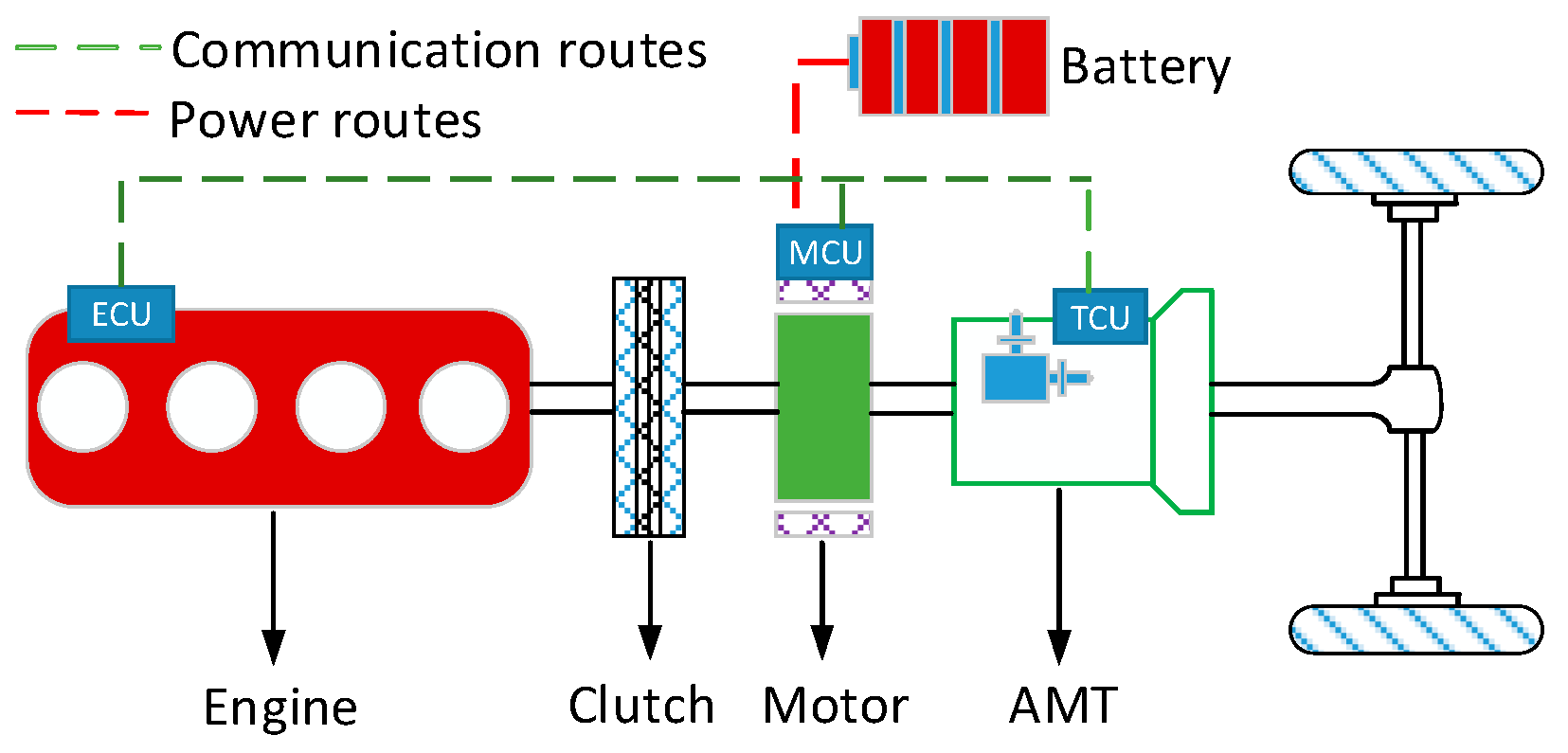
PMP aims to obtain the optimal solution by optimizing the instantaneous Hamilton function. The traditional PMP for HEV is usually implemented using the interpolation method, leading the distortion to engine map and higher computation burden. Moreover, the drivability (e.g., frequent gearshift) and battery aging degradation are not well considered in the optimization formulation. With the proposed approximation method utilized in PMP solution, we obtain a continuous Hamilton function for PMP with the extracted gearshift map by incorporating the battery aging. This is called approximate PMP (A-PMP) in this paper. Thus, the EMS of HEVs yields a potential in real-time control while improving the computation efficiency. In this paper, the engine fuel rate and SOC derivative are approximated by a linear function of its associated torque (given below) for parallel HEVs.
(1) First, the optimal results are obtained by PMP to optimize the gearshift command and torque distribution by considering drivability and fuel economy simultaneously. This is realized under China Typical City Cycle (CTCC), which offers an extracted gearshift map for approximate PMP.
(2) Second, the engine and motor piecewise linear models are introduced into the optimization of torque distribution, aiming to enhance the fuel and computation efficiencies. Based on the piecewise linear models, a computationally efficient energy management approach is then formulated with the extracted gearshift map.
(3) Lastly, the approximate Hamilton function is derived by piecewise linear models, and a control-oriented battery aging model is then incorporated by explicitly including the battery aging degradation into the design. The proposed strategy results in a better control performance for fuel economy and battery lifetime. This is indeed essential to ensure the potential in real-time control.
3.1. The Principle of PMP
As a global optimization method, PMP can be implemented by transforming the global optimization problem into instantaneous optimization. In this section, PMP is formulated for a parallel HEV to jointly optimize gearshift command and torque distribution. The optimization objective (Hamilton function) is formulated as follows (Equation (11)).
where
consists of the optimal gearshift command and torque split, respectively;
λ(
t) is the co-state, and
is the battery dynamic.
The dynamic of co-state is presented in Equation (12).
The state dynamic is shown in Equation (13).
For optimality, to determine the optimal control, Equation (14) should be considered.
The constraints should be satisfied in Equation (15) as follows.
where
Te(
t) and
Tm(
t) are the engine torque and motor torque, respectively;
Te_
max(
ne(
t)) is the engine maximum torque at the current speed,
Tm_
max(
nm(
t)) is the motor maximum torque at the current speed,
Tm_
min(
nm(
t)) is the motor minimum torque at the current speed,
nm_
max is the motor maximum speed,
ne_max and
ne_min are the engine maximum and minimum speed, respectively, and
SOCmin,
SOCmax are the minimum and maximum SOC, respectively.
3.2. Optimization of Gearshift Command and Torque Distribution
To optimize the torque distribution, the torque demand at the input shaft of the transmission is adopted as shown in Equations (16) and (17).
As previously mentioned, the optimal control input includes gearshift command and torque split. Thus, the optimal gearshift number
g(
t) can be obtained by Equation (18), which is constrained as seen in Equation (19). The value {−1,0,1} denotes downshift, maintaining, and upshift, respectively.
Correspondingly, motor torque and gearshift command are selected as an optimal control input shown in Equation (20), which can be obtained by Equation (21) by satisfying the constraints in Equation (15).
The engine torque is obtained as follows:
Based on the instantaneous optimization of PMP, the optimal gearshift command can be determined at each time instant with the driving cycle. An optimal torque distribution is then calculated accordingly. Furthermore, a gearshift map is extracted from the optimal results under a specific driving cycle, and employed in approximate PMP to obtain the optimal torque split.
3.3. Approximate PMP
A. Models Approximation
To derive the optimal control of PMP, the piecewise linear approximation is introduced to the engine fuel rate and the SOC derivative, which can be approximated as a function of the corresponding torque. As a result, the Hamiltonian function equals to a piecewise linear function as a summation of the two terms. The engine fuel rate can be approximated by engine torque, as shown in Equation (23). The fitting coefficients that depend on the engine speed are shown in
Table 1.
where
a(
ne) and
b(
ne) are fitting coefficients related to the engine speed.
To further show the fitting results, the engine fuel rate fitting curve is created by the piecewise linear approximation, as shown in
Figure 5.
Similarly, the approximation of SOC derivative (
) is simplified by piecewise linear approximation, which can be presented as Equation (24).
where
c(
nm),
d(
nm),
g(
nm),
f(
nm) are fitting coefficients associated with the motor speed.
It is observed that the SOC derivative curve (deltSOC) is divided into two regions by the zero motor torque due to the opposite directions of power flow on both sides. The released battery power is equal to the output motor mechanical power, which is divided by the motor efficiency if the motor torque is positive. For the opposite direction, the absorbed battery power is equal to the motor power multiplied by the motor efficiency. To clearly present the results, the fitting curve is obtained by the piecewise linear approximation shown in
Figure 6. It can be observed from
Table 1;
Table 2 that the
R-square for engine fuel rate and SOC derivative is around 0.99, achieving a good fitting. Thus, piecewise linear fitting is considered to be an appropriate approximation approach.
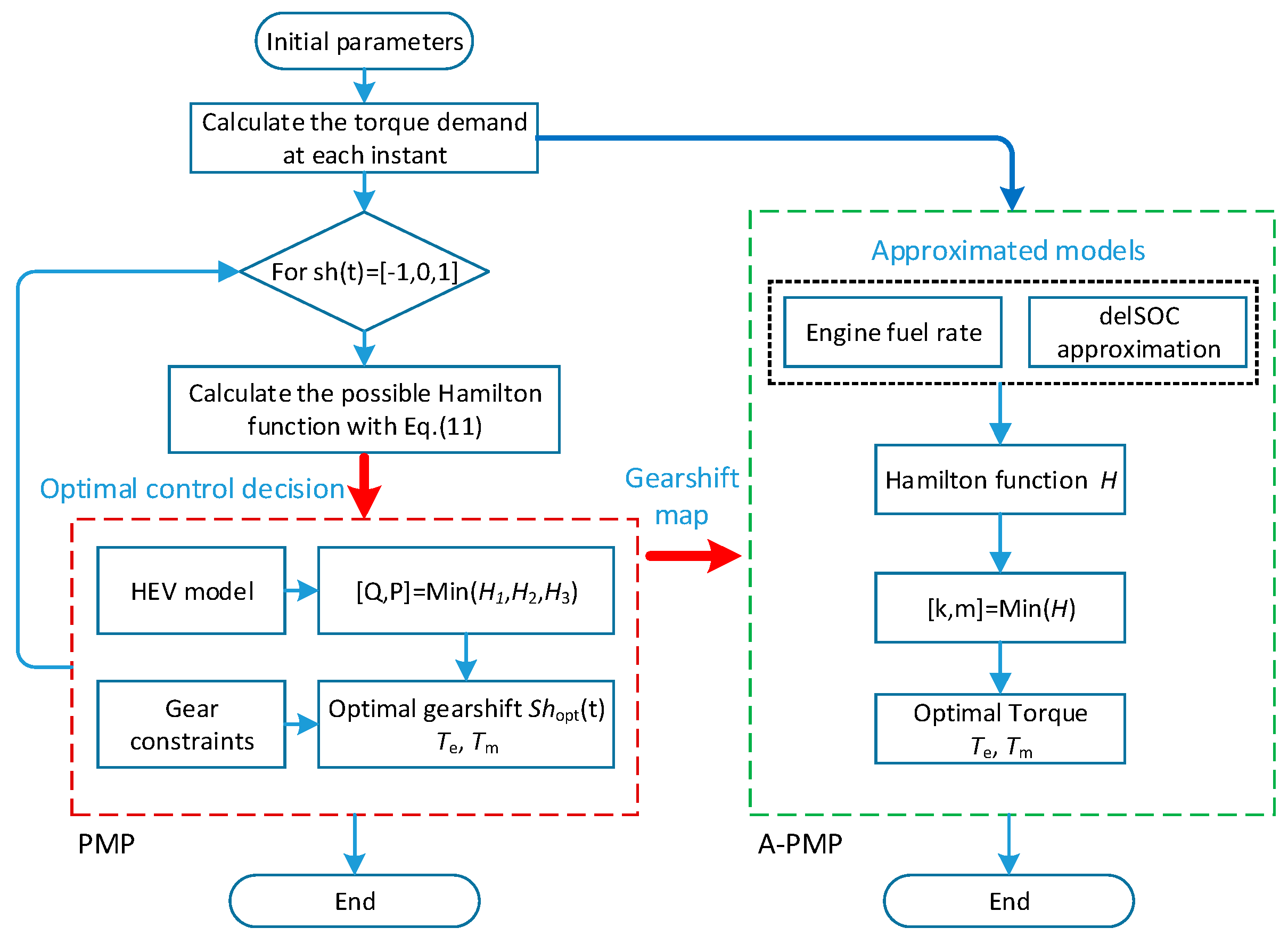
Based on the approximated engine and motor models, the detailed procedure of A-PMP is summarized in
Figure 7.
B. A-PMP Formulation
Basically, the A-PMP has the same optimization structure as the standard PMP except for the instantaneous Hamiltonian optimization. By introducing linear approximation models to the local optimization problem and calculating the Hamiltonian; thus, the computational load is reduced. In the optimization scheme, the extracted gearshift map is employed in the A-PMP, and only the torque split is enforced by minimizing the Hamilton function. According to the principle of PMP, the Hamilton function is formulated as Equation (25).
where
u(
t) includes the engine torque and motor torque (
Nm).
Correspondingly, with the approximated models of Equations (23) and (24), the Hamilton function can be reformulated as a piecewise linear function shown in Equation (26).
The co-state dynamic is presented in Equation (27).
The optimal engine and motor torque can be determined as follows.
where
Rratio represents the motor torque divided by the total torque demand.
In this method, the torque distribution can be optimized by minimizing the instantaneous Hamilton function Equation (26) to guarantee the drivability.
In addition, the optimal engine torque and motor torque should satisfy the following constraint.
C. The Battery Aging Model
In this part, a multi-objective optimization problem by including the battery aging is constructed. To this aim, a battery aging model is required to blend the battery life into energy management. Generally, the battery is a complex electrochemical system. Two types of battery model are usually used to predict battery degradation: cycle life aging and calendar aging model. In this paper, a control-oriented battery cycle life aging is considered in optimizing the power split. For these models, electrochemical aging models and semi-empirical aging models are proposed in the literature [
33,
34]. The latter one is more suitable for HEV control design. Thus, we adopted the cycle semi-empirical battery aging model, presented in [
35]. The battery pack adopts the LiFePO4 cells in this study. To measure the battery degradation, the battery capacity loss
Qloss is presented in Equation (32).
where
is the battery capacity loss (%),
α,
β and
η are the fitting coefficients related to SOC, and
Ea is the activation energy (J/mol),
Rg is the gas constant,
T is the battery temperature in Kelvin [K],
Ah is the accumulated charge throughput, i.e., the total amount of charge that can flow in and out of the battery during its operation,
is the current rate,
z is the power law factor.
The accumulated charge throughput is calculated in Equation (33) and
is defined as the ratio of the current (A) to the nominal charge capacity (
Ah) in Equation (34).
where
is the current during the trip.
For an HEV application, it is generally realized that the battery should be replaced with a new one when the battery capacity reaching 80% of the original value [
36]. Therefore, the end of life is defined as 20% loss of capacity. The nominal conditions defined in this study are
Irate,norm = 2.5[1/h],
SOCnorm = 0.35, and
Tnorm = (273.15 + 25) K [
37], and the nominal battery life is then calculated in Equation (35). In this paper, the battery temperature is assumed to be constant (25 °C).
The battery life is defined in Equation (36) in terms of Ah-throughput related to specific operating conditions.
Thus, the severity factor is obtained using Equation (37) for a given cycle, which indicates the battery relative aging effect.
To consider the battery aging, the effective Ah-throughput can be expressed by Equation (38). Generally, minimizing the battery aging degradation is to minimize the effective Ah-throughput.
Therefore, the approximated Hamilton function is reformulated in Equation (39) by considering fuel economy and battery aging simultaneously. The optimal control of A-PMP is then solved by minimizing Equation (39).
where
K is the weight factor for battery aging cost,
Ca is the ratio of battery replacement cost of 1 kg of gasoline.