A Health Indicator for the Online Lifetime Estimation of an Electric Vehicle Power Li-Ion Battery
Abstract
1. Introduction
2. ERL-Based Lifetime Estimator
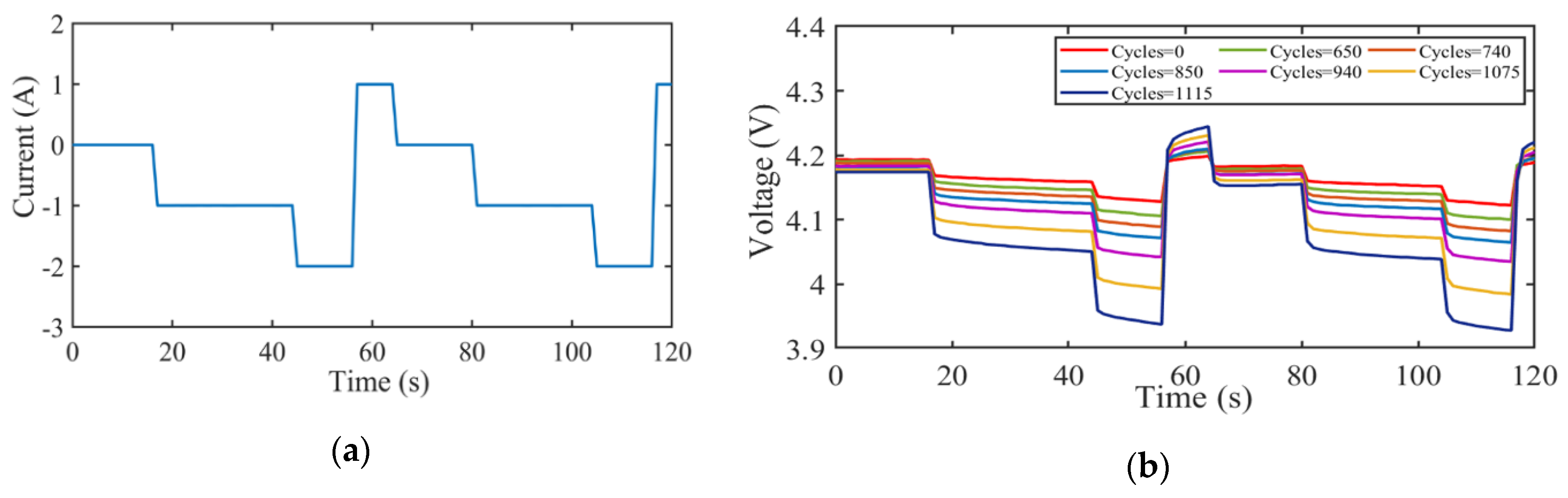
2.1. ERL Extraction
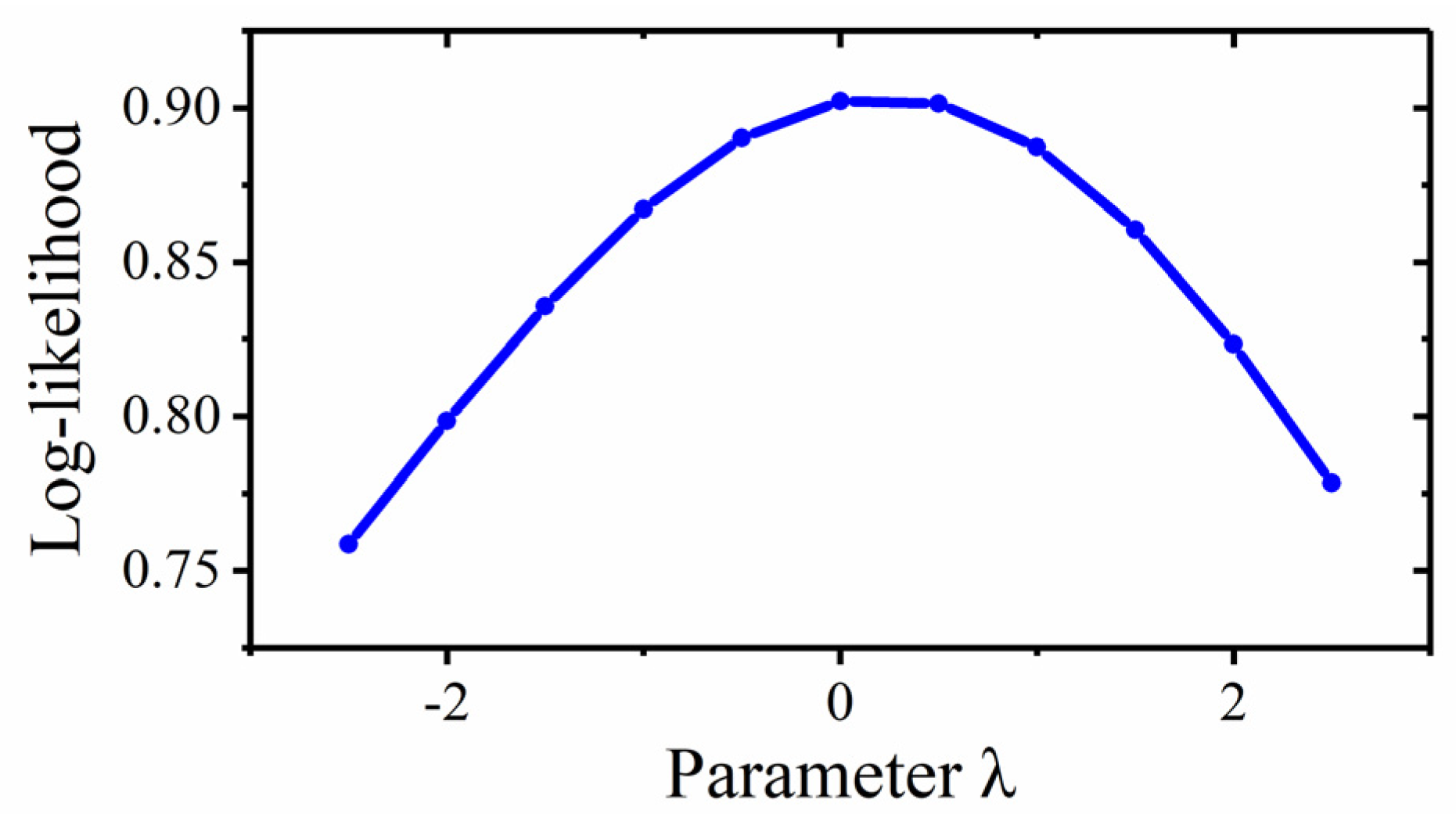
2.2. Box–Cox Transformation
- (a)
- Choose an initial value of λ within a suitable range (such as [–5,5]).
- (b)
- Substitute the initial λ to calculate the corresponding g(λ).
- (c)
- Calculate all g(λ) corresponding to the remaining λ in turn.
- (d)
- Plot the correlation curve of g(λ) and λ.
- (e)
- Select the λ that maximizes g(λ).
3. Experimental Section
4. Results and Discussion
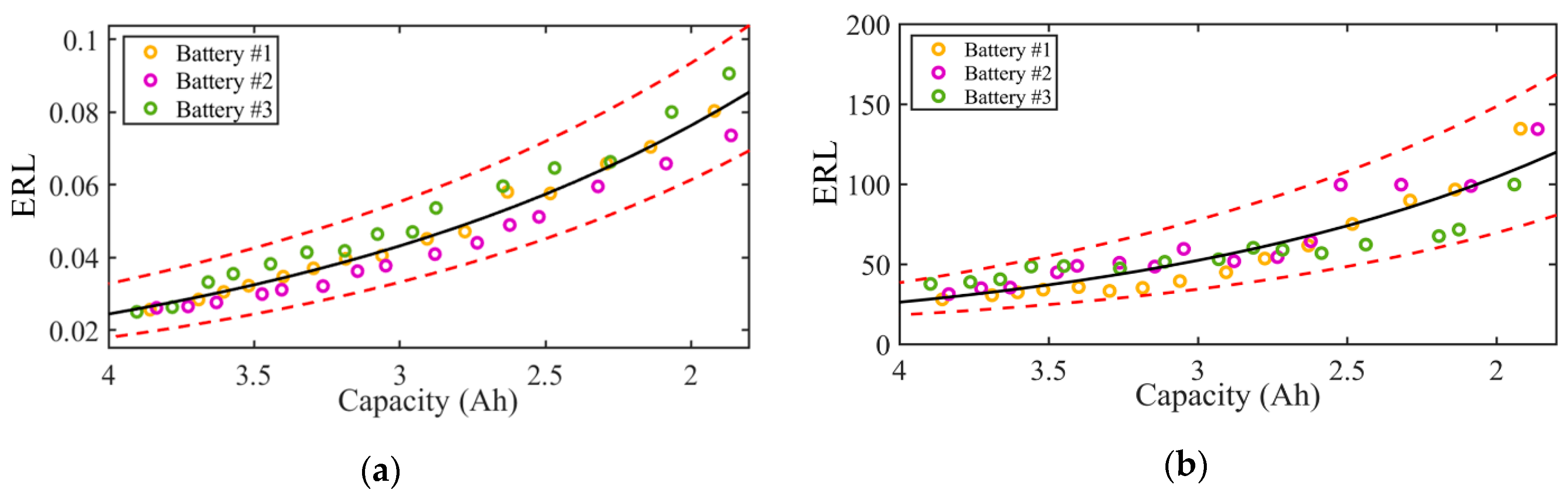
4.1. Estimation Dispersion of ERL
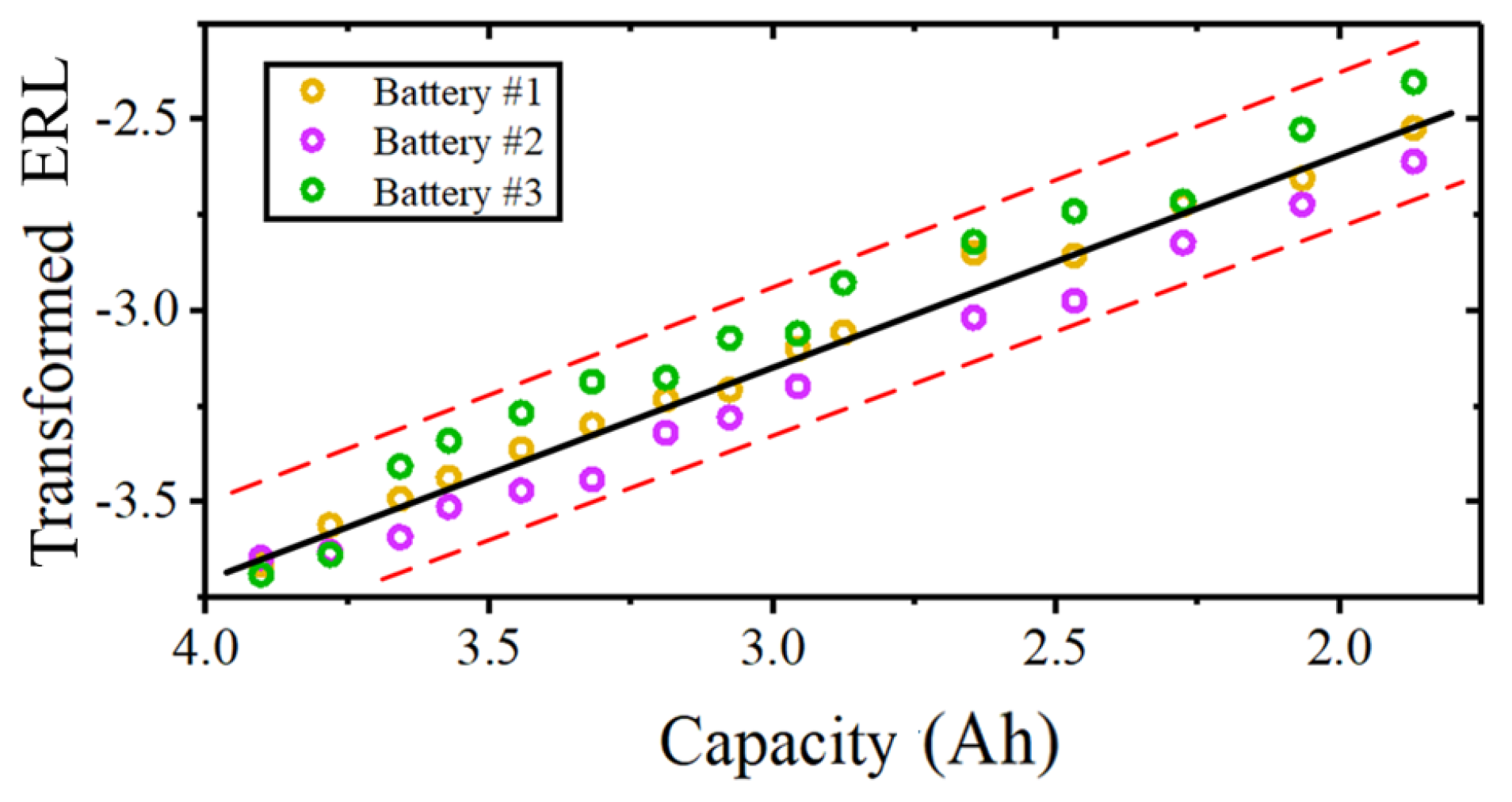
4.2. Optimization of ERL
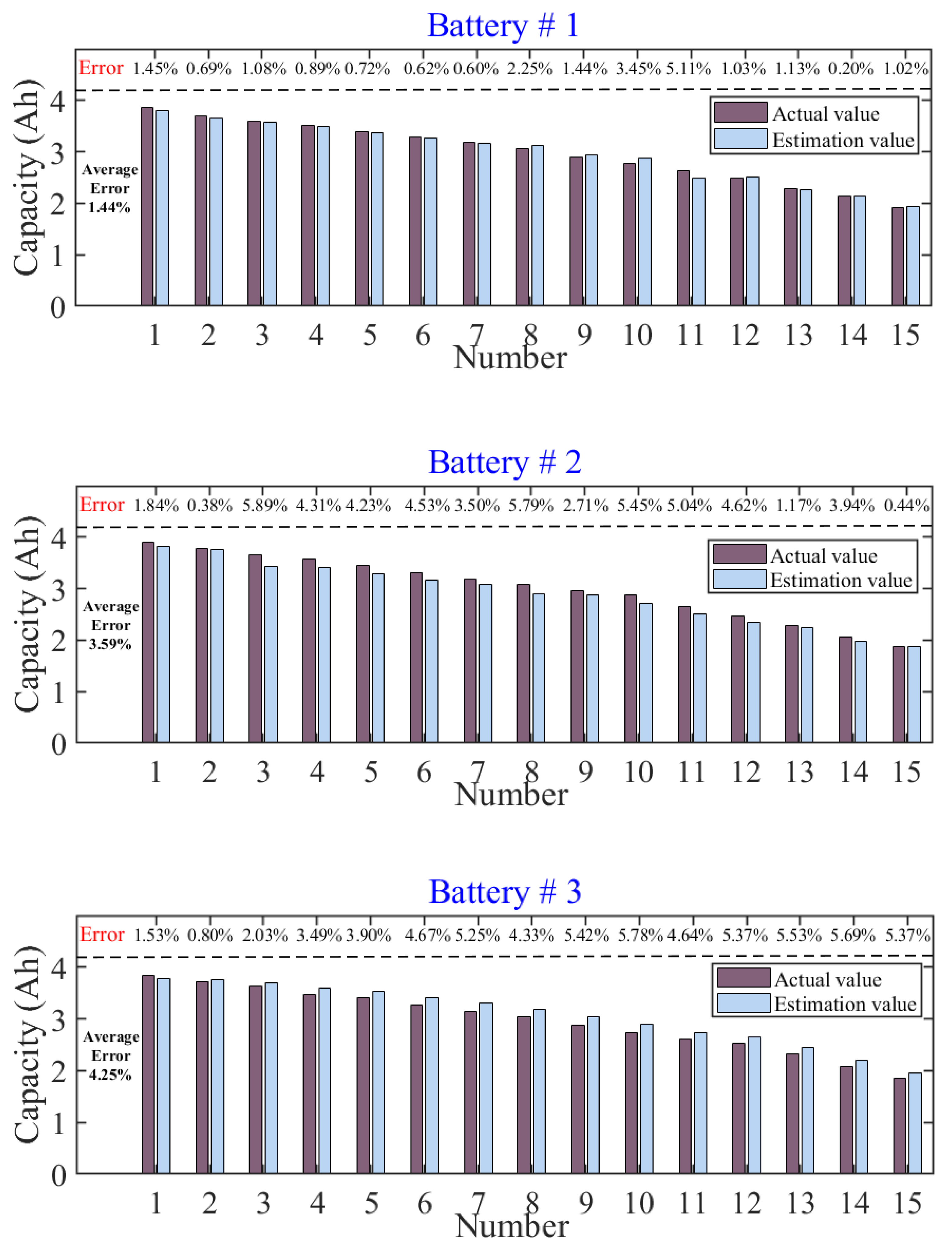
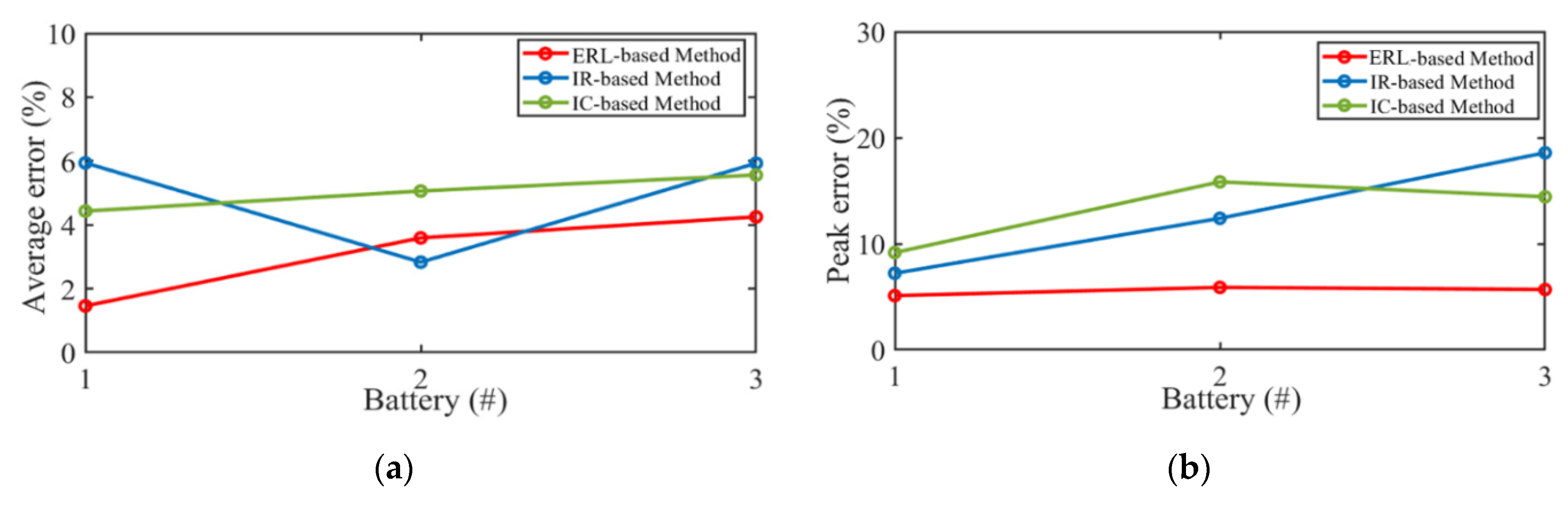
4.3. Estimation Result
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kim, Y.; Raghunathan, V.; Raghunathan, A. Design and Management of Battery-Supercapacitor Hybrid Electrical Energy Storage Systems for Regulation Services. IEEE Trans. Multi Scale Comput. Syst. 2016, 3, 12–24. [Google Scholar] [CrossRef]
- Meng, H.; Li, Y.F. A review on prognostics and health management (PHM) methods of lithium-ion batteries. Renew. Sustain. Energy Rev. 2019, 116, 109405. [Google Scholar] [CrossRef]
- Wang, D.; Miao, Q.; Pecht, M. Prognostics of lithium-ion batteries based on relevance vectors and a conditional three-parameter capacity degradation model. J. Power Sources 2013, 239, 253–264. [Google Scholar] [CrossRef]
- Zhang, J.; Lee, J. A review on prognostics and health monitoring of Li-ion battery. J. Power Sources 2011, 196, 6007–6014. [Google Scholar] [CrossRef]
- Ma, J.; Xu, S.; Shang, P.; Ding, Y.; Qin, W.; Cheng, Y.; Lu, C.; Su, Y.; Chong, J.; Jin, H.; et al. Cycle life test optimization for different Li-ion power battery formulations using a hybrid remaining-useful-life prediction method. Appl. Energy 2020, 262, 114490. [Google Scholar] [CrossRef]
- Lucu, M.; Martinez-Laserna, E.; Gandiaga, I.; Liu, K.; Marco, J. Data-driven nonparametric Li-ion battery ageing model aiming at learning from real operation data—Part B: Cycling operation. J. Energy Storage 2020, 30, 101410. [Google Scholar] [CrossRef]
- Yuan, H.F.; Dung, L.R. Off-Line State-of-Health Estimation for High Power Lithium-Ion Batteries Using Three-Point Impedance Extraction Method. IEEE Trans. Veh. Technol. 2017, 66, 2019–2032. [Google Scholar] [CrossRef]
- Sun, L.; Li, G.; You, F. Combined internal resistance and state-of-charge estimation of lithium-ion battery based on extended state observer. Renew. Sustain. Energy Rev. 2020, 131, 109994. [Google Scholar] [CrossRef]
- Qian, K.; Huang, B.; Ran, A.; He, Y.; Li, B.; Kang, F. State-of-health (SOH) evaluation on lithium-ion battery by simulating the voltage relaxation curves. Electrochim. Acta 2019, 303, 183–191. [Google Scholar] [CrossRef]
- Zhou, Y.; Huang, M.; Chen, Y.; Tao, Y. A novel health indicator for on-line lithium-ion batteries remaining useful life prediction. J. Power Sources 2016, 321, 1–10. [Google Scholar] [CrossRef]
- Tian, J.; Xiong, R.; Yu, Q. Fractional-Order Model-Based Incremental Capacity Analysis for Degradation State Recognition of Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 2018, 66, 1576–1584. [Google Scholar] [CrossRef]
- Li, Y.; Abdel-Monem, M.; Gopalakrishnan, R.; Berecibar, M.; Nanini-Maury, E.; Omar, N.; van den Bossche, P.; van Mierlo, J. A quick on-line state of health estimation method for Li-ion battery with incremental capacity curves processed by Gaussian filter. J. Power Sources 2018, 373, 40–53. [Google Scholar] [CrossRef]
- Bloom, I.; Jansen, A.N.; Abraham, D.P. Differential voltage analyses of high-power, lithium-ion cells. 1. Technique and application. J. Power Sources 2005, 139, 295–303. [Google Scholar] [CrossRef]
- Han, X.; Ouyang, M.; Lu, L.; Li, J.; Zheng, Y.; Li, Z. A comparative study of commercial lithium ion battery cycle life in electrical vehicle: Aging mechanism identification. J. Power Sources 2014, 251, 38–54. [Google Scholar] [CrossRef]
- Tong, S.; Klein, M.P.; Park, J.W. On-line optimization of battery open circuit voltage for improved state-of-charge and state-of-health estimation. J. Power Sources 2015, 293, 416–428. [Google Scholar] [CrossRef]
- Lee, S.; Kim, J.; Lee, J.; Cho, B.H. State-of-charge and capacity estimation of lithium-ion battery using a new open-circuit voltage versus state-of-charge. J. Power Sources 2008, 185, 1367–1373. [Google Scholar] [CrossRef]
- Yunlong, S.; Gaopeng, L.; Yongzhe, K.; Zhongkai, Z.; Bin, D.; Chenghui, Z. A multi-fault diagnosis method based on modified Sample Entropy for lithium-ion battery strings. J. Power Sources 2020, 446, 227275. [Google Scholar]
- Widodo, A.; Shim, M.C.; Caesarendra, W.; Yang, B.S. Intelligent prognostics for battery health monitoring based on sample entropy. Expert Syst. Appl. Int. J. 2011, 38, 11763–11769. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, R.; He, H.; Pecht, M.G. Lithium-Ion Battery Remaining Useful Life Prediction with Box–Cox Transformation and Monte Carlo Simulation. IEEE Trans. Ind. Electron. 2018, 66, 1585–1597. [Google Scholar] [CrossRef]
- Banaei, A.; Fahimi, B. Real time condition monitoring in Li-Ion batteries via battery impulse response. In Proceedings of the 2010 IEEE Vehicle Power and Propulsion Conference, Lille, France, 1–3 September 2010. [Google Scholar]
- Lavigne, L.; Sabatier, J.; Francisco, J.M.; Guillemard, F.; Noury, A. Lithium-ion Open Circuit Voltage (OCV) curve modelling and its ageing adjustment. J. Power Sources 2016, 324, 694–703. [Google Scholar] [CrossRef]
- Coleman, M.; Hurley, W.G.; Lee, C.K. An Improved Battery Characterization Method Using a Two-Pulse Load Test. IEEE Trans. Energy Convers. 2008, 23, 708–713. [Google Scholar] [CrossRef]
- Liu, D.; Zhou, J.; Liao, H.; Peng, Y.; Peng, X. A Health Indicator Extraction and Optimization Framework for Lithium-Ion Battery Degradation Modeling and Prognostics. IEEE Trans. Syst. Man Cybern. Syst. 2015, 45, 915–928. [Google Scholar]
- Morozova, M.; Koschutnig, K.; Klein, E.; Wood, G. Monotonic non-linear transformations as a tool to investigate age-related effects on brain white matter integrity: A Box–Cox investigation. NeuroImage 2016, 125, 1119–1130. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Wang, J.; Liu, Q.; Tang, J.; Liu, H.; Fang, Z. Deep-Discharging Li-Ion Battery State of Charge Estimation Using a Partial Adaptive Forgetting Factors Least Square Method. IEEE Access 2019, 7, 47339–47352. [Google Scholar] [CrossRef]
- Liu, S.; Wang, J.; Liu, Q.; Tang, J.; Liu, H.; Zhou, Y.; Pan, X. A Novel Discharge Mode Identification Method for Series-connected Battery Pack Online State of Charge Estimation over A Wide Life Scale. IEEE Trans. Power Electron. 2020. [Google Scholar] [CrossRef]
- Jiang, Y.; Jiang, J.; Zhang, C.; Zhang, W.; Gao, Y.; Li, N. State of health estimation of second-life LiFePO4 batteries for energy storage applications. J. Clean. Prod. 2018, 205, 754–762. [Google Scholar] [CrossRef]


| Type | Size | Terminal Voltage (V) | Operating Voltage (V) | Capacity (Ah) | Maximum Discharge Rate (C) |
|---|---|---|---|---|---|
| Li(NiCoMn)O2 (NCM) | 21,700 | 3.7 | 2.7–4.2 | 4 | 4 |
| Battery | Depth of Discharge (DOD) | State of Charge (SOC) Ranges |
|---|---|---|
| # 1 | 50% | 25–75% |
| # 2 | 50% | 35–85% |
| # 3 | 40% | 30–70% |
| Error | IR-Based Method | IC-Based Method | ERL-Based Method |
|---|---|---|---|
| Peak error | 18.58% | 15.84% | 5.89% |
| Average error | 4.90% | 5.02% | 2.95% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, B.; Qiu, H.; Weng, L.; Huo, K.; Liu, S.; Liu, H. A Health Indicator for the Online Lifetime Estimation of an Electric Vehicle Power Li-Ion Battery. World Electr. Veh. J. 2020, 11, 59. https://doi.org/10.3390/wevj11030059
Yu B, Qiu H, Weng L, Huo K, Liu S, Liu H. A Health Indicator for the Online Lifetime Estimation of an Electric Vehicle Power Li-Ion Battery. World Electric Vehicle Journal. 2020; 11(3):59. https://doi.org/10.3390/wevj11030059
Chicago/Turabian StyleYu, Bin, Haifeng Qiu, Liguo Weng, Kailong Huo, Shiqi Liu, and Haolu Liu. 2020. "A Health Indicator for the Online Lifetime Estimation of an Electric Vehicle Power Li-Ion Battery" World Electric Vehicle Journal 11, no. 3: 59. https://doi.org/10.3390/wevj11030059
APA StyleYu, B., Qiu, H., Weng, L., Huo, K., Liu, S., & Liu, H. (2020). A Health Indicator for the Online Lifetime Estimation of an Electric Vehicle Power Li-Ion Battery. World Electric Vehicle Journal, 11(3), 59. https://doi.org/10.3390/wevj11030059




