Sideslip Angle Fusion Estimation Method of an Autonomous Electric Vehicle Based on Robust Cubature Kalman Filter with Redundant Measurement Information
Abstract
1. Introduction
2. Vehicle Model
2.1. Three-Degree-of-Freedom Vehicle Dynamics Model
2.2. Tire Model
3. Vehicle Sideslip Angle Fusion Estimation Method
3.1. Robust Cubature Kalman Filter for Vehicle Running State Estimation
3.2. Adaptive Measurement-Update Solution to Improve the Robustness of Estimation
3.3. Sideslip Angle Fusion Estimation Method Using Redundant Measurement Information
4. Simulation Results
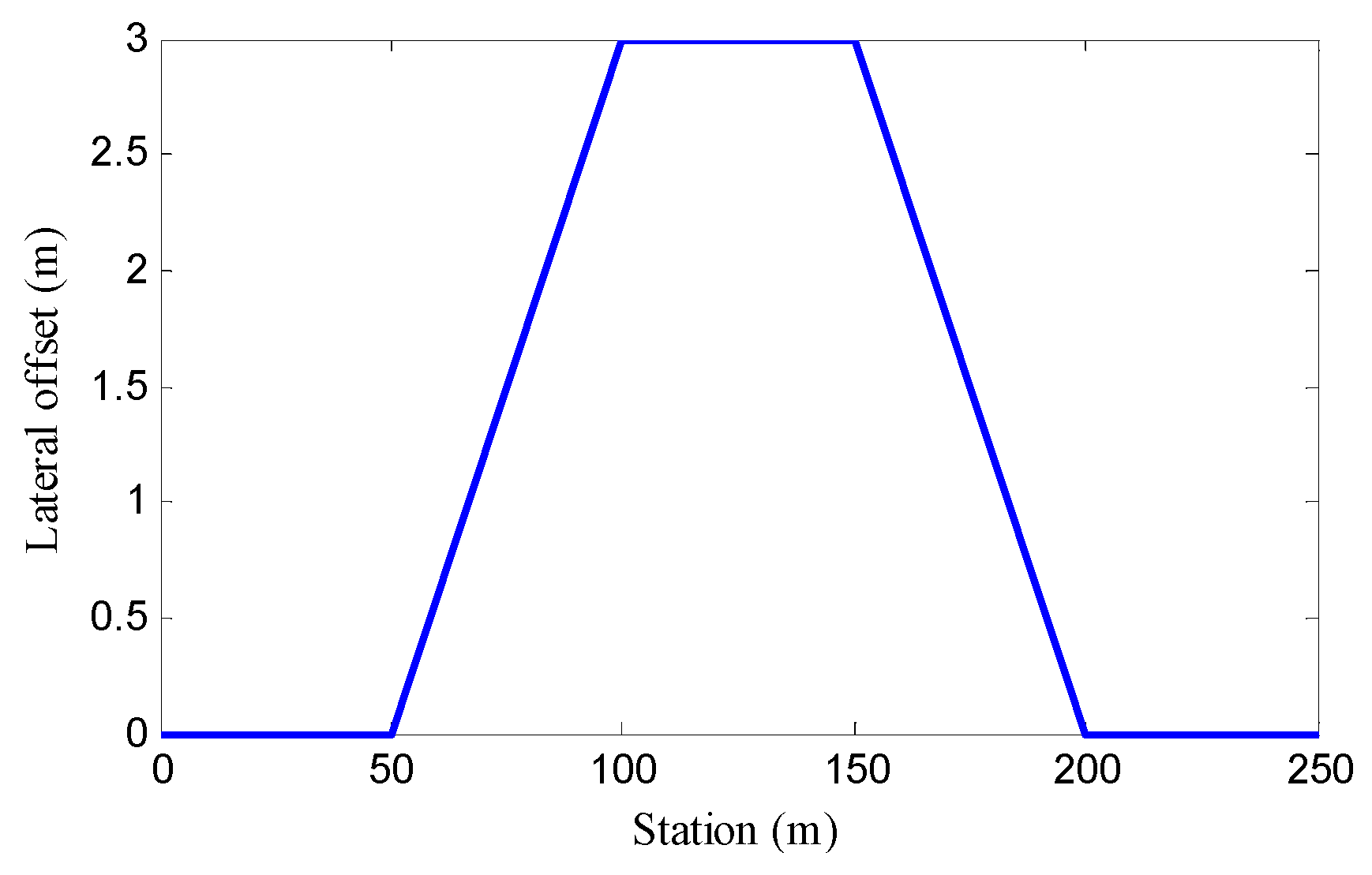
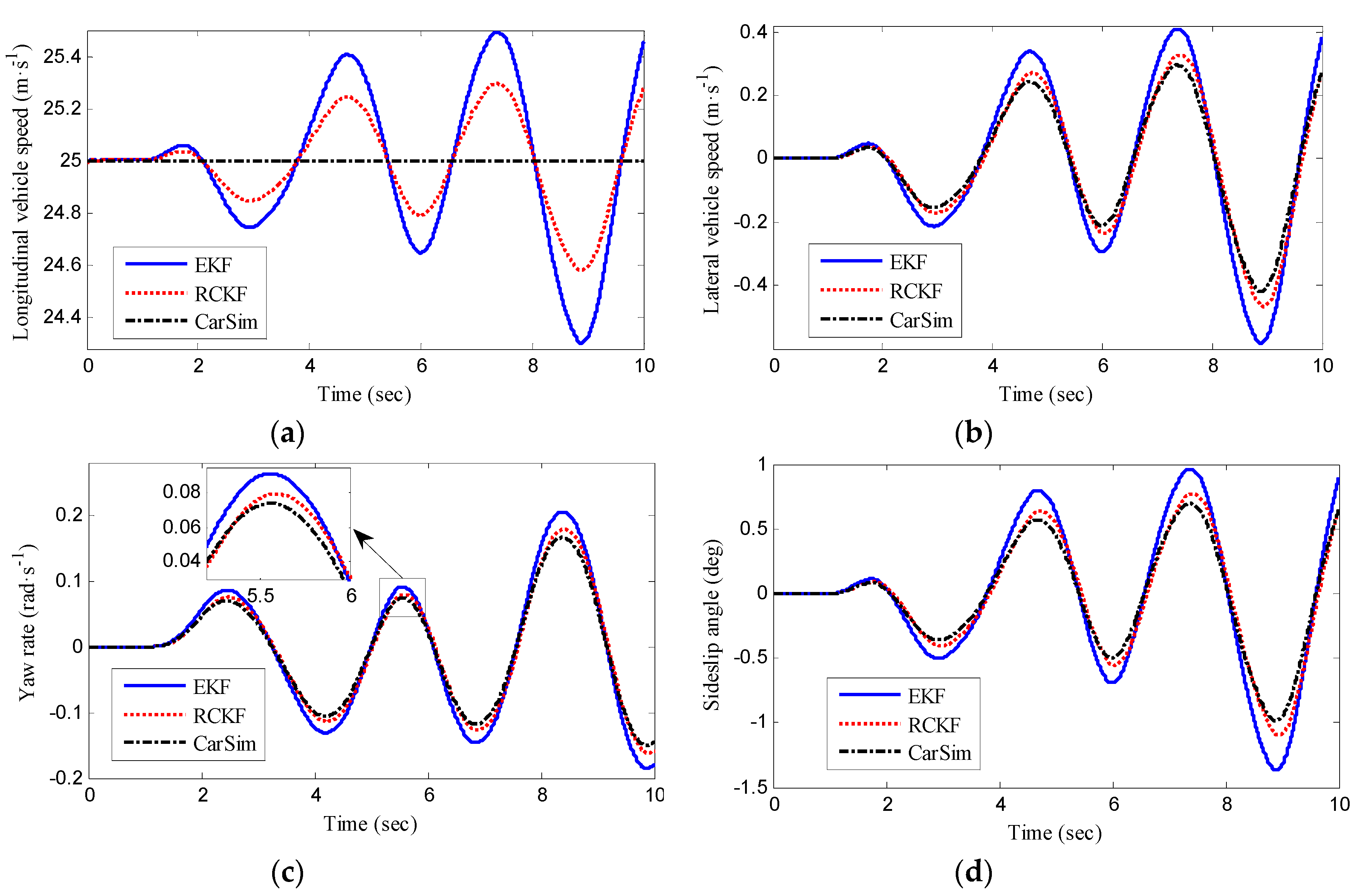
4.1. Case Study 1: Double Lane Changes Maneuver
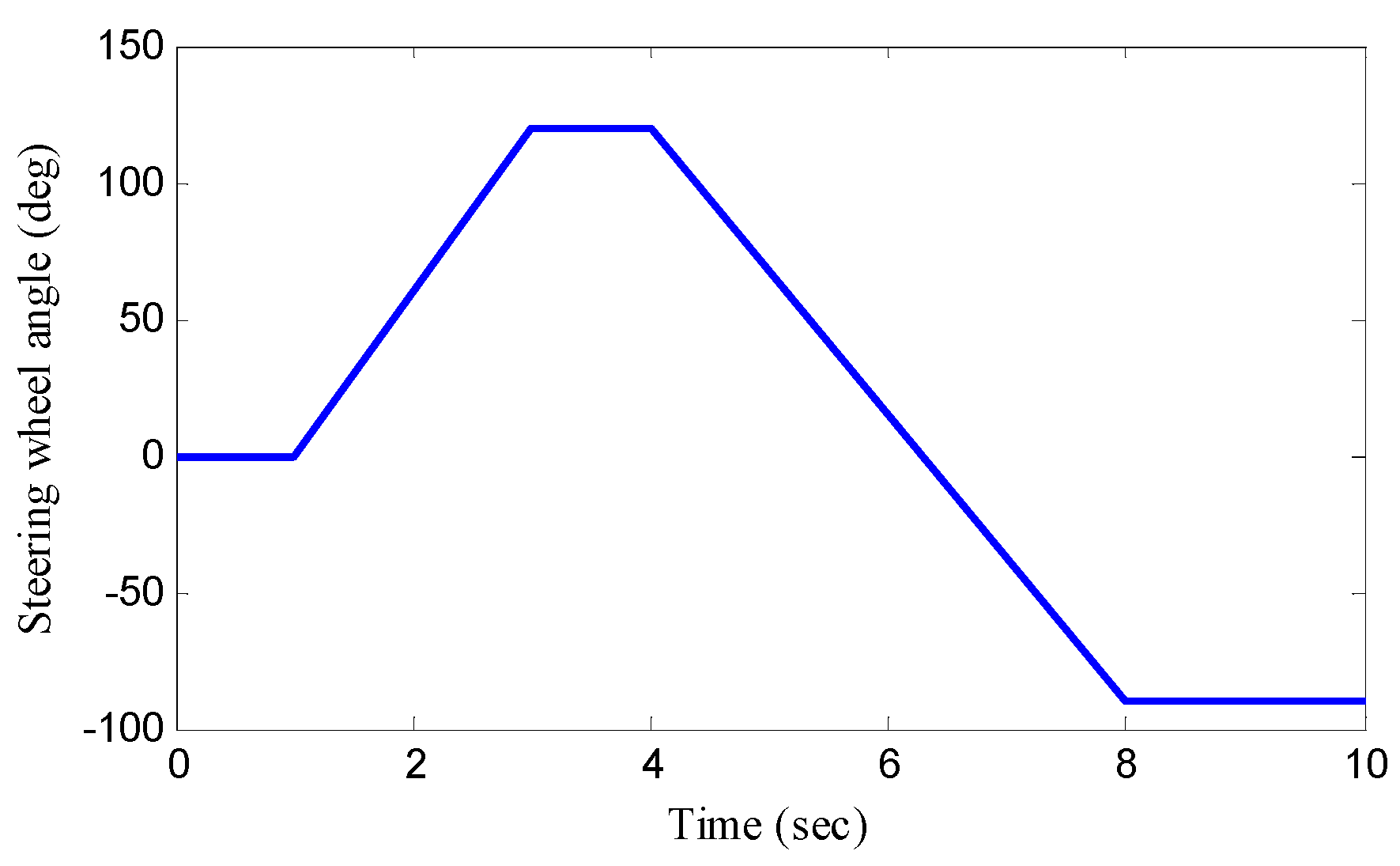
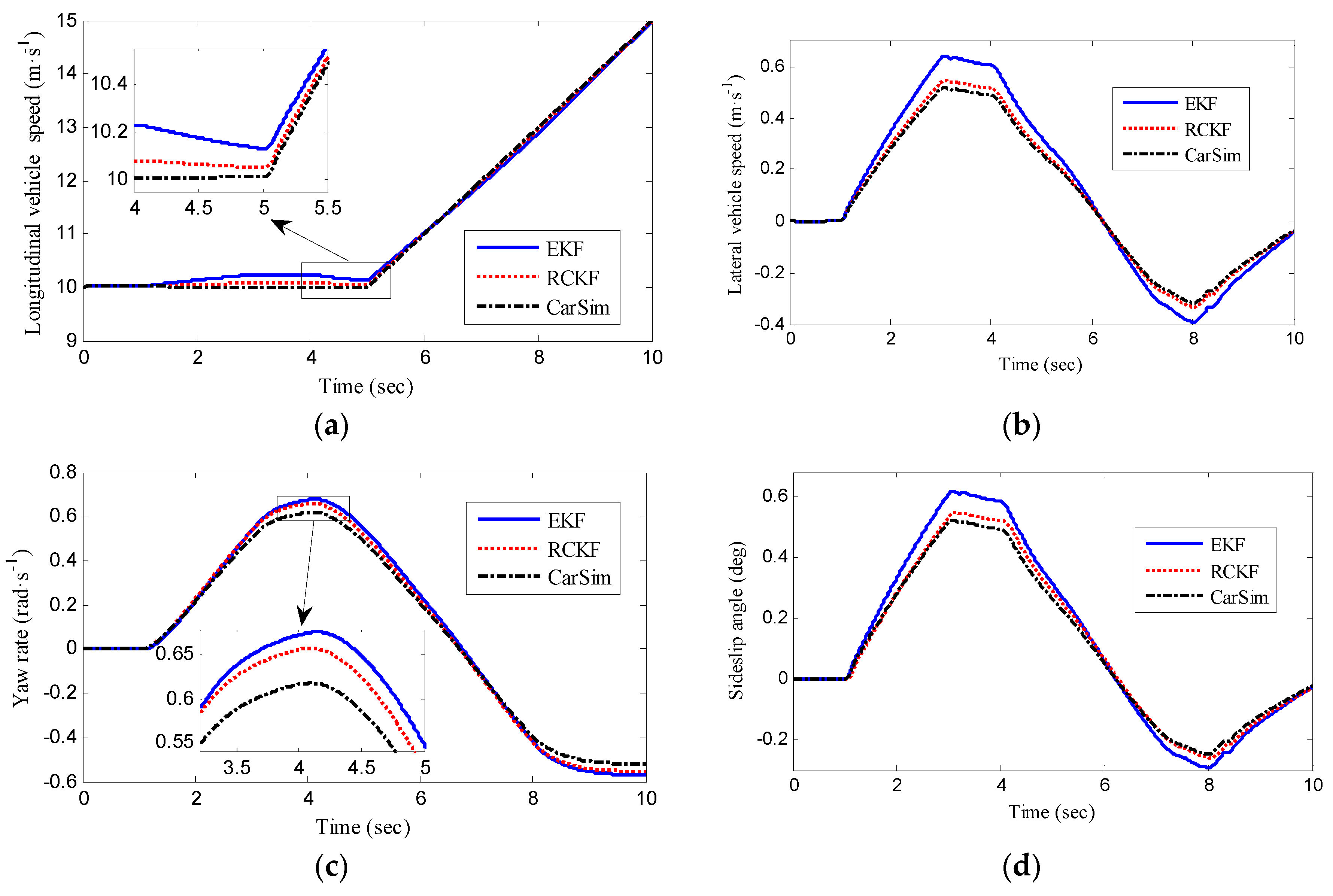
4.2. Case Study 2: Fishhook Maneuver
5. Experimental Verifications
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, T.; Chen, L.; Cai, Y.; Xu, X. Estimation of vehicle sideslip angle via pseudo-multisensor information fusion method. Metrol. Meas. Syst. 2018, 25, 499–516. [Google Scholar]
- Zhang, H.; Wang, J. Vehicle lateral dynamics control through AFS/DYC and robust gain-scheduling approach. IEEE Trans. Veh. Technol. 2016, 65, 489–494. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, Z.; Chai, J.; Kan, Z. Risk Identification and Analysis for PPP Projects of Electric Vehicle Charging Infrastructure Based on 2-Tuple and the DEMATEL Model. World Electr. Veh. J. 2019, 10, 4. [Google Scholar] [CrossRef]
- Qiu, H.; Dong, Z.; Lei, Z. Simulation and experiment of integration control of ARS and DYC for electrical vehicle with four wheel independent drive. J. Jiangsu Univ. Nat. Sci. Ed. 2016, 37, 268–276. [Google Scholar]
- Xu, X.; Chen, T.; Chen, L.; Wang, W. Longitudinal force estimation for motorized wheels driving electric vehicle based on improved closed-loop subspace identification. J. Jiangsu Univ. Nat. Sci Ed. 2016, 37, 650–656. [Google Scholar]
- Chen, Y.; Wang, J. Adaptive vehicle speed control with input injections for longitudinal motion independent road frictional condition estimation. IEEE Trans. Veh. Technol. 2011, 60, 839–848. [Google Scholar] [CrossRef]
- Shen, K.; Selezneva, M.; Neusypin, K.; Proletarsky, A. Novel variable structure measurement with intelligent components flight vehicles. Metrol. Meas. Syst. 2017, 24, 347–356. [Google Scholar] [CrossRef]
- Chen, T.; Xu, X.; Li, Y.; Wang, W.; Chen, L. Speed-dependent coordinated control of differential and assisted steering for in-wheel motor driven electric vehicles. Proc. Inst. Mech. E Part D J. Automob. Eng. 2018, 232, 1206–1220. [Google Scholar] [CrossRef]
- Yang, L.; Tang, Y.; Tang, L.; Wu, C. Brushless DC motor drive characteristics and system for reel-type irrigator. J. Drain. Irrig. Mach. Eng. 2018, 36, 690–695. [Google Scholar]
- Gu, Z.; Yuan, S.; Tang, L.; Tang, Y. Intelligent solar drive control system of hose reel irrigator. J. Drain. Irrig. Mach. Eng. 2018, 36, 969–974. [Google Scholar]
- Iora, P.; Tribioli, L. Effect of ambient temperature on electric vehicles’ energy consumption and range: Model definition and sensitivity analysis based on nissan leaf data. World Electr. Veh. J. 2019, 10, 2. [Google Scholar] [CrossRef]
- Jiang, H.; Li, A.; Ma, S.; Chen, L. Design and performance analysis of airflow energy recovery device of electric vehicle. J. Jiangsu Univ. Nat. Sci. Ed. 2017, 38, 125–132. [Google Scholar]
- Chen, T.; Chen, L.; Xu, X.; Cai, Y.; Sun, X. Simultaneous path following and lateral stability control of 4WD-4WS autonomous electric vehicles with actuator saturation. Adv. Eng. Softw. 2019, 128, 46–54. [Google Scholar] [CrossRef]
- Anil, K.; Matteo, C.; Edward, H. Vehicle sideslip estimator using load sensing bearings. Control Eng. Pract. 2016, 54, 46–57. [Google Scholar]
- Wang, J.; Li, J. Hierarchical coordinated control method of in-wheel motor drive electric vehicle based on energy optimization. World Electr. Veh. J. 2019, 10, 15. [Google Scholar] [CrossRef]
- Chen, T.; Xu, X.; Chen, L.; Jiang, H.; Cai, Y. Estimation of longitudinal force, lateral vehicle speed and yaw rate for four-wheel independent driven electric vehicles. Mech. Syst. Signal Process. 2018, 101, 377–388. [Google Scholar] [CrossRef]
- Chen, T.; Chen, L.; Cai, Y.; Xu, X. Robust sideslip angle observer with regional stability constraint for an uncertain singular intelligent vehicle system. IET Control Theory Appl. 2018, 12, 1802–1811. [Google Scholar] [CrossRef]
- Fan, Y.; Huang, X.; Li, J.; Wang, T.; Du, F. Stability analysis on light weight and small size watering cart for dual purpose of both sprinkling irrigation and hose irrigation. J. Drain. Irrig. Mach. Eng. 2010, 28, 256–259. [Google Scholar]
- Li, L.; Jia, G.; Ran, X.; Song, J.; Wu, K. Avariable structure extended Kalman filter for vehicle side slip angle estimation on a low friction road. Veh. Syst. Dyn. 2014, 52, 280–308. [Google Scholar] [CrossRef]
- Martin, H.; Johannes, E.; Manfred, P.; Manuel, H. Vehicle side-slip angle estimation on a banked and low-friction road. Proc. Inst. Mech. E Part D J. Automob. Eng. 2017. [Google Scholar] [CrossRef]
- Wang, R.R.; Zhang, H.; Wang, J. Linear parameter-varying controller design for four-wheel independently actuated electric ground vehicles with active steering systems. IEEE Trans. Control Syst. Technol. 2014, 22, 1281–1296. [Google Scholar]
- Zhang, H.; Wang, J. Active steering actuator fault detection for an automatically-steered electric ground vehicle. IEEE Trans. Veh. Technol. 2017, 66, 3685–3702. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, X.; Wang, J. Robust energy-to-peak sideslip angle estimation with applications to ground vehicles. Mechatronics 2015, 30, 338–347. [Google Scholar] [CrossRef]
- Yoon, J.; Peng, H. Robust vehicle sideslip angle estimation through a disturbance rejection filter that integrates a magnetometer with GPS. IEEE Trans. Intell. Transp. Syst. 2014, 15, 191–204. [Google Scholar] [CrossRef]
- Liu, W.; He, H.; Sun, F. Vehicle state estimation based on minimum model error criterion combining with extended Kalman filter. J. Frankl. Inst. 2016, 353, 834–856. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, G.; Wang, J. Sideslip angle estimation of an electric ground vehicle via finite-frequency H∞ approach. IEEE Trans. Transp. Electr. 2016, 2, 200–209. [Google Scholar] [CrossRef]
- Cheli, F.; Braghin, F.; Brusarosco, M.; Mancosu, F.; Sabbioni, E. Design and testing of an innovative measurement device for tyre-road contact forces. Mech. Syst. Signal Process. 2011, 25, 1956–1972. [Google Scholar] [CrossRef]
- Zhu, H.; Li, L.; Jin, M.; Li, H.; Song, J. Real-time yaw rate prediction based on a non-linear model and feedback compensation for vehicle dynamics control. Proc. Inst. Mech. Eng. D J. Automob. Eng. 2013, 227, 1431–1445. [Google Scholar] [CrossRef]
- Rath, J.; Veluvolu, K.; Defoort, M.; Soh, Y. Higher-order sliding mode observer for estimation of tyre friction in ground vehicles. IET Control Theory Appl. 2014, 8, 399–408. [Google Scholar] [CrossRef]
- Leung, K.; Whildborne, J.; Purdy, D.; Barber, P. Road vehicle state estimation using low-cost GPS/INS. Mech. Syst. Signal Process. 2011, 25, 1988–2004. [Google Scholar] [CrossRef]
- Nam, K.; Fujimoto, H.; Hori, Y. Lateral stability control of in-wheel-motor-driven electric vehicles based on sideslip angle estimation using lateral tire force sensors. IEEE Trans. Veh. Technol. 2012, 61, 1972–1985. [Google Scholar]
- Chen, L.; Bian, M.; Luo, Y.; Li, K. Real-time identification of the tyre-road friction coefficient using an unscented Kalman filter and mean-square-error-weighted fusion. Proc. Inst. Mech. Eng. D J. Automob. Eng. 2015, 230, 788–802. [Google Scholar] [CrossRef]
- Chen, T.; Chen, L.; Xu, X.; Cai, Y.; Jiang, H.; Sun, X. Estimation of longitudinal force and sideslip angle for intelligent four-wheel independent drive electric vehicles by observer iteration and information fusion. Sensors 2018, 2018, 1268. [Google Scholar] [CrossRef]
- Li, X.; Song, X.; Chan, C. Reliable vehicle sideslip angle fusion estimation using low-cost sensors. Measurement 2014, 51, 241–258. [Google Scholar] [CrossRef]
- Li, X.; Chan, C.; Wang, Y. A reliable fusion methodology for simultaneous estimation of vehicle sideslip and yaw angles. IEEE Trans. Veh. Technol. 2016, 65, 4440–4458. [Google Scholar] [CrossRef]
- Boada, B.; Boada, M.; Diaz, V. Vehicle side slip angle measurement based on sensor data fusion using an integrated ANFIS and an Unscented Kalman Filter algorithm. Mech. Syst. Signal Process. 2016, 72, 832–845. [Google Scholar] [CrossRef]
- Jin, X.; Yin, G. Estimation of lateral tire-road forces and sideslip angle for electric vehicles using interacting multiple model filter approach. J. Frankl. Inst 2015, 352, 686–707. [Google Scholar] [CrossRef]
- Yoon, J.H.; Li, S.E.; Ahn, C. Estimation of vehicle sideslip angle and tire-road friction coefficient based on magnetometer with GPS. Int. J. Automot. Technol. 2016, 17, 427–435. [Google Scholar] [CrossRef]
- Liu, Y.; Li, T.; Yang, Y.; Ji, X.; Wu, J. Estimation of tire-road friction coefficient based on combined APF-IEKF and iteration algorithm. Mech. Syst. Signal Process. 2017, 88, 25–35. [Google Scholar] [CrossRef]
- Cheng, S.; Li, L.; Chen, J. Fusion algorithm design based on adaptive SCKF and integral correction for side-slip angle observation. IEEE Trans. Ind. Electron. 2018, 65, 5754–5763. [Google Scholar] [CrossRef]
- Nam, K.; Oh, S.; Fujimoto, H.; Hori, Y. Estimation of sideslip angle and roll angles of electric vehicles using lateral tire force sensors through RLS and Kalman filter approaches. IEEE Trans. Ind. Electron. 2013, 60, 988–1000. [Google Scholar] [CrossRef]

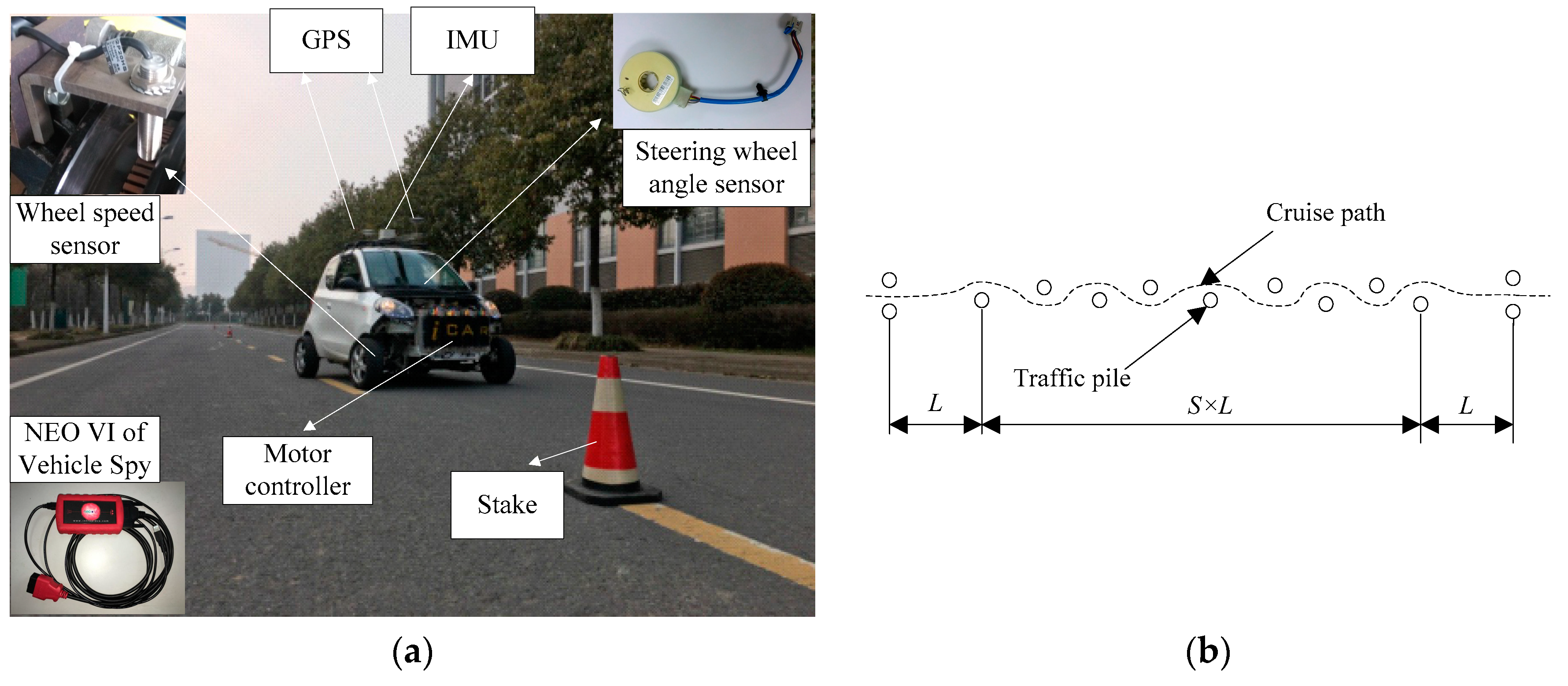
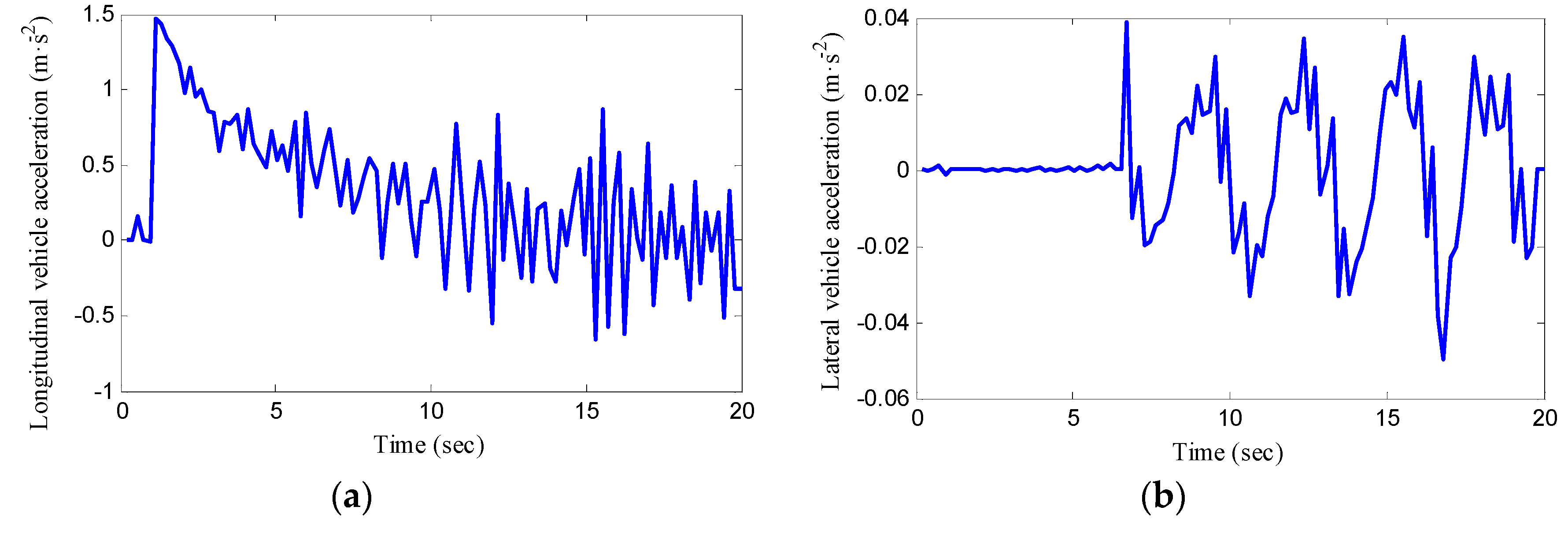
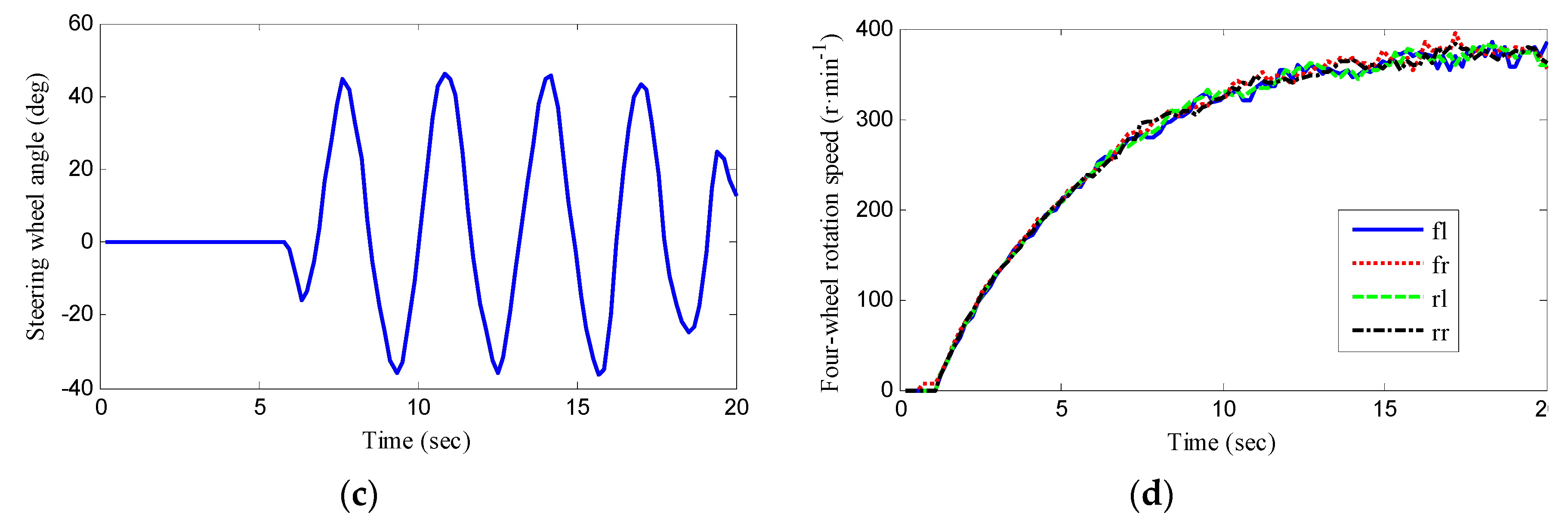
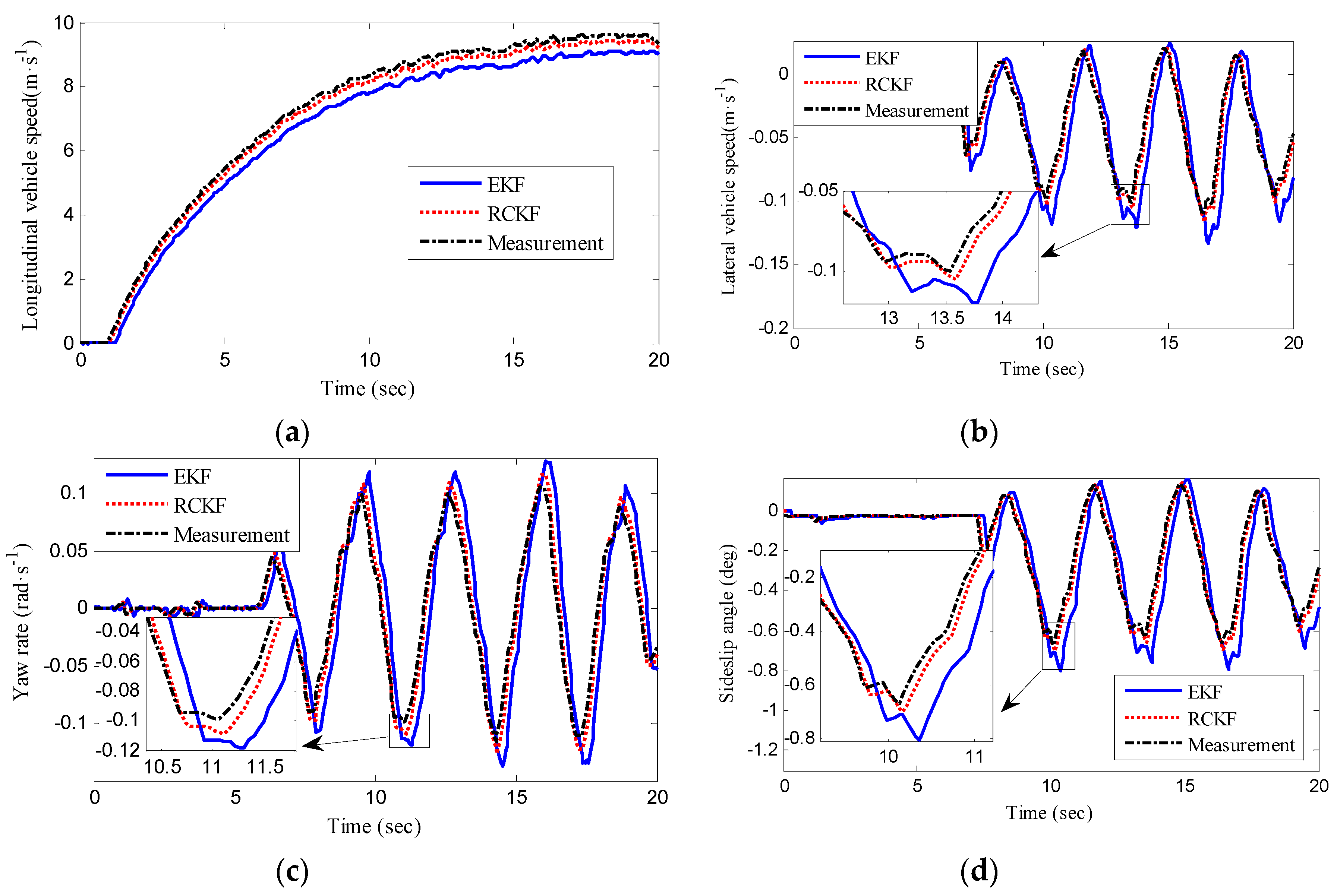
| Symbol | Parameters | Value and Units |
|---|---|---|
| m | Vehicle mass | 800 kg |
| r | Effective radius of wheel | 0.245 m |
| lf | Distances from vehicle gravity center to the front axle | 0.795 m |
| lr | Distances from vehicle gravity center to the rear axle | 0.975 m |
| bf, br | Half treads of the front(rear) wheels | 0.775 m |
| Cf | Equivalent cornering stiffness of front wheel | 60000 N/rad |
| Cr | Equivalent cornering stiffness of rear wheel | 40000 N/rad |
| Iz | Moment of inertia | 1000 kg·m2 |
| Vehicle State | AE | RMSE | ||
|---|---|---|---|---|
| EKF | ACKF | EKF | ACKF | |
| vx | 0.1837 | 0.1294 | 0.1962 | 0.1308 |
| vy | 0.0506 | 0.0219 | 0.1329 | 0.0973 |
| γ | 0.0168 | 0.0121 | 0.1034 | 0.0965 |
| β | 0.1213 | 0.0464 | 0.1377 | 0.1011 |
| Vehicle State | AE | RMSE | ||
|---|---|---|---|---|
| EKF | ACKF | EKF | ACKF | |
| vx | 0.1507 | 0.1013 | 0.1752 | 0.1223 |
| vy | 0.0627 | 0.0201 | 0.1398 | 0.1090 |
| γ | 0.0514 | 0.0316 | 0.1085 | 0.0919 |
| β | 0.2811 | 0.0932 | 0.1453 | 0.0916 |
| Vehicle State | AE | RMSE | ||
|---|---|---|---|---|
| EKF | ACKF | EKF | ACKF | |
| vx | 0.4776 | 0.1615 | 0.2078 | 0.1404 |
| vy | 0.0121 | 0.0029 | 0.1958 | 0.1299 |
| γ | 0.0155 | 0.0063 | 0.2295 | 0.1341 |
| β | 0.0612 | 0.0172 | 0.1891 | 0.1153 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.; Chen, L.; Xu, X.; Cai, Y.; Jiang, H.; Sun, X. Sideslip Angle Fusion Estimation Method of an Autonomous Electric Vehicle Based on Robust Cubature Kalman Filter with Redundant Measurement Information. World Electr. Veh. J. 2019, 10, 34. https://doi.org/10.3390/wevj10020034
Chen T, Chen L, Xu X, Cai Y, Jiang H, Sun X. Sideslip Angle Fusion Estimation Method of an Autonomous Electric Vehicle Based on Robust Cubature Kalman Filter with Redundant Measurement Information. World Electric Vehicle Journal. 2019; 10(2):34. https://doi.org/10.3390/wevj10020034
Chicago/Turabian StyleChen, Te, Long Chen, Xing Xu, Yingfeng Cai, Haobin Jiang, and Xiaoqiang Sun. 2019. "Sideslip Angle Fusion Estimation Method of an Autonomous Electric Vehicle Based on Robust Cubature Kalman Filter with Redundant Measurement Information" World Electric Vehicle Journal 10, no. 2: 34. https://doi.org/10.3390/wevj10020034
APA StyleChen, T., Chen, L., Xu, X., Cai, Y., Jiang, H., & Sun, X. (2019). Sideslip Angle Fusion Estimation Method of an Autonomous Electric Vehicle Based on Robust Cubature Kalman Filter with Redundant Measurement Information. World Electric Vehicle Journal, 10(2), 34. https://doi.org/10.3390/wevj10020034







