Abstract
This paper proposes TSKT-oblivious RAM (ORAM), an efficient multi-server ORAM construction, to protect a client’s access pattern to outsourced data. TSKT-ORAM organizes each of the server storages as a k-ary tree and adopts XOR-based private information retrieval (PIR) and a novel delayed eviction technique to optimize both the data query and data eviction process. TSKT-ORAM is proven to protect the data access pattern privacy with a failure probability of when system parameter . Meanwhile, given a constant-size local storage, when N (i.e., the total number of outsourced data blocks) ranges from –, the communication cost of TSKT-ORAM is only 22–46 data blocks. Asymptotic analysis and practical comparisons are conducted to show that TSKT-ORAM incurs lower communication cost, storage cost and access delay in practical scenarios than the compared state-of-the-art ORAM schemes.
1. Introduction
Many corporations and individuals are using cloud storage services to host their business or personal data. As the first line of defense for data secrecy, these cloud storage clients can encrypt their sensitive data before outsourcing them. This, unfortunately, is not sufficient, because the clients’ access pattern to the outsourced data can still be observed by the cloud service providers and the attackers who compromise the service. Moreover, researcher have reported that even the content of encrypted data could be inferred from the exposed access pattern [1].
Researchers have found the private information retrieval (PIR) [2,3,4,5,6,7,8,9,10,11] and the oblivious RAM (ORAM) [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28] to be security-provable methods for hiding the data access pattern from the data storage server. While some studies indicate that the PIR schemes may be infeasible for large-scale datasets as they need to process the whole dataset in order to hide just one data request [19], the ORAM approaches still appear to be promising as more and more resource-efficient constructions have been proposed. Particularly, communication cost is the most important metric to evaluate the feasibility of an ORAM construction. In the literature, the most communication-efficient ORAM constructions are C-ORAM [29] and CNE-ORAM [30], both consuming bandwidth for each data query, when the total number of exported data blocks is N and each data block is of size bits for some constant . Though C-ORAM and CNE-ORAM have achieved better communication efficiency than prior works, further reducing the requirement of the data block size and the query delay is still desirable to make the ORAM construction more feasible to implement in cloud storage systems.
In this paper, we propose a new ORAM construction, named TSKT-ORAM, in which data blocks are out-sourced to two independent servers where the data blocks are stored in k-ary trees and evictions are delayed and aggregated to reduce its cost. The design can further reduce the costs of data access pattern protection and simultaneously accomplish the following performance goals in practical scenarios:
- Communication efficiency: Under a practical scenario, the communication cost per data query is about 22 blocks–46 blocks when and the block size bits for some constant . In practice, this is lower or comparable to constant communication ORAM constructions C-ORAM and CNE-ORAM. Furthermore, in TSKT-ORAM, there is no server-server communication cost incurred.
- Low access delay: Compared to both the C-ORAM and CNE-ORAM schemes with constant client-server communication cost, TSKT-ORAM has a low access latency.
- Small data block size requirement: Compared to C-ORAM and CNE-ORAM, TSKT-ORAM only requires each data block size KB.
- Constant storage at the client: TSKT-ORAM only requires the client storage to store a constant number of data blocks, while each server needs to store data blocks.
- Low failure probability guarantee: TSKT-ORAM is proven to achieve a failure probability given system parameter .
In the rest of the paper, Section 2 briefly reviews the related work. Section 3 presents the problem definition. Section 4 and Section 5 present our proposed scheme. Section 6 reports the security analysis. Section 7 makes a detailed comparison between our proposed scheme with existing ORAMs. Finally, Section 8 concludes the paper.
2. Related Work
2.1. Oblivious RAM
Based on the data lookup technique adopted, existing ORAMs can be classified into two categories: hash-based and index-based ORAMs. Hash-based ORAMs [12,13,14,15,16,17,18,19,20,21] require some data structures such as buckets or stashes to deal with hash collisions. Among them, the balanced ORAM (B-ORAM) [17] proposed by Kushilevitz et al. achieves the lowest asymptotical communication cost, which is , where B is the size of a data block. Index-based ORAMs [22,23,24,25,26,27] use index structure for data lookup. They require the client to either store the index or outsource the index to the server recursively in a way similar to storing data, at the expense of increased communication cost. The state-of-the-art index-based ORAMs are binary tree ORAM (T-ORAM) [22], path ORAM [23] and SCORAM [28]. When (constant ) is assumed, the communication cost for T-ORAM is with failure probability (), while path ORAM and SCORAM incur communication cost with failure probability and client-side storage.
2.2. Private Information Retrieval
PIR protocols were proposed mainly to protect the pattern in accessing read-only data at remote storage. There are two variations of PIR: information-theoretic PIR (iPIR) [2,3,5,6], assuming multiple non-colluding servers each holding one replica of the shared data; computational PIR (cPIR) [4,7,8,9], which usually assumes a single server in the system. cPIR is more related to our work and thus is briefly reviewed in the following. The first cPIR scheme was proposed by Kushilevitz and Ostrovsky in [7]. Designed based on the hardness of the quadratic residuosity decision problem, the scheme has () communication cost, where n is the total number of outsourced data in bits. Since then, several other single-server cPIRs [8,9] have been proposed based on different intractability assumptions. Even though cPIRs are impractical when the database size is large, they are acceptable for small databases. Recently, several partial homomorphic encryption-based cPIRs [10,11] have been proposed to achieve satisfactory performance in practice, when the database size is small. Due to the property of partial homomorphic encryption, [31,32] show that these cPIR schemes can also be adapted for data updating.
2.3. Hybrid ORAM-PIR Designs
Designs based on a hybrid of ORAM and PIR techniques have emerged recently. Among them, C-ORAM [29] has the best known performance. However, due to the complexity of PIR primitives, one data query would require the server to take about 7 min to process. In addition, the data block size in C-ORAM is bits, where N is the total number of outsourced data blocks. Thus, this imposes another strict requirement on C-ORAM.
2.4. Multi-Server ORAMs
There are several multi-server ORAM schemes in the literature. Lu and Ostrovsky proposed one of the earliest multiple-server ORAM constructions [33], in which there is no server-to-server communication, but the client-server communication incurs at the cost of per query. Despite the asymptotic result, as pointed out in [27], this construction actually incurs very high client-server communication overhead in practice.
Stefanov and Shi propose another multi-server ORAM construction [27], which follows the basic design of partition-ORAM [25]. In this scheme, the client-server communication cost is reduced to a constant number, but the server-server communication cost is . In addition, it requires the client to store data blocks in the local storage.
Recently, another multi-server ORAM called CNE-ORAM was proposed, which incurs client-server communication cost using at least four non-colluding servers. In CNE-ORAM, each data block is split into two parts using secret sharing techniques. Each part of one data block is further copied into two copies, and each copy is stored onto two out of the four servers. The remaining part is also copied and stored onto the other two servers. At the server side, the storage is organized as a binary tree with of a height , and each tree node can store data blocks. For each data query, the target data block is retrieved using the mechanism of XOR-based private information retrieval (PIR). The client then writes data blocks to the root node of each server. After queries, the data eviction process is executed to prevent the root node from overflowing. During data eviction, the client guides the servers to merge nodes on the evicting path. In the post eviction process, the client retrieves a block for the leaf node of the evicting path and replaces it with an empty block if it is a noise block. The computation cost is mainly contributed by data XOR operations, where for each data query, more than blocks are XORed, and the communication cost is mainly contributed by uploading data blocks to the root per query, where is the height of the tree.
3. Problem Definition
We consider a system model as follows. A client exports N equally-sized data blocks to two remote storage servers, where the two servers do not collude with each other. Note that such an architecture is feasible in practice, since the client can select two servers in a way that they will not know the existence of each other. For example, a client can simply select Amazon S3 and Google Drive as two independent storage servers. Each of the two servers has an identical copy of the data storage.
The client accesses the exported data every now and then and wishes to hide the pattern of the accesses from the server. Specifically, the client has two types of private accesses to the data stored at the server, as follows:
- private read ;
- private write .
Here, i and D denote the ID and content of the accessed data block, respectively. These two types can be uniformly denoted as , where can be either or and should be kept secret.
To hide each private access to data, the client usually needs to access the storage server multiple times. As the server can observe the locations accessed by the client, we shall prevent the pattern of location access from leaking any information about the data access. There are two types of location access:
- retrieval from a location, denoted as ;
- uploading to a location, denoted as .
Here, l and D denote the accessed location and the data block retrieved or uploaded, respectively. The two types can also be generalized to , where is either or .
As the ORAM construction is to protect the client’s data access pattern from the cloud storage server, we assume the client to be trustworthy, while assuming the server to be honest but curious. That is, though the server may attempt to find out the client’s data access pattern, it honestly stores data and responds to the client’s requests for location access. We assume the client-server connection to be secure, which can be accomplished using mechanisms like SSL [34].
Following the definitions adopted by existing ORAM constructions [12,23,25], the security of our proposed ORAM is formalized as follows.
Definition 1.
Given:
- security parameter λ;
- two arbitrary equal-length sequences of private data access denoted as , , ⋯⟩ and , , ⋯⟩; and
- two sequences of the client’s access to storage locations that correspond to and , denoted as , and , .
An ORAM construction is secure if:
- and are computationally indistinguishable; and
- the construction fails with a probability no greater than .
4. Preliminary Construction: TSBT-ORAM
Before presenting our proposed TSKT-ORAM scheme, we first present a preliminary scheme: TSBT-ORAM (multi-server binary tree ORAM). TSBT-ORAM follows the framework of P-PIR [32], but aims to improve the data access delay. Based on the observation that the access delay in P-PIR is mainly caused by the expensive homomorphic operations, TSBT-ORAM replaces the homomorphic encryptions with XOR operations on the server. The rest of this section presents TSBT-ORAM in terms of storage organization, the data query process and the data eviction process.
4.1. Storage Organization
Storage is organized at both the server and client sides.
4.1.1. Server-Side Storage
Two servers denoted as and are needed. Since the servers are almost identical to each other, we only describe how storage is organized in and call the “server”. Later, we will show the differences between and .
The server storage is organized as a binary tree with layers. Each node stores blocks, where c is a system parameter related to the security parameter . Within a node, each block has a unique position offset ranging from zero to .
Recall that the total number of exported data blocks is assumed to be N, but the capacity of the storage is larger than N blocks. Hence, dummy blocks, each a block of random bits, are introduced in order to fill up the storage. Hereafter, we call the aforementioned N blocks real blocks to differentiate them from the dummy ones. Before being stored in the server storage, each real data block is encrypted with a probabilistic symmetric encryption scheme; that is, each data block is stored as , where E denotes the encryption function. To initialize the server storage, all the real blocks are randomly distributed to the leaf nodes while the dummy blocks are distributed to the rest of the storage space. Note that the blocks distributed to each node are randomly permuted before uploading, which hides the distribution of real blocks from the server.
Each node also contains a symmetrically-encrypted index block that records the IDs of the data blocks stored at each position of the node; as the index block is also encrypted, the index information is not known to the server.
Figure 1 shows an example, where data blocks are exported and stored in a binary tree-based storage with six layers. Starting from the top layer, i.e., Layer 0, each node is denoted as , where l is the layer index and i is the node index on the layer.
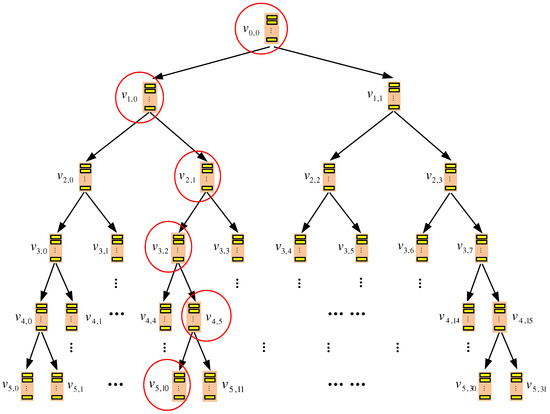
Figure 1.
TSBT-oblivious RAM (ORAM)’s server-side storage structure. Circled nodes represent the ones accessed by the client during a query process when the target data block is mapped to leaf node .
4.1.2. Client-Side Storage
TSBT-ORAM requires the client to maintain an index table with N entries, where each entry i () records the ID of a leaf node on the tree such that data block is stored at some node on the path from the root to this leaf node. As in T-ORAM [22] and P-PIR [32], the index table can be exported to the server, as well; this way, the client-side storage can be of constant size and only needs to store at most two data blocks, as well as some secret information such as encryption keys.
4.2. Data Query Process
A data query process is launched by a client, and responded by the two servers.
4.2.1. Client’s Launching of Query
To query a certain data block , the client first checks its index table to find out the leaf node to which is mapped. Hence, a path from the root to is identified. To facilitate the presentation, we denote the selected path as follows:
For each node () on , the client retrieves the encrypted index block from the server and checks if is in the node. Then, it generates two query vectors and , where each vector is a binary stream of bits and each bit corresponds to one block in the node. The contents of the vectors are determined as follows:
- is generated randomly.
- is first made as a copy of . Further, if the query target is in node (supposing the offset of in the block is m), bit m of is flipped.
Note that, if contains , and differ only at one bit, which corresponds to ; if does not contain , the two query vectors are the same. Then, the client sends to server for , respectively.
4.2.2. Servers’ Response to Query
Upon receiving query vectors for , server needs to conduct bit-wise XOR operations on some data blocks and return the resulting block. Before elaborating the operations, let us introduce the bit-wise XOR operator on blocks as follows.
Definition 2.
Let ⨁ denote a bit-wise XOR operator on blocks. More specifically, assume:
where each , is a bit-stream representation of block D. The bit-wise XOR of a set of blocks denoted as , i.e.,
is a block whose bit-stream representation is:
where each , i.e., the XOR of the bits with offset i in every block of set .
Responding to the query, server first conducts the following computations for each layer . Recall that is the node queried by the client from layer l, and the node contains blocks. Let:
denote the set of all blocks in and:
denote the subset of blocks that are selected by query vector . The server computes:
Once has been computed for each layer , the server further computes:
and then sends back to the client.
4.2.3. Client’s Computation of the Query Result
Upon receiving and from the servers, the client computes and decrypts it to get the query target data block. After the target block has been accessed, the client re-encrypts it, assigns a path randomly for the block and uploads it to the root node of each server.
An example of the query process is illustrated in Figure 1, where the query target is mapped to leaf node . Hence, each node on the path is involved in the data query. Finally, data block is found at node . After being accessed, it is re-encrypted and added to root node .
4.3. Data Eviction Process
To prevent any node on the tree from overflowing, the client launches an eviction process after each query process.
4.3.1. Basic Idea
The basic idea of data eviction is as follows. For each non-leaf layer l, up to two evicting nodes and are randomly selected (note that the top layer has only one node, and thus, only one node is selected); one data block is evicted from each selected node to one of its two child nodes, while a dummy block is evicted to the other child node. In the following, we focus on the eviction operations involving , as the operations involved are similar. Note that, and are the child nodes of .
Figure 2 shows an example of the eviction process, where circled nodes are selected to evict data blocks to their child nodes. Let us consider how node evicts its data block. The index block in the node is first retrieved to check if the node contains any real data block. If there is a real block in and is mapped to leaf node , will be obliviously evicted to , which is ’s child and is on the path from to , while a dummy eviction is performed on another child node . Otherwise, two dummy evictions will be performed on nodes and .
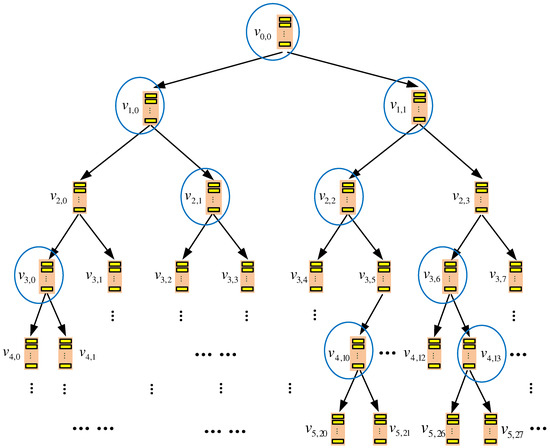
Figure 2.
An example of the eviction process in TSBT-ORAM.
For obliviousness, the eviction process should further meet the following requirements:
- which real data block is evicted from an evicting node should be hidden;
- which one of two child nodes of an evicting node that receives the evicted real data block should be hidden.
To meet these requirements, the design of TSBT-ORAM involves the following two aspects:
- For each evicting node (e.g., ), the position where the evicted data block resides should be hidden from any server.
- For each receiving node (e.g., ), each position that can be used to receive the evicted data block should be selected with an equal probability. In other words, each position of the receiving node should have an equal probability to be written during data eviction. This way, the behavior of a receiving node is independent of whether it receives a real or dummy block.
4.3.2. Oblivious Retrieval of Evicted Data Block
In the eviction process, the client first obliviously retrieves an evicting data block D from each evicting node . If there is at least one real data block in this node, D is a randomly selected real data block; otherwise, D is a dummy data block.
MSTK-ORAM accomplishes the obliviousness in data block retrieval via an approach similar to the query process. In a nutshell, the process is as follows. Suppose the offset of D at is m. The client composes an eviction vector , which also has bits, and sends it to server . Another eviction vector is composed to differ from in only one bit m, and is then sent to server . On receiving for , server conducts the bit-wise XOR operation on the blocks selected by and returns the resulting block. The client then conducts bit-wise XOR operation on the returned blocks to obtain D.
4.3.3. Oblivious Receiving of Evicted Data Block
After the client has retrieved D, the block should be re-encrypted and then evicted to a child of the evicting node . On the high level, there are the following two cases:
- Case I: D is a real data block.Without loss of generality, suppose D needs to be evicted to ; meanwhile, a dummy block needs to be evicted to to achieve obliviousness. To reduce the communication cost, D is treated also as the dummy data block when evicted to .
- Case II: D is a dummy data block. In this case, D is evicted to both and as a dummy data block.
Next, we explain the details of the above process.
The storage space of each node on the server storage tree is logically partitioned into three equally-sized parts, denoted as , and , and each part can store data blocks.
- : This part is used by the node to store the latest evicted data blocks, which could be dummy or real, from its parent.
- : This part is used to store each real data block that still remains in the node after more than (dummy or real) blocks have been evicted to the node since the arrival of this real block. Since the number of real data blocks stored in any node is at most , this part may contain dummy blocks.
- : This is the storage space other than and in the node. This part contains only dummy data blocks.
Note that the servers only know and the union of and ; the partitioning between and is known only to the client. A node uses only or to receive data blocks evicted from its parent. Furthermore, , and are only logical partitions, and they could change from time to time. For example, when one position in or is used to accept a data block evicted from the parent node, this position is transferred to ; meanwhile, the oldest position in is automatically transferred from to or .
Based on the above logical partitioning, the client evicts the data block D from to or as follows. First, if D is a real data block, there are the following two cases:
- If D should be evicted to (i.e., D is assigned to the path passing ), one position in partition of node is randomly picked to receive D, and meanwhile, one position in partition or of node is randomly picked to receive a dummy block.
- Otherwise (i.e., D should be evicted to ), one position in partition of is randomly picked to receive D, while one position in partition or of is randomly picked to receive a dummy block.
Second, if D is a dummy data block (i.e., has no real block to evict), for (and respectively), the client randomly picks a position from partitions and of (and , respectively) to receive a dummy block. After the reception, the positions of nodes and join partition of the two nodes, respectively, and the least-recently receiving position in each of the two nodes joins partition .
As will be proven in Section 6, each position in has the same probability to be selected to receive a data block evicted from the parent; thus, the eviction process is oblivious and is independent of the data access pattern.
5. Final Construction: TSKT-ORAM
To improve the communication efficiency and further reduce the access delay, we propose TSKT-ORAM, which replaces the binary tree in TSBT-ORAM with a k-ary tree to reduce the height of the tree. As the tree height is decreased, the communication cost for each query can be reduced and so for the access delay. Replacing the binary tree by the k-ary tree requires the data eviction process to change accordingly. Hence, we also design a new data eviction algorithm. Next, we present the scheme in detail.
5.1. Storage Organization
The data storage of each server is organized as a k-ary tree, with height , where k is a power of two. As shown in Figure 3, each node on the k-ary tree, called a k-node, can be mapped to a binary subtree with nodes called b-nodes; also, each k-node contains the following data structures:
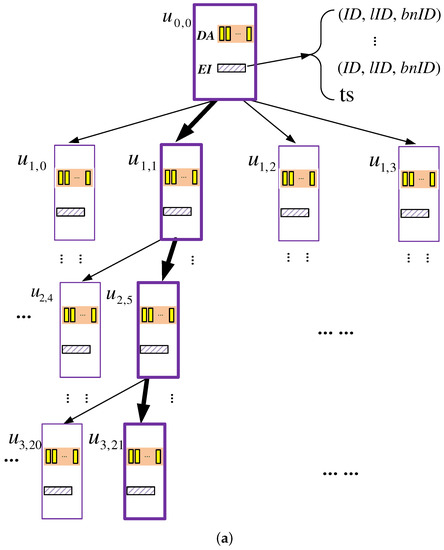
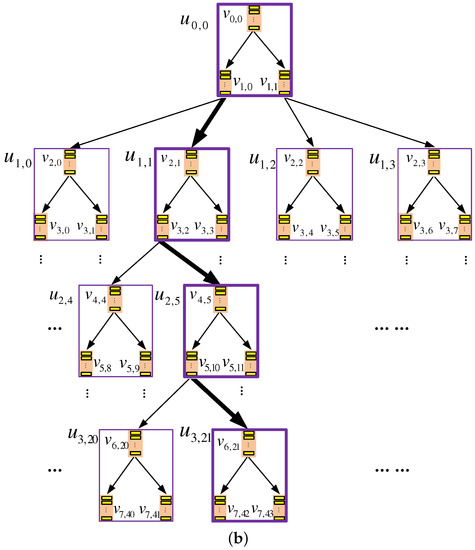
Figure 3.
An example TSKT-ORAM scheme with a quaternary-tree storage structure. Each k-node in the physical view (a) corresponds to a two-tier binary subtree shown in the logical view (b). Bold boxes represent the k-nodes accessed when a client queries a target data block stored at k-node ; that is, nodes , , and need to be accessed. (a) Quaternary tree: physical view of the server storage; (b) binary tree: logical view of the server storage.
- Data array (DA): a data container that stores data blocks, where c is a system parameter. As c gets larger, the failure probability of the scheme gets smaller, and meanwhile, more storage space gets consumed; hence, an appropriate value should be picked for c. As demonstrated by the security analysis presented later, when , the failure probability can be upper-bounded by . Therefore, we use four as the default value of c.
- Encrypted index table (EI): a table of entries recording the information for each block stored in the DA. Specifically, each entry is a tuple of format , which records the following information of each block:
- −
- : ID of the block;
- −
- : ID of the leaf k-node to which the block is mapped;
- −
- : ID of the b-node (within ) to which the block logically belongs.
In addition, the EI has a ts field, which stores a time stamp indicating when this k-node was accessed the last time.
5.2. Client-Side Storage
Similar to TSBT-ORAM, the client maintains an index table that records the mapping between data block IDs and the paths assigned to the blocks, some buffer space that temporarily stores data blocks downloaded from the server and a small permanent storage for secrets. In addition, the client maintains a counter that keeps track of the number of queries issued by the client.
5.3. System Initialization
To initialize the system, the client acts as follows. It first encrypts each real data block to , as in TSBT-ORAM, and then randomly assigns it to a leaf k-node on the k-ary tree maintained at each server. The rest of the DA spaces on the tree shall all be filled with dummy blocks.
For each k-node, its EI entries are initialized to record the information of blocks stored in the node. Specifically, the entry for a real data block shall record the block ID to the field, the ID of the assigned leaf k-node to the field and the ID of an arbitrary leaf b-node within the k-node to the field. In an entry for a dummy data block, the block ID is marked as “” while the and fields are filled with arbitrary values. The field of the EI shall be initialized to zero.
For the client-side storage, the index table is initialized to record the mapping from real data blocks to leaf k-nodes, and the keys for data and index table encryption are also recorded to a permanent storage space. Finally, the client initializes its counter to zero.
5.4. Data Query
To query a data block with ID t, the client increments the counter and searches the index table to find out the leaf k-node that is mapped to, and then, for each k-node u on the path from the root k-node to this leaf node, the XOR operations similar to those in TSBT-ORAM are performed to retrieve . The only difference is that the query bit vector size of TSKT-ORAM is bits per vector. As shown in Figure 3a, to query a data block stored at k-node , the EIs at , , and are accessed, as these k-nodes are on the path from the root to the leaf node to which is mapped. A dummy data block is retrieved obliviously from , , and , respectively, while is retrieved obliviously from .
5.5. Data Eviction
The same as in TSBT-ORAM, each server launches a data eviction process after each query.
5.5.1. Overview
The purpose of data eviction in TSKT-ORAM is essentially the same as in TSBT-ORAM. Thus, it could be conducted as follows: Over the logical binary tree view of the k-ary tree, the eviction process requires the root b-node and two randomly selected b-nodes from each non-leaf layer to each evict a data block to its child nodes. The evicted data block is ideally a real data block; but a dummy block is evicted if a selected node does not have a real data block. The eviction process is ensured to be oblivious with the same techniques used in TSBT-ORAM.
Adopting the above approach, however, would not take advantage of the k-ary tree structure and would incur a client-server communication cost of blocks per query, which is similar to the eviction cost incurred by existing binary tree-based ORAM constructions. In order to leverage the k-ary tree structure to reduce the eviction cost, we propose to opportunistically delay and aggregate evictions that occur within a k-node. We call such kinds of evictions as intra k-node evictions, while call other evictions as inter k-node evictions. Next, we use the examples in Figure 4 to explain the idea.
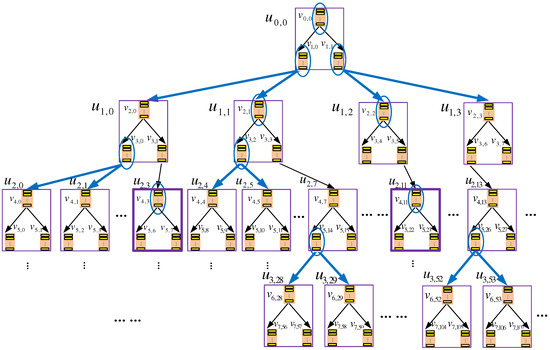
Figure 4.
An example data eviction process in TSKT-ORAM with a quaternary-tree storage structure. In the logical view (i.e., binary-tree view) of the tree, the root b-node and two b-nodes from each layer, which are circled in the figure, are selected to evict data blocks to their child nodes; thus, the k-nodes that contain these selected b-nodes or their child nodes are also involved in the eviction. With the delay eviction mechanism, not all of these evictions have to be performed immediately. Instead, the evictions that occur within the same k-node, for example, the evictions from to its child nodes and from to its child nodes, occur in k-nodes and , respectively, which are highlighted with bold boundaries, can be delayed to reduce the eviction overhead.
In the figure, b-node is selected to evict a data block to its child nodes, and this node and its child nodes all belong to the same k-node . Hence, the eviction from is an intra k-node eviction. Because b-nodes belonging to the same k-node share one DA space to store their data blocks, an intra k-node eviction can be conducted by only updating the EI of the k-node to reflect the change of the field of the evicted block, without physically moving the block. That is, an intra k-node eviction can be conducted more efficiently. On the other hand, evicting a data block from b-node to its child nodes is an inter k-node eviction, because this b-node and its child nodes belong to three different k-nodes. These b-nodes do not share DA space, and thus, the eviction has to be conducted by moving blocks across k-nodes. This is less efficient than an intra k-node eviction.
Furthermore, we find that it is not always necessary to immediately conduct intra k-node eviction. Instead, such evictions can be delayed and aggregated opportunistically. More specifically, we may find that a k-node is not involved in any inter k-node eviction during an eviction process; that is, its root b-node is not a child of any node selected to evict data block, and meanwhile, its leaf b-nodes do not evict data blocks. For example, k-node and are such k-nodes in Figure 4. For intra-k-node evictions occurring within such k-nodes (e.g., the evictions from and to their child nodes), we do not have to conduct them immediately; rather, they can be conducted (i.e., updating the EIs of the k-nodes) later when the k-node is next accessed in a query process or an inter-k-node eviction. Note that such a delay does not affect the correctness of the eviction process, because the EIs will not be accessed before the updates are made; moreover, the delay could allow more intra k-node evictions to be conducted at once, i.e., intra-k-node evictions could be aggregated, which could further reduce the cost.
5.5.2. The Algorithm
Based on the previously-explained idea, the eviction algorithm is designed to include the following three phases.
- Phase I, selecting b-nodes for inter-k-node eviction: In this phase, the client randomly selects two b-nodes from each layer on the binary tree; that is, each selected b-node must be on the bottom layer of the binary subtree within a certain non-leaf k-node. Each selected b-node needs to evict a data block to its child nodes, which are in other k-nodes. Hence, the eviction has to be an inter k-node eviction and should be conducted immediately.
- Phase II, conducting delayed intra-k-node evictions: Each inter-k-node eviction planned in the previous phase involves three k-nodes: the k-node that contains the evicting b-node and the two other k-nodes that contain the child b-nodes of the evicting b-node. Before the inter-k-node eviction is executed, we need to make sure that the three involved k-nodes have completed all delayed evictions within them, and this is the purpose of this phase.More specifically, the following three steps should be taken for each k-node, denoted as , which is involved in an inter-k-node eviction planned in the previous phase. Note that, here, l denotes the layer of the k-node on the k-ary tree.
- The client downloads the EI of , decrypts it and extracts the value of field .
- The client computes . Note that, counts the number of queries issued by the client, which is also the number of eviction processes that have been launched, and is the discrete timestamp for the latest access of . Hence, r is the number of eviction processes for which may have delayed its intra-k-node evictions.
- The client simulates the r eviction processes to find out and execute the delayed intra-k-node evictions. In particular, for each of the eviction processes:
- (a)
- The client randomly selects two b-nodes from each binary-tree layer . Note that layer is not a leaf binary-tree layer within a k-node, and therefore, any b-node selecting from the layer only has child nodes within the same k-node; in other words, the eviction from the selected b-node must be an intra-k-node eviction.
- (b)
- For each previously selected b-node that is within k-node , one data block is picked from it, and the field of the block is updated to one of its child nodes that the block can be evicted to; this way, the delayed eviction from the selected b-node is executed.
- After the previous step completes, all the delayed evictions within k-node have been executed. Therefore, the field in the EI of is updated to .
- Phase III, conducting inter-k-node evictions: For each inter-k-node eviction planned in the first phase, its involved k-nodes should have conducted all of their delayed evictions in the second phase. Hence, the planned inter-k-node eviction can be conducted now. Essentially, each selected evicting b-node should evict one of its data blocks from the DA space of its k-node to the DA space of the k-node containing the child b-node that accepts the block, and the eviction should be oblivious. The detail is similar to the oblivious data eviction process in TSBT-ORAM that is elaborated in Section 4.3 and therefore is skipped here.
6. Security Analysis
In this section, we first study the failure probability of TSKT-ORAM, which is followed by the study of its obliviousness. These studies finally lead to the main theorem.
Lemma 1.
The probability for a DA in any k-node to overflow is no greater than , as long as the parameters of TSKT-ORAM meet the following conditions:
- data blocks are stored in each DA;
- ;
- ; and
- .
Proof.
The proof considers non-leaf and leaf k-nodes separately.
Non-leaf k-nodes:
The proof for non-leaf k-node proceeds in the following two steps.
In the first step, we consider the binary tree that a k-ary tree in TSKT-ORAM is logically mapped to and study the number of real data blocks (denoted as a random variable ) logically belonging to an arbitrary b-node v on an arbitrary level l of the binary tree.
As the eviction process of TSKT-ORAM completely simulates the eviction process of T-ORAM and P-PIR over the logical binary tree, the results of [22] of the theoretical study on the number of real data blocks in a binary tree node can still apply. Specifically, can be modeled as a Markov chain denoted as . In the chain, the initial one is , The transition from to occurs with probability , and the transition from to occurs with probability , for every non-negative integer i. Here, and for any level l. Furthermore, for any , a unique stationary distribution exists for the chain; that is,
where:
In the second step, we consider an arbitrary k-node u on the k-ary tree and study the number of real data blocks stored at the DA of u, which is denoted as a random variable .
The binary subtree that u is logically mapped to contains b-nodes, which are denoted as for simplicity. Then . Furthermore, as k should be greater than two to make TSKT-ORAM nontrivial, any of the b-nodes should be on a level greater than or equal to one on the logical binary tree (those b-nodes on Levels 0 and 1 never overflow).
Now, we compute the probability:
Note that there are different combinations of () such that . Hence, we have:
Here, Equation (12) is due to , which is due to Equation (9). Inequality (13) is due to for all . Hence, we have:
Here, Inequality (14) is due to in the scheme, Inequality (15) is due to and .
Then, the following inequalities follow:
Leaf k-nodes:
At any time, all the leaf k-nodes contain at most N real blocks, and each of the blocks is randomly placed into one of the leaf k-nodes. Thus, we can apply the standard balls and bins model to analyze the overflow probability. In this model, N balls (real blocks) are thrown into bins (i.e., leaf k-nodes) in a uniformly random manner.
We study one arbitrary bin and let be N random variables such that:
Note that are independent of each other, and hence, for each , . Let . The expectation of X is:
According to the Chernoff bound, when , it holds that:
Hence, letting , we have:
Finally, we have the following equation:
The first inequality is due to the union bound. The second inequality is due to the fact that .
According to the above two parts, we have proven that the overflow probability is . ☐
Lemma 2.
Any query process in TSKT-ORAM accesses k-nodes from each layer of the k-ary tree, uniformly at random.
Proof.
(Sketch) In TSKT-ORAM, each real data block is initially mapped to a leaf k-node uniformly at random; and after a real data block is queried, it is re-mapped to a leaf k-node also uniformly at random. When a real data block is queried, all k-nodes on the path from the root to the leaf k-node that the real data block is currently mapped to are accessed. Due to the uniform randomness of the mapping from real data blocks to leaf k-nodes, the set of k-nodes accessed during a query process is also uniformly at random. ☐
Lemma 3.
Any eviction process in TSKT-ORAM accesses a sequence of k-nodes independently of the client’s private data request.
Proof.
(Sketch) During an eviction process, the accessed sequence of k-nodes is independent of the client’s private data request due to: (i) the selection of b-nodes for eviction (i.e., Phase I of the eviction process) is uniformly random on the fixed set of layers of the logical binary tree and thus is independent of the client’s private data request; and (ii) the rules determining which evictions should be executed immediately (and hence, the involved k-nodes should be accessed) and which can be delayed are also independent of the client’s private data requests. ☐
Lemma 4.
For any k-node with k-node as its parent, each position in of has the equal probability of to be selected to access.
Proof.
During an eviction process, may evict a real or dummy block to one of its child nodes (i.e., or ). In the following, we consider these two cases respectively.
Case I: evicts a real block to a child node. There are two subcases as follows.
Case I-1: the real block is evicted to ; this subcase occurs with the probability of . In this subcase, according to the previously described eviction policy, a position is randomly selected from to accept the evicted block.
Case I-2: the real block is evicted to , i.e., a dummy block is evicted to ; this occurs with the probability of . In this subcase, according to the eviction policy, a position is randomly selected from to access.
Case II: does not evict any real block to its child nodes. That is, both and are evicted with dummy blocks. In this case, according to the eviction policy, a position is randomly selected from to access.
Furthermore, because and have the same size, each position in has equal probability to be selected to access. ☐
Theorem 1.
TSKT-ORAM is secure under Definition 1, if and .
Proof.
Given any two equal-length sequence and of the client’s private data requests, their corresponding observable access sequences and are computationally indistinguishable, because both of the observable sequences are independent of the client’s private data request sequences. This is due to the following reasons:
- According to the query and eviction algorithms, sequences and should have the same format; that is, they contain the same number of observable accesses, and each pair of corresponding accesses has the same access type.
- According to Lemma 2, the sequence of locations (i.e., k-nodes) accessed by each query process is uniformly random and thus independent of the client’s private data request.
- According to Lemma 3, the sequence of locations (i.e., k-nodes) accessed by each eviction process after a query process is also independent of the client’s private data request.
Moreover, according to Lemma 1, the TSKT-ORAM construction fails with a probability of , when and . ☐
7. Comparisons
In this section, we present detailed performance comparisons between TSKT-ORAM and several state-of-the-art ORAMs including T-ORAM [22], path ORAM [23], P-PIR [32], C-ORAM [29], MSS-ORAM [27] and CNE-ORAM [30].
7.1. Asymptotic Comparisons
Table 1 shows the asymptotic comparison between TSKT-ORAM and some existing ORAM schemes. First, we compare TSKT-ORAM with single-server ORAMs, which include T-ORAM, path ORAM, P-PIR and C-ORAM. As we can see, the communication costs of T-ORAM, path ORAM and P-PIR are not constant, while TSKT-ORAM is in practice. Though C-ORAM incurs constant communication cost, it requires expensive homomorphic encryptions, which incurs a huge amount of computations at the server side and results in long data access delay. For example, with C-ORAM, each data access has to incur a delay as long as seven minutes.

Table 1.
Asymptotic comparisons in terms of client-server communication cost, server-server communication cost, client storage cost, server storage cost and the minimum number of non-colluding servers required. N is the total number of data blocks and B is the size of each block in the unit of bits. for some . For TSKT-ORAM, where and . For all tree structure ORAMs, the index table is outsourced to the server with recursion depth. A scheme marked with the asterisk symbol requires homomorphic encryption.
Second, we compare TSKT-ORAM with other multi-server ORAMs, which include MS-ORAM, MSS-ORAM and CNE-ORAM. MS-ORAM and MSS-ORAM both require server-server communication; additionally, MSS-ORAM incurs high storage cost at the client side, while TSKT-ORAM does not require server-server communication and incurs only constant cost at the client. Compared to CNE-ORAM, which requires at least four non-colluding servers, TSKT-ORAM requires only two; also, TSKT-ORAM incurs lower computational costs (which is translated to lower data access delay) and smaller server storage costs, as will be discussed next.
7.2. Practical Comparisons
Among all the ORAMs that are considered in the above asymptotical comparisons, CNE-ORAM is the one most comparable to TSKT-ORAM. Thus, we make a more detailed comparison between TSKT-ORAM and CNE-ORAM in practical scenarios. The comparisons are conducted in terms of communication cost, storage cost and access delay. The access delay comparison includes all non-implementation factors that result in the access delay. In the comparison, we consider the following parameter settings: (1) N ranges from –; (2) B is set to 1 MB for both schemes; (3) security parameter is set to 80; (4) system parameter k in TSKT-ORAM is set to 128. Table 2 shows the communication and computation costs of these schemes.

Table 2.
Practical comparisons (, MB). The communication cost in the table is the client-server communication cost per query. The computational cost is the number of XOR operations needed on the server side.
7.2.1. Communication Cost
CNE-ORAM reports a communication cost of more than per query. TSKT-ORAM incurs a lower or comparable communication cost with . Specifically, when , the communication cost of TSKT-ORAM is about per query; when , the cost is less than per query; when , the cost is less than per query.
7.2.2. Computational Cost
Because the bit-wise XOR operations on data blocks are the major contributors of computational cost for both TSKT-ORAM and CNE-ORAM, we here only compare the amount of such operations with both schemes.
In TSKT-ORAM, the server needs to conduct such operations. Due to and , . Therefore, the total number of XOR operations ranges from 4572–9144.
In CNE-ORAM, the XOR operations are determined by the binary tree height and the node size denoted as . is related to the security parameter. From the regression evaluation in the CNE-ORAM work, . Furthermore, the XOR operations need to be performed on half of these blocks. Hence, the total number of such operations is . For fairness, we set security parameter in CNE-ORAM to 80. Then, the total number of operations ranges from 11,200–23,800.
Therefore, we can see that TSKT-ORAM incurs a computational cost less than half of that incurred by CNE-ORAM.
7.2.3. Access Delay Comparison
The access delay for both TSKT-ORAM and CNE-ORAM is mainly contributed by the communication and computation delays.
Suppose the network bandwidth between the client and each of the servers is 10 MB/s and the data block size MB. For each query, CNE-ORAM needs at least four seconds to transfer the data blocks needed, while TSKT-ORAM needs about 2.2~4.6 s.
To estimate the delay caused by computation, the authors of CNE-ORAM [30] measure the delay of an XOR operation to be about one millisecond using a 2012 MacBook Pro with a 2.4-GHz Intel i7 processor. For fairness, we adopt the same hardware to compare the computation delays of both schemes. The delay for TSKT-ORAM is about ~9 s, while the delay for CNE-ORAM ranges from ~ s.
Therefore, we can see that TSKT-ORAM incurs a delay that is less than half of that caused by CNE-ORAM.
Note that, for comparison fairness, we assume the above values of network bandwidth and computational power, which may be very different from the practical settings. Particularly, a client with high-level security concerns could use a much better network service to have much higher communication bandwidth with the servers, and the servers typically have much more powerful computational capacity than a MacBook.
7.2.4. Storage Cost
The storage cost of CNE-ORAM depends on the size of each node on the binary tree and the number of tree nodes, which can be computed as follows:
where L is the tree height, and . Hence, the number of tree nodes is greater than or equal to . Therefore, the storage cost per server in CNE-ORAM is:
Since there are four servers in CNE-ORAM, the storage cost in total is .
As for TSKT-ORAM, each server stores a k-ary tree that can be logically mapped to a binary tree, where each k-ary tree node is equivalent to binary tree nodes. The size of each k-ary tree node is , which means each binary tree node has a size of . The total number of binary tree nodes is . Hence, the storage cost at each server is ; further, since as required for security, the cost is less than . Considering there are two servers required, the total storage cost for TSKT-ORAM is less than .
Therefore, we can see that the storage cost of TSKT-ORAM is only about one fourth of that of CNE-ORAM.
8. Conclusions
This paper proposes a new multi-server ORAM construction named TSKT-ORAM, which organizes the server storage as a k-ary tree with each node acting as a fully-functional XOR-based PIR storage. It also adopts a novel delayed eviction technique to optimize the eviction process. TSKT-ORAM is proven to protect the data access pattern privacy at a failure probability of (N is the number of exported data blocks), when . the communication cost of TSKT-ORAM is only 22–46 data blocks, when N (i.e., the total number of outsourced data blocks) ranges from –. Detailed asymptotic and practical comparisons are conducted to show that TSKT-ORAM achieves better communication, storage and computational efficiency in practical scenarios than the compared state-of-the-art ORAM schemes.
TSKT-ORAM, however, requires each of the two servers to allocate a storage space of 24 N blocks, in order to store only N real data blocks. In the future work, we plan to develop new ORAM constructions that are not only communication-efficient, but also storage-efficient.
Author Contributions
All authors made roughly equal contributions to the design of the schemes and the writing of the paper. J.Z. developed the proofs. J.Z. and Q.M. performed the cost analysis and comparisons.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Islam, M.S.; Kuzu, M.; Kantarcioglu, M.K. Access pattern disclosure on searchable encryption: Ramification, attack and mitigation. In Proceedings of the NDSS Symposium, San Diego, CA, USA, 5–8 February 2012. [Google Scholar]
- Chor, B.; Goldreich, O.; Kushilevitz, E.; Sudan, M. Private information retrieval. In Proceedings of the 36th FOCS 1995, Milwaukee, WI, USA, 23–25 October 1995. [Google Scholar]
- Beimel, A.; Ishai, Y.; Kushilevitz, E.; Raymond, J.F. Breaking the barrier for information-theoretic private information retrieval. In Proceedings of the 43rd FOCS 2002, Vancouver, BC, Canada, 16–19 November 2002. [Google Scholar]
- Chor, B.; Gilboa, N. Computationally private information retrieval. In Proceedings of the Twenty-Ninth Annual ACM Symposium on Theory of Computing, El Paso, TX, USA, 4–6 May 1997. [Google Scholar]
- Gertner, Y.; Ishai, Y.; Kushilevitz, E.; Malkin, T. Protecting data privacy in private information retrieval schemes. In Proceedings of the 30th Annual ACM Symposium on Theory of Computing, Dallas, TX, USA, 24–26 May 1998. [Google Scholar]
- Goldberg, I. Improving the robustness of private information retrieval. In Proceedings of the IEEE Symposium on Security and Privacy, Berkeley, CA, USA, 20–23 May 2007. [Google Scholar]
- Kushilevitz, E.; Ostrovsky, R. Replication is not needed: Single database, computationally-private information retrieval (extended abstract). In Proceedings of the FOCS 1997, Miami, FL, USA, 19–22 October 1997. [Google Scholar]
- Cachin, C.; Micali, S.; Stadler, M. Computationally private information retrieval with polylogarithmic communication. In Proceedings of the Eurocrypt 1999, Prague, Czech Republic, 2–6 May 1999. [Google Scholar]
- Lipmaa, H. An oblivious transfer protocol with log-squared communication. In Proceedings of the ISC 2005, Berlin, Germany, 9–11 June 2005. [Google Scholar]
- Trostle, J.; Parrish, A. Efficient computationally private information retrieval from anonymity or trapdoor groups. In Information Security; Springer: Heidelberg, Germany, 2011; Volume 6531, pp. 114–128. [Google Scholar]
- Hoffstein, J.; Pipher, J.; Silverman, J.H. NTRU: A ring-based public key cryptosystem. In Algorithmic Number Theory; Springer: Heidelberg, Germany, 1998; Volume 1423, pp. 267–288. [Google Scholar]
- Goldreich, O.; Ostrovsky, R. Software protection and simulation on oblivious RAMs. J. ACM 1996, 43, 431–473. [Google Scholar] [CrossRef]
- Goodrich, M.T.; Mitzenmacher, M. Mapreduce parallel cuckoo hashing and oblivious RAM simulations. arXiv, 2010; arXiv:1007.1259. [Google Scholar]
- Goodrich, M.T.; Mitzenmacher, M.; Ohrimenko, O.; Tamassia, R. Privacy-preserving group data access via stateless oblivious RAM simulation. In Proceedings of the SODA 2012, Kyoto, Japan, 17–19 January 2012. [Google Scholar]
- Goodrich, M.T.; Mitzenmacher, M. Privacy-preserving access of outsourced data via oblivious RAM simulation. In Proceedings of the ICALP 2011, Zurich, Switzerland, 4–8 July 2011. [Google Scholar]
- Goodrich, M.T.; Mitzenmacher, M.; Ohrimenko, O.; Tamassia, R. Oblivious RAM simulation with efficient worst-case access overhead. In Proceedings of the CCSW 2011, Chicago, IL, USA, 21 October 2011. [Google Scholar]
- Kushilevitz, E.; Lu, S.; Ostrovsky, R. On the (in)security of hash-based oblivious RAM and a new balancing scheme. In Proceedings of the Twenty-Third Annual ACM-SIAM Symposium on Discrete Algorithms, Kyoto, Japan, 17–19 January 2012. [Google Scholar]
- Pinkas, B.; Reinman, T. Oblivious RAM revisited. In Proceedings of the CRYPTO 2010, Santa Barbara, CA, USA, 15–19 August 2010. [Google Scholar]
- Williams, P.; Sion, R. Building castles out of mud: Practical access pattern privacy and correctness on untrusted storage. In Proceedings of the CCS 2008, Alexandria, VA, USA, 27–31 October 2008. [Google Scholar]
- Williams, P.; Sion, R.; Tomescu, A. PrivateFS: A parallel oblivious file system. In Proceedings of the CCS 2012, Releigh, NC, USA, 16–18 October 2012. [Google Scholar]
- Williams, P.; Sion, R.; Tomescu, A. Single round access privacy on outsourced storage. In Proceedings of the CCS 2012, Releigh, NC, USA, 16–18 October 2012. [Google Scholar]
- Shi, E.; Chan, T.H.H.; Stefanov, E.; Li, M. Oblivious RAM with O((logN)3) worst-case cost. In Proceedings of the ASIACRYPT 2011, Seoul, Korea, 4–8 December 2011. [Google Scholar]
- Stefanov, E.; van Dijk, M.; Shi, E.; Fletcher, C.; Ren, L.; Yu, X.; Devadas, S. Path ORAM: An extremely simple oblivious RAM protocol. In Proceedings of the CCS 2013, Berlin, Germany, 4–8 November 2013. [Google Scholar]
- Stefanov, E.; Shi, E. ObliviStore: High performance oblivious cloud storage. In Proceedings of the IEEE Symposium on Security and Privacy, San Francisco, CA, USA, 19–23 May 2013. [Google Scholar]
- Stefanov, E.; Shi, E.; Song, D. Towards practical oblivious RAM. In Proceedings of the NDSS 2011, San Diego, CA, USA, 6–9 February 2011. [Google Scholar]
- Gentry, C.; Goldman, K.; Halevi, S.; Julta, C.; Raykova, M.; Wichs, D. Optimizing ORAM and using it efficiently for secure computation. In Proceedings of the PETS 2013, Bloomington, IN, USA, 10–23 July 2013. [Google Scholar]
- Stefanov, E.; Shi, E. Multi-Cloud Oblivious Storage. In Proceedings of the CCS 2013, Berlin, Germany, 4–8 November 2013. [Google Scholar]
- Wang, X.; Huang, Y.; Chan, T.H.H.; Shelat, A.; Shi, E. SCORAM: Oblivious RAM for secure computations. In Proceedings of the CCS 2014, Scotsdale, AZ, USA, 3–7 November 2014. [Google Scholar]
- Moataz, T.; Mayberry, T.; Blass, E.O. Constant communication ORAM with small blocksize. In Proceedings of the CCS 2015, Denver, CO, USA, 12–16 October 2015. [Google Scholar]
- Moataz, T.; Blass, E.O.; Mayberry, T. Constant Communication ORAM without Encryption. In IACR Cryptology ePrint Archive; International Association for Cryptologic Research: Rüschlikon, Switzerland, 2015. [Google Scholar]
- Lipmaa, H.; Zhang, B. Two new efficient PIR-writing protocols. In Proceedings of the ACNS 2010, Beijing, China, 22–25 June 2010. [Google Scholar]
- Mayberry, T.; Blass, E.O.; Chan, A.H. Efficient private file retrieval by combining ORAM and PIR. In Proceedings of the NDSS 2014, San Diego, CA, USA, 23–26 February 2014. [Google Scholar]
- Lu, S.; Ostrovsky, R. Distributed Oblivious RAM for Secure Two-Party Computation. In IACR Cryptology ePrint Archive 2011/384; International Association for Cryptologic Research: Rüschlikon, Switzerland, 2011. [Google Scholar]
- Freier, A.; Karlton, P.; Kocher, P. The Secure Sockets Layer (SSL) Protocol Version 3.0; RFC 6101; Internet Engineering Task Force (IETF): Fremont, CA, USA, 2011. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).