Abstract
The expansion of telecommunication technologies touches almost all aspects life that we are living nowadays. Indeed, such technologies have emerged as a fourth essential utility alongside the traditional utilities of electricity, water, and gas. In this context, Cloud Data Center Networks (cloud-DCNs) have been proposed as a promising way to cope with such a high-tech era and with any expected trends in future computing networks. Resources of cloud-DCNs are leased to the interested users in the form of services, such services come in different models that vary between software, platform, and infrastructure. The leasing process of any service model starts with the users (i.e., service tenants). A tenant asks for the service resources, and the cloud-provider allocates the resources with a charge that follows a predefined cost policy. Cloud resources are limited, and those cloud providers have profit objectives to be satisfied. Thus, to comply with the aforementioned promise, the limited resources need to be carefully allocated. Existing allocation proposals in the literature dealt with this problem in varying ways. However, none proposes a win-win allocation model that satisfies both the providers and tenants. This work proposes A Rational Allocation Approach in Cloud Data Center Networks (ARAAC) that efficiently allocates the available cloud resources, in a way that allows for a win-win environment to satisfy both parties: the providers and tenants. To do so, ARAAC deploys the Second Best-Price (SBP) mechanism along with a behavioral-based reputation model. The reputation is built according to the tenants’ utilization history throughout their previous service allocations. The reputation records along with the adoption of the SBP mechanism allows for a locally free-equilibrium approach that allocates the available cloud-DCN resources in an efficient and fair manner. In ARAAC, through an auction scenario, tenants with positive reputation records are awarded by having the required resources allocated at prices that are lower than what they have offered. Compared to other benchmark models, simulation results show that ARAAC can efficiently adapt the behavior of those rational service-tenants to provide for better use of the cloud resources, with an increase in the providers’ profits.
1. Introduction and Problem Statement
The technological era we are living these days in almost all aspects of life necessitates the need of powerful, scalable, highly available, and easily accessible computing environments. In this context, cloud computing has emerged as a promising choice for a computing platform that satisfies the aforementioned requirements, with big savings in cost and power. A clear convergence of such cloud-based computing environments and the advancement in information technologies can be deeply touched in people’s life styles nowadays, especially when it comes to their social aspects and work activities, which tend to be overwhelmed by a completely new smart-space. Moreover, developments in Big-Data and Internet of Things applications have allowed for a huge and smart era in other life aspects, such as economy, health, and education. This implicitly means higher dependencies on the existing communication and computing technologies. Typically, cloud computing environments are hosted in Data Centers (DCs) that interconnect massive amounts of networked computing resources laid in servers to support a huge number of applications. The provisioning process of these kind of applications does not only depend on the computing resources that run the applications, but also on the communication resources offered by the network infrastructures necessary for efficient service delivery [1,2]. This includes both: (1) the communication between the DC components, and (2) the communication between the DC as an entity and its users. Moreover, through high speed network infrastructures, servers of various DCs may get connected together to allow for parallel implementation of cloud-services. Such a combination of networking and cloud computing DC resources is referred to as cloud Data Center Networking (cloud-DCN) [3]. Through this, both network and cloud computing resources are provisioned to the users in the forms of services. Hence, provision of these kinds of networked computing resources may cover both intra- and/or inter-data center networking. However, our study is mainly concerned with the intra-data center networking services.
In cloud-DCNs, network and server resources are allocated to the interested users in the form of services (e.g., Infrastructure as a Service (IaaS)). Such allocation scenarios mainly depend on the users reveals for their service requirements (i.e., network and server resources). However, statistics are showing tremendous increases in the traffic every year. To cope with this, sufficient capacities are required in the cloud-DCN infrastructures. Now, with these expectations for huge growth in the global network traffic, and with the absence of an efficient resource allocation model in such scenarios, entering a resource depletion age is becoming inevitable sooner than ever. Proposals for the auction-based resource allocation in the literature are no longer satisfying, as they do not provide real win-win models that consider the interest of both parties, that is, the cloud-DCN providers and their service-tenants. A few proposals provide for greedy profit maximization that targets either the providers or the tenants, but not both. Moreover, such proposals lack efficient policies that stress the issue of resource utilization, which has a direct impact on resultant profit rates/service price units, and resource availability that greatly affects the users’ satisfaction rates. In summary, proposals in the literature have the following limitations: (1) they do not provide real profit maximization for the cloud-DCN providers, as they lack the proper mechanisms that create forms of competition among the service tenants; (2) they do not provide the real satisfaction requirements of the service tenants, which are represented by both competing price units and guaranteed resource availability; (3) they do not provide efficient mechanisms that encourage resource utilization behaviors, which are proven to be necessary in such environments. To handle this, and to maintain acceptable service levels while allowing for a win-win approach, managers of cloud-DCNs need to adopt new models that guarantee: (1) efficient resource utilization, (2) satisfying profit targets, and (3) the tenants’ quality of service (QoS) requirements.
The authors of [4] proposed an allocation model that attempts to model an auction scenario played by a cloud provider (i.e., the service seller) and a set of tenants (i.e., the service consumers). In this, the allocation process follows a multi-stage uniform price sealed bid approach to allocate the services (i.e., cloud resources) among the bidders. The allocation function is formulated on the basis of the bidders’ resource requests and their offered bid prices. As long as there is enough bandwidth to provide, the model chooses those bidders who offer bid prices higher than a predefined market clearing price. However, to accommodate for more requests, the chosen bidders may not receive the full amount of resources they requested. Instead, the allocation might be for partial amounts only. This is motivated by the claim that such an allocation scenario can maximize the provider’s profit. We believe that the proposal of [4] has the following limitations:
- Allocating the network resources on the basis of the market clearing price may help the cloud-DCN provider avoid losses, however, it can never achieve profit maximization. Indeed, knowing that the offered bid prices will not be considered for the charging issues, bidders will always tend to offer high bid prices simply to win the auction. Then all those who win the auction pay the same price defined by that market clearing price.
- The absence of a competition environment in such an allocation scenario can motivate exaggeration actions. Bidders with no incentives to truthfully reveal their true needs and real resource requirements, may tend to exaggerate their needs and ask for more resources. Living with such huge growth in the global network traffic, exaggerated actions may impose real waste for the available cloud resources.
- Cutting portions from the requested network resources contradicts the tenants’ satisfaction goals. In truth, those bidders who receive only portions of what they have asked for may not be satisfied as this may affect their QoS requirements.
In this work, we propose A Rational Allocation Approach in Cloud data center networks (ARAAC) that provides a different auction scenario to allocate the cloud-services among a set of service tenants. In ARAAC, we chose to adopt the second-best price (SBP) sealed-bid auction. This allows for an environment of competition, through which, the service tenants (i.e., bidders) compete to win the allocation auction through their offered bid prices. In this way, the auction strategy can: (1) maximize the provider’s profit, and (2) enforce an incentive compatible solution. Moreover, to better utilize the providers’ resources and to suppress any waste of the cloud-DCN resources, in ARAAC, we propose injecting an additional factor into the selection process of the candidate service tenants. This new factor that we have called a reputation provides information about the historical behaviour of the tenants in the context of resource utilization history. Hence, those tenants with poor utilization records are excluded from the auction regardless of their offered prices, and those with good records and reasonable price offers stay and get charged with prices less than what they offered in their bids.
Consequently, service tenants will be motivated to ask for no more resources than their real needs, as this would lead to poor utilization rates that create low reputation records in the future, thus depriving them from participating in the coming allocation auctions. In summary, the contribution of ARAAC comes from the following:
- ARAAC provides for strategy-proofness [5] and an incentive-compatible [6] solution that encourages truthful reveals for the required cloud-DCN resources, thus leading to high utilization rates. This comes through the competition environment enforced throughout the SBP [7] and the behavior-based reputation mechanisms.
- ARAAC allows for a fair allocation model that motivates the tenants’ positive behaviour, while it does not affect their required service levels. Fairness comes from the fact that ARRAC allocates the resources to those bidders with positive behavior and competing offered prices.
- ARAAC motivates reasonable bid prices that maximizes the cloud-DCN providers profits while not being a greedy allocation approach [8]. ARAAC chooses the winning bidders not only through their offered bid prices, but according to their usages’ behavior.
The paper is organized as follows: Section 1 briefly placed the proposal in a broad context, highlighted the tackled problem, and clearly showed the proposed contributions in points. Next, Section 2 presents the proposed resource allocation model and ARAAC allocation algorithm. Section 3 presents empirical simulation results. In Section 4, we present the related work. Finally, we conclude the paper in Section 5.
2. ARAAC: A Rational Allocation Approach in Cloud-Service Networks
This section presents our proposed model, the ARAAC, in which we allocate the cloud-DCN services to the service tenants through multi-round sealed-bid auctions. Usually, scenarios of such an interaction among competing parties are modeled as a game in which the players can deterministically choose either to cooperate or not. Accordingly, we model the allocation process as a game with two players: (1) a cloud-DCN provider, and (2) a set of service tenants.
2.1. Definitions and Mathematical Modeling
ARAAC assumes the game players to all be rational in that they always aim to maximize their own profits [9]. In this context, cloud-DCN providers aim to maximize their collected profits from those chosen service-tenants. However, to achieve such high profits, the provider needs to deliver acceptable service levels with competing service prices. In the same way, service-tenants also seek to maximize their profits. This is achieved when the required resources are fully granted, and satisfy their QoS requirements in low price-units.
Accordingly, the objectives of the cloud-DCN providers and the service-tenants are formed by maximizing their utilities, which are defined as follows:
- Definition 1: (Provider’s Utility.) The utility of the cloud-DCN provider in such a game is represented in the charges collected from the cooperative tenants nominated for allocation. In ARAAC, this is calculated as shown in Equation (1), which adds the different charges collected per accepted request i, ∀i∈N:where refers to the requested resource units by bidder i, and is the price-unit chosen by the pricing policy of the cloud-DCN provider. This function is bounded by the following constraints:Behavior-Based Threshold:For each bidder i, an identification reference is used to link i to a database that collects information related to the bidder’s previous history, in regard to its resource utilization behavior throughout a certain time window predefined by the market providers. For bidder i to be listed among the candidates for allocation, its behavior score needs to pass the behavioral threshold value . At each auction round t, the threshold value may be revised by the providers according to the market state. The formulation of this constraint is given by:Leasing Price-unit Threshold:For each bidder i, to be considered for allocation among the set of candidates, its offered price-unit needs to be higher than or at least equal a predefined price-unit threshold . The process of defining such threshold follows the providers’ profit objectives and market state at the allocation period t. With such threshold, ARAAC allows to maintain the providers’ profit objectives and avoids losses. Such constraint is given by:Resource Availability:To control the allocation decision, those bidders who satisfy the aforementioned two constraints are sorted in N according to their offered price-units . After having the bidders sorted, and according to their required resource units , for each bidder i, the provider checks if it has sufficient resource capacities for allocation in accordance to the residual resources after previous allocations. At each auction round t, the cloud-DCN provider defines the portion of the resources available for allocation . Hence, each candidate bidder i needs to pass the following:Those bidders who pass the aforementioned three constraints are stored in the candidate list C, and thus are charged for their granted services according to the pricing policy set by the cloud-DCN providers. In ARAAC, the model chooses the SBP policy to set the charges for its service tenants.
- Definition 2: (Tenants’ Utility.) The utility of the service-tenants (i.e., the bidders) in the allocation game is represented by the gain a tenant can collect from participating in the auction. Being a candidate for allocation, and besides the service granted by the allocation itself, the financial-utility is calculated in Equation (5) below as the difference between the sum of the offered price unit and the charged price for the required service resource units . Intuitively, the objective for each tenant i is to maximize the value of given below:The calculation of the tenants’ utility is also bounded by the constraint discussed next:Partial Allocation is Not Accepted:To ease the presentation of such constraint, we define as a set of entities referred to by where . It is worth to highlighting that allocation in this work is for service instances, and such instances require various types of network and computing resources. This includes resources such as bandwidth, switching capacities, memory space, and CPU cycles. Hence, the allocation of is met only when all the j entities are granted, otherwise the allocation is not considered. Such constraint is described by:
- Definition 3: (Incentive Compatible Approach). The proposal of ARAAC provides an incentive compatible [6] approach that motivates the rational service-tenants to reveal their truthful valuation of the required services (i.e., resource units). Indeed, bids with low price units may be excluded from the auction, as they do not satisfy a predefined price-unit threshold , while others with reasonable offered price units are rewarded by having the required resources allocated, and only pay the next highest price (i.e., the SBP in row). This allows for positive utilities. Moreover, ARAAC also motivates efficient resource utilization. True, bidders with bad utilization behavior records may find themselves deprived of being candidates for allocation in this round and others, regardless of their offered prices units.
- Definition 4: (Individual Rationality [10]). ARAAC can be considered as an approach that provides for rational allocation. Regardless of the offered price-units, it excludes those bidders with low reputation records, and instead, it allows others with potentially lower offered prices for allocation, as they have attained certain levels of reputation. Accordingly, we can clearly state that ARAAC maximizes the providers’ profits while not being greedy. Indeed, among the bids with high offered price units, only those with acceptable reputation records remain; others are excluded regardless of their offered bids.
2.2. ARAAC’s Allocation Algorithm
The theme of a sealed-bid auction allows for a kind of privacy. Indeed, bidders submit their bids in private, and no other bidder has the privilege to know the other bidders’ offers. It is only the cloud-DCN provider who has such a privilege and who is hereby authorized to make the allocation decision. The decision defines who among the bidders win the auction, as well as the corresponding service price-units that differ from what has already been offered in their bids. The auction is held for multiple rounds t, , that are periodically carried out. The durations of such periods are defined according to the offered services and the market requirements.
To start the allocation process, in each round t, the cloud-DCN provider calls the service tenants to submit their requests in a sealed-bid manner. Each bidder is required to reveal: (1) its identification reference (used to link with a reputation database), (2) its required service (i.e., resource units), and (3) its offered price-unit . Having the aforementioned three pieces of information, the model follows the algorithm presented in Table 1 to choose the candidate bidders for allocation.

Table 1.
ARAAC’s Allocation Algorithm.
As described in Table 1, the model receives the bidders’ profiles as an input. In steps 3–7, it sorts the received bids in descending order according to the offered price unit values , and updates the set N accordingly. For those sorted bids, steps 8 to 12 state that the model checks for the bidders’ behavioral record and excludes those who do not satisfy the behavior threshold . Steps 13 to 16 show that the model also excludes those bidders who offer low price units that do not satisfy the threshold . Next, it checks who among the remaining bidders in N fit within the available resource space to be served. Hence, in step 18, the model finds the reference that refers to the last bidder that fits for allocation in round t. Then in step 19, all those who passed the aforementioned check points are stored in a new candidates’ set called C. Finally, all those in C are charged according to the SBP mechanism, through which bidder i pays the cost unit . ARAAC is modeled to charge the last candidate bidder the threshold price unit .
2.3. Benchmark Mechanisms
In ARAAC, the service allocation process is modeled as a game between two parties. One is the cloud-DCN provider, and the other is a set of service tenants. The cloud-DCN provider aims to maximize its collected profits by asking for competing service prices, with acceptable service levels. On the other hand, service tenants also seek to maximize their utilities, but while receiving acceptable service levels. To achieve this, ARAAC proposes a conservative selection algorithm presented in Table 1, that adopts the SBP mechanism along with the behavior-based reputation mechanism. Through such mechanisms, together, ARAAC motivates: (1) truthful revealing of price units (achieved by the SBP’s pricing policy), and (2) high utilization rates for the available resources (achieved by the reputation records). To evaluate the efficiency of our model, we chose to compare ARAAC’s performance with two other models as a benchmark: (1) a model that deploys the SBP mechanism [7] alone to select its set of candidate tenants for allocation, and (2) a model that deploys the Tit-for-Tat strategy [11] along with the SBP mechanism being deployed.
2.3.1. SBP: Second Best Price
To be consistent, we chose to use the same set of tenants’ profiles as was chosen for the ARAAC proposal. Hence, both models deal with the same set of bidders and have the same parameters. However, in the SBP mechanism, the selection algorithm is somehow different. As for that in ARAAC, the model receives the bidders’ profiles and then sorts them according to the offered price unit () values. Having the bids sorted, the model excludes those who have their price unit values that are less than the threshold value . It then checks the for resource availability according to the value. However, it does not perform any checks for the bidder’s resource utilization record, it only seeks those bidders that maximize its current utility . Hence, it expects high profit values but low utilization rates. Being less selective compared with ARAAC, blocking rates may also be lower.
In ARAAC, we believe that profit gains are certainly important, but we also believe that resource utilization in such cloud-DCNs environments is important too. Eventually, those allocation models that do not stress the importance of resource utilization reach a depletion point that forces expensive updates in the cloud-DCN structures. Aside from being very expensive, such updates may require massive changes in the whole network infrastructure. With the absence of an efficient utilization mechanism, it is unlikely that such updates will satisfy the rapidly increasing growth for long. It is more likely that such updates will be frequent sooner than expected.
2.3.2. Tit-for-Tat & Second-Best Price
In this benchmark model, we also chose to use the same set of tenants’ profiles as was chosen for the ARAAC proposal. Hence, both models deal with the same set of bidders and have the same parameters. However, this model is concerned in the tenants’ utilization behavior only (i.e., no price unit threshold). Additionally, the behavior scores are built with a different way compared to those of ARAAC. In this model, the behavioral score is not accumulative; it describes the tenant’s utilization behavior in the last allocation only (i.e., the last allocation won). If i utilized the allocated resources efficiently (e.g., ), then it is considered as a cooperative tenant, otherwise it is non-cooperative. Hence, at allocation round t, only those bids of the cooperative tenants (i.e., having a behavior score ) are considered for allocation, non-cooperative tenants (i.e., having a behavior score ) are not considered, regardless of the price units they offer.
Accordingly, as presented in the allocation algorithm in Table 2, the model performs the same checks as ARAAC for the offered price units and resource availability. However, when it comes to the behavior-based attribute of a tenant i, the model checks only for its behavior in the last allocation it gets, and accordingly decides to whether or not consider its offer.

Table 2.
Tit-for-Tat selection algorithm.
3. Simulation Results
3.1. Service and Tenant Instances
To access the efficiency of the proposed ARAAC service allocation model, we carried out an experimental assessment that simulated the allocation of service instances among a set of competing service tenants throughout a sealed-bid auction scenario. In this, we assumed a pool of 400 different bidders’ profiles representing a wide sample of possible service-tenants. Among them, at each auction round t, the model randomly chose 40 profiles as bidders to compete for a limited space of service-instance resources. As illustrated in Algorithm 1, the bidders’ profiles were described by the bidder’s identification number , the required amount of service resources , and the offered price unit . The allocation was assumed to be periodic; the service instances were allocated for certain predefined periods t that suited the types of the offered services. Accordingly, each allocation period starts with a new auction round that did not hold any allocations from previous rounds. Hence, dependencies between consecutive auctions was not allowed, and all bidders were treated as fresh according to their up-to-date profiles.
3.2. Discussion
This section presents the performance results of the simulated allocation scenarios. Through this, we show the efficiency of our proposal, the ARAAC, by comparing its performance metrics to the two other benchmark mechanisms presented in Section 2.3: the SBP and the Tit-for-Tat [11] mechanisms.
To do so, we choose to study the performance of the aforementioned three proposals in terms of: (1) total profit gains. (2) bandwidth usage rates and (3) blocking ratios. The simulation was developed to randomly choose 40 bids among a pre-generated database that contained 400 bidders’ profiles. As mentioned in Section 2, each bidder’s profile provides a price unit , required service resources , and an identification reference that was used to link to a behavior-based reputation records’ database. Such behavior-based records come in two different streams, the first that shows an average value for the bidder’s accumulative behavior over a certain time window (i.e., ARAAC’s philosophy), and the second that reflects the bidder’s behavior in the previously won allocation round in which the bidder participated (i.e., Tit-for-Tat’s philosophy). The behavior describes the bidder’s utilization of its allocated resources in the previous allocation rounds; on the basis of this, the bidder is tagged as a cooperative or non-cooperative player. Being cooperative or not is determined after monitoring the bidder’s usage of the allocated resources throughout the previous auction round(s). For a given allocation period, the system considered a usage of or more of the allocated resources as cooperative behavior, otherwise it reflected an exaggerated request that led to the wasting of allocated resources and thus this was considered as non-cooperative behavior.
To simulate real-life scenarios, the bidders’ profiles were generated by a function that provides representative profiles to simulate: (1) cooperative bidders with reasonable price units, (2) cooperative bidders but offering low price units, (3) non-cooperative bidders with reasonable price units, and (4) non-cooperative bidders with low price-units. Accordingly, the SBP model that motivates revealing high price-units chose those bidders who offer the highest prices regardless of their behavior. Hence, it was highly expected that profiles 1 and 3 were candidates for allocation in this model. On the other hand, profiles 1 and 2 would more likely suit the Tit-for-Tat model that only targets the bidders’ behavior, no matter was the offered price units. In this context, it is worth noting that deploying the Tit-for-Tat model in such auction scenarios may lead to a deadlock state. Indeed, if we assume the case in which a group of bidders show a non-cooperative behavior at auction round t, this necessarily means no allocation for such bidders in the next round(s). Having such case repeated for a few rounds with other bidders leads to a state in which the majority of the bidders have a non-cooperative behavior record that certainly puts the model in a deadlock state [6]. ARAAC has a different selection criteria, it deploys a hybrid selection algorithm that looks for those bidders who offer reasonable price-units and who have a positive accumulative reputation record. This allows a room for forgiveness. Such selection criteria are expected to choose those who can provide for both: profits gains and resource utilization.
To evaluate these assumptions, Figure 1, Figure 2 and Figure 3 present the performance outcomes when the aforementioned three mechanisms (ARAAC, Tit-for-Tat, and SBP) were deployed in the conducted simulation environment. Figure 1 shows the resource utilization rates of five different auction rounds, t, labeled on the time axis from 1 to 5. Analyzing the figure, we can conclude that the Tit-for-Tat mechanism scored the highest records, while the SBP scored the lowest. This was predictable; indeed, the Tit-for-Tat mechanism is very selective when it comes to the bidders’ behavior in the last won auction round, and it only accepts those bidders with a positive behavioral record. Thus it results in high utilization rates. On the contrary, the SBP does not show any attention to the bidders behavior but for the offered price-units which justifies the low scores it provided. When it comes to ARAAC, the offered price-units and the bidders’ behavior are both important, however, the behavior here is accumulative. Therefore, if compared to the other two mechanism, ARAAC shows an intermediate score at the first few rounds, and with the time, it begins to approach the Tit-for-Tat rates as its behavioral policy prevails and the tenants’ behavior becomes more mature.
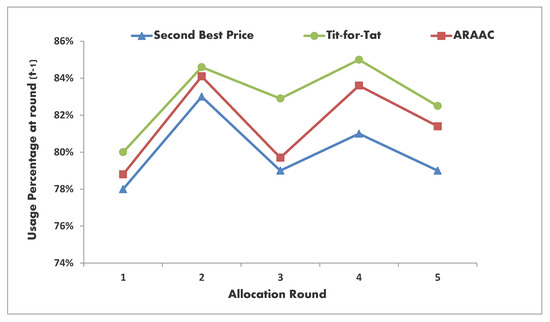
Figure 1.
Bandwidth utilization rates of the simulated allocation mechanisms.
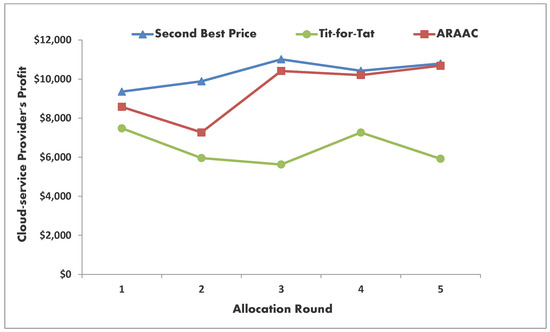
Figure 2.
Profit gains of the simulated allocation mechanisms.
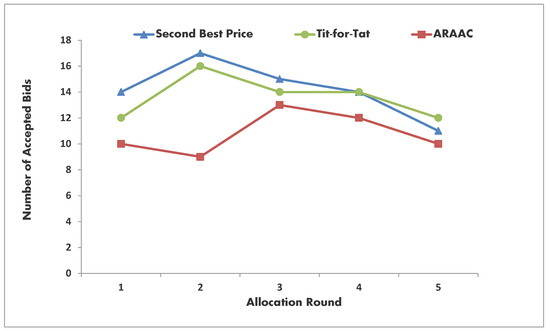
Figure 3.
Acceptance rates of the simulated allocation mechanisms.
In Figure 2, we show the resulting profit values for the cloud-DCN providers at the five auction rounds labeled on the time axis from 1 to 5. Analyzing the figure, we can easily notice that the Tit-for-Tat mechanism earned the lowest profits, while it was clearly higher for the SBP which seeks only the high bid offers. Intuitively, adopting a mechanism that selects the bidders according to their behavioral records regardless of their offered price-units provides no guarantees of profit maximization. In turn, the SBP won the maximum profits in almost all the auction rounds. This is also intuitive, as it seeks for the bids with the highest offered price-units no matter their behavioral records. At the first few rounds, ARAAC earnings were averagely between those of the other two mechanisms. However, at rounds 4 and 5, ARAAC showed close results to those of the SBP. This agrees with our claim that ARAAC provides for an incentive compatible allocation model. Indeed, as the time continued, ARAAC’s behavior-based selection policy prevailed, and thus, it motivated those rational bidders who wanted to win the allocation auctions to adapt their behavior accordingly.
Figure 3 plots the acceptance rates of the three different allocation mechanisms. The results show that ARAAC has the lowest number of highly selected accepted bids. This sheds light on the selectiveness of the proposed allocation criteria. Obtaining such low acceptance ratio, with increasing resource utilization rates that approach those of the Tit-for-Tat mechanism with high profits, puts the ARAAC first when compared to the other two allocation mechanisms. Never the less, it is worth highlighting that for a cloud-service provider, it is much more preferable to serve/manage fewer cooperative numbers of service tenants as long as they provide for high utilization and profit rates.
4. Related Work
Being overwhelmed by the ideas of virtualized networks and cloud computing triggered new directions for networking and computing resource management. Research proposals that tackle such directions in the literature are numerous. In this context, and in regard to the resource allocation problem we discuss the following. In [12], the authors studied the problem of bandwidth resource reservation in cloud networks. In their work, the authors proposed an auction based mechanism to distribute the bandwidth resource. To motivate the users’ revealing the truth about their resource valuation, the proposed auction model deploys the Vickrey-Clarke-Groves (VCG) truth-telling mechanism. According to the amount of required resources, and the effect (i.e., the inconvenience) of this on others, the mechanism calculates additional charge that is added to the bidders’ price offers, together with what to be paid for the required resources. The same mechanism was already proposed by Quttoum et al. in [13] for bandwidth allocation in Virtual Private Networks (VPNs). The mechanism can truly provide a social welfare, economic, and strategy-proof solution. However, deploying the proposal in cloud service allocation problems may get become computationally intractable. Others may claim such a proposal to be greedy, indeed, it only tackles the providers’ profit maximization, giving zero weight to the issues of resource price-units and the tenants’ utilization behavior. The proposal of [14] comes with another payment strategy that calculates the Shapley value [15] incurred by the traffic of each bidder, and accordingly the resource providers decide whether to accept or reject the bid. This is somehow similar to the philosophy of the VCG truth-telling mechanism, however, no charges are added to the bids, as it focusses on comparing the offered bide with the bidder’s Shapley value. If the later is larger, the bid is rejected; otherwise the bid is accepted. Again, such a pricing policy does not provide for profit maximization; it follows the average marginal charge for the allocation decisions. Moreover, the issue of resource utilization behavior was also not addressed in their proposal.
In [4], the authors propose a model that supports both bandwidth reservation (i.e., ahead reservation for resource guarantees) and allocation (i.e., for real time requirements) scenarios. In their work, resources are distributed among the users on the basis of auction scenarios. Firstly, the model runs in the reservation mode; then, what remains from the available pool of resources after reservation decisions are revealed is auctioned again for allocations. In the reservation mode, the model defines a high price unit value called the image pricing value with the goal of maximizing the provider’s profits. In allocation auctions, the selling price-unit is fixed for the same auctioned items, and it is defined according to its market clearing prices. This assumes the offering of fair pricing among all bidders; fairness is always required especially in such scenarios. However, fairness does not originate through charged prices only; in global auction markets, such as eBay and others, the process of resource allocation or even reservation, considers the bidders’ other attributes, such as their feedback records or history alongside their offered prices. In our context, such feedback and historical behavioral records may match the tenants’ willingness to pay and their resource utilization attitudes. Such attributes are of great importance when it comes to environments with limited capacities, such as cloud-DCNs. What is more, the allocation proposal of [4] assumes that as long as there is enough bandwidth to provide, the model chooses those bidders who offer bid prices higher than the predefined market clearing price [16]. However, to accommodate for more requests, those chosen bidders may not receive the full amount of resources they requested. Instead, the allocation is for partial amounts only! This is motivated with the claim that such an allocation scenario can maximize the provider’s profit. Such a proposal may increase the acceptance ratio, but, the customers’ satisfaction will be sharply decreased. Those who are assumed to be winning bidders with partial fulfilments of their requests will not be satisfied. Absolutely, as resources in such cloud scenarios are translated to services, and less resources means ask for a lower level of services. What is more, adopting the market clearing price strategy to define the winning bids is not sufficient at all. Indeed, such a strategy may help us avoid losses; however, it can never achieve profit maximization. Knowing that the offered bid prices will not be considered for the charging issues, bidders will always tend to offer high bid prices simply to win the auction. Then all those who win the auction pay the same price defined by the market clearing price.
We note that none of the aforementioned proposals stress that importance of the network users’ cooperation in utilizing the available cloud-resources efficiently. They all tackle the price issues with no regard to the concept of resource utilization or any other related attribute. Allocation scenarios in such cloud-based environments need to be tackled seriously, and perhaps from a different perspective that gives the utilization issue greater importance. Resources of the cloud-based networks are rich indeed, however, they are not unlimited. The market witnesses a huge migration from the traditional networks and all other sorts of computing applications toward these cloud-based networks. Therefore, to keep the pool of resources rich and ready to host new requests with reasonable costs, allocation methodologies need to be modified. We agree that profit objectives are of high priority, but by no means of higher priority than the resource availability. Scarce resources means less space, more expensive units, and thus fewer tenants and lower profits as a result. A misuse of the cloud-DCN resources can be considered as a threat that requires security-based behavior mechanisms to resist. Indeed, in such a context, security does not always relate to the traditional encryption/decryption algorithms; it extends to cloud data protection [17,18] and resource integrity. These resources are network and computing resources. It is also worth highlighting that none of the aforementioned proposals provide for a win-win strategy; such a strategy allows both parties involved in the resource allocation process to be rewarded. In all of them, it is either the cloud provider or the tenant who is rewarded but not both. Win-win allocation strategies help to enforce cooperation among non-cooperative parties [19,20]. When cooperation prevails, systems leave no incentives for tenants to lie or exaggerate their requirements, and thus incentive-compatible [6] solutions become feasible.
5. Conclusions
Our belief in the importance of resource utilization in cloud-DCNs comes from the impression that the users of such types of networks always seek guarantees that resource availability at their providers’ side is definite. Guaranteeing this, with reasonable price units is enough to provide high satisfaction rates. Indeed, such an environment allows for a peace of mind that motivates rational users to remain systematic (i.e., following the true allocation rules), in a way that keeps their anticipated payoffs untouched. Existing service allocation models may provide for non-negative profits and/or acceptable rates of user satisfaction. In this work, ARAAC provides a win-win proposal that cloud-DCN providers can deploy to gain high profits while delivering high satisfaction rates represented by resource availability along with reasonable price units. This comes form the selection mechanism ARAAC proposes, in which, it uses a behavior-based accumulative database to motivate the service tenants’ cooperative behavior that is interpreted in their truthful resource requirement, and provides incentives for those tenants with high price offers by charging them the second highest price in the row. Truthful resource requirements allows for better resource utilization at the provider’s side, which means availability and reasonable prices. Therefore, the proposal of ARAAC represents an incentive compatible solution that motivates the revealing of the truth for the required service resources and a truthful valuation for the offered price-units. Otherwise, those who choose not to reveal the truth put themselves under the risk of being excluded from the allocation auctions, either because of a low behavioral record or weak non-competitive price offers. Simulation results showed interesting performance records of ARAAC when compared to the Tit-for-Tat and the SBP allocation mechanisms. ARAAC provides superior profit gains to that of the Tit-for-Tat mechanism, close gains to those of the SBP, and moderate resource utilization records that approaches those for the Tit-for-Tat mechanism.
Author Contributions
Ahmad Nahar Quttoum conceived and designed the experiments; Ahmad Nahar Quttoum performed the experiments; Ahmad Nahar Quttoum, Ayoub AlSarhan, and AbidAlrahman Mohammad analyzed the data; Ahmad Nahar Quttoum wrote the paper; Ahmad Nahar Quttoum, Ayoub AlSarhan, and AbidAlrahman Mohammad reviewed and revised the paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Duan, Q. Modeling and Delay Analysis for Converged Network-Cloud Service Provisioning Systems. In Proceedings of the IEEE International Conference on Computing, Networking, and Communications (ICNC’13), San Diego, CA, USA, 28–31 January 2013. [Google Scholar]
- Duan, Q. Cloud Service Performance Evaluation: Status, Challenges, and Opportunities—A Survey from the System Modeling Perspective. J. Digit. Commun. Netw. 2017, 32, 101–111. [Google Scholar] [CrossRef]
- Luong, N.C.; Wang, P.; Niyato, D.; Yonggang, W.; Han, Z. Resource Management in Cloud Networking Using Economic Analysis and Pricing Models: A Survey. IEEE Commun. Surv. Tutor. 2017, 19, 954–1001. [Google Scholar] [CrossRef]
- Wee, K.T.; Dinil, M.D.; Mohan, G. Uniform Price Auction for Allocation of Dynamic Cloud Bandwidth. In Proceedings of the 2014 IEEE International Conference on Communications (ICC), Sydney, NSW, Australia, 10–14 June 2014. [Google Scholar]
- Marian, M.; Yong, M.T. Strategy-Proof Dynamic Resource Pricing of Multiple Resource Types on Federated Clouds. In Algorithms and Architectures for Parallel Processing (ICA3PP) 2010; Hsu, C.H., Yang, L.T., Park, J.H., Yeo, S.S., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 337–350. ISBN 978-3-642-13119-6. [Google Scholar]
- Robert, J.M.; Otrok, H.; Quttoum, A.N.; Boukhris, R. A distributed resource management model for Virtual Private Networks: Tit-for-Tat strategies. J. Comput. Netw. 2012, 56, 927–939. [Google Scholar] [CrossRef]
- Alvin, E.R.; Axel, O. Last-Minute Bidding and the Rules for Ending Second-Price Auctions: Evidence from eBay and Amazon Auctions on the Internet. Am. Econ. Rev. 2002, 92, 1093–1103. [Google Scholar]
- Wee, K.T.; Dinil, M.D.; Mohan, G. Near-Optimal Dynamic Spectrum Allocation in Cellular Networks. In Proceedings of the 3rd IEEE Symposium on New Frontiers in Dynamic Spectrum Access Networks, DySPAN 2008, Chicago, IL, USA, 14–17 October 2008. [Google Scholar]
- Hai-Ya, S.; Wan-Liang, W.; Ngai-Ming, K.; Sheng-Yong, C. Game Theory for Wireless Sensor Networks: A Survey. J. Sens. 2012, 12, 9055–9097. [Google Scholar] [CrossRef]
- Roger, B.M. Game Theory: Analysis of Conflict; Harvard University Press: Cambridge, MA, USA, 1991; ISBN 9780674728615 0674728610. [Google Scholar]
- Robert, M.A. The Evolution of Cooperation: Revised Edition; Basic Books: New York, NY, USA, 2006; ISBN 0-465-02122-0. [Google Scholar]
- Yang, G.; Zhenzhe, Z.; Fan, W.; Xiaofeng, G.; Guihai, C. SOAR: Strategy-proof auction mechanisms for distributed cloud bandwidth reservation. In Proceedings of the 2014 IEEE International Conference on Communication Systems (ICCS), Macau, China, 19–21 November 2014. [Google Scholar]
- Quttoum, A.N.; Otrok, H.; Dzion, Z. ARMM: An Autonomic Resource Management Model for Virtual Private Networks. In Proceedings of the 2010 IEEE International Conference on Consumer Communications and Networking Conference (CCNC), Las Vegas, NV, USA, 12–15 January 2010. [Google Scholar]
- SHI, W.; Wu, C.; Li, Z. A Shapley-value Mechanism for Bandwidth On Demand between Datacenters. IEEE Trans. Cloud Comput. 2015. [Google Scholar] [CrossRef]
- Jinwu, G.; Xiangfeng, Y.; Di, L. Uncertain Shapley value of coalitional game with application to supply chain alliance. J. Sens. 2017, 56, 551–556. [Google Scholar] [CrossRef]
- Ilan, K.; Kjell, G.N. Underpricing and Market Power in Uniform Price Auctions; Oxford Academic: Oxford, UK, 2003; pp. 849–877. [Google Scholar]
- Kabir, M.E.; Mahmood, A.N.; Mustafa, A.K.; Wang, H. Micoraggregation Sorting Framework for K-Anonymity Statistical Disclosure Control in Cloud Computing. IEEE Trans. Cloud Comput. 2015. [Google Scholar] [CrossRef]
- Wang, H.; Yi, H.; Bertino, E.; Sun, L. Protecting Outsourced Data in Cloud Computing Through Access Management. Concurr. Comput. Pract. Exp. 2014, 137–153. [Google Scholar] [CrossRef]
- Jian, G.; Fangming, L.; Dan, Z.; John, C.S.L.; Hai, J. A cooperative game based allocation for sharing data center networks. In Proceedings of the IEEE 2013 INFOCOM Conference, Turin, Italy, 14–19 April 2013. [Google Scholar]
- Jian, G.; Fangming, L.; Haowen, T.; Yingnan, L.; Hai, J.; John, C.; Lui, S. Falloc: Fair network bandwidth allocation in IaaS datacenters via a bargaining game approach. In Proceedings of the 21st Internation IEEE Conference on Network Protocols (ICNP), Goettingen, Germany, 7–10 October 2013. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).