1. Introduction
In cognitive radio networks (CRNs), secondary users (SUs) may access a potentially large number of frequency bands or channels that are not occupied by primary users (PUs) at given time and space. Therefore, the coexistence of PUs and SUs becomes one of the key challenges while accessing the same part of the spectrum [
1]. In an ideal condition, SUs must sense all channels before deciding which channel to access based on accessing strategy. However, in actuality, because of wide-band spectrum and hardware constraints, it is difficult for SUs to sense the entire operating spectrum band (300GHz) in a given period of time. Although compressive sensing is adopted as a wideband spectrum sensing technology for CRNs to solve this problem [
2,
3], little research has been done to implement feasible wide band spectrum sensing, as it is especially difficult to perform compressive sensing when prior knowledge of the primary signals is lacking. In fact, spectrum statistical information as a priori knowledge may not always be securable in a decentralized cognitive radio network. Hence, the blind sub-Nyquist wideband sensing is still an open issue in the field of compressive sensing for CRNs [
4]. Some efforts [
5] have been made to solve this problem. Cognitive compressive sensing has been formulated as a restless multi-armed bandit (rMAB) problem, which makes compressive sensing adaptive and cognitive.
In this paper, we investigate the blind spectrum selection problem for classical narrow-band spectrum sensing technology considering the handoff cost. In a decentralized CRN, prior knowledge of spectrum statistical information maybe not acquirable; in this context, many scholars have developed the multi-armed bandit (MAB) framework for opportunistic spectrum access (OSA) of CRN [
6,
7,
8,
9]. Anandkumar et al. [
8] proposed a distributed algorithm named ρ
PRE policy based on the
-greedy policy [
10]. Gai et al. [
9] proposed a SL(K) subroutine and then established the prioritized access policy (DLP) and fair access policy (DLF) based on SL(K) and a pre-allocation order. Chen et al. [
11] then proposed
kth-UCB1 policy combined the
-greedy and UCB1 policy and evaluated its performance both for real-time applications and best-effort applications. All of them achieve logarithmic regret in the long run.
Due to the spectrum varying nature of CRN, SUs are required to perform proactive spectrum handoffs when the spectrum band is occupied by PUs in the MAB framework, which results in a handoff delay consisting of RF reconfiguration or negotiation between transceiver In the above work [
9,
10,
11], the handoff delay is not taken into consideration in their paper, i.e., the spectrum handoff is assumed to be costless. In this paper, by including a fixed handoff delay, SUs have to make the choice of either staying foregoing spectrum with low availability or handing off to a spectrum with higher availability and tolerating the handoff delay. We formulate this problem and investigate the performance of the above policies, i.e., ρ
PRE, SL(K), and
kth-UCB1. To the best of our knowledge, the influence of the handoff delay on the above policies in the MAB framework has not been investigated yet.
The rest of this paper is organized as follows:
Section 2 describes the system model, which is similar to related works [
9,
12] except that the handoff delay is included as a handoff cost. In
Section 3, we formulate the problem and present the three policies. In
Section 4, we examine the proposed scheme through simulation. Finally, the paper concludes with a summary in
Section 5.
2. System Model
The channel model of a cognitive radio network with
independent and orthogonal channels that are licensed to a primary network following a synchronous slot structure is illustrated in
Figure 1. We model the channel availability
as an i.i.d. Bernoulli process with mean value
:
, in which
denotes the “free”(denoted by 1) or “busy”(denoted by 0) state at time
of channel
. The SUs can access the free slot, which will yield a handoff delay if they access a channel that they did not access in the previous slot.
The cognitive radio network is a composite of secondary users. They access the channels in a decentralized way, i.e., there is no centralized entity collecting channel availability and channel state information (CSI) and then dispatching channels to SUs. In a slot cognitive radio network, a centralized entity will heavily impact the network performance. Regardless, we assume each SU has a pre-allocated rank that is dispatched by the network when the network forming or SU joins the network. For simplicity, we assume the priority of is ranked by , i.e., the priority of is higher than if for either type of application. This rank is prior to learning and transmission processes and will not be changed afterwards.
The SUs behave in a proactive way to access the channels: They record past channel access histories and then utilize them to make predictions on future spectrum availability following a given policy. In addition, because of the inclusion of the handoff delay, SUs have to make the choice of either staying foregoing spectrum with relatively low availability or handing off to a spectrum with higher availability and tolerating the handoff delay. We denote the proportion of the handoff delay to the entire slot as fixed handoff cost for simplicity.
The cognitive radio frame structure is shown in
Figure 2. At the beginning of the frame, an SU chooses a channel to sense. Once the sensing result indicates that the channel is idle, the SU transmits pilot to receiver to probe CSI. The CSI is fed back through a dedicated error-free feedback channel without delay. The length of the data transmission is scalable and will be adopted by a transceiver according to the handoff delay or the data length in this scheme. At the end of the frame, the receiver acknowledges every successful or unsuccessful transmission as
for a collision that occurs; otherwise, it is 1.
3. Problem Formulation and Policies
Blind spectrum selection in decentralized cognitive radio networks can be formulated as a decentralized MAB problem for multiple distributed SUs [
8,
9,
12,
13,
14], and in this paper the terms “channel” and “arm” are used interchangeably. Denote
as the decentralized policy for SU
and
as the set of homogeneous policies of all users. Arm
yields reward
at slot
according to its distribution, whose expectation is
,
. Thus, the sum of the actual reward obtained by all users after
slots following policy
is
where
is defined to be 1 if user
is the only one to play arm
at slot
; otherwise, it is 0.
In the ideal scenario where the availability statistics
are known, the SUs are orthogonally allocated to the
channels, where
is the set of
arms with
largest expected rewards. Then, the expected reward after the
slots is
Then, we can define the performance of the policy
as regret
:
where
is the expectation operator.
We call a policy
uniformly good if for every configuration
, the regret satisfies
Such policies do not allow the total regret to increase rapidly for any
.
This problem is widely studied and several representative policies that are uniformly good are proposed: the distributed ρ
PRE policy [
8], the SL(K) policy [
9], and the
kth-UCB1 policy [
11]. The distributed ρ
PRE policy based on the
-greedy policy, which prescribes to play the highest average reward arm with probability
and a random arm with probability
, and
decreases as the experiment proceeds. However, one parameter of the policy requires prior evaluation of the arm reward means. To avoid this problem, the SL(K) policy is proposed based on the classical UCB1 policy of the MAB problem. Through it guarantees logarithm regret in the long run, it leads to a larger leading constant in the logarithmic order. The
kth-UCB1 policy makes a good tradeoff on both policies.
| Algorithm 1: ρPRE policy for the user with rank . |
//Define: : the number of arm is played after slots. : sample mean availabilities after slots. , where decay rate is prior valuated according to the arm reward means //Init: play each arm once For Play arm and let , EndFor //Main loop For Step1: play the arm of the highest index values in with probability and play a channel uniformly at random with probability Step2: Update , and EndFor
|
| Algorithm 2: SL(K) policy for the user with rank . |
//Define: : the number of arm is played after slots. : sample mean availabilities after slots. // Init: play each arm once For Play arm and let , EndFor // Main loop For Step1: Select the set contains arms with the highest index values:
Step2: Play the arm with the minimal index value in according to
Step3: Update and . EndFor
|
| Algorithm 3: kth-UCB1 policy for the user with rank . |
//Define: : the number of arm is played after slots. : sample mean availabilities after slots. , where decay rate is prior valuated according to the arm reward means // Init: play each arm once For Play arm and let , EndFor // Main loop For Step1: Select the set contains arms with the highest index values.
Step2: with probability play the arm with minimum index value in and with probability play an arm uniformly at random in . Step3: Update , and . EndFor
|
The above policies are derived and investigated in the scenario where there is no expense when the player switches from one arm to another. However, in CRNs, the handoff cost should be taken into consideration as illustrated in
Section 2. Therefore, let
be the sum of handoff cost of all users at slot
, where
is the indicator if user
switches to arm
from other arms. Then, define the handoff regret as
We define the total regret as
Since the inclusion of the handoff delay
,
, and
are correlatively related, it is difficult to make a theoretical analysis of the total regret in a distributed multi-user case, although the authors of [
15] considered this problem in a single-user case. In the next section, we examine the above policies by simulation and discuss their performance.
4. Simulation Results and Analysis
In this section, we present simulation results for the scheme proposed in this work. Simulations are done using Matlab, and we assume
channels with channel availabilities
= [0.5, 0.2, 0.8, 0.6, 0.9, .03, 0.4, 0.1, 0.7] and
SUs. The policy parameter configuration is the decay rate
for the ρ
PRE policy and
for the
kth-UCB1 policy, which is an optimal configuration according to the authors of [
11], and the SL(K) policy is parameterless. The time scope is
. Every experiment is repeated 50 times.
As the regret of one user already takes the collision into consideration, the total regret of a CRN is simply the sum of all users in that CRN. Therefore, we present the regret and actions of one user in CRN where we take SU with the rank
.
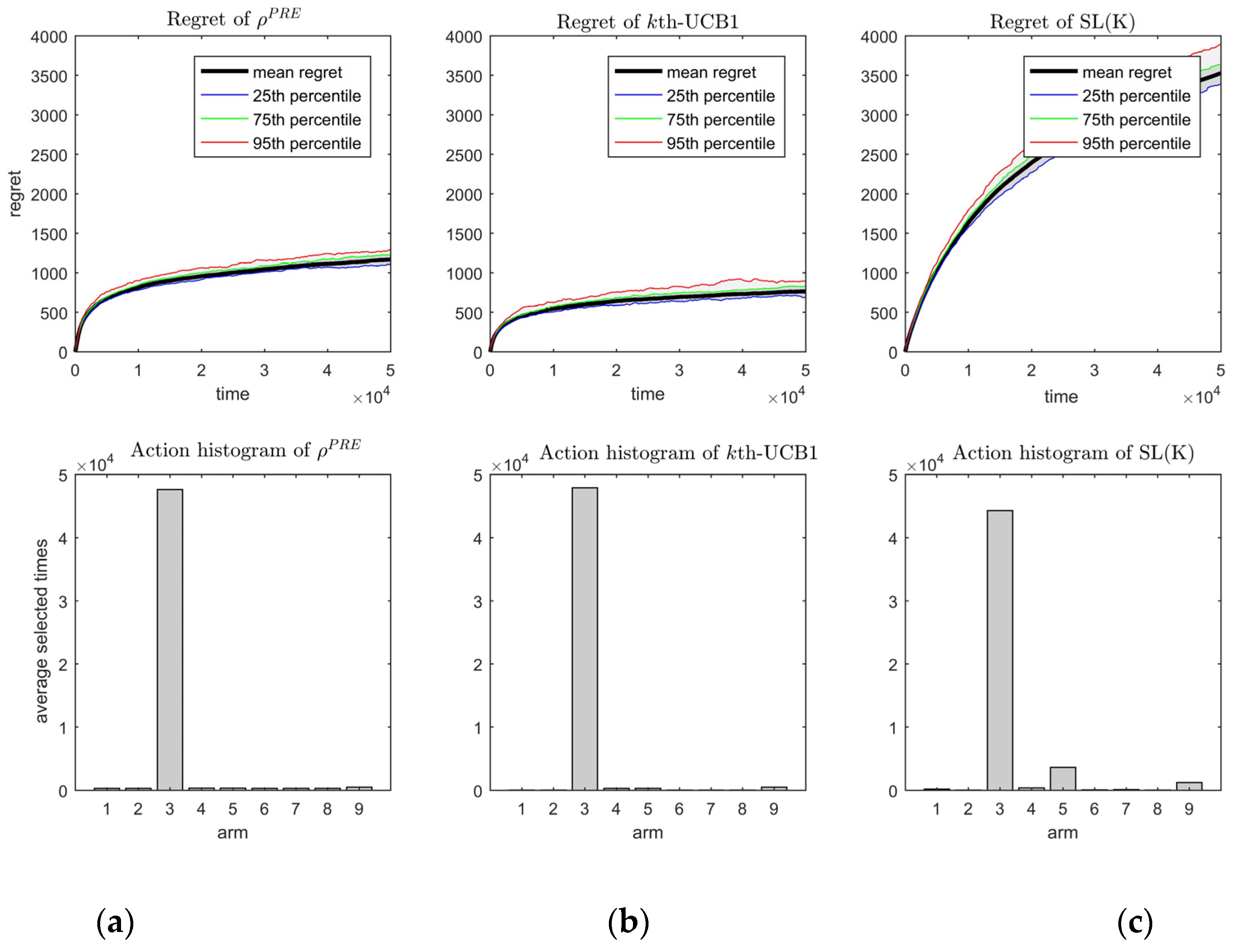
Figure 3 shows the regrets and actions of these policies under fixed handoff cost
.
From
Figure 3, we can see that the three policies all achieve the logarithm regret and the actions converge to the third arm, which is the arm with the second-best channel availability. The regret of policy
kth-UCB1 (
Figure 3b) is smaller than that of policy ρ
PRE (
Figure 3a). This is caused by two aspects. Firstly, the decay rate
in
kth-UCB1 can be smaller than ρ
PRE and does not make the policy diverge. Secondly, the
kth-UCB1 policy can distinguish the order-optimal arm from other arms more precisely than the ρ
PRE policy by comparing the action histogram of
Figure 3a,b, in which the number of arm 9 selected by the
kth-UCB1 policy is smaller than that of policy ρ
PRE. The regret of policy SL(K) in
Figure 3c is largest, which means it has the largest leading constant in the logarithmic order.
We also investigated the regret of the three policies with varying handoff cost
as shown in
Figure 4. As handoff cost is meaningless when the value is larger than 0.5, an
between 0 and 0.5 is chosen. From
Figure 4, we see that the regret increases as
increases. Moreover, the growth rates of the three policies are all small when
, which shows that these policies perform well. However, they become considerably large when
. Intuitively, this is because a large
causes the arms to become indistinguishable.
5. Conclusions
In this work, we studied the blind spectrum selection in a decentralized cognitive radio networks in the MAB framework considering the handoff delay as a fixed handoff cost. We formulate this problem and investigate three representative policies and prove the uniform goodness of these policies for our scenario. Through simulation, we further show that, despite the inclusion of the fixed handoff cost, ρPRE, SL(K), and kth-UCB1 achieve the same asymptotic performance as they do without handoff cost. Through comparison of these three policies, we found that the kth-UCB1 policy has better overall performance.