A Reliability Calculation Method for Web Service Composition Using Fuzzy Reasoning Colored Petri Nets and Its Application on Supercomputing Cloud Platform
Abstract
:1. Introduction
2. Related Work
- We gradually define the concepts of reliability calculation. Based on the definition of formalized description for Web services, we define the semantic threshold similarity and semantic threshold equality for Web services. We first give the definition of FRCPN and the definition of FRCPN activity. Then, we propose the conditions of the activity. We analyze the reliability calculation of some elements in five kinds of production rules in FRCPN. According to the requirements of reliability calculation for FRCPN, we redefine the formalized definition of transition and the formalized definition of Web services.
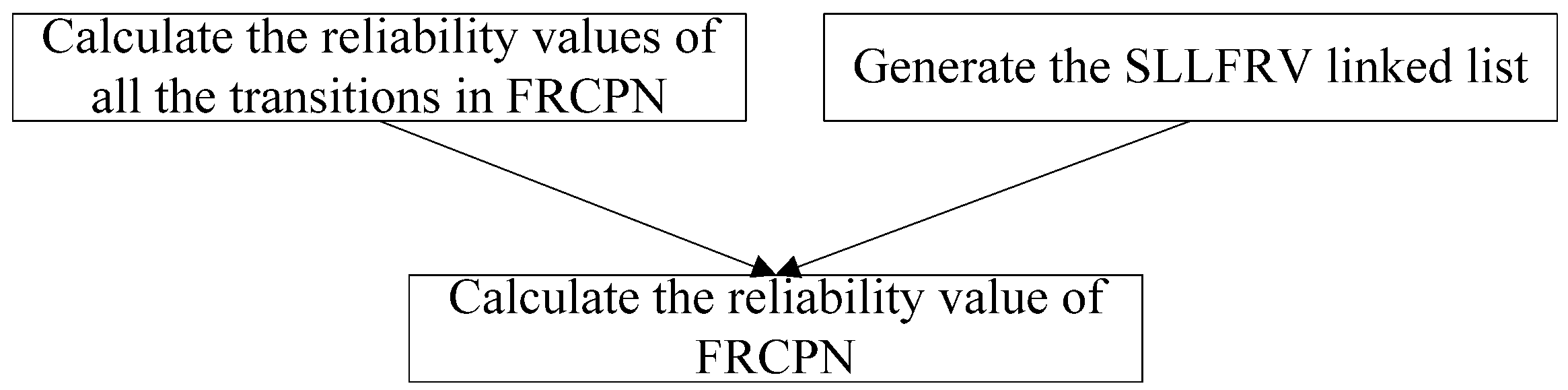
- A reliability calculation method for FRCPN is proposed. Firstly, the method calculates the reliability values of the transitions in FRCPN, and uses an algorithm to generate a Sequential Linked List for Filling Reliability Value (SLLFRV) linked list. According to the SLLFRV linked list, we propose an algorithm to calculate the reliability values of all Web services. Finally, we use the reliability value of the end Web service in FRCPN as the reliability value of FRCPN.
- We apply and analyze the reliability calculation method. The reliability value of a FRCPN graph is calculated as an example. We analyze the execution process of the method. We analyze the implementation effect of the method for different size FRCPNs and obtain some rules. We give the application description for the method in SCP.
3. Related Definition
3.1. Definition of Semantic Threshold Similarity and Definition of Semantic Threshold Equality
3.2. Definition of FRCPN and Definition of FRCPN Activity
- (1)
- represents the place set, and each place represents a Web service.
- (2)
- represents the transition set, and each transition represents the matching relationships among Web services.
- (3)
- F is a dependence relation set, represented as an If-Then form.
- (4)
- is a function of , and the function’s value is in the range of [0,1], which is the triggered threshold of the transition. The function is also the semantic similarity threshold for Web services, and we can control the minimum triggered threshold using the function.
- (5)
- is the precondition set defined on the , which represents all preconditions being satisfied before the transitions are triggered.
- (6)
- is the QoS set defined on the ; it indicates all QoS of the Web services that need to be satisfied before the transitions are triggered.
3.3. Production Rule of FRCPN
3.3.1. The First Production Rule
3.3.2. The Second Production Rule
3.3.3. The Third Production Rule
3.3.4. The Fourth Production Rule
3.3.5. The Fifth Production Rule
- (1)
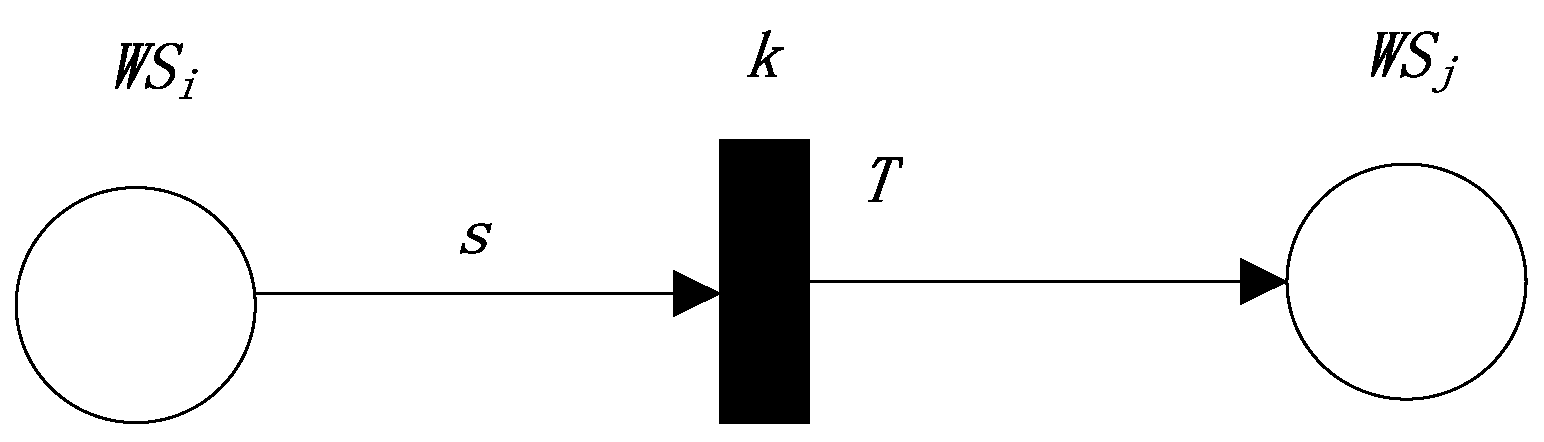
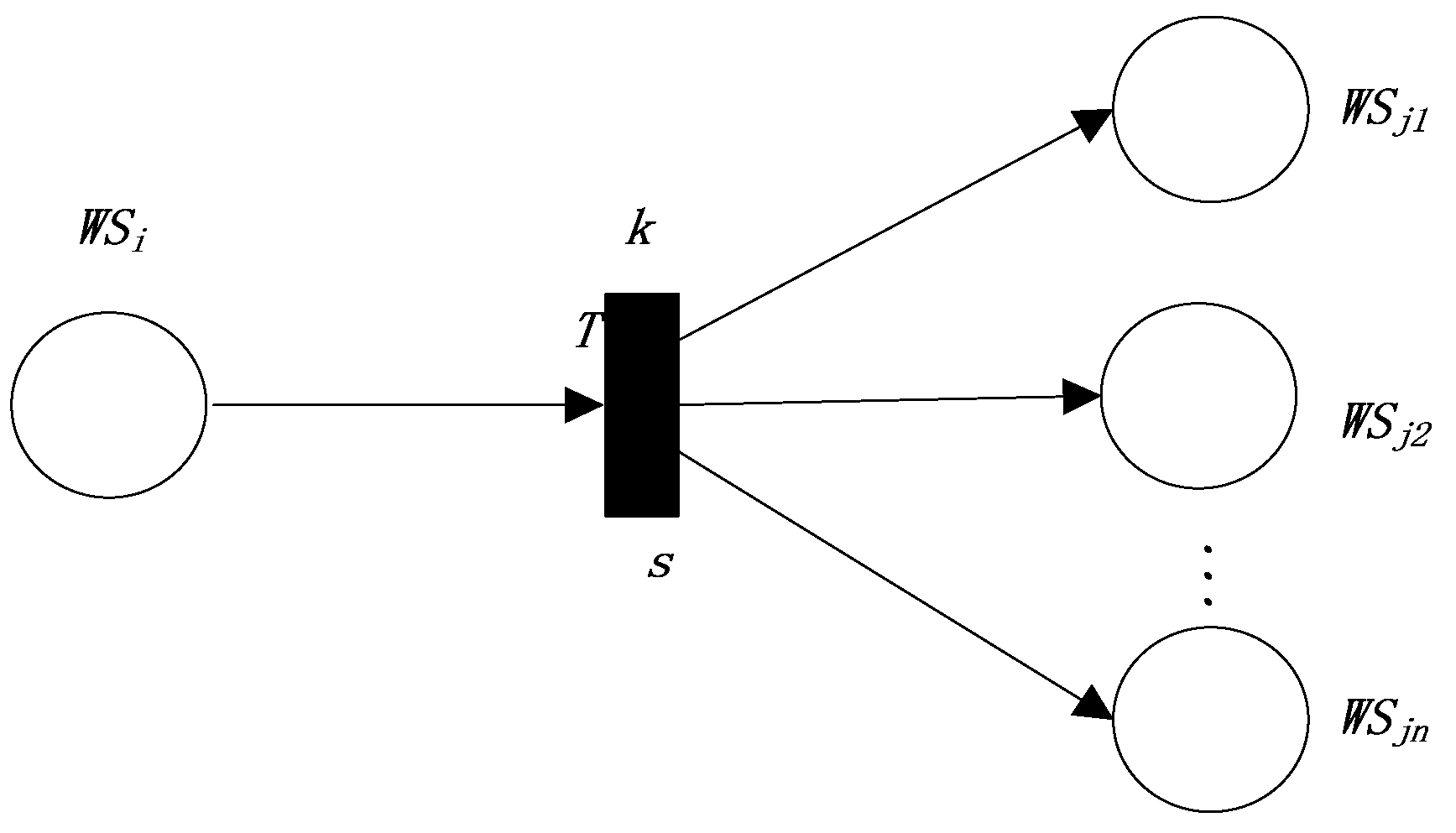
- In the first, fourth, and fifth production rules, the reliability value of the postpositional Web service of the transition equals the product of the reliability of the prepositional Web service of the transition and the reliability value of the transition.
- (2)
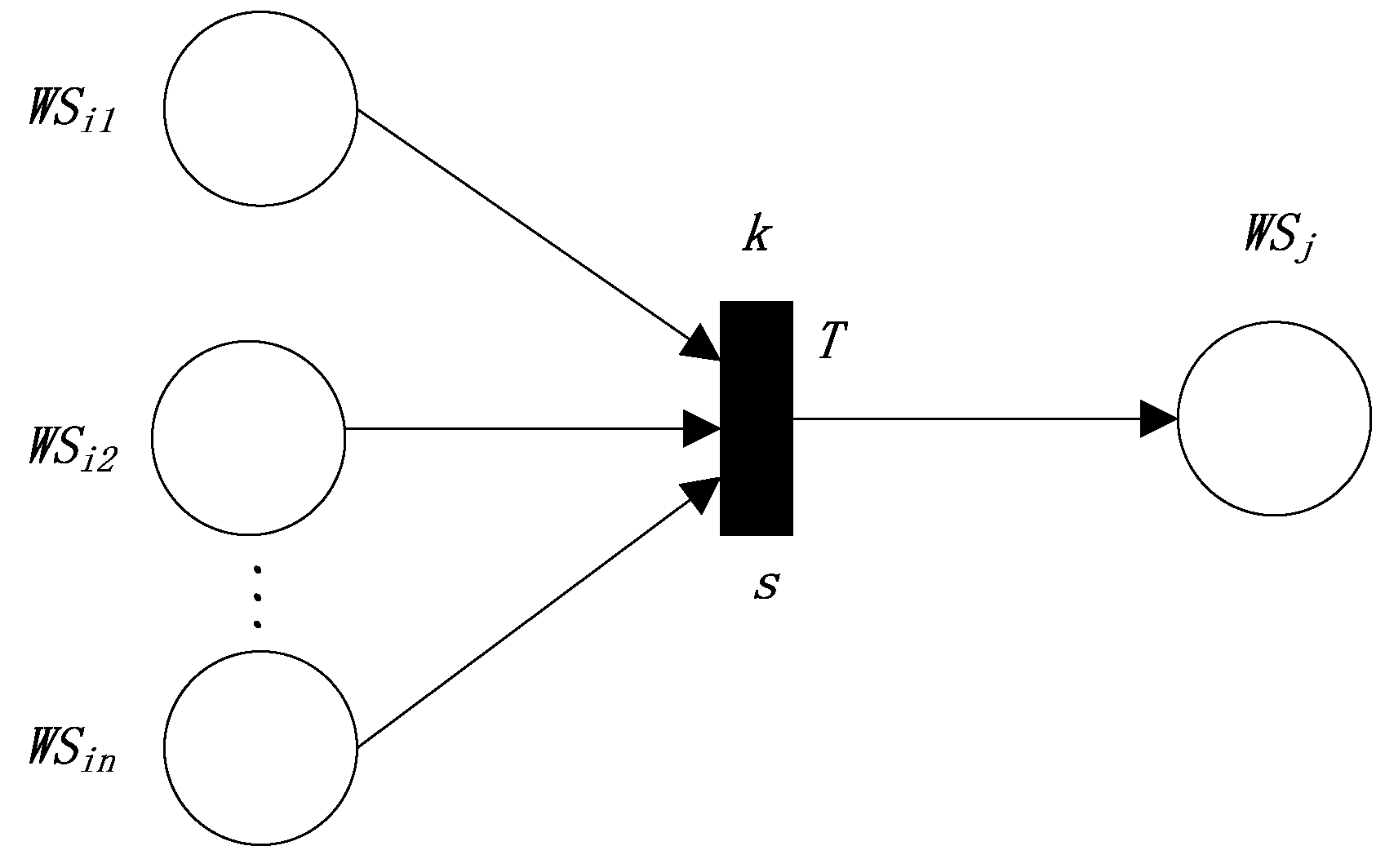
- In the second production rule, the reliability value of the postpositional Web service of the transition equals the minimum reliability value of all the prepositional Web services multiplied by the reliability value of the transition.
- (3)
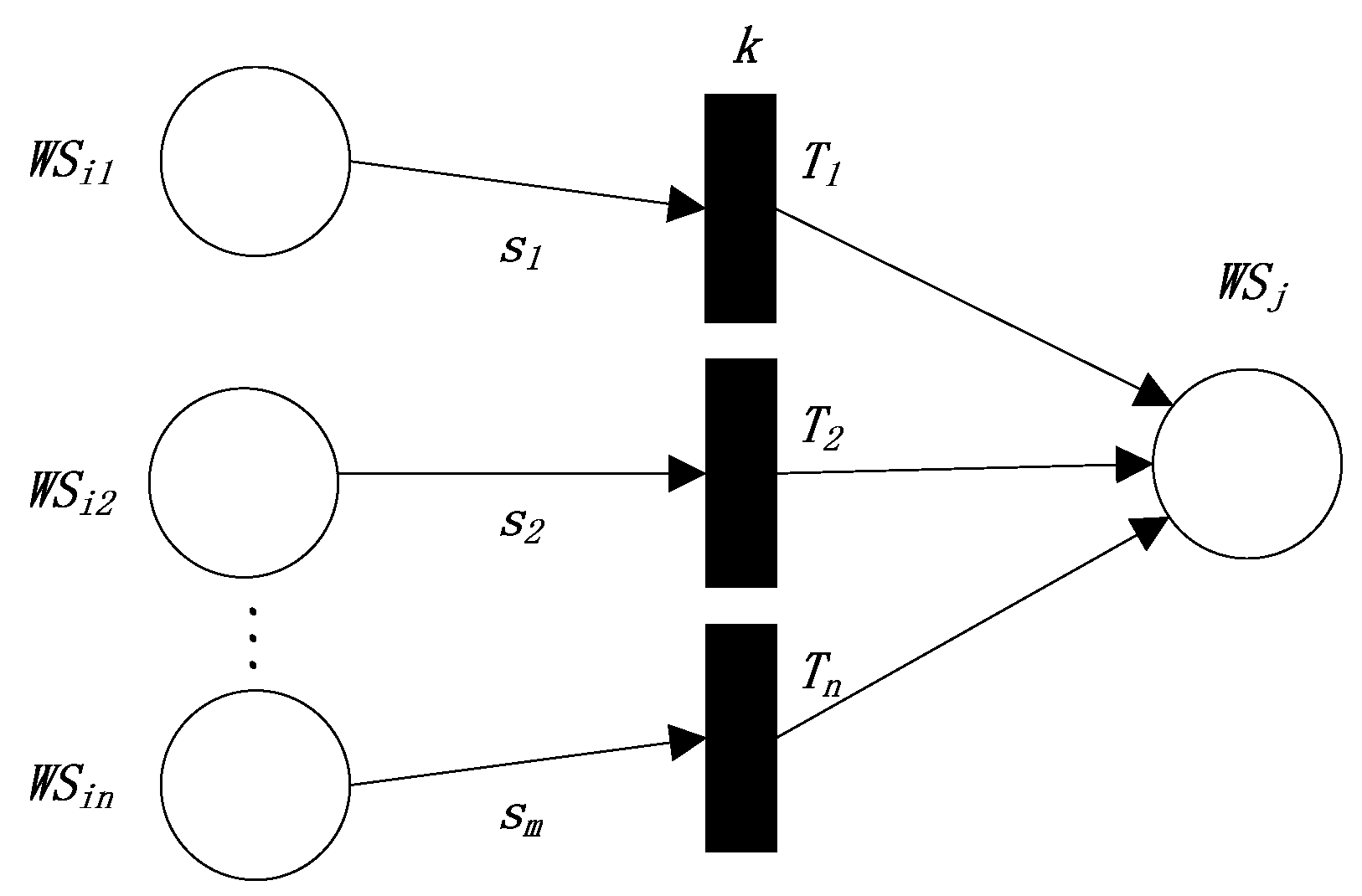
- In the third production rule, the reliability value of the postpositional Web service of the transitions equals the maximum value of the reliability values of the respective prepositional Web services multiplied by the reliability values of the transitions.
- (1)
- WS, Web Service represents a Web service in FRCPN.
- (2)
- IRS, Immediate Reachability Set. For a current Web service WS, if there exists a transition t satisfying some conditions, including and , then we call the immediate reachability Web service of WS. All of the immediate reachability Web services of WS are called an immediate reachability set of WS, denoted as IRS.
- (3)
- PRTS, PRepositional Transition Set. For a current Web service WS, if there exists a transition t satisfying , we call t the prepositional transition of WS. All of the prepositional transitions of WS are called a prepositional transition set of WS, denoted as PRTS.
- (4)
- POTS, POstpositional Transition Set. For a current Web service WS, if there exists a transition t satisfying , we call t the postpositional transition of WS. All of the postpositional transitions of WS are called a postpositional transition set of WS, denoted as POTS.
- (5)
- PIRS, Prepositional Immediate Reachability Set. For a current Web service WS, if there exists a transition t satisfying some conditions, including and , we call the prepositional immediate reachability Web service of WS. All of the prepositional immediate reachability Web services of WS are called a prepositional immediate reachability Web service set, denoted as PIRS.
- (6)
- , the reliability value of the current Web service. Before calculating the reliability value of all Web services in the graph, we set the initial Web service’s reliability to 1, and the reliability value of other Web services to 0.
- (1)
- T, Transition, represents a transition in FRCPN.
- (2)
- PRWSS, PRepositional Web Service Set. For a current transition t, if there exists a Web service WS satisfying , we call WS the prepositional Web service of t. All of the prepositional Web services of t are called the prepositional Web service set of t, denoted as PRWSS.
- (3)
- POWSS, POstpositional Web Service Set. For a current transition t, if there exists a Web service WS satisfying , we call WS s the postpositional Web Service of t. All of the postpositional Web Services of t are called the postpositional Web Service set of t, denoted as POWSS.
- (4)
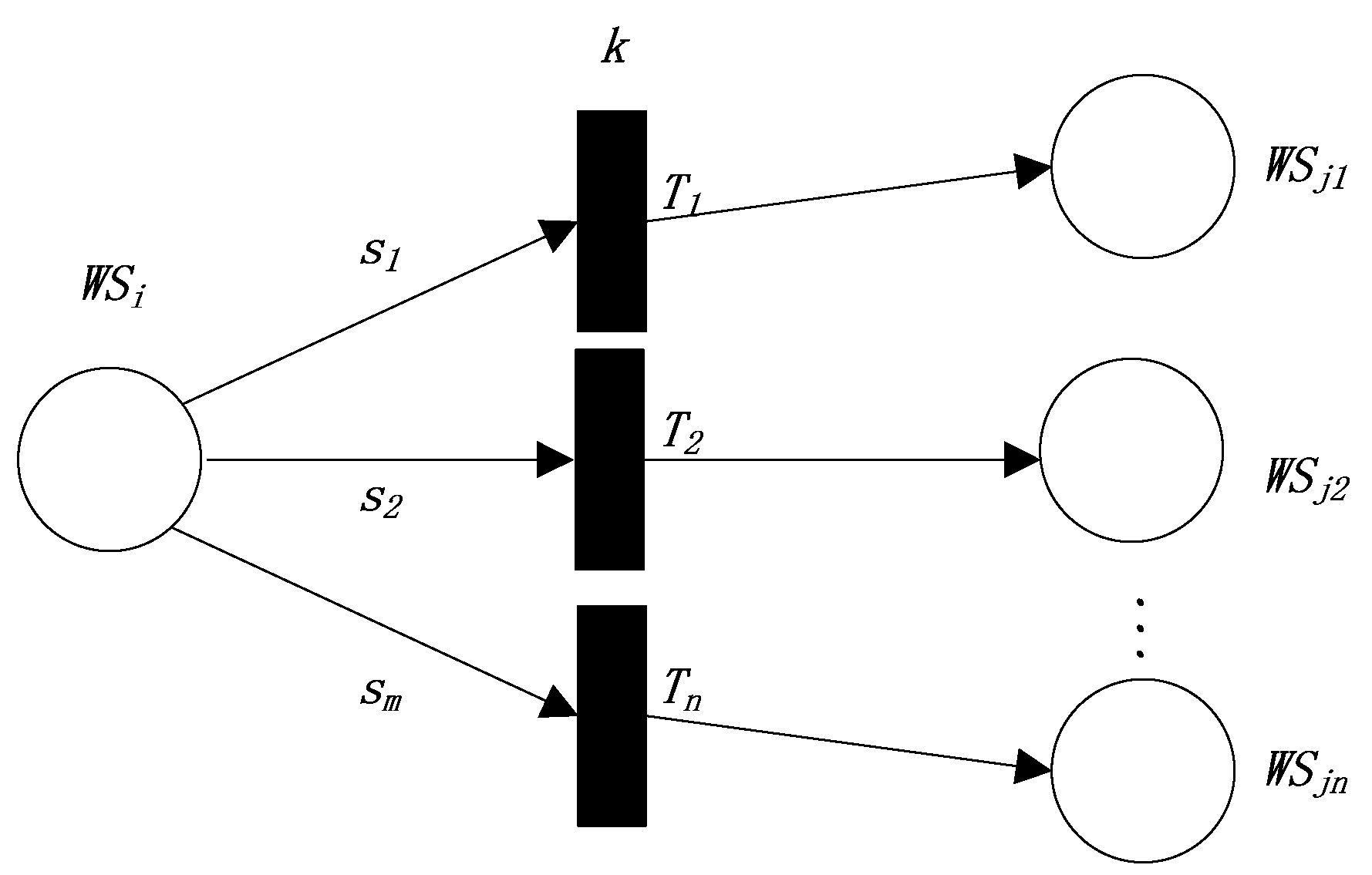
- Type, the type of current transition. There are five types of transition. The first type of transition is shown in Figure 1, the second type of transition is shown in Figure 2, the third type of transition is shown in Figure 3, the fourth type of transition is shown in Figure 4, and the fifth type of transition is shown in Figure 5.
- (5)
- , the reliability value of the current transition.
4. Reliability Calculation Method for FRCPN
4.1. Reliability Calculation Algorithm for All the Transitions in FRCPN
| Algorithm 1 TSet fillTransitionValue(FRCPN frcpn) |
| Algorithm’s name: The reliability calculation algorithm for all the transitions in FRCPN |
| Input parameter: FRCPN graph frcpn |
| Output parameter: TSet, The transition set filled with reliability values in FRCPN |
| //Get the transition set of FRCPN graph frcpn |
| 1 TSet tSet = frcpn.getTransitionSet() |
| //Set successively the reliability values of all the transitions in frcpn using a loop |
| 2 for int k = 0 to |tSet| − 1 step 1 |
| 3 Transition t = tSet.get(k) |
| //Get the type of the transition |
| 4 int type = t.getType() |
| //Set the reliability value of the transition according to the type of the transition |
| //If the type of the transition is the first type, the third type or the fifth type |
| 5 if type = 1 or type = 3 or type = 5 then |
| //The PRWSS has only a Web service |
| 6 WS wsi = t.getPRWSS.get(0) |
| //The POWSS has only a Web service |
| 7 WS wsj = t.getPOWSS.get(0) |
| //Set the reliability value of the transition. In the expression, |
| 8 t.setReliablityValue() |
| 9 end if |
| //If the type of the transition is the second type |
| 10 if type = 2 then |
| //Get the PRWSS of current transition |
| 11 WSSet preWSS = t.getPRWSS() |
| //The POWSS has only a Web service |
| 12 WS wsj = t.getPOWSS.get(0) |
| //Set the reliability value of the transition. In the expression, |
| //|preWSS| = n |
| //The elements in preWSS are represented as preWSS1, preWSS2,…, preWSSn |
| 13 t.setReliablityValue() |
| 14 end if |
| // If the type of the transition is the fourth type |
| 15 if type = 4 then |
| //The PRWSS has only a Web service |
| 16 WS wsi = t.getPRWSS.get(0) |
| //Get the POWSS of current transition |
| 17 WSSet postWSS = t.getPOWSS () |
| // Set the reliability value of the transition. In the expression, |
| //|postWSS| = n |
| //The elements in postWSS are represented as postWSS1, postWSS2,…, postWSSn |
| 18 t.set Reliablity Value() |
| 19 end if |
| 20 end for |
| 21 return tSet |
4.2. Generation Algorithm for SLLFRV Linked List
- (1)
- If the reliability values of some Web services in the PIRS of current Web service are not set, this situation will lead to non-generation of the reliability value for the current Web service.
- (2)
- A transition has several possible postpositional Web Services, and different transitions may have the same postpositional Web Service, so we need to consider the situation for setting the reliability value of Web service many times.
| Algorithm 2 LinkT generateLinkT(FRCPN frcpn, Transition t, LinkT linkT) |
| Algorithm’s name: The generation algorithm for SLLFRV |
| Input parameters: FRCPN graph frcpn, current transition t, SLLFRV linked list linkT. When the algorithm is called first, we set the input parameter t is ∅, and set the input parameter linkT is ∅. |
| Output parameter: the SLLFRV linked list generated |
| //If t is ∅ and linkT is ∅, then it is the first time to call this algorithm |
| 1 if t is ∅ and linkT is ∅ then |
| 2 linkT = newLinkT() |
| //Get starting Web service of frcpn |
| 3 WS ws = frcpn.getStartWebService() |
| //Get the POTS of starting Web service |
| 4 TSet postTSet = ws.getPOTS() |
| 5 for int i = 0 to|postTSet| − 1 step 1 |
| 6 if i = 0 then |
| 7 linkT = postTSet.get(0) |
| 8 linkT.top = postTSet.get(0) |
| 9 linkT.last = postTSet.get(0) |
| 10 else |
| 11 linkT.last.next = postTSet.get(i) |
| 12 linkT.last = postTSet.get(i) |
| 13 end if |
| 14 end for |
| //Continue to iterative generate linkT |
| 15 for int i = 0 to|postTSet| − 1 step 1 |
| 16 generateLinkT(fcpn,postTSet.get(i),linkT) |
| 17 end for |
| 18 else //It is not first time to call generateLinkT() |
| // Generate linkT and return to the superior function |
| 19 if t is ∅ then |
| 20 return linkT |
| 21 end if |
| //Get the POWSS of the current transition |
| 22 WSSet wsSet = t.getPOWSS () |
| 23 for int i = 0 to |wsSet| − 1 step 1 |
| 24 WS ws = wsSet.get(i) |
| //Get the POTS of the current Web service |
| 25 TSet postTSet = ws.getPOTS() |
| //Get the PRTS of the current Web service |
| 26 TSet preTSet = ws.getPRTS() |
| //If PRTS of the current Web service is not in linkT |
| 27 if preTSet not in linkT then |
| 28 break |
| 29 end if |
| //If the current Web service does not have a postpositional transition |
| 30 if postTSet is ∅ then |
| 31 break |
| 32 end if |
| 33 for int j = 0 to |postTSet| − 1 step 1 |
| 34 Transition ct = postTSet.get(j) |
| //Get the union of POWSS of all the transitions in linkT |
| 35 WSSet linkTPreWSSet = |
| //Set the initial value of the judgment flag to false |
| /*The judgment flag indicates whether the PRWSS of the current transition is included in preWSSet*/ |
| 36 boolean flag = false |
| 37 WSSet tPreWSSet = ct.getPRWSS() |
| // If tPreWSSet is a subset of linkTPreWSSet, then set the flag to true |
| 38 if tPreWSSet in linkTPreWSSet then |
| 39 flag = true |
| 40 end if |
| /*If the current transition is not included in linkT, and the judgment flag is |
| true*/ |
| 41 if ct not in linkT and flag is true then |
| 42 linkT.last.next = ct |
| 43 linkT.last = ct |
| 44 end if |
| 45 end for |
| // Continue to iterative generate linkT |
| 46 for int i = 0 to |postTSet| − 1 step 1 |
| 47 generateLinkT(fcpn,postTSet.get(i),linkT) |
| 48 end for |
| 49 end for |
| 50 end if |
| 51 return linkT |
4.3. Reliability Calculation Algorithm for All the Web Services in FRCPN
| Algorithm 3 FRCPN fillWSValue(FRCPN frcpn, LinkT linkT) |
| Algorithm’s name: the reliability calculation algorithm for FRCPN frcpn |
| Input parameters: FRCPN graph frcpn, SLLFRV linked list linkT |
| Output parameter: FRCPN graph frcpn that the graph has generated the reliability values of Web services |
| //According to SLLFRV linkT, generate successively the reliability values of Web services |
| 1 for Transition t = linkT.top to t = null step t = t.next |
| //If the current transition is of the first, fourth, or fifth type |
| 2 if t.getType() = 1 or t.getType() = 4 or t.getType() = 5 then |
| /*Get the reliability value of the prepositional Web service of the current transition*/ |
| 3 float trustValue = t.getPRWSS().get(0).getTrustValue() × t.getTrustValue() |
| //Get the POWSS of the transition t |
| 4 WSSet postWSSet = t. |
| //Set the reliability values of the Web services in POWSS of transition t |
| 5 for int i = 0 to |postWSSet| − 1 step 1 |
| 6 WS ws = postWSSet.get(i) |
| 7 ws.setTrustValue( Max{ ws.getTrustValue, trustValue} ) |
| 8 end for |
| 9 end if |
| //If the current transition is of the second type |
| 10 if t.getType() = 2 then |
| //Get the PRWSS of the current transition |
| 11 WSSet preWSSet = t.getPRWSS() |
| /*The reliability value of the postpositional Web service of the transition equals the minimum value of reliability values of all the prepositional Web services of the transition*/ |
| //|preWSSet| = |
| 12 float trustValue = Min( preWSSet.get(0).getTrustValue(), |
| preWSSet.get(1).getTrustValue(), …,preWSSet.get(n).getTrustValue()) |
| ×t.getTrustValue() |
| //The POWSS of the current transition has only one Web service |
| 13 WS ws = t.getPOWSS.get(0) |
| 14 ws.setTrustValue( Max{ ws.getTrustValue, trustValue} ); |
| 15 end if |
| // If the current transition is of the third type |
| 16 if t.getType() = 3 then |
| //The POWSS of the current transition only has one Web service |
| 17 WS ws = t.getPOWSS().get(0) |
| //Get the PRTS of the current transition |
| 18 TSet tSet = ws.getPRTS() |
| //Get the reliability value of ws, |tSet| = n |
| 19 float trustValue = Max( |
| tSet.get(0).getPRWSS().get(0).getTrustValue()×tSet.get(0).getTrustVale(), |
| tSet.get(1).getPRWSS().get(0).getTrustValue()×tSet.get(1).getTrustVale(), |
| …, |
| tSet.get(n).getPRWSS().get(0).getTrustValue()×tSet.get(n).getTrustVale()); |
| 20 ws.setTrustValue( Max{ ws.getTrustValue, trustValue} ); |
| 21 end if |
| 22 end for |
| 23 return frcpn |
5. An Example of the Application of the Method
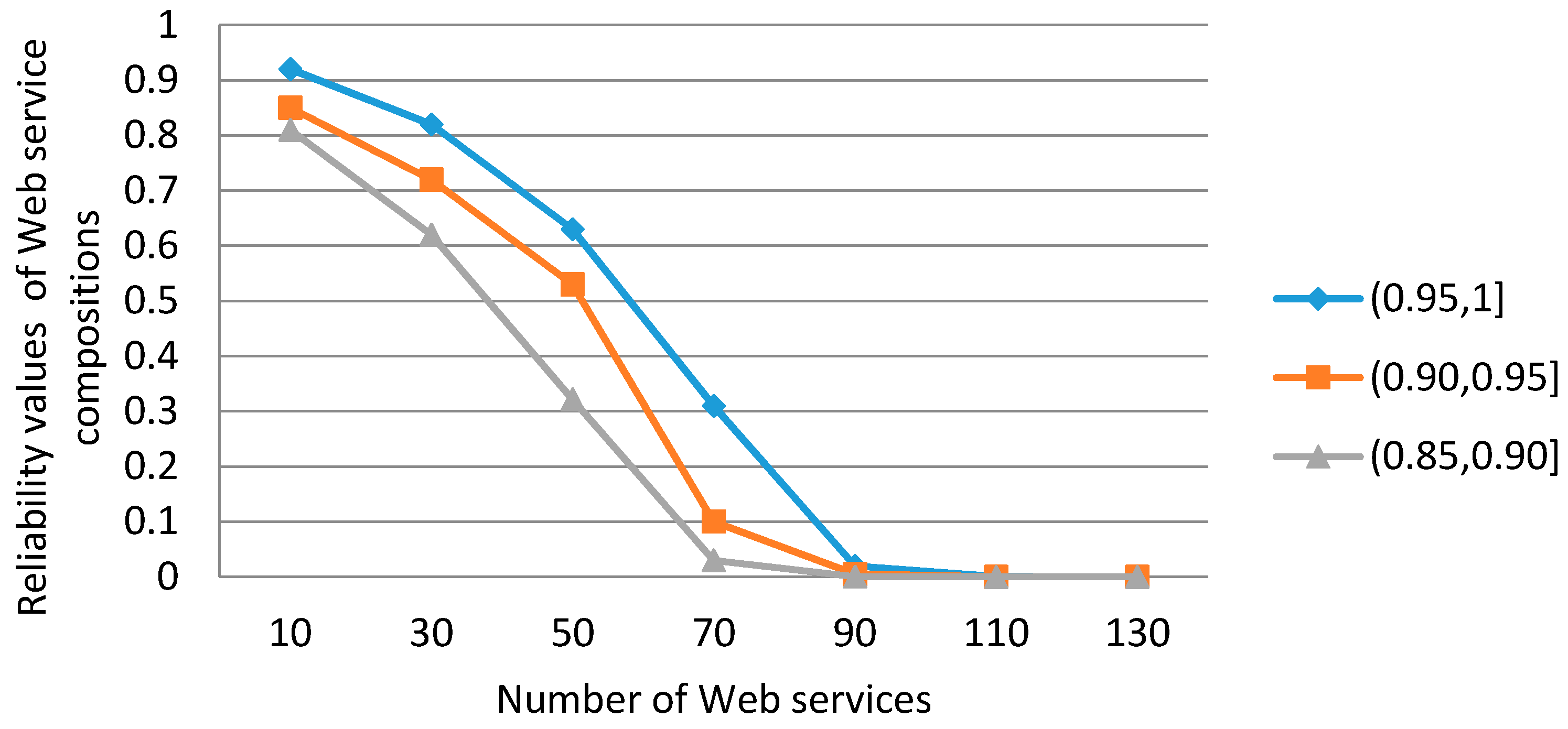
6. Simulated Experiments
- (1)
- Under the same reliability range of transitions, if the number of Web services is greater, then the length of SLLFRV is longer and the reliability values of the Web service compositions are smaller.
- (2)
- Under different reliability ranges of transitions, if the minimum range is smaller, then as the number of Web services increases, the reliability values of the service compositions decrease more rapidly.
- (3)
- We should proper control the scale of Web services in FRCPN. For example, if we set the reliability threshold of Web service compositions as 0.6, then in the reliability range (0.95, 1.0] of transitions, the number of Web services should be controlled below 30 and the length of SLLFRV is below 6.
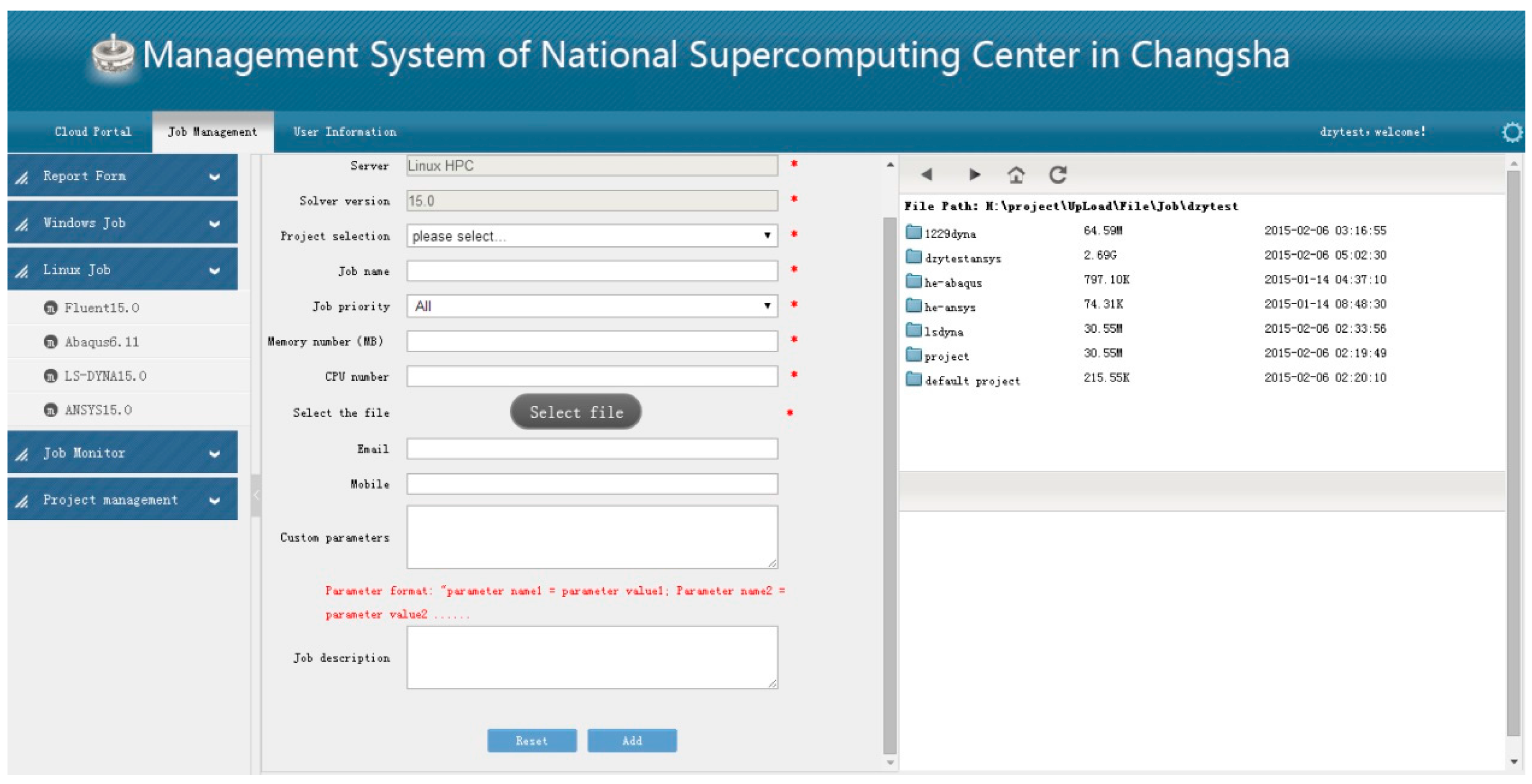
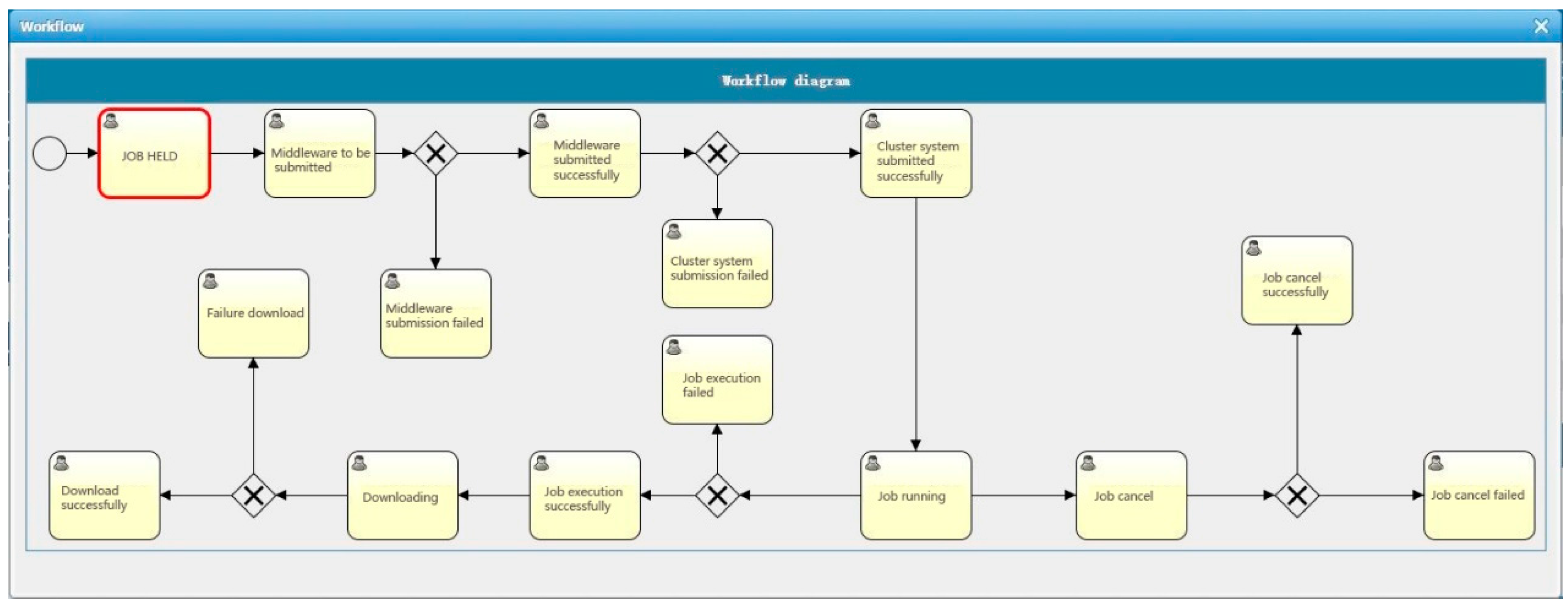
7. Application in SCP
8. Conclusions and Further Work
- (1)
- Study the transaction model of Web service compositions and the exception recovery mechanism of Web service compositions, to facilitate the fallback handling for the jobs in the SCP prototype.
- (2)
- Carry out research into the structural verification algorithm of FRCPN to verify the validity of the structure.
- (3)
- Create a comprehensive summary of existing research works to form the theory and application system behind service compositions in the cloud platform, including modeling, searching, matching, automatic composition, validation, transaction handling, exception handling, etc.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Li, B.; Chai, X.; Zhang, L.; Hou, B.; Lin, T.Y.; Yang, C.; Xiao, Y.; Xing, C.; Zhang, Z.; Zhang, Y.; et al. New advances of the research on cloud simulation. In Advanced Methods, Techniques, and Applications in Modeling and Simulation; Springer: New York, NY, USA, 2014; Volume 4, pp. 1597–1606. [Google Scholar]
- Juan, Y.; Gang, G. Design a new manufacturing model: Cloud manufacturing. In Proceedings of the 2012 International Conference on Cybernetics and Informatics; Springer: New York, NY, USA, 2014; Volume 14, pp. 1597–1606. [Google Scholar]
- Zhang, L.; Luo, Y.; Tao, F.; Li, B.; Ren, L.; Zhang, X.; Guo, H.; Cheng, Y.; Hu, A.; Liu, Y. Cloud manufacturing: A new manufacturing paradigm. Enterp. Inf. Syst. 2014, 8, 167–187. [Google Scholar] [CrossRef]
- Ren, L.; Zhang, L.; Tao, F.; Zhao, C.; Chai, X.; Zhao, X. Cloud manufacturing: From concept to practice. Enterp. Inf. Syst. 2015, 9, 186–209. [Google Scholar] [CrossRef]
- Lu, Y.; Xu, X.; Xu, J. Development of a hybrid manufacturing cloud. J. Manuf. Syst. 2014, 33, 551–566. [Google Scholar] [CrossRef]
- Cho, S.-H. CAE services on cloud computing platform in South Korea. In AsiaSim 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 440–446. [Google Scholar]
- Yu, J.; Cha, J.; Lu, Y.; Xu, W.; Sobolewski, M. A CAE-integrated distributed collaborative design system for finite element analysis of complex product based on SOOA. Adv. Eng. Softw. 2010, 41, 590–603. [Google Scholar] [CrossRef]
- Wahab, O.A.; Bentahar, J.; Otrok, H.; Mourad, A. Towards trustworthy multi-cloud services communities: A trust-based hedonic coalitional game. IEEE Trans. Serv. Comput. 2016. [Google Scholar] [CrossRef]
- Lee, S.; Kim, H.-G.; Jung, H.; Lee, M.; Song, S.; You, B.-J. OntoPipeliner: An ontology-based automatic semantic service pipeline generator. Expert Syst. Appl. 2011, 38, 9472–9482. [Google Scholar] [CrossRef]
- Angelo, F.; Eugenio, Z. Context-aware composition of semantic web services. Mob. Netw. Appl. 2014, 19, 235–248. [Google Scholar]
- Lin, S. Research on Semantic Similarity Computation and Applications. Ph.D. Thesis, Shangdong University, Shangdong, China, October 2009. [Google Scholar]
- Xia, Y.; Liu, Y.; Liu, J.; Zhu, Q. Modeling and performance evaluation of BPEL processes: A stochastic-petri-net-based approach. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2012, 42, 503–510. [Google Scholar] [CrossRef]
- Du, Y.; Li, X.; Xiong, P. A petri net approach to mediation-aided composition of web services. IEEE Trans. Autom. Sci. Eng. 2012, 9, 429–435. [Google Scholar] [CrossRef]
- Du, Y.; Tan, W.; Zhou, M. Timed compatibility analysis of web service composition: A modular approach based on petri nets. IEEE Trans. Autom. Sci. Eng. 2014, 11, 594–606. [Google Scholar] [CrossRef]
- Yu, W.; Yan, C.; Ding, Z.; Jiang, C.; Zhou, M. Modeling and validating e-commerce business process based on petri nets. IEEE Trans. Syst. Man Cybern. Syst. 2014, 44, 327–341. [Google Scholar] [CrossRef]
- Xia, Y.; Luo, X.; Li, J.; Zhu, Q. A petri-net-based approach to reliability determination of ontology-based service compositions. IEEE Trans. Syst. Man Cybern. Syst. 2013, 43, 1240–1247. [Google Scholar]
- Feng, L.; Masanao, O.; Takashi, K.; Kobayashi, K. A learning fuzzy petri net model. IEEE Trans. Electr. Electron. Eng. 2012, 7, 274–282. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, G. A petri net approach to reliable execution for web service composition. In Proceedings of the 2013 9th International Conference on Computational Intelligence and Security (CIS), Sichuan, China, 14–15 December 2013; pp. 105–109.
- Nematzadeh, H.; Motameni, H.; Mohamad, R.; Nematzadeh, Z. QoS Measurement of workflow-based web service compositions using colored petri net. Sci. World J. 2014, 2014, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Vidal, J.C.; Lama, M.; Bugarín, A. Toward the use of petri nets for the formalization of OWL-S choreographies. Knowl. Inf. Syst. 2012, 32, 629–665. [Google Scholar] [CrossRef]
- Zhu, L.; Sun, L. Hierarchical colored petri nets based modeling and analyzing for web service composition. Key Eng. Mater. 2011, 467, 1206–1211. [Google Scholar] [CrossRef]
- Li, B.; Ji, S.; Qiu, D.; Cai, J. Generating test cases of composite services based on owl-s and eh-cpn. Int. J. Softw. Eng. Knowl. Eng. 2010, 20, 921–941. [Google Scholar] [CrossRef]
- Xia, Y.; Zhang, X.; Luo, X.; Zhu, Q. Modelling of ontology-based service compositions using petri net. Elektron. Elektrotech. 2013, 19, 75–78. [Google Scholar] [CrossRef]
- Xia, Y.; Wan, N.; Dai, G.; Luo, X.; Sun, T. A non-markovian stochastic petri net-based approach to performance evaluation of ontology-based service composition. Concurr. Comput. Pract. Exp. 2012, 24, 2255–2267. [Google Scholar] [CrossRef]
- Wahab, O.A.; Bentahar, J.; Otrok, H.; Mourad, A. A survey on trust and reputation models for Web services: Single, composite, and communities. Decis. Support Syst. 2015, 74, 121–134. [Google Scholar] [CrossRef]
- Hang, C.-W.; Kalia, A.K.; Singh, M.P. Behind the curtain: Service selection via trust in composite services. In Proceedings of the 2012 IEEE 19th International Conference on Web Services (ICWS), Honolulu, HI, USA, 24–29 June 2012; pp. 9–16.
- Stantchev, V. Effects of Replication on Web Service Performance in WebSphere; International Computer Science Institute: Berkeley, CA, USA, 2008. [Google Scholar]
- Stantchev, V.; Malek, M. Translucent replication for service level assurance. In High Assurance Services Computing; Springer: New York, NY, USA, 2009; pp. 1–18. [Google Scholar]
- Werner, M.; Richling, J.; Milanovic, N.; Stantchev, V. Composability concept for dependable embedded systems. In Proceedings of the International Workshop on Dependable Embedded Systems at the 22nd Symposium on Reliable Distributed Systems (SRDS 2003), Florence, Italy, 5 October 2003; pp. 20–25.
- Haddad, J.E.I.; Manouvrier, M.; Rukoz, M. TQoS: Transactional and QoS-aware selection algorithm for automatic web service composition. IEEE Trans. Serv. Comput. 2010, 3, 73–85. [Google Scholar] [CrossRef]
- Fan, G.; Yu, H.; Chen, L.; Liu, D. Petri net based techniques for constructing reliable service composition. J. Syst. Softw. 2013, 86, 1089–1106. [Google Scholar] [CrossRef]
- Kim, Y.; Choi, J.-S.; Shin, Y. Trustworthy service discovery for dynamic web service composition. KSII Trans. Internet Inf. Syst. 2015, 9, 1260–1281. [Google Scholar]
- Silic, M.; Delac, G.; Srbljic, S. Prediction of atomic web services reliability for QoS-aware recommendation. IEEE Trans. Serv. Comput. 2015, 8, 425–438. [Google Scholar] [CrossRef]
- Xu, J.; Yao, S. Reliability of SOA systems using SPN and GA. In Proceedings of the IEEE 10th World Congress on Services, Anchorage, AK, USA, 27 June–2 July 2014; pp. 370–377.
- Garg, H. Reliability analysis of repairable systems using petri nets and vague Lambda—Tau methodology. ISA Trans. 2013, 52, 6–18. [Google Scholar] [CrossRef] [PubMed]
- Gan, M.; Wang, S.; Zhou, M.; Li, J.; Li, Y. A survey of reachability trees of unbounded petri nets. Acta Autom. Sin. 2015, 41, 686–693. [Google Scholar]
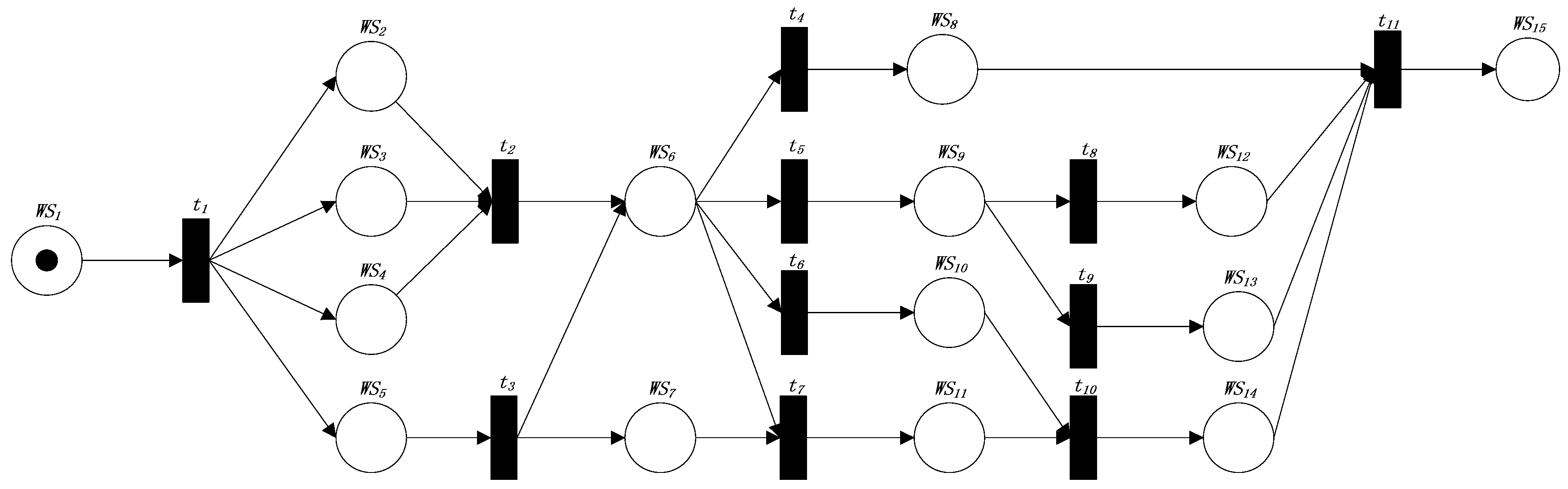
| Web Services’ Name | IRS (Immediate Reachability Set) | PRTS (PRepositional Transition Set) | POTS (POstpositional Transition Set) | PIRS (Prepositional Immediate Reachability Set) |
|---|---|---|---|---|
| WS1 | {WS2, WS3, WS4, WS5} | ∅ | {t1} | ∅ |
| WS2 | {WS6} | {t1} | {t2} | {WS1} |
| WS3 | {WS6} | {t1} | {t2} | {WS1} |
| WS4 | {WS6} | {t1} | {t2} | {WS1} |
| WS5 | {WS6, WS7} | {t1} | {t3} | {WS1} |
| WS6 | {WS4, WS5, WS6, WS7} | {t2,t3} | {t4,t5,t6,t7} | {WS2,WS3,WS4,WS5} |
| WS7 | {WS11} | {t3} | {t7} | {WS5} |
| WS8 | {WS15} | {t4} | {t11} | {WS6} |
| WS9 | {WS12, WS13} | {t5} | {t8,t9} | {WS6} |
| WS10 | {WS14} | {t6} | {t10} | {WS6} |
| WS11 | {WS14} | {t7} | {t10} | {WS6,WS7} |
| WS12 | {WS15} | {t8} | {t11} | {WS9} |
| WS13 | {WS15} | {t9} | {t11} | {WS9} |
| WS14 | {WS15} | {t10} | {t11} | {WS10,WS11} |
| WS15 | {t11} | {WS8,WS12,WS13,WS14} |
| Transition’s Name | Known Similarity | PRWSS | POWSS | Type |
|---|---|---|---|---|
| t1 | {WS1} | {WS2,WS3,WS4,WS5} | fourth | |
| t2 | {WS2,WS3,WS4} | {WS6} | second | |
| t3 | {WS5} | {WS6,WS7} | fourth | |
| t4 | {WS6} | {WS8} | fifth | |
| t5 | {WS6} | {WS9} | fifth | |
| t6 | {WS6} | {WS10} | fifth | |
| t7 | {WS6,WS7} | {WS11} | second | |
| t8 | {WS9} | {WS12} | fifth | |
| t9 | {WS9} | {WS13} | fifth | |
| t10 | {WS10,WS11} | {WS14} | second | |
| t11 | {WS8,WS12,WS13,WS14} | {WS15} | second |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, Z.; Chen, L.; He, T.; Meng, T. A Reliability Calculation Method for Web Service Composition Using Fuzzy Reasoning Colored Petri Nets and Its Application on Supercomputing Cloud Platform. Future Internet 2016, 8, 47. https://doi.org/10.3390/fi8040047
Deng Z, Chen L, He T, Meng T. A Reliability Calculation Method for Web Service Composition Using Fuzzy Reasoning Colored Petri Nets and Its Application on Supercomputing Cloud Platform. Future Internet. 2016; 8(4):47. https://doi.org/10.3390/fi8040047
Chicago/Turabian StyleDeng, Ziyun, Lei Chen, Tingqing He, and Tao Meng. 2016. "A Reliability Calculation Method for Web Service Composition Using Fuzzy Reasoning Colored Petri Nets and Its Application on Supercomputing Cloud Platform" Future Internet 8, no. 4: 47. https://doi.org/10.3390/fi8040047
APA StyleDeng, Z., Chen, L., He, T., & Meng, T. (2016). A Reliability Calculation Method for Web Service Composition Using Fuzzy Reasoning Colored Petri Nets and Its Application on Supercomputing Cloud Platform. Future Internet, 8(4), 47. https://doi.org/10.3390/fi8040047





