A Novel QoS Provisioning Algorithm for Optimal Multicast Routing in WMNs
Abstract
:1. Introduction
- We present a model for the MCOMR problem from the approximate perspective. This model allows multiple QoS metrics to be considered in WMNs with guaranteed multicast service performance.
- We formulate the problem of the MCOMR problem and develop a novel multicast heuristic approximation (NMHA) algorithm based on the technique of auxiliary graph construction, scaling, rounding and the MPH algorithm to solve the problem.
- We analyze the theoretical properties of the proposed algorithm. Analytical results show that our algorithm is effective and achieves lower complexity and the approximate optimal solution for WMNs.
- We conduct experiments to evaluate the performance of the proposed algorithm and compare the algorithm against variations of current best known algorithms. Obtained numerical results indicate that the proposed algorithm is efficient and accurate for multicast service in WMNs.
2. Preliminaries
2.1. Problem Formulation
2.2. Deterministic Algorithm with Auxiliary Graph
2.3. Description of MPH Algorithm
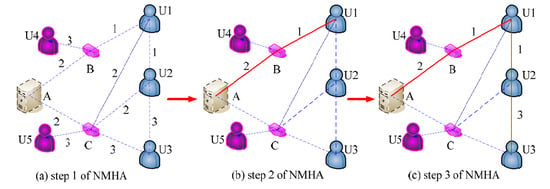
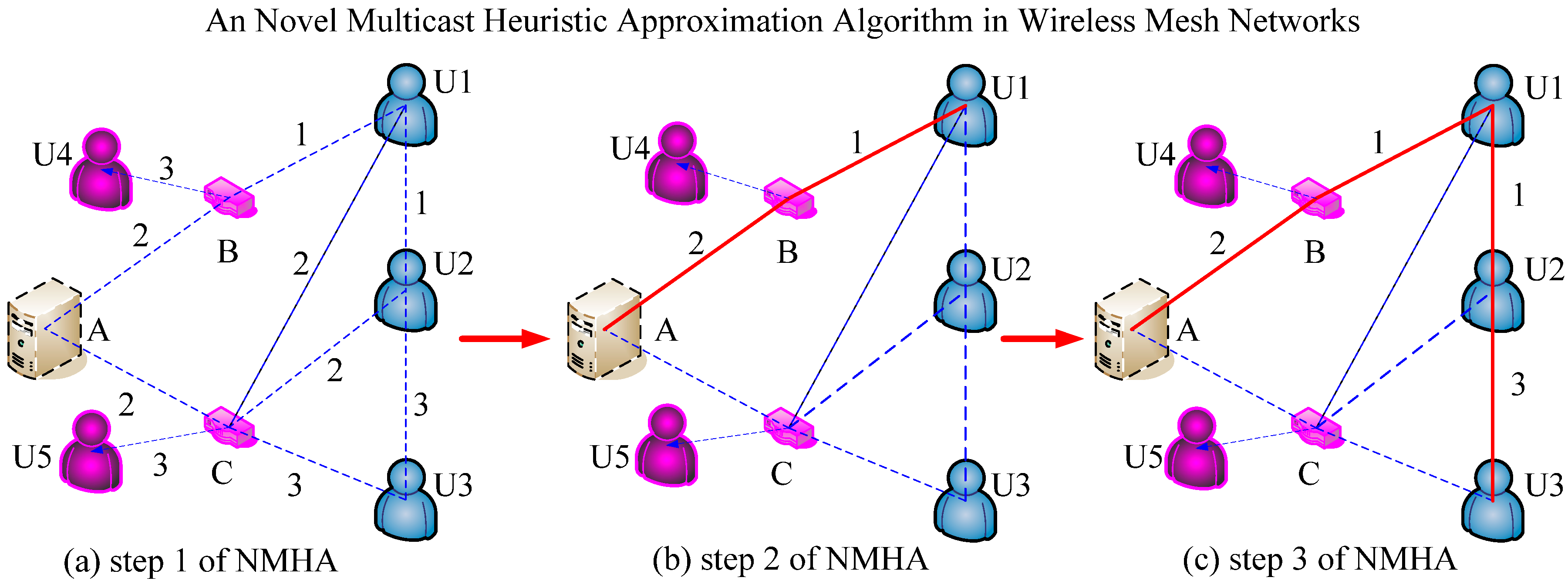
3. The Proposed NMHA Algorithm
3.1. Description of NMHA Algorithm
3.2. The Procedure of the NMHA Alogorithm
| Algorithm 1 NMHA algorithm |
| Input: , the source node s and the set of destination nodes D, and the approximation ratio Output: 1. For each in 2. ; 3. set ; 4. end for 5. ; 6. Choose any node from the set D of multicast destination nodes, initialize generating tree , ; 7. for every node and to , , do 8. ; ; 9. end for 10. for do 11. for every adjacent node of node , where and do 12. if where 13. then 14. ; 15. node and edge ; 16. end if 17. end for 18. ; 19. end for 20. if 21. then return. No feasible multicast routing tree, exit; 22. else, ; ; 23. end if 24. end for 25. OUTPUT ; |
3.3. Analysis of the NMHA Algorithm
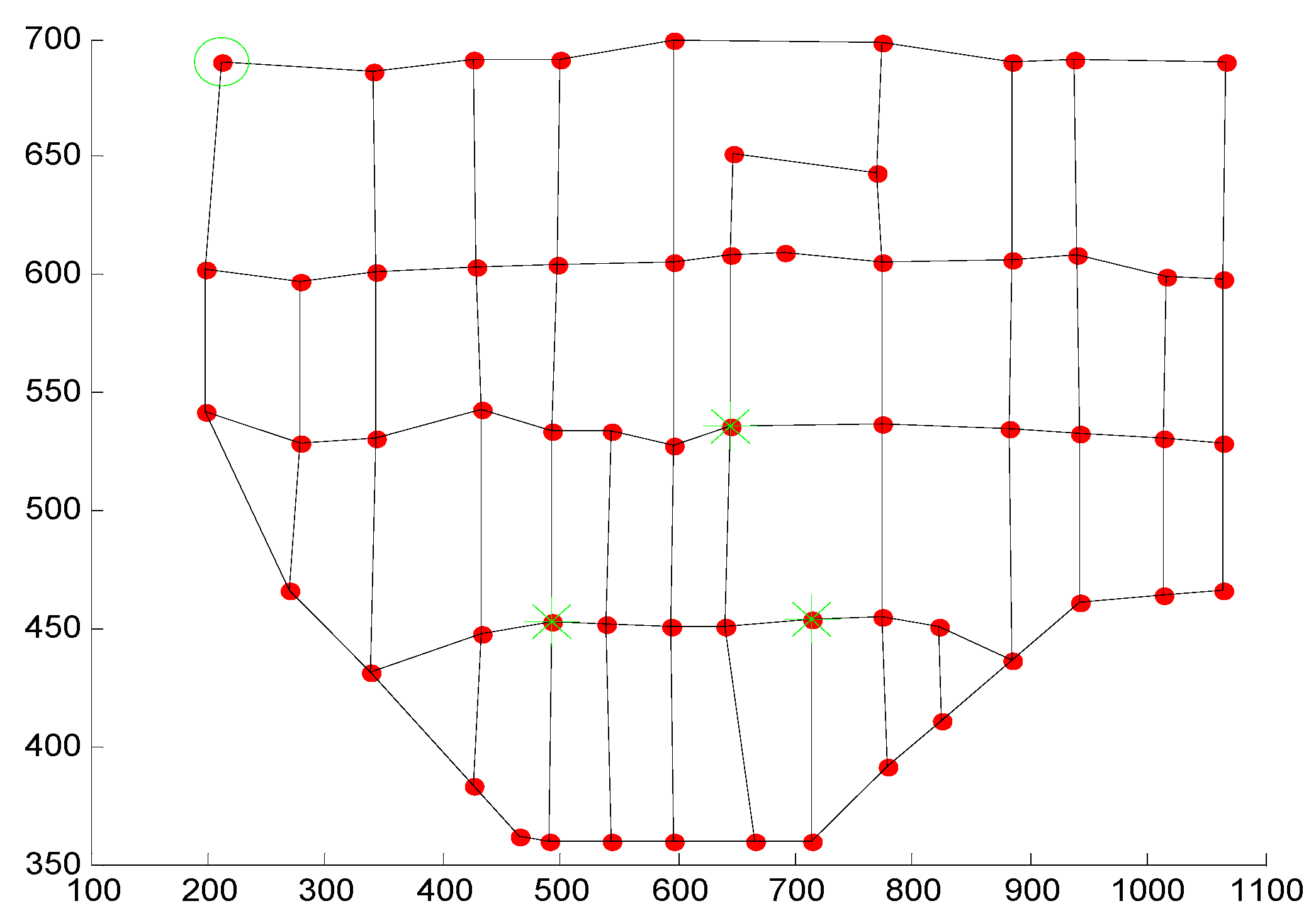
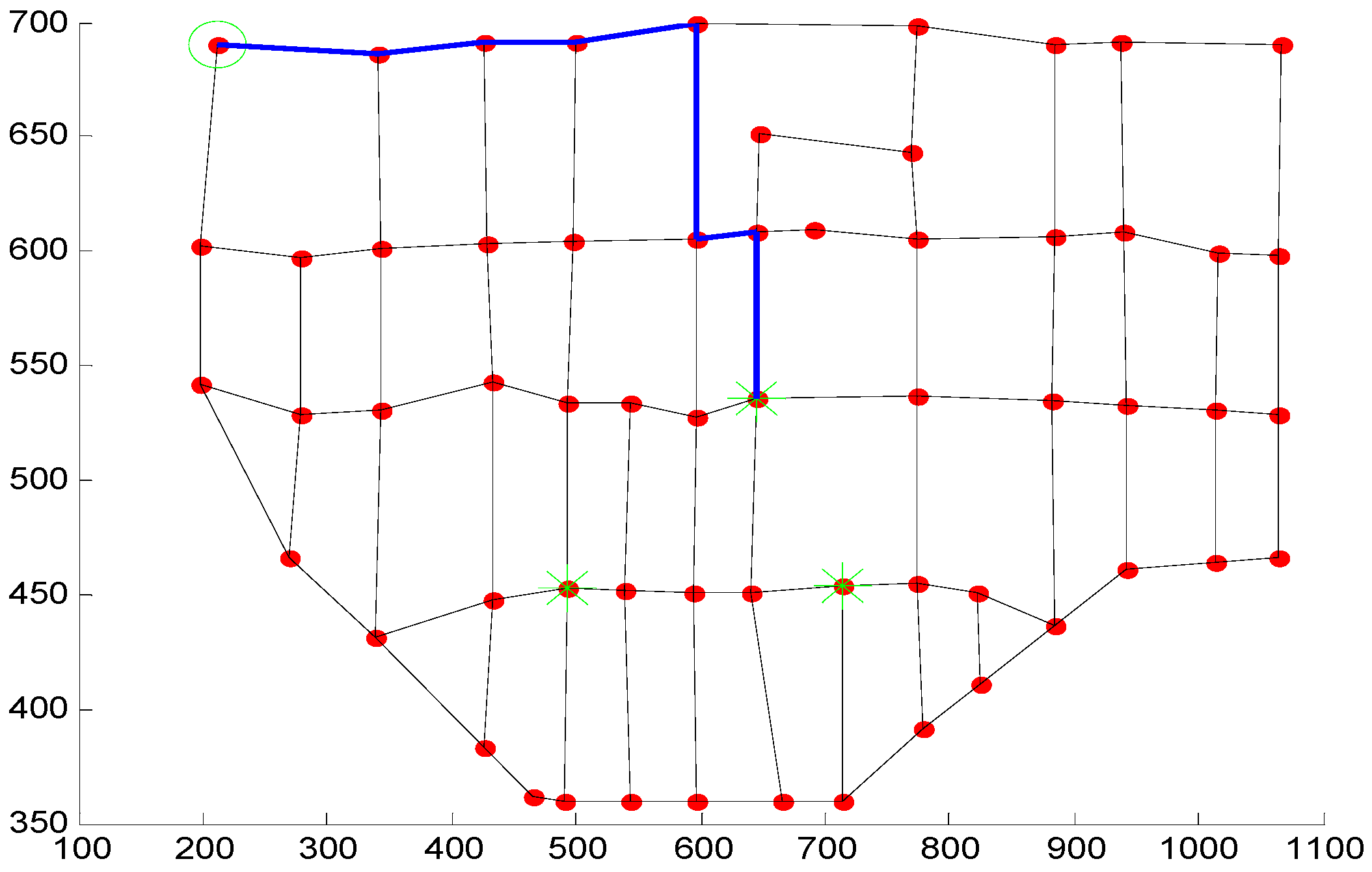
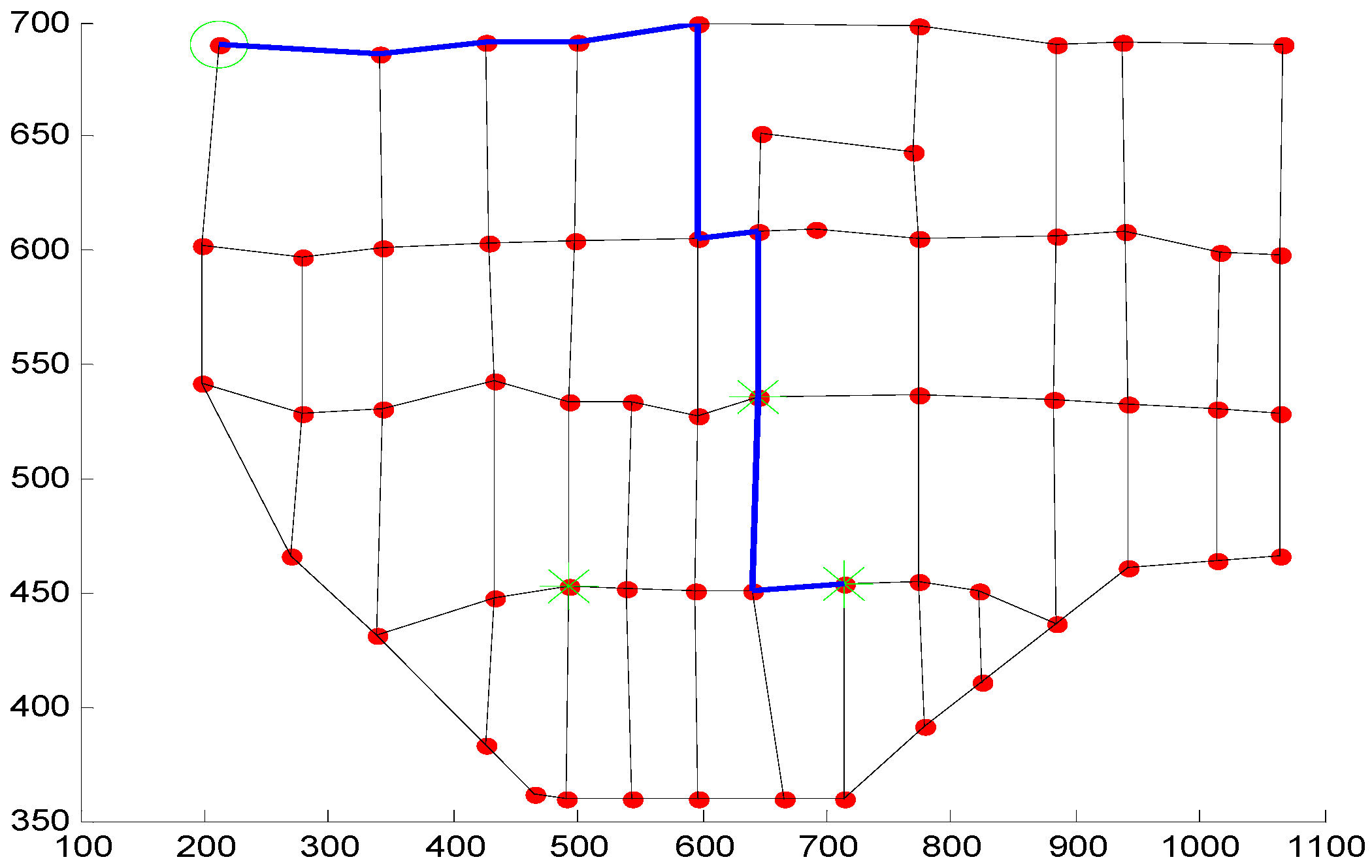
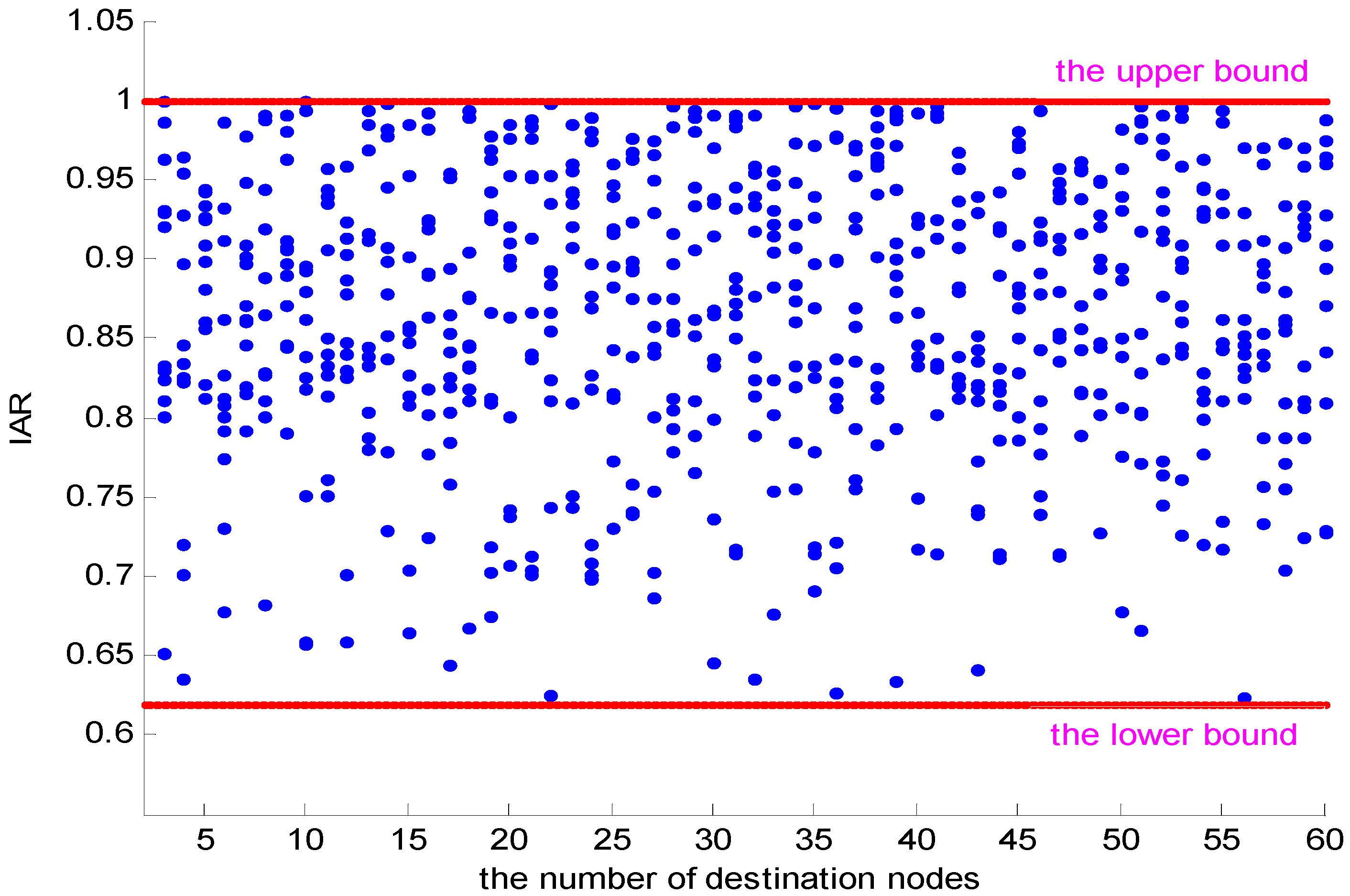
4. The Simulation Experiments
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhu, Z.; Li, S.; Chen, X. Design QoS-Aware Muli-Path Provisioning Strategies for Efficient CLOUD-Assisted SVC Video Streaming to Heterogeneous Clients. IEEE Trans. Multimedia 2013, 15, 758–768. [Google Scholar]
- Huang, J.; Huang, X.; Ma, Y. Routing with multiple quality of services constraints: An approximation perspective. J. Netw. Comput. Appl. 2012, 35, 465–475. [Google Scholar] [CrossRef]
- Fang, X.; Yang, D.; Xue, G. MAP: Multiconstrained Anypath Routing in Wireless Mesh Networks. IEEE Trans. Mob. Comput. 2012, 12, 1893–1906. [Google Scholar] [CrossRef]
- Lu, T.; Zhu, J. Genetic Algorithm for Energy-Efficient QoS Multicast Routing. IEEE Commun. Lett. 2013, 17, 31–34. [Google Scholar] [CrossRef]
- Su, Y.-S.; Su, S.-L.; Li, J.-S. Joint Topology-Transparent Scheduling and QoS Routing in Ad Hoc Networks. IEEE Trans. Veh. Technol. 2014, 63, 372–389. [Google Scholar] [CrossRef]
- Huijun, D.; Hua, Q.; Jihong, Z. QoS routing algorithm with multi-dimensions for overlay networks. China Commun. 2013, 10, 167–176. [Google Scholar] [CrossRef]
- Xiao, Y.; Thulasiraman, K.; Fang, X.; Yang, D.; Xue, G. Computing a Most Probable Delay Constrained Path: NP-Hardness and Approximation Schemes. IEEE Trans. Comput. 2012, 61, 738–744. [Google Scholar] [CrossRef]
- Chen, S.; Song, M.; Sahni, S. Two techniques for fast computation of constrained shortest paths. IEEE/ACM Trans. Netw. 2008, 16, 105–115. [Google Scholar] [CrossRef]
- Huang, J.; Liu, Y. MOEAQ: A QoS-aware multicast routing algorithm for MANET. Expert Syst. Appl. 2010, 37, 1391–1399. [Google Scholar] [CrossRef]
- Liu, L.; Song, Y.; Zhang, H.; Ma, H.; Vasilakos, A.V. Physarum Optimization: A Biology-inspired Algorithm for the Steiner Tree Problem in Networks. IEEE Trans. Comput. 2015, 64, 818–831. [Google Scholar]
- Youssef, M.; Ibrahim, M.; Abdelatif, M.; Lin, C.; Vasilakos, A.V. Routing Metrics of Cognitive Radio Networks: A Survey. IEEE Commun. Surv. Tutor. 2014, 16, 92–109. [Google Scholar] [CrossRef]
- Zhang, X.M.; Zhang, Y.; Yan, F.; Vasilakos, A.V. Interference-based topology control algorithm for delay-constrained mobile Ad hoc networks. IEEE Trans. Mob. Comput. 2015, 14, 742–754. [Google Scholar] [CrossRef]
- Pei, G.; Parthasarathy, S.; Srinivasan, A.; Vullikanti, A.K.S. Approximation Algorithms for Throughput Maximization in Wireless Networks with Delay Constraints. IEEE/ACM Trans. Netw. 2013, 21, 1988–2000. [Google Scholar] [CrossRef]
- Takahashi, H.; Matsuyama, A. An approximate solution for the Steiner problem in graphs. Math Jpn. 1980, 24, 573–577. [Google Scholar]
- Yuan, X. Heuristic algorithms for multiconstrained quality-of-service routing. IEEE/ACM Trans. Netw. 2002, 10, 244–256. [Google Scholar] [CrossRef]
- Xue, G.; Sen, A.; Zhang, W.; Tang, J.; Thulasiraman, K. Finding a path subject to many additive QoS constraints. IEEE/ACM Trans. Netw. 2007, 15, 201–211. [Google Scholar] [CrossRef]
- Xue, G.; Zhang, W.; Tang, J.; Thulasiraman, K. Polynomial time approximation algorithms for multi-constrained QoS routing. IEEE/ACM Trans. Netw. 2008, 16, 656–669. [Google Scholar]
- Feng, G.; Korkmaz, T. A Fast Hybrid ε-Approximation Algorithm for Computing Constrained Shortest Paths. IEEE Commun. Lett. 2013, 17, 1471–1474. [Google Scholar] [CrossRef]
- Szymanski, T.H. Max-Flow Min-Cost Routing in a Future-Internet with Improved QoS Guarantees. IEEE Trans. Commun. 2013, 61, 1485–1497. [Google Scholar] [CrossRef]
- Yang, W.; Zhang, Y. A Fast Algorithm for the Optimal Constrained Path Routing in Wireless Mesh Networks. J. Commun. 2016, 11, 126–131. [Google Scholar]
- Li, P.; Guo, S.; Yu, S.; Vasilakos, A.V. Reliable Multicast with Pipelined Network Coding Using Opportunistic Feeding and Routing. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 3264–3273. [Google Scholar] [CrossRef]
- Meng, T.; Wu, F.; Yang, Z.; Chen, G.; Vasilakos, A. Spatial Reusability-Aware Routing in Multi-Hop Wireless Networks. IEEE Trans. Comput. 2015, 65. [Google Scholar] [CrossRef]
- Liu, J.; Wan, J.; Wang, Q.; Zeng, B.; Fang, S. A Time-recordable Cross-Layer Communication Protocol for the Positioning of Vehicular Cyber-Physical Systems. Future Gener. Comput. Syst. 2016, 56, 438–448. [Google Scholar] [CrossRef]
- Liu, J.; Wan, J.; Wang, Q.; Li, D.; Qiao, Y.; Cai, H. A Novel Energy-saving One-Sided Synchronous Two-Way Ranging Algorithm for Vehicular Positioning. ACM/Springer Mob. Netw. Appl. 2015, 20, 661–672. [Google Scholar] [CrossRef]
- Wan, J.; Liu, J.; Shao, A.; Vasilakos, A.V.; Imran, M.; Zhou, K. Mobile Crowd Sensing for Traffic Prediction in Internet of Vehicles. Sensors 2016, 16, 88. [Google Scholar] [CrossRef] [PubMed]
- Alasaad, A.; Nicanfar, H.; Gopalakrishnan, S.; Leung, V.C.M. A ring-based multicast routing topology with QoS support in wireless mesh networks. Wirel. Netw. 2013, 19, 1627–1651. [Google Scholar] [CrossRef]
- Hwang, I.S.; Nikoukar, A.; Chen, K.C.; Liem, A.T.; Lu, C.H. QoS enhancement of live IPTV using an extended real-time streaming protocol in Ethernet passive optical networks. IEEE/OSA J. Opt. Commun. Netw. 2014, 6, 695–704. [Google Scholar] [CrossRef]
- Xiang, Z.; Tao, M.; Wang, X. Coordinated Multicast Beamforming in Multicell Networks. IEEE Trans. Wirel. Commun. 2013, 12, 12–21. [Google Scholar] [CrossRef]
- Cao, Y.; Blostein, S.D.; Chan, W.Y. Optimization of unequal error protection rateless codes for multimedia multicasting. J. Commun. Netw. 2015, 17, 221–230. [Google Scholar] [CrossRef]
- Afolabi, R.O.; Dadlani, A.; Kim, K. Multicast Scheduling and Resource Allocation Algorithms for OFDMA-Based Systems: A Survey. IEEE Commun. Surv. Tutor. 2013, 15, 240–254. [Google Scholar] [CrossRef]
- Al-Fuqaha, A.; Khreishah, A.; Guizani, M.; Rayes, A.; Mohammadi, M. Toward better horizontal integration among IoT services. IEEE Commun. Mag. 2015, 53, 72–79. [Google Scholar] [CrossRef]
- Mahboobi, B.; Mehrizi, S.; Ardebilipour, M. Multicast Relay Beamforming in CDMA Networks: Nonregenerative Approach. IEEE Commun. Lett. 2015, 19, 1418–1421. [Google Scholar] [CrossRef]
- Bornhorst, N.; Pesavento, M.; Gershman, A.B. Distributed Beamforming for Multi-Group Multicasting Relay Networks. IEEE Trans. Signal Proc. 2012, 60, 221–232. [Google Scholar] [CrossRef]
- Chuah, S.P.; Chen, Z.; Tan, Y.P. Energy-Efficient Resource Allocation and Scheduling for Multicast of Scalable Video Over Wireless Networks. IEEE Trans. Multimed. 2012, 14, 1324–1336. [Google Scholar] [CrossRef]
- Quang, P.T.A.; Piamrat, K.; Singh, K.D.; Viho, C. Video Streaming over Ad-hoc Networks: A QoE-based Optimal Routing Solution. IEEE Trans. Veh. Technol. 2016. [Google Scholar] [CrossRef]


| s | the source node |
| the kth destination nodes | |
| D | the set of destination nodes |
| m, n | the edge and the node number of graph G, respectively |
| q | the number of terminal nodes |
| ith link weight of edge ex | |
| K | the number of Quality-of-Service (QoS) requirements |
| the set of weights of the edges | |
| the set of constrains | |
| ith QoS requirement | |
| the multicast tree with all nodes in the set of destination nodes D | |
| the Steiner tree with j destination nodes in the set D | |
| , | all the nodes and the edges of the multicast trees T, respectively |
| , | the optimal and the approximate optimal multicast routing tree, respectively |
| the total weights from to | |
| the short path connected node to the | |
| , | the ith weight of path length from source s to any node u in |
| all the K weight of path length from source s to any node u in |
| NO. | q = 2 | q = 5 | q = 8 | q = 11 | q = 14 | q = 17 | q = 20 | q = 23 |
| NMHA | 42 | 107 | 163 | 233 | 297 | 366 | 419 | 492 |
| Xue’s | 58 | 751 | 1850 | 3611 | 4443 | 8772 | 12,054 | 15,779 |
| NO. | q = 26 | q = 30 | q = 34 | q = 38 | q = 42 | q = 46 | q = 50 | q = 54 |
| NMHA | 569 | 627 | 725 | 799 | 889 | 963 | 1052 | 1138 |
| Xue’s | 21,136 | 28,412 | 33,689 | 39,956 | 51,896 | 63,512 | 75,412 | 87,512 |
| NO. | q = 2 | q = 5 | q = 8 | q = 11 | q = 14 | q = 17 | q = 20 | q = 23 |
| NMHA | 24 | 33 | 34 | 56 | 58 | 59 | 70 | 59 |
| FMPH | 24 | 35 | 38 | 64 | 66 | 69 | 80 | 75 |
| NO. | q = 26 | q = 29 | q = 32 | q = 35 | q = 38 | q = 42 | q = 46 | q = 47 |
| NMHA | 72 | 80 | 81 | 90 | 95 | 101 | 109 | 110 |
| FMPH | 85 | 98 | 105 | 103 | 117 | 124 | 134 | 136 |
| NO. | q = 2 | q = 35 | q = 70 | q = 105 | q = 140 | q = 175 | q = 210 | q = 245 |
| NMHA | 1009 | 1490 | 1822 | 2201 | 2330 | 2474 | 2819 | 2837 |
| FMPH | 1067 | 1490 | 2230 | 2485 | 2764 | 3310 | 3545 | 3355 |
| NO. | q = 270 | q = 305 | q = 340 | q = 375 | q = 410 | q = 445 | q = 496 | q = 497 |
| NMHA | 3320 | 3349 | 3610 | 3535 | 3894 | 4041 | 4488 | 4492 |
| FMPH | 4128 | 4129 | 4824 | 4877 | 5139 | 5212 | 5985 | 5989 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, W.; Chen, Y. A Novel QoS Provisioning Algorithm for Optimal Multicast Routing in WMNs. Future Internet 2016, 8, 38. https://doi.org/10.3390/fi8030038
Yang W, Chen Y. A Novel QoS Provisioning Algorithm for Optimal Multicast Routing in WMNs. Future Internet. 2016; 8(3):38. https://doi.org/10.3390/fi8030038
Chicago/Turabian StyleYang, Weijun, and Yuanfeng Chen. 2016. "A Novel QoS Provisioning Algorithm for Optimal Multicast Routing in WMNs" Future Internet 8, no. 3: 38. https://doi.org/10.3390/fi8030038
APA StyleYang, W., & Chen, Y. (2016). A Novel QoS Provisioning Algorithm for Optimal Multicast Routing in WMNs. Future Internet, 8(3), 38. https://doi.org/10.3390/fi8030038