Conflict and Computation on Wikipedia: A Finite-State Machine Analysis of Editor Interactions
Abstract
:1. Introduction
2. Methods
2.1. Tracking Conflict through Page Reverts
2.2. Hidden Markov Models
2.3. Fitting and Characterizing HMMs
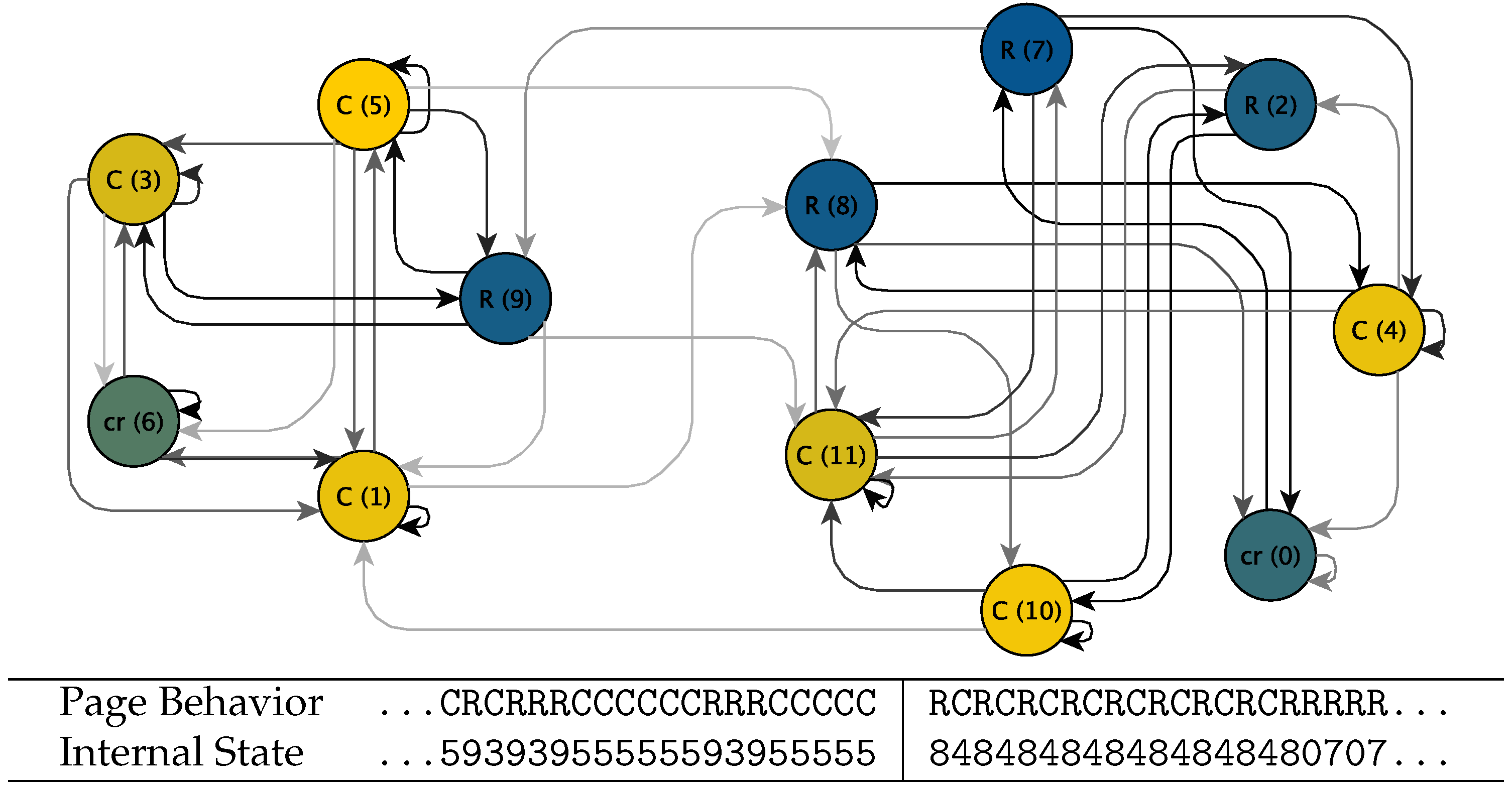
2.4. Subspaces, Trapping Time, and Viterbi Reconstruction for HMMs
2.5. Causes of State Transitions
3. Results
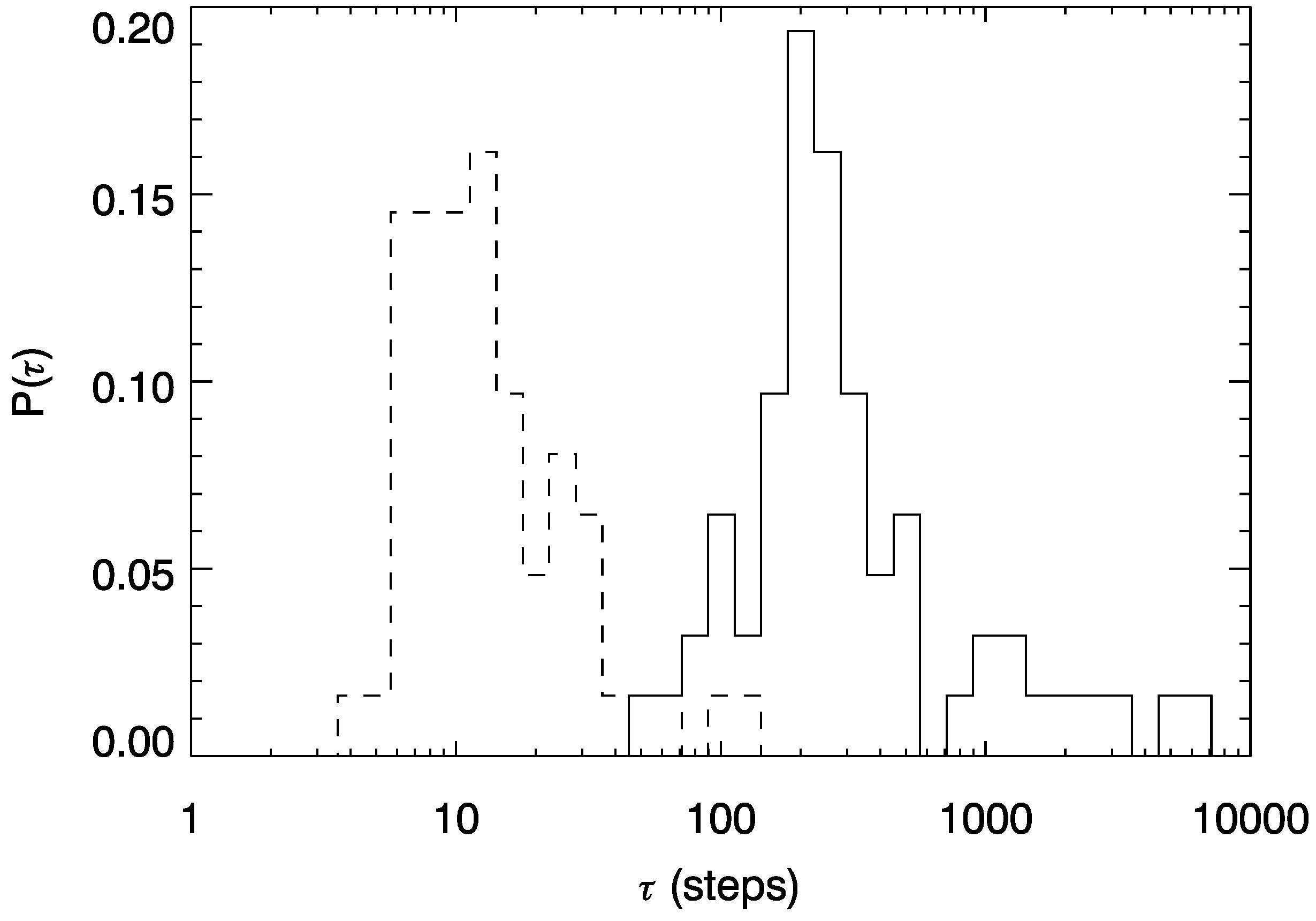
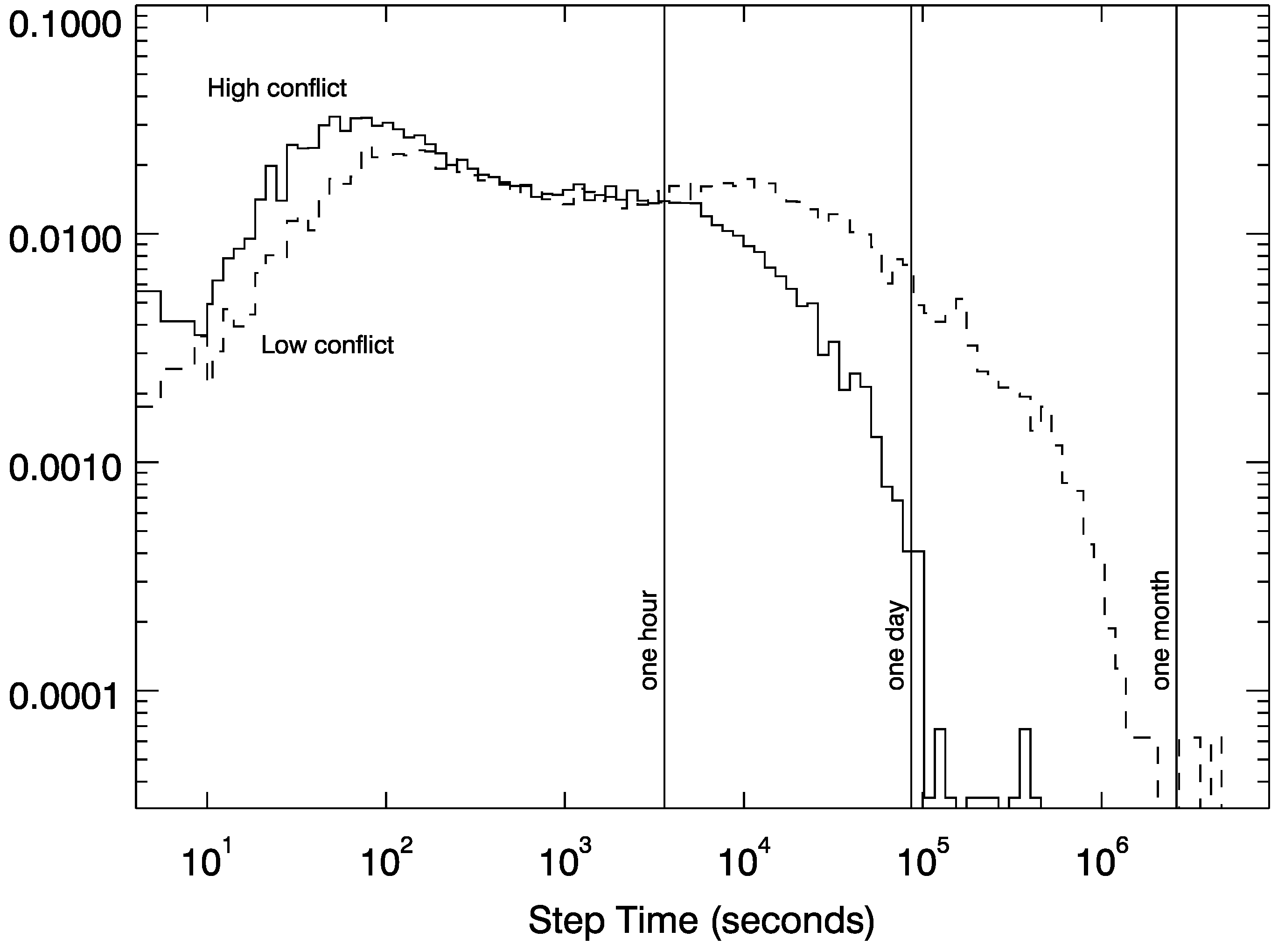
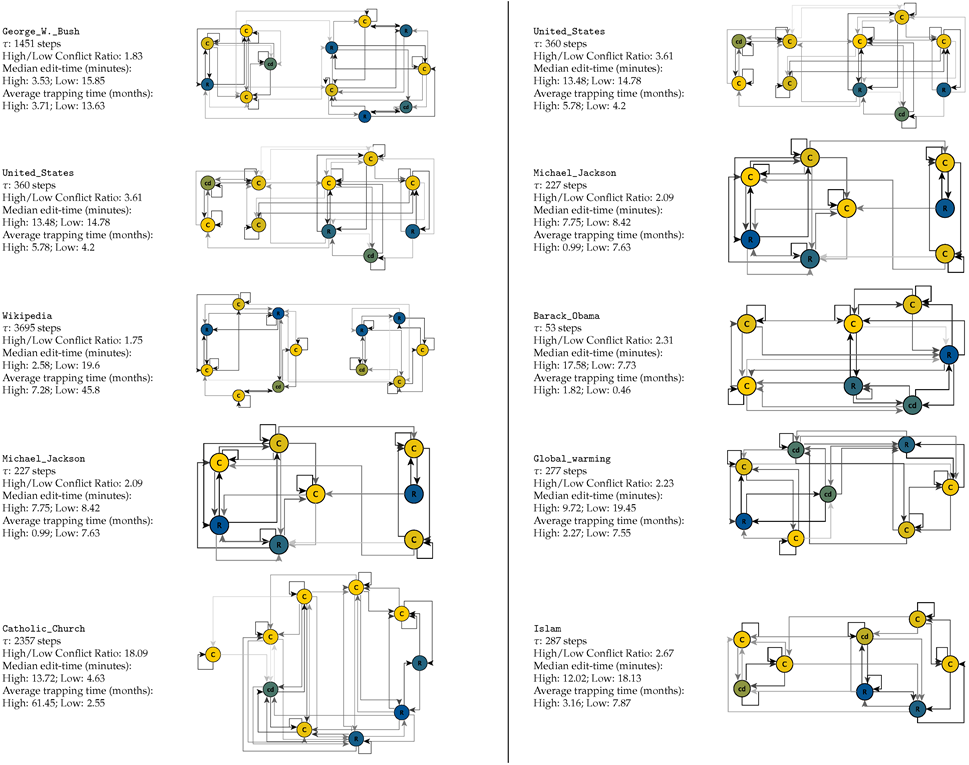
3.1. Epoch Detection
3.2. Drivers of Conflict Transitions
- How many events are there and what fraction are associated with a transition? (Effectiveness)
- What fraction of transitions are associated with an event? (Explanatory power)
- For those transitions that we can associate with an event, what fraction have the expected effect? (Valence)
3.2.1. Page Protection Events
3.2.2. Anti-Social User Events
3.2.3. Major External Events
4. Discussion
5. Conclusions
Acknowledgments
Conflicts of Interest
Appendix A. Articles in Our Analysis
Appendix B. Choosing the Number of States in an HMM
| Number of States | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 (Truth) | 9 | 10 |
| AIC | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 37.5% | 7.2% | 45.8% | 9.3% | 0.0% |
| BIC | 0.0% | 0.0% | 0.0% | 20.8% | 54.1% | 23.9% | 1.0% | 0.0% | 0.0% | 0.0% |
Appendix C. Relaxation Time, Mixing Time, Decay Time, Trapping Time
References
- DeDeo, S. Collective Phenomena and Non-Finite State Computation in a Human Social System. PLoS ONE 2013, 8, e75818. [Google Scholar] [CrossRef] [PubMed]
- Keegan, B.C.; Lev, S.; Arazy, O. Analyzing Organizational Routines in Online Knowledge Collaborations: A Case for Sequence Analysis in CSCW. In Proceedings of the 19th ACM Conference on Computer-Supported Cooperative Work and Social Computing, San Francisco, CA, USA, 27 February–2 March 2016.
- Jelinek, F. Continuous speech recognition by statistical methods. Proc. IEEE 1976, 64, 532–556. [Google Scholar] [CrossRef]
- Bahl, L.; Baker, J.; Cohen, P.; Dixon, N.; Jelinek, F.; Mercer, R.; Silverman, H. Preliminary results on the performance of a system for the automatic recognition of continuous speech. In Proceedings of the ICASSP ’76 IEEE International Conference on Acoustics, Speech, and Signal Processing, Philadelphia, PA, USA, 12–14 April 1976; Volume 1, pp. 425–429.
- DeRose, S.J. Grammatical category disambiguation by statistical optimization. Comput. Linguist. 1988, 14, 31–39. [Google Scholar]
- Church, K.W. A Stochastic Parts Program and Noun Phrase Parser for Unrestricted Text. In Proceedings of the ANLC ’88 Second Conference on Applied Natural Language Processing, Association for Computational Linguistics, Stroudsburg, PA, USA, 22–27 August 1988; pp. 136–143.
- Salzberg, S.L.; Delcher, A.L.; Kasif, S.; White, O. Microbial gene identification using interpolated Markov models. Nucleic Acids Res. 1998, 26, 544–548. [Google Scholar] [CrossRef] [PubMed]
- Darmon, D.; Sylvester, J.; Girvan, M.; Rand, W. Predictability of user behavior in social media: Bottom-up v. top-down modeling. In Proceedings of the 2013 IEEE International Conference on Social Computing (SocialCom), Washington, DC, USA, 8–14 September 2013; pp. 102–107.
- Reagle, J.M. Good Faith Collaboration: The Culture of Wikipedia; MIT Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Kittur, A.; Suh, B.; Pendleton, B.A.; Chi, E.H. He Says, She Says: Conflict and Coordination in Wikipedia. In Proceedings of the CHI ’07 SIGCHI Conference on Human Factors in Computing Systems, San Jose, CA, USA, 30 April–3 May 2007; ACM: New York, NY, USA, 2007; pp. 453–462. [Google Scholar]
- Kane, G.C.; Johnson, J.; Majchrzak, A. Emergent Life Cycle: The Tension Between Knowledge Change and Knowledge Retention in Open Online Coproduction Communities. Manag. Sci. 2014, 60, 3026–3048. [Google Scholar] [CrossRef]
- Kriplean, T.; Beschastnikh, I.; McDonald, D.W.; Golder, S.A. Community, Consensus, Coercion, Control: Cs*W or How Policy Mediates Mass Participation. In Proceedings of the GROUP ’07 2007 International ACM Conference on Supporting Group Work, Sanibel Island, FL, USA, 4–7 November 2007; ACM: New York, NY, USA, 2007; pp. 167–176. [Google Scholar]
- Viégas, F.B.; Wattenberg, M.; Dave, K. Studying Cooperation and Conflict Between Authors with History Flow Visualizations. In Proceedings of the CHI ’04 SIGCHI Conference on Human Factors in Computing Systems, Vienna, Austria, 24–29 April 2004; ACM: New York, NY, USA, 2004; pp. 575–582. [Google Scholar]
- Kane, G.C. A Multimethod Study of Information Quality in Wiki Collaboration. ACM Trans. Manag. Inf. Syst. 2011, 2. [Google Scholar] [CrossRef]
- Arazy, O.; Nov, O.; Patterson, R.; Yeo, L. Information Quality in Wikipedia: The Effects of Group Composition and Task Conflict. J. Manag. Inf. Syst. 2011, 27, 71–98. [Google Scholar] [CrossRef]
- DeDeo, S. Group Minds and the Case of Wikipedia. Hum. Comput. 2014, 1, 5–29. [Google Scholar] [CrossRef]
- Open Data for the paper Conflict and Computation on Wikipedia:A Finite-State Machine Analysis of Editor Interactions. Available online: https://bit.ly/wikihmm (accessed on 5 July 2016).
- SFIHMM. high-speed C code for the estimation of Hidden Markov Models (finite state machines) on arbitrary time series, for Viterbi Path Reconstruction, PCCA+ (Perron-Cluster Cluster Analysis), and for the generation of simulated data from HMMs. Available online: http://bit.ly/sfihmm (accessed on 5 July 2016).
- Geertz, C. Thick description: Toward an interpretive theory of culture. In Readings in the Philosophy of Social Science; Martin, M., McIntyre, L.C., Eds.; MIT Press: Cambridge, MA, USA, 1994; pp. 213–231. [Google Scholar]
- Yasseri, T.; Sumi, R.; Rung, A.; Kornai, A.; Kertész, J. Dynamics of Conflicts in Wikipedia. PLoS ONE 2012, 7, e38869. [Google Scholar] [CrossRef] [PubMed]
- Kittur, A.; Chi, E.H.; Suh, B. What’s in Wikipedia?: Mapping Topics and Conflict Using Socially Annotated Category Structure. In Proceedings of the CHI ’09 SIGCHI Conference on Human Factors in Computing Systems, Boston, MA, USA, 4–9 April 2009; ACM: New York, NY, USA, 2009; pp. 1509–1512. [Google Scholar]
- Brandes, U.; Lerner, J. Visual Analysis of Controversy in User-Generated Encyclopedias? Inf. Vis. 2008, 7, 34–48. [Google Scholar] [CrossRef]
- Suh, B.; Chi, E.H.; Pendleton, B.A.; Kittur, A. Us vs. them: Understanding social dynamics in Wikipedia with revert graph visualizations. In Proceedings of the IEEE Symposium on Visual Analytics Science and Technology, Sacramento, CA, USA, 30 October–1 November 2007; pp. 163–170.
- Heaberlin, B.; DeDeo, S. The Evolution of Wikipedia’s Norm Network. Future Internet 2016, 8. [Google Scholar] [CrossRef]
- Hinds, P.J.; Bailey, D.E. Out of sight, out of sync: Understanding conflict in distributed teams. Organ. Sci. 2003, 14, 615–632. [Google Scholar] [CrossRef]
- Jehn, K.A. A qualitative analysis of conflict types and dimensions in organizational groups. Adm. Sci. Q. 1997, 42, 530–557. [Google Scholar] [CrossRef]
- Kittur, A.; Kraut, R.E. Beyond Wikipedia: Coordination and Conflict in Online Production Groups. In Proceedings of the CSCW ’10 2010 ACM Conference on Computer Supported Cooperative Work, Savannah, GA, USA, 6–10 February 2010; ACM: New York, NY, USA, 2010; pp. 215–224. [Google Scholar]
- Collier, B.; Bear, J. Conflict, Criticism, or Confidence: An Empirical Examination of the Gender Gap in Wikipedia Contributions. In Proceedings of the CSCW ’12 ACM 2012 Conference on Computer Supported Cooperative Work, Seattle, WA, USA, 11–15 February 2012; ACM: New York, NY, USA, 2012; pp. 383–392. [Google Scholar]
- Auray, N.; Poudat, C.; Pons, P. Democratizing scientific vulgarization. The balance between cooperation and conflict in French Wikipedia. Obs. (OBS*) J. 2007, 1. [Google Scholar] [CrossRef]
- Reagle, J.M., Jr. “Be Nice”: Wikipedia norms for supportive communication. New Rev. Hypermedia Multimedia 2010, 16, 161–180. [Google Scholar] [CrossRef]
- Viégas, F.B.; Wattenberg, M.; Kriss, J.; van Ham, F. Talk before you type: Coordination in Wikipedia. In Proceedings of the 40th IEEE Annual Hawaii International Conference on System Sciences, Waikoloa, HI, USA, 3–6 January 2007; p. 78.
- Baum, L.E.; Petrie, T. Statistical Inference for Probabilistic Functions of Finite State Markov Chains. Ann. Math. Stat. 1966, 37, 1554–1563. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes, 3rd edition: The Art of Scientific Computing; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Mills, T.C. time series Techniques for Economists; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Deuflhard, P.; Dellnitz, M.; Junge, O.; Schütte, C. Computation of essential molecular dynamics by subdivision techniques. In Computational Molecular Dynamics: Challenges, Methods, Ideas; Springer: New York, NY, USA, 1999; pp. 98–115. [Google Scholar]
- Cordes, F.; Weber, M.; Schmidt-Ehrenberg, J. Metastable Conformations via Successive Perron-Cluster Cluster Analysis of Dihedrals; Konrad-Zuse-Zentrum für Informationstechnik Berlin (ZIB): Berlin, Germany, 2002. [Google Scholar]
- Deuflhard, P.; Weber, M. Robust Perron cluster analysis in conformation dynamics. Linear Algebra Appl. 2005, 398, 161–184. [Google Scholar] [CrossRef]
- Noé, F.; Horenko, I.; Schütte, C.; Smith, J.C. Hierarchical analysis of conformational dynamics in biomolecules: Transition networks of metastable states. J. Chem. Phys. 2007, 126, 155102. [Google Scholar] [CrossRef] [PubMed]
- Forney, G.D., Jr. The Viterbi algorithm. Proc. IEEE 1973, 61, 268–278. [Google Scholar] [CrossRef]
- DeDeo, S.; Hawkins, R.X.D.; Klingenstein, S.; Hitchcock, T. Bootstrap Methods for the Empirical Study of Decision-Making and Information Flows in Social Systems. Entropy 2013, 15, 2246–2276. [Google Scholar] [CrossRef]
- Klingenstein, S.; Hitchcock, T.; DeDeo, S. The civilizing process in London’s Old Bailey. Proc. Natl. Acad. Sci. USA 2014, 111, 9419–9424. [Google Scholar] [CrossRef] [PubMed]
- Hill, B.M.; Shaw, A. Page Protection: Another Missing Dimension of Wikipedia Research. In Proceedings of the OpenSym ’15 11th International Symposium on Open Collaboration, San Francisco, CA, USA, 25 May 2015; ACM: New York, NY, USA, 2015; pp. 15:1–15:4. [Google Scholar]
- New York Times Developer Network. Search interface for New York Times Archives. Available online: http://developer.nytimes.com (accessed on 5 July 2016).
- The Guardian Open Platform. Search interface for Guardian Archives. Available online: http://open-platform.theguardian.com (accessed on 5 July 2016).
- Hillary Clinton: Revision history. Available online: https://en.wikipedia.org/w/index.php?title=HillaryClintonoffset=20070217204656limit=87action=history (accessed on 5 July 2016).
- DeDeo, S. Major Transitions in Political Order. In From Matter to Life: Information and Causality; Walker, S.I., Davies, P.C.W., Ellis, G., Eds.; Cambridge University Press: Cambridge, UK,, 2015; Available online: http://arxiv.org/abs/1512.03419 (accessed on 5 July 2016).
- Keegan, B.; Gergle, D.; Contractor, N. Staying in the Loop: Structure and Dynamics of Wikipedia’s Breaking News Collaborations. In Proceedings of the WikiSym ’12 Eighth Annual International Symposium on Wikis and Open Collaboration, Linz, Austria, 27–29 August 2012.
- Axelrod, R.; Hamilton, W. The evolution of cooperation. Science 1981, 211, 1390–1396. [Google Scholar] [CrossRef] [PubMed]
- Sumi, R.; Yasseri, T.; Rung, A.; Kornai, A.; Kertész, J. Characterization and prediction of Wikipedia edit wars. In Proceedings of the ACM WebSci ’11, Koblenz, Germany, 14–17 June 2011; pp. 1–3.
- Sumi, R.; Yasseri, T.; Rung, A.; Kornai, A.; Kertész, J. Edit Wars in Wikipedia. In Proceedings of the IEEE Third International Conference on Social Computing (SocialCom), Boston, MA, USA, 9–11 October 2011; pp. 724–727.
- Yasseri, T.; Kertész, J. Value production in a collaborative environment. J. Stat. Phys. 2013, 151, 414–439. [Google Scholar] [CrossRef]
- Jackendoff, R. Language, Consciousness, Culture: Essays on Mental Structure; MIT Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Scheffer, M.; Bascompte, J.; Brock, W.A.; Brovkin, V.; Carpenter, S.R.; Dakos, V.; Held, H.; van Nes, E.H.; Rietkerk, M.; Sugihara, G. Early-warning signals for critical transitions. Nature 2009, 461, 53–59. [Google Scholar] [CrossRef] [PubMed]
- Lade, S.J.; Gross, T. Early warning signals for critical transitions: A generalized modeling approach. PLoS Comput. Biol. 2012, 8, e1002360. [Google Scholar] [CrossRef] [PubMed]
- Dakos, V.; van Nes, E.H.; Donangelo, R.; Fort, H.; Scheffer, M. Spatial correlation as leading indicator of catastrophic shifts. Theor. Ecol. 2010, 3, 163–174. [Google Scholar] [CrossRef]
- Dakos, V.; Scheffer, M.; van Nes, E.H.; Brovkin, V.; Petoukhov, V.; Held, H. Slowing down as an early warning signal for abrupt climate change. Proc. Natl. Acad. Sci. USA 2008, 105, 14308–14312. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Dearing, J.A.; Langdon, P.G.; Zhang, E.; Yang, X.; Dakos, V.; Scheffer, M. Flickering gives early warning signals of a critical transition to a eutrophic lake state. Nature 2012, 492, 419–422. [Google Scholar] [CrossRef] [PubMed]
- Van de Leemput, I.A.; Wichers, M.; Cramer, A.O.; Borsboom, D.; Tuerlinckx, F.; Kuppens, P.; van Nes, E.H.; Viechtbauer, W.; Giltay, E.J.; Aggen, S.H.; et al. Critical slowing down as early warning for the onset and termination of depression. Proc. Natl. Acad. Sci. USA 2014, 111, 87–92. [Google Scholar] [CrossRef] [PubMed]
- Feldman, M.S.; Pentland, B.T. Reconceptualizing organizational routines as a source of flexibility and change. Adm. Sci. Q. 2003, 48, 94–118. [Google Scholar] [CrossRef]
- Pentland, B.T.; Hærem, T. Organizational Routines as Patterns of Action: Implications for Organizational Behavior. Annu. Rev. Organ. Psychol. Organ. Behav. 2015, 2, 465–487. [Google Scholar] [CrossRef]
- Wikipedia:BOLD, revert, discuss cycle. Available online: https://en.wikipedia.org/wiki/Wikipedia:BOLD,revert,discusscycle (accessed on 5 July 2016).
- Faraj, S.; Jarvenpaa, S.; Majchrzak, A. Knowledge Collaboration in Online Communities. Organ. Sci. 2011, 22, 1224–1239. [Google Scholar] [CrossRef]
- Gerald, C.; Kane, R.G.F. The Shoemaker’s Children: Using Wikis for Information Systems Teaching, Research, and Publication. MIS Q. 2009, 33, 1–17. [Google Scholar]
- Majchrzak, A.; Faraj, S.; Kane, G.C.; Azad, B. The Contradictory Influence of Social Media Affordances on Online Communal Knowledge Sharing. J. Comput. Med. Commun. 2013, 19, 38–55. [Google Scholar] [CrossRef]
- Hansen, S.; Berente, N.; Lyytinen, K. Wikipedia, Critical Social Theory, and the Possibility of Rational Discourse. Inf. Soc. 2009, 25, 38–59. [Google Scholar] [CrossRef]
- Ransbotham, S.; Kane, G.C. Membership turnover and collaboration success in online communities: Explaining rises and falls from grace in Wikipedia. MIS Q. 2011, 35, 613–627. [Google Scholar]
- Ransbotham, S.; Kane, G.; Lurie, N. Network Characteristics and the Value of Collaborative User-Generated Content. Mark. Sci. 2012, 31, 387–405. [Google Scholar] [CrossRef]
- Chomsky, N. Aspects of the Theory of Syntax; MIT Press: Cambridge, MA, USA, 1965. [Google Scholar]
- Rabin, M.O.; Scott, D. Finite Automata and Their Decision Problems. IBM J. Res. Dev. 1959, 3, 114–125. [Google Scholar] [CrossRef]
- Crutchfield, J.P.; Young, K. Inferring statistical complexity. Phys. Rev. Lett. 1989, 63. [Google Scholar] [CrossRef] [PubMed]
- Crutchfield, J.P. The calculi of emergence: Computation, dynamics and induction. Phys. D Nonlinear Phenom. 1994, 75, 11–54. [Google Scholar] [CrossRef]
- Crutchfield, J.P.; Shalizi, C.R. Thermodynamic depth of causal states: Objective complexity via minimal representations. Phys. Rev. E 1999, 59. [Google Scholar] [CrossRef]
- Marzen, S.E.; Crutchfield, J.P. Predictive Rate-Distortion for Infinite-Order Markov Processes. J. Stat. Phys. 2016, 163, 1312–1338. [Google Scholar] [CrossRef]
- Marzen, S.E.; Crutchfield, J.P. Statistical signatures of structural organization: The case of long memory in renewal processes. Phys. Lett. A 2016, 380, 1517–1525. [Google Scholar] [CrossRef]
- Török, J.; Iñiguez, G.; Yasseri, T.; San Miguel, M.; Kaski, K.; Kertész, J. Opinions, conflicts, and consensus: Modeling social dynamics in a collaborative environment. Phys. Rev. Lett. 2013, 110, 088701. [Google Scholar] [CrossRef] [PubMed]
- Iñiguez, G.; Török, J.; Yasseri, T.; Kaski, K.; Kertész, J. Modeling social dynamics in a collaborative environment. EPJ Data Sci. 2014, 3, 1–20. [Google Scholar] [CrossRef]
- Barabasi, A.L. The origin of bursts and heavy tails in human dynamics. Nature 2005, 435, 207–211. [Google Scholar] [CrossRef] [PubMed]
- Leskovec, J.; McGlohon, M.; Faloutsos, C.; Glance, N.; Hurst, M. Patterns of Cascading Behavior in Large Blog Graphs. In Proceedings of the 2007 SIAM International Conference on Data Mining, Minneapolis, MN, USA, 26–28 April 2007; Chapter 60. pp. 551–556.
- Stehlé, J.; Barrat, A.; Bianconi, G. Dynamical and bursty interactions in social networks. Phys. Rev. E 2010, 81, 035101. [Google Scholar] [CrossRef] [PubMed]
- Zhi-Dan, Z.; Hu, X.; Ming-Sheng, S.; Tao, Z. Empirical analysis on the human dynamics of a large-scale short message communication system. Chin. Phys. Lett. 2011, 28, 068901. [Google Scholar]
- Karsai, M.; Kaski, K.; Barabási, A.L.; Kertész, J. Universal features of correlated bursty behaviour. Sci. Rep. 2012, 2. [Google Scholar] [CrossRef] [PubMed]
- Wellman, B.; Salaff, J.; Dimitrova, D.; Garton, L.; Gulia, M.; Haythornthwaite, C. Computer Networks as Social Networks: Collaborative Work, Telework, and Virtual Community. Annu. Rev. Sociol. 1996, 22, 213–238. [Google Scholar] [CrossRef]
- Wellman, B. Computer Networks As Social Networks. Science 2001, 293, 2031–2034. [Google Scholar] [CrossRef] [PubMed]
- Flack, J.C.; Krakauer, D.C.; de Waal, F.B. Robustness mechanisms in primate societies: A perturbation study. Proc. R. Soc. B Biol. Sci. 2005, 272, 1091–1099. [Google Scholar] [CrossRef] [PubMed]
- Flack, J.C.; Girvan, M.; De Waal, F.B.; Krakauer, D.C. Policing stabilizes construction of social niches in primates. Nature 2006, 439, 426–429. [Google Scholar] [CrossRef] [PubMed]
- DeDeo, S.; Krakauer, D.; Flack, J. Inductive game theory and the dynamics of animal conflict. PLoS Comput. Biol. 2010, 6, e1000782. [Google Scholar] [CrossRef] [PubMed]
- Hobson, E.A.; DeDeo, S. Social Feedback and the Emergence of Rank in Animal Society. PLoS Comput. Biol. 2015, 11, e1004411. [Google Scholar] [CrossRef] [PubMed]
- DeDeo, S.; Krakauer, D.; Flack, J. Evidence of strategic periodicities in collective conflict dynamics. J. R. Soc. Interface 2011, 8, 1260–1273. [Google Scholar] [CrossRef] [PubMed]
- Flack, J.C. Multiple time-scales and the developmental dynamics of social systems. Philos. Trans. R. Soc. B Biol. Sci. 2012, 367, 1802–1810. [Google Scholar] [CrossRef] [PubMed]
- Celeux, G.; Durand, J.B. Selecting hidden Markov model state number with cross-validated likelihood. Comput. Stat. 2008, 23, 541–564. [Google Scholar] [CrossRef]
- Bacci, S.; Pandolfi, S.; Pennoni, F. A comparison of some criteria for states selection in the latent Markov model for longitudinal data. Adv. Data Anal. Classif. 2014, 8, 125–145. [Google Scholar] [CrossRef]
- MacKay, D.J. Information Theory, Inference and Learning Algorithms; Cambridge University Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach; Springer Science & Business Media: New York, NY, USA, 2003. [Google Scholar]
- Levin, D.A.; Peres, Y.; Wilmer, E.L. Markov Chains and Mixing Times; American Mathematical Society: Providence, RI, USA, 2009. [Google Scholar]
| Size | Type One Motifs | Type Two Motifs |
|---|---|---|
| 2 | CR, RC | CC, RR |
| 3 | CRC, RCR, RCC, CCR | CCC, RRR, RRC, CRR |
| 4 | RCRC, CRCR, CRCC, CCRC, RCCR | CCCC, RRRR, RRCC, RCRR, CRRC |
| 5 | CRCRC, RCRCR, RCRCC, CCRCR, CRCCR | CCCCC, RRCRR, RRRRR, CRRRR, RRRRC |
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
DeDeo, S. Conflict and Computation on Wikipedia: A Finite-State Machine Analysis of Editor Interactions. Future Internet 2016, 8, 31. https://doi.org/10.3390/fi8030031
DeDeo S. Conflict and Computation on Wikipedia: A Finite-State Machine Analysis of Editor Interactions. Future Internet. 2016; 8(3):31. https://doi.org/10.3390/fi8030031
Chicago/Turabian StyleDeDeo, Simon. 2016. "Conflict and Computation on Wikipedia: A Finite-State Machine Analysis of Editor Interactions" Future Internet 8, no. 3: 31. https://doi.org/10.3390/fi8030031
APA StyleDeDeo, S. (2016). Conflict and Computation on Wikipedia: A Finite-State Machine Analysis of Editor Interactions. Future Internet, 8(3), 31. https://doi.org/10.3390/fi8030031





