Substring Position Search over Encrypted Cloud Data Supporting Efficient Multi-User Setup †
Abstract
:1. Introduction
- We present a Substring Position Searchable Symmetric Encryption (SSP-SSE) scheme that allows a substring search over an encrypted document collection. The scheme is based on a position heap tree data structure recently proposed by Ehrenfeucht et al. [21].
- We formally define two leakage functions and security against the adaptive chosen-query attack of a tree-based SSP-SSE scheme. Apart from the traditional access and search patterns, we include the definition of the path pattern in the leakage functions of a tree-based searchable encryption. We show that SSP-SSE enjoys the strong notion of semantic security [6].
- We present a construction that is very efficient and does not require large ciphertext space. Our encryption takes time, and the ciphertext is of size , where k is the security parameter and n is the size of stored data. The search protocol takes time and three rounds of communication, where m is the length of the queried substring and is the number of occurrences of the substring in the document collection. We perform a thorough experimental evaluation of our solution on a real-world genomic dataset.
- We consider a natural extension of the SSP-SSE scheme, where an arbitrary group of data users can submit substring queries to search the encrypted collection. We design a scheme support distributed setup, where data users choose their own secret key rather than receive the key from a trusted authority. We formally define a Multi-User Substring Position Searchable Symmetric Encryption (MSSP-SSE) and present an efficient construction.
2. Related Work
3. Background and Building Blocks
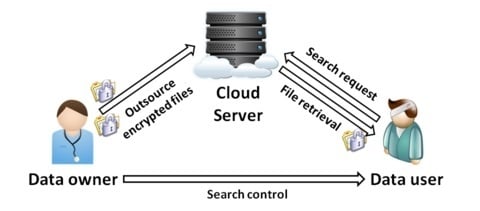
3.1. System and Threat Models
3.2. Preliminaries and Notations
- Given a key and an input , there is an algorithm to compute .
- For any t-time oracle algorithm A, we have:
- a key generation algorithm that inputs a security parameter k and outputs a secret key K.
- a probabilistic algorithm that inputs a secret key K and message m, and outputs a ciphertext c.
- a deterministic algorithm that inputs a secret key K and ciphertext c, and outputs a message m or special symbol ⊥ (if decryption failed).
- Use secret parameter k to output the secret key .
- The adversary A is given oracle access to .
- The adversary A outputs a message m.
- Let and . C denotes the set of all possible ciphertexts. A bit b is chosen at random, and is given to the adversary A.
- The adversary A is again given to the oracle access to , and A runs the number of polynomial queries to output a bit .
- The experiment outputs one if b = , otherwise zero.
4. Substring Search Algorithms
4.1. Suffix Tree
- Each edge is labeled with a non-empty substring of t, named the edge label.
- Every internal node has at least two children.
- No two edges out of a node have edge labels starting with the same character.
- The tree has n leaves, labeled from 1 to n.
4.2. Suffix Array
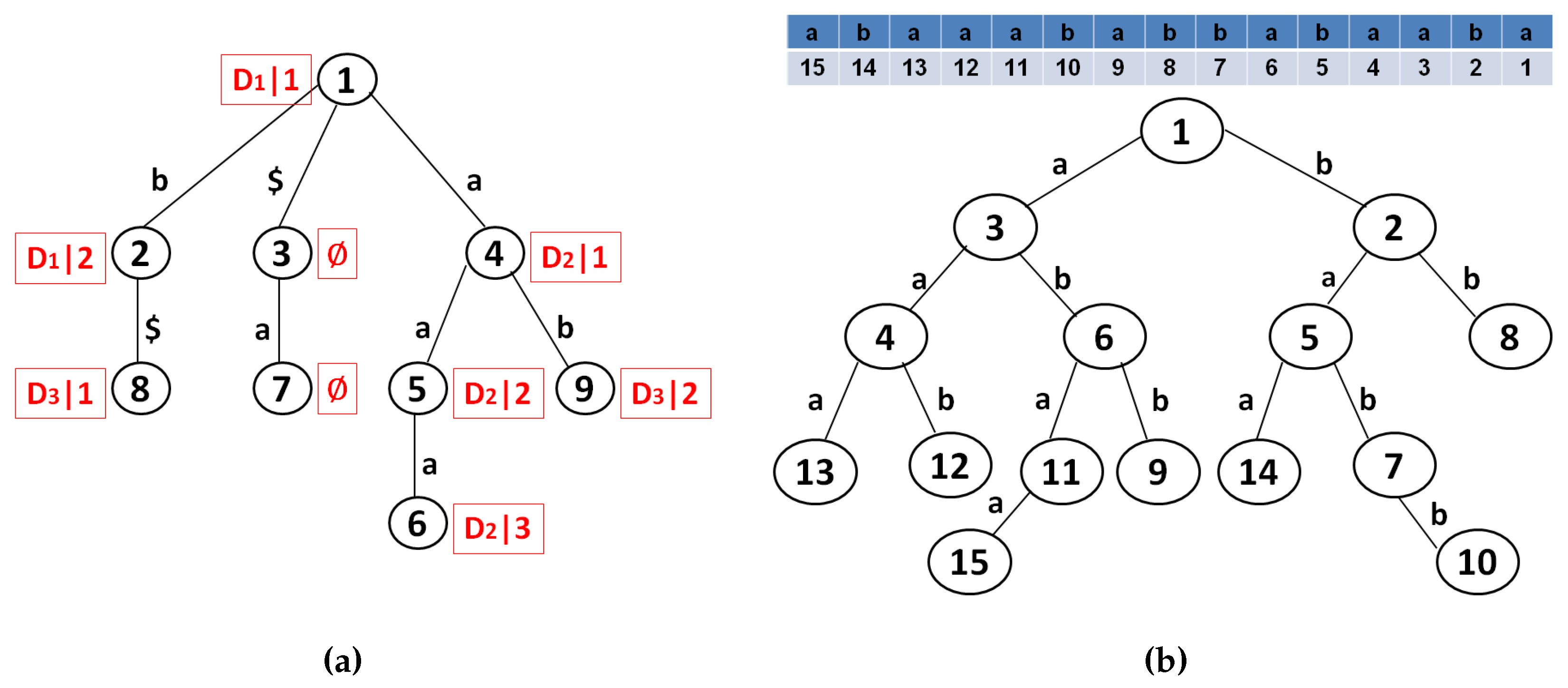
4.3. Position Heap Tree
- Index into the position heap Λ to find the longest prefix p of χ that is a node of Λ. For each ancestor of p, lookup the position i stored in . Here, position i is an occurrence of . Determine if this occurrence is followed by . If yes, report i as an occurrence of χ.
- If , also report all positions of the descendants of p.
4.4. Discussion
5. Substring Position Searchable Symmetric Encryption
5.1. Algorithm Definitions
- K←: a probabilistic key generation algorithm to setup the SSP-SSE scheme. The algorithm takes a secret parameter k and outputs a set of secret keys K.
- ←: a deterministic algorithm to build a position heap tree Λ. The algorithm takes a document collection D = and outputs a position heap tree Λ.
- ←: a probabilistic algorithm to encrypt a position heap tree Λ and document corpus D. The algorithm inputs a set of secret keys K, a position heap tree Λ and a documents corpus D. The output of algorithm is a searchable index I and encrypted collection C = .
- ←↔←: two deterministic algorithms that are executed interactively between the cloud user and the cloud provider. The ConstructQuery algorithm inputs a set of secret keys K, a substring χ, and it outputs a search query Q. The Search is an algorithm that inputs a searchable index I and a search query Q. The algorithm finds the set of matching encrypted document identifiers .
- ←: a deterministic algorithm that takes a set of secret keys K and a ciphertext as input and outputs an original document , and a set of χ’s positions in .
5.2. Security Model Definitions
- Leakage . Given the encrypted collection C = and the searchable index I, the leakage consists of the following information: the number of encrypted documents, the size of encrypted documents and the identifier of each encrypted document.
- Leakage . Given the encrypted collection C = , the searchable index I and the search query Q, the leakage function outputs the access pattern , search pattern and path pattern .
5.3. SSP-SSE Construction
| Algorithm 1: Notations. |
|
5.3.1. Setup Phase
| Algorithm 2: SSP-SSE setup phase. |
| Let = be a PCPA-secure symmetric-key encryption scheme; let F: × → be a PRF; and let P: × → be a PRP. SETUP PHASE. : given the security parameter k, generate , , , ← and , , , . Output the key set K = , , , , , , , . BuildTree(D) : given the document collection D = :
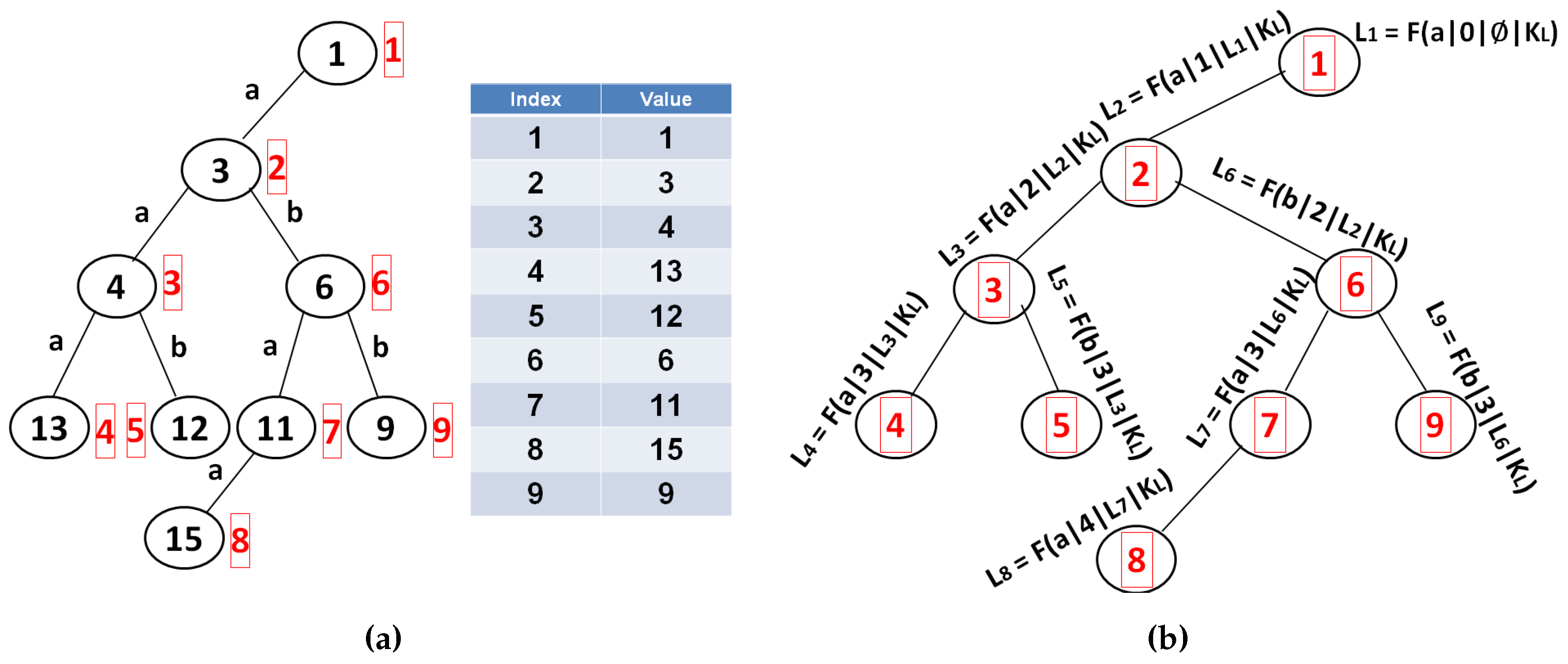
Encrypt(K, Λ, D) : given the secret key set K, position heap tree Λ and the set of documents D = . Build encrypted tree:
Build encrypted arrays:
Encrypt document collection:
Output: index I = and encrypted document collection C = . |
5.3.2. Search Phase
| Algorithm 3: SSP-SSE search phase. |
| SEARCH PHASE. [(Q) ← ConstructQuery(K, χ)] ↔ [(L) ← Search(I,Q)] is an interactive protocol between the cloud user and the cloud provider. The cloud user keeps the key set K = , , , , , , , and queries cloud provider for a substring χ. The cloud provider executes search on searchable index I = and returns results back to the cloud user.
:
|
6. Security and Performance Analysis
6.1. Security
- : The simulator has a leakage , which gives the simulator information about the number and size of documents, as well as identifier of each encrypted document. The simulator randomly generates a set of simulated ciphertexts and simulated searchable index as follows:
- –
- Simulator outputs the set of ciphertexts , where .
- –
- Simulator sets the simulated encrypted position heap tree , where each node is set as and each path label of node is set as , where . The simulator outputs the encrypted position heap tree .
- –
- Simulator then constructs simulated arrays and : = and = , where .
- –
- Simulator outputs simulated searchable index = and the set of simulated ciphertexts .
- : The adversary sends a new query Q to the simulator . The simulator then starts collecting various dependencies between the incoming search query and the resulting output.
- –
- With given search query Q, simulator traverses the simulated encrypted position heap tree starting from the root node, following the simulated path labels to find the set of matching encrypted nodes in . The simulator outputs the set of simulated matching nodes: and .
- –
- With given search requests , the simulator performs a search in simulated array and returns matching elements .
- –
- With given search requests , the simulator performs a search in simulated array and returns matching elements .
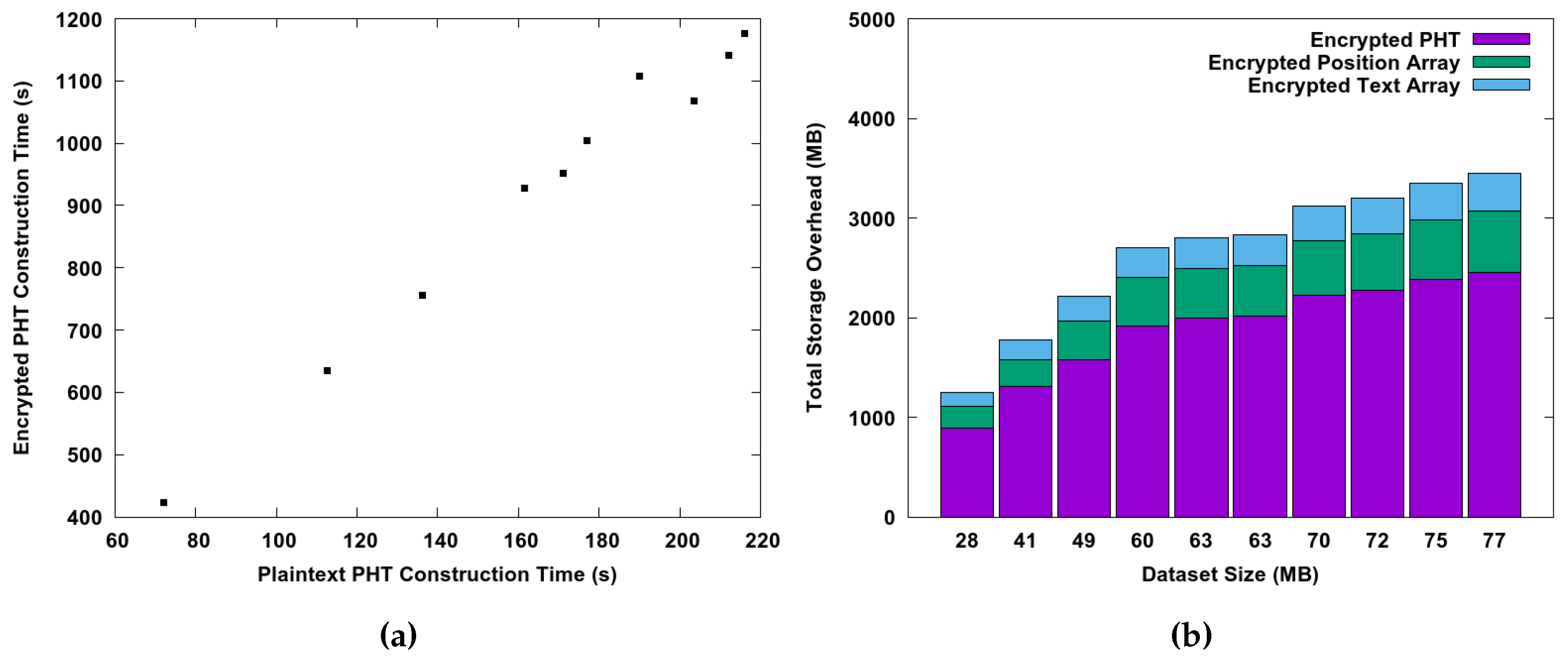
6.2. Performance
7. Multi-User Substring Position Searchable Symmetric Encryption
7.1. Preliminaries
- : a probabilistic algorithm that inputs a security parameter λ and a circuit × → , and outputs a secret function key and a public evaluation key .
- F: a deterministic algorithm that inputs the function key and an input and outputs some output for some set .
- : a deterministic algorithm that inputs the evaluation key , an input and a witness and that produces an output or ⊥.
- : a probabilistic algorithm to output public and secret keys. The algorithm inputs the security parameter λ and the group order g. It computes . Next, it picks a random seed and computes z←. It outputs a secret key and public values , where is kept secret and are published to the bulletin board.
- : a deterministic algorithm that inputs group g and user’s secret . It outputs a group key k = .
- : a probabilistic algorithm to setup the BE-NIKE-WPRF scheme. The algorithm outputs a secret parameter λ and group order g.
- : a probabilistic algorithm to join the scheme that is executed by each participant. The algorithm inputs a secret parameter λ and group order g. The algorithm invokes to output secret and public values . The user makes publicly available to other participants.
- : a probabilistic algorithm to encrypt message m under the shared key. The algorithm inputs the set of public values , secret key and plaintext message m. The algorithm runs to derive the shared key k. The algorithm outputs a ciphertext c, which is the encryption of message m using the shared key k.
- : a deterministic algorithm to decrypt . The algorithm invokes to derive k. If , then the algorithm decrypts using k and outputs the original message m.
7.2. Algorithm Definitions
- ← : a probabilistic key generation algorithm to setup the SSP-SSE scheme. The algorithm takes a secret parameter k and outputs a set of secret keys K, secret parameter λ and group g.
- ← : a deterministic algorithm to build a position heap tree Λ. The algorithm takes a document collection D = and constructs a position heap tree Λ.
- ← : a probabilistic algorithm to encrypt a position heap tree and document corpus. The algorithm inputs a set of secret keys K, a position heap tree Λ and a documents corpus D. The output of algorithm is a searchable index I and encrypted collection C = .
- ← : a probabilistic algorithm run by each data user to participate in the scheme. The algorithm invokes with an input of secret parameter λ and group order g. It outputs a pair .
- ← : a probabilistic algorithm run by the group owner to establish the group of authorized data users. The algorithm runs with an input of public values , group owner’s secret key and a sampled secret r. The output is encrypted ciphertext .
- ← : a probabilistic algorithm run by the group owner to remove a user o from the set of authorized users. The algorithm invokes that inputs the set of public values , group owner’s secret key and a new secret r. The output is encrypted ciphertext .
- ← ↔ ← : two deterministic algorithms that are executed interactively between the authorized cloud user and the cloud provider. The algorithm inputs a set of secret keys K, ciphertext and a substring χ, and it outputs a search query Q. The algorithm uses a query Q, searchable index I and ciphertext . It outputs a sequence of identifiers .
- ← : a deterministic algorithm that takes a set of secret keys K and a ciphertext as input, and it outputs an original document , , and a set of χ’s positions in .
- Given searchable index I and the set of encrypted documents C = , the adversary should learn nothing about the original document collection D = .
- Given the set of incoming search queries Q = , access pattern, search pattern and path pattern, the adversary should learn nothing about the content of each search query or the content of resulted documents.
- Once a user is removed from the set of authorized cloud users, he/she is no longer allowed to invoke a search over encrypted documents in the cloud. Thus, we require the revocation of the cloud users.
| Algorithm 4: . |
| ← ← ← ← ← ← ← Q ← L ← if L ≠ ⊥, output one, otherwise output zero |
7.3. MSSP-SSE Construction
| Algorithm 5: MSSP-SSE construction. |
:
BuildTree(D) : Given a document collection D = , output Λ ← . Encrypt(K, Λ, D) :
Output . Join(λ, g) :
Keep private; output to the cloud server. :
Output new to the cloud server.
Output ← . |
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Strizhov, M.; Ray, I. Substring Position Search over Encrypted Cloud Data Using Tree-Based Index. In Proceedings of the 2015 IEEE International Conference on Cloud Engineering (IC2E), Tempe, AZ, USA, 9–13 March 2015.
- Song, D.X.; Wagner, D.; Perrig, A. Practical Techniques for Searches on Encrypted Data. In Proceedings of the 2000 IEEE Symposium on Security and Privacy, Berkeley, CA, USA, 14–17 May 2000.
- Goh, E.J. Secure Indexes. Cryptology ePrint Archive, Report 2003/216. 2003. Available online: http://eprint.iacr.org/2003/216/ (accessed on 10 January 2016).
- Moataz, T.; Shikfa, A. Boolean Symmetric Searchable Encryption. In Proceedings of the 8th ACM SIGSAC Symposium on Information, Computer and Communications Security, Hangzhou, China, 8–10 May 2013.
- Orencik, C.; Kantarcioglu, M.; Savas, E. A Practical and Secure Multi-keyword Search Method over Encrypted Cloud Data. In Proceedings of the 6th IEE International Conference on Cloud Computing, Santa Clara, CA, USA, 28 June–3 July 2013.
- Curtmola, R.; Garay, J.; Kamara, S.; Ostrovsky, R. Searchable Symmetric Encryption: Improved Definitions and Efficient Constructions. In Proceedings of the 13th ACM Conference on Computer and Communications Security, Alexandria, VA, USA, 30 October–3 November 2006.
- Boneh, D.; Waters, B. Conjunctive, Subset, and Range Queries on Encrypted Data. In Proceedings of the 4th IACR Theory of Cryptography Conference, Amsterdam, The Netherlands, 21–24 February 2007.
- Boneh, D.; Crescenzo, G.D.; Ostrovsky, R.; Persiano, G. Public Key Encryption with Keyword Search. In Proceedings of the EUROCRYPT 2004, Jeju Island, Korea, 5–9 December 2004.
- Lai, J.; Zhou, X.; Deng, R.H.; Li, Y.; Chen, K. Expressive Search on Encrypted Data. In Proceedings of the 8th ACM SIGSAC Symposium on Information, Computer and Communications Security, Hangzhou, China, 8–10 May 2013.
- Cao, N.; Wang, C.; Li, M.; Ren, K.; Lou, W. Privacy-Preserving Multi-keyword Ranked Search over Encrypted Cloud Data. In Proceedings of the 30th IEEE International Conference on Computer Communications, Shanghai, China, 31 July–2 August 2011.
- Cash, D.; Jarecki, S.; Jutla, C.; Krawczyk, H.; Rosu, M.C.; Steiner, M. Highly-Scalable Searchable Symmetric Encryption with Support for Boolean Queries. In Proceedings of the 33rd Annual International Cryptology Conference CRYPTO 2013, Santa Barbara, CA, USA, 18–22 August 2013.
- Kamara, S.; Papamanthou, C.; Roeder, T. Dynamic Searchable Symmetric Encryption. In Proceedings of the 2012 ACM Conference on Computer and Communications Security, Raleigh, NC, USA, 16–18 October 2012.
- Chang, Y.C.; Mitzenmacher, M. Privacy Preserving Keyword Searches on Remote Encrypted Data. In Proceedings of the 3rd International Conference on Applied Cryptography and Network Security, New York, NY, USA, 7–10 June 2005.
- Shi, E.; Bethencourt, J.; Chan, T.H.H.; Song, D.; Perrig, A. Multi-Dimensional Range Query over Encrypted Data. In Proceedings of the 2007 IEEE Symposium on Security and Privacy, Berkeley, CA, USA, 20–23 May 2007.
- Agrawal, R.; Kiernan, J.; Srikant, R.; Xu, Y. Order-Preserving Encryption for Numeric Data. In Proceedings of the ACM SIGMOD International Conference on Management of Data, Paris, France, 13–18 June 2004.
- Blanton, M. Achieving Full Security in Privacy-Preserving Data Mining. In Proceedings of the 3rd IEEE International Conference on Privacy, Security, Risk and Trust, Boston, MA, USA, 9–11 October 2011.
- Li, J.; Wang, Q.; Wang, C.; Cao, N.; Ren, K.; Lou, W. Fuzzy Keyword Search over Encrypted Data in Cloud Computing. In Proceedings of the 29th Conference on Information Communications, London, UK, 7–9 September 2010.
- Wang, C.; Ren, K.; Yu, S.; Urs, K. Achieving Usable and Privacy-assured Similarity Search over Outsourced Cloud Data. In Proceedings of the 31th Conference on Information Communications, Hertfordshire, UK, 29–31 October 2012.
- Boldyreva, A.; Chenette, N. Efficient Fuzzy Search on Encrypted Data. In Proceedings of the 21st International Workshop on Fast Software Encryption, London, UK, 3–5 March 2014.
- Strizhov, M.; Ray, I. Multi-keyword Similarity Search over Encrypted Cloud Data. In Proceedings of the ICT Systems Security and Privacy Protection, Marrakech, Morocco, 2–4 June 2014.
- Ehrenfeucht, A.; McConnell, R.M.; Osheim, N.; Woo, S.W. Position Heaps: A Simple and Dynamic Text Indexing Data Structure. J. Discret. Algorithms 2011, 9, 100–121. [Google Scholar] [CrossRef]
- Bloom, B.H. Space/Time Trade-offs in Hash Coding with Allowable Errors. Commun. ACM 1970, 13, 422–426. [Google Scholar] [CrossRef]
- Wang, C.; Cao, N.; Li, J.; Ren, K.; Lou, W. Secure Ranked Keyword Search over Encrypted Cloud Data. In Proceedings of the 2010 IEEE 30th International Conference on Distributed Computing Systems, Genoa, Italy, 21–25 June 2010.
- Moataz, T.; Justus, B.; Ray, I.; Cuppens-Boulahia, N.; Cuppens, F.; Ray, I. Privacy-Preserving Multiple Keyword Search on Outsourced Data in the Clouds. In Proceedings of the Data and Applications Security and Privacy XXVIII, Vienna, Austria, 14–16 July 2014.
- Crescenzo, G.D.; Saraswat, V. Public Key Encryption with Searchable Keywords Based on Jacobi Symbols. In Proceedings of the 8th International Conference on Cryptology in India, Chennai, India, 9–13 December 2007.
- Golle, P.; Staddon, J.; Waters, B. Secure Conjunctive Keyword Search over Encrypted Data. In Proceedings of the Applied Cryptography and Network Security 2004, Yellow Mountain, China, 8–11 June 2004.
- Hwang, Y.H.; Lee, P.J. Public Key Encryption with Conjunctive Keyword Search and Its Extension to a Multi-user System. In Proceedings of the First International Conference on Pairing-Based Cryptography, Tokyo, Japan, 2–4 July 2007.
- Weiner, P. Linear Pattern Matching Algorithms. In Proceedings of the 14th Annual Symposium on Switching and Automata Theory (Swat 1973), Washington, DC, USA, 15–17 October 1973; pp. 1–11.
- Manber, U.; Myers, G. Suffix Arrays: A New Method for On-Line String Searches. SIAM J. Comput. 1993, 22, 935–948. [Google Scholar] [CrossRef]
- Gusfield, D. Algorithms on Strings, Trees, and Sequences: Computer Science and Computational Biology; Cambridge University Press: New York, NY, USA, 1997. [Google Scholar]
- Ukkonen, E. On-line Construction of Suffix Trees. Algorithmica 1995, 14, 249–260. [Google Scholar] [CrossRef]
- Gentry, C.; Goldman, K.; Halevi, S.; Julta, C.; Raykova, M.; Wichs, D. Optimizing ORAM and Using It Efficiently for Secure Computation. In Proceedings of the 13th Privacy Enhancing Technologies Symposium, Bloomington, IN, USA, 10–12 July 2013.
- LibTomCrypt. Cryptographic Toolkit. 2016. Available online: https://github.com/libtom/libtomcrypt (accessed on 10 May 2016).
- NCBI. Genome Database. 2016. Available online: http://www.ncbi.nlm.nih.gov/genome (accessed on 10 May 2016). [Google Scholar]
- Fiat, A.; Naor, M. Broadcast Encryption. In Proceedings of the 13th Annual International Cryptology Conference CRYPTO ’93, Santa Barbara, CA, USA, 22–26 August 1993.
- Zhandry, M. How to Avoid Obfuscation Using Witness PRFs. In Proceedings of the 13th International Conference on Theory of Cryptography TCC 2016, Tel Aviv, Israel, 10–13 January 2016.
- Morris, B.; Rogaway, P.; Stegers, T. How to Encipher Messages on a Small Domain. In Proceedings of the CRYPTO 2009, Santa Barbara, CA, USA, 16–20 August 2009.


| Data Structure | Construction | Search | Cloud Storage |
|---|---|---|---|
| Suffix Tree | |||
| Suffix Array | |||
| Position Heap Tree |
| Organism Name | Description | mRNA Size (MB) | Organism Name | Description | mRNA Size (MB) |
|---|---|---|---|---|---|
| Dufourea novaeangliae |  | 28 | Papilio Polytes |  | 41 |
| Bactrocera dorsalis |  | 49 | Fopius arisanus |  | 60 |
| Halyomorpha halys |  | 63 | Tribolium castaneum |  | 63 |
| Stomoxys calcitrans |  | 70 | Orussus abietinus |  | 72 |
| Nasonia vitripennis |  | 75 | Linepithema humile |  | 77 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Strizhov, M.; Osman, Z.; Ray, I. Substring Position Search over Encrypted Cloud Data Supporting Efficient Multi-User Setup. Future Internet 2016, 8, 28. https://doi.org/10.3390/fi8030028
Strizhov M, Osman Z, Ray I. Substring Position Search over Encrypted Cloud Data Supporting Efficient Multi-User Setup. Future Internet. 2016; 8(3):28. https://doi.org/10.3390/fi8030028
Chicago/Turabian StyleStrizhov, Mikhail, Zachary Osman, and Indrajit Ray. 2016. "Substring Position Search over Encrypted Cloud Data Supporting Efficient Multi-User Setup" Future Internet 8, no. 3: 28. https://doi.org/10.3390/fi8030028
APA StyleStrizhov, M., Osman, Z., & Ray, I. (2016). Substring Position Search over Encrypted Cloud Data Supporting Efficient Multi-User Setup. Future Internet, 8(3), 28. https://doi.org/10.3390/fi8030028