Supporting Privacy of Computations in Mobile Big Data Systems †
Abstract
:1. Introduction
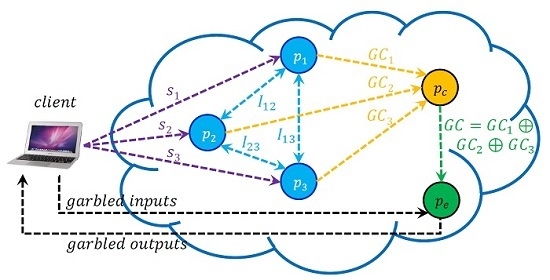
2. A High-Level Overview of Our System
2.1. Our Adversarial Model
2.2. Main Characteristics of Our System
- Offloaded Computation: The client delegates the intensive computational tasks to the cloud servers of creating and evaluating the garbled circuit. The client only chooses the cloud servers, provides them with unique seed values, generates garbled inputs during evaluation, and interprets garbled outputs returned by the evaluator.
- Compact Cipher Text: While Gentry’s scheme has an extremely large cipher text size, the cipher text size can be as small as a few hundred bits with our scheme (Section 5.6). Thus, our proposed method is far more practical for cloud computing in mobile systems in comparison to FHE schemes.
- Decoupling: The process of creating the garbled circuit is decoupled from the process of evaluating the garbled circuit. While the servers, , interact with one another for creating the garbled circuit, the server evaluates the garbled circuit, independently.
- Advance Construction: Since evaluation of the garbled circuit requires no interaction among the servers, if several versions of the garbled circuit for a given computation are precomputed and stored at the evaluator, in advance, then it can readily carry out the requested computation. Thus, the client will only incur the relatively short time taken to evaluate the garbled circuit. In other words, precomputation will drastically improve the response time for the client.
- Collusion Resistance: To interpret any garbled value, the evaluator, , must collude with each of the n servers, . Thus, even if out of the n servers are corrupt and collude with the evaluator, the privacy of the client’s inputs and the result of the computation are still preserved.
- Verification of Outputs: The client has the ability to verify that the evaluator actually carried out the requested computation.
3. Background
3.1. Yao’s Garbled Circuit
3.2. 1-Out-Of-2 Oblivious Transfer
3.3. 1-Out-Of-4 Oblivious Transfer
4. Secure and Verifiable Cloud Computing for Mobile Systems
4.1. Construction and Evaluation of Garbled Circuits
4.1.1. Construction of the Garbled Circuit,
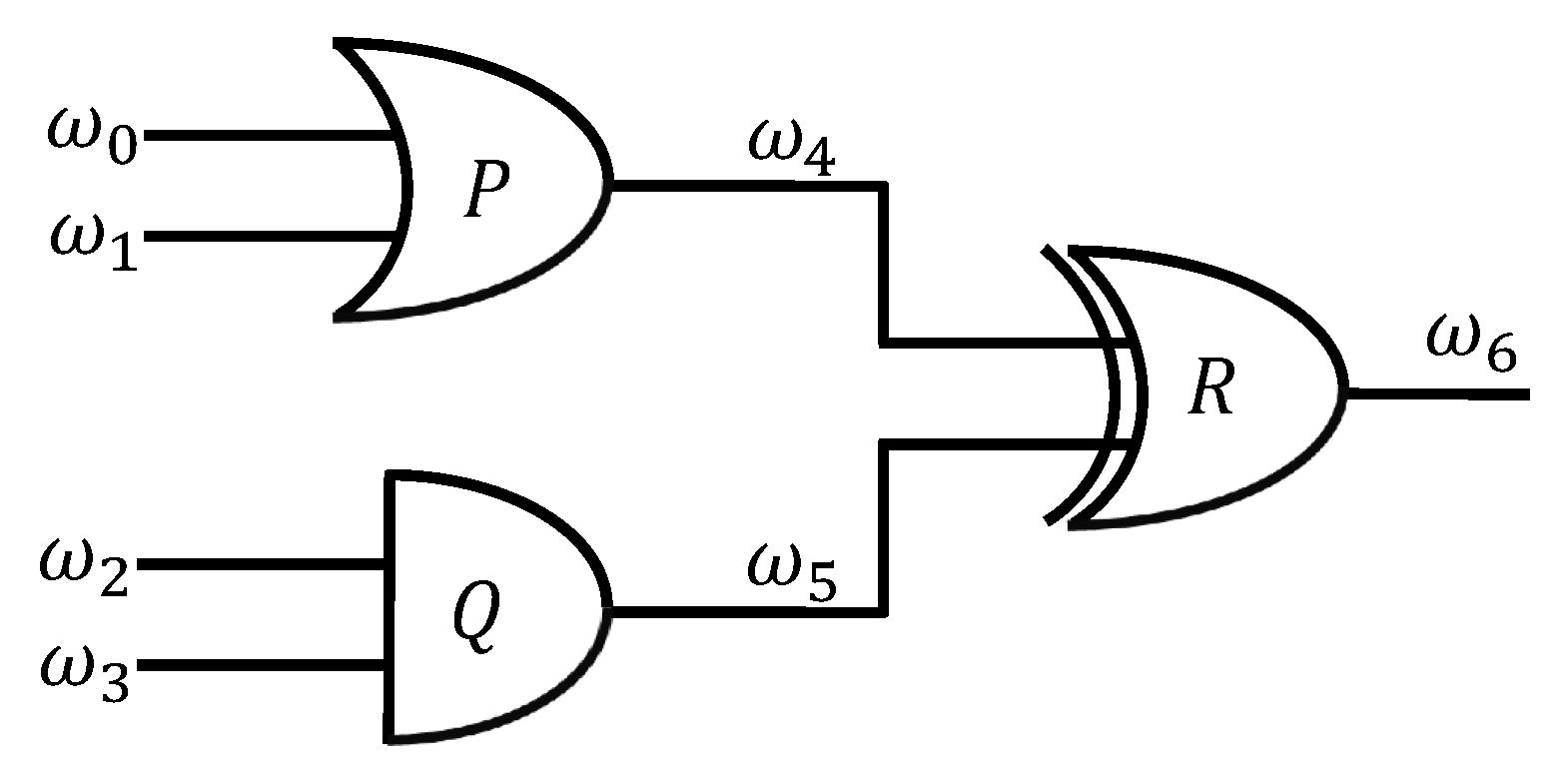
4.1.2. Secure Multiparty Computation of an Entry,
4.1.3. Evaluation of the Garbled Circuit,
- split the most significant bits of α into n parts, ; each part has k bits; similarly, split the most significant bits of β into n parts, ; each part has k bits; i.e., , where .
- compute .
4.2. Secure and Verifiable Cloud Computing through Secure Multiparty Computation
4.3. Recovery and Verification of Outputs
- How does the client efficiently recover the result of the computation without carrying out the delegated computations by itself?
- How does the client verify that the evaluator, in fact, evaluated the garbled circuit? Stated differently, is it possible for the client to determine whether the evaluator returned arbitrary numbers without carrying out any computation at all, instead of the actual garbled output for each output wire?
4.4. Summary of Our Proposed System
- The client chooses , a set of servers in the cloud. Then, to each server , the client provides a unique seed value , and a description of the desired computation. To each pair of servers, , the client also provides another seed value .
- For the requested computation, each server, , creates (or retrieves from its repository, if available already) a corresponding Boolean circuit (B).
- Using the pseudo random generator of Blum, Blum, Shub, each server, , uses the seed value to generate its shares for the pair of garbled values and a λ value for each wire in the circuit (B). Each server, , generates a pseudorandom bit sequence of length bits using seed value ; here W denotes the number of wires in the Boolean circuit (B).
- The client instructs the n servers to construct the shares () of a BMR garbled circuit, , using their shares as private inputs for the secure multiparty computation protocol of Goldreich. Each pair of servers, , generates pseudorandom bits using pairwise seed values while using the protocol of Goldreich. Let denote the shares of server corresponding to the four garbled table entries of gate A. Then, equals the concatenation of all bit strings of the form , where the concatenation operation is carried out over all the gates in the circuit.
- The client instructs each of the n servers, to send their shares to the server . Performing only XOR operations, the server creates the desired circuit, , which is sent to server for evaluation.
- The client generates garbled input values for each input wire in the circuit using the unique seed values , and sends them to the server for evaluation. The client also generates the λ values and the two possible garbled values for each output wire in the circuit using these seed values, and keeps the λ values as secret.
- The server evaluates using the garbled inputs to obtain the garbled output for every output wire in the circuit and sends them to the client. The client now translates these garbled values into plaintext bits, using the λ values, to recover the result of the requested computation.
- For each output wire in the circuit, the client checks whether the garbled output that is received from the evaluator, , matches with one of the two expected garbled values that it computed on its own. If the client determines that there is a match for all output wires, it declares that the evaluator in fact carried out the computation.
5. Complexity
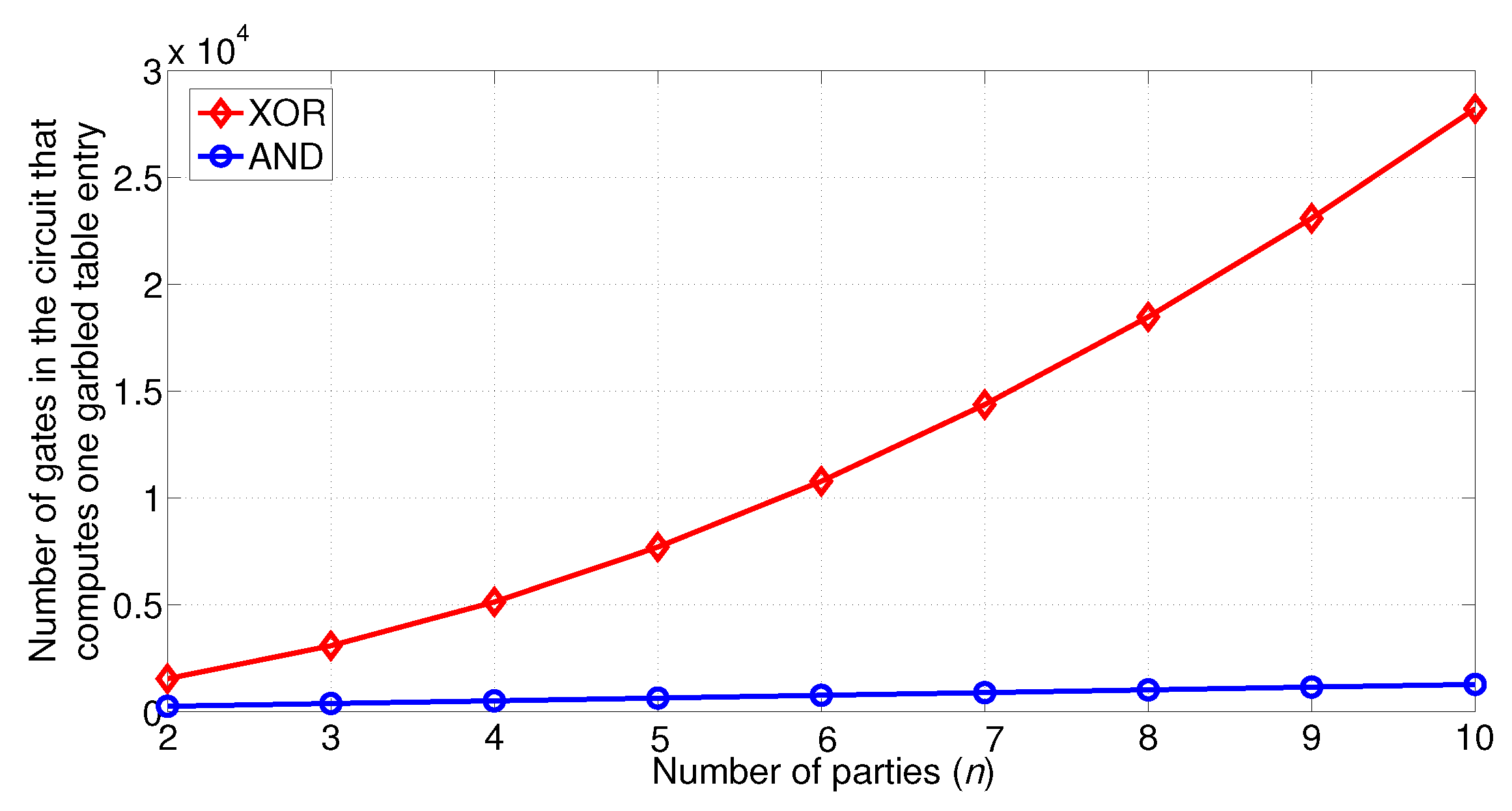
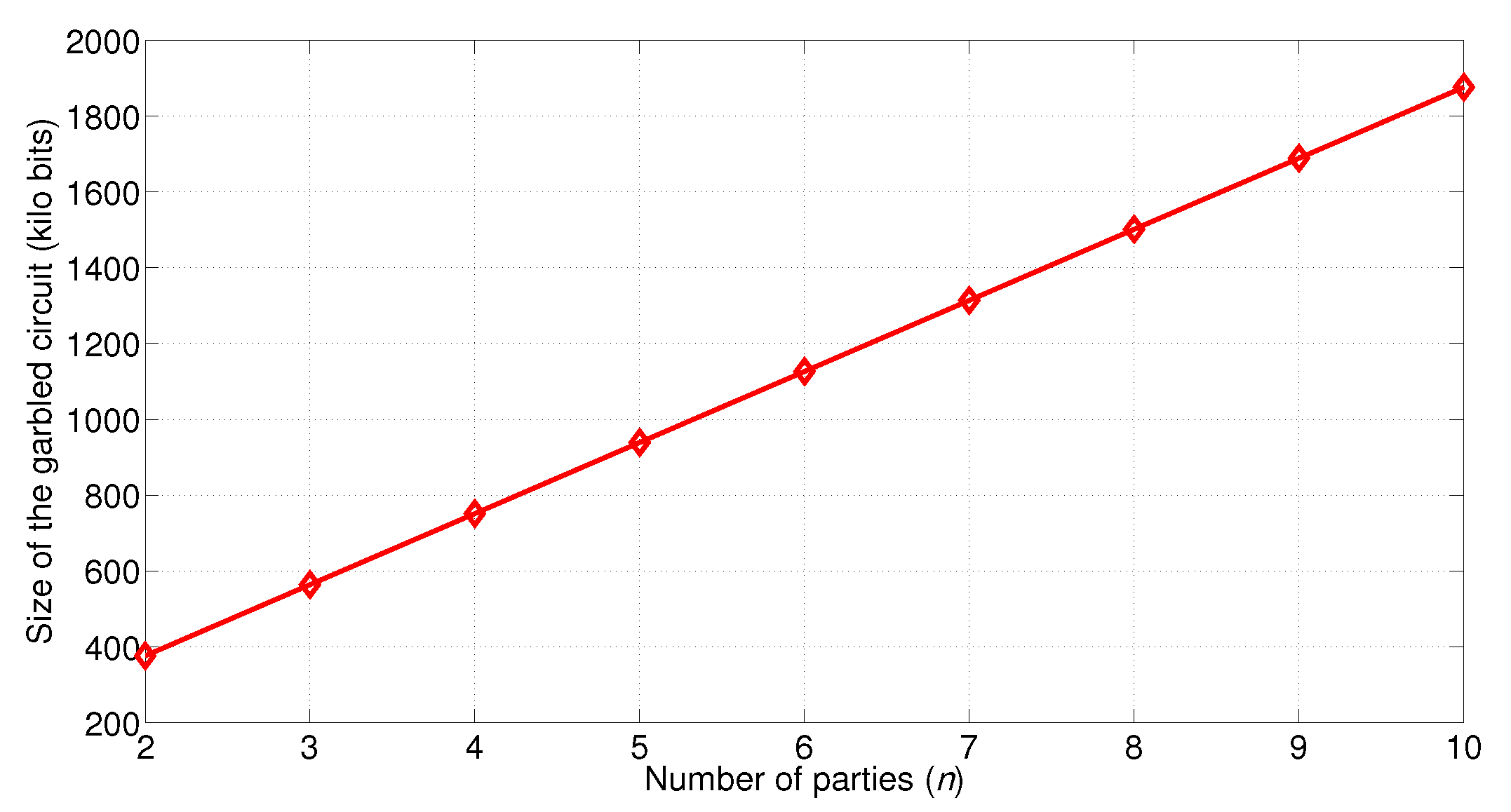
5.1. Circuit Size of One Garbled Table Entry
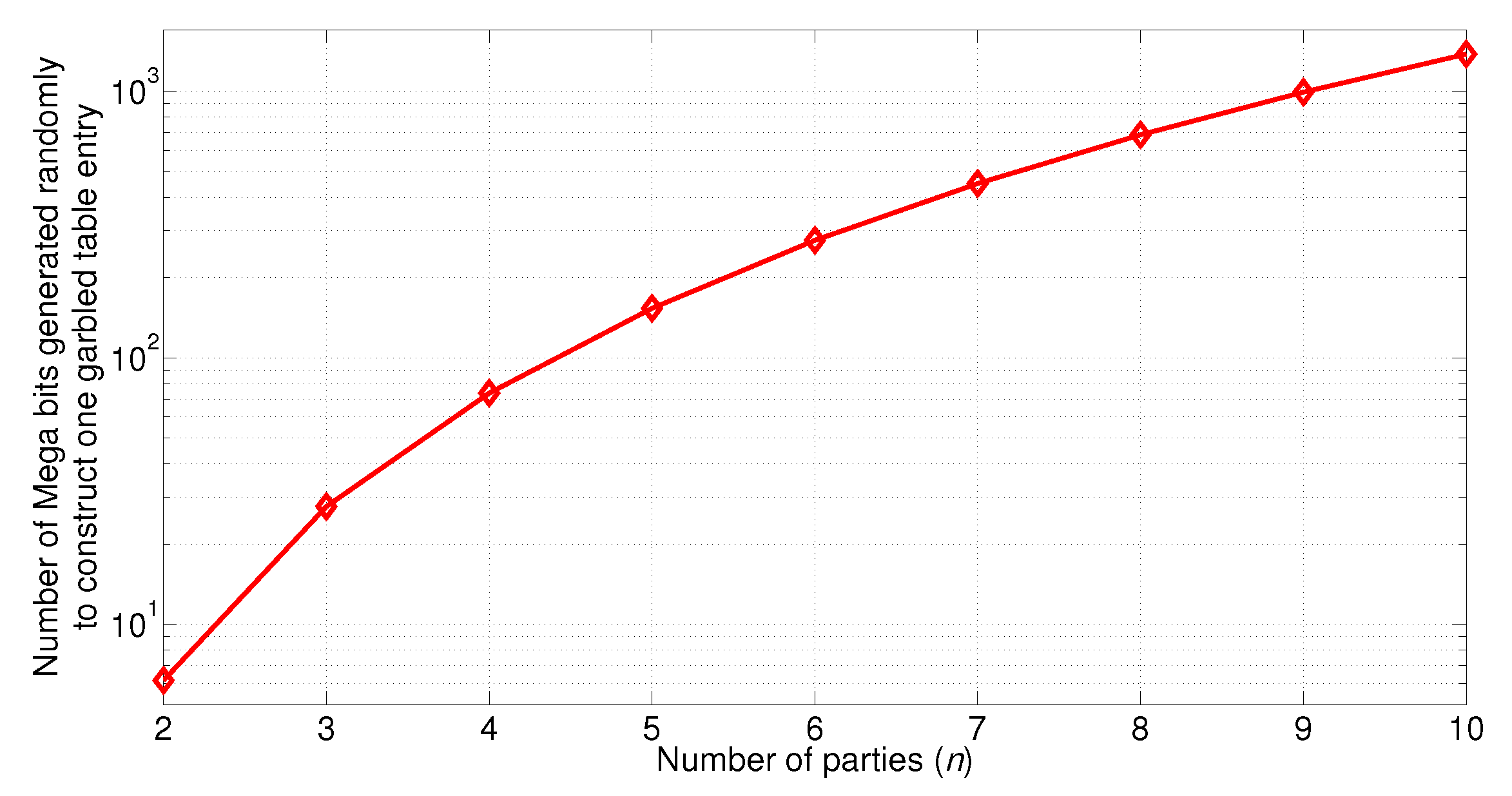
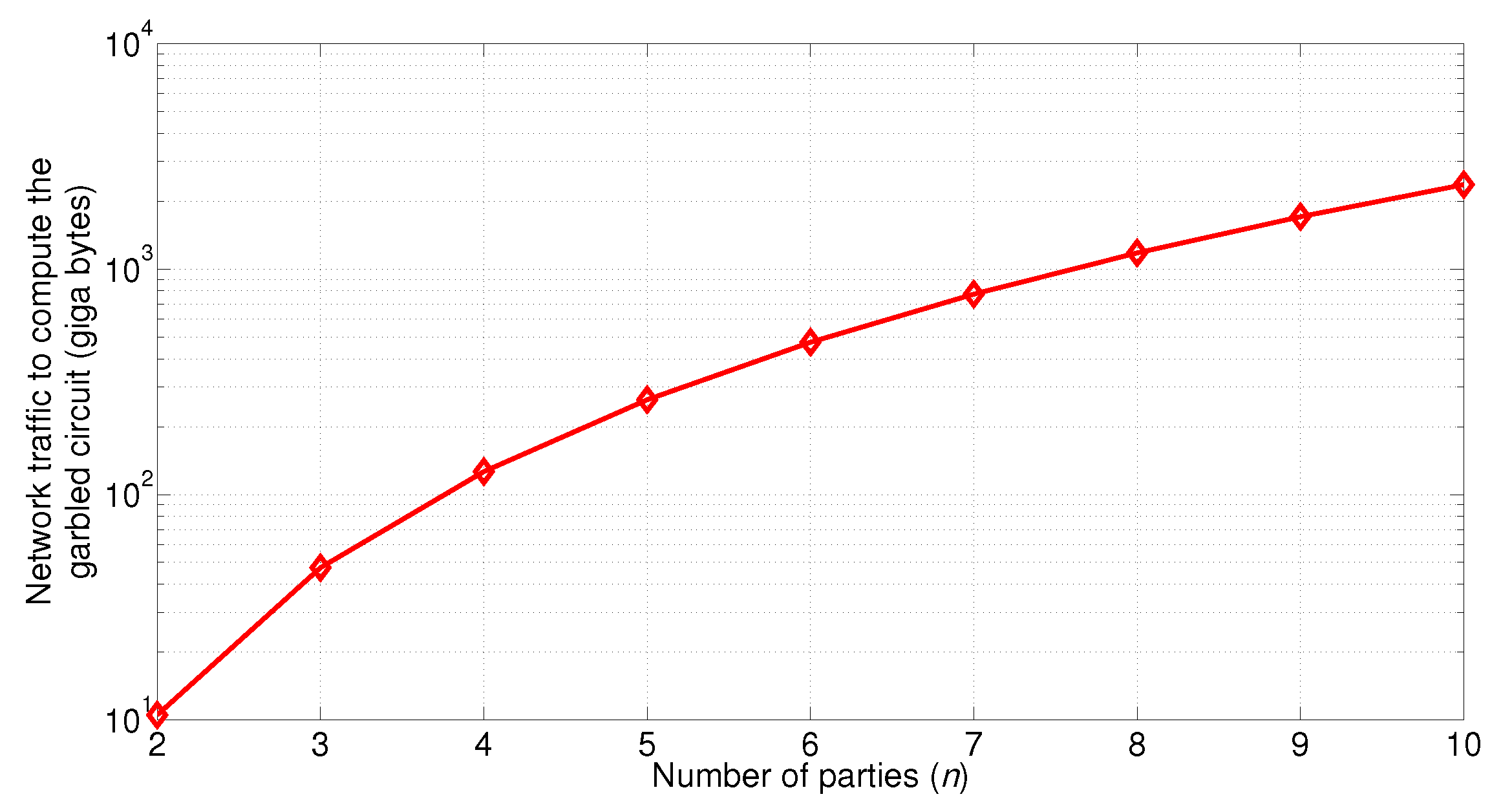
5.2. Communication Cost to Compute One Garbled Table Entry
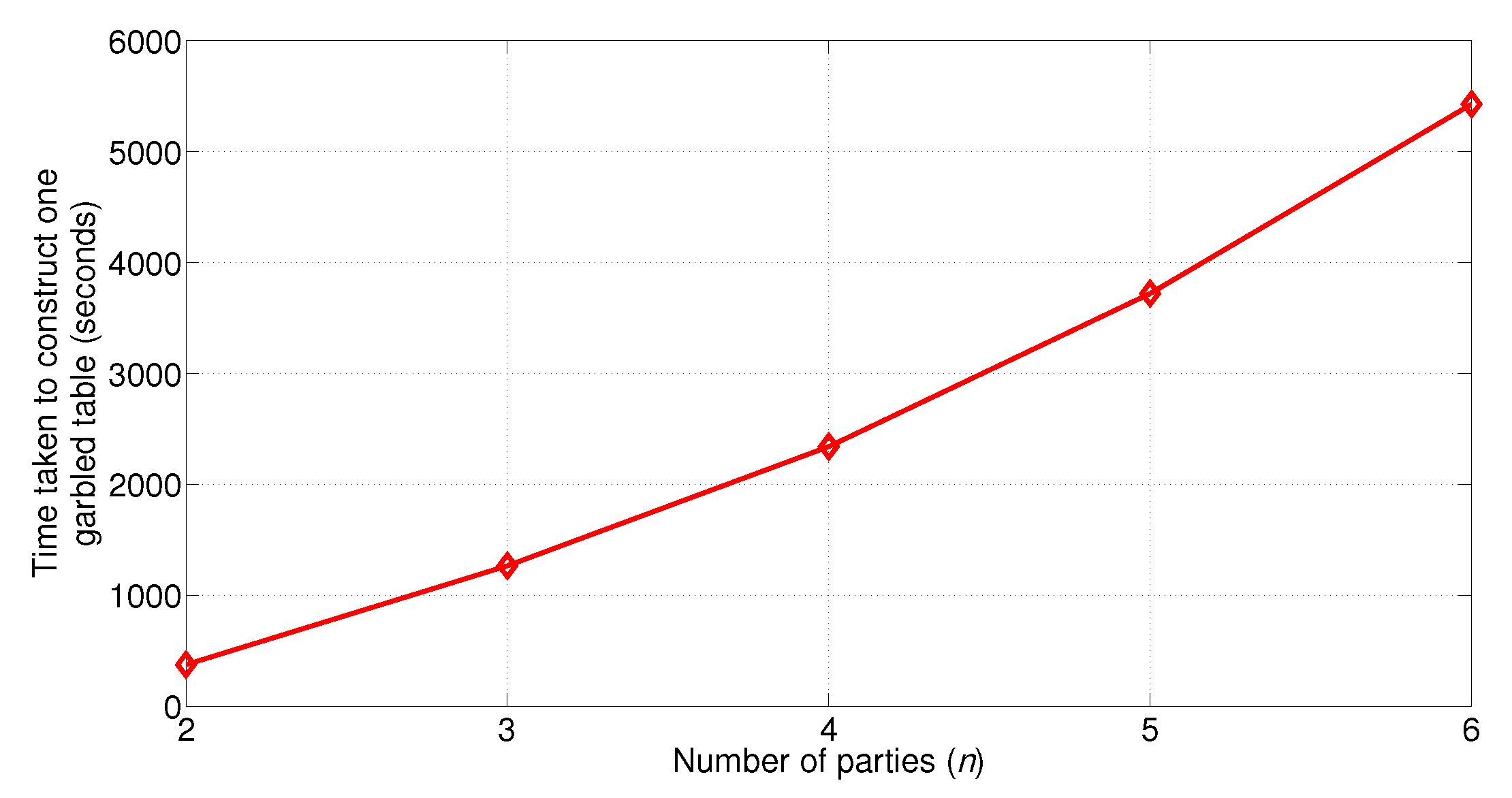
5.3. Computation Cost of Creating the Garbled Circuit
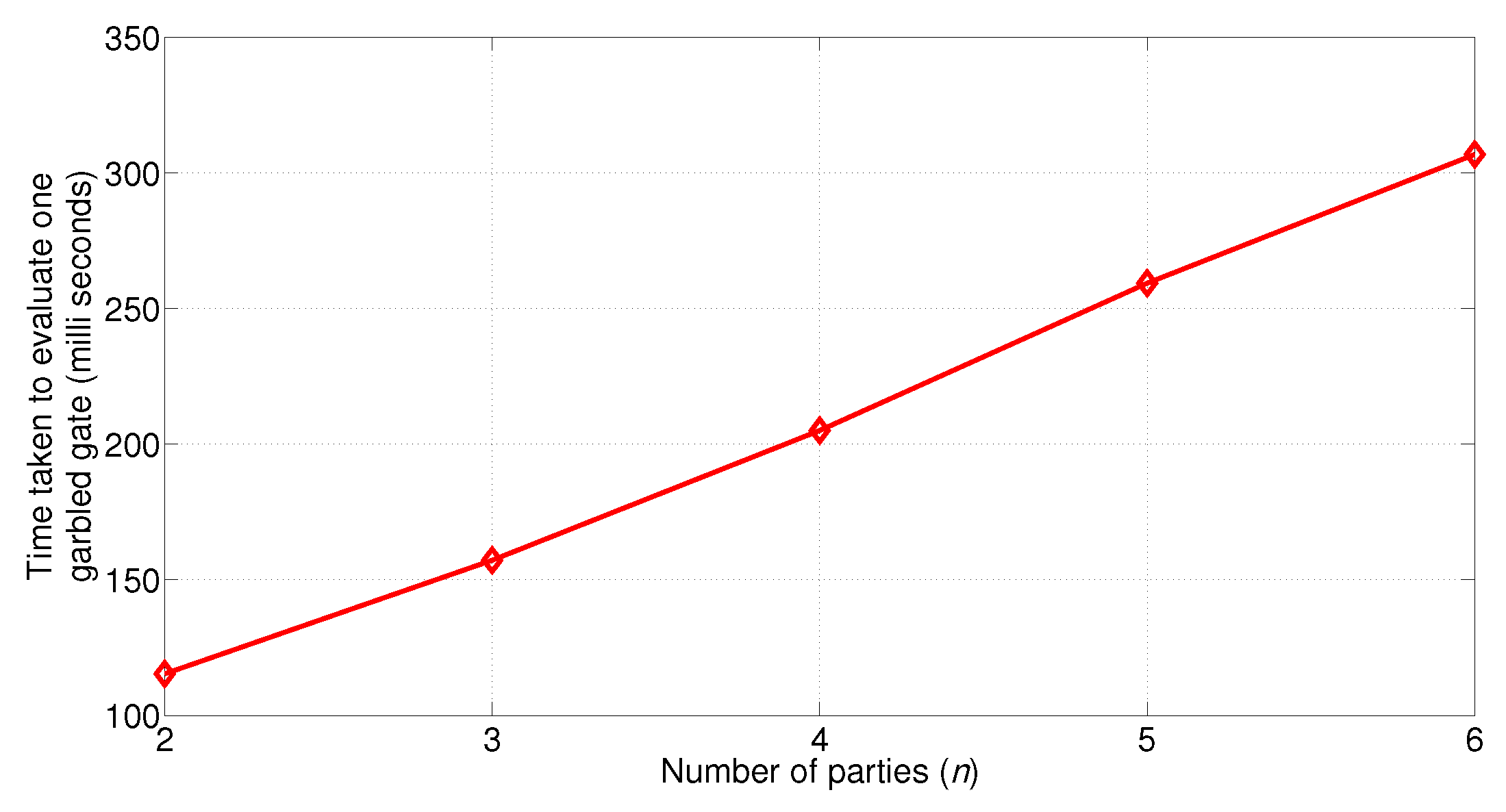
5.4. Cost of Evaluating the Garbled Circuit
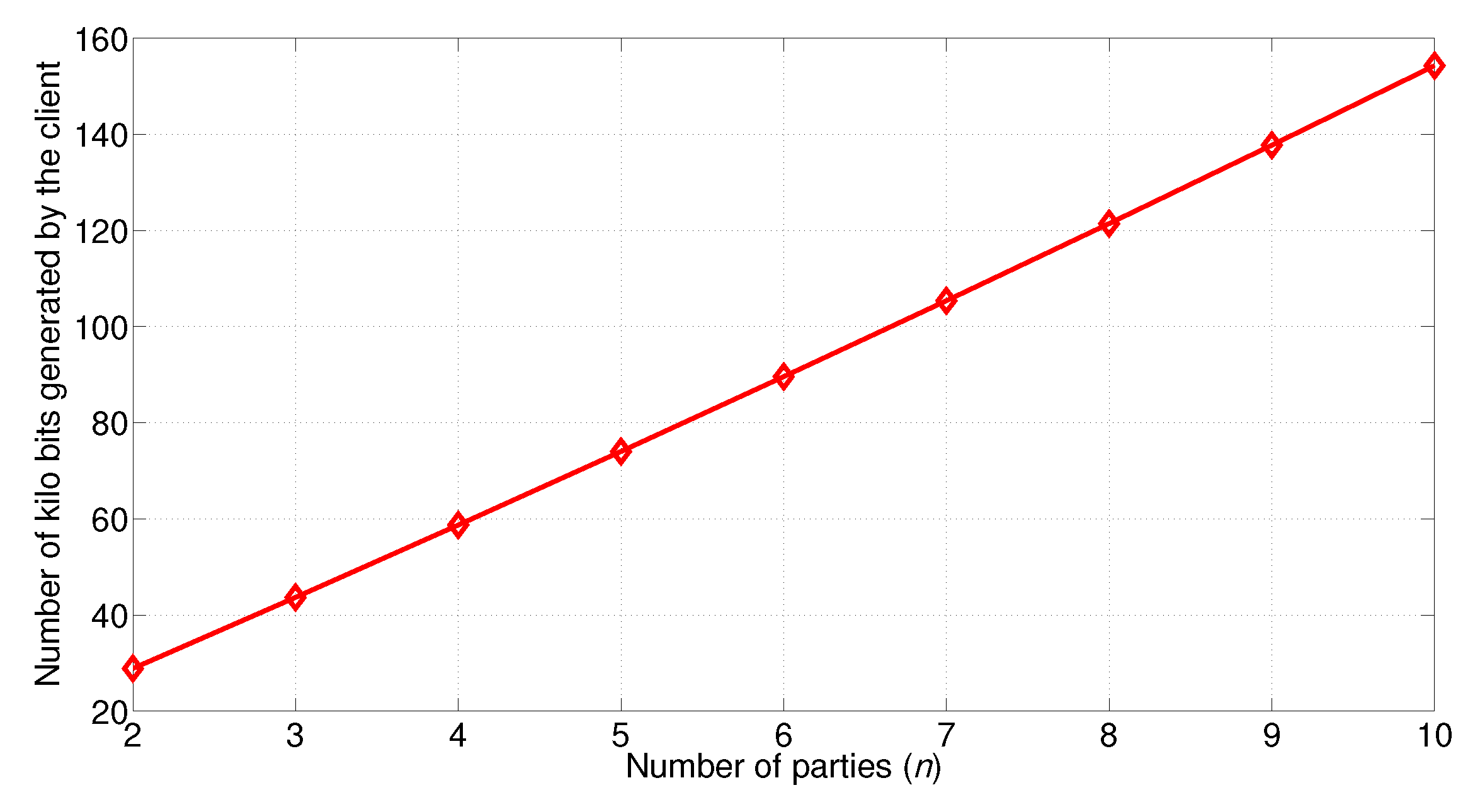
5.5. Cost for the Client
5.6. Comparison of Our Scheme with Gentry’s FHE Scheme
5.7. Construction and Evaluation Time
6. Privacy Preserving Search for the Nearest Bank/ATM
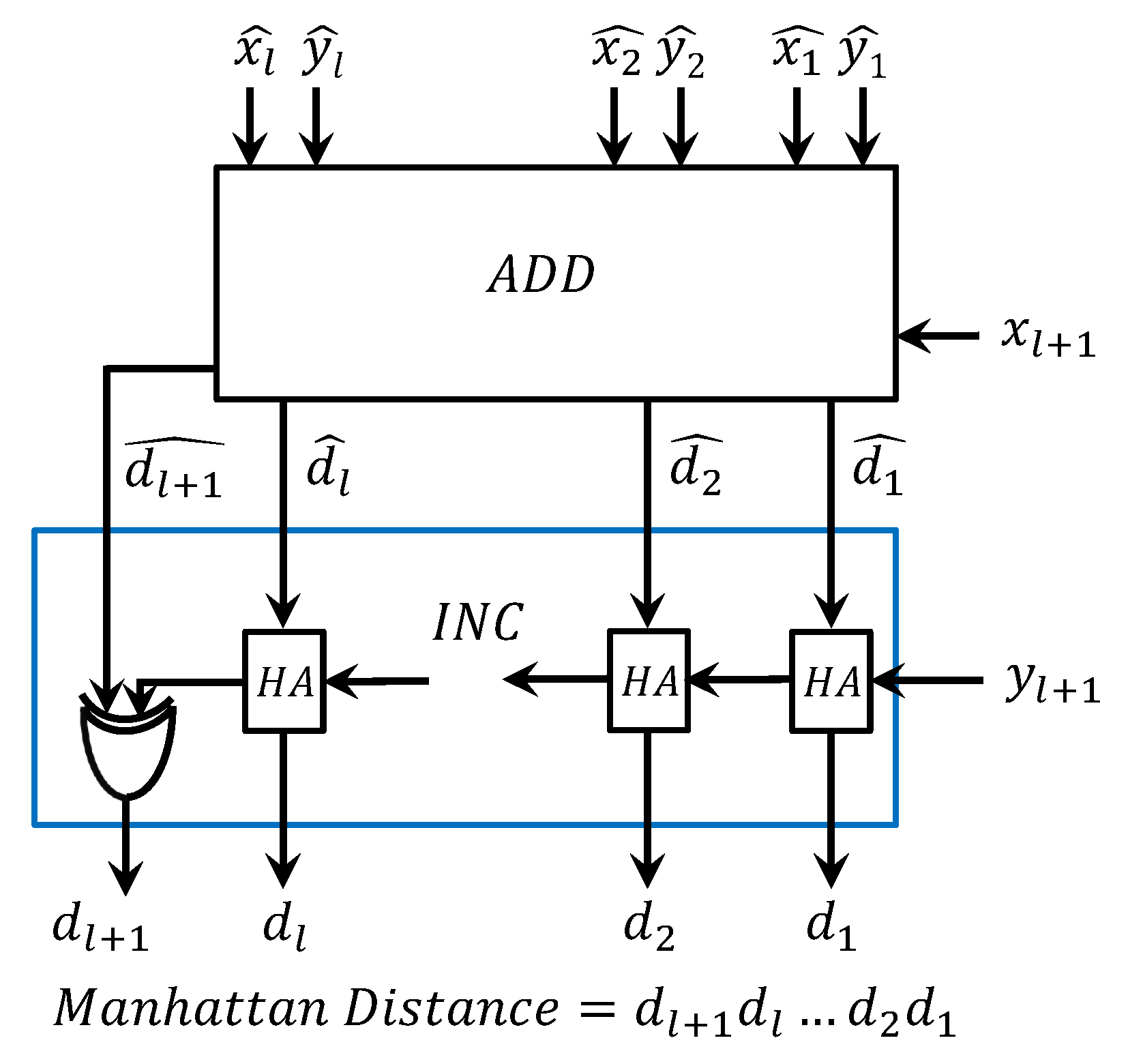
6.1. Circuit for Computing Manhattan Distance
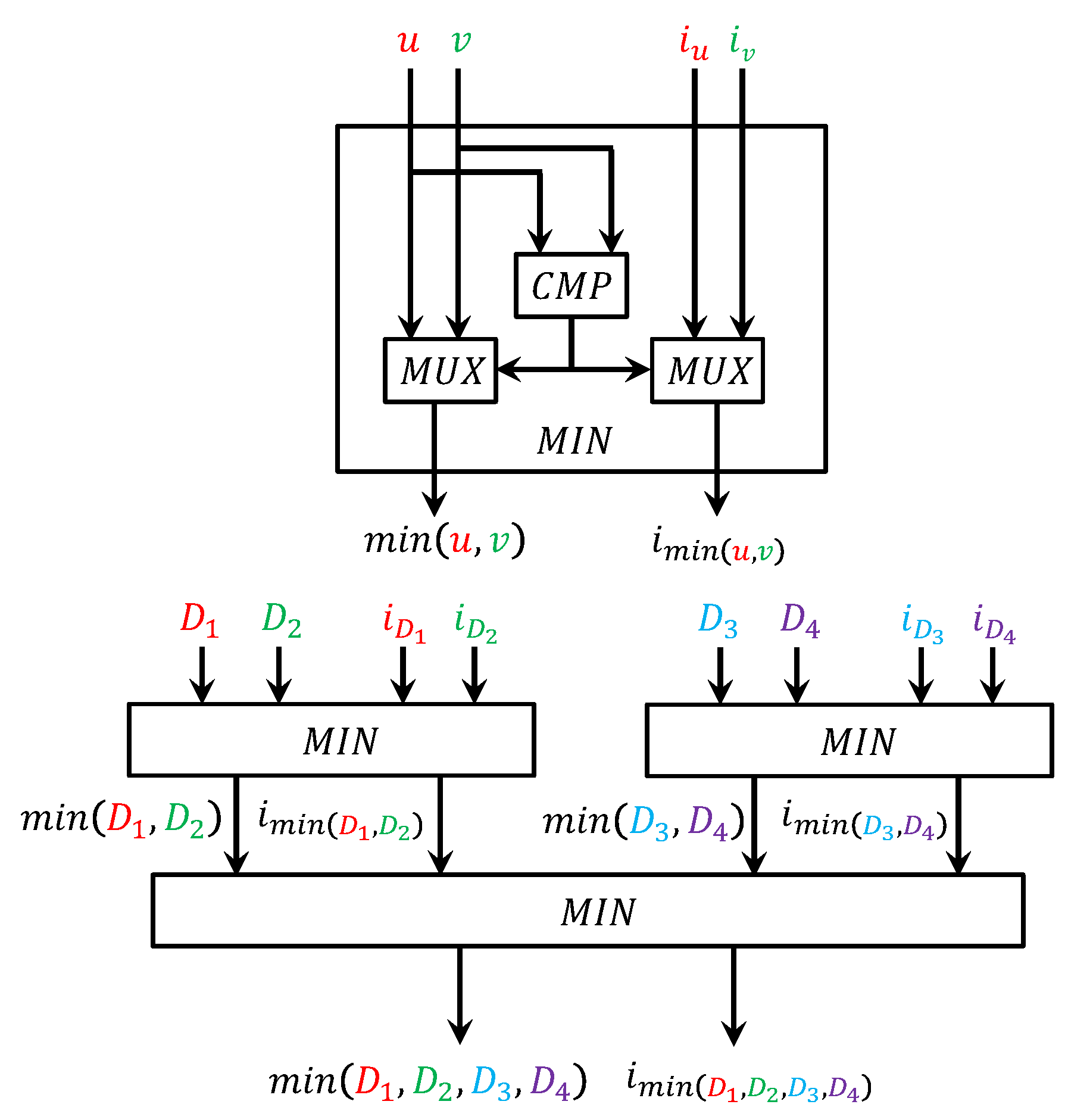
6.2. Circuit for Computing the Nearest ATM
6.3. Server-Side and Client-Side Cost
7. Related Work
8. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Armbrust, M.; Fox, A.; Griffith, R.; Joseph, A.D.; Katz, R.; Konwinski, A.; Lee, G.; Patterson, D.; Rabkin, A.; Stoica, I.; Zaharia, M. A view of cloud computing. Commun. ACM 2010, 53, 50–58. [Google Scholar] [CrossRef]
- Rivest, R.L.; Adleman, L.; Dertouzos, M.L. On data banks and privacy homomorphisms. Found. Secur. Comput. 1978, 4, 169–180. [Google Scholar]
- Gentry, C. Computing arbitrary functions of encrypted data. Commun. ACM 2010, 53, 97–105. [Google Scholar] [CrossRef]
- Brakerski, Z.; Vaikuntanathan, V. Efficient fully homomorphic encryption from (standard) LWE. In IEEE 52Nd Annual Symposium on Foundations of Computer Science; IEEE Computer Society: Washington, DC, USA, 2011; pp. 97–106. [Google Scholar]
- Zhang, X.; Xu, C.; Jin, C.; Xie, R.; Zhao, J. Efficient fully homomorphic encryption from {RLWE} with an extension to a threshold encryption scheme. Future Gener. Comput. Syst. 2014, 36, 180–186. [Google Scholar] [CrossRef]
- Yao, A.C. Protocols for secure computations. In Proceedings of the 23rd Annual Symposium on Foundations of Computer Science, SFCS ’08, Chicago, IL, USA, 3–5 November 1982.
- Yao, A.C.-C. How to generate and exchange secrets. In Proceedings of the 27th Annual Symposium on Foundations of Computer Science, Toronto, ON, Canada, 27–29 October 1986.
- Goldreich, O. Foundations of Cryptography: Volume 2, Basic Applications; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Goldreich, O.; Micali, S.; Wigderson, A. How to play ANY mental game. In Proceedings of the Nineteenth Annual ACM Symposium on Theory of Computing, New York, NY, USA, 25–27 May 1987; pp. 218–229.
- Premnath, S.N.; Haas, Z.J. A Practical, Secure, and Verifiable Cloud Computing for Mobile Systems. In Proceedings of the 9th International Conference on Future Networks and Communications (FNC’14)/The 11th International Conference on Mobile Systems and Pervasive Computing (MobiSPC’14)/Affiliated Workshops, Niagara Falls, Canada, 17–20 August 2014; Series Procedia Computer Science. Volume 34, pp. 474–483.
- Beaver, D.; Micali, S.; Rogaway, P. The round complexity of secure protocols. In Proceedings of the Twenty-Second Annual ACM Symposium on Theory of Computing, Baltimore, MD, USA, 13–17 May 1990; pp. 503–513.
- Rogaway, P. The Round Complexity of Secure Protocols. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 22 April 1991. [Google Scholar]
- Blum, L.; Blum, M.; Shub, M. A simple unpredictable pseudo random number generator. SIAM J. Comput. 1986, 15, 364–383. [Google Scholar] [CrossRef]
- Schneier, B. Applied Cryptography: Protocols, Algorithms, and Source Code in C, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1995. [Google Scholar]
- Naor, M.; Pinkas, B. Efficient oblivious transfer protocols. In Proceedings of the Twelfth Annual ACM-SIAM Symposium on Discrete Algorithms, Washington, DC, USA, 7–9 January 2001; pp. 448–457.
- Naor, M.; Pinkas, B. Computationally secure oblivious transfer. J. Cryptol. 2005, 18, 1–35. [Google Scholar] [CrossRef]
- Barker, E.; Barker, W.; Burr, W.; Polk, W.; Smid, M. Recommendation for key management—Part 1: General (Revision 3). NIST Spec. Publ. 2012, 700–857. Available online: http://www.amazon.com/Recommendation-Key-Management-General-Revision/dp/1499160224 (accessed on 5 May 2016). [Google Scholar]
- Tillich, S.; Smart, N. Circuits of Basic Functions Suitable For MPC and FHE. Available online: http://www.cs.bris.ac.uk/Research /CryptographySecurity/MPC/ (accessed on 15 April 2014).
- Chase. Available online: http://www.chase.com (accessed on 15 April 2014).
- Wells Fargo. Available online: http://www.wellsfargo.com (accessed on 15 April 2014).
- Kolesnikov, V.; Sadeghi, A.R.; Schneider, T. Improved garbled circuit building blocks and applications to auctions and computing minima. In Cryptology and Network Security; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–20. [Google Scholar]
- Huang, Y.; Evans, D.; Katz, J. Private set intersection: Are garbled circuits better than custom protocols. In NDSS; The Internet Society: San Diego, CA, USA, 2012. [Google Scholar]
- Domingo-Ferrer, J. A provably secure additive and multiplicative privacy homomorphism. In Information Security; Springer: Berlin/Heidelberg, Germany, 2002; pp. 471–483. [Google Scholar]
- Lindell, Y.; Pinkas, B. A proof of security of yao’s protocol for two-party computation. J. Cryptol. 2009, 22, 168–188. [Google Scholar] [CrossRef]
- Lindell, Y.; Pinkas, B. Secure multiparty computation for privacy-preserving data mining. J. Priv. Confid. 2009, 1, 59–98. [Google Scholar]
- Henecka, W.; Sadeghi, A.R.; Schneider, T.; Wehrenberg, I. TASTY: Tool for automating secure two-party computations. In Proceedings of the 17th ACM Conference on Computer and Communications Security, Chicago, IL, USA, 4–8 October 2010; pp. 451–462.
- Malkhi, D.; Nisan, N.; Pinkas, B.; Sella, Y. Fairplay—A secure two-party computation system. In USENIX Security Symposium; USENIX Association: San Diego, CA, USA, 2004. [Google Scholar]
- Ben-David, A.; Nisan, N.; Pinkas, B. FairplayMP: A system for secure multi-party computation. In Proceedings of the 15th ACM Conference on Computer and Communications Security, Alexandria, VA, USA, 27–31 October 2008; pp. 257–266.
- Burkhart, M.; Strasser, M.; Many, D.; Dimitropoulos, X. SEPIA: Privacy-preserving aggregation of multi-domain network events and statistics. In Proceedings of the 19th USENIX conference on Security, Washington, DC, USA, 11–13 August 2010.
- Damgård, I.; Pastro, V.; Smart, N.; Zakarias, S. Multiparty computation from somewhat homomorphic encryption. In Advances in Cryptology–CRYPTO 2012; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Ames, S.; Venkitasubramaniam, M.; Page, A.; Kocabas, O.; Soyata, T. Secure health monitoring in the cloud using homomorphic encryption, a branching-program formulation. In Enabling Real-Time Mobile Cloud Computing through Emerging Technologies; Soyata, T., Ed.; IGI Global: Hershey, PA, USA, 2015; pp. 116–152. [Google Scholar]
- Bugiel, S.; Nürnberger, S.; Sadeghi, A.R.; Schneider, T. Twin clouds: Secure cloud computing with low latency. In Communications and Multimedia Security; Springer: Berlin/Heidelberg, Germany, 2011; pp. 32–44. [Google Scholar]
- Goldwasser, S.; Kalai, Y.; Popa, R.A.; Vaikuntanathan, V.; Zeldovich, N. Reusable garbled circuits and succinct functional encryption. In Proceedings of the Forty-Fifth Annual ACM Symposium on Theory of Computing, Palo Alto, CA, USA, 1–4 June 2013; pp. 555–564.
- Gennaro, R.; Gentry, C.; Parno, B. Non interactive verifiable computing: Outsourcing computation to untrusted workers. In Advances in Cryptology–CRYPTO 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 465–482. [Google Scholar]
- Naehrig, M.; Lauter, K.; Vaikuntanathan, V. Can homomorphic encryption be practical? In Proceedings of the 3rd ACM Workshop on Cloud Computing Security Workshop, Chicago, IL, USA, 17–21 October 2011; pp. 113–124.
- Duan, Y.; Canny, J.; Zhan, J. P4P: Practical large-scale privacy-preserving distributed computation robust against malicious users. In Proceedings of the 19th USENIX conference on Security, Washington, DC, USA, 11–13 August 2010.
- Carter, H.; Mood, B.; Traynor, P.; Butler, K. Secure outsourced garbled circuit evaluation for mobile devices. In Proceedings of the 22nd USENIX Conference on Security, Washington, DC, USA, 14–16 August 2013.
- Computing in the Cloud. Available online: https://people.ece.cornell.edu/haas/wnl/CiC (accessed on 15 July 2014).



| P | Q | R |
|---|---|---|
| Bank/ATM | Location |
|---|---|
| Chase | 201 South 0 East |
| Chase | 185 South 100 East |
| Chase | 376 East 400 South |
| Chase | 531 East 400 South |
| Wells Fargo | 299 South 0 East |
| Wells Fargo | 381 East 300 South |
| Wells Fargo | 79 South 0 East |
| Wells Fargo | 778 South 0 East |
| Wells Fargo | 570 South 700 East |
| Wells Fargo | 235 South 1300 East |
| Block | Gates | Gates |
|---|---|---|
| 0 | ||
| l | ||
| l | ||
| Block | Gates | Gates |
|---|---|---|
| Block | Gates | Gates |
|---|---|---|
| 2596 | 854 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nandha Premnath, S.; Haas, Z.J. Supporting Privacy of Computations in Mobile Big Data Systems. Future Internet 2016, 8, 17. https://doi.org/10.3390/fi8020017
Nandha Premnath S, Haas ZJ. Supporting Privacy of Computations in Mobile Big Data Systems. Future Internet. 2016; 8(2):17. https://doi.org/10.3390/fi8020017
Chicago/Turabian StyleNandha Premnath, Sriram, and Zygmunt J. Haas. 2016. "Supporting Privacy of Computations in Mobile Big Data Systems" Future Internet 8, no. 2: 17. https://doi.org/10.3390/fi8020017
APA StyleNandha Premnath, S., & Haas, Z. J. (2016). Supporting Privacy of Computations in Mobile Big Data Systems. Future Internet, 8(2), 17. https://doi.org/10.3390/fi8020017