Using Financial Instruments to Transfer the Information Security Risks
Abstract
:1. Introduction
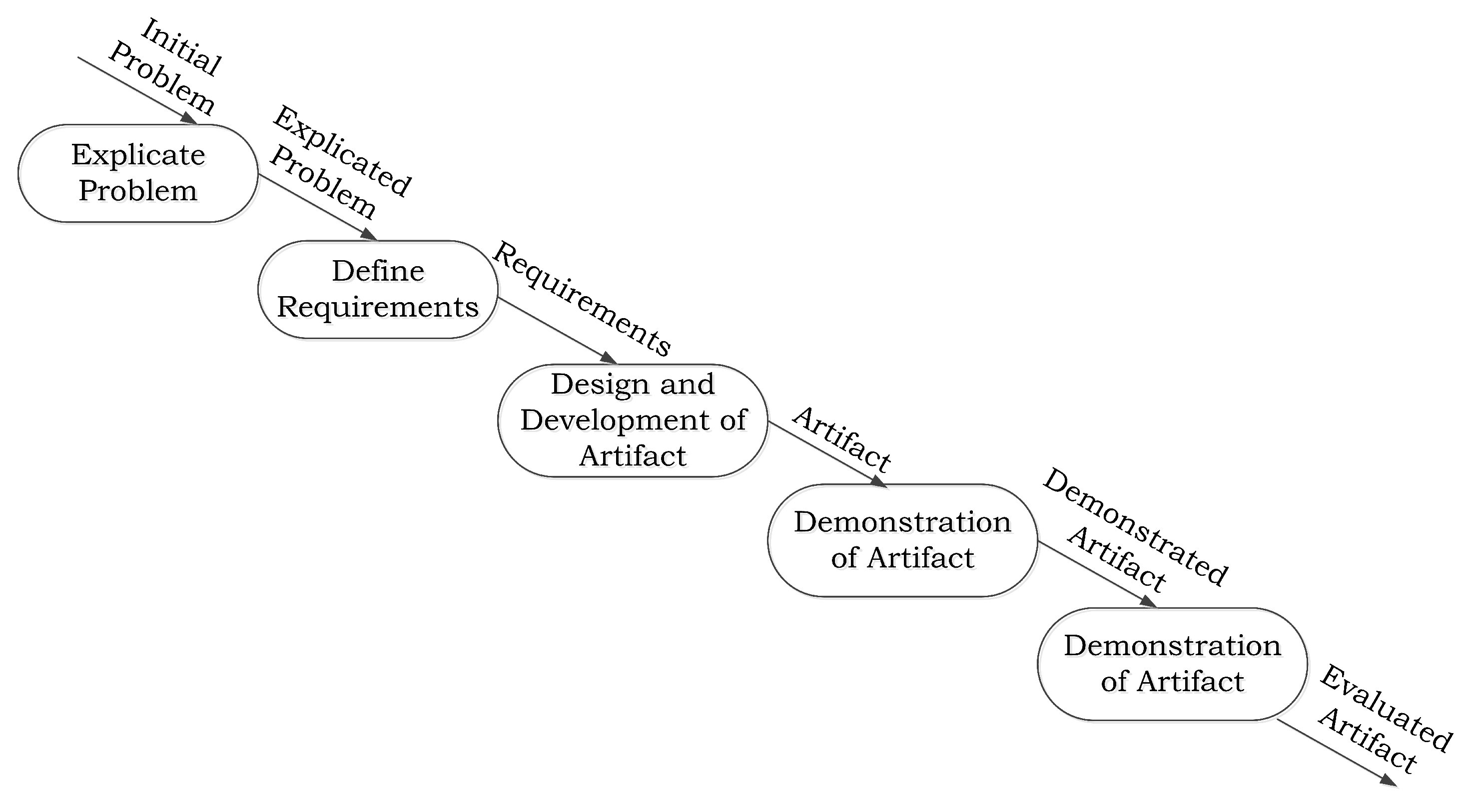
2. Research Method
2.1. Explicate Problem
2.2. Define Requirements
2.3. Design and Development of the Artifact
2.4. Demonstration of the Artifact
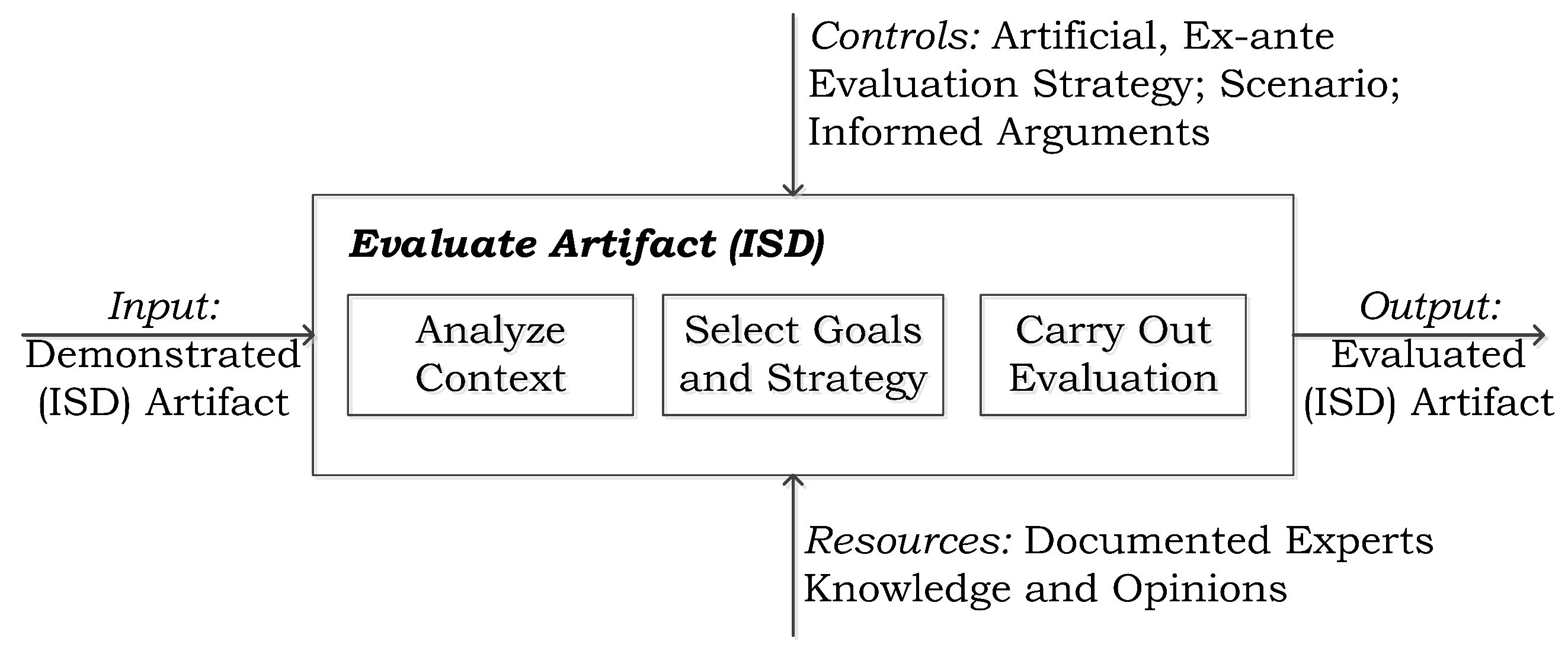
2.5. Evaluation of the Artifact
3. Related Work
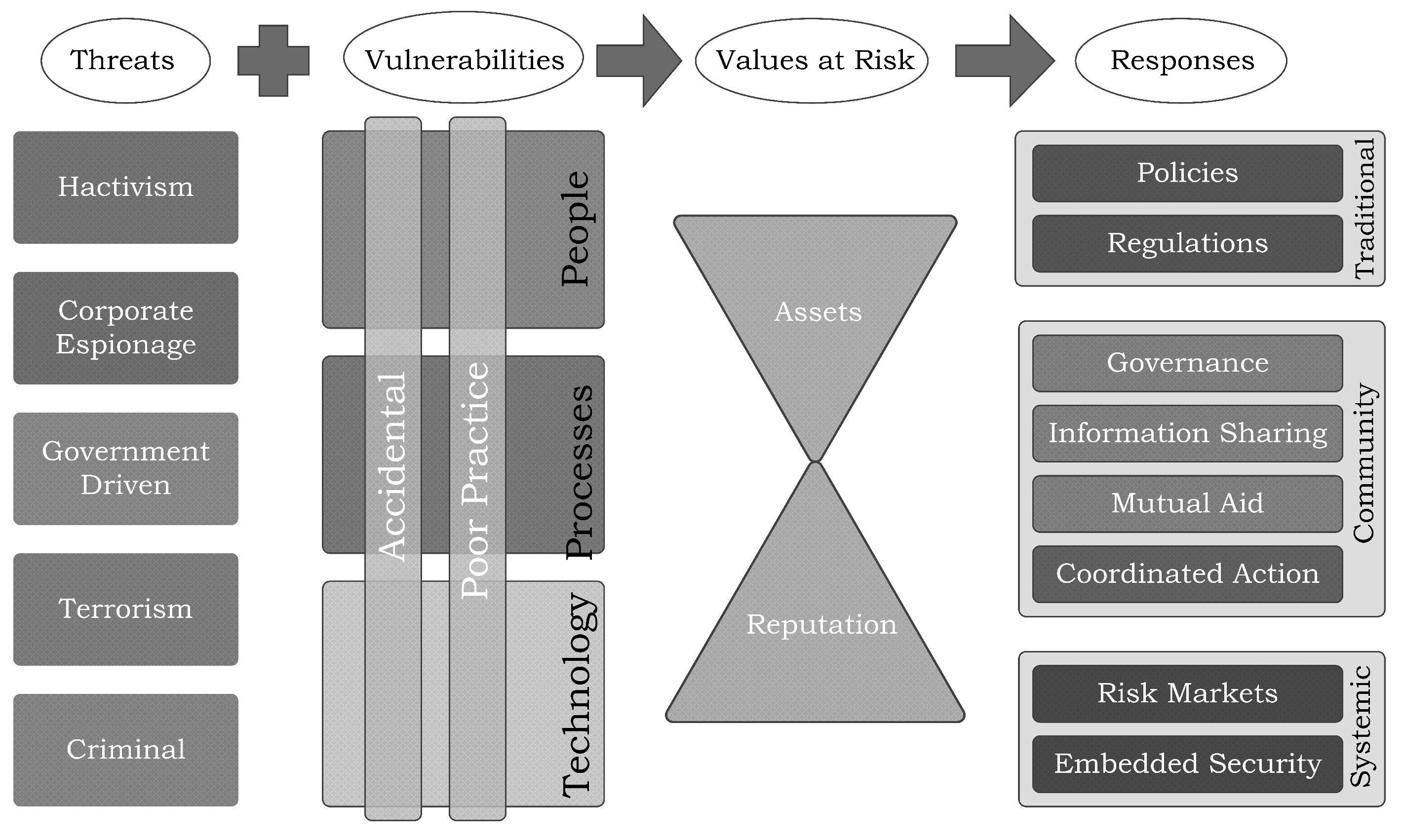
3.1. Information Security Risk Management
3.1.1. Risk Identification
3.1.2. Risk Estimation
3.1.3. Risk Response
- Avoidance: This strategy involves avoiding the possible threats and attacks. The source of risk or the asset’s exposure to the risk is eliminated. This strategy is usually used in the cases where the impact of the risk is more than the benefit of having that particular asset, such as full internet connectivity to all the computer systems in the company.
- Acceptance: This strategy involves accepting the security risk and its potential impact as a cost of doing the business. This strategy is applied in the cases where the cost of implementing the security control is likely to be higher than the potential impact of the risk materialization.
- Reduction (Mitigation): This strategy aims to reduce the risk exposure by implementing the appropriate security controls, security policies and compliance with regulatory requirements. It is a primary and commonly applied risk management strategy.
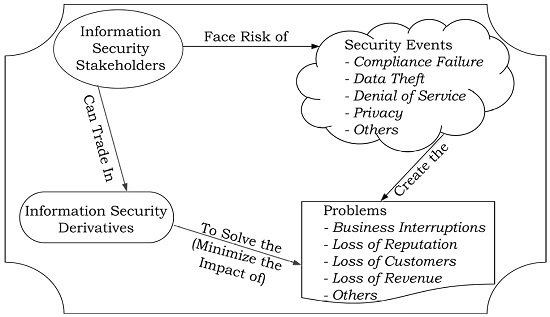
- Transference: Risk transferring strategy is applied to partially transfer the risk exposure to a third party by outsourcing the security services or purchasing a cyber-insurance or taking an appropriate position in the information security financial instruments. In the light of various cyber security incidents where technical defenses failed to prevent the attacks, risk-transference strategy can play a vital role in mitigating the residual risk.
3.2. Financial Engineering and Risk Management
3.3. Financial Derivatives to Hedge Risks
3.3.1. Macro Market
3.3.2. Economic Derivatives
3.3.3. Weather Derivatives
3.3.4. Electricity Derivatives
3.3.5. Cloud Computing Derivatives
3.3.6. Natural Disaster Risk Management Instruments
3.3.7. Terrorism Risk Management Instruments
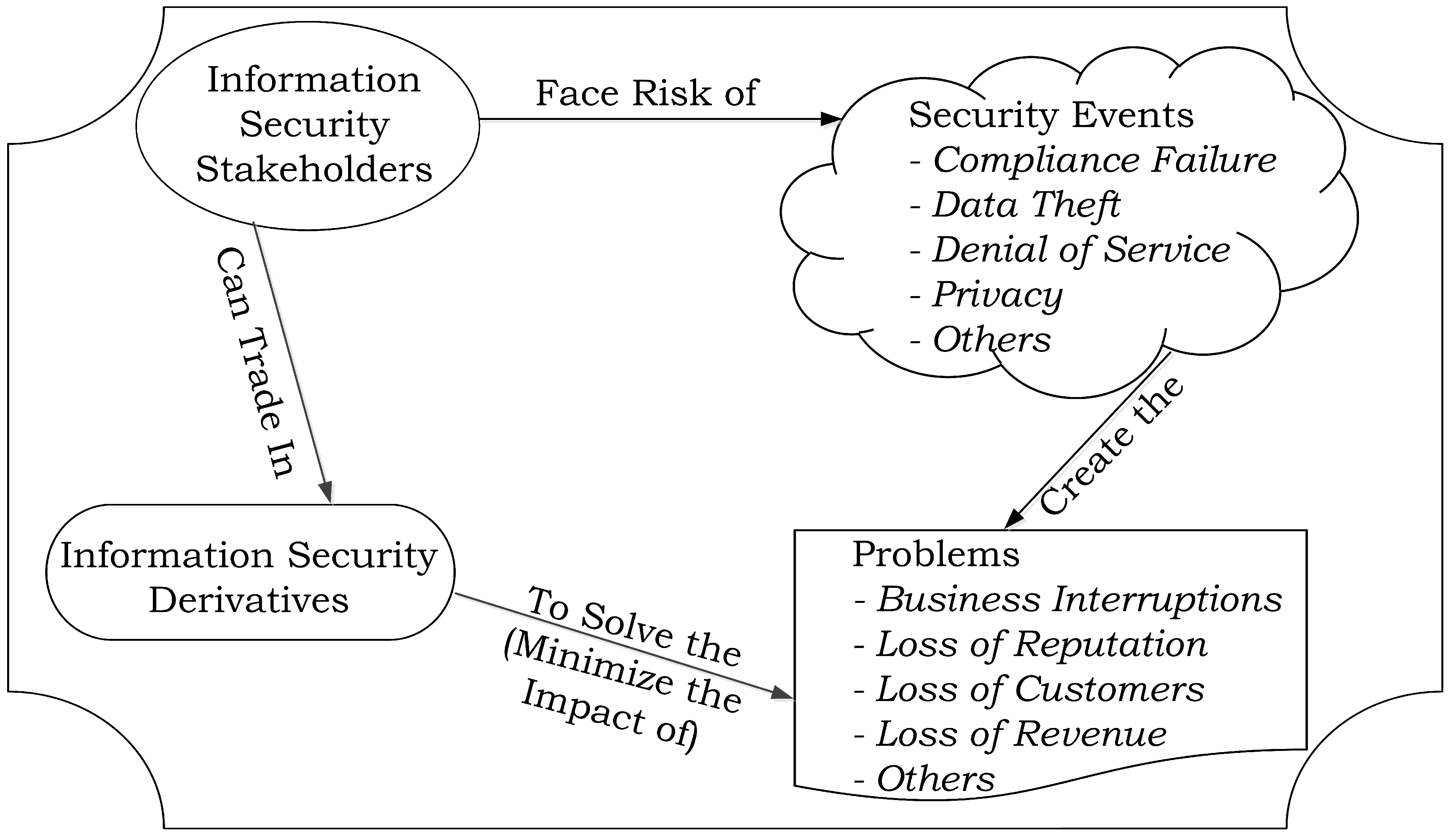
4. Problem Elicitation
- Limited Efficiency and Effectiveness of Cyber-Insurance: Cyber-insurance is the “statistical” approach to hedge the risks, and it relies on the law of large numbers. For the mechanism to work successfully, the risks covered must be reasonably independent to each other and the frequencies (estimation) must be known. All that is required for the success of insurance products is a reliable actuarial table, and a large pool of insureds to distribute the risk. However, unlike other insurance products, cyber-insurance products are designed in absence of proven actuarial tables. There is a lack of historical cyber-incidents data which limits the variety of cyber-insurance products and cyber-insurer’s are exposed to a risk of insolvency due to interconnected and high impact nature of cyber-risks. Thus, the correlated nature of cyber-risks negatively affects the efficiency and effectiveness of cyber-insurance products. The overall problem of inefficiency and ineffectiveness can be better understood in the light of following problems in the cyber-insurance products.
- Information Asymmetry: Cyber-insurance markets are inefficient and incur additional costs due to information asymmetry. The cyber-insurance products are often customized to address the specific requirements of the client, however, if the cyber-insurance buyer does not know all about the product coverage, then there is an information asymmetry between the client and the provider. This can be explained with the theory of “The Market for Lemons” proposed by George A. Akerlof [66]. Akerlof introduced “The Market for Lemons” with the question of why there is a “large price difference between new cars and those which have just left the showroom” [66]. It suggests that cyber-insurance products are a trust good, and all the coverage details are not visible to the buyer. As a buyer cannot differentiate between a “good” coverage and “less” coverage products, the product is traded at the price of “less” coverage products (and high risk) (lemons). The famous case of Sony and Zurich Insurance is a relevant example [67].In addition to the problem of lemons market, the cyber-insurance domain suffers from the problem of “adverse selection”. An adverse selection arises when the client has some relevant information and the information is not disclosed to the cyber-insurance provider, i.e., the client knows about the risk for which it wants to acquire a cyber-insurance policy. The adverse selection can be explained with the theory of “The Market for Insurance” [68].The third type of information asymmetry in the cyber-insurance field is “moral hazard”. A moral hazard arises when the buyer is purchasing a coverage based on the experience of losses. Thus, the buyer of the insurance product may have no or less incentive in mitigating the risk, instead the buyer prefers to transfer the risk to the insurer.
- Incomplete Markets: Cyber-insurance products available in the market are very limited in terms of variety of risks and their coverage [69,70]. In other words, the cyber-insurance markets do not provide an opportunity to hedge “all” (wide variety) of risks for which hedging mechanisms are required. In such a scenario, information security stakeholders have to bear the risk, or they use the less optimal mechanisms to transfer/hedge the risks [69]. This discrepancy in risk exposure and actual risk coverage is usually termed as “Basis Risk”.
- Lack of Liquidity: It is crucial to have liquid markets to achieve effective risk hedging. However, once a cyber-insurance policy is purchased, the client has no mechanism during the contract period to adjust (buy or sell) his position according to the latest risk scenario.
- High Transaction Cost: Currently, transaction costs are high in cyber-insurance and reinsurance markets. Typically, the risk is transferred through contracts, credit risk of counterparties is evaluated, and risk management systems are deployed and maintained. However, due to the interdependent and correlated nature of information security risks, the capitalization levels to support the insurance liabilities may be dramatically out of equilibrium [69,70,71].
- Regulatory Capital Requirements: Regulatory requirements, such as Solvency-II [72] require (re-)insurers to meet the capital requirements. These capital requirements and requirements to maintain a risk management system increases the cost of capital. Also, this creates barriers to entry for new entrants into the cyber-(re)insurance market.
- Counterparty Credit Risk: A counterparty to an insurance contract is exposed to the risk that its counterparty will go bankrupt during the life of the contract. In other words, an insurance cover can only be realized if the insurer is solvent when the risk is materialized. However, due to inefficient risk estimation [69,71], failure to comply with regulatory requirements [72], and simultaneous claims filed by multiple clients due to interdependent nature/materialization of risk [69,70,71], the insurer may not be able to settle all the claims.
- Lack of Data: The cyber-(re)insurance industry faces a unique challenge of lack of actuarial data. In absence of relevant historical data cyber-(re)insurer’s may not be close to actual risk probabilities and their risk assessment may either be an overestimate or an underestimate of the risk exposure, and its impact [69,71].
5. Requirements for Information Security Derivatives
- The financial instrument should allow an effective and efficient hedging mechanism for the risk exposure to the underlying information security event.The information security derivatives should perform better than the cyber-insurance products on the following properties.
- Increased information elicitation and aggregation
- Strong manipulation resistance
- Increased market products and size
- Increased scalability
- Rapid implementation
- Increased liquidity
- Reduced transaction cost
- Increased price transparency
- Reduced cost of capital
- Reduced risk to the issuer or market operator
- Reduced settlement and clearing costs
- Diversification of counterparty credit risk
- Increased data generation
6. Design Specifications for Information Security Derivatives
6.1. Risk Mitigation with ISD
- Determine the hedge amount to be invested in the complementary states
- Distribution of the said amount among the complementary states
- There are four possible states (outcomes) of the underlying event, namely s1, s2, s3, and s4.
- The states to be hedged are s1 and s2. Thus, the complementary states are s3 and s4.
- Existing investment in each state is $40, $50, $30, and $60 respectively.
- A trader has previously invested $10 (IH) in s1 and s2.
- Allocation of $10 in s1 and s2 is proportionate to existing investment in respective states. s1 is allocated $4.444 (=10 * (40/(40 + 50))) and s2 is allocated $5.555 (=10 * (50/(40 + 50))).
- Therefore, the amounts invested in each state minus the trader’s investment is $35.555, $44.444, $30, and $60 for the states s1, s2, s3, and s4, respectively.
6.2. ISD Design Process
6.2.1. Identification of Security Events
6.2.2. Defining States
6.2.3. Types of ISD
6.2.4. Pricing of ISD
6.2.5. Payout Trigger
6.2.6. Payout Structure
6.2.7. Decision Criteria
6.2.8. Specification of Derivatives
6.2.9. Trading of ISD
7. Demonstration: An Example Application
7.1. Information Security Options
7.1.1. Scenario
7.1.2. Contract Specification
7.1.3. Participants and Incentives
7.1.4. Risk Hedging
- S1 = Unit-1 suffers a (pre-specified type of) cyber-attack and production at the unit is adversely affected.
- S2 = Unit-1 suffers no cyber-attack or the production at the unit is not affected.
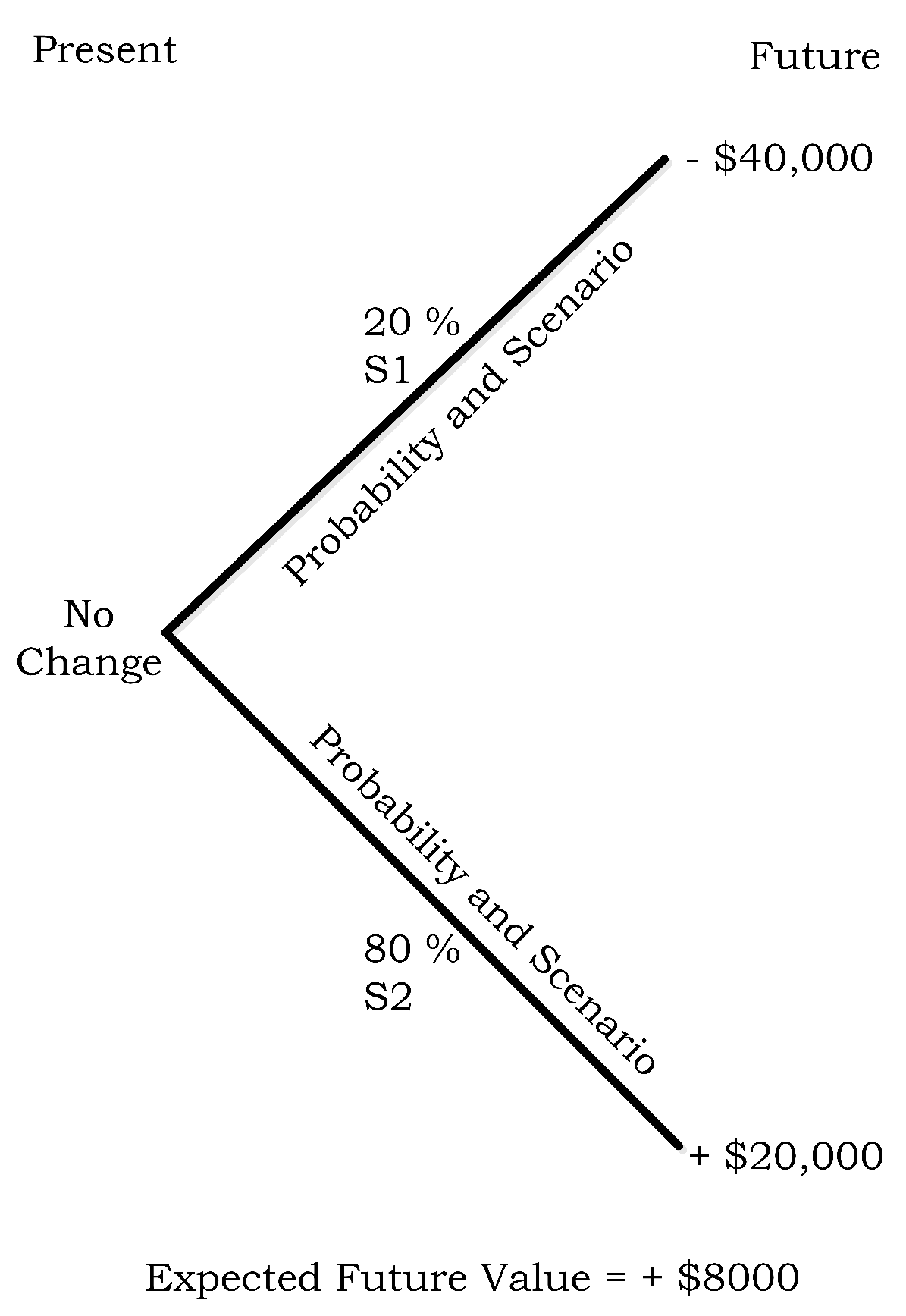
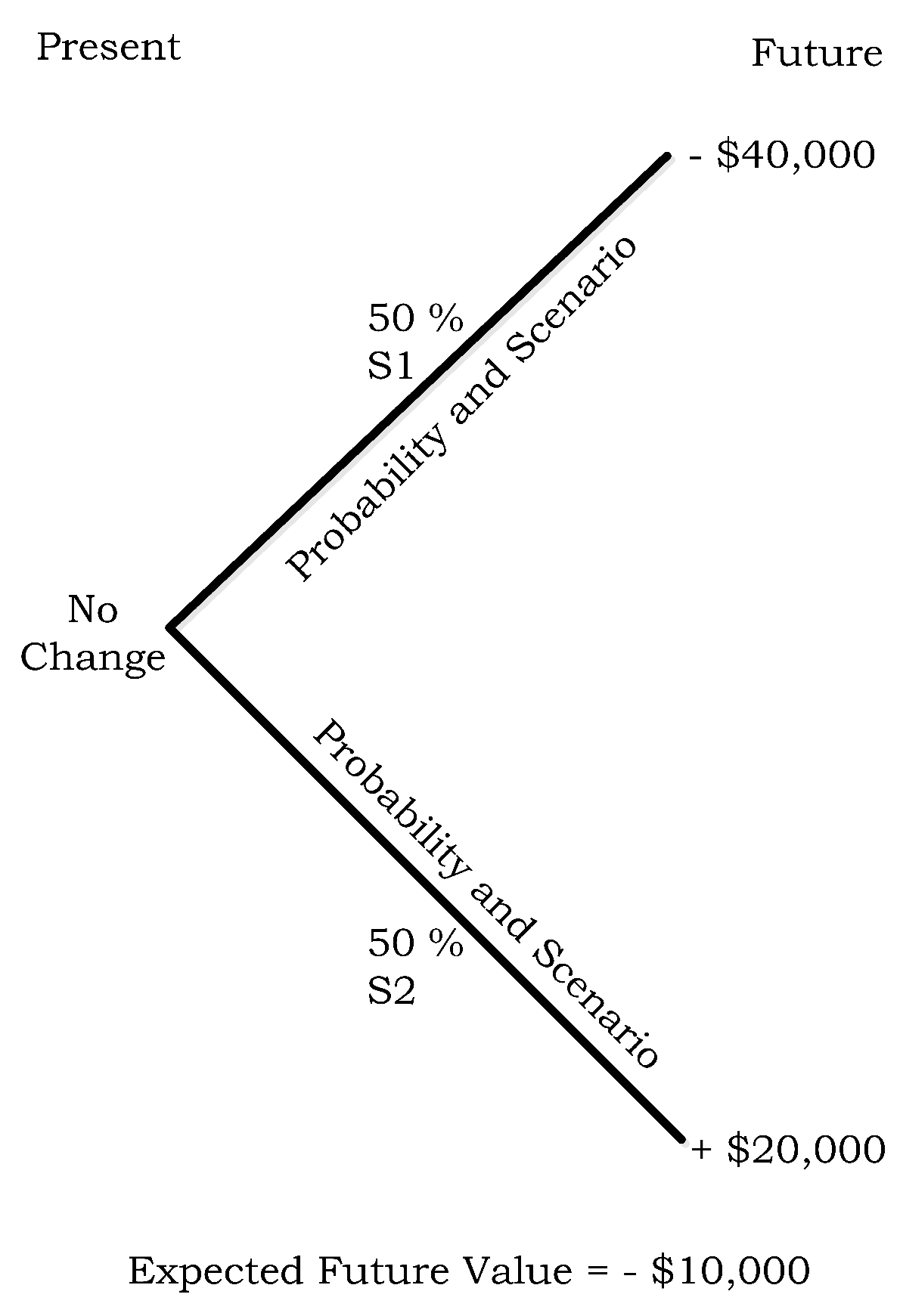
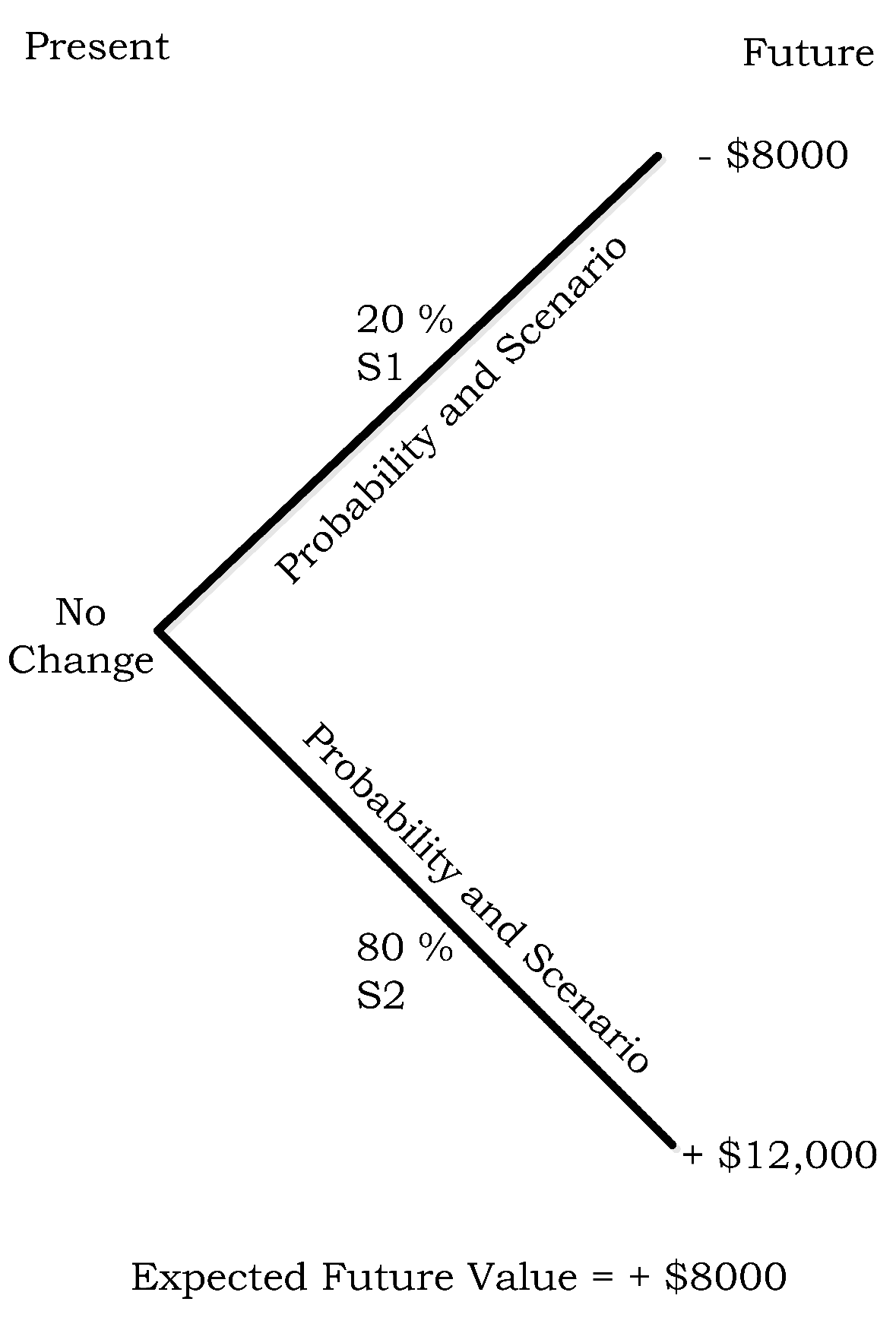
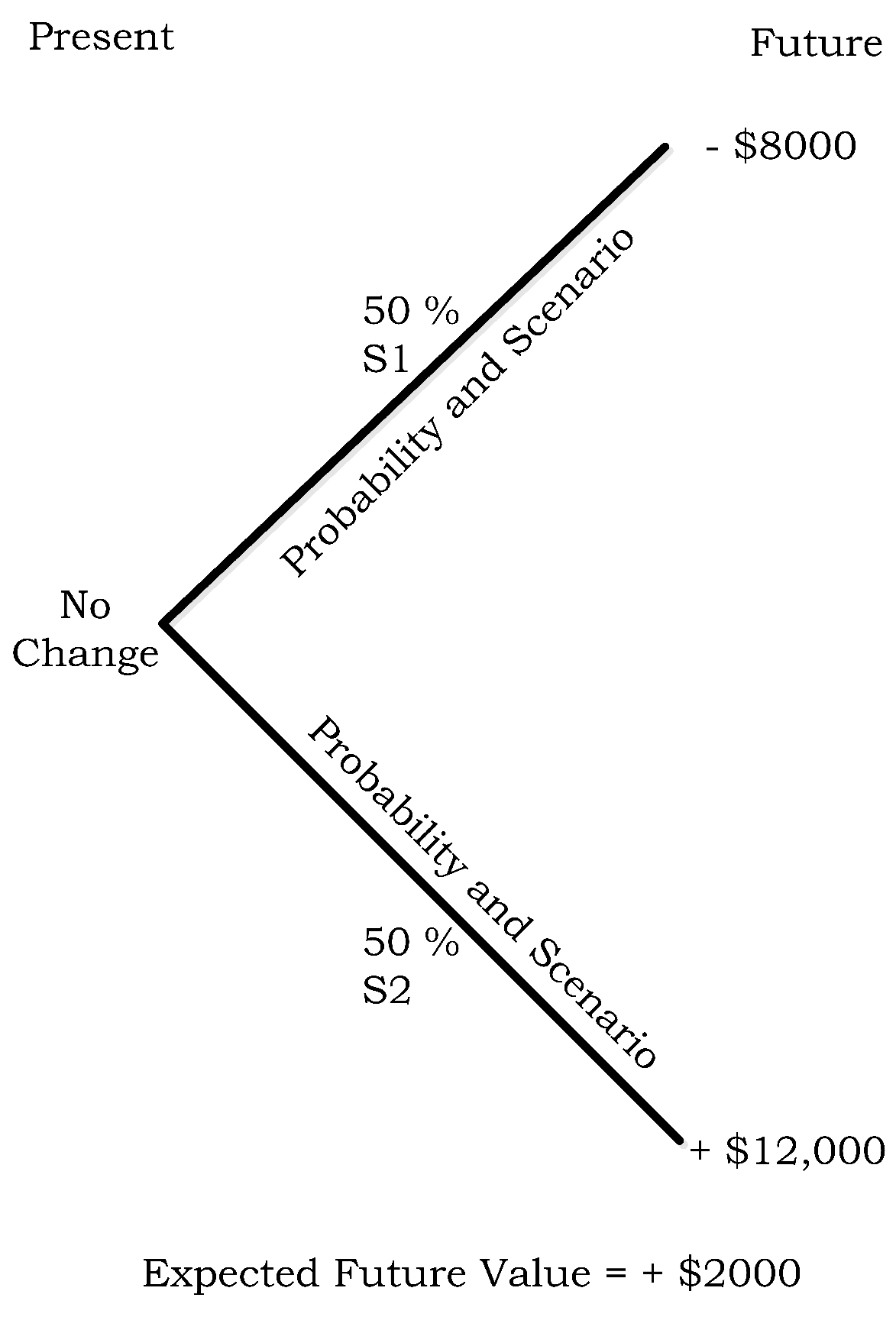
- µh1 = −$8000 (=−$40,000 loss + $40,000 payout from 400 ISO contracts − $8000 paid to purchase 400 ISO contracts).
- µh2 = $12,000 (=$20,000 revenue earned − $8000 (=$20 * 400) cost of 400 ISO contracts)
- µh1 = −$8000 (−$40,000 loss + $40,000 payout from 400 ISO contracts − $8000 paid to purchase 400 ISO contracts).
- µh2 = $12,000 ($20,000 revenue − $8000 (=$20*400) cost of 400 ISO contracts.
7.2. Information Security Vanilla Options
7.2.1. Scenario
7.2.2. Contract Specifications
7.2.3. Participants and Incentives
7.2.4. Risk Hedging
- S1 = C does not suffers a cyber-attack in the trading period or its services are not adversely affected if attacked.
- S2 = C suffers a cyber-attack and its services are unavailable for 1 h.
- S3 = C suffers a cyber-attack and its services are unavailable for 3 h.
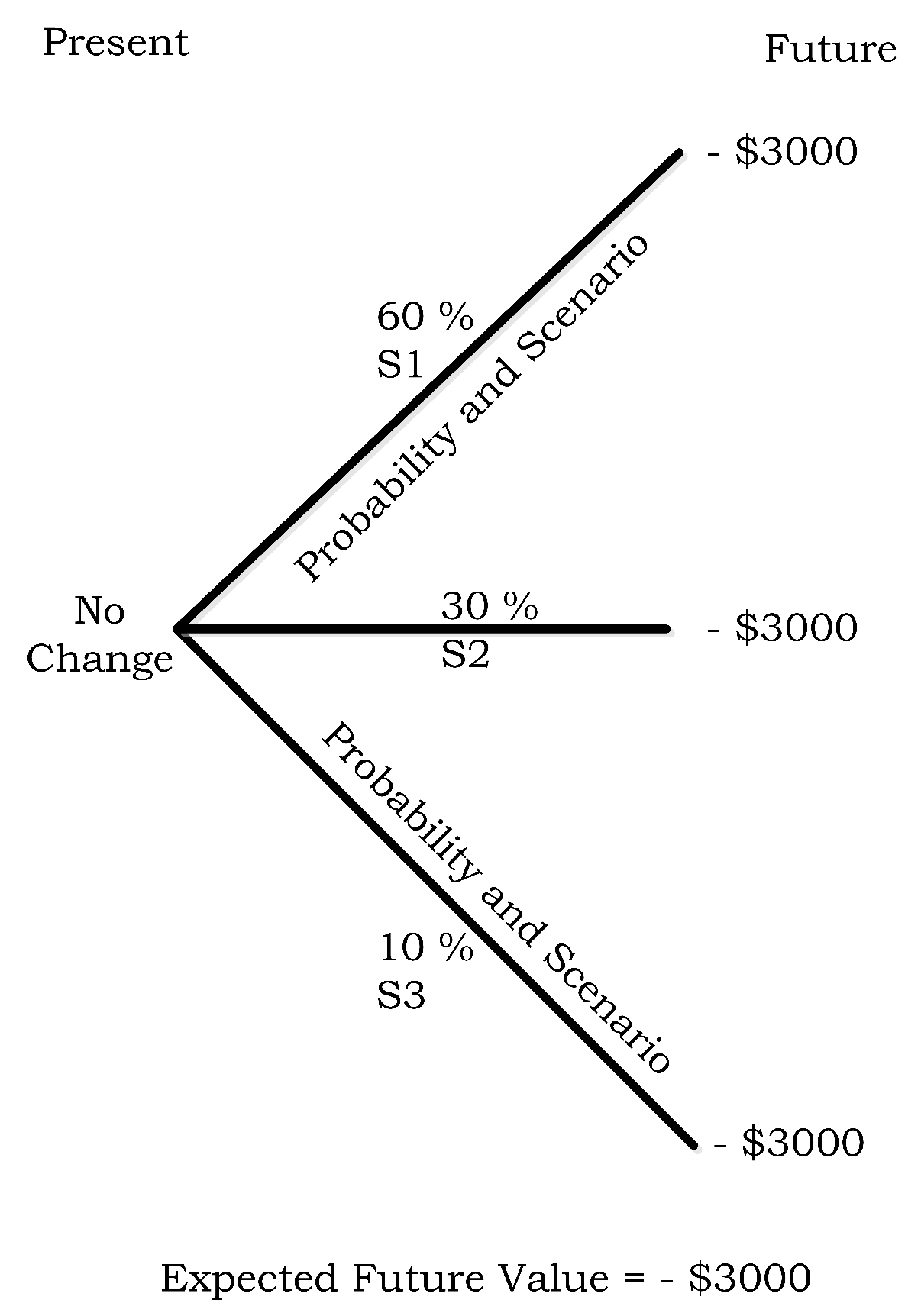
- µh1 = $0 loss due to no cyber-attack − $3000 cost to buy 100 ISVO contracts.
- µh2 = −$10,000 loss due to unavailability of services for one hour + $10,000 payout from 100 ISVO contracts − $3000 cost of purchasing 100 ISVO contracts.
- µh3 = −$30,000 loss due to unavailability of services for three hours + $30,000 payout from the 100 ISVO contracts − $3000 cost of purchasing 100 ISVO contracts.
- µh1 = $0 loss due to no cyber-attack − $3000 cost to buy 100 ISVO contracts.
- µh2 = −$10,000 loss due to unavailability of services for one hour + $10,000 payout from 100 ISVO contracts − $3000 cost of purchasing 100 ISVO contracts.
- µh3 = −$30,000 loss due to unavailability of services for three hours + $30,000 payout from the 100 ISVO contracts − $3000 cost of purchasing 100 ISVO contract.
7.3. Information Security Swaps
7.3.1. Scenario
7.3.2. Contract Specification
7.3.3. Participants and Incentives
7.3.4. Risk Hedging
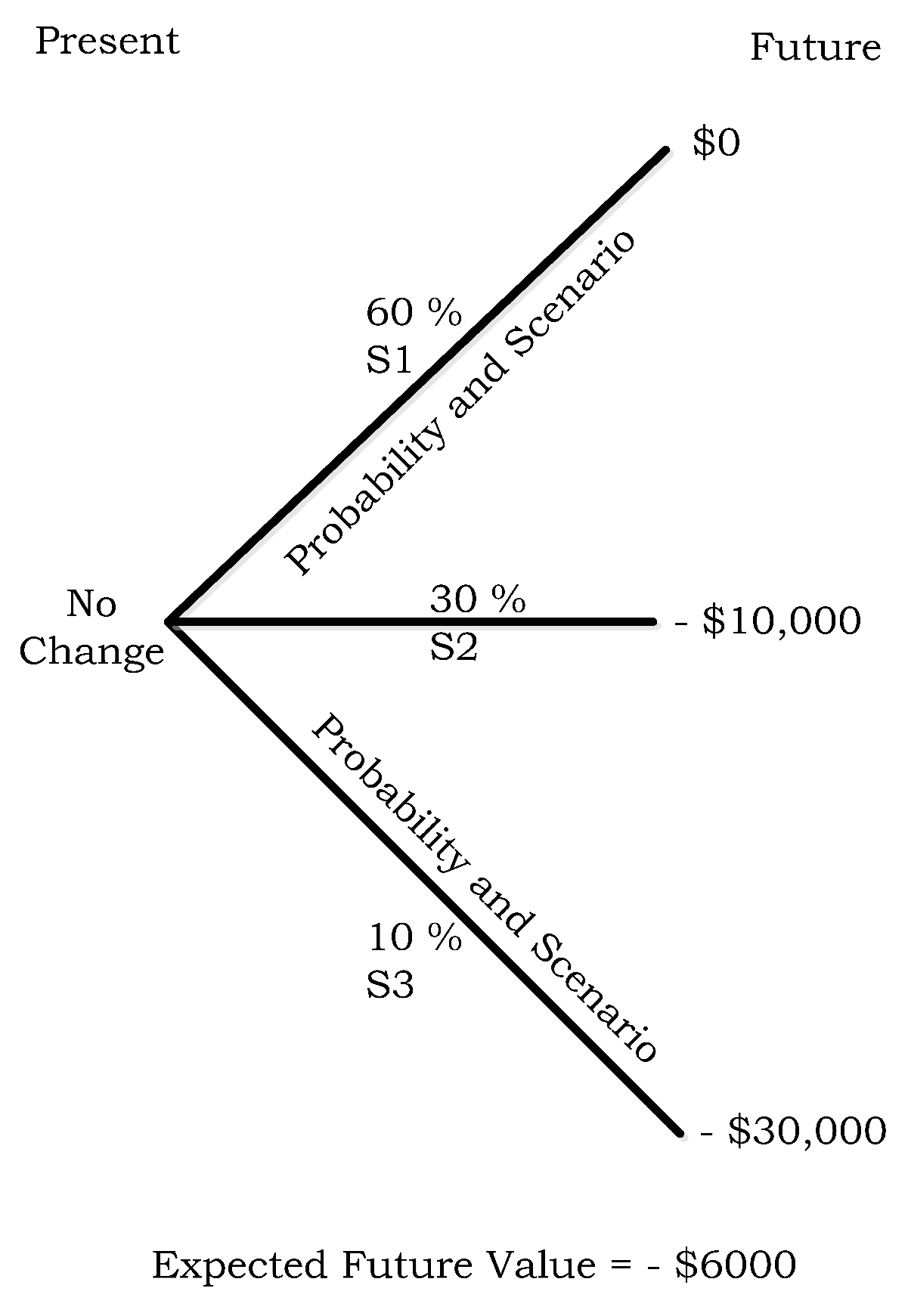
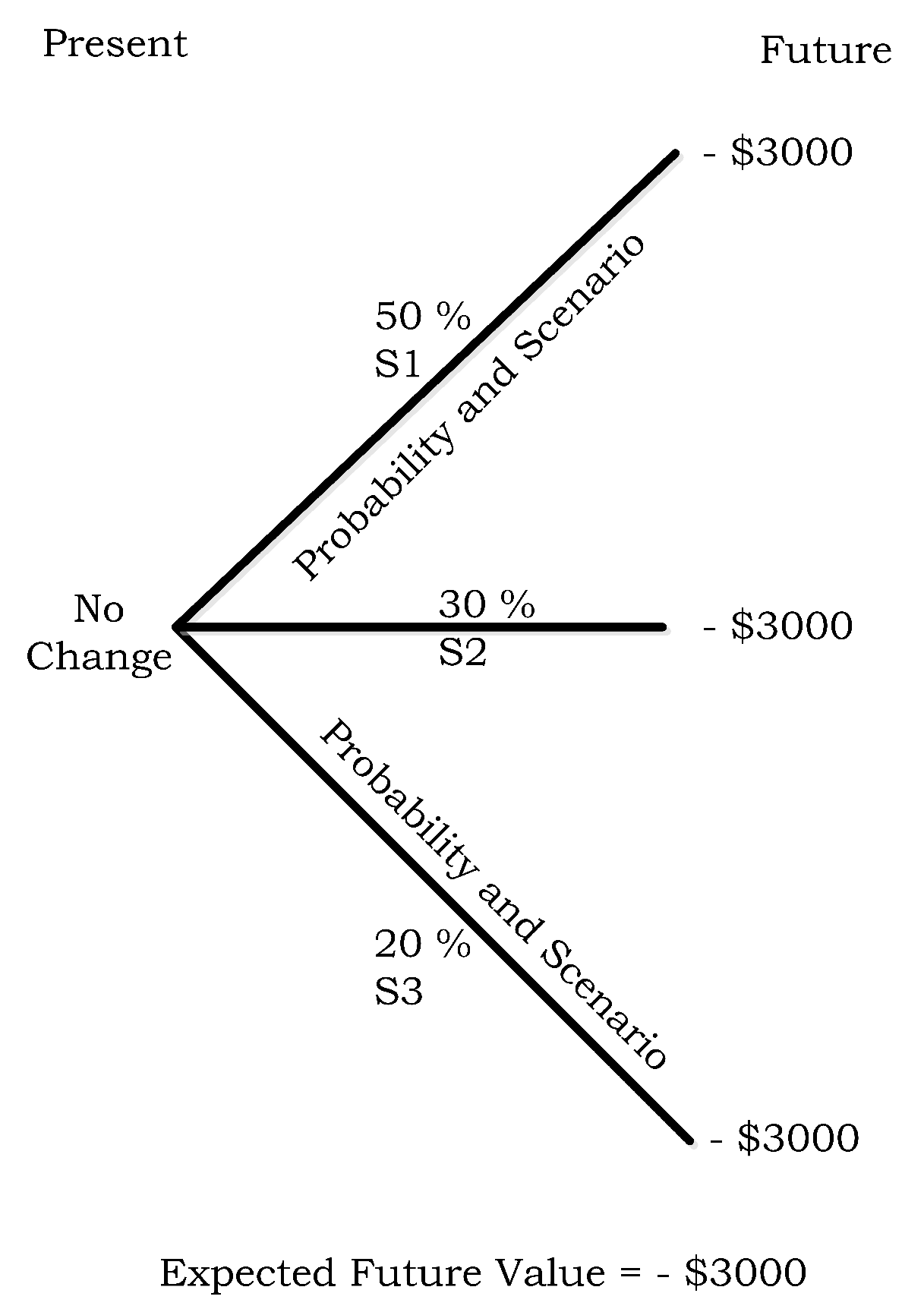
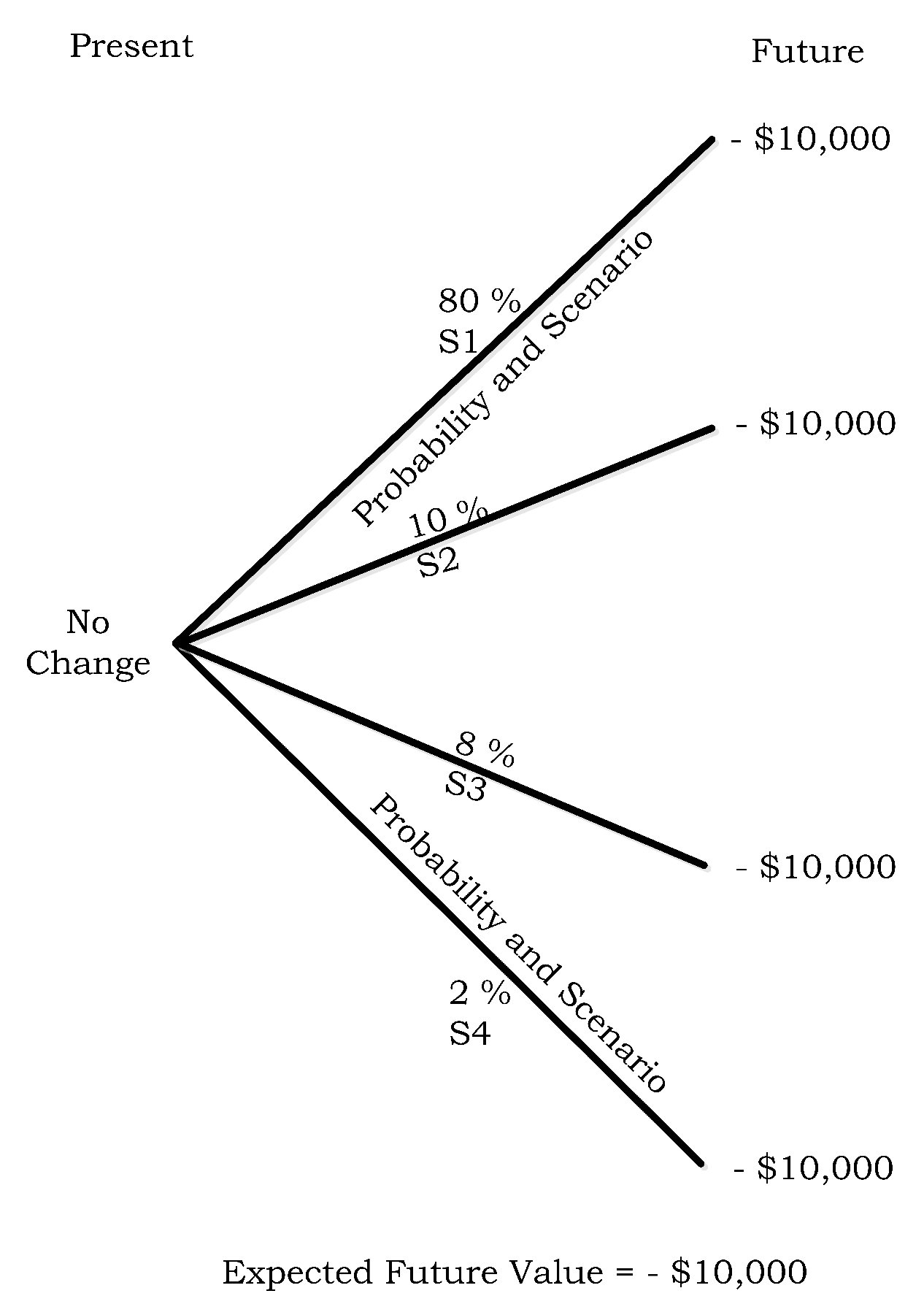
- µh1 = $0 loss due to no cyber-attack − $10,000 paid for the premium.
- µh2 = −$150,000 loss due to cyber-attack + $150,000 payout from ISS contract − $10,000 paid for the premium.
- µh3 = −$350,000 loss due to cyber-attack + $350,000 payout from ISS contract − $10,000 paid for the premium.
- µh4 = −$500,000 loss due to cyber-attack + $500,000 payout from ISS contract − $10,000 paid for the premium.
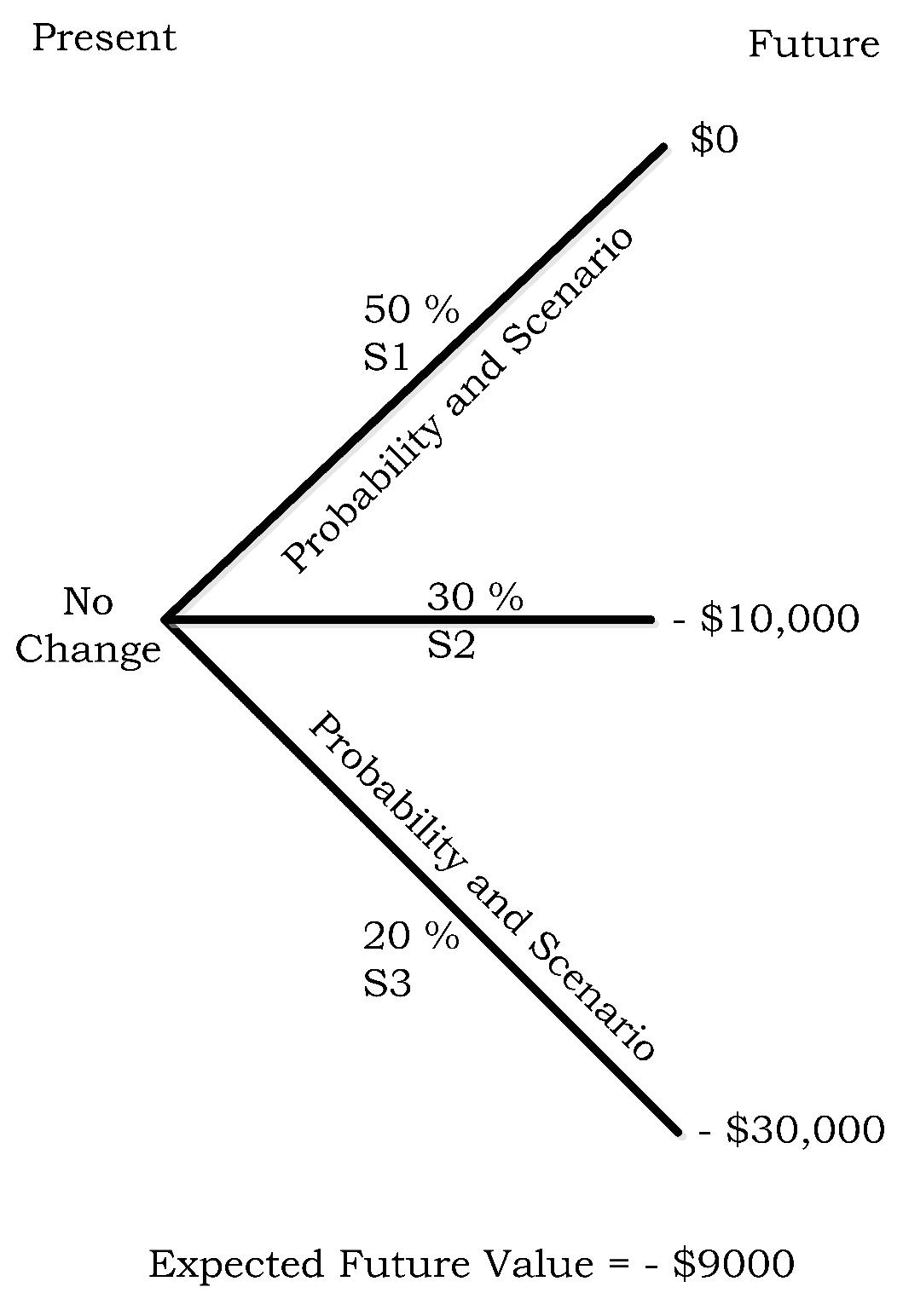
- µh1 = $0 loss due to no cyber-attack − $10,000 paid for the premium.
- µh2 = −$150,000 loss due to cyber-attack + $150,000 payout from ISS contract − $10,000 paid for the premium.
- µh3 = −$350,000 loss due to cyber-attack + $350,000 payout from ISS contract − $10,000 paid for the premium.
- µh4 = −$500,000 loss due to cyber-attack + $500,000 payout from ISS contract − $10,000 paid for the premium.
7.4. Information Security Futures
7.4.1. Scenario
7.4.2. Contract Specification
7.4.3. Participants and Incentives
7.4.4. Risk Hedging
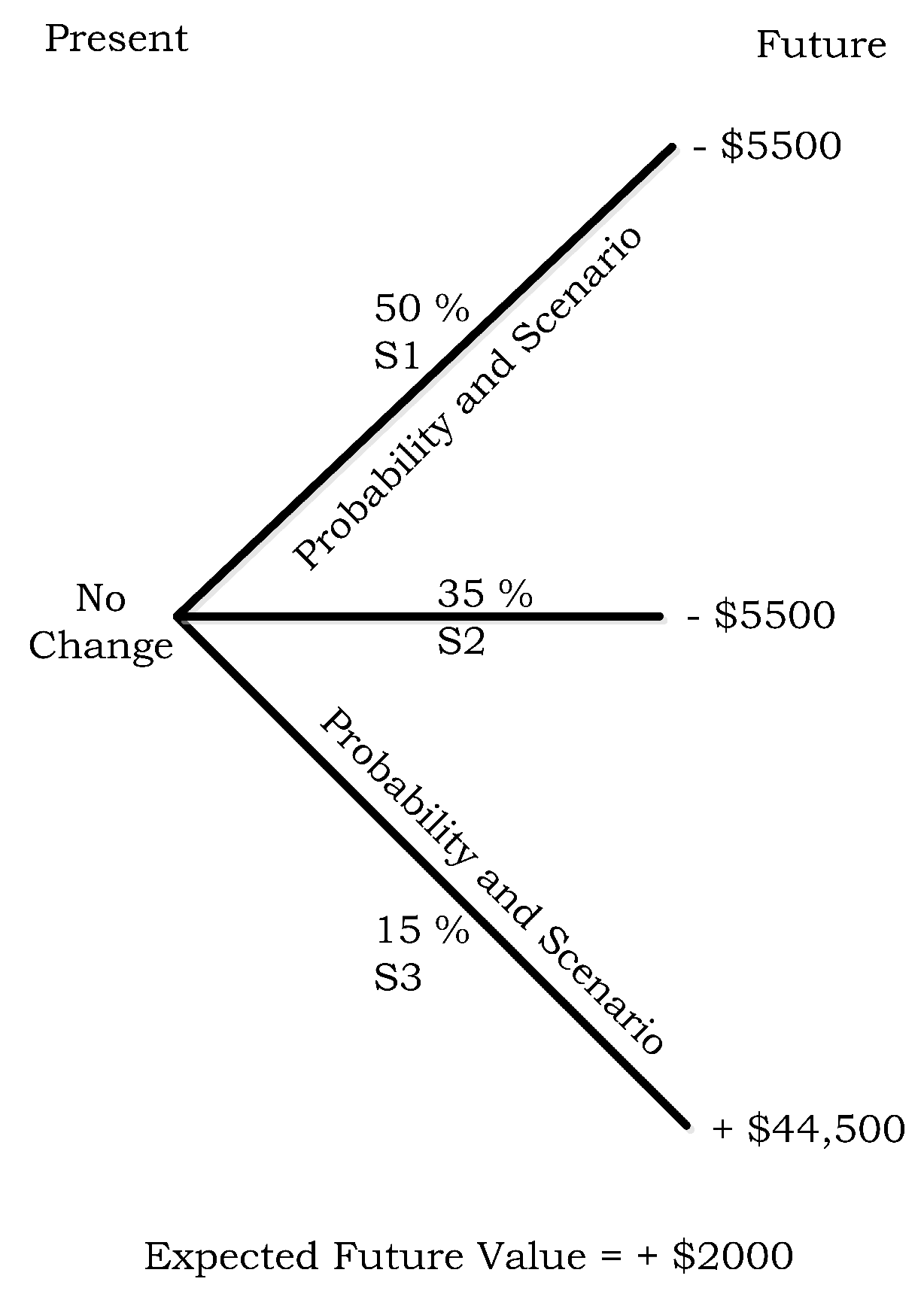
- µh1 = $0 loss − $5500 cost to buy 100 ISF contracts.
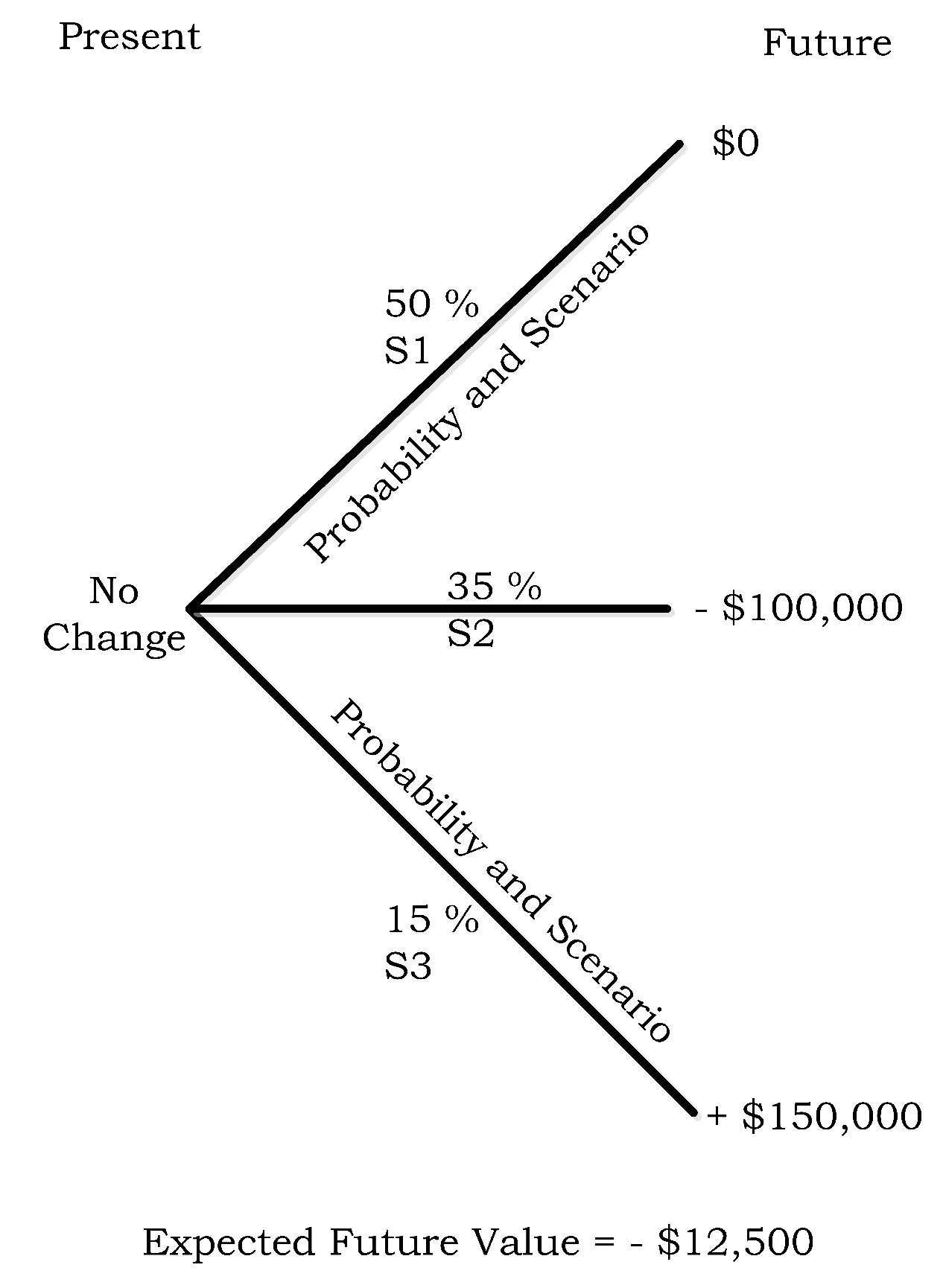
- µh2 = −$100,000 loss due to 1000 cars sold less than the strike + $100,000 payout from 100 ISF contracts − $5500 cost of purchasing 100 ISF contracts.
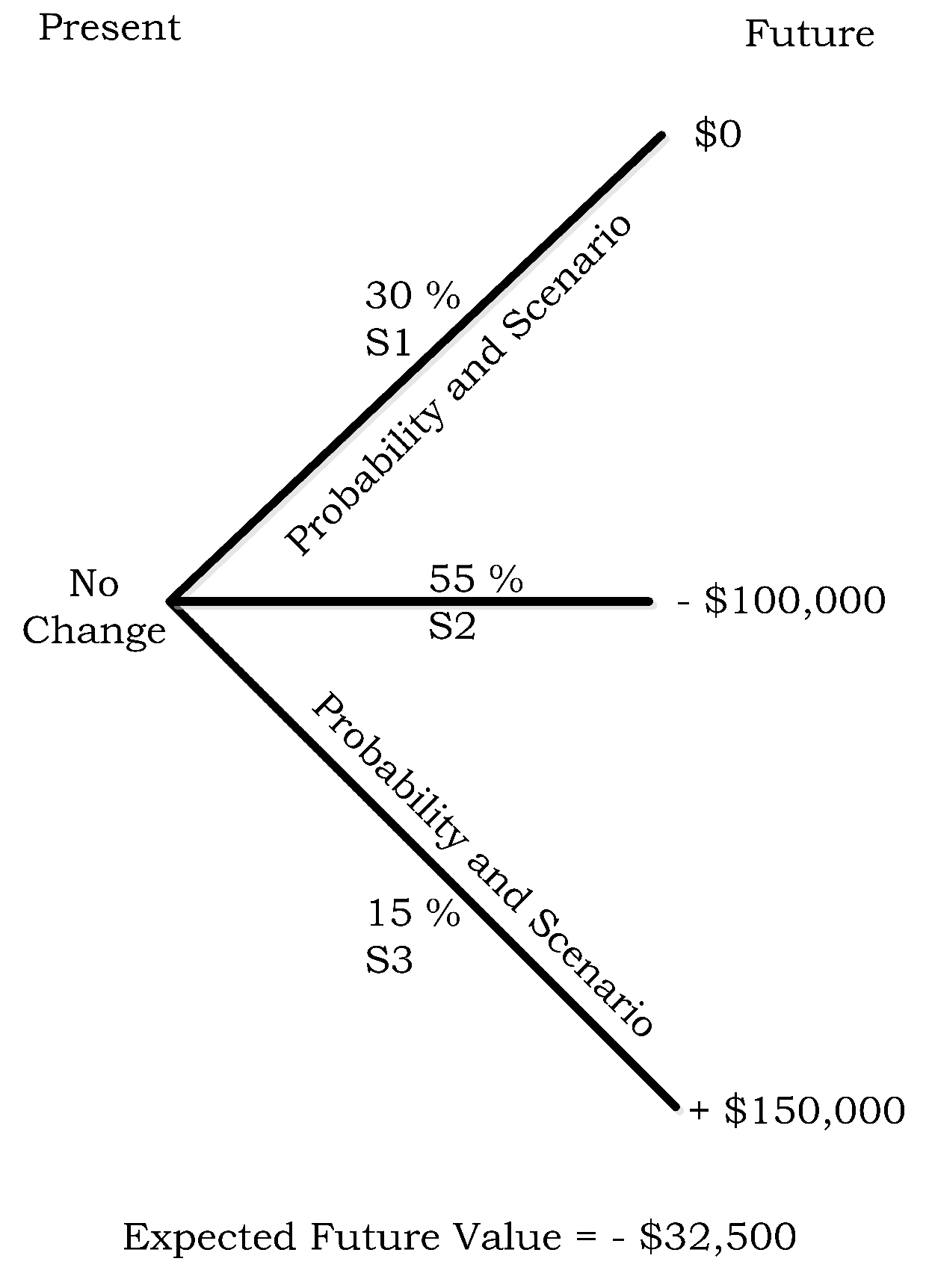
- µh3 = +$150,000 profit due to 1000 cars sold over the strike − $100,000 payout to the counterparty − $5500 cost of purchasing 100 ISF contracts.
- µh1 = $0 loss − $5500 cost to buy 100 ISF contracts.
- µh2 = −$100,000 loss due to 1000 cars sold less than the strike + $100,000 payout from 100 ISF contracts − $5500 cost of purchasing 100 ISF contracts.
- µh3 = +$150,000 profit due to 1000 cars sold over the strike − $100,000 payout to the counterparty − $5500 cost of purchasing 100 ISF contracts.
8. Evaluation
8.1. Analyze Context
8.2. Select Goals and Strategy
- Lack of relevant historical data.
- Availability of limited time for this study.
- Availability of limited resources, such as limited availability of vulnerability information, market participants, etc.
- The underlying security events may not occur during the experiment period.
- Participants may not have any information relevant to the underlying event.
- Participants would not have their skin in the game, i.e., they would not suffer the consequences of revealing incorrect information or market manipulation.
- The limited size of participants would lead to very thin markets, i.e., liquidity issues.
- Listed contracts and participants may have a bias due to limited period study.
- Lack of knowledge on legal aspects of running an information security prediction market.
8.3. Carry out Evaluation
8.3.1. Improved Information Aggregation
8.3.2. Manipulation Resistant
8.3.3. Increased Market Products and Size
8.3.4. Increased Scalability
8.3.5. Rapid Implementation
8.3.6. Increased Liquidity
8.3.7. Reduced Transaction Costs
8.3.8. Increased Price Transparency
8.3.9. Reduced Cost of Capital
8.3.10. Reduced Risk to Issuer/Market Operator
8.3.11. Reduced Settlement and Clearing Costs
8.3.12. Diversification of Counterparty Credit Risks
8.3.13. Increased Data Generation
9. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Department for Business, Innovation and Skills. 2015 Information Security Breaches Survey; Technical Report URN BIS/15/302; HM Government: London, UK, 2015.
- Gray, A. Government Resists Calls to Fund Backstop for Cyber Disaster Losses. 2015. Available online: http://www.ft.com/cms/s/0/7f9d8326-d096-11e4-a840-00144feab7de.html (accessed on 29 December 2015).
- WEF and Partners. Global Risks 2014. sight Report, 9th ed.; World Economic Forum (WEF): Cologny/Geneva, Switzerland, 2014. [Google Scholar]
- Gadanecz, B.; Moessner, R.; Upper, C. Economic derivatives. In BIS Quarterly Review; Bank for International Settlements: Basel, Switzerland, 2007; pp. 69–81. [Google Scholar]
- Dubil, R. Economic derivatives markets—New opportunities for individual investors: A research agenda. Financ. Serv. Rev. 2007, 16, 89. [Google Scholar]
- Cao, M.; Li, A.; Wei, J. Weather derivatives: A new class of financial instruments. Soc. Sci. Res. Netw. 2003. Available online: http://papers.ssrn.com/sol3/papers.cfm?abstractid=1016123 (accessed on 29 December 2015). [Google Scholar] [CrossRef]
- Andersen, T. Innovative Financial Instruments for Natural Disaster Risk Management; Technical Report; Inter-American Development Bank: Washington, DC, USA, 2002. [Google Scholar]
- Liu, M.; Wu, F.F.; Ni, Y. A survey on risk management in electricity markets. In Proceedings of the Power Engineering Society General Meeting, Montreal, Canada, 18–22 June 2006.
- Cusatis, P.; Thomas, M. Hedging Instruments and Risk Management: How to Use Derivatives to Control Financial Risk in Any Market; McGraw-Hill Education: New York, NY, USA, 2005. [Google Scholar]
- Pandey, P.; Snekkenes, E.A. Applicability of prediction markets in information security risk management. In Proceedings of the 25th International Workshop on Database and Expert Systems Applications (DEXA), Munich, Germany, 1–4 September 2014; Tjoa, A.M., Morvan, F., Wagner, R.R., Eds.; pp. 296–300.
- Pandey, P.; Snekkenes, E.A. Using prediction markets to hedge information security risks. In Security and Trust Management; Mauw, S., Jensen, C., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Wroclaw, Poland, 2014; Volume 8743, pp. 129–145. [Google Scholar]
- Pandey, P.; Snekkenes, E.A. Design and performance aspects of information security prediction markets for risk management. In Proceedings of the 12th International Conference on Security and Cryptography, Colmar, France, 20–22 July 2015; pp. 273–284.
- Johannesson, P.; Perjons, E. An Introduction to Design Science, 1st ed.; Springer International Publishing: Cham, Switzerland, 2014. [Google Scholar]
- Samuel-Ojo, O.; Shimabukuro, D.; Chatterjee, S.; Muthui, M.; Babineau, T.; Prasertsilp, P.; Ewais, S.; Young, M. Meta-analysis of design science research within the IS community: trends, patterns, and outcomes. In Global Perspectives on Design Science Research; Springer-Verlag: Berlin/Heidelberg, Germany, 2010; pp. 124–138. [Google Scholar]
- Vaishnavi, V.; Kuechler, B. Design Science Research in Information Systems. 2013. Available online: http://desrist.org/desrist/content/design-science-research-in-information-systems.pdf (accessed on 29 December 2015).
- Rossi, M.; Sein, M.K. Design research workshop: A proactive research approach. Present. Deliv. IRIS 2003, 26, 9–12. [Google Scholar]
- Purao, S. Design Research in the Technology of Information Systems: Truth or Dare; Technical Report; Georgia State University: Atlanta, GA, USA, 2002. [Google Scholar]
- March, S.T.; Smith, G.F. Design and natural science research on information technology. Decis. Support Syst. 1995, 15, 251–266. [Google Scholar] [CrossRef]
- Hevner, A.; March, S.; Park, J.; Ram, S. Design science in information systems research. MIS Q. 2004, 28, 75–105. [Google Scholar]
- Vaishnavi, V.K.; William, J.K. Design Science Research Methods and Patterns: Innovating Information and Communication Technology; Auerbach Publications, Taylor & Francis Group: Boca Raton, FL, USA, 2007. [Google Scholar]
- Venable, J.; Pries-Heje, J.; Baskerville, R. A comprehensive framework for evaluation in design science research. In Design Science Research in Information Systems. Advances in Theory and Practice; Springer-Verlag: Berlin/Heidelberg, Germany, 2012; pp. 423–438. [Google Scholar]
- UK Cyber Security. The Role of Insurance in Managing and Mitigating the Risk; Technical Report; UK HM Government and Marsh, 2015. Available online: https://www.gov.uk/government/uploads/system/uploads/attachment_data/file/415354/UK_Cyber_Security_Report_Final.pdf (accessed on 29 December 2015).
- Piquito, N.P. Financial Product Development: A Strategically Competitive System Engineering Approach to Innovative Risk Based Financial Engineering. Ph.D. Thesis, Faculty of Engineering, Rand Afrikaans University, Johannesburg, South Africa, 1999. [Google Scholar]
- Ross, S.A.; Jordan, B.D.; Westerfield, R. Fundamentals of Corporate Finance; McGraw-Hill/Irwin Publishing: New York, NY, USA, 2012. [Google Scholar]
- Silber, W.L. The process of financial innovation. Am. Econ. Rev. 1983, 73, 89–95. [Google Scholar]
- Horne, J.C. Of financial innovations and excesses. J. Financ. 1985, 40, 621–631. [Google Scholar] [CrossRef]
- Ross, S.A. Institutional markets, financial marketing, and financial innovation. J. Financ. 1989, 44, 541–556. [Google Scholar] [CrossRef]
- Merton, R.C. Financial innovation and economic performance. J. Appl. Corp. Financ. 1992, 4, 12–22. [Google Scholar] [CrossRef]
- Allen, F.; Gale, D. Financial Innovation and Risk Sharing; The MIT Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Davis, K. Innovations in derivative securities: successes and failures. In Proceeding of the 6th Melbourne Money and Finance Conference, Supplement to the Journal of Applied Finance and Investment, Melbourne, Australia, July 1996.
- Shiller, R.J. Macro Markets: Creating Institutions for Managing Society’s Largest Economic Risks; Oxford University Press: New York, NY, USA, 1998. [Google Scholar]
- Myers, R. What Every CFO Needs to Know Now about Weather Risk Management. Available online: https://www.celsiuspro.com/Portals/0/Downloads/WeatherRisk_What_Every_CFO_Needs_to_Know_Now.pdf (accessed on 29 December 2015).
- Group, CME. Weather Products: Managing Global Weather Exposures, Growing Opportunties, Reducing Risks; Technical Report; CME Group: Chicago, IL, USA, 2009. [Google Scholar]
- Deng, S.; Oren, S.S. Electricity derivatives and risk management. Energy 2006, 31, 940–953. [Google Scholar] [CrossRef]
- Ghosh, K.; Ramesh, V. An options model for electric power markets. Int. J. Electri. Power Energy Syst. 1997, 19, 75–85. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhou, H. Analysis of forward option trades in electricity markets. In Proceedings of the 2004 IEEE International Conference on Electric Utility Deregulation, Restructuring and Power Technologies, Hong Kong, China, 5–8 April 2004; Volume 2, pp. 500–504.
- Oum, Y.; Oren, S.; Deng, S. Hedging quantity risks with standard power options in a competitive wholesale electricity market. Nav. Res. Logist. NRL 2006, 53, 697–712. [Google Scholar] [CrossRef]
- Oum, Y.; Oren, S.S. Optimal static hedging of volumetric risk in a competitive wholesale electricity market. Decis. Anal. 2010, 7, 107–122. [Google Scholar] [CrossRef]
- Bhanot, K. Value of an option to purchase electric power—The case of uncertain consumption. Energy Econ. 2002, 24, 121–137. [Google Scholar] [CrossRef]
- Chung, T.; Zhang, S.; Yu, C.; Wong, K. Electricity market risk management using forward contracts with bilateral options. IEE Proc. Gen. Transm. Distrib. 2003, 150, 588–594. [Google Scholar] [CrossRef]
- Oren, S.S. Integrating real and financial options in demand-side electricity contracts. Decis. Support Syst. 2001, 30, 279–288. [Google Scholar] [CrossRef]
- Spinler, S.; Huchzermeier, A.; Kleindorfer, P. Risk hedging via options contracts for physical delivery. Spectrum 2003, 25, 379–395. [Google Scholar]
- Buyya, R.; Yeo, C.S.; Venugopal, S. Market-oriented cloud computing: Vision, hype, and reality for delivering it services as computing utilities. In Proceedings of the 10th IEEE International Conference on High Performance Computing and Communications, Dalian, China, 25–27 September 2008; pp. 5–13.
- Buyya, R.; Pandey, S.; Vecchiola, C. Cloudbus toolkit for market-oriented cloud computing. In Cloud Computing; Springer-Verlag: Berlin/Heidelberg, Germany, 2009; pp. 24–44. [Google Scholar]
- Dash, D.; Kantere, V.; Ailamaki, A. An economic model for self-tuned cloud caching. In Proceedings of the IEEE 25th International Conference on Data Engineering, Shanghai, China, 29 March–2 April 2009; pp. 1687–1693.
- Krieger, O.; McGachey, P.; Kanevsky, A. Enabling a marketplace of clouds: VMware’s vCloud director. SIGOPS Oper. Syst. Rev. 2010, 44, 103–114. Available online: http://doi.acm.org/10.1145/1899928.1899942 (accessed on 29 December 2015). [Google Scholar] [CrossRef]
- Zhang, Q.; Gürses, E.; Boutaba, R.; Xiao, J. Dynamic resource allocation for spot markets in clouds. In Proceedings of the 11th USENIX Conference on Hot Topics in Management of Internet, Cloud, and Enterprise Networks and Services, Hot-ICE’11, Boston, MA, USA, 29 March 2011; USENIX Association: Berkeley, CA, USA, 2011; pp. 1–6. [Google Scholar]
- Haque, A.; Alhashmi, S.M.; Parthiban, R. A survey of economic models in grid computing. Futur. Gen. Comput. Syst. 2011, 27, 1056–1069. [Google Scholar] [CrossRef]
- Amazon EC2 Spot Instances. Available online: http://aws.amazon.com/ec2/spot/ (accessed on 29 December 2015).
- Cohen, R. Compute Derivatives: The Next Big Thing in Commodities? 2013. Available online: http://www.forbes.com/sites/reuvencohen/2013/10/02/compute-derivatives-the-next-big-thing-in-commodities/ (accessed on 29 December 2015).
- Song, B.; Hassan, M.M.; Huh, E.N. A novel Cloud market infrastructure for trading service. In Proceedings of the International Conference on Computational Science and Its Applications, Yongin, South Korea, 29 June–2 July 2009; pp. 44–50.
- Mihailescu, M.; Teo, Y.M. Dynamic resource pricing on federated clouds. In Proceedings of the 10th IEEE/ACM International Conference on Cluster, Cloud and Grid Computing, Melbourne, Australia, 17–20 May 2010; pp. 513–517.
- Gomes, E.R.; Vo, Q.B.; Kowalczyk, R. Pure exchange markets for resource sharing in federated clouds. Concurr. Comput. Pract. Exp. 2012, 24, 977–991. [Google Scholar] [CrossRef]
- Vanmechelen, K.; Depoorter, W.; Broeckhove, J. Combining futures and spot markets: A hybrid market approach to economic grid resource management. J. Grid Comput. 2011, 9, 81–94. [Google Scholar] [CrossRef]
- Rahman, M.R. Risk Aware Resource Allocation for Clouds; Technical Report; University of Illinois: Champaign, IL, USA, 2011; Available online: https://www.ideals.illinois.edu/handle/2142/25754 (accessed on 29 December 2015).
- Bossenbroek, A.; Tirado-Ramos, A.; Sloot, P. Grid resource allocation by means of option contracts. IEEE Syst. J. 2009, 3, 49–64. [Google Scholar] [CrossRef]
- Toosi, A.N.; Thulasiram, R.K.; Buyya, R. Financial option market model for federated cloud environments. In Proceedings of the 2012 IEEE/ACM Fifth International Conference on Utility and Cloud Computing, Chicago, IL, USA, 5–8 November 2012; pp. 3–12.
- Du, A.Y.; Das, S.; Gopal, R.D.; Ramesh, R. Risk hedging in storage grid markets: Do options add value to forwards? ACM Trans. Manag. Inf. Syst. 2011, 2, 10. [Google Scholar] [CrossRef]
- Du, A.Y.; Das, S.; Ramesh, R. Efficient risk hedging by dynamic forward pricing: A study in cloud computing. INFORMS J. Comput. 2012, 25, 625–642. [Google Scholar] [CrossRef]
- Kauffman, R.; Ma, D.; Shang, R.; Huang, J.; Yang, Y. On the financification of cloud computing: An agenda for pricing and service delivery mechanism design research. Int. J. Cloud Comput. 2014, 2, 1–14. [Google Scholar]
- Cummins, J.D.; Weiss, M.A. Convergence of insurance and financial markets: Hybrid and securitized risk-transfer solutions. J. Risk Insur. 2009, 76, 493–545. [Google Scholar] [CrossRef]
- Bouriaux, S.; Scott, W.L. Capital market solutions to terrorism risk coverage: A feasibility study. J. Risk Financ. 2004, 5, 34–44. [Google Scholar] [CrossRef]
- David, M. The potential for new derivatives instruments to cover terrorism risks. Policy Issues Insur. 2005, 163–169. [Google Scholar] [CrossRef]
- Gerrish, A. Terror cats: TRIA’s failure to encourage a private market for terrorism insurance and how federal securitization of terrorism risk may be a viable alternative. Washing. Lee Law Rev. 2011, 68, 1825–1873. [Google Scholar]
- Biener, C.; Eling, M.; Wirfs, J.H. Insurability of cyber risk: An empirical analysis. Geneva Pap. Risk Insur. Issues Pract. 2015, 40, 131–158. [Google Scholar] [CrossRef]
- Akerlof, G.A. The Market for ’Lemons’: Quality Uncertainty and the Market Mechanism. Q. J. Econ. 1970, 84, 488–500. [Google Scholar] [CrossRef]
- New York Supreme Court. Zurich American Insurance Company vs. Sony Corporation of America; NY Court: New York, NY, USA, 2011; No. 651982/2011. [Google Scholar]
- Rothschild, M.; Stiglitz, J. Equilibrium in competitive insurance markets: An essay on the economics of imperfect information. Q. J. Econ. 1976, 90, 629. [Google Scholar] [CrossRef]
- Chon, G. Cyber Attack Risk Requires $1bn of Insurance Cover, Companies Warned. 2015. Available online: http://www.ft.com/intl/cms/s/0/61880f7a-b3a7-11e4-a6c1-00144feab7de.html (accessed on 29 December 2015).
- King, R. Cyber Insurance Capacity Is ‘very Small’: AIG CEO. CIO J. 2015. Available online: http://blogs.wsj.com/cio/2015/04/02/cyber-insurance-capacity-is-very-small-aig-ceo/ (accessed on 29 December 2015).
- DiPietro, B. Lack of Data Hampers Buyers, Sellers of Cyber and Reputation Policies. 2014. Available online: http://blogs.wsj.com/riskandcompliance/2014/07/01/lack-of-data-hampers-buyers-sellers-of-cyber-and-reputation-insurance/ (accessed on 29 December 2015).
- Solvency II: A Closer Look at the Evolving Process Transforming the Global Insurance Industry; Technical Report; KPMG LLP, 2011; Available online: https://www.kpmg.com/US/en/IssuesAndInsights/ArticlesPublications/Documents/solvency-II.pdf (accessed on 29 December 2015).
- Stapleton, T. Data Breach Cost : Risks, Costs and Mitigation Strategies for Data Breaches. Technical Report. 2012. Available online: http://www.zurichna.com/internet/zna/sitecollectiondocuments/en/products/securityandprivacy/data-breach-costs-wp-part-201-20-28risks-costs-and-mitigation-strategies.pdf (accessed on 29 December 2015).
- Hurtaud, S.; Flamand, T.; de la Vaissiere, L.; Hounka, A. Cyber Insurance as One Element of the Cyber Risk Management Strategy; Technical Report; Deloitte Luxembourg, 2015; Available online: http://rmas.fad.harvard.edu/files/rmas/files/lu-cyber-insurance-cyber-risk-management-strategy-03032015.pdf (accessed on 29 December 2015).
- Floresca, L. Data Breach Settlements: A New Cost in Cyber Risk. 2014. Available online: http://www.wsandco.com/about-us/news-and-events/cyber-blog/cyber-cost (accessed on 29 December 2015).
- WEF and Partners. Risk and Responsibility in a Hyperconnected World; Technical Report; World Economic Forum in collaboration with McKinsey & Company: Geneva, Switzerland, 2014. [Google Scholar]
- WEF and Partners. Partnering for Cyber Resilience: Risk and Responsibility in a Hyperconnected World—Principles and Guidelines; Technical Report Ref. 270912; World Economic Forum: Geneva, Switzerland, 2012. [Google Scholar]
- Durbin, M. All about Derivatives; McGraw-Hill Education: New York, NY, USA, 2010. [Google Scholar]
- Fabozzi, F.J. The Handbook of Financial Instruments; John Wiley & Sons, Inc.,: New York, NY, USA, 2002. [Google Scholar]
- Merton, R.C. Continuous-Time Finance; Wiley-Blackwell: Hoboken, NJ, USA, 1992. [Google Scholar]
- Pandey, P.; DeHaes, S. A novel financial instrument to incentivize investments in information security controls and mitigate residual risk. In Proceedings of the Ninth International Conference on Emerging Security Information, Systems and Technologies (SECUREWARE), Venice, Italy, 23–28 August 2015; Falk, R., Westphall, C.M., Hof, H.J., Eds.; pp. 166–175.
- Black, F.; Scholes, M. The pricing of options and corporate liabilities. J. Political Eco. 1973, 81, 637–654. Available online: http://www.jstor.org/stable/1831029 (accessed on 29 December 2015). [Google Scholar] [CrossRef]
- Pandey, P.; Snekkenes, E.A. A performance assessment metric for information security financial instruments. In Proceedings of the International Conference on Information Society (i-Society), London, UK, 9–11 November 2015; pp. 138–145.
- Sidney, C. The Art of Legging; Rotex Publishing: London, UK, 2003. [Google Scholar]
- Index of Cyber Security. 2015. Available online: http://www.cybersecurityindex.org/ (accessed on 29 December 2015).
- Embrechts, P.; Klüppelberg, C.; Mikosch, T. Modelling Extremal Events for Insurance and Finance; Applications of Mathematics; Springer: Berlin, Germany; Heidelberg, Germany, 1997; Volume 33, pp. 285–286. [Google Scholar]
- PureFunds ISE Cyber Security ETF; Technical Report; Pure Funds, 2014; Available online: http://pureetfs.com/etfs/hack.html (accessed on 29 December 2015).
- KPMG Consulting. UK Cyber Vulnerability Index 2013; Business and Industry Issue, KPMG Consulting: London, UK, 2014. [Google Scholar]
- ABI Research. Global Cybersecurity Index; Technical Report; International Telecommunication Union and ABI Research: New York, NY, USA, 2014. [Google Scholar]
- ETSI. A Full Set of Operational Indicators for Organizations to Use to Benchmark their Security Posture; Technical Report DGS/ISI-001-1; European Telecommunications Standards Institute (ETSI): Sophia Antipolis, France, 2013; version 1.1.1 (2013-04). [Google Scholar]
- Perloth, N. In Cyberattack on Saudi Firm, U.S. Sees Iran Firing Back. 2012. Available online: http://www.nytimes.com/2012/10/24/business/global/cyberattack-on-saudi-oil-firm-disquiets-us.html (accessed on 29 December 2015).
- Mathew, J. Oil Industry Has Become Hackers’ Favourite Because of Potential to Create Blackouts or Spills. 2015. Available online: http://www.ibtimes.co.uk/oil-industry-has-become-hackers-favourite-because-potential-create-blackouts-spills-1505737 (accessed on 29 December 2015).
- Davis, C. NatGas, Oil Industry in ’Crosshairs’ of Malicious Cyber Attacks. 2015. Available online: http://www.naturalgasintel.com/articles/102592-natgas-oil-industry-in-crosshairs-of-malicious-cyber-attacks (accessed on 29 December 2015).
- BBC News. Oil Cyber-Attacks Could Cost Lives, Shell Warns. 2012. Available online: http://www.bbc.com/news/technology-16137573 (accessed on 29 December 2015).
- Byres, E. Next Generation Cyber Attacks Target Oil and Gas SCADA. 2012. Available online: http://www.pipelineandgasjournal.com/next-generation-cyber-attacks-target-oil-and-gas-scada (accessed on 29 December 2015).
- Arnsdorf, I. Hackers’ Favorite Target: Big Oil and All That Deadly Equipment. 2015. Available online: http://www.bloomberg.com/news/articles/2015-06-10/hackers-favorite-target-big-oil (accessed on 29 December 2015).
- Hechinger, J. Harvard Makes Professor Disclose More After Blinkx Slides. 2014. Available online: http://www.bloomberg.com/news/2014-02-06/harvard-makes-professor-disclose-more-after-blinkx-slides.html (accessed on 29 December 2015).
- Wolfers, J.; Zitzewitz, E. Prediction Markets. J. Econ. Perspect. 2004, 18, 107–126. [Google Scholar] [CrossRef]
- Malkiel, B.G. The efficient market hypothesis and its critics. J. Econ. Perspect. 2003, 17, 59–82. [Google Scholar] [CrossRef]
- Dembo, R.; Freeman, A. Seeing Tomorrow: Rewriting the Rules of Risk; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1998. [Google Scholar]
- Palmer, D. Hackers See Cloud as ’a Fruit-Bearing Jackpot’ for Cyber Attacks. 2015. Available online: http://www.computing.co.uk/ctg/news/2429256/hackers-see-cloud-as-a-fruit-bearing-jackpot-for-cyber-attacks (accessed on 29 December 2015).
- Palmer, D. Venom Security Vulnerability Allows Hackers to Infiltrate Networks via the Cloud. 2015. Available online: http://www.computing.co.uk/ctg/news/2408602/venom-security-vulnerability-allows-hackers-to-infiltrate-networks-via-the-cloud (accessed on 29 December 2015).
- Vogel, P.S. The Increasing Business Risk of Cloud Cyberattacks. 2014. Available online: http://www.ecommercetimes.com/story/80107.html (accessed on 29 December 2015).
- Zetter, K. Russian Spy Gang Hijacks Satellite Links to Steal Data. 2015. Available online: http://www.wired.com/2015/09/turla-russian-espionage-gang-hijacks-satellite-connections-to-steal-data/ (accessed on 2 November 2015).
- Stuart, J. Comment: Satellite Industry Must Invest in Cyber Security. 2015. Available online: http://www.ft.com/intl/cms/s/0/659ab77e-c276-11e4-ad89-00144feab7de.html (accessed on 29 December 2015).
- Dougherty, J.E. Chinese Military Planning Cyber Attacks Against U.S. Satellites and Computer Systems to Degrade Pentagon’s Superiority. 2015. Available online: http://www.cyberwar.news/2015-10-20-chinese-military-planning-cyber-attacks-against-u-s-satellites-and-computer-systems-to-degrade-pentagons-superiority.html (accessed on 29 December 2015).
- Rabinovvitch, A. Hackers Find New Battleground in Space, Targeting Satellites in ’Trophy Attacks’. 2015. Available online: http://www.insurancejournal.com/news/international/2015/10/27/386240.htm (accessed on 29 December 2015).
- Cuthbertson, A. China’s Star Wars Weapons Include ’Missile-Loaded Satellites Able to Crash into International Space Station’. 2015. Available online: http://www.ibtimes.co.uk/chinas-star-wars-weapons-include-missile-loaded-satellites-able-crash-into-international-space-524304 (accessed on 29 December 2015).
- Flaherty, M.P.; Samenow, J.; Rein, L. Chinese Hack U.S. Weather Systems, Satellite Network. 2014. Available online: https://www.washingtonpost.com/local/chinese-hack-us-weather-systems-satellite-network/2014/11/12/bef1206a-68e9-11e4-b053-65cea7903f2e_story.html (accessed on 29 December 20155).
- Greenberg, A. Hackers Remotely Kill a Jeep on the Highway-With Me in It. 2015. Available online: http://www.wired.com/2015/07/hackers-remotely-kill-jeep-highway/ (accessed on 2 November 2015).
- Mearian, L. Hacker: ’Hundreds of Thousands’ of Vehicles Are at Risk of Attack. 2015. Available online: http://www.computerworld.com/article/2951489/telematics/hacker-hundreds-of-thousands-of-vehicles-are-at-risk-of-attack.html (accessed on 29 December 2015).
- Wright, R.; Sharman, A. Cyber Hack Triggers Mass Fiat Chrysler Car Recall. 2015. Available online: http://www.ft.com/intl/cms/s/0/2bafe3e0-321f-11e5-8873-775ba7c2ea3d.html (accessed on 29 December 2015).
- Gibbs, S. Jeep Owners Urged to Update Their Cars after Hackers Take Remote Control. 2015. Available online: http://www.theguardian.com/technology/2015/jul/21/jeep-owners-urged-update-car-software-hackers-remote-control (accessed on 29 December 2015).
- Slamka, C.; Soukhoroukova, A.; Spann, M. Event studies in real-and play-money prediction markets. J. Pred. Mark. 2008, 2, 53–70. [Google Scholar]
- Wolfers, J.; Zitzewitz, E. Prediction Markets in Theory and Practice; Technical Report; National Bureau of Economic Research: London, UK, 2006. [Google Scholar]
- Chen, Y.; Mullen, T.; Chu, C.H. An in-depth analysis of information markets with aggregate uncertainty. Electron. Commerce Res. 2006, 6, 201–221. [Google Scholar] [CrossRef]
- Fama, E.F. Efficient capital markets: A review of theory and empirical work. J. Financ. 1970, 25, 383–417. [Google Scholar] [CrossRef]
- Plott, C.R. Markets as information gathering tools. South. Econ. J. 2000, 2–15. [Google Scholar] [CrossRef]
- Gruca, T.S.; Berg, J.E.; Cipriano, M. Consensus and differences of opinion in electronic prediction markets. Electron. Mark. 2005, 15, 13–22. [Google Scholar] [CrossRef]
- Bondarenko, O.; Bossaerts, P. Expectations and Learning in Iowa. J. Bank. Financ. 2000, 24, 1535–1555. [Google Scholar] [CrossRef]
- Ho, T.H.; Chen, K.Y. Discovering and managing new product blockbusters: The magic and science of prediction markets. Calif. Manag. Rev. 2007, 50, 144–158. [Google Scholar] [CrossRef]
- Rhode, P.W.; Strumpf, K.S. Historical presidential betting markets. J. Econ. Perspect. 2004, 18, 127–141. [Google Scholar] [CrossRef]
- Yang, S. Information Aggregation Efficiency of Prediction Markets. Ph.D. Thesis, Erasmus Research Institute of Management, Rotterdam, The Netherlands, 2014. [Google Scholar]
- Shi, P.; Conitzer, V.; Guo, M. Prediction mechanisms that do not incentivize undesirable actions. In Internet and Network Economics; Springer-Verlag: Berlin/Heidelberg, Germany, 2009; pp. 89–100. [Google Scholar]
- Dimitrov, S.; Sami, R. Composition of markets with conflicting incentives. In Proceedings of the 11th ACM Conference on Electronic Commerce, Cambridge, MA, USA, 7–11 June 2010; pp. 53–62.
- Rhode, P.W.; Strumpf, K.S. Manipulating Political Stock Markets: A Field Experiment and a Century of Observational Data; University of Arizona: Tucson, AZ, USA, 2006. [Google Scholar]
- Hanson, R.; Oprea, R. Manipulators Increase Information Market Accuracy; George Mason University: Fairfax, VA, USA, 2004. [Google Scholar]
- Abramowicz, M. The hidden beauty of the quadratic market scoring rule: A uniform liquidity market maker with variations. GWU Law School Public Law Res. Pap. 2007. [Google Scholar] [CrossRef]
- Berg, H.; Proebsting, T. Hanson’s automated market maker. J. Predict. Mark. 2009, 3, 45–59. [Google Scholar]
- Hanson, R. On Market Maker Functions. J. Predict. Mark. 2009, 3, 61–63. Available online: http://EconPapers.repec.org/RePEc:buc:jpredm:v:3:y:2009:i:1:p:61-63 (accessed on 29 December 2015). [Google Scholar]
- Hanson, R. Book Orders for Market Scoring Rules; George Manson University: Fairfax, VA, USA, 2003. [Google Scholar]
- Chakraborty, M.; Das, S.; Peabody, J. Price evolution in a continuous double auction prediction market with a scoring-rule based market maker. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015.
- Hanson, R. Combinatorial information market design. Inf. Syst. Front. 2003, 5, 107–119. Available online: http://dx.doi.org/10.1023/A:1022058209073 (accessed on 29 December 2015). [Google Scholar] [CrossRef]
- Ledyard, J.; Hanson, R.; Ishikida, T. An experimental test of combinatorial information markets. J. Econ. Behav. Organ. 2009, 69, 182–189. [Google Scholar] [CrossRef]
- Pennock, D.M. A dynamic pari-mutuel market for hedging, wagering, and information aggregation. In Proceedings of the 5th ACM Conference on Electronic Commerce (EC ’04), New York, NY, USA, 17–20 May 2004; ACM: New York, NY, USA, 2004; pp. 170–179. [Google Scholar]
- Tetlock, P.C.; Hahn, R.W.; Lien, D.D. Designing information markets for decision making. AEI Brook. Jt. Center Work. Pap. 2005. [Google Scholar] [CrossRef]
- Hanson, R. Logarithmic market scoring rules for modular combinatorial information aggregation. J. Predict. Markets 2012, 1, 3–15. [Google Scholar]
- Bloomfield, R.; O’Hara, M. Market transparency: Who wins and who loses? Rev. Financ. Stud. 1999, 12, 5–35. [Google Scholar] [CrossRef]
- Madhavan, A. Consolidation, fragmentation, and the disclosure of trading information. Rev. Financ. Stud. 1995, 8, 579–603. [Google Scholar] [CrossRef]
- Pagano, M.; Röell, A. Transparency and liquidity: A comparison of auction and dealer markets with informed trading. J. Financ. 1996, 51, 579–611. [Google Scholar] [CrossRef]



| Outputs | Description | March and Smith [18] | Rossi and Sein [16], Purao [17] |
|---|---|---|---|
| Constructs | The conceptual vocabulary of domain | ✓ | ✓ |
| Models | A set of propositions or statements expressing relationships between constructs | ✓ | ✓ |
| Methods | A set of steps used to perform a task - how to knowledge | ✓ | ✓ |
| Instantiations | The operationalization of constructs, models, and methods | ✓ | ✓ |
| Better Theories | Artifact construction as analogous to experimental natural science, coupled with reflection and abstraction | ✗ | ✓ |
| Core Methodology | Sub-Methodologies |
|---|---|
| Observational | Case Study: Study artifact in depth in business environment |
| Field Study: Monitor use of artifact in multiple projects | |
| Analytical | Static Analysis: Examine structure of artifact for static qualities (e.g., complexity) |
| Architecture Analysis: Study fit of artifact into technical IS architecture | |
| Optimization: Demonstrate inherent optimal properties of artifact or provide optimality bounds on artifact behavior | |
| Dynamic Analysis: Study artifact in use for dynamic qualities (e.g., performance) | |
| Experimental | Controlled Experiment: Study artifact in controlled environment for qualities (e.g., usability) |
| Simulation: Execute artifact with artificial data | |
| Testing | Functional (Black Box) Testing: Execute artifact interfaces to discover failures and identify defects |
| Structural (White Box) Testing: Perform coverage testing of some metric (e.g., execution paths) in the artifact implementation | |
| Descriptive | Informed Argument: Use information from the knowledge base (e.g., relevant research) to build a convincing argument for the artifact’s utility |
| Scenarios: Construct detailed scenarios around the artifact to demonstrate its utility |
| Objective | Reduce the Probability of Risk Event | Reduce the Financial Impact of Risk Event |
|---|---|---|
| Strategies | Technical Controls | Technical Controls |
| Security Policy | Cyber-Insurance | |
| Others | Derivatives |
| Insurability Criteria | Main Findings | Assessment |
|---|---|---|
| Randomness of Loss Occurrence | - Correlation among risks hinders efficient pooling | Problematic |
| - Risk pools are too small and cannot be diversified; also, lack of adequate reinsurance | ||
| - Lack of data | ||
| - Changing nature of cyber risks (e.g., new standards, regulations) | ||
| Maximum Possible Loss | - Maximum possible loss for cyber risk lower than for other operational risks | Not Problematic |
| - Insurers protect against extreme loses by cover limits | ||
| Average Loss Per Event | - Average loss for cyber risk lower than for other operational risks | Not Problematic |
| - Dependent on company size, self-protection, and institutional commitment for information security | ||
| Loss Exposure | - Increasing number of cyber risk events | Not Problematic |
| - Dependent on event catgory (i.e., human actions dominate other event categories) | ||
| Information Asymmetry | - Moral hazard poses a strong theoretical threat; regular risk assessments, deductibles, and caps on coverage help reduce moral hazard | Problematic |
| - Adverse selection poses a strong theoretical threat; upfront risk assessments (screening) and signaling (e.g., ISO certificates) help reduce adverse selection | ||
| Insurance Premium | - High premiums and other costs due to large uncertainties; expected to decline | Increasingly Less Problematic |
| - Large geographic and industry variations in availability of policies | ||
| - Low number of competitors; expected to increase over time | ||
| - Additional costs (e.g., upfront risk assessments) | ||
| Cover Limits | - Policies typically cover a maximum (e.g., US $ 50 Million) | Problematic |
| - Policies contain exclusions (e.g., self-inflicted loss, accessing unsecure websites, terrorism) | ||
| - Indirect costs (e.g., reputational effects) cannot be measured and often not covered | ||
| - Product complexity can be problematic (lots of exclusions, dynamic risk nature, both for the insurance seller and buyer uncertainty regarding the actual coverage) | ||
| Public Policy | - Increase in overall industry exposure through cyber insurance is conceivable due to moral hazard incentives and high loss correlations in interrelated networks | Less Problematic |
| - Insurance fraud might be incentivized, since hacking attacks or physical attacks are difficult to detect and to trace back | ||
| Legal Restrictions | - In many countries it is not allowed to insure regulatory fines | Less Problematic |
| - Risk of change (e.g., new legal standards and regulations) | ||
| - Complexity and dynamic nature of this novel risk type might pose a potential legal threat for insurance brokers that limits their willingness to offer the product; only few specialists willing and able to sell cyber insurance | ||
| - Disclosure of sensitive information |
| Cyber-Insurance Problems | Functional Requirements for ISD |
|---|---|
| Inefficient and Ineffective | Efficient and Effective Risk Hedging |
| Information Asymmetry | Increased Information Elicitation and Aggregation |
| Strong Manipulation Resistance | |
| Incomplete Markets | Increase in Products (Variety) |
| Scalability | |
| Rapid Implementation | |
| Lack of Liquidity | Increased Liquidity |
| High Transaction Cost | Reduced Transaction Cost |
| Increased Price Transparency | |
| Regulatory Capital Requirements | Low Cost of Capital |
| Reduced Risk to Market Operator | |
| High Settlement Cost | Low Settlement and Clearing Cost |
| High Counterparty Credit Risk | Low Counterparty Credit Risk |
| Lack of Data | Increased Data Generation |
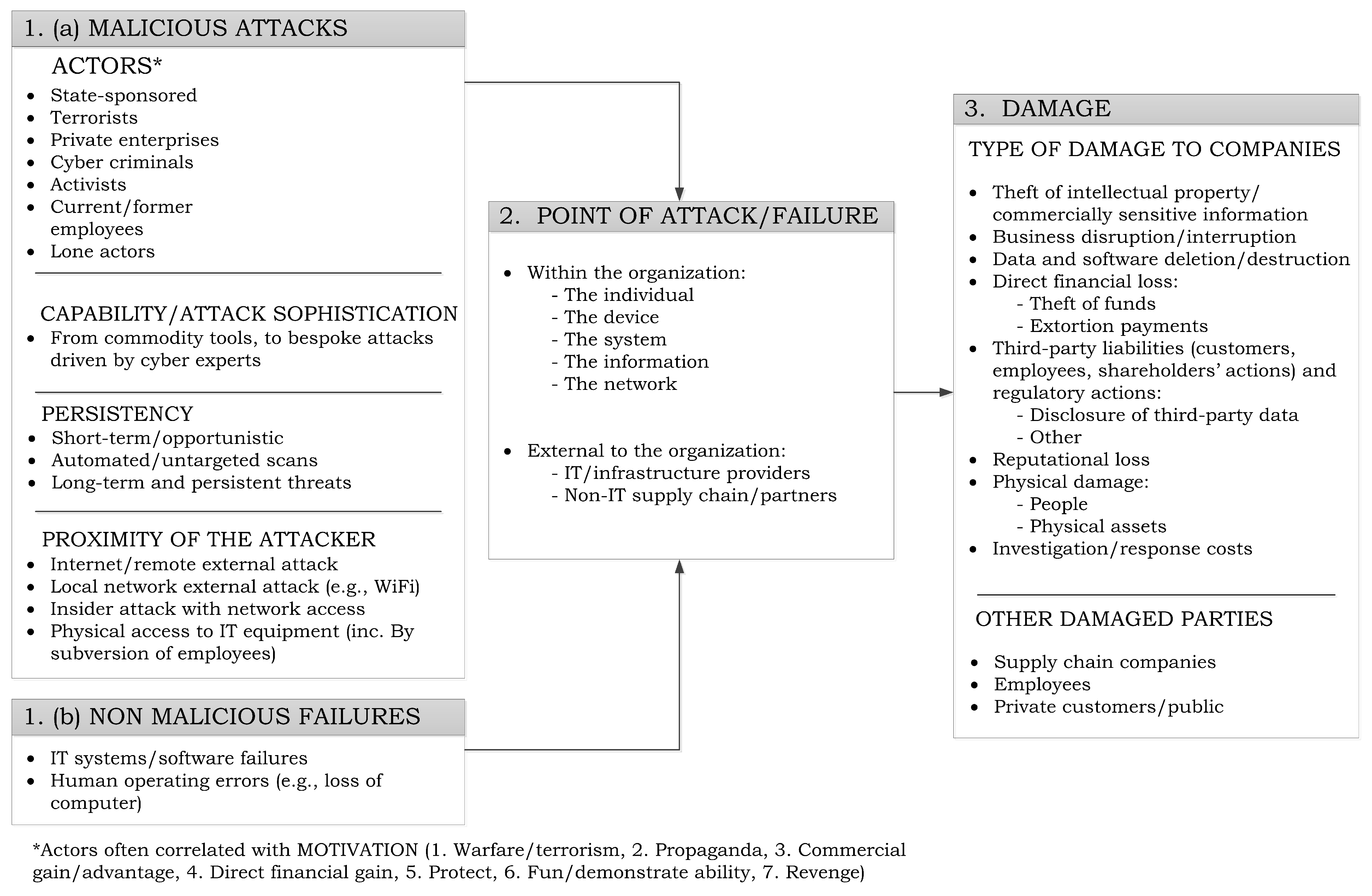
| Loss Category | Description |
|---|---|
| Intellectual Property (IP) Theft | Loss of value of an IP asset, expressed in terms of loss of revenue as a result of reduced market share. |
| Business Interruption | Lost profits or extra expenses incurred due to the unavailability of IT systems or data as a result of cyber attacks or other non-malicious IT failures. |
| Data and Software Loss | The cost to reconstitute data or software that has been deleted or corrupted. |
| Cyber Extortion | The cost of expert handling for an extortion incident, combined with the amount of the ransom payment. |
| Cyber Crime/Cyber Fraud | The direct financial loss suffered by an organisation arising from the use of computers to commit fraud or theft of money, securities, or other property. |
| Breach of Privacy Event | The cost to investigate and respond to a privacy breach event, including IT forensics and notifying affected data subjects. Third-party liability claims arising from the same incident. Fines from regulators and industry associations. |
| Network Failure Liabilities | Third-party liabilities arising from certain security events occurring within the organisation’s IT network or passing through it in order to attack a third party. |
| Impact on Reputation | Loss of revenue arising from an increase in customer churn or reduced transaction volumes, which can be directly attributed to the publication of a defined security breach event. |
| Physical Asset Damage | First-party loss due to the destruction of physical property resulting from cyber attacks. |
| Death and Bodily Injury | Third-party liability for death and bodily injuries resulting from cyber attacks. |
| Incident Investigation and Response Costs | Direct costs incurred to investigate and “close” the incident and minimise post-incident losses. Applies to all the other categories/events. |
| Trigger Criteria | Examples |
|---|---|
| Index | Such as Company Specific Risk Index, ISE Cyber Security ETF (HACK) [87], |
| UK Cyber Vulnerability Index [88], | |
| Global Cybersecurity Index (GCI) [89], Index of Cyber Security [85] | |
| Results Indicators | Such as Technological Indicators (performance of security controls, etc.), |
| Process and Procedural Indicators (compliance with regulatory requirements, etc.), so on. | |
| Information Security Indicators [90] | |
| Customized Indicators | Such as a combination of performance index and result indicators, |
| Qualitative analysis of security strength, | |
| penetration testing of security defense systems, Forensics, so on. | |
| Information Security Indicators [90] |
| Payout Structure | Payout Structure Definition | ISO | ISVO | ISF | ISS |
|---|---|---|---|---|---|
| Fixed | Payouts are fixed and based on occurrence of pre-specified “state(s)” | ✓ | ✗ | ✗ | ✓ |
| Increasing | Payouts are proportionately linked to occurrence of “state(s)” above the trigger level | ✗ | ✓ | ✓ | ✓ |
| Tiered | Payouts depend on the level of outcomes, i.e., the payout structure is tiered (increase or decrease) | ✗ | ✓ | ✓ | ✓ |
| Decreasing | Payouts decreases with decrease/falling-short from the trigger level | ✗ | ✓ | ✓ | ✓ |
| Fixed Specifications | Variable Specifications |
|---|---|
| Issuer | |
| Information Security Derivative Type | |
| Contract ID | |
| Underlying Event or Condition | |
| Trading Start Date and Time | YYYY-MM-DD |
| HH-MM-SS | |
| Trading End Date and Time | YYYY-MM-DD |
| HH-MM-SS | |
| Minimum Investment Required | Amount : |
| Currency : | |
| Maximum Investment Permitted | Amount : |
| Currency : | |
| Contract Trading Unit (Lot Size) | |
| Transaction Fee | |
| Payout Trigger Criteria | |
| Decision Criteria | |
| Payout (Return) Structure | |
| Pay-Off Horizon | |
| Settlement Date | |
| Independent Third Party Verification Required | Yes/No |
| Eligible Investors/Traders | |
| Know Your Trader/Investor Required | Yes/No |
| Transferable Instrument | Yes/No |
| Other Relevant Information |
| Fixed Specifications | Variable Specifications |
|---|---|
| Issuer | Information Security Prediction Market |
| Information Security Derivative Type | Information Security Option |
| Contract ID | ISO 123 |
| Underlying Event or Condition | The unit-1 of the company “O” suffers a (pre-defined type of) cyber-attack and the production at the unit is adversely affected for one or more days on or before 31 December 2015. |
| Trading Start Date and Time | 1 October 2015 00-00-01 CET |
| Trading End Date and Time | 31 December 2015 23-59-59 CET |
| Minimum Investment Required | Amount : 1000 (One Thousand) |
| Currency : USD | |
| Maximum Investment Permitted | Amount : 500,000 (Five Hundred Thousand) |
| Currency : USD | |
| Contract Trading Unit (Lot Size) | One (01) |
| Transaction Fee | 0% (Zero for the sake of easy calculation and demonstration) |
| Payout Trigger Criteria | Failure of production system, thus affecting the production by at least 30% at the Unit-1 of company O for three or more hours during the normal work (production hours) would count as a failure for one full day. |
| Decision Criteria | (i) Press release by the company. |
| (ii) Company’s reporting to a regulator, such as stock market regulator. | |
| Payout (Return) Structure | Fixed; $100 per contract if the predefined (cyber-attack) event occurs, $0 otherwise. |
| Pay-Off Horizon | On the day of settlement |
| Settlement Date | If there is no news/report of cyber-attack within the trading period, then the settlement would be on the fourth business day after the last trading day. However, if there is any news/report of the incident within the trading period then the settlement would take place on the fourth business day from the last trading day or from the day of production recovery whichever is earlier. |
| Independent Third Party Verification Required | No |
| Eligible Investors/Traders | Only verified |
| Know Your Trader/Investor Required | Yes |
| Transferable Instrument | Yes, to other verified traders only |
| Other Relevant Information | Nil |
| Participant | Trading Side | Incentive/Motivation |
|---|---|---|
| Oil Company “O” | Buy | To hedge the cyber-risk exposure to the unit-1. |
| Oil Company’s Cyber-Security Product Vendor “V” | Sell | To convince others through the display of strong faith that their system is strong and will meet the pre-specified performance requirements for the oil industry. |
| Competitors of Vendor “V” | Buy | To convince others through the display of strong signal that the system of “V” is not able to meet the desired performance and they can develop or have better products to meet the desired requirements. |
| Investors in Company “O” | Buy/Sell | To hedge their risk or to profit from trading in the contract. The buy or sell decision depends on investor’s individual belief. Investors try to earn profit by predicting the future price movements or the probability of the underlying event based on the any relevant information they may have. |
| Cyber-Insurers and Re-insurers | Buy/Sell | To hedge their risk or to profit from trading in the contract. The buy or sell decision is based on their individual risk portfolio. |
| Speculators | Buy/Sell | This category includes a range of market participants, such as hedge funds, proprietary trading firms, individual traders, and so on. These traders participate (buy or sell) to earn a profit by predicting the future price movements or the probability of the underlying event based on the any relevant information they may have. |
| Security Researchers | Buy/Sell | Security researchers in possession of some relevant information may participate in trading of the contract. Moral and ethical aspects, such as [97], are ignored. |
| Fixed Specifications | Variable Specifications |
|---|---|
| Issuer | Information Security Prediction Market |
| Information Security Derivative Type | Information Security Vanilla Option |
| Contract ID | ISVO 123 |
| Underlying Event or Condition | The company “C” suffers a (pre-defined type of) cyber-attack during the trading period of the contract and its cloud services are unavailable to its clients. |
| Trading Start Date and Time | 1 October 2015 00-00-01 CET |
| Trading End Date and Time | 31 December 2015 23-59-59 CET |
| Minimum Investment Required | Amount : 1000 (One Thousand) |
| Currency : USD | |
| Maximum Investment Permitted | Amount : 500,000 (Five Hundred Thousand) |
| Currency : USD | |
| Contract Trading Unit (Lot Size) | One (01) |
| Transaction Fee | 0% (Zero for the sake of easy calculation and demonstration) |
| Payout Trigger Criteria | Cloud computing services of “C” are unavailable for at least continues 60 min in one day. |
| Decision Criteria | Press release by the company “C” or a regulatory filing by the company “C”, such as to the stocks trading regulator. |
| Payout (Return) Structure | Scaling-Increasing; Payout of $100 per contract for per hour of service unavailability, $0 otherwise. |
| Pay-Off Horizon | On the day of settlement |
| Settlement Date | If there is no news/report of any cyber-attack on the company ‘C’ then the settlement will be on the fourth business day from the last day of trading. However, if there is any news/report of any cyber-attack during the trading period then the settlement will be on the fourth business day after the incident’s report is released or the fourth business day from the last trading date, whichever is earlier. |
| Independent Third Party Verification Required | No |
| Eligible Investors/Traders | Only verified |
| Know Your Trader/Investor Required | Yes |
| Transferable Instrument | Yes, to other verified traders only |
| Other Relevant Information | Nil |
| Participant | Trading Side | Incentive/Motivation |
|---|---|---|
| Company “C” | Buy | To hedge the risk exposure. |
| Cyber-security product vendor’s of “C” | Sell | To convince others through the display of strong faith that their products are of high quality and can strongly defend against cyber-attacks. |
| Competitors of security product vendors of “C” | Buy | To convince others through the display of strong signal that the products of cloud service provider’s are not strong enough and can not defend against the advance cyber-attacks. |
| Investors in “C” | Buy/Sell | To hedge their risk or to profit from trading in the contract. The buy or sell decision depends on investor’s individual belief. |
| Cyber-Insurer and Cyber-Reinsurer | Buy/Sell | To hedge their risk or to profit from trading in the contract. The buy or sell decision is based on the company’s risk portfolio. |
| Speculators | Buy/Sell | This category includes a range of market participants, such as speculators, hedge funds, proprietary trading firms, individual traders, and so on. These traders participate (buy or sell) to earn a profit from the relevant information they may have. |
| Security Researchers | Buy/Sell | Security researchers in possession of some relevant information may participate in the trading of the contract. |
| Fixed Specifications | Variable Specifications |
|---|---|
| Issuer | Information Security Prediction Market |
| Information Security Derivative Type | Information Security Swap |
| Contract ID | ISS 123 |
| Underlying Event or Condition | The satellite services providing company “S” suffers a (pre-specified type of) cyber-attack during the trading period of the contract and its services are completely unavailable to its clients for continuous six hours at least. |
| Trading Start Date and Time | 1 January 2016 00-00-01 CET |
| Trading End Date and Time | 31 December 2016 23-59-59 CET |
| Minimum Investment Required | Amount : 1000 (One Thousand) |
| Currency : USD | |
| Maximum Investment Permitted | Amount : 50,000 (Fifty Thousand) |
| Currency : USD | |
| Contract Trading Unit (Lot Size) | One (01) |
| Transaction Fee | 0% to the exchange(Zero for the sake of easy calculation and demonstration), Premium of 2% to the counterparty. |
| Payout Trigger Criteria | For the calculation of payout, the disruption of services for a continuous period of six or more hours during the contract trading period. |
| Decision Criteria | At least one of the following: |
| (i) Press release by the company “S”. | |
| (ii) A filing by the company “C” to a regulator, such as stocks trading regulator. | |
| (iii) A third party verification report. | |
| Payout (Return) Structure | Maximum payout of $500,000 or the actual impact, whichever is lower. |
| Pay-Off Horizon | On the day of settlement |
| Settlement Date | If there is no news/report of any cyber-attack on the company “S” then the contract will automatically settle on the first business day from the last trading day) from the last date of the contract period. If any of the states S2, S3, or S4 occur during the trading period then the settlement would occur on the fourth business day from the date of incident reporting. |
| Independent Third Party Verification Required | Yes, if the counterparties want to verify the incident. |
| Eligible Investors/Traders | Only verified |
| Know Your Trader/Investor Required | Yes |
| Transferable Instrument | Yes, to other verified traders only |
| Other Relevant Information | Nil |
| Participant | Trading Side | Incentive/Motivation |
|---|---|---|
| Company “S” | Buy | To hedge the risk exposure. |
| Security Product Vendors of “S” | Sell | To convince others that their products are of high quality and can strongly defend against cyber-attacks. |
| Cyber-Insurer and Cyber-Reinsurers | Sell | To hedge the risk exposure due to new developments in the company/technology/regulatory requirements, etc. To diversify their investment and profit from trading in the contract, if they believe that the company “S” has strong security system. |
| Speculators | Sell | To diversify their investment portfolio. |
| State | Limited Period Interruption | Satellite Hijacking (Permanent Loss) |
|---|---|---|
| S1 | ✗ | ✗ |
| S2 | ✓ | ✗ |
| S3 | ✗ | ✓ |
| S4 | ✓ | ✓ |
| State | Loss Probability | Impact Value |
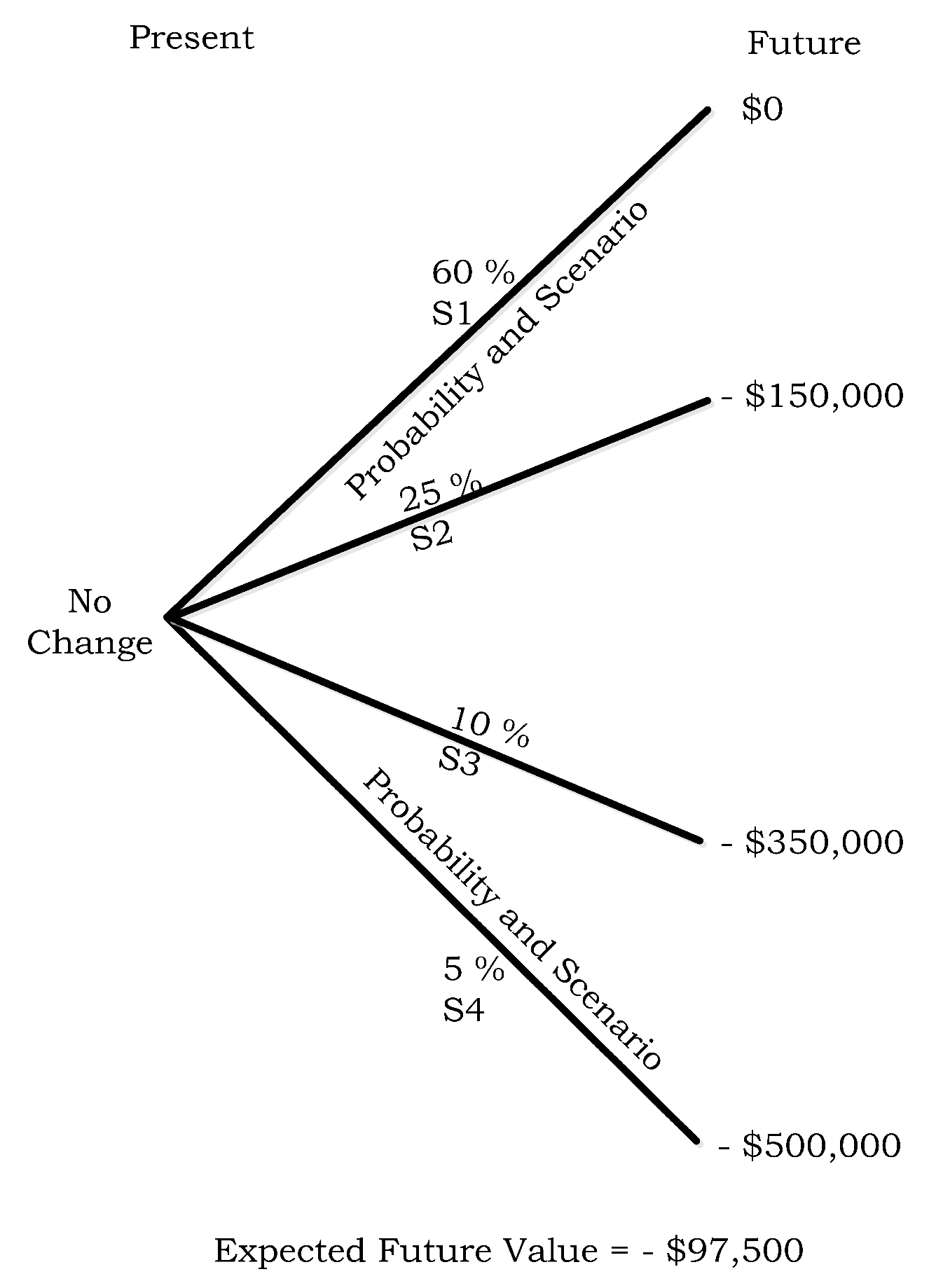
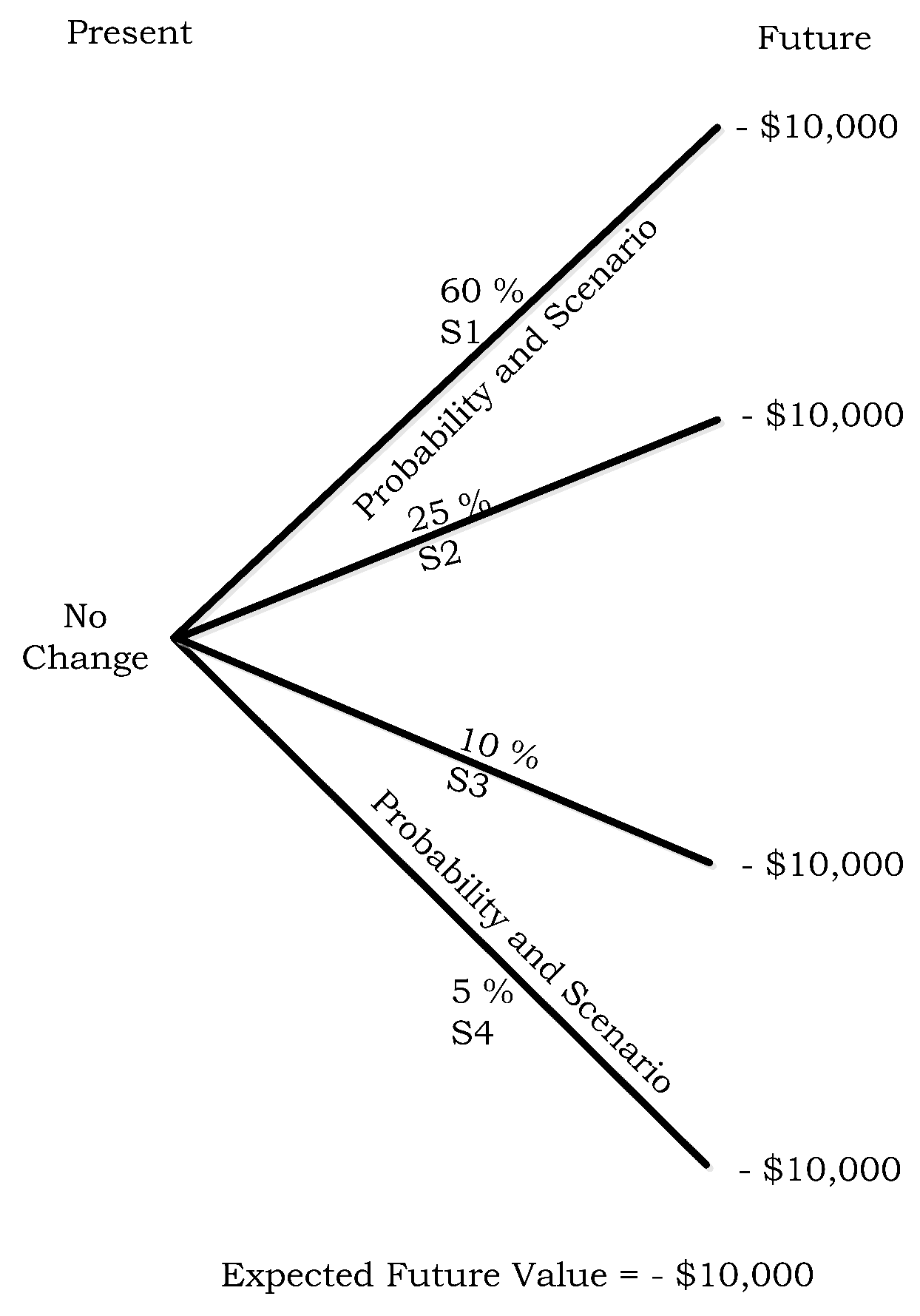
|---|---|---|
| S1 | 60% | $0 |
| S2 | 25% | −$150,000 |
| S3 | 10% | −$350,000 |
| S4 | 5% | −$500,000 |
| State | Loss Probability | Impact Value |
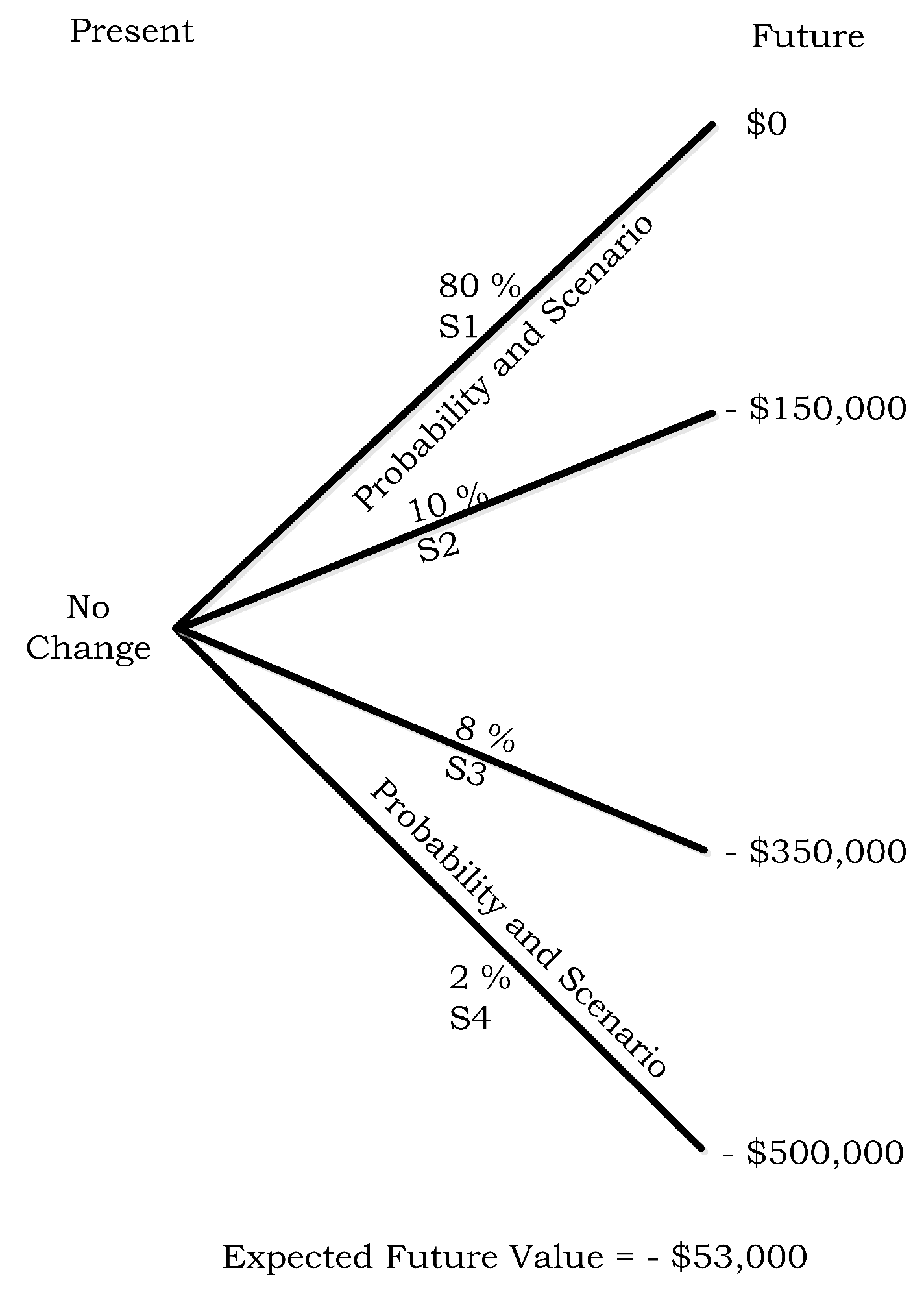
|---|---|---|
| S1 | 80% | $0 |
| S2 | 10% | −$150,000 |
| S3 | 8% | −$350,000 |
| S4 | 2% | −$500,000 |
| Fixed Specifications | Variable Specifications |
|---|---|
| Issuer | Information Security Prediction Market |
| Derivative Type | Information Security Future |
| Contract ID | ISF 123 |
| Underlying Event or Condition | The contract has a strike fixed at the sale of 10,000 cars. One counterparty, say C1, pays $1000 to the second counterparty, say C2, for every 1000 cars sold above the strike. Similarly, the counterparty, C2 pays $1,000 to C1 for every 1000 cars falling short of the strike. The payout can only be a multiple of 1000, and sales of 500 or more cars will be considered as equivalent of 1000 for the payout calculation. |
| Trading Start Date and Time | 1 October 2015 00-00-01 CET |
| Trading End Date and Time | 31 December 2016 23-59-59 CET |
| Minimum Investment Required | Amount : 100,000 (One Thousand) |
| Currency : USD | |
| Maximum Investment Permitted | Amount : 500,000 (Five Hundred Thousand) |
| Currency : USD | |
| Contract Trading Unit (Lot Size) | One (01) |
| Transaction Fee | 0% (Zero for the sake of easy calculation and demonstration) |
| Payout Trigger Criteria | Strike fixed at car sales figure of 10,000. |
| Decision Criteria | Sales figures as reported by the company in its quarterly and annual reports. |
| Payout (Return) Structure | Scaling |
| Pay-Off Horizon | On the day of settlement |
| Settlement Date | The settlement takes place on the fourth trading day from the date of company filling its report (sales figures)until 31 December 2016. If the company fails to file its sales report by the end of 31 January 2017 then the median estimates of analysts (A1, A2, and A3) tracking the company will be taken into consideration to settle the contract, no later than five trading days from the 31 January 2017. |
| Independent Third Party Verification Required | No |
| Eligible Investors/Traders | Only verified |
| Know Your Trader/Investor Required | Yes |
| Transferable Instrument | Yes, to other verified traders only |
| Other Relevant Information | Nil |
| Participant | Trading Side | Incentive/Motivation |
|---|---|---|
| Car Manufacturer | Buy | To hedge the adverse impact of software vulnerabilities on the company’s reputation and sales. |
| Competitors of Car Manufacturer | Sell | To convince others through the display of strong signal that the electronic system in the cars manufactured by “M” have severe vulnerabilities and security risks. The competitors would trade the contracts to signal that they can develop or have better products which are stronger (less or no vulnerability) than “M’s” system. |
| Investors in Car Manufacturer | Buy/Sell | To hedge their risk or to profit from trading in the contract. The buy or sell decision depends upon investor’s individual belief. |
| Cyber-Security Researchers | Buy/Sell | Security researchers in possession of some relevant information may participate in trading of the contract. However, they may like to participate in trading of the contract which is related to the vulnerability discovery in the said product. Trading in that particular contract would allow them to “responsibly” disclose the vulnerability to the car manufacturer “M”. |
| Cyber-(Re)Insurer | Buy/Sell | To hedge their risk or to profit from trading in the contract. The buy or sell decision depends upon insurer’s risk portfolio. |
| Speculators | Buy/Sell | To diversify their investment portfolio. |
| State | State Description |
|---|---|
| S1 | Number of cars sold by the end of 31 December 2016 is 10,000 |
| S2 | Number of cars sold by the end of 31 December 2016 is 9000 (less than 10,000) |
| S3 | Number of cars sold by the end of 31 December 2016 is 11,000 (more than 10,000) |
| State | Event Probability | Impact Value |
|---|---|---|
| S1 | 50% | $0 |
| S2 | 35% | −$100,000 |
| S3 | 15% | +$150,000 |
| State | Event Probability | Impact Value |
|---|---|---|
| S1 | 30% | $0 |
| S2 | 55% | −$100,000 |
| S3 | 15% | +$150,000 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pandey, P.; Snekkenes, E. Using Financial Instruments to Transfer the Information Security Risks. Future Internet 2016, 8, 20. https://doi.org/10.3390/fi8020020
Pandey P, Snekkenes E. Using Financial Instruments to Transfer the Information Security Risks. Future Internet. 2016; 8(2):20. https://doi.org/10.3390/fi8020020
Chicago/Turabian StylePandey, Pankaj, and Einar Snekkenes. 2016. "Using Financial Instruments to Transfer the Information Security Risks" Future Internet 8, no. 2: 20. https://doi.org/10.3390/fi8020020
APA StylePandey, P., & Snekkenes, E. (2016). Using Financial Instruments to Transfer the Information Security Risks. Future Internet, 8(2), 20. https://doi.org/10.3390/fi8020020