Enabling Horizontal Collaboration in Logistics Through Secure Multi-Party Computation

Abstract

The road transport sector is currently facing significant challenges, due in part to CO₂ emissions, high fuel prices, and a shortage of staff. These issues are partially caused by more than 40% of truck journeys being “empty runs” in some member states of the European Union and heavy under-utilization of deck space for non-empty runs. In order to overcome said inefficiency, this paper proposes a decentralized platform to facilitate collaborative transport networks (CTNs), i.e., to enable horizontal collaboration to increase load factors and reduce costs and CO₂ emissions. Our solution leverages secure multi-party computation (MPC) to guarantee that no sensitive business information is leaked to competing hauliers. The system optimizes truck assignments by modeling logistics as a weighted graph that considers orders and truck capacities while maintaining strict confidentiality. Our approach addresses key barriers to CTN adoption, such as lack of trust and data privacy. Implemented using MPyC without extensive optimizations, we demonstrate the efficiency and effectiveness in increasing the average load factor, while achieving acceptable running times (in the order of hours) for arguably meaningful instance sizes (up to 1000 orders). After leveraging a rather simplistic modeling inspired by previous work, we finally give an outlook of possible extensions toward more realistic models and estimate their impact on efficiency.

1. Introduction

As of 2020, more than 20% of all truck rides in the European Union were empty runs, as measured by the total amount of kilometers covered (https://trans.info/en/eu-empty-runs-267211 (accessed on 30 June 2025)), and a significant fraction of non-empty runs was underutilized—that is, they had unused deck space. The situation is even worse for domestic transport, where almost one out of four runs is an empty run, with even higher figures in certain countries, e.g., Cyprus (44% of empty runs), Greece (40%), or Bulgaria (39%). Given that the global freight traffic demand is expected to triple between 2015 and 2050, improving this situation is of critical importance for ecological, economic, and social reasons; cf. also Section 2.2.

While the aforementioned empty runs are partially due to stringent European legislation (https://transport.ec.europa.eu/transport-modes/road/mobility-package-i_en (accessed on 30 June 2025)), another reason is insufficient horizontal collaboration among competing transport companies. The potential benefits of collaborative transport networks (CTNs), e.g., for cost reduction [1] or decarbonization [2] have been well acknowledged. A recent study by Teppan et al. [3] defined the Collaborative Freighter Delivery Problem (CFDP) and provided a simplistic yet highly effective heuristic optimization algorithm to quantify the potential of collaboration.

Focusing on the CFDP rather than actual deployments, their approach assumes all participating hauliers share all information about their orders with a trusted entity that carries out the optimization and assigns specific orders to specific hauliers. However, a recent study by Karam et al. [4] identified a total of 31 barriers in 5 different domains for why CTNs do not see widespread adoption, including, e.g., competition law and trust in coordinators. While different in nature, one core aspect of these two barriers is the need for keeping all information strictly confidential, to avoid being accused of forbidden collaboration and to protect business secrets, respectively. Thus, the approach of Teppan et al. [3] fails to satisfy these central real-world requirements.

1.1. Our Contribution

In this work we aim at overcoming this central limitation by developing a distributed and provably secure variant of the heuristic by Teppan et al. [3]. This is achieved by deploying secure multi-party computation (commonly shortened to MPC) for executing the assignment of orders to trucks, following a heuristic designed to support “MPC-friendly” implementations.

More specifically, similar to previous work, we consider a weighted graph in which each node constitutes a potential origin or destination of an order, and the weights correspond to distances (or journey times) between these locations. Each order specifies its origin and destination, size (e.g., required deck space or weight), as well as the owning haulier. Furthermore, each haulier owns a set of trucks, each having a specified capacity and starting position. Logistic companies can now contribute their orders to the CTN platform, and will receive a set of orders they are responsible for carrying out, together with (suggested) assignments for trucks. The developed heuristic only slightly deviates from that of Teppan et al. [3] to allow for better compatibility with MPC.

We implemented our heuristic in MPyC (https://mpyc.readthedocs.io/ (accessed on 30 June 2025)), and provide benchmarks for different instance sizes from a publicly available reference dataset [5], proving the efficiency and effectiveness of our approach. Specifically, we show that the objective value for the CFDP achieved by our implementation is almost identical to that of previous work ($0.1162$ vs. $0.1126$, cf. Section 4.4.3). Furthermore, for arguably sufficiently large instance sizes (cf. also Section 3.3), our implementation achieves runtimes in the orders of a few hours on standard hardware, allowing, e.g., for daily overnight executions.

Finally, we want to stress that, similar to [3], we followed a simplified modeling, not covering all real-world constraints in collaborative logistics, ignoring, e.g., physical constraints (such as temperature) or timing requirements (such as just-in-time-delivery). This design choice was necessary to enable direct comparison of our results with previous work. However, in Section 5, we explain how our modeling can be extended to also cover more complex external constraints, for which impacts on runtime are to be expected.

Overall, the presented work represents a valuable first step toward the realization of collaborative transport networks based on secure multi-party computation, enabling joint optimization while safeguarding the participants’ critical business information. Despite current limitations in terms of efficiency and the scope of modeling, we believe that this approach can contribute meaningfully to the development of future product-grade solutions in this domain.

1.2. Related Work

Horizontal collaboration in the transport domain is a highly active field for research and development, and we refer to Karam et al. [4] for an introduction and overview.

Regarding optimization, transport logistics [6] planning problems [7,8] have become extremely large and complex due to, for example, the sheer problem size and the amount of involved network partners or complex optimization criteria that might be in opposition to each other (e.g., timeliness vs. load factors or carbon footprint). State-of-the-art approaches for (company-internal) optimization are built upon a number of techniques, e.g., (mixed) integer linear programming [9] like IBM’s CPLEX LS2010 (https://www.ibm.com/products/ilog-cplex-optimization-studio (accessed on 30 June 2025)); constraint programming [10] like IBM’s CP Optimizer targeting scheduling and timetabling problems [11]; or Google’s OR Tools [12], targeting vehicle routing or bin-packing problems. In addition to that, there are many existing highly effective heuristic search algorithms [13] for many classic optimization problems like scheduling, routing, or packing problems [14]. However, all of these mentioned approaches consider in-house optimization and have not been designed for federated computation in CTNs.

A first approach toward privacy-preserving optimization has been taken by Gojković and Schranz [15] using the Artificial Bee Colony Algorithm from swarm intelligence. However, their work leaves many questions unanswered, especially related to the formal modeling of the precise information revealed to the stakeholders or the actual deployment of the algorithm, so it can only be seen as an innovative first step. We will also use the same underlying reference dataset [5] to validate the results of our heuristic.

1.3. Structure of This Paper

This document is structured as follows. Section 2 gives a concise introduction to secure multi-party computation and provides some more background on the motivation of this work. In Section 3, we recap the modeling underlying our optimization problem and briefly summarize the potential of CTNs to increase the load factor in the logistics sector. Section 4 presents the main contribution of this paper, including a secure MPC-based solver for the CFDP (Section 4.1), security considerations (Section 4.2), deployment considerations (Section 4.3), and performance evaluation (Section 4.4). In Section 5 we explain how additional constraints can be integrated into our modeling. Finally, we briefly conclude in Section 6.

2. Preliminaries

In the following we give a brief introduction to secure multi-party computation in Section 2.1. Readers familiar with the topic can safely skip this section upon first reading and come back later if needed. Subsequently, in Section 2.2, we provide some more motivation for the need for horizontal collaboration in the logistics domain.

2.1. Introduction to MPC

MPC consists of a family of cryptographic techniques that address the following general problem: given a set of parties ${\mathcal{P}}_1,\dots ,{\mathcal{P}}_n$, with each party ${\mathcal{P}}_i$ holding an input value $x^{\left(i\right)}$, the goal is to compute $y=f\left(x^{\left(1\right)},\dots ,x^{\left(n\right)}\right)$ without resorting to an external third party and without revealing any information on the input values (aside from what can be deduced from the output value y).

MPC was introduced by Yao in 1982 [16], who also presented the first important technique to realize an MPC solution, namely garbled circuits. Research has flourished since, with the first couple of decades focusing on theoretical possibilities and limits of MPC, as well as new solution families [17,18,19,20,21,22,23] based on cryptographic techniques such as secret sharing [24]. The first decade of the 21st century witnessed some important advancements in general constructions and efficiency [25,26], with MPC being deployed for the first time to solve a practical problem in 2009 [27].

Since its introduction in the 1980s, MPC has reached a high level of maturity, with the introduction of several efficient schemes [28,29] and software platforms implementing general-purpose MPC protocols; online overviews (https://github.com/rdragos/awesome-mpc?tab=readme-ov-file (accessed on 30 June 2025)) are available for the interested reader. Furthermore, MPC-based solutions have been proposed in pilots and demonstrators for various sectors; in particular, an application to collaborative resource optimization for air traffic management has been proposed [30], a scenario which bears some resemblance to the collaborative freighter assignment problem. Finally, several start-ups and companies such as Cybernetica (https://cyber.ee/ (accessed on 30 June 2025)), Partisia (https://www.partisia.com/ (accessed on 30 June 2025)), Roseman Labs (https://rosemanlabs.com/ (accessed on 30 June 2025)), and Linksight (https://www.linksight.nl/en/ (accessed on 30 June 2025)) offer MPC services. For a more in-depth overview of the topic, cf. [31,32].

It is important to remark that different MPC constructions offer different security guarantees under various assumptions on the adversarial model and on the communication channels in place. Dishonest behavior is modeled by assuming that an entity known as the adversary takes control of a number of parties, and is therefore able to read all information seen by these corrupted parties; if the adversary can further instruct corrupted parties to disregard the instructions of the MPC protocol, we speak of an active adversary, while if this is not the case, and corrupted parties exchange information with the adversary but do follow the steps of the MPC protocol correctly, we speak of a passive adversary. Guaranteeing security against an active adversary comes at a price: this is generally possible only if the adversary controls a smaller fraction of parties compared to passive adversaries. Similar considerations apply if information-theoretic security is required, hence guaranteeing that not even a computationally unbounded adversary can break the MPC protocol.

The most widespread approach to MPC follows the share-compute-reveal paradigm. The idea is that any secret value x can be “split” into n elements $x_1,\dots ,x_n$ called shares using a secret sharing scheme [24], in such a way that no “small” coalition of parties can recover any information on x based on the shares in their possession, while larger coalitions can completely reconstruct x given their set of shares. This sharing system is also supposed to support the evaluation of sums and products, meaning that given shares of two values x and y, it is possible to compute shares of $x+y$ and of $x·y$ without revealing any information on x nor y. The idea is then to express the function f as a circuit, compute shares of each input value, and evaluate the circuit on these shares; once shares of the output value $f\left(x^{\left(1\right)},\dots ,x^{\left(n\right)}\right)$ are obtained, parties can then reveal these shares and reconstruct the output. Security is guaranteed under the assumption that the adversary can only control a “small” coalition.

Comparison to Other Privacy-Preserving Technologies

In addition to MPC, a variety of other privacy-enhancing technologies (PETs) has been introduced in the academic literature and found various applications in different domains in the real world. Thus, we will next briefly justify the choice for our MPC-based solution presented in the subsequent sections.

The main alternative paradigm for secure computation besides MPC is that of fully homomorphic encryption (FHE), which enables computations on encrypted data without decrypting them, hence preserving privacy throughout the process. This allows data owners to outsource sensitive data processing, such as to cloud services, while keeping the underlying information confidential. The encrypted results can then be decrypted only by the data owner’s secret key. Since its conceptual introduction by Rivest et al. [33] and its first practical realization in 2009 [34], FHE has seen many advances but remains computationally expensive and slower than working with plaintext data. In the context of our scenario, protecting sensitive business information is crucial. Yet, while FHE could theoretically allow computations on encrypted inputs from multiple parties, it is not a fully natural choice here, as the master secret key (needed for decrypting the final computation result) needs to be handled securely, thus again requiring either a trusted entity managing the key—the avoidance of which is the main ambition of this work—or a distributed setup resembling to MPC.

Another main approach used for federated computations, especially in the context of federated learning, is that of differential privacy (DP) [35]. This is a technique for protecting individual data entries in a dataset by adding carefully calibrated randomness to the output of computations. It ensures that the inclusion or exclusion of a single data point does not significantly affect the result, thereby providing strong privacy guarantees. DP is particularly well-suited for statistical analysis, aggregate queries, and releasing anonymized datasets. However, in collaborative logistics optimization—where multiple hauliers aim to jointly optimize truck utilization—DP is not ideal: our use case requires precise, per-instance decisions (e.g., matching specific orders to trucks), where even small inaccuracies introduced by DP noise can degrade the quality of the solution.

Another option would be to use Trusted Execution Environments (TEEs) [36], such as Intel’s Software Guard Extensions (SGX) (https://www.intel.com/content/www/us/en/products/docs/accelerator-engines/software-guard-extensions.html (accessed on 30 June 2025)), AMD Secure Encrypted Virtualization (SEV) (https://www.amd.com/en/developer/sev.html (accessed on 30 June 2025)), ARM TrustZone (https://www.arm.com/technologies/trustzone-for-cortex-m (accessed on 30 June 2025)), or IBM Secure Service Container (https://www.ibm.com/docs/en/systems-hardware/linuxone/3932-LA2?topic=container-secure-service-technology-deploying-appliances (accessed on 6 August 2025)). These offer secure enclaves for isolated data processing and are often used to protect sensitive computations from untrusted system components. However, they rely on a centralized hardware root of trust, requiring all parties to place faith in the security and integrity of a single chip vendor, contradicting our goal of avoiding a central trusted entity—even though, admittedly, their role would be different from that in the case of plaintext computations by a central authority. However, TEEs have been repeatedly shown to be vulnerable to side-channel and hardware-level attacks.

Finally, functional encryption (FE) [37] allows users to compute specific functions on encrypted data without revealing the data itself. While powerful in theory, FE is still largely impractical for complex, real-world applications like collaborative logistics optimization due to limited expressiveness and a lack of efficient general-purpose implementations. Additionally, FE typically assumes a central authority to manage keys and functions, conflicting with the decentralized trust requirements of multi-party collaboration.

2.2. Extended Motivation and Background

As already mentioned earlier, collaboration in logistics may be beneficial on various levels. In the following, we briefly introduce three main dimensions in which such collaborative efforts may generate impact.

2.2.1. Ecological Dimension

In 2019, transport was responsible for about one quarter of the European Union’s total CO₂ emissions, and more than 7% of the EU’s total emissions were caused by trucks (https://www.europarl.europa.eu/topics/en/article/20190313STO31218/co2-emissions-from-cars-facts-and-figures-infographics (accessed on 30 June 2025)). Furthermore, transport was the only sector with a significant increase of CO₂ emissions between 1990 and 2019, and current projections put the decrease in emissions by 2050 far behind the EU’s ambitious goals, which would be necessary to achieve the Paris Agreement of limiting the global temperature increase below 2 degrees Celsius compared to the pre-industrial era. This situation contradicts the European Green Deal, which aims to transform Europe into a sustainable and climate-neutral economy by 2050, by, for instance, reaching a 90% reduction in transport-related greenhouse gas emissions (https://commission.europa.eu/strategy-and-policy/priorities-2019-2024/european-green-deal/transport-and-green-deal_en (accessed on 30 June 2025)).

2.2.2. Economical Dimension

Operational costs, including fuel, maintenance, road tolls, and driver wages, are major expenses for transport companies [38]. These costs only partially depend on the load factor of the truck, leading to inefficiencies and higher freight prices for partially empty runs, which in particular increases pressure on small logistics companies that cannot optimize in-house. Maximizing the average utilization of trucks would thus lower logistics expenses; in turn, this could translate into reduced consumer prices, especially in sectors heavily reliant on freight transport. The savings from cutting empty runs would also help stabilize costs across industries, especially in times of high energy prices.

2.2.3. Social Dimension

Europe is experiencing a shortage of truck drivers, and about one third of all truck drivers is expected to retire in the next ten years (https://www.iru.org/news-resources/newsroom/half-european-truck-operators-cant-expand-due-driver-shortages (accessed on 30 June 2025)), while at the same time the freight traffic demand is growing. Decreasing the fraction of empty truck runs can thus help mitigate the EU’s truck driver shortage because it maximizes efficiency, reduces unnecessary workload, optimizes the use of available drivers, and thus alleviates pressure on the existing workforce, allowing companies to meet growing transport demands without overburdening drivers.

3. Optimization Problem

Real-world optimization problems, including those in the logistics domain, often have a very high computational complexity, cf. [39,40]. More precisely, these problems are especially difficult to solve in worst-case scenarios, where they are often considered intractable for meaningful instance sizes, which is, in particular, the case in our scenario, where inputs from many parties are pooled.

In the following we recap the Collaborative Freighter Delivery Problem (CFDP), which is known to be NP-hard [3]; we tackle it with a heuristic later in Section 4.

3.1. CFDP Instances and Valid Solutions

On a high level, the CFDP [3] is defined by a directed weighted graph $\mathcal{M}:=\left\{\mathcal{N},\mathcal{E}\right\}$ specifying a map. The nodes $\mathcal{N}$ specify locations (e.g., regions/cities, warehouses, etc.) for senders and receivers, while the edges $\mathcal{E}\subseteq \left\{\right({\mathcal{N}}_1,{\mathcal{N}}_2,w):{\mathcal{N}}_1\ne {\mathcal{N}}_2\in \mathcal{N},w\in \mathbb{N}\}$ represent roads between locations, together with the time w required to move from the origin N₁ to the destination N₂. We assume a complete graph, i.e., every pair of nodes is connected by a unique edge.

The relevant actors in a CTN are collaborating freight hauliers, each managing a fleet of trucks and a set of customer orders. Hauliers, trucks, and orders all have unique identifiers, modeled as positive integers.

A haulier $\mathrm{HAULIER}$ is a pair $\left(\mathrm{HAULIERID},\left(\mathrm{TRUCKI}{\mathrm{D}}_1,\dots ,\mathrm{TRUCKI}{\mathrm{D}}_{\ell }\right)\right)$, where the value $\mathrm{HAULIERID}\in \mathbb{N}$ denotes the haulier identifier and $\left(\mathrm{TRUCKI}{\mathrm{D}}_1,\dots ,\mathrm{TRUCKI}{\mathrm{D}}_{\ell }\right)$ is the list of identifiers of the trucks that are controlled by the haulier.

A truck $\mathrm{TRUCK}$ is described by a truck identifier $\mathrm{TRUCKID}\in \mathbb{N}$, the identifier $\mathrm{HAULIERID}$ of the haulier that controls the truck, the current truck position $\mathrm{POSITION}\in \mathcal{N}$, and the truck capacity $\mathrm{CAPACITY}\in \mathbb{N}$. The latter can be thought of as, e.g., the number of pallets that fit on the loading area. Furthermore, each truck has a dedicated starting position (e.g., corresponding to its home base).

An order $\mathrm{ORDER}$ consists of an identifier $\mathrm{ORDERID}\in \mathbb{N}$, its origin and destination $\mathrm{ORIGIN}\ne \mathrm{DEST}\in \mathcal{N}$, its volume $\mathrm{VOL}\in \mathbb{N}$, and the identifier $\mathrm{HAULIERID}$ of the haulier that the order is assigned to (including ⊥ for “unassigned”).

Finally, a truck drive $\mathrm{DRIVE}$ is a tuple of the form $(\mathrm{TRUCKID},(\mathrm{ORIGIN},\mathrm{DEST}),(\mathrm{ORDERI}{\mathrm{D}}_1,\dots ,\mathrm{ORDERI}{\mathrm{D}}_k))$, where $\mathrm{TRUCKID}$ is the identifier of the truck assigned to the drive, $\mathrm{ORIGIN}\in \mathcal{N}$ is the drive departure node, $\mathrm{DEST}\in \mathcal{N}$ is its destination, and the list $\left(\mathrm{ORDERI}{\mathrm{D}}_1,\dots ,\mathrm{ORDERI}{\mathrm{D}}_k\right)$ denotes orders that need to be carried from the departure node to the destination node.

Intuitively, a valid solution to a collaborative freighter delivery problem instance is now a set of consistent truck drives respecting the trucks’ maximum capacity, such that each order is picked up at its origin and delivered to its destination address. We omit the formal modeling of CFDP instances and valid solutions here, and refer the interested reader to [3,5].

3.2. Optimization Goal

The optimization goal of the plain CFDP problem is to minimize the average empty space on a truck. For this, let $\mathcal{A}$ denote all truck rides in a valid solution. For each ride $A\in \mathcal{A}$, $C_{T_A}$ denotes the capacity of the truck used for this ride, and ${\mathcal{O}}_A$ are the orders of this ride, where $v_O$ is the volume of an order $O\in {\mathcal{O}}_A$.

The optimization goal is then the fraction ${\displaystyle \frac{C_{T_A}-{\sum }_{O\in {\mathcal{O}}_A}{v}_O}{C_{T_A}}}$ of empty space for a specific truck ride, averaged over all truck rides $A\in \mathcal{A}$, resulting in a normalized value in the interval $[0,1]$. Specifically, the optimization goal is given by the following:

$$\mathrm{minimize}{\displaystyle \frac{1}{\left|\mathcal{A}\right|}}·\sum _{A\in \mathcal{A}}{\displaystyle \frac{C_{T_A}-{\sum }_{O\in {\mathcal{O}}_A}{v}_O}{C_{T_A}}}=1-{\displaystyle \frac{1}{\left|\mathcal{A}\right|}}·\sum _{A\in \mathcal{A}}\sum _{O\in {\mathcal{O}}_A}{\displaystyle \frac{v_O}{C_{T_A}}}.$$

(1)

An objective value of 0 indicates that all trucks are completely filled, whereas an objective value of 1 indicates that all trucks are completely empty.

Note that Equation (1) minimizes the fraction of empty deck space per truck ride. Minimizing the fraction of empty deck space per truck-kilometer is easily achieved by adding appropriate scaling factors to the summands.

Clearly, as an extension to the above CFDP, the prioritization of orders can be reflected in the objective function, with adjustable weights to adjust the relative importance of those two aspects (i.e., timing and load factor). However, while being under ongoing development, for the sake of brevity, we will not elaborate on the prioritization aspects in more detail in this paper, as it does not change the overall approach and validity of our results, and was also not considered in [3], which we use as a baseline for our evaluation.

3.3. On the Potential of Horizontal Collaboration

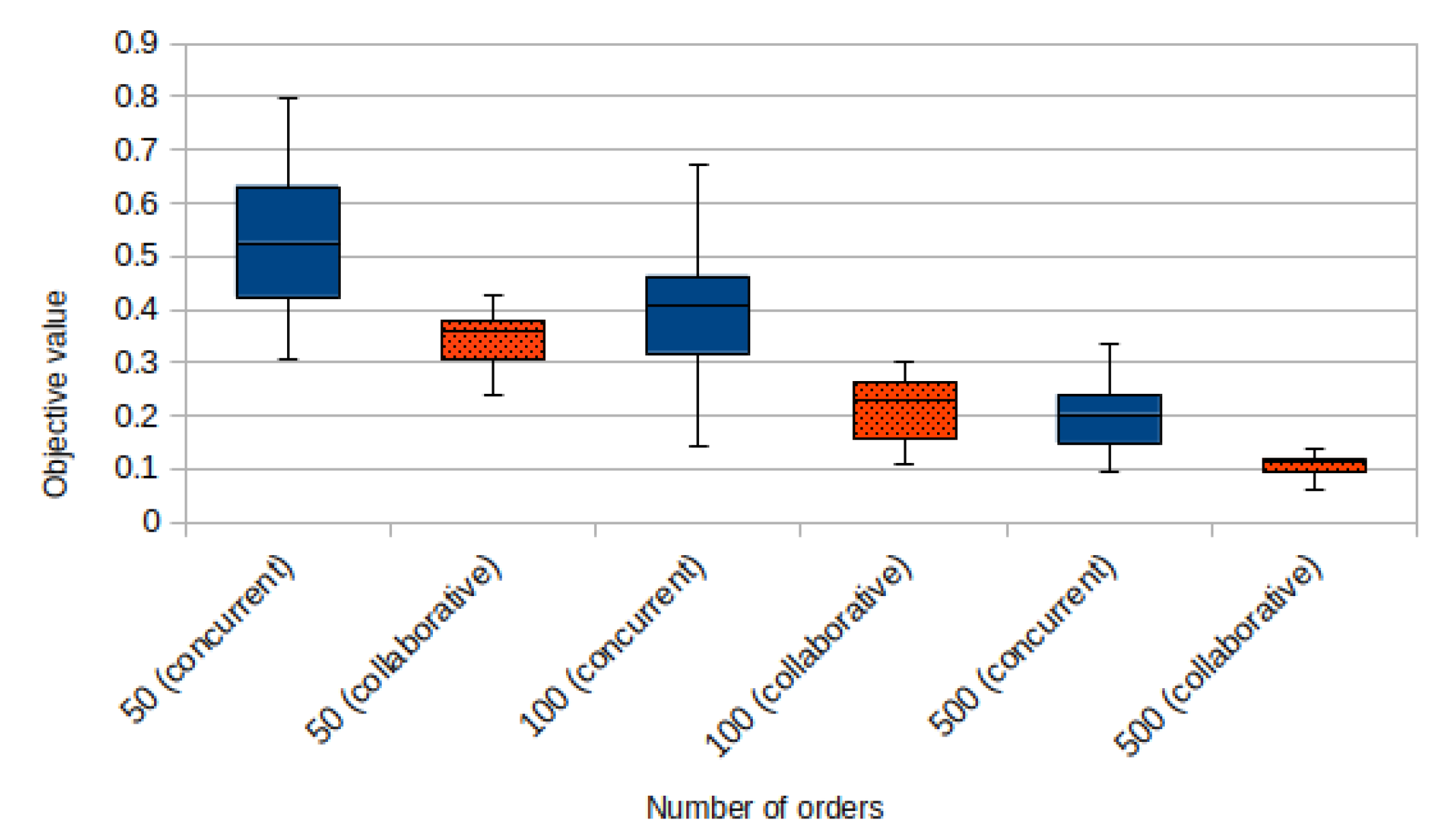
When aiming for a privacy-preserving solution enabling competing hauliers to jointly assign their orders to companies, a natural question to ask is whether this actually brings any benefit regarding the optimization goal in Equation (1). The answer to this question can be seen in Figure 1, derived from [3]: for different instance sizes, the left (blue) box marks the objective value if each haulier optimizes locally, while the right (orange, dotted) box marks the objective value if the same orders are processed in a collaborative manner. These results underpin the intuition that a collaborative approach, where empty space on one truck can be used for an order from another haulier, increases the efficiency and optimality of the entire solution. Note that this collaborative heuristic not only optimizes Equation (1) but also significantly contributes to all the dimensions listed in Section 1, underscoring its potential for sustainable logistics solutions.

An important observation is revealed by a closer look at the figure. Namely, collaboration pays off more for instances with fewer orders, an aspect that is also reflected in the diminishing differences in the collaborative and concurrent objective values as the number of orders increases. This is not surprising, since higher numbers of orders per haulier already allow for reasonably efficient in-house optimization.

This observation can now be used to further incentivize hauliers to participate in a CTN through the following approach:

• In a first step, each haulier performs in-house optimizations, maximizing the load factor of their own trucks, which will result in good results for most of the truck drives if they have a sufficiently large number of orders to process.
• Only in a second step, orders that cannot be efficiently processed in-house—e.g., because they are based in outlier destinations, or because they just do not fit on the optimized trucks—are submitted to the collaborative platform, together with available trucks.

The benefits of this two-step approach are now twofold:

• From a company point of view, this allows one to hide the actual order situation (being sensitive economic information) as only “left-over” orders are provided to the system, and no information about pre-processed orders is revealed.
• From an optimization point of view, this brings the advantage of reduced instance sizes given the NP-hardness of the CFDP and the additional overhead of cryptographically secured implementations.

In particular, looking at Figure 1, instances with about 500 orders already achieve a very good overall load factor (<12% of empty deck space), so that not too much additional improvements are possible. Therefore, scalability in terms of the number of orders is only needed for up to several hundred, or at most 1000, orders. In case a higher number of orders is submitted to the platform by different hauliers, these can be processed independently in (randomized) batches of 500 to 1000 orders, without relevant negative impact on the quality of the solution.

4. Toward an MPC-Based Solution for the CFDP

A main obstacle for the adoption of collaborative approaches in competitive sectors is confidentiality: collaboration often demands sharing sensitive operational data with business competitors, a requirement that would often be unacceptable. This is in particular the case for the logistics sector, where hauliers would most likely be highly reluctant to share such data with any party, let alone with business competitors, cf. Karam et al. [4].

However, outputting to each haulier only the orders assigned to it within a valid solution of the CFDP does not disclose any other sensitive information like order situation or availability. Hence, the root of the problem lies in the sensitivity of the input data, not the output.

This duality of sensitive input vs. non-sensitive (to some extent) output is addressed by so-called privacy-enhancing technologies, or PETs. In particular secure multi-party computation is a canonical candidate technology to address the logistic challenge we are interested in.

In the following we describe our solution, argue its security, discuss practical deployment considerations, and finally provide efficiency and effectiveness benchmarks.

4.1. Description of Our Solution

This subsection discusses our MPC solution to the CTN described in the previous sections in a way that is as agnostic as possible of the MPC protocol (and software) that can be used to instantiate and implement it. We will therefore only assume that an MPC solution is available that can turn secret values x into “scrambled” values $\left[x\right]$; for simplicity, one can think of a secret-sharing process as described in Section 2.1, where $\left[x\right]=\left(x_1,\dots ,x_n\right)$ is the collection of shares. It is assumed that sum- and multiplication gates can be securely evaluated on scrambled values, and that a value y can be reconstructed from its scrambled version $\left[y\right]$ if all parties holding shares of y cooperate. Moreover, we also assume that a scrambled value $\left[x\right]$ can be reconstructed either publicly, meaning that all MPC parties will obtain the value of x, or to a single party, meaning that other parties will obtain no information whatsoever on x; this is a standard property of many MPC protocols.

The first step consists of scrambling the data related to orders and trucks; this means that the owner of each order $\mathrm{ORDER}=\left(\mathrm{ORDERID},\left(\mathrm{ORIGIN},\mathrm{DEST}\right),\mathrm{VOL},\perp \right)$ will ensure that all data (except for the haulier value, which is unassigned at this point) is scrambled, hence obtaining $\left[\mathrm{ORDER}\right]=\left(\left[\mathrm{ORDERID}\right],\left(\left[\mathrm{ORIGIN}\right],\left[\mathrm{DEST}\right]\right),\left[\mathrm{VOL}\right]\right)$. Similarly, each haulier will scramble the truck data, and also initialize a “destination” variable $\mathrm{DEST}est$ to the unassigned value ⊥, hence obtaining $\left[\mathrm{TRUCK}\right]=\left(\left[\mathrm{HAULIERID}\right],\left[\mathrm{POSITION}\right],\left[\mathrm{DEST}\right],\left[\mathrm{CAPACITY}\right]\right)$; notice that there is no need to scramble (or share in any other way) the truck identifier. Finally, the map data is assumed to be public.

In the following we now describe the main steps of our solution; the interested reader can refer to our implementation (https://github.com/ait-crypto/MUPOL-MPC (accessed on 30 June 2025)) for additional implementation-specific details. We assume that a number of fundamental building blocks are available in the MPC framework used:

• A secure non-exclusive OR subroutine that, on input two scrambled bits $\left[x\right],\left[y\right]$, outputs $\left[x\vee y\right]$. For simplicity, we denote this OR operation on scrambled values with ∨.
• A secure-equality sub-routine, i.e., an MPC sub-routine $\mathtt{eq}$ that takes as input two scrambled integers $\left[x\right],\left[y\right]$ and outputs a scrambled bit $\left[b\right]$ where $b=1$ if $x=y$, and 0 otherwise.
• A secure comparison sub-routine, i.e., an MPC sub-routine $\mathtt{greater}\_\mathtt{eq}$ that takes as input two scrambled integers $\left[x\right],\left[y\right]$ and outputs a scrambled bit $\left[b\right]$ where $b=1$ if $x\ge y$, and 0 otherwise.
• A secure if-else subroutine, i.e., an MPC sub-routine $\mathtt{if}\_\mathtt{else}$ that takes as input a scrambled bit $\left[b\right]$ and two scrambled values $\left[x\right],\left[y\right]$, and outputs $\left[x\right]$ if $b=1$ and $\left[y\right]$ if $b=0$.
• A secure sorting sub-routine, i.e., an MPC sub-routine $\mathtt{sort}$ that takes a list of scrambled values $L:=\left(\left[x^{\left(1\right)}\right],\dots ,\left[x^{\left(\ell \right)}\right]\right)$ as input, with $x^{\left(i\right)}\in \mathbb{N}$ for all i, and outputs a permutation $\left(\left[x^{\left(i_1\right)}\right],\dots ,\left[x^{\left(i_{\ell }\right)}\right]\right)$ of L where $x^{\left(i_j\right)}\le x^{\left(i_{j+1}\right)}$ for all j.

Note that these basic functionalities are common to most modern generic MPC frameworks such as MPyC or MP-SPDZ [41].

Our solution now consists of two core components:

$\mathtt{fill}\_\mathtt{truck}$.

The sub-routine $\mathtt{fill}\_\mathtt{truck}$ (Sub-routine 1) takes as input an order and a truck and checks whether the order can be processed by this truck. To do so, the algorithm checks whether the truck is at the same position as the order, whether the destination of the order and the truck are consistent (or, in case the truck has not yet been assigned a destination because it has no orders already assigned, it defines the destination accordingly), whether the available deck space of the truck is sufficient to process the order, and whether the order has not already been assigned to another truck. If all conditions are satisfied, the order is obliviously assigned to the truck, and all respective variables (remaining capacity, etc.) are updated; otherwise, the order is not processed in the specific activation of the function.

$\mathtt{create}\_\mathtt{empty}\_\mathtt{truck}\_\mathtt{drive}$.

The sub-routine $\mathtt{create}\_\mathtt{empty}\_\mathtt{truck}\_\mathtt{drive}$ (Sub-routine 2) is only called when no further orders can be processed, i.e., if for all unprocessed orders there is no truck available at the same position. In this case, this algorithm moves an empty truck to the position of an order awaiting distribution. In line with the optimization goal in Equation (1), the algorithm sends an empty truck minimizing the distance, i.e., a truck closest to the waiting order.

While the $\mathtt{fill}\_\mathtt{truck}$ sub-routine can be fully described by leveraging the building blocks described above, $\mathtt{create}\_\mathtt{empty}\_\mathtt{truck}\_\mathtt{drive}$, on the other hand, requires a number of auxiliary sub-routines that we describe below.

• $\mathtt{find}\_\mathtt{unproc}\_\mathtt{origin}$ takes as input the list of scrambled orders, and outputs the first order for which the $\mathrm{PROCESSED}$ flag is set to 0.
• $\mathtt{find}\_\mathtt{dist}\_\mathtt{to}\_\mathtt{order}$ takes as input the list of scrambled trucks and a scrambled order object, and adds to each truck object a scrambled flag $\left[\mathrm{DIST}\right]=\left[e.w\right]$, where $e.w$ denotes the weight of the edge with origin equal to the position of the truck, and destination equal to the position of the order.
• $\mathtt{arg}\_\mathtt{min}$ is a secure arg-min function, i.e., given a list of scrambled integers $\left[x^{\left(1\right)}\right],\dots ,\left[x^{\left(N\right)}\right]$, it returns $\left[i\right]$ where $x^{\left(i\right)}=min\left(x^{\left(1\right)},\dots ,x^{\left(N\right)}\right)$.

Sub-routine 1 fill_truck

Inputs: 1. A scrambled truck object [TRUCK]; 2. A scrambled order object [ORDER].

Computation: 1. Compute the following scrambled Boolean values: eq([TRUCK.POSITION], [ORDER.ORIGIN]), i.e., compute (without revealing it) whether the truck position coincides with the order origin. eq([TRUCK.DEST], [⊥]) ∨ eq([TRUCK.DEST], [ORDER.DEST]), i.e., compute whether the truck has destination equal to that of the order, or whether the destination has not yet been set; in this case the truck would be available for delivering the given order. greater_eq([TRUCK.CAPACITY]—[ORDER.VOL], [0]), i.e., compute whether the remaining truck capacity is larger or equal to the order volume.

2. Multiply these Boolean values, and multiply the result with ([1]—[ORDER.PROCESSED]); denote the obtained scrambled Boolean value by [ISCOMPATIBLE]. Notice that the result is equal to [1] if all of the conditions described above are met and the order has not already been assigned to a different truck drive and to [0] otherwise. 3. If truck and order are compatible, update the truck destination to match the order destination; this is performed by setting [TRUCK.DEST] ← if_else([ISCOMPATIBLE], [ORDER.DEST], [TRUCK.DEST]). 4. Update the truck capacity by setting [TRUCK.CAPACITY] ← [TRUCK.CAPACITY]—[ORDER.VOL] · [ISCOMPATIBLE]. 5. Update the order haulier indicator to match the truck haulier, if order and truck are compatible; this is performed by setting [ORDER.HAULIER] ← if_else([ISCOMPATIBLE], [TRUCK.HAULIER], [ORDER.HAULIER]) 6. Update the order status with [ORDER.PROCESSED] ← [ORDER.PROCESSED] ∨ [ISCOMPATIBLE].

Sub-routine 2 create_empty_truck_drive

Inputs: 1. The array of scrambled order objects [ORDERSET] = ([ORDER(1)],...,[ORDER(ℓ)] 2. The array of scrambled truck objects [TRUCKSET] = ([TRUCK(1)],...,[TRUCK(t)] 3. An array [DRIVESET] of scrambled truck drive objects.

Computation: 1. Call find_unproc_origin([ORDERSET]) to obtain the scrambled object describing the position [UNPROCPOS] of the first unprocessed order 2. Call find_dist_to_order([TRUCKSET], [UNPROCPOS]) to add a [DIST] flag to each truck object. 3. Compute [i] = arg_min([TRUCK.DIST] for [TRUCK] ∈ [TRUCKSET]) to identify a truck closest to the unprocessed order. 4. Select the truck [TRUCK(i)] with index i; this step can be securely performed with MPC using standard methods. 5. Add the tuple ([TRUCK(i).HAULIERID], [TRUCK(i).POSITION], [UNPROCPOS] to the list of scrambled truck drives [DRIVESET]. 6. “Move” the i-th truck to the position of the first unprocessed order by setting [TRUCK(i).POSITION] = [UNPROCPOS].

By leveraging the sub-routines $\mathtt{fill}\_\mathtt{truck}$ and $\mathtt{create}\_\mathtt{empty}\_\mathtt{truck}\_\mathtt{drive}$, we can now define our solver $\mathtt{MPC}\_\mathtt{solver}$ (Protocol 3) for the CFDP. The algorithm is initialized with the scrambled orders and trucks provided by each haulier, where each order is labeled as unprocessed. Furthermore, the algorithm internally maintains a list of created truck drives and counts the number of orders that have already been processed.

The algorithm is then carried out in cycles. In each cycle, it iterates over all trucks and orders, and assigns the order to the given truck using the $\mathtt{fill}\_\mathtt{truck}$ subroutine. The protocol then checks whether any order has been assigned (i.e., whether a truck drive has been created) during this iteration. If this is the case, the next cycle is started; otherwise, $\mathtt{create}\_\mathtt{empty}\_\mathtt{truck}\_\mathtt{drive}$ is called to avoid a deadlock. This procedure is repeated until all orders are processed. Finally, each party now receives its assigned orders.

Full details are presented in Protocol 3.

Protocol 3 MPC_solver

Inputs: a collaborative freighter delivery instance, given by a map $\mathcal{M}$, a set of orders ORDERSET, a set of trucks TRUCKSET, and a set of hauliers HAULIERSET

Initialization: 1. The owner of each order object ORDER and truck object TRUCK uploads them to the MPC framework; scrambled objects [ORDER] and [TRUCK] are obtained. 2. For each order object [ORDER], the [PROCESSED] flag is initialized to [0]. 3. the parties initialize an empty list of scrambled truck drives [DRIVESET]$\leftarrow \varnothing$ 4. the parties initialize a counter of processed order NUMPROCESSED ←0

Computation: 1. For each [TRUCK] ∈ [TRUCKSET] and each [ORDER] ∈ [ORDERSET], parties run fill_truck ([TRUCK], [ORDER]). 2. Parties compute the (scrambled) number of orders that have been processed in this round, and reconstruct its value; if this number is equal to 0, parties run create_empty_truck_drive ([ORDERSET], [TRUCKSET], [DRIVESET]). 3. Parties update the number of processed orders NUMPROCESSED by adding the number of orders processed in this round (computed in the previous step) to it. If NUMPROCESSED = |ORDERSET|, they proceed to the output phase; otherwise, they update each truck location and reset their volume and destination, and go back to step 1

Output phase: 1. The parties reconstruct the scrambled haulier ID [ORDER.HAULIERID] of each order. Notice that this only reveals how many orders are assigned to each haulier, with no other information on the orders or trucks. Similarly, the parties reconstruct the haulier ID associated to each empty drive. 2. Each order object [ORDER] and each empty drive object [DRIVE] = (HAULIERID, [ORIGIN], [DEST]) is entirely reconstructed only to the haulier assigned to it.

4.2. Security Consideration

By the definition of security for multi-party computation [16,17,18,19,20,21,22,23], it is guaranteed that no information beyond the defined computation outputs is revealed to any participant in the system. Assuming a software framework that securely implements these protocols, we thus only need to argue that the data explicitly revealed to the computing nodes during the protocol execution does not contain any sensitive information.

Assigned orders. 

At the end of the output phase, Protocol 3 discloses a full description of the truck drives assigned to a specific haulier only to this party, i.e., each haulier learns the orders that it is responsible for. This is an immediate functional requirement and the expected output of the computation, and thus does not violate confidentiality.

It should also be observed that repeated executions of the protocol could reveal recurring patterns in order volumes and routes, and in the matching between orders and trucks. There does not seem to be an obvious solution to this issue, since hauliers have to know which orders are assigned to which trucks, and hiding these patterns would arguably require adding some form of noise or randomization, which would degrade the quality of the solution. This, however, is an inherent issue of the CFDP problem itself and is thus orthogonal to the goals of our solution; moreover, as argued in Section 3.3, our solution is arguably best suited for a setting where most of the orders have already been individually processed by each haulier with separate, in-house optimization, and where only a limited total number of orders (in the order of a few thousands) is left to be processed. Hence, the revealed patterns would only concern a fraction of the number of orders submitted to the hauliers.

Number of orders and empty drives per haulier. 

Similarly, Protocol 3 explicitly outputs the number of empty drives as well as the number of orders per haulier to all participants, but no information about the specific orders to be processed or their origins/destinations. Initial discussions with domain experts showed that (average case) fairness is one of the key features requested by hauliers, e.g., to ensure that no systematic biases (e.g., with a specific haulier systematically getting more empty rides than another) in case of malicious computing nodes exist. This request is addressed by outputting such audit information, without violating the confidentiality of sensitive information.

At the same time, this output helps to increase efficiency, as otherwise “fake” orders and truck drive objects would need to be created to mask the actual number of orders and empty drives of each haulier.

Given that this is a functional requirement for certain stakeholders as well as an efficiency booster, we therefore chose to reveal this piece of information.

Number of processed orders per iteration. 

During each iteration of the solver, the number of orders processed during this iteration is revealed (Step 2 of the computation phase). This could be avoided, but it would lead to a very inefficient oblivious while-loop construction, where we would need to set an upper bound on the number of iterations necessary to obtain a solution (roughly $2·\left|\mathrm{ORDERSET}\right|$ as in the worst case every single order would cause an empty truck drive before it can be processed), and then run each iteration for this fixed number of times, accepting the worst-case complexity for every given instance, while our experiments show that significantly better average-case performance can be achieved (cf. Section 4.4).

However, arguably, this piece of information does not reveal sensitive data, as it neither includes the number of truck rides nor information about origins, destinations, or owners of orders. Rather, it solely reveals a single inequality on the relative distribution of trucks, orders, and order sizes (basically indicating that no remaining order would fit into any truck), which does not allow one to infer information about single orders. While revealing this information is thus not inherent, we chose to do it, given the high benefit of this choice on efficiency and the practical irrelevance of the disclosed information.

In summary, only three types of information are disclosed during the computation process—two of which are necessary for functionality, while the third arguably does not reveal sensitive data—whereas all other inputs remain protected by the inherent security of MPC.

4.3. Deployment Considerations

A key question to be answered when developing an MPC-based platform is who would host the computing nodes in a practical deployment.

One option could consist of each participating haulier hosting one node, making sure that each haulier can fully trust at least the node under their control. However, this is arguably unrealistic from multiple points of view. Firstly, from an efficiency point of view, the complexity of secret sharing-based MPC protocols generally scales quadratically in the number of nodes, so that a high number of nodes is unfavorable; while significant, this drawback might be overcome, e.g., by randomly selecting a subset of hauliers to host the computing nodes for each execution of the protocol.

However, secondly, this option would require each haulier to possess the necessary knowledge and IT infrastructure to host such a node, which might be especially unrealistic for micro to small companies employing up to 5 or 25 drivers, respectively [38]. Considering the discussion in Section 3.3, such companies might be the ones with the highest relative benefit from a collaborative platform, since they might not have sufficiently many orders for extensive in-house optimization.

We thus consider a more realistic scenario where a small number of MPC nodes (e.g., 3) is hosted by independent service providers. These parties should not be active members of the transport ecosystem, to avoid their own interests and conflicts of interest. Possible candidates might, e.g., be notaries, who already enjoy a high level of trust. This approach is also aligned with other related initiatives such as the PhysICAL (https://physical-project.at/ (accessed on 30 June 2025)) project, which is developing a trusted broker for optimizing multi-modal transport challenges (although the PhysICAL approach relies on a single fully trusted entity collecting, processing, and storing sensitive business information from logistics companies, which might pose a significant risk for large-scale adoption [4]).

Overall, we thus believe that this approach constitutes a good balance between trust challenges and efficiency, and at the same time allows parties to reduce costs and increase usability compared to a fully decentralized deployment due to economies of scale.

Finally, given the established trust in notaries—especially in contrast to a setting where nodes are controlled by competing hauliers—we consider instantiations with passive security to be a suitable choice. In this model, computing nodes may attempt to infer information from the data they process but otherwise adhere to the protocol specifications. However, as we discuss below, this is not a fundamental constraint of our heuristic but rather of the choice of the implementation framework, and could easily be adjusted by adopting alternative implementation frameworks at the cost of higher computational complexity.

4.4. Implementation and Evaluation

The solution discussed in the previous sub-section can be applied to any MPC protocol supporting evaluation of arbitrary arithmetic circuits, and therefore to any MPC software implementation with the same properties.

4.4.1. Software Framework

We have selected the MPyC platform for our purposes; MPyC is a Python library that allows for fast prototyping and proof-of-concept implementation, hence being very suitable for our needs. MPyC implements the protocol described in [18,19], both of which were proven secure with a simulation argument in the stand-alone model (and also in the universal-composability framework of Canetti [42] for [18], under the assumption that the message delivery between honest parties cannot be influenced by the adversary [43]). These secret sharing-based protocols are secure against a passive adversary controlling a minority of the parties, where the security guarantees hold in an information-theoretic sense, i.e., even against computationally unbounded adversaries. In particular any coalition of less than half of the MPC parties, who exchange information with each other but further follow the instructions of our MPC solution, gains no information on the participants’ inputs other than what can be deduced from the output values of the MPC solution. Within the MPyC, we have made use of the “secure integer” construct, with a bit-length of 10, which is sufficient to express the relatively small numbers (order volumes, node and haulier IDs, etc.) of our solution; MPyC then makes use of a suitable finite field “under the hood” to securely compute operations on these values. We remark that there are standard mechanisms, based on zero-knowledge proofs, to make this protocol actively secure, meaning that not even a coalition of parties that deviate from the instructions of the protocol can break its security [18]. These mechanisms, however, are not implemented in MPyC and would therefore require the usage of a different software framework. Given the purpose of this article, we believe security against passive adversaries to be sufficient.

While MPyC is generally not deemed suitable for production code, it does simulate several MPC parties as separate processes and is therefore a suitable tool to assess the feasibility of a solution. We have fully implemented the solution described earlier and made the code available.

4.4.2. Efficiency Analysis

For benchmarking and better comparison with the plaintext variant, we re-used the reference map defined by Teppan et al. [3], and ran the solver on problem instances with an increasing number of orders (10, 50, 100, 500 and 1000) and of trucks (from 5, 50, and 500) defined in a publicly available reference dataset for the CFDP (https://github.com/nrike67/CollaborativeFreightDeliveryProblem-Benchmark (accessed on 30 June 2025)).

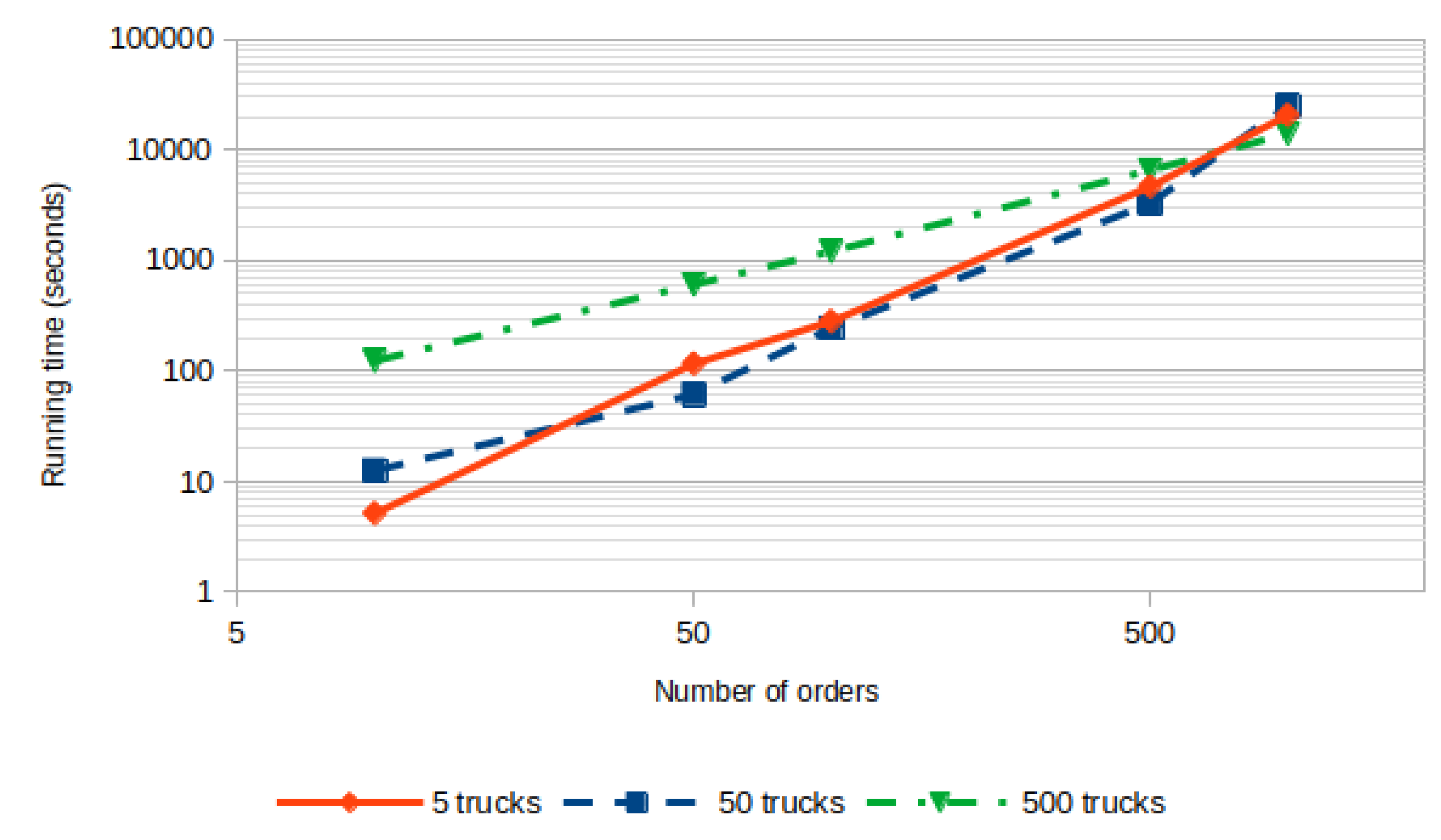
The solution was executed on a virtual machine equipped with a single-core CPU at 2.8 GHz, and with 16GiB of RAM, running Ubuntu 24.04 and Python 3.10. The results of the experiment are reported in Figure 2. There, a log-log plot was chosen because both axes span multiple orders of magnitude, and smaller values would otherwise be difficult to distinguish on a linear scale. For each choice of number of orders and of trucks, 10 experiments were run, and we report the median running time, although we remark that the variation was very small, with a standard deviation of less than 2% of the mean figures (and almost always less than 1%).

The longest running time is obtained with 1000 orders and 50 trucks, totaling 25,002 s, i.e., slightly less than 7 h. However, when the number of trucks increases, the complexity is actually lowered, reaching 13,990 s, i.e., less than 4 h (note here the log-scale on the y-axis). This is due to a combination of inherent MPC problems and the current design of our solution: on one hand, the running time of the MPC sub-routine $\mathtt{fill}\_\mathtt{truck}$ is a constant, independent of the number of trucks that it actually fills, something inherent to MPC protocols; this means that the total running time of our solution is higher when $\mathtt{fill}\_\mathtt{truck}$ is executed many times, regardless of how many trucks are filled in each execution. On the other hand, a problem instance with a lower number of trucks will necessitate to create an empty truck drive earlier, since it is less likely that sufficiently many trucks are available at the order positions; since our current solution creates a single empty truck drive at a time, this leads to frequent executions of the $\mathtt{fill}\_\mathtt{truck}$ sub-routine. The connecting line in Figure 2 corresponds to a measured polynomial relationship of the running time with respect to the number of orders, ranging from an approximate power of 3 for 50 trucks, to an increase which is slightly above linear for 500 trucks. While a formal analysis of the projected running time for larger instances would be beyond the scope of this paper (cf. also the discussion on the limited gains for large instances as discussed in Section 3.3), we remark that these experiments indicate that instances with, for example, 10,000 orders, could be processed in reasonable time, if enough many trucks are available.

Future work could modify the solution in order to create a higher number of empty truck drives in a single batch; however, given our current purpose of a feasibility study, we are primarily interested in the order of magnitude of the running time, to first ascertain whether the approach is feasible at all. Our experiments show a running time of some hours for thousands of orders and dozens of trucks, and we hence deem it a suitable basis for further improvements and optimization.

4.4.3. Quality of the Solution

In order to validate the effectiveness of our approach, we re-used a problem instance with a comparable regime of parameters as the one used in the “plaintext” heuristic approach of [3], compute a solution and its associated objective value (cf. Equation (1)), and compare it to the objective value of the plaintext approach. Given that the MPC approach securely implements a heuristic that is quite similar to the plaintext approach, we do not expect any significant difference between the results of the two, and therefore only focus on a specific regime of parameters for validation purposes.

In particular, in a similar spirit as Figure 1, we consider a setting with a total of 500 orders and compute the mean objective value for varying number of trucks (ranging from 1 to 5) and maximum order volume (10, 20, or 32 units). We obtain a mean value of $0.1162$, very close to the $0.1126$ of [3], and almost halving the empty runs compared to the non-collaborative approach, thereby proving that we can achieve the same improvement as Teppan et al. [3] without requiring plaintext access.

5. Extensions and Future Directions

As mentioned earlier, this paper aims at proving the feasibility and practicability of a secure realization of a solver for the CFDP as specified by Teppan et al. [3], thereby overcoming the trust-related challenges highlighted by Karam et al. [4], and compare the efficiency and effectiveness of the modified heuristic to their results. However, we acknowledge that the modeling used in [3] (and thus also our paper) oversimplifies certain aspects of real-world large-scale collaborative transport networks. In the following we thus briefly outline some of the most immediate tasks in increasing order of complexity of integration into our solution, arguing that all but the last extension can be achieved without breaking the practicability claims made earlier.

Firstly, in practice, many transport orders pose requirements regarding the physical and operational conditions. Such requirements can be related to temperature (e.g., refrigerated or frozen goods), humidity (e.g., protection from high humidity for electronic devices or paper), shock and vibration protection (e.g., fragile goods such as glass), or hygiene standards (e.g., related to food safety). However, especially when assuming sufficiently large numbers of orders per category in large-scale networks, this can trivially be realized in our solution by simply running an independent instance per requirement class. Furthermore, if hauliers wish to hide the types of orders that they provided to the network, a relatively cost-efficient single round of sorting of all orders can be performed in MPC prior to the independent execution of the instances.

Secondly, time management needs to be reflected more carefully. It is important to note here that our implementation already includes the concept of time in the sense that each truck has a variable $\mathrm{NEXTAVAILABILITY}$ that is increased by the driving time between different regions after each truck drive. However, this is not presented in Section 3 as “time” is neither included in the modeling in [3] nor is it part of the optimization criterion in Equation (1). Nevertheless, as the overall modeling considers regions rather than pick-up locations, our current internal modeling ignores journey times between different locations within the same region. This can be addressed in our heuristic at minimal costs by adding some fixed additional time period per order to model the time a truck needs to pick up different orders within a city. Investigating the feasibility of advanced routing algorithms using, e.g., Dijkstra’s algorithm [44] on complex maps without disclosing origin or destination, leveraging results by Keller and Scholl [45], could be an interesting direction for future research.

Thirdly, and closely related to the previous aspect, time constraints of orders should be considered to accurately reflect just-in-time delivery requirements. While highly complex constraints might be hard to realize in MCP, a compromise already foreseen in our implementation is as follows. Each order contains an additional variable $\mathrm{PRIO}$ from some predefined domain, e.g., $1,\dots ,10$. Now, as an already available optional pre-processing step before entering our presented approach, all orders are sorted by $\mathrm{PRIO}$, making sure that high priorities tend to be processed earlier. As potential future extensions, when selecting a truck to be filled next, the one with the lowest $\mathrm{NEXTAVAILABILITY}$ could be selected; similarly, when introducing an empty truck drive, the truck minimizing its $\mathrm{NEXTAVAILABILITY}$ plus the necessary journey time could be selected. Note that the computational overhead of this approach should be manageable, as all loops in Protocols 2 and 3 obliviously iterate over all trucks already in our current version to maximize confidentiality.

Fourthly, external constraints should be added as future work. Certain legal obligations (e.g., maximum driving times and mandatory breaks) seems feasible at least on a conceptual level, e.g., by adding the pause times to $\mathrm{NEXTAVAILABILITY}$ if the variable exceeds the allowed continuous driving time, or setting $\mathrm{NEXTAVAILABILITY}\leftarrow \infty$ if the maximum driving time is reached, and only selecting trucks with sufficient available driving time for the next order. However, more complex extensions (e.g., requiring that trucks need to be back at their home base in the evening) to be realized in a privacy-preserving setting, while at the same time respecting the optimization goal defined in Equation (1), would be an interesting yet highly challenging research question.

Orthogonal to the aforementioned functional extensions, further enhancements regarding the computational efficiency of the current approach could also be investigated. For instance, by simultaneously introducing multiple empty truck drives, the number of iterations of the MPC protocol could be reduced, thereby increasing efficiency. However, introducing multiple such drives at once might lead to a worse average usage factor as defined in Equation (1), and was thus omitted for a fairer comparison with [3]. Yet it might be interesting to precisely quantify the trade-off between the computational efficiency of the MPC solver and the quality of the obtained solution.

As explained in Section 4.2, our current solution outputs the number of orders assigned to each haulier to allow for a detection of a systematic bias for or against a specific haulier. Yet, from a more research-oriented point of view, and in the spirit of verifiable MPC [30,46,47], it would be interesting to output a cryptographic proof together with the assigned orders, showing that the presented heuristic was properly executed by all nodes, and allowing for public verifiability and auditability of the computation, leveraging primitives such as zero-knowledge proofs of knowledge (ZK-PoKs). However, such approaches typically come with significant computational overhead, negatively impacting their practical applicability. Investigating the feasibility and costs could thus be an interesting area for future research.

Also related to auditability, yet in an orthogonal sense, the haulier contributing a specific order might have a legitimate interest in learning the executing haulier in case of a contract violation, e.g., because the order was not delivered on time. At the moment, this piece of information is not explicitly output to any entity. Two solutions could easily be integrated at minimal costs into our system. Firstly, the owner of an order receives an additional output indicating the executing haulier. Alternatively, the MPC nodes could locally store their shares of the final assignment of orders to hauliers, and simply reveal this information if some proof of misconduct is submitted by the owner of an order. While additional processes, e.g., clarifying which evidence of misconduct to accept, are needed in this case, it is quite straightforward to implement the computational adjustments needed to maintain an assignment of order identifiers to haulier IDs among the MPC.

A final point that should be investigated in subsequent research for practical applicability is the issue of regulations on the protection of confidential data. The CFDP problem does not, per se, involve personal data, and legislation such as the GDPR is therefore out of scope; however, other, possibly sector-specific, regulations might need to be taken into account when using a solution like ours on actual company data.

6. Conclusions

In this work, we presented an approach toward solving the collaborative freighter delivery problem in a fully confidentiality-preserving manner based on secure multi-party computation. Our prototypical implementation in MPyC shows that the problem can be solved in a reasonable time for sufficiently large instance sizes to realize the full potential of collaborative planning. By re-using modeling, parameters, and problem instances from previous work [3], we were able to show that our approach achieves the same quality of solutions as its plaintext alternative.

We expect that the efficiency can be increased substantially by applying further optimizations or by switching the underlying MPC framework to MP-SPDZ [41], which has been shown to outperform MPyC in many situations [48].

Similar to previous work, our modeling faces limitations when applied to real-world scenarios, particularly with respect to timing aspects. To address this, we outlined a broad range of potential future extensions and provided indications of their technical feasibility. While some enhancements could be integrated with relatively low effort, others may require substantial research and engineering to achieve practical efficiency. However, we believe that, in the long term, the suggested approach indicates a potential path toward reducing the number of empty runs in logistics and increasing the average load factor of trucks, thereby reducing the carbon footprint of the sector and reducing costs.