Abstract
With continuous advancements in semiconductor technology, mastering efficient designs of high-quality and advanced chips has become an important part of science and technology education. Chip performances will determine the futures of various aspects of societies. However, novice students often encounter difficulties in learning digital chip designs using Verilog programming, a common hardware design language. An efficient self-study system for supporting them that can offer various exercise problems, such that any answer is marked automatically, is in strong demand. In this paper, we design and implement a web-based Verilog programming learning assistant system (VPLAS), based on our previous works on software programming. Using a heuristic and guided learning method, VPLAS leads students to learn the basic circuit syntax step by step, until they acquire high-quality digital integrated circuit design abilities through self-study. For evaluation, we assign the proposal to 50 undergraduate students at the National Taipei University of Technology, Taiwan, who are taking the introductory chip-design course, and confirm that their learning outcomes using VPLAS together are far better than those obtained when following a traditional method. In our final statistics, students achieved an average initial accuracy rate of over 70% on their first attempts at answering questions after learning through our website’s tutorials. With the help of the system’s instant automated grading and rapid feedback, their average accuracy rate eventually exceeded 99%. This clearly demonstrates that our system effectively enables students to independently master Verilog circuit knowledge through self-directed learning.
1. Introduction
With the rapid growth of semiconductor industries and innovative technologies, chip design has become an indispensable facet of technology sectors for engineers. Advances in semiconductor processes have not only enhanced the performances of consumer electronics but also exerted a profound influence on various technological fields, including artificial intelligence, the Internet of Things (IoT), and communications. Consequently, the demand for professionals with strong digital-circuit design capabilities has emerged as a central priority in science and technology education.
With the evolution of digital circuit design technologies, hardware description languages (HDLs) have become indispensable for the design and verification of digital systems. Among the various HDLs, Verilog stands out as one of the most widely adopted HDLs, finding extensive applications in developing field-programmable gate arrays (FPGAs) and application-specific integrated circuits (ASICs). Verilog supports designs at the behavioral level, register-transfer level (RTL), and gate level [1], which allows for precise specifications of circuit functionalities. Through the use of synthesis tools [2], the Verilog descriptions can be converted into standard-cell netlists, culminating in complete chip designs and layouts.
Despite the widespread availability of teaching resources and learning tools for software programming languages, such as Python and Java, HDLs, like Verilog, remain relatively underserved. Although Verilog is invaluable in practical digital circuit designs, its specialized syntax and limited learning pathways impose a steep learning curve for beginners. In traditional instructional settings, students can often be discouraged by a lack of hands-on experience and immediate feedback. A system to assist the self-studies of Verilog programming has been strongly requested in both academia and industry.
Recent studies have explored various methods to support student learning, showing promising results. Some have proposed gamified adaptive learning systems that leverage AI to personalize learning without the need for instructor intervention, effectively improving learning outcomes and self-efficacy [3,4]. Others have integrated active learning strategies and hands-on projects into traditional courses, helping students better understand and apply complex concepts such as digital system design [5]. These approaches demonstrate the value of combining technology, interactivity, and personalization to enhance student engagement and performance, providing useful references for the design of our proposed system.
Previously, we developed a web-based Programming Learning Assistant System (PLAS) to offer a dedicated self-learning environment for novice students to learn key software programming languages, including C, Java, Python, and JavaScript [6]. PLAS provides several types of exercise problems that have different levels and learning goals for step-by-step study. For any problem, an answer from a student is marked automatically in the system, and the result is immediate feedback to the student.
In this paper, we design and implement a web-based Verilog Programming Learning Assistant System (VPLAS) by extending our work on PLAS for software and programming to address the common challenges students face when learning Verilog. In our earlier study in [7], we proposed an initial version of VPLAS, focusing on providing simple exercise problems. Building upon this foundation, we enhance this VPLAS by refining its instructional design and adopting a layered, progressive teaching approach. These improvements allow students to engage in effective self-directed learning and strengthen their overall learning experiences. It delivers a structured set of exercise problems coupled with automated answer evaluations, creating a highly interactive, self-directed learning environment.
Furthermore, VPLAS employs heuristic and guided-learning strategies to help students progressively grasp the main syntax and common logic in Verilog, thereby transcending the limitations of traditional lecture-centric instructions so that learners acquire foundational digital-circuit design skills. VPLAS is specifically tailored for students who are new to Verilog. It employs a section-based structure to sequentially guide learners through the language’s basic syntax and common logic. Sections are organized in a progressive manner—moving from simple topics to complex ones—so that students can gradually assimilate the main concepts and implementation techniques in Verilog. Each section has clearly defined learning objectives, ensuring that students maintain a clear sense of direction and experience measurable milestones throughout their learning journey.
In each section in VPLAS, the learning model integrates illustrative examples with targeted exercises. In the example segments, annotated code snippets demonstrate Verilog’s syntax and its practical applications, enabling students to grasp structural patterns through concrete cases. The exercises employ fill-in-the-blank questions, referring to the questions set in [8]. Using a highly interactive format, the segments focus on learners’ attention to critical language constructs and provide immediate automated feedback. This instant response mechanism helps students monitor their progress and identify errors in real-time, enhancing overall learning efficiency.
The exercises in VPLAS are carefully designed, with increasing difficulty, and the tasks remain sufficiently challenging to sustain engagement. They ensure a smooth and accessible learning curve. The system features real-time evaluations of student submissions, which, in comparison to traditional manual grading, can substantially reduce instructors’ workloads and enhance instructional efficiency. Under conventional workflows, students must wait for feedback from instructors on assignments, impeding learning momentum and delaying the correction of misconceptions.
By leveraging real-time learning data analytics, instructors can immediately gauge each student’s progress and deliver targeted guidance, while learners benefit from iterative practice that reinforces correct understanding. In summary, this approach not only streamlines the assessment process for educators but also cultivates a highly interactive, immediate-feedback learning environment, improving the overall effectiveness of digital-circuit design education.
The primary contribution of VPLAS is the provision of an efficient, beginner-focused Verilog learning aid by combining example-based instructions and fill-in-the-blank exercises with automated grading to deepen students’ understanding of Verilog syntax and implementation. Through a carefully sequenced section design, VPLAS systematically guides learners from fundamental concepts to advanced applications, while real-time feedback mechanisms reduce frustrations and accelerate acquisitions of core digital-circuit design skills. Furthermore, by offering a smooth learning curve and a highly interactive environment, the system transcends traditional lecture-centric pedagogy and delivers an innovative, practical solution for Verilog instruction.
To evaluate the effectiveness of our learning platform, we administered the same set of test questions to two distinct undergraduate cohorts. In each group, approximately 50 Verilog novice students joined. Throughout the evaluation, we recorded and analyzed the key performance and behavioral metrics, including the first-attempt accuracy, the final accuracy, and the total number of attempts, to quantify learning progression and the system’s supportive impacts. Our analysis results demonstrate that the proposed platform substantially improved students’ learning outcomes, demonstrating its feasibility and advantages for use in learning introductory digital circuit designs.
The structure of this paper is organized as follows: Section 2 reviews the related literature regarding the theoretical foundations of this study. Section 3 presents the core concepts and design thinking of the proposed approach. Section 4 evaluates the proposal through applications to novice students. Section 5 provides a comprehensive analysis of the evaluation outcomes and explores potential directions for future improvements. Section 6 concludes the thesis by summarizing the research outcomes and contributions.
2. Related Works
This section begins by examining the importance of Hardware Description Languages (HDLs) in digital circuit design. It then reviews recent research developments related to HDLs and Large Language Models (LLMs), followed by a survey of the relevant literature on their applications in educational contexts. Subsequently, systems designed to support programming education are introduced. Finally, an overview of existing HDL learning platforms is provided as a foundational reference for this study.
2.1. The Importance of Hardware Description Languages
HDLs, such as Verilog and VHDL, play a crucial role in digital chip design flows, directly affecting design efficiency, quality, and final product performance. In [9], Quevedo et al. employed MLIR technology to conduct control and data flow analysis at the early design stage, combining resource estimation with multiple scheduling algorithms. This approach effectively supports designers in optimizing area, latency, and power consumption, emphasizing the importance of HDLs in early-stage design exploration and optimization to significantly enhance design outcomes.
Meanwhile, with the increasing complexity of chip designs, the efficiency of HDL code development has become a bottleneck in design cycles and quality. In [10], Xu et al. analyzed the inefficiencies in current design practices and proposed optimization strategies based on language features and design specifications, such as syntax restructuring, module reuse, and improved compilation and simulation efficiency. The experimental results demonstrate that these enhancements not only shorten development time but also improve code readability and maintainability, thereby accelerating the overall design flow.
In conclusion, mastering and continuously optimizing the use of HDLs is indispensable for improving the performance and productivity of modern digital chip design workflows.
2.2. Research on HDLs and Large Language Models
The automatic generation of HDL code has emerged as a prominent area of research, highlighting both the importance and the inherent challenges of HDL in the hardware design process. Compared to other programming languages, HDLs are characterized by unique symbolic representations, timing constraints, and concurrency, making code generation tasks significantly more complex and domain-specific. In response, paper [11] introduces an open-source, LLM-assisted RTL generation technique that runs efficiently on standard laptops, outperforming GPT-3.5 and even GPT-4 in certain tasks, promoting accessible and open hardware design automation. In [12], Yang et al. addressed hallucination issues in LLM-generated Verilog by applying Chain-of-Thought reasoning and domain-specific training data, achieving improved accuracy in symbolic tasks such as state diagrams and truth tables.
These two studies underscore the critical role of HDLs in modern hardware design and emphasize their distinct challenges compared to general-purpose programming languages. They highlight HDL code generation as a key driver in advancing intelligent and automated hardware development.
2.3. Exploration of Instructional Strategies
In recent years, a growing body of research has focused on instructional strategies aimed at enhancing student learning outcomes in hardware and electronics-related courses, addressing the limitations of traditional lecture-based approaches.
In [13], Pearce adopted a scaffolded instructional design that integrates theoretical review, foundational practice, and staged assessments. This structured guidance effectively supports students in overcoming technical and cognitive challenges, significantly improving project completion rates and student satisfaction in computer engineering courses. Reference [14] proposes a “learning-by-doing” pedagogical model that combines virtual laboratories with multimedia resources. Through hands-on practice and periodic evaluations, this method fosters students’ motivation and comprehension, yielding positive learning outcomes and feedback.
In [15], researchers introduce a challenge-based blended learning approach in an introductory digital circuits course. By combining task-oriented learning with practical exercises, the course deepens students’ understanding of core concepts and enhances their problem-solving abilities. Experimental results indicate significant improvements in motivation and conceptual clarity. Furthermore, paper [16] presented a case-based instructional strategy tailored for students without an electronics background. By using real-world design cases alongside lab experiments and FPGA implementation, the approach reduces the abstraction of HDL learning and improves both comprehension and engagement. Surveys and experimental data confirm its effectiveness across diverse student groups.
Collectively, these studies highlight the critical role of guided practice, hands-on activities, and timely feedback across various teaching models, including scaffolded instruction, experiential learning, challenge-based approaches, and case-based methods. The findings consistently suggest that traditional lecture-based teaching alone is insufficient for achieving optimal learning outcomes. Instead, incorporating structured, interactive teaching strategies can significantly enhance students’ motivation, depth of understanding, and overall satisfaction, demonstrating their practical value and importance in hardware and electronics education.
2.4. Technology-Supported Programming Learning Systems
In the field of programming education, the integration of technological tools has increasingly been shown to enhance both learning efficiency and instructional quality. Recent studies suggest that interactive platforms, automated resources, and multimodal learning environments can effectively aid students in grasping abstract concepts and increasing learning motivation.
In [17], Pădurean et al. developed a dialogue-based learning platform that allows students to engage in programming exercises through system interactions. The platform encourages the iterative refinement of problem-solving processes. The results indicate that such interactive mechanisms promote active thinking and critical evaluation, thereby strengthening students’ programming comprehension and problem-solving skills.
In [18], Hrvacević et al. proposed a web-based system featuring automated question generation to improve the efficiency and diversity of test item creation. By leveraging large language models, the system significantly reduces the manual burden of question design while increasing the scalability and accessibility of educational resources—which is particularly valuable for large-scale courses.
In [19], Perera et al. conducted a systematic analysis of introductory programming languages for novice learners. Their findings reveal that block-based visual tools can effectively lower entry barriers for beginners, although learners may face difficulties when transitioning to text-based programming. To address this, the study advocates for the development of dual-modality learning environments that balance accessibility for novices with smooth progression to more advanced skills.
Collectively, these studies demonstrate that various forms of technological support—ranging from interactive platforms to automation and multimodal systems—can shorten the learning curve, enhance conceptual understanding, and boost learner engagement, highlighting the potential of technology as a valuable aid in programming education.
2.5. Overview of Online HDL Learning Resources
With the advancement of internet technologies and cloud services, numerous online learning platforms for HDL have emerged, aiming to reduce learning barriers and enhance practical skills. HDLBits (Available online: https://hdlbits.01xz.net/wiki/Main_Page (accessed on 19 May 2024)) offers interactive Verilog exercises directly via the browser, with automatic code-checking and no need for local installation. EDA Playground (Available online: https://edaplayground.com/ (accessed on 26 May 2024)) provides a cloud-based development environment for HDL simulation and testing. DigitalJS (Available online: https://digitaljs.tilk.eu/ (accessed on 26 May 2024)) allows users to design and simulate digital circuits via an intuitive web interface. ChipVerify (Available online: https://www.chipverify.com/ (accessed on 26 May 2024)) delivers comprehensive Verilog and SystemVerilog tutorials with practical examples, helping learners build a solid foundation in digital design and verification.
To further enhance hands-on experiences in hardware education, several studies have explored the integration of HDL platforms with remote learning.
In [20], El-Medany et al. proposed a mobile learning laboratory enabling students to remotely access and interact with FPGA boards via mobile devices, overcoming traditional lab constraints and improving course accessibility.
In [21], Lee presents DEVBOX, a browser-based Verilog learning platform tailored to pre-university and early undergraduate students, simplifying the HDL learning process and promoting early engagement with logic design.
In [22], Zhang et al. introduced Verilog OJ, an online judge system that compiles, simulates, and verifies Verilog code using open-source tools, supporting large-scale classroom use with thousands of submissions and integrated peer discussion features.
In [23], Al Amin et al. conducted a requirement analysis of FPGA RLab, a collaborative remote lab supporting real-time video, multi-user hardware control, and cross-platform compatibility, the highlighting key design considerations for future remote HDL education systems.
In summary, online HDL platforms have become indispensable tools in modern digital design education. These systems effectively lower hardware and spatial barriers while promoting active learning through immediate practice and feedback, offering critical insights for the development of this study’s proposed system.
3. Design of the Learning System and Content Structure
In this section, we systematically introduce and explain the learning contents of Verilog, ranging from basic concepts for beginners to advanced syntax applications. This design is intended to gradually lead students to master the core skills of digital circuit design. The sections containing the contents are designed in a step-by-step manner, and adopt combinations of example explanations and exercises, ensuring that students can make steady progress and gain a thorough understanding of the learning process.
3.1. System Interface Introduction
The user interface of this system, as shown in Figure 1, is mainly divided into the three main sections—Source Coding, Answer, and Related Information—to enhance learning experiences and students’ understanding of Verilog syntax and digital circuit design.
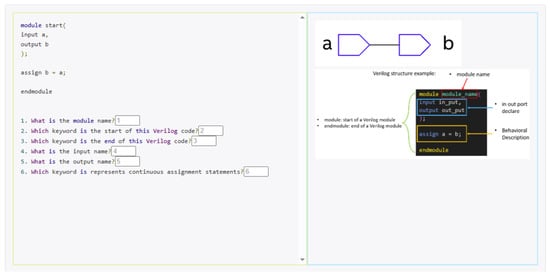
Figure 1.
User interface for Problem 1.
- Source Coding: This section provides a complete Verilog code corresponding to the implementation of a specific digital circuit. The fill-in-the-blank sections request students to supplement the missing code according to the requirements of the question to enhance their understanding of grammar and program logic.
- Answer: This section contains quizzes on concepts related to the code and is designed to assess students’ understanding of grammatical structures, digital circuit behaviors, and key design concepts. Learners must apply their knowledge to interpret the provided code and solve each problem, with the platform’s real-time feedback mechanism immediately verifying the correctness of their answers.
- Related Information: This section offers supplementary learning materials aligned with each exercise, including an annotated example code, in-depth conceptual explanations, and digital-circuit schematics or timing waveforms. Designed to support self-directed studies, it enables students to consult these resources during problem-solving, reinforcing their understanding of programming constructs and digital-logic fundamentals.
Through the interactive design of the above sections, the system can not only strengthen students’ understanding of Verilog syntax and digital circuit behaviors, but also improve learners’ code-writing and error correction capabilities through real-time evaluation and feedback mechanisms, further optimizing their learning effects.
3.2. Answering Process
The answering process of this system is designed to guide students to master Verilog syntax and digital circuit design concepts through a step-by-step learning mechanism. Students will learn and take the test through to the following steps:
- Concept Acquisition: Students first browse the Reference Material Section and learn the background knowledge, sample codes, or digital circuits and timing waveforms related to the question to grasp the core concepts covered in the question. This stage aims to help students establish basic cognition and lay the foundation for subsequent program reading and problem-solving.
- Code Analysis: After understanding the basic concepts, students move to the Source Code Section to observe and analyze the provided Verilog code. In some questions, the code will include fill-in-the-blank sections, requiring students to infer the missing program fragments to further deepen their understanding of Verilog syntax and circuit operation logic.
- Answer and Submission: Students fill in their answers in the Answer Section. After completing all questions, they click the “Answer” button to submit their answers, as shown in Figure 2. The system will automatically compare the answers entered by students with the correct answers, which are stored in the system in the background, and output the accuracy rate in real time. If there are wrong answers, the system will mark them in red to help students identify and correct them.
 Figure 2. Answer button to submit answers.
Figure 2. Answer button to submit answers. - Iterative Learning and Mastery: Students can make multiple attempts until all answers are correct. This system provides instant feedback and correction opportunities, helping students consolidate their learning through repeated practice and ensuring a complete understanding of Verilog syntax and digital circuit concepts.
- Section Score and Tracking: When students have completed all questions in a section, they can enter their personal ID to record their learning outcomes, and the system will output the student’s final answers for the section, as shown in Figure 3. This mechanism can be used for students’ self-assessment and can also serve as a reference for teachers to monitor learning progress and effectiveness.
 Figure 3. Submission section.
Figure 3. Submission section.
Through the above design, this system provides an interactive and autonomous learning environment. Through conceptual understanding, program analysis, real-time evaluations, and multiple attempts, it will assist in students’ mastery of Verilog syntax and digital logic design, and cultivate their program reasoning and error correction capabilities, achieving the best learning effect.
3.3. Question Generation Process
The question generation process of this system follows the design principles of standardization and automation to ensure the consistency, accuracy, and teaching applicability of the question content. The following steps are used to generate questions:
- Definition of Learning Concepts: According to the course requirements, teachers determine the Verilog syntax, digital circuit concepts, or design methods covered by the questions to ensure that students can master the target knowledge points through answering these questions.
- Verilog Code Generation: According to the defined teaching concepts, teachers write Verilog codes to implement the corresponding digital circuit functions and ensure that the codes match the teaching contents.
- Code Simulation and Verification: Teachers use professional digital circuit simulation tools such as ModelSim, Vivado, and Quartus to run the Verilog program to confirm that its functions and logic are correct, preventing incorrect programs from affecting students’ learning.
- Question Design: Teachers design targeted test questions based on the code contents or related concepts to ensure that students can strengthen their understanding of grammar and logic through answering the questions.
- Ensuring Unique Answers: Teachers ensure that all questions have unique answers to avoid students’ learning outcomes and automatic assessment accuracy being affected by ambiguous answers.
- Supplementary Learning Resources: Teachers add relevant supplementary learning resources, such as concept descriptions, images, tables, or sample code, to help students understand the topic backgrounds and core concepts.
- Automated Conversion to HTML Format: Automated tools are used to convert the contents into HTML formats to generate an interactive web-based quiz environment where students can answer questions directly, ensuring that the platform can provide real-time assessments and visual learning experiences.
Through this mention systematic question generation process, this system can ensure the accuracy, consistency, and learning effect of the test contents, and improve the efficiency of question generation and management through automation technologies, making Verilog teaching more structured, interactive, and efficient.
3.4. Section Introduction
The following section will delineate each section’s core content and corresponding instructional objectives in detail.
3.4.1. Section 1: Verilog Introduction
This section establishes the foundational knowledge required for digital-circuit design using Verilog. The specific topics addressed in this section’s exercises are listed in Table 1. It begins with an explanation of the Verilog module construct, detailing the syntax and declaration of input and output ports to familiarize students with the basic building blocks of any design. The section then examines the four essential logic gates—NOT, AND, OR, and XOR—clarifying their roles and behaviors within combinational circuits. As shown in Figure 4, through practical circuit diagrams and guided questions, students can clearly understand the functions of logic gates and their corresponding operators.

Table 1.
Summary of topics in Section 1.
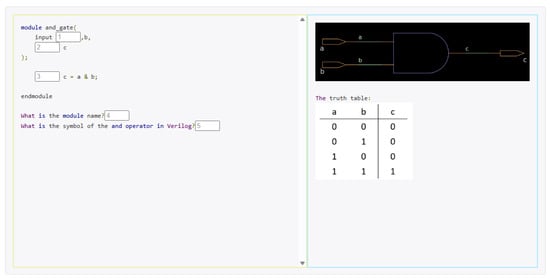
Figure 4.
A and gate problem.
Next, it systematically introduces the reg and wire data types, explaining their respective functions in signal storage versus transmissions and the conditions under which each should be used. This enables students to accurately distinguish between the two core data types. The section then extends to the always block, offering an in-depth comparison of combinational and sequential logic, so learners can obtain a preliminary understanding of how each is described at the RTL.
Finally, the section presents the three principal design abstraction levels—gate level, dataflow level, and behavioral level—contrasting their characteristics and typical application scenarios. By the end of this section, students will have a coherent overview of Verilog’s syntax and abstraction hierarchy, laying the groundwork for deeper exploration in subsequent sections and ensuring they possess the basic skills needed to proceed.
3.4.2. Section 2: Basic Architecture
This section focuses on the value declaration and the basic architecture design of Verilog to help students become familiar with the core concepts of data representations in digital circuit design. The specific topics addressed in this section’s exercises are listed, along with the corresponding number of generated questions, in Table 2.

Table 2.
Summary of topics in Section 2.
First, the four signal types in Verilog are introduced—1 (logic high potential), 0 (logic low potential), X (unknown value) and Z (high impedance)—and their application scenarios and significance in different circuit designs are explained. Next, the course explains how to define the bit size, the base, and the numerical representation of data to help students understand how to effectively describe the structure and range of data.
In addition, the course systematically introduces the definition and usage of vectors and arrays in Verilog, and explains their applications in multi-bit data representations and processing, further strengthening students’ programming capabilities. This section also covers advanced concepts regarding numerical processing, such as truncation and extension, and provides detailed guidance on comment-writing and variable naming rules in program code to help students develop good programming habits. As shown in Figure 5, through detailed explanations of Verilog value definitions and practical demonstrations, students can strengthen their knowledge of this section via direct question-and-answer interactions.
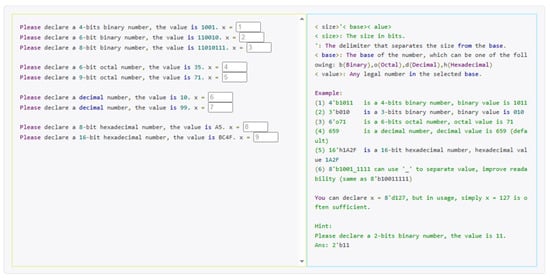
Figure 5.
A value declaration problem.
To help students strengthen their understanding of the concepts in Section 1 while learning new knowledge, the exercises in this section will incorporate previous content to consolidate basic concepts and grammar. This section is designed to increase students’ understanding of Verilog value declaration and processing.
3.4.3. Section 3: Data Conversion
This section focuses on the representation and conversion of the values in different bases in Verilog to help students master the core concepts of digital system conversion. The specific topics addressed in this section’s exercises are listed in Table 3.

Table 3.
Summary of topics in Section 3.
First, how to express binary, decimal, and hexadecimal values in Verilog, and their applications in digital circuit design, are introduced. Next, the methods used to convert binary and decimal, hexadecimal, and floating-point numbers are explained, and two complementary numbers are used to convert between signed and unsigned numbers to help students understand the processing logic of positive and negative numbers in hardware design.
The base conversion is very important in digital signal processing. Although daily calculations are mainly based on the decimal system, in the computer world, binary is the cornerstone of all calculations and hexadecimal is a widely used base to express binary data more efficiently. Therefore, being familiar with various base representations and conversion methods is a basic and essential skill for digital circuit designers. As shown in Figure 6, in the teaching section, we will list out a step-by-step procedures for converting a binary number to a fixed-point number, including both the integer and fractional parts, and provide a complete demonstration along with an example. In the exercise section, students will be required to solve problems based on the numbers we specify.

Figure 6.
Data conversion between binary and fixed point number problem.
In order to strengthen students’ understanding of these concepts, this section designs a variety of exercises to help students consolidate their knowledge of base conversion and signed and unsigned number processing in actual operations. The goal of this section is to enable students to master numerical conversion while understanding how these concepts are applied in digital circuit design.
3.4.4. Section 4: Verilog Operator
This section focuses on the various types of operators and their operation methods in Verilog programming, and systematically introduces important concepts such as arithmetic, relational, equality, shift, bit-wise, and logical operations. The specific topics addressed in this section’s exercises are listed in Table 4. Through detailed code examples and exercises, students can understand the functions and applications of operators in practice.

Table 4.
Summary of topics in Section 4.
The arithmetic operations section covers basic operations, such as addition, subtraction, multiplication, and division, and explores the operating modes of signed and unsigned numbers in depth. Unlike software design, hardware operations require special attention to the handling of overflow and signed bits. These details are crucial to the correct design of digital circuits. Shift operation is a common and efficient operation method in Verilog. Students will learn how to use shift operation to replace complex multiplication and division, thereby reducing the consumption of hardware resources. As shown in Figure 7, in the teaching section, we present the differences between logical left shift and right shift using binary numbers for illustration. We also explain when to use each operation and the advantages of using bit shifts. A practical example is provided in the source code area to help students gain a concrete understanding of this concept.
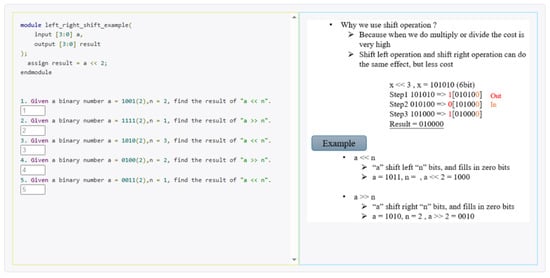
Figure 7.
A logic shift problem.
In addition, this section focuses on the differences between bit operations and logical operations, and analyzes their application scenarios in conditional judgment and hardware design. For example, bit operations are mostly used for data processing, while logical operations are more suitable for conditional judgment and control logic. This section helps students understand the role of operators in digital circuit design and consolidates their practical ability in RTL design by emphasizing the differences between, and practical applications of, these operations.
3.5. Related Work Comparison
This section reviews and synthesizes a range of research and applications related to Verilog-based educational platforms. As summarized in Table 5, the analysis focuses on the functionalities, instructional objectives, and key advantages of each approach.

Table 5.
Functional objectives and advantages of HDL learning platforms.
This study presents VLPAS, a beginner-oriented Verilog learning platform that emphasizes modular instruction, guided problem sets, and an instant feedback mechanism. The system is designed to address the limitations in existing platforms, particularly the lack of a structured pedagogy and support for learning progression. VLPAS aims to provide a more organized and supportive learning experience for Verilog, and may serve as a useful supplementary tool for future online HDL education.
4. Evaluation
In this section, we evaluate the proposal through an analysis of question types and the results obtained by students. Here, all values are statistically averaged to obtain the final result.
4.1. Evaluation Subjects and Methodology Design
The participants in this evaluation were 112 students who were taking the undergraduate electronics digital logic design course in the Department of Electronic Engineering at the National Taipei University of Technology (NTUT), Taiwan. We divided them into two groups. Group 1 consisted of students with relevant programming backgrounds who were all Verilog language beginners. Group 2 mainly consisted of students with a basic programming background who were all Verilog language beginners, and a small number of them were interdisciplinary learners with no prior experience in computer science.
The assessment of the proposal is one of the compulsory activities of the course. Each student connected to the system through their own device to complete the test online. After completing the test, the answer process was sent back for subsequent analysis. By analyzing the test results, we can understand their initial learning effects and their degree of mastery of basic knowledge of Verilog. The use of different test groups increases the diversity of test results, making the results more consistent with the normal distribution and making the system evaluation results closer to the actual situation.
4.2. Evaluation Indicators
For each question, students were permitted to make multiple submissions, with the system providing immediate feedback on the correctness of each attempt. This real-time feedback mechanism enabled students to promptly identify and correct misunderstandings, fostering self-directed learning. The primary metrics employed in this study were as follows:
- First-Attempt Accuracy: This examines the proportion of questions answered correctly upon the student’s initial submission, reflecting intuitive understanding or prior knowledge.
- Final Accuracy: This examines the proportion of questions answered correctly upon the student’s final submission, after multiple attempts, indicating the level of understanding achieved through iterative learning and correction.
- Number of Submissions: This represents the total number of attempts made for each question, which reflects both the student’s level of engagement and the relative difficulty of the item.
During the research process, the above data were integrated to obtain the average first and final correct rates for each question, the average number of submissions for each question, the overall number of submissions for each student, and the number of questions that were improved from incorrect to correct, in order to more deeply evaluate the students’ learning process.
4.3. Results Analysis
The test results of each section will be displayed, analyzed, and evaluated. The results for Group 1 and Group 2 will be analyzed and discussed.
4.3.1. Results Analysis for Section 1
This section contains a total of 22 questions, covering basic syntax, such as simple wire connections, data-type differences such as wire and reg, design levels, including gate-level, dataflow, and behavioral, and the differences between combinational logic and sequential logic. Finally, there is a test comparing the differences between each design level.
Test Results of Group 1
The test results for Section 1 obtained by Group 1 are presented in Figure 8, where the x-axis represents the question numbers and the y-axis indicates the average number of attempts per question, as well as the average accuracy rates. In this figure, the gray bar depicts the average number of submissions for each question, the blue line represents the average submission time, and the red line indicates the average accuracy of the last submission.
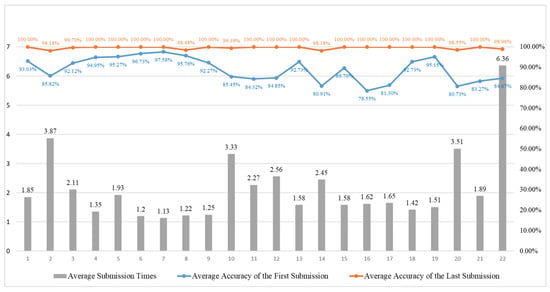
Figure 8.
Solution results for Group 1 in Section 1.
It is evident that, for most questions, students achieved a first-attempt accuracy exceeding 80%, demonstrating that the instructional explanations provided with the questions significantly supported students’ comprehension. Additionally, Questions 2 to 4 and 16 to 18 constituted sets of similar question types. As observed in the figure, the average number of submissions for these grouped questions consistently decreased, while the first-attempt accuracy gradually increased across the sequence. This suggests that the design and sequencing of these question sets effectively facilitate students’ rapid mastery of related concepts. An analysis of the overall test results reveals that questions with lower first-attempt accuracy primarily include the following.
Question 14 requires students to determine whether a circuit was synchronous or asynchronous. We infer that many students struggled to effectively distinguish between these two types of circuits, as the concepts of synchrony and asynchrony can be particularly challenging for beginners.
Questions 16, 17, and 18 assess students’ understanding of Verilog variable types for wire and reg and their differences, which are also closely related to the concepts of synchronous and asynchronous circuits. This may account for the lower accuracy rates observed. However, with repeated practice on similar question sets, the first-attempt accuracy improved from 78.55% on question 16 to 92.73% on question 18, indicating that such targeted exercises significantly enhance conceptual understanding and highlight the effectiveness of the learning system.
Question 20 requires students to identify three different design levels in Verilog. We speculate that students had less exposure to gate-level representations compared to the other, more commonly encountered design levels, leading to a relatively lower accuracy rate for this question.
Overall, the first-attempt correct rate was higher than 85% for most questions, and the final correct rate was close to 100%, indicating that the difficulty of this test was moderate and students had a solid foundation in terms of the basic concepts.
Individual Student Performance in Group 1
In Figure 9, the x-axis represents student IDs, while the y-axis shows each student’s average number of submissions and accuracy rate. The orange line in the figure indicates that students’ final accuracy is highly consistent, with the vast majority achieving or approaching 100%, demonstrating that repeated practice enabled most students to reach excellent learning outcomes.
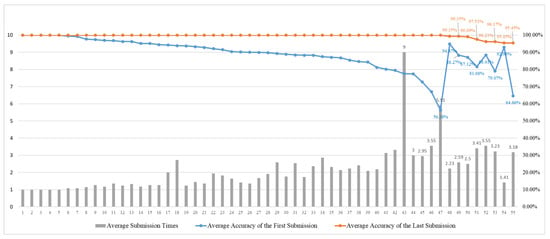
Figure 9.
Individual student results for Group 1 in section 1.
For the majority of students, the first-attempt accuracy exceeded 80%, indicating a strong initial understanding of the material. A small subset of students, for example ID 43 and ID 47, exhibited notably higher average submission counts and comparatively lower first-attempt accuracies. This suggests that, although these students were initially unfamiliar with Verilog, the iterative practice and explanatory support of the proposal ultimately enabled them to master the section’s content and achieve successful learning results.
Overall, Group 1 students demonstrated a strong foundational understanding of this section. Through the system’s provision of targeted practice sets and real-time feedback, the students were able to progressively overcome challenging topics and ultimately achieve a high level of final accuracy.
Group 2 Test Results
The test results of Group 2 are shown in Figure 10, where the x-axis represents question numbers and the y-axis indicates both the average number of attempts per question and the average accuracy rates. The overall response patterns are generally consistent with those observed in Group 1. However, the data distribution in Group 2 is more polarized. We observed that first-attempt accuracy for certain units was lower than that of Group 1. More students had no relevant background knowledge. The main difficulties were concentrated in the following section.
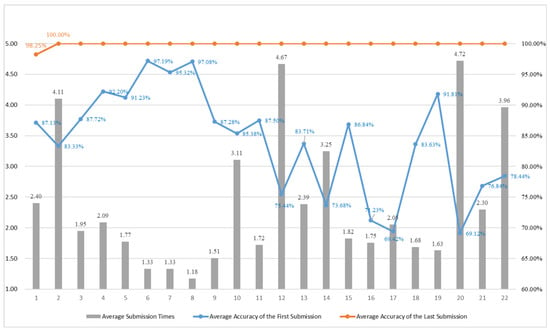
Figure 10.
Solution results of Group 2 in Section 1.
Questions 12 and 14 pertain to combinational logic, a concept not typically encountered in general programming courses. For beginners, unfamiliar subject matters often result in lower accuracy and higher average submission counts. Nevertheless, through the system’s effective instructions and opportunities for repeated practice, students were ultimately able to develop a sound understanding of these topics.
Questions 16, 17, and 18 showed relatively weak performances in both groups, indicating that the content relating to synchronous and asynchronous circuits poses a particular challenge, as it is specific to Verilog and more conceptually demanding. After working through the consecutive practice set designed by the system, the first-attempt accuracy improved significantly, further demonstrating the positive impact of targeted question sequencing on comprehension.
Question 20 obtained the lowest accuracy due to students’ limited exposure to gate-level circuit representations compared to more familiar design levels, such as dataflow or behavioral. However, as students progressed through the subsequent related questions, their accuracy steadily improved, reflecting the effectiveness of the system’s instructional explanations and sequencing in helping students correct misconceptions and solidify their understanding of the underlying concepts.
Overall, most of the students were able to achieve close to full marks in the end, while the groups with a higher average number of submissions usually had lower first-submission scores and needed repeated revisions to approach 100%. The multiple attempts mechanism can effectively help students gradually improve their accuracy in answering questions. Different students have different initial levels of understanding, but the overall final effects are quite good, which means that this system can achieve similar results for students of different levels.
Individual Student Performance in Group 2
As shown in Figure 11, approximately 62% of students achieved a first-attempt accuracy of 85% or higher. The result was close to the one observed in Group 1. This indicates that the majority of students were able to comprehend the question requirements on their initial attempt and reach fully correct answers within two to three submissions. However, in contrast to Group 1, students with lower first-attempt accuracy in Group 2 exhibited a marked increase in their average number of submissions. This suggests that, compared to students with a background in computer science, these learners were less familiar with the contents and required more iterative attempts to fully understand and correctly solve the problems. Notably, despite facing unfamiliar materials, these students did not give up. Instead, they persisted, with the support of the system, ultimately achieving correct solutions. This outcome underscores the system’s clear and positive impact as an effective learning aid for students seeking to acquire Verilog proficiency.
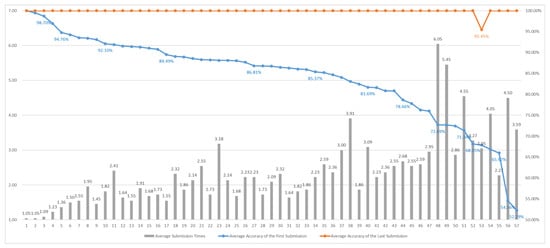
Figure 11.
Individual student performance for Group 2 in Section 1.
4.3.2. Section 2 Analysis
This section’s assessment is composed of 13 questions covering the following topics: (1) definitions of numerical data types; (2) declarations of vectors and arrays; (3) methods for the truncation and extension of numerical values in Verilog; (4) effective variable naming conventions; (5) characteristics and applications of different design abstraction levels for gate-level, dataflow, and behavioral; (6) distinctions between combinational and sequential logics. Finally, practical comparisons of the features and differences among these design levels are provided through the applied test questions.
Group 1 Test Results
The test results are shown in Figure 12. It can be clearly observed from the figure that the accuracy rate of most students reached more than 80% for first-time answers, and the average number of submissions between each question is quite stable, indicating that the students are familiar with the operation of the system and the means of answering.
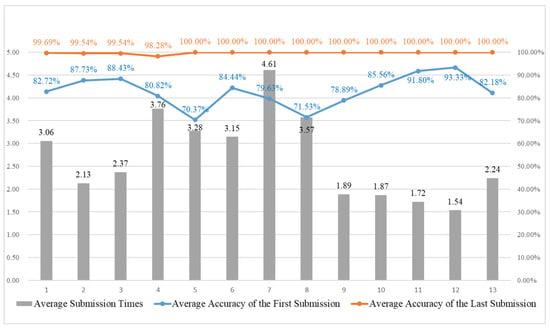
Figure 12.
Solution results for Group 1 in Section 2.
In addition, students can review what they previously learned while absorbing new knowledge through the introduction of question types that are similar to those in Section 1 for Questions 10 to 12. From the results in the figure, we can see that the average accuracy upon first submission is higher and the average submission times were significantly lower than those for other questions, which means that while students are learning new knowledge, they can also strengthen their understanding of related concepts by reviewing their previous knowledge.
From the overall analysis of the test results, the questions with a low average accuracy upon first submission achieved these results for the following reasons:
- Question 5: This question lists various situations, including different numbers of bits and different radix systems, and requires students to declare the corresponding numbers in this format. We believe that some students may only be familiar with binary and hexadecimal systems, and are unfamiliar with octal systems.This results in a lower number of correct answers being achieved compared to other questions.
- Question 8: This question explains the “truncation” and “extension” mechanisms that occur when variables of different bit widths are assigned to each other in Verilog. Students need to judge whether the description is correct or incorrect. We think that students may not have paid attention to the difference between signed and unsigned. Students often think that the sign extension will be performed when the bit width is insufficient. However, the sign extension will only be performed when the target variable is signed and the source data has a signed value. Otherwise, the zero extension will occur.
Individual Student Performance in Group 1
As shown in Figure 13, it can be observed from the chart that the average number of submissions for most students was about two, and only a few students exceeded four submissions. In addition, about 60% of the students achieved an accuracy rate of more than 85% on the first attempt, which suggests that the system can effectively provide students with a good testing environment, and the questions and topic descriptions provided are clear and easy to understand. Students could quickly grasp the meaning of the questions and successfully obtain the answers. As can be seen from the orange line graph, the students’ average accuracy upon final submission is close to 100%, which highlights that most students were able to fully understand the content of the questions and achieve good learning results through the repeated exercises provided by the system.
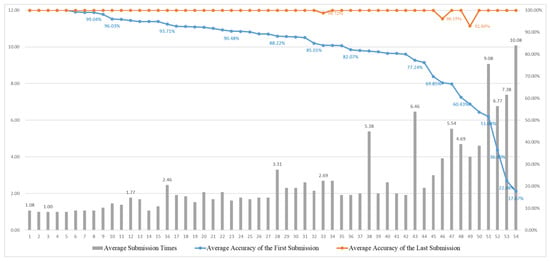
Figure 13.
Individual student performance for Group 1 in Section 2.
Further analysis of students’ average accuracy upon first submission revealed that there was a large performance gap among students. Some students performed well in their first attempt, but others needed multiple attempts before gradually improving their performance. This diverse first-time answer performance and the high levels of final results indicate that the teaching and exercise design of the proposed system has a good learning assistance effect, enabling students to quickly adjust their mistakes and significantly improve their learning outcomes.
Group 2 Test Results
The test results are shown in Figure 14. The overall answer curve is roughly consistent with the trend of Group 1, indicating that the challenges faced by the students in the two groups in conceptual understanding are highly consistent. However, since Group 2 includes students that have no computer science background, the Average Accuracy of the First Submission is significantly lower than that of Group 1. This reflects the lack of basic programming and hardware logic knowledge, which creates a high hurdle for beginners.
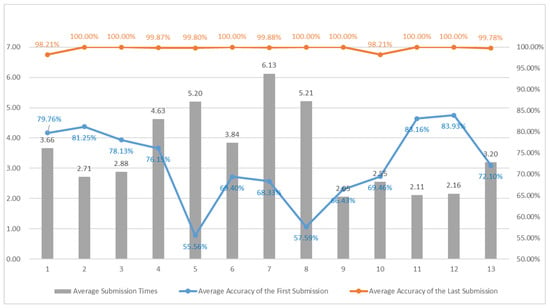
Figure 14.
Solution results for Group 2 in Section 2.
From the data, we can see that both Group 1 and Group 2 have a higher average number of comparisons for Question 7, but they are able to achieve a very high final accuracy rate. It was found that the question contained a trap and students were required to confirm the definition again and again before they could provide the correct answer, which should be improved in future works.
To assess students’ ability to integrate prior knowledge, we designed Questions 10, 11, and 12 as review questions, similarly to those in Section 1. Figure 14 shows the average accuracy upon first submission for these three questions significantly improved after repeated practice, demonstrating that alternating new and previously learned concepts can effectively reinforce understanding. Compared to Group 1, Group 2 had more difficulty with questions related to numerical definition and bit manipulation in Verilog, such as value declaration, truncation, and extension, indicating that such abstract conversion and symbol extension mechanisms are particularly challenging for students without any information technology background. To reduce this gap, we are considering adding more practical exercises regarding “hardware data types” and “bit operations” and using visual waveform figures to increase students’ intuitive understanding. Additionally, introducing small tests to help students review and reinforce their knowledge is another direction for future improvement.
In summary, students in Group 2 were still able to achieve a high accuracy rate, comparable to that of Group 1, through the repeated practice and instant feedback provided by the system, indicating that this learning platform has good adaptability and teaching effectiveness for students from different backgrounds.
Individual Student Performance in Group 2
As can be observed from Figure 15, the vast majority of students eventually achieved 90% or even close to 100%, with only a few students achieving slightly below 80%. Taken together, the results indicate that (1) some students already had a good understanding upon their initial submission and can maintain high scores with only one or two attempts, (2) although some students do not score well in their first submission, they can significantly improve their accuracy after multiple revisions, and (3) the number of submissions often reflects the depth of students’ initial understanding, and more attempts mean that they need more attempts to get close to full marks. Overall, this chart highlights the value of multiple attempts and immediate feedback, proving that even if the initial performance gap is quite large, most learners can eventually improve their performance to a level similar to that of higher-scoring students through subsequent efforts.
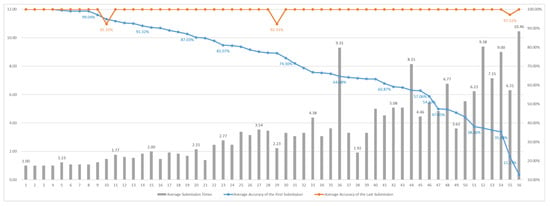
Figure 15.
Individual student performance for Group 2 in Section 2.
4.3.3. Section 3 Analysis
There are eight test questions in this section. They cover the conversion of values between binary, decimal, and hexadecimal, including fixed-point number conversion and signed number conversion.
Group 1 Test Results
The test results are shown in Figure 16. From the chart, we can see the answer status of the questions. The overall number of submissions is lower than that in the previous sections because this section is about basic base conversion, with fixed formulas that can be applied and fewer special situations. Students can directly obtain the correct answers using the formulas they have learned. The final correct answer rate was close to 100%. The first three questions had a high rate of correct answers on the first submission. These three questions involved 4-bit numerical conversions and were relatively simple, so the rates of correct answers were quite high.
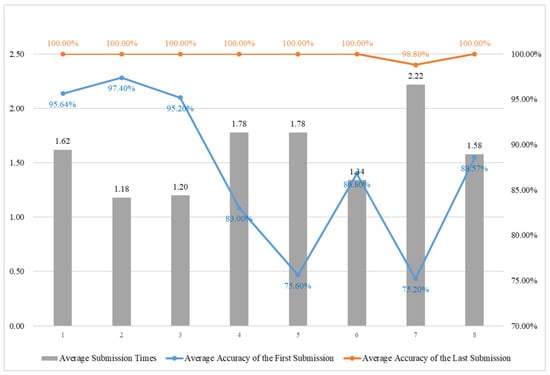
Figure 16.
Solution results for Group 1 in Section 3.
From the overall test results analysis, the main reasons for low average accuracy upon first submission in certain questions are as follows:
- Question 5: This question asks participants to convert a binary value into a fixed-point number. The average accuracy of the first submission is 75.6%. This question is more difficult for students who are exposed to fixed-point numbers for the first time. However, the next question, Question 6, asks students to convert fixed-point numbers back to binary values. It can be seen that the correct answer rate for the first answer significantly improved, to 86.8%. It can be concluded that after practice, students’ understanding of the concept can be greatly improved, and they can perform better when they are exposed to similar questions again.
- Question 7: This question asks students to convert a binary value into a corresponding signed number. The first-time correct answer rate is 75.2%. For students who are encountering two complementary numbers for the first time, this question requires them to learn a new concept, so the first-time correct answer rate is lower. Similar to previous situations, such as Questions 5 and 6, Question 8 is a reverse conversion of the results. After obtaining an initial understanding of the concept, the results significantly improve upon a second exposure to similar questions.
Individual Student Performance in Group 1
Figure 17 shows the answers of individual students in Group 1 in Section 3. It can be observed from the figure that the average number of submissions for most students is less than 1.5, which means that most students can obtain a correct answer within one or two attempts. The top students (around the top 20%) showed high levels of accuracy, mostly above 95%, on their first submissions. The initial accuracy of other students dropped slightly; however, after repeated revisions, most of them were still able to achieve a high accuracy rate, showing that they have good learning potential and improvement abilities. This proves that the content of this system is not too difficult and good results can be obtained as long as more attempts are made.
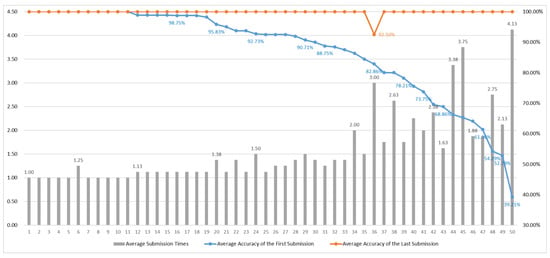
Figure 17.
Individual student performance for Group 1 in Section 3.
Group 2 Test Results
As shown in Figure 18, the overall response curve for Group 2 is close to the trend observed in Group 1. However, Group 2 exhibited a slightly lower average accuracy of the first submission and a higher average number of submissions per question, although the final accuracy still approached 100%. This outcome is expected, as some students in Group 2 did not have a background in computer science. The results highlight that prior knowledge significantly impacts the first-attempt accuracy for beginners. Nevertheless, our consistent instructional approach and concept sequencing enabled students from different backgrounds to ultimately achieve comparable outcomes.
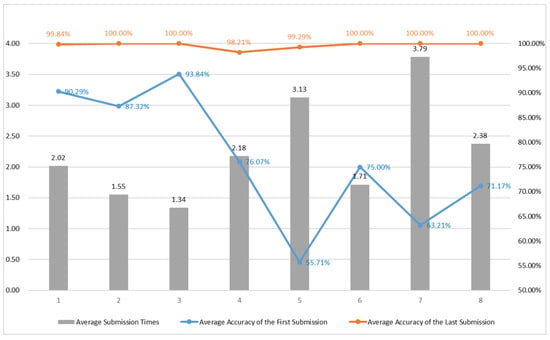
Figure 18.
Solution results for Group 2 in Section 3.
Similar to Group 1, Questions 5 and 7 had a lower average accuracy upon first submission, likely due to their more complex concepts. After practicing these topics, students demonstrated a notable increase in accuracy on subsequent, similar questions, such as Questions 6 and 8, illustrating the effectiveness of the exercise structure in reinforcing understanding.
Individual Student Performance in Group 2
Figure 19 presents the average Submission Times, the average accuracy of the first submission, and the average accuracy of the last submission for each student in Group 2. Compared to Group 1, Group 2 exhibits larger variability in learning outcomes, with a wider range of performance across students. Specifically, while some students were able to complete their responses in one attempt, the average number of submissions noticeably increased for students beyond ID 30, with certain individuals, such as student ID 37, requiring more than seven attempts. This indicates that this group needed more iterations and revisions during the learning process.
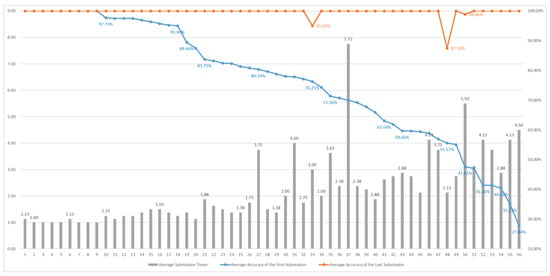
Figure 19.
Individual student performance for Group 2 in Section 3.
The primary reason for this disparity is likely the inclusion of students without relevant academic backgrounds in Group 2, making the initial learning curve steeper for some. Nevertheless, examinations of the final accuracy rates show that the majority of students were ultimately able to achieve satisfactory results through repeated practice. This suggests that, despite a weaker starting point, students demonstrated significant improvements with sufficient practice and time investments, which is consistent with the conclusions drawn from earlier analyses.
4.3.4. Section 4: Analysis
This section’s assessment comprised 23 questions focused on arithmetic and logical operations in Verilog, including addition, subtraction, multiplication, division, and modulus, with both unsigned and signed number representations. Additional topics covered shift operations, relational comparisons, and bit-wise and logical operations. Due to the broad range of Verilog operations addressed, the assessment was more extensive and complex compared to previous sections.
Group 1 Test Results
As shown in Figure 20, most questions did not achieve an average accuracy upon first submission above 90%. This is primarily because the arithmetic operations in Verilog involve numerous underlying concepts; simply memorizing procedures is insufficient, and a deeper, integrated understanding is required to achieve higher accuracy. While repeated practice enabled the final accuracy rates to approach 100%, some items still fell short of complete mastery.
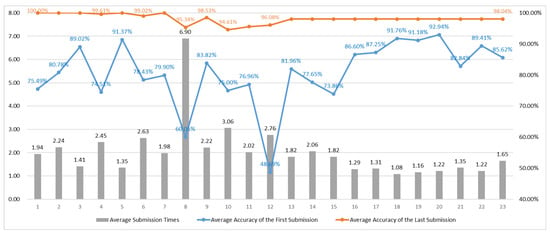
Figure 20.
Solution results for Group 1 in Section 4.
The following provides a more detailed analysis of these questions. From the overall assessment results, the reasons for certain questions obtaining notably lower average accuracy upon first submission are as follows:
- Question 4: This topic focused on how division is performed in binary, which differs somewhat from traditional decimal division. This unfamiliarity resulted in a lower initial accuracy. However, after students understood the underlying computational method, the final accuracy rose to 99%, indicating that although the problem was challenging, students were able to master the concept through guided practice.
- Question 6: This question addressed signed binary addition, which requires students to account for sign extension and overflow conditions not present in unsigned addition. The need for additional reasoning resulted in a lower first-attempt accuracy. Nevertheless, after multiple attempts and conceptual clarification, students’ final accuracy neared 100%.
- Question 8: Students performed signed multiplication—a more complex process requiring a comprehensive understanding of the binary arithmetic rules. As expected, both the average number of attempts and initial accuracy were less favorable; the final accuracy for this item was 95.3%. This may be attributed to the complexity of the problem, insufficiently detailed guidance, or gaps in the design of the problem, suggesting areas for improvement.
- Question 12: This question involved binary signal concatenation and replication. The first-attempt accuracy was only 48.6%, which is relatively low. Upon review, the item itself did not appear excessively complex. The lower accuracy may have resulted from unclear wording in the question, leading to overlooked details, or from the abstract nature of the concept for beginners.
- Questions 8, 10, 11, and 12: These questions had the lowest final accuracy rates, all below 98%. These topics primarily concerned signed operations, which students found more challenging, as expected given their increased complexity. To address this, future improvements could include breaking down complex concepts into more granular subtopics for smoother learning curves, or increasing the number of practice problems to reinforce understanding through repetition.
Individual Student Performance in Group 1
Figure 21 displays the performance of individual Group 1 students in Section 4. Several key observations can be made:
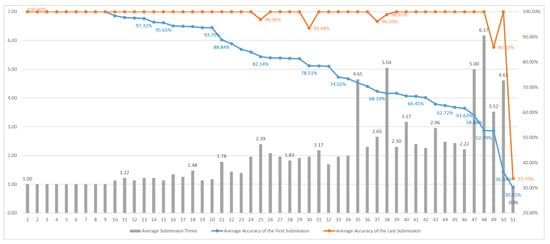
Figure 21.
Individual student performance for Group 1 in Section 4.
- Increased Number of Submissions Indicates Greater Learning Challenges: The chart shows that most students required more submissions per question than in previous sections. For the students beyond ID 24, the average number of submissions commonly exceeded two, with those in the latter part of the group needing four to six attempts or more. This reflects the heightened difficulty of this section, which covers a wide range of complex arithmetic and logic operations, necessitating repeated practice to arrive at correct solutions.
- Higher Topic Difficulty Reveals Greater Variability Among Students: The average accuracy of the first submission drops from about 97% for the leading students to approximately 70% for those toward the end, indicating a clear gap in students’ comprehension of operations, bit manipulations, and signed versus unsigned calculations. For some students, even the final accuracy remained quite low, suggesting that certain problems may have been excessively difficult or overly complex, hindering effective problem-solving.
- Summary: Overall, Section 4 represents a significant increase in learning difficulty within the system’s curriculum. The trends in average submission count and first-attempt accuracy suggest that additional instructional supports are warranted for advanced operations, such as more detailed worked examples, targeted error correction strategies, and the pre-class categorization of problem types to help students gradually build the necessary computational skills.
Group 2 Test Results
As shown in Figure 22, both the average submission times and the average accuracy of the first submission for Group 2 were slightly lower than those observed in Group 1. Consistent with the results from Group 1, Questions 4, 6, 8, and 12 exhibited lower accuracy rates. In addition, for Group 2, Question 10 presented a significant challenge; this topic involved signed division, one of the more complex problem types in the section, which resulted in a notably high number of attempts.
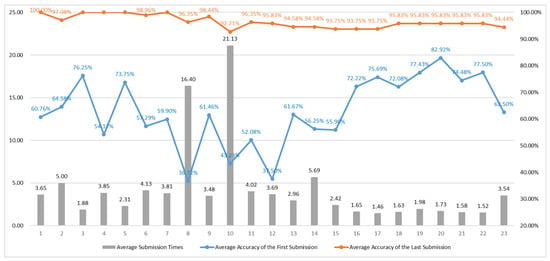
Figure 22.
Solution results for Group 2 in Section 4.
Beyond the inherent complexity of these questions, potential ambiguities or short-comings in the problem statements or design may have contributed to these outcomes. In terms of the final accuracy, several of the later questions did not reach the expected target (ideally 97%), likely due to the incomplete problem design or insufficiently clear conceptual explanations. Addressing these issues through refined question design and improved instructional clarity will be a focus for future revisions.
Individual Student Performance in Group 2
Figure 23 illustrates the learning performances of Group 2 students in Section 4, high-lighting pronounced individual differences and challenges. The chart reveals that some students had average submission times exceeding seven attempts, indicating a need for extensive trial-and-error during problem-solving. The average accuracy of the first submission exhibited a clear downward trend, dropping from 100% among the leading students to approximately 30–50% for those in the latter portion of the group, reflecting a substantial gap in initial comprehension. While most students were ultimately able to achieve 100% final accuracy, a few did not attain complete mastery, resulting in lower final scores.
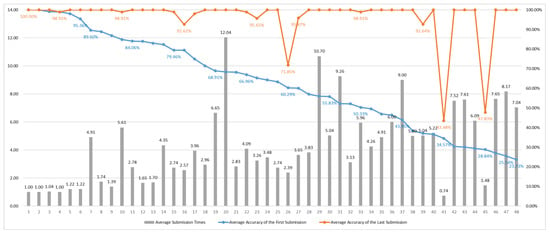
Figure 23.
Individual student performance in Group 2 in Section 4.
Compared to Group 1 students, Group 2 students displayed higher average submission times, lower average accuracy in their first submission, and greater disparities among the lower-performing students in this section. This difference is likely attributable to the inclusion of students without relevant backgrounds in Group 2; lacking foundational computer science knowledge, they may have found certain concepts more challenging, which manifested as a steeper learning curve. To address this, future instructions should incorporate more detailed examples and tiered supports to help students from diverse backgrounds gradually develop both a computational understanding and practical skills. Additionally, there was one student (ID 41) with an average submission count of 0.74. Upon investigation, this was due to their incomplete responses to several questions, resulting in anomalously low data. Going forward, data from students with incomplete responses should be treated accordingly to ensure more accurate analysis.
4.3.5. Comparative Analysis
Figure 24 summarizes the overall learning performance of Group 1 and Group 2 students across Section 1 to Section 4. The horizontal axis represents the section index, while the left vertical axis indicates the average accuracy and the right vertical axis corresponds to the average submission count.
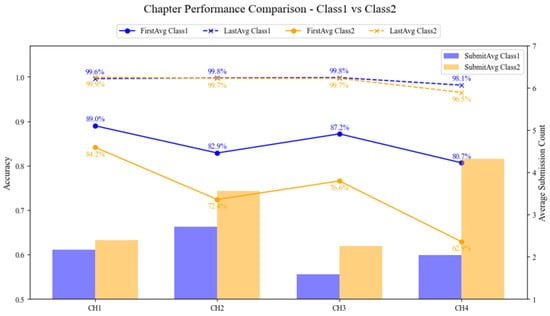
Figure 24.
Section performance comparison between Group 1 and Group 2.
In the figure, the line graphs illustrate each group’s first-attempt (FirstAvg) and final (LastAvg) accuracy for each section, the blue solid and dashed lines denote Group 1, and the orange solid and dashed lines represent Group 2. The bar charts show the average number of submissions per section for each group, with the blue bars representing Group 1 and the orange bars representing Group 2. To enhance clarity, specific percentage values are annotated at each line node. Subsequent sections will provide comparative analyses both across sections and between groups based on these results.
Analysis Across Sections
Table 6 presents the average analytical metrics for each section, calculated as the mean values of both Group 1 and Group 2. “FirstAvg” represents the average first-attempt accuracy, “LastAvg” is the average final accuracy, and “SubmitAvg” denotes the average number of submissions. This approach enables the identification of inter-section differences and highlights areas that may require instructional adjustment.

Table 6.
Performance analysis across sections.
In terms of first-attempt accuracy, Section 1 showed the strongest performance, with an average of 86.57%. This indicates that students had a solid grasp of basic concepts and syntax, enabling them to answer correctly on their initial attempt. In contrast, Section 4 had the lowest first-attempt accuracy, at just 71.17%, reflecting the increased cognitive load and error propensity associated with more complex topics such as arithmetic operations such as addition, subtraction, multiplication, division, signed and unsigned arithmetic, and logical operations.
The results for the average submission count further corroborate these observations. Section 4 exhibited the highest average submission count, at 3.18, indicating that students required more attempts and corrections to complete the tasks successfully. Section 2 ranked second in submission count, likely due to the abstract nature of multiple signal declarations and vector array operations. Conversely, Section 3 had the lowest average submission count, at only 1.92, suggesting that its content, which was mainly focused on number system conversions, was more straightforward for students to master.
Despite the differences in initial performance, all sections achieved a final accuracy of 97% or higher, demonstrating that repeated practices enabled students to effectively master the key concepts of each section and achieve positive learning outcomes. Overall, this analysis provides a valuable reference for ranking section difficulty and allocating instructional resources, allowing for data-driven adjustments to curriculum design.
Analysis of Performance Differences Between Groups
Table 7 presents the average analytical metrics for both groups, allowing for a direct comparison of learning outcomes across sections. The data clearly reveal significant differences in performance between Group 1 and Group 2.

Table 7.
Performance comparison between two groups.
In terms of the average first-attempt accuracy, Group 1 achieved an average of 84.82%, markedly higher than Group 2’s 74.01%. This suggests that Group 1 students possessed stronger initial comprehensions and greater proficiency in applying syntax when faced with new questions. This difference is likely attributable to the composition of the cohorts, as Group 1 comprised mostly students with relevant backgrounds and stable foundational abilities, whereas Group 2 included students with backgrounds of non-related disciplines, who often required additional time to interpret questions and grasp syntactic structures during their first attempts.
However, with respect to the average final accuracy, both groups performed exceptionally well, with only a 0.4% difference between them. This indicates that even students with limited initial understanding were able to successfully correct their errors and achieve the learning objectives through the system’s iterative practices and real-time feedback. These results further demonstrate the platform’s capacity to support learners of varying proficiency levels, providing strong guidance for self-directed study and a forgiving learning environment.
A closer examination of the average number of submissions shows that Group 2 students averaged 3.13 submissions per question, substantially higher than Group 1’s average of 2.12. This suggests that Group 2 students required more attempts and corrections to arrive at the correct answers, likely reflecting greater challenges in understanding the intent of the questions and/or mastering the syntactic details. This phenomenon reinforces the importance of recognizing differences in students’ backgrounds and highlights the potential benefits of differentiated instructional strategies to shorten learning curves and reduce error rates.
In summary, this analysis not only uncovers disparities in initial comprehensions and problem-solving processes between the two groups but also confirms that, with effective learning interfaces and instructional designs, students from different backgrounds can ultimately achieve high learning standards. The findings provide valuable insights for the future development of individualized tutoring approaches and targeted adjustments in the section design.
5. Discussion
After completing an analysis of all four sections and both groups, we summarized the strengths and potential areas for improvement observed during the implementation of this Verilog instructional system. This section presents the discussions from three perspectives: the effectiveness of the question design, the summary and analysis of overall results, and observations and future improvements.
5.1. Effectiveness and Advantages of Question Design
The system employs a diverse range of question types to enhance student learning outcomes. The use of question sets facilitates the consolidation and integration of knowledge within related topics, while more challenging, varied questions are designed to assess students’ ability to flexibly apply the concepts. The immediate feedback mechanism enables learners to promptly identify and correct errors, thereby promoting deeper understanding. Additionally, repeated practice questions help reinforce memory retention and support self-assessment, ultimately fostering a positive and effective learning cycle.
5.2. Summary and Analysis of Overall Results
The findings of this study indicate that the majority of students achieved a final accuracy rate close to 99%, demonstrating that the difficulty level of the system’s questions was appropriately set to effectively differentiate student proficiencies without causing excessive frustration. Furthermore, students were able to achieve a stable and satisfactory performances regardless of their background in computer science, underscoring the strong instructional versatility of the system.
Overall, students experienced a smooth learning curve and were able to sequentially master key concepts. The platform’s fully online operation, which requires no additional hardware or software resources, enables both instructional experiments and learning assessments to be completed with ease, offering flexibility in implementation and significant potential for broader adoption.
5.3. Observations and Future Improvements
Although the overall learning outcomes were satisfactory, certain items did not achieve expected accuracy levels. This may be attributed to ambiguous wording in questions or gaps in students’ understanding of specific concepts. Additionally, some anomalies were observed in the testing data, highlighting the need for subsequent data screening and cleaning to improve the accuracy and representativeness of the analysis. To further optimize the system and its evaluation mechanisms, the following improvements are recommended.
- Enhance the design of learner questionnaires to gain deeper insights into potential difficulties encountered during the answering process.
- Incorporate the tracking of response time as a basis for analyzing learning behaviors and progress.
- Implement appropriate restrictions in the testing environment, such as clearly prohibiting collaboration during assessment periods, to ensure the authenticity of the data.
- Introduce a midterm and final exams mechanism to complement ongoing practices and provide more comprehensive and credible evidence of the learning achievements.
6. Conclusions
This paper developed an online Verilog practice and learning system that employs immediate feedback, multiple-attempt mechanisms, and structured question sets to guide students in gradually mastering fundamental syntax and logic concepts. The system automatically assesses the correctness of responses and provides real-time feedback on learning progress, enabling students to make timely adjustments to their learning strategies. Organized into sections based on learning topics and featuring various types of questions, the system reinforces conceptual understanding through a step-by-step practice model.
Empirical evaluation results from 112 students across two groups taking the introductory chip-design course at the National Taipei University of Technology, Taiwan, demonstrated that, regardless of students’ prior backgrounds, the system effectively improved learning outcomes, with final accuracy rates consistently reaching up to 99%. The results confirm the system’s strong support for their learning and its general applicability. Future works will focus on expanding the diversity of the question types and introducing more sophisticated diagnostic and assessment mechanisms to further enhance learning effectiveness.
Author Contributions
Conceptualization, S.J., Y.W. and N.F.; methodology, P.-C.H., T.-L.F. and Y.-C.F.; software, S.J. and Y.W.; formal analysis, S.J.; investigation, P.-C.H., T.-L.F. and Y.-C.F.; writing—original draft preparation, P.-C.H. and T.-L.F.; writing—review and editing, P.-C.H., T.-L.F. and S.J.; supervision, N.F. and Y.-C.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wilson, P. Design Recipes for FPGAs: Using Verilog and VHDL; Newnes: Oxford, UK, 2015. [Google Scholar]
- Brayton, R.K.; Rudell, R.; Sangiovanni-Vincentelli, A.; Wang, A.R. MIS: A multiple-level logic optimization system. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2004, 6, 1062–1081. [Google Scholar] [CrossRef]
- Tang, Y.; Hare, R.; Ferguson, S. Classroom evaluation of a gamified adaptive tutoring system. In Proceedings of the 2022 IEEE Frontiers in Education Conference (FIE), Uppsala, Sweden, 8–11 October 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–5. [Google Scholar]
- Hare, R.; Tang, Y.; Ferguson, S. An intelligent serious game for digital logic education to enhance student learning. IEEE Trans. Educ. 2024, 67, 387–394. [Google Scholar] [CrossRef]
- Ismail, I.; Zabidi, M.M.A.; Paraman, N.; Mohd-Yusof, K.; Rahman, N.F.A. Active and project-based learning implementation in a constructively aligned digital systems design course. IEEE Trans. Educ. 2023, 66, 602–611. [Google Scholar] [CrossRef]
- Funabiki, N.; Matsushima, Y.; Nakanishi, T.; Watanabe, K.; Amano, N. A Java programming learning assistant system using test-driven development method. IAENG Int. J. Comput. Sci. 2013, 40, 38–46. [Google Scholar]
- Jin, S.; Funabiki, N.; Fang, T.; Hsieh, P.; Fan, Y.; Kao, W.; Lee, Y. An implementation of grammar-concept understanding problems in Verilog programming learning assistant system. In Proceedings of the 13th International Conference on Information and Education Technology (ICIET), Fukuyama, Japan, 18–20 April 2025; pp. 280–284. [Google Scholar]
- Rodríguez-Vidal, J.; Martínez, R.; García-Beltrán, Á. C-programming self-assessment exercises versus final exams: 12 years of experience. Comput. Appl. Eng. Educ. 2023, 31, 1272–1288. [Google Scholar] [CrossRef]
- Quevedo, J.A.; Maldonado, Y. From MLIR to scheduled CDFG: A design flow for hardware resource estimation. IEEE Embed. Syst. Lett. 2025. Early Access. [Google Scholar] [CrossRef]
- Xu, X.; Peng, X. Research and practice on improving the efficiency of digital chip design description language. In Proceedings of the 2023 9th Annual International Conference on Network and Information Systems for Computers (ICNISC), Wuhan, China, 27–29 October 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 451–456. [Google Scholar]
- Liu, S.; Fang, W.; Lu, Y.; Wang, J.; Zhang, Q.; Zhang, H.; Xie, Z. Rtlcoder: Fully open-source and efficient LLM-assisted RTL code generation technique. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2024, 44, 1448–1461. [Google Scholar] [CrossRef]
- Yang, Y.; Teng, F.; Liu, P.; Qi, M.; Lv, C.; Li, J.; Zhang, H.; He, Z. Haven: Hallucination-mitigated LLM for Verilog code generation aligned with HDL engineers. In Proceedings of the 2025 Design, Automation & Test in Europe Conference (DATE), Lyon, France, 31 March–2 April 2025; IEEE: Piscataway, NJ, USA, 2025; pp. 1–7. [Google Scholar]
- Pearce, H. Experiences scaffolding a computer engineering project course to improve student outcomes. In Proceedings of the 2025 IEEE International Symposium on Circuits and Systems (ISCAS), London, UK, 25–28 May 2025; IEEE: Piscataway, NJ, USA, 2025; pp. 1–5. [Google Scholar]
- Chowdhury, S.R.; Wardhan, H.; Karri, S.K.; Kode, S.; Nagaraju, K. Smart learning environments for teaching electronics to students. In Proceedings of the 2013 IEEE Fifth International Conference on Technology for Education (T4E), Kharagpur, India, 18–20 December 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 174–175. [Google Scholar] [CrossRef]
- Hoefer, J.; Gauß, M.; Adams, M.; Kreß, F.; Kempf, F.; Karle, C.; Harbaum, T.; Barth, A.; Becker, J. A challenge-based blended learning approach for an introductory digital circuits and systems course. In Proceedings of the 2024 IEEE International Symposium on Circuits and Systems (ISCAS), Singapore, 19–22 May 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–5. [Google Scholar]
- Chen, S.L.; Lai, Y.K.; Hu, W.C.; Chung, W.Y. Case-based instruction of digital integrated circuit design courses for non-major undergraduates. In Proceedings of the 2013 Learning and Teaching in Computing and Engineering, Macau, Macao, 21–24 March 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 172–177. [Google Scholar]
- Pădurean, V.-A.; Denny, P.; Gotovos, A.; Singla, A. Prompt programming: A platform for dialogue-based computational problem solving with generative AI models. arXiv 2025, arXiv:2503.04267. [Google Scholar]
- Hrvacević, L.; Cincović, J.; Milaković, A.; Jocović, V.; Matveiev, V.; Drašković, D. Development of a web system with an automated question generator based on large language models. In Proceedings of the 2024 11th International Conference on Electrical, Electronic and Computing Engineering (IcETRAN), Nis, Serbia, 3–6 June 2024; pp. 1–6. [Google Scholar]
- Perera, P.; Tennakoon, G.; Ahangama, S.; Panditharathna, R.; Chathuranga, B. A systematic mapping of introductory programming languages for novice learners. IEEE Access 2021, 9, 88121–88136. [Google Scholar] [CrossRef]
- El-Medany, W.M.; Ismail, Y. Mobile learning laboratory for hardware courses. In Proceedings of the 2013 Fourth International Conference on e-Learning “Best Practices in Management, Design and Development of e-Courses: Standards of Excellence and Creativity”, Manama, Bahrain, 7–9 May 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 51–54. [Google Scholar]
- Lee, K. The DEVBOX Development Education Platform: An Environment for Introducing Verilog to Young Students. Master’s Thesis, University of British Columbia, Vancouver, BC, Canada, 2016. [Google Scholar]
- Zhang, H.; Lu, J.; Xu, W. Verilog OJ: Research and implementation of a Verilog HDL online judge system. In Proceedings of the 2023 IEEE International Conference on Image Processing and Computer Applications (ICIPCA), Changchun, China, 1–13 August 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1398–1401. [Google Scholar]
- Al Amin, R.; Wiese, V.; Jacobs, S.; Hardebusch, T.; Jaschke, S.; Obermaisser, R. Requirement analysis and didactic evaluation of a collaborative remote laboratory for FPGAs. In Proceedings of the 2025 IEEE Global Engineering Education Conference (EDUCON), London, UK, 22–25 April 2025; IEEE: Piscataway, NJ, USA, 2025; pp. 1–5. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).