Research on Advancing Radio Wave Source Localization Technology Through UAV Path Optimization
Abstract
1. Introduction
1.1. Significance and Motivation
1.2. Purpose and Objectives
- To improve localization accuracy beyond prior work by incorporating a hybrid approach that integrates RSSI, AOA, and EOA with appropriate weighting.
- To construct a high-efficiency and high-accuracy localization system by leveraging UAV mobility for LoS (line-of-sight) acquisition and path optimization.
- To assess the impact of factors such as UAV orbit radius and sequential estimation on localization performance.
2. Literature Review
2.1. Fingerprinting-Based Localization
2.2. UAV-Assisted Methods
2.3. UAV Trajectory Optimization
2.4. Positioning of This Study
3. Materials and Methods
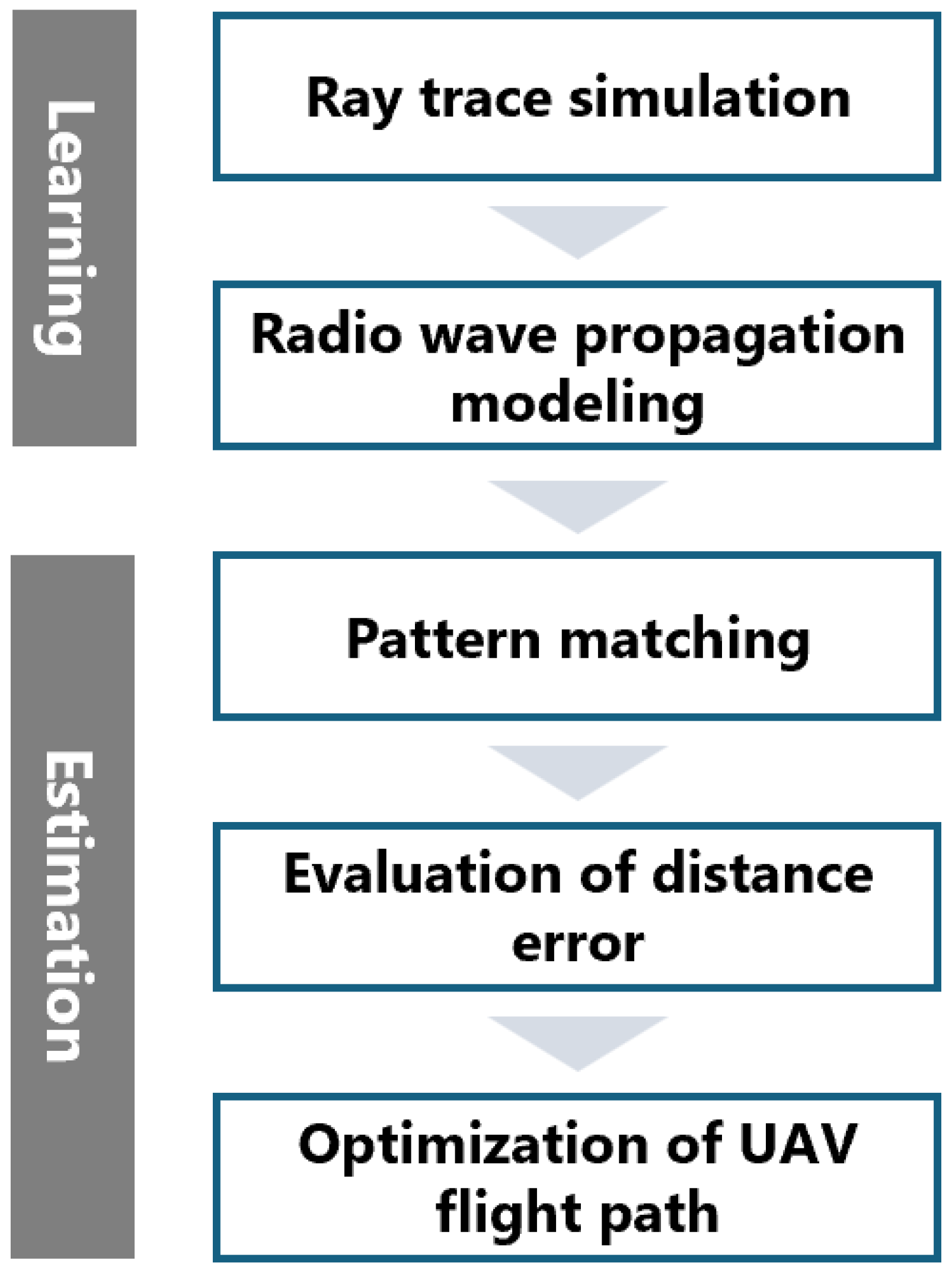
3.1. Overall Flowchart
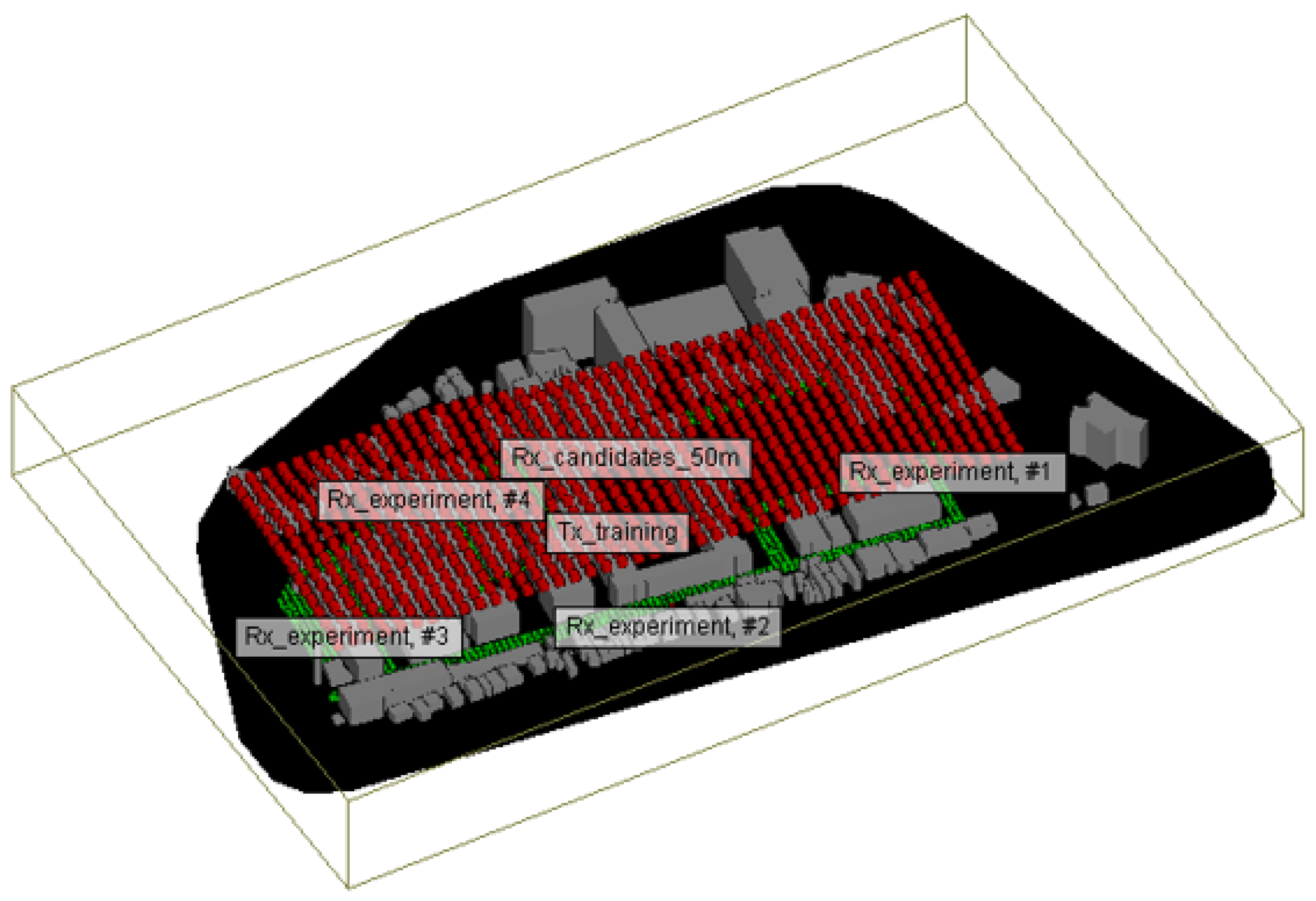
3.2. Ray Tracing Model
3.3. Radio Propagation Modeling
3.4. Location Fingerprinting Method
3.5. LoS Probability
3.6. Solution to the Optimization Problem
3.7. Particle Swarm Optimization (PSO)
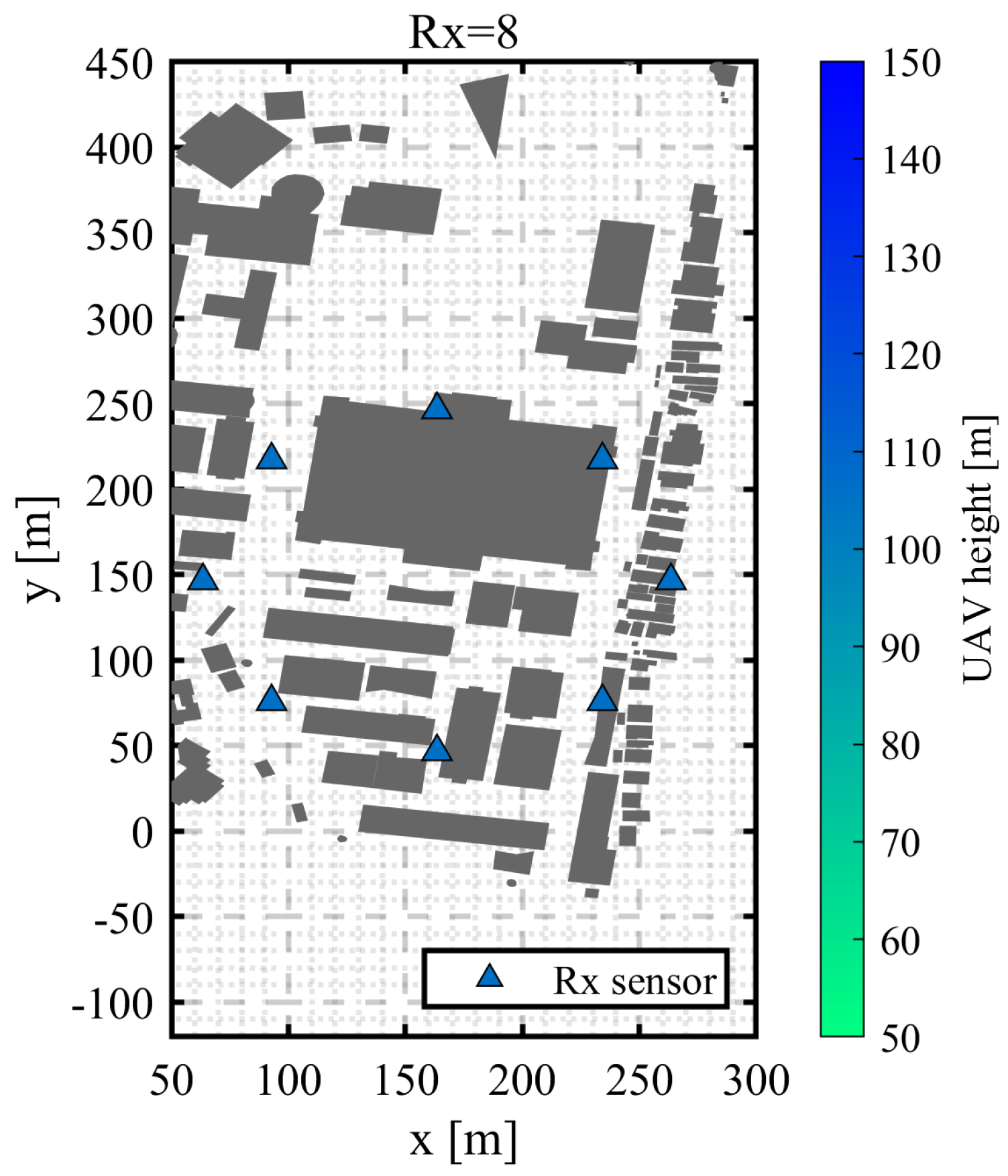
3.8. UAV Orbit
3.9. Objective Function
3.10. Estimation Method for Source Coordinates Using RSSI
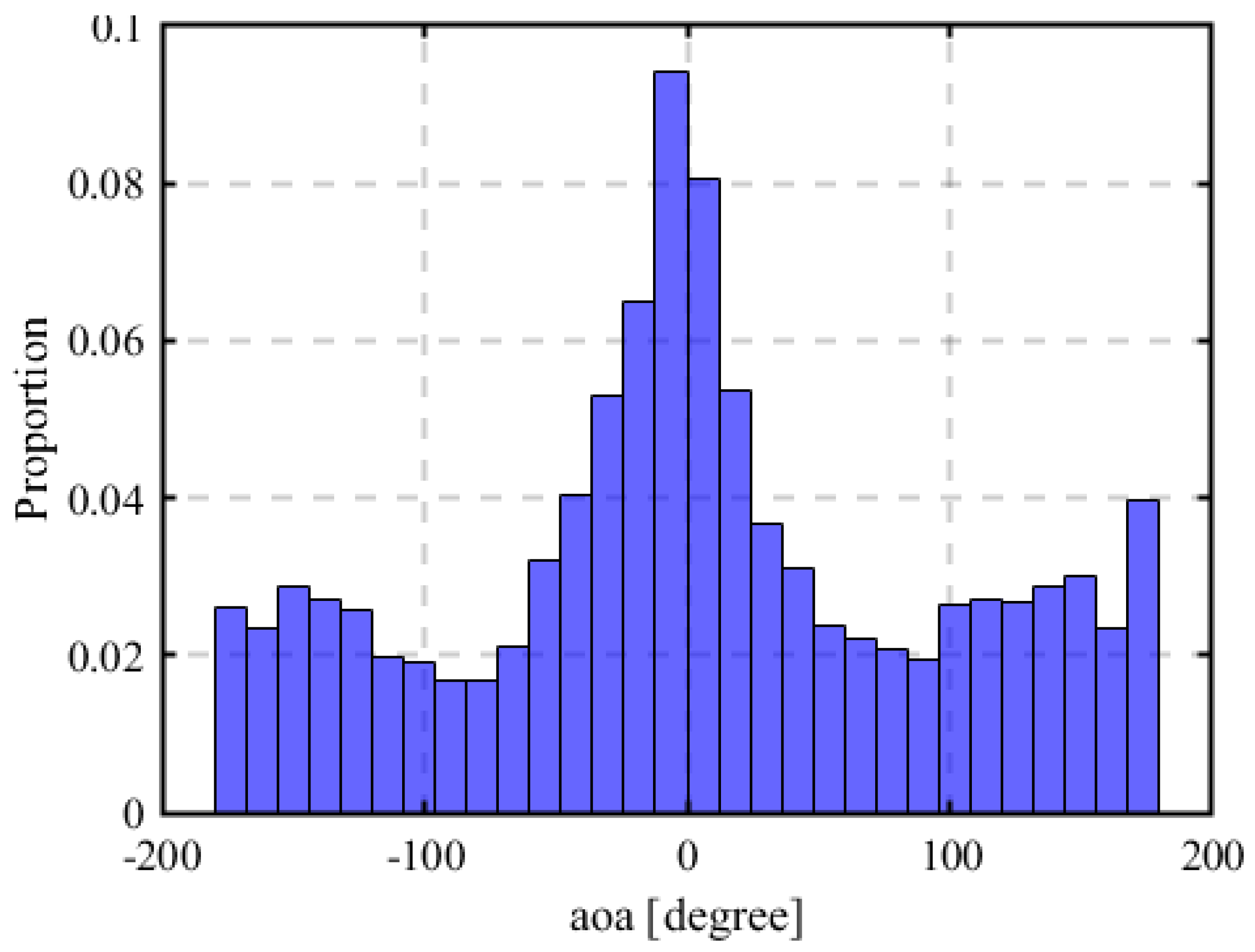
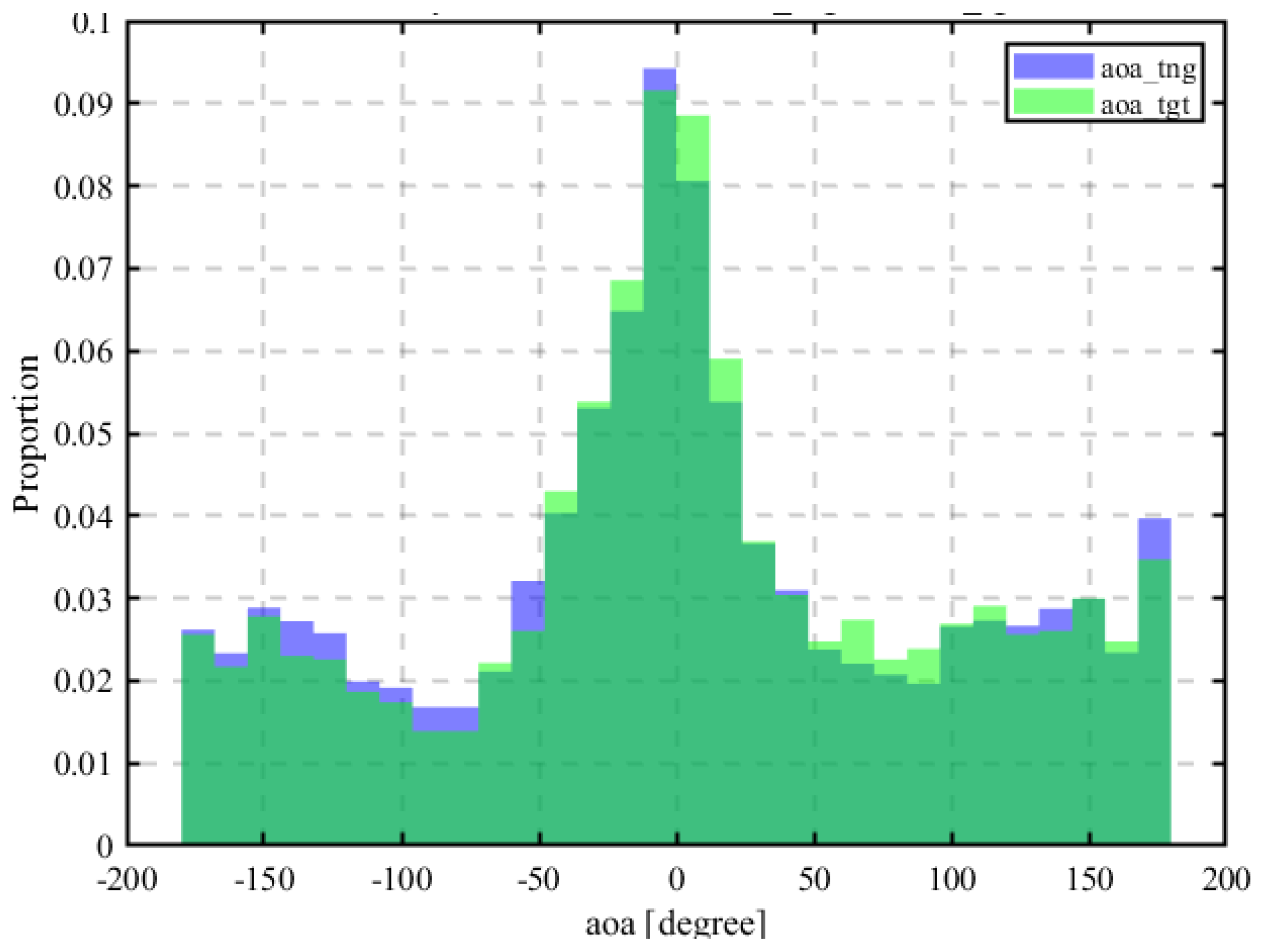
3.11. AOA Model
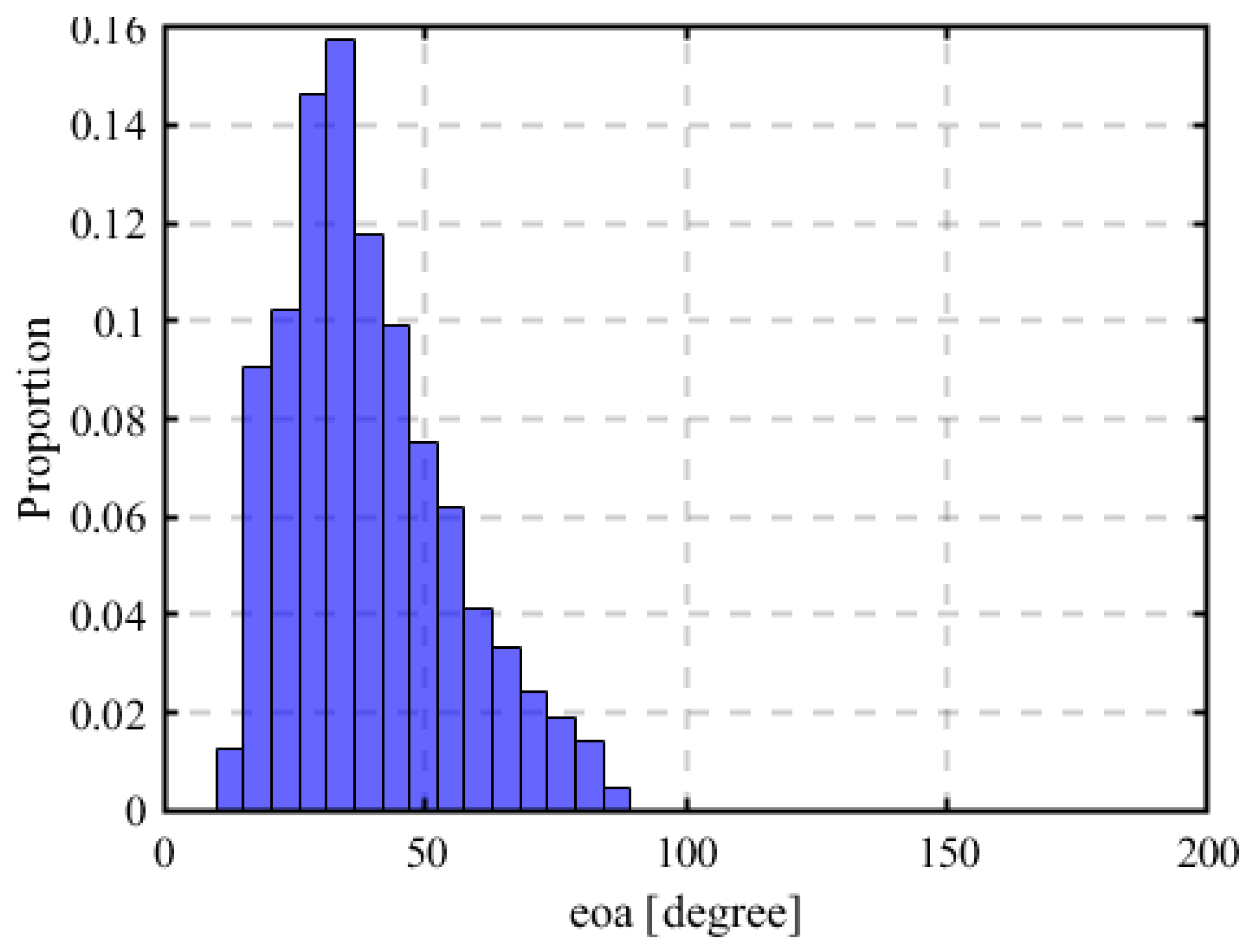
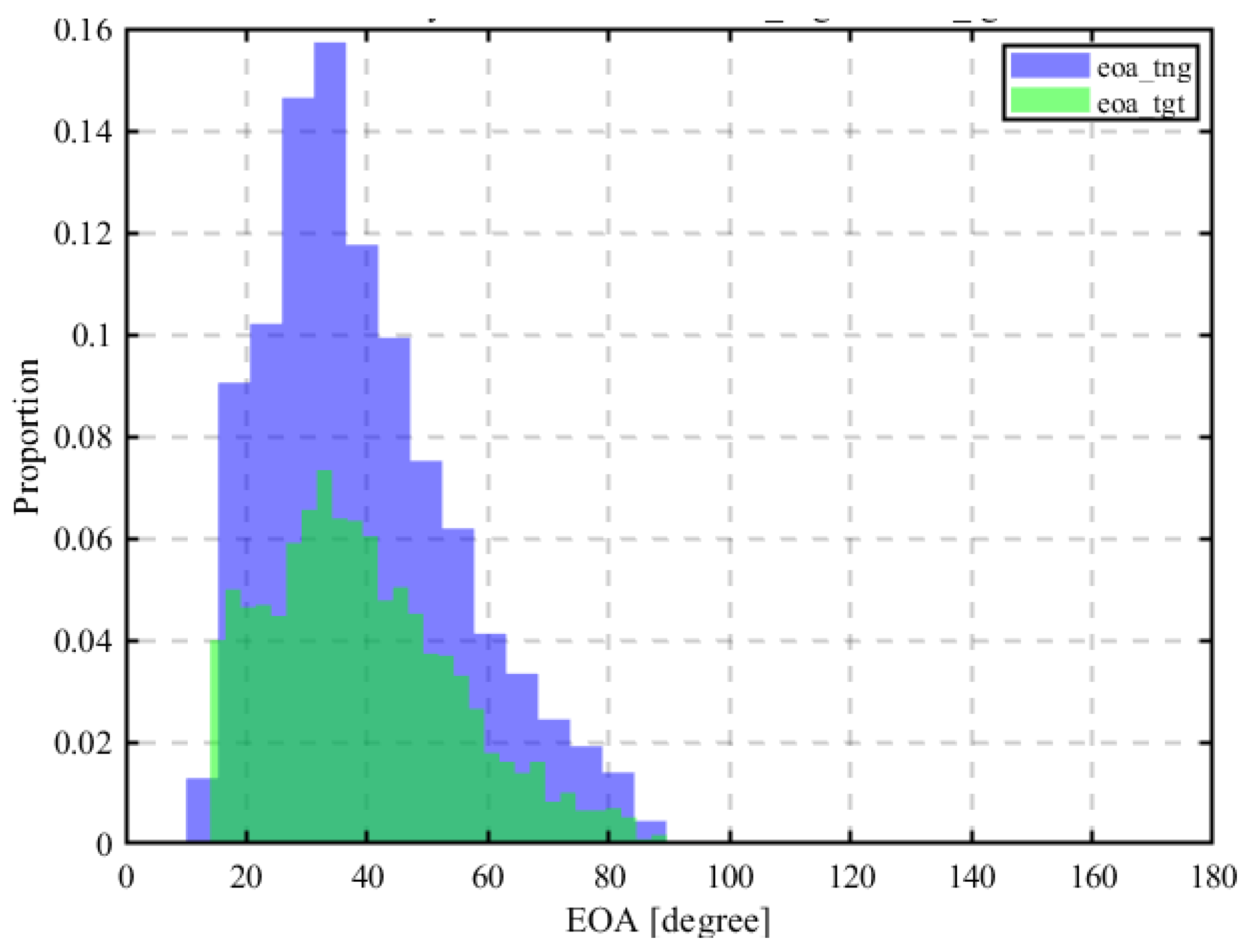
3.12. Estimation Using Elevation of Arrival (EOA)
3.13. HYBRID Model
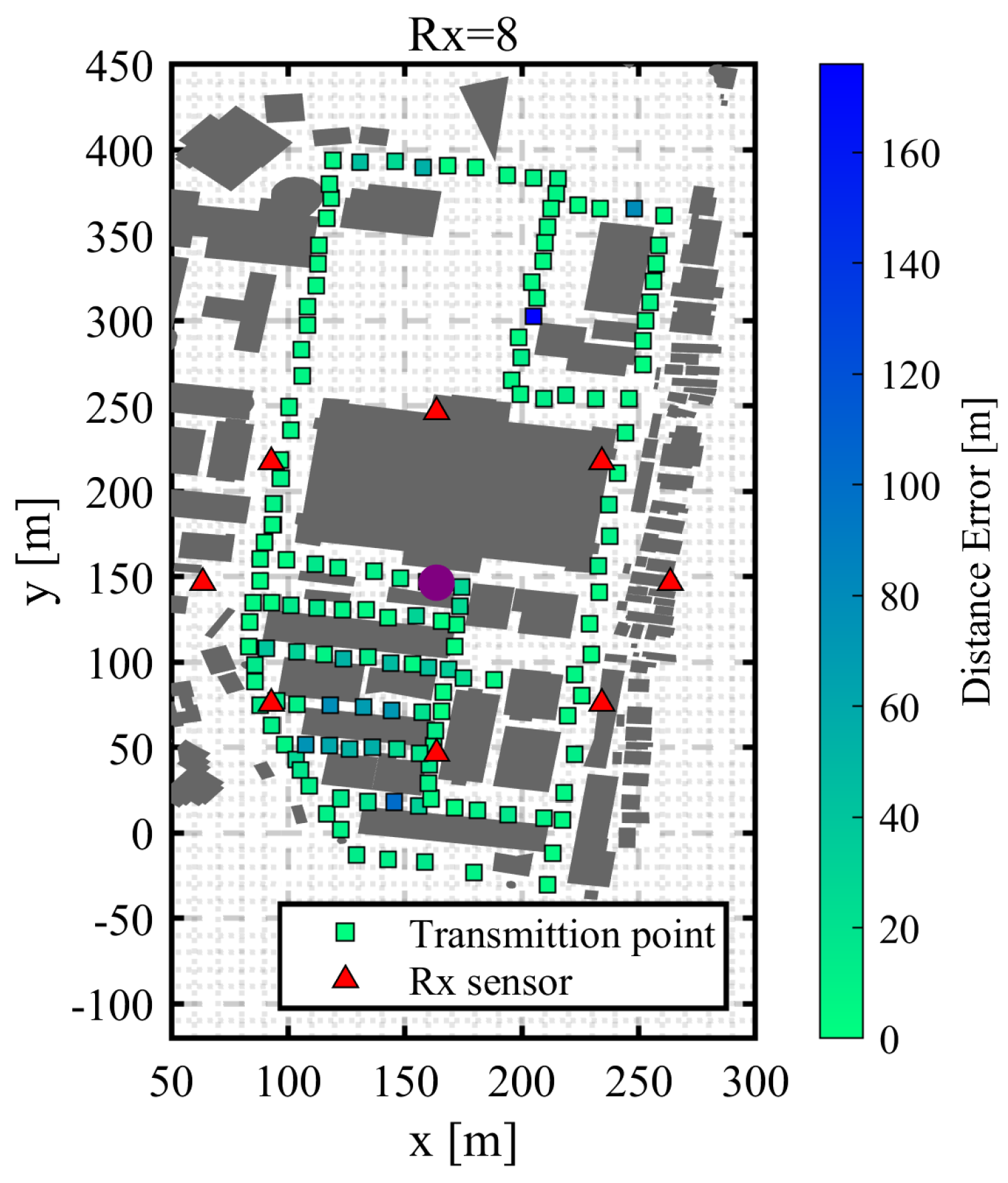
3.14. Computation and Evaluation of Estimation Error
3.15. Sequential Estimation Model
4. Results
4.1. Circular Trajectory Placement with a Radius of 100 m
4.1.1. Using Only RSSI
4.1.2. Using Only AOA
4.1.3. Hybrid
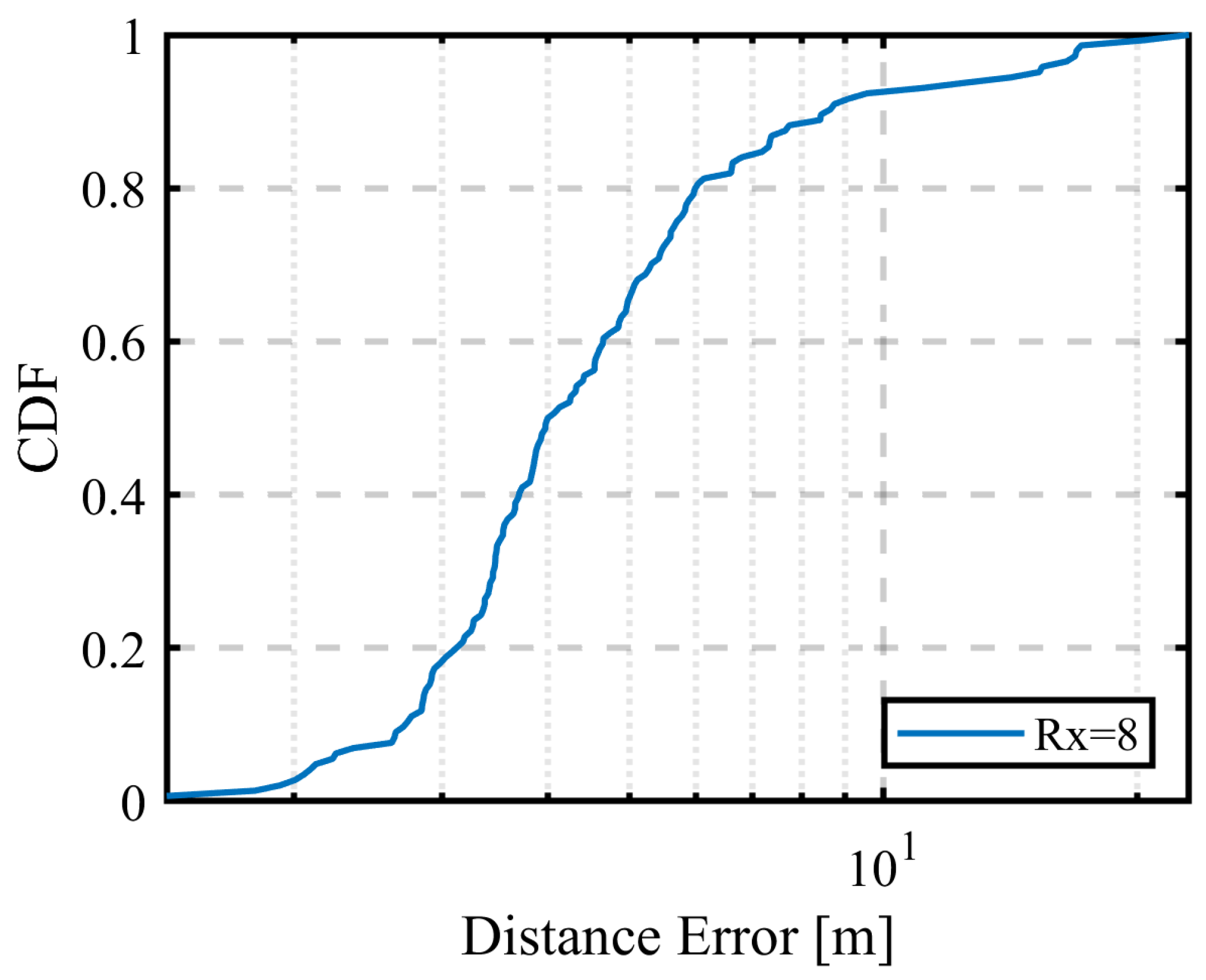
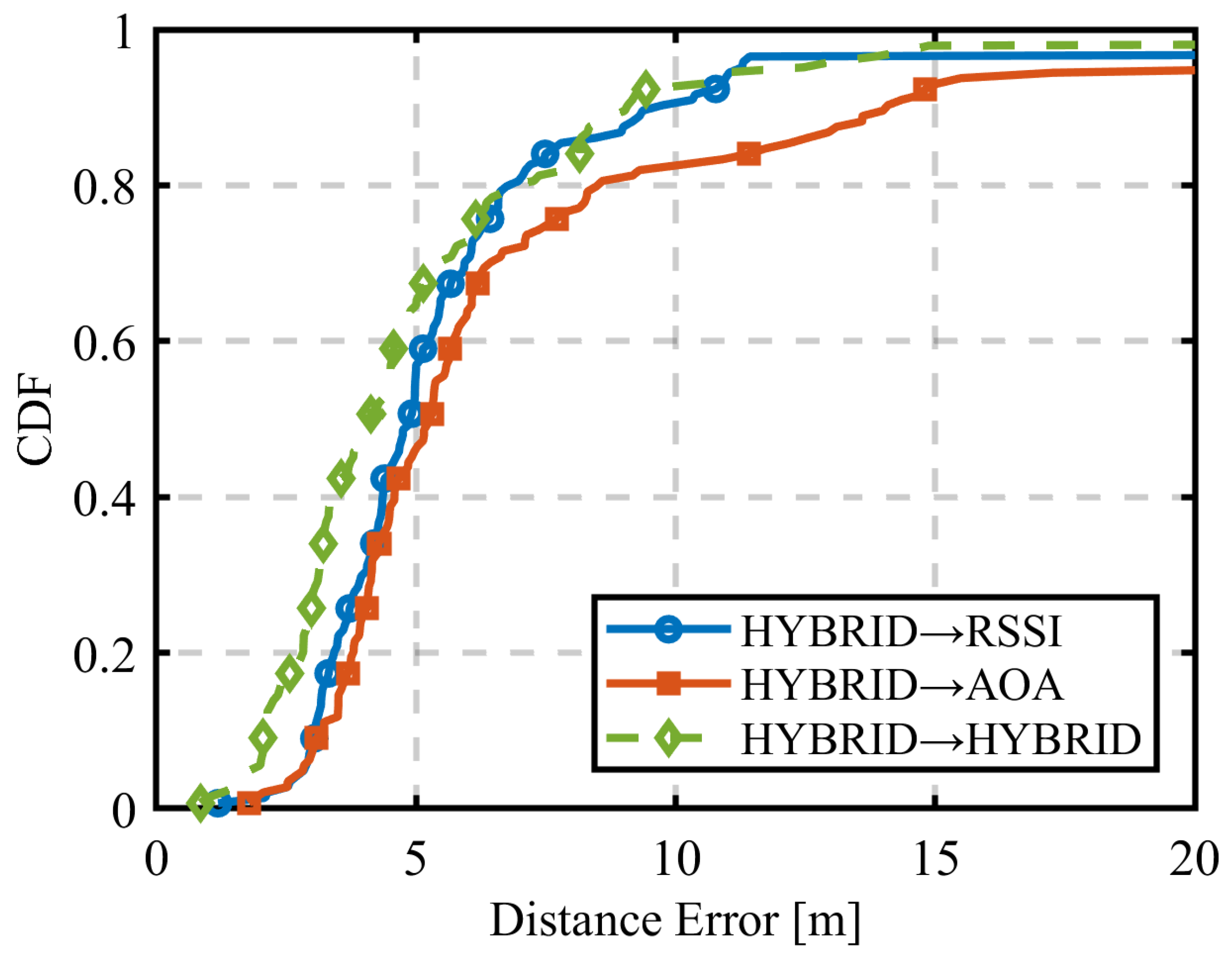
4.1.4. Comparison of RSSI, AOA, and HYBRID Results
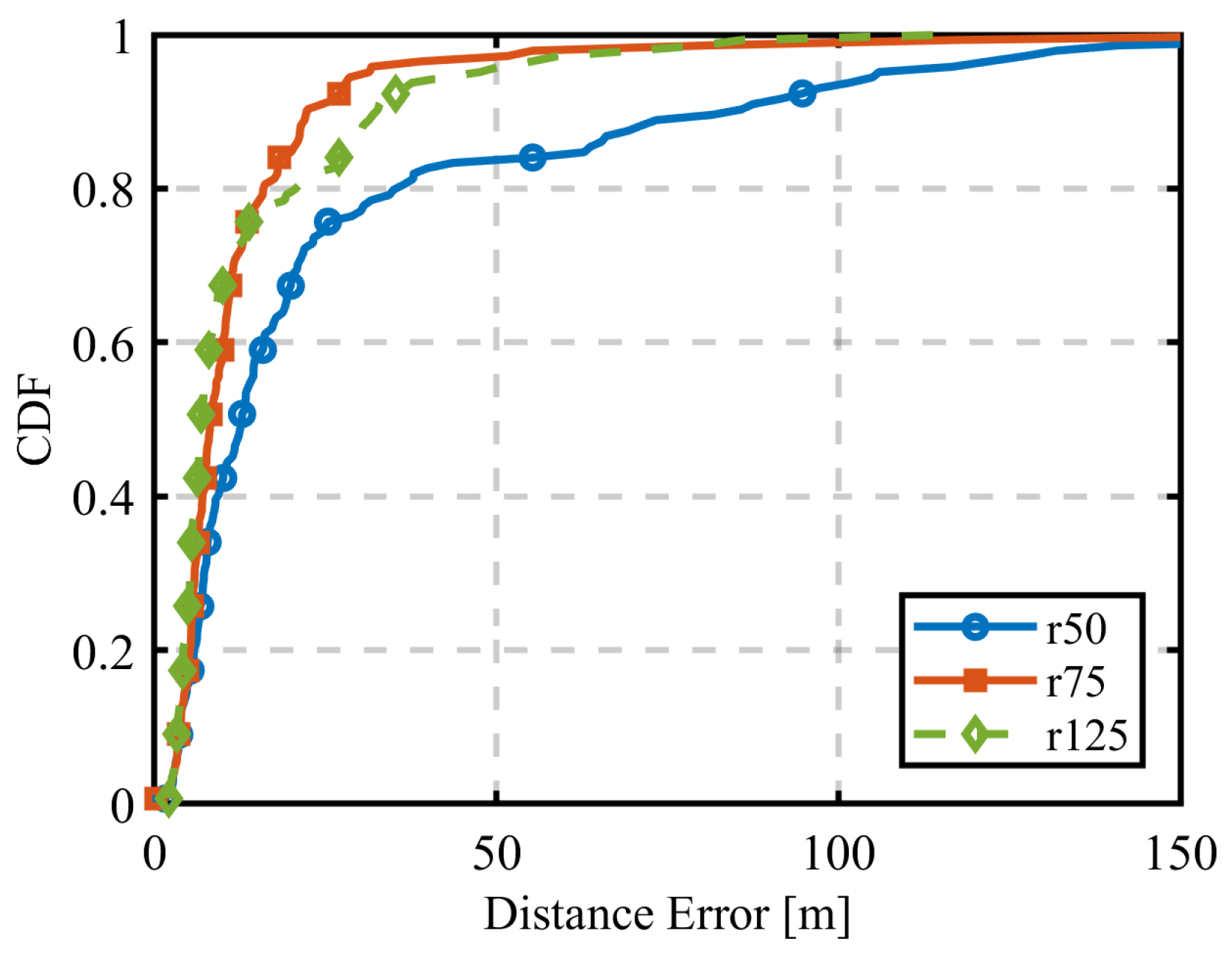
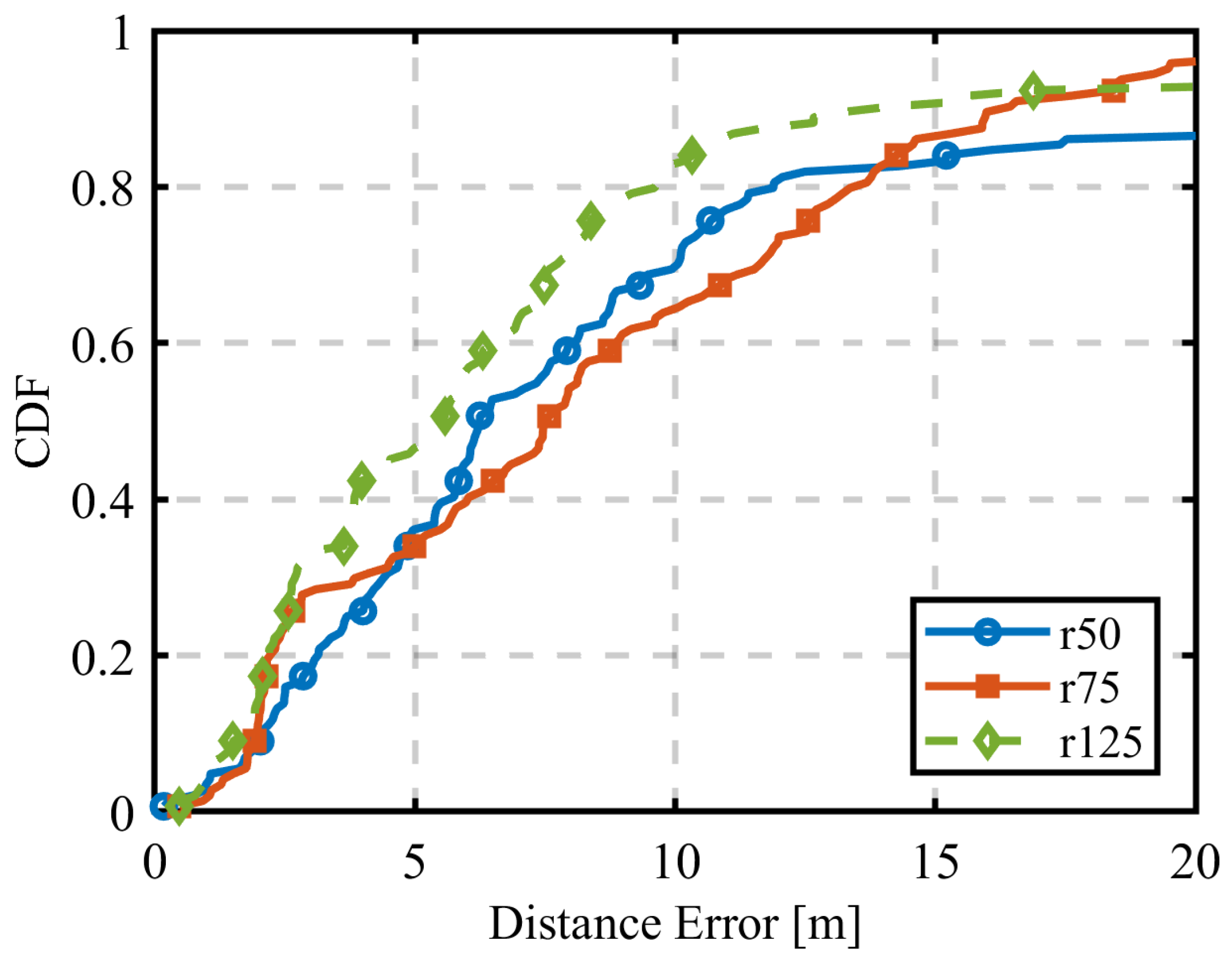
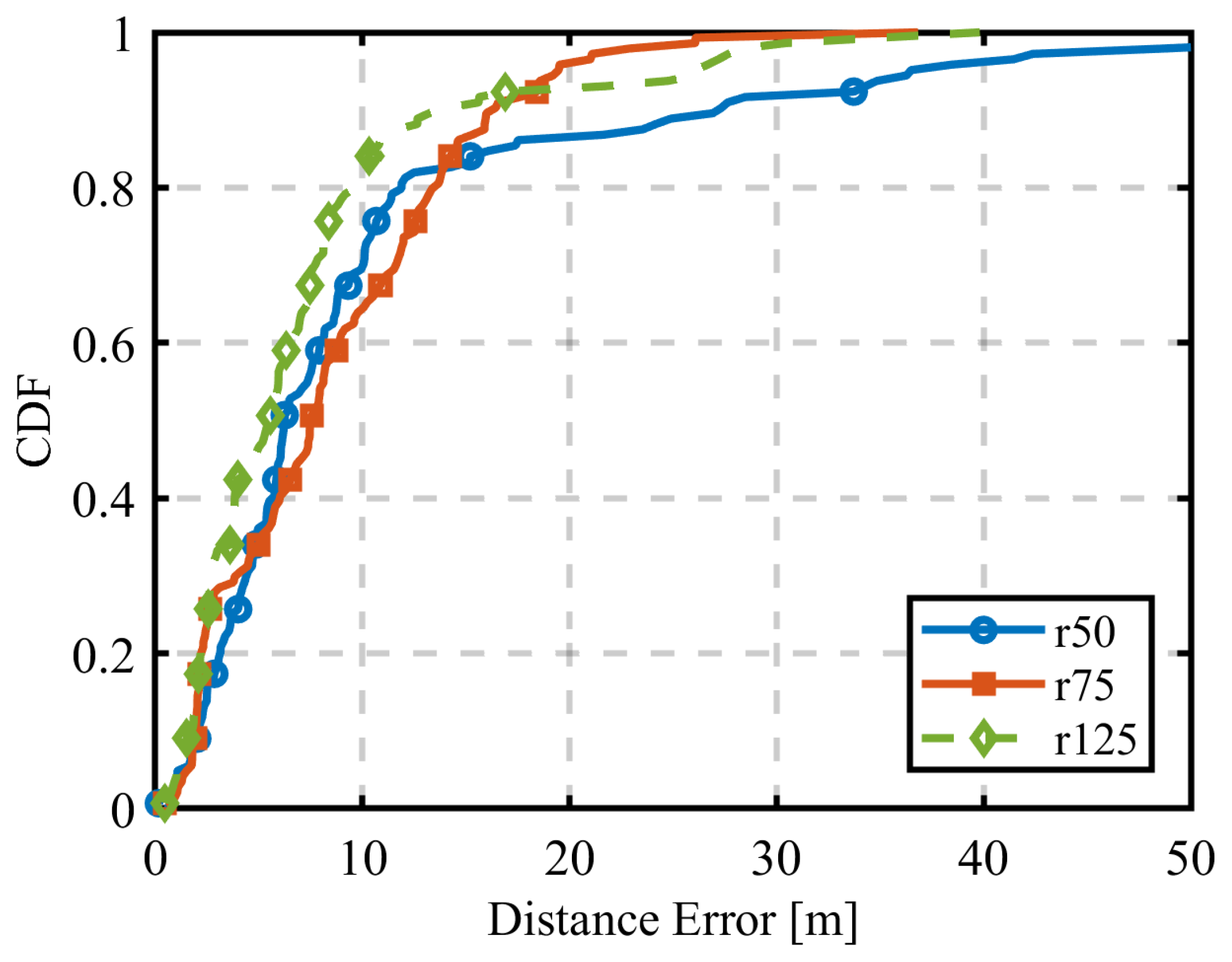
4.2. Circular Trajectory Placement with Varying Radius
4.3. Sequential Estimation
4.3.1. Results for the First Estimation Using RSSI
4.3.2. Results for the First Estimation Using AOA
4.3.3. Results for the First Estimation Using HYBRID
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ministry of Internal Affairs and Communications, Japan. Latest Trends in Radio Policy. Available online: https://www.soumu.go.jp/main_content/000932571.pdf (accessed on 17 March 2025).
- Ministry of Internal Affairs and Communications, Japan. Overview of Illegal Radio Station Countermeasures. Available online: https://www.tele.soumu.go.jp/j/adm/monitoring/summary/ad_pro/index.htm (accessed on 17 March 2025).
- Tan, J.; Zhao, H. UAV Localization with Multipath Fingerprints and Machine Learning in Urban NLOS Scenario. In Proceedings of the 2020 IEEE 6th International Conference on Computer and Communications (ICCC), Chengdu, China, 11–14 December 2020; pp. 1551–1557. [Google Scholar] [CrossRef]
- He, S.; Chan, S.-H.G. Wi-Fi Fingerprint-Based Indoor Positioning: Recent Advances and Comparisons. IEEE Commun. Surv. Tutor. 2015, 18, 466–490. [Google Scholar] [CrossRef]
- Murata, S.; Matsuda, T.; Hiraguri, T. Multiple-wave source localization using UAVs in NLOS environments. IEICE Commun. Express ComEX 2020, 13, 375–378. [Google Scholar] [CrossRef]
- Zhou, L.; Ning, X.; You, M.Y.; Zhang, R.; Shi, Q. Robust Multi-UAV Placement Optimization for AOA-Based Cooperative Localization. IEEE Trans. Intell. Veh. 2024; 1–15, Early Access. [Google Scholar] [CrossRef]
- Azari, A.; Ghavimi, F.; Ozger, M.; Jantti, R.; Cavdar, C. Machine Learning assisted Handover and Resource Management for Cellular-Connected Drones. In Proceedings of the 2020 IEEE 91st Vehicular Technology Conference (VTC2020-Spring), Antwerp, Belgium, 25–28 May 2020. [Google Scholar]
- Kamei, T. Investigation on Outdoor Positioning Using Fingerprinting Method and UAV Flight Path Optimization. Master’s Thesis, Tokyo Institute of Technology, Tokyo, Japan, 2022. [Google Scholar]
- Fujita, N.; Chauvet, N.; Röhm, A.; Horisaki, R.; Li, A.; Hasegawa, M. Efficient Pairing in Unknown Environments: Minimal Observations and TSP-Based Optimization. IEEE Access 2022, 10, 57630–57640. [Google Scholar] [CrossRef]
- Tanaka, S. Study on Sensor Placement for Outdoor Radio Source Localization Using UAVs. Master’s Thesis, Tokyo Institute of Technology, Tokyo, Japan, 2020. [Google Scholar]
- Thomas, T.; Vook, F.; Mellios, E.; Hilton, G.S.; Nix, A.R.; Visotsky, E. 3D Extension of the 3GPP/ITU Channel Model. In Proceedings of the IEEE Vehicular Technology Conference (VTC Spring), Dresden, Germany, 2–5 June 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Zhang, R.; Lu, X.; Zhao, J.; Cai, L.; Wang, J. Measurement and Modeling of Angular Spreads of 3D Urban Street Channels. IEEE Trans. Veh. Technol. 2017, 66, 3555–3570. [Google Scholar] [CrossRef]
- Tran, G.K.; Kamei, T.; Tanaka, S. Route Optimization of Unmanned Aerial Vehicle Sensors for Localization of Wireless Emitters in Outdoor Environments. Network 2023, 3, 326–342. [Google Scholar] [CrossRef]
- Holis, J.; Pechac, P. Elevation Dependent Shadowing Model for Mobile Communications via High Altitude Platforms in Built-up Areas. IEEE Trans. Antennas Propag. 2008, 56, 1078–1084. [Google Scholar] [CrossRef]
- Gu, Y.; Lo, A.; Niemegeers, I. A Survey of Indoor Positioning Systems for Wireless Personal Networks. IEEE Commun. Surv. Tutor. 2009, 11, 13–32. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Shimizu, Y. Introduction to Optimization Engineering: A Smart Decision-Making Workbench; Corona Publishing Co.: San Antonio, TX, USA, 2010. [Google Scholar]
- Chuku, N.; Nasipuri, A. RSSI-Based Localization Schemes for Wireless Sensor Networks Using Outlier Detection. J. Sens. Actuator Netw. 2021, 10, 10. Available online: https://www.mdpi.com/2224-2708/10/1/10 (accessed on 17 March 2025). [CrossRef]
- Nanos, N.; Isik, O.K.; Verdeguer Moreno, R.; Petrunin, I.; Tsourdos, A. UAV Path Planning Optimization based on GNSS Quality and Mission Requirements. In AIAA Scitech 2021 Forum; ARC: Kent, UK, 2021. [Google Scholar] [CrossRef]
- Le, A.T.; Tran, L.C.; Huang, X.; Ritz, C.; Dutkiewicz, E.; Phung, S.L.; Bouzerdoum, A.; Franklin, D. Unbalanced Hybrid AOA/RSSI Localization for Simplified Wireless Sensor Networks. Sensors 2020, 20, 3838. [Google Scholar] [CrossRef] [PubMed]
- Dhital, A.; Closas, P.; Fernández-Prades, C. Bayesian Filtering for Indoor Localization and Tracking in Wireless Sensor Networks. EURASIP J. Wirel. Commun. Netw. 2012, 2012, 21. [Google Scholar] [CrossRef]
- Yu, J.; Feng, Z.; Wang, J.; Zhang, P. Sequential Localization of Wireless Transmitters with UAVs Using Gaussian Processes. In Proceedings of the 2021 IEEE Global Communications Conference (GLOBECOM), Madrid, Spain, 7–11 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Qiu, M.; Liu, B. Multi-Sensor Adaptive Weighted Data Fusion Based on Biased Estimation. Sensors 2024, 24, 3275. [Google Scholar] [CrossRef] [PubMed]












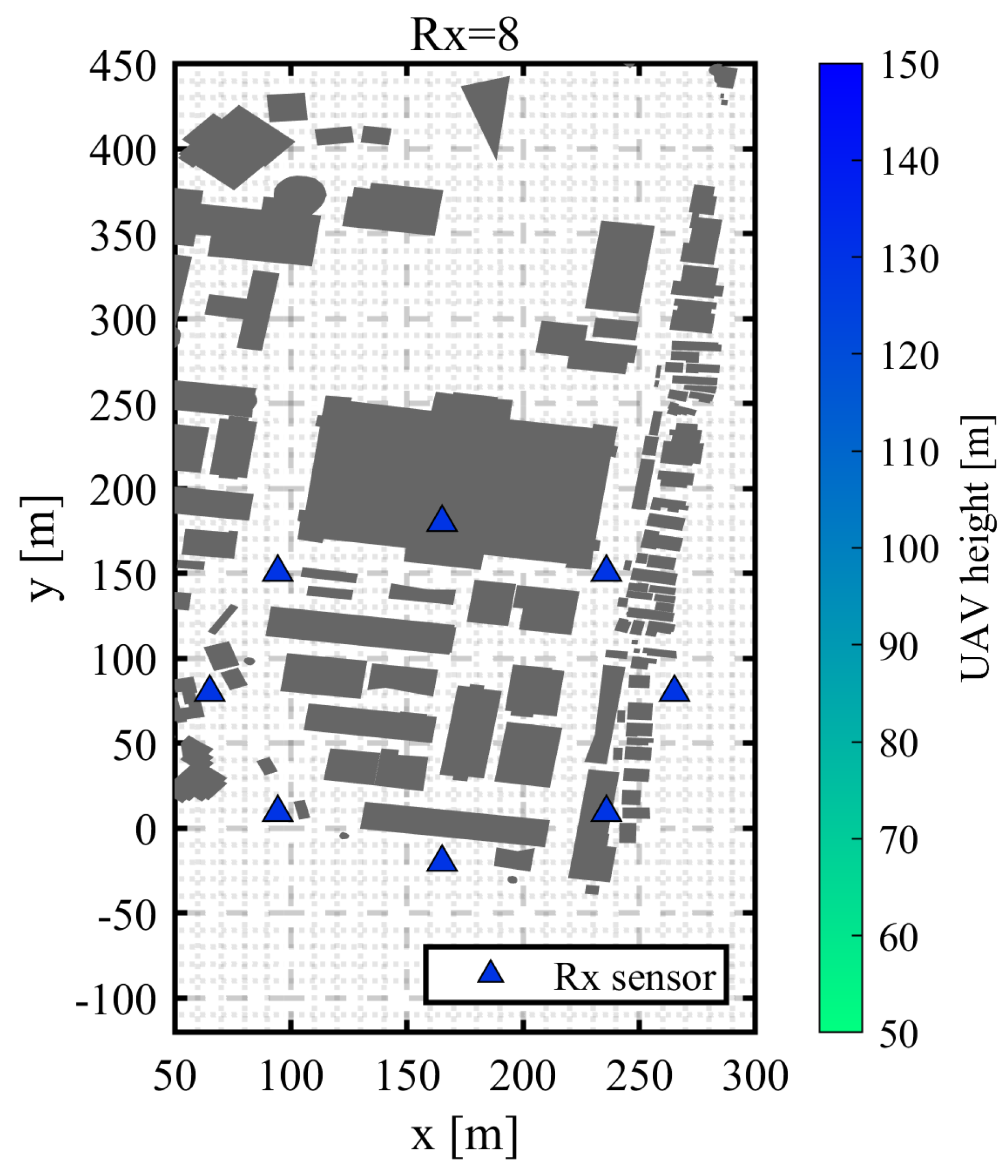
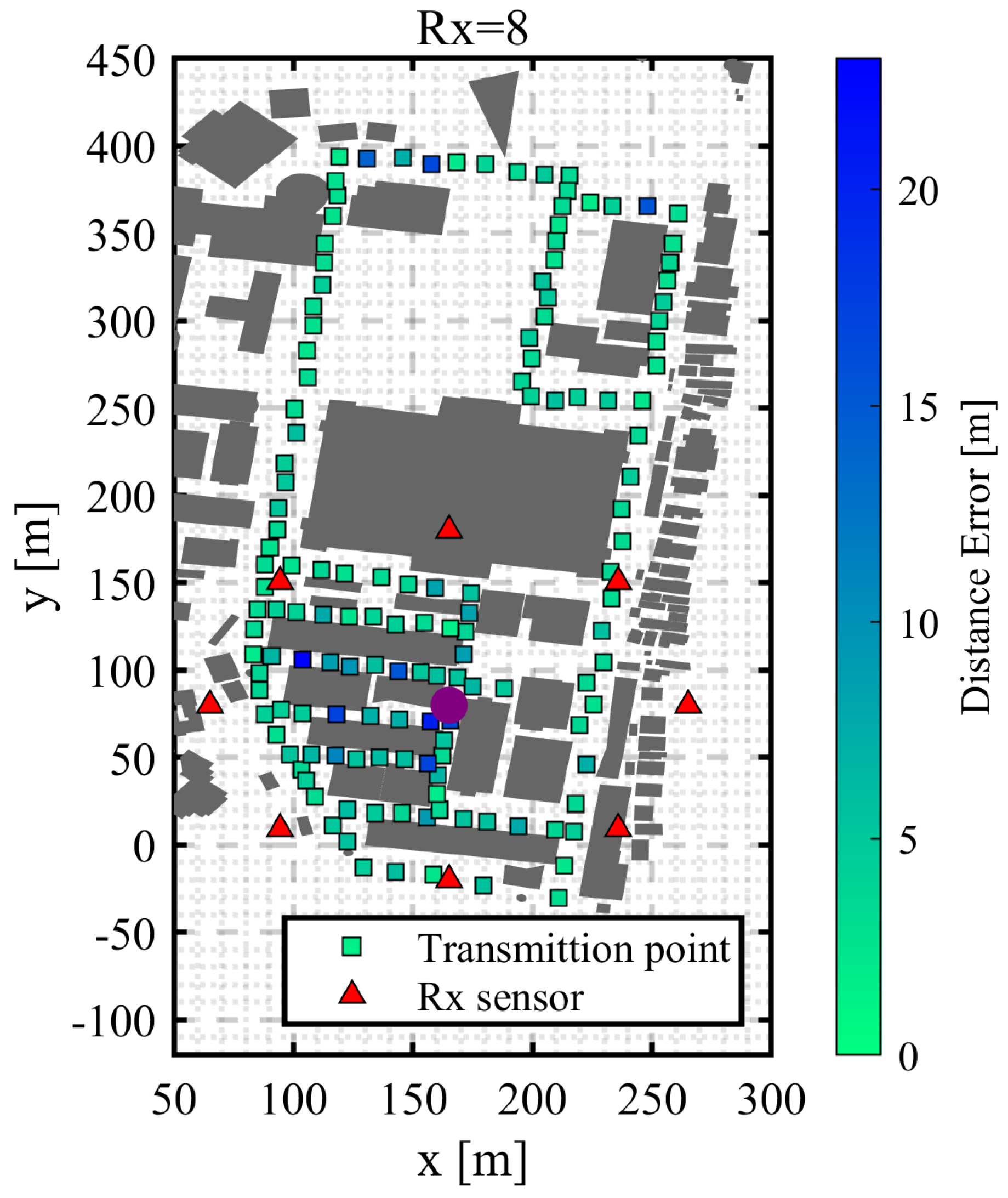



| Item | Value |
|---|---|
| Model | 3D (Ray launching) |
| Frequency [GHz] | 2.487 |
| Bandwidth [MHz] | 5.00 |
| Number of Reflections | 6 |
| Number of Diffractions | 1 |
| Number of Transmissions | 0 |
| Rx | Antenna Type: Isotropic |
| Height [m]: 50/75/100/125/150 | |
| Antenna Gain [dBi]: 2.0 | |
| Tx | Antenna Type: Isotropic |
| Transmission Power [dBm]: 27 |
| Parameters | Values |
|---|---|
| Initial position , Initial velocity | |
| w | 0.5 |
| Number of particles | 100 |
| 10 |
| Radio Signal Information | Mean Error [m] | CDF 90% Value [m] |
|---|---|---|
| RSSI | 16.4 | 41.9 |
| AOA | 7.5 | 14.8 |
| HYBRID | 5.3 | 8.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takahashi, T.; Tran, G.K. Research on Advancing Radio Wave Source Localization Technology Through UAV Path Optimization. Future Internet 2025, 17, 224. https://doi.org/10.3390/fi17050224
Takahashi T, Tran GK. Research on Advancing Radio Wave Source Localization Technology Through UAV Path Optimization. Future Internet. 2025; 17(5):224. https://doi.org/10.3390/fi17050224
Chicago/Turabian StyleTakahashi, Tomoroh, and Gia Khanh Tran. 2025. "Research on Advancing Radio Wave Source Localization Technology Through UAV Path Optimization" Future Internet 17, no. 5: 224. https://doi.org/10.3390/fi17050224
APA StyleTakahashi, T., & Tran, G. K. (2025). Research on Advancing Radio Wave Source Localization Technology Through UAV Path Optimization. Future Internet, 17(5), 224. https://doi.org/10.3390/fi17050224






