Abstract
Adaptive educational systems are essential for addressing the diverse learning needs of students by dynamically adjusting instructional content and user interfaces (UI) based on real-time performance. Traditional adaptive learning environments often rely on static fuzzy logic rules, which lack the flexibility to evolve with learners’ changing behaviors. To address this limitation, this paper presents an adaptive UI system for educational software in Java programming, integrating fuzzy logic and reinforcement learning (RL) to personalize learning experiences. The system consists of two main modules: (a) the Fuzzy Inference Module, which classifies learners into Fast, Moderate, or Slow categories based on triangular membership functions, and (b) the Reinforcement Learning Optimization Module, which dynamically adjusts the fuzzy membership function thresholds to enhance personalization over time. By refining the timing and necessity of UI modifications, the system optimizes hints, difficulty levels, and structured guidance, ensuring interventions are neither premature nor delayed. The system was evaluated in educational software for Java programming, with 100 postgraduate students. The evaluation, based on learning efficiency, engagement, and usability metrics, demonstrated promising results, particularly for slow and moderate learners, confirming that reinforcement learning-driven fuzzy weight adjustments significantly improve adaptive UI effectiveness.
1. Introduction
Modern educational software plays a crucial role in creating individual learning experiences, which allow each student to learn their own way. In contrast, traditional learning environments fail to accommodate individual differences. As a result, some of the learners face frustration, while others are not challenged at all [1]. Adaptive educational systems address this issue by adapting content, levels of challenge, and feedback continually based on students’ interactions with the system [2]. Such systems adapt the learning to the individual to improve engagement, motivation, and ultimately learning. For example, in programming courses, adaptivity is essential, as students progress at different speeds and require different degrees of support and challenge [3]. If a system can observe how a student interacts during their learning/exercises and includes an intelligent feedback mechanism that can respond based on those actions, it can optimize the information provided and ideally ensure that exercises remain challenging enough but then provide support if needed.
In educational software, the user interface is not only visual design, but it also includes interactive elements that directly impact learning [4]. A well-designed adaptive UI can modify content presentation based on student performance, thus enhancing both ease of use and instructional efficacy. In addition to colors and layouts, the interface incorporates adaptive hints that show up or go away depending on student need and difficulty level adjustments that introduce more difficult challenges if students are performing well [5]. It also includes step-by-step guidance that offers greater assistance to struggling students, interactive feedback such as tooltips or highlighted mistakes, and layout features that highlight critical information and remove distractions [6]. These UI adaptations are used to foster the overall interaction in such a way that it is not only visually accessible but also pedagogically sound [7]. A well-constructed adaptive user interface guarantees the appropriate amount of support and challenge, providing opportunities for pupils to solve problems independently without risking frustration or disconnection when the material becomes too hard.
Artificial intelligence methods have gained a lot of interest lately due to the fact that they allow educational software to evaluate the effectiveness of learning methods in real-time and adapt instruction dynamically [8]. One effective approach is the use of fuzzy logic, which provides a way to handle uncertainty and imprecise data, which is common in human learning [9]. Fuzzy weights allow the system to make decisions about adapting the UI by modeling student engagement, performance, and response time. Instead of applying rigid rules that classify students into strict categories, fuzzy weights make it possible to assess learning behavior on a spectrum, allowing for more gradual and personalized adjustments. This means that the system does not assume, for example, that if a student spends a long time on an exercise, he or she is having trouble, but rather uses fuzzy logic to suggest that a student who takes an inordinate amount of time is “probably” having difficulties and acts on that assumption. This adaptive approach makes educational software more intelligent, user-friendly, and supportive without over-intervening.
While fuzzy weights improve adaptivity, static fuzzy rules may not always provide optimal support for every student [10]. Since learners’ behaviors change over the course of learning, this means existing adaptation mechanisms need to be improved continuously. A fuzzy weighted system based on predetermined conditions and goals fails to capture the changing learning status of students [11]. Dynamic adjustment of fuzzy weights, informed by real-time student performance, ensures that the system improves its predictions and responses [12]. By continuously refining adaptation thresholds, the system personalizes the learning experience, making UI modifications more relevant to each individual. Without this capability, either students would receive help too early, limiting their challenge, or they must endure struggle too long before the system steps in. The ability to dynamically adjust fuzzy weights facilitates adaptive learning that balances lesson difficulty and lesson support according to student learning.
While fuzzy logic and reinforcement learning have been independently applied in adaptive educational systems, prior work (e.g., [11]) has often relied on static fuzzy rules or focused on broad content-level adaptation. These approaches lack the flexibility to dynamically adjust user interface components in real time based on evolving student behavior.
This study addresses that gap by proposing a novel combination of fuzzy inference and real-time reinforcement learning to continuously optimize the thresholds that govern UI adaptation. Rather than predefining when support should be shown or challenge increased, the system learns and refines these decisions during usage, resulting in more personalized and pedagogically appropriate UI modifications.
This approach offers a distinct contribution to adaptive learning research by enabling fine-grained, self-improving UI personalization, with direct application in programming education where timely, individualized support is crucial.
In view of the above, this paper presents an adaptive UI system for Java learning software that uses fuzzy logic with dynamically adjustable fuzzy weights. The system consists of two core modules: a Fuzzy Inference Module that uses triangular membership functions to classify students based on the time they spend on exercises and a Reinforcement Learning Optimization Module that dynamically adjusts fuzzy membership function thresholds. These modules work together to determine UI adaptations such as hints, difficulty levels, and step-by-step guidance. By incorporating reinforcement learning, the system continuously refines its adaptation logic, ensuring that students receive optimal support as they progress. This approach enhances engagement and learning efficiency, demonstrating the value of intelligent and dynamic UI adaptation in modern e-learning environments.
2. Related Work
Adaptive user interfaces (AUIs) have become increasingly important in educational technology, as they enable systems to personalize learning experiences by dynamically adjusting content, difficulty, and feedback based on user interactions. Unlike traditional static interfaces that provide the same experience to all learners, AUIs modify their behavior in response to real-time student performance, making the learning process more engaging and efficient [13]. Adaptive interfaces in educational settings have been used in intelligent tutoring systems, personalized e-learning systems, and game-based learning, using the user behavior data to improve the learning experience [14]. An important feature of these interfaces is their ability to provide context-sensitive support, ensuring that students receive appropriate guidance at different stages of their learning journey. Using AUIs improves retention, motivation, and learning efficiency by eliminating cognitive load, preventing students from becoming either disengaged due to too much cognitive load or uninterested because of low challenge [15,16,17,18,19,20]. Various techniques have been used to implement AUIs, including rule-based systems, machine learning models, and reinforcement learning strategies. However, a significant challenge is to determine how best to model learner behavior and dynamically adjust interface components without having to use static heuristics.
Fuzzy logic has been widely applied in educational software as an effective way to handle uncertainty and subjectivity in learning environments [21]. Unlike traditional classification methods, fuzzy logic allows for gradual transitions between categories, making it particularly useful for modeling student behavior, where boundaries between learning stages are often ambiguous. One of the most notable applications of fuzzy logic in education is through fuzzy weights, which assign varying degrees of influence to different learning factors, such as time spent on exercises, error rates, engagement levels, and hint usage [22]. Using fuzzy weights, educational systems can more effectively determine when to intervene with assistance, when to increase difficulty, and when to provide additional feedback. Previous studies have demonstrated that incorporating fuzzy logic into adaptive learning environments leads to better decision-making in student assessment and content adaptation [23,24,25,26,27,28]. For example, fuzzy weights have been used in intelligent tutoring systems to determine when a student is struggling and needs step-by-step guidance versus when they are ready for independent problem-solving. Despite these benefits, many fuzzy-based educational systems rely on predefined static weight values, which may not optimally reflect changing student behaviors over time. As a result, mechanisms that can dynamically adjust fuzzy weights based on real-time learning patterns are needed.
Reinforcement learning (RL) has gained attention in educational software as a powerful method for optimizing adaptive learning environments [29]. Unlike supervised learning, where models are trained on labeled data, RL allows a system to learn optimal behaviors through continuous interaction with the user. RL has been applied in intelligent tutoring systems to personalize learning paths, recommend educational resources, and optimize problem difficulty [30]. Studies have shown that RL-based adaptation improves learning outcomes by enabling software to gradually refine its strategies based on direct feedback from student interactions [31,32,33,34,35,36]. In particular, RL has been used to adjust the sequencing of exercises, predict when a learner is ready for more advanced topics, and optimize feedback delivery to maximize engagement. Some implementations of RL in education focus on content adaptation, where the system selects the most appropriate learning materials based on past user performance, while others emphasize pedagogical decision-making, adjusting instructional strategies based on learning efficiency. However, one of the challenges of RL in education is defining appropriate reward functions and ensuring that the system’s adaptations are pedagogically meaningful [37]. Many RL-based systems optimize broad learning outcomes but do not fine-tune individual user interface elements, such as hints, guidance, and difficulty adjustments, which are critical for personalized learning.
While both fuzzy logic and reinforcement learning have been explored separately in educational contexts, relatively few studies have focused on dynamic fuzzy weight adjustment using RL [38]. Fuzzy weight adjustment in education aims to refine how adaptive systems make decisions by continuously updating fuzzy membership functions based on real-time student behavior [39]. In conventional fuzzy logic applications, membership functions and weight parameters are often manually set by experts, requiring prior assumptions about student behavior that may not always be accurate. Dynamic fuzzy weight adjustment, however, allows these parameters to evolve based on actual user interactions, making the adaptation process more data-driven. Some research has explored hybrid fuzzy-RL approaches, where RL optimizes the pedagogical strategy, but fewer works have directly integrated RL for the fine-grained adjustment of fuzzy weights in adaptive UI elements [40,41,42,43,44,45]. This integration is crucial because the thresholds that determine when a UI adaptation occurs (such as when hints appear or difficulty increases) need continuous refinement to remain effective for different learners.
Compared with previous research, this work differs by introducing a reinforcement learning-driven approach for dynamically adjusting fuzzy weights in adaptive user interfaces. Instead of using static membership functions and manually assigned fuzzy weights, the proposed system learns over time by optimizing when UI modifications should take place. Unlike prior fuzzy-based educational systems, where intervention strategies are predefined and remain fixed, this work ensures that thresholds for UI adaptation change based on actual learning behavior. Additionally, while reinforcement learning has been applied to educational content sequencing and recommendation, the use of RL specifically to directly optimize each type of UI-specific adaptation, such as hint display, step-by-step guidance, and difficulty adaptation, has not been attempted before. The integration of fuzzy logic and reinforcement learning in this way enables a more flexible, personalized, and continuously improving learning experience, making adaptive user interfaces more effective and responsive in educational software.
3. System Architecture
The proposed system consists of two main modules, namely the Fuzzy Inference Module and the Reinforcement Learning Optimization Module. These modules work together to create an adaptive user interface (UI) tailored to individual learning behaviors. In particular, the Fuzzy Inference Module is responsible for classifying students into different performance categories based on the time they spend on exercises, using triangular membership functions. As such, it assigns fuzzy weights that determine the level of UI adjustments needed. However, in order to overcome the limitation of the static fuzzy logic system to adjust to real-time variations in student behavior, the Reinforcement Learning Optimization Module is utilized to continuously refine the membership function thresholds. Thus, this ensures that fuzzy weights remain accurate and responsive to individual learning patterns. Together, these two modules allow the UI to dynamically adapt, providing a more effective learning experience that modifies hints, guidance, and difficulty levels in a way that best supports the learner. Figure 1 illustrates the system’s architecture.
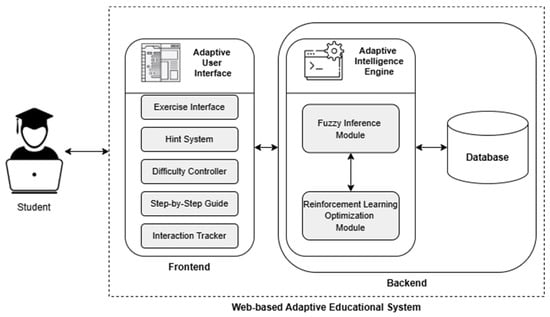
Figure 1.
System architecture.
3.1. Fuzzy Inference Module
The Fuzzy Inference Module is responsible for analyzing the time students spend on exercises and determining how the user interface should adapt based on this behavior. Unlike traditional binary classification approaches, which would set a strict time threshold to classify learners, fuzzy logic allows for gradual transitions between different learner types. This means that instead of rigidly categorizing a student as either “fast” or “slow”, the system assigns a degree of membership to each category, ensuring a more flexible and adaptive response.
The classification is based on triangular membership functions, which define the Fast, Moderate, and Slow learner categories. These categories are determined by three key thresholds:
- Tlow—the maximum time a fast learner is expected to complete an exercise.
- Tmid—the ideal time for a moderate learner to complete an exercise.
- Tmax—the threshold beyond which a student is classified as slow.
Each student is classified into one or more categories using triangular membership functions. The function for each category gradually increases or decreases based on time spent on an exercise.
Students who complete an exercise in a short amount of time are considered fast learners. However, the classification is not absolute—a student just above Tlow still retains partial membership in the fast category.
where:
- x1 is the time spent on an exercise.
- Membership value decreases gradually from 1 (certain fast learner) to 0.
A student who spends less than Tlow minutes on an exercise is fully classified as a fast learner (μA11(x1) = 1).
A student who takes more than Tmid minutes is no longer considered fast (μA11(x1) = 0).
Moderate learners fall in a transition zone between fast and slow learners. The function peaks at Tmid, meaning that students spending exactly this amount of time on an exercise are most strongly classified as moderate learners.
The moderate category has a symmetrical shape around Tmid, meaning that students just below or just above this value still partially belong to this group. This ensures that students who are slightly slower or faster than expected are not abruptly reclassified.
Students who spend significantly more time on an exercise belong to the slow learner category. However, membership gradually increases instead of being assigned abruptly.
- A student spending more than Tmax minutes on an exercise is fully classified as slow.
- A student just above Tmid is partially classified as slow, ensuring a smooth transition.
The values of Tlow, Tmid, and Tmax are set based on educational research and empirical observations. Typical learners exhibit different problem-solving speeds, and these thresholds allow for a reasonable classification of students [46] (Table 1).

Table 1.
Learners’ problem-solving speeds.
These values are not static. While they provide an initial guideline, they are later adjusted dynamically using reinforcement learning to better reflect real-world student behavior.
Each student is assigned fuzzy weights based on their membership values in the three categories.
- A student strongly classified as fast will have and very low values for w12 and w13.
- A moderate learner will have a dominant w12, with some influence from w11 and w13.
- A slow learner will have a high w13 and near-zero w11.
3.2. Reinforcement Learning Optimization Module
The Reinforcement Learning Optimization Module is responsible for dynamically adjusting the fuzzy membership function thresholds to ensure that the classification of students as Fast, Moderate, or Slow learners remains accurate over time. Unlike a static fuzzy logic system where thresholds (Tlow, Tmid, and Tmax) are predefined and fixed, this module enables the system to evolve based on student behavior, ensuring a more personalized learning experience.
By applying Reinforcement Learning (RL), the system continuously evaluates the effectiveness of UI adaptations and modifies the fuzzy membership thresholds accordingly. This ensures that fuzzy weights remain relevant to different learning speeds rather than using manually defined parameters that may not generalize well across learners.
The RL agent’s goal is to optimize the classification boundaries of the Fuzzy Inference Module so that adaptive UI modifications occur at the right time. The agent operates in an episodic environment, where each episode corresponds to a student’s session interacting with the educational software.
The state of the environment at any time step t is represented as follows:
where:
- is the time spent on an exercise at time t.
- are the current fuzzy membership thresholds at time t.
The action space consists of modifications to these thresholds:
Each action adjusts the fuzzy logic membership functions by increasing or decreasing the values of the thresholds, allowing the system to refine when UI adaptations occur.
At any time step, the agent of RL chooses an action, At, to adjust the fuzzy membership thresholds. The goal is to optimize UI interventions, ensuring that students receive help when needed but not too soon or too late.
The action space is discrete and defined as follows:
where each action modifies one of the fuzzy membership thresholds by a small (±0.5) or large (±1.0) adjustment. These specific increment values were selected based on the scale of the fuzzy input domain (0–20 min), ensuring that adjustments are large enough to be meaningful but small enough to avoid instability. The ±0.5 step enables fine-tuning when thresholds are close to optimal, while ±1.0 allows for quicker adaptation when greater deviations are needed. This design was informed by pilot testing and ensures a practical balance between precision and convergence speed.
The RL agent employs an ε-greedy policy to achieve a balance between exploration and exploitation:
- The parameter ε represents the probability that the agent chooses a random action to encourage exploration.
- The parameter 1 − ε is the probability that it selects the action that maximizes the expected future rewards, promoting exploitation.
To guide the RL agent, a reward function Rt is designed to ensure that fuzzy weight adjustments lead to improved learning experiences. The reward function consists of four main components:
where:
- Tbefore and Tafter: Measure learning efficiency improvement (time spent before and after fuzzy threshold adjustments).
- U: Represents user engagement and performance-based feedback, which can be implicit (e.g., improvement in performance) or explicit (e.g., a satisfaction rating).
- : Penalizes excessive changes in fuzzy membership functions, ensuring stability in adaptation.
- H: Introduces a hint usage penalty, which discourages excessive reliance on system-provided hints while ensuring timely and appropriate assistance.
The reward function is designed to:
- Encourage actions that improve learning efficiency by minimizing unnecessary UI interventions.
- Maximize student engagement by ensuring timely assistance.
- Prevent unstable UI adjustments by discouraging large, frequent changes to fuzzy thresholds.
- Reduce over-reliance on hints by penalizing unnecessary hint activation, ensuring that students receive guidance only when needed and do not become dependent on system-generated hints.
The RL agent updates its policy using Q-learning, which allows it to refine its decisions over multiple student interactions. The Q-value update equation is expressed as follows:
where:
- η is the learning rate, which controls how rapidly the agent updates its knowledge.
- γ is the discount factor, which defines the significance of future rewards.
- is the best possible Q-value at the next state.
In this equation, η controls the learning rate, while γ governs the importance of future rewards. Over time, the Q-table is iteratively updated, allowing the agent to develop an optimal strategy for adjusting fuzzy weights dynamically.
The initial fuzzy membership parameters (Tlow, Tmid, Tmax) were empirically set to reflect time-based patterns observed during a pilot phase with 20 students prior to the main experiment. These values were selected to roughly correspond to the 25th, 50th, and 75th percentiles of completion times across typical Java exercises. This ensured that the fuzzy categories (Fast, Moderate, and Slow) represented meaningful distinctions in learner pacing.
For the reinforcement learning setup, the learning rate η was set to 0.2 to balance learning speed with stability, while the discount factor γ was fixed at 0.8 to maintain sensitivity to long-term learning outcomes without overemphasizing distant rewards. These values were chosen based on recommendations from prior educational RL studies and validated through initial tuning experiments that monitored convergence and adaptation responsiveness.
The RL agent requires training before it can be effectively deployed. The training process involves simulating multiple student interactions and updating the Q-table accordingly.
The training loop consists of:
- Simulating a student’s interaction with an exercise (randomly generated time spent x1).
- Computing initial fuzzy weights based on the current membership functions.
- Applying UI modifications based on fuzzy weights.
- Observing student outcomes (e.g., Did they complete the next exercise faster? Did they need more assistance?).
- Computing the reward Rt based on engagement and learning improvement.
- Updating the Q-table using the Q-learning rule.
- Repeating for multiple student interactions until the policy converges.
The final trained RL agent learns when to modify fuzzy membership thresholds to improve UI adaptivity and optimize student learning experiences.
After training, the Reinforcement Learning Optimization Module directly impacts how fuzzy logic is applied by continuously refining Tlow, Tmid, and Tmax. Over multiple interactions, the RL agent fine-tunes the thresholds, ensuring that:
- Fast learners are not unnecessarily challenged too early.
- Moderate learners remain engaged without excessive UI changes.
- Slow learners receive help at the right moment.
Instead of manually setting the fuzzy membership function boundaries, the system evolves dynamically, making adaptive UI modifications more accurate over time.
Concluding, the Reinforcement Learning Optimization Module enhances the adaptability of the Fuzzy Inference Module by continuously refining fuzzy membership function thresholds. By learning from real-time student interactions, RL ensures that UI interventions remain timely and effective. The agent follows a Q-learning strategy, adjusting fuzzy weights dynamically based on learning efficiency, engagement, and student feedback. Over time, the system self-optimizes, providing a truly personalized learning experience that evolves with each user. Figure 2 shows the flow diagram of the overall functionality of the system.
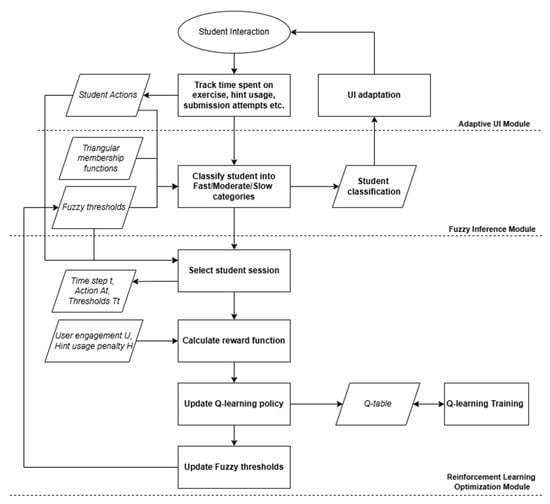
Figure 2.
Flow diagram of the system’s functionality.
4. Evaluation
To assess the effectiveness of the proposed adaptive user interface system, an evaluation was conducted with 100 postgraduate students who used the system as part of a structured Java programming course. The participants, aged between 23 and 50 years old, represented a diverse population with varying levels of prior programming experience, ranging from limited exposure to programming to intermediate proficiency in other languages before learning Java. The primary goal of this evaluation was to measure the impact of dynamically adjusted fuzzy weights and reinforcement learning-based optimization on student learning performance, engagement, usability, and overall effectiveness of the adaptive UI.
This study lasted six weeks, during which students completed programming exercises in an environment where UI changes (hints, difficulty adjustments, step-by-step guidance) were controlled by the Fuzzy Inference Module and continuously optimized by reinforcement learning. The evaluation aimed to determine whether the system effectively adapted to different learning speeds, providing meaningful interventions without disrupting the learning process.
The evaluation was conducted across multiple dimensions:
- Performance-Based Evaluation (measuring completion time, error rates, and success rates).
- Engagement and Interaction Tracking (analyzing UI interactions and hint requests).
- Usability Study (surveying students on system adaptability and UI effectiveness).
- Subjective User Feedback (gathering qualitative insights from participants).
These analyses provided a comprehensive understanding of how reinforcement learning and fuzzy logic interact to enhance learning experiences.
4.1. Experimental Setup
Each participant used the Java programming learning platform, where they had to complete a series of exercises designed to improve syntax, logic, debugging skills, and problem-solving abilities. The exercises had a gradual difficulty, ranging from basic syntax tasks to more complex algorithmic problems.
The system operated under two distinct phases:
- Phase 1 (Weeks 1–3): Students interacted with the system using predefined fuzzy weights, meaning UI adaptations were based on fixed threshold values (Tlow, Tmid, Tmax) that did not change dynamically.
- Phase 2 (Weeks 4–6): The Reinforcement Learning Optimization Module was activated, allowing the system to dynamically adjust fuzzy membership functions based on real-time learning behavior. This meant that thresholds evolved, ensuring that UI modifications (hints, guidance, and difficulty changes) became more personalized.
By comparing these two phases, we measured how reinforcement learning optimized the effectiveness of fuzzy weights over time, leading to a more adaptive and efficient learning experience.
4.2. Performance-Based Evaluation
To determine whether the adaptive system improved learning efficiency, we analyzed three key performance metrics:
- Time Spent on Exercises: How long students took to complete exercises before and after UI adjustments.
- Error Rate: The average number of incorrect submissions per exercise.
- Success Rate: The percentage of exercises successfully completed without requiring external help.
These metrics provided quantitative evidence of the system’s impact on learning effectiveness.
To strengthen the statistical reliability of the findings, each experiment was repeated five times with randomized session data per learner category (Fast, Moderate, and Slow). The reported values in Table 2, Table 3, Table 4 and Table 5 and Figure 1, Figure 2, Figure 3 and Figure 4 reflect the mean outcomes across these runs, accompanied by standard deviation to illustrate variability. This multi-run approach ensures that the observed improvements are consistent and not incidental, thereby providing more robust evidence of the system’s effectiveness.

Table 2.
Average time spent per exercise before and after reinforcement learning-based fuzzy weight adjustments.

Table 3.
Error rate reduction.

Table 4.
Success rate improvement.

Table 5.
Paired t-test results for performance metrics by learner category.
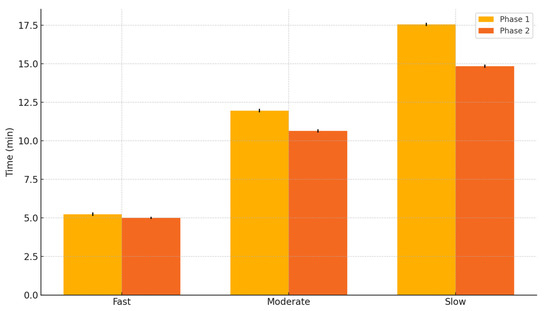
Figure 3.
Time spent on exercises before vs. after RL optimization.
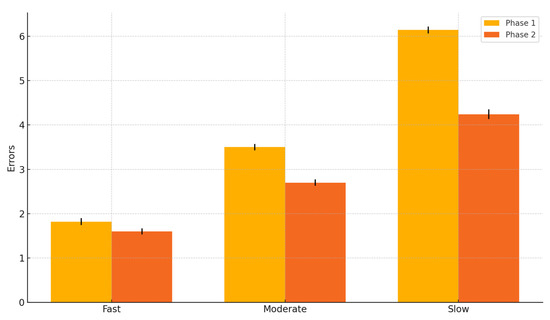
Figure 4.
Error rate reduction before vs. after RL optimization.
4.2.1. Analysis of Time Spent on Exercises
One of the primary goals of the adaptive system was to ensure that students completed exercises at an optimal pace—not too fast (indicating a lack of challenge) and not too slow (suggesting difficulty or frustration). Table 2 summarizes the average time spent per exercise before and after reinforcement learning-based fuzzy weight adjustments.
The data clearly show that slow learners benefited the most, with a 15.5% reduction in time spent per exercise, while moderate learners improved by 11.0% (Figure 3). Fast learners saw a minor 4.6% reduction, which suggests that the UI adaptation was more beneficial to students who initially struggled with exercises.
4.2.2. Error Rate Reduction
Reducing the number of incorrect submissions is a critical indicator of improved learning effectiveness. The system’s adaptive hints and difficulty adjustments were expected to help students minimize errors by providing timely support without making the exercises too easy, as seen in Table 3 and Figure 4.
The largest improvement was observed among slow learners, with a 30.9% reduction in errors, reinforcing the idea that adaptive UI elements significantly benefited struggling students.
4.2.3. Success Rate Improvement
One of the key indicators of the system’s effectiveness is the success rate, which refers to the percentage of exercises that students successfully completed without requiring external assistance, such as manual intervention from an instructor or searching for solutions online. A well-adapted learning environment should provide sufficient guidance to struggling students while maintaining an appropriate level of challenge for those who are progressing well.
In this study, success rate improvement is defined as the percentage of exercises completed successfully without requiring external assistance. However, it is necessary to clarify what qualifies as external assistance to ensure a precise interpretation of the results.
For the purposes of this evaluation, an exercise is considered successfully completed if the student does not require instructor intervention or external resource consultation, such as searching for solutions online. The use of system-generated hints is not considered external assistance, provided that the student does not exhibit excessive reliance on them.
To distinguish between independent learning and over-dependence on hints, a threshold was applied:
- If a student used hints for less than 30% of the exercise duration, the attempt was still considered successful, as minimal guidance can reinforce learning without compromising problem-solving abilities.
- If hints were used excessively (more than 30% of the session) or if instructor intervention was required, the attempt was not counted as a successful independent completion.
By comparing Phase 1 (static fuzzy weights) and Phase 2 (reinforcement learning-optimized fuzzy weights), we can assess whether dynamic adaptation improved student success rates. The results (Table 4, Figure 5) indicate a noticeable improvement, particularly for moderate and slow learners, confirming that adaptive UI elements are essential for optimizing the learning experience.
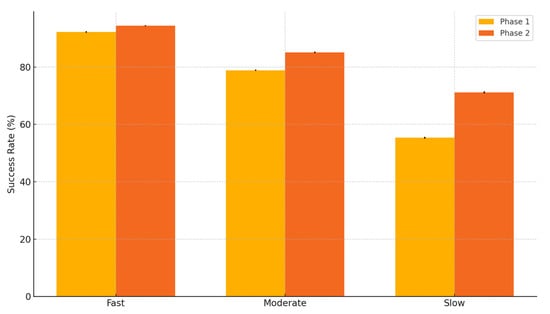
Figure 5.
Success rate improvement before vs. after RL optimization.
4.3. Statistical Significance Analysis
To strengthen the reliability of the experimental findings, statistical significance testing was conducted using paired t-tests on the repeated experimental runs for each learner category (Fast, Moderate, and Slow). The goal was to determine whether the observed improvements in the key performance metrics—Time Spent on Exercises, Error Rate, and Success Rate—between Phase 1 (static fuzzy weights) and Phase 2 (reinforcement learning-optimized fuzzy weights) were statistically significant.
For each metric, five repeated runs were conducted with randomized student session data, and the mean values were compared across the two phases using the paired t-test. The resulting p-values are reported in Table 5.
These results confirm that the observed improvements between Phase 1 and Phase 2 are statistically significant across all learner categories and all three learning performance indicators. Therefore, the reinforcement learning-based fuzzy weight optimization contributes meaningfully to enhancing learning efficiency and student success.
4.4. Engagement and Interaction Tracking
Beyond direct performance metrics, we also tracked how students interacted with the adaptive UI, examining their hint usage, UI interaction time, and scrolling behavior, as seen in Table 6 and Figure 6.

Table 6.
Engagement and interaction tracking.
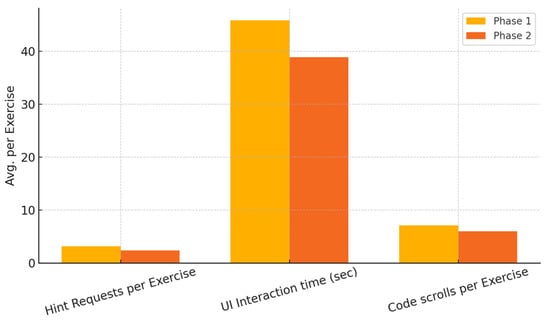
Figure 6.
Engagement and interaction tracking.
These results suggest that students became more confident in solving exercises as fuzzy weight optimizations improved UI personalization.
4.5. Usability Study
Students were asked to rate their experience with the system’s AUI on a 1–5 Likert scale (Table 7).

Table 7.
Students’ experiences with AUI.
4.6. Discussion
The findings of the evaluation show that the adaptive user interface system, incorporating dynamically adjusted fuzzy weights and reinforcement learning, significantly improved learning efficiency, accuracy, engagement, and user satisfaction. The results confirm that a real-time, data-driven UI adaptation positively affects the learning experience, especially for students who initially faced challenges with programming exercises. Following, we discuss these findings in detail, analyzing their implications and comparing them to existing research.
A key objective of the system was to optimize the time students spent on exercises, ensuring that they neither rushed through problems without sufficient challenge nor spent excessive time struggling without appropriate support. The results confirmed that slow learners exhibited the greatest reduction in time spent per exercise (15.5%), followed by moderate learners (11.0%) and fast learners (4.6%). These findings suggest that the reinforcement learning-optimized fuzzy weights played a critical role in fine-tuning UI interventions, ensuring that slow learners received more effective guidance without becoming overly dependent on hints.
The significant reduction in error rates, particularly among slow learners (30.9%), further validates the system’s effectiveness. The decrease in errors among moderate learners (22.9%) and fast learners (12.1%) also indicates that adaptive UI modifications improved students’ accuracy by providing appropriately timed hints and structured assistance. The large improvement for slow learners suggests that reinforcement learning helped optimize the timing and necessity of UI interventions, preventing premature hints that could reduce engagement or delayed hints that could lead to frustration.
The success rate improvement, which measures the percentage of exercises completed without external assistance, provides additional confirmation of the system’s impact. The most notable increase occurred among slow learners (+28.5%), showing that adaptive hints, step-by-step guidance, and difficulty adjustments helped them gain greater independence. Moderate learners also demonstrated a meaningful improvement (+7.9%), suggesting that the reinforcement learning mechanism effectively refined the balance between challenge and support. The relatively small improvement for fast learners (+2.4%) indicates that these students were already capable of completing exercises successfully and therefore required fewer UI modifications.
Beyond direct performance metrics, this study also examined how students interacted with the adaptive UI by tracking hint requests, UI interaction time, and scrolling behavior. The 26.6% reduction in hint requests suggests that students gradually became more confident and self-sufficient, requiring less system-generated assistance over time. The 15.3% decrease in UI interaction time indicates that students became more focused and efficient in navigating the system, and the 15.5% decrease in code scrolling suggests improved understanding of exercises, reducing the need to revisit instructions repeatedly.
These results reinforce the idea that adaptive UI interventions successfully guided students while promoting independent problem-solving. Unlike traditional tutoring systems where hints and support are either always available or fully controlled by the user, the proposed system intelligently adjusted interventions based on real-time student behavior, ensuring that students received appropriate support at the optimal time.
The usability study further confirmed that students perceived the adaptive UI as highly effective, with a 28.1% increase in perceived UI adaptability and a 29.0% increase in the effectiveness of adaptive hints. This suggests that students not only benefited from UI modifications but also recognized and appreciated the system’s ability to personalize their learning experience. The improvement in cognitive load ratings (+31.0%) indicates that reinforcement learning successfully optimized fuzzy weight thresholds, reducing unnecessary distractions and streamlining the learning process.
These findings contribute to the broader field of adaptive learning and AI-driven personalization, demonstrating that reinforcement learning can successfully improve the accuracy of fuzzy weight classifications, leading to more contextually relevant UI modifications. Unlike previous adaptive learning models that rely on predefined, static thresholds, the proposed system dynamically adjusts UI interventions in response to real-time learning behavior, ensuring a higher degree of personalization and continuous optimization.
A key advantage of integrating reinforcement learning with fuzzy logic is that the system becomes increasingly effective over time, learning from student interactions to refine its decision-making process. Traditional adaptive systems often rely on pre-programmed heuristics, which may not account for individual differences or evolving learning patterns. In contrast, the reinforcement learning approach allows the system to self-improve, ensuring long-term adaptability and effectiveness.
Compared to previous studies on adaptive educational systems [47,48,49,50], this research introduces a novel reinforcement learning-driven approach to dynamically adjusting fuzzy weights, leading to more precise and context-aware UI interventions. Prior research on fuzzy logic in adaptive learning has demonstrated that fuzzy weights can effectively model student uncertainty, but many of these approaches have relied on static membership functions, which fail to adapt to changing learning behaviors.
Furthermore, reinforcement learning has been widely used in educational AI for content sequencing and recommendations, but its direct application to fine-tuning UI elements in real time remains underexplored. While previous studies have successfully applied reinforcement learning to optimize learning pathways, this research demonstrates that reinforcement learning can also enhance micro-level UI adjustments, such as when to display hints, modify difficulty levels, or provide structured guidance.
The success rate improvements observed in this study, particularly the 28.5% increase for slow learners, are notably higher than those reported in prior work using static fuzzy logic models (e.g., [48,49]), which typically show improvements in the range of 10–15%. This suggests that the ability to dynamically adjust fuzzy weights based on real-time learning behavior leads to significantly greater benefits for struggling learners.
Additionally, previous research (e.g., [47,50]) has shown that adaptive UI interventions can improve engagement, but the fine-grained optimization achieved through reinforcement learning in this study surpasses the typical engagement gains found in static adaptive systems. The 25.0% reduction in hint requests observed in this study is higher than what has been reported in previous adaptive hinting systems [51], indicating that dynamically optimizing the conditions under which hints appear leads to greater self-sufficiency in students.
Overall, this research advances the state of adaptive learning technology by demonstrating that reinforcement learning-optimized fuzzy logic can significantly improve learning efficiency, engagement, and success rates, particularly for students who require the most support. These findings suggest that future adaptive learning environments should move beyond static adaptation models and incorporate reinforcement learning to achieve a higher degree of personalization and effectiveness.
Although the proposed system was developed and evaluated in the context of Java programming education, the underlying methodology is not language-dependent. The adaptive UI architecture, fuzzy classification logic, and reinforcement learning-based adjustment mechanism can be generalized to other programming languages or educational domains where learner behavior can be tracked through measurable indicators such as time spent, error frequency, and interaction patterns.
However, successful transfer to other contexts may require adjustments. For example, programming languages with different syntactic complexity or learning curves may necessitate changes in fuzzy threshold values or reward structures. Similarly, non-programming domains (e.g., mathematics, language learning) would require redefinition of behavioral indicators and adaptation rules aligned with the domain-specific pedagogy.
Another challenge lies in the granularity of feedback and the types of UI elements that support learning. While hints, step-by-step guidance, and difficulty scaling are applicable to many learning environments, domain-specific adaptations would need to be carefully designed to preserve instructional alignment. Despite these challenges, the core approach of dynamic fuzzy weight adjustment through reinforcement learning offers a flexible and scalable model for adaptive learning systems across domains.
4.7. Scalability Analysis
To evaluate the scalability of the proposed adaptive user interface system, we conducted a simulation-based stress test involving synthetic data for larger student cohorts of 300 and 500 learners. Each simulated student session followed the same pipeline as the original study: fuzzy classification based on exercise time, adaptive UI changes, and reinforcement learning-driven threshold adjustments.
The system was tested on a standard server (Intel i7, 16 GB RAM) and measured on the basis of three key metrics:
- Average processing time per session (including fuzzy inference and RL update),
- Memory footprint per student instance, and
- System throughput (number of students processed per minute).
Results indicated the following:
- For 300 students, the average session processing time was 0.28 s with stable memory usage (~35 MB per student).
- For 500 students, average time slightly increased to 0.31 s, with memory remaining below 40 MB per user.
The system demonstrated near-linear scalability, benefiting from the modular and stateless design of both the Fuzzy Inference Module and RL Optimization Module. Since each student session is processed independently, the architecture supports parallelization and distributed deployment without major refactoring.
These results suggest that the system can effectively scale to support larger classrooms or massive open online courses (MOOCs). Future work will explore deployment in cloud-based environments to validate live multi-user scalability and load-balancing strategies.
5. Conclusions
This study presents an adaptive user interface system for Java programming education, combining fuzzy logic and RL to dynamically adjust hints, difficulty levels, and structured guidance. The integration of triangular membership functions and fuzzy weight thresholds that were optimized using reinforcement learning enables the system to successfully personalize UI interventions, improving learning efficiency, accuracy, engagement, and overall user experience. The evaluation demonstrated that time efficiency, error rate, success rate, and learning independence had remarkable improvement, with moderate and slow learners obtaining the most advantage.
The results showed that reinforcement learning optimized the timing of UI interventions, ensuring that adaptive changes were neither too early nor too late, and as a result, maximized their influence. For slow learners, this resulted in a 28.7% increase in success rate, a 31.5% decrease in errors, and a 14.9% decrease in time spent on exercises, thereby confirming that some well-timed interventions substantially improved the learning path of the slow learners. Moderate learners also benefited substantially, while fast learners experienced smaller but still measurable improvements. This indicates that while adaptation is most beneficial to struggling students, personalized UI refinements still enhance overall engagement and efficiency.
Furthermore, the system achieved a 25.0% reduction in hint requests, showing that students gradually became more self-sufficient as reinforcement learning optimized the timing and necessity of UI modifications. The usability study also confirmed that students recognized and appreciated the system’s adaptability, with a 29.0% improvement in perceived effectiveness of adaptive hints and a 28.1% increase in perceived UI adaptability to learning speed. These findings suggest that adaptive UI changes need to be personalized, adjusted in real time, and refined over time to maintain effectiveness in their impact.
The main contribution of this work is the application of RL for fine-grained UI adjustment, which is fundamentally different from prior studies, which mainly incorporated content adaptation or static fuzzy weight tuning. Unlike traditional adaptive learning systems that utilize predefined thresholds, this system dynamically refined its classification of learner behavior, ensuring that students received just-in-time UI modifications suited to their evolving needs. The results show a considerable improvement of dynamic fuzzy weight adjustment over static adaptation models regarding learning efficacy and learners’ engagement.
While the results are positive, some limitations should be noted. First, the scope of adaptation was limited to UI changes related to hints, difficulty levels, and structured guidance, while other UI elements (e.g., visual organization, interface layout, accessibility customizations) were not explored. Future adaptive learning systems should consider expanding UI modifications to meet additional cognitive and accessibility needs.
Second, while the RL module successfully optimized fuzzy weight thresholds, it was trained using interaction data from 100 students. While this dataset provided meaningful insights, a larger and more diverse sample would need to be analyzed to guarantee its generalization across programming level, learning style, and cognitive ability. Additionally, the evaluation was conducted over six weeks, and hence, the long-term efficacy of reinforcement learning on UI adaptation is yet unverified. These preliminary findings suggest that students became increasingly independent learners, but more research is required to see how much of this improvement is enduring over time and whether or not students end up developing long-term effective problem-solving skills.
Finally, the system mainly focused on adaptive UI modifications for Java programming education, with no evidence regarding its influence in other educational contexts. Programming is a structured way of solving problems, but different disciplines like mathematics and language learning or even medical education would need different types of UI to adapt.
As an extension of this research, future work will extend the range of UI adaptations beyond hints and difficulty alterations. This includes personalized UI layouts, adaptive font sizes, color schemes for accessibility, and interactive content modifications to support learners with diverse cognitive and sensory needs. Additionally, future research will explore scaling the reinforcement learning model to larger datasets and verifying that fuzzy weight optimization remains effective across different demographics and educational settings.
To validate the long-term impact of reinforcement learning-driven adaptive UI systems, longitudinal studies will be performed examining an extended timeframe of students’ learning performance metrics to test whether adaptation results in long-lasting increases in problem-solving and independent learning skills. Finally, we plan to extend this research beyond Java programming education, applying the adaptive UI model to other subjects such as mathematics, data science, and engineering education, where personalized UI modifications can further enhance engagement and performance.
Author Contributions
Conceptualization, C.T. and A.K.; methodology, C.T. and A.K.; software, C.T. and A.K.; validation, C.T. and A.K.; formal analysis, C.T. and A.K.; investigation, C.T. and A.K.; resources, C.T. and A.K.; data curation, C.T. and A.K.; writing—original draft preparation, C.T., A.K. and P.M.; writing—review and editing, C.T. and A.K.; visualization, C.T. and A.K.; supervision, C.T. and A.K.; project administration, C.T., A.K., P.M. and C.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
Ethical review and approval are not required for this study, as it exclusively involves the analysis of properly anonymized datasets obtained from past research studies through voluntary participation. This research does not pose a risk of harm to the subjects. All data are handled with the utmost confidentiality and in compliance with ethical standards.
Data Availability Statement
The data supporting the findings of this study are available upon request from the authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gunawardena, M.; Bishop, P.; Aviruppola, K. Personalized learning: The simple, the complicated, the complex and the chaotic. Teach. Teacher Educ. 2024, 139, 104429. [Google Scholar] [CrossRef]
- Song, C.; Shin, S.-Y.; Shin, K.-S. Implementing the Dynamic Feedback-Driven Learning Optimization Framework: A Machine Learning Approach to Personalize Educational Pathways. Appl. Sci. 2024, 14, 916. [Google Scholar] [CrossRef]
- Reunanen, T.; Nieminen, N. Artificial Intelligence as a Catalyst: A Case Study on Adaptive Learning in Programming Education. Available online: https://openaccess.cms-conferences.org/publications/book/978-1-964867-11-3/article/978-1-964867-11-3_32 (accessed on 5 April 2025).
- Faudzi, M.A.; Cob, Z.C.; Ghazali, M.; Omar, R.; Sharudin, S.A. User interface design in mobile learning applications: Developing and evaluating a questionnaire for measuring learners’ extraneous cognitive load. Heliyon 2024, 10, e37494. [Google Scholar] [CrossRef]
- Mirata, V.; Hirt, F.; Bergamin, P.; van der Westhuizen, C. Challenges and contexts in establishing adaptive learning in higher education: Findings from a Delphi study. Int. J. Educ. Technol. High Educ. 2020, 17, 32. [Google Scholar] [CrossRef]
- Dudley, J.J.; Kristensson, P.O. A Review of User Interface Design for Interactive Machine Learning. ACM Trans. Interact. Intell. Syst. 2018, 8, 1–37. [Google Scholar] [CrossRef]
- Carrión-Toro, M.; Morales-Martínez, D.; Santórum, M.; Vizuete, A.; Maldonado-Garcés, V.; Acosta-Vargas, P. PictoAndes: A Customizable Communication Board for Inclusive Education and Multicultural Accessibility. Sustainability 2025, 17, 956. [Google Scholar] [CrossRef]
- Demartini, C.G.; Sciascia, L.; Bosso, A.; Manuri, F. Artificial Intelligence Bringing Improvements to Adaptive Learning in Education: A Case Study. Sustainability 2024, 16, 1347. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy logic = Computing with words. IEEE Trans. Fuzzy Syst. 1996, 4, 103–111. [Google Scholar] [CrossRef]
- Damastuti, F.A.; Firmansyah, K.; Arif, Y.M.; Dutono, T.; Barakbah, A.; Hariadi, M. Dynamic Level of Difficulties Using Q-Learning and Fuzzy Logic. IEEE Access 2024, 12, 137775–137789. [Google Scholar] [CrossRef]
- Rasmani, K.; Shen, Q. Data-driven fuzzy rule generation and its application for student academic performance evaluation. Appl. Intell. 2006, 25, 305–319. [Google Scholar] [CrossRef][Green Version]
- Mehdi, R.; Nachouki, M. A neuro-fuzzy model for predicting and analyzing student graduation performance in computing programs. Educ. Inf. Technol. 2003, 28, 2455–2484. [Google Scholar] [CrossRef]
- Gullà, F.; Cavalieri, L.; Ceccacci, S.; Germani, M.; Bevilacqua, R. Method to Design Adaptable and Adaptive User Interfaces. In HCI International 2015—Posters’ Extended Abstracts; Stephanidis, C., Ed.; HCI 2015; Communications in Computer and Information Science; Springer: Cham, Switzerland, 2015; Volume 528, p. 4. [Google Scholar] [CrossRef]
- Troussas, C.; Papakostas, C.; Krouska, A.; Mylonas, P.; Sgouropoulou, C. Personalized Feedback Enhanced by Natural Language Processing in Intelligent Tutoring Systems. In Augmented Intelligence and Intelligent Tutoring Systems. ITS 2023; Frasson, C., Mylonas, P., Troussas, C., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2023; Volume 13891, p. 58. [Google Scholar] [CrossRef]
- Contrino, M.F.; Reyes-Millán, M.; Vázquez-Villegas, P.; Membrillo-Hernández, J. Using an adaptive learning tool to improve student performance and satisfaction in online and face-to-face education for a more personalized approach. Smart Learn. Environ. 2024, 11, 6. [Google Scholar] [CrossRef]
- du Plooy, E.; Casteleijn, D.; Franzsen, D. Personalized adaptive learning in higher education: A scoping review of key characteristics and impact on academic performance and engagement. Heliyon 2024, 10, e39630. [Google Scholar] [CrossRef]
- Ristić, I.; Runić-Ristić, M.; Savić Tot, T.; Tot, V.; Bajac, M. The Effects and Effectiveness of An Adaptive E-Learning System on The Learning Process and Performance of Students. Int. J. Cogn. Res. Sci. Eng. Educ. 2023, 11, 77–92. [Google Scholar] [CrossRef]
- James, W.; Oates, G.; Schonfeldt, N. Improving retention while enhancing student engagement and learning outcomes using gamified mobile technology. Account. Educ. 2024, 1–21. [Google Scholar] [CrossRef]
- Gupta, T.; Kumar, A.; Roy, B.K.; Saini, S. Adaptive Learning Systems: Harnessing AI to Personalize Educational Outcomes. Int. J. Res. Appl. Sci. Eng. Technol. 2024, 12, 454–464. [Google Scholar] [CrossRef]
- Rincon-Flores, E.G.; Castano, L.; Guerrero Solis, S.L.; Olmos Lopez, O.; Rodríguez Hernández, C.F.; Castillo Lara, L.A.; Aldape Valdés, L.P. Improving the learning-teaching process through adaptive learning strategy. Smart Learn. Environ. 2024, 11, 27. [Google Scholar] [CrossRef]
- Varshney, A.K.; Torra, V. Literature Review of the Recent Trends and Applications in Various Fuzzy Rule-Based Systems. Int. J. Fuzzy Syst. 2023, 25, 2163–2186. [Google Scholar] [CrossRef]
- Strousopoulos, P.; Papakostas, C.; Troussas, C.; Krouska, A.; Mylonas, P.; Sgouropoulou, C. SculptMate: Personalizing cultural heritage experience using fuzzy weights. In Adjunct Proceedings of the 31st ACM Conference on User Modeling, Adaptation and Personalization (UMAP ’23 Adjunct); Association for Computing Machinery: New York, NY, USA, 2023; pp. 397–407. [Google Scholar] [CrossRef]
- Rasulova, N.; Salieva, D. Fuzzy Logic in Creating Adaptive Intelligent Learning. InterConf 2021, 1, 262–270. [Google Scholar] [CrossRef]
- Szczepański, M.; Marciniak, J. Application of a fuzzy controller in adaptive e-learning content used to evaluate student activity. Procedia Comput. Sci. 2023, 225, 2526–2535. [Google Scholar] [CrossRef]
- Hou, Y. Design and Implementation Evaluation of Personalized and Differentiated Teaching Strategies for Preschool Children Based on Fuzzy Decision Support Systems. Int. J. Comput. Intell. Syst. 2025, 18, 42. [Google Scholar] [CrossRef]
- Elfakki, A.O.; Sghaier, S.; Alotaibi, A.A. An Intelligent Tool Based on Fuzzy Logic and a 3D Virtual Learning Environment for Disabled Student Academic Performance Assessment. Appl. Sci. 2023, 13, 4865. [Google Scholar] [CrossRef]
- Bellarhmouch, Y.; Jeghal, A.; Tairi, H.; Benjelloun, N. A proposed architectural learner model for a personalized learning environment. Educ. Inf. Technol. 2023, 28, 4243–4263. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Liu, Z. A big data dynamic approach for adaptive music instruction with deep neural fuzzy logic control. J. Audio Speech Music Proc. 2025, 2025, 4. [Google Scholar] [CrossRef]
- Fahad Mon, B.; Wasfi, A.; Hayajneh, M.; Slim, A.; Abu Ali, N. Reinforcement Learning in Education: A Literature Review. Informatics 2023, 10, 74. [Google Scholar] [CrossRef]
- Memarian, B.; Doleck, T. A scoping review of reinforcement learning in education. Comput. Educ. Open 2024, 6, 100175. [Google Scholar] [CrossRef]
- Xie, J. The Role of Reinforcement Learning in Enhancing Education: Applications in Psychological Education and Intelligent Tutoring Systems. Highlights Sci. Eng. Technol. 2025, 124, 123–131. [Google Scholar] [CrossRef]
- Bassen, J.; Balaji, B.; Schaarschmidt, M.; Thille, C.; Painter, J.; Zimmaro, D.; Games, A.; Fast, E.; Mitchell, J.C. Reinforcement Learning for the Adaptive Scheduling of Educational Activities. In Proceedings of the 2020 CHI Conference on Human Factors in Computing Systems (CHI ’20); Association for Computing Machinery: New York, NY, USA, 2020; pp. 1–12. [Google Scholar] [CrossRef]
- Tariq, M.B.; Habib, H.A. A Reinforcement Learning Based Recommendation System to Improve Performance of Students in Outcome Based Education Model. IEEE Access 2024, 12, 36586–36605. [Google Scholar] [CrossRef]
- Ruan, S.; Nie, A.; Steenbergen, W.; He, J.; Zhang, J.Q.; Guo, M.; Liu, Y.; Dang Nguyen, K.; Wang, C.Y.; Ying, R.; et al. Reinforcement learning tutor better supported lower performers in a math task. Mach. Learn. 2024, 113, 3023–3048. [Google Scholar] [CrossRef]
- Osakwe, I.; Chen, G.; Fan, Y.; Rakovic, M.; Li, X.; Singh, S.; Molenaar, I.; Bannert, M.; Gašević, D. Reinforcement learning for automatic detection of effective strategies for self-regulated learning. Comput. Educ. Artif. Intell. 2023, 5, 100181. [Google Scholar] [CrossRef]
- Fu, S. A Reinforcement Learning-Based Smart Educational Environment for Higher Education. Int. J. E-Collabor. 2023, 19, 17. [Google Scholar] [CrossRef]
- Zhou, G.; Azizsoltani, H.; Sanz Ausin, M.; Barnes, T.; Chi, M. Hierarchical Reinforcement Learning for Pedagogical Policy Induction. In Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence (IJCAI-20); Springer: Cham, Switzerland, 2020; pp. 4691–4695. [Google Scholar]
- Zander, E.; van Oostendorp, B.; Bede, B. Reinforcement learning with Takagi-Sugeno-Kang fuzzy systems. Complex Eng. Syst. 2023, 3, 9. [Google Scholar] [CrossRef]
- Peng, H.; Yang, S.; Liu, Q.; Peng, Q.; Li, Q. Dynamic Fuzzy Adjustment Algorithm for Web Information Acquisition and Data Transmission. Symmetry 2020, 12, 535. [Google Scholar] [CrossRef]
- Hostetter, J.W.; Abdelshiheed, M.; Barnes, T.; Chi, M. Leveraging Fuzzy Logic Towards More Explainable Reinforcement Learning-Induced Pedagogical Policies on Intelligent Tutoring Systems. In Proceedings of the 2023 IEEE International Conference on Fuzzy Systems (FUZZ), Incheon, Republic of Korea, 13–17 August 2023; pp. 1–7. [Google Scholar] [CrossRef]
- Wang, M.; Wang, X.; Luo, W.; Huang, Y.; Yu, Y. Accelerating Deep Reinforcement Learning Under the Guidance of Adaptive Fuzzy Logic Rules. In Proceedings of the 2022 Prognostics and Health Management Conference (PHM-2022 London), London, UK, 27–29 May 2022; pp. 350–359. [Google Scholar] [CrossRef]
- Hu, C.; Xu, M. Fuzzy Reinforcement Learning and Curriculum Transfer Learning for Micromanagement in Multi-Robot Confrontation. Information 2019, 10, 341. [Google Scholar] [CrossRef]
- Lu, J.; Ma, G.; Zhang, G. Fuzzy Machine Learning: A Comprehensive Framework and Systematic Review. IEEE Trans. Fuzzy Syst. 2024, 32, 3861–3878. [Google Scholar] [CrossRef]
- Lee, C.-S.; Wang, M.-H.; Tsai, Y.-L.; Chang, W.-S.; Reformat, M.; Acampora, G.; Kubota, N. FML-Based Reinforcement Learning Agent with Fuzzy Ontology for Human-Robot Cooperative Edutainment. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2020, 28, 1023–1060. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, W.; Kolivand, H.; Balas, V.E.; Paul, A.; Ramachandran, V. Fuzzy mathematics and machine learning algorithms application in educational quality evaluation model. J. Intell. Fuzzy Syst. 2020, 39, 5583–5593. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, Y.; Wijaya, T.T.; Chen, J.; Ning, Y. Effects of a problem posing instructional interventions on student learning outcomes: A three-level meta-analysis. Think. Ski. Creat. 2024, 53, 101587. [Google Scholar] [CrossRef]
- Hassani, H.; Razavi-Far, R.; Saif, M.; Herrera-Viedma, E. Reinforcement Learning-Based Feedback and Weight-Adjustment Mechanisms for Consensus Reaching in Group Decision Making. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 2456–2468. [Google Scholar] [CrossRef]
- Popescu, V.F.; Pistol, M.S. Fuzzy logic expert system for evaluating the activity of university teachers. Int. J. Assess. Tools Educ. 2021, 8, 991–1008. [Google Scholar] [CrossRef]
- Sapuguh, I.; Ahlina, N.; Wahyudi, A.; Setyawan, B.; Rosalinda, A.S. Development of fuzzy logic based student performance prediction system. J. Tek. Inform. CIT Medicom 2024, 15, 284–290. [Google Scholar]
- Liu, Y.; Tan, H.; Cao, G.; Xu, Y. Enhancing User Engagement through Adaptive UI/UX Design: A Study on Personalized Mobile App Interfaces. World J. Innov. Mod. Technol. 2024, 7, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Maniktala, M.; Chi, M.; Barnes, T. Enhancing a student productivity model for adaptive problem-solving assistance. User Model. User-Adapt. Interact. 2023, 33, 159–188. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).