Abstract
For efficient radio network planning, empirical path loss (PL) prediction models are utilized to predict signal attenuation in different environments. Alternatively, machine learning (ML) models are proposed to predict path loss. While empirical models are transparent and require less computational capacity, their predictions are not able to generate accurate forecasting in complex environments. While ML models are precise and can cope with complex terrains, their opaque nature hampers building trust and relying assertively on their predictions. To fill the gap between transparency and accuracy, in this paper, we utilize glass box ML using Microsoft research’s explainable boosting machines (EBM) together with the PL data measured for a university campus environment. Moreover, polar coordinate transformation is applied in our paper, which unravels the superior explanation capacity of the feature transmitting angle beyond the feature distance. PL predictions of glass box ML are compared with predictions of black box ML models as well as those generated by empirical models. The glass box EBM exhibits the highest performance. The glass box ML, furthermore, sheds light on the important explanatory features and the magnitude of their effects on signal attenuation in the underlying propagation environment.
1. Introduction
The evolution of mobile communication systems has progressed from the first generation (1G) to the fifth generation (5G). In light of integrating the Internet of Things (IoT) in various domains such as smart factories, precision agriculture, transport systems, etc., optimizing connectivity is becoming of prime importance [1]. However, there are many challenges for mobile communication systems of the future to meet this trend. Knowing the path loss behavior of a communication channel is one among many challenging characteristics of wireless communications. Here, path loss (PL) refers to the decrease in reception over distance, which is dependent on many environmental factors [2]. Empirical models and ML models have been applied frequently to perform PL predictions. Empirical models use empirical data to establish a relationship between the signal strength at a transmitter and a receiver based on features like distance, frequency, environmental conditions, and obstacles [3]. These models are transparent predictors as they incorporate a small number of parameters, and the equations of these models are concise. Machine learning models are alternative models to analyze vast amounts of empirical data to identify complex patterns and dependencies that may not be easily captured by empirical models [3]. Shaibu et al. have demonstrated that ML models are more accurate than empirical models [3]. Though, ML models, despite being highly accurate, are not sufficiently interpretable (or explainable) [4]. In recent research, explainable artificial intelligence (XAI) has received high attention to address the interpretability of ML models. Interpretability is defined by Miller [4] as “the degree to which a human can understand the cause of a decision”. The terms explainability and interpretability are often used interchangeably. Explainability is also referred to in the literature as interpretability, intelligibility, causability, or understandability [5,6,7]. Extension of XAI to the PL predictions made by ML models in wireless communication remains a research gap in the existing literature.
In our work we propose to integrate accuracy and transparency in PL predictions by applying intrinsically interpretable ML models. Intrinsically interpretable ML models are glass box models per se due to their intrinsic structure [8]. In order to convey a comparative understanding, we utilize three categories of models, each of them represented by three concrete models to predict measured PL data from a university campus environment [9,10]. We utilize empirical PL prediction models (represented in Section 4.1 by Okumura–Hata, COST-231 Hata, and ECC-33 models), ML-based PL prediction models (represented in Section 4.2 by random forest (RF), extreme gradient boosting (XGB), and multi-layer perception (MLP)), and glass box ML-based PL prediction models (represented in Section 4.3 by generalized additive model (GAM), generalized neural additive model (GNAM), and explainable boosting machine (EBM)).
As visualized in Figure 1, our work contributes to the existing literature of PL models by demonstrating the high prediction accuracy of glass box ML models (compared to the empirical PL models and black box ML models), beside showing the advantage of glass box ML models to have intrinsic explanation power in order to shed light on the rationale behind the ML model predictions. Thereby, and to the best of our knowledge, our paper is the first to demonstrate the possible robustness of applying glass box ML models in PL prediction modeling.
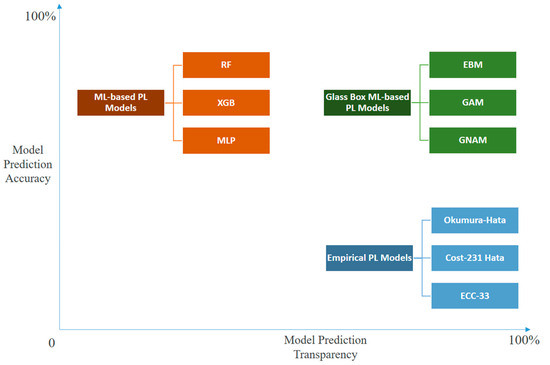
Figure 1.
Model prediction accuracy versus model prediction transparency by different PL modeling approaches.
The remainder of this paper is structured as follows: Section 2 provides a literature review of explainable ML models of PL prediction. Section 3 provides insight into the data used in our study. Section 4 concisely introduces the prediction models applied to the data, consisting of empirical models, black box ML, and glass box ML models. Section 5 presents the accuracy results of the aforementioned prediction models. Section 6 is devoted to the interpretation of the results of the glass box EBM model by highlighting the significance and magnitude of the effects of the explanatory variables on signal attenuation in the study environment. Concluding remarks are summarized in Section 7.
2. Literature Review
The identification of relevant papers regarding the application of explainable ML models to PL prediction tasks is carried out by filtering titles and content in the IEEE Xplore, ScienceDirect, ACM, and Google Scholar databases in the time between 1 January 2020 and 31 October 2024. The goal of our literature review was to identify the researches in the intersection of ML, XAI, and PL modeling (Figure 2).
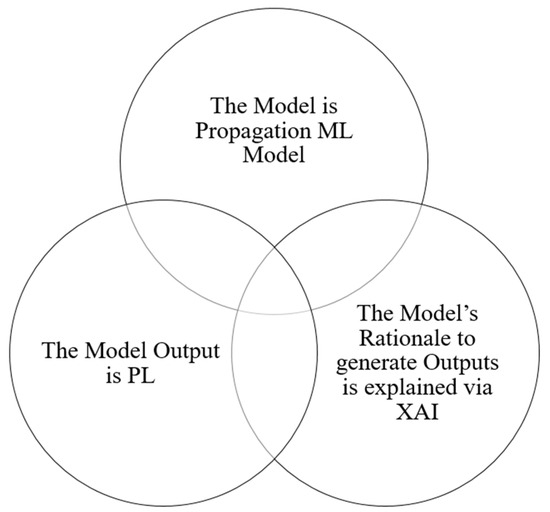
Figure 2.
Scope of the literature review: identify the researches in the intersection of ML, XAI, and PL modeling.
Thereby, we opted for broad coverage by using the search term “path loss” in the title as well as each of the search terms “explainable”, “interpretable”, “feature importance”, and “SHAPley” in the full body of the papers’ text (accessed on 31 October 2024) without using AI-related terms (e.g., “machine learning” or “deep learning”). The term “SHAPley” is applied as a search term as it addresses one of the most prominent XAI techniques, which is elaborated below. Databases, search terms, and the number of relevant results from searching explainable studies of PL prediction are presented in Table 1.

Table 1.
Overview of databases, search terms, and the number of relevant results by searching explainable ML studies of PL prediction along the literature scanning process.
After searching the relevant papers according to the search strategy presented in Table 1, we removed the duplicates, and scanned the remaining papers based on the criterion of whether the paper applies XAI to ML models to predict PL. We found 11 papers that jointly include ML, XAI, and PL modeling. The propagation context, model training, and model interpretation methods of these relevant studies are presented in Table 2.

Table 2.
Overview of the explainable ML studies of PL prediction.
While existing ML methods in XAI-based PL prediction studies are by default opaque models, they often use model-agnostic explanation techniques to unveil the logic behind decisions made by them. Model-agnostic techniques presume ML models to be of a black box nature and try to convey explanations by building surrogate models, either through employing intrinsically interpretable meta models (e.g., by employing linear regression as applied in [11]) or through employing perturbation mechanisms. Perturbation-based mechanisms (applied in [14,17,19]) analyze the importance of each input on the model outcome by systematically modifying the input of the model and observing the changes in the output. If the permutation of a specific part of the input considerably alters the model output, then the specified part is considered to be important.
Several studies [12,13,15,16] utilize the Shapley value-based explanations (SHAP) concept. SHAP can be considered a perturbation-based concept as well, which computes the average marginal contribution of a feature to the output predicted by the ML model, considering all possible combinations of features [22]. ALE [18] and LIME [12] are further model-agnostic methods used in the literature of PL prediction, which are built based on perturbation and meta-modeling [22].
An ensemble of tree-based models, e.g., GTB, XGB, and RF, can be explained to some degree by means of mean decrease impurity methods [20,21]. The mean decrease impurity method describes how heavily the model relies on a certain feature to make its prediction by counting the times a feature is used to split a node, weighted by the number of samples it splits [23].
Ensemble tree-based models are basically characterized as black box models in the literature [24] as they are composed of a high number of trees in the forest. This makes the complete transparency of their predictions challenging from a user’s point of view. Ongoing research in the literature aims to make ensemble tree-based models more explainable—e.g., through extracting decision rules from the RF [24] and by proposing a single associated decision tree (DT) to represent tree-based models [25].
Hence, the signal propagation studies summarized in Table 2 can be categorized as inherently opaque ML models. These models are served by a surrogate explanation model to explain their results. In contrast, in this paper, we incorporate intrinsically glass box ML for PL prediction, which is self-reliant in terms of interpretation. Henceforth, showcasing the feasibility of high prediction accuracy together with enhanced transparency through using intrinsically explainable ML models of PL prediction is pioneered in our paper. Our departing point from the existing literature is highlighted in Figure 3.
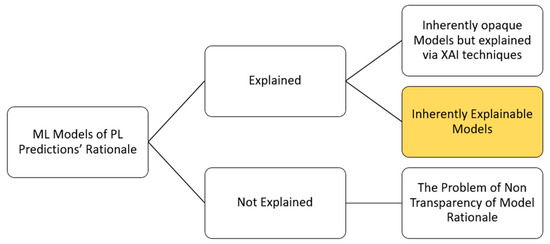
Figure 3.
Positioning our contribution of intrinsically explainable ML models of PL prediction within the existing literature.
3. Data
In this paper, we use the published measured data from Covenant University, Ota, Ogun State, Nigeria [9,10]. The reason for choosing this dataset in our study is that a smart campus environment approximately resembles urban microenvironments comprising spatially distributed buildings alongside roads, trees, parking lots, etc. This can characterize complex electromagnetic propagation phenomena, which might not be easily captured only based on empirical PL models. Measurement campaigns in [9,10] are conducted by means of smooth drive tests with an average speed of 40 km/h along three survey routes (A, B, and C) within the university campus as a mobile receiver moves away from three collocated directional 1800 MHz base station transmitters.
The measurement routes (A, B, and C) can be distinguished based on a Digital Terrain Map (DTM) of the study area presented in [9]. Based on a comparison between the original reference with the Google Satellite View of Covenant University’s main campus location, the measurement routes (A, B, and C) as well as the position of the three collocated transmitters (marked by Tx) are shown in Figure 4. Thereby, the approximated transmitter’s location is indicated by Tx. Route A, route B, and route C are marked by green, blue, and orange, respectively.
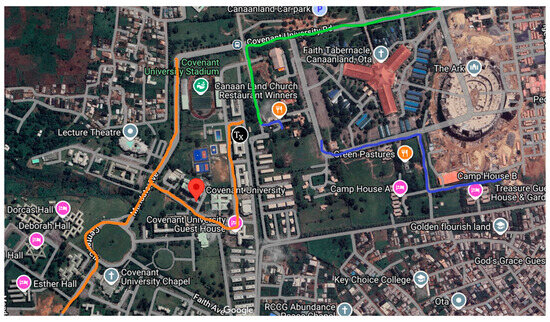
Figure 4.
Google satellite view of the study terrain describing drive tests moving away from the three collocated transmitters (marked by Tx) along the three survey routes (A, B, and C) within the university campus marked by green, blue, and orange, respectively.
The PL data and the terrain information about the smart campus environment include longitude, latitude, elevation, altitude, clutter height, and distance of separation between the corresponding transmitter and the receiver points [9]. There are a total of 3617 measurements along with the three different routes. Further details regarding experimental design, test materials, as well as exploratory data analysis in terms of distributions of variables and correlation statistical analysis, are available in the original published data set study [9].
4. Evaluation Models
In this section, we introduce three categories of models, each of them represented by three concrete models to predict measured PL data from a university campus environment.
4.1. Empirical Models
We utilize the following three empirical models in our study: Okomura–Hata, COST-231 Hata, and ECC-33.
- (1)
- Okumura–Hata Model
The Okumura–Hata model is frequently employed for path loss prediction. A basic formulation of the Okumura–Hata model, in general form, is presented in Equation (1) [3]:
where A, B, C, D, E, and F are model-specific constants that can be tailored based on specific environmental factors as well as the frequency of operation and the receiver height. f is the frequency of the signal in MHz. h is the height of the transmitting antenna in meters. d is the distance between the transmitter and receiver in kilometers. The application of Okumura–Hata includes urban and suburban as well as open rural areas in the frequency bands from 150 MHz to 1500 MHz.
- (2)
- COST-231 Hata Model
The COST-231 Hata Model is an extension of the Okumura–Hata model to the frequency bands of 1500 MHz ≤ f ≤ 2000 MHz [3]. The proposed model for path loss is designed for mobile communication networks in urban areas and is presented in Equation (2):
where f, d, , , and Cm are the frequency in MHz, distance from the transmitting station to the receiving antenna, transmitting antenna height, receiver antenna height, and an environment-specific constant term. The correction factor is as follows:
- (3)
- ECC-33 Model
The ECC-33 path loss model, which is applicable for the 700–3000 MHz frequency band, is developed by the Electronic Communication Committee (ECC). The model is based on a modification of Okumura’s original measurements to more accurately represent a fixed wireless access (FWA) system. The path loss equation is given as [26]:
, , , and represent free space attenuation, medial PL, transmitter antenna height gain, and receiver antenna gain factor. The functions are separately defined:
Note that the specific version of the Okumura–Hata, COST231 Hata, and ECC-33 models is presented in [10]. The three aforementioned models are used by us as a basis to evaluate the results of our study. However, in our study, we do not replicate the results corresponding to each of these models. We only use the spreadsheet containing the real measured PL data versus the PL data prognosis by the three models in [10]’s Supplementary Material to compute accuracy metrics in our result section.
4.2. Black Box ML Models
We utilize three black box ML models in our study comprising MLP, XGB, and RF models.
- (1)
- MLP (multi-layer perception)
We replicate a modified version of the ANN training applied by [27] to the PL prediction by means of the same training data set in our study. While in the aforementioned study, the features longitude and altitude are dropped by a feature selection step before training the model, we abstain from dropping any of the input explanatory variables through our study as longitude and latitude are containing site-specific information of the training, which leads to accounting for shadowing effects by modeling PL behavior. Hence, the ML models’ input features through our paper are longitude, latitude, elevation, altitude, clutter height, and distance of separation between the corresponding transmitter and the receiver points. The model output feature is path loss throughout.
The fully connected neural network applied in our study consists of two hidden layers, each comprising 32 neurons and the rectified linear unit-based activation function.
- (2)
- XGB (extreme gradient boosting)
We apply the XGB model, which is one of the most prominent ensemble of tree- based models. Its high performance is based on parallelization, tree pruning, and hardware optimization, while requiring minimal data pre-processing [28].
XGB is applied in multiple XAI researches of PL predictions [6,7,19]. The model trained in this paper is hyper-parametrized by using the randomized search function of the Python Sklearn 1.3.2 package through the parameter space within the search grid: . This results in utilizing 42 decision trees, incorporating the maximum depth attribute of the trees to 4, and setting the learning rate equal to 0.023.
- (3)
- RF (random forest)
We apply the RF model in our study, as it represents one of the most prominent ensembles of tree-based models [29]. It is applied frequently for XAI research of PL predictions [14,15,16,17,18,19,20,21]. The model trained in this paper is hyper-parametrized by using the randomized search function of the Python Sklearn package through the parameter space within the search grid: . It results in utilizing 1000 decision trees, incorporating the maximum depth attribute of the trees to 60, and setting the minimum sample leaf as well as the sample split equal to 2.
4.3. Glass Box ML Models
We introduce the following three glass Bbox ML models in our study: GAM, GNAM, and EBM.
- (1)
- GAM (generalized additive model)
GAMs are a semi-parametric extension of the generalized linear models that allow for nonparametric fittings of complex dependencies of response variables. A GAM adopts a sum of arbitrary functions of variables (possibly nonlinear) that represent different features via splines, which altogether describe the magnitude and variability of the response variables [30]. For a univariate response variable of multiple features, GAM is expressed by Equation (9):
where is the intercept parameter, represents independent variables, is the dependent variable, g() is the link function that relates the independent variables to the expected value of the dependent variable, and represents a random variable [31].
GAMs are interpretable by design because of their functional forms that make it easy to reason about the contribution of each feature to the prediction. The analysis of the data in our study based on GAM is performed by using the pyGAM module with the source code available at https://github.com/dswah/pyGAM/tree/master (accessed on 20 February 2025).
The model’s hyper-parameters are not optimized by us and are set to default values.
- (2)
- GNAM (generalized neural additive model)
GNAMs [32] are a neural network-based extension of GAMs through replacing the mathematical exploration of in Equation (9) by MLPs. The GNAM can be expressed by the following:
where is the MLP network. The architecture of the GNAM with k input explanatory variables and presuming just one hidden layer and as a corresponding activation function is presented in Figure 5.
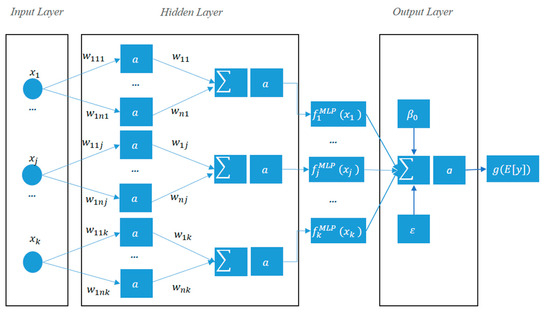
Figure 5.
The architecture of the GNAMs with k input explanatory variables and presuming just one hidden layer.
The analysis of the data in our study based on GNAM is performed by using the NAMpy package with the source code available at https://github.com/AnFreTh/NAMpy/tree/main (accessed on 20 February 2025). The MLP’s hyper-parameters are not optimized by us and are set to default values.
- (3)
- EBM (explainable boosting machine)
The basic idea behind EBM is similar to GAM and GNAM. However, EBMs offer a few major improvements over the traditional GAMs family [33]. First, EBMs learn each feature function using gradient-boosted ensembles of bagged trees. Similar to gradient-boosted tree models, EBMs’ training comprises a large number of trees in a sequential manner, each explaining the errors of the previous one. Though, in contrast, in EBM, each tree is built based on a single input feature. It first builds a small tree with the input feature x1 and computes the residuals (ε). It then fits the second tree with a different input feature x2 to the residuals and goes on through all input features to complete the ongoing iteration. To mitigate the effect of each input feature’s order in the sequence, EBM incorporates a small learning rate. Moreover, sequentially estimating each feature one-at-a-time in a round-robin fashion mitigates potential collinearity issues between predictors [34]. Once the first iteration is complete, the training is reiterated for a large number of iterations to ensure an acceptable accuracy. The EBM’s training procedure of decision trees (DTs) with k input explanatory variables is visualized in Figure 6.
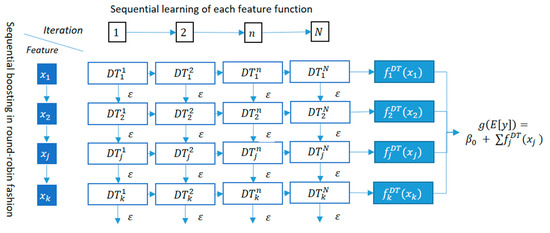
Figure 6.
The architecture of the EBM with k input explanatory variables and N iterations.
In addition, EBMs take the combined impacts of two or more independent variables known as the interaction effect (GA2Ms). To compute the interactive effects, first, the additive model, which merely incorporates one-dimensional elements, is fitted. In the next phase, the one-dimensional functions are taken into account as frozen model terms, and models are trained to account for the remaining pairwise interactions. Thereby, an algorithm called FAST [35] is used to rank the pairs based on their relationship with residuals. The EBM can be expressed by the following:
The direct impact of an input feature on the target feature is known as the main effect, while the combined impact of two or more features is known as the interaction effect.
EBMs are highly interpretable because the contribution of each independent variable or combination of independent variables to a final prediction can be visualized and understood by plotting and , respectively. The analysis of the data in our study based on EBM is performed by using the toolkit called InterpretML from Microsoft [33]. The model’s hyper-parameters are not optimized by us and are set to default values. In addition, based on decaying characteristics of the signal strength when it propagates from the base station towards different angles, we applied polar coordinate transformation to transform the geographical data into a polar coordinate system before training the model. Thereby, image axis-independent variables (longitude and latitude) are converted into polar coordination consisting of distance and the transmitting signal direction, i.e., Tx-Rx Angle. The Tx-Rx angle is computed by us through translating the longitude and latitude of the points to X-Y geographic points and setting the (X, Y) coordinate values of the transmitter location equal to the reference point (0, 0).
5. Model Accuracy Results
The prediction accuracies of the black box ML and glass box ML models are evaluated based on splitting the data by a 1:4 training: testing ratio and by means of MAE (mean absolute error), RMSE (root mean square error), and R squared. The prediction accuracies of the empirical models are computed based on the Supplementary Materials in [10]. The values of the performance metrics for the measurement routes A, B, and C are presented in Table 3, Table 4 and Table 5. The code and the input data to replicate the model accuracy results can be downloaded at the Supplementary Material of this paper.

Table 3.
Evaluation of prediction models along route A.

Table 4.
Evaluation of prediction models along route B.

Table 5.
Evaluation of prediction models along route C.
Overviewing the accuracy results in Table 3, Table 4 and Table 5 by means of the obtained mean absolute errors as well as the R-squared and root mean squared error demonstrates the capability of the EBM model in terms of achieving the foremost precise predictions along the routes A and B. For route C, we attained comparable results with tree-based models, i.e., RF and XGB, which are the best predictors along route C.
The superiority of EBM exactness compared to GAM and GNAM can be referred to as its ability to account for interactive interaction of independent variables in addition to considering their isolated effects. In addition, tree-based models (RF, XGB, and EBM) demonstrate higher precision in comparison with deep models (MLP, GNAM).
Furthermore, all models show deteriorating results when it comes to route C. Negative R-squared values observed by empirical models indicate that the sum of the squares of the vertical distances of the points from the fitted curve (residuals) exceeds the sum of the squares of the vertical distances of the points from a horizontal line drawn at the mean PL predicted value. This can be interpreted as no suitability of empirical models to explain the PL behavior by means of the independent variables of the study. Moreover, the Okumura–Hata model, which is initially thought to be for frequencies in between 150 MHz and 1500 MHz, shows partly comparable and superior results along route A and route B, respectively, in comparison with COST 231 and ECC-33 models, which are supposed to be more suitable PL prediction candidates due to the applied center frequency of our study, which is 1800 MHz.
6. Model Interpretation Results
This section is devoted to shedding light on the rationale behind the EBM model to generate its predictions. We first elaborate on the EBM model interpretation at the local level, which explains how the model makes a prediction based on an individual input. We then explain the EBM model’s rationale at the global level, which explains how the model works over the entire dataset. The code and the input data to replicate the model interpretation results can be downloaded at the Supplementary Material of this paper.
6.1. Local Explanations
Local explanations explain the reasoning of the model prediction based on a distinct input. Given an arbitrary input value for a receiver point, the local explanation declares the contribution of each input feature’s value to the generated prediction. Figure 7 depicts EBM local explanations by means of exemplary input-output from the test dataset. EBM illustrates how much each input feature’s value contributes to the predicted single PL in the positive (orange bar) or negative term (blue bar) beyond the regression’s intercept term () (gray bar), which is described in Equation (11). In this case, the value of the angle (+108.75 degrees), from which the signals traverse towards the receiver points, plays a significant role in generating PL prediction by contributing −10.055 dB to the predicted PL value. However, the contribution of the angle is offset by the feature elevation of the receiver point (63 m), having a +13.429 dB effect on signal weakening, as well as the feature distance from the transmitter (720 m), having a +2.658 dB contribution on PL. The altitude of the receiver (57 m) is shown to have a negative effect equal to −2.890 dB on PL prediction. The interactive incorporation of distance between transmitter and receiver and the corresponding transmitting angle is shown to have a −1.850 dB effect on signal attenuation. Further, the presented horizontal bars in Figure 7 can be read accordingly.
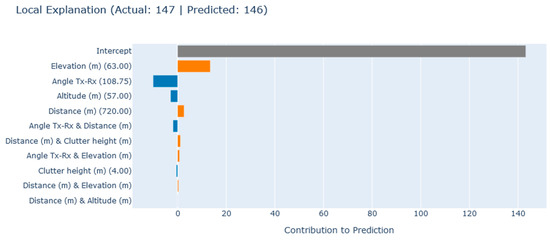
Figure 7.
EBM Local explanation by means of an exemplary input-output from the study’s test set (gray bar: intercept, orange bar: positive contributing input value, blue bar: negative contributing input value).
6.2. Global Explanations
Global explanations explain the model predictions’ reasoning, consisting of feature significance, feature marginal contributions, and interactive feature marginal contributions based on the entire training data set.
- (1)
- Feature Significance
The global significance of input features is computed based on the average absolute value of each input feature’s contribution across the entire training set. Thereby, both large positive and large negative effects by individual predictions are considered important by this measure and are summed up. Figure 8 presents the conveyed global importance of features to predict PL in our study.
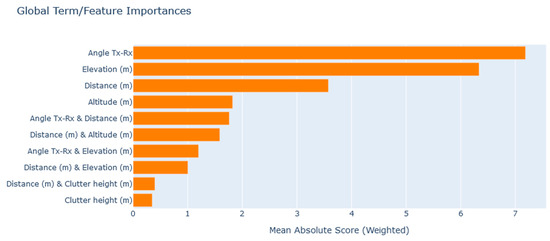
Figure 8.
EBM global importance of independent features in predicting PL.
The transmitting to receiver angle plays the most significant role in generating prediction, showing on average, a 7.185 dB contribution. The receiver point’s elevation, distance to the transmitter, and its altitude are further important features by globally contributing equal to 6.335 dB, 3.574 dB, and 1.821 dB in PL predictions, respectively. In addition, interaction of angle and distance is considered the most important interactive term (Equation (11)) by contributing 1.760 dB on average to the predictions. In contrast, the feature Clutter height (0.349 dB) is apparently playing minimal effects to generate PL predictions. Further presented horizontal bars in Figure 8 can be read accordingly.
- (2)
- Feature Marginal Contribution
Feature marginal contribution maps each possible value of an input feature to a corresponding contribution (in a look-up table manner) to generate PL predictions. Figure 9 and Figure 10 demonstrate the marginal effects of angle Tx-Rx, elevation, distance, altitude, and clutter height, respectively.
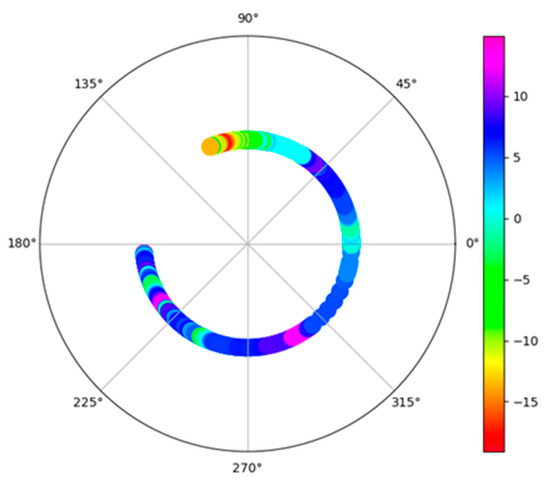
Figure 9.
Transmitting Tx-Rx angle values corresponding to contribution to generate PL prediction.
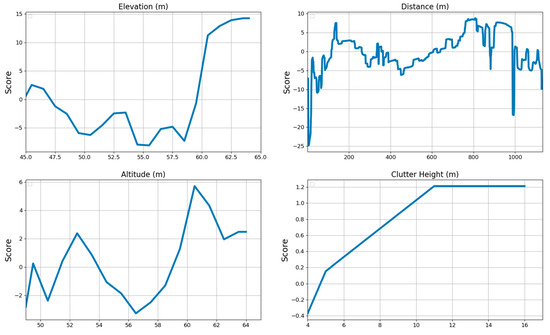
Figure 10.
Independent feature values and their contribution to generating PL prediction.
The center point in Figure 9 represents the location of the transmitter. The ring around the center point represents the PL strengthening or weakening when it transmits from the base station towards a specific direction. The effect of the Tx-Rx angle on PL can be understood based on the path profile (represented by buildings, trees, roads, etc.) in the area between the transceivers. For instance, the light green colored transmitting angles close to 90 degrees can be referred to the locations on the route A next to the label ‘Canaan Land Church’ in Figure 4 and next to the “Coverant University Gate’ in the corresponding DTM. These locations often lie on the line of sight (LoS) path between Tx and Rx. The pink or dark blue colored transmission angles in between 180–225 degrees in Figure 9 can be referred to multiple buildings under way from Tx towards the receivers in the route C, causing strong non-line-of-sight (NLoS) effects, e.g., in the locations next to the ‘Coverant University Center for Learning’ (in DTM map), ‘Esther Hall’, and ‘Coverant University Chapel’ (in Figure 4), respectively.
The overall elevation’s effect is shown in the upper left-hand panel in Figure 10. It can be divided into three parts consisting of elevations under 50 m, between 50 m and 58 m, and above 58 m. While we observe an absolute decreasing contribution to PL up to 50 meters’ level, the contribution of elevation to PL in the range between 50 m and 58 m shows volatilities. From above 58 meters’ levels onward up to 65 m, the effect of elevation on signal weakening amplifies drastically to make this feature the second most important PL determinant above others. The feature distance (upper right panel in Figure 10) reveals a typical logarithmic characteristic, with a rapid rise from the minimum distance up to around 200 m and then with slightly increasing (but fluctuating) overall slopes from that point onward.
The effect of increasing the receiver’s altitude (lower left panel in Figure 10) shows a sinus-shaped (but globally increasing) contribution with less than ca 6 dB and 4 dB impacts above and below the zero line, respectively.
The effect of clutter height is shown in the lower right panel in Figure 10. Up to 11 m, clutter height has zero influence on the PL behavior of the terrain. From 11 m to 16 m, clutter height has a constant impact of under 2 dB on the PL.
- (3)
- Interactive Feature Marginal Contribution
Figure 11 demonstrates the contribution of the interaction effect (explained by Equation (11)) between the independent features. The value of the color represents the average contribution of the combination of the corresponding feature values in dB units to the model’s PL predictions. The interaction effects must be interpreted beyond the net effect of each single independent feature, which has been incorporated in model decisions beforehand. The interaction of distance and the Tx-Rx angle, which is identified as the foremost interactive effect in our model, is represented in the foremost panel in Figure 11. The combination of distance and the Tx-Rx angle can be understood as a proxy feature of site-specific attributes, e.g., a building’s density, shape, material, etc., at each receiver’s location point. The trained EBM model based on the measurements along the survey routes suggests receiver location-specific effects on PL ranging from −20 dB up to +20 dB, depending on the receiver point, with most of the locations in the average range. The result shows distinct spatial zones depending on distance and the Tx-Rx angle ranges. For example, the area with the highest interactive effect on increasing PL is the region comprising the locations with a distance above 600 m from the transmitter location and Tx-Rx degrees ranging from −120 degrees up to −175 degrees, while the region with a distance above 600 m from the transmitter location and Tx-Rx degrees ranging from 50 degrees up to 100 degrees are the receiver locations with the highest interactive effect on decreasing PL. Further interpretation of the interactive results requires more detailed spatial information of the area between the transmitter and the receiver, as well as the specific attributes of the receiver location.
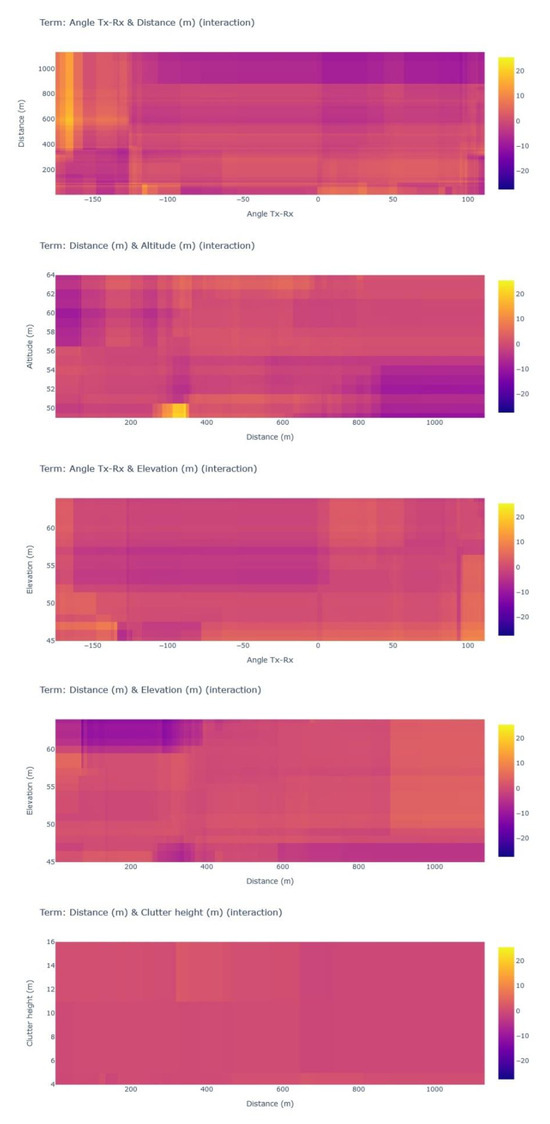
Figure 11.
Interactive contribution of independent features to generate PL prediction.
7. Conclusions
While contributions of ML-driven PL models in the literature of communication systems are increasing, our paper, by means of a systematic literature research, shows that only a subset of the studies apply XAI to clarify the logic behind the corresponding ML models to predict PL. The literature analysis in this paper furthermore indicates that, while the usage of intrinsically interpretable XAI methods to understand the ML model’s decision rationale is pivotal, it is not yet applied. This paper takes a first step to exemplify the feasibility of balancing the prediction accuracy and explanation power of PL modeling via inherently explainable ML models. In addition, transforming longitude-latitude information to polar coordinates is applied in this paper. We thereby disentangle the primary role of the Tx-Rx transmitting angle as the foremost significant feature to explain signal strengthening or weakening in the studied university campus area. Elevation of receiver locations and their distance from the transmitter are explained as the second and third influential features, in the underlying environment, respectively. In addition, the magnitude of the effects of each of the significant features on signal propagation in the underlying environment of our study is illuminated.
In future research, the glass box models applied in our paper can be further examined by applying them to multiple further signal attenuation problems comprising multiple terrains, frequencies, and transceiver configurations. Also, the comparison to deterministic modeling via ray tracing (RT) techniques could be interesting. We have tested our models in this paper on synthetically generated data based on the empirical 3GPP model, which demonstrates accurate and transparent results in the same way as shown in this paper (The code and the input data to replicate the 3GPP model can be downloaded at the Supplementary Material of this paper). The results provide a foundational basis for our further research on examining the applied models in the implemented propagation environment and radio system setup in the project NoLa (Nomadic 5G Networks for Small-Scale Rural Areas https://nola-5g.de/, accessed on 20 February 2025). Thereby, we aim to explore multiple parameters, including signal strength, data throughput, latency, and packet loss. Adding additional information to the input part, e.g., the receiver points’ degree of LoS or NLoS information, the terrain occupancy map, and vegetation distribution on the path between the transceivers, can enhance the efficiency of our modelling in the next step.
The feasibility of applying GNAMs to incorporate the bilateral interactive effects of the influencing features (GA2Ms), as well as higher orders of interactions within PL prediction environments, can be a further research subject. GNAMs can incorporate a variety of networks as alternatives to MLP, e.g., CNN, ResNet, RandomFourierNet, etc., as the default, which can render more computational flexibility in dealing with more complex tasks.
Supplementary Materials
The supporting information including the data and code can be downloaded at: https://gitlab.uni-koblenz.de/hamedkhalili/nola (accessed on 25 March 2025).
Author Contributions
Conceptualization, H.F., M.A.W. and H.K.; methodology, H.F. and H.K.; software, H.K.; validation, M.A.W. and H.F.; formal analysis, H.K.; investigation, H.K.; resources, M.A.W. and H.F.; data curation, H.K.; writing—original draft preparation, H.K.; writing—review and editing, M.A.W. and H.F.; visualization, H.K.; supervision, M.A.W. and H.F.; project administration, M.A.W.; funding acquisition, M.A.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was conducted within the NoLa project, funded in the InnoNT program of the German Federal Ministry for Digital and Transport (BMDV), grant 19OI23015A.
Data Availability Statement
The datasets analyzed in the current study are available at https://doi.org/10.1016/j.dib.2018.02.026.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Khanh, Q.V.; Hoai, N.V.; Manh, L.D.; Le, A.N.; Jeon, G. Wireless Communication Technologies for IoT in 5G: Vision, Applications, and Challenges. Wirel. Commun. Mob. Comput. 2022, 2022, 3229294. [Google Scholar] [CrossRef]
- Phillips, C.; Sicker, D.; Grunwald, D. A survey of wireless path loss prediction and coverage mapping methods. IEEE Commun. Surv. Tutor. 2013, 15, 255–270. [Google Scholar] [CrossRef]
- Shaibu, F.E.; Onwuka, E.N.; Salawu, N.; Oyewobi, S.S.; Djouani, K.; Abu-Mahfouz, A.M. Performance of Path Loss Models over Mid-Band and High-Band Channels for 5G Communication Networks: A Review. Future Internet 2023, 15, 362. [Google Scholar] [CrossRef]
- Miller, T. Explanation in artificial intelligence: Insights from the social sciences. Artif. Intell. 2019, 267, 1–38. [Google Scholar] [CrossRef]
- Allgaier, J.; Mulansky, L.; Draelos, R.L.; Pryss, R. How does the model make predictions? A systematic literature review on the explainability power of machine learning in healthcare. Artif. Intell. Med. 2023, 143, 102616. [Google Scholar] [CrossRef]
- Confalonieri, R.; Coba, L.; Wagner, B.; Besold, T.R. A historical perspective of explainable Artificial Intelligence. WIREs Data Min. Knowl. Discov. 2021, 11, e1391. [Google Scholar] [CrossRef]
- Angelov, P.P.; Soares, E.A.; Jiang, R.; Arnold, N.I.; Atkinson, P.M. Explainable artificial intelligence: An analytical review. WIREs Data Min. Knowl. Discov. 2021, 11, e1424. [Google Scholar] [CrossRef]
- Vollert, S.; Atzmueller, M.; Theissler, A. Interpretable Machine Learning: A brief survey from the predictive maintenance perspective. In Proceedings of the 2021 26th IEEE International Conference on Emerging Technologies and Factory Automation (ETFA), Vasteras, Sweden, 7–10 September 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Popoola, S.I.; Atayero, A.A.; Arausi, Q.D.; Matthews, V.O. Path loss dataset for modeling radio wave propagation in smart campus environment. Data Brief 2018, 17, 1062–1073. [Google Scholar] [CrossRef]
- Popoola, S.I.; Atayero, A.A.; Popoola, O.A. Comparative assessment of data obtained using empirical models for path loss predictions in a university campus environment. Data Brief 2018, 18, 380–393. [Google Scholar] [CrossRef]
- Juang, R.T. Explainable Deep-Learning-Based Path Loss Prediction from Path Profiles in Urban Environments. Appl. Sci. 2021, 11, 6690. [Google Scholar] [CrossRef]
- Yazici, I.; Özkan, E.; Gures, E. Enhancing Path Loss Prediction Through Explainable Machine Learning Approach. In Proceedings of the 2024 11th International Conference on Wireless Networks and Mobile Communications (WINCOM), Leeds, UK, 23–25 July 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Sani, U.S.; Malik, O.A.; Lai, D.T.C. Improving Path Loss Prediction Using Environmental Feature Extraction from Satellite Images: Hand-Crafted vs. Convolutional Neural Network. Appl. Sci. 2022, 12, 7685. [Google Scholar] [CrossRef]
- Nuñez, Y.; Lisandro, L.; da Silva Mello, L.; Orihuela, C. On the interpretability of machine learning regression for path-loss prediction of millimeter-wave links. Expert Syst. Appl. 2023, 215, 119324. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, Y.; Yu, L.; Yuan, Z.; Liu, G.; Wang, Q. Environment Features-Based Model for Path Loss Prediction. IEEE Wirel. Commun. Lett. 2022, 11, 2010–2014. [Google Scholar] [CrossRef]
- Liao, X.; Zhou, P.; Wang, Y.; Zhang, J. Path Loss Modeling and Environment Features Powered Prediction for Sub-THz Communication. IEEE Open J. Antennas Propag. 2024, 5, 1734–1746. [Google Scholar] [CrossRef]
- Elshennawy, W. Large Intelligent Surface-Assisted Wireless Communication and Path Loss Prediction Model Based on Electromagnetics and Machine Learning Algorithms. Prog. Electromagn. Res. C 2022, 119, 65–79. [Google Scholar] [CrossRef]
- Nuñez, Y.; Lisandro, L.; da Silva Mello, L.; Ramos, G.; Leonor, N.R.; Faria, S.; Caldeirinha, F.S. Path Loss Prediction for Vehicular-to-Infrastructure Communication Using Machine Learning Techniques. In Proceedings of the 2023 IEEE Virtual Conference on Communications (VCC), Virtual, 28–30 November 2023; pp. 270–275. [Google Scholar] [CrossRef]
- Hussain, S.; Bacha, S.F.N.; Cheema, A.A.; Canberk, B.; Duong, T.Q. Geometrical Features Based-mmWave UAV Path Loss Prediction Using Machine Learning for 5G and Beyond. IEEE Open J. Commun. Soc. 2024, 5, 5667–5679. [Google Scholar] [CrossRef]
- Turan, B.; Uyrus, A.; Koc, O.N.; Kar, E.; Coleri, S. Machine Learning Aided Path Loss Estimator and Jammer Detector for Heterogeneous Vehicular Networks. In Proceedings of the 2021 IEEE Global Communications Conference (GLOBECOM), Madrid, Spain, 7–11 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Wieland, F.; Drescher, Z.; Houser, J. Comparing Path Loss Prediction Methods for Low Altitude UAS Flights. In Proceedings of the 2021 IEEE/AIAA 40th Digital Avionics Systems Conference (DASC), San Antonio, TX, USA, 3–7 October 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Khalili, H.; Wimmer, M.A. Towards Improved XAI-Based Epidemiological Research into the Next Potential Pandemic. Life 2024, 14, 783. [Google Scholar] [CrossRef]
- Perrier, A. Feature Importance in Random Forests. Cit. on p. 6. 2015. Available online: https://scholar.google.com/scholar?q=Perrier,%20A.%20Feature%20Importance%20in%20Random%20Forests.%20Cit.%20on%20p.%206.%202015 (accessed on 28 February 2025).
- Ahmed, N.S.; Sadiq, M.H. Clarify of the Random Forest Algorithm in an Educational Field. In Proceedings of the 2018 International Conference on Advanced Science and Engineering (ICOASE), Duhok, Iraq, 9–11 October 2018; pp. 179–184. [Google Scholar] [CrossRef]
- Rostami, M.; Oussalah, M.A. Novel explainable COVID-19 diagnosis method by integration of feature selection with random forest. Inform. Med. Unlocked 2022, 30, 100941. [Google Scholar] [CrossRef]
- Sharma, P.; Singh, R.K. Comparative Analysis of Propagation Path loss Models with Field Measured Data. Int. J. Eng. Sci. Technol. 2010, 2, 2008–2013. [Google Scholar]
- Singh, H.; Gupta, S.; Dhawan, C.; Mishra, A. Path Loss Prediction in Smart Campus Environment: Machine Learning-based Approaches. In Proceedings of the 2020 IEEE 91st Vehicular Technology Conference (VTC2020-Spring), Antwerp, Belgium, 25–28 May 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Molnar, C. Interpretable Machine Learning. A Guide for Making Black Box Models Explainable. 2022. Available online: https://christophmolnar.com/books/ (accessed on 9 January 2025).
- Hastie, T.J.; Tibshirani, R.J. Generalized Additive Models, 1st ed.; Routledge: London, UK, 2017. [Google Scholar]
- Agarwal, R.; Melnick, L.; Frosst, N.; Zhang, X.; Lengerich, B.; Caruana, R.; Hinton, G. Neural Additive Models: Interpretable Machine Learning with Neural Nets. arXiv 2021, arXiv:2004.13912. [Google Scholar]
- Nori, H.; Jenkins, S.; Koch, P.; Caruana, R. InterpretML: A Unified Framework for Machine Learning Interpretability; Microsoft Corporation: Redmond, WA, USA, 2019; Available online: https://arxiv.org/pdf/1909.09223 (accessed on 9 January 2025).
- Greenwell, B.M.; Dahlmann, A.; Dhoble, S. Explainable Boosting Machines with Sparsity: Maintaining Explainability in High-Dimensional Settings. arXiv 2023, arXiv:2311.07452. [Google Scholar]
- Lou, Y.; Caruana, R.; Gehrke, J.; Hooker, G. Accurate intelligible models with pairwise interactions. In Proceedings of the 19th ACMSIGKDD International Conference on Knowledge Discovery and Data Mining, Chicago, IL, USA, 11–14 August 2013; pp. 623–631. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).