Distributed Denial of Service Attack Detection in Software-Defined Networks Using Decision Tree Algorithms
Abstract
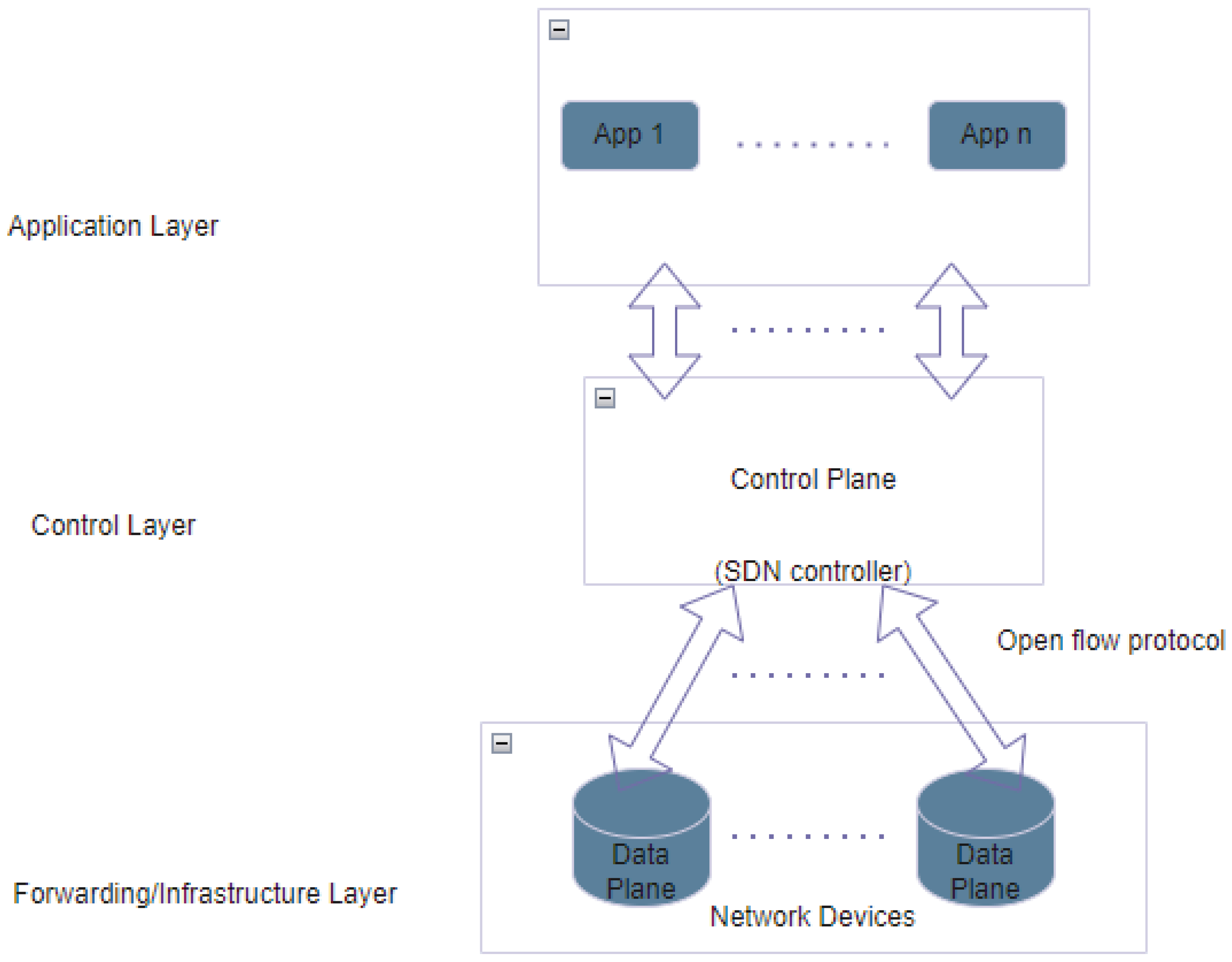
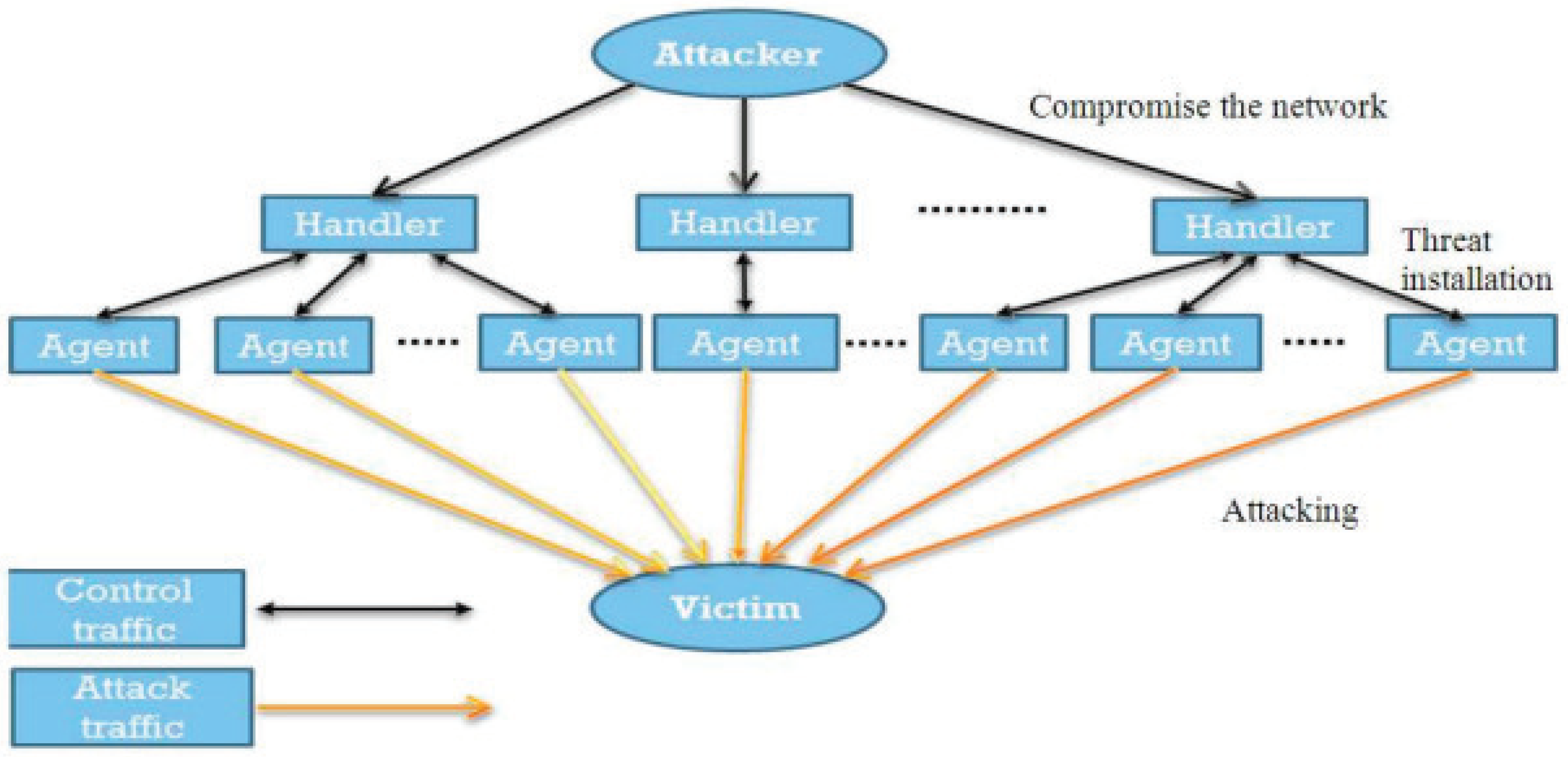
1. Introduction
2. Background and Description of Datasets
2.1. The Study of Ahuja et al. [1]
2.2. The Study of Elsayed et al. [2]
3. Novelty and Contributions
- In the past studies on the detection of DDoS attacks, SDN-specific datasets were not available or not utilized. As such, the main focus in those studies was the creation of datasets. In the present study, our contribution is in utilizing two recent and core datasets for the underyling problem while utilizing a decision-tree-based approach. The availability of two datasets has enabled us to verify that the detection of malicious and benign network traffic is closer to how it appears in reality, as opposed to being biased towards how it is represented in a single dataset.
- The previous technique by Ahuja et al. [1] had multiple steps involved, which increased the complexity of the overall algorithm. In the technique proposed herein, certain algorithmic layers and encoding techniques have been removed altogether, and there is no implementation of t-SNE (see details in the next section). This removal results in the proposed approach being simpler. Furthermore, Elsayed et al. [2] applied RF directly to their dataset, but random forest requires certain parameters’ selection, which leads to a grid search for optimization. Our contribution is in proposing a technique that avoids the above issues, leading to a simpler and time-efficient approach.
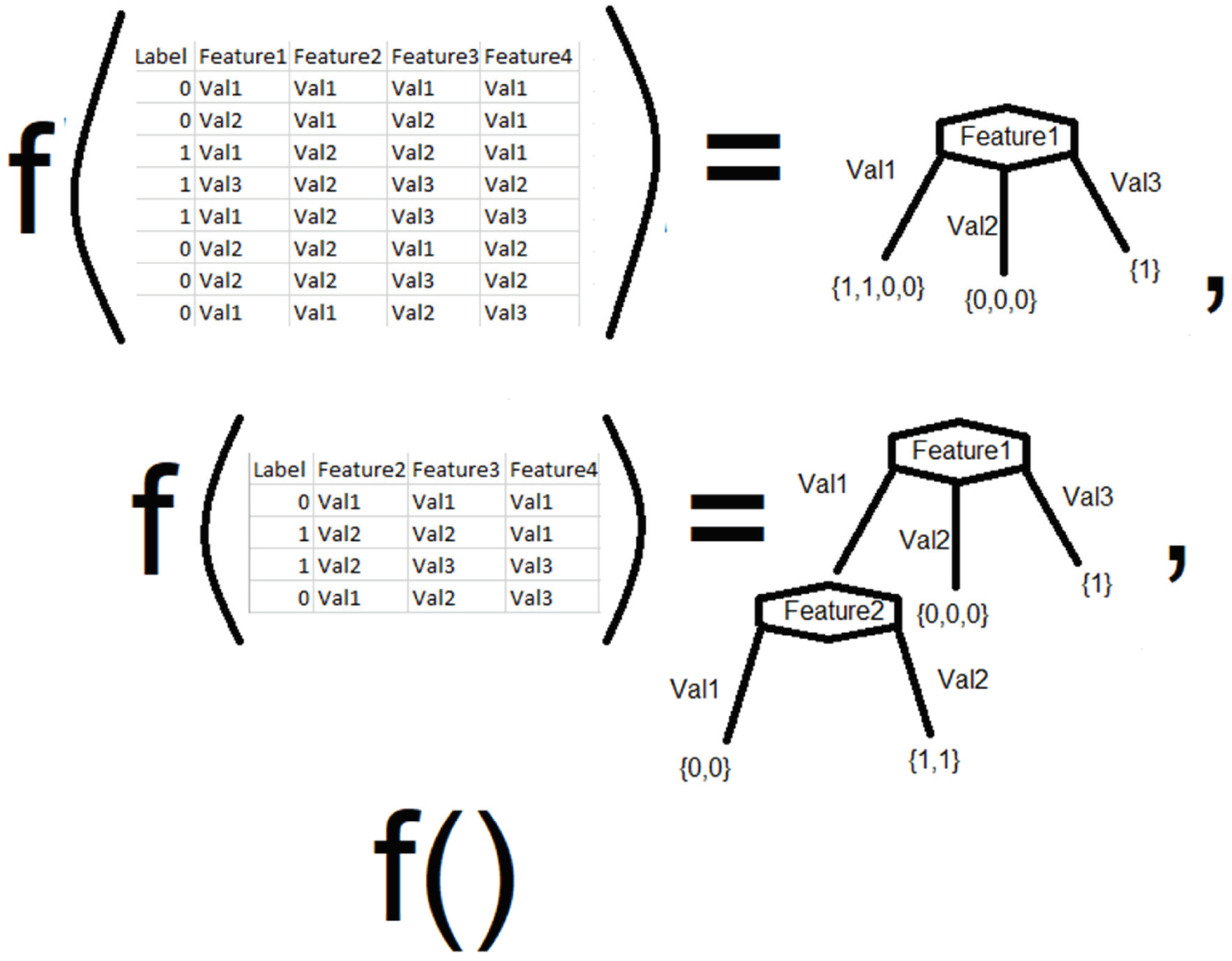
- In the present study, a simple algorithm enhancement to the decision tree algorithm, called the greedy decision tree (GDT), is proposed. The GDT technique involves iteratively constructing a DT, selecting features that give the best results when added to the previously constructed DT. It is shown that the results of this approach are comparable or better than those obtained by Ahuja et al. and Elsayed et al. [1,2].
- Stability analysis of the GDT algorithm is performed to demonstrate its behavior under different conditions while using the aforementioned two SDN-specific datasets.
4. Proposed Approach
4.1. Motivation
4.1.1. Why Decision Tree?
4.1.2. Reduction in Computational Complexity
4.2. Algorithm Selection
- Select the attribute with the lowest Gini index/highest information gain/gain ratio.
- Split the initial data into subsets.
- Apply the same technique to the subsets, leaving out the attribute that has already been selected.
- Stop when entropy becomes 0 or no more attributes are left.
| Algorithm 1 Greedy Decision Tree (F). |
|
5. Performance Measures
- True positive (): legitimate traffic correctly classified as legitimate.
- True negative (): illegitimate traffic correctly classified as illegitimate.
- False positive (): legitimate traffic incorrectly classified as illegitimate.
- False negative (): illegitimate traffic incorrectly classified as legitimate.
6. Results and Discussion
6.1. Comparison of CART and Modified CART Algorithms
6.2. Comparison of Proposed Greedy Decision Tree with Other Techniques
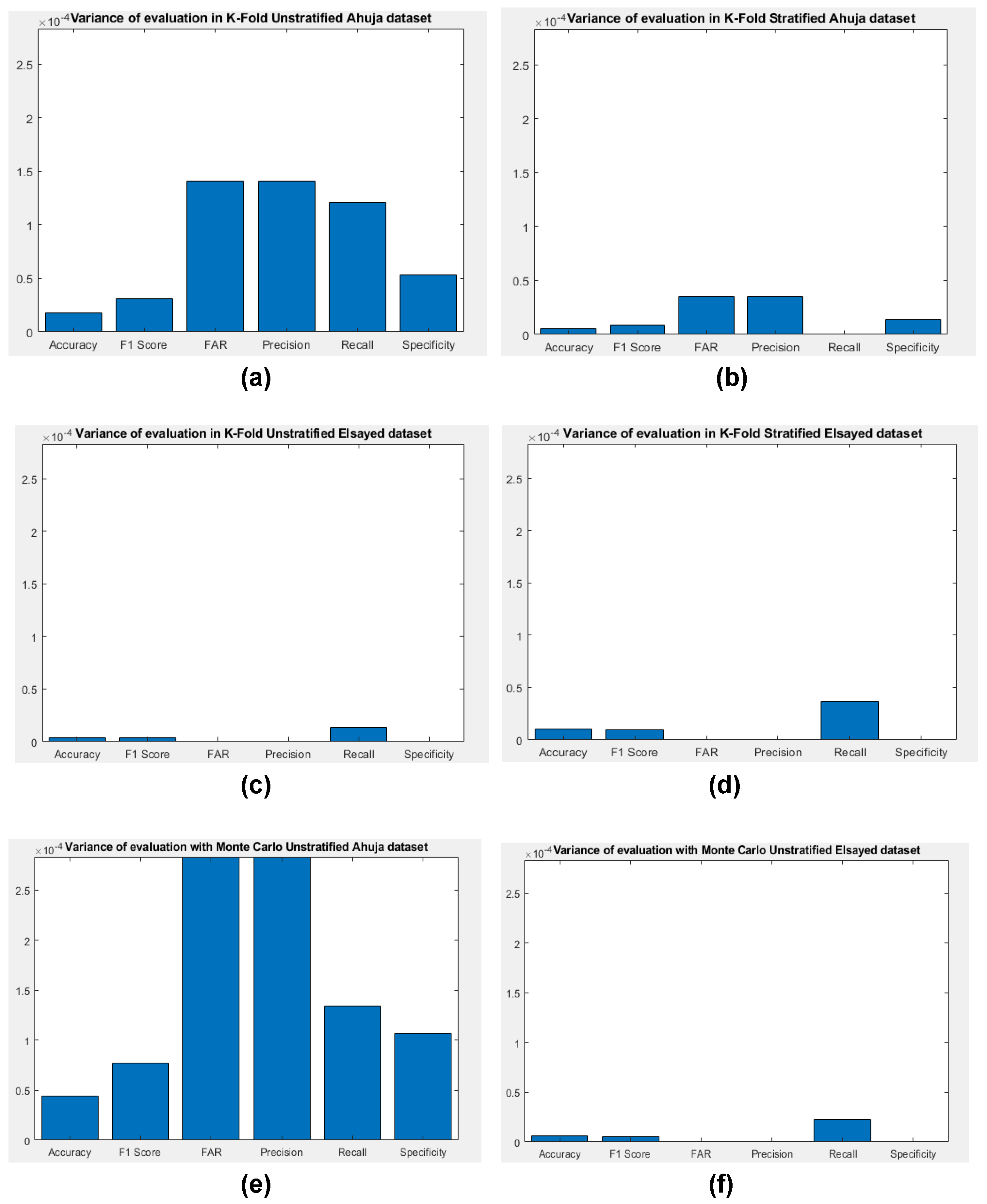
6.3. Stability Analysis of the Greedy Decision Tree Algorithm
7. Limitations of the Proposed Method
8. Conclusions and Future Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial neural network |
| CART | Classification and regression tree |
| CNN | Convolutional neural network |
| DDoS | Distributed denial of service |
| DL | Deep learning |
| DNN | Deep neural network |
| DT | Decision tree |
| EL | Ensemble learning |
| FNN | Feedforward neural network |
| GDT | Greedy decision tree |
| GLM | General linear model |
| GRU | Gated recurrent unit |
| KNN | K-nearest neighbors |
| LDA | Linear discriminant analysis |
| LSTM | Long short-term memory |
| ML | Machine learning |
| MLP | Multi-layer perceptron |
| NB | Naive Bayes |
| PCA | Principal component analysis |
| RF | Random forest |
| RNN | Recurrent neural network |
| SDN | Software-defined network |
| SVC | Support vector classifier |
| SVM | Support vector machine |
| t-SNE | t-distributed stochastic neighborhood embedding |
References
- Ahuja, N.; Singal, G.; Mukhopadhyay, D.; Kumar, N. Automated DDOS attack detection in software defined networking. J. Netw. Comput. Appl. 2021, 187, 103108. [Google Scholar] [CrossRef]
- Elsayed, M.S.; Le-Khac, N.A.; Jurcut, A.D. InSDN: A novel SDN intrusion dataset. IEEE Access 2020, 8, 165263–165284. [Google Scholar] [CrossRef]
- Javaid, S.; Afzal, H.; Babar, M.; Arif, F.; Tan, Z.; Jan, M.A. ARCA-IoT: An attack-resilient cloud-assisted IoT system. IEEE Access 2019, 7, 19616–19630. [Google Scholar] [CrossRef]
- Babar, M.; Tariq, M.U.; Jan, M.A. Secure and resilient demand side management engine using machine learning for IoT-enabled smart grid. Sustain. Cities Soc. 2020, 62, 102370. [Google Scholar] [CrossRef]
- Eliyan, L.F.; Di Pietro, R. DoS and DDoS attacks in Software Defined Networks: A survey of existing solutions and research challenges. Future Gener. Comput. Syst. 2021, 122, 149–171. [Google Scholar] [CrossRef]
- Nicholson, P. AWS hit by Largest Reported DDoS Attack of 2.3 Tbps. 2023. Available online: https://www.a10networks.com/blog/aws-hit-by-largest-reported-ddos-attack-of-2-3-tbps/ (accessed on 3 October 2023).
- Bhaya, W.; Manaa, M.E. Review clustering mechanisms of distributed denial of service attacks. J. Comput. Sci. 2014, 10, 2037. [Google Scholar] [CrossRef]
- Rehman, A.; Haseeb, K.; Alam, T.; Alamri, F.S.; Saba, T.; Song, H. Intelligent secured traffic optimization model for urban sensing applications with Software Defined Network. IEEE Sens. J. 2024, 24, 5654–5661. [Google Scholar]
- Nadeem, M.W.; Goh, H.G.; Ponnusamy, V.; Aun, Y. DDoS Detection in SDN using Machine Learning Techniques. Comput. Mater. Contin. 2021, 71, 771–789. [Google Scholar]
- Palmieri, F. Network anomaly detection based on logistic regression of nonlinear chaotic invariants. J. Netw. Comput. Appl. 2019, 148, 102460. [Google Scholar]
- Santos, R.; Souza, D.; Santo, W.; Ribeiro, A.; Moreno, E. Machine learning algorithms to detect DDoS attacks in SDN. Concurr. Comput. Pract. Exp. 2019, 32, e5402. [Google Scholar] [CrossRef]
- Niyaz, Q.; Sun, W.; Javaid, A. A deep learning based DDoS detection system in software-defined networking (SDN). arXiv 2016, arXiv:1611.07400. [Google Scholar]
- da Silva, A.S.; Wickboldt, J.A.; Granville, L.Z.; Schaeffer-Filho, A. ATLANTIC: A framework for anomaly traffic detection, classification, and mitigation in SDN. In Proceedings of the NOMS 2016-2016 IEEE/IFIP Network Operations and Management Symposium, Istanbul, Turkey, 25–29 April 2016; pp. 27–35. [Google Scholar]
- Bahashwan, A.A.; Anbar, M.; Manickam, S.; Al-Amiedy, T.A.; Aladaileh, M.A.; Hasbullah, I.H. A Systematic Literature Review on Machine Learning and Deep Learning Approaches for Detecting DDoS Attacks in Software-Defined Networking. Sensors 2023, 23, 4441. [Google Scholar] [CrossRef] [PubMed]
- Karan, B.; Narayan, D.; Hiremath, P. Detection of DDoS attacks in software defined networks. In Proceedings of the 2018 3rd International Conference on Computational Systems and Information Technology for Sustainable Solutions (CSITSS), Bengaluru, India, 20–22 December 2018; pp. 265–270. [Google Scholar]
- Yang, L.; Zhao, H. DDoS attack identification and defense using SDN based on machine learning method. In Proceedings of the 2018 15th International Symposium on Pervasive Systems, Algorithms and Networks (I-SPAN), Yichang, China, 16–18 October 2018; pp. 174–178. [Google Scholar]
- Sudar, K.M.; Beulah, M.; Deepalakshmi, P.; Nagaraj, P.; Chinnasamy, P. Detection of Distributed Denial of Service Attacks in SDN using Machine learning techniques. In Proceedings of the 2021 International Conference on Computer Communication and Informatics (ICCCI), Coimbatore, India, 27–29 January 2021; pp. 1–5. [Google Scholar]
- Kavitha, M.; Suganthy, M.; Biswas, A.; Srinivsan, R.; Kavitha, R.; Rathesh, A. Machine Learning Techniques for Detecting DDoS Attacks in SDN. In Proceedings of the 2022 International Conference on Automation, Computing and Renewable Systems (ICACRS), Pudukkottai, India, 13–15 December 2022; pp. 634–638. [Google Scholar]
- Wang, S.; Balarezo, J.F.; Chavez, K.G.; Al-Hourani, A.; Kandeepan, S.; Asghar, M.R.; Russello, G. Detecting flooding DDoS attacks in software defined networks using supervised learning techniques. Eng. Sci. Technol. Int. J. 2022, 35, 101176. [Google Scholar]
- Revathi, M.; Ramalingam, V.; Amutha, B. A machine learning based detection and mitigation of the DDOS attack by using SDN controller framework. Wirel. Pers. Commun. 2022, 127, 2417–2441. [Google Scholar] [CrossRef]
- Gebremeskel, T.G.; Gemeda, K.A.; Krishna, T.G.; Ramulu, P.J. DDoS Attack Detection and Classification Using Hybrid Model for Multicontroller SDN. Wirel. Commun. Mob. Comput. 2023, 9965945. [Google Scholar] [CrossRef]
- Elubeyd, H.; Yiltas-Kaplan, D. Hybrid Deep Learning Approach for Automatic DoS/DDoS Attacks Detection in Software-Defined Networks. Appl. Sci. 2023, 13, 3828. [Google Scholar]
- Hassan, A.I.; El Reheem, E.A.; Guirguis, S.K. An entropy and machine learning based approach for DDoS attacks detection in software defined networks. Sci. Rep. 2024, 14, 18159. [Google Scholar]
- Luong, T.K.; Tran, T.D.; Le, G.T. DDoS attack detection and defense in SDN based on machine learning. In Proceedings of the 2020 7th NAFOSTED Conference on Information and Computer Science (NICS), Ho Chi Minh City, Vietnam, 26–27 November 2020; pp. 31–35. [Google Scholar]
- Alamri, H.A.; Thayananthan, V. Analysis of machine learning for securing software-defined networking. Procedia Comput. Sci. 2021, 194, 229–236. [Google Scholar] [CrossRef]
- Karki, D.; Dawadi, B.R. Machine Learning based DDoS Detection System in Software-Defined Networking. In Proceedings of the 11th IOE Graduate Conference, Pokhara, Nepal, 9–10 March 2022; pp. 228–246. [Google Scholar]
- Dheyab, S.A.; Abdulameer, S.M.; Mostafa, S. Efficient Machine Learning Model for DDoS Detection System Based on Dimensionality Reduction. Acta Inform. Pragensia 2022, 11, 348–360. [Google Scholar]
- Sanmorino, A.; Marnisah, L.; Di Kesuma, H. Detection of DDoS Attacks using Fine-Tuned Multi-Layer Perceptron Models. Eng. Technol. Appl. Sci. Res. 2024, 14, 16444–16449. [Google Scholar] [CrossRef]
- Mehmood, S.; Amin, R.; Mustafa, J.; Hussain, M.; Alsubaei, F.S.; Zakaria, M.D. Distributed Denial of Services (DDoS) attack detection in SDN using Optimizer-equipped CNN-MLP. PLoS ONE 2025, 20, e0312425. [Google Scholar] [CrossRef] [PubMed]
- Rahman, O.; Quraishi, M.A.G.; Lung, C.H. DDoS attacks detection and mitigation in SDN using machine learning. In Proceedings of the 2019 IEEE World Congress on Services (SERVICES), Milan, Italy, 8–13 July 2019; Volume 2642, pp. 184–189. [Google Scholar]
- Almadhor, A.; Altalbe, A.; Bouazzi, I.; Hejaili, A.A.; Kryvinska, N. Strengthening network DDOS attack detection in heterogeneous IoT environment with federated XAI learning approach. Sci. Rep. 2024, 14, 24322. [Google Scholar] [CrossRef]
- Kyaw, A.T.; Oo, M.Z.; Khin, C.S. Machine-learning based DDOS attack classifier in software defined network. In Proceedings of the 2020 17th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Phuket, Thailand, 24–27 June 2020; pp. 431–434. [Google Scholar]
- Firdaus, D.; Munadi, R.; Purwanto, Y. Ddos attack detection in software defined network using ensemble k-means++ and random forest. In Proceedings of the 2020 3rd International Seminar on Research of Information Technology and Intelligent Systems (ISRITI), Yogyakarta, Indonesia, 10–11 December 2020; pp. 164–169. [Google Scholar]
- Nugraha, B.; Murthy, R.N. Deep learning-based slow DDoS attack detection in SDN-based networks. In Proceedings of the 2020 IEEE Conference on Network Function Virtualization and Software Defined Networks (NFV-SDN), Leganes, Spain, 10–12 November 2020; pp. 51–56. [Google Scholar]
- Alshra’a, A.S.; Farhat, A.; Seitz, J. Deep learning algorithms for detecting denial of service attacks in software-defined networks. Procedia Comput. Sci. 2021, 191, 254–263. [Google Scholar] [CrossRef]
- Altamemi, A.J.; Abdulhassan, A.; Obeis, N.T. DDoS attack detection in software defined networking controller using machine learning techniques. Bull. Electr. Eng. Inform. 2022, 11, 2836–2844. [Google Scholar] [CrossRef]
- Karthika, P.; Arockiasamy, K. Simulation of SDN in mininet and detection of DDoS attack using machine learning. Bull. Electr. Eng. Inform. 2023, 12, 1797–1805. [Google Scholar] [CrossRef]
- Kannan, C.; Muthusamy, R.; Srinivasan1, V.; Chidambaram, V.; Karunakaran, K. Machine learning based detection of DDoS attacks in software defined network. Indones. J. Electr. Eng. Comput. Sci. 2023, 32, 1503–1511. [Google Scholar] [CrossRef]
- Hassan, H.A.; Hemdan, E.E.D.; El-Shafai, W.; Shokair, M.; Abd El-Samie, F.E. Detection of attacks on software defined networks using machine learning techniques and imbalanced data handling methods. Secur. Priv. 2024, 7, e350. [Google Scholar] [CrossRef]
- Haq, I.; Khan, S.A.; Mohammad, N.; Zaman, A. Optimizing Distributed Denial of Service (DDoS) Attack Detection Techniques on Software Defined Network (SDN) Using Feature Selection. In Proceedings of the 2024 4th International Conference on Innovations in Computer Science (ICONICS), Karachi, Pakistan, 13–14 November 2024; pp. 1–7. [Google Scholar]
- Potdar, K.; Pardawala, T.S.; Pai, C.D. A comparative study of categorical variable encoding techniques for neural network classifiers. Int. J. Comput. Appl. 2017, 175, 7–9. [Google Scholar] [CrossRef]
- Hancock, J.T.; Khoshgoftaar, T.M. Survey on categorical data for neural networks. J. Big Data 2020, 7, 1–41. [Google Scholar] [CrossRef]
- Duan, J. Financial system modeling using deep neural networks (DNNs) for effective risk assessment and prediction. J. Frankl. Inst. 2019, 356, 4716–4731. [Google Scholar] [CrossRef]
- Trunk, G.V. A problem of dimensionality: A simple example. IEEE Trans. Pattern Anal. Mach. Intell. 1979, PAMI-1, 306–307. [Google Scholar]
- Wheeler, A. PCA Does Not Make Sense After One Hot Encoding. 2021. Available online: https://andrewpwheeler.com/2021/06/22/pca-does-not-make-sense-after-one-hot-encoding/ (accessed on 12 December 2023).
- Ghosh, A.M.; Grolinger, K. Deep learning: Edge-cloud data analytics for iot. In Proceedings of the 2019 IEEE Canadian Conference of Electrical and Computer Engineering (CCECE), Edmonton, AB, Canada, 5–8 May 2019; pp. 1–7. [Google Scholar]
- Linting, M.; Meulman, J.J.; Groenen, P.J.; van der Koojj, A.J. Nonlinear principal components analysis: Introduction and application. Psychol. Methods 2007, 12, 336. [Google Scholar] [PubMed]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Xu, X.; Xie, Z.; Yang, Z.; Li, D.; Xu, X. A t-SNE based classification approach to compositional microbiome data. Front. Genet. 2020, 11, 620143. [Google Scholar]
- Vidyala, R. What, Why and How of t-SNE. 2020. Available online: https://medium.com/data-science/what-why-and-how-of-t-sne-1f78d13e224d#:~:text=t%2DSNE%20plots%20are%20highly,parameter%20for%20all%20the%20runs (accessed on 11 November 2023).
- Shah, R.; Silwal, S. Using dimensionality reduction to optimize t-sne. arXiv 2019, arXiv:1912.01098. [Google Scholar]
- Waagen, D.; Hulsey, D.; Godwin, J.; Gray, D.; Barton, J.; Farmer, B. t-SNE or not t-SNE, that is the question. In Proceedings of the Automatic Target Recognition XXXI, SPIE, Online, 12–16 April 2021; Volume 11729, pp. 62–71. [Google Scholar]
- Bahashwan, A.A.; Anbar, M.; Manickam, S.; Issa, G.; Aladaileh, M.A.; Alabsi, B.A.; Rihan, S.D.A. HLD-DDoSDN: High and low-rates dataset-based DDoS attacks against SDN. PLoS ONE 2024, 19, e0297548. [Google Scholar]
- Negera, W.G.; Schwenker, F.; Debelee, T.G.; Melaku, H.M.; Feyisa, D.W. Lightweight model for botnet attack detection in software defined network-orchestrated IoT. Appl. Sci. 2023, 13, 4699. [Google Scholar] [CrossRef]
- Abtahi, S.M.; Rahmani, H.; Allahgholi, M.; Alizadeh Fard, S. ENIXMA: ENsemble of EXplainable Methods for detecting network Attack. Comput. Knowl. Eng. 2024, 7, 1–8. [Google Scholar]
- Navia-Vázquez, A.; Parrado-Hernández, E. Support vector machine interpretation. Neurocomputing 2006, 69, 1754–1759. [Google Scholar]
- Brüggenjürgen, S.; Schaaf, N.; Kerschke, P.; Huber, M.F. Mixture of Decision Trees for Interpretable Machine Learning. In Proceedings of the 2022 21st IEEE International Conference on Machine Learning and Applications (ICMLA), Nassau, Bahamas, 12–14 December 2022; pp. 1175–1182. [Google Scholar]
- Zhou, Q.; Li, R.; Xu, L.; Nallanathan, A.; Yang, J.; Fu, A. Towards Interpretable Machine-Learning-Based DDoS Detection. SN Comput. Sci. 2023, 5, 115. [Google Scholar]
- Pandey, P. Interpretable or Accurate? Why Not Both? 2021. Available online: https://towardsdatascience.com/interpretable-or-accurate-why-not-both-4d9c73512192 (accessed on 16 February 2024).
- Dinov, I.D.; Dinov, I.D. Black box machine-learning methods: Neural networks and support vector machines. In Data Science and Predictive Analytics: Biomedical and Health Applications using R; Springer: Cham, Switzerland, 2018; pp. 383–422. [Google Scholar]
- Siklar, M. Why Building Black-Box Models Can Be Dangerous. 2021. Available online: https://towardsdatascience.com/why-building-black-box-models-can-be-dangerous-6f885b252818 (accessed on 16 February 2024).
- Molnar, C. Interpretable Machine Learning. 2020. Available online: https://christophm.github.io/interpretable-ml-book/ (accessed on 25 January 2025).
- Anonymous. 2024. Available online: https://www.geeksforgeeks.org/iterative-dichotomiser-3-id3-algorithm-from-scratch/ (accessed on 27 October 2024).
- Abdullah, A.S.; Selvakumar, S.; Karthikeyan, P.; Venkatesh, M. Comparing the efficacy of decision tree and its variants using medical data. Indian J. Sci. Technol. 2017, 10, 1–8. [Google Scholar]
- MARS, vs. CART Regression Predictive Power. Available online: https://stats.stackexchange.com/questions/584597/mars-vs-cart-regression-predictive-power?newreg=089b481e966f41f1a224a90d681f7c09 (accessed on 8 March 2025).
- Breiman, L. Classification and Regression Trees; Routledge: Abingdon, UK, 2017. [Google Scholar]
- Tırınk, C.; Önder, H.; Francois, D.; Marcon, D.; Şen, U.; Shaikenova, K.; Omarova, K.; Tyasi, T.L. Comparison of the data mining and machine learning algorithms for predicting the final body weight for Romane sheep breed. PLoS ONE 2023, 18, e0289348. [Google Scholar]
- Rashid, R. Digital Analytics Decision Trees; CHAID vs CART. 2017. Available online: https://www.linkedin.com/pulse/digital-analytics-decision-trees-chaid-vs-cart-raymond-rashid/ (accessed on 8 March 2025).
- Shmueli, G. Classification Trees: CART vs. CHAID. 2007. Available online: https://www.bzst.com/2006/10/classification-trees-cart-vs-chaid.html (accessed on 8 March 2025).
- González, A.; Pérez, R. An experimental study about the search mechanism in the SLAVE learning algorithm: Hill-climbing methods versus genetic algorithms. Inf. Sci. 2001, 136, 159–174. [Google Scholar]
- Giarelis, N.; Kanakaris, N.; Karacapilidis, N. An innovative graph-based approach to advance feature selection from multiple textual documents. In Proceedings of the IFIP international Conference on Artificial Intelligence Applications and Innovations, Halkidiki, Greece, 5–7 June 2020; pp. 96–106. [Google Scholar]
- Kumar, R.R.; Tarang, G.R.; Adipudi, K.K.; Parvathaneni, V.; Steven, G. Performance Comparison of A* Search Algorithm and Hill-Climb Search Algorithm: A Case Study. In Multifaceted approaches for Data Acquisition, Processing & Communication; CRC Press: Boca Raton, FL, USA, 2024; pp. 185–194. [Google Scholar]
- Khan, S.A.; Iqbal, K.; Mohammad, N.; Akbar, R.; Ali, S.S.A.; Siddiqui, A.A. A Novel Fuzzy-Logic-Based Multi-Criteria Metric for Performance Evaluation of Spam Email Detection Algorithms. Appl. Sci. 2022, 12, 7043. [Google Scholar] [CrossRef]
- Haseeb-Ur-Rehman, R.M.A.; Aman, A.H.M.; Hasan, M.K.; Ariffin, K.A.Z.; Namoun, A.; Tufail, A.; Kim, K.H. High-speed network ddos attack detection: A survey. Sensors 2023, 23, 6850. [Google Scholar] [CrossRef]
- Adedeji, K.B.; Abu-Mahfouz, A.M.; Kurien, A.M. DDoS attack and detection methods in internet-enabled networks: Concept, research perspectives, and challenges. J. Sens. Actuator Netw. 2023, 12, 51. [Google Scholar] [CrossRef]
- Lapolli, Â.C.; Marques, J.A.; Gaspary, L.P. Offloading real-time DDoS attack detection to programmable data planes. In Proceedings of the 2019 IFIP/IEEE Symposium on Integrated Network and Service Management (IM), Arlington, VA, USA, 8–12 April 2019; pp. 19–27. [Google Scholar]
- Fonseca-Delgado, R.; Gomez-Gil, P. An assessment of ten-fold and Monte Carlo cross validations for time series forecasting. In Proceedings of the 2013 10th International Conference on Electrical Engineering, Computing Science and Automatic Control (CCE), Mexico City, Mexico, 30 September–4 October 2013; pp. 215–220. [Google Scholar]
- Patro, R. Cross-Validation: K Fold vs. Monte Carlo. 2021. Available online: https://towardsdatascience.com/cross-validation-k-fold-vs-monte-carlo-e54df2fc179b (accessed on 11 November 2023).
- Ensemble Algorithms. 2024. Available online: https://www.mathworks.com/help/stats/ensemble-algorithms.html (accessed on 7 March 2025).
- How Do You Choose Between Simple Random and Stratified Sampling? Available online: https://www.linkedin.com/advice/3/how-do-you-choose-between-simple-random-stratified-sampling (accessed on 13 December 2023).
- Elfil, M.; Negida, A. Sampling methods in clinical research; an educational review. Emergency 2017, 5, e52. [Google Scholar]
- Forman, G.; Scholz, M. Apples-to-apples in cross-validation studies: Pitfalls in classifier performance measurement. ACM SIGKDD Explor. Newsl. 2010, 12, 49–57. [Google Scholar]
- Last, M.; Maimon, O.; Minkov, E. Improving stability of decision trees. Int. J. Pattern Recognit. Artif. Intell. 2002, 16, 145–159. [Google Scholar]
- Jacobucci, R. Decision Tree Stability and Its Effect on Interpretation. Ph.D. Thesis, University of Notre Dame, Notre Dame, IN, USA, 2018. [Google Scholar]
- Szeghalmy, S.; Fazekas, A. A comparative study of the use of stratified cross-validation and distribution-balanced stratified cross-validation in imbalanced learning. Sensors 2023, 23, 2333. [Google Scholar] [CrossRef]
- Impact of Dataset Size on Classification Performance. Available online: https://dspace.mit.edu/bitstream/handle/1721.1/131330/applsci-11-00796.pdf?sequence=1 (accessed on 7 March 2025).
- Kusumura, Y. Maintain Model Robustness: Strategies to Combat Feature Drift in Machine Learning. 2023. Available online: https://dotdata.com/blog/maintain-model-robustness-strategies-to-combat-feature-drift-in-machine-learning/ (accessed on 7 March 2025).
- Ahmadi, A.; Sharif, S.S.; Banad, Y.M. A Comparative Study of Sampling Methods with Cross-Validation in the FedHome Framework. IEEE Trans. Parallel Distrib. Syst. 2025, 36, 570–579. [Google Scholar] [CrossRef]
- Decision Trees. Available online: https://www.ibm.com/think/topics/decision-trees (accessed on 7 March 2025).
- 8 Key Advantages and Disadvantages of Decision Trees. Available online: https://insidelearningmachines.com/advantages_and_disadvantages_of_decision_trees/ (accessed on 7 March 2025).
- Williams, S. Global Surge in DDoS Attacks Causes Dire Financial Consequences. 2024. Available online: https://securitybrief.in/story/global-surge-in-ddos-attacks-causes-dire-financial-consequences (accessed on 14 March 2024).
- Smith, G. DDoS Statistics: How Large a Threat Are DDoS Attacks? 2024. Available online: https://www.stationx.net/ddos-statistics/ (accessed on 14 March 2024).
- Blum, D.; Holling, H. Spearman’s law of diminishing returns. A meta-analysis. Intelligence 2017, 65, 60–66. [Google Scholar] [CrossRef]
- Hernández-Orallo, J. Is Spearman’s law of diminishing returns (SLODR) meaningful for artificial agents? In Proceedings of the ECAI —22nd European Conference on Artificial Intelligence, The Hague, The Netherlands, 29 August–2 September 2016; pp. 471–479. [Google Scholar]
| Reference | Year | Algorithms | Datasets |
|---|---|---|---|
| [15] | 2018 | SVM, DNN | KDD-Cup99, Mininet for SDN |
| [16] | 2018 | SVM | KDD-Cup99 |
| [11] | 2019 | SVM, MLP, DT (CART), RF | Scapy tool, Mininet |
| [30] | 2019 | DT (J48), RF, SVM, KNN | hping |
| [32] | 2020 | SVM (linear, polynomial) | Scapy tool |
| [33] | 2020 | K-means++, RF | InSDN |
| [24] | 2020 | DNN, linear SVM, DT, NB | CICIDS2018 |
| [34] | 2020 | CNN-LSTM, MLP, SVM | Self-generated |
| [2] | 2020 | KNN, NB, AdaBoost, DT, RF, rbf-SVM, lin SVM, MLP | InSDN (self-generated) |
| [35] | 2021 | RNN, LSTM, GRU | InSDN |
| [25] | 2021 | KNN, SVM, DT, NB, RF, XGBoost | CIC-DDoS2019 |
| [17] | 2021 | SVM, DT | KDD-Cup99 |
| [1] | 2021 | SVC-RF, LR, SVC, KNN, RF, ANN | New dataset |
| [18] | 2022 | KNN, logistic regression, DT | KDD-Cup99 |
| [19] | 2022 | SVM, GLM, NB, DA, FNN, DT, KNN, BT | 1999
DARPA, InSDN, DASD |
| [36] | 2022 | LR, NB, DT | Mininet for SDN |
| [26] | 2022 | RF, KNN-SVM, NB | CIC-DDoS2019 |
| [20] | 2022 | SVM (Ensemble), DT (J48), KNN | KDD-Cup99 |
| [9] | 2022 | SVM, KNN, NB, RF and DT | NSL-KDD |
| [27] | 2022 | PCA, KPCA, LDA, DT, RF | CIC-DDoS2019 |
| [37] | 2023 | SVM, NB, MLP | Mininet |
| [38] | 2023 | SVM, DT, Gaussian NB, RF, extra tree classifier, ANN | Mininet |
| [21] | 2023 | RNN, GRU, MLP, LSTM | CICIDS2017, CIC-DDoS2019 |
| [22] | 2023 | GRU, hybrid DL | CICIDS2017, NSL-KDD |
| [39] | 2024 | LR, LDA, NB, KNN, CART, AdaBoost, RF, SVM | InSDN |
| [23] | 2024 | KNN | CICIDS2017, CICIDS2018, CIC-DDoS2019 |
| [28] | 2024 | MLP | CIC-DDoS2019 |
| [31] | 2024 | XGBoost-SHAP | CIC-IOT-2023 |
| [40] | 2024 | SVM, random forest, KNN | Dataset by Ahuja et al. [1] |
| [29] | 2025 | SHAP, CNN-BiLSTM, AE-MLP, CNN-MLP | InSDN, CIC-DDoS2019 |
| Traffic Class | Number of Instances |
|---|---|
| Benign | 63,561 |
| Malicious | 40,784 |
| TCP | 29,436 (18,897 benign, 10,539 malicious) |
| UDP | 33,588 (22,772 benign, 10,816 malicious) |
| ICMP | 41,321 (24,957 benign, 16,364 malicious) |
| No. | Feature | Description |
|---|---|---|
| 1 | dt | Date and time |
| 2 | switch | Datapath ID of the switch in the topology |
| 3 | src | Source IP address of the flow |
| 4 | dst | Destination IP address of the flow |
| 5 | pktcount | Number of packets sent during the flow |
| 6 | bytecount | Number of bytes sent during the flow |
| 7 | dur | Duration of the flow in seconds |
| 8 | dur_nsec | Duration of the flow in nanoseconds |
| 9 | tot_dur | Total duration of the flow in nanoseconds |
| 10 | flows | Total number of flows in the switch |
| 11 | packetins | Number of packet_in messages to the controller |
| 12 | pktperflow | Packet count per flow |
| 13 | byteperflow | Byte count per flow |
| 14 | pktrate | Packet rate calculated using packet counts |
| 15 | Pairflow | Boolean value |
| 16 | Protocol | Protocol associated with the traffic flow |
| 17 | port_no | Port number of the switch |
| 18 | tx_bytes | Number of bytes transmitted on the port |
| 19 | rx_bytes | Number of bytes received on the port |
| 20 | tx_kbps | Transmit bandwidth of the port |
| 21 | rx_kbps | Receive bandwidth of the port |
| 22 | tot_kbps | Total bandwidth of the port |
| 23 | label | The label of the attack |
| Data Group | Number of Instances | Percentage |
|---|---|---|
| Normal | 68,424 | 19.9% |
| Metasploitable-2 | 136,743 | 39.76% |
| OVS | 138,772 | 40.34% |
| No. | Attribute Name | No. | Attribute Name |
|---|---|---|---|
| 1 | Protocol | 25 | Fwd-IAT-Min |
| 2 | Flow-duration | 26 | Bwd-IAT-Tot |
| 3 | Tot-Fwd-pkts | 27 | Bwd-IAT-Mean |
| 4 | Tot-Bwd-Pkts | 28 | Bwd-IAT-Std |
| 5 | TotLen-Fwd-Pkts | 29 | Bwd-IAT-Max |
| 6 | TotLen-Bwd-Pkts | 30 | Bwd-IAT-Min |
| 7 | Fwd-Pkt-Len-Max | 31 | Fwd-Header-Len |
| 8 | Fwd-Pkt-Len-Min | 32 | Bwd-Header-Len |
| 9 | Fwd-Pkt-Len-Mean | 33 | Fwd-Pkts/s |
| 10 | Fwd-Pkt-Len-Std | 34 | Bwd-Pkts/s |
| 11 | Bwd-Pkt-Len-Max | 35 | Pkt-Len-Min |
| 12 | Bwd-Pkt-Len-Min | 36 | Pkt-Len-Max |
| 13 | Bwd-Pkt-Len-Mean | 37 | Pkt-Len-Mean |
| 14 | Bwd-Pkt-Len-Std | 38 | Pkt-Len-Std |
| 15 | Flow-Bytes/s | 39 | Pkt-Len-Var |
| 16 | Flow-Pkts/s | 40 | Pkt-Size-Avg |
| 17 | Flow-IAT-Mean | 41 | Active-Mean |
| 18 | Flow-IAT-Std | 42 | Active-Std |
| 19 | Flow-IAT-Max | 43 | Active-Max |
| 20 | Flow-IAT-Min | 44 | Active-Min |
| 21 | Fwd-IAT-Tot | 45 | Idle-Mean |
| 22 | Fwd-IAT-Mean | 46 | Idle-Std |
| 23 | Fwd-IAT-Std | 47 | Idle-Max |
| 24 | Fwd-IAT-Max | 48 | Idle-Min |
| Algorithm | Accuracy % | Recall % | Specificity % | FAR % | Precision % | F1 Score % | No. of Features |
|---|---|---|---|---|---|---|---|
| Ahuja | 98.8 | - | 98.18 | 0.02 | 98.27 | 97.65 | 23 |
| CART | 99.990 | 99.984 | 99.994 | 0.009 | 99.990 | 99.987 | 16 |
| Modified CART | 99.989 | 99.985 | 99.991 | 0.014 | 99.986 | 99.985 | 10 |
| Algorithm | Validation | Sampling | Accuracy % | Recall % | Specificity % | FAR % | Precision % | F1-Score % |
|---|---|---|---|---|---|---|---|---|
| GDT | K-Fold | Stratified | 99.999 | 100 | 99.998 | 0.00263 | 99.997 | 99.999 |
| GDT | K-Fold | Random | 99.993 | 99.989 | 99.996 | 0.0052 | 99.994 | 99.992 |
| GDT | Monte | Random | 99.993 | 99.995 | 99.993 | 0.011 | 99.980 | 99.990 |
| Carlo | ||||||||
| AdaBoost | K-Fold | Stratified | 97.99 | 98.13 | 98.13 | 2.33 | 97.66 | 97.90 |
| LogitBoost | K-Fold | Stratified | 98.73 | 98.80 | 98.80 | 1.46 | 98.53 | 98.66 |
| GentleBoost | K-Fold | Stratified | 99.32 | 99.32 | 99.32 | 0.75 | 99.24 | 99.28 |
| RUSBoost | K-Fold | Stratified | 88.78 | 90.77 | 90.77 | 11.44 | 88.55 | 89.64 |
| SVC-RF (Ahuja) | Not specified | Not specified | 98.8 | 97.91 | 98.18 | 0.02 | 98.27 | 97.65 |
| Algorithm | Validation | Sampling | Accuracy % | Recall % | Specificity % | FAR % | Precision % | F1-Score % |
|---|---|---|---|---|---|---|---|---|
| GDT | K-fold | Stratified | 99.997 | 99.995 | 100 | 0 | 100 | 99.997 |
| GDT | K-fold | Random | 99.997 | 99.995 | 100 | 0 | 100 | 99.997 |
| GDT | Monte Carlo | Random | 99.997 | 99.995 | 100 | 0 | 100 | 99.998 |
| AdaBoost | K-fold | Stratified | 99.998 | 99.998 | 99.998 | 0.001 | 99.998 | 99.998 |
| LogitBoost | K-fold | Stratified | 99.996 | 99.996 | 99.996 | 0.003 | 99.996 | 99.996 |
| GentleBoost | K-fold | Stratified | 99.995 | 99.995 | 99.995 | 0.004 | 99.995 | 99.995 |
| RUSBoost | K-fold | Stratified | 99.341 | 99.323 | 99.301 | 0.617 | 99.332 | 99.341 |
| RF (Elsayed) | K-fold | - | - | 99.995 | - | - | 99.99 | 99.997 |
| Algorithm | Validation | Sampling | Average Training Time | Throughput (Predictions/Sec) | ||
|---|---|---|---|---|---|---|
| Ahuja | Elsayed | Ahuja | Elsayed | |||
| GDT | K-fold | Stratified | 8.0 | 7.6 | 2,658,798 | 5,723,790 |
| GDT | K-fold | Random | 8.0 | 7.6 | 2,509,367 | 5,714,573 |
| GDT | Monte Carlo | Random | 8.0 | 7.6 | 2,753,333 | 5,718,750 |
| AdaBoost | K-fold | Stratified | 10.1 | 9.7 | 147,618 | 252,850 |
| LogitBoost | K-fold | Stratified | 11.5 | 8.5 | 164,636 | 283,262 |
| GentleBoost | K-fold | Stratified | 8.9 | 7.9 | 193,814 | 294,309 |
| RUSBoost | K-fold | Stratified | 13.1 | 16.4 | 195,295 | 269,154 |
| SVC-RF (Ahuja) | - | - | - | - | - | - |
| RF (Elsayed) | K-fold | - | - | 42.5 | - | - |
| Dataset | Sampling | Validation | Feature Variance | Tree Size Variance |
|---|---|---|---|---|
| Ahuja | Stratified | K-fold | 0.2 | 57.2 |
| Ahuja | Not stratified | K-fold | 0.7 | 215.2 |
| Ahuja | Not stratified | Monte Carlo | 0.3447 | 685.47 |
| Elsayed | Stratified | K-fold | 0.2 | 156 |
| Elsayed | Not stratified | K-fold | 0.3 | 270.8 |
| Elsayed | Not stratified | Monte Carlo | 0.213 | 152.78 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaman, A.; Khan, S.A.; Mohammad, N.; Ateya, A.A.; Ahmad, S.; ElAffendi, M.A. Distributed Denial of Service Attack Detection in Software-Defined Networks Using Decision Tree Algorithms. Future Internet 2025, 17, 136. https://doi.org/10.3390/fi17040136
Zaman A, Khan SA, Mohammad N, Ateya AA, Ahmad S, ElAffendi MA. Distributed Denial of Service Attack Detection in Software-Defined Networks Using Decision Tree Algorithms. Future Internet. 2025; 17(4):136. https://doi.org/10.3390/fi17040136
Chicago/Turabian StyleZaman, Ali, Salman A. Khan, Nazeeruddin Mohammad, Abdelhamied A. Ateya, Sadique Ahmad, and Mohammed A. ElAffendi. 2025. "Distributed Denial of Service Attack Detection in Software-Defined Networks Using Decision Tree Algorithms" Future Internet 17, no. 4: 136. https://doi.org/10.3390/fi17040136
APA StyleZaman, A., Khan, S. A., Mohammad, N., Ateya, A. A., Ahmad, S., & ElAffendi, M. A. (2025). Distributed Denial of Service Attack Detection in Software-Defined Networks Using Decision Tree Algorithms. Future Internet, 17(4), 136. https://doi.org/10.3390/fi17040136








