Optimizing LoRaWAN Performance Through Learning Automata-Based Channel Selection
Abstract
1. Introduction
2. Related Work
3. Methods
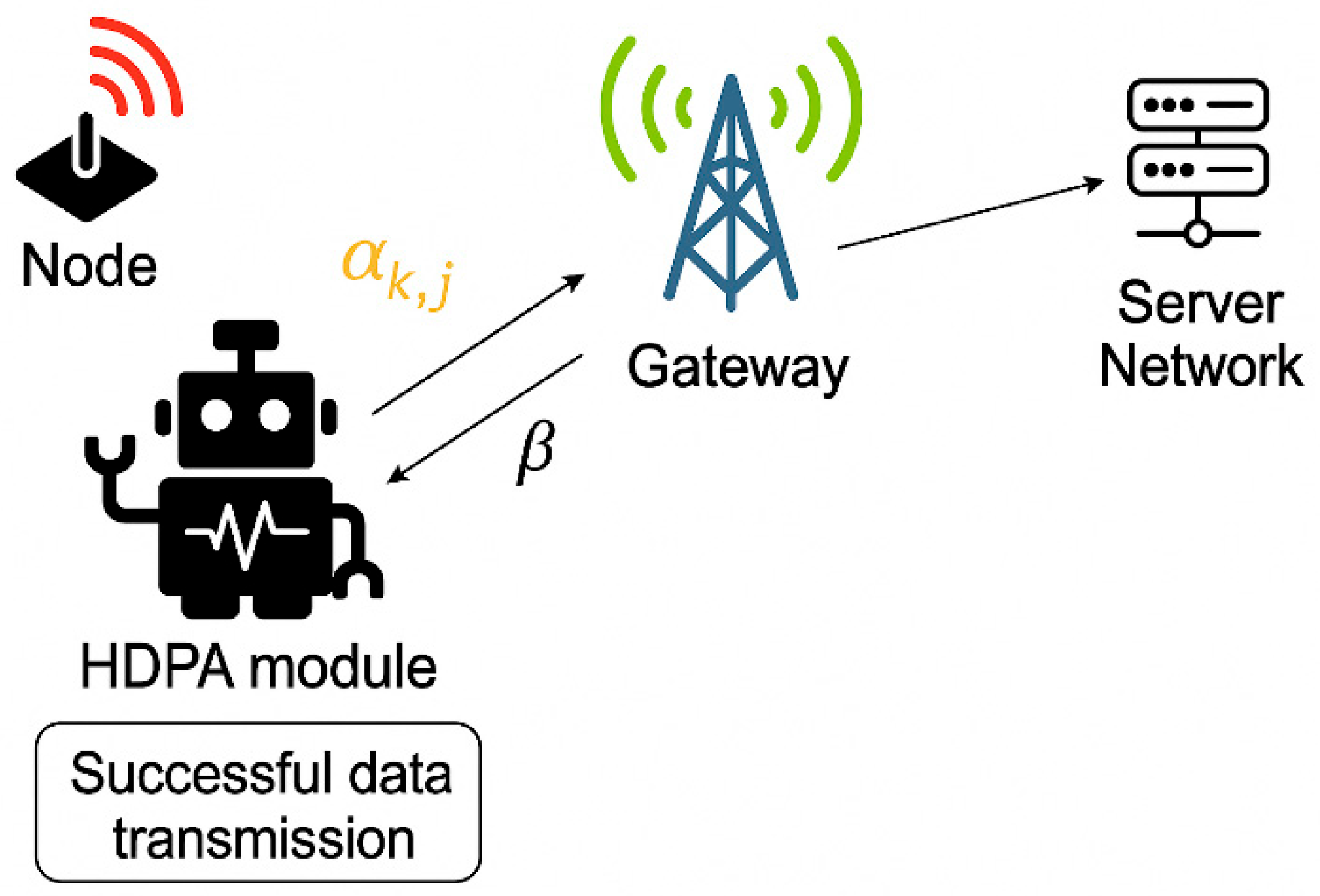
3.1. System Model
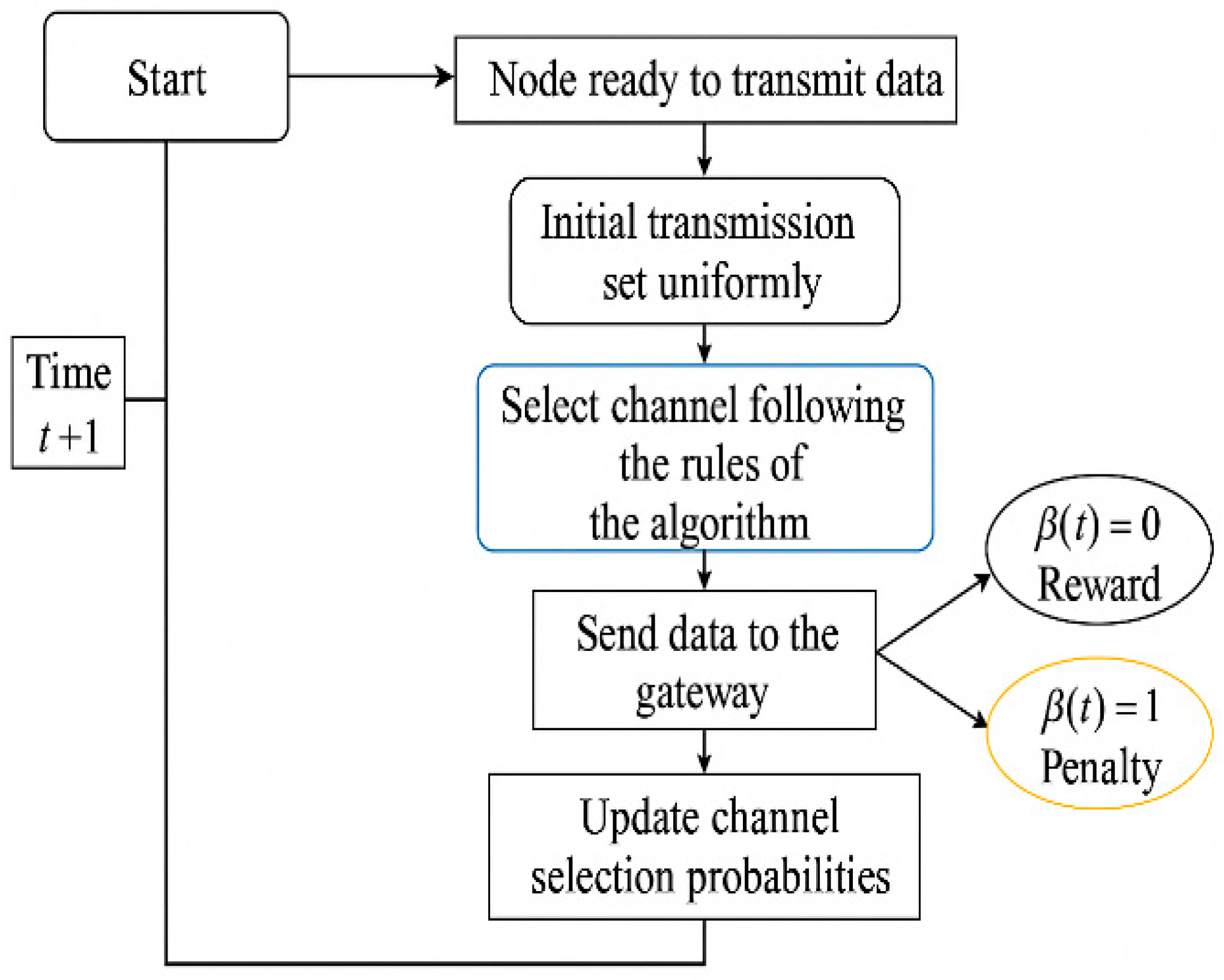
3.2. Proposed Algorithm Flowchart
3.3. Mathematical Development
| Algorithm 1: Hierarchical Learning Automata-Based Channel Selection | |||||
| Input: System structure (tree depth K, learning rates δ, Δ), initial probabilities, and environment feedback β(t). | |||||
| Output: A stable (converged) policy that selects the best-performing channel with the highest learned reward estimate. | |||||
| 1 | Initialize: Set . Initialize all probability vectors and reward estimates. | ||||
| 2 | Loop | ||||
| 3 |
| ||||
| 4 | selects a channel by randomly sampling as per its channel probability vector . | ||||
| 5 | We denote as the chosen channel at depth 0 with . , chooses a channel and activates the next LA at depth «2». The process continues until K − 1, which is the level that chooses the channel. | ||||
| 6 |
| ||||
| 7 | The index of the channel chosen at depth K is denoted . | ||||
| 8 | Update the estimated chance of reward based on the response received from the environment at leaf depth K: . For the other channel at the leaf, where and : | ||||
| 9 |
The reward estimate and attempt count are updated as: | ||||
| 10 |
We denote the larger element between and as and the lower reward estimate as . | ||||
| Update and using the estimate and for all as: | |||||
| 11 | If Then | ||||
| 12 | |||||
| 13 | |||||
| 14 | Else | ||||
| 15 | If β(t) = 1 Then | ||||
| 16 | |||||
| 17 | |||||
| 18 | |||||
| 19 | |||||
| 20 | End if | ||||
| 21 |
| ||||
| 22 |
| ||||
| 23 | End Loop | ||||
| Return: Optimal channel with maximum estimated reward. | |||||
3.4. Channel Propagation
3.5. Software Environment
3.6. System Simulation
3.7. Simulation Variable
3.8. Implementation Feasibility on End Devices
4. Results and Discussion
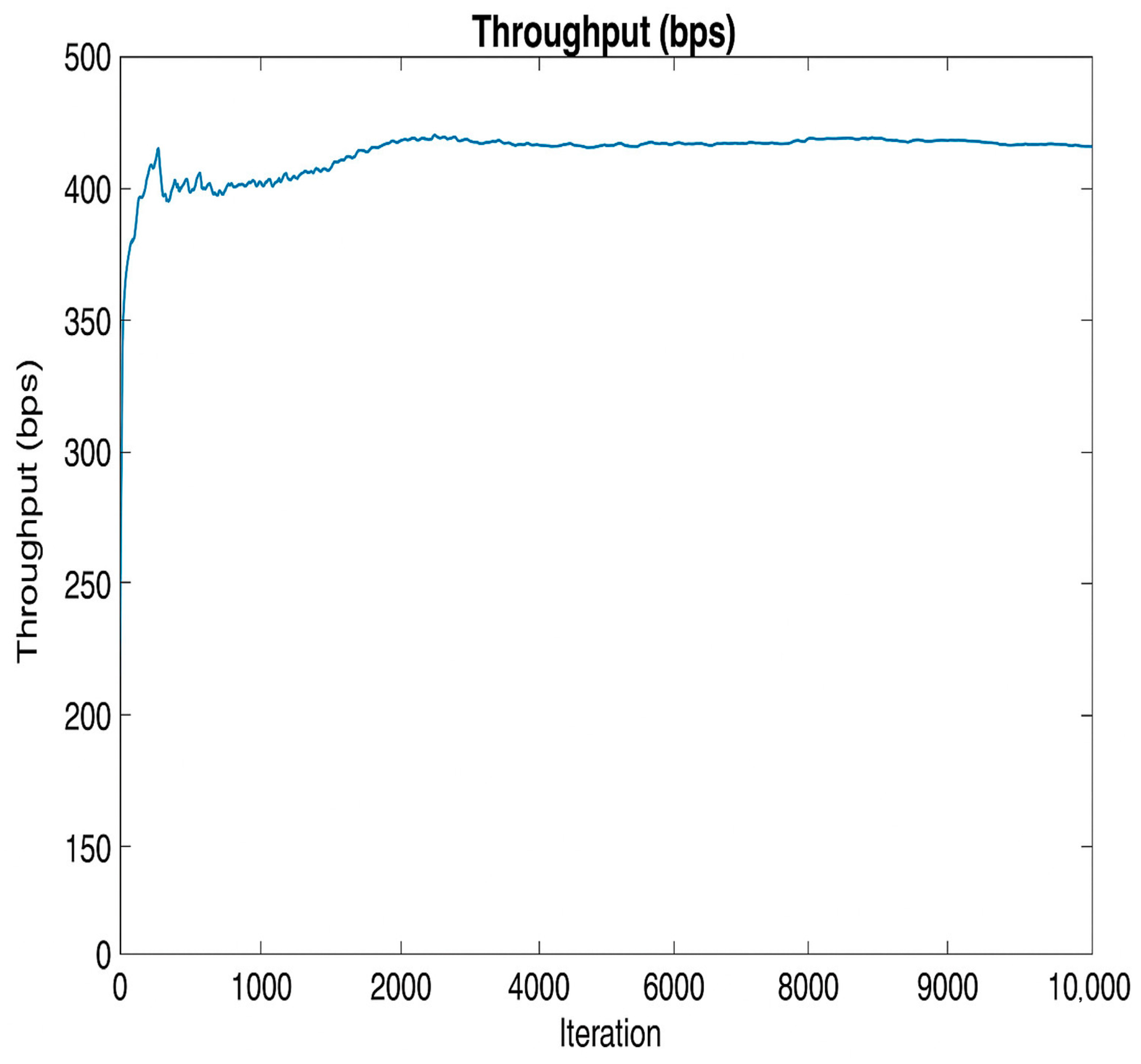
4.1. Performance Evaluation and Comparison Analysis
4.2. Sensitivity Analysis
5. Conclusions and Future Work
5.1. Conclusions
5.2. Future Works
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cheikh, I.; Sabir, E.; Aouami, R.; Sadik, M.; Roy, S. Throughput-Delay Tradeoffs for Slotted-Aloha-based LoRaWAN Networks. In Proceedings of the 2021 International Wireless Communications and Mobile Computing (IWCMC), Harbin City, China, 28 June–2 July 2021. [Google Scholar] [CrossRef]
- Wang, H.; Pei, P.; Pan, R.; Wu, K.; Zhang, Y.; Xiao, J.; Yang, J. A Collision Reduction Adaptive Data Rate Algorithm Based on the FSVM for a Low-Cost LoRa Gateway. Mathematics 2022, 10, 3920. [Google Scholar] [CrossRef]
- Zhang, X.; Jiao, L.; Granmo, O.-C.; Oommen, B.J. Channel selection in cognitive radio networks: A switchable Bayesian learning automata approach. In Proceedings of the IEEE 24th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), London, UK, 8–11 September 2013; IEEE: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Diane, A.; Diallo, O.; Ndoye, E.H.M. A systematic and comprehensive review on low power wide area network: Characteristics, architecture, applications and research challenges. Discov. Internet Things 2025, 5, 7. [Google Scholar] [CrossRef]
- Bai, H.; Cheng, R.; Jin, Y. Evolutionary reinforcement learning: A survey. Intell. Comput. 2023, 2, 0025. [Google Scholar] [CrossRef]
- Omslandseter, R.O.; Jiao, L.; Zhang, X.; Yazidi, A.; Oommen, B.J. The hierarchical discrete pursuit learning automaton: A novel scheme with fast convergence and epsilon-optimality. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 8278–8292. [Google Scholar] [CrossRef] [PubMed]
- Yazidi, A.; Zhang, X.; Jiao, L.; Oommen, B.J. The hierarchical continuous pursuit learning automation: A novel scheme for environments with large numbers of actions. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 512–526. [Google Scholar] [CrossRef] [PubMed]
- Prakash, A.; Choudhury, N.; Hazarika, A.; Gorrela, A. Effective Feature Selection for Predicting Spreading Factor with ML in Large LoRaWAN-based Mobile IoT Networks. In Proceedings of the 2025 National Conference on Communications (NCC), New Delhi, India, 6–9 March 2025. [Google Scholar] [CrossRef]
- Lavdas, S.; Bakas, N.; Vavousis, K.; Khalifeh, A.; Hajj, W.E.; Zinonos, Z. Evaluating LoRaWAN Network Performance in Smart City Environments Using Machine Learning. IEEE Internet Things J. 2025, 12, 27060–27074. [Google Scholar] [CrossRef]
- Garlisi, D.; Pagano, A.; Giuliano, F.; Croce, D.; Tinnirello, I. Interference Analysis of LoRaWAN and Sigfox in Large-Scale Urban IoT Networks. IEEE Access 2025, 13, 44836–44848. [Google Scholar] [CrossRef]
- Keshmiri, H.; Rahman, G.M.; Wahid, K.A. LoRa Resource Allocation Algorithm for Higher Data Rates. Sensors 2025, 25, 518. [Google Scholar] [CrossRef] [PubMed]
- Li, A.; Fujisawa, M.; Urabe, I.; Kitagawa, R.; Kim, S.-J.; Hasegawa, M. A lightweight decentralized reinforcement learning based channel selection approach for high-density LoRaWAN. In Proceedings of the 2021 IEEE International Symposium on Dynamic Spectrum Access Networks (DySPAN), Los Angeles, CA, USA, 13–15 December 2021. [Google Scholar] [CrossRef]
- Oyewobi, S.S.; Hancke, G.P.; Abu-Mahfouz, A.M.; Onumanyi, A.J. An effective spectrum handoff based on reinforcement learning for target channel selection in the industrial Internet of Things. Sensors 2019, 19, 1395. [Google Scholar] [CrossRef] [PubMed]
- Hasegawa, S.; Kim, S.-J.; Shoji, Y.; Hasegawa, M. Performance evaluation of machine learning based channel selection algorithm implemented on IoT sensor devices in coexisting IoT networks. In Proceedings of the 2020 IEEE 17th Annual Consumer Communications & Networking Conference (CCNC), Las Vegas, NV, USA, 10–13 January 2020. [Google Scholar] [CrossRef]
- Loh, F.; Mehling, N.; Geißler, S.; Hoßfeld, T. Simulative performance study of slotted aloha for LoRaWAN channel access. In Proceedings of the NOMS 2022—2022 IEEE/IFIP Network Operations and Management Symposium, Budapest, Hungary, 25–29 April 2022. [Google Scholar] [CrossRef]
- Yurii, L.; Anna, L.; Stepan, S. Research on the Throughput Capacity of LoRaWAN Communication Channel. In Proceedings of the 2023 IEEE East-West Design & Test Symposium (EWDTS), Batumi, Georgia, 22–25 September 2023. [Google Scholar] [CrossRef]
- Gaillard, G.; Pham, C. CANL LoRa: Collision Avoidance by Neighbor Listening for Dense LoRa Networks. In Proceedings of the 2023 IEEE Symposium on Computers and Communications (ISCC), Gammarth, Tunisia, 9–12 July 2023. [Google Scholar] [CrossRef]
- LoRa Alliance, Inc. LoRaWAN® L2 1.0.4 Specification (TS001-1.0.4). White Paper, October 2020. Available online: https://lora-alliance.org/wp-content/uploads/2021/11/LoRaWAN-Link-Layer-Specification-v1.0.4.pdf (accessed on 20 May 2025).
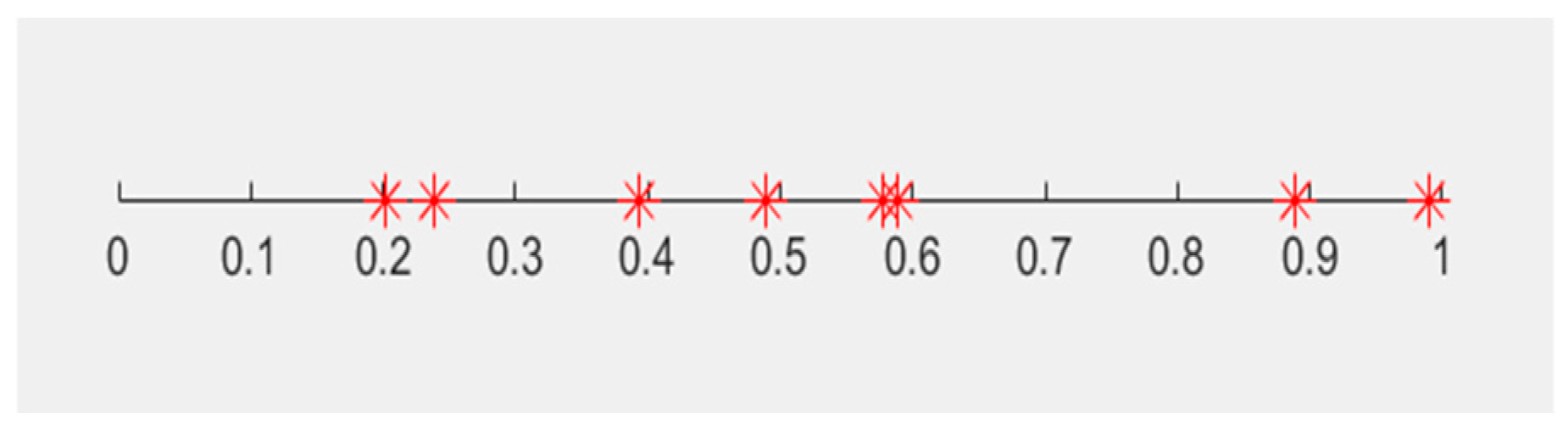
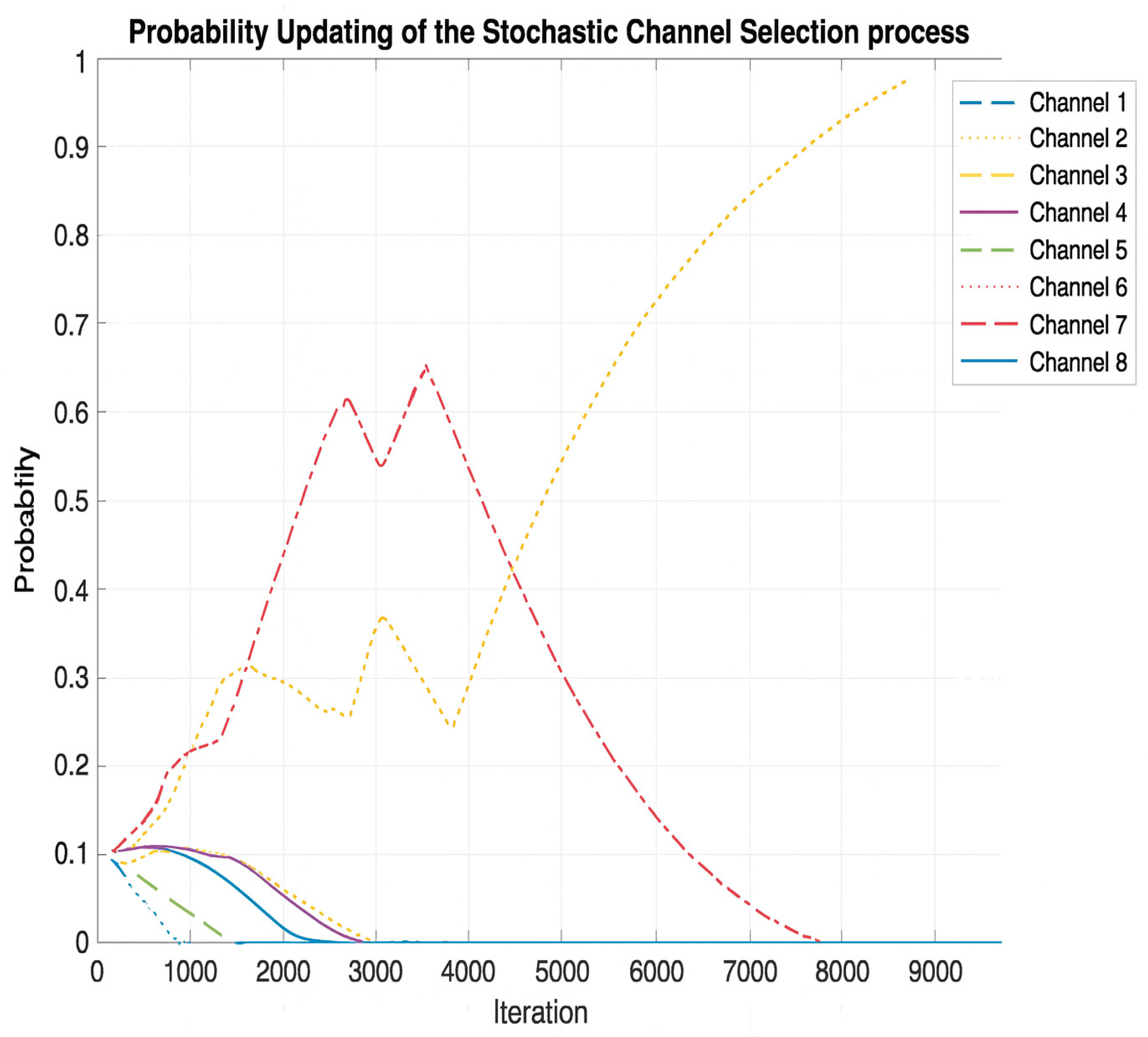
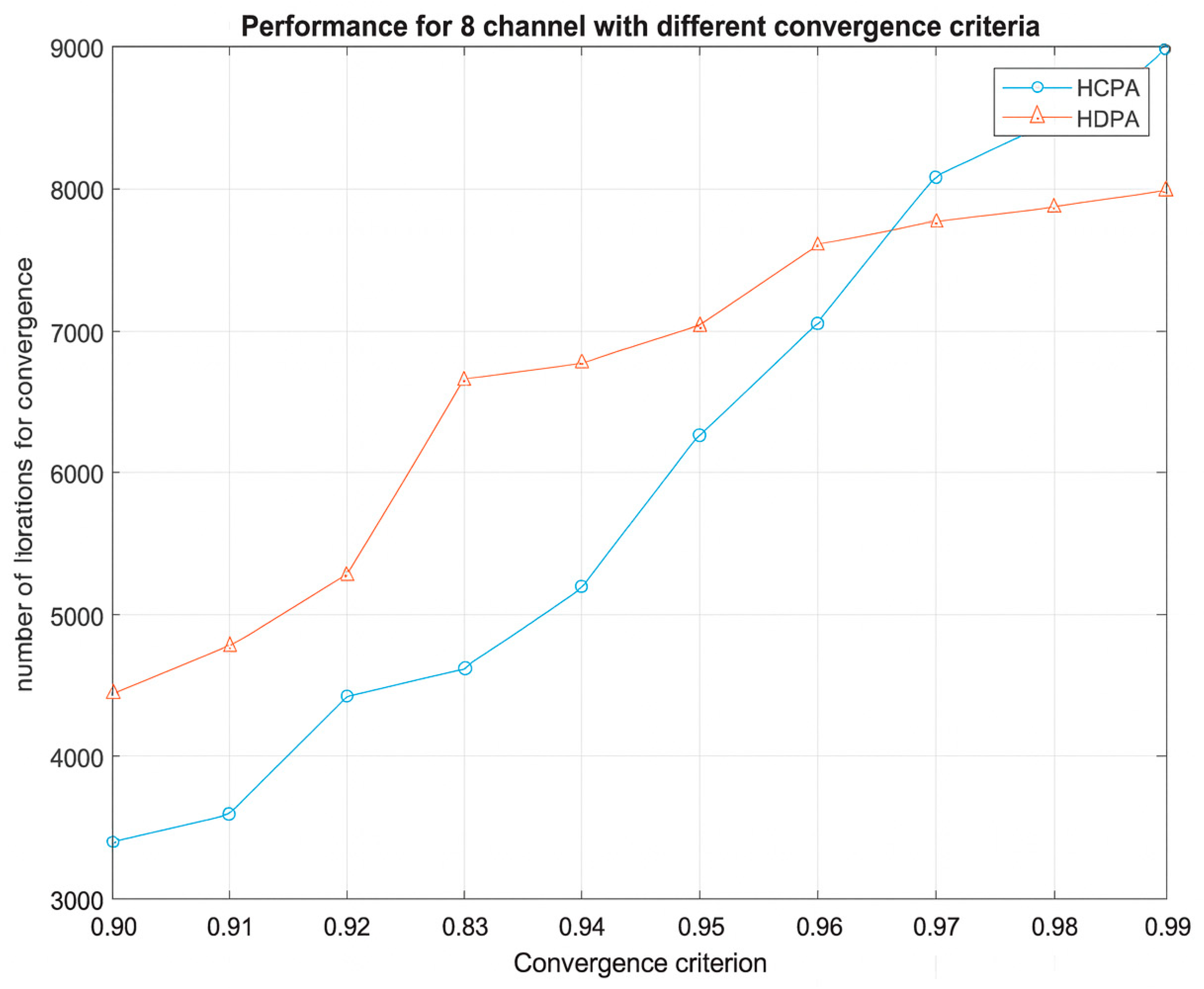
| 0.199 | 0.282 | 0.394 | 0.499 | 0.681 | 0.698 | 0.971 | 0.999 |
| Variable | Symbol | Description |
|---|---|---|
| Number of channels | Total number of available channels in the network. | |
| Initial channel probability | Initial probability vector for channel selection, | |
| Reward | Binary value: 0 for successful transmission (ACK), 1 otherwise | |
| Learning Rate | Step size for probability updates. | |
| Hierarchical levels | Number of levels , e.g., for 8 channels | |
| Convergence threshold | Probability threshold set (0.99) for stopping updates once a channel is confidently optimal | |
| Maximum iteration | Maximum number of iterations for the simulation. | |
| Action selection probability | Probability of selecting channels at iteration. | |
| Reward estimate | Estimate of the reward for channel i. | |
| Channel State | The state of each channel is either idle or busy. |
| Parameter | HDPA |
|---|---|
| Mean | 6279.64 |
| Std | 131.36 |
| Accuracy | 98.78% |
| Learning parameter | 8.7 × 10−4 |
| Parameters | HDPA | HCPA |
|---|---|---|
| Mean | 6279.64 | 6778.34 |
| STD | 131.36 | 117.12 |
| Accuracy | 98.78% | 93.89% |
| Learning parameter | 8.7 × 10−4 | 6.9 × 10−4 |
| Parameters | HDPA | TOW-MAB |
|---|---|---|
| Parameter sensitivity: | Learning rate, Convergence threshold | Frame Success Rate (FSR) Fairness Index (FI) |
| Environment Type: | Simulated LoRaWAN Under stochastic Channel states | Real-world deployment with coexisting IoT networks |
| Hardware Implementation: | Simulation-based | Raberry Pi + Lazurite 920J Modules |
| Network Model: | Single gateway, adaptive Channel selection, reward-based feedback | Multiple gateways, fixed sensor deployment, and real interference patterns |
| Learning structure: | Hierarchical tree with recursive probability updates | Single-layer with oscillatory decision dynamics |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Atadet, L.A.; Musabe, R.; Hitimana, E.; Gatera, O. Optimizing LoRaWAN Performance Through Learning Automata-Based Channel Selection. Future Internet 2025, 17, 555. https://doi.org/10.3390/fi17120555
Atadet LA, Musabe R, Hitimana E, Gatera O. Optimizing LoRaWAN Performance Through Learning Automata-Based Channel Selection. Future Internet. 2025; 17(12):555. https://doi.org/10.3390/fi17120555
Chicago/Turabian StyleAtadet, Luka Aime, Richard Musabe, Eric Hitimana, and Omar Gatera. 2025. "Optimizing LoRaWAN Performance Through Learning Automata-Based Channel Selection" Future Internet 17, no. 12: 555. https://doi.org/10.3390/fi17120555
APA StyleAtadet, L. A., Musabe, R., Hitimana, E., & Gatera, O. (2025). Optimizing LoRaWAN Performance Through Learning Automata-Based Channel Selection. Future Internet, 17(12), 555. https://doi.org/10.3390/fi17120555







