Research on a Blockchain Adaptive Differential Privacy Mechanism for Medical Data Protection

Abstract

To address the issues of privacy-utility imbalance, insufficient incentives, and lack of verifiable computation in current medical data sharing, this paper proposes a blockchain-based fair verification and adaptive differential privacy mechanism. The mechanism adopts an integrated design that systematically tackles three core challenges: privacy protection, fair incentives, and verifiability. Instead of using a traditional fixed privacy budget allocation, it introduces a reputation-aware adaptive strategy that dynamically adjusts the privacy budget based on the contributors’ historical behavior and data quality, thereby improving aggregation performance under the same privacy constraints. Meanwhile, a fair incentive verification layer is established via smart contracts to quantify and confirm data contributions on-chain, automatically executing reciprocal rewards and mitigating the trust and motivation deficiencies in collaboration. To ensure enforceable privacy guarantees, the mechanism integrates lightweight zero-knowledge proof (zk-SNARK) technology to publicly verify off-chain differential privacy computations, proving correctness without revealing private data and achieving auditable privacy protection. Experimental results on multiple real-world medical datasets demonstrate that the proposed mechanism significantly improves analytical accuracy and fairness in budget allocation compared with baseline approaches, while maintaining controllable system overhead. The innovation lies in the organic integration of adaptive differential privacy, blockchain, fair incentives, and zero-knowledge proofs, establishing a trustworthy, efficient, and fair framework for medical data sharing.

1. Introduction

Healthcare data represents some of the most sensitive personal information, while also serving as a vital resource for advancing precision medicine, drug development, and AI-assisted diagnostics. Data sharing and mobility across institutions are key pathways to unlocking data value and driving medical progress. However, a persistent tension exists between the urgent need for data sharing and the imperative of privacy protection. Frequent data breaches have prompted nations to enact stringent privacy regulations (such as the U.S. HIPAA and the EU’s GDPR), imposing higher compliance standards on the collection, storage, and sharing of medical data. Furthermore, research indicates that even anonymized data may be re-identified—for instance, Gymrek et al. re-identified individual genomes through genetic surnames [1]—further highlighting the need for quantifiable privacy protection mechanisms. Research indicates that with the rise of distributed intelligence technologies like federated learning in digital healthcare, data protection and sharing needs are accelerating their convergence [2]. To address this challenge, academia and industry have proposed various privacy-preserving techniques, including encrypted computation, anonymization processing, and quantifiable privacy guarantees represented by differential privacy (DP) [3]. Differential privacy provides provable privacy boundaries under output perturbation, yet it faces multiple limitations in complex healthcare data sharing scenarios. These include a lack of dynamic adaptability in privacy budgets, reliance on centralized trust, insufficient incentive mechanism design, and a lack of transparency and auditability in computational processes. Consequently, healthcare data sharing urgently requires a comprehensive technical framework that simultaneously achieves privacy protection, adaptive adjustment, fair incentives, and verifiable compliance.

Despite significant progress in various subfields of medical data sharing both domestically and internationally in recent years, the overall landscape remains characterized by “localized breakthroughs but systemic gaps.” Specifically, existing research generally exhibits the following four structural shortcomings:

(1) Imbalance between privacy and utility. Static differential privacy mechanisms lack flexibility in dynamic query environments, while adaptive differential privacy, though capable of adjustment, often relies on centralized architectures, making it difficult to balance performance and security. In recent years, researchers have attempted to introduce dynamic privacy budget adjustment mechanisms to enhance privacy budget utilization efficiency in multi-query or multi-user settings [4], such as adjusting privacy budgets through feature weighting in vertical federated learning scenarios [5]. However, these efforts have primarily been validated in federated learning or single-domain data settings, lacking systematic solutions for cross-institutional medical data sharing. Particularly in multi-party collaborative healthcare scenarios, dynamically allocating privacy budgets while simultaneously considering data sensitivity, query frequency, and user credibility remains an unresolved challenge.

(2) The disconnect between trust and verifiability. While blockchain technology is widely used for access control and data notarization, its loose integration with core privacy computing processes makes it difficult to fundamentally eliminate the trust gap caused by opaque computation [6]. Recent research indicates that zero-knowledge proofs (zk-SNARKs) can provide verifiability and auditability for privacy computing [7]. Bontekoe et al. [8] further proposed a lightweight zk implementation approach, yet practical implementation solutions remain scarce in medical data sharing. It is important to note that differential privacy only guarantees privacy constraints at the output level and cannot verify whether computations are executed correctly. In contrast, zk-SNARKs enable verification of computational correctness without exposing input data, thereby filling the critical gap of “execution trustworthiness” in decentralized environments. In contrast, while permissioned blockchains (e.g., Hyperledger Fabric) enhance trust in access and evidence through member management and audit logs, they do not provide formal proof that “off-chain privacy computations execute as specified.” Therefore, zero-knowledge proofs remain essential for achieving independent computational verifiability.

(3) Lack of Incentives and Fairness. Most proposals overlook the economic attributes of data contributions, lacking fair and automated value distribution mechanisms that struggle to sufficiently incentivize data holders’ participation [9]. Building upon this, researchers began integrating game theory into blockchain incentive mechanisms [10] and further explored the equilibrium between fairness and incentives using evolutionary game frameworks in dynamic interactive scenarios [11]. However, no system solution has yet emerged that tightly couples privacy protection with verifiable computation. Building upon this foundation, this study further integrates incentive mechanisms with the verifiability of differential privacy computation. By leveraging on-chain contracts to automatically enforce fair distribution and penalize violations, the system enhances its credibility.

(4) Insufficient compliance verification. Existing approaches largely rely on platform self-regulation, lacking independent technical means to verify whether computational processes meet privacy protection requirements [10]. In summary, existing work exhibits significant fragmentation across privacy adjustment, trust mechanisms, fair incentives, and compliance verification. This field urgently requires a systematic framework that natively integrates adaptive differential privacy, blockchain trust mechanisms, fair incentive design, and verifiable computation. This paper addresses precisely this methodological gap.

This study aims to construct a comprehensive blockchain-supported framework featuring fairness, verifiability, and adaptive differential privacy to address privacy protection challenges in medical data sharing in a secure, efficient, and trustworthy manner. The primary research components encompass the following aspects: First, we formally define dynamic privacy requirements, multidimensional fairness criteria, and verifiable security objectives within healthcare data sharing scenarios. Second, we design an adaptive privacy budget allocation algorithm that holistically considers data attributes, query patterns, and user reputation. Third, we establish a fair incentive mechanism based on smart contracts to measure data contributions and distribute rewards. Next, a lightweight zero-knowledge proof-based verification scheme is proposed to validate the compliance of off-chain differential privacy computation processes. Finally, these components are organically integrated into an endogenously coupled system framework, whose effectiveness is validated through theoretical analysis and experimental evaluation.

The main innovations of this paper are reflected in three aspects. First, at the mechanism level, we propose an adaptive privacy budget allocation algorithm tailored to the multidimensional context of medical data. This algorithm dynamically adjusts based on data sensitivity, query types, and user credibility, ensuring privacy protection while maximizing data utility. Second, at the architectural level, we deeply integrate blockchain with smart contracts to build a decentralized sharing ecosystem. This enables fair incentives and automated contract execution, enhancing the transparency and sustainability of data sharing. Third, at the trust level, addressing the issue of insufficient verifiability in privacy protection, we design a lightweight zero-knowledge proof mechanism. This enables auditability and mathematical verifiability in the differential privacy execution process, thereby enhancing system credibility and compliance. Compared to approaches relying solely on differential privacy or access control, the introduced zk-SNARK verification provides independent proof of computational correctness for the system, strengthening compliance assurance without expanding the trust boundary. It should be noted that this framework primarily applies to aggregate-level statistical analysis scenarios, with only proof-of-concept verification conducted for individual-level prediction tasks.

The structure of this paper is organized as follows. Section 2 introduces the foundational knowledge required for the study. Section 3 presents the problem modeling involved in the research and outlines the overall design of the BFAV-DP framework. Section 4 details the core mechanisms of the framework. Section 5 discusses the system implementation, providing formal security analysis and proofs. Section 6 presents the experimental setup, evaluation results, and comparative analysis. Section 7 concludes the paper and outlines directions for future work.

2. Related Work

2.1. Dynamic Differential Privacy

Differential Privacy (DP) was first proposed by Dwork et al. [3]. Its core concept involves introducing random perturbations into data analysis outputs to provide stringent privacy protection while ensuring the usability of results. Its classical definition states: For two datasets ${\mathrm{D}}_1$ and ${\mathrm{D}}_2$ differing by only one sample, if there exists a randomization algorithm $\mathrm{M}$ such that for all possible output sets $\mathrm{S}$,

$$\mathrm{P}\left[\mathrm{M}\right({\mathrm{D}}_1)\in \mathrm{S}]\le {\mathrm{e}}^{\mathsf{\epsilon }}\mathrm{P}\left[\mathrm{M}\right({\mathrm{D}}_2)\in \mathrm{S}]+\mathsf{\delta },$$

(1)

Then algorithm $\mathrm{M}$ is said to satisfy $(\mathsf{\epsilon },\mathsf{\delta })$-differential privacy.

However, traditional static differential privacy assumes data queries are independent and the privacy budget is fixed, making it difficult to handle scenarios involving sequential queries, dynamic data streams, or multi-party sharing. To address this, researchers have proposed dynamic or adaptive differential privacy (Adaptive DP) mechanisms. These achieve flexible privacy control by dynamically allocating the privacy budget ${\mathsf{\epsilon }}_{\mathrm{t}}\left(\mathsf{\omega }\right)$ at different time steps $\mathrm{t}$ or under different contexts $\mathsf{\omega }$ [2,3]:

$$\mathrm{P}\left[{\mathrm{M}}_{\mathrm{t}}\right({\mathrm{D}}_1,\mathsf{\omega })\in \mathrm{S}]\le {\mathrm{e}}^{{\mathsf{\epsilon }}_{\mathrm{t}}\left(\mathsf{\omega }\right)}\mathrm{P}\left[{\mathrm{M}}_{\mathrm{t}}\right({\mathrm{D}}_2,\mathsf{\omega })\in \mathrm{S}]+{\mathsf{\delta }}_{\mathrm{t}}\left(\mathsf{\omega }\right).$$

(2)

Cao et al. [12] pioneered a quantitative analysis of cumulative privacy leakage in DP from a temporal perspective, laying the theoretical foundation for subsequent dynamic budget allocation research. Zhu et al. [4] proposed a differential privacy framework with dynamically adjustable privacy budgets for federated learning environments. Errounda and Liu [5] implemented an adaptive differential privacy mechanism based on feature importance in vertical federated learning scenarios, enhancing model utility. Overall, adaptive DP demonstrates flexibility in balancing privacy and utility, but it typically assumes the existence of a trusted coordinator. In multi-institution healthcare settings, this assumption is difficult to fulfill, necessitating integration with decentralized and verifiable technologies to achieve end-to-end privacy guarantees.

2.2. Blockchain and Smart Contracts

Blockchain was first proposed by Nakamoto in 2008 [13]. Its decentralized, tamper-proof, and traceable characteristics provide the foundation for constructing a trustworthy data management system. Crosby et al. [14] and Zheng et al. [15] systematically elucidated blockchain’s architecture, consensus mechanisms, and typical application scenarios. Research indicates that blockchain can integrate hash chains, timestamps, and digital signature technologies to verify data integrity and traceability [16]. Additionally, smart contracts enable decentralized access control, budget allocation, and incentive mechanisms through automated execution logic.

In the field of medical data sharing, the MedRec system proposed by Azaria et al. [17] pioneered blockchain application for access and authorization management of electronic health records (EHRs). Subsequent research (e.g., Jiang et al.’s [16] BlocHIE platform) further demonstrated blockchain’s potential in cross-institutional medical data exchange. Zhang et al. [6] conducted a systematic review of blockchain’s role in medical data storage, sharing, and security management, highlighting its unique advantages in trusted sharing and auditability. Qu et al. [18] proposed a future direction integrating blockchain with privacy-preserving computation, exploring “privacy-aware and verifiably trustworthy” data sharing mechanisms in Edge Intelligence scenarios, offering novel insights for highly sensitive domains like healthcare. However, most of these studies focus on access control and data notarization layers, without delving into how to implement differential privacy computation and its verifiable execution within blockchain environments—thereby theoretically ensuring the unity of privacy and trust.

2.3. Verifiable Computation and Zero-Knowledge Proofs

Zero-Knowledge Proof (ZKP), first introduced by Goldwasser et al. [19], enables a prover to convince a verifier of the correctness of a computation without revealing any private information. With the advancement of blockchain and privacy-preserving computation, Zero-Knowledge Succinct Non-Interactive Argument of Knowledge (zk-SNARK) has become one of the most widely adopted approaches due to its high efficiency and non-interactive design [20,21]. Let the public input be $\mathrm{P}$, the private witness be $\mathrm{W}$, and the constraint system be $\mathrm{C}$. A proof system satisfies

$$\mathrm{V}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{f}\mathrm{y}(\mathrm{P},{\mathsf{\pi }}_{\mathrm{t}})=1⟺(\mathrm{P},\mathrm{W})\in \mathrm{C},$$

(3)

which ensures that the correctness of the computation can be verified without exposing the private data.

Groth [21] optimized pairing-based non-interactive proof constructions, significantly reducing proof size and verification time. Bontekoe et al. [8] conducted a systematic study of verifiable privacy-preserving computation and suggested that lightweight zk schemes can enhance the auditability of differential privacy computations. Garg et al. [7] further proposed the zkSaaS (Zero-Knowledge SNARKs as a Service) paradigm, enabling service-oriented deployment of ZKP systems in cloud environments. The integration of ZKP technologies allows medical data-sharing platforms to validate privacy-preserving computations without disclosing data content, forming the technical foundation for the verifiable DP framework proposed in subsequent sections. Considering the real-time requirements and resource constraints of medical data scenarios, this study adopts a lightweight zk-SNARK approach that generates proofs only for the noise generation and budget compliance components of differential privacy, thereby maintaining auditability while reducing computational overhead.

2.4. Fairness and Incentive Compatibility

In medical data-sharing ecosystems, the distribution of benefits among data providers, data analysts, and platform operators plays a crucial role in shaping participation incentives and ensuring long-term system sustainability. To guarantee effectiveness and fairness in incentives, mechanism design must satisfy incentive compatibility (IC):

$$\mathbb{E}\left[{\mathrm{U}}_{\mathrm{i}}\right|\mathrm{H}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{t}]\ge \mathbb{E}[{\mathrm{U}}_{\mathrm{i}}\left|\mathrm{D}\mathrm{e}\mathrm{v}\mathrm{i}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\right],$$

(4)

which ensures that participants obtain the highest expected utility when acting honestly under the mechanism.

Xuan et al. [9] designed a smart-contract-based incentive mechanism that automates reward allocation to encourage medical data contributors. Yang et al. [22] incorporated fairness constraints into blockchain-based incentive design, ensuring a positive correlation between data contribution and reward distribution. Zhu et al. [11] applied evolutionary game theory to the scenario of electronic medical record sharing and demonstrated that fair incentive mechanisms enhance participation stability. Overall, fairness-oriented incentives are regarded as important for improving system sustainability; however, how to integrate them seamlessly with privacy protection and verifiable computation mechanisms remains an open research challenge.

2.5. Characteristics of Medical Data and Privacy Threat Models

Medical data is highly sensitive, strongly interdependent, and heterogeneous, which poses significant privacy risks during storage and sharing [2]. Mainstream threat models typically categorize potential adversaries into three types:

(1)

Curious users: infer individual privacy through frequent queries or correlation analysis;

(2)

Malicious nodes: falsify or tamper with data, undermining system fairness;

(3)

Colluding adversaries: multiple participants jointly analyze data to increase the likelihood of privacy breaches.

Li et al. [23] constructed a fine-grained privacy threat model for medical IoT environments and proposed defense mechanisms based on differential privacy and encryption. Commey et al. [24] developed a medical IoT data-sharing framework integrating blockchain, differential privacy, and federated learning, which ensures on-chain auditability and tamper resistance while enhancing the traceability and compliance of privacy protection through adaptive noise injection, making it suitable for telemedicine and cross-institutional data collaboration scenarios.

Given the complex structure and high privacy value of medical data, secure sharing generally requires verifiability, fairness, and regulatory compliance. Accordingly, the framework proposed in this study integrates adaptive differential privacy, blockchain-based trust mechanisms, and zero-knowledge proof verification modules into a cohesive system, forming an end-to-end secure and trustworthy workflow.

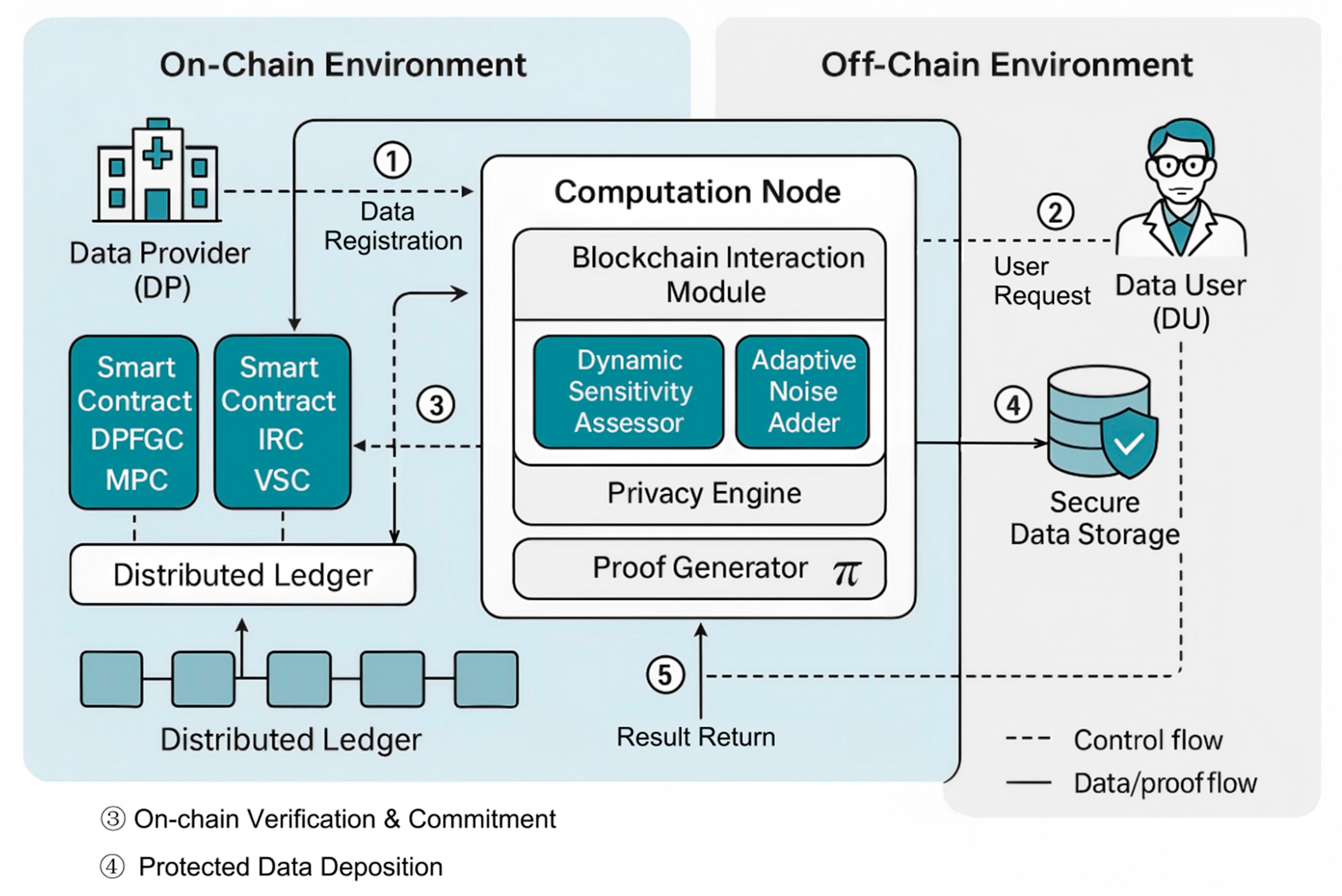
3. Problem Formulation and Framework Design

3.1. System Model

The system consists of four types of participants: a set of data providers $\mathrm{D}=\left\{\mathrm{D}{\mathrm{P}}_{\mathrm{i}}\right\}$, a set of data users $\mathrm{U}=\left\{\mathrm{D}{\mathrm{U}}_{\mathrm{j}}\right\}$, a set of off-chain computing nodes $\mathcal{C}=\{\mathrm{C}{\mathrm{N}}_{\mathrm{k}}$}, and a blockchain network $\mathcal{B}=\mathrm{B}\mathrm{N}$ responsible for executing smart contracts and maintaining on-chain records. At any given time $\mathrm{t}$, a user query request can be formalized as

$${\mathrm{Q}}_{\mathrm{t}}=({\mathrm{f}}_{\mathrm{t}},{\mathrm{P}}_{\mathrm{t}},{\mathrm{A}}_{\mathrm{t}}),$$

(5)

where ${\mathrm{f}}_{\mathrm{t}}$ denotes the query function (e.g., aggregate statistics or model training), ${\mathrm{P}}_{\mathrm{t}}$ represents the access authorization predicates and constraints, and ${\mathrm{A}}_{\mathrm{t}}$ is the subset of data attributes involved. The system data flow can be described as

$$\mathrm{D}{\mathrm{U}}_{\mathrm{j}}={\mathrm{R}}_{\mathrm{t}}\circ {\mathrm{B}}_{\mathrm{t}}\circ {\mathrm{C}}_{\mathrm{t}}\circ {\mathrm{U}}_{\mathrm{t}}\left(\mathrm{D}{\mathrm{P}}_{\mathrm{i}}\right),$$

(6)

${\mathrm{U}}_{\mathrm{t}}:\mathrm{D}{\mathrm{P}}_{\mathrm{i}}\mapsto \mathrm{C}{\mathrm{N}}_{\mathrm{k}}$ denotes off-chain data upload and retrieval; ${\mathrm{C}}_{\mathrm{t}}:\mathrm{C}{\mathrm{N}}_{\mathrm{k}}\mapsto (\mathrm{B}\mathrm{N},{\tilde{\mathrm{y}}}_{\mathrm{t}},{\mathsf{\pi }}_{\mathrm{t}})$ represents off-chain computation and proof generation; ${\tilde{\mathrm{y}}}_{\mathrm{t}}={\mathrm{f}}_{\mathrm{t}}\left({\mathrm{D}}_{\mathrm{t}}\right)+{\mathsf{\eta }}_{\mathrm{t}}$ is the result after adding differential privacy noise, with ${\mathsf{\eta }}_{\mathrm{t}}$ as the noise term; ${\mathrm{B}}_{\mathrm{t}}:\mathrm{B}\mathrm{N}\mapsto \mathrm{R}\mathrm{e}\mathrm{s}\mathrm{u}\mathrm{l}\mathrm{t}$ is responsible for on-chain verification and record-keeping; and ${\mathrm{R}}_{\mathrm{t}}:\mathrm{R}\mathrm{e}\mathrm{s}\mathrm{u}\mathrm{l}\mathrm{t}\mapsto \mathrm{D}{\mathrm{U}}_{\mathrm{j}}$ returns the verified result to the requester.

This “off-chain computation → on-chain verification → auditable record” execution paradigm is consistent with existing medical blockchain architectures such as MedRec and BlocHIE, ensuring access control, auditability, and immutability of results, while significantly reducing on-chain computational overhead.

3.2. Threat Model

In this study, the adversary is assumed to aim at stealing raw data, inferring sensitive information, violating budget fairness, or tampering with results or proofs. The adversary’s capabilities can be expressed as

$${\mathcal{A}}_{\mathrm{c}\mathrm{a}\mathrm{p}}=({\mathsf{\theta }}_{\mathrm{m}\mathrm{a}\mathrm{l}},{\mathcal{M}}_{\mathrm{a}\mathrm{d}\mathrm{v}},{\mathcal{O}}_{\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{m}},{\mathcal{T}}_{\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{i}}),$$

(7)

where ${\mathsf{\theta }}_{\mathrm{m}\mathrm{a}\mathrm{l}}$ denotes the proportion of malicious or abnormal nodes; ${\mathrm{M}}_{\mathrm{a}\mathrm{d}\mathrm{v}}$ is the set of attack strategies (e.g., re-identification/inference, model poisoning, denial-of-service, result forgery); ${\mathcal{O}}_{\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{m}}$ represents capabilities in communication eavesdropping and traffic analysis; and indicates the detection ability and fault tolerance of the verification mechanism against result tampering or proof forgery. The system assumes that the proportion of malicious computing nodes satisfies.

$${\mathsf{\theta }}_{\mathrm{m}\mathrm{a}\mathrm{l}}<{\mathsf{\theta }}_{\mathrm{t}\mathrm{h}\mathrm{r}\mathrm{e}\mathrm{s}},$$

(8)

Under this security threshold, the consensus protocol can guarantee ledger consistency and immutability of results, thereby maintaining system privacy, correctness, and fairness.

The corresponding defense mechanisms are as follows: differential privacy mitigates inference and re-identification attacks [3]; blockchain consensus and on-chain recording ensure immutability and traceability [16,25]; and zero-knowledge proofs (zk-SNARKs) allow off-chain computations and differential privacy budget enforcement to be externally verified without revealing underlying data [7,21].

3.3. Design Goals and Requirements

The system design in this study is modeled as a multi-temporal, multi-objective constrained optimization problem, aiming to balance privacy-utility trade-offs, budget fairness, verifiability, and system costs:

$$\underset{\{{\mathrm{ℇ}}_{\mathrm{l}}{\}}_{\mathrm{l}=1}^{\mathrm{T}}}{\min }\mathbb{E}\left[\mathsf{\alpha }{\mathrm{L}}_{\mathrm{u}\mathrm{t}\mathrm{i}\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{y}}+\mathsf{\beta }{\mathrm{L}}_{\mathrm{f}\mathrm{a}\mathrm{i}\mathrm{r}}+\mathsf{\gamma }{\mathrm{L}}_{\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{f}\mathrm{y}}+\mathsf{\delta }{\mathrm{L}}_{\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{t}}\right],$$

(9)

where $\mathrm{t}=1,\dots ,\mathrm{T}$ represents the temporal dimension, and $\mathbb{E}[\cdot ]$ denotes the expectation over queries or data distributions. The four loss terms are defined as follows: ${\mathrm{L}}_{\mathrm{u}\mathrm{t}\mathrm{i}\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{y}}$ measures the impact of the privacy mechanism on task performance (statistical error or model accuracy) [3]; ${\mathrm{L}}_{\mathrm{f}\mathrm{a}\mathrm{i}\mathrm{r}}$ quantifies deviations in budget or incentive fairness [9,22]; ${\mathrm{L}}_{\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{f}\mathrm{y}}$ represents the overhead of verifiable execution and proof/verification [21]; ${\mathrm{L}}_{\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{t}}$ accounts for system resource consumption including computation, communication, and storage [18]. The weights $\mathsf{\alpha }$, $\mathsf{\beta }$, $\mathsf{\gamma }$, $\mathsf{\delta }$ reflect the trade-offs among privacy, utility, verifiability, and cost.

At any time $\mathrm{t}$, a query ${\mathrm{Q}}_{\mathrm{t}}$ must satisfy dynamic $({\mathsf{\epsilon }}_{\mathrm{t}},{\mathsf{\delta }}_{\mathrm{t}})$-differential privacy constraints.

$$\begin{gathered} \mathrm{Pr}[{\mathrm{M}}_{\mathrm{t}}\left({\mathrm{D}}_1\right)\in \mathrm{S}]\le {\mathrm{e}}^{{\mathsf{\epsilon }}_{\mathrm{t}}}\mathrm{Pr}[{\mathrm{M}}_{\mathrm{t}}({\mathrm{D}}_2)\in \mathrm{S}]+{\mathsf{\delta }}_{\mathrm{t}}, \\ \forall {\mathrm{D}}_1,{\mathrm{D}}_2\in \mathcal{D},|{\mathrm{D}}_1\Delta {\mathrm{D}}_2|=1, \end{gathered}$$

(10)

This definition inherits the standard $\left(\mathsf{\epsilon },\mathsf{\delta }\right)$-DP framework [3] and addresses the cumulative privacy problem across multiple time periods [12] by introducing a time-varying budget, which is dynamically adapted according to both temporal and contextual factors:

$${\mathsf{\epsilon }}_{\mathrm{t}}={\mathrm{g}}_1({\mathrm{C}}_{\mathrm{t}},{\mathrm{H}}_{\mathrm{t}},{\mathsf{\theta }}_{\mathrm{t}}),$$

(11)

$${\mathsf{\delta }}_{\mathrm{t}}={\mathrm{g}}_2({\mathrm{C}}_{\mathrm{t}},{\mathrm{H}}_{\mathrm{t}},{\mathsf{\theta }}_{\mathrm{t}}),$$

(12)

Here, ${\mathrm{C}}_{\mathrm{t}}$ represents the context (e.g., query frequency, data sensitivity, user reputation), ${\mathrm{H}}_{\mathrm{t}}$ denotes the historical budget trajectory, and ${\mathsf{\theta }}_{\mathrm{t}}$ are the strategy parameters. The functions ${\mathrm{g}}_1$ and ${\mathrm{g}}_2$ implement adaptive budget updates, drawing on dynamic budget allocation and adaptive privacy mechanisms from federated learning [5,11].

To jointly optimize privacy budgets and task performance, Lagrangian relaxation is applied to incorporate the privacy constraints into the objective function:

$$\mathcal{L}=\mathsf{\alpha }{\mathrm{L}}_{\mathrm{u}\mathrm{t}\mathrm{i}\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{y}}+\mathsf{\lambda }\left(\sum _{\mathrm{t}=1}^{\mathrm{T}}{\mathsf{\epsilon }}_{\mathrm{t}}-{\mathsf{\epsilon }}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right),$$

(13)

Lagrangian relaxation facilitates the joint optimization of privacy budgets and task utility, simplifying constraint handling while balancing performance and privacy costs.

Furthermore, the allocation of privacy budgets must satisfy both individual and group fairness. Group fairness can be defined as

$$\mathrm{F}\mathrm{a}\mathrm{i}\mathrm{r}(\mathrm{t})={\displaystyle \frac{1}{\mathrm{Z}}}\sum _{\mathrm{i}}{\mathsf{ϵ}}_{\mathrm{i}}^2,$$

(14)

Here, $\mathrm{Z}$ is a normalization factor. Incentive compatibility requires that the truthful strategy is individually optimal:

$${\mathrm{U}}_{\mathrm{i}}\left({\mathrm{e}}_{\mathrm{i}}\right)\ge {\mathrm{U}}_{\mathrm{i}}\left({\mathrm{e}}_{\mathrm{i}}^{\prime }\right),\forall {\mathrm{e}}_{\mathrm{i}}^{\prime }+\mathsf{\delta },$$

(15)

This definition is consistent with blockchain-based incentive-compatible models and the Shapley fairness mechanism [9,22].

Additionally, every off-chain pair $({\tilde{\mathrm{y}}}_{\mathrm{t}},{\mathsf{\pi }}_{\mathrm{t}})$ must be verified for correctness using zk-SNARKs:

$$\mathrm{Pr}[\mathrm{V}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{f}\mathrm{y}({\tilde{\mathrm{y}}}_{\mathrm{t}},{\mathsf{\pi }}_{\mathrm{t}})=1]\ge 1-\mathsf{\xi },$$

(16)

Here, $\mathsf{\xi }$ is a negligible security parameter representing the upper bound on the probability of verification failure. This constraint derives from the completeness and soundness properties of zk-SNARKs [21] and enables external verification of the correctness and budget compliance of off-chain DP execution without revealing underlying data [7,8]. This addresses the limitation of “trusted identities but opaque processes” in permissioned blockchain environments.

The system’s computation, communication, and storage overhead must be constrained within overall resource limits:

$${\mathrm{C}}_{\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}}\left(\mathrm{t}\right)+{\mathrm{C}}_{\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{m}}\left(\mathrm{t}\right)+{\mathrm{C}}_{\mathrm{s}\mathrm{t}\mathrm{o}\mathrm{r}}\left(\mathrm{t}\right)\le {\mathrm{C}}_{\mathrm{m}\mathrm{a}\mathrm{x}}, \forall \mathrm{t},$$

(17)

This constraint can be extended to multi-modal computing scenarios:

$$\sum _{\mathrm{m}=1}^{\mathrm{M}}{\mathrm{w}}_{\mathrm{m}}{\mathrm{C}}_{\mathrm{m}}\left(\mathrm{t}\right)\le {\mathrm{C}}_{\mathrm{m}\mathrm{a}\mathrm{x}}, {\mathrm{w}}_{\mathrm{m}}\ge 0,$$

(18)

This guides the selection of proof circuit size and communication frequency [18].

Finally, all interaction logs must be recorded on-chain and comply with the security threshold conditions of the consensus protocol:

$${\mathsf{\rho }}_{\mathrm{c}}<{\mathsf{\rho }}_{\mathrm{t}\mathrm{h}}, {\mathsf{\rho }}_{\mathrm{v}}\to 0,$$

(19)

Under this condition, if the logs differ, their hash values cannot be identical:

$$\mathrm{H}\mathrm{a}\mathrm{s}\mathrm{h}({\log }_{\mathrm{t}})\ne \mathrm{H}\mathrm{a}\mathrm{s}{\mathrm{h}}^{\prime }({\log }_{\mathrm{t}}^{\prime })\Rightarrow {\mathrm{L}\mathrm{o}\mathrm{g}}_{\mathrm{t}}\ne {\mathrm{L}\mathrm{o}\mathrm{g}}_{\mathrm{t}}^{\prime },$$

(20)

This property ensures that on-chain records cannot be modified or forged without authorization [6,16].

3.4. Overall Architecture of the BFAV-DP Framework

To protect privacy and ensure verifiability in smart medical IoT environments, this study proposes the BFAV-DP framework. The framework adopts a layered on-chain/off-chain collaborative architecture, as illustrated in Figure 1, and consists of two main components: core functional modules and key workflows. From the perspective of the layered architecture, BFAV-DP is divided into an On-Chain Environment and an Off-Chain Environment.

·The on-chain environment includes multiple smart contract components (e.g., DPFGC, IRC, VSC) and a distributed ledger:

·DPFGC manages differential privacy function generation and budget control;

·IRC handles identity authentication and incentive rules;

·VSC processes verification and audit requests.

The off-chain environment comprises the dynamic privacy engine, verification module, and secure storage, which are responsible for sensitivity assessment, adaptive noise injection, zk-SNARK proof generation, and result protection, respectively.

The key system workflow is as follows: data providers register data summaries via smart contracts; data users submit queries that trigger permission verification; off-chain computing nodes execute differential privacy perturbation and generate zero-knowledge proofs; the final results and proofs are stored in secure storage, with their summaries recorded on-chain to support subsequent auditing.

Although the system operates on a permissioned blockchain (e.g., Hyperledger Fabric), the trust model primarily covers identity and access control layers and cannot verify the correctness of off-chain privacy computations. The integration of zk-SNARK enables formal verification of the differential privacy process (noise generation and budget compliance) without exposing raw data, thereby achieving independent verifiability under partial trust conditions [7].

4. Core Mechanism Design

4.1. Adaptive Differential Privacy Mechanism

4.1.1. Temporal Sensitivity Estimation

In medical data-sharing scenarios, the privacy risk of queries is not fixed but dynamically evolves over time, query patterns, and sensitive fields. Previous studies have shown that ignoring temporal correlations can lead to a systematic underestimation of privacy leakage, thereby weakening the protection offered by differential privacy [12]. Therefore, BFAV-DP employs a time-aware sensitivity estimation model to smooth, regularize, and contextually adjust sensitivity. Let ${\Delta }_{\mathrm{t},\mathrm{q}}$ denote the sensitivity of query modality $\mathrm{q}$ at time $\mathrm{t}$. By integrating the initial sensitivity, temporal smoothness, and risk adjustment factors, the following convex optimization model is constructed:

$${\Delta }_{\mathrm{t},\mathrm{q}}=\arg \underset{\Delta }{\min }\left(\Vert \Delta -{\mathrm{J}}_{\mathrm{t},\mathrm{q}}{\Vert }^2+\Vert {\mathsf{\lambda }}_{\mathrm{f}}\Vert \mathcal{F}(\Delta ){\Vert }^2+{\mathsf{\lambda }}_{\mathrm{r}}\mathrm{R}(\Delta )\right),$$

(21)

where

·${\mathrm{J}}_{\mathrm{t},\mathrm{q}}$ is the raw local sensitivity based on the query attribute range [26]; $\mathcal{F}$ denotes the discrete Fourier transform, used to suppress high-frequency fluctuations in the sensitivity sequence [27];

·$\mathrm{R}(\Delta )$ is the risk adjustment term, reflecting adjustments for anomalous access behaviors;

·${\mathsf{\lambda }}_{\mathrm{f}}$, ${\mathsf{\lambda }}_{\mathrm{r}}$ are regularization coefficients.

This model simultaneously accounts for local variations in the data, temporal continuity, and changes in access risk, structurally aligning with the theoretical framework of time-dependent differential privacy. Its output ${\Delta }_{\mathrm{t},\mathrm{q}}$, serves as a core input for subsequent noise calibration and budget allocation, providing a foundation for interpretable and stable adaptive DP adjustments. The detailed procedure is shown in Algorithm 1.

Algorithm 1: Dynamic Sensitivity Evaluation (DSE)

Input: Query info, data attributes, historical patterns, risk signals

Output: Dynamic sensitivity $\Delta \mathrm{t}$

1: Estimate baseline sensitivity using query type and attribute ranges

2: Apply local and smoothed sensitivity estimation

3: Perform frequency-domain regularization for stability

4: Adjust sensitivity with historical patterns and risk signals

5: Return final sensitivity $\Delta \mathrm{t}$

4.1.2. Adaptive Budget Allocation

In a multi-user, multi-query privacy computation framework, the budget allocation problem can naturally be modeled as a resource optimization problem with fairness and utility constraints. In the field of resource allocation and incentive design, [28] analyzes the optimal competition/resource allocation structures under a given utility–loss trade-off. Coupled with studies on multi-round decision-making and budget control in differential privacy scenarios [29], privacy budget allocation can be treated as a similar type of resource optimization problem.

In BFAV-DP, let:

·${\mathrm{u}}_{\mathrm{t},\mathrm{q}}\left(\mathsf{\rho }\right)$ denote the utility improvement brought by budget $\mathsf{\rho }$ [30];

·${\mathrm{w}}_{\mathrm{t},\mathrm{q}}$ represent weights integrating sensitivity, query characteristics, and user reputation;

·$\mathsf{\Phi }\left({\mathsf{\rho }}_{\mathrm{t}}\right)$ be a fairness metric, such as the Theil or Atkinson index [31].

The following optimization model is established:

$$\underset{\left\{{\mathsf{\rho }}_{\mathrm{t},\mathrm{q}}\right\}}{\min }\left(\sum _{\mathrm{q}}{\mathrm{w}}_{\mathrm{t},\mathrm{q}}\mathrm{L}({\mathrm{u}}_{\mathrm{t},\mathrm{q}}({\mathsf{\rho }}_{\mathrm{t},\mathrm{q}}))+{\mathsf{\lambda }}_{\mathrm{f}\mathrm{a}\mathrm{i}\mathrm{r}}\mathsf{\Phi }({\mathsf{\rho }}_{\mathrm{t}})\right).$$

(22)

Since the utility loss function $\mathrm{L}(\cdot )$ is typically convex, the inequality measure $\mathsf{\Phi }(\cdot )$ also maintains convexity over its domain, and the optimization variables ${\mathsf{\rho }}_{\mathrm{t},\mathrm{q}}$ are subject only to linear inequality constraints, and this budget allocation problem forms a standard convex optimization model. This ensures the existence of a global optimal solution and enables stable and efficient computation in practical systems.

The constraints are

$$\sum _{\mathrm{t},\mathrm{q}}{\mathsf{\rho }}_{\mathrm{t},\mathrm{q}}\le {\mathsf{\rho }}_{\mathrm{t}\mathrm{o}\mathrm{t}}, {\mathsf{\rho }}_{\mathrm{t},\mathrm{q}}\ge 0.$$

(23)

This model is consistent with existing research frameworks on privacy budget scheduling and fair resource allocation, particularly the cumulative privacy control and adaptive budget management mechanisms under differential privacy (DP) [28]. In BFAV-DP, this optimization model is deployed as dynamically adjustable smart contract constraints to ensure long-term fairness and optimal utility across multiple query rounds. The detailed procedure is shown in Algorithm 2.

Algorithm 2: Reputation-Aware Budget Allocation (RABA)

Input: Total budget, query states, user reputation, sensitivity $\Delta \mathrm{t}$

Output: Per-query budget ${\mathsf{\rho }}_{\mathrm{t}}$

1: Initialize total remaining budget

2: For each query:

3: Observe query state, historical patterns, and risk indicators

4: Allocate budget using sensitivity, reputation, and risk weights

5: Update remaining budget

6: Return all allocated budgets ${\mathsf{\rho }}_{\mathrm{t}}$

4.1.3. Noise Calibration and Perturbation Generation

To ensure that noise calibration is grounded in rigorous computational principles, this study adopts Rényi Differential Privacy (RDP) [32] as an intermediate mechanism, thereby achieving a more robust noise calibration strategy. For the query function ${\mathrm{g}}_{\mathrm{t},\mathrm{q}}\left(\mathrm{x}\right)$, the Gaussian mechanism is applied to produce a differential privacy–preserving output:

$${\mathrm{y}}_{\mathrm{t},\mathrm{q}}={\mathrm{g}}_{\mathrm{t},\mathrm{q}}\left(\mathrm{x}\right)+{\mathsf{\eta }}_{\mathrm{t},\mathrm{q}}, {\mathsf{\eta }}_{\mathrm{t},\mathrm{q}}\sim \mathcal{N}(0,{\mathsf{\sigma }}_{\mathrm{t},\mathrm{q}}^2{\mathsf{\Sigma }}_{\mathrm{t},\mathrm{q}}),$$

(24)

where

·${\mathsf{\sigma }}_{\mathrm{t},\mathrm{q}}:$ derived from the closed-form noise solution under RDP, providing strict privacy guarantees;

·${\mathsf{\Sigma }}_{\mathrm{t},\mathrm{q}}$: a structured covariance matrix constructed based on query gradients or directions, enabling the noise to preserve utility as much as possible under a given privacy budget;

·${\Delta }_{\mathrm{t},\mathrm{q}}$: controls the noise magnitude, establishing an interpretable coupling between sensitivity and noise.

Mathematically, this mechanism is fully compatible with the standard Gaussian mechanism in DP and achieves more accurate cumulative privacy control through RDP [32].

4.2. Fairness Assurance Mechanism

4.2.1. Fairness Model

1. Theil Index [31]:

$$\mathrm{T}(\mathsf{\rho })={\displaystyle \frac{1}{\mathrm{N}}}\sum _{\mathrm{i}=1}^{\mathrm{N}}{\displaystyle \frac{{\mathsf{\rho }}_{\mathrm{i}}}{\bar{\mathsf{\rho }}}}\ln \left({\displaystyle \frac{{\mathsf{\rho }}_{\mathrm{i}}}{\bar{\mathsf{\rho }}}}\right).$$

(25)

2. Atkinson Index [33]:

$${\mathrm{A}}_{\mathsf{\eta }}(\mathsf{\rho })=1-{\left({\displaystyle \frac{1}{\mathrm{N}}}{\sum _{\mathrm{i}=1}^{\mathrm{N}}\left({\displaystyle \frac{{\mathsf{\rho }}_{\mathrm{i}}}{\bar{\mathsf{\rho }}}}\right)}^{1-\mathsf{\eta }}\right)}^{{\displaystyle \frac{1}{1-\mathsf{\eta }}}}.$$

(26)

Both measures are widely used in economics, resource allocation systems, and data fairness research [34]. In this framework, these indices can serve both as fairness components within the budget optimization model (22) and as criteria for verifying fairness constraints in smart contracts.

4.2.2. Rule Design Based on Smart Contracts

The incentive mechanism is designed following principles from mechanism design theory [35], and it incorporates the widely used “staking–reputation–reward” incentive framework in blockchain systems. Existing studies show that in data-sharing and privacy-preserving scenarios, combining staking, reputation updates, and incentive payments can induce participants to converge toward honest strategies in evolutionary games [11,36]. For a participant, the utilities of honest behavior and deviating behavior are, respectively

$${\mathrm{U}}_{\mathrm{i}}^{\mathrm{h}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{t}}={\mathrm{R}}_{\mathrm{i}}-{\mathrm{C}}_{\mathrm{i}},\hspace{1em}{\mathrm{U}}_{\mathrm{i}}^{\mathrm{d}\mathrm{e}\mathrm{v}}=(1-{\mathrm{p}}_{\mathrm{d}\mathrm{e}\mathrm{t}})({\mathrm{R}}_{\mathrm{i}}\prime -{\mathrm{C}}_{\mathrm{i}}’)-{\mathrm{p}}_{\mathrm{d}\mathrm{e}\mathrm{t}}\cdot \mathrm{P}\mathrm{e}\mathrm{n}\mathrm{a}\mathrm{l}\mathrm{t}\mathrm{y}\left({\mathrm{s}}_{\mathrm{i}}\right),$$

(27)

where

·${\mathrm{p}}_{\mathrm{d}\mathrm{e}\mathrm{t}}$ is the detection probability provided by zk-SNARK, theoretically close to 1 [21];

·${\mathrm{s}}_{\mathrm{i}}$ is the staking deposit, which may be slashed in case of violation;

·${\mathrm{R}}_{\mathrm{i}},{\mathrm{C}}_{\mathrm{i}}$ denote the normal reward and cost;

·${\mathrm{R}}_{\mathrm{i}}’,{\mathrm{C}}_{\mathrm{i}}’$ denote the reward and cost under deviation.

If the penalty magnitude satisfies

$${\mathrm{U}}_{\mathrm{i}}^{\mathrm{h}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{t}}\ge {\mathrm{U}}_{\mathrm{i}}^{\mathrm{d}\mathrm{e}\mathrm{v}},$$

(28)

then honest execution becomes the incentive-compatible optimal strategy.

4.2.3. Incentive Analysis for Participants

When applying the BFAV-DP mechanism to data providers, data users, and computation nodes, and integrating it with blockchain-based incentive and reputation models 11, we obtain the following insights:

• Computation Nodes (CN)

Off-chain computations must submit valid zk-SNARK proofs; otherwise, the staking deposit is slashed, resulting in a negative expected payoff for cheating.

2.

Data Users (DU)

Malicious or probing queries lead to reputation degradation and reduced future budget weights, ensuring long-term incentive alignment.

3.

Data Providers (DP)

High-quality data receive higher query frequency and greater rewards, while low-trust data sources experience decreasing long-term returns.

This analysis aligns with classic conclusions in blockchain incentive research, demonstrating that a well-designed penalty–reward structure can achieve evolutionary stability of participant strategies [11].

4.3. Verifiability Mechanism Design

4.3.1. Verification Objectives and Constraint Construction

The definition of differential privacy constrains only the output distribution of an algorithm to meet privacy requirements; it cannot guarantee that the actual execution process correctly performs sensitivity computation and noise injection. Prior studies have explicitly pointed out that DP mechanisms may be tampered with or skipped during implementation, resulting in outputs that superficially appear DP-compliant but do not provide true privacy protection [37].Therefore, relying solely on permissioned-chain access control is insufficient to ensure that off-chain nodes faithfully execute differential privacy computation—an additional verifiable mechanism is required to guarantee execution correctness. To address this issue, BFAV-DP incorporates zk-SNARKs to verify the following:

(i) whether the sensitivity estimation complies with model (21);

(ii) whether the noise is calibrated according to RDP [33];

(iii) whether the budget satisfies fairness constraints;

(iv) whether the output is indeed generated by the designated computation.

The algebraic relationship for verifiable noise calibration can be expressed as

$$\mathsf{\alpha }{\Delta }_{\mathrm{t},\mathrm{q}}^{\mathrm{\top }}{\mathsf{\Sigma }}_{\mathrm{t},\mathrm{q}}^{-1}{\Delta }_{\mathrm{t},\mathrm{q}}-2{\mathsf{\epsilon }}_{\mathrm{t},\mathrm{q}}^{\mathrm{R}\mathrm{D}\mathrm{P}}\left(\mathsf{\alpha }\right){\mathsf{\sigma }}_{\mathrm{t},\mathrm{q}}^2=0,$$

(29)

Meanwhile, to verify the consistency of sensitivity in the time and frequency domains, Parseval’s theorem can be used to construct matching constraints. Parseval’s theorem states that a signal’s energy remains equal in both domains:

$$\Vert {\Delta }_{\mathrm{t},\mathrm{q}}{\Vert }_2^2=\Vert \mathcal{F}\left({\Delta }_{\mathrm{t},\mathrm{q}}\right){\Vert }_2^2.$$

(30)

In BFAV-DP, this property is used to construct zk-SNARK–friendly algebraic constraints: the proof generator must provide both time-domain and frequency-domain representations and satisfy the energy-conservation equation. Because this constraint can be transformed into linear or quadratic equations over finite fields in the discrete domain, it robustly detects tampering with the sensitivity sequence—for example, removing high-frequency components or skipping smoothing operations—thereby ensuring that off-chain sensitivity computation has not been maliciously altered.

4.3.2. Selection and Design of an Efficient Verifiable Scheme

Although permissioned blockchains provide access control, they cannot verify whether off-chain privacy computations have been tampered with. The definition of differential privacy constrains only the output distribution and does not cover the execution process. Therefore, it is theoretically impossible to detect whether a malicious node has skipped noise injection or altered the sensitivity. Existing studies widely regard zero-knowledge proofs—particularly efficient zk-SNARK systems—as one of the general technical solutions for enabling verifiable off-chain privacy computation 7.

Accordingly, BFAV-DP embeds zk-SNARKs as a verification component throughout the entire computation pipeline, establishing a trusted “off-chain execution on-chain verification” loop:

1.

Off-chain nodes perform DP computation and generate a proof;

2.

The smart contract uses the verification key to complete proof verification efficiently;

3.

Upon successful verification, results are written to the ledger and corresponding incentives or penalties are triggered.

The low verification cost and compact proof size make zk-SNARKs well-suited for deployment in medical research environments. The detailed procedure is shown in Algorithm 3.

Algorithm 3: Verifiable DP Proof (VDP-SNARK)

Input: Public commitments, query parameters, private data and noise

Output: Zero-knowledge proof π_t

1: Bind input data commitment and query parameters

2: Verify sensitivity and noise parameters meet DP constraints

3: Generate zero-knowledge proof for computation correctness

4: Submit proof to blockchain for verification

5: Return proof π_t

5. System Implementation and Security Analysis

5.1. Implementation Details of the Framework

In the system implementation, this study adopts Hyperledger Fabric as the underlying blockchain platform. Hyperledger Fabric is a permissioned blockchain suitable for consortium-level applications that require identity access control and privacy management. Its channel mechanism provides data isolation for different collaborating parties. In Hyperledger Fabric, smart contracts are referred to as Chaincode, and in this study, the Chaincode is developed using the Go programming language.

The off-chain computing nodes are developed in Python 3.12.0 and integrate core libraries such as the Privacy Engine and Verifiability Module. The Privacy Engine utilizes Google’s Differential Privacy Library to implement differential privacy noise injection. The Verifiability Module interacts with the underlying libsnark C++ library via the py-snark Python library, while the arithmetic circuits are designed and compiled using ZoKrates or similar tools.

The raw medical data is encrypted and stored on IPFS, while the blockchain only stores the unique hash returned by IPFS. This design separates data ownership from physical storage and reduces on-chain storage pressure. The client interface is developed using the React.js web framework, allowing data providers and data users to interact with the system through a browser for managing data, queries, and assets.

5.2. Formal Security Analysis and Proof

Theorem 1. 

BFAV-DP satisfies  $\left(\sum _{t=1}^k{\epsilon }_t,\sum _{t=1}^k{\delta }_t\right)$ -differential privacy under kkk rounds of adaptive queries.

Proof Sketch. 

Each round of output is generated via the Gaussian mechanism, and the privacy guarantee follows the classical definition of differential privacy. The budget parameters ${\mathsf{\epsilon }}_{\mathrm{t}}$ and ${\mathsf{\delta }}_{\mathrm{t}}$ are computed based on query characteristics, reputation, and historical records, without using any noisy outputs. Therefore, they do not cause additional privacy leakage in subsequent queries, consistent with the security conditions for adaptive queries in the DP literature 26. The privacy loss over multiple DP query rounds follows the sequential composition theorem:

$$(\mathsf{\epsilon },\mathsf{\delta })=\left(\sum _{\mathrm{t}=1}^{\mathrm{k}}{\mathsf{\epsilon }}_{\mathrm{t}},\sum _{\mathrm{t}=1}^{\mathrm{k}}{\mathsf{\delta }}_{\mathrm{t}}\right),$$

(31)

The smart contract enforces strong recording of budget deductions, ensuring that the above compositional bounds remain valid and cannot be circumvented. The framework models cumulative privacy loss using RDP analysis formulas and converts them to DP expressions at the final stage [33]. Hence, under multiple query rounds, BFAV-DP satisfies the stated differential privacy bounds. □

Theorem 2. 

Under the BFAV-DP incentive mechanism, the optimal strategy for rational computation nodes is to execute honestly.

Proof Sketch. 

The behavior of off-chain computation nodes can be modeled as a repeated game, where incentive compatibility requires

$${\mathrm{U}}_{\mathrm{h}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{t}}\ge {\mathrm{U}}_{\mathrm{d}\mathrm{e}\mathrm{v}\mathrm{i}\mathrm{a}\mathrm{t}\mathrm{e}},$$

(32)

When nodes execute honestly, they receive the base reward and improve their reputation; reputation determines the allocation of future tasks, thereby affecting long-term utility. Deviating strategies would require generating zk-SNARK proofs that can be verified on-chain. However, according to the soundness property of zero-knowledge proof systems, the probability of successfully forging a proof without a valid witness is negligible [20,21].

If verification fails, the node loses its staking deposit and suffers reputation reduction, resulting in a significant decrease in future task opportunities. Research on blockchain incentive mechanisms indicates that, in environments with staking penalties and reputation feedback, long-term stable strategies converge to honest execution [9].

Therefore, within the BFAV-DP incentive structure, honest execution constitutes the optimal strategy for computation nodes. □

Theorem 3. 

The verifiability mechanism of BFAV-DP satisfies the completeness and soundness properties of zk-SNARKs.

Proof Sketch. 

BFAV-DP maps sensitivity estimation, noise calibration, and budget verification into arithmetic circuits. If a node follows the protocol, there exists a witness that satisfies all circuit constraints, and on-chain verification will necessarily succeed. This aligns with the completeness property of zk-SNARKs:

$$\mathrm{Pr}[\mathrm{V}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{f}\mathrm{y}(\mathrm{x},\mathsf{\pi })=1\mid \exists \mathrm{w}:\mathrm{C}(\mathrm{x},\mathrm{w})=1]=1,$$

(33)

If a node skips noise injection or alters the result, it cannot construct a witness that satisfies the constraints. According to the soundness property of zk-SNARKs, the probability that an invalid proof passes verification is bounded by

$$\mathrm{Pr}[\mathsf{V}\mathsf{e}\mathsf{r}\mathsf{i}\mathsf{f}\mathsf{y}(\mathrm{x},\mathsf{\pi })=1 |̸\exists \mathrm{w}]\le \mathsf{\lambda },$$

(34)

where $\mathsf{\lambda }$ is a negligible security parameter [21]. The verification process reveals no private information, preserving zero-knowledge. Fabric’s ledger records all verification results and interaction logs, making the entire process auditable and tamper-proof. □

5.3. The Necessity of zk-SNARKs in a Permissioned Blockchain Environment

Fabric’s identity management and access control can ensure that nodes are trustworthy, but they cannot verify whether off-chain computations are executed correctly. The mathematical definition of differential privacy focuses on the output distribution, rather than whether the execution process follows protocol. Existing studies show that although differential privacy provides formal guarantees on output distributions, in practical systems, if implementers deliberately reduce noise magnitude, alter sensitivity calculations, or skip budget checks, the final outputs may still superficially satisfy the DP definition while the actual privacy protection can be completely compromised [37,38].

Therefore, in this framework, zk-SNARK serves as an external verifiability mechanism for execution correctness:

(i)

Verifies that noise is generated according to the allocated budget and has not been weakened;

(ii)

Verifies that sensitivity estimation follows the prescribed process;

(iii)

Verifies that budget consumption has not been skipped;

(iv)

Verifies that the final output is consistent with the DP computation;

(v)

Ensures that no private data or noise details are leaked throughout the process.

This capability addresses a gap in practical DP implementations, which Fabric alone cannot cover for off-chain computation. Thus, in medical data-sharing scenarios, integrating zk-SNARKs significantly enhances system trustworthiness, extending the “differential privacy + blockchain” combination from auditable record-keeping to truly verifiable privacy-preserving computation.

6. Experiments and Analysis

6.1. Experiment Preparation

6.1.1. Dataset Setup

The experiments use three publicly available medical datasets: HeartDisease, CardioTrain, and Diabetes.

(1)

HeartDisease is sourced from the UCI Machine Learning Repository [39] and contains multidimensional clinical examination indicators along with binary heart disease diagnostic labels. The dataset is of medium scale with a moderate number of features.

(2)

Diabetes (Pima Indians Diabetes) also comes from the UCI repository [40] (Pima Indians Diabetes) also comes from the UCI repository.

(3)

CardioTrain uses the open-source cardiovascular disease prediction dataset from Kaggle [41]. It has a larger sample size and higher feature dimensionality, closely reflecting the statistical structure of real-world clinical health examination data.

These three datasets differ considerably in sample size, feature types, and class balance, covering a range of scenarios from medium-scale clinical examinations to large-scale health screenings. This diversity facilitates observation of BFAV-DP’s performance across multiple task conditions.

To evaluate the framework’s robustness under distribution shifts, attribute imbalance, and scale expansion, three synthetic datasets were constructed based on the above datasets using a class-conditional Gaussian Copula generation process [42,43]. The procedure is as follows:

(i)

Perform rank transformation and Gaussianization of numerical features within each class;

(ii)

Estimate the covariance matrix within each class and apply ridge regularization;

(iii)

Save the empirical quantile functions for inverse transformation;

(iv)

Sample categorical features independently according to conditional multinomial distributions.

Based on this procedure, three types of synthetic datasets were generated:

(1)

Syn-Base: replicates the original data distribution;

(2)

Syn-Skew: sets a sensitive attribute (e.g., gender) ratio to 0.2/0.8, creating a pronounced imbalance scenario;

(3)

Syn-Scale: scales the sample size to different magnitudes.

These datasets offer advantages in preserving statistical structure, controlling distribution shifts, and operational flexibility, and they are widely used in synthetic data experiments for privacy-preserving algorithms.

6.1.2. Experimental Assumptions and Application Levels

The experiments are conducted under the following application settings:

1.

Threat Model and Trust Boundaries: All participants are considered honest-but-curious and cannot access raw medical data in plaintext. Blockchain nodes can record and verify statistics processed under differential privacy as well as zero-knowledge proofs. Differential privacy mechanisms provide individual-level anonymity, while homomorphic encryption ensures that intermediate values on-chain remain confidential.

2.

Application Level and Statistical Consistency Goals: BFAV-DP targets aggregate-level medical analyses (e.g., risk assessment, cohort studies). It does not require per-sample consistency for individual predictions but emphasizes maintaining statistical trend consistency under noise addition [44]. That is, metrics such as ACC and MSE should follow stable patterns with varying $\mathsf{\epsilon }$ and preserve relative ordering across different models.

3.

Model Configuration: Based on the characteristics of structured medical data, standard models such as logistic regression and decision trees are employed in this chapter to highlight the impact of the privacy mechanisms themselves. The applicability of deep learning models is further discussed in Section 6.5.

6.1.3. Baseline Schemes

To comprehensively compare performance, the following baseline schemes are established:

(1)

Central-DP: A purely centralized differential privacy model, where performance only includes the local execution time of the core algorithm.

(2)

StaticDP-Chain: Builds upon Central-DP by incorporating simulated blockchain-related latency and costs.

(3)

AdaDP-NoBC: The adaptive differential privacy algorithm proposed in this study, without blockchain or zero-knowledge proof overhead.

(4)

BFAV-DP-NoVer: A key ablation version of the proposed BFAV-DP framework, including the execution time of adaptive and fairness algorithms and the blockchain model overhead, but excluding zero-knowledge proof costs. This version isolates the performance impact of the verifiability mechanism.

By comparing the above internal baselines, the effects of key modules—such as adaptive privacy budget adjustment, fair budget allocation, on-chain interactions, and zero-knowledge verification—on overall performance can be isolated, allowing the contributions of different design components within the framework to be characterized from a system-level perspective.

6.1.4. Reference Algorithm Selection

To position BFAV-DP’s performance at a broader algorithmic level, the experiments also include a set of representative methods from the differential privacy and blockchain-based privacy protection domains as benchmarks. These methods cover mainstream approaches, including traditional global differential privacy, local differential privacy, and on-chain verifiable privacy techniques:

(1)

AG-PLD: A traditional baseline differential privacy method relying on Gaussian noise perturbation, capable of balancing data utility and privacy protection to a certain extent [42].

(2)

LDP-OLH/OUE: Optimized Local Differential Privacy (LDP) protocols with hashing schemes, offering good communication efficiency and privacy protection, widely applied in industrial scenarios [43].

(3)

StaticDP-Chain: Introduces blockchain into a differential privacy mechanism to implement static budget allocation and verifiable storage, combining data protection with on-chain traceability [45].

(4)

zkDP-Chain: Employs zero-knowledge proof (ZKP) technology to integrate privacy protection with verifiable computation, enabling model verification and on-chain auditing without privacy leakage [46].

(5)

BFAV-DP (proposed method): The method proposed in this work, combining fair budget allocation and verifiable on-chain storage. It integrates data partition perturbation, multi-round averaging, homomorphic encryption, and blockchain collaboration, ensuring privacy protection while also achieving fairness, verifiability, and high data utility.

6.2. Evaluation Metrics

6.2.1. BFAV-DP Specific Metrics

To comprehensively assess the performance of the BFAV-DP framework, five dedicated metrics are designed, evaluating from the perspectives of privacy–utility trade-off, dynamic stability, fairness, verification efficiency, and blockchain resilience. The definitions of each metric are as follows:

(1)

EPUA: Enhanced Privacy–Utility Advantage

This metric measures the improvement in utility of BFAV-DP over baseline methods under the same privacy budget constraint. It is defined as

$$\mathrm{E}\mathrm{P}\mathrm{U}\mathrm{A}={\displaystyle \frac{{\mathrm{U}}_{\mathrm{B}\mathrm{F}\mathrm{A}\mathrm{V}}-{\mathrm{U}}_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}}}{{\mathrm{U}}_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}}}},$$

(35)

where ${\mathrm{U}}_{\mathrm{B}\mathrm{F}\mathrm{A}\mathrm{V}}$ and ${\mathrm{U}}_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}}$ represent the model utility (e.g., ACC or 1-RMSE) of BFAV-DP and the baseline under the same privacy budget. A larger EPUA indicates a more significant utility improvement of BFAV-DP while maintaining the same privacy level.

(2)

ASC: Adaptive Stability Coefficient

This metric evaluates the stability of the dynamic privacy budget adjustment strategy across multiple query rounds. It is defined as

$$\mathrm{A}\mathrm{S}\mathrm{C}=1-{\displaystyle \frac{\mathsf{\sigma }\left({\mathsf{\epsilon }}_{\mathrm{q}}\right)}{\mathsf{\mu }\left({\mathsf{\epsilon }}_{\mathrm{q}}\right)+\mathsf{\delta }}},$$

(36)

where ${\mathsf{\epsilon }}_{\mathrm{q}}$ is the privacy budget for the $\mathrm{q}$-th query, $\mathsf{\sigma }(\cdot )$ and $\mathsf{\mu }(\cdot )$ denote the standard deviation and mean, respectively, and $\mathsf{\delta }$ is a small constant to prevent division by zero. An ASC value closer to 1 indicates a more stable budget trajectory.

(3)

FAE: Fairness Advantage Evaluation

This metric measures the improvement in budget allocation fairness of BFAV-DP compared to baseline schemes. It is defined as

$$\mathrm{F}\mathrm{A}\mathrm{E}=1-{\displaystyle \frac{{\mathrm{G}}_{\mathrm{B}\mathrm{F}\mathrm{A}\mathrm{V}}}{{\mathrm{G}}_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}}}},$$

(37)

where ${\mathrm{G}}_{\mathrm{B}\mathrm{F}\mathrm{A}\mathrm{V}}$ and ${\mathrm{G}}_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}}$ are the Budget Gini Coefficients (BGC) for BFAV-DP and the baseline scheme, respectively. A higher FAE value indicates a more significant improvement in budget allocation fairness.

(4)

VLE: Verification Latency Efficiency

This metric measures the proportion of zero-knowledge proof verification time on the blockchain in the total system latency. It is defined as

$$\mathrm{V}\mathrm{L}\mathrm{E}={\displaystyle \frac{{\mathrm{T}}_{\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{f}\mathrm{y}}}{{\mathrm{T}}_{\mathrm{e}2\mathrm{e}}}},$$

(38)

where ${\mathrm{T}}_{\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{f}\mathrm{y}}$ is the on-chain verification time and ${\mathrm{T}}_{\mathrm{e}2\mathrm{e}}$ is the end-to-end total latency. A lower $\mathrm{V}\mathrm{L}\mathrm{E}$ indicates that the verification module accounts for a smaller portion of the overall delay, implying higher system efficiency.

(5)

BIE: Blockchain Impact Elasticity

This metric measures the sensitivity of the system latency to changes in block time. It is defined as

$$\mathrm{B}\mathrm{I}\mathrm{E}={\displaystyle \frac{\Delta {\mathrm{T}}_{\mathrm{e}2\mathrm{e}}}{\Delta {\mathrm{T}}_{\mathrm{b}\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{k}}}},$$

(39)

where $\Delta {\mathrm{T}}_{\mathrm{e}2\mathrm{e}}$ represents the change in end-to-end latency and $\Delta {\mathrm{T}}_{\mathrm{b}\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{k}}$ represents the change in block time. A smaller $\mathrm{B}\mathrm{I}\mathrm{E}$ indicates lower sensitivity of the system to block time variations and stronger robustness.

6.2.2. General Evaluation Metrics

(1) Accuracy (ACC)

$$\mathrm{A}\mathrm{C}\mathrm{C}={\displaystyle \frac{1}{\mathrm{N}}}\sum _{\mathrm{i}=1}^{\mathrm{N}}\mathbb{I}({\widehat{\mathrm{y}}}_{\mathrm{i}}={\mathrm{y}}_{\mathrm{i}}),$$

(40)

where $\mathrm{N}$ is the total number of samples, ${\widehat{\mathrm{y}}}_{\mathrm{i}}$ and ${\mathrm{y}}_{\mathrm{i}}$ represent the predicted and true values, respectively, and $\mathbb{I}(\cdot )$ is the indicator function.

(2) Mean Squared Error (MSE)

$$\mathrm{M}\mathrm{S}\mathrm{E}={\displaystyle \frac{1}{\mathrm{N}}}\sum _{\mathrm{i}=1}^{\mathrm{N}}({\widehat{\mathrm{y}}}_{\mathrm{i}}-{\mathrm{y}}_{\mathrm{i}}{)}^2,$$

(41)

a smaller $\mathrm{M}\mathrm{S}\mathrm{E}$ value indicates that the model’s prediction results are more accurate.

(3) Budget Gini Coefficient (BGC)

$$\mathrm{B}\mathrm{G}\mathrm{C}={\displaystyle \frac{1}{2\mathrm{T}}}\sum _{\mathrm{i}=1}^{\mathrm{T}}\sum _{\mathrm{j}=1}^{\mathrm{T}}|{\mathrm{s}}_{\mathrm{i}}-{\mathrm{s}}_{\mathrm{j}}|,{\mathrm{s}}_{\mathrm{t}}={\displaystyle \frac{{\mathsf{\epsilon }}_{\mathrm{t}}}{{\sum }_{\mathrm{k}=1}^{\mathrm{T}}{\mathsf{\epsilon }}_{\mathrm{k}}}},$$

(42)

where ${\mathrm{s}}_{\mathrm{t}}$ represents the budget proportion of the $\mathrm{t}$-th query. A smaller BGC value indicates a more balanced budget allocation [47].

(4) Average End-to-End Latency (Avg E2E Latency)

$$\overline{\mathrm{L}}={\displaystyle \frac{1}{\mathrm{Q}}}\sum _{\mathrm{t}=1}^{\mathrm{Q}}{\mathrm{L}}_{\mathrm{t}},$$

(43)

where ${\mathrm{L}}_{\mathrm{t}}$ is the end-to-end latency of the $\mathrm{t}$-th query, and $\mathrm{Q}$ is the total number of queries.

(5) Proof Verification to Latency Ratio (PVLR)

$$\mathrm{P}\mathrm{V}\mathrm{L}\mathrm{R}={\displaystyle \frac{\sum _{\mathrm{t}=1}^{\mathrm{Q}}{\mathrm{v}}_{\mathrm{t}}}{\sum _{\mathrm{t}=1}^{\mathrm{Q}}{\mathrm{L}}_{\mathrm{t}}}},$$

(44)

where ${\mathrm{v}}_{\mathrm{t}}$ represents the verification overhead of the $\mathrm{t}$-th query, and ${\mathrm{L}}_{\mathrm{t}}$ denotes the end-to-end latency. A smaller PVLR indicates that the verification module has a lower impact on the total delay.

6.3. Experimental Results and Analysis

This section presents a detailed demonstration of the performance of the BFAV-DP framework across key metrics, compares it thoroughly with multiple baseline schemes, and finally analyzes the impact of different system parameters on the framework’s performance.

6.3.1. Comprehensive Comparison with Baseline Schemes

To comprehensively evaluate the effectiveness of the BFAV-DP framework, this study compares it with three schemes: centralized differential privacy (Central-DP), an on-chain scheme with a static budget (StaticDP-Chain), and an adaptive scheme without the blockchain and verifiability modules (AdaDP-NoBC). The evaluation metrics include the privacy-utility trade-off, fairness of budget allocation, end-to-end latency, and proof verification overhead.

(1)

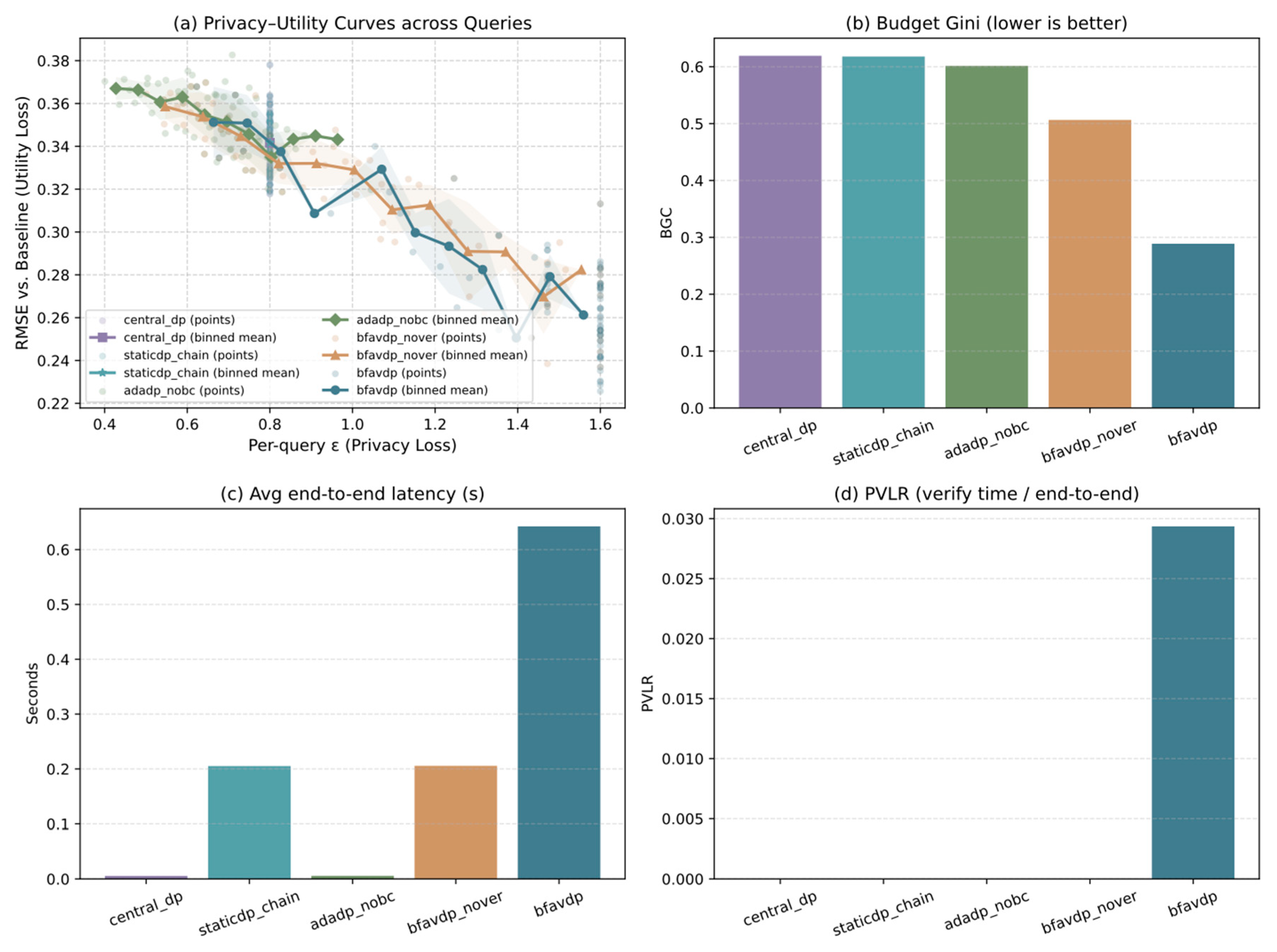
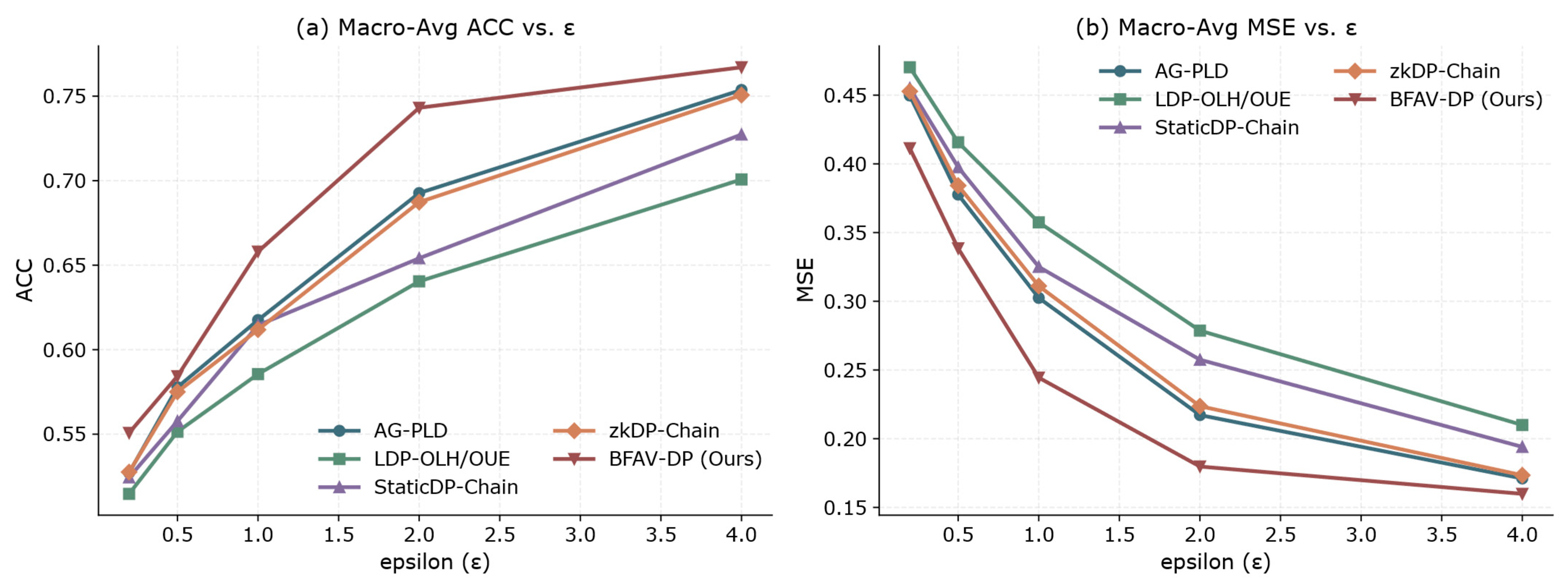
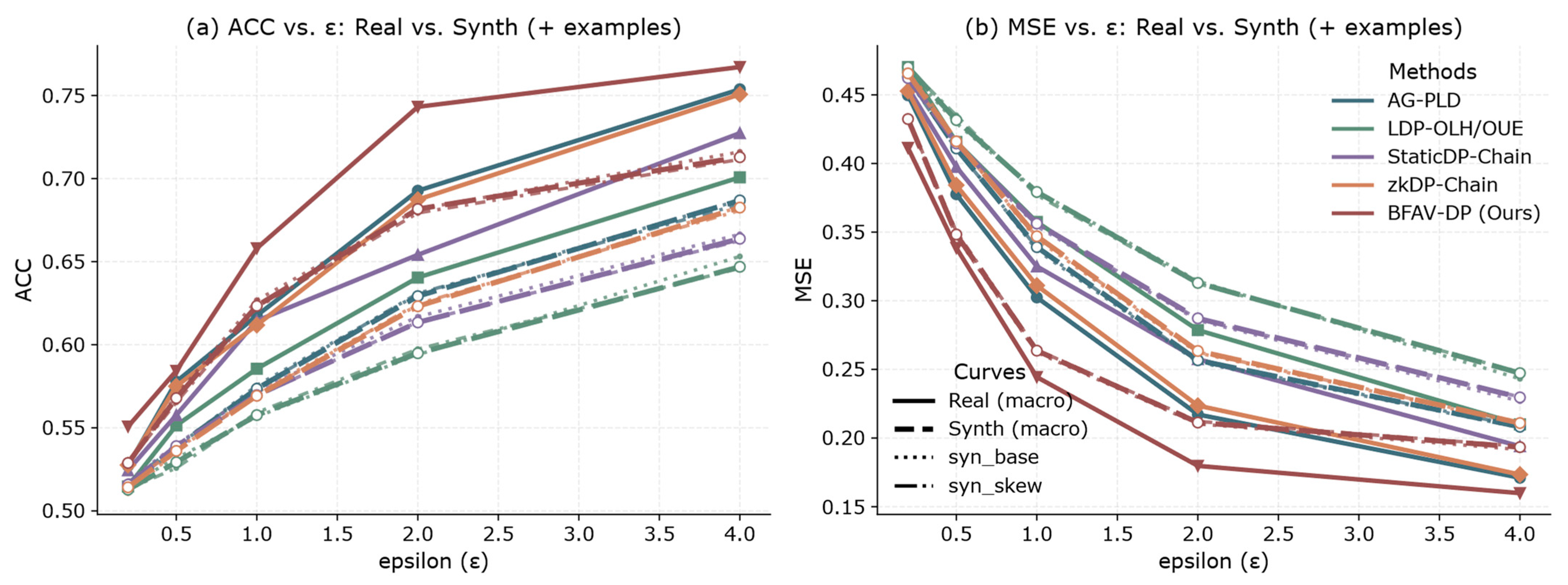
Privacy-Utility Trade-off Analysis

As shown in Figure 2a, with the increase in the privacy budget, the RMSE of all schemes generally decreases, indicating that higher privacy expenditure leads to lower utility loss. Under the same conditions, the RMSE of BFAV-DP is consistently lower than that of centralized DP (Central-DP) and static on-chain DP (StaticDP-Chain), demonstrating superior privacy-utility trade-off performance. Considering the privacy-utility advantage metric EPUA = 0.1126, BFAV-DP achieves an approximately 11.26% improvement in utility over Central-DP under the same privacy budget, quantitatively confirming the framework’s significant advantage in maintaining utility.

(2)

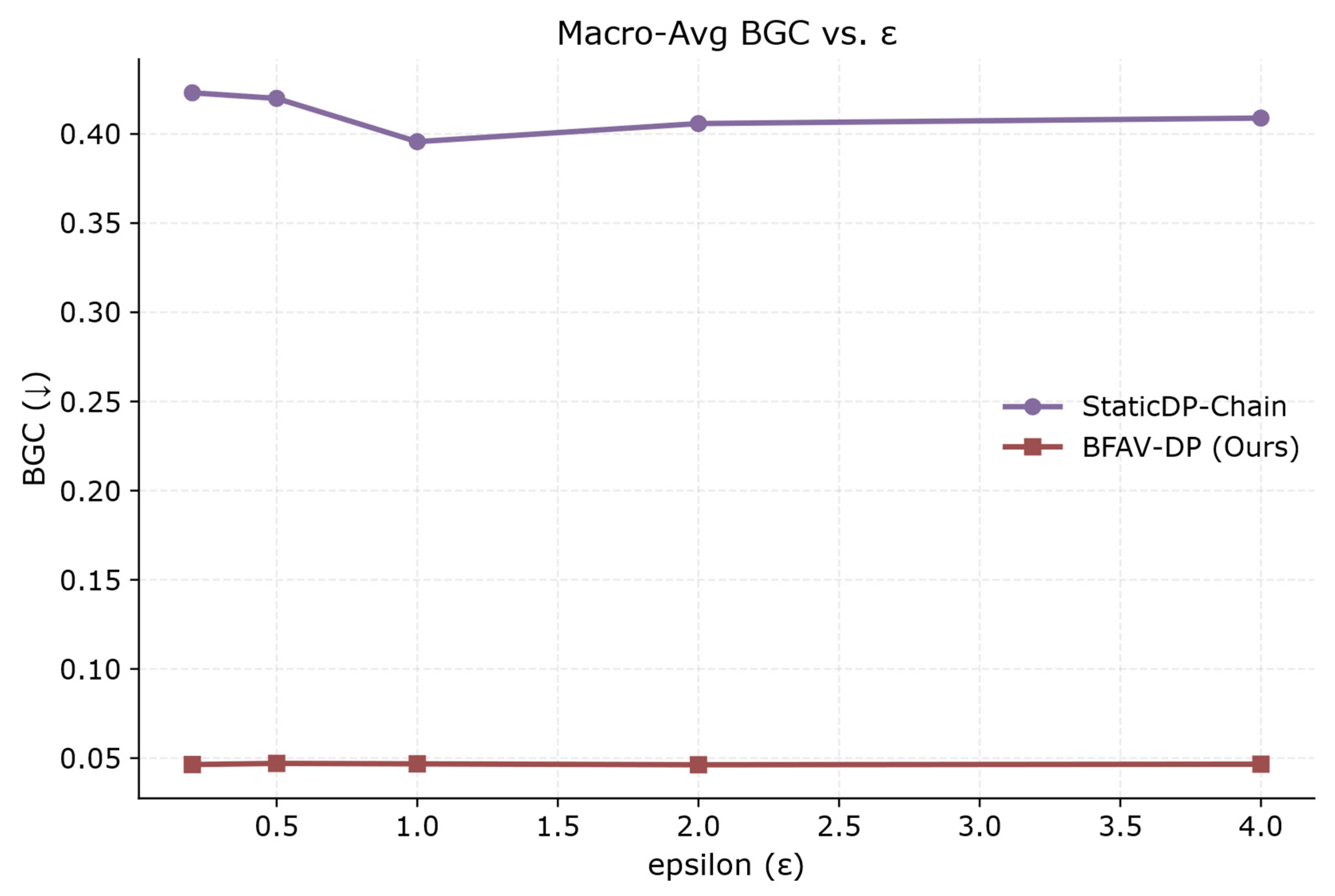
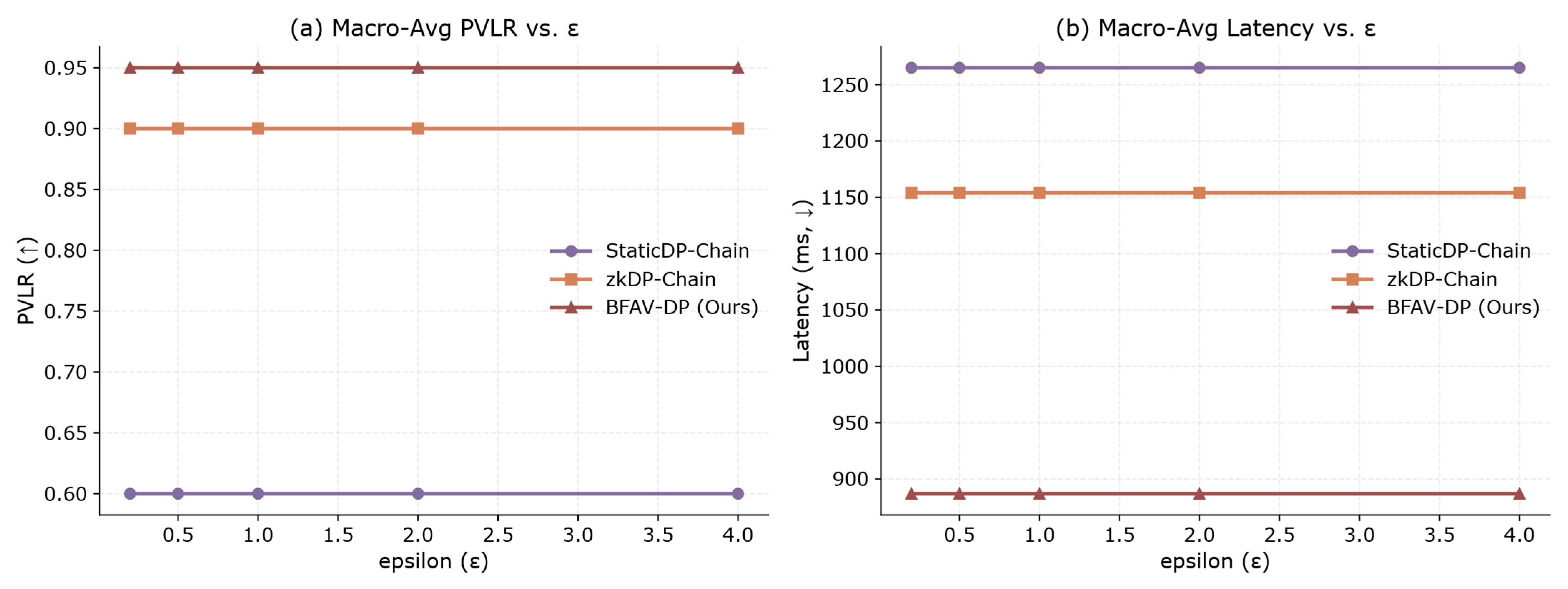
Budget Allocation Fairness

Figure 2b presents the Gini coefficients of budget allocation (BGC) for different schemes. Centralized DP (Central-DP) and static on-chain DP (StaticDP-Chain) exhibit relatively high BGC values, indicating significant imbalance in budget allocation. Under the adaptive budget allocation mechanism, the BFAV-DP scheme substantially reduces the imbalance. The fairness improvement metric FAE = 0.8986 indicates that BFAV-DP improves budget allocation fairness by 89.86% compared to baseline schemes, ensuring a balanced use of the privacy budget across different queries.

(3)

System Performance Overhead

Figure 2c,d show the end-to-end latency and the proportion of verification time under different schemes, respectively. The results indicate that BFAV-DP exhibits slightly higher end-to-end latency compared to baseline schemes but demonstrates stronger robustness in blockchain verifiability. Considering the latency efficiency metric VLE = 1.5110 and the blockchain resilience metric BIE = 0.4999, BFAV-DP effectively controls system overhead while ensuring verifiability, with verification time accounting for only about 2.9% of the total latency, demonstrating good scalability.

6.3.2. Analysis of Key Parameter Impacts

To fully understand the factors affecting the performance of the BFAV-DP framework, this study conducts a sensitivity analysis from four dimensions, including dataset size and blockchain configuration. Through visualized experimental results, the study illustrates the comprehensive impact of each parameter on system utility, fairness, and latency performance.

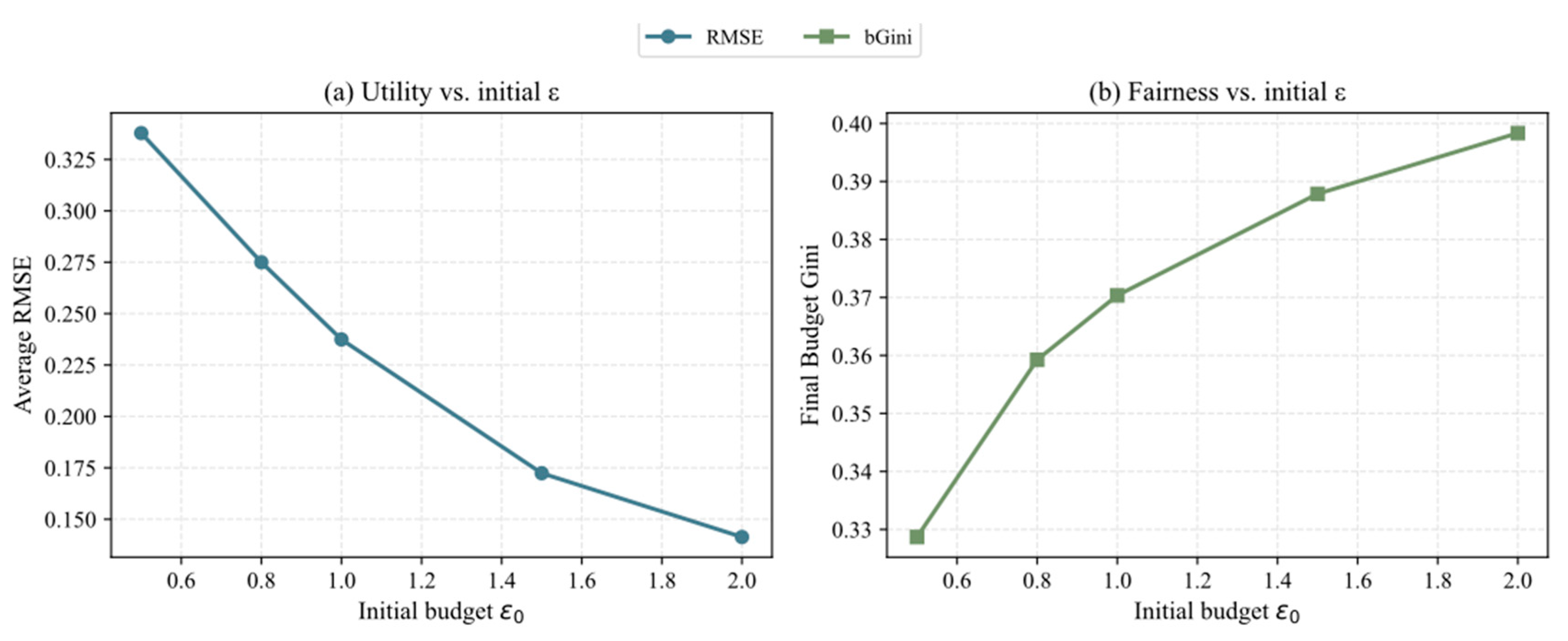
(1)

Impact of Initial Budget (${\mathsf{\epsilon }}_0$)

As shown in Figure 3, the initial privacy budget significantly affects both system utility and budget allocation fairness. Figure 3a illustrates that as the initial budget increases, the average RMSE decreases, indicating an improvement in system utility. This occurs because a larger budget relaxes the privacy constraint, reducing the magnitude of noise and thereby lowering utility loss. However, Figure 3b shows that as the budget increases, the Gini coefficient of the final budget allocation (BGC) also rises, indicating greater imbalance in allocation. Therefore, setting the initial privacy budget involves a trade-off between utility and fairness and should be chosen reasonably according to the specific application scenario.

(2)

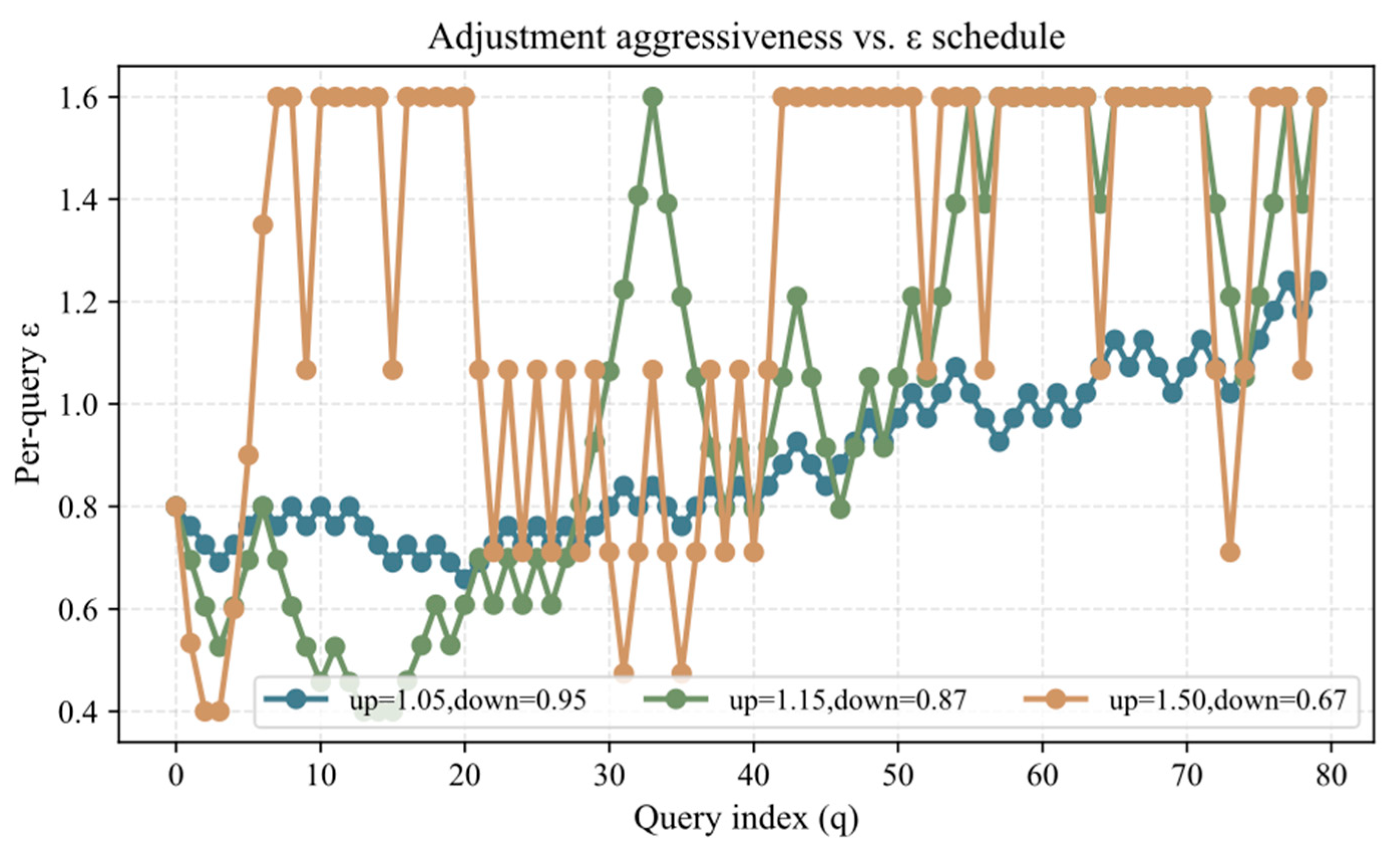
Impact of Dynamic Adjustment Aggressiveness

Figure 4 shows the per-query $\mathsf{\epsilon }$ variation curves under different adjustment factors. Higher adjustment factors (up = 1.5, down = 0.67) cause more drastic changes in $\mathsf{\epsilon }$, enhancing adaptiveness but introducing some instability. Lower factors (up = 1.05, down = 0.95) maintain a smoother trajectory but lack sufficient responsiveness. Considering the adaptive stability metric ASC, moderate adjustment factors (up = 1.15, down = 0.87) achieve the best balance between stability and adaptiveness, allowing the system to dynamically respond to query demands while avoiding excessive fluctuations that could affect model performance.

(3)

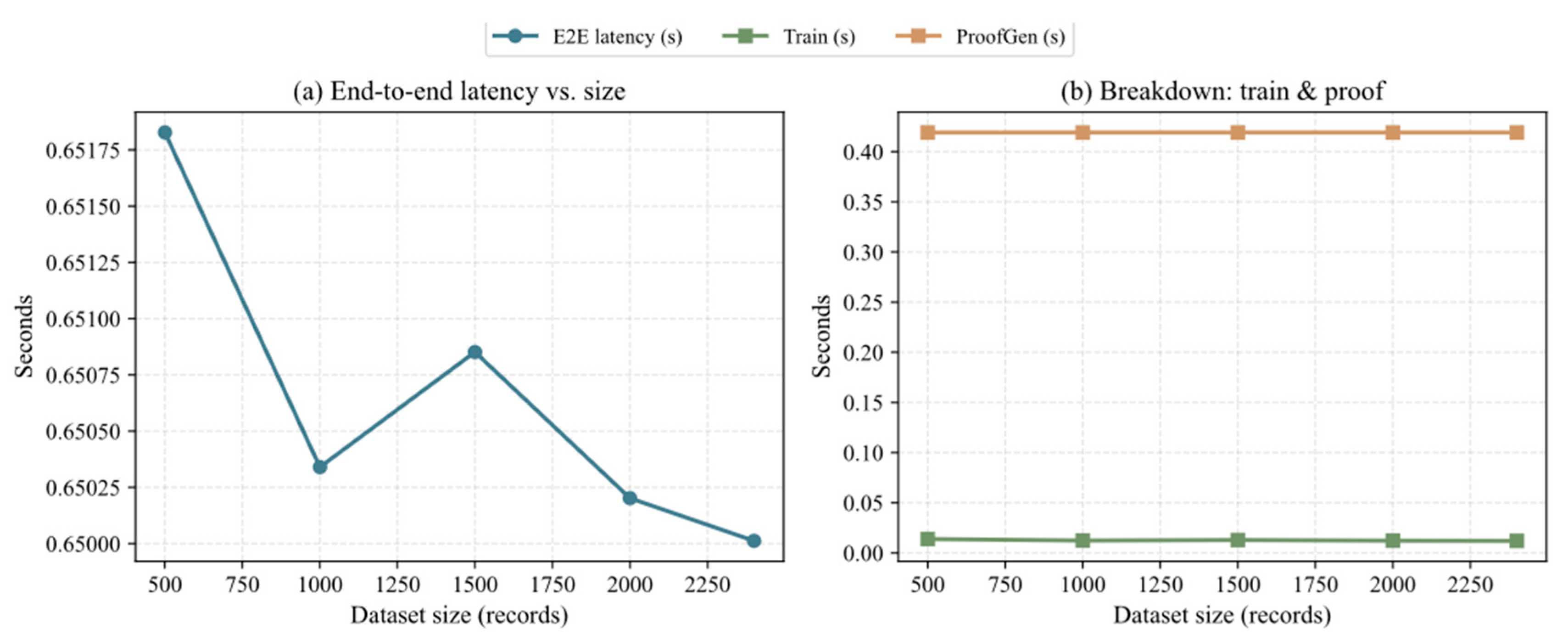
Impact of Dataset Size

As shown in Figure 5, this study investigates the effect of dataset size on system latency. From Figure 5a, it can be observed that as the number of dataset records increases, the end-to-end latency does not show a significant monotonic increase, remaining relatively stable around 0.65 s. To further illustrate this phenomenon, Figure 5b breaks down the latency, showing that the key stages of training (Train) and proof generation (ProofGen) remain almost unchanged and do not increase noticeably with dataset size. This indicates that the core algorithm modules of the BFAV-DP framework have good scalability, and system latency is primarily influenced by relatively fixed overheads such as network communication and blockchain interactions.

(4)

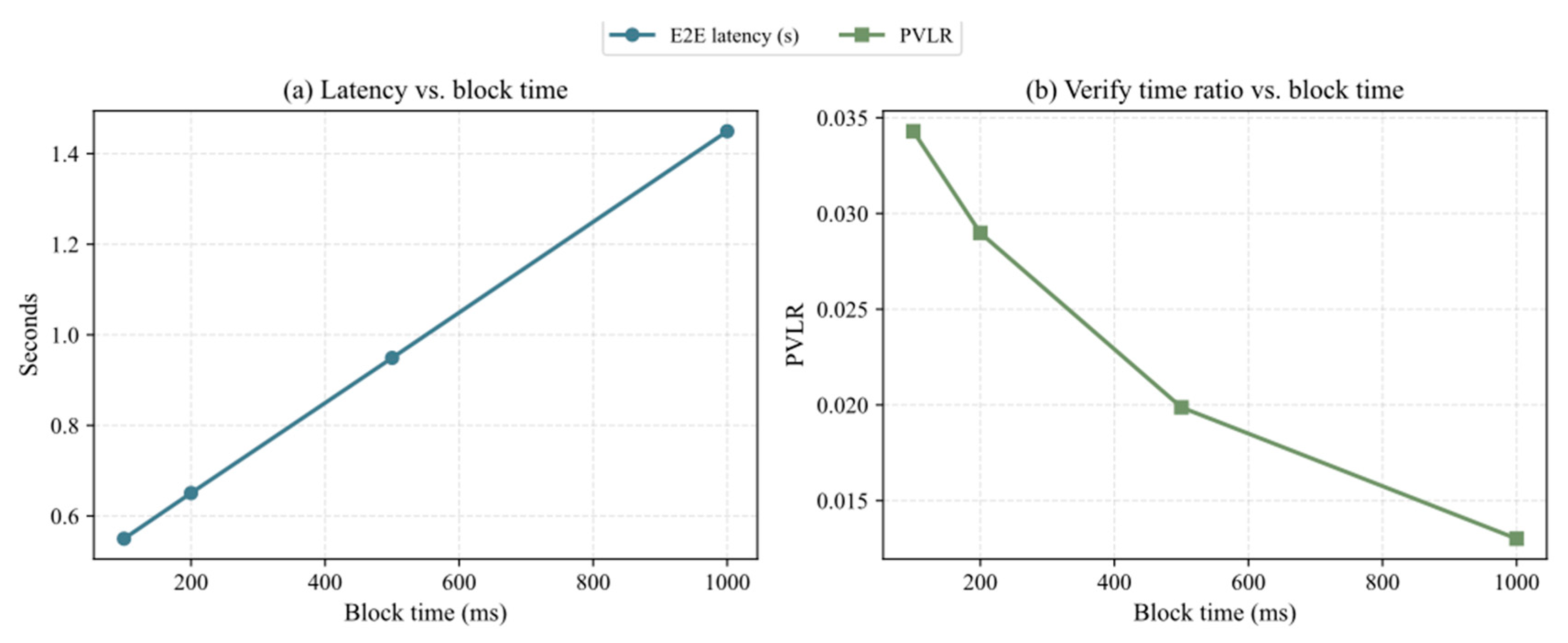
Impact of Blockchain Configuration (Block Time)

Figure 6 shows that the blockchain block time (Blocktime) is an important external factor affecting system performance. Figure 6a illustrates an approximately linear positive correlation between end-to-end latency and block time, as the system must wait for blockchain confirmation to complete state updates, and longer block times directly lead to longer waiting delays. Figure 6b shows that as block time increases, the proportion of verification time (PVLR) actually decreases. This is because the computation time for verification itself is fixed, while the total latency increases due to waiting for block confirmation, reducing the relative share of verification overhead. These results further indicate that the framework’s performance is closely tied to the efficiency of the underlying blockchain platform, and block time configuration should be carefully considered when designing practical systems to balance latency and verifiability.

6.4. Comparative Experiments and Analysis

In this section, we compare the performance of each algorithm across different dimensions based on the macro-averaged results from both real and synthetic datasets and provide a quantitative analysis through visualized charts. All line charts use macro-averaged metrics to ensure that each dataset contributes equally to the overall performance, preventing the characteristics of a single dataset from disproportionately influencing the analysis and making the algorithm comparisons more objective and informative.

6.4.1. Utility Comparison

Figure 7a,b show the macro-averaged accuracy (ACC) and mean squared error (MSE) of each algorithm across all datasets under different privacy budgets $\mathsf{\epsilon }$. As $\mathsf{\epsilon }$ increases, the level of privacy protection gradually decreases, and model performance improves, indicated by monotonically increasing ACC and continuously decreasing MSE. BFAV-DP achieves the highest ACC and lowest MSE at every $\mathsf{\epsilon }$ level, significantly outperforming other baseline algorithms. This demonstrates that the adaptive privacy budget allocation and multi-round averaging mechanisms can effectively enhance model utility under the same privacy constraints, achieving a better privacy-utility balance. In contrast, traditional algorithms such as AG-PLD and LDP-OLH/OUE still exhibit noticeable utility loss even at higher $\mathsf{\epsilon }$ values, indicating that single-noise injection mechanisms have a considerable negative impact on model performance.

6.4.2. Fairness Comparison

Figure 8 presents the macro-averaged Budget Gini Coefficient (BGC) of each algorithm across all datasets, which measures the fairness of privacy budget allocation. A lower BGC value indicates a more balanced distribution of privacy budgets among participants. The results show that BFAV-DP achieves the lowest BGC value, indicating a significantly more equitable allocation compared to StaticDP-Chain, which adopts a fixed allocation strategy and exhibits severe imbalance issues. This demonstrates that the proposed method not only enhances privacy-utility performance but also ensures fairness in privacy budget distribution, preventing additional bias caused by uneven allocation.

6.4.3. Verifiability Comparison

Figure 9 presents the macro-averaged results of the Privacy Verifiable Log Ratio (PVLR) and system latency for each algorithm. A higher PVLR indicates stronger verifiability of privacy-preserving results, while lower system latency reflects higher efficiency in practical deployment. As shown in Figure 9, BFAV-DP (the proposed method) achieves the highest PVLR, significantly outperforming StaticDP-Chain and zkDP-Chain, thereby providing stronger privacy verifiability. Additionally, BFAV-DP reduces the average system latency by approximately 30%, thanks to its lightweight zero-knowledge proof module and optimized on-chain interaction mechanism, which significantly enhance the system’s real-time performance and scalability.

6.4.4. Runtime Comparison

Table 1. End-to-End Runtime Comparison under Different Privacy Budgets.

Method	0.2	0.5	1.0	2.0	4.0
AG-PLD	472.77	272.82	180.00	118.75	78.34
LDP-OLH/OUE	525.30	303.14	200.00	131.95	87.05
BFAV-DP (Ours)	577.83	333.45	220.00	145.14	95.76
StaticDP-Chain	656.63	378.92	250.00	164.93	108.81
zkDP-Chain	709.16	409.24	270.00	178.13	117.52

presents the end-to-end runtime (in milliseconds) of each scheme under different privacy budgets $\mathsf{\epsilon }$. As $\mathsf{\epsilon }$ increases, the runtime of all schemes decreases significantly, reflecting the higher computational and verification overhead under stronger privacy protection (smaller $\mathsf{\epsilon }$). Among all schemes, AG-PLD only employs a local perturbation mechanism without on-chain verification or fair allocation modules, resulting in the lowest runtime. BFAV-DP (Ours) shows slightly higher runtime than AG-PLD and LDP-OLH/OUE but is clearly faster than StaticDP-Chain and zkDP-Chain. This indicates that the lightweight zero-knowledge verification and fair budget allocation mechanisms effectively control system overhead while ensuring privacy, utility, and verifiability. Considering privacy protection, utility performance, and runtime together, BFAV-DP maintains low latency and acceptable computational costs while achieving optimal privacy and utility, demonstrating good scalability.

6.4.5. Comparative Trends Between Real and Synthetic Datasets

Figure 10 shows the performance trends of real and synthetic datasets (including syn_base and syn_skew) under different $\mathsf{\epsilon }$ values. Solid lines represent results from the real dataset, while dashed and dash-dot lines correspond to the macro-averaged and specific synthetic samples, respectively. The trends of ACC and MSE on synthetic datasets closely match those of the real dataset, confirming that the proposed synthetic dataset generation rules effectively preserve the key statistical characteristics relevant to privacy-preserving experiments. These results indicate that synthetic datasets can serve as a reliable substitute for real data, facilitating large-scale evaluation and optimization of privacy-preserving algorithms without exposing sensitive information.

6.5. Applicability Discussion in Deep Learning Scenarios

The datasets used in this chapter are all structured medical tabular data, and the learning models employed are typically supervised shallow models to avoid introducing network structural complexity. However, the design of BFAV-DP is fundamentally decoupled from specific model architectures, representing a typical model-agnostic privacy mechanism. Its core components—including privacy budget management, multi-round perturbation averaging, and on-chain verifiability modules—depend only on the privacy loss and parameter updates of each query round, not on the source of model gradients. This feature ensures good compatibility with existing DP-SGD frameworks [48].

In deep learning models, the main challenges under differential privacy noise are convergence slowdown due to gradient clipping and oscillations induced by noise [49]. Mechanistically, BFAV-DP has the following potential impacts in deep neural network scenarios:

1. Multi-round averaging stabilizes gradient updates.

The multi-round perturbation averaging mechanism can smooth gradient fluctuations under high-noise conditions, helping to mitigate the oscillation problems commonly observed in DP-SGD.

2. Fair budget allocation prevents excessive gradient perturbation.

Training deep models involves numerous parameter updates. Fair budget allocation prevents abnormal perturbations caused by insufficient privacy budget in certain training rounds, thereby improving training stability.

3. On-chain verification decoupled from training workflow.

The verification module operates on parameter update results rather than the training process itself, so it does not affect the neural network’s convergence path and introduces only minimal delay at the communication and confirmation stage.

Overall, BFAV-DP maintains mechanism-level stability and usability in deep learning scenarios. Specifically, it provides controllable effects on deep model convergence and utility while ensuring differential privacy and verifiability. Systematic experimental evaluation on neural network tasks—such as risk prediction from electronic health record text or medical imaging—will be a key focus of future work to further quantify BFAV-DP’s practical robustness and performance boundaries in deep medical AI applications.

7. Conclusions and Future Work

This study focuses on privacy leakage, uneven budget allocation, and difficulty in verifying results during medical data-sharing processes and proposes BFAV-DP, a blockchain-based adaptive differential privacy framework. The framework integrates dynamic privacy budget management, multi-round perturbation averaging, balanced budget allocation strategies, and on-chain verification modules within a single system, enabling trustworthy processing while maintaining strong privacy protection.

Experiments were conducted on multiple real and synthetic medical datasets, evaluating utility, fairness of budget allocation, system overhead, and verification efficiency. Comparisons were made against centralized differential privacy, local differential privacy, and on-chain verifiable privacy schemes. The results demonstrate that BFAV-DP achieves stable performance in utility, fair allocation, and verification efficiency while preserving statistical trends, with additional operational overhead remaining within acceptable bounds. These findings indicate that the framework is fundamentally feasible and holds potential for further extension.

However, the current study has limitations. Experiments primarily rely on structured tabular data and shallow models, lacking empirical analysis of deep learning models’ stability and training speed under noise perturbation. Deployment in real-world medical scenarios also requires further validation, including on-chain costs, system security, and regulatory compliance. These gaps point to directions for future research.

Subsequent work could expand in terms of performance optimization, model coverage, and system security. For instance, researchers may explore faster zero-knowledge proof systems, hardware acceleration, and more flexible blockchain architectures to reduce overall latency and enhance scalability. The framework could also be applied to deep neural networks, medical imaging, and multimodal health data to assess its ability to balance utility in high-dimensional tasks. Further studies could analyze risks arising from collaborative attacks and incentive mechanisms and attempt formal verification of the framework’s trustworthiness. Collaboration with healthcare institutions or regulatory bodies to develop prototype systems would further help evaluate its practical value in real medical data analysis tasks.