Hybrid Sensor Fusion Beamforming for UAV mmWave Communication
Abstract
1. Introduction
1.1. Background
1.2. Related Research
2. Materials and Methods
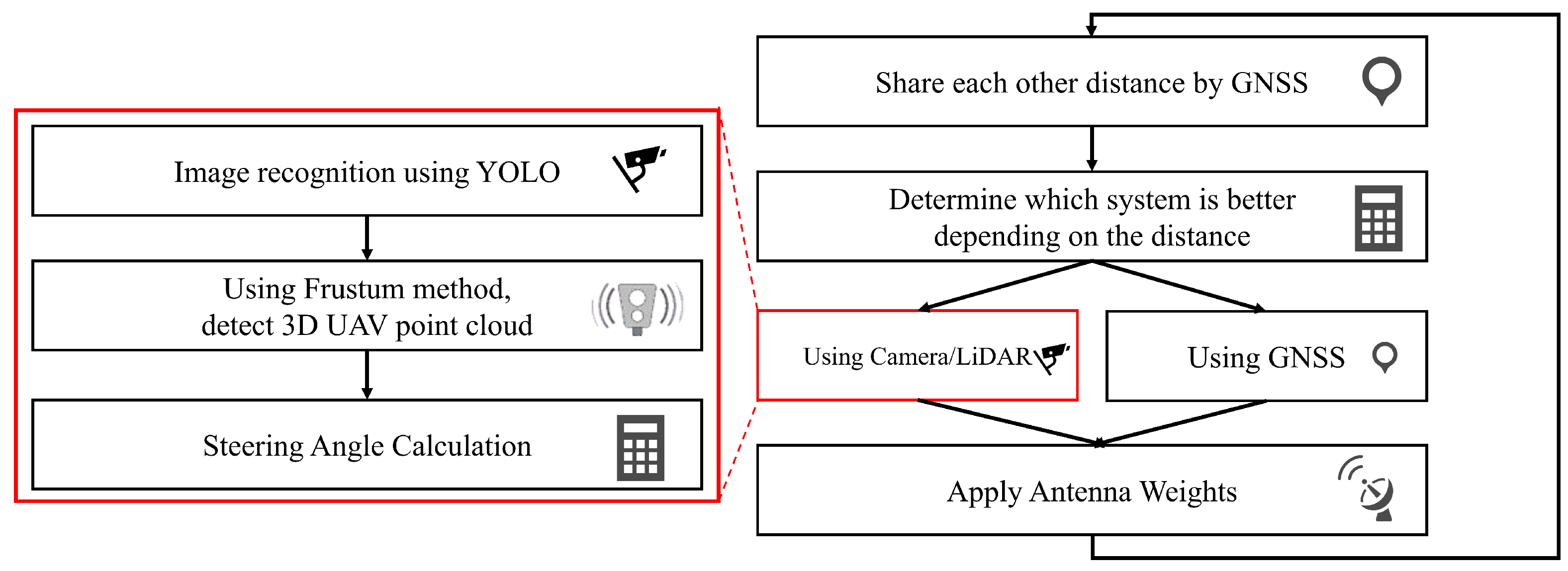
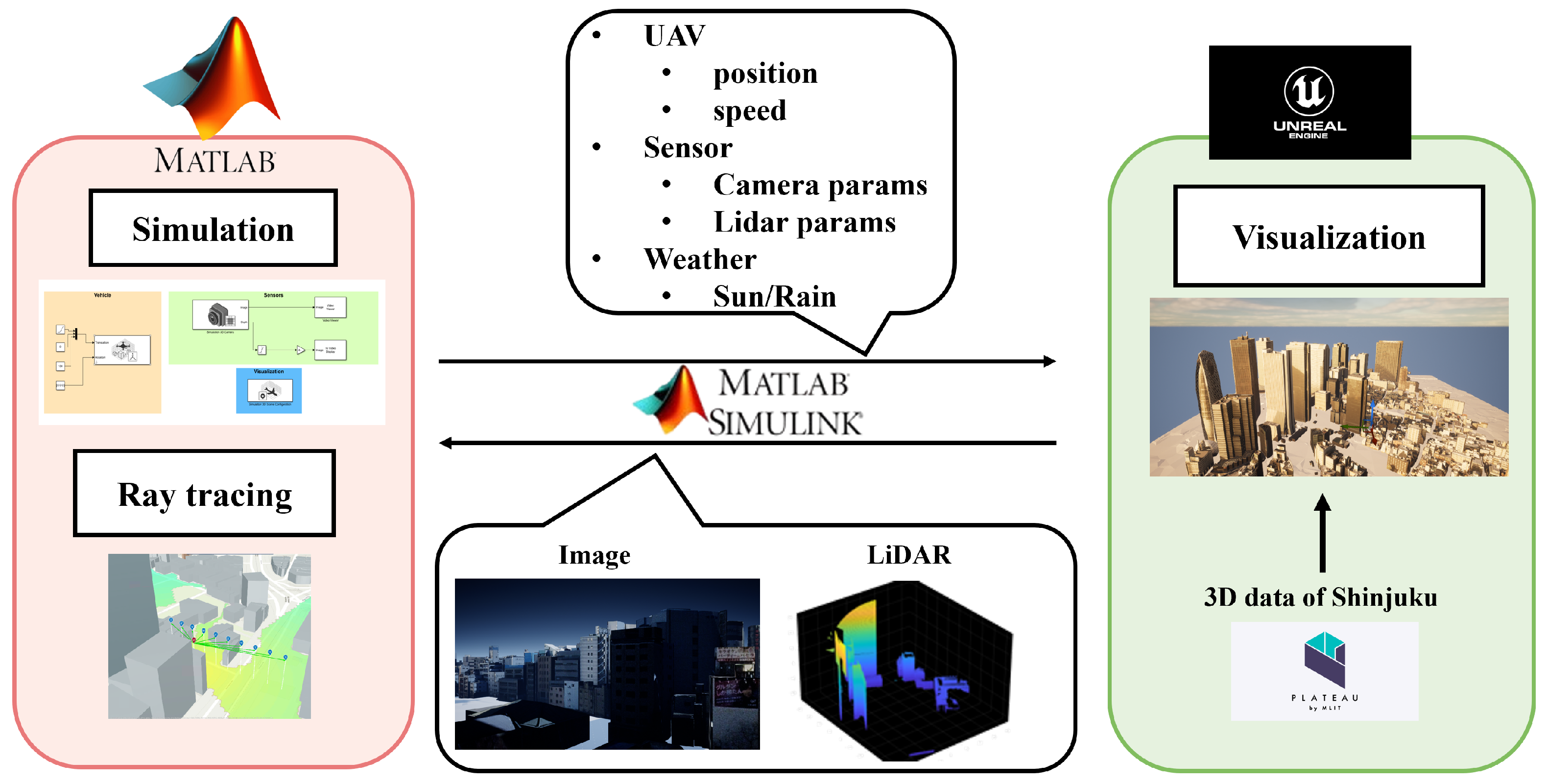
2.1. System Pipeline Overview
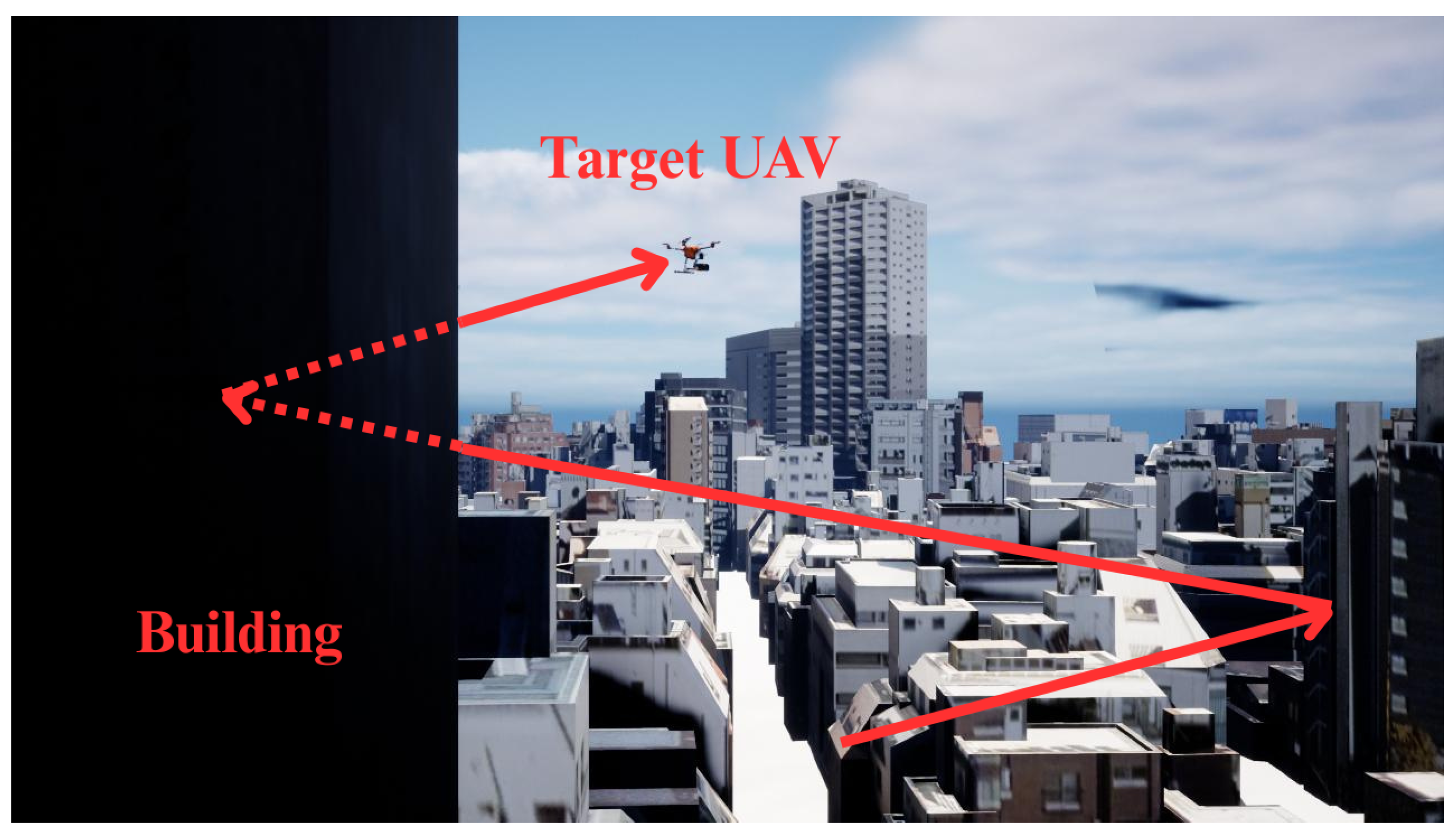
- 2D Vision-based Detection: In the initial stage, the onboard camera of the ego UAV detects the target UAV within the image plane using a computer vision algorithm. This provides the general direction of the target, but at this point, it yields only a 2D bounding box, lacking essential depth information.
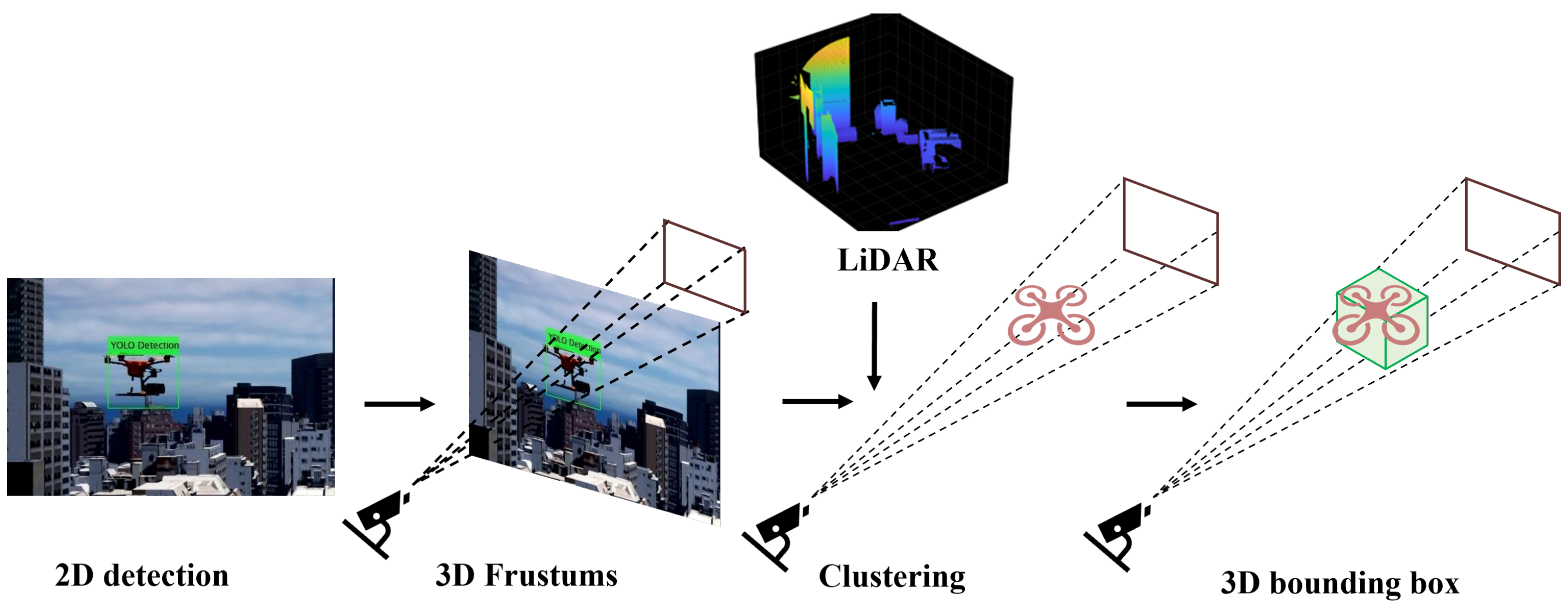
- 3D Localization via Sensor Fusion: Next, the system fuses the 2D detection results from Stage 1 with the 3D point cloud data obtained from the onboard LiDAR. This sensor fusion process enables the precise localization of the target UAV, yielding its 3D relative coordinates (x, y, z).
- Beamforming Control: In the final stage, based on the 3D relative coordinates calculated in Stage 2, the system electronically steers a phased array antenna to direct the main lobe of the millimeter-wave beam toward the target UAV, maximizing the received signal strength.
2.2. Perception Module: Sensor-Based UAV Detection
2.3. Beam Control Module
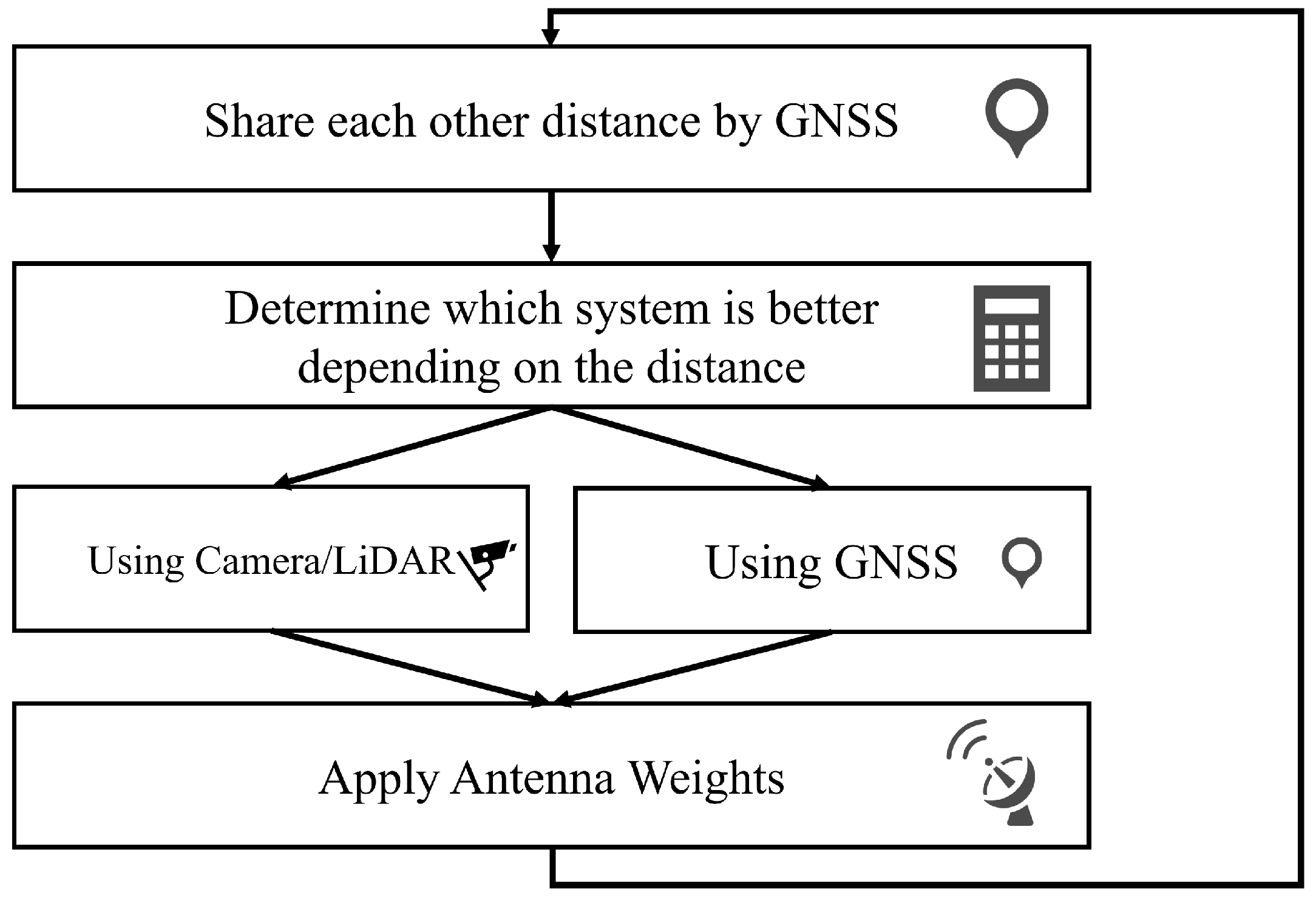
2.4. Baseline Method for Comparison
2.4.1. Pilot-Based Beam Sweeping
2.4.2. GNSS-Based Beam Steering
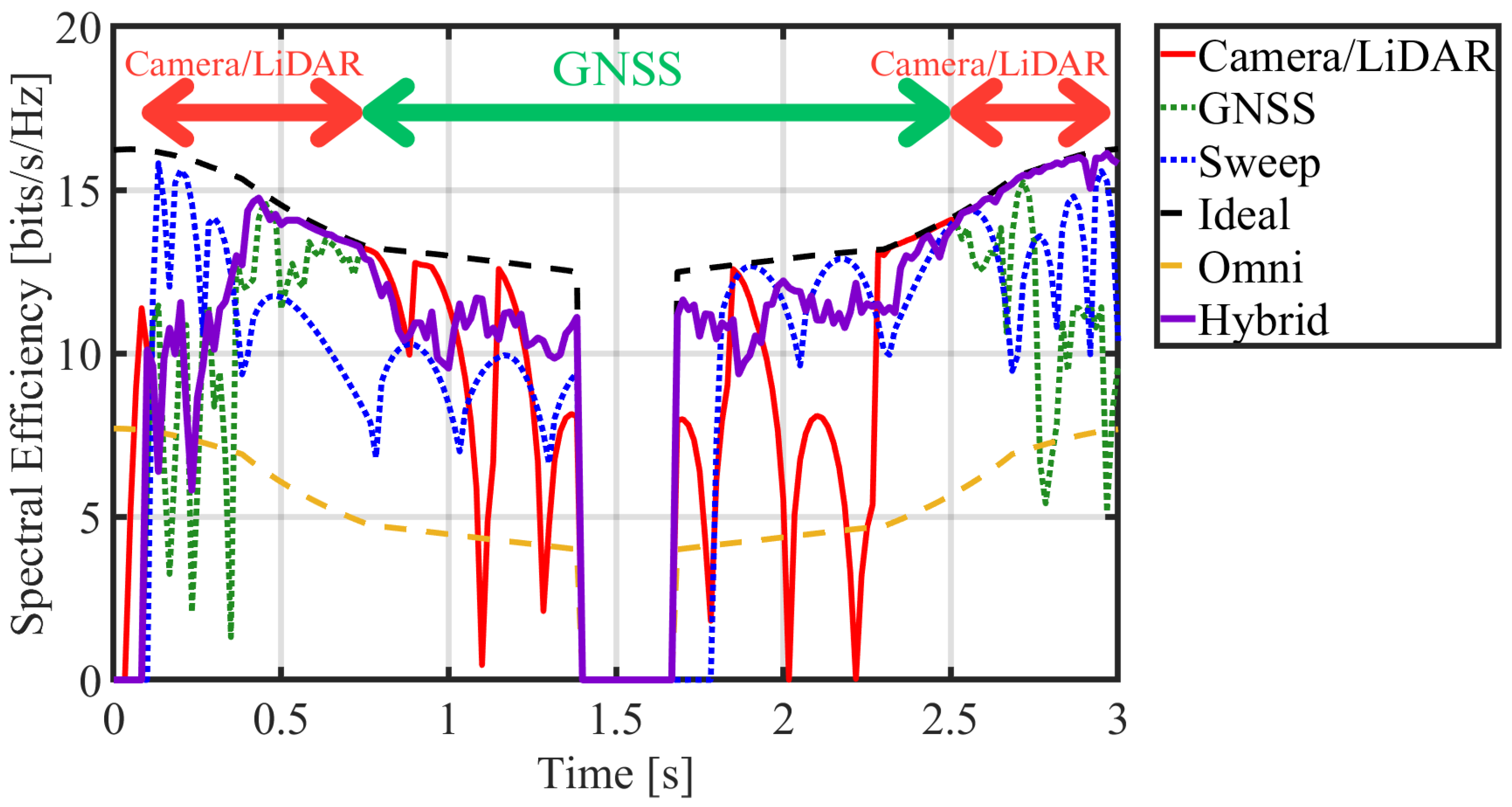
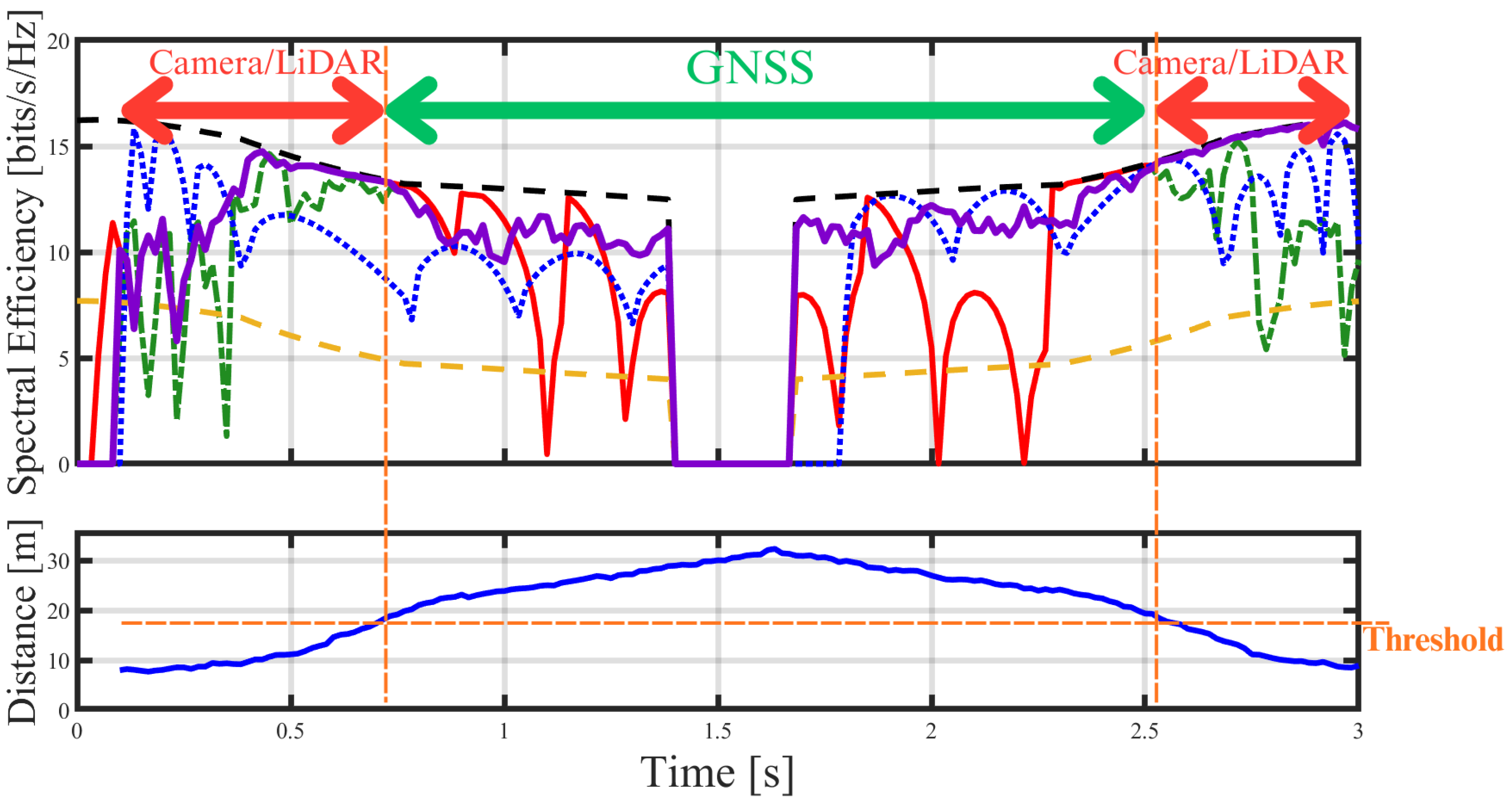
2.5. Hybrid Approach
3. Simulation Setup
3.1. Simulation Environment
3.2. Scenarios and Parameters
3.3. Processing Latency Model
3.4. Evaluation Metrics
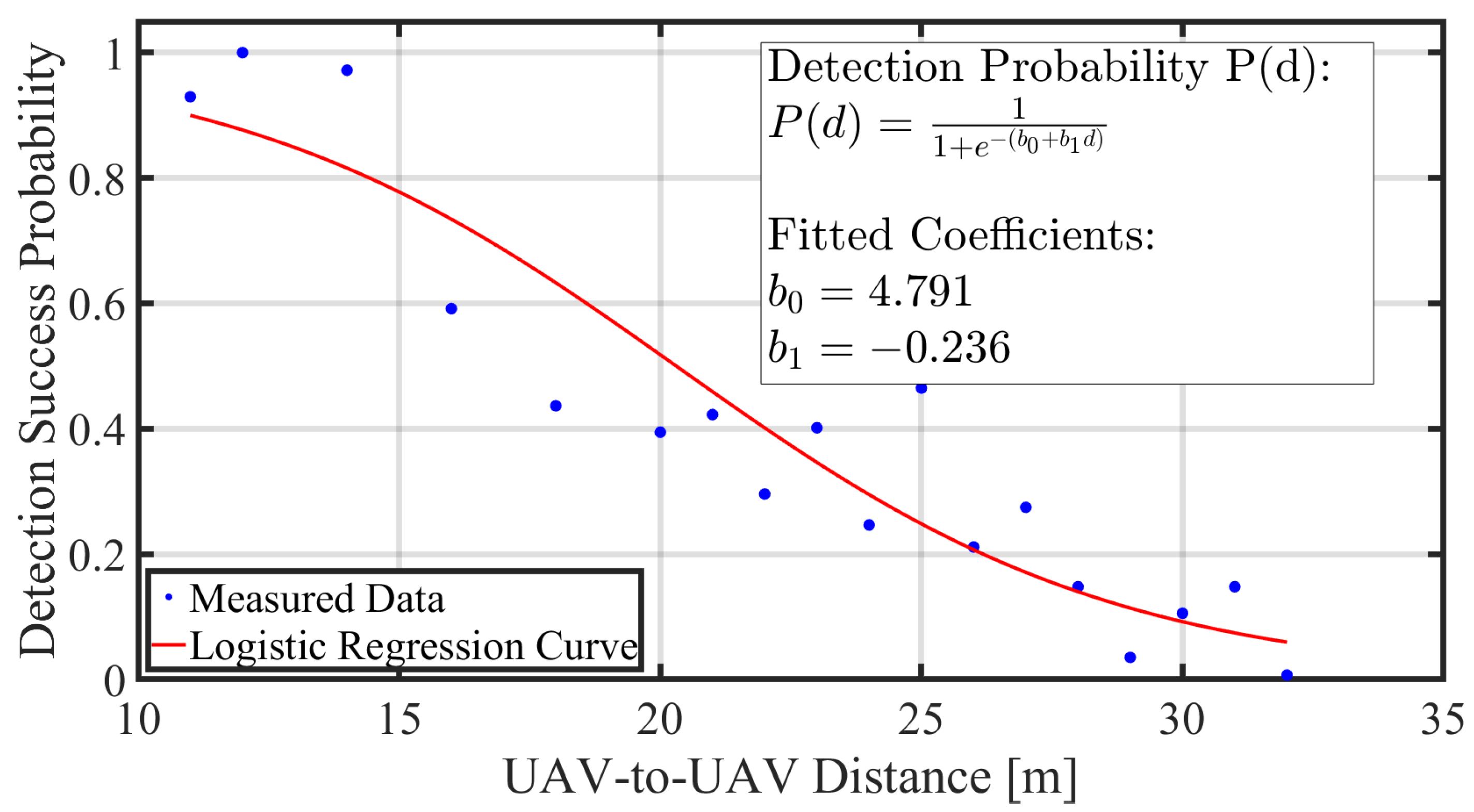
3.4.1. Detection Performance Metrics
3.4.2. Communication Link Performance Metrics
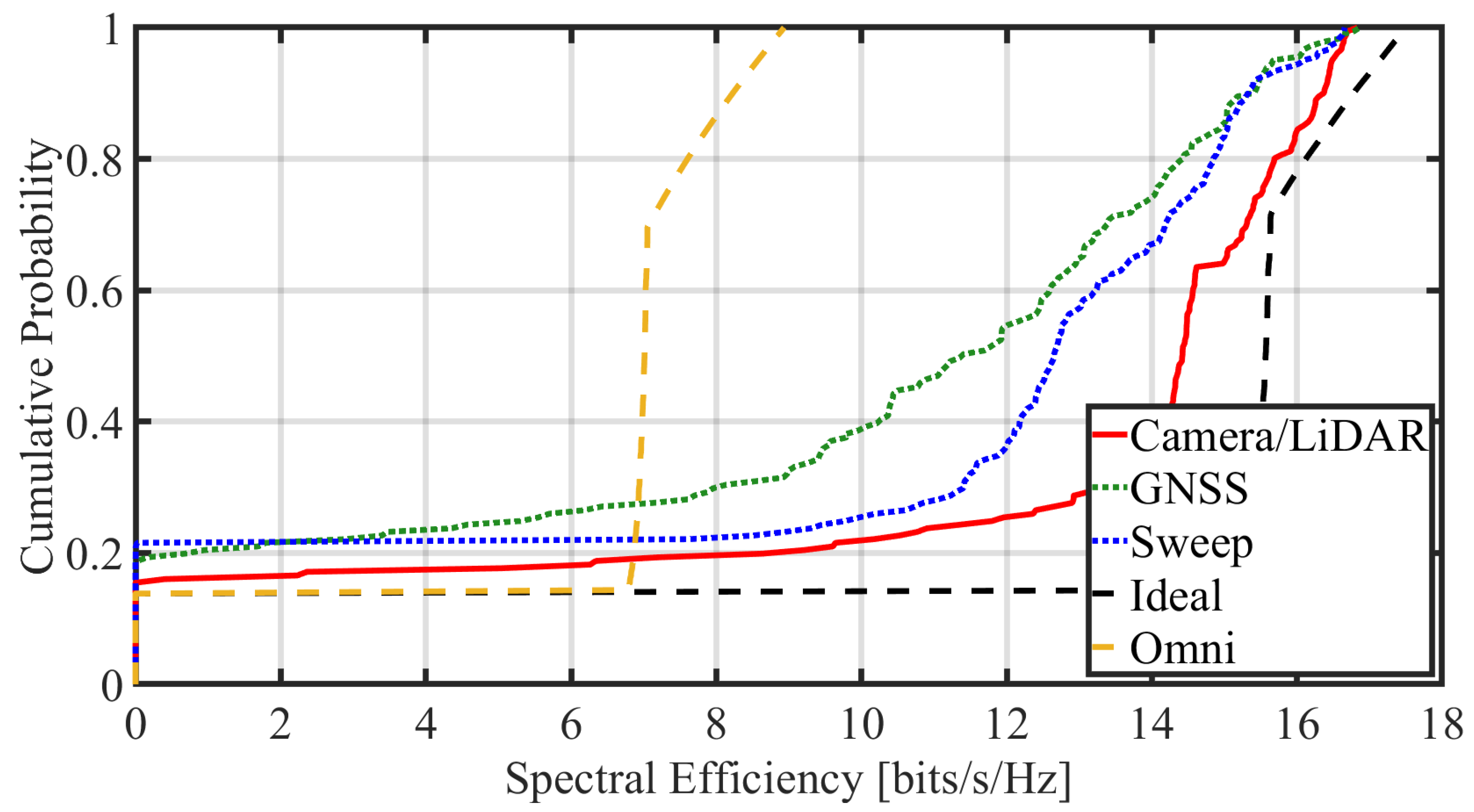
- Spectral Efficiency (): A measure of how efficiently a given bandwidth is utilized. It is calculated by dividing the throughput by the bandwidth. We calculate the theoretical maximum channel capacity (C) based on the Shannon–Hartley theorem as the throughput.where B is the bandwidth and is the Signal-to-Noise Ratio.
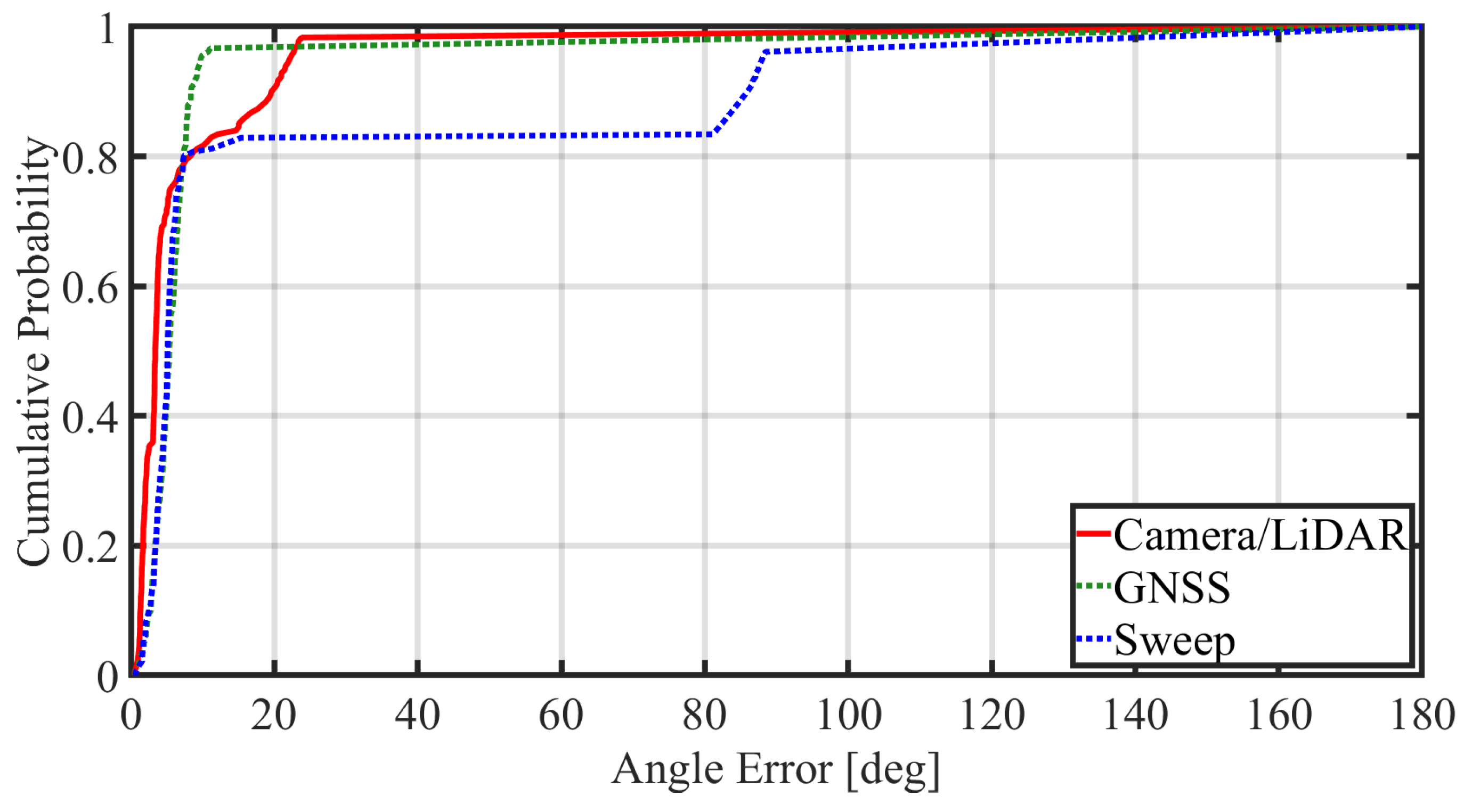
- Angular Pointing Error (): An indicator of beam alignment accuracy. It is calculated as the angle between the steered beam vector () and the ground-truth vector to the target UAV ().
4. Results
4.1. Detection Performance
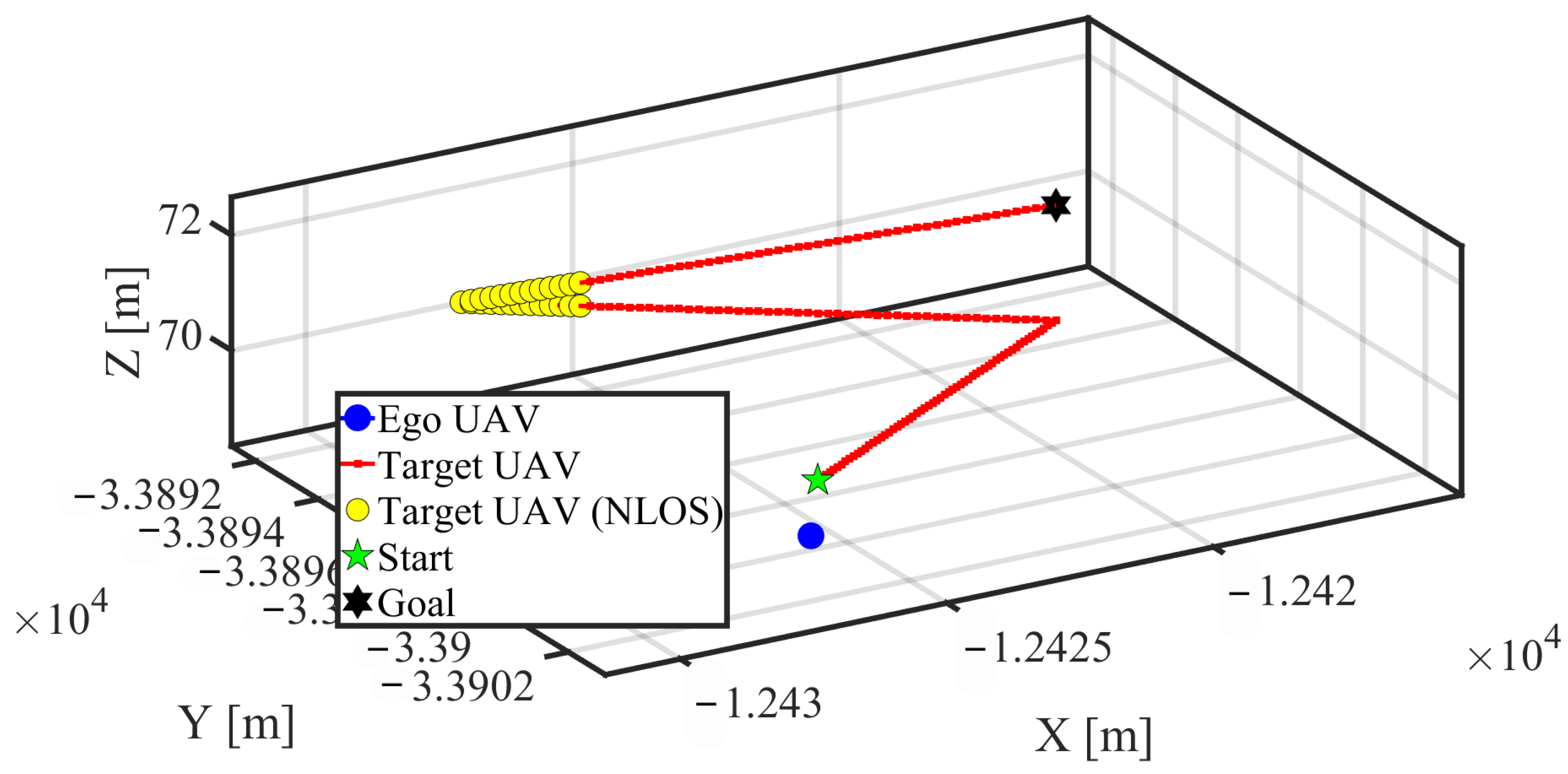
4.2. Communication Link Performance (Scenario 1)
4.2.1. Analysis of Angular Pointing Error
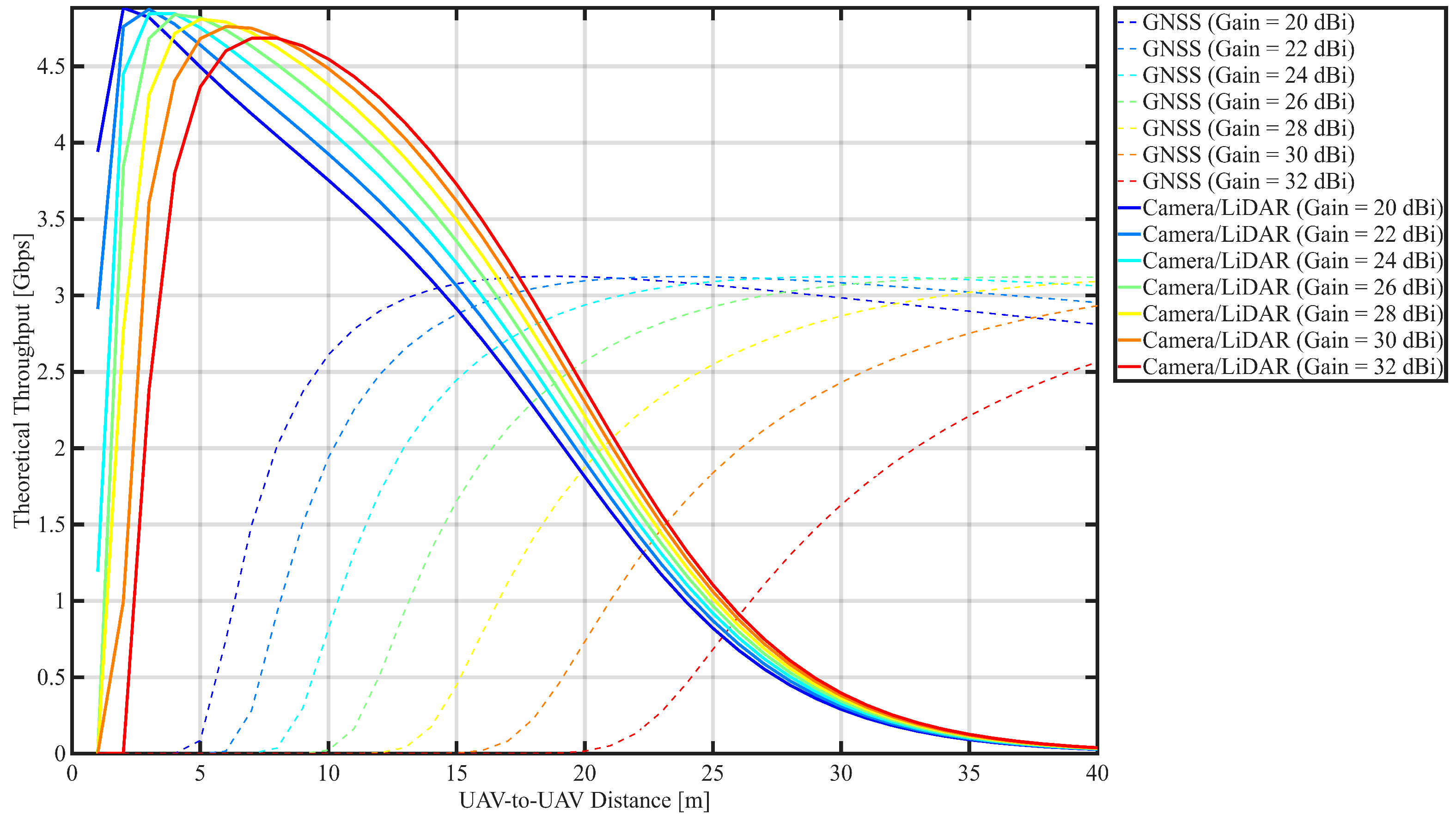
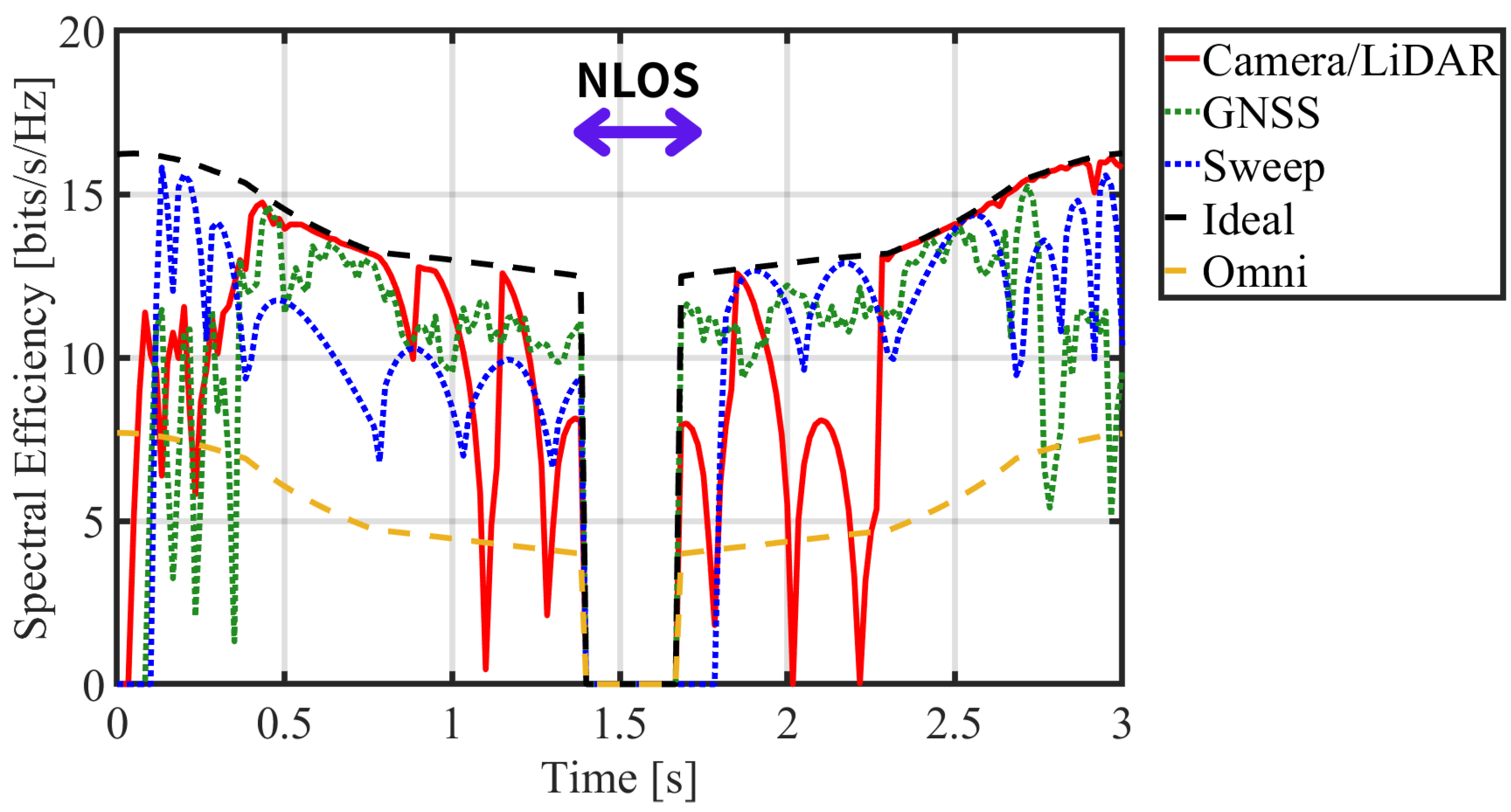
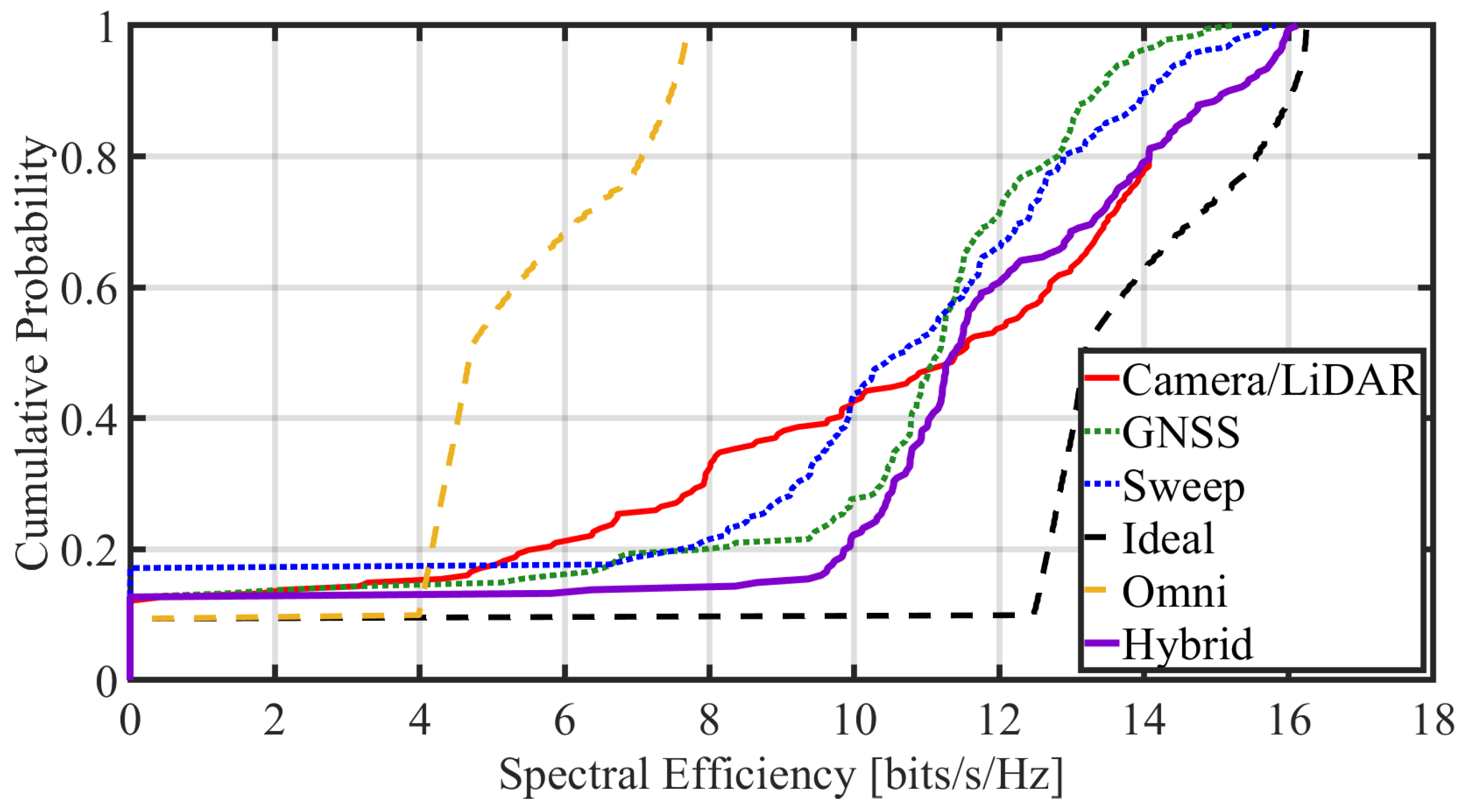
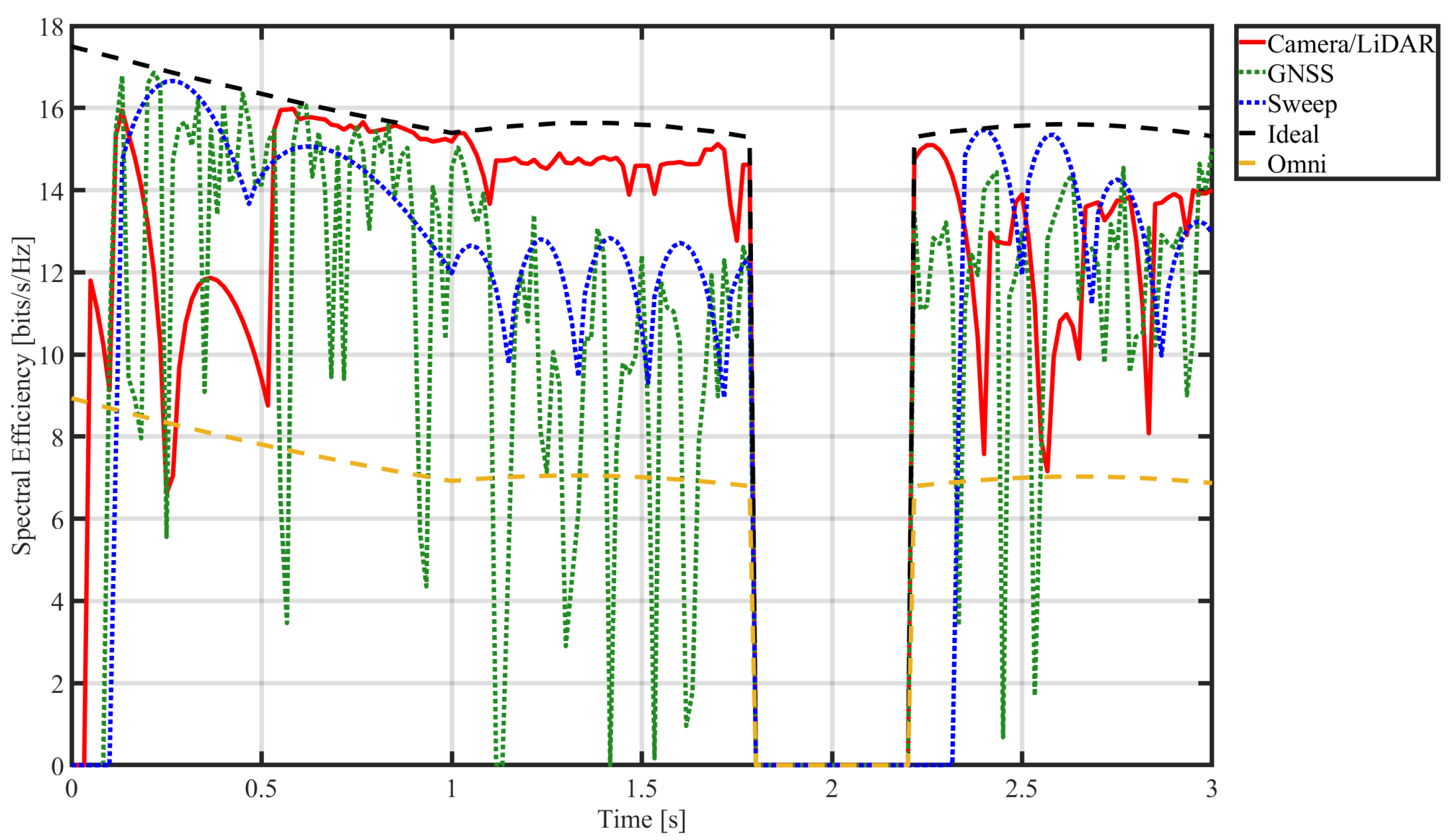
4.2.2. Comparison of Spectral Efficiency
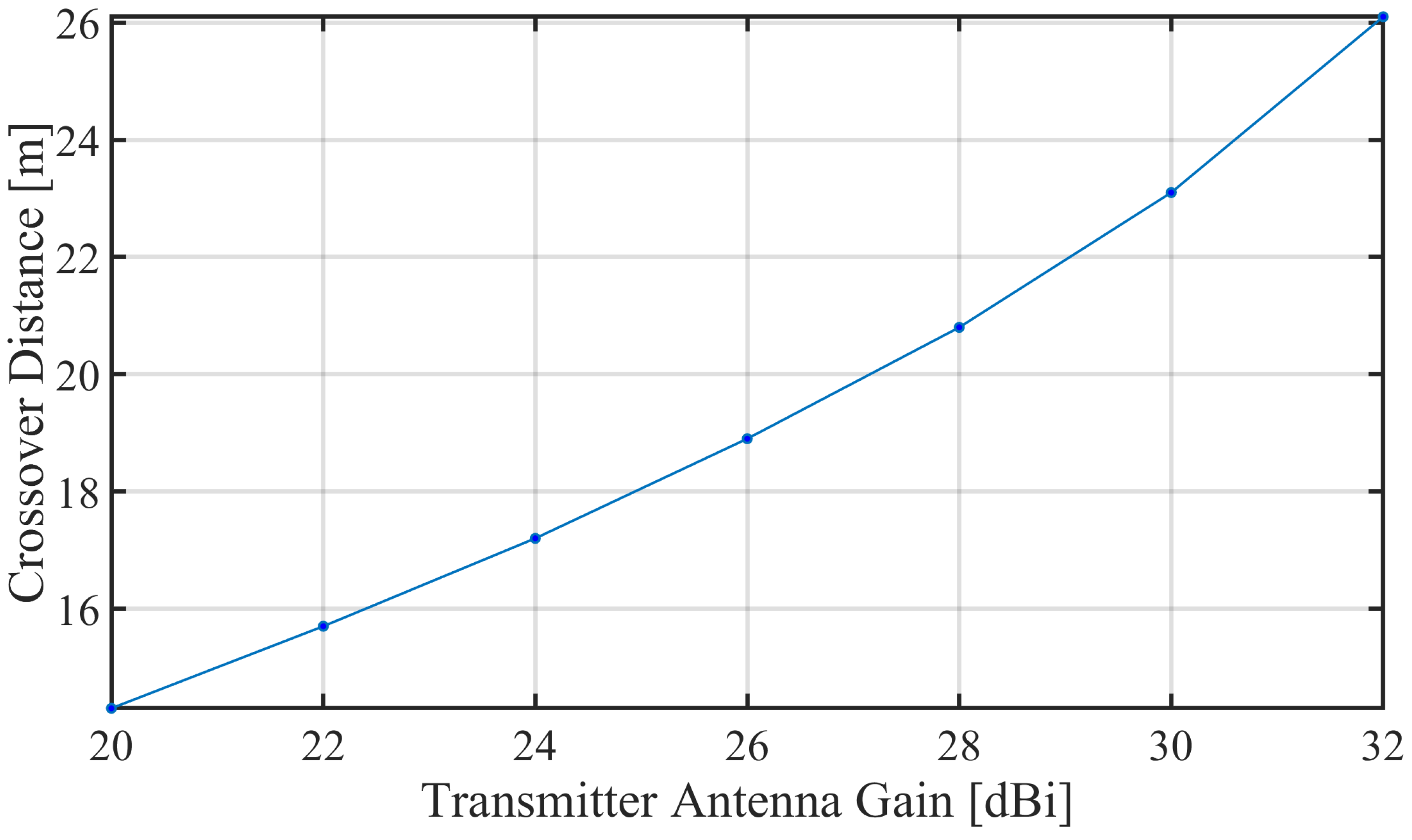
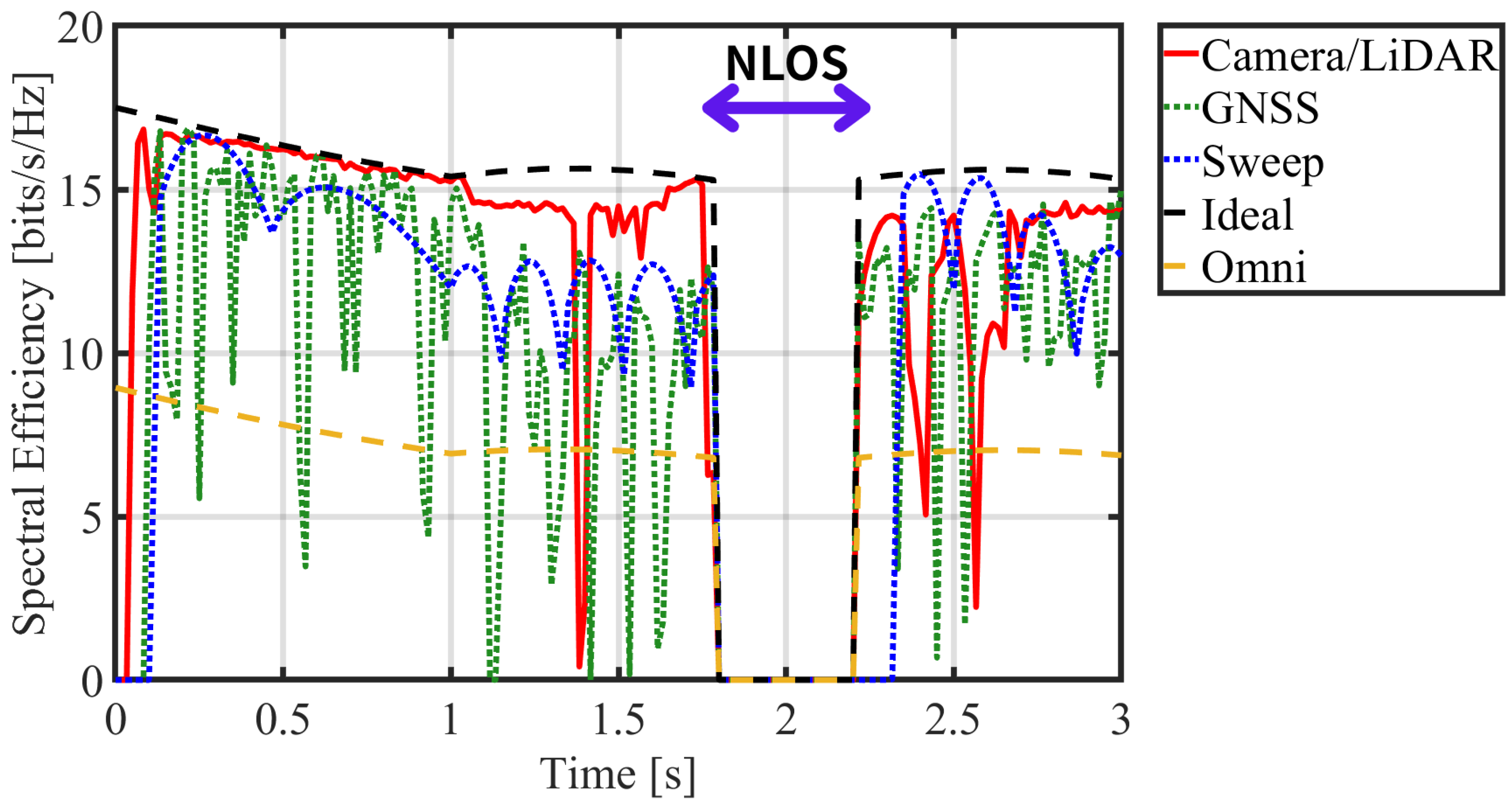
4.2.3. Link Acquisition and Recovery Speed
4.3. Communication Link Performance (Scenario 2)
4.4. Resistance to Rain
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tran, G.K. Temporary Communication Network Using Millimeter-Wave Drone Base Stations. In Proceedings of the 2024 IEEE VTS Asia Pacific Wireless Communications Symposium (APWCS), Singapore, 21–23 August 2024. [Google Scholar]
- Tran, G.K.; Nakazato, J.; Sou, H.; Iwamoto, H. Research on smart wireless aerial networks facilitating digital twin construction. IEICE Trans. Commun. 2026, E109-B, 4. [Google Scholar] [CrossRef]
- Tran, G.K.; Ozasa, M.; Nakazato, J. NFV/SDN as an Enabler for Dynamic Placement Method of mmWave Embedded UAV Access Base Stations. Network 2022, 2, 479–499. [Google Scholar] [CrossRef]
- Sumitani, T.; Tran, G.K. Study on the construction of mmWave based IAB-UAV networks. In Proceedings of the AINTEC 2022, Hiroshima, Japan, 19–21 December 2022. [Google Scholar]
- Amrallah, A.; Mohamed, E.M.; Tran, G.K.; Sakaguchi, K. UAV Trajectory Optimization in a Post-Disaster Area Using Dual Energy-Aware Bandits. Sensors 2023, 23, 1402. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Zhang, W. Beam Tracking and Optimization for UAV Communications. IEEE Trans. Wirel. Commun. 2019, 18, 5367–5379. [Google Scholar] [CrossRef]
- Zhou, S.; Yang, H.; Xiang, L.; Yang, K. Temporal-Assisted Beamforming and Trajectory Prediction in Sensing-Enabled UAV Communications. IEEE Trans. Commun. 2025, 73, 5408–5419. [Google Scholar] [CrossRef]
- Miao, W.; Luo, C.; Min, G.; Zhao, Z. Lightweight 3-D Beamforming Design in 5G UAV Broadcasting Communications. IEEE Trans. Broadcast. 2020, 66, 515–524. [Google Scholar] [CrossRef]
- Dovis, F. GNSS Interference Threats and Countermeasures; Artech House: Norwood, MA, USA, 2015. [Google Scholar]
- Zhou, J.; Wang, W.; Zhang, C. A GNSS Anti-Jamming Method in Multi-UAV Cooperative System. IEEE Trans. Veh. Technol. 2025; early access. [Google Scholar] [CrossRef]
- Abdelfatah, R.; Moawad, A.; Alshaer, N.; Ismail, T. UAV Tracking System Using Integrated Sensor Fusion with RTK-GPS. In Proceedings of the International Mobile, Intelligent, and Ubiquitous Computing Conference (MIUCC), Cairo, Egypt, 26–27 May 2021; pp. 352–356. [Google Scholar] [CrossRef]
- Zou, J.; Wang, C.; Liu, Y.; Zou, Z.; Sun, S. Vision-Assisted 3-D Predictive Beamforming for Green UAV-to-Vehicle Communications. IEEE Trans. Green Commun. Netw. 2023, 7, 434–443. [Google Scholar] [CrossRef]
- Liu, C.; Yuan, W.; Wei, Z.; Liu, X.; Ng, D.W.K. Location-Aware Predictive Beamforming for UAV Communications: A Deep Learning Approach. IEEE Wirel. Commun. Lett. 2021, 10, 668–672. [Google Scholar] [CrossRef]
- Zang, J.; Gao, D.; Wang, J.; Sun, Z.; Liang, S.; Zhang, R.; Sun, G. Real-Time Beam Tracking Algorithm for UAVs in Millimeter-Wave Networks with Adaptive Beamwidth Adjustment. In Proceedings of the 2025 International Wireless Communications and Mobile Computing (IWCMC), Abu Dhabi, United Arab Emirates, 12–16 May 2025; pp. 770–775. [Google Scholar] [CrossRef]
- Iwamoto, H. A Study on Characteristic Evaluation of Aerial Back-Haul Links by UAV for Digital Twin Construction. Master’s Thesis, Institute of Science Tokyo, Tokyo, Japan, 2025. (In Japanese). [Google Scholar]
- Zhong, W.; Zhang, L.; Jin, H.; Liu, X.; Zhu, Q.; He, Y.; Ali, F.; Lin, Z.; Mao, K.; Durrani, T.S. Image-Based Beam Tracking with Deep Learning for mmWave V2I Communication Systems. IEEE Trans. Intell. Transp. Syst. 2024, 25, 19110–19116. [Google Scholar] [CrossRef]
- Seidaliyeva, U.; Ilipbayeva, L.; Utebayeva, D.; Smailov, N.; Matson, E.T.; Tashtay, Y.; Turumbetov, M.; Sabibolda, A. LiDAR Technology for UAV Detection: From Fundamentals and Operational Principles to Advanced Detection and Classification Techniques. Sensors 2025, 25, 2757. [Google Scholar] [CrossRef]
- Zermas, D.; Izzat, I.; Papanikolopoulos, N. Fast segmentation of 3D point clouds: A paradigm on LiDAR data for autonomous vehicle applications. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 5067–5073. [Google Scholar]
- Shao, S.; Zhou, Y.; Li, Z.; Xu, W.; Chen, G.; Yuan, T. Frustum PointVoxel-RCNN: A High-Performance Framework for Accurate 3D Object Detection in Point Clouds and Images. In Proceedings of the 2024 4th International Conference on Computer, Control and Robotics (ICCCR), Shanghai, China, 19–21 April 2024; pp. 56–60. [Google Scholar]
- Sugimoto, Y.; Tran, G.K. A study on visual sensors based link quality prediction for UAV-to-UAV communications. In Proceedings of the 8th International Workshop on Smart Wireless Communications (SmartCom 2025), Eindhoven, The Netherlands, 4–6 June 2025. [Google Scholar]
- Sugimoto, Y.; Tran, G.K. Autonomous mmWave Beamforming for UAV-to-UAV Communication Using LiDAR-Camera Sensor Fusion. In Proceedings of the IEEE Global Communications Conference. 2025. Available online: https://t2r2.star.titech.ac.jp/cgi-bin/publicationinfo.cgi?lv=en&q_publication_content_number=CTT100937900 (accessed on 12 November 2025).
- Cai, X.; Zhu, X.; Yao, W. Distributed time-varying group formation tracking for multi-UAV systems subject to switching directed topologies. In Proceedings of the 27th International Conference on Computer Supported Cooperative Work in Design (CSCWD), Tianjin, China, 8–10 May 2024; pp. 127–132. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, R.; Ai, B.; Lian, Z.; Zeng, L.; Niyato, D.; Peng, Y. Deep Reinforcement Learning for Energy Efficiency Maximization in RSMA-IRS-Assisted ISAC System. In Proceedings of the IEEE Transactions on Vehicular Technology, Chengdu, China, 19–22 October 2025. [Google Scholar] [CrossRef]
- Ma, Z.; Liang, Y.; Zhu, Q.; Zheng, J.; Lian, Z.; Zeng, L.; Fu, C.; Peng, C.; Ai, B. Hybrid-RIS-Assisted Cellular ISAC Networks for UAV-Enabled Low-Altitude Economy via Deep Reinforcement Learning with Mixture-of-Experts. IEEE Trans. Cogn. Commun. Netw. 2025; early access. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, Q.; Lin, Z.; Chen, J.; Ding, G.; Wu, Q.; Gu, G.; Gao, Q. Sparse Bayesian Learning-Based Hierarchical Construction for 3D Radio Environment Maps Incorporating Channel Shadowing. IEEE Trans. Wirel. Commun. 2024, 23, 14560–14574. [Google Scholar] [CrossRef]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Cahyadi, M.N.; Asfihani, T.; Suhandri, H.F.; Navisa, S.C. Analysis of GNSS/IMU Sensor Fusion at UAV Quadrotor for Navigation. IOP Conf. Ser. Earth Environ. Sci. 2023, 1276, 012021. [Google Scholar]
- Lopez-Perez, D.; Guvenc, I.; Chu, X. Mobility management challenges in 3GPP heterogeneous networks. IEEE Commun. Mag. 2012, 50, 70–78. [Google Scholar] [CrossRef]
- Qi, K.; Liu, T.; Yang, C. Federated Learning Based Proactive Handover in Millimeter-wave Vehicular Networks. In Proceedings of the 2020 15th IEEE International Conference on Signal Processing (ICSP), Beijing, China, 6–9 December 2020; pp. 401–406. [Google Scholar] [CrossRef]
- Sony. Airpeak. RTK-1. Available online: https://www.sony.jp/airpeak/products/RTK-1/spec.html (accessed on 1 October 2025).
- Khawaja, W.; Ozdemir, O.; Guvenc, I. UAV Air-to-Ground Channel Characterization for mmWave Systems. In Proceedings of the 2017 IEEE 86th Vehicular Technology Conference (VTC-Fall), Toronto, ON, Canada, 24–27 September 2017; pp. 1–5. [Google Scholar] [CrossRef]
- 802.11ad-2012; IEEE Standard for Information Technology–Telecommunications and Information Exchange Between Systems–Local and Metropolitan Area Networks–Specific Requirements-Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications Amendment 3: Enhancements for Very High Throughput in the 60 GHz Band. IEEE: New York, NY, USA, 2012.
- Haitham, H.; Omid, A.; Michael, R.; Mohammed, A.; Dina, K.; Piotr, I. Fast millimeter wave beam alignment. In Proceedings of the 2018 Conference of the ACM Special Interest Group on Data Communication (SIGCOMM’18), Budapest, Hungary, 20–25 August 2018; pp. 432–445. [Google Scholar]
- Luo, K.; Luo, R.; Zhou, Y. UAV detection based on rainy environment. In Proceedings of the 2021 IEEE 4th Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Chongqing, China, 18–20 June 2021; pp. 1207–1210. [Google Scholar] [CrossRef]
- Singh, P.; Gupta, K.; Jain, A.K.; Vishakha; Jain, A.; Jain, A. Vision-based UAV Detection in Complex Backgrounds and Rainy Conditions. In Proceedings of the 2024 2nd International Conference on Disruptive Technologies (ICDT), Greater Noida, India, 15–16 March 2024; pp. 1097–1102. [Google Scholar] [CrossRef]






| Category | Parameter | Value |
|---|---|---|
| RF Parameters | Frequency | 60 GHz |
| Bandwidth | 300 MHz | |
| Transmit Power | 20 dBm | |
| Antenna Parameters | Antenna | 16 × 16 URA |
| Element Spacing | 0.5 | |
| Antenna Gain | 25.9 dBi | |
| HPBW |
| Method | Actual UAV | Actual Non-UAV | Total (Detections) | |
|---|---|---|---|---|
| Detected (predicted as UAV) | LiDAR-only | 970 (TP *) | 541 (FP) | 1511 |
| Camera/LiDAR | 909 (TP) | 22 (FP) | 931 | |
| Not Detected | LiDAR-only | 641 (FN) | ||
| Camera/LiDAR | 547 (FN) | |||
| Total (Actual UAV) | LiDAR/(Camera/LiDAR) | 1611/1456 (GT) |
| Method | Recall (TP/GT) | Precision (TP/Detections) | F1 Score |
|---|---|---|---|
| LiDAR-only method | 0.602 | 0.642 | 0.620 |
| Camera/LiDAR method | 0.624 | 0.976 | 0.761 |
| Method | Avg. Angel Error | Avg. Spectral Efficiency |
|---|---|---|
| Camera/LiDAR | 8. | 11.98 bits/s/Hz |
| GNSS-based | 9.54 bits/s/Hz | |
| Beam Sweep | 10.52 bits/s/Hz | |
| Ideal | 13.66 bits/s/Hz | |
| Omni | 6.30 bits/s/Hz |
| Method | Avg. Spectral Efficiency |
|---|---|
| Hybrid | 10.71 bits/s/Hz |
| Camera/LiDAR | 9.87 bits/s/Hz |
| GNSS-based | 9.75 bits/s/Hz |
| Beam Sweep | 9.45 bits/s/Hz |
| Ideal | 12.71 bits/s/Hz |
| Omni | 5.00 bits/s/Hz |
| Method | Avg. Spectral Efficiency (Clear) | Avg. Spectral Efficiency (Rain) |
|---|---|---|
| Camera/LiDAR | 11.98 bits/s/Hz | 11.58 bits/s/Hz |
| GNSS-based | 9.54 bits/s/Hz | 9.54 bits/s/Hz |
| Beam Sweep | 10.52 bits/s/Hz | 10.52 bits/s/Hz |
| Ideal | 13.66 bits/s/Hz | 13.66 bits/s/Hz |
| Omni | 6.30 bits/s/Hz | 6.30 bits/s/Hz |
| Method | 10-Percentile Value (Clear) | 10-Percentile Value (Rain) |
|---|---|---|
| Camera/LiDAR | 10.54 bits/s/Hz | 10.28 bits/s/Hz |
| GNSS-based | 3.40 bits/s/Hz | 3.40 bits/s/Hz |
| Beam Sweep | 8.55 bits/s/Hz | 8.55 bits/s/Hz |
| Ideal | 15.40 bits/s/Hz | 15.40 bits/s/Hz |
| Omni | 6.89 bits/s/Hz | 6.89 bits/s/Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sugimoto, Y.; Tran, G.K. Hybrid Sensor Fusion Beamforming for UAV mmWave Communication. Future Internet 2025, 17, 521. https://doi.org/10.3390/fi17110521
Sugimoto Y, Tran GK. Hybrid Sensor Fusion Beamforming for UAV mmWave Communication. Future Internet. 2025; 17(11):521. https://doi.org/10.3390/fi17110521
Chicago/Turabian StyleSugimoto, Yuya, and Gia Khanh Tran. 2025. "Hybrid Sensor Fusion Beamforming for UAV mmWave Communication" Future Internet 17, no. 11: 521. https://doi.org/10.3390/fi17110521
APA StyleSugimoto, Y., & Tran, G. K. (2025). Hybrid Sensor Fusion Beamforming for UAV mmWave Communication. Future Internet, 17(11), 521. https://doi.org/10.3390/fi17110521






