A DLT-Aware Performance Evaluation Framework for Virtual-Core Speedup Modeling

Abstract

Scheduling computing is a well-studied area focused on improving task execution by reducing processing time and increasing system efficiency. Divisible Load Theory (DLT) provides a structured analytical framework for distributing partitionable computational and communicational loads across processors, and its adaptability has allowed researchers to integrate it with other models and modern technologies. Building on this foundation, previous studies have shown that Amdahl-like laws can be effectively combined with DLT to produce more realistic performance models. This paper further develops analytical models that further extend such integration by incorporating Gustafson’s Law and Juurlink’s Law into DLT to capture broader scaling behaviors. It also extends the analysis to workload distribution in virtual multicore systems, providing a more structured basis for evaluating parallel performance. Methods include analytically computing speedup as a function of the number of cores and the parallelizable fraction under different scheduling strategies, with comparisons across workload conditions. Results show that combining DLT with speedup laws and virtual core design offers a deeper and more structured approach for analytical parallel system evaluation. While the analysis remains theoretical, the proposed framework establishes a mathematical foundation for future empirical validation, heterogeneous workload modeling, and sensitivity analysis.

1. Introduction

Multiprocessor systems and data-intensive tasks require scheduling methods that account for both computation and communication. Divisible Load Theory (DLT) provides a linear and closed-form framework to divide workloads into fractions and to optimally distribute them across processors and links [1]. Over three decades, DLT has been applied to parallel and distributed computing, cloud systems, and sensor networks, showing its usefulness as a performance modeling tool. Its strength lies in its ability to offer closed-form analytical results that explicitly capture the effect of communication delay, bandwidth, and load partitioning, making it one of the few theories that describe distributed performance quantitatively [2,3,4].

Parallel speedup laws give another view of scalability. Amdahl’s Law [5] emphasizes the constraint of serial fractions, while Gustafson’s Law [6] shifts the focus to problem scaling with processor count. Juurlink extended Gustafson’s model by including heterogeneity effects [7]. Embedding these laws into DLT creates an integrated framework that links workload distribution with scaling analysis, offering a more realistic picture of parallel performance [8].

Modern multicore architectures add further complexity. Symmetric, asymmetric, and dynamic designs change how workloads are balanced and how theoretical speedups are achieved [9,10,11,12]. Combining DLT with these speedup laws under multicore designs enables the evaluation of scheduling strategies in terms of both efficiency and scalability.

The objective of this study is to develop such integrated models. We analyze how DLT interacts with Gustafson’s and Juurlink’s laws and extend the framework to multicore environments. Results demonstrate how load distribution strategies and processor organization influence achievable speedup, providing insights for scheduling in multicore and cloud systems. Ultimately, this work bridges idealized scaling laws and realistic distributed computation, contributing a unified mathematical perspective for analyzing performance in modern heterogeneous systems.

Our contributions in this work:

• We integrate Divisible Load Theory (DLT) with Gustafson’s and Juurlink’s speedup laws, providing a unified framework that links workload distribution with scalability analysis.
• We extend DLT to symmetric, asymmetric, and dynamic virtual multicore designs, showing how processor configuration and scheduling strategies affect achievable speedup.
• We present numerical evaluations that illustrate how different load distribution models interact with scaling laws, offering practical insights for scheduling in multicore and cloud environments.

2. Related Works

Divisible Load Theory (DLT) has evolved over three decades as a foundational analytical tool for modeling distributed computation and communication delays. Early studies established its linear partitioning framework and explored extensions to heterogeneous systems and multi-installment scheduling [1,2,3,4]. Building on this foundation, Cao, Wu, and Robertazzi [8] demonstrated that Amdahl-like laws can be effectively integrated with DLT to provide more realistic speedup estimations.

Recent research has further diversified its applications: Wang et al. [13] extended DLT from fine-grained to coarse-grained divisible workloads on networked systems, while Kazemi et al. [14] applied DLT to fog computing environments with linear and nonlinear load models to optimize resource allocation. At a more experimental level, Chinnappan et al. [15] validated a multi-installment DLT-based scheduling strategy through synthetic aperture radar (SAR) image reconstruction on distributed clusters, bridging the gap between theoretical analysis and practical deployment.

Together, these studies reinforce DLT’s analytical role in understanding communication-bounded performance and scalability.

Beyond chip-level modeling, recent studies have explored communication–computation overlapping in large-scale numerical solvers [16] and task mapping in heterogeneous architectures for visual systems [17]. In parallel, reliability-aware scheduling and task offloading for distributed edge and UAV-assisted computing continue to highlight the broader challenge of balancing computation and communication under non-ideal conditions [18]. These diverse efforts share the same analytical motivation as the present study: to quantify scalability through explicit modeling of delay, heterogeneity, and architectural design.

3. Divisible Load Theory Models

3.1. Real-World Applicability of Divisible Load Theory

Although Divisible Load Theory (DLT) is an analytical framework, it was originally motivated by the need to model realistic computing and communication processes in distributed systems [4]. DLT provides a mathematically tractable framework that captures key performance behaviors observed in distributed and parallel systems. Rather than serving as an empirical model, it offers analytical insight into how computation and communication jointly determine system efficiency under various network and processor configurations. Its practical relevance can be summarized in several aspects.

First, DLT inherently captures the combined effects of computation and communication, allowing designers to analyze heterogeneous processors, link speeds, and topological constraints in a unified manner.

Second, the linearity of the model enables closed-form solutions that remain valid under latency, propagation delay, and finite link capacity, providing quantitative insight into performance saturation in congested networks.

Third, DLT has been extended to include time-varying loads and stochastic effects, Previous studies have shown that DLT-based analytical predictions closely match simulation and experimental trends in distributed systems, typically within single-digit percentage deviations [2,3].

Finally, its equivalence with circuit and queuing models makes it suitable for hybrid analysis of networks exhibiting nonlinear transmission characteristics.

Together, these attributes make DLT not only a mathematical abstraction but also a framework that remains robust under real-world constraints such as congestion, link asymmetry, and resource variability.

3.2. Preliminaries

We consider a single-level tree (star) network consisting of a root processor $P_0$ and m child processors $P_1,\dots ,P_m$, as illustrated in Figure 1.

The total workload is arbitrarily divisible. Processor i receives fraction ${\alpha }_i$ of the load, with

$$\sum _{i=0}^m{\alpha }_i=1.$$

Inverse processing speed of processor i is denoted $w_i$, and inverse link speed is $z_i$. Constants $T_{cp}$ and $T_{cm}$ scale computation and communication. The computation and communication times are

$$T_{comp}^{\left(i\right)}=w_i{T}_{cp}{\alpha }_i,T_{comm}^{\left(i\right)}=z_i{T}_{cm}{\alpha }_i.$$

(1)

The finishing time $T_f$ is when the slowest processor completes. The baseline sequential time $T_{seq}$ gives the DLT speedup

$$S_{DLT}={\displaystyle \frac{T_{seq}}{T_f}}.$$

(2)

These expressions follow the classical DLT formulation introduced by Agrawal and Jagadish [1], where workloads are treated as continuously divisible and communication delays are explicitly modeled. The framework has since been extended to heterogeneous and sensor-driven systems [2,3] and formally summarized in recent texts on distributed scheduling [4,19].

DLT incorporates three main distribution strategies.

3.3. Sequential Distribution (SDLT1)

In SDLT1, the root distributes the load to one child at a time; each child computes only after receiving the full load. Load balance requires (see [4] Section 5.2.1):

$${\alpha }_0{w}_0{T}_{cp}={\alpha }_1{w}_1{T}_{cp},{\alpha }_{i-1}{w}_{i-1}{T}_{cp}={\alpha }_{i-1}{z}_{i-1}{T}_{cm}+{\alpha }_i{w}_i{T}_{cp},i=2,\dots ,m.$$

(3)

Normalization $\sum {\alpha }_i=1$ closes the system. The equivalent processing rate is

$${\gamma }_{eq}={\displaystyle \frac{1}{1+w_0{T}_{cp}{\sum }_{i=1}^m\frac{1}{w_i{T}_{cp}+z_i{T}_{cm}}}}.$$

(4)

Hence the speedup is

$$S_{DLT1}=1+w_0{T}_{cp}\sum _{i=1}^m{\displaystyle \frac{1}{w_i{T}_{cp}+z_i{T}_{cm}}}.$$

(5)

For a homogeneous system ($w_i=w$, $z_i=z$),

$$S_{DLT1}=1+m·{\displaystyle \frac{w_0{T}_{cp}}{w{T}_{cp}+z{T}_{cm}}}.$$

(6)

3.4. Simultaneous Distribution, Staggered Start (SDLT2)

In SDLT2, the root sends to all children simultaneously; each child starts computing only after receiving its load. Timing relations are

$${\alpha }_0{w}_0{T}_{cp}={\alpha }_1(z_1{T}_{cm}+w_1{T}_{cp}),{\alpha }_{i-1}(z_{i-1}{T}_{cm}+w_{i-1}{T}_{cp})={\alpha }_i(z_i{T}_{cm}+w_i{T}_{cp}).$$

(7)

Defining

$$k_1={\displaystyle \frac{w_0{T}_{cp}}{w_1{T}_{cp}+z_1{T}_{cm}}},q_i={\displaystyle \frac{w_{i-1}{T}_{cp}+z_{i-1}{T}_{cm}}{w_i{T}_{cp}+z_i{T}_{cm}}},$$

the closed form speedup is

$$S_{DLT2}=1+k_1\left(1+\sum _{i=2}^m\prod _{l=2}^i{q}_l\right).$$

(8)

For a homogeneous system,

$$S_{DLT2}=1+m·{\displaystyle \frac{w_0{T}_{cp}}{w{T}_{cp}+z{T}_{cm}}}.$$

(9)

3.5. Simultaneous Distribution, Simultaneous Start (SDLT3)

In SDLT3, each child processor begins computation as soon as the first portion of its assigned load arrives, allowing full overlap between communication and computation. The load balance equations for this model are

$${\alpha }_{i-1}{w}_{i-1}{T}_{cp}={\alpha }_i{w}_i{T}_{cp},i=1,2,\dots ,m,$$

(10)

with normalization ${\sum }_{i=0}^m{\alpha }_i=1$. Solving recursively yields

$${\alpha }_i=\left(\prod _{j=2}^i{q}_j\right){\alpha }_1,q_i={\displaystyle \frac{w_{i-1}}{w_i}}.$$

(11)

The corresponding speedup for a single-level tree is then

$$S_{DLT3}=1+k_1\left[1+\sum _{i=2}^m\left(\prod _{j=i}^m{q}_j\right)\right],$$

(12)

where $k_1=w_1/w_0$. For the homogeneous case ($w_i=w$) and negligible communication delay, this reduces to

$$S_{DLT3}=1+m{\displaystyle \frac{w_0}{w}}.$$

(13)

3.6. DLT Summary

The three models differ in their treatment of communication and overlap:

• SDLT1 suffers from the root bottleneck and scales poorly.
• SDLT2 eliminates sequential transmissions, giving linear scaling in homogeneous systems.
• SDLT3 achieves the closest to ideal linear speedup under overlapping assumptions.

All formulas above are complete for both heterogeneous and homogeneous systems, and can be directly used in subsequent integrations with speedup laws.

4. Integration with Classical Speedup Laws

Classical laws, including those of Amdahl, Gustafson, and Juurlink, split a workload into serial and parallel parts and then ask how speed scales [5,6,7]. The usual input is the processor count p, which implicitly assumes that p processors deliver close to p times performance. In real systems, this is not true. Communication, load imbalance, and heterogeneity result in losses. DLT provides a system-aware speedup that includes these losses. Our approach follows the integration concept proposed by Cao, Wu, and Robertazzi [8], replacing p with $S_{DLT}$ so that the laws preserve their intuition but reflect realistic constraints. Similar considerations about practical scalability in multicore design have also been emphasized by Hill and Marty [11,12].

4.1. Amdahl’s Law with DLT

Amdahl assumes a fixed-size problem with parallel fraction f [5]:

$$S_{Amdahl}\left(p\right)={\displaystyle \frac{1}{(1-f)+\frac{f}{p}}}.$$

(14)

We replace p by the effective speedup from DLT:

$$S_{Amdahl-DLT}={\displaystyle \frac{1}{(1-f)+\frac{f}{S_{DLT}}}}.$$

(15)

This keeps the serial/parallel split but removes the ideal-core assumption, making Amdahl’s framework compatible with realistic distributed and multicore environments.

4.2. Gustafson’s Law with DLT

Gustafson points out that problem size typically scales with resources [6]. The scaled-speedup form follows from fixing the normalized p-core time to 1 and letting parallel work grow with p, yielding

$$S_{Gustafson}\left(p\right)=(1-f)+fp,$$

(16)

as derived from the ratio $T\left(1\right)/T\left(p\right)$ with a scaled parallel term. Substituting $S_{DLT}$ gives

$$S_{Gustafson-DLT}=(1-f)+f{S}_{DLT}.$$

(17)

This keeps the scaled-workload interpretation but grounds the scaling in measured distribution efficiency rather than a raw core count.

4.3. Juurlink’s General Law (GSEE) with DLT

Juurlink generalizes the growth of the parallel portion via a scale function $scale\left(p\right)$ with bounds $1\le scale\left(p\right)\le p$, it serves as a middle ground between Amdahl (constant) and Gustafson (linear) [7]. A common example is $scale\left(p\right)=\sqrt{p}$ to capture diminishing returns. From the same $T\left(1\right)/T\left(p\right)$ construction one obtains the generalized scaled speedup equation (GSEE):

$$S_{General-DLT}\left(p\right)={\displaystyle \frac{(1-f)+fscale\left(p\right)}{(1-f)+{\displaystyle \frac{fscale\left(p\right)}{p}}}}.$$

(18)

which reduces to Amdahl for $scale\left(p\right)=1$ and to Gustafson for $scale\left(p\right)=p$. Replacing p by $S_{DLT}$ yields the DLT-aware form:

$$S_{General-DLT}={\displaystyle \frac{(1-f)+fscale\left(S_{DLT}\right)}{(1-f)+{\displaystyle \frac{fscale\left(S_{DLT}\right)}{S_{DLT}}}}}.$$

(19)

This links the shape of scaling (via $scale(·)$) with the achievable parallelism under communication/heterogeneity (via $S_{DLT}$).

4.4. Why Replace p $S_{DLT}$?

The reason is practical and direct:

• Realism. p implicitly means “about $p\times$ performance,” which is not achievable once communication and imbalance are involved. $S_{DLT}$ is an attainable speedup that already accounts for distribution cost and overlap.
• Model continuity. Different DLT policies (SDLT1–3) give different $S_{DLT}$; the laws remain the same algebraically, so we can compare policies without changing the law itself.
• Parameter transparency. The resulting formulas retain f (serial/parallel mix) while adding measurable system parameters $(w,z,T_{cp},T_{cm})$ through $S_{DLT}$.

This substitution is the glue between classical laws and system-level constraints. It retains the clarity of Amdahl/Gustafson/Juurlink while making the predictions match real multicore and network systems.

4.5. Bridging Theoretical and Architectural Limits

This study is divided into two tightly connected parts, each addressing a different layer of performance limitation in multicore systems.

The first part establishes a baseline model by integrating Divisible Load Theory (DLT) with the classical speedup laws of Amdahl, Gustafson, and Juurlink. DLT and the speedup laws approach scalability from two complementary perspectives: DLT quantifies system-level bottlenecks introduced by communication and scheduling, while speedup laws describe computational scaling under idealized assumptions. By embedding DLT into the structure of the classical laws, the model captures both scheduling constraints and parallel scalability within a unified analytical framework. This section therefore defines the theoretical ceiling of multicore performance when both computation and communication are taken into account.

The second part builds directly on this foundation by incorporating architectural constraints through the concept of virtual core design. While the first model represents the global scalability limit of a system, the virtual core model translates that limit into realizable performance under different chip organizations. By modeling symmetric, asymmetric, and dynamic multicore configurations, this section demonstrates how architectural structure determines how close real systems can approach the theoretical bounds established in the first part.

Together, the two parts form a complete and hierarchical methodology: the first defines the upper limit imposed by scheduling and communication, and the second measures the extent to which actual multicore designs can reach that limit. This separation ensures conceptual clarity while maintaining continuity between theoretical scalability and practical architectural realizability, bridging idealized performance models with real-world multicore implementations.

4.6. Introduction to Multicore Speedup Modeling

The classical speedup laws of Amdahl, Gustafson, and Juurlink [5,6,7] provide important insights into the scalability of parallel systems, but they all share a strong simplification: the number of processors p is treated as a direct proxy for performance. In the multicore era, this assumption is no longer valid. Chip design involves fundamental trade-offs in area, power, and complexity, and the simple idea that “p processors yield $p\times$ performance” fails to reflect reality.

Hill and Marty [11] addressed this gap by introducing the concept of Base Core Equivalents (BCE). A base core is the smallest, most efficient unit of computation, and the chip as a whole is constrained by a budget of n such cores. Different design choices—many small cores, a few large cores, or dynamically reconfigurable cores—must all fit within this BCE budget. This framework bridges classical laws with the realities of chip architecture and has since inspired further analytical and design extensions [10,12].

In their model, three design styles are distinguished:

• Symmetric multicore, where the chip is partitioned into identical cores;
• Asymmetric multicore, where a single large core is combined with many small ones;
• Dynamic multicore, where cores can fuse into a wide pipeline for sequential work and split for parallel work.

Each design leads to a distinct formula for speedup, extending Amdahl’s structure into the multicore domain. In the following subsections, we summarize these results and then introduce our own extension by integrating Divisible Load Theory (DLT).

4.7. Symmetric Multicore Design (BCE)

We adopt the Base Core Equivalents (BCE) framework: a chip has a fixed budget of n BCEs; a core that uses r BCEs delivers sequential performance $perf\left(r\right)$ with $perf\left(r\right)\le r$ (a common assumption is $perf\left(r\right)=\sqrt{r}$). With r BCEs per core, the chip implements $n/r$ identical cores. The serial and parallel phases do not overlap: one r-BCE core runs the serial part; all $n/r$ cores (each r BCEs) execute the parallel part.

• Amdahl form.

Let f be the parallel fraction. The speedup relative to one BCE (baseline) is

$$S_{sym}^{Amdahl}(f,n,r)={\displaystyle \frac{1}{{\displaystyle \frac{1-f}{perf\left(r\right)}}+{\displaystyle \frac{f}{perf\left(r\right)·(n/r)}}}}={\displaystyle \frac{1}{{\displaystyle \frac{1-f}{perf\left(r\right)}}+{\displaystyle \frac{fr}{perf\left(r\right)n}}}}.$$

(20)

Equivalently,

$$S_{sym}^{Amdahl}(f,n,r)={\displaystyle \frac{perf\left(r\right)}{(1-f)+f·\frac{r}{n}}}.$$

(21)

• Gustafson form (scaled workload).

Replacing f by $fn$ for the parallel component (speedup measured w.r.t. one BCE), the scaled speedup is

$$S_{sym}^{Gustafson}(f,n,r)={\displaystyle \frac{(1-f)+fn}{{\displaystyle \frac{1-f}{perf\left(r\right)}}+{\displaystyle \frac{fn}{perf\left(r\right)·(n/r)}}}}={\displaystyle \frac{(1-f)+fn}{{\displaystyle \frac{1-f}{perf\left(r\right)}}+{\displaystyle \frac{fr}{perf\left(r\right)}}}}.$$

(22)

Multiplying numerator and denominator by $perf\left(r\right)$ gives the compact form

$$S_{sym}^{Gustafson}(f,n,r)={\displaystyle \frac{\left((1-f)+fn\right)perf\left(r\right)}{(1-f)+fr}}.$$

(23)

• General law (Juurlink/GSEE).

For a growth function $1\le scale\left(n\right)\le n$,

$$S_{sym}^{General}(f,n,r)={\displaystyle \frac{(1-f)+fscale\left(n\right)}{(1-f)+{\displaystyle \frac{fscale\left(n\right)}{perf\left(r\right)·(n/r)}}}}={\displaystyle \frac{\left((1-f)+fscale\left(n\right)\right)perf\left(r\right)}{(1-f)+{\displaystyle \frac{frscale\left(n\right)}{n}}}}.$$

(24)

• Interpretation.

Equations (20)–(24) capture the trade-off between how many cores ($n/r$) and how strong each core is ($perf\left(r\right)$). Larger r accelerates the serial part (numerator effect via $perf\left(r\right)$), but reduces the number of parallel workers (denominator effect via $n/r$). Amdahl’s form models fixed-size problems; Gustafson’s form models scaled problems; the general law interpolates via $scale(·)$ between Amdahl ($scale=1$) and Gustafson ($scale=n$).

4.8. Integration of DLT into Multicore Models

While the BCE framework of Hill and Marty successfully maps classical speedup laws to chip design constraints, it still assumes that the parallel portion of a workload executes ideally once the number of cores is fixed. In practice, communication and scheduling overheads limit the achievable parallelism. Divisible Load Theory (DLT) provides a systematic way to quantify this effect. By explicitly modeling computation and communication costs, DLT produces an effective speedup, denoted as $S_{DLT}$, which replaces the idealized core count n in the multicore formulas.

The general mapping is

$$n⟶S_{DLT},scale\left(n\right)⟶scale\left(S_{DLT}\right),$$

(25)

where $scale(·)$ is the growth function in Juurlink’s generalized law. When communication costs vanish, $S_{DLT}\to n$, and the formulas reduce to their original forms. When communication dominates, $S_{DLT}\to 1$, and the speedup collapses to unity.

4.9. Symmetric Multicore with DLT

For the symmetric design, the original BCE-based laws can be extended by substituting n with $S_{DLT}$. With parallel fraction f and performance of an r-sized core denoted by $perf\left(r\right)$, the results are

• Amdahl form:

$$S_{sym-DLT}^{Amdahl}(f,S_{DLT},r)={\displaystyle \frac{perf\left(r\right)}{(1-f)+f{\displaystyle \frac{r}{S_{DLT}}}}}.$$

(26)

• Gustafson form:

  $$S_{sym-DLT}^{Gustafson}(f,S_{DLT},r)={\displaystyle \frac{\left((1-f)+f{S}_{DLT}\right)perf\left(r\right)}{(1-f)+fr}}.$$

  (27)
• General form:

  $$S_{sym-DLT}^{General}(f,S_{DLT},r)={\displaystyle \frac{\left((1-f)+fscale\left(S_{DLT}\right)\right)perf\left(r\right)}{(1-f)+f{\displaystyle \frac{rscale\left(S_{DLT}\right)}{S_{DLT}}}}}.$$

  (28)
• Interpretation:

These expressions preserve the consistency of the original symmetric multicore laws. They collapse to the baseline formulas when $S_{DLT}=n$, and they reduce to unity when $S_{DLT}=1$, showing that the framework correctly interpolates between the ideal and communication-limited extremes.

4.10. Asymmetric Multicore with DLT

In the asymmetric design, one large core of size r executes the sequential part, while the parallel part is executed by this large core together with the remaining $S_{DLT}-r$ base-equivalent units. The integration with DLT yields

• Amdahl form:

$$S_{asym-DLT}^{Amdahl}(f,S_{DLT},r)={\displaystyle \frac{1}{{\displaystyle \frac{1-f}{perf\left(r\right)}}+{\displaystyle \frac{f}{perf\left(r\right)+S_{DLT}-r}}}}.$$

(29)

• Gustafson form:

$$S_{asym-DLT}^{Gustafson}(f,S_{DLT},r)={\displaystyle \frac{(1-f)+f{S}_{DLT}}{{\displaystyle \frac{1-f}{perf\left(r\right)}}+{\displaystyle \frac{f{S}_{DLT}}{perf\left(r\right)+S_{DLT}-r}}}}.$$

(30)

• General form:

$$S_{asym-DLT}^{General}(f,S_{DLT},r)={\displaystyle \frac{(1-f)+fscale\left(S_{DLT}\right)}{{\displaystyle \frac{1-f}{perf\left(r\right)}}+{\displaystyle \frac{fscale\left(S_{DLT}\right)}{perf\left(r\right)+S_{DLT}-r}}}}.$$

(31)

• Interpretation:

These formulas capture the heterogeneous trade-off: a large core accelerates the sequential phase, while the remaining BCE budget contributes to parallel execution. DLT ensures that the effective parallelism is limited by communication overhead rather than raw resource count.

4.11. Dynamic Multicore with DLT

In the dynamic design, r base cores can be fused into a large core for the sequential part, and the chip reconfigures into all $S_{DLT}$ units for the parallel part. The DLT-integrated formulas are

• Amdahl form:

$$S_{dyn-DLT}^{Amdahl}(f,S_{DLT},r)={\displaystyle \frac{1}{{\displaystyle \frac{1-f}{perf\left(r\right)}}+{\displaystyle \frac{f}{S_{DLT}}}}}.$$

(32)

• Gustafson form:

$$S_{dyn-DLT}^{Gustafson}(f,S_{DLT},r)={\displaystyle \frac{(1-f)+f{S}_{DLT}}{{\displaystyle \frac{1-f}{perf\left(r\right)}}+f}}.$$

(33)

• General form:

$$S_{dyn-DLT}^{General}(f,S_{DLT},r)={\displaystyle \frac{(1-f)+fscale\left(S_{DLT}\right)}{{\displaystyle \frac{1-f}{perf\left(r\right)}}+{\displaystyle \frac{fscale\left(S_{DLT}\right)}{S_{DLT}}}}}.$$

(34)

• Interpretation:

Dynamic multicore represents the most flexible design, combining the advantages of symmetric and asymmetric organizations. With DLT integration, the model reflects the fact that even under ideal reconfiguration, communication and distribution costs cap the achievable performance.

4.12. Summary

In summary, the DLT-augmented framework unifies the workload aspects (Amdahl, Gustafson, and Juurlink), architectural design choices (symmetric, asymmetric, dynamic), and system-level realities (communication and scheduling). This provides a more realistic picture of multicore performance than either classical laws or virtual core design models alone.

5. Results

In this section, we evaluate the performance of the proposed DLT-extended multicore speedup models. Following the structure of the classical laws, we first present results for symmetric, asymmetric, and dynamic designs, and then compare their behavior under different workload scenarios (Amdahl, Gustafson, and General). Figures and tables are provided to illustrate trends in speedup as functions of the parallel fraction f, the large-core size r, and the effective parallelism $S_{DLT}$.

5.1. Algorithmic Framework for SDLT Models

To enhance theoretical operability and reproducibility, Algorithm 1 summarizes a unified computational framework for the three principal models—SDLT1, SDLT2, and SDLT3. Given processor speeds $w_i$, link speeds $z_i$, and the computation and communication intensities $T_{cp}$ and $T_{cm}$, the algorithm produces the analytical speedup curves for each scheduling strategy. The pseudocode follows MATLAB-style notation and was implemented and tested in MATLAB R2023a (MathWorks, Natick, MA, USA) for ease of reproducibility.

Algorithm 1 Unified Computation of SDLT1, SDLT2, and SDLT3 Speedups

1: Input: $w_0$, $T_{cp}$, $T_{cm}$, ${\{w_i,z_i\}}_{i=1}^N$ 2: Output: $SDLT1\left(n\right)$, $SDLT2\left(n\right)$, $SDLT3\left(n\right)$ 3: Initialize $k_1\leftarrow w_0/w_1$ 4: for $n=1$ to N do 5:       $sumProduct\leftarrow 0$ 6:       $sumSDLT2\leftarrow 0$ 7:       $sumSDLT3\leftarrow 0$ 8:       for $i=1$ to n do 9:          $sumSDLT2+=1/(w_i{T}_{cp}+z_i{T}_{cm})$ 10:         $sumSDLT3+=1/w_i$ 11:         if $i>1$ then 12:              $product\leftarrow 1$ 13:              for $l=2$ to i do 14:                    $q_l\leftarrow (w_{l-1}{T}_{cp}-z_{l-1}{T}_{cm})/\left(w_l{T}_{cp}\right)$ 15:                    $product \ast =q_l$ 16:              end for 17:              $sumProduct+=product$ 18:         end if 19:     end for 20:     $SDLT1\left[n\right]\leftarrow 1+k_1(1+sumProduct)$ 21:     $SDLT2\left[n\right]\leftarrow 1+w_0{T}_{cp}sumSDLT2$ 22:     $SDLT3\left[n\right]\leftarrow 1+w_{0}sumSDLT3$ 23: end for 24: return all $SDLT1$, $SDLT2$, and $SDLT3$ curves

The algorithm corresponds to the analytical formulations in Equations (1)–(13) and provides an operational procedure for computing SDLT, SDLT2, and SDLT3 speedups.

The parameters used in the simulations are summarized in

Table 1. Parameter settings used for the DLT-extended speedup simulations.

System Type	n	${\mathit{\omega }}_0$	${\mathit{\omega }}_1,{\mathit{\omega }}_2,\dots ,{\mathit{\omega }}_{\mathit{n}}$	${\mathit{z}}_1,{\mathit{z}}_2,\dots ,{\mathit{z}}_{\mathit{n}}$	${\mathit{T}}_{\mathbf{cp}}$	${\mathit{T}}_{\mathbf{cm}}$	f
Heterogeneous	50	4.2	4.2, 4.4, 4.6, …, 14	2.2, 2.4, 2.6, …, 12	2	1.5	0.7
Homogeneous	50	4.2	4.2, 4.2, …, 4.2	2.2, 2.2, …, 2.2	2	1.5	0.7

. For both heterogeneous and homogeneous configurations, the number of child processors is $n=50$, and the parallel fraction is fixed at $f=0.7$ unless otherwise stated. All numerical results presented here are derived from deterministic solutions of the proposed analytical equations rather than stochastic or discrete-time simulations, ensuring full reproducibility of the reported outcomes.

5.2. DLT-Extended Classical Speedup Laws

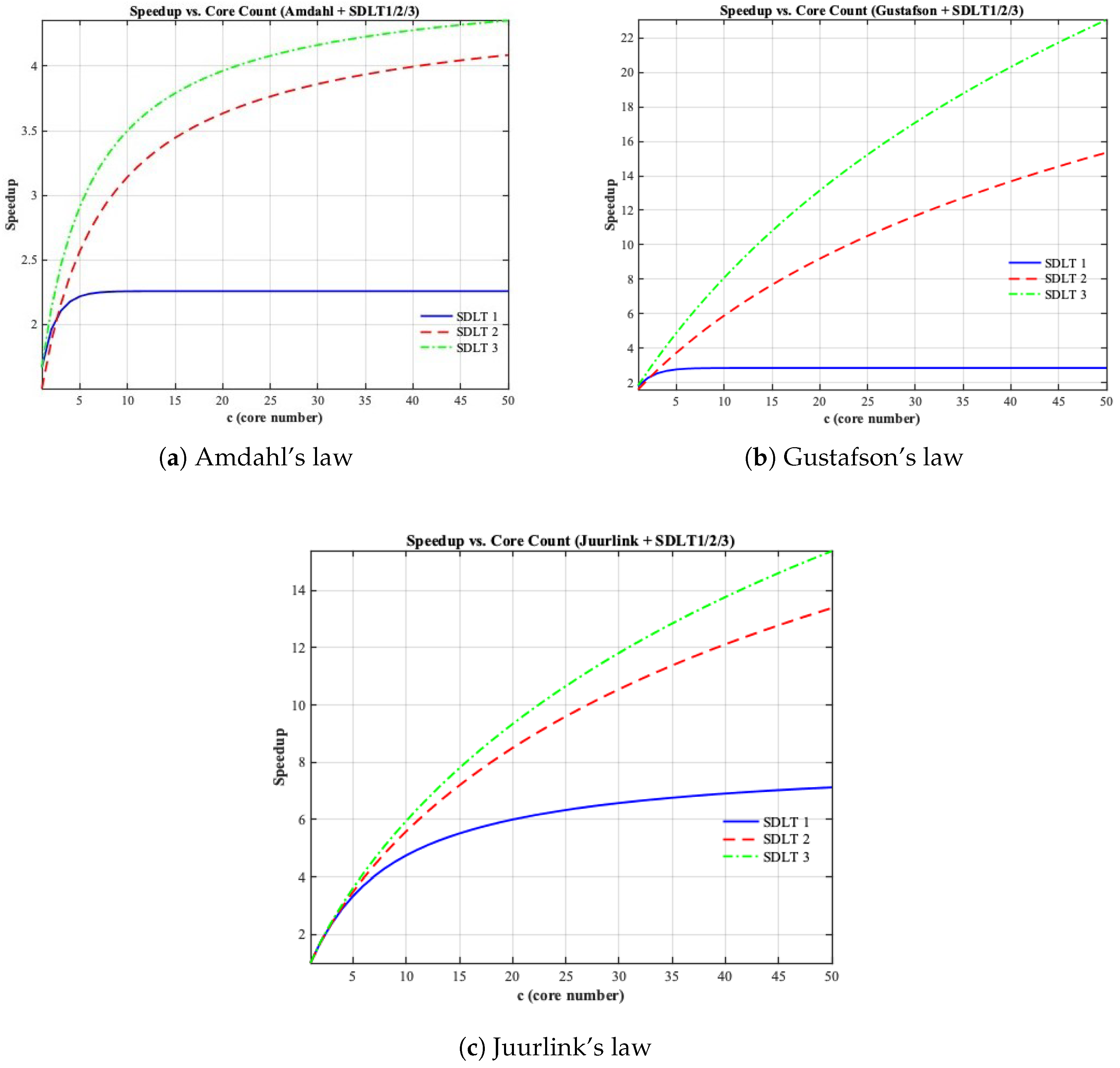
Before turning to multicore design trade-offs, it is instructive to examine the direct integration of Divisible Load Theory (DLT) with the classical speedup laws of Amdahl, Gustafson, and Juurlink. Figure 2 presents the results for their combinations. In this case, the idealized processor count c is replaced directly by the effective parallelism $S_{DLT}$, without incorporating the BCE resource model. This produces three DLT-adjusted baselines that illustrate how communication overhead modifies workload semantics.

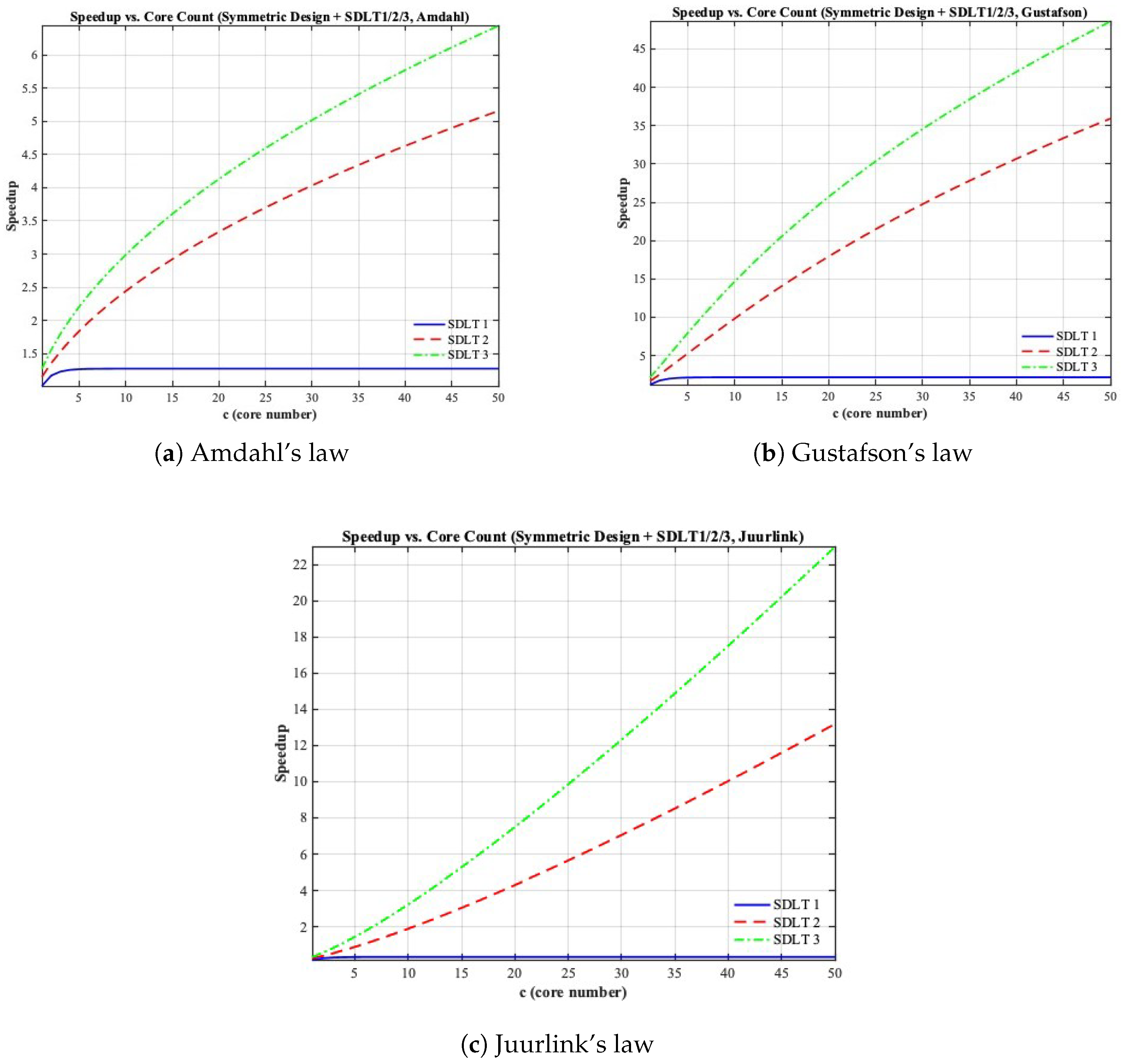
5.3. Symmetric Multicore Results

Figure 3 presents the symmetric multicore results obtained by integrating DLT with three classical scaling laws. The analysis assumes a fixed parallelizable fraction $f=0.8$ while varying the number of cores determined by r. Each curve replaces the ideal processor count in the original law with the DLT-based effective speedup $S_{DLT}$, which reflects both computation and communication effects.

For Amdahl’s law (Figure 3a), speedup increases as r decreases (i.e., more cores) but quickly saturates due to the serial component. When DLT is integrated, the achievable speedup drops further, showing how communication overhead amplifies the limitation of fixed-size workloads.

Under Gustafson’s law (Figure 3b), the speedup grows almost linearly as the workload scales with the number of cores. With DLT integration, the slope becomes smaller, indicating that scalability is partially offset by the communication delay inherent in distributed systems.

Juurlink’s law (Figure 3c) extends both models by introducing a tunable scaling parameter p that transitions between Amdahl’s and Gustafson’s behaviors. The DLT-adjusted curves capture the realistic interaction between workload scalability and communication delay, forming a more accurate reflection of actual multicore performance.

5.4. Asymmetric Multicore Results

Figure 4 shows the performance of the asymmetric multicore design with DLT integration under Amdahl’s, Gustafson’s, and Juurlink’s speedup laws. In this configuration, one large r-sized core executes the serial phase, while multiple smaller cores handle the parallel portion. Compared with the symmetric design, the asymmetric approach consistently achieves higher speedup for the same $S_{DLT}$, as the larger core effectively reduces the serial bottleneck.

Under Amdahl’s law (Figure 4a), this configuration extends the saturation point of speedup, showing that heterogeneous cores mitigate the serial limitation more efficiently. For Gustafson’s law (Figure 4b), the speedup grows faster with increasing cores but remains bounded by communication overhead captured in $S_{DLT}$. Juurlink’s model (Figure 4c) lies between these two extremes, where the combined effects of scalability and DLT constraints yield a balanced and realistic estimate of system performance. Overall, the results confirm that heterogeneous multicore designs maintain higher efficiency under DLT-adjusted scaling laws, especially in communication-limited scenarios.

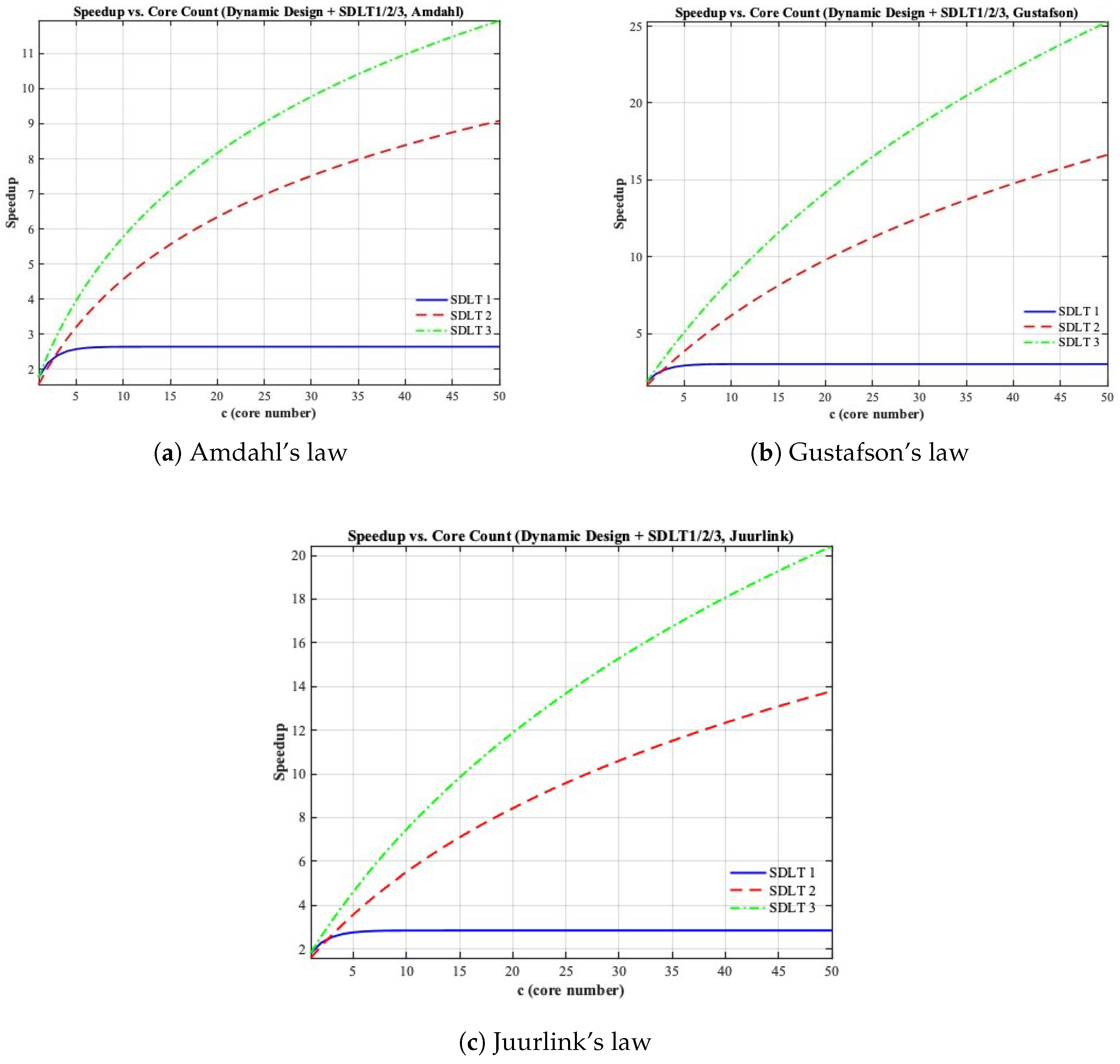
5.5. Dynamic Multicore Results

Figure 5 illustrates the performance of the dynamic multicore design integrated with DLT under Amdahl’s, Gustafson’s, and Juurlink’s laws. This configuration allows the system to dynamically reconfigure its r BCEs: during the serial phase, BCEs are fused into a large core for sequential execution, and during the parallel phase, all $S_{DLT}$ units are redistributed across smaller parallel cores. This flexibility maximizes resource utilization and represents the upper limit of multicore scalability under communication constraints.

For Amdahl’s law (Figure 5a), the dynamic design alleviates the serial bottleneck entirely within the BCE budget, extending the achievable speedup beyond symmetric and asymmetric configurations. Under Gustafson’s law (Figure 5b), the model achieves nearly ideal linear scaling, with DLT integration slightly reducing the slope as communication costs grow. Juurlink’s formulation (Figure 5c) provides a smooth transition between these limits, confirming that dynamic reconfiguration consistently outperforms static organizations across all workload types. Even under DLT-imposed delays, this model remains the most optimistic yet realistic upper bound on multicore performance.

To compare the three virtual core design strategies more directly,

Table 2. Representative speedups of three multicore architectures under Juurlink’s law with DLT integration (estimated from Figure 4c).

Design	Juurlink’s Law (SDLT1)	Juurlink’s Law (SDLT3)
Symmetric	1	22
Asymmetric	4	23
Dynamic	3	20

summarizes their representative speedups under Juurlink’s law with DLT integration. Among the three scaling laws, Juurlink’s formulation is the most representative, as it generalizes both Amdahl’s and Gustafson’s behaviors by incorporating a tunable scalability parameter. It therefore provides a balanced evaluation of realistic multicore performance, capturing both partial workload scalability and communication overheads modeled by $S_{DLT}$. Across all three architectures, the asymmetric design achieves the highest attainable speedup, followed by the dynamic and symmetric configurations.

6. Discussion

This work integrates Amdahl’s, Gustafson’s, and Juurlink’s scaling laws and their virtual-core design augments with the Divisible Load Theory (DLT) framework to capture how computation and communication jointly determine achievable performance in multicore systems. Classical laws treat processor count as an ideal performance multiplier, assuming no cost for synchronization or data transfer. In contrast, DLT provides a more precise view of how delays, bandwidth, and load partitioning shape the effective speedup observed in practice.

The combined models show that when communication is explicitly considered, the theoretical boundaries of multicore speedup shift significantly. Across symmetric, asymmetric, and dynamic designs, similar performance trends emerge: communication overhead compresses the difference between architectures, and efficiency becomes a function of how each design manages both computation time and transfer delay. The asymmetric design remains the most adaptable and efficient, while the symmetric configuration is the most constrained under DLT-adjusted scaling.

These results highlight that reduced performance gaps among multicore architectures are not a limitation but rather a reflection of communication-constrained realism. Architectural design choices, though important, become secondary when communication delays dominate system performance—a phenomenon that classical scaling laws fail to expose. This integration thus forms a bridge between idealized scaling theory and the real, delay-bound behavior of modern processors, extending the reach of classic speedup laws into architectures where communication cannot be ignored.

7. Future Work

While the analysis provides theoretical insight into communication-constrained scalability, it remains idealized in several respects. The current framework assumes perfectly divisible workloads and does not incorporate stochastic heterogeneity or benchmark-based validation. These simplifications make the model mathematically tractable but inevitably limit realism. Future research may extend the DLT-based scaling laws toward heterogeneous-core and stochastic-load environments, sensitivity studies on parameter variations, and empirical verification through benchmark traces or hardware measurements.

8. Conclusions

Overall, this study establishes a unified mathematical foundation connecting classical speedup theory with communication-aware performance modeling. By integrating Amdahl’s, Gustafson’s, and Juurlink’s laws within the DLT framework, the proposed models clarify how computation and communication jointly determine achievable performance in multicore systems. This integration not only refines the theoretical interpretation of speedup but also provides a structured approach for analyzing scalability and efficiency in modern multicore and distributed architectures. The results emphasize that communication-aware models are essential for understanding realistic performance behavior, offering a foundation upon which future empirical and heterogeneous-system studies can build.