Sparse Regularized Autoencoders-Based Radiomics Data Augmentation for Improved EGFR Mutation Prediction in NSCLC

Abstract

Lung cancer (LC) remains a leading cause of cancer mortality worldwide, where accurate and early identification of gene mutations such as epidermal growth factor receptor (EGFR) is critical for precision treatment. However, machine learning-based radiomics approaches often face challenges due to the small and imbalanced nature of the datasets. This study proposes a comprehensive framework based on Generic Sparse Regularized Autoencoders with Kullback–Leibler divergence (GSRA-KL) to generate high-quality synthetic radiomics data and overcome these limitations. A systematic approach generated 63 synthetic radiomics datasets by tuning a novel kl_weight regularization hyperparameter across three hidden-layer sizes, optimized using Optuna for computational efficiency. A rigorous assessment was conducted to evaluate the impact of hyperparameter tuning across 63 synthetic datasets, with a focus on the EGFR gene mutation. This evaluation utilized resemblance-dimension scores (RDS), novel utility-dimension scores (UDS), and t-SNE visualizations to ensure the validation of data quality, revealing that GSRA-KL achieves excellent performance (RDS > 0.45, UDS > 0.7), especially when class distribution is balanced, while remaining competitive with the Tabular Variational Autoencoder (TVAE). Additionally, a comprehensive statistical correlation analysis demonstrated strong and significant monotonic relationships among resemblance-based performance metrics up to moderate scaling (≤1.0*), confirming the robustness and stability of inter-metric associations under varying configurations. Complementary computational cost evaluation further indicated that moderate kl_weight values yield an optimal balance between reconstruction accuracy and resource utilization, with Spearman correlations revealing improved reconstruction quality (MSE $\rho =-0.78$, $p<0.001$) at reduced computational overhead. The ablation-style analysis confirmed that including the KL divergence term meaningfully enhances the generative capacity of GSRA-KL over its baseline counterpart. Furthermore, the GSRA-KL framework achieved substantial improvements in computational efficiency compared to prior PSO-based optimization methods, resulting in reduced memory usage and training time. Overall, GSRA-KL represents an incremental yet practical advancement for augmenting small and imbalanced high-dimensional radiomics datasets, showing promise for improved mutation prediction and downstream precision oncology studies.

1. Introduction

Lung cancer remains the leading cause of cancer mortality worldwide, and non-small cell lung cancer (NSCLC) constitutes nearly 85% of all cases [1,2]. Advances in precision oncology have revealed that epidermal growth factor receptor (EGFR) mutations are key molecular drivers in NSCLC, enabling targeted therapies such as gefitinib, erlotinib, and osimertinib that significantly improve survival outcomes [3,4,5]. Identifying EGFR mutation status is therefore critical for optimal treatment planning [6,7]. However, molecular testing through biopsy is invasive, spatially limited, and sometimes infeasible in advanced disease.

Radiomics has emerged as a transformative approach that converts medical images into high-dimensional quantitative features reflecting tumor heterogeneity [8,9,10]. These features, when integrated with machine learning, enable noninvasive prediction of molecular alterations and clinical outcomes [11,12,13]. In NSCLC, numerous studies have shown that radiomic models can distinguish EGFR-mutant from wild-type tumors with promising accuracy [14,15,16,17]. Despite this progress, radiomics-based EGFR prediction remains limited by small sample sizes, class imbalance, and high feature dimensionality, which collectively hinder model generalizability and robustness [18,19,20].

To overcome these challenges, synthetic data generation has been increasingly explored to augment limited radiomics datasets [21,22,23]. Generative models such as Conditional Tabular GAN (CTGAN) and Tabular Variational Autoencoder (TVAE) [24] have demonstrated potential for producing statistically realistic samples. However, GAN-based models often struggle with tabular data sparsity and mode collapse [25], leading to degraded resemblance and limited predictive utility. In this context, autoencoder-based frameworks have attracted attention for their ability to learn smooth latent representations and reconstruct complex high-dimensional structures. In our prior work, we introduced the Generic Sparse Regularized Autoencoder with KL divergence (GSRA-KL) as a generator for radiomics augmentation [26]. That study, however, was limited to a small balanced PET/CT metastasis dataset and used a computationally expensive particle-swarm-optimization (PSO) strategy for hyperparameter selection. To translate generative radiomics methods into practical, time-constrained clinical workflows, few needs remain: (i) systematic evaluation on small, highly imbalanced CT-derived datasets (e.g., EGFR mutation prediction), and (ii) more efficient, reproducible hyperparameter tuning.

This study addresses these gaps by extending and validating GSRA-KL for CT-based, small-sample, imbalanced EGFR mutation prediction tasks. Concretely, we introduce a scalable kl_weight hyperparameter to control KL-regularization strength, adopt Optuna-based Bayesian optimization to reduce tuning cost [27], and compare GSRA-KL against GSRA and Tabular VAE (TVAE) baselines [24]. The synthetic radiomics datasets were rigorously evaluated based on comprehensive metrics (resemblance- and utility-dimension metrics) defined by Hernández et al. [21], which were previously modified by Munir et al. [26]. The current study also defines a novel utility-dimension score (UDS) as a single unit to effectively assess downstream predictive modeling. Furthermore, a visual investigation of the quality of synthetic radiomics datasets is also conducted through t-SNE plots in lower-dimensional space [22]. In addition to methodological refinements, this study incorporates rigorous statistical evaluations to ensure the reliability and interpretability of performance trends. Non-parametric statistical tests, including the Friedman test [28] and Spearman rank correlation analysis [29], were applied to assess consistency and significance across evaluations of resemblance and computational resources, providing a robust basis for comparative analysis of model behavior under varying configurations.

Our goal is to demonstrate practical, computationally feasible synthetic augmentation that meaningfully improves downstream prediction in challenging radiomics scenarios.

Main Contributions

This study extends our previously published GSRA-KL framework [26] by introducing methodological and analytical innovations that enhance both generative fidelity and computational efficiency. The major contributions are:

• Introducing a scalable kl_weight hyperparameter into the GSRA-KL loss function to adaptively balance sparse regularization and reconstruction fidelity.
• Enhancing synthetic data faithfulness through systematic generation across mutation subtypes by jointly adjusting GSRA-KL hyperparameters, particularly tuning kl_weight values relative to hidden-layer sizes.
• Integrating an Optuna-based Bayesian optimization framework for hyperparameter tuning, which significantly reduces computational cost compared to the PSO-based approach used previously.
• Conducting a comprehensive evaluation across 63 synthetic datasets for EGFR gene mutation using resemblance-dimension score (RDS), the novel utility-dimension score (UDS), and t-SNE visualizations.
• Performing additional quantitative validation using non-parametric Friedman and Spearman rank-based statistical analyses to assess consistency across resemblance and computational cost dimensions.
• Comparing the effectiveness of GSRA-KL, GSRA, and TVAE models to address prediction enhancement challenges in small, imbalanced CT-based radiomics datasets.
• Performing an ablation-like analysis demonstrating that setting kl_weight = 0.0 reverts GSRA-KL to the baseline GSRA model, enabling an isolated evaluation of KL divergence regularization effects on model performance and robustness.

The remainder of the paper is organized as follows: Section 2 describes the dataset, model architectures, and evaluation protocols; Section 3 presents the experimental results; Section 4 integrates resemblance trends, computational cost analysis, and practical implications of the GSRA–KL framework; and Section 5 provides concluding remarks.

2. Materials and Methods

The approach adopted to assess the efficacy of the GSRA-KL-based algorithm is divided into three phases: data preparation and preprocessing, synthetic data generation, and quality evaluation through resemblance, utility-dimension metrics, and t-SNE plots (see Figure 1).

2.1. Data-Preprocessing Phase

The proposed study utilized radiomics data (Features Transpose EGFR) cohorts of 83 patients, with established mutation status from a previous study [16] and accessible at https://www.mdpi.com/article/10.3390/tomography7020014/s1 (accessed on 7 June 2022). The datasets comprise 266 radiomics signatures, including both texture and non-texture features. Three features with constant values were removed using filter methods, leaving 263 radiomics features from the cohort of 83 NSCLC patients. In EGFR, 12 patients (14%) had mutant status while 71 (86%) were classified as wild-type. The data is normalized using standard scaling before model training. These small and highly imbalanced dataset was chosen to evaluate the efficacy of our previously proposed GSRA-KL algorithm, a synthetic radiomics data-generation method based on generic sparse regularized autoencoders with Kullback–Leibler divergence [26].

2.2. Synthetic Data Generation

The previously proposed GSRA-KL algorithm used a default weightage value of the KL divergence loss term [26]. In the current study, we introduced a hyperparameter termed kl_weight (see Equations (1) and (2)) to assess its impact on the quality of synthetic data. It may lead to an optimal value for a faithful synthetic radiomics dataset to effectively counter machine learning prediction performance issues on small and class-imbalanced datasets in diagnosis and precision treatment options. For an extensive range of kl_weight hyperparameters with a step size of 0.05, we generated 21 synthetic datasets for each hidden dimension. Three hidden dimension sizes (input * 0.5, input * 1, and input * 2) were experimented with. Moreover, for a robust comparison and validation against state-of-the-art deep learning techniques, such as TVAE, we also generated synthetic data.

$$\begin{array}{cc}\hfill {\mathrm{Loss}}_{\mathrm{Novel}}=& \underset{\mathrm{Mean} \mathrm{Squared} \mathrm{Error}}{\underbrace{{\displaystyle \frac{1}{N}}\sum _{i=1}^N\sum _{j=1}^d{(x_{ij}-{\widehat{x}}_{ij})}^2}}+\underset{\mathrm{Sparsity} \mathrm{Regularization}}{\underbrace{\beta {\mathsf{\Omega }}_{\mathrm{sparsity}}}}\hfill \\ & +\underset{\mathrm{Weight} \mathrm{Regularization}}{\underbrace{\lambda {\mathsf{\Omega }}_{\mathrm{weights}}}}+\underset{\mathrm{KL} \mathrm{Regularization}}{\underbrace{\mathrm{kl}\text{\_}\mathrm{weight}\mathrm{KL}(p_k \Vert q_k)}}\hfill \end{array}$$

(1)

$$\mathrm{KL}(p_k \Vert q_k)=\sum _{k=1}^n\left[p_{k}log{\displaystyle \frac{p_k}{q_k}}+(1-p_k)log{\displaystyle \frac{1-p_k}{1-q_k}}\right]$$

(2)

where $p_k$ and $q_k$ are the probability distributions of input and output features across all samples at the input and output layers, respectively. The GSRA–KL pipeline integrates KL regularization and Optuna-based hyperparameter tuning for controlled radiomics synthesis (see Algorithm 1), and to generate multiple synthetic datasets with varying values of kl_weight. This enables an evaluation of the effectiveness of incorporating the KL term into the loss function of GSRA and the impact of synthetic data generation on improving predictions in small, imbalanced CT radiomics for NSCLC patients. Further to assess the consistency and significance of computational cost and resource utilization trends across hidden-layer sizes and hyperparameter settings, non-parametric Friedman tests were employed to assess group-wise differences, followed by Spearman rank correlation analysis to examine monotonic relationships between kl_weight and computational metrics [28,29].

Algorithm 1 Pseudocode for GSRA–KL-Based Synthetic Radiomics Data Generation with Custom Loss and Optuna Optimization

Input: $X_{\mathrm{train}}$, $N_{\mathrm{synthetic}}$, $N_{\mathrm{trials}}$, $d_{\mathrm{input}}$, $d_{\mathrm{hidden}}$, $\lambda$, $\beta$, $p_{\mathrm{sparsity}}$, $kl\text{\_}weight$, epochs E, batch size B, random seed. Initialize: Fix random seed; set $\epsilon ={10}^{-10}$; preprocess $X_{\mathrm{train}}$; define $kl\text{\_}range$. Output: Trained encoder/decoder, best hyperparameters, synthetic datasets $\tilde{X}$, and resource metrics. Process: For each $kl\text{\_}value\in kl\text{\_}range$: – Define Optuna objective: * Sample $\lambda ,\beta ,p_{\mathrm{sparsity}}$ from search space. * Build autoencoder ← create_autoencoder($d_{\mathrm{input}},d_{\mathrm{hidden}},\lambda ,\beta ,p_{\mathrm{sparsity}},kl\text{\_}value$). * Train model ← train(model, $X_{\mathrm{train}},E,B$). * Compute loss: $L_{\mathrm{Novel}}=L_{\mathrm{recon}}+L_{L2}+L_{\mathrm{sparsity}}+L_{KL}$. * Return $L_{\mathrm{Novel}}$ to Optuna. – Run Optuna for $N_{\mathrm{trials}}$ to minimize validation loss. – Select best parameters ← select_best_params(). – Retrain final model with best parameters. – Generate $\tilde{X}$ ← sample_synthetic_data(model, $N_{\mathrm{synthetic}}$). – Log resource usage ← compute_resource_usage().

2.3. Synthetic Data Evaluation

The evaluation of generated synthetic samples is crucial for assessing the effectiveness of the proposed GSRA-KL data augmentation model compared to GSRA and TVAE, thereby improving predictions for scenarios such as small and imbalanced radiomics-based gene mutations. In this study, the synthetic data quality is evaluated along two primary dimensions—resemblance and utility—based on methods adapted from [21], with specific modifications. Moreover, different parameters are computed for the computational cost analysis of the proposed algorithm. To evaluate consistency and significance of computational performance trends, non-parametric Friedman tests were applied across different hidden-layer sizes, followed by Spearman rank correlation analysis to quantify monotonic relationships between kl_weight and performance metrics such as reconstruction loss, runtime, and memory usage [28,29]. The t-SNE plots were also used to visually inspect the distributional pattern comparisons between real and synthetic radiomics datasets. All algorithms are implemented in Google Colab using Python 3, along with the necessary libraries and packages.

2.4. Resemblance-Dimension Evaluation

The resemblance-dimension score (RDS) measures the degree to which the synthetic data resembles the real radiomics dataset. It combines four levels of analysis:

2.4.1. Univariate Resemblance Analysis

Each radiomics feature in each Mutation from real and synthetic datasets is individually assessed using Student’s t-test (ST) to compare means, Mann–Whitney U-test (MW) to test distribution similarity, Kolmogorov–Smirnov test (KS) to compare feature distributions, and Wasserstein Distance (WD) to measure distributional similarity. Statistical tests are conducted using Python’s SciPy library. Suppose the p-value > 0.05, the null hypothesis (H0) is accepted. The higher similarity is interpreted as indicating better feature resemblance, as evidenced by higher KS and lower WD scores. IWD scores are inversely normalized (1-WD) for consistency. The Univariate Score (US) is calculated by assigning 40% weightage to the KS test as it is assessing distributional level comparison, while 20% each to ST, MW, and IWD. To evaluate the consistency and significance of resemblance-dimension trends across models and three hidden-layer sizes, non-parametric Friedman tests were employed to assess group-wise differences, followed by Spearman rank correlation analysis to quantify monotonic relationships between kl_weight and resemblance metrics [28,29].

2.4.2. Bivariate Effectiveness (BE)

Pearson correlation coefficients are compared between features across real and synthetic datasets. The similarity of the correlation matrices is assessed using the KS test, with higher p-values indicating greater similarity [23].

2.4.3. Multivariate Resemblance

The Maximum Mean Discrepancy (MMD) test measures the differences between the multivariate distributions of real and synthetic datasets [23]. Lower MMD scores indicate a closer resemblance. For consistency, IMMD uses an inverse MMD score (1-MMD).

2.4.4. Resemblance Score (RS)

The RS score is calculated by assigning a weight of 40% to the US score, while 30% each to BE and IMMD.

2.4.5. Data-Labeling Analysis (DLA)

Real and synthetic samples are combined and binary labelled to assess semantic feature preservation. Machine learning models are trained to distinguish between real and synthetic samples. The data-labeling score (DLS) was calculated based on evaluation metrics, including accuracy, AUC, precision, recall, and F1-score, all of which were equally weighted. Lower classification performance implies a higher semantic resemblance between real and synthetic data. Then, the inverse score (IDLS) was computed as 1-DLS for consistency and comparison with other scores in the resemblance dimension. The synthetic data generation model is considered excellent if its data-labeling score (DLS) is below 0.6, categorized as good for a score in the range of 0.6 to 0.8, and poor otherwise. The machine learning models and configurations used in data-labeling analysis include:

• Logistic Regression—Default;
• Decision Tree—random_state = 9;
• Random Forest—n_estimators = 100, random_state = 9;
• Support Vector Machine—C = 100, max_iter = 300, kernel = ’linear’, probability = True, random_state = 9;
• K-Nearest Neighbors—n_neighbors = 10;
• Multi-layer Perceptron—hidden_layer_sizes = (128, 64, 32), max_iter = 300, random_state = 9;
• Naive Bayes—Default (GaussianNB);
• Gaussian Process—Default;
• XGBoost—Default;
• LightGBM—Default.

2.4.6. Computation of Resemblance-Dimension Score (RDS)

The final RDS is computed with 60% weight assigned to the resemblance score (RS) and 40% to IDLS. The model is excellent if its RDS is above 0.45, categorized as good for a score of 0.4 to 0.45, and poor otherwise.

2.5. Utility-Dimension Evaluation

Utility evaluation assesses the synthetic dataset’s effectiveness in preserving predictive capability.

2.5.1. Evaluation Strategy

This study compares two strategies: Training on Real Data and Testing on Real Data (TRTR) versus Training on Synthetic Data and Testing on Real Data (TSTR). We implemented the same machine learning models used in the DLA for evaluating utility dimensions. The real radiomics dataset has a small sample size and is imbalanced, resulting in poor performance of the machine learning models. To address this issue, we balanced the real radiomics dataset by using high-quality synthetic data from GSRA-KL models that demonstrated stable and higher RDS scores. We compared the performance gap of the machine learning models between the imbalanced and balanced radiomics cohorts.

2.5.2. Training and Testing Protocol

Data splits: 80% of the real and synthetic datasets were used for training, and 20% of the real datasets were reserved for testing. Performance metrics (accuracy, AUC, precision, recall, and F1-score) were averaged across all models. Given the high dimensionality of radiomics features, we opted to apply Principal Component Analysis (PCA) before training, which accounted for 95% of the variance.

2.5.3. Utility Score Interpretation

A novel utility-dimension score (UDS) is defined and computed by assigning equal weight to the mean of all evaluation metrics across all TRTR and TSTR strategy models. The synthetic data-generation algorithm is termed excellent if its UDS is above 0.7, and it is categorized as good for a score in the range of 0.6 to 0.7, while it is poor otherwise. A comparative ROC-AUC plot is presented for imbalanced and balanced classes to demonstrate the effectiveness of synthetic radiomics data augmentation in addressing class imbalance while enhancing prediction accuracy.

In addition to evaluating resemblance and utility dimensions, visual inspection based on t-SNE plots of high-dimensional synthetic versus real radiomics datasets highlighted the comparison of distributional patterns. All metrics are calculated based on a wide range of kl_weight values and plotted for a thorough analysis. By integrating resemblance and utility-dimension evaluation along with t-SNE plots, our evaluation framework comprehensively assesses the fidelity and predictive usability of the synthetic radiomics data generated by GSRA-KL and other models, providing a strong foundation for clinical translation.

3. Results

The proposed study investigates the effectiveness of the GSRA-KL algorithm in generating synthetic radiomics datasets for the highly imbalanced EGFR gene mutation dataset (12 positive cases out of 83 total samples). We investigated the GSRA-KL algorithm to assess how manual tuning of the kl_weight hyperparameter influences the quality of generated synthetic datasets. To ensure a thorough analysis, we generated a total of 63 synthetic datasets, varying the hidden-layer sizes (input dimension * 0.5, input dimension * 1.0, and input dimension * 2.0) and systematically adjusting kl_weight across a defined range. The quality of each synthetic dataset was assessed through the resemblance- and utility-dimension metrics alongside visual validation using t-SNE plots. As per the findings in our previous study [26], computational cost challenges the optimization of GSRA-KL algorithms through PSO. Therefore, in the current study, we opted for Optuna-based Bayesian optimization to address this issue. For each kl_weight value-based training, the computational cost was calculated.

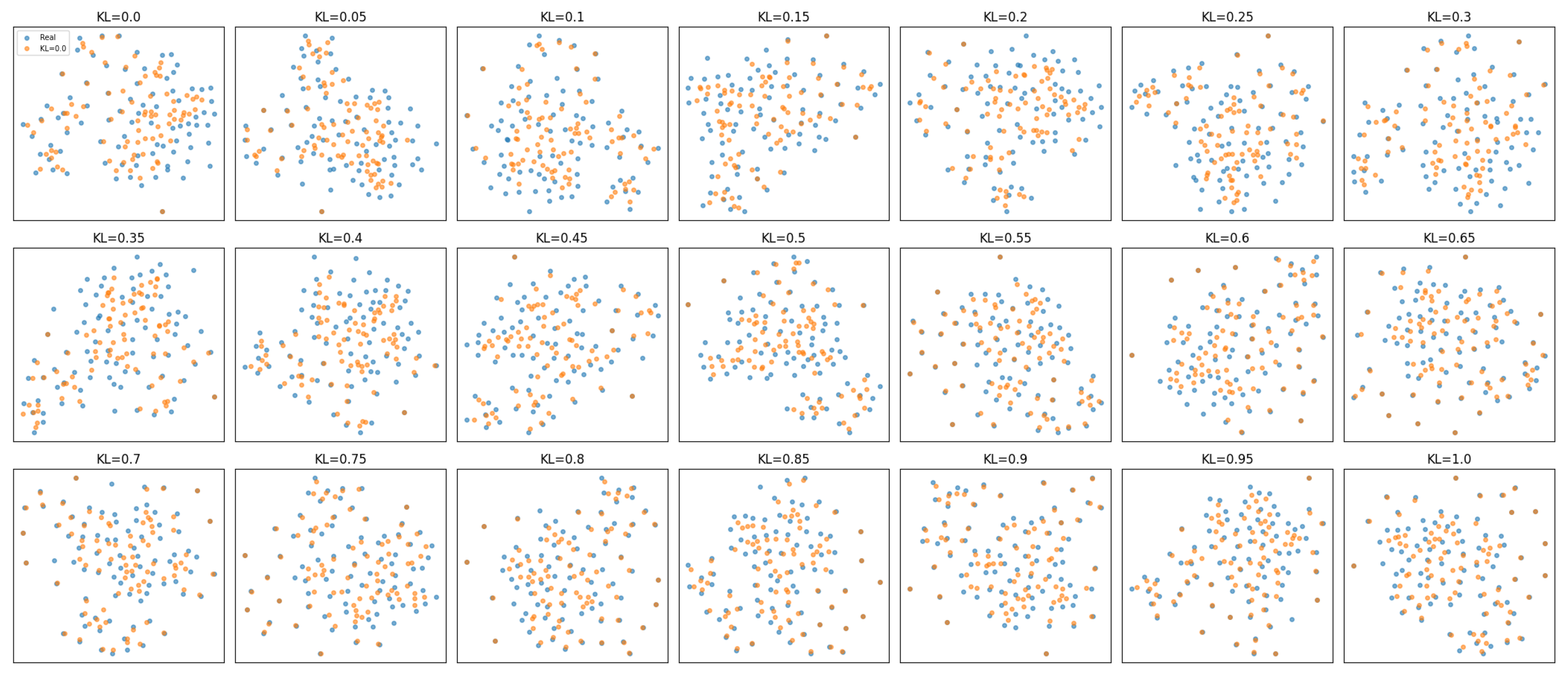
3.1. Resemblance-Dimension Evaluation

To evaluate the influence of KL divergence weighting on model behavior, a series of resemblance analyses were conducted across varying hidden-layer scaling factors (0.5*, 1.0*, 2.0*) (see

Table 1. Univariate analysis.

Algorithm	Similar Features				Metrics
	ST (↑)	MW (↑)	KS (↑)	ST (↑)	MW (↑)	KS (↑)	WD (↓)	IWD (↑)	US (↑)
kl_weight = 0.0
GSRA-KL*0.5	263	225	177	0.7302	0.4235	0.2918	0.0399	0.9601	0.5395
GSRA-KL*1	252	168	145	0.5157	0.2933	0.2422	0.0416	0.9584	0.4504
GSRA-KL*2	215	124	114	0.3742	0.2003	0.2048	0.0478	0.9526	0.3708
kl_weight = 1.0
GSRA-KL*0.5	263	251	229	0.7125	0.6144	0.4896	0.0294	0.9706	0.6553
GSRA-KL*1	246	201	188	0.5775	0.4634	0.4146	0.0304	0.9696	0.5837
GSRA-KL*2	232	171	143	0.4373	0.2739	0.2735	0.0356	0.9644	0.4445
TVAE	263	251	229	0.5942	0.5866	0.5248	0.0331	0.9699	0.6395

,

Table 2. Resemblance score (RS).

Algorithm	kl_weight	BE (↑)	MMD (↓)	IMMD (↑)	RS (↑)
GSRA-KL*0.5	0.0	0.1525	0.2746	0.7254	0.4792
GSRA-KL*1	0.0	0.1418	0.2622	0.7378	0.4440
GSRA-KL*2	0.0	0.1245	0.2507	0.7493	0.4105
GSRA-KL*0.5	1.0	0.1097	0.1995	0.8005	0.5352
GSRA-KL*1	1.0	0.0891	0.1829	0.8171	0.4990
GSRA-KL*2	1.0	0.0796	0.1750	0.8250	0.4492
TVAE	-	0.0730	0.1819	0.8181	0.5200

,

Table 3. Data-labeling analysis (DLA).

Algorithm	Accuracy (↓)	AUC (↓)	Precision (↓)	Recall (↓)	F1-Score (↓)	DLS (↓)	IDLS (↑)	Comments
kl_weight = 0.0
GSRA-KL*0.5	0.7026	0.7923	0.6495	0.9762	0.7601	0.77614	0.22386	Good
GSRA-KL*1	0.7320	0.8435	0.6915	0.9762	0.7859	0.80582	0.19418	Poor
GSRA-KL*2	0.7288	0.8425	0.6869	1.0000	0.7796	0.8028	0.1972	Poor
kl_weight = 1.0
GSRA-KL*0.5	0.6914	0.7679	0.6302	0.9500	0.7405	0.756	0.244	Good
GSRA-KL*1	0.6592	0.7016	0.5998	0.8955	0.7048	0.71218	0.28782	Good
GSRA-KL*2	0.6322	0.6900	0.5747	0.8336	0.6689	0.68008	0.31992	Good
TVAE	0.4235	0.5125	0.3758	0.6000	0.4604	0.47444	0.52556	Excellent

and

Table 4. Resemblance-dimension score (RDS).

Algorithm	KL Weight	RDS	Comments
GSRA-KL*0.5	0.0	0.3892	Poor
	1.0	0.4596	Excellent
GSRA-KL*1	0.0	0.3654	Poor
	1.0	0.4235	Good
GSRA-KL*2	0.0	0.3492	Poor
	1.0	0.2695	Poor
TVAE	–	0.5241	Excellent

). Figure 2 presents a four-panel summary illustrating the behavior of component resemblance metrics, aggregate resemblance scores, inverse data-labeling performance, and the final resemblance-dimension score (RDS) across the entire KL range.

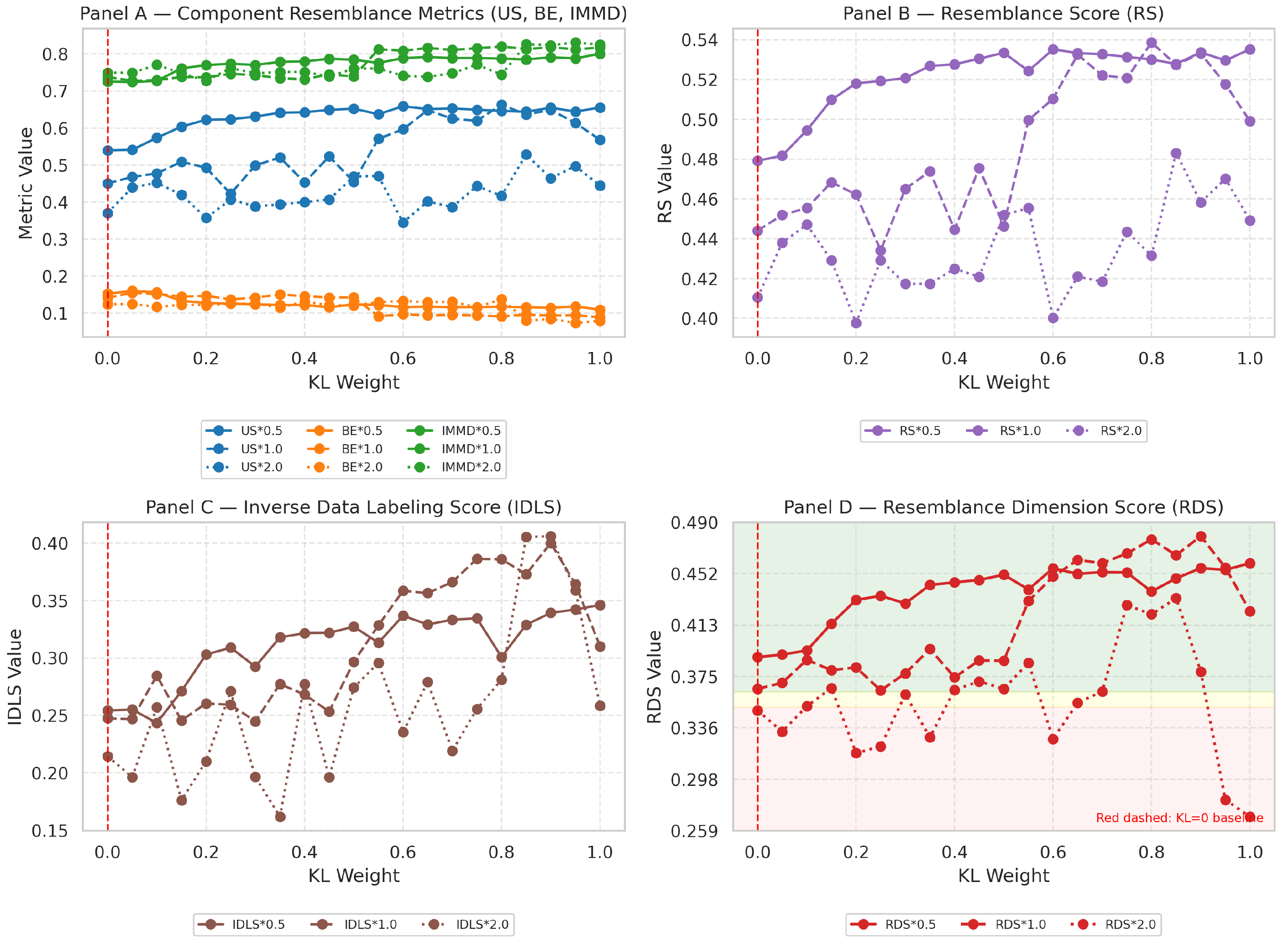
3.2. Panel A—Component-Level Metrics (US, BE, IMMD)

This subsection focuses on the individual resemblance components—Univariate Score (US), Bivariate Effectiveness (BE), and Inverse Maximum Mean Discrepancy (IMMD)—to characterize how feature-level resemblance varies with increasing KL weight and model scaling. Panel A shows that IMMD remained the most stable and consistently high metric across KL weights, while BE exhibited a minor decline and US displayed greater variability. Notably, IMMD increased slightly with higher KL values for the 1.0* and 2.0* hidden-layer size scalings, suggesting moderate regularization enhances latent structure consistency. The component resemblance metrics exhibit stable trends across the KL weight range, with IMMD and BE maintaining higher metric values (above 0.7 and 0.6, respectively), indicating consistent feature-wise resemblance between synthetic and real distributions. In contrast, US demonstrates moderate fluctuation, suggesting sensitivity to parameter scaling.

The quantitative results in Table 1 reveal that at kl_weight = 1.0, both GSRA and GSRA-KL attain higher Univariate Scores (US), particularly for the moderate hidden-layer size scaling (1.0*), with values approximating 0.58–0.65, comparable to the competitive baseline TVAE (0.64). The concurrent increase in IWD and decrease in WD across KL-scaled variants indicate improved feature alignment and reduced distributional divergence. These outcomes substantiate that moderate KL regularization enhances subcomponent-level resemblance and stabilizes the generative mapping without compromising feature diversity.

3.3. Panel B—Aggregate Resemblance Score (RS)

The overall resemblance behavior was evaluated using an aggregated resemblance score (RS) that integrates multiple component-level measures. Panel B shows a gradual upward trend of RS with increasing KL weight, indicating improved global similarity between synthetic and real datasets. The 1.0* scaling configuration yielded consistently higher RS values compared with smaller (0.5*) or larger (2.0*) networks, supporting its stability as a balanced architecture. The composite resemblance score (RS), which increases gradually with $kl\text{\_}weight$ and attains a relatively stable plateau for weights beyond 0.3, implying that moderate KL regularization promotes better alignment between the generated and real feature spaces.

As summarized in Table 2, the GSRA-KL framework achieves higher RS values at kl_weight = 1.0, particularly for the 0.5* and 1.0* configurations (0.53 and 0.50, respectively), which are comparable to the competitive baseline TVAE (0.52). The concurrent reduction in MMD and increase in IMMD with stronger KL regularization reflect improved global alignment between real and synthetic feature distributions. Overall, these results confirm that moderate regularization yields a favorable balance between resemblance strength and model generalization.

3.4. Panel C—Inverse Data-Labeling Score (IDLS)

To examine the separability of data between synthetic and real samples, the inverse data-labeling score (IDLS) was computed across the KL range. Panel C demonstrates that IDLS increases with KL weight for all scalings, implying increased model discriminability between synthetic and real data—an indicator of improved generative realism. Nevertheless, higher IDLS variability at the *2.0 scaling suggests that excessive network complexity introduces stochastic fluctuations. Panel C highlights the inverse data-labeling score (IDLS), showing an increasing trend with higher KL weights, which signifies improved separability and realism in synthetic samples. However, marginal fluctuations suggest possible over-regularization effects beyond $kl\text{\_}weight=0.8$.

As presented in Table 3, the IDLS exhibits a consistent increase with higher KL weighting, rising from approximately 0.22 at kl_weight = 0.0 to 0.32 at kl_weight = 1.0 for the GSRA-KL2 configuration, reflecting enhanced discriminability and realism in generated data. The moderate-scaled GSRA-KL1 achieves balanced performance, while the larger configuration introduces marginal instability, corroborating the observed variability trends. Comparatively, TVAE attains the highest IDLS (0.53), reaffirming its strong separability but with less control over feature-level regularization.

3.5. Panel D—Resemblance-Dimension Score (RDS) with Quality Bands

The RDS metric integrates multiple resemblance indicators into a single dimensionless scale, allowing for a straightforward interpretation of generative quality. Panel D shows that RDS gradually improves with higher KL weight and often transitions from moderate (yellow) to high-quality (green) zones. The *1.0 and *2.0 models exhibit consistent improvements beyond the baseline (KL = 0), confirming that moderate KL regularization promotes both representational compactness and sample fidelity. The RDS peaks at $kl\text{\_}weight=0.376$ with a value of $0.449$, representing an optimal balance between reconstruction fidelity and distributional regularization. Values below this peak indicate under-regularization, whereas higher KL weights lead to a gradual decline due to excessive penalization of the latent representation.

Collectively, these findings indicate that the GSRA–KL framework achieves its best generalization and resemblance balance at moderate KL weighting ($kl\text{\_}weight\approx 0.3$–$0.4$), beyond which performance saturates or slightly degrades.

As summarized in Table 4, the GSRA-KL variants demonstrate a clear improvement in RDS with increasing KL weight, where the *0.5 configuration attains the highest value (0.46) and transitions into the “Excellent” quality band. The *1.0 model follows closely with an RDS of 0.42, confirming stable resemblance performance under moderate regularization, while the *2.0 variant exhibits degradation due to over-penalization. Although TVAE achieves the highest overall RDS (0.52), the GSRA-KL models exhibit a more controlled and interpretable trade-off between compactness and fidelity.

Statistical Correlation Analysis

Spearman’s rank correlation analysis was conducted to assess the monotonic relationships among the performance metrics (US, IMMD, BE, RS, IDLS, and RDS) under varying scaling factors (0.5*, 1.0*, and 2.0*). The results are summarized in

Table 5. Spearman’s rank correlation analysis of performance metrics (US, IMMD, BE, RS, IDLS, and RDS) under three hidden-layer sizes (0.5*, 1.0*, and 2.0*). Bold values indicate statistically significant correlations ($p<0.05$).

Metric	Layer Size	Correlation ($\mathit{\rho }$)	p-Value
US	0.5*	0.819	5.50 × 10−6
	1.0*	0.794	1.77 × 10−5
	2.0*	0.431	0.051
IMMD	0.5*	0.899	3.14 × 10−8
	1.0*	0.855	8.16 × 10−7
	2.0*	0.394	0.078
BE	0.5*	–0.871	2.71 × 10−7
	1.0*	–0.809	8.96 × 10−6
	2.0*	–0.270	0.236
RS	0.5*	0.823	4.54 × 10−6
	1.0*	0.794	1.77 × 10−5
	2.0*	0.516	0.0167
IDLS	0.5*	0.865	4.21 × 10−7
	1.0*	0.831	3.06 × 10−6
	2.0*	0.662	0.00107
RDS	0.5*	0.878	1.70 × 10−7
	1.0*	0.823	4.54 × 10−6
	2.0*	0.219	0.339

.

Strong and statistically significant positive correlations were observed for most metrics at the 0.5* and 1.0* scales, indicating a stable monotonic association between these performance indicators and the underlying dataset configurations. Specifically, the US metric exhibited strong positive correlations at both 0.5* ($\rho$ = 0.819, p = 5.5 × 10⁻⁶) and 1.0* ($\rho$ = 0.794, p = 1.8 × 10⁻⁵), while the association weakened and became statistically non-significant at 2.0× (p > 0.05). Similarly, IMMD demonstrated high correlations at 0.5× ($\rho$ = 0.899, p = 3.1 × 10⁻⁸) and 1.0* ($\rho$ = 0.855, p = 8.2 × 10⁻⁷), but a reduced relationship at 2.0× ($\rho$ = 0.394, p = 0.078).

Comparable results were obtained for RS ($\rho$ = 0.823, p = 4.5 × 10⁻⁶ at 0.5×) and IDLS ($\rho$ = 0.865, p = 4.2 × 10⁻⁷ at 0.5*), confirming their consistent correlation across scaling levels up to 1.0*. However, at 2.0* scaling, the correlation strength notably decreased ($\rho$ = 0.516 for RS and $\rho$ = 0.662 for IDLS), indicating reduced robustness of metric associations at higher scaling factors.

In contrast, the BE metric exhibited a strong negative correlation at 0.5* ($\rho$ = –0.871, p = 2.7 × 10⁻⁷) and 1.0* ($\rho$ = –0.809, p = 8.9 × 10⁻⁶), suggesting that higher BE values inversely relate to performance stability. This relationship, however, diminished at 2.0* (p = 0.236).

Finally, the RDS metric also showed significant positive correlations at 0.5* ($\rho$ = 0.878, p = 1.7 × 10⁻⁷) and 1.0* ($\rho$ = 0.823, p = 4.5 × 10⁻⁶), but the association weakened at 2.0* (p = 0.339), reinforcing that moderate scaling (≤1.0×) maintains stronger inter-metric dependencies.

Overall, these findings indicate that the correlation among evaluation metrics remains robust and statistically significant up to 1.0* scaling, while further upscaling (2.0*) leads to attenuation in these relationships. This suggests that the optimal stability range for data scaling and metric consistency lies within the lower to intermediate scaling levels.

3.6. Computational Efficiency Analysis

Various essential parameters were computed during the GSRA-KL training and optimization process to effectively assess the impact of the kl_weight hyperparameter on the computational cost of the proposed algorithm. A representative set of optimal hyperparameters for kl_weight values (0.0, 1.0) is summarized in

Table 6. Optuna-based hyperparameter optimization (HiddenSize = Input*1.0).

Algorithm: GSRA-KL	Best Hyperparameters
	Sparsity Regularization	L2 Weight Regularization	Sparsity Proportion
kl_weight = 0.0	2.46 × 10−4	2.16 × 10−4	1.31 × 10−1
kl_weight = 1.0	1.28 × 10−3	1.01 × 10−4	1.05 × 10−1

. The GSRA-KL algorithm was evaluated across three hidden-layer configurations, with the KL divergence weight (kl_weight) systematically varied from 0.0 to 1.0 in increments of 0.05 to capture its influence on computational efficiency and model stability.

Table 7. Performance summary (mean ± SD) across hidden-layer size scaling factors. Bold indicates statistically significant Friedman test ($p<0.05$).

Metric	0.5*	1.0*	2.0*	p-Value
mse	0.007682 ± 0.000694	0.007452 ± 0.001735	0.007976 ± 0.001502	7.165 × 10−1
optimization_time	220.788208 ± 41.293179	237.399137 ± 58.739415	278.671245 ± 19.188771	4.115 × 10−2
training_time	11.237552 ± 3.404399	10.945072 ± 3.145071	12.941548 ± 1.542467	5.385 × 10−1
total_execution_time	232.026462 ± 43.408871	248.344791 ± 61.702421	291.613893 ± 20.362463	1.290 × 10−1
ram_usage_gb	3.251824 ± 1.181036	3.294094 ± 1.285505	4.207957 ± 1.640278	1.727 × 10−7
disk_usage_gb	29.107617 ± 0.003875	29.111608 ± 0.006725	29.121750 ± 0.012597	1.727 × 10−7

presents the aggregated performance metrics (mean ± SD) computed across all kl_weight levels for three scaling factors. While the table summarizes overall computational trends, the detailed analysis indicated that varying kl_weight (0–1.0) influenced both optimization stability and resource utilization. Specifically, increases in kl_weight were associated with gradual improvements in reconstruction loss (MSE) up to mid-range values, after which performance plateaued. In contrast, optimization and total execution times exhibited more pronounced variability, consistent with the statistically significant Friedman test results ($p<0.05$) observed for these metrics. Furthermore, both RAM and disk utilization increased significantly with higher KL-weight scaling, reflecting the additional computational overhead introduced by stronger regularization constraints in the GSRA-KL optimization process. Overall, these findings suggest that moderate kl_weight values achieve a balanced trade-off between computational cost and model stability, making them more suitable for efficient GSRA-KL training.

Computational Efficiency—Spearman Analysis: 

Table 8. Spearman correlation analysis of computational performance metrics across scaling factors.

Metric	Layer Size	Correlation ($\mathit{\rho }$)	p-Value
MSE	0.5*	−0.784	2.56 × 10−5
	1.0*	−0.743	1.15 × 10−4
	2.0*	−0.332	0.141
Optimization Time	0.5*	0.823	4.54 × 10−6
	1.0*	0.722	2.19 × 10−4
	2.0*	−0.705	3.56 × 10−4
Training Time	0.5*	0.745	1.05 × 10−4
	1.0*	0.649	1.45 × 10−3
	2.0*	−0.471	0.0310
Total Execution Time	0.5*	0.842	1.74 × 10−6
	1.0*	0.701	3.97 × 10−4
	2.0*	−0.690	5.43 × 10−4
RAM Usage (GB)	0.5*	0.500	0.0210
	1.0*	0.312	0.169
	2.0*	0.421	0.0575
Disk Usage (GB)	0.5*	0.357	0.112
	1.0*	0.217	0.345
	2.0*	0.392	0.0787

summarizes the Spearman’s rank correlations between the kl_weight parameter and key computational performance metrics across different hidden-layer scaling factors. Strong negative correlations were observed between kl_weight and MSE for 0.5* and 1.0* layers ($\rho$ = –0.78 and –0.74, $p<0.001$), indicating improved reconstruction quality with moderate KL divergence penalization. In contrast, optimization and total execution times showed a strong positive correlation at more minor scales ($p<0.01$) that reversed at 2.0, suggesting an increased computational burden with deeper layers. RAM and disk usage exhibited weak to moderate associations, implying that memory and storage demands remained relatively stable across configurations.

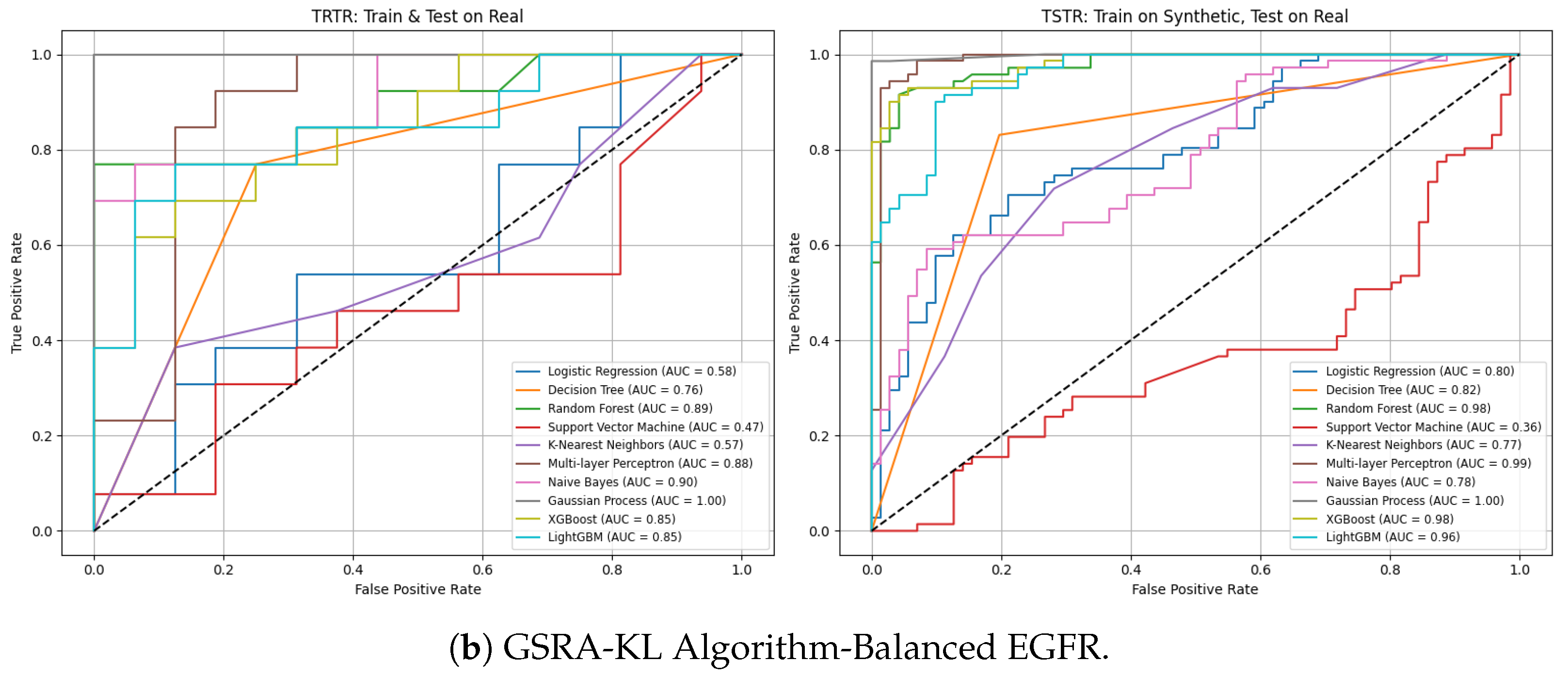
3.7. Utility-Dimension Evaluation

To evaluate the effectiveness of synthetic data generation, the utility-dimension was assessed using six performance metrics: accuracy, AUC, precision, recall, and F1-score, each contributing equally (20%) to the utility-dimension score (UDS) (see

Table 9. Utility-dimension analysis (GSRA-KL (HiddenSize-input*0.5 with kl_weight = 1.0)).

Overall Means of Testing Metrics with Standard Deviation (SD)
Dataset with Imbalanced Class Distribution					Dataset with Balanced Class Distribution
Strategy	Accuracy	AUC	Precision	Recall	F1-Score	Accuracy	AUC	Precision	Recall	F1-Score
Real Radiomics Dataset
TRTR	0.8000	0.4700	0.0250	0.0500	0.0333	0.6621	0.7750	0.6120	0.8077	0.6884
SD	0.1182	0.1638	0.0750	0.1500	0.1000	0.1270	0.1667	0.1171	0.0988	0.0873
GSRA-KL based Synthetic Radiomics Dataset
TSTR	0.8434	0.7437	0.4987	0.4250	0.4233	0.7958	0.8426	0.7934	0.8296	0.8075
SD	0.0733	0.1706	0.2918	0.2341	0.2119	0.1354	0.1833	0.1527	0.1024	0.1201
TVAE based Synthetic Radiomics Dataset
TSTR	0.7867	0.8863	0.4060	0.9083	0.5585	0.7789	0.8488	0.7524	0.8451	0.7928
SD	0.0598	0.0578	0.0734	0.0870	0.0818	0.0687	0.0707	0.0742	0.0854	0.0611

and

Table 10. Utility-dimension score (UDS).

Dataset with Imbalanced Class Distribution				Dataset with Balanced Class Distribution
Algorithm	Strategy	UDS	Comments	Strategy	UDS	Comments
EGFR Mutation
-	TRTR	0.2757	Poor	TRTR	0.7090	Excellent
GSRA-KL	TSTR	0.5868	Poor	TSTR	0.8138	Excellent
TVAE	TSTR	0.7092	Excellent	TSTR	0.8036	Excellent

). The EGFR mutation cohort was considered under imbalanced and balanced class distributions. Additionally, a ROC-AUC plot (see Figure 3) is generated for visual comparison, enhancing the understanding of model performance under both mutation conditions.

As shown in Table 9, the GSRA–KL model demonstrated consistently higher mean accuracy and AUC compared to the real data baseline under both class distributions, indicating the robustness of synthetic feature representations. For the imbalanced setting, the GSRA–KL model achieved a noticeable improvement in AUC (0.7437) relative to the real dataset (0.4700), suggesting that synthetic augmentation effectively mitigates class imbalance effects. Under balanced conditions, both GSRA–KL and TVAE maintained competitive results across all metrics, with F1-scores exceeding 0.80, reflecting strong generalization and stability across training–testing scenarios. These quantitative outcomes emphasize the practical viability of synthetic radiomics data for enhancing model reliability and downstream predictive performance.

TRTR Versus TSTR Strategy

• Under an imbalanced class distribution, TRTR performance was notably poor, with a UDS of 0.2757.
• In contrast, balanced distribution significantly improved performance to an excellent UDS of 0.7090.
• Under imbalanced data, GSRA-KL resulted in a UDS of 0.5868 (poor), while TVAE achieved 0.7092 (excellent).
• Under balanced data, GSRA-KL and TVAE delivered excellent UDS values of 0.8138 and 0.8036, respectively.

For visually inspecting high-dimensional synthetic radiomics datasets and identifying distributional patterns similar to those in real data, t-SNE plots are drawn for each kl_weight-based synthetic dataset. In this case, the hidden-layer size of the GSRA-KL algorithm is set to match the input dimension, with no compression applied at the code layer (see Figure 3a,b). It is observed that the preservation of distributional patterns improves with the application of KL weight regularization.

4. Discussion

This section provides a comprehensive discussion of the experimental findings, integrating resemblance trends, computational cost analysis, and the practical utility of the proposed GSRA–KL framework. It interprets the observed correlations and statistical patterns in the context of computational efficiency and generative performance. By synthesizing quantitative resemblance metrics with runtime and resource utilization analyses, this section identifies trade-offs between generative fidelity, scalability, and utility, ensuring a balanced evaluation of the framework’s methodological and practical implications.

4.1. Statistical Analysis—Resemblance Dimension

The correlation analysis of the trends depicted in Figure 2 confirms a generally monotonic relationship between KL weight and resemblance metrics, supporting the utility of controlled KL regularization in improving generative efficiency. The Spearman coefficients ($\rho$) between KL weight and key resemblance metrics are summarized in

Table 11. Spearman correlation coefficients ($\rho$) between KL weight and resemblance metrics across three scaling configurations.

Metric	Scale 0.5*	Scale 1.0*	Scale 2.0*
IMMD	0.90	0.85	0.39
US	0.82	0.79	0.43
BE	–0.87	–0.81	–0.27
RS	0.82	0.79	–
IDLS	0.86	0.66	–
RDS	0.88	0.82	–

. Positive correlations for IMMD, US, RS, IDLS, and RDS indicate consistent enhancement of resemblance with increasing regularization, while BE exhibits an inverse dependence, decreasing as resemblance improves.

While these upward trends are statistically meaningful, the absolute magnitudes of change are relatively modest. Oscillatory patterns, particularly at higher network complexities (*2.0 scaling), likely reflect stochastic optimization variability rather than deterministic KL effects. Moreover, aggregating component-level metrics (US, BE, IMMD) into composite indices such as RDS may obscure nuanced trade-offs between feature resemblance and latent-space alignment. Therefore, both granular and composite analyses are crucial for an accurate assessment of model behavior.

Overall, moderate KL regularization (KL ≈ 0.5–1.0) yields the most stable and consistent balance between feature-level resemblance and latent distribution stability. These findings empirically justify the KL-weight configurations adopted in subsequent GSRA–KL experiments, achieving a favorable trade-off between generative fidelity and computational efficiency.

4.2. Computational Cost Efficiency

The results in Table 7, averaged across all kl_weight levels and scaling factors, reveal that while reconstruction accuracy (MSE) remains largely consistent, computational demands vary with model complexity. Optimization and total execution times increase with larger hidden-layer configurations, reflecting higher parameterization and resource consumption. The significant Friedman test results ($p<0.05$) for optimization time, RAM usage, and disk usage highlight these as key contributors to computational cost. Nonetheless, the moderate increases in memory and storage requirements demonstrate that GSRA–KL retains practical efficiency and scalability even at higher complexities.

The correlation analysis in Table 8 further indicates that moderate kl_weight values improve reconstruction efficiency without markedly increasing computational load. At higher complexities (2.0* layers), correlations between time-based metrics and KL weight reverse direction, suggesting diminishing returns beyond optimal regularization. The weak associations for RAM and disk usage imply that GSRA–KL’s resource utilization remains efficient and well-optimized under varying KL strengths, underscoring its suitability for large-scale radiomics applications.

Moreover, the adoption of Optuna-based hyperparameter optimization markedly enhances computational efficiency relative to the PSO-driven approach in the prior study. As summarized in

Table 12. Optuna-based computational cost optimization.

Algorithm	PSO-Based Previous Study [26]			Optuna-Based Current Study
	RAM (GB)	Disk (GB)	Time (s)	RAM (GB)	Disk (GB)	Time (s)
GSRA-KL ($kl\text{\_}weight=0.0$)	2.70	32.60	1729	1.45	29.10	168.59
GSRA-KL ($kl\text{\_}weight=1.0$)	3.60	36.60	2731	2.83	29.11	278.14
Retraining time (s) with best hyperparameters
GSRA-KL ($kl\text{\_}weight=0.0$)	–	–	15.63	–	–	7.59
GSRA-KL ($kl\text{\_}weight=1.0$)	–	–	6.79	–	–	12.09

, the Optuna implementation reduces memory usage by up to 46%, disk utilization by 11–20%, and optimization time by approximately 90%, without compromising reconstruction quality. This demonstrates the advantage of adaptive, sample-efficient search algorithms in accelerating model convergence and resource performance.

4.3. Utility-Dimension Analysis

The utility-dimension evaluation employed six performance metrics—accuracy, AUC, precision, recall, and F1-score—each contributing equally (20%) to the overall utility-dimension score (UDS), with comparisons made across imbalanced and balanced EGFR mutation datasets (see Table 9 and Table 10). A ROC-AUC plot (Figure 3) complements this quantitative analysis to visualize classifier performance under both conditions.

The results in Table 9 reveal distinct performance patterns between GSRA–KL, TVAE, and real radiomics data. Under imbalanced conditions, GSRA–KL improved the AUC from 0.47 (real) to 0.74 and the F1-score from 0.03 to 0.42, indicating a substantial gain in model discrimination and overall utility. TVAE further enhanced AUC to 0.89 and F1-score to 0.56, though with a noticeable precision–recall imbalance (0.41 vs. 0.91), suggesting over-sensitivity to minority classes. In contrast, under balanced distributions, both GSRA–KL and TVAE achieved high and stable performance (AUC ≈ 0.84–0.85, F1 ≈ 0.80), with GSRA–KL showing slightly better accuracy (0.80 vs. 0.78) and metric consistency across folds. These findings highlight that GSRA–KL yields a more uniform performance profile, excelling in balanced datasets, whereas TVAE exhibits marginally higher recall but less balanced precision under class imbalance.

The findings in the utility-dimension evaluation (Table 10, Figure 3) underscore the importance of data balance in determining the predictive performance of real and synthetic datasets. Under imbalanced conditions, models employing the TRTR strategy exhibit poor utility (e.g., EGFR UDS = 0.2757), indicating that structural imbalance adversely affects classifier generalization. Conversely, under balanced conditions, GSRA–KL consistently achieves excellent UDS scores, outperforming TVAE in EGFR mutation prediction (0.8138 vs. 0.8036). This performance gain demonstrates the effectiveness of KL-regularized augmentation and adaptive hyperparameter optimization in improving synthetic data utility.

Interestingly, TVAE performs slightly better under imbalanced data (0.7092 vs. 0.5868), implying that GSRA–KL is more sensitive to imbalance but excels once balance is restored. The t-SNE visualizations (Figure 4) further support this trend, revealing tighter real–synthetic overlap as kl_weight tuning progresses. Overall, these results affirm that the GSRA–KL framework enhances synthetic radiomics fidelity and practical utility, particularly in balanced datasets used for clinically relevant classification tasks such as EGFR mutation prediction.

Taken together, the resemblance, computational, and utility analyses establish the GSRA–KL framework as a stable and scalable generative strategy for synthetic radiomics augmentation. The observed improvements in resemblance metrics and classification performance, coupled with significant gains in computational efficiency, indicate that the proposed model effectively balances fidelity and practicality. Nevertheless, certain dependencies on dataset composition and regularization sensitivity warrant further investigation, which are discussed in the following subsection on future research directions.

4.4. Observations and Future Research Direction

The present study primarily aimed to overcome the challenges of small-sample radiomics datasets and the inherent imbalance in EGFR mutation status by proposing the GSRA–KL framework with a scalable hyperparameter (kl_weight). Some aspects need further investigation while incorporating larger radiomics datasets from multiple modalities and institutions. These aspects need elaboration to strengthen the study’s rigor and highlight directions for future validation, as outlined below:

• Mitigation of Sample Scarcity and Class Imbalance: Although the dataset comprised only 83 patients with 12 EGFR-positive cases, the proposed GSRA–KL framework was specifically designed to address the challenges of sample scarcity and class imbalance. The scalable kl_weight hyperparameter was systematically varied over 21 values ($0:0.05:1.0$). Each configuration was evaluated under three distinct hidden-layer sizes—equal to half of and double the input dimensionality—resulting in a total of 63 synthetic datasets derived from the limited CT radiomics cohort. This extensive experimentation enabled the framework to learn stable latent representations across diverse network complexities and varying strengths of KL-regularization. The generated datasets were comprehensively validated using resemblance metrics, the proposed utility-dimension score (UDS), and t-SNE visualizations to ensure distributional fidelity. These results demonstrate that GSRA–KL effectively mitigates small-sample constraints while maintaining statistical and predictive consistency. Nonetheless, validation on larger, multi-institutional datasets remains an important direction for confirming generalizability and clinical translation.
• Categorization of RDS Metrics: The RDS thresholds (excellent $>0.45$; good $0.40$–$0.45$; poor $<0.40$) were empirically determined based on our experiments and adaptations from previous studies [21,26]. While these ranges reflect the quality of synthetic datasets in the context of small, imbalanced EGFR mutation cohorts, they have not yet been established as universal clinical or technical benchmarks and require further investigation on multiple modalities and disease radiomics datasets.
• Baseline Comparison and Rationale: While this study primarily compares GSRA-KL with GSRA and TVAE, we acknowledge the relevance of other widely used generative and augmentation methods such as GANs, CTGAN, and SMOTE. The current selection was guided by methodological proximity, as both GSRA and TVAE can be used for radiomics feature synthesis and share architectural similarities with GSRA-KL. In contrast, GAN- and SMOTE-based models are generally optimized for lower-dimensional or class-imbalanced tabular datasets, and are less suited to the complex, high-dimensional correlations characteristic of radiomics features (263 in this study). Moreover, GAN-based models are known to exhibit instability during training and suffer from mode collapse, particularly when applied to limited or highly correlated feature spaces, leading to reduced diversity and fidelity in the generated data [30,31,32]. For these reasons, their full-scale inclusion was beyond the scope of this work. Nonetheless, both GAN and CTGAN (as representative tabular synthesis models) will be considered in future research to contrast further their performance and suitability for generating high-dimensional radiomics features.
• Training Instability: The proposed GSRA-KL framework establishes a pipeline for effective synthetic radiomics data generation, emphasizing that parameter and hyperparameter selection remain subjective and dataset-dependent. The current study proposes an evaluation framework for generating effective and high-quality synthetic dataset generation strategies, as well as for selecting viable techniques, as outlined in the current work. Although results show unstable performance at higher KL weights (especially for hidden size $*2.0$), future work will explore stability enhancements through additional regularization (e.g., dropout tuning, early stopping) and cross-validation across multiple random seeds to improve the robustness and reproducibility of GSRA-KL training, as similar techniques have been shown to mitigate mode collapse and training variance in generative models [30,32]. Furthermore, future research will focus on formalizing this process by integrating adaptive and Bayesian optimization techniques [33,34] to automatically identify stable and optimal configurations for diverse radiomics datasets.
• Evaluation Metric Validation: While the proposed utility-dimension score (UDS) demonstrates promising results in evaluating the practical utility of synthetic data within this study, its validation remains confined to the datasets and models explored herein. To enhance its credibility and general applicability, future studies should extend UDS evaluation to diverse datasets and compare it against established measures such as FID, MMD, and discriminability indices. Such comparative analyses across various generative frameworks would provide deeper insight into the robustness and generalizability of UDS as a reliable metric for synthetic data assessment.
• Clinical Utility and Data Imbalance: In utility-dimension analysis, the UDS under imbalanced EGFR mutation data (UDS = 0.2757) appears poor. However, this result actually highlights the critical importance of balancing strategies, such as those implemented within the GSRA–KL framework. When the same data were balanced, UDS markedly improved to 0.7090 (excellent), demonstrating the framework’s capacity to enhance predictive performance once class imbalance is mitigated. This transition from poor to excellent UDS supports GSRA–KL’s intended role as a data-level augmentation approach rather than a classifier itself. Furthermore, future work will integrate GSRA–KL–generated balanced datasets into clinically relevant endpoints (e.g., treatment response and survival prediction), thereby extending its validation beyond TRTR and TSTR strategies and toward real-world clinical translation.
• Runtime Comparison and Optimization Environment: The reported 90% reduction in optimization runtime when employing Optuna compared to the PSO-based implementation was obtained under identical Google Colab computational settings using the same dataset, preprocessing pipeline, and GSRA-KL architecture. Both approaches optimized equivalent hyperparameters (e.g., $L_2$ penalty weight, sparsity weight, and sparsity target) with the same validation loss objective. The observed difference primarily reflects algorithmic design rather than hardware bias: the PSO implementation in pyswarm executes particle evaluations sequentially without adaptive stopping, whereas Optuna’s Tree-structured Parzen Estimator (TPE) sampler performs adaptive and asynchronous trial evaluation, enabling faster convergence within the same search space. While every effort was made to maintain consistent runtime conditions, minor variations in TPU/CPU scheduling inherent to the Colab environment may introduce marginal timing differences. Nonetheless, the comparative efficiency observed for Optuna is attributed to its inherently more scalable and sample-efficient search strategy. Future work will extend this analysis by performing fully normalized benchmarking across optimization algorithms and compute backends further to validate the fairness and reproducibility of runtime comparisons.

5. Conclusions

This study extended the GSRA-KL framework to improve synthetic radiomics generation for small and imbalanced EGFR mutation datasets. The enhanced version introduces a tunable kl_weight hyperparameter within the GSRA loss function to adaptively balance sparsity and reconstruction fidelity, coupled with an Optuna-based Bayesian optimization scheme that substantially reduces computational cost compared to the earlier PSO-based approach. A comprehensive evaluation encompassing 63 synthetic datasets was conducted using resemblance-dimension score (RDS), the proposed utility-dimension score (UDS), and t-SNE visualizations to assess both feature-level fidelity and predictive utility.

Experimental findings show that GSRA-KL attains excellent RDS scores (up to 0.4596) and competitive UDS performance—0.7090 under balanced and 0.5868 under imbalanced conditions—compared to TVAE (0.8036 and 0.7092, respectively). These results indicate that GSRA-KL preserves data resemblance effectively and performs comparably to existing generative baselines, though TVAE demonstrates relatively higher robustness in highly imbalanced settings. The ablation analysis confirms that setting kl_weight=0.0 reverts GSRA-KL to the baseline GSRA model, allowing for the isolation of the KL regularization effect on model stability and generalization. Optimal hyperparameter tuning remains dataset-dependent, underscoring the need for adaptive search to strike a balance between fidelity and utility.

From a computational standpoint, Optuna-based optimization reduced runtime from 1729 s to 168.6 s and RAM usage from 2.7 GB to 1.45 GB, demonstrating marked efficiency gains without compromising reconstruction stability. Statistical validation using Friedman and Spearman correlation tests further confirmed significant performance trends across three hidden-layer sizes, reinforcing the robustness of the computational analysis. Despite these practical advantages, we recognize that GSRA-KL represents an incremental, though meaningful, advancement rather than a fundamentally novel architecture.

In summary, GSRA-KL provides a tunable and computationally efficient framework for radiomics data augmentation, capable of generating high-fidelity synthetic datasets that support mutation prediction and model generalization under limited data conditions. Future work will extend this framework to other disease domains, explore integration of domain-aware priors, and investigate federated or privacy-preserving deployment for collaborative radiomics research.