Abstract
This article examines the role of fairness in software across diverse application contexts, with a particular emphasis on healthcare, and introduces the concept of algorithmic (individual) meta-fairness. We argue that attaining a high degree of fairness—under any interpretation of its meaning—necessitates higher-level consideration. We analyze the factors that may guide the choice of a fairness definition or bias metric depending on the context, and we propose a framework that additionally highlights quality criteria such as accountability, accuracy, and explainability, as these play a crucial role from the perspective of individual fairness. A detailed analysis of requirements and applications in healthcare forms the basis for the development of this framework. The framework is illustrated through two examples: (i) a specific application to a predictive model for reliable lower bounds of BRCA1/2 mutation probabilities using Dempster–Shafer theory, and (ii) a more conceptual application to digital, feature-oriented healthcare twins, with the focus on bias in communication and collaboration. Throughout the article, we present a curated selection of the relevant literature at the intersection of ethics, medicine, and modern digital society.
Keywords:
fairness; bias; meta-fairness; risk prediction; healthcare; digital twins; quality criteria 1. Introduction
Fairness in software is an interdisciplinary and rapidly evolving field with far-reaching implications across many domains of modern life, including law (e.g., assessing the risk of criminal re-offence), finance (evaluating creditworthiness), engineering (autonomous driving decisions), medicine (predicting cancer risk), and even social media (mitigating filter bubbles). There are many definitions of algorithmic fairness, some of which can be shown to be contradictory [1,2], particularly when established ethical principles or standards of social responsibility are in conflict. In non-polar prediction settings, where the interests of individuals and decision-makers coincide (as in many medical applications), fairness may be interpreted as the absence of bias.
When algorithmic fairness is considered, the primary focus is on evaluating the decisions, assignments, or allocations generated by an algorithm or model in a broad sense. In practice, fairness is rarely the sole consideration; other quality criteria such as accuracy, efficiency, or usability are also assumed or explicitly required from the algorithm. A well-designed fairness metric must therefore reflect these performance aspects, while remaining sensitive to the specific context and the viewpoints of relevant stakeholders. Additionally, contradictions between different fairness metrics lead to the question of what fairness understanding is fair. This question cannot be answered without considering the situation and its context [3].
To address these demands and potential conflicts among existing fairness definitions, we propose a meta-level approach, which we term meta-fairness (MF). Meta-fairness should provide a principled and explainable framework for selecting or combining fairness metrics based on the social and application context, prevailing conceptions of justice, and the utilities of both decision-makers and decision recipients. The foundation for this definition is given by an extensive literature overview of the subject of fairness from [4].
One of the first mentions of the term in the context of algorithms appears in the 2004 paper by Naeve-Steinweg [5]. From a game-theoretic perspective, she highlighted the need to address how agents should be treated when they disagreed on what constituted a fair solution, introducing the demand for “a new kind of properties” capturing “meta-fairness and meta-equity.” In the same year, Hyman [6] explored parallel challenges in mediation, asking, first, how parties and mediators addressed their own sense of justice and fairness; and second, whether and why mediators brought such notions into the process. He stated that “no meta-ethics tells mediators which measures of fairness are appropriate;” “they must choose.” The task of MF is to support this choice.
Recently, the concept of MF has gained increased attention in the literature, with studies such as [7,8] and others exploring its implications. This paper provides a comprehensive review of existing methodologies that, although employing different vocabulary, aim to achieve the goals we understand as the task of MF. Note that the majority of publications do not explicitly use the term ‘meta-fairness’, highlighting the need for a unified terminology and understanding of this concept.
In this paper, we propose a definition of (individual) MF designed to serve as a guiding principle for achieving fairness, even when potential conflicts between criteria arise. Drawing on a literature review on meta-fairness, our goal is to integrate existing approaches into a more comprehensive perspective rather than introducing yet another framework tailored to a specific case. Furthermore, our approach allows for the combination of not only different fairness metrics but also additional quality criteria (e.g., explainability) depending on the application context. We employ a score-based questionnaire system and the Dempster-Shafer theory (DST) [9,10] for this combination.
The MF definition, including its contextual component, is intentionally broad to accommodate diverse application domains and levels of decision-making risk. Its general components, collectively organized under the MF framework, are illustrated here using healthcare as a concrete example. While the framework itself is broadly applicable, the specific questionnaires presented are primarily tailored to healthcare, particularly medical risk assessment tools. We illustrate the application of the framework using a case study on predicting mutation probabilities in the BRCA1/2 tumor-suppressor genes for a low level of decision-making risk, focusing on the challenge of ensuring correct and fair assignment of patients to the low-risk class. An example of applying the MF framework in a broader, conceptual context is its use for digital twins (DTs) in healthcare, where we propose applying meta-fairness to overarching DT principles, allowing fairness and bias to be quantified across each DT category.
The paper is structured as follows. Section 2 reviews related work on the transition from fairness to MF, highlighting that the pursuit of fairness under any interpretation ultimately calls for higher-level reasoning. This part also introduces a working definition of MF that serves as the basis for our analysis. Section 3 provides an outline of the methods used and details the proposed MF framework, including possible questionnaires and DST employment. The concepts are then illustrated through the two mentioned applications, including discussion, in Section 4. The paper concludes with a summary and perspectives for future work.
Note that our intention, as in [7], is to make the MF approach as broadly applicable as possible. Initially, it is independent of any specific application domain and can be employed in finance, healthcare, or other areas, accommodating both polar and non-polar decision settings. Only in Section 3.3, which discusses specific questionnaires, is the approach directly linked to healthcare; even there, several questions and bias lists are applicable beyond this domain. Section 3.4 can again be interpreted in a general context. Section 4.1 illustrates the application of MF to a specific model, while Section 4.2 explores its application to another concept (DT), further highlighting the generality of the proposed approach.
2. Related Work: From Fairness to Meta-Fairness in Medical Risk Assessment
This section aims to demonstrate the need for a meta-level analysis in order to achieve greater flexibility and better results in the application of fairness principles and metrics. We begin by examining how fairness is commonly understood, with the focus on risk prediction, highlighting that authors who seek to achieve a high degree of fairness often implicitly adopt a higher-level perspective. In Section 2.1, we motivate the necessity to consider the concept of MF by analyzing publications that address the questions of what fairness is and which definition of fairness can itself be considered fair, under what conditions, and depending on which factors. A possible definition of MF is introduced in Section 2.2. Section 2.3 then provides a literature overview of works that propose frameworks aligning with our idea of MF (frequently without explicitly using the term). Finally, an overview of software and benchmarks for assessing algorithmic fairness is given in Section 2.4. In Table 1 at the end of this section, the papers reviewed here are categorized according to their topic, and our MF proposal is positioned in relation to them.
2.1. Fairness and Beyond: A Short Analysis
In general language terms, fairness is understood as the quality of being just, impartial, and equitable. It represents a desired property of decisions, typically defined with respect to a chosen ethical and/or statistical standard. In society, fairness ideally serves as a normative principle governing the distribution of resources, opportunities, and treatment. In the context of algorithms, it refers to ensuring that software-based decisions or predictions do not unjustly disadvantage individuals or groups. Fairness is closely related to bias, which can be broadly defined as a systematic deviation, preference, or prejudice that skews results, judgments, or processes. Russo and Vidal [11], who attempt an ontological, formal description and documentation of biases, identify three general bias categories: human, systemic, and statistical. Bias is a cause of unfairness, but the elimination of bias alone does not always guarantee fairness [12].
2.1.1. Algorithmic Bias
The fairness of non-polar predictions is frequently reduced to the simplified notion of the absence of bias. Algorithmic bias occurs when software discriminates against specific groups of individuals due to flaws in its model design, data, or statistical sampling methods, as well as issues with user-software interaction [1,11,13,14], resulting in invalid outcomes for these groups. (This definition corresponds to the category of statistical bias from [11]. We touch upon human and systemic ones in Section 3.3). In particular, Paulus and Kent [1] point out four most prominent sources of bias: due to outcome variables having different meanings across groups (label bias), group differences in the meaning of group variables (feature bias), absence of data impacting a certain group (differential missingness), and models tailored to the majority group (sampling bias). Anderson and Visweswaran [13] provide more examples of bias for each of its main causes mentioned above. Preventing algorithmic bias is often a more tractable goal than ensuring fairness, as the quality of predictions, decisions, or classifications from software can be assessed separately for each subgroup.
Further notable publications on bias are [15,16,17]. Zliobaite [15] provides a systematic review of existing discrimination measures, clarifying the conceptual distinctions between different fairness metrics and evaluating their suitability for algorithmic decision-making. The study focuses primarily on conceptual analysis and taxonomy rather than empirical testing. Arnold et al. [16] propose a quantitative approach to measuring racial discrimination through deviations from fairness criteria such as equality of opportunity and sufficiency. Their contribution lies in formalizing a method that connects fairness theory to empirical assessment, though it is tied to specific fairness metrics. Mosley and Wenman [17] take an even more applied perspective, using a publicly available French vehicle insurance dataset to demonstrate a price-based linear model for assessing and mitigating bias in predictive systems. While their work illustrates how fairness metrics can inform practical model adjustments, its conclusions are constrained by the specific characteristics of the dataset and domain.
2.1.2. Group and Individual Fairness
Contemporary researchers distinguish between group fairness and individual fairness, cf. Figure 1 in green. Group fairness is typically defined as a variation on the concept of parity between groups that differ in a so-called sensitive (or protected) attribute (SA). Parity is a simple way to check if an algorithm is fair by ensuring that its evaluation metrics do not depend on a specific group. However, this measure is static and can be unsuitable, for example, if base rates truly differ across the groups [2] or if populations change with time [18,19]. Passing a parity test does not guarantee fairness, but it can help to broadly identify potential biases in software for groups, although they may still conflict in the context of the chosen definition of fairness [1]. Well-established group fairness metrics, such as equal opportunity (parity in true positive rates), among others, are derived from the corresponding confusion matrix.
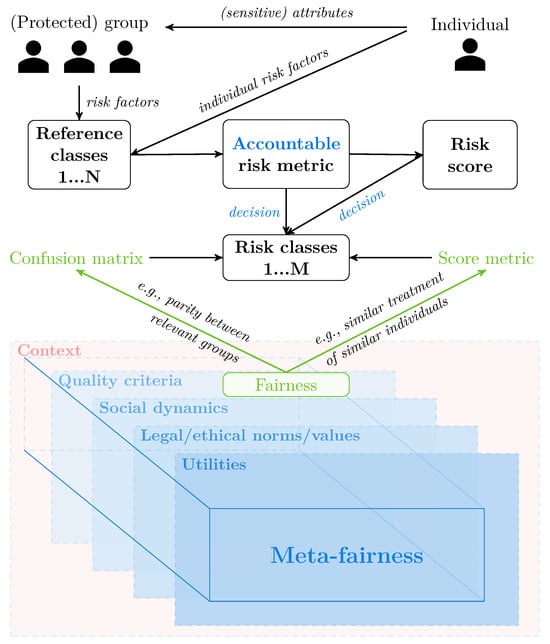
Figure 1.
Risk prediction for groups and individuals in relation to group and individual fairness; necessity of meta-fairness. See Figure 2 for more details on MF.
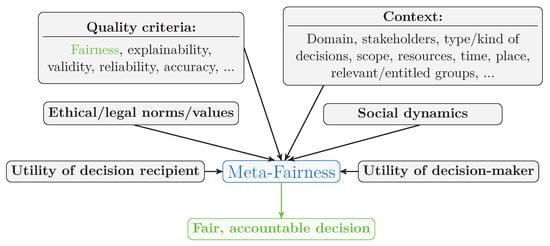
Figure 2.
The concept of meta-fairness in algorithmic decision support.
SA is a characteristic that requires special consideration to ensure fairness, often due to legal, ethical, or social reasons. Not all attributes are inherently sensitive, but certain ones may be designated as such based on the specific use case. In the US, for example, federal law recognizes nine SAs, including sex, race, and age. In medical contexts, however, these same attributes may function as risk factors (RFs). That is, they may legitimately influence clinical outcomes or software predictions for specific groups. For instance, although there have been calls to exclude SA ‘race’ from all clinical prediction models, research indicates that race-unaware estimates can worsen disparities [20]. This highlights the importance of context: Rather than relying on a fixed set of protected groups, Hertweck et al. [7] suggest considering relevant groups based on the specific use case. In the following, we define an RF as a characteristic that directly influences the risk associated with an individual.
Group fairness does not automatically translate to fairness for an individual within that group [21], as statistical definitions provide guarantees on average for groups only. Individual fairness is often defined as the principle that similar individuals should be treated similarly (e.g., by the software). Although various metrics have been proposed to assess both group and individual fairness [3,21], the majority of authors focus on group fairness [13], even though some of them term what they do “individual fairness” [2].
The assessment of individual fairness proves to be rather challenging, especially from the point of view of medical risk prediction software. This is because risk is an attribute that cannot be directly quantified in an individual, unlike measurable characteristics such as blood pressure or specific genetic markers, such as pathogenic variants in tumor suppressor genes. Rather, individual risk is often inferred through an individual’s subset of risk factors (also termed a feature vector in literature), each RF defining a subgroup (reference class), cf. Figure 1) to which the individual belongs. This contradicts the ideal definition of individual fairness, to the extent that Paulus and Kent [1] note that there is an “overlap between the concepts of reference class forecasting and prejudice.”
A clear illustration of this issue is provided by the following observation. Anderson and Visweswaran [13] state that individual fairness “means the algorithm’s decision is not affected by group membership, but only by the relevant characteristics of an individual.” This understanding is obviously at odds with defining risk for individuals through their reference classes as necessary in risk prediction. Moreover, this definition fails when familial risks are relevant, as an individual’s risk may then depend on the characteristics of others. As a solution, Hertweck et al. [7] propose the concept of approximate (individual) fairness: it preserves the use of group fairness metrics derived from the confusion matrix but emphasizes the careful selection of groups. This includes focusing on weakly causally relevant groups and incorporating a mechanism to identify individuals who have a moral claim to equal treatment (called a claim differentiator). Additionally, it underscores the need to clarify context-specific justice objectives, such as whether to prioritize equality, maximize benefits for the worst-off group, or pursue alternative criteria (called patterns of justice).
2.1.3. Fairness in Risk Assessment
In Figure 1, the main steps in the risk assessment process for a group or an individual are illustrated using black boxes with a white background. For identified RFs, reference classes are formed from the considered cohort of patients, which can be the original group from a medical study or a protected subgroup chosen for further examination within a fairness study. These classes influence the choice of the risk class, which, in the case of the individual risk assessment, is determined through a risk score obtained using a risk metric. The risk score models are typically developed from standardized examination data of well-defined cohorts in international medical databases. They often use approaches such as log-log regression to relate patient and family health data to risk classes [22]. Model performance can be assessed for fairness and bias using standard metrics, comparing predicted risks with actual disease occurrences in sufficiently large cohorts, and, in the most rigorous cases, through individual clinical validation. Several domain-independent formalizations of the general risk-score computation process have been proposed, applicable across fields such as medicine, law, or banking, with notable examples provided by Kleinberg et al. [2] and Baumann et al. [23].
Note that, in observational studies, risk factors may correlate with health outcomes for reasons unrelated to direct causality. While distinguishing between prediction and causal inference is essential [20], it is equally important to differentiate between the risk score and the decisions derived from it [24]. Many commonly used fairness metrics are functions of classification decisions, rather than of the underlying risk scores themselves. This might be problematic for a number of reasons, most notably because the embedded assumptions about costs and benefits may not be made explicit [24]. Separating fairness in modeling from fairness in decision-making allows for better analysis of unfairness sources. The risk metric should satisfy predefined quality standards (i.e., be accountable, as discussed, for example, in [25]) to ensure appropriate assignment of an individual to the risk class. The specific quality standards to be applied depend on the context. Moreover, the uncertainty associated with the (potentially partial) assignment to the risk class should be quantified and communicated to the patient [26]. In other words, beyond the context-specific component of risk-prediction software described above, there are also communication- and collaboration-oriented components that become relevant when considering the complete process involving such software.
The fairness of assigning an individual to a risk class is a critical aspect of individual fairness. In the context of cancer treatment and prevention, for instance, accurately grouping individuals into a low-risk category is essential to avoid causing undue insecurity. For this, accurate lower bounds for risk probabilities need to be estimated. Here, methods based on DST offer a promising approach since they can help incorporate not only aleatory but also epistemic uncertainty into predictions [27,28]. Additionally, the so-called intersectional fairness needs to be considered for assignment to reference classes and protected groups, since there might be multiple possibilities to do so. Finally, many researchers emphasize that it is necessary to “engage with the broader context surrounding machine learning use in healthcare” [29], which we take as the necessity to perform a meta-level analysis leading to the concept of meta-fairness.
2.1.4. Accountable Algorithms
Fairness is only one of the principles for creating accountable algorithms [25]. The next essential principle is explainability. Explainability means ensuring “that algorithmic decisions as well as any data driving those decisions can be explained to end-users and other stakeholders in non-technical terms” [25]. Interpretability is a closely related concept and is sometimes used interchangeably, although there is a difference between them, primarily concerning the degree of transparency. Explainability usually refers to the ability to clarify a model’s output, also through post-hoc analysis, without necessarily understanding the internal workings of the model. In contrast, interpretability implies a deeper, more direct understanding of how the model internally processes inputs to generate outputs. Together, explainability and interpretability help transform an algorithm from a black box into a trustworthy, human-centered precision tool. Also towards this goal, DST-based methods have gained more and more importance in the last decades [30]. Throughout this paper, we will use the term explainability, although DST-based methods are in most cases also interpretable.
Diakopoulos and Friedler [25] identify three further principles for accountable algorithms: accuracy, defined as identifying and communicating sources of error and uncertainty to clarify potential impacts and guide mitigation; responsibility, the establishment of external remedies for algorithmic harm and designation of supervising humans; and auditability, the ability for third parties to examine algorithm behavior through transparent documentation, accessible APIs, and permissive terms of use.
Expanding on this, Baniasadi et al. [31,32] identify fairness, but also reliability and validity as central to assessing efficacy in assessment, which also enhances the notion of accuracy in accountable software. Reliability refers to achieving consistent and repeatable results from a (risk) metric, accounting for epistemic uncertainty, with similar results obtained by different evaluators or at different times for the same individual. Validity ensures that the chosen metric accurately measures what it is intended to measure and that decisions are made in accordance with established rules and guidelines. It reflects the accuracy with such components as content validity and consistency of assessment for the same evaluator. For complex processes or classification tasks, efficiency may also be essential. Additionally, incorporating data provenance or data lineage [33,34,35,36] helps to ensure reproducibility, that is, improve findability, accessibility, interoperability, and reuse of data, known as FAIR principles of data management (cf. https://www.go-fair.org/fair-principles/ (accessed on 21 October 2025)).
Furthermore, sustainability should be an important concern, encompassing not only the responsible management of natural resources and the minimization of negative ecological impacts (e.g., with respect to energy) but also social and economic considerations. In software-driven systems, sustainability can refer both to the intrinsic qualities of algorithms and to their interaction with digital twins and physical systems. Internally, an algorithm is sustainable if it operates in a maintainable and resource-efficient manner [37], while also being robust, fair, explainable, and adaptive over time. Externally, in combination with digital twins, sustainability is realized when the system makes decisions that optimize long-term performance, resilience, and resource efficiency, while minimizing negative impacts on society, stakeholders, and the environment [38]. Fairness is also an important consideration in this context, cf. https://sustainabilitydirectory.medium.com/could-algorithmic-bias-affect-sustainability-outcomes-13dcae4550c5 (accessed on 21 October 2025). In this paper, we understand sustainability in its internal sense, considering it as part of the set of quality criteria (QCs).
In addition to the content of an application or a digital twin, the roles of decision-makers and recipients are significant. Decisions are often made collaboratively by a team and must be communicated effectively; consequently, the concepts of communication and collaboration become particularly important. Human communication is the exchange of information between individuals or groups, using various media such as spoken or written language, images, gestures, or music. It conveys facts, opinions, and conclusions, and often serves as the basis for joint projects. Successful communication requires that participants share a common language or be proficient in each other’s language. It also depends on factors such as comprehensibility, honesty, completeness, agreement on underlying principles and goals, and consensus on the conclusions or outcomes to be achieved. Collaboration is a purposeful, inter-dependent, and coordinated interaction in which information is exchanged and actions are mutually adjusted to achieve a shared objective. Collaboration is characterized by goal alignment, inter-dependence, communication, coordination, and mutual influence.
2.2. Meta-Fairness: Possible Definition
The so-called quality criteria such as accuracy or explainability, together with additional concepts illustrated in Figure 1 and Figure 2, can be integrated under the broader notion of MF, which we introduce in this paper.
Definition 1.
Meta-fairness encompasses fairness itself, its defining attributes, foundations, and prerequisites. While addressing algorithmic deficiencies such as bias and discrimination, it guides the selection of appropriate quality criteria and metrics based on the specific application and social context. Moreover, it allows for the integration of contemporary justice goals (‘patterns of justice’ along with ethical values) and the interests of relevant stakeholders (‘utilities’).
Some authors (cf. [7] and relevant references therein) do not consider fairness and other quality criteria from Figure 2 to be conceptually in the same category. Fairness is seen as parallel to the metric according to which the decision-makers determine if their goals (such as accuracy) have been achieved. Whereas we agree with the necessity to consider this so-called decision-maker utility [7], we argue that the ‘fairness’ that considers additional quality criteria, resources, ethical norms, and other factors should rather be called ‘meta-fairness’. That is, fairness in our sense comprises a set of group or individual fairness metric-based strategies, out of which the appropriate one can be chosen (or more than one of them combined) depending on MF considerations.
Our purpose in introducing meta-fairness is to unify the currently fragmented fairness frameworks, which define fairness under specific conditions, and to provide guidance for selecting or combining appropriate approaches depending on the context. Ideally, this definition should not depend on whether fairness is pursued in low-risk tasks (e.g., diagnostic support) or in high-stakes settings involving greater ethical and legal responsibility (e.g., treatment decision-making). Although the core MF principles should apply uniformly across contexts, their practical implementation needs to be adapted to the specific task. For instance, in low-risk applications, greater emphasis may be placed on explainability alongside fairness. In high-risk applications, more weight should be given to accuracy, accountability, responsibility, and empirical validation to uphold fairness under stricter ethical and clinical constraints. Finally, in socio-technical systems where decisions influence future data (e.g., resource allocation), social dynamics should warrant particular attention to identify and mitigate potential feedback loops that could reinforce bias. The precise weighting of these aspects should ultimately be determined by experts in the respective domains. Details on how, exactly, these considerations can be reflected in our MF framework are in Section 3.3 and Section 3.4.
In the remainder of the paper, we do not explicitly consider trade-offs between the decision-maker’s objectives and fairness since this is not relevant for non-polar decisions. However, the proposed approach can accommodate such trade-offs and could be further extended in this direction, which is the subject of future work.
2.3. Approaches to Meta-Fairness
A comprehensive overview of contemporary research on fairness is provided in [4]. However, even in the non-polar case, relying on a single fairness metric is insufficient, particularly when fairness considerations for an individual may conflict with those of their family. The literature review in this subsection aims to substantiate the MF concept given by Definition 1, which builds on and extends the approach proposed in [4], and is detailed in Section 3.3 for the healthcare domain.
It is important to note that MF remains a new and evolving concept without a universally accepted definition or standard at the moment. (Neto and Souza Neto [39] provide general guidelines to best practices on building meta-models.) Nevertheless, several authors have already addressed this concept using a different terminology [7,23,40,41]. In this subsection, we describe these and further key publications and show that they align with our understanding of MF.
Several studies touching on the idea of MF emerged during the COVID-19 pandemic [42,43]. While they address a polar case, some of the findings are also applicable to a non-polar setting. Emanuel and Persad [43] outline a three-step ethical framework for allocating scarce resources: identifying core ethical values, establishing priority tiers based on those values, and implementing allocation strategies accordingly. Key procedural principles include transparency and engagement. The implementation phase poses particular challenges, including the need to clearly define eligible/relevant groups and to avoid open access methods that usually benefit the wealthy. Carroll et al. [42], drawing on a systematic review of over 150 publications, largely support these findings. They emphasize the complexity of equitable resource allocation in public health emergencies and highlight the necessity of applying multiple ethical principles simultaneously. Moreover, they advocate for the development of an evidence-based tool to guide difficult allocation decisions.
Both Carroll et al. [42] and Emanuel and Persad [43] primarily emphasize group fairness. However, individual MF metrics could also be valuable in polar decision-making contexts, as illustrated by the COVID-19 pandemic. During the pandemic, scarce resources were allocated through centralized plans that prioritized groups based on disease severity. Hospitals published detailed criteria outlining allocation protocols. Notably, these plans varied across regions—particularly regarding preferences for patient age, health status, or interpretations of social benefit—introducing spatial and temporal inconsistencies. Individual-level decisions were not permitted on a case-by-case basis, even for patients already at hospital doors. Mathematically, the situation can be modeled as a constrained random queuing system at the individual level. We argue that such a system could have benefited from a context-sensitive individual fairness metric (i.e., fairness enhanced by MF). Key measures to improve fairness could have included building emergency resource reserves and enabling short-term reallocations to less burdened hospitals. Adapting our definition of MF for polar decisions and medical triage is a topic of our future work.
Kirat et al. [44] demonstrate in detail and with many examples that “achieving fairness in machine learning algorithms cannot be handled by isolated disciplines” (e.g., law versus algorithms’ development), but do not explain how exactly to handle this. They suggest better legislation on the explainability of algorithmic decisions and outline several interdisciplinary research paths. Modén et al. [45] show how to involve teachers during the first development stages for AI through participatory design in order “to identify how teachers interpret fairness in their local situations and to ensure that their interpretations underlie concrete system functionalities.”
The works mentioned above serve as classical use cases for the broader fairness framework recently proposed in [7,23], which applies to both polar and non-polar settings. Additional examples are Waytz et al. [40] focusing on a polar trade-off between fairness and loyalty, while Zhang and Sang [41] provide an example of a trade-off between accuracy and fairness. The latter provides a particularly relevant illustration for understanding that non-polar decisions also involve trade-offs and the nature of such compromises.
Padh et al. [46] present a fairness framework that operates independently of the underlying model and is capable of optimizing with respect to multiple fairness criteria and different sensitive attributes. Their implementation supports a wide range of statistical parity-based group fairness notions. For example, they can achieve good accuracy results by combining the demographic-parity-based fairness for different relevant groups on several public data sets. However, the authors point out limitations of the approach arising from conflicting definitions of fairness. These limitations can potentially be mitigated by adopting the strategies outlined in [23] a couple of years later.
As noted by Hertweck et al. [7], the concept of fairness has been extensively explored in both computer science, where various fairness metrics have been developed recently, and philosophy, where it has been a subject of discussion for a long time. That is, fairness is largely not a mathematical concept. The authors propose a novel approach to decision-making, where processes are designed to prioritize not only the objectives of the decision-maker, but also fairness towards individuals affected by the decisions. This dual objective can create a conflict, which can be mitigated by explicitly articulating the values of both the decision-maker and those impacted. To be able to do so, the values of decision-makers and decision subjects should be quantifiable and expressible as mathematical formulas. The reconciliation of these two perspectives, which balances the need for fairness with the need for objective decision-making, can be termed MF (not explicitly used in [7]).
We have already mentioned several concepts from [7] in Section 2.1 and incorporated them into our proposed understanding of MF (cf. Figure 2, Definition 1). The authors propose a framework for making underlying value judgments explicit, consisting of six questions that detail the utility of the decision-maker, the utility of the decision recipients, relevant groups, the claim differentiator, patterns of justice, and, finally, the trade-off decision, of which the first five may explicitly concern the non-polar case. Drawing on theories of distributive justice and algorithmic fairness, they define a fairness score to compare with utility outcomes. Using Pareto efficiency, they evaluate decision rules derived from a fixed model.
While this procedure is highly effective at making typically hidden goals and values explicit, it does not necessarily make the employed quality criteria explicit. Using the framework from [7], these criteria can be incorporated as components of the utilities of both decision-makers and recipients, which is usually sufficient in the context of group fairness. However, in the case of individual fairness, additional qualities of accountable software, such as explainability, play a more significant role in shaping fairness itself, and therefore, in our opinion, should be considered explicitly. The same is true for the context, which is integrated only implicitly into each of the procedure steps from [7].
Another group of approaches relevant in this context originates from the area of reinforcement learning (RL). RL is a method for learning optimal actions through agent-environment interactions to maximize cumulative rewards. On the one hand, fairness in RL is especially important, since a learning algorithm’s actions can influence both its environment and future rewards. The authors of an early work [47] showed, however, that enforcing exact fairness in an RL-based algorithm required exponential time to approximate the optimal policy non-trivially. A comprehensive overview of the current challenges in this area can be found in [48].
On the other hand, RL principles can also be applied directly to ensure fairness. In fair classification, for example, RL can be employed either to mitigate bias in model representations [49] or to adjust the training process [50]. Especially in works like [51], where RL is used to accommodate multi-objective goals without the need for linear scalarization, the purpose of applying RL may resemble that of MF. However, MF aims at a much broader and less formal application, incorporating additional quality criteria beyond accuracy and potentially accounting for social dynamics as well.
Aside from the already mentioned works, new research (e.g., [52]) is continually appearing, emphasizing the urgent need for a common terminology.
2.4. Fairness Software and Benchmarks
We propose to interpret the term ‘fairness’ as a set of available metrics, such as equal opportunity, without implying any judgment of their relevance in particular contexts. Numerous implementations of fairness metrics exist, some of which may already implicitly address aspects of MF. Broadly, three main strategies have been proposed for incorporating fairness into algorithms. Pre-processing methods aim to modify the input or training data to ensure fairness before the model is used or trained [53]. In-processing approaches integrate fairness constraints directly into the algorithm itself [54,55]. Finally, post-processing techniques adjust algorithms based on their output (such as risk scores) and SA. This approach avoids the need to modify potentially complex training pipelines while preserving utility [56,57]. We adopt the last approach for our MF framework.
Examples of existing work illustrate these three strategies. For instance, FairDo [58], available at https://github.com/mkduong-ai/fairdo (accessed on 21 October 2025) is a recent Python package designed to mitigate bias in datasets before model training, representing a typical pre-processing approach. The Fair Fairness Benchmark (FFB) [55], a PyTorch-based framework available at https://github.com/ahxt/fair_fairness_benchmark (accessed on 21 October 2025) embodies an in-processing strategy for assessing and enforcing group fairness in machine learning models. Meanwhile, post-processing approaches are exemplified by the FairnessLab toolkit and its variants [23,57], available as open-source software at https://github.com/joebaumann (accessed on 21 October 2025) and implemented in Python. Similarly, the implementation accompanying [7], accessible at https://github.com/hcorinna/utility-based-fairness (accessed on 21 October 2025) can be regarded as a concrete realization of an MF concept, referred to as “utility-based fairness.” Additionally, AIF360 (AI Fairness 360 [59]) to be found at https://github.com/Trusted-AI/AIF360/tree/main (accessed on 21 October 2025), offers a comprehensive collection of fairness metrics and algorithms for both pre- and post-processing, implemented in Python and R.
A wide variety of datasets (benchmarks) have been developed for evaluating fairness in algorithmic decision-making. Current initiatives increasingly focus on unifying these resources while enhancing their accessibility, applicability, and ease of use. We highlight three recent examples of such benchmark efforts in the following section. CEB (Compositional Evaluation Benchmark) [60] is a dataset designed to assess bias in large language models (LLMs) applied to natural language processing tasks with respect to bias types, demographic subgroups associated with given SAs, and task categories. The dataset is publicly available at https://github.com/SongW-SW/CEB (accessed on 21 October 2025), and the evaluation is conducted using the provided Bash scripts. FairMT-Bench [61] is a benchmark for evaluating LLM fairness capabilities across three stages: context understanding, user interaction, and instruction trade-offs. It is implemented in Python and is available at https://github.com/FanZT6/FairMT-bench (accessed on 21 October 2025). FairMedFM [62] integrates with 17 widely used medical imaging datasets to assess fairness in medical imaging foundation models and can be accessed at https://github.com/FairMedFM/FairMedFM (accessed on 21 October 2025).
Table 1 summarizes the body of related work according to their respective main subjects. Note that while several papers span multiple subjects, we organize them mostly by their principal topic. If more than one topic seems important, we reference the paper multiple times. If not otherwise mentioned, the papers prioritize group fairness. For studies addressing meta-fairness (whether or not they explicitly use this term), we additionally highlight how their approaches differ from the current proposal. None of these studies relies on DST, which we therefore do not mention explicitly. The MF framework, described in the following section, aims to meaningfully integrate the strengths of existing methods while extending them through the explicit consideration of QCs.

Table 1.
From fairness (F) to meta-fairness (MF): references considered in Section 2 sorted according to their subject (arranged in the order of their appearance in the paper).
Table 1.
From fairness (F) to meta-fairness (MF): references considered in Section 2 sorted according to their subject (arranged in the order of their appearance in the paper).
| Topic | Reference | |
|---|---|---|
| General alg. F; bias; F metrics | [1,2,4,11,12,13,14,15,16,17] | |
| (Social) dynamics | [18,19,52,63] | |
| Individual F | [3,13,21] | |
| F in risk score models | [2,4,20,24] | |
| Accountable algorithms; QCs | [25,31,33,34,35,36,37,38] | |
| Application to healthcare | [1,4,13,20,29,42,43,62] | |
| Topic | Reference | Difference to this MF proposal |
| Approaches to MF | [3] | Focused on classification of different fairness definitions and their interconnections, not on combining them; no guidance on what/how to choose |
| [4] | Focused on accountability; no explicit consideration of QCs, utilities, social dynamics; structured differently | |
| [5] | A purely game-theoretic perspective; one of the first mentions of MF in algorithms | |
| [6] | Focused on mediation; one of the first mentions of meta-ethics | |
| [7,23] | No explicit consideration of QCs and social dynamics; not focused on combining F definitions; not focused on individual fairness | |
| [8] | Interpolates between three preset fairness criteria; focused on law | |
| [40] | (Narrowly) focused on a polar trade-off between fairness and loyalty | |
| [41] | (Narrowly) focused on a trade-off between accuracy and fairness | |
| [44] | No concrete way for achieving fairness depending on context proposed; the need for interdisciplinary work outlined | |
| [45] | Focus on teaching; no concrete framework proposed | |
| [46] | Focused on limitations arising from conflicting definitions of fairness | |
| [49,50,51] | Focused on the fairness-accuracy trade-off only; no social dynamics; not frameworks (narrower focus) | |
| [52] | Focused on social objectives; not a framework per se | |
| Topic | Reference | |
| F in reinforcement learning | [47,48] | |
| F software/benchmarks | [53,54,55,56,57,58,59,60,61,62] | |
3. Materials and Methods
In addition to the extensive literature review in Section 2, we present a concise overview of the relevant methods in the context of DST, while also introducing our notation in Section 3.1. In the next Subsection, we reintroduce and improve the metric for medical risk tools’ assessment from [4] since it plays an important role in the proposed methodology for assessing (individual) fairness using MF, which we describe in the last subsection.
3.1. DST Enhanced by Interval Analysis
Interval analysis (IA) [64] is a widely used technique for result verification. By applying suitable fixed-point theorems, whose conditions can be reliably checked by a computer, IA allows for formal proofs that the outcomes of simulations are correct, assuming the underlying code is sound. IA accounts for errors due to rounding, conversion, discretization, and truncation. The results are expressed as intervals with floating-point bounds guaranteed to enclose the exact solution of the coded computer-based model. Since IA operates on sets, it enables deterministic propagation of bounded uncertainties from inputs to outputs. Some methods also support inverse uncertainty propagation. However, a well-known limitation of basic IA is the excessive widening of interval bounds, due to overestimation (the dependency problem and the wrapping effect). More advanced techniques, such as those based on affine arithmetic or Taylor models, have been developed to mitigate these effects and improve result tightness.
A real interval , with and, normally, , is defined as
A real number can be represented as a point interval with . For , the interval operation between two intervals and is defined as
which results in another interval:
For division, it is usually required that though extended interval arithmetic can handle zero in the denominator. For some operations, simplified formulas exist (e.g., ). Using outward rounding, floating-point bounds can be computed to enclose real intervals reliably. Based on this arithmetic, interval methods can be extended to verified function evaluations and automatic error bounding in solving algebraic or differential equation systems.
DST [65] combines evidence from different sources to measure confidence that a certain event occurs. In the finite case, DST assigns a (crisp) probability to whether a realization of a random variable X lies in a set . The result is expressed through lower and upper bounds (belief and plausibility) on the probability of a subset of the frame of discernment . A random DST variable is characterized by its basic probability assignment (BPA) M. If are the sets of interest where each , then M is defined by
The mass of the impossible event ∅ is equal to zero. Every with is called a focal element (FE). The plausibility and belief functions can be defined with the help of the BPAs for all and any as
These two functions allow defining upper and lower non-additive monotone measures [65] on the true probability. The FE masses must sum to one. If expert-provided BPAs exceed one, normalization is applied as
If the sum is below one, either the same normalization is used, or a new FE is added to absorb the deficit. The latter is meaningful only for computing the lower limit , while the former may overly inflate the belief function. If there is evidence for the same issue from two or more sources (e.g., given as BPAs , ), the BPAs have to be aggregated. A common method is Dempster’s rule:
with , .
Interval BPAs (IBPAs) generalize crisp BPAs by allowing to be intervals, reflecting uncertainty about the probability that X belongs to a given set. Computations of , , and aggregations proceed as in the crisp case, but with interval arithmetic. Since interval arithmetic lacks additive inverses [64], the condition is relaxed to .
Adopting the open-world interpretation of DST may be necessary when the number of FEs n cannot be fixed in advance [66,67]. Furthermore, several approaches have been proposed to address the limitation that Dempster’s rule emphasizes similarities in evidence while disregarding potential conflicts [68].
3.2. A Metric for Medical Risk Tools’ Assessment
A score metric for healthcare software is presented in [4] and extended in the next subsection by integrating the concept of MF from Definition 1. It appears necessary to assign weights to the individual quality criteria and other relevant factors shown in Figure 2, based on constraints such as personal and material effort, availability of on-site resources over the required period, retrievability, and other considerations. These weights should reflect the relative importance of each factor in achieving healthcare success and well-being, and should be determined by experts from the relevant disciplines. If there are different approaches for the evaluations, two basic probability assignments can be used and combined using Dempster’s rule of combination (or any other variant of a combination rule, e.g., [68]) from the DST.
Three popular fairness conditions in risk assessment are formulated in [2]:
- Calibration within groups (if the algorithm assigns probability x to a group of individuals for being positive with respect to the property of interest, then approximately an x fraction of them should actually be positive);
- Balance for the positive class (in the positive class, there should be equal average scores across groups);
- Balance for the negative class (the same as above for the negative class).
In the same article, it is demonstrated that “except in highly constrained special cases, there is no method that can satisfy these three conditions simultaneously.” In other words, determining which fairness condition (or combination of conditions) should be used in a given situation must rely on factors beyond purely mathematical or philosophical definitions of fairness, leading to the proposed concept of MF. Our framework is intended to support the choice of metrics, which is a goal similar to that of the framework introduced in [7]. However, it is important to note that the framework in [7] does not explicitly consider QCs as an aspect of MF. Our approach does not seek to identify the one true combination of fairness conditions for a given situation, but rather aims to find a compromise among multiple possibilities that may be equally suitable (or quantifiably unequal) in their applicability to that situation.
Luther and Harutyunyan [4] formulate the following three requirements for fairness, of which the first one may be assessed by any of the three conditions from [2] mentioned above:
- R1
- Subgroups within the cohort that possess unique or additional characteristics, especially those leading to higher uncertainty or requiring specialized treatment, should not be disadvantaged.
- R2
- Validated lower and upper bounds are specified for the risk classes.
- R3
- The employment of suitable or newly developed technologies and methods is continuously monitored by a panel of experts; the patient’s treatment is adjusted accordingly if new insights become available.
Although originally formulated for healthcare, these requirements are generalizable to any domain employing risk-score–based decision-making software. The latter two requirements extend beyond fairness, reflecting broader criteria for accountable risk assessment systems. Within the proposed MF framework, they can thus be interpreted as steps toward achieving meta-fairness. In the following, we reproduce the metric from Luther and Harutyunyan [4], with enhancements and explanations.
The score fairness metric is defined as a minimal set of requirements and yields a value between 0 and 15, with the higher score indicating a higher fairness degree. Its key advantage lies in its flexibility: it can be readily adapted to incorporate new developments, medical insights, and the increasing relevance of individual genetic markers while maintaining comparability with earlier versions. As a prerequisite, the following should be determined:
- If the risk is sufficiently specified;
- If the model for computing the risk factors and calculating the overall risk is valid/accurate;
- If assignment to a risk class is valid/accurate.
The scoring procedure described below is not applicable unless the conditions specified above are met. This covers the quality criterion of accuracy described in Section 2.1. (All considered QCs are visualized in Figure 3 for a better overview.) In general, these prerequisites imply that the algorithm or software system in use has been developed in accordance with verification and validation (V&V) principles [69,70,71,72,73]. For example, it may mean that the software must produce consistent, accurate, and reproducible risk scores. A detailed discussion of how to achieve that lies beyond the scope of this paper, although this does not mean that some aspects of the QC Accuracy cannot be considered within MF.
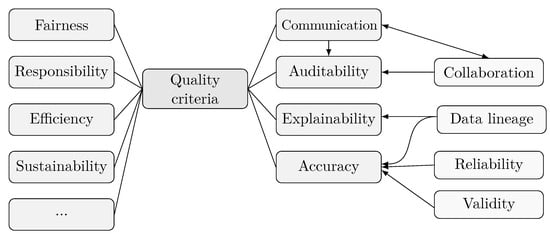
Figure 3.
A selection of quality criteria considered in Section 2.1, along with a selection of possible interconnections between them (non-exhaustive). Aside from fairness, our literature analysis delivered 49 further keywords for possible QCs (alphabetically): ability, accessibility, accountability, accuracy, applicability, auditability, authority, availability, awareness, causality, comparability, compatibility, completeness, complexity, effectiveness, efficiency, equality, equity, explainability, findability, flexibility, functionality, innovativity, interoperability, interpretability, loyalty, missingness, opportunity, parity, performance, plausibility, privacy, reliability, representativeness, reproducibility, responsibility, retrievability, security, severity, similarity, sustainability, transparency, trustworthiness, uncertainty, usability, utility, validity, willingness, and worthiness.
The overall ‘fairness’ score is calculated by summing the points assigned to responses for the questions below that evaluate various aspects of the algorithm or software system under review. To make later integration into the MF process easier, we specify the QC(s) the questions are aimed at.
- General information, 1 point: Does the algorithm/system offer adequate information about its purpose, its target groups, patients and their diseases, disease-related genetic variants, doctors, medical staff, experts, their roles, and their tasks? Are the output results appropriately handled? Can FAQs, knowledge bases, and similar information be easily found? (QC Explainability, Auditability)
- Risk factors:
- 2 pts Is there accessible and fair information specifying what types of data are expected regarding an individual’s demographics, lifestyle, health status, previous examination results, family medical history, and genetic predisposition, and over what time period this information should be collected? (QC Auditability, Data Lineage, Explainability)
- 1 pt Does the risk model include risk factors for protected or relevant/eligible groups? (QC Fairness)
- Assignment to risk classes:
- 0.5 pts Depending on the disease pattern, examination outcomes, and patients’ own medical samples (e.g., biomarkers), and using transparent risk metrics, are patients assigned to a risk class that is clearly described? (QC Explainability)
- 0.5 pts If terms such as high risk, moderate risk, or low risk are used, are transition classes provided to avoid assigning similar individuals to dissimilar classes and to include the impact of epistemic uncertainty or missing data? (QC Fairness)
- 1 pt Are the assignments to (transitional) risk classes made with the help of the risk model validated for eligible patient groups over a longer period of time in accordance with international quality standards? (QC Fairness, Accuracy, Validity)
- Assistance:
- 1 pt Can questionnaires be completed in a collaborative manner by patients and doctors together? (QC Auditability, Collaboration)
- 1 pt Can the treating doctor be involved in decision-making and risk interpretation beyond questionnaire completion; are experts given references to relevant literature on data, models, algorithms, validation, and follow-up? (QC Auditability)
- Data handling, 2 pts: Is the data complete and of high quality, and was it collected and stored according to relevant standards? Are data and results at disposal over a longer period of time? Are cross-cutting requirements such as data protection, privacy, and security respected? (QC Accuracy, Data Lineage)
- Result consequences:
- 1 pt Are the effects of various sources of uncertainty made clear to the patient and/or doctor? (QC Accuracy, Explainability, Auditability)
- 2 pts Does the output information also include counseling possibilities and help services over an appropriate period of time depending on the allocated risk class? (QC Responsibility, Sustainability)
- 1 pt Are arbitration boards and mediation procedures in the case of disputes available? (QC Responsibility, Sustainability)
As can be seen from the above, this individual-focused metric emphasizes accountability (particularly auditability) in response to the growing shift in the research from ‘formal fairness’ toward participatory approaches. However, it does not make explicit the context, the goals of decision-makers and decision recipients as well as the applicable patterns of justice and legal norms, as suggested by Hertweck et al. [7]. Therefore, at least for the individual case, it is reasonable to combine both views with each other, since the framework in [7] lacks explicit consideration of context and QCs. Moreover, the questions listed above are organized according to general-language concepts rather than MF categories. What becomes apparent is that, if fairness is understood merely as a set of metrics, then the proposal from [4] extends beyond it.
3.3. The MF Framework: (Individual) Fairness Enhanced Through Meta-Fairness
Discrimination arises when groups or individuals are treated dissimilarly. If a compromise can be found between different metrics reflecting varying degrees of fairness, it is essential to clarify what this implies for the affected person(s). A philosophical question remains as to whether the task of MF is to identify the optimal set of procedures that maximizes fairness for the individual or group, or to pursue a principled compromise among the available alternatives. Our approach is aimed at the latter.
As discussed in Section 2, the concept of algorithmic fairness, both group and individual, has been the subject of extensive literature, numerous implementations, and a wide range of perspectives, philosophies, and debates. Virtually every proposed approach has faced criticism at some point, with some critiques later retracted or revised. In particular, formal mathematical definitions of fairness have been strongly criticized for neglecting crucial aspects such as social context, social dynamics, and historical injustice [52,63]. We do not aim to introduce yet another formalization. Instead, our goal is to build upon and integrate existing approaches in a principled and flexible manner that should accommodate evolving understandings and easily allow the substitution or inclusion of different fairness metrics. Score-based questionnaires, together with DST methods that offer various mechanisms for combining expert opinions under uncertainty, seem particularly well-suited for this purpose.
In the case of non-polar predictions, the utilities of decision-makers and recipients can be assumed to align. When they do not, the DST allows the construction of two BPAs representing the viewpoints of the decision-makers and the decision subjects, which can then be combined using an appropriate DST combination rule (Section 3.1, [68]).
We assume that the same prerequisites as for the metric in Section 3.2 apply. This includes the requirement for the measurement from [52] that “developers are well advised to ensure that the measured properties are meaningful and predictively useful.” Grote [52] formulates relevant adequacy conditions for social objectives, QC Accuracy (referred to as ‘measurement’), social dynamics, and the utility of decision-makers, which we incorporate into the questionnaires presented in this subsection alongside the already mentioned ideas from [4,7].
In our MF framework, the aspects of meta-fairness illustrated in Figure 1 and Figure 2 are initially defined using a checklist and a score-based questionnaire, and, if necessary, subsequently combined with the aid of DST. A key component of each questionnaire is the specification of biases considered by each QC. Since the same bias may appear under slightly different names in the literature, and conversely, biases with identical names may have differing definitions across publications, we provide a list of the considered biases along with their definitions and references in Table 2 to establish a common ground. For each bias, we provide a single reference deemed most relevant, although other references could also be applicable. Examples of biases in the healthcare context, sometimes expressed using alternative terminology, are discussed in [13,74]; in such cases, the definition in the table, rather than the name in Column 2, should be considered authoritative. In the following, we refer to biases by their corresponding numbers in the table. The final column of the table indicates how each bias is associated with the relevant QCs.

Table 2.
Biases (‘b’) considered in Section 3.3 and Section 4, with definitions and references, in the alphabetical order. ‘Ref’ means ‘reference;’ ‘C’ stands for ‘category’ according to [11], out of ‘H’ human, ‘SY’ systemic, ‘ST’ statistical. The abbreviations for QCs are: ‘A’ accuracy, ‘Au’ auditability, ‘C’ communication/collaboration, ‘D’ data, ‘E’ explainability, ‘F’ fairness, ‘RS’ responsibility/sustainability, ‘S’ social dynamics.
Definition 2.
The MF Framework is the set of instruments specifying the MF components Context (including Utilities), QCs, Legal/Ethical norms and values, and Social dynamics. In particular, a checklist for Context helps determine the relevance of each subsequent questionnaire about QCs, Legal/Ethical norms and values, and Social dynamics, which in turn give structure to the BPAs used to derive the final score if different opinions or interpretations are possible.
Note that Definitions 1 and 2 have, up to this point, been independent of the healthcare domain. At the stage of the context checklist, however, the domain must be specified, and the subsequent QC questionnaires need to be relevant to this domain—in our case, healthcare. Nevertheless, the bias lists for the QCs, as well as some of the other questions, can be readily generalized to other domains. In the following, we detail the context checklist and the questionnaires.
3.3.1. A Checklist for Context, Utilities from Figure 2
Based on the aspects shown in Figure 1 and Figure 2 and Definition 2, it is necessary to establish the context first, which takes the form of a checklist. The context aspect should include at least the components listed below, but can be extended if required. The actual utilities of decision-makers and recipients are considered to be parts of the context.
- Domain: healthcare/finance/banking/…
- Stakeholders: Decision-makers and -recipients
- Kind of decisions: Classification, ranking, allocation, recommendation
- Type of decisions: Polar/non-polar
- Relevant groups: Sets of individuals representing potential sources of inequality (e.g., rich/poor, male/female; cf. [7])
- Eligible groups: Subgroups in relevant groups having a moral claim to being treated fairly (cf. the concept of a claim differentiator from [7]; e.g., rich/poor at over 50 years of age)
- Notion of fairness: What is the goal of justice depending on the context (cf. the concept of patterns of justice from [7]; e.g., demographic parity, equal opportunity, calibration, individual fairness)
- Legal and ethical constraints: Relevant regulatory requirements, industry standards, or organizational policies
- Time: Dynamics in the population
- Resources: What is available?
- Location: Is the problem location-specific? How?
- Scope: Model’s purpose; short-term or long-term effects? groups or individuals? Real-time or batch processing? High-stakes or low-stakes?
- Utilities: What are they for decision-makers, decision-recipients?
- QCs: What is relevant?
- Social objectives: What are social goals?
3.3.2. Questionnaires for Quality Criteria from Figure 2
As discussed earlier, QCs play a crucial role in the MF framework. Our literature review identified 50 candidate QCs used by researchers (cf. Figure 3). Below, we present questionnaires for a subset of QCs that are particularly relevant from the perspective of meta-fairness, which domain experts may refine further. Such refinements could alter the resulting scores, which can then be normalized within the proposed framework. We provide scoring possibilities for QCs’ fairness, accuracy, explainability, auditability, responsibility/sustainability, and communication/collaboration only.
3.3.3. QC Fairness ()
The first component of the score for QC fairness is any actual optimal value of fairness scores obtained by any formal fairness procedure, for example, using the tools described in Section 2.4. If it is not directly given like that, it needs to be rescaled accordingly; the simplest way is to use a linear (min–max) transformation. For an original range and a target range , the transformation is given by: If more than one value is available (there are several interesting points on the Pareto front), then an interval containing them can be chosen (weight ). Then, the following assessment questions should be answered and the total scores summed up (, weight ). The score is computed as the weighted sum .
- Utilities: Are the correct functions used? (1 pt for the decision-maker’s and -recipient’s each)
- Patterns of justice: Are they correctly chosen and made explicit? (2 pt)
- Model: Does the risk model include risk factors to reflect relevant groups? (1 pt)
- Risk classes: If terms such as high risk, moderate risk, or low risk are used, are transition classes provided to avoid assigning similar individuals to dissimilar classes? (2 pt)
- Type: Is group (0 pt) or individual (1 pt) fairness assessed? (Individual fairness prioritized.)
- Bias: What biases out of the following list are tested for and are not exhibited by the model (here and in the following: 1 pt each if both true; 0 otherwise): 1/13/22/26/31/35/39
3.3.4. QC Accuracy ()
- General: Does the variable used by the model accurately represent the construct it intends to measure, and is it suitable for the model’s purpose (2 pt)?
- Uncertainty: Are the effects of various sources of uncertainty made clear to the patient and/or doctor (2 pt)?
- Data
- quality, representativeness: are FAIR principles upheld (1 pt each)?
- lineage: Are data and results at disposal over a longer period of time (1 pt)? Are cross-cutting requirements, e.g., data protection/privacy/security, respected (1 pt)?
- bias: 20/27/29/37 (1 pt each)
- Reliabilty: Is the model verified? Formal/code/result/uncertainty quantification (1 pt each)
- Validity: As the variable validated through appropriate (psychometric) testing (1 pt)? Are the assignments to (transitional) risk classes made with the help of the risk model validated for eligible patient groups over a longer period of time in accordance with international quality standards (1 pt)?
- Society: Does the model align with and effectively contribute to the intended social objectives? I.e., is the model’s purpose clearly defined (1 pt)? Does its deployment support the broader social goals it aims to achieve (1 pt)?
- Bias: Pertaining to accuracy: 8/11/14/18/24/33/42/43 (1 pt each)
3.3.5. QC Explainability
- Data: Are FAIR principles upheld with the focus on explainability (1 pt)?
- Information: Does the algorithm/system offer adequate information about its purpose, its target groups, patients and their diseases, disease-related genetic variants, doctors, medical staff, experts, their roles, and their tasks (4 pt)?
- Risk classes: Depending on the disease pattern, examination outcomes, and patients’ own medical samples (e.g., biomarkers), and using transparent risk metrics, are patients assigned to a risk class that is clearly described (4 pt)?
- Effects: Are the effects of various sources of uncertainty made clear to the patient and/or doctor (1 pt)?
- Bias: 7/15/21/28/30 (1 pt each)
3.3.6. QC Auditability
- Information: Are the output results appropriately handled (1 pt)? Can FAQs, knowledge bases, and similar information be easily found (1 pt)?
- Data types: Is there accessible and fair information specifying what types of data are expected regarding an individual’s demographics, lifestyle, health status, previous examination results, family medical history, and genetic predisposition, and over what time period should this information be collected (2 pt)?
- Expert involvement: Are experts given references to relevant literature on data, models, algorithms, validation, and follow-up (2 pt)?
- Bias: 3/4/5/25 (1 pt each)
3.3.7. QCs Responsibility/Sustainability
- Counseling: Does the output information also include counseling possibilities and help services over an appropriate period of time depending on the allocated risk class?
- Mediation: Are arbitration boards and mediation procedures in the case of disputes available?
- Trade-offs: Is optimization with respect to sustainability, respect, and fairness goals?
- Sustainability: Are environmental, economic, and social aspects of sustainability all taken into account?
- Bias: 2/10/17/36/38
3.3.8. QCs Communication/Collaboration
- Type of interaction: Are humans ‘out of the loop,’ ‘in the loop,’ ‘over the loop’?
- Adequacy: Are the model’s outputs used appropriately by human decision-makers? I.e., how are the model’s recommendations or predictions interpreted and acted upon by users? Are they integrated into decision-making processes fairly and responsibly?
- Collaboration: Can questionnaires be completed in a collaborative manner by patients and doctors together?
- Integrity: Is third-party interference excluded?
- Bias: 6/9/12/16/19/23/user 24/32/40
3.3.9. Legal/Ethical Norms and Values from Figure 2
Key legal norms for algorithms in healthcare are still evolving and aim to balance innovation with patient well-being. While specific requirements vary across countries and jurisdictions, they generally cover patient safety and treatment efficacy, data protection and privacy, transparency and explainability, fairness, accountability and liability, informed consent and autonomy, and cybersecurity. Algorithms’ ethics similarly encompasses values, principles, and practices that apply shared standards of right and wrong to their design and use. As noted by Hanna et al. [74], recurrent ethical topics—respect for autonomy, beneficence and non-maleficence, justice, and accountability—are particularly relevant in healthcare. This again highlights the importance of incorporating QCs within an MF framework.
At least the following two questions are relevant here:
- Adequacy: Are appropriate legal norms taken into account?
- Relevance: Are relevant and entitled groups correctly identified and made explicit?
Further definition of this component of the MF framework should be grounded in a multi-stakeholder process. Binding requirements can be provided by legal and regulatory standards, such as anti-discrimination law or data protection regulation. Professional standards and ethical guidelines issued by domain-specific associations (e.g., in medicine, finance, or computer science) can offer further orientation. In addition, ethics committees and review boards play a central role in operationalizing these norms in practice. Finally, the inclusion of perspectives from affected stakeholders and civil society ensures that broader societal values are represented.
3.3.10. Social Dynamics from Figure 2
Considering the final component of MF, social dynamics, means uncovering structural biases, recognizing feedback effects, and preventing ‘fairwashing.’ Structural bias arises from the systemic rules, norms, and practices that shape how data is collected, how decisions are made, and how opportunities are distributed. For instance, in healthcare, clinical studies have historically underrepresented women, resulting in diagnostic models that perform worse for them. At the same time, algorithms influence the very societies that employ them. For example, predictive models often equate past healthcare costs with patient needs. Because marginalized groups historically receive less care, the model underestimates their health risks, leading to fewer resources being allocated. This, in turn, worsens outcomes and feeds back into future training data, reinforcing inequities in a self-perpetuating loop. By uncovering such structural and dynamic effects, we can reduce the risk of fairwashing, that is, presenting an algorithm as fair when it is not. Therefore, considering multiple metrics (or combinations of them), applying explainability tools responsibly, and maintaining a strong focus on accountability, as emphasized in the MF framework proposed here, also helps to take into account social dynamics. Further considerations may be as follows:
- Time influence: Is the model designed to maintain stable performance across varying demographic groups over time?
- Interaction: Is the influence of the model on user behavior characterized? To what extent are these effects beneficial or appropriate?
- Utility: Is the social utility formulated?
- Purpose fulfillment: Is it assessed if it can be aligned with the functionality of the software under consideration?
- Feedback effects: Are there any studies characterizing changes induced by the model in the society?
- Bias: 34/41
The questionnaires presented above, which specify the components of the MF framework according to Definition 2, indicate vital MF areas that may require further refinement by experts and are not intended to be exhaustive.
3.4. DST for Meta-Fairness
According to Definition 2, there should be a possibility to combine different views on what is fair. DST, especially with imprecise probabilities, provides a suitable means for combining diverse views, as it can represent uncertainty and partial belief without requiring fully specified probability distributions. Its ability to aggregate evidence from multiple sources makes it particularly useful for integrating notions arising from different stakeholders or ethical perspectives, while its explicit treatment of conflict helps to uncover tensions between competing objectives. At the same time, the computational complexity grows quickly with the size of the hypothesis space, the resulting belief and plausibility intervals may be difficult to interpret for non-technical audiences, and Dempster’s rule of combination can yield counterintuitive results under high conflict. Moreover, the DST obviously cannot resolve any normative questions about which fairness notion ought to take precedence.
There are several ways to apply the DST within the MF framework.
3.4.1. Augmented Fairness Score
One approach is to obtain scores (cf. Section 3.3, QC Fairness) in a more sophisticated manner. Metaphorically, unfairness can be viewed as a disease, allowing us to apply the same DST methodology as described in Section 4.1 for breast cancer. In this analogy, the RFs correspond to different types of bias present in an algorithm. We can then assign one BPA to individual unfairness and another to group unfairness, and combine them using Dempster’s rule. Finally, the fairness score can be calculated as one minus the unfairness mass, which includes ambiguous situations, as illustrated in the example below. If ambiguity is not to count as fairness, the fairness mass itself can be used directly as the score.
Let us consider a simple, hypothetical example of this approach in healthcare. In this example, we draw inspiration from Wang et al. [81], who quantified racial disparities in mortality prediction among chronically ill patients, but we instead focus on a hypothetical diabetes screening use case. Note that Wang et al. [81] did not apply DST methods, but instead relied on logistic regression and other similarly less interpretable approaches.
Suppose we have a predictive model that recommends patients for early diabetes screening. Unfairness can arise at both the individual and group levels: at the individual level, two patients with nearly identical medical profiles (e.g., age, BMI, glucose levels nearly the same for a Black and a White patient) may receive substantially different screening recommendations, while at the group level, patients sharing a particular SA may be systematically under-recommended for screening compared to others. For illustration, we examine disparities with respect to ethnicity (Black vs. White).
We define the FEs for the first BPA based on the three following individual unfairness metrics (or RFs in the analogy).
- Feature similarity inconsistency (FS): A patient with a nearly identical profile to another patient receives a substantially different risk score;
- Counterfactual bias (CB): If a single attribute is changed while all other features are held fixed (e.g., recorded ethnicities flipped from Black to White), the model recommendation changes, even though it should not medically matter; and
- Noise sensitivity (NS): Small, clinically irrelevant perturbations (e.g., rounding a glucose level from 125.6 to 126) lead to disproportionately different predictions.
For the group view , the metrics/RFs may be selected as follows (cf. the three commonly used fairness conditions on page 15).
- Demographic parity gap: One group is recommended for screening at a substantially lower rate than another, despite having similar risk profiles;
- Equal opportunity difference: The model fails to identify true positive cases more frequently in one group than in others; and
- Calibration gap: Predicted risk scores are systematically overestimated for one group and underestimated for another.
In general, the choice of metrics can be motivated by the lists of biases described in Section 3.3. As shown above, the FEs of individual and group BPAs are generally not identical. A transparent way to address this is to construct a mapping , where (unfair/fair) represents the hypothesis frame of discernment. An example mapping for can be defined as follows: (feature-similarity inconsistency is considered unfair); (this is also regarded as unfair); (noise sensitivity is ambiguous); (strong evidence of unfairness); (total ignorance). For brevity, we omit this step for .
Suppose the masses for the individual BPA are defined as , , , . We take the mass of as the remainder (). In the simplest case, the transferred masses can be defined as the sum of the masses of all FEs that map exactly to each hypothesis set. That is, , , .
If the group BPA is defined by , , , we can proceed to combine the evidence. To select an appropriate combination rule, we first compute the conflict K as in Equation (4). A high value of K indicates strong disagreement among the sources, in which case Dempster’s rule may produce extreme belief values, and an alternative combination rule should be considered. In this example, the conflict is relatively low: . After applying Dempster’s rule, the combined BPA is given as , , (rounding outwards).
The final belief in fairness can be interpreted as excluding ambiguity, lying in the interval , or, if ambiguity is included, as (both values are low in this example). The actual fairness score must be recalibrated for the MF framework to be in the range from 0 to 15: when the interpretation excluding ambiguity is used.
This approach offers the advantage of high explainability by encoding both the information about the considered evidence types (BPAs) and the underlying reasoning (r). On the other hand, the choice of the mapping r is subjective and must be justified. All masses can be represented as intervals, and the mapping r itself can be defined probabilistically. Dynamical developments can be taken into account by creating cumulative evidence curves, as described in Section 4.1 for prediction of gene mutation probabilities.
3.4.2. General MF Score
Another way to incorporate DST into the proposed MF framework is to use its components from Definition 2 as FEs of an (I)BPA. This can involve, in a first step, using questionnaires to obtain scores for those components as described in Section 3.3. Each questionnaire can be associated with a probability , computed as the ratio of the achieved score to the total possible score. This probability may be expressed as an interval to reflect the (un)certainty of the expert completing the questionnaire. Alternatively, these probabilities can be provided directly by an expert evaluating the system, without using a questionnaire. Note that consisting of more than one MF-related aspect can also be considered if an isolated assessment is not feasible.
In the second step, the weights associated with each are determined by the expert based on the context. Here, the weights can be either crisp numbers or intervals. For crisp weights, the condition must hold; for interval weights, . A weight can be set to zero if a particular aspect is not to be considered in the current assessment. The mass associated with is then computed as (in either the crisp or interval version). To avoid inflating the resulting belief-based score, the mass of the frame of discernment should be assigned as the remainder, without applying any redistribution function.
Finally, we use the BPAs/IBPAs defined in this manner to produce the final assessment score or interval. First, we combine all defined , , which may reflect N expert opinions, different interpretations of fairness (if not already captured by the QC Fairness score), or group versus individual perspectives, using an appropriate DST combination rule depending on the degree of conflict K. Afterward, we can compute the (or ) functions for the relevant aspects of interest, or combinations thereof, which can be considered as the general MF score. An example for the approach is in the Discussion to Section 4.1.
More sophisticated approaches to computing the general score are conceivable, drawing inspiration from methods in data fusion. For example, one could incorporate additional assessment criteria for MF expressed in the BPAs dynamically, following the open-world interpretation of DST, or account for differences in their FEs differently from the example in this subsection. We leave these directions for future work.
4. Results: Meta-Fairness, Applied
Alongside advancing the concept of MF, we aim to examine its application in healthcare and risk prevention. First, we revisit our earlier DST-based risk prediction models, asking whether these methods ensure the fair and appropriate assignment of patient groups—as well as individuals and their families—into risk classes. We also consider whether DST provides a better solution compared to logistic regression, or whether it requires further generalization, for example, through the use of interval bounds for probabilities and/or additional evidence combination rules.
Second, building on our experience with DTs in virtual museums [82], we outline an application of the MF concept to DTs in healthcare. Although a substantial body of literature exists on DT fairness, there seems to be limited knowledge of overarching DT principles. Modern DTs rely heavily on AI, including generation and modeling, communication, and collaboration, which introduces multiple levels of consideration and competing metrics, as emphasized in [82]. Each DT feature can now be analyzed additionally from the point of view of MF.
4.1. Predicting BRCA1/2 Mutation Probabilities
Pathogenic variants, or mutations, are a major cause of human disease, particularly cancer. When present in germline cells, such variants are heritable and increase cancer risk both for individuals and within families. Mutations in BRCA1 and BRCA2 are the most well-established causes of hereditary breast cancer (BC) and also confer an elevated risk of ovarian cancer (OC). This condition, formerly known as hereditary breast and ovarian cancer syndrome (HBOC), is increasingly referred to as King syndrome (KS) in recognition of Mary-Claire King, who first identified these genes, and to avoid the misleading implication that the syndrome affects only women or is limited to breast and ovarian cancers.
In [27,28], we introduced a two-stage (interval) DST model that estimates the likelihood of pathogenic variants in BRCA1/2 genes under epistemic uncertainty, with particular focus on the RF of age of cancer onset. In addition, we developed a decision-tree-based approach for classifying individuals into appropriate risk categories [27]. This work was based on a literature review and informed through established online tools such as BOADICEA (via CanRisk https://www.canrisk.org/ (accessed on 21 October 2025)) or Penn II (https://pennmodel2.pmacs.upenn.edu/penn2/ (accessed on 21 October 2025)) in the manner detailed in [27,28]. Implementations of models and methods, as well as all data, are to be found at https://github.com/lorenzgillner/UncertainEvidence.jl (accessed on 21 October 2025), https://github.com/lorenzgillner/BRCA-DST (accessed on 21 October 2025). In this subsection, we illustrate the application of the MF framework from Section 3.3 and Section 3.4 using this example. Here, the question of interest is if reliable assignment to the low-risk class is ensured.
4.1.1. Model Outline
The age at first cancer diagnosis is one of the most important indicators of a BRCA1/2 mutation. It must be accounted for carefully, even when the exact age is unknown, as is often the case for information regarding family members. The model in [28] proposes handling this using a two-stage procedure.
In Stage 1, we define cumulative curves by age for each RF, including BC, OC, BC/OC occurring in the same individual (sp), and additive factors for bilateral BC (bBC) and male BC (mBC). The curves are calculated in 5-year age increments and connected by straight lines. Separate sets of curves are provided for Ashkenazi and non-Ashkenazi Jewish ancestry (cf. Figure 4). In the figure, example probabilities from the literature are indicated for potential genetic test referral, illustrating that, at these thresholds, referrals would almost always occur even without considering multiple RFs. These thresholds appear to be too low, making it especially important to ensure reliable assignment to the low-risk class, as misclassification into a higher-risk category can lead to unnecessary emotional, medical, financial, and social burdens.
Figure 4.
Cumulative curves for RF of BC, OC, sp as well as additive factors mBC, bBC for non-Ashkenazi ancestry.
In Stage 2, the lower risk bound is calculated in two steps. First, individual and familial BPAs, and , are derived from the cumulative curves. Next, and are combined using an appropriate combination rule (e.g., Dempster’s) to compute the final . If the age of onset is uncertain, the resulting value is expressed as an interval. Since we relied on manually collected data from open-access publications, supplemented with predictions from Penn II where necessary, we consider this model a proof-of-concept for the proposed approach, although it shows good agreement with the literature [28].
4.1.2. Example
Consider a non-Ashkenazi Jewish patient diagnosed with breast and ovarian cancer at age 22, whose mother was diagnosed with bilateral breast cancer at age 50. To compute the lower-risk probability of a BRCA1/2 mutation, we generate for the patient and for her mother from the curves in Figure 4 (see Table 3). For the patient, the exact age is known, resulting in a crisp BPA (Column 2). For the mother, however, only an approximate age is available. Instead of providing only the worst-case estimate by assuming the age to be 51, we construct the BPA over an interval of years, which yields the intervals shown in Column 3. Note that in our model, the curves at 60 also cover ages above 60.

Table 3.
Basic probability assignments for the patient, her mother, and combined.
Using Dempster’s rule in Equation (4), we combine the patient’s history with her family history (Column 4). From this, we compute the final belief value as lying in the interval according to Equation (2) by choosing the set of RF {BC, OC, sp, bBC}. Note that interval arithmetic is used in Equations (2) and (4). The interval corresponds to a best-case BRCA1/2 mutation risk probability of approximately 45% and a worst-case lower risk probability of approximately 55%. For comparison, the crisp estimate from Penn II for the same case is 54%.The key advantages of our approach are that both best-case and worst-case bounds are explicitly visible, and the model remains explainable.
4.1.3. Discussion
The model described above does not entirely satisfy the criteria R1–R3 outlined in Section 3.2. While the model corresponds reasonably well to the literature, it remains a proof of concept and can be further refined. The primary reason is that establishing a reliable ground truth for the considered RFs is inherently challenging [28], for instance, because ethnicity is both an important RF and an SA with limited availability in most databases. This discussion is not intended to demonstrate the fairness of our model; rather, it serves to illustrate how the MF framework can be applied.
Specifically, with respect to R1, the model currently distinguishes only two subgroups: the general population and the Ashkenazi Jewish population (with unspecified location). Further work is needed to assess whether this limitation disproportionately disadvantages other groups, such as Black or Latin American populations, and to examine whether geographic context (e.g., the USA vs. Mexico for Latin Americans) plays a significant role. Nonetheless, extending the model to include cumulative curves tailored to these populations should be straightforward once the relevant data become available. Regarding R2, the literature is not fully consistent about the thresholds defining risk classes. For the low-risk class, the probability of a BRCA1/2 mutation is often set below 10%, though in some cases the threshold is 7.5%. The advantage of our model is that this uncertainty can be expressed as the interval . Criterion R3 likewise cannot be fully ensured in a simple academic context. New RFs continue to be identified. For example, triple-negative breast cancer (i.e., cancer cells lacking all three common receptors—estrogen, progesterone, and HER2) has been found to be strongly associated with BRCA1 mutations, but this factor is not yet included in the model. (Receptors are proteins that “detect” molecules such as hormones.) Furthermore, the possibility of multiple, distinct BCs in the same patient is not currently captured, since each FE is considered only once within the DST framework. This, too, could be addressed by extending the model in the same manner as for other RFs, provided suitable data are available to construct the cumulative curves in Figure 4.
Suppose that the considered, hypothetical context is as follows: Doctors and patients (stakeholders) act together (non-polar decisions; same utilities) to check if similar individuals are appropriately assigned to the low-risk class (notion of fairness: individual; kind of decision: classification). In this context, relevant/eligible groups do not play a role; further, we assume that resources are not limited, there are no further legal norms and ethical values to consider, and the location is not relevant. Dynamics in the population cannot be sufficiently reflected at the current state-of-the-art.
The model’s purpose is to assess the BRCA1/2 mutation probability to help the doctors reach the decision of sending the patient for the genetic test or not. In the considered context, the stakes are medium-high, but long-term: If a person is erroneously assigned a higher risk class than necessary, there will not be any life-threatening developments missed. However, this still has negative consequences both for the treating clinic and for the patient. Psychologically, it can create unnecessary anxiety, stress, or lifestyle changes. Medically, the risk of overtreatment and a strain on resources increases. So, the utilities of all stakeholders are obviously aligned. The overarching social goal is to minimize BC in the population. The relevant QCs are fairness, accuracy, and explainability. In this context, the next steps are to fill out appropriate questionnaires from Section 3.3 for the QCs given above.
QC Fairness. Individual fairness requires a good similarity measure for individuals. Using the DST model, it is easy to establish similarity: patients having the same RF combinations can be considered as similar and are treated the same, so that can be assumed 15. From the questionnaire, the value is 10, the model scoring 7 in its non-bias part. The score 0 is given for the following biases:
- 1
- Aggregation bias, since it cannot be excluded at the moment that false conclusions are drawn about individuals from the population;
- 22
- Inductive bias, since there are still assumptions built into the model structure that we consider general, and the Ashkenazi Jewish population only;
- 35
- Representation bias, since we cannot test for this at the moment; and
- 39
- Simplification bias, for the similar reason as 1.
The overall score is therefore , that is, approx. 83%. Note that the model systematically gives higher risk class estimations for the Ashkenazi Jewish population, which is not a sign of discrimination in this case because this group has truly higher base rates. That is, any definition of fairness based on equal base rates is not relevant in the context.
QC Accuracy. Combining various risk prevention approaches and using decision trees [27], we can offer a reliable lower bound for the transition between low risk and average risk. It is easier to determine intermediate risk classes if interval information on the probability bounds is available. Therefore, we can give the score of 4 for the first two questions; the group of questions about the data scores 6. Note that the score for the general question about FAIR principles can be assumed as 4 because the model is available under https://github.com/lorenzgillner/BRCA-DST (accessed on 21 October 2025). Reliability score is 1.5; validity 0; society relevance 2. The score 0 is given to the following biases: 20/29/37 for data and 14/42 for accuracy, summing up overall to and 65%.
QC Explainability. DST methods offer a clear advantage in explainability compared to, for example, a logistic-regression–based model, where the underlying formula is not transparent, potentially introducing implicit dependencies among variables and making the results harder to interpret. The explainability score is therefore relatively high for the model, namely, or 60%, with biases 21 and 30 being given the score of 0.
The first use case illustrates the possible employment of transition classes. Consider two patients, A and B: both are women of the same age, with similar health profiles and no personal history of cancer. Both have a family history of breast cancer, as their mothers were diagnosed at ages 48 and 49, respectively. Using the Penn II model to estimate the probability of a BRCA1/2 mutation for each family, the results are 10% for A and 9% for B. Consequently, A would be referred for genetic testing while B would not, despite their striking similarities. The situation would be even worse for A if the exact age at which her mother was diagnosed were uncertain, for example, if it were only known that the diagnosis occurred at age 45 or later. In such cases, the youngest possible age (45) is used in the calculation, which results in a probability of 11%. This approach is conservative, as using the earliest plausible age ensures the risk is not underestimated.
In our model, the upper bound of the belief-based risk is 7.5% at age 49 and 7.9% at age 48, which is somewhat lower than the estimates produced by the logistic-regression–based model Penn II. If the exact age is unknown, the result can be expressed as an interval, , which reflects both the best-case and worst-case scenarios. Furthermore, if a transition class is introduced between low risk and average risk, all patients with similar profiles would be classified into this category, ensuring fair treatment. Note that the psychological impact of being classified into a transition class is less severe than that of being placed directly into the ‘worse’ class, since it implies that one was never fully part of the ‘better’ category. Additionally, it allows us to take into account differences in thresholds from the literature.
As an illustration of the second approach outlined in Section 3.4, consider the following example. In the discussion above, we evaluated our model from the perspective of an individual patient. For this purpose, we define a BPA with the FEs QCF (QC Fairness), QCA (QC Accuracy), QCE (QC Explainability), and C (Context). The corresponding probabilities are derived from the previously obtained scores, and an expert assigns them equal weights (see Table 4, Columns 2 and 3) (We assign probability 1 to C, as it has been thoroughly described.) A different expert, however, considers context to be central to the assessment and therefore distributes the weights differently, while remaining uncertain about the relative importance of fairness in this setting (see Columns 4 and 5 of the table). Finally, the model can also be evaluated from the perspective of the patient’s family. Since formally, the framework does not distinguish between the patient and their family, an expert may assign different probabilities to the FEs when viewed from this perspective (see Columns 6 and 7).

Table 4.
(I)BPAs for the example for the second use of DST from Section 3.4.
From these assignments, we see that Expert 1 is fairly confident the model is fair to individuals—about 21% certain, with plausibility reaching up to 45%. Expert 2 is less confident, estimating the lower bound of fairness between 8% and 17%. Group fairness (from the family perspective, using the lower bound) is assessed between 12% and 15%. Note that this scale differs from that used in the questionnaires above because of weighting. We combine these opinions using Dempster’s rule, since the overall conflict is average. The individual views are combined first, followed by the group perspective. The resulting belief function for the model’s fairness (whether for the patient or for the family) lies between 12% and 28%. The belief that the model is both fair and accurate ranges from 22% in the worst case to 47% in the best case (all values rounded outward). Overall, we see that a medium level of uncertainty in the inputs approximately doubles the uncertainty present in the final score.
4.2. Meta-Fairness Applied to Communication in Digital Healthcare Twins
The review by Katsoulakis et al. [83] examines the applications, challenges, and future directions of DT technology in healthcare. Although it does not explore the topic of fairness in depth, the authors emphasize that “ensuring that the digital twin models are free from biases and do not discriminate against individuals or groups is vital.” Key considerations include transparency and fairness in data usage, equitable access to the necessary technology and data, and ethical concerns such as privacy and informed consent. Similarly, the overview publication by Bibri et al. [84] highlights that, in addition to privacy and security, ethical and social aspects of DTs in healthcare should address fairness, bias mitigation, transparency, and accountability in decision-making processes. From a broader perspective, as human DTs and other augmented DTs populate and enhance the digital parallel universe, the Metaverse, Islam et al. [85] emphasizes that algorithmic bias, limited system transparency, and persistent data privacy concerns remain central obstacles to achieving an inclusive and ethical application of AI in this context. These concerns can be conceptually addressed through the MF framework introduced in Section 3.3, as outlined in this subsection.
In recent papers [82,86], we considered feature-oriented DTs of various kinds of virtual museums and formulated an approach for assessing them from the viewpoint of appropriate quality criteria. The features fit into three broad categories of content, communication, and collaboration that have further, subordinate features. A risk-informed virtual museum supports the communication and perception of different types of risks from a variety of threat categories and collaborative risk management. The approach can also be applied to healthcare DTs, since communication and collaboration are important features of such DTs, too. In the following, we take a closer look at them and their subordinate features (cf. Figure 5). Each individual feature can now be examined in terms of MF and related ethical principles.
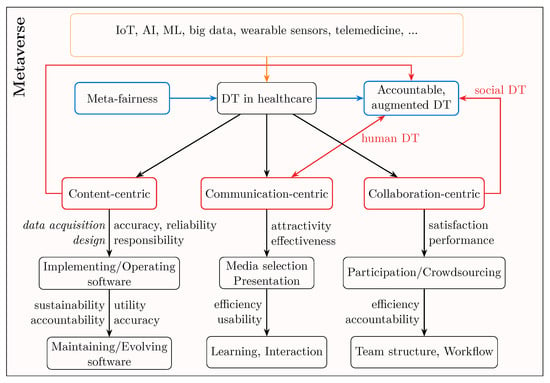
Figure 5.
Possible healthcare DT categories (in red), subordinate features and their quality criteria.
4.2.1. DTs and MF
In Figure 5, a layered model of healthcare DTs within the Metaverse is presented, illustrating how MF can guide the evolution from core digital twin concepts to accountable, augmented implementations. Three focus categories—content, communication, and collaboration—link the central DT to subordinate components such as software operation, media presentation, participation, learning, and workflow management, highlighting where quality criteria like accuracy, efficiency, usability, sustainability, and accountability are addressed within this framework. Furthermore, digital twins utilize overarching technologies, including the Internet of Things (IoT) and AI. AI, for instance, plays a big role in DTs, encompassing content generation and modeling, as well as communication and collaboration. The remaining meta-fairness aspects (beyond the quality criteria) are not explicitly depicted in the figure; Table 2 and the dedicated questionnaire in Section 3.3 summarize the potential biases associated with the communication and collaboration categories to address the QC Fairness. In the following, we discuss these biases in greater detail.
4.2.2. Communication, Collaboration, and Bias
Bias in communication can arise from differing assessments of the situation, cultural or social differences, prejudice, aversion, incomplete or distorted messages, missing information, unreliable channels, or content that is unintentionally or deliberately manipulated. Therefore, it is cognitive in nature. Meier [76] provides information on eighteen different communication biases that influence and affect how the communication partners perceive and interpret mutual information.
As pointed out by Paulus et al. [87], biases or confirmation errors can reinforce each other. This is particularly harmful when path dependencies arise, whereby the initial data bias not only influences the initial decisions, but also leads to erroneous decision paths due to confirmation errors. The authors argue that the interplay of data bias and confirmation bias threatens the digital resilience of crisis response organizations. The risk of confirmation bias is high if data collection is based on undisclosed criteria, resulting in distorted data sets that do not properly reflect the population or cohort under investigation, for example. Further, unjustified beliefs about one’s own abilities, opinions, talents, or values, along with erroneous judgments or inappropriate generalizations about others, can lead to misjudgment of oneself or one’s position in relation to others. In addition, communication may also be distorted by third-party interference, which can exploit or obstruct it. To counter this risk, coding theory techniques such as redundancy and encryption can make communication more secure and error-tolerant.
For the category of collaboration, the top ten biases are identified in [77]. Some of these, such as confirmation and overconfidence biases, are similar to those highlighted by Meier [76] for communication. The key distinction is that communication biases primarily influence how messages are exchanged and interpreted (e.g., stereotyping or framing), whereas collaboration biases affect how groups organize, make decisions, and act collectively (e.g., groupthink or authority bias).
Note that although the biases cataloged in [76,77] are primarily human-oriented, they can be directly translated into checks for algorithmic fairness, since algorithmic bias often originates from human bias. For example, confirmation bias, that is, favoring information that supports pre-existing beliefs, can cause developers to unintentionally overlook evidence that a model is discriminatory. This connection has been widely relied on in the literature. For instance, Lin et al. [88] applies two fairness metrics to collaborative learning and model personalization, demonstrating that both fairness and accuracy of the resulting models can be improved. Similarly, Chen et al. [89] examines the problem of caching and request routing in DT services, incorporating both resource constraints and fairness-awareness in the context of collaboration between multi-access edge computing servers.
Crowdsourcing is a concern in collaboration-oriented DTs, since companies and cooperating public institutions are increasingly relying on it to address staff shortages and to develop innovative products and services at a lower cost. Fairness can be associated with various aspects of crowdsourcing, such as remuneration or recognition [90]. The authors observe that participants’ perceptions of fairness are significantly related to their interest in the products, their perception of innovativeness, and their loyalty intentions. The influence of two different fairness understandings is found to be asymmetric: distributive justice is a fundamental prerequisite to avoid negative behavioral consequences, while procedural justice motivates participants and positively affects their commitment.
Since avoiding bias is a prerequisite for fairness, various bias metrics have been developed that differ in how they weight different types of bias. The overview above demonstrates that, by using the MF framework described in Section 3.3, and in particular the DST approach for combining different conceptions of unfairness illustrated in Section 3.4, it is possible to achieve a more comprehensive understanding of potential discrimination and bias-related risks within the DTs.
4.2.3. Discussion
The concept of augmented DTs provides a highly flexible and illustrative framework for selecting specific features across the three DT categories and for evaluating associated biases or constructing bias metrics for these features. Realizing this potential in the sense of the methods proposed in Section 3.4, however, requires further empirical studies, as well as access to their findings and underlying data.
In practical applications, the MF framework can be complemented by augmented (healthcare) DTs. The overarching technologies, such as IoT, AI, and ML, should also be seen through the lens of MF before they are used to augment healthcare DTs. These technologies, along with big data, wearable sensors, and telemedicine, function as cross-cutting elements that support medical professionals in collecting and monitoring health data, identifying patient risks, and communicating treatment plans effectively between patients and clinicians.
By integrating these technological and methodological layers, augmented healthcare DTs offer a more comprehensive, data-informed, and ethically aware approach to patient care, while also providing a structured means to detect, quantify, and mitigate potential biases in the system. We argue that it may be more useful to consider fairness and related concepts not in terms of application domains or contexts and their associated technologies, but rather based on the MF framework and the features of augmented digital twins extending into the Metaverse.
5. Conclusions
The concept of fairness is situated at the intersection of ethical norms, government regulations, political perspectives, and social challenges within a heterogeneous society whose members vary widely in age, background, education, opinions, and purchasing power. These differences often give rise to conflicts, distributional struggles, and neglect of others’ interests. The debate over fairness is further influenced by heterogeneous structures in academia, professional associations with their scientific committees, and lobbyists representing business, employers, and employees. These actors participate with differing objectives and sometimes controversial positions, further complicating the discourse. In this respect, it becomes necessary to examine and discuss fairness and potential discrimination against individuals or groups at a meta-level across various contexts, in order to capture the complex interplay of social, political, and institutional factors.
To evaluate these issues, we proposed a meta-fairness framework that incorporates multiple quality criteria, including accuracy, explainability, responsibility, and auditability, alongside the often competing metrics for assessing fairness and avoiding discrimination. To demonstrate the framework in practice, we provided detailed questionnaires for medical risk assessment tools and outlined strategies for weighting and combining the criteria using DST. While the questionnaire-based evaluation is comprehensive, it is designed to be modular and adaptable, allowing domain experts to prioritize the MF components most relevant to their context. Evaluating all criteria simultaneously may not always be feasible, but missing information can be accommodated through DST and appropriate weighting. Importantly, the subjective expert assessments required to create basic probability assignments in DST are justified not by eliminating subjectivity, but by making it explicit, structured, and open to validation. We took a first step toward this by employing standardized questionnaires and well-defined procedures for processing expert input related to meta-fairness.
We illustrated potential applications of the MF framework in two ways. First, we examined a specific case: risk assessment for genetic mutations influencing early-onset breast cancer. Second, we explored broader, conceptual applications of MF to modern technologies, particularly digital twins (DTs), and assessed their significance in healthcare, where DTs with diverse features are starting to partially replace physical models, systems, and processes.
First and foremost, it is essential to incorporate expert insights from the relevant scientific disciplines into the discussion and to subsequently refine the MF framework and illustrate the concept of meta-fairness. At the moment, our research is based on an extensive literature review described in Section 2. Addressing the fairness-related challenges requires an interdisciplinary scientific discourse, aimed at developing practical concepts for identifying and combating discrimination across its various forms, as well as providing points of contact and effective access to arbitration procedures within institutional settings.
Despite the complexity of this task, our MF framework makes a meaningful contribution by providing a structured view of the various factors influencing fairness in different contexts. A promising direction for future research is the application of the MF framework within reinforcement learning. Real-world RL-enabled systems are highly complex, as agents operate in dynamic environments over extended periods. Ensuring the responsible development and deployment of such systems will therefore require a deeper understanding of fairness in RL, which the MF framework could help to structure and guide. Conversely, it would also be valuable to investigate how principles from RL can inform and enrich the concept of MF. Our long-term objective is to enable the automatic implementation of transparent fairness principles and bias mitigation in AI- and ML-based decision-making processes.
Author Contributions
W.L. and E.A. contributed equally to the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
https://github.com/lorenzgillner (accessed on 21 October 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following common abbreviations are used in this manuscript. This list is not exhaustive.
| AI | Artificial Intelligence |
| BC | Breast Cancer |
| BPA | Basic Probability Assignment |
| BRCA1/2 | BReast CAncer Gene 1 and 2 |
| COVID-19 | COronaVIrus Disease 2019 |
| DST | Dempster-Shafer Theory |
| DT | Digital Twin |
| FAIR | Findable, Accessible, Interoperable, Reusable |
| FAQ | Frequently Asked Questions |
| FE | Focal Element |
| IA | Interval Analysis |
| IoT | Internet of Things |
| KS | King Syndrome |
| MF | Meta-Fairness |
| ML | Machine Learning |
| OC | Ovarian Cancer |
| PT | Physical Twin |
| QC | Quality Criteria |
| RF | Risk Factor |
| RL | Reinforcement Learning |
| SA | Sensitive Attribute |
| V&V | Verification and Validation |
References
- Paulus, J.; Kent, D. Predictably unequal: Understanding and addressing concerns that algorithmic clinical prediction may increase health disparities. npj Digit. Med. 2020, 3, 99. [Google Scholar] [CrossRef]
- Kleinberg, J.; Mullainathan, S.; Raghavan, M. Inherent Trade-Offs in the Fair Determination of Risk Scores. In Proceedings of the 8th Innovations in Theoretical Computer Science Conference (ITCS 2017), Berkeley, CA, USA, 9–11 January 2017; Papadimitriou, C.H., Ed.; Schloss Dagstuhl–Leibniz-Zentrum für Informatik: Wadern, Germany, 2017; Volume 67, pp. 43:1–43:23. [Google Scholar] [CrossRef]
- Castelnovo, A.; Crupi, R.; Greco, G.; Regoli, D.; Penco, I.; Cosentini, A. A clarification of the nuances in the fairness metrics landscape. Sci. Rep. 2022, 12, 4209. [Google Scholar] [CrossRef]
- Luther, W.; Harutyunyan, A. Fairness in Healthcare and Beyond—A Survey. JUCS, 2025; to appear. [Google Scholar]
- Naeve-Steinweg, E. The averaging mechanism. Games Econ. Behav. 2004, 46, 410–424. [Google Scholar] [CrossRef]
- Hyman, J.M. Swimming in the Deep End: Dealing with Justice in Mediation. Cardozo J. Confl. Resolut. 2004, 6, 19–56. [Google Scholar]
- Hertweck, C.; Baumann, J.; Loi, M.; Vigano, E.; Heitz, C. A Justice-Based Framework for the Analysis of Algorithmic Fairness-Utility Trade-Offs. arXiv 2022. [Google Scholar] [CrossRef]
- Zehlike, M.; Loosley, A.; Jonsson, H.; Wiedemann, E.; Hacker, P. Beyond incompatibility: Trade-offs between mutually exclusive fairness criteria in machine learning and law. Artif. Intell. 2025, 340, 104280. [Google Scholar] [CrossRef]
- Shafer, G. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976. [Google Scholar] [CrossRef]
- Ferson, S.; Kreinovich, V.; Ginzburg, L.; Myers, D.S.; Sentz, K. Constructing Probability Boxes and Dempster-Shafer Structures; Sandia National Laboratories: Albuquerque, NM, USA, 2003. [Google Scholar] [CrossRef]
- Russo, M.; Vidal, M.E. Leveraging Ontologies to Document Bias in Data. arXiv 2024. [Google Scholar] [CrossRef]
- Newman, D.T.; Fast, N.J.; Harmon, D.J. When eliminating bias isn’t fair: Algorithmic reductionism and procedural justice in human resource decisions. Organ. Behav. Hum. Decis. Process. 2020, 160, 149–167. [Google Scholar] [CrossRef]
- Anderson, J.W.; Visweswaran, S. Algorithmic individual fairness and healthcare: A scoping review. JAMIA Open 2024, 8, ooae149. [Google Scholar] [CrossRef] [PubMed]
- AnIML. Bias and Fairness—AnIML: Another Introduction to Machine Learning. Available online: https://animlbook.com/classification/bias_fairness/index.html (accessed on 21 October 2025).
- Zliobaite, I. Measuring discrimination in algorithmic decision making. Data Min. Knowl. Discov. 2017, 31, 1060–1089. [Google Scholar] [CrossRef]
- Arnold, D.; Dobbie, W.; Hull, P. Measuring Racial Discrimination in Algorithms; Working Paper 2020-184; University of Chicago, Becker Friedman Institute for Economics: Chicago, IL, USA, 2020. [Google Scholar] [CrossRef]
- Mosley, R.; Wenman, R. Methods for Quantifying Discriminatory Effects on Protected Classes in Insurance; Research paper; Casualty Actuarial Society: Arlington, VA, USA, 2022. [Google Scholar]
- Sanna, L.J.; Schwarz, N. Integrating Temporal Biases: The Interplay of Focal Thoughts and Accessibility Experiences. Psychol. Sci. 2004, 15, 474–481. [Google Scholar] [CrossRef]
- Mozannar, H.; Ohannessian, M.I.; Srebro, N. From Fair Decision Making to Social Equality. arXiv 2020. [Google Scholar] [CrossRef]
- Ladin, K.; Cuddeback, J.; Duru, O.K.; Goel, S.; Harvey, W.; Park, J.G.; Paulus, J.K.; Sackey, J.; Sharp, R.; Steyerberg, E.; et al. Guidance for unbiased predictive information for healthcare decision-making and equity (GUIDE): Considerations when race may be a prognostic factor. npj Digit. Med. 2024, 7, 290. [Google Scholar] [CrossRef]
- Dwork, C.; Hardt, M.; Pitassi, T.; Reingold, O.; Zemel, R. Fairness Through Awareness. arXiv 2011, arXiv:1104.3913. [Google Scholar] [CrossRef]
- Baloian, N.; Luther, W.; Peñafiel, S.; Zurita, G. Evaluation of Cancer and Stroke Risk Scoring Online Tools. In Proceedings of the 3rd CODASSCA Workshop on Collaborative Technologies and Data Science in Smart City Applications, Yerevan, Armenia, 23–25 August 2022, Yerevan, Armenia, 23–25 August 2022; Hajian, A., Baloian, N., Inoue, T., Luther, W., Eds.; Logos Verlag: Berlin, Germany, 2022; pp. 106–111. [Google Scholar]
- Baumann, J.; Hertweck, C.; Loi, M.; Heitz, C. Distributive Justice as the Foundational Premise of Fair ML: Unification, Extension, and Interpretation of Group Fairness Metrics. arXiv 2023, arXiv:2206.02897. [Google Scholar] [CrossRef]
- Petersen, E.; Ganz, M.; Holm, S.H.; Feragen, A. On (assessing) the fairness of risk score models. arXiv 2023, arXiv:2302.08851. [Google Scholar] [CrossRef]
- Diakopoulos, N.; Friedler, S. Principles for Accountable Algorithms and a Social Impact Statement for Algorithms. Available online: https://www.fatml.org/resources/principles-for-accountable-algorithms (accessed on 21 October 2025).
- Alizadehsani, R.; Roshanzamir, M.; Hussain, S.; Khosravi, A.; Koohestani, A.; Zangooei, M.H.; Abdar, M.; Beykikhoshk, A.; Shoeibi, A.; Zare, A.; et al. Handling of uncertainty in medical data using machine learning and probability theory techniques: A review of 30 years (1991–2020). arXiv 2020. [Google Scholar] [CrossRef]
- Auer, E.; Luther, W. Uncertainty Handling in Genetic Risk Assessment and Counseling. JUCS J. Univers. Comput. Sci. 2021, 27, 1347–1370. [Google Scholar] [CrossRef]
- Gillner, L.; Auer, E. Towards a Traceable Data Model Accommodating Bounded Uncertainty for DST Based Computation of BRCA1/2 Mutation Probability with Age. JUCS J. Univers. Comput. Sci. 2023, 29, 1361–1384. [Google Scholar] [CrossRef]
- Pfohl, S.R.; Foryciarz, A.; Shah, N.H. An empirical characterization of fair machine learning for clinical risk prediction. J. Biomed. Inform. 2021, 113, 103621. [Google Scholar] [CrossRef]
- Penafiel, S.; Baloian, N.; Sanson, H.; Pino, J. Predicting Stroke Risk with an Interpretable Classifier. IEEE Access 2020, 9, 1154–1166. [Google Scholar] [CrossRef]
- Baniasadi, A.; Salehi, K.; Khodaie, E.; Bagheri Noaparast, K.; Izanloo, B. Fairness in Classroom Assessment: A Systematic Review. Asia-Pac. Educ. Res. 2023, 32, 91–109. [Google Scholar] [CrossRef]
- University of Minnesota Duluth. Reliability, Validity, and Fairness. 2025. Available online: https://assessment.d.umn.edu/about/assessment-resources/using-assessment-results/reliability-validity-and-fairness (accessed on 8 September 2025).
- Moreau, L.; Ludäscher, B.; Altintas, I.; Barga, R.S.; Bowers, S.; Callahan, S.; Chin, G., Jr.; Clifford, B.; Cohen, S.; Cohen-Boulakia, S.; et al. Special Issue: The First Provenance Challenge. Concurr. Comput. Pract. Exp. 2008, 20, 409–418. [Google Scholar] [CrossRef]
- Pasquier, T.; Lau, M.K.; Trisovic, A.; Boose, E.R.; Couturier, B.; Crosas, M.; Ellison, A.M.; Gibson, V.; Jones, C.R.; Seltzer, M. If these data could talk. Sci. Data 2017, 4, 170114. [Google Scholar] [CrossRef] [PubMed]
- Jacobsen, A.; de Miranda Azevedo, R.; Juty, N.; Batista, D.; Coles, S.; Cornet, R.; Courtot, M.; Crosas, M.; Dumontier, M.; Evelo, C.T.; et al. FAIR Principles: Interpretations and Implementation Considerations. Data Intell. 2020, 2, 10–29. [Google Scholar] [CrossRef]
- Wilkinson, M.D.; Dumontier, M.; Jan Aalbersberg, I.J.; Appleton, G.; Axton, M.; Baak, A.; Blomberg, N.; Boiten, J.-W.; da Silva Santos, L.; Bourne, P.E.; et al. The FAIR Guiding Principles for scientific data management and stewardship. Sci. Data 2016, 3, 160018. [Google Scholar] [CrossRef]
- Sculley, D.; Holt, G.; Golovin, D.; Davydov, E.; Phillips, T.; Ebner, D.; Chaudhary, V.; Young, M.; Dennison, D. Hidden Technical Debt in Machine Learning Systems. In Proceedings of the NIPS’15: 29th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 2494–2502. [Google Scholar]
- Qi, Q.; Tao, F.; Hu, T.; Anwer, N.; Liu, A.; Wei, Y.; Wang, L.; Nee, A. Enabling technologies and tools for digital twin. J. Manuf. Syst. 2021, 58, 3–21. [Google Scholar] [CrossRef]
- Neto, A.; Souza Neto, J. Metamodels of Information Technology Best Practices Frameworks. J. Inf. Syst. Technol. Manag. 2011, 8, 619. [Google Scholar] [CrossRef]
- Waytz, A.; Dungan, J.; Young, L. The whistleblower’s dilemma and the fairness–loyalty tradeoff. J. Exp. Soc. Psychol. 2013, 49, 1027–1033. [Google Scholar] [CrossRef]
- Zhang, Y.; Sang, J. Towards Accuracy-Fairness Paradox: Adversarial Example-based Data Augmentation for Visual Debiasing. In Proceedings of the 28th ACM International Conference on Multimedia, New York, NY, USA, 12–16 October 2020; MM ’20. pp. 4346–4354. [Google Scholar] [CrossRef]
- Carroll, A.; McGovern, C.; Nolan, M.; O’Brien, A.; Aldasoro, E.; O’Sullivan, L. Ethical Values and Principles to Guide the Fair Allocation of Resources in Response to a Pandemic: A Rapid Systematic Review. BMC Med. Ethics 2022, 23, 1–11. [Google Scholar] [CrossRef]
- Emanuel, E.; Persad, G. The shared ethical framework to allocate scarce medical resources: A lesson from COVID-19. Lancet 2023, 401, 1892–1902. [Google Scholar] [CrossRef]
- Kirat, T.; Tambou, O.; Do, V.; Tsoukiàs, A. Fairness and Explainability in Automatic Decision-Making Systems. A challenge for computer science and law. arXiv 2022, arXiv:2206.03226. [Google Scholar] [CrossRef]
- Modén, M.U.; Lundin, J.; Tallvid, M.; Ponti, M. Involving teachers in meta-design of AI to ensure situated fairness. In Proceedings of the Sixth International Workshop on Cultures of Participation in the Digital Age: AI for Humans or Humans for AI? Co-Located with the International Conference on Advanced Visual Interfaces (CoPDA@AVI 2022), Frascati, Italy, 7 June 2022; Volume 3136, pp. 36–42. [Google Scholar]
- Padh, K.; Antognini, D.; Lejal Glaude, E.; Faltings, B.; Musat, C. Addressing Fairness in Classification with a Model-Agnostic Multi-Objective Algorithm. arXiv 2021, arXiv:2009.04441. [Google Scholar]
- Jabbari, S.; Joseph, M.; Kearns, M.; Morgenstern, J.; Roth, A. Fairness in Reinforcement Learning. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; Precup, D., Teh, Y.W., Eds.; JMLR.org: New York, NY, USA, 2017; Volume 70, pp. 1617–1626. [Google Scholar] [CrossRef]
- Reuel, A.; Ma, D. Fairness in Reinforcement Learning: A Survey. arXiv 2024. [Google Scholar] [CrossRef]
- Petrović, A.; Nikolić, M.; M, J.; Bijanić, M.; Delibašić, B. Fair Classification via Monte Carlo Policy Gradient Method. Eng. Appl. Artif. Intell. 2021, 104, 104398. [Google Scholar] [CrossRef]
- Eshuijs, L.; Wang, S.; Fokkens, A. Balancing the Scales: Reinforcement Learning for Fair Classification. arXiv 2024. [Google Scholar] [CrossRef]
- Kim, W.; Lee, J.; Lee, J.; Lee, B.J. FairDICE: Fairness-Driven Offline Multi-Objective Reinforcement Learning. arXiv 2025. [Google Scholar] [CrossRef]
- Grote, T. Fairness as adequacy: A sociotechnical view on model evaluation in machine learning. AI Ethics 2024, 4, 427–440. [Google Scholar] [CrossRef]
- Kamiran, F.; Calders, T. Data preprocessing techniques for classification without discrimination. Knowl. Inf. Syst. 2012, 33, 1–33. [Google Scholar] [CrossRef]
- Menon, A.K.; Williamson, R.C. The cost of fairness in binary classification. In Proceedings of the 1st Conference on Fairness, Accountability and Transparency, New York, NY, USA, 23–24 February 2018; Friedler, S.A., Wilson, C., Eds.; PMLR: New York, NY, USA, 2018; Volume 81, pp. 107–118. [Google Scholar]
- Han, X.; Chi, J.; Chen, Y.; Wang, Q.; Zhao, H.; Zou, N.; Hu, X. FFB: A Fair Fairness Benchmark for In-Processing Group Fairness Methods. arXiv 2024, arXiv:2306.09468. [Google Scholar]
- Hardt, M.; Price, E.; Srebro, N. Equality of Opportunity in Supervised Learning. arXiv 2016, arXiv:1610.02413. [Google Scholar] [CrossRef]
- Baumann, J.; Hannák, A.; Heitz, C. Enforcing Group Fairness in Algorithmic Decision Making: Utility Maximization Under Sufficiency. In Proceedings of the 2022 ACM Conference on Fairness, Accountability, and Transparency, Seoul, Republic of Korea, 21–24 June 2022; FAccT ’22. pp. 2315–2326. [Google Scholar] [CrossRef]
- Duong, M.K.; Conrad, S. Towards Fairness and Privacy: A Novel Data Pre-processing Optimization Framework for Non-binary Protected Attributes. In Data Science and Machine Learning; Springer Nature: Singapore, 2023; pp. 105–120. [Google Scholar] [CrossRef]
- Bellamy, R.K.E.; Dey, K.; Hind, M.; Hoffman, S.C.; Houde, S.; Kannan, K.; Lohia, P.; Martino, J.; Mehta, S.; Mojsilovic, A.; et al. AI Fairness 360: An Extensible Toolkit for Detecting, Understanding, and Mitigating Unwanted Algorithmic Bias. arXiv 2018, arXiv:1810.01943. [Google Scholar] [CrossRef]
- Wang, S.; Wang, P.; Zhou, T.; Dong, Y.; Tan, Z.; Li, J. CEB: Compositional Evaluation Benchmark for Fairness in Large Language Models. arXiv 2025, arXiv:2407.02408. [Google Scholar]
- Fan, Z.; Chen, R.; Hu, T.; Liu, Z. FairMT-Bench: Benchmarking Fairness for Multi-turn Dialogue in Conversational LLMs. arXiv 2025, arXiv:2410.19317. [Google Scholar]
- Jin, R.; Xu, Z.; Zhong, Y.; Yao, Q.; Dou, Q.; Zhou, S.K.; Li, X. FairMedFM: Fairness Benchmarking for Medical Imaging Foundation Models. arXiv 2024, arXiv:2407.00983. [Google Scholar]
- Weinberg, L. Rethinking Fairness: An Interdisciplinary Survey of Critiques of Hegemonic ML Fairness Approaches. J. Artif. Intell. Res. 2022, 74, 75–109. [Google Scholar] [CrossRef]
- Moore, R.E.; Kearfott, R.B.; Cloud, M.J. Introduction to Interval Analysis; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2009. [Google Scholar] [CrossRef]
- Ayyub, B.M.; Klir, G.J. Uncertainty Modeling and Analysis in Engineering and the Sciences; Chapman & Hall/CRC: Boca Raton, FL, USA, 2006. [Google Scholar] [CrossRef]
- Smets, P. The Transferable Belief Model and Other Interpretations of Dempster-Shafer’s Model. arXiv 2013. [Google Scholar] [CrossRef]
- Skau, E.; Armstrong, C.; Truong, D.P.; Gerts, D.; Sentz, K. Open World Dempster-Shafer Using Complementary Sets. In Proceedings of the Thirteenth International Symposium on Imprecise Probability: Theories and Applications, Oviedo, Spain, 11–14 July 2023; de Cooman, G., Destercke, S., Quaeghebeur, E., Eds.; PMLR: New York, NY, USA, 2023; Volume 215, pp. 438–449. [Google Scholar]
- Xiao, F.; Qin, B. A Weighted Combination Method for Conflicting Evidence in Multi-Sensor Data Fusion. Sensors 2018, 18, 1487. [Google Scholar] [CrossRef]
- IEEE Computer Society. IEEE Standard for System, Software, and Hardware Verification and Validation; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar] [CrossRef]
- Auer, E.; Luther, W. Towards Human-Centered Paradigms in Verification and Validation Assessment. In Collaborative Technologies and Data Science in Smart City Applications; Hajian, A., Luther, W., Han Vinck, A.J., Eds.; Logos Verlag: Berlin, Germany, 2018; pp. 68–81. [Google Scholar]
- Barnes, J.J.I.; Konia, M.R. Exploring Validation and Verification: How they Differ and What They Mean to Healthcare Simulation. Simul. Heal. J. Soc. Simul. Healthc. 2018, 13, 356–362. [Google Scholar] [CrossRef]
- Riedmaier, S.; Danquah, B.; Schick, B.; Diermeyer, F. Unified Framework and Survey for Model Verification, Validation and Uncertainty Quantification. Arch. Comput. Methods Eng. 2020, 28, 1–26. [Google Scholar] [CrossRef]
- Kannan, H.; Salado, A. A Theory-driven Interpretation and Elaboration of Verification and Validation. arXiv 2025, arXiv:2506.10997. [Google Scholar]
- Hanna, M.G.; Pantanowitz, L.; Jackson, B.; Palmer, O.; Visweswaran, S.; Pantanowitz, J.; Deebajah, M.; Rashidi, H.H. Ethical and Bias Considerations in Artificial Intelligence/Machine Learning. Mod. Pathol. 2025, 38, 100686. [Google Scholar] [CrossRef] [PubMed]
- Mehrabi, N.; Morstatter, F.; Saxena, N.; Lerman, K.; Galstyan, A. A Survey on Bias and Fairness in Machine Learning. ACM Comput. Surv. (CSUR) 2021, 54, 1–35. [Google Scholar] [CrossRef]
- Meier, J.D. Communication Biases. Sources of Insight. 2025. Available online: https://sourcesofinsight.com/communication-biases/ (accessed on 21 October 2025).
- Sokolovski, K. Top Ten Biases Affecting Constructive Collaboration. 2018. Available online: https://innodirect.com/top-ten-biases-in-collaboration/ (accessed on 21 October 2025).
- Balagopalan, A.; Zhang, H.; Hamidieh, K.; Hartvigsen, T.; Rudzicz, F.; Ghassemi, M. The Road to Explainability is Paved with Bias: Measuring the Fairness of Explanations. In Proceedings of the FAccT ’22: 2022 ACM Conference on Fairness, Accountability, and Transparency, Seoul, Republic of Korea, 21–24 June 2022; pp. 1194–1206. [Google Scholar] [CrossRef]
- Spranca, M.; Minsk, E.; Baron, J. Omission and Commission in Judgment and Choice. J. Exp. Soc. Psychol. 1991, 27, 76–105. [Google Scholar] [CrossRef]
- Caton, S.; Haas, C. Fairness in Machine Learning: A Survey. ACM Comput. Surv. 2024, 56, 1–38. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, L.; Zhou, Z.; Laurentiev, J.; Lakin, J.R.; Zhou, L.; Hong, P. Assessing fairness in machine learning models: A study of racial bias using matched counterparts in mortality prediction for patients with chronic diseases. J. Biomed. Inform. 2024, 156, 104677. [Google Scholar] [CrossRef]
- Luther, W.; Baloian, N.; Biella, D.; Sacher, D. Digital Twins and Enabling Technologies in Museums and Cultural Heritage: An Overview. Sensors 2023, 23, 1583. [Google Scholar] [CrossRef]
- Katsoulakis, E.; Wang, Q.; Wu, H.L.; Shahriyari, L.; Fletcher, R.; Liu, J.; Achenie, L.; Liu, H.; Jackson, P.; Xiao, Y.; et al. Digital twins for health: A scoping review. npj Digit. Med. 2024, 7, 77. [Google Scholar] [CrossRef]
- Bibri, S.; Huang, J.; Jagatheesaperumal, S.; Krogstie, J. The Synergistic Interplay of Artificial Intelligence and Digital Twin in Environmentally Planning Sustainable Smart Cities: A Comprehensive Systematic Review. Environ. Sci. Ecotechnol. 2024, 20, 100433. [Google Scholar] [CrossRef]
- Islam, K.M.A.; Khan, W.; Bari, M.; Mostafa, R.; Anonthi, F.; Monira, N. Challenges of Artificial Intelligence for the Metaverse: A Scoping Review. Int. Res. J. Multidiscip. Scope 2025, 6, 1094–1101. [Google Scholar] [CrossRef]
- Luther, W.; Auer, E.; Sacher, D.; Baloian, N. Feature-oriented Digital Twins for Life Cycle Phases Using the Example of Reliable Museum Analytics. In Proceedings of the 8th International Symposium on Reliability Engineering and Risk Management (ISRERM 2022), Hannover, Germany, 4–7 September 2022; Beer, M., Zio, E., Phoon, K.K., Ayyub, B.M., Eds.; Research Publishing: Singapore, 2022; Volume 9, pp. 654–661. [Google Scholar]
- Paulus, D.; Fathi, R.; Fiedrich, F.; Walle, B.; Comes, T. On the Interplay of Data and Cognitive Bias in Crisis Information Management. Inf. Syst. Front. 2024, 26, 391–415. [Google Scholar] [CrossRef] [PubMed]
- Lin, F.; Zhao, C.; Vehik, K.; Huang, S. Fair Collaborative Learning (FairCL): A Method to Improve Fairness amid Personalization. INFORMS J. Data Sci. 2024, 4, 67–84. [Google Scholar] [CrossRef]
- Chen, L.; Zheng, S.; Wu, Y.; Dai, H.N.; Wu, J. Resource and Fairness-Aware Digital Twin Service Caching and Request Routing with Edge Collaboration. IEEE Wirel. Commun. Lett. 2023, 12, 1881–1885. [Google Scholar] [CrossRef]
- Faullant, R.; Füller, J.; Hutter, K. Fair play: Perceived fairness in crowdsourcing competitions and the customer relationship-related consequences. Manag. Decis. 2017, 55, 1924–1941. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).