TRIDENT-DE: Triple-Operator Differential Evolution with Adaptive Restarts and Greedy Refinement

Abstract

This paper introduces TRIDENT-DE, a novel ensemble-based variant of Differential Evolution (DE) designed to tackle complex continuous global optimization problems. The algorithm leverages three complementary trial vector generation strategies best/1/bin, current-to-best/1/bin, and pbest/1/bin executed within a self-adaptive framework that employs jDE parameter control. To prevent stagnation and premature convergence, TRIDENT-DE incorporates adaptive micro-restart mechanisms, which periodically reinitialize a fraction of the population around the elite solution using Gaussian perturbations, thereby sustaining exploration even in rugged landscapes. Additionally, the algorithm integrates a greedy line-refinement operator that accelerates convergence by projecting candidate solutions along promising base-to-trial directions. These mechanisms are coordinated within a mini-batch update scheme, enabling aggressive iteration cycles while preserving diversity in the population. Experimental results across a diverse set of benchmark problems, including molecular potential energy surfaces and engineering design tasks, show that TRIDENT-DE consistently outperforms or matches state-of-the-art optimizers in terms of both best-found and mean performance. The findings highlight the potential of multi-operator, restart-aware DE frameworks as a powerful approach to advancing the state of the art in global optimization.

1. Introduction

Global optimization remains a central challenge in computational science, offering indispensable tools for addressing problems of high complexity in diverse domains ranging from engineering and physics to economics, biology, and artificial intelligence. Unlike local search methods that tend to converge toward nearby minima and thus risk entrapment in suboptimal solutions, global optimization seeks to explore the search space more comprehensively in order to identify the true global optimum. The inherent difficulty of such tasks arises from the presence of multimodality, discontinuities, nonconvex structures, and high dimensionality, all of which demand algorithmic strategies that balance exploration with exploitation in a highly adaptive manner.

Global optimization is most clearly grounded in its mathematical formulation. Let $f:S\to \mathbb{R}$ be a continuous real-valued function defined on a feasible region $S\subset {\mathbb{R}}^n$. The goal is to determine a global minimizer $x^{★}\in S$ such that $f\left(x^{★}\right)\le f\left(x\right)$ for all $x\in S$. The feasible region is typically modeled as a Cartesian product of closed and bounded intervals, $S={\prod }_{i=1}^n[a_i,b_i]$, ensuring that S is compact (and convex under interval bounds). Under these conditions, optimization becomes the systematic pursuit of the minimizer within a well-defined, yet potentially rugged and high-dimensional, landscape.

Over the past decades, a wide variety of optimization algorithms have been introduced, evolving from traditional deterministic approaches to powerful modern metaheuristics. Classical derivative-based methods, such as steepest descent [1] and Newton’s method [2], are efficient for smooth and convex problems but struggle in the absence of gradient information or in the presence of multiple minima. Stochastic search methods like Monte Carlo sampling [3] and simulated annealing [4] introduced robustness to noise and multimodality but at the expense of slower convergence.

A particularly influential family of methods has been population-based metaheuristics. Genetic Algorithms (GA) [5], Differential Evolution (DE) [6,7,8,9], and Particle Swarm Optimization (PSO) [10,11,12] remain standard references in this field, each exploiting collective dynamics of populations to efficiently explore the solution space. Within this lineage, numerous refinements have been proposed to enhance adaptivity and performance. Self-adaptive Differential Evolution (SaDE) [13] and jDE [14] introduced mechanisms whereby control parameters co-evolve alongside candidate solutions, leading to more resilient search dynamics. Comprehensive Learning Particle Swarm Optimization (CLPSO) [15] extended the PSO paradigm by enhancing the information-sharing process across the swarm, thus improving the ability to escape local minima. The Covariance Matrix Adaptation Evolution Strategy (CMA-ES) [16], often regarded as one of the most sophisticated evolutionary optimizers, dynamically adapts covariance structures to guide search more effectively in anisotropic landscapes.

DE has evolved through several influential variants that improved either adaptation, sampling, or selection. JADE introduced the DE/current-to-pbest mutation with an external archive and on-the-fly parameter adaptation, substantially strengthening convergence and diversity control [17]. Building on JADE’s ideas, SHADE proposed success-history-based adaptation for F and CR, while L-SHADE further coupled this with linear population-size reduction to enhance late-stage exploitation [18,19]. In parallel, ensemble-style approaches such as CoDE and EPSDE combined multiple trial generators and parameter pools within a single framework, often yielding robust performance across heterogeneous landscapes [20,21]. More recently, jSO distilled the SHADE/L-SHADE family into an efficient adaptive scheme that performed strongly on CEC benchmarks [22], while lines such as LSHADE-RSP and multi-operator LSHADE variants integrated restart and local-search mechanisms [23,24]. Against this background, TRIDENT-DE is positioned as a complementary design: it employs a two-stage acceptance (a greedy refinement step followed by evaluation of the raw trial vector) and integrates this acceptance logic with our DE pipeline. This differs from success-history adaptation and ensemble selection in that it explicitly structures acceptance pressure at the variation level, which we show can improve stability of best and mean performance on real-world problems considered in this work. These developments provide the immediate backdrop against which more specialized and hybrid designs have emerged.

Recent years have also seen the development of highly specialized and hybrid approaches that push the limits of global optimization. The EA4Eig algorithm [25] exploits eigenspectrum information to adjust search directions more intelligently. The UDE3 (also known as UDE-III) method [26] introduces novel recombination schemes that maintain diversity while emphasizing convergence. Such developments underscore a continuing trend toward hybridization and adaptivity, in which classical frameworks are enriched by dynamic control, learning mechanisms, or hybrid ensembles of operators.

Derivative-free approaches such as the Nelder-Mead simplex [27] retain relevance in low-dimensional and gradient-free scenarios, while biologically and physically inspired heuristics such as ant colony optimization [28] and artificial bee colony [29] continue to provide innovative perspectives by mimicking natural processes [30]. These diverse algorithmic families collectively form the backbone of contemporary global optimization research, where robustness, scalability, and adaptivity remain the primary objectives.

The present article introduces TRIDENT-DE, a novel algorithmic framework that distinguishes itself from the aforementioned methodologies through its explicit reliance on a triple-operator ensemble structure combined with adaptive restart and greedy refinement strategies. Unlike standard Differential Evolution variants that typically rely on a single trial vector generation scheme, TRIDENT-DE simultaneously employs best/1/bin, current-to-best/1/bin, and pbest/1/bin within a self-adaptive mechanism, ensuring a dynamic balance between exploration and exploitation. This triadic structure, metaphorically represented as a “trident,” allows the algorithm to probe the search space from complementary perspectives, thereby reducing the likelihood of premature convergence. Furthermore, TRIDENT-DE incorporates a micro-restart mechanism that reinitializes a fraction of the population around the elite solution with Gaussian perturbations, preserving diversity without discarding accumulated information. An additional greedy line-refinement operator accelerates convergence by projecting solutions along base-to-trial directions, enabling more aggressive exploitation of promising regions. In contrast to hybrid algorithms that often combine unrelated strategies in ad hoc ways, TRIDENT-DE presents a cohesive framework where each component synergistically reinforces the others, yielding a method that is not only adaptive and robust but also computationally efficient. This conceptual and practical novelty positions TRIDENT-DE as a competitive advancement in the landscape of global optimization, capable of addressing high-dimensional, multimodal problems with a level of aggressiveness and resilience that surpasses existing methods.

The remainder of this paper is organized as follows: Section 2 details TRIDENT-DE, including design rationale and implementation aspects. Section 3 introduces the experimental protocol and results: Section 3.1 summarizes settings and computational environment, Section 3.2 enumerates the benchmark suites with emphasis on real-world instances, Section 3.3 analyzes parameter sensitivity, Section 3.4 examines time complexity and scaling behavior, Section 3.6 investigates neural network training with TRIDENT-DE on public classification datasets and Section 3.5 reports the comparative assessment against state-of-the-art solvers. Finally, Section 4 concludes with key findings and directions for future work.

2. The TRIDENT-DE Method

We now present the pseudocode of TRIDENT-DE to make the full control loop explicit. Before diving into it, recall that updates are executed in mini-batches: each agent builds multiple trials using three complementary Differential Evolution operators and retains the best one. A low-cost greedy line refinement is then applied along the base-to-trial direction, while parameters are perturbed via light self-adaptation. Iteration-level progress is assessed explicitly, when stagnation is detected, adaptive micro-restarts refresh diversity without disrupting exploitation around the elite. Feasibility is enforced by box projection, and termination follows an evaluation budget or a maximum-iteration cap. With this context, the pseudocode in Algorithm 1 below summarizes the stages and decision points implemented in TRIDENT-DE.

Algorithm 1 TRIDENT-DE (Triple-Operator, Restart-Aware DE)

Input: objective f, dimension n, population N, max iters $I_{max}$, max evals $F{E}_{max}$, bounds $\ell ,u$ Params: base F, crossover C, operator probs $r,q,p$ (best/1, cur2best/1, pbest/1), stagnation trigger $\tau$, restart fraction $\rho$, elite size $\kappa$, jitter amplitude $\lambda$, elite-kick prob $\pi$, line-refine factor $\beta$ 01 For i = 1…N do 02    For j = 1…n do 03         sample $x_{i,j}$ from Uniform (${\ell }_j,u_j$) 04    End for 05 $y_i\leftarrow f\left(x_i\right)$ 06 End for 07 $i^{★}\leftarrow arg{min}_i{y}_i$, $x^{★}$← $x_{i^{★}}$, $f^{★}\leftarrow y_{i^{★}}$, $A\leftarrow \left\{x^{★}\right\}$ $t\leftarrow 0$, $\mathrm{FE}\leftarrow N$, $s\leftarrow 0$ 08 While ($t<I_{max}$) and ($FE<F{E}_{max}$) do 09     $t\leftarrow t+1$, update $i^{★},x^{★},f^{★}$ // refresh incumbent 10     For i = 1…N do 11         If i = $i^{*}$ then continue 12             $x^0\leftarrow x_i$, $f^0\leftarrow y_i$ // cache current 13             Draw op ∈ {best/1, cur2best/1, pbest/1, none} with probs (r, q, p, $1-r+q+p$) 14             $F\leftarrow \mathrm{clip}(F+\lambda \mathcal{N}(0,1),0,2)$, $C_i\leftarrow \mathrm{clip}(C+\lambda \mathcal{N}(0,1),0,1)$ 15             $r_1\ne i$, $r_2\ne i$, $r_2\ne r_1$ 16             If op = best/1 then $v\leftarrow x^{★}+F_i(x_{r_1}-x_{r_2})$ 17             Else if op = cur2best/1 then $v\leftarrow x_i+F_i·(x^{★}-x_i)+F_i·(x_{r_1}-x_{r_2})$ 18             Else if op = pbest/1 then pick $p^{★}\in A\cup x^{★}$, $v\leftarrow p^{★}+F_i·(x_{r_1}-x_{r_2})$ 19             Else $v\leftarrow x_i$ 20        End if 21         Pick $j_{rand}$ uniformly from {1…n} 22         For j = 1…n do 23             If Uniform(0,1) < $C_i$orj = $j_{rand}$ then $z_j\leftarrow v_j$else$z_j\leftarrow x_{i,j}$ 24         $z_j\leftarrow clamp(z_j,{\ell }_j,u_j)$ 25         End for 26         $g\leftarrow z-x_i$, $x^{\top }\leftarrow clamp(x_i+\beta ·g,\ell ,u)$, 27         // ============= Two-Stage Acceptance (explicit) ============= 28         // =====Stage 1: Greedy refinement along base-to-trial direction==== 29         $f^{\top }\leftarrow f\left(x^{\top }\right)$, $FE\leftarrow FE+1$ 30         If $f^{\top }<f^0$ then 31             $x_i\leftarrow x^{\top }$, $y_i\leftarrow f^{\top }$ 32             If $y_i<f^{*}$then $x^{*}\leftarrow x_i$, $f^{★}\leftarrow y_i$, $s\leftarrow 0$, update elite ring A keeping $\left|A\right|\le \kappa$ 33         Else 34             // =====Stage 2: Evaluate and consider the raw trial vector z===== 35             $f^z\leftarrow f\left(z\right)$, $FE\leftarrow FE+1$ 36             If $f^z<f^0$ then 37                 $x_i\leftarrow z$, $y_i\leftarrow f^z$ 38                 If $y_i<f^{*}$ then $x^{★}\leftarrow x_i$, $f^{★}\leftarrow y_i$, $s\leftarrow 0$ 39             Else 40                 $x_i\leftarrow x^0$, $y_i\leftarrow f^0$ // explicit revert if neither stage improves 41             End if 42         End if 43     End for 44     If no $y_i$ improved then$s\leftarrow s+1$ else $s\leftarrow 0$ 45     If $s\ge \tau$ then 46         $m\leftarrow \lfloor \rho ·N\rfloor$, pick worst m indices set W 47         For each i in W do 48             If Uniform (0, 1) < $\pi$ then 49                 sample $x_i$ from $\mathcal{N}(x^{\prime }{\sigma }^2·{(u-\ell )}^2)$ 50             Else 51                 sample each $x_{i,j}$ from Uniform(${\ell }_j,u_j$) 52             End if 53             Project $x_i$ to box $[\ell ,u]$, 54             $y_i\leftarrow f\left(x_i\right)$, $FE\leftarrow FE+1$ 55         End for 56         $s\leftarrow 0$ 57     End if 58 End while 59 Return $x^{★},f^{★}$

• Notes for pseudocode.
• Objective and domain. $f:S\to \mathbb{R}$, $S=[\ell ,u]={\prod }_{j=1}^n[{\ell }_j,u_j]$. A candidate is $x\in {\mathbb{R}}^n$.
• Population and elite. Size N, $x_i$ is the i-th individual, $y_i=f\left(x_i\right)$. Best index $i^{★}=arg{min}_i{y}_i$, elite $x^{★}=x_{i^{★}}$, $f^{★}=f\left(x^{★}\right)$. Elite archive A holds up to $\kappa$ best solutions (ties by f).
• Operators. One of best/1, current-to-best/1, pbest/1, or none, drawn with probabilities $(r,q,p,1-(r+q+p\left)\right)$. With $r_1\ne r_2\ne i$:

  $$\begin{array}{cc}\hfill \mathit{best}/1:& v=x^{★}+F_i(x_{r_1}-x_{r_2}),\hfill \\ \hfill \mathit{current}-\mathit{to}-\mathit{best}/1:& v=x_i+F_i(x^{★}-x_i)+F_i(x_{r_1}-x_{r_2}),\hfill \\ \hfill \mathit{pbest}/1:& p^{★}\sim \mathrm{Unif}(A\cup \left\{x^{★}\right\}),v=p^{★}+F_i(x_{r_1}-x_{r_2}),\hfill \\ \hfill \mathit{none}:& v=x_i.\hfill \end{array}$$
• Controls. Per-individual jitter $F_i=\mathrm{clip}(F+{\lambda }_F{\xi }_F,0,2)$ and $C_i=\mathrm{clip}(C+{\lambda }_C{\xi }_C,0,1)$ with ${\xi }_F,{\xi }_C\sim \mathcal{N}(0,1)$. Scalar $\mathrm{clip}(x,a,b)=min\{max\{x,a\},b\}$; vector $\mathrm{clamp}(x,\ell ,u)$ applies $\mathrm{clip}$ component-wise.
• Crossover and projection. Binomial crossover with rate $C_i$ and one forced index $j_{\mathrm{rand}}$ from v ensures $z\ne x_i$. Project: $z\leftarrow \mathrm{clamp}(z,\ell ,u)$.
• Greedy refinement (one step). With $g=z-x_i$, $x^{\mathrm{ref}}=\mathrm{clamp}(x_i+\beta g,\ell ,u)$, $\beta \in (0,1]$; greedy selection against the snapshot $(x_i^0,f_i^0)$.
• Stagnation and micro-restarts. If no $y_i$ improves, stagnation counter $s\uparrow$; if $s\ge \tau$, restart worst $m=\lfloor \rho N\rfloor$ individuals by

  $$x_{i,j}\sim \mathcal{N}\left(x_j^{★},{\sigma }^2{(u_j-{\ell }_j)}^2\right)\mathrm{with}\mathrm{prob}.\pi ,\mathrm{else}{x}_{i,j}\sim \mathcal{U}({\ell }_j,u_j),$$

  then project $x_i\leftarrow \mathrm{clamp}(x_i,\ell ,u)$.
• Termination. Primary: $\mathrm{FE}\ge {\mathrm{FE}}_{max}$; secondary: $t\ge I_{max}$.

TRIDENT-DE is a population-based, derivative-free optimizer designed for box-constrained minimization of a continuous objective $f:S\to \mathbb{R}$ over $S=[\ell ,u]={\prod }_{j=1}^n[{\ell }_j,u_j]$. At iteration t, the algorithm maintains a population ${\left\{x_i^{\left(t\right)}\right\}}_{i=1}^N\subset S$ with fitness values $y_i^{\left(t\right)}=f\left(x_i^{\left(t\right)}\right)$. The incumbent elite is

$$i^{★}=arg\underset{i}{min}{y}_i^{\left(t\right)},x^{★}=x_{i^{★}}^{\left(t\right)},f^{★}=f\left(x^{★}\right).$$

An elite archive A of capacity $\kappa$ stores the best solutions seen so far (ties resolved by f) to support pbest sampling, feasibility is enforced throughout by componentwise projection $\mathrm{clamp}(x,\ell ,u)$, where for each coordinate j we set $x_j\leftarrow min\{max\{x_j,{\ell }_j\},u_j\}$.

Initialization.

Each coordinate is drawn independently as $x_{i,j}^{\left(0\right)}\sim \mathcal{U}({\ell }_j,u_j)$; then $y_i^{\left(0\right)}=f\left(x_i^{\left(0\right)}\right)$ is evaluated, the elite $x^{★}$ is set, and the archive is seeded as $A\leftarrow \left\{x^{★}\right\}$. This uniform seeding spreads initial mass across S without imposing structural priors on f.

Per-iteration control flow.

At the start of iteration t, the elite is refreshed so that all subsequent operators are anchored to the most recent best. For each individual i, a rollback snapshot $(x_i^0,f_i^0)=(x_i^{\left(t\right)},y_i^{\left(t\right)})$ is taken to guarantee non-worsening replacement. A trial-vector generator $\mathrm{op}\in \{\mathit{best}/1, \mathit{current}-\mathit{to}-\mathit{best}/1, \mathit{pbest}/1, \mathit{none}\}$ is selected by a categorical draw with probabilities $(r,q,p,1-(r+q+p\left)\right)$. This triad yields complementary pressures: best/1 concentrates exploitation around $x^{★}$; current-to-best/1 steers $x_i$ toward $x^{★}$ while retaining a differential term, pbest/1 exploits $A\cup \left\{x^{★}\right\}$ to distribute attraction over multiple high-quality anchors, the none branch stabilizes dynamics when parameter jitter is aggressive.

Light self-adaptation.

Control parameters are perturbed at the individual level using one Gaussian deviate per parameter:

$$F_i=\mathrm{clip}(F+{\lambda }_F{\xi }_F,0,2),C_i=\mathrm{clip}(C+{\lambda }_C{\xi }_C,0,1),$$

with ${\xi }_F,{\xi }_C\sim \mathcal{N}(0,1)$ independent and ${\lambda }_F,{\lambda }_C>0$ controlling jitter amplitude. This preserves evaluation efficiency while adapting to local roughness.

Donor formation, crossover and projection.

With mutually distinct indices $r_1\ne r_2\ne i$ drawn uniformly from $\{1,\dots ,N\}$, the donor v is

$$\begin{array}{cc}\hfill \mathit{best}/\mathbf{1}:& v=x^{★}+F_i(x_{r_1}^{\left(t\right)}-x_{r_2}^{\left(t\right)}),\hfill \\ \hfill \mathit{current}-\mathit{to}-\mathit{best}/1:& v=x_i^{\left(t\right)}+F_i(x^{★}-x_i^{\left(t\right)})+F_i(x_{r_1}^{\left(t\right)}-x_{r_2}^{\left(t\right)}),\hfill \\ \hfill \mathit{pbest}/1:& p^{★}\sim \mathrm{Unif}\left(A\cup \left\{x^{★}\right\}\right),v=p^{★}+F_i(x_{r_1}^{\left(t\right)}-x_{r_2}^{\left(t\right)}),\hfill \end{array}$$

and $v=x_i^{\left(t\right)}$ if $\mathrm{op}=\mathit{none}$. Binomial crossover with rate $C_i$ forms z from $(v,x_i^{\left(t\right)})$, forcing one dimension $j_{\mathrm{rand}}$ from v to ensure $z\ne x_i^{\left(t\right)}$; feasibility is restored by $z\leftarrow \mathrm{clamp}(z,\ell ,u)$.

One-step greedy refinement and acceptance.

Let $g=z-x_i^{\left(t\right)}$. A low-cost, one-evaluation line refinement proposes

$$x^{\mathrm{ref}}=\mathrm{clamp}\left(x_i^{\left(t\right)}+\beta g,\ell ,u\right),\beta \in (0,1],$$

and evaluates $f\left(x^{\mathrm{ref}}\right)$. If $f\left(x^{\mathrm{ref}}\right)<f_i^0$, we accept $(x_i^{(t+1)},y_i^{(t+1)})=(x^{\mathrm{ref}},f\left(x^{\mathrm{ref}}\right))$; otherwise we evaluate the raw trial once, $f\left(z\right)$, accepting z if $f\left(z\right)<f_i^0$ and rolling back to $(x_i^0,f_i^0)$ otherwise. Whenever a replacement improves the global best, we set $x^{★}\leftarrow x_i^{(t+1)}$, update $f^{★}$, and update the archive A (insert if $\left|A\right|<\kappa$, else replace the worst).

Stagnation and adaptive micro-restarts.

A stagnation counter s increments when no $y_i$ improves within an iteration; otherwise it resets. If $s\ge \tau$, we restart the worst $m=\lfloor \rho N\rfloor$ individuals. For each restarted index i, with probability $\pi$ we sample an elite-centred Gaussian kick

$$x_{i,j}\sim \mathcal{N}\left(x_j^{★},{\sigma }^2{(u_j-{\ell }_j)}^2\right)\mathrm{independently}\mathrm{for}j=1,\dots ,n,$$

and with probability $1-\pi$ we reinitialize uniformly $x_{i,j}\sim \mathcal{U}({\ell }_j,u_j)$; in both cases we project with $x_i\leftarrow \mathrm{clamp}(x_i,\ell ,u)$ and refresh $y_i=f\left(x_i\right)$.

Budget and ordering.

Termination is governed primarily by the evaluation budget $\mathrm{FE}\ge {\mathrm{FE}}_{max}$ and secondarily by an iteration cap $t\ge I_{max}$. The ordering elite refresh, operator selection, parameter jitter, donor formation, crossover, projection, greedy refinement, fallback raw-trial, acceptance/archive update, stagnation accounting, and (if needed) micro-restart ensures that refinement reuses a precomputed direction, projection preserves feasibility at every stage, and diversity is injected only under verified stagnation.

As shown in Figure 1, after initialization and elite refresh, each agent undergoes operator selection, parameter jitter, trial construction, and greedy line refinement, followed if necessary by a single raw-trial evaluation. Iteration-level progress is assessed at node U, to avoid ambiguity, the “Yes” and “No” branches lead to separate actions V (reset stagnation counter) and Y (increase stagnation counter) which both feed into W (restart trigger). When the trigger fires, micro-restarts (X) rejuvenate a worst fraction near the elite (or uniformly), after which the loop returns to the main termination check. This organization clarifies control flow, emphasizes the low-cost refinement step, and shows precisely how stagnation governs diversity injection.

Figure 1. TRIDENT-DE flowchart: triple-operator DE with greedy refinement and adaptive micro-restarts.

3. Experimental Setup and Benchmark Results

3.1. Setup

Table 1 summarizes the core settings of TRIDENT-DE, grouping the population size, the box bounds, and the default DE controls (F, C) together with the jDE-style self-adaptation (resampling probabilities and sampling ranges). It also lists the hyperparameters governing the triple trial-vector ensemble, the greedy line-refinement, and the adaptive micro-restart policy (restart fraction $\rho$, Gaussian kick scale $\sigma$, stagnation trigger $\tau$). Note that operator scheduling follows a round-robin (three operators) scheme in the manuscript, while the implementation uses a round-robin (three operators) to balance exploration and exploitation across iterations. The defaults ${\mathrm{FE}}_{max}$ = $1.5·{10}^5$ and $I_{max}$ = 500 standardize the computational budget across problems and act as termination criteria, with priority given to the evaluation budget (see Table 1).

Table 1. Default TRIDENT-DE settings: exploration-exploitation balance and restart mechanisms.

Name	Value	Description
N	100	Population size
n	problem	Problem dimension (from instance).
$[\ell ,u]$	from problem, fallback ${[-1,1]}^n$	Box bounds, fallback used if margins missing.
F	$F^0=0.9$	Baseline scale, per-individual $F_i$ (jDE-style control in code).
C	$C^0=0.7$	Baseline crossover, per-individual $C_i$ (jDE-style control in code).
$r,q,p$	(round-robin)	Operator selection in manuscript, implementation uses 3-operator cycle.
$\tau$	18	Stagnation trigger (no-improvement iterations before restart).
$\rho$	0.10	Fraction of worst individuals to restart.
$\sigma$	0.20	Gaussian kick scale at restart (× box range).
$\beta$	$\{1.0,0.5\}$	One-step greedy line-refine factors.
${\mathrm{FE}}_{max}$	150,000	Evaluation-budget termination (code default).
$I_{max}$	500	Iteration cap (used in manuscript, not enforced by code).
$\alpha$	0.55	Mini-batch ratio.
t	4	Trials per agent.
${\tau }_F$	0.10	jDE resampling prob. for $F_i$.
${\tau }_C$	0.10	jDE resampling prob. for $C_i$.
$F_{\ell },F_u$	$0.1,1.2$	Bounds for jDE resampling of $F_i$.
$C_{\ell },C_u$	$0.0,0.95$	Bounds for jDE resampling of $C_i$.
$\phi$	0.10	Top-p fraction for pbest/1.

We adopted a two-part policy for parameter selection. First, when broadly accepted defaults exist in the DE literature (e.g., ranges for F and C and pbest-style sampling), we used those settings to ensure comparability. Second, for TRIDENT-DE–specific knobs the operator probabilities (r, q, p), jitter amplitude $\lambda$, line-refine factor $\beta$, stagnation threshold $\tau$, restart fraction $\rho$, elite size $\kappa$, and elite-kick probability $\pi$ we ran a small pilot grid on held-out problems to pick robust values. Afterwards, the very same configuration was kept fixed across all benchmarks (synthetic and real-world), avoiding per-problem tuning and supporting fair and reproducible comparisons. Intuitively, F/C remain in safe exploration–exploitation zones, (r, q, p) balance best/1, current-to-best/1, and pbest/1, a modest $\lambda$ prevents instability, $\beta$ leverages a low-cost base→trial direction, and ($\tau$, $\rho$, $\pi$) trigger gentle micro-restarts only under verified stagnation.

Table 2 reports the configurations of all competitor methods to ensure reproducibility and fairness with respect to population size and iteration budget. For each algorithm, we list its internal controls (e.g., the comprehensive-learning probability for CLPSO, population sizing and coefficients for CMA-ES, JADE-style parameters for EA4Eig, success-history memories and p-best ranges for mLSHADE_RL and UDE3, and adaptation schemes for SaDE) as used in our experiments. Harmonizing the population at N = 100 and the iteration cap at $I_{max}$ = 500 guarantees comparability, while per-method settings follow the literature and publicly available implementations.

Table 2. Parameters of other methods.

Name	Value	Description
N	100	Population size for all methods
$I_{max}$	500	Maximum number of iterations for all methods
CLPSO
clProb	0.3	Comprehensive learning probability
cognitiveWeight	1.49445	Cognitive weight
inertiaWeight	0.729	Inertia weight
mutationRate	0.01	Mutation rate
socialWeight	1.49445	Social weight
CMA-ES
$N_{CMA-ES}$	$4+⌊3·log\left(dim\right)⌋$	Population size
EA4Eig
archiveSize	100	Archive size for JADE-style mutation
eig_interval	5	Recompute eigenbasis every k iterations
maxCR	1	Upper bound for CR
maxF	1	Upper bound for F
minCR	0	Lower bound for CR
minF	0.1	Lower bound for F
pbest	0.2	p-best fraction (current-to-pbest/1)
tauCR	0.1	Self-adaptation prob. for CR
tauF	0.1	Self-adaptation prob. for F
mLSHADE_RL
archiveSize	500	Archive size
memorySize	10	Success-history memory size (H)
minPopulation	4	Minimum population size
pmax	0.2	Maximum p-best fraction
pmin	0.05	Minimum p-best fraction
SaDE
crSigma	0.1	Std for CR sampling
fGamma	0.1	Scale for Cauchy F sampling
initCR	0.5	Initial CR mean
initF	0.7	Initial F mean
learningPeriod	25	Iterations per adaptation window
UDE3
minPopulation	4	Minimum population size.
memorySize	10	Success-history memory size (H).
archiveSize	100	Archive size.
pmin	0.05	Minimum p-best fraction.
pmax	0.2	Maximum p-best fraction.

All experiments were conducted on a high-performance node featuring a cpu with 32 threads running Debian Linux. The evaluation protocol was designed for statistical rigor and reproducibility: each benchmark function was executed 30 times independently, using distinct random seeds to capture the stochastic variability of the algorithms.

The proposed method and all baselines were implemented in optimized ANSI C++ and integrated into the open-source OPTIMUS framework [31]. The source code is hosted at https://github.com/itsoulos/GLOBALOPTIMUS (accessed 25 September 2025), ensuring transparency and reproducibility. Parameter settings exactly follow Table 1 and Table 2. Build environment: Debian 12.12 with GCC 13.4.

The primary performance indicator is the average number of objective-function evaluations over 30 runs for each test function. In all ranking tables comparing solvers, best values are highlighted in green (1st place) and second-best values in blue (2nd place).

3.2. Benchmark Functions

Table 3 compiles the real-world optimization problems used in our evaluation. For each case, we report a brief description, the dimensionality and variable types (continuous/mixed-integer), the nature and count of constraints (inequalities/equalities), salient landscape properties (nonconvexity, multi-modality), as well as the evaluation budget and comparison criteria. The set spans, indicatively, mechanical design, energy scheduling, process optimization, and parameter estimation with black-box simulators, ensuring that conclusions extend beyond synthetic test functions. Where applicable, we also note any normalizations or constraint reformulations adopted for fair comparison.

Table 3. The real world benchmark functions used in the conducted experiments.

Problem	Formula	Dim	Constraints/Bounds
Parameter Estimation for Frequency-Modulated Sound Waves [32,33,34]	${min}_{x\in {[-6.4,6.35]}^6}f\left(x\right)={\displaystyle \frac{1}{N}}{\sum }_{n=1}^N{\left|y(n;x)-y_{\mathrm{target}}\left(n\right)\right|}^2$ $y(n;x)=x_{0}sin\left(x_{1}n+x_{2}sin(x_{3}n+x_{4}sin\left(x_{5}n\right))\right)$	6	$x_i\in [-6.4,6.35]$
Lennard-Jones Potential (atoms: 10, 13, 38) [35]	${min}_{x\in {\mathbb{R}}^{3N-6}}f\left(x\right)=4{\sum }_{i=1}^{N-1}{\sum }_{j=i+1}^N\left[{\left({\displaystyle \frac{1}{r_{ij}}}\right)}^{12}-{\left({\displaystyle \frac{1}{r_{ij}}}\right)}^6\right]$	24, 43, 108	$x_0\in (0,0,0)$ $x_1,x_2\in [0,4]$ $x_3\in [0,\pi ]$ $x_{3k-3}$ $x_{3k-2}$ $x_i\in [-b_k,+b_k]$
Bifunctional Catalyst Blend Optimal Control [36,37,38]	${\displaystyle \frac{d{x}_1}{dt}}=-k_1{x}_1$, ${\displaystyle \frac{d{x}_2}{dt}}=k_1{x}_1-k_2{x}_2+k_3{x}_2+k_4{x}_3$, ${\displaystyle \frac{d{x}_3}{dt}}=k_2{x}_2$, ${\displaystyle \frac{d{x}_4}{dt}}=-k_4{x}_4+k_5{x}_5$, ${\displaystyle \frac{d{x}_5}{dt}}=-k_3{x}_2+k_6{x}_4-k_5{x}_5+k_7{x}_6+k_8{x}_7+k_9{x}_5+k_{10}{x}_7$ ${\displaystyle \frac{d{x}_6}{dt}}=k_8{x}_5-k_7{x}_6$, ${\displaystyle \frac{d{x}_7}{dt}}=k_9{x}_5-k_{10}{x}_7$ $k_i\left(u\right)=c_{i1}+c_{i2}u+c_{i3}{u}^2+c_{i4}{u}^3$	1	$u\in [0.6,0.9]$
Optimal Control of a Non-Linear Stirred Tank Reactor [39,40,41]	$J\left(u\right)={\int }_0^{0.72}\left[x_1{\left(t\right)}^2+x_2{\left(t\right)}^2+0.1u^2\right]dt$ ${\displaystyle \frac{d{x}_1}{dt}}=-2x_1+x_2+1.25u+0.5exp\left({\displaystyle \frac{x_1}{x_1+2}}\right)$ ${\displaystyle \frac{d{x}_2}{dt}}=-x_2+0.5exp\left({\displaystyle \frac{x_1}{x_1+2}}\right)$ $x_1\left(0\right)=0.9,x_2\left(0\right)=0.09$, $t\in [0,0.72]$	1	$u\in [0,5]$
Tersoff Potential for model Si (B) [42,43]	${min}_{\mathbf{x}\in \mathrm{\Omega }}f\left(\mathbf{x}\right)={\sum }_{i=1}^{N}E\left({\mathbf{x}}_i\right)$ $E\left({\mathbf{x}}_i\right)={\displaystyle \frac{1}{2}}{\sum }_{j\ne i}{f}_c\left(r_{ij}\right)\left[V_R\left(r_{ij}\right)-B_{ij}{V}_A\left(r_{ij}\right)\right]$ where $r_{ij}=\parallel {\mathbf{x}}_i-{\mathbf{x}}_j\parallel$, $V_R\left(r\right)=Aexp(-{\lambda }_{1}r)$ $V_A\left(r\right)=Bexp(-{\lambda }_{2}r)$ $f_c\left(r\right)$: cutoff function with $f_c\left(r\right)$: angle parameter	30	$x_1\in [0,4]$ $x_2\in [0,4]$ $x_3\in [0,\pi ]$ $x_i\in \left[{\displaystyle \frac{4(i-3)}{4}},4\right]$
Tersoff Potential for model Si (C) [42,43]	${min}_{\mathbf{x}}V\left(\mathbf{x}\right)={\sum }_{i=1}^N{\sum }_{j>i}^N{f}_C\left(r_{ij}\right)\left[a_{ij}{f}_R\left(r_{ij}\right)+b_{ij}{f}_A\left(r_{ij}\right)\right]$ $f_C\left(r\right)=\left\{\begin{array}{cc}1,\hfill & r<R-D\hfill \\ {\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{2}}cos\left({\displaystyle \frac{\pi (r-R+D)}{2D}}\right),\hfill & |r-R|\le D\hfill \\ 0,\hfill & r>R+D\hfill \end{array}\right.$ $f_R\left(r\right)=Aexp(-{\lambda }_{1}r)$ $f_A\left(r\right)=-Bexp(-{\lambda }_{2}r)$ $b_{ij}={\left[1+\left({\beta }^n\right){\zeta }_{ij}^n\right]}^{-1/\left(2n\right)}$ ${\sum }_{k\ne i,j}{f}_C\left(r_{ik}\right)g\left({\theta }_{ijk}\right)exp\left[{\lambda }_3^3{(r_{ij}-r_{ik})}^3\right]$	30	$x_1\in [0,4]$ $x_2\in [0,4]$ $x_3\in [0,\pi ]$ $x_i\in \left[{\displaystyle \frac{4(i-3)}{4}},4\right]$
Spread Spectrum Radar Polyphase Code Design [44]	${min}_{x\in X}f\left(x\right)=max\left\{|{\phi }_1\left(x\right)|,|{\phi }_2\left(x\right)|,\dots ,|{\phi }_m\left(x\right)|\right\}$ $X=\{x\in {\mathbb{R}}^n\mid 0\le x_j\le 2\pi ,j=1,\dots ,n\}m=2n-1$ ${\phi }_j\left(x\right)=\left\{\begin{array}{cc}{\displaystyle \sum _{k=1}^{n-j}cos(x_k-x_{k+j})}\hfill & \mathrm{for}j=1,\dots ,n-1\hfill \\ {\displaystyle n}\hfill & \mathrm{for}j=n\hfill \\ {\displaystyle {\phi }_{2n-j}\left(x\right)}\hfill & \mathrm{for}j=n+1,\dots ,2n-1\hfill \end{array}\right.$ ${\phi }_j\left(x\right)={\sum }_{k=1}^{n-j}cos(x_k-x_{k+j}),j=1,\dots ,n-1$ ${\phi }_n\left(x\right)=n$, ${\phi }_{n+\ell }\left(x\right)={\phi }_{n-\ell }\left(x\right),\ell =1,\dots ,n-1$	20	$x_j\in [0,2\pi ]$
Transmission Network Expansion Planning [45]	$min{\sum }_{l\in \mathrm{\Omega }}{c}_l{n}_l+W_1{\sum }_{l\in OL}|f_l-{\overline{f}}_l|+W_2{\sum }_{l\in \mathrm{\Omega }}max(0,n_l-{\overline{n}}_l)$ $Sf=g-d$ $f_l={\gamma }_l{n}_l\mathrm{\Delta }{\theta }_l,\forall l\in \mathrm{\Omega }$ $|f_l|\le {\overline{f}}_l{n}_l,\forall l\in \mathrm{\Omega }$ $0\le n_l\le {\overline{n}}_l,n_l\in \mathbb{Z},\forall l\in \mathrm{\Omega }$	7	$0\le n_i\le {\overline{n}}_l$ $n_i\in \mathbb{Z}$
Electricity Transmission Pricing [46]	${min}_{x}f\left(x\right)={\sum }_{i=1}^{N_g}{\left({\displaystyle \frac{C_i^{gen}}{P_i^{gen}}}-R_i^{gen}\right)}^2+{\sum }_{j=1}^{N_d}{\left({\displaystyle \frac{C_j^{load}}{P_j^{load}}}-R_j^{load}\right)}^2$ ${\sum }_{j}G{D}_{i,j}+{\sum }_{j}B{T}_{i,j}=P_i^{gen},\forall i$ ${\sum }_{i}G{D}_{i,j}+{\sum }_{i}B{T}_{i,j}=P_j^{load},\forall j$ $G{D}_{i,j}^{max}=min(P_i^{gen}-B{T}_{i,j},P_j^{load}-B{T}_{i,j})$	126	$G{D}_{i,j}\in [0,G{D}_{i,j}^{max}]$
Circular Antenna Array Design [47]	${min}_{r_1,\dots ,r_6,{\phi }_1,\dots ,{\phi }_6}f\left(\mathbf{x}\right)={max}_{\theta \in \mathrm{\Omega }}AF(\mathbf{x},\theta )$ $AF(\mathbf{x},\theta )=\left|{\sum }_{k=1}^{6}exp\left(j\left[2\pi r_{k}cos(\theta -{\theta }_k)+{\phi }_k{\displaystyle \frac{\pi }{180}}\right]\right)\right|$	12	$r_k\in [0.2,1]$ ${\phi }_k\in [-180,180]$
Cassini 2: Spacecraft Trajectory Optimization Problem [48]	$x={\left[t_0,\mathrm{\Delta }{t}_1,\dots ,\mathrm{\Delta }{t}_5,p_1,\dots ,p_4\right]}^{\top },$ ${min}_{x}J\left(x\right)=\mathrm{\Delta }{v}_{\mathrm{launch}}+{\sum }_{\ell =1}^4\mathrm{\Delta }{v}_{\ell }^{\mathrm{DSM}}+\mathrm{\Delta }{v}_{\mathrm{arrival}},$ $E\to V\to E\to V\to J\to S$ $t_0\in [850,2000],\mathrm{\Delta }{t}_{\ell }\in [20,1200],p_{\ell }\in [1.0,10.0].$	10	$r_{p,\ell }\ge R_{P_{\ell }}+h_{min,P_{\ell }},$ ${\delta }_{\ell }\le {\delta }_{max,P_{\ell }},$ $t_0^{min}\le t_0\le t_0^{max},$ $\mathrm{\Delta }{t}_{\ell }^{min}\le \mathrm{\Delta }{t}_{\ell }\le \mathrm{\Delta }{t}_{\ell }^{max}.$
Wireless Coverage Antenna Placement [49,50]	$x_i,y_i\in \mathbb{R}\left(\mathrm{position}\right),P_i\in {\mathbb{R}}_{\ge 0}\left(\mathrm{transmission}\mathrm{power}\right).$ $S_{iu}(x_i,y_i,P_i)={\displaystyle \frac{G{P}_i}{{\left({(x_i-x_u)}^2+{(y_i-y_u)}^2\right)}^{\alpha /2}+\epsilon }},$ ${min}_{x,y,P}\underset{\stackrel{⏟}{\mathrm{coverage}\mathrm{deficiency}}}{{\displaystyle \sum _{u\in \mathcal{U}}}{\left[\tau -S_u(x,P)\right]}_{+}}+{\lambda }_P{\sum }_{i=1}^N{P}_i+,$ ${\lambda }_O{\sum }_{u\in \mathcal{U}}{\sum }_{i<j}{\left[min\{S_{iu},S_{ju}\}-\kappa \right]}_{+}$ $S_u(x,P)={max}_{i=1,\dots ,N}{S}_{iu}(x_i,y_i,P_i).$	30	$0\le x_i\le W,$ $0\le y_i\le H,$ $0\le P_i\le P_{max}$
Dynamic Economic Dispatch 1 [51]	${min}_{\mathbf{P}}f\left(\mathbf{P}\right)={\sum }_{t=1}^{24}{\sum }_{i=1}^5\left(a_i{P}_{i,t}^2+b_i{P}_{i,t}+c_i\right)$ $P_i^{min}\le P_{i,t}\le P_i^{max},\forall i=1,\dots ,5,t=1,\dots ,24$ ${\sum }_{i=1}^5{P}_{i,t}=D_t,\forall t=1,\dots ,24$ $P_{min}=[10,20,30,40,50]$ $P_{max}=[75,125,175,250,300]$	120	$P_i^{min}\le P_{i,t}\le P_i^{max}$
Dynamic Economic Dispatch 2 [51]	${min}_{\mathbf{P}}f\left(\mathbf{P}\right)={\sum }_{t=1}^{24}{\sum }_{i=1}^9\left(a_i{P}_{i,t}^2+b_i{P}_{i,t}+c_i\right)$ $P_i^{min}\le P_{i,t}\le P_i^{max},\forall i=1,\dots ,5,t=1,\dots ,24$ ${\sum }_{i=1}^5{P}_{i,t}=D_t,\forall t=1,\dots ,24$ $P_{min}=[150,135,73,60,73,57,20,47,20]$ $P_{max}=[470,460,340,300,243,160,130,120,80]$	216	$P_i^{min}\le P_{i,t}\le P_i^{max}$
Static Economic Load Dispatch (1,2,3,4,5)[51]	${min}_{P_1,\dots ,P_{N_G}}F={\sum }_{i=1}^{N_G}{f}_i\left(P_i\right)$ $f_i\left(P_i\right)=a_i{P}_i^2+b_i{P}_i+c_i,i=1,2,\dots ,N_G$ $f_i\left(P_i\right)=a_i{P}_i^2+b_i{P}_i+c_i+|e_{i}sin\left(f_i(P_i^{min}-P_i)\right)|$ $P_i^{min}\le P_i\le P_i^{max},i=1,2,\dots ,N_G$ ${\sum }_{i=1}^{N_G}{P}_i=P_D+P_L$ $P_L={\sum }_{i=1}^{N_G}{\sum }_{j=1}^{N_G}{P}_i{B}_{ij}{P}_j+{\sum }_{i=1}^{N_G}{B}_{0i}{P}_i+B_{00}$ $P_i-P_i^0\le U{R}_i{P}_i^0-P_i\le D{R}_i$	6 13 15 40 140	See Technical Report of CEC2011

3.3. Parameter Sensitivity Analysis of TRIDENT-DE

Following Lee et al.’s [52] parameter-sensitivity methodology, we construct a structured analysis to quantify responsiveness to parameter changes and the preservation of reliability across diverse operating regimes.

The parameter sensitivity study probes the stability of TRIDENT-DE under controlled variations of key hyperparameters and quantifies whether reliability is preserved across heterogeneous operating conditions. We focus on the stagnation counter before restart $\tau$, the restart fraction $\rho$, the elite-centred Gaussian kick scale $\sigma$ at restart, the number of trials per agent t, and the top-p fraction $\phi$ that governs the pbest/1 sampling. Each factor is swept over representative values around the defaults in Table 1 while the remaining factors are kept fixed, and we record the impact on mean performance, extrema, and the main-effect range for three complementary test classes: a molecular Lennard-Jones cluster at N = 10, the Tersoff potential for silicon (model B), and the Static Economic Load Dispatch (ELD-1) problem. These three benchmarks span rugged, multimodal physical landscapes and heavily constrained industrial testbeds, making the observed trends transferable rather than instance-specific. For Lennard-Jones, perturbations around $\tau$ = 12/18/30, $\rho$ = 0.05/0.1/0.2, $\sigma$ = 0.1/0.2/0.3, t = 2/4/6/8, and $\phi$ = 0.06/0.10/0.18 induce only minor shifts in mean objective value and very small main-effect ranges across all factors, indicating inherent robustness of the method in this multimodal setting. The tight concentration of means around ~−27.08 together with the lack of systematic movement in extremes suggests that the triple-operator ensemble, the mild jDE-style control on F and C, and the one-step greedy line refinement act as dampers against parameter oversensitivity, especially because the refinement reuses a precomputed direction at negligible variance cost. These observations are evident in Table 4 and Figure 2.

Table 4. Sensitivity analysis of the method parameters for the “Lennard-Jones Potential, Dim:10” problem.

Parameter	Value	Mean	Min	Max	Iters	Main Effect Range
$\tau$	12	−27.0878	−28.4225	−24.0293	3240	0.0137
	18	−27.0741	−28.4225	−23.2567	3240
	30	−27.0871	−28.4225	−23.0968	3240
$\rho$	0.05	−27.0741	−28.4225	−23.0968	3240	0.0143
	0.1	−27.0885	−28.4225	−23.1044	3240
	0.2	−27.0864	−28.4225	−23.6869	3240
$\sigma$	0.1	−27.0913	−28.4225	−23.6906	3240	0.0138
	0.2	−27.0803	−28.4225	−23.1044	3240
	0.3	−27.0775	−28.4225	−23.0968	3240
t	2	−27.0823	−28.4225	−23.1044	3240	0.0066
	4	−27.0861	−28.4225	−23.2567	3240
	6	−27.0842	−28.4225	−23.0968	3240
	8	−27.0794	−28.4225	−23.6906	3240
$\phi$	0.06	−27.0916	−28.4225	−23.0968	3240	0.0145
	0.1	−27.0803	−28.4225	−23.2567	3240
	0.18	−27.0771	−28.4225	−23.1044	3240

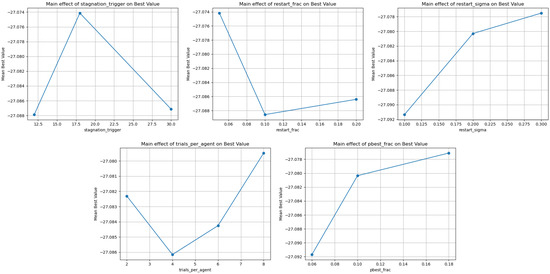
Figure 2. Graphical representation of $\tau$, $\rho$, $\sigma ,$ t and $\phi$ for the “Lennard-Jones Potential, Dim:10” problem.

In the Tersoff-Si (model B) potential, the overall robustness pattern persists, with the number of trials per agent t showing the most noticeable albeit still small effect on mean performance and main-effect range. Increasing t slightly improves exploitation of promising directions, occasionally trading off diversity, yet exploration remains safeguarded by adaptive micro-restarts, so the dynamics do not collapse. The gentle drift in mean with t does not overturn the defaults of Table 1, whereas $\rho$ and $\sigma$ exert only marginal influence within the probed ranges, underscoring that restarts serve as a safety valve rather than a dominant driver. The quantitative evidence is given in Table 5 and Figure 3.

Table 5. Sensitivity analysis of the method parameters for the “Tersoff Potential for model Si (C)” problem.

Parameter	Value	Mean	Min	Max	Iters	Main Effect Range
$\tau$	12	−31.6851	−34.1571	−27.5111	3240	0.0171
	18	−31.6897	−34.5056	−27.9642	3240
	30	−31.6725	−34.1820	−28.0777	3240
$\rho$	0.05	−31.6850	−34.2058	−27.6689	3240	0.0118
	0.1	−31.6752	−34.5056	−28.2521	3240
	0.2	−31.6870	−34.2775	−27.5111	3240
$\sigma$	0.1	−31.6830	−34.1571	−27.5111	3240	0.0139
	0.2	−31.6890	−34.5056	−28.0084	3240
	0.3	−31.6751	−34.2775	−27.6689	3240
t	2	−31.6994	−34.2775	−27.6689	3240	0.0524
	4	−31.7036	−34.5056	−28.0084	3240
	6	−31.6753	−34.1820	−27.9642	3240
	8	−31.6512	−34.1365	−27.5111	3240
$\phi$	0.06	−31.6887	−34.1365	−27.5111	3240	0.0127
	0.1	−31.6825	−34.1820	−28.0777	3240
	0.18	−31.6760	−34.5056	−27.6689	3240

Figure 3. Graphical representation of $\tau$, $\rho$, $\sigma ,$ t and $\phi$ for the “Tersoff Potential for model Si (C)” problem.

The picture changes more distinctly for ELD-1. Here, the lack of time coupling removes inter-temporal interactions, yet feasibility remains tight due to the power-balance equality and unit output bounds. Depending on the presence of valve-point effects, the landscape can be markedly nonconvex, with ripple-like undulations around local extrema. In this setting, the stagnation threshold $\tau$ still acts as a reliable trigger for rejuvenation when the population gets trapped in shallow basins, but its relative influence is smaller than in dynamic DED-type problems because there are no time-linked plateaus reinforcing stagnation. By contrast, the top-p fraction $\phi$ becomes the primary control knob: it governs how strongly the search is pulled toward p-best elites, mediating the trade-off between aggressive exploitation near top units and the preservation of diversity across alternative feasible corridors. Increasing t (trials per agent) further improves the use of local directions without collapsing exploration, as adaptive micro-restarts with calibrated $\rho$ and $\sigma$ inject gentle diversity whenever stagnation is detected. The results in Table 6 and the corresponding Figure 4 indicate that defaults around $\tau$ ≈ 18 and $\phi$ ≈ 0.10 are safe operating points for ELD-1, small local retunings of these two parameters can yield more stable quality jumps when valve-point ripples make the landscape more “toothed,” without requiring adjustments to $\rho$ and $\sigma$ beyond the probed ranges.

Table 6. Sensitivity analysis of the method parameters for the “Static Economic Load Dispatch 1” problem.

Parameter	Value	Mean	Min	Max	Iters	Main Effect Range
$\tau$	12	2977.7669	2967.2491	3002.3335	3240	0.3580
	18	2977.5983	2967.2491	3039.8430	3240
	30	2977.9563	2967.2491	3167.0430	3240
$\rho$	0.05	2977.7981	2967.2491	3167.0430	3240	0.1440
	0.1	2977.8338	2967.2491	3039.8430	3240
	0.2	2977.6897	2967.2491	3039.8430	3240
$\sigma$	0.1	2977.7085	2967.2491	3167.0430	3240	0.1282
	0.2	2977.8367	2967.2491	3031.7766	3240
	0.3	2977.7764	2967.2491	3039.8430	3240
t	2	2977.6721	2967.2491	3039.8430	3240	0.1995
	4	2977.7556	2967.2491	3039.8430	3240
	6	2977.7959	2967.2491	3039.8430	3240
	8	2977.8717	2967.2491	3167.0430	3240
$\phi$	0.06	2977.9287	2967.2491	3039.8430	3240	0.3351
	0.1	2977.7994	2967.2491	3167.0430	3240
	0.18	2977.5935	2967.2491	3031.7766	3240

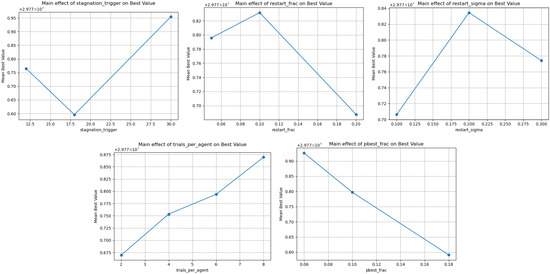
Figure 4. Graphical representation of $\tau$, $\rho$, $\sigma ,$ t and $\phi$ for the “Static Economic Load Dispatch 1” problem.

Taken together, the sensitivity profile shows that the defaults in Table 1 are well-balanced across diverse problems: $\rho$ and $\sigma$ regulate a gentle injection of diversity without disrupting exploitation, $\phi$ shapes the attraction lattice of pbest/1 across multiple elites, and t enhances the utility of the already computed direction $z\to x\top$ at modest additional cost. The small main-effect ranges observed in Lennard-Jones and Tersoff confirm that the triple-operator design, combined with light jDE-style jitter on F and C, yields a self-stabilising regime in which parameter effects are largely second-order. Conversely, in heavily constrained energy scheduling, $\tau$ and $\phi$ become active control knobs, consistent with a landscape featuring broad plateaus and tight feasibility margins. The practical implication is twofold: first, the proposed defaults deliver portable reliability with minimal pre-tuning, second, when constraints dominate, a narrow local retuning of $\tau$ and $\phi$ around their nominal values preserves the best search rate without sacrificing stability. These conclusions align with the architecture of TRIDENT-DE, where interactions among three trial generators, one-step greedy refinement, and adaptive micro-restarts distribute the burden of adaptation and, as a result, insulate the system from sharp nonlinearities in any single hyperparameter.

3.4. Analysis of Complexity of TRIDENT-DE

Below we provide a bullet-style specification of two real-world optimization problems adopted as representative testbeds for the time-complexity and scaling analysis of the proposed method, we summarise the key decision variables, admissible bounds/domains, and objective functions, and explicitly note relevant modeling assumptions and feasibility penalty terms, so that the ensuing bullets serve as a quick “map” of practical constraints and goals prior to the runtime evaluation.

• GasCycle Thermal Cycle
  Vars: $\mathbf{x}={[T_1,T_3,P_1,P_3]}^{\top }$. $r=P_3/P_1,\gamma =1.4.$

  $$\eta \left(\mathbf{x}\right)=1-r^{-(\gamma -1)/\gamma }{\displaystyle \frac{T_1}{T_3}},\underset{\mathbf{x}}{min}f\left(\mathbf{x}\right)=-\eta \left(\mathbf{x}\right).$$
  Bounds: $300\le T_1\le 1500,1200\le T_3\le 2000,1\le P_1,P_3\le 20.$
  Penalty: infeasible $\Rightarrow f={10}^{20}$.
• Tandem Space Trajectory (MGA-1DSM, EVEEJ + 2 × Saturn)
  Vars($D=18$):$\mathbf{x}={[t_0,T_1,T_2,T_3,T_4,T_{5A},T_{5B},s_1,s_2,s_3,s_4,s_{5A},s_{5B},r_p,k_{A1},k_{A2},k_{B1},k_{B2}]}^{\top }$.

  $$\begin{array}{cc}& 7000\le t_0\le 10000,\hfill \\ & 30\le T_1\le 500,30\le T_2\le 600,30\le T_3\le 1200,\hfill \\ & 30\le T_4\le 1600,30\le T_{5A},T_{5B}\le 2000,\hfill \\ & 0\le s_{1..4},s_{5A},s_{5B},r_p,k_{A1},k_{A2},k_{B1},k_{B2}\le 1.\hfill \end{array}$$
  Objective:

  $$\underset{\mathbf{x}}{min}\mathrm{\Delta }{V}_{\mathrm{tot}}=\mathrm{\Delta }{V}_{\mathrm{launch}}\left(T_1\right)+\mathrm{\Delta }{V}_{\mathrm{legs}}(T_1:T_4)+\mathrm{\Delta }{V}_A+\mathrm{\Delta }{V}_B+\mathrm{\Delta }{V}_{\mathrm{DSM}}(\mathbf{s},r_p)-G_{\mathrm{GA}}-G_J+P_{\mathrm{hard}}+P_{\mathrm{soft}},$$

  $$P_{\mathrm{soft}}=\beta max\left\{0,(T_1+\dots +T_4+\frac{1}{2}(T_{5A}+T_{5B}))-3500\right\}.$$
  Notes: $\mathrm{\Delta }{V}_{\mathrm{launch}}$ decreases (log-like) in $T_1$ (≥6 km/s floor), leg/branch costs decrease with TOF.

The time-complexity Figure 5 reveals an almost linear growth of wall-clock time with respect to problem size (40–400) for both GasCycle Thermal Cycle and Tandem Space Trajectory. The monotonic trend and near-constant increments per size step indicate that the proposed architecture scales effectively with $O\left(n\right)$ in the investigated size parameter, with no signs of exponential or strongly super-linear behavior. Across the two cases, Tandem Space Trajectory consistently exhibits slightly higher times, which is naturally explained by a larger per-evaluation cost of the underlying simulator/objective in that domain. In other words, the dominant contributor to total runtime is the evaluation cost, while the search mechanism itself preserves an approximately constant slope with respect to size. The absence of kinks or abrupt escalations at larger sizes further suggests that components such as the triple trial-vector ensemble, the one-step greedy line refinement, and the adaptive micro-restarts do not introduce hidden overhead that would manifest as degraded asymptotic scaling. Practically, the method remains predictable and efficient as the problem grows, with performance primarily governed by the problem-dependent evaluation burden. The mild, roughly constant offset between the two benchmarks over the 40–400 range reinforces the view that this is a domain-dependent additive cost rather than a change in the algorithm’s scaling rate. Overall, the evidence supports a favorable scaling profile: linear complexity in the examined size parameter, stability under heavier loads, and a clean separation between a stable algorithmic overhead and the variable evaluation cost imposed by each application.

Figure 5. Time scaling under a fixed iteration budget.

3.5. Comparative Performance Analysis of TRIDENT-DE

This section introduces the experimental component that assesses the proposed method across alternative configurations and problem sets, emphasizing behavioral consistency and reproducibility. Table 7 compiles the corresponding comparative figures and summary evaluation metrics.

Table 7. Comparison Based on Best and Mean after 1.5 × 10⁵ FEs.

	TRIDENT-DE Best/Mean	UDE3 Best/Mean	EA4Eig Best/Mean	mLSHADE_RL Best/Mean	SaDE Best/Mean	CMA-ES Best/Mean	jDE Best/Mean	CLPSO Best/Mean
Lennard -Jones Potential (10 atoms)	−28.42253189	−17.60964115	−22.47842596	−28.42252711	−22.86077544	−28.42253189	−15.91366007	−16.59269921
	−27.19833972	−16.33758634	−19.48663385	−23.77189104	−21.22806787	−27.52754934	−13.75563015	−13.55503647
Lennard-Jones Potential (13 atoms)	−41.39220729	−21.90945922	−28.01101572	−40.6992486	−29.31393114	−44.32680142	−18.77073675	−18.00250514
	−39.14390841	−19.49372047	−24.58810405	−30.67706246	−27.48874237	−41.44245617	−15.4243072	−15.86691988
Lennard-Jones Potential (38 atoms)	−125.1886792	−2.015038465	−55.05415428	−120.0680452	−68.91313107	−167.7369019	9186.25096	330.9934848
	−107.1751456	140.2211284	−3.350181902	−73.95117658	−45.80265994	−163.6091673	9186.25096	1087.035295
Tersoff Potential for model Si (B)	−28.93480467	−25.43447342	−26.90746941	−28.12281867	−26.65687822	−28.33045002	−24.75133772	−22.67387001
	−27.70615763	−23.30318979	−24.69059932	−25.49977206	−25.27422603	−27.38991233	−22.94168766	−21.21150428
Tersoff Potential for model Si (C)	−33.8820283	−29.30227462	−30.88865174	−31.70444684	−30.94469385	−32.50963421	−29.44789882	−26.88039528
	−31.91749393	−27.53891341	−29.0199918	−29.44303263	−29.70029831	−31.53772845	−29.44789882	−24.653633
Parameter Estimation for Frequency-Modulated Sound Waves finalstrutarstrutbox	0.116157535	0	0.15272453	0.116157535	0.148007602	0.210122687	0	0.131483748
	0.134324544	0.103406319	0.213099692	0.208210846	0.148007602	0.267329914	0.132539923	0.212498169
Circular Antenna Array Design	0.006809638	0.006809665	0.006809638	0.006809662	0.006814682	0.007253731	0.00681715	0.006933401
	0.006809683	0.006817385	0.006809638	0.006825338	0.00790701	0.008755359	0.006835764	0.051815518
Spread Spectrum RadarPolyphase Code Design	0.014426836	0.953872709	0.601567824	0.074552911	0.550837019	0.062519409	1.005739785	0.860294378
	0.26254527	1.206577385	0.869257599	0.535028919	0.803527605	0.197713522	1.331416957	1.273200439
Cassini 2: Spacecraft Trajectory Optimization Problem finalstrutarstrutbox	0	0.000926598	0	0	0.039231105	0	0.000026961	1.22633022
	0.000011205	0.008206106	0	0.00001729	0.070230417	5.929143722	0.000285411	3.639687905
Wireless Coverage Antenna Placement	0.946350736	0.946350736	0.946655032	0.946350736	0.946361987	1.18939375	0.946350736	0.946365969
	0.94662124	0.946502884	0.946659575	0.946875107	0.946688757	1.190699803	0.946401452	0.946727502
Transmission Network Expansion Planning	4.485304003	4.485295106	4.485292926	4.485292926	4.485299525	4.485292926	4.485292926	4.486699087
	4.485292926	4.485304003	4.485292926	4.485292926	4.485311924	4.485292948	4.485292926	4.495857336
Dynamic Economic Dispatch 1	130,850.0389	130,693.5423	130,694.29	130,882.0646	131,010.8769	130,650.9354	131,225.2453	131,834.4235
	130,931.1074	130,717.6052	130,862.9893	130,955.331	131,099.1959	130,654.2758	131,225.2453	132,151.5397
Dynamic Economic Dispatch 2	165,980.9574	164,946.164	172,067.4426	167,519.3281	167,908.0605	165,847.1092	186,121.2812	177,120.3822
	166,478.1534	165,614.9256	172,931.6964	168,275.5429	168,495.9731	166,233.691	190,793.5621	178,190.4198
Static Economic Load Dispatch 1	2967.249196	2967.249196	2979.803369	2967.249196	2967.249196	2967.249586	2967.249196	2967.249197
	2975.721343	2976.057657	2979.803369	2976.956221	2976.139816	3108.931917	2967.659992	2973.33009
Static Economic Load Dispatch 2	17,879.73679	17,864.69687	18,006.65976	17,882.28384	17,892.38129	17,960.84734	17,867.57447	17,910.47794
	17,928.65603	17,890.83413	18,063.12085	17,950.15892	17,958.94204	18,077.58006	17,992.09486	18,089.83526
Static Economic Load Dispatch 3	32,367.57735	32,367.57735	32,415.80367	32,367.57765	32,376.02197	32,645.34102	32,391.64981	32,384.85409
	32,440.87752	32,400.86337	32,573.03572	32,491.57235	32,491.28971	32,867.1729	32,476.58405	32,532.19143
Static Economic Load Dispatch 4	121,071.4654	121,066.9247	121,197.2468	121,085.9922	12,1195.4656	12,2350.1013	121,234.0466	121,328.7006
	121,422.9908	121,197.2468	121,545.1315	121,308.5801	121,517.4918	122,957.6217	121,526.7414	121,541.4182
Static Economic Load Dispatch 5	508,663.8176	508,661.3113	508,872.6908	508,851.668	508,985.9092	508,717.1467	511,174.5326	509,025.7426
	508,703.0424	508,676.4938	508,986.6092	508,988.5396	509,125.2079	508,770.1661	562,012.6548	509,080.3439

Table 7 reports best and mean performance under a common budget of $1.5\times {10}^5$ evaluations across synthetic and real-world problems. On the Lennard-Jones suite (N = 10, 13, 38), TRIDENT-DE reaches energy minima on par with the strongest baselines while keeping the best-mean gap tight evidence that top results are reliably repeatable rather than isolated lucky runs. This contrasts with the pronounced variability seen in some competitors (e.g., large outliers for jDE on LJ-38), underscoring how the triple trial-vector ensemble, one-step greedy refinement, and micro-restarts absorb multi-modality without sacrificing diversity.

For the Tersoff-Si (B/C) potentials, the pattern remains favorable: TRIDENT-DE’s best values are competitive or superior, and, crucially, the mean is often lower than that of many baselines, implying a higher probability of obtaining high-quality solutions in a typical run. The detailed rankings corroborate this view: by mean performance, TRIDENT-DE stays among the top ranks on physical potentials and several real-world tasks (e.g., TNEP, wireless coverage), highlighting robustness under constraints and irregular landscapes (see Table 8 and Table 9).

Table 8. Detailed Ranking of Algorithms Based on Best after 1.5 × 10⁵ FEs. The values highlighted in green indicate the best performance, while those in blue denote the second-best performance.

	TRIDENT-DE	UDE3	EA4Eig	mLSHADE_RL	SaDE	CMA-ES	jDE	CLPSO
Lennard-Jones Potential (10 atoms)	1	6	5	3	4	1	8	7
Lennard-Jones Potential (13 atoms)	2	6	5	3	4	1	7	8
Lennard-Jones Potential (38 atoms)	2	6	5	3	4	1	8	7
Tersoff Potential for model Si (B)	1	6	4	3	5	2	7	8
Tersoff Potential for model Si (C)	1	7	5	3	4	2	6	8
Parameter Estimation for Frequency-Modulated Sound Waves	3	1	7	3	6	8	1	5
Circular Antenna Array Design	1	4	2	3	5	8	6	7
Spread Spectrum Radar Polyphase Code Design	1	7	5	3	4	2	8	6
Cassini 2: Spacecraft Trajectory Optimization Problem	1	6	1	1	7	1	5	8
Wireless Coverage Antenna Placement	1	1	7	1	5	8	1	6
Transmission Network Expansion Planning	7	5	1	1	6	1	1	8
Dynamic Economic Dispatch 1	4	2	3	5	6	1	7	8
Dynamic Economic Dispatch 2	3	1	6	4	5	2	8	7
Static Economic Load Dispatch 1	1	1	8	1	1	7	1	6
Static Economic Load Dispatch 2	3	1	8	4	5	7	2	6
Static Economic Load Dispatch 3	1	1	7	3	4	8	6	5
Static Economic Load Dispatch 4	2	1	5	3	4	8	6	7
Static Economic Load Dispatch 5	2	1	5	4	6	3	8	7

Table 9. Detailed Ranking of Algorithms Based on Mean after 1.5 × 10⁵ FEs. The values highlighted in green indicate the best performance, while those in blue denote the second-best performance.

	TRIDENT-DE	UDE3	EA4Eig	mLSHADE_RL	SaDE	CMA-ES	jDE	CLPSO
Lennard-Jones Potential (10 atoms)	2	6	5	3	4	1	7	8
Lennard-Jones Potential (13 atoms)	2	6	5	3	4	1	8	7
Lennard-Jones Potential (38 atoms)	2	6	5	3	4	1	8	7
Tersoff Potential for model Si (B)	1	6	5	3	4	2	7	8
Tersoff Potential for model Si (C)	1	7	6	5	3	2	4	8
Parameter Estimation for Frequency-Modulated Sound Waves	3	1	7	5	4	8	2	6
Circular Antenna Array Design	2	3	1	4	6	7	5	8
Spread Spectrum Radar Polyphase Code Design	2	6	5	3	4	1	8	7
Cassini 2: Spacecraft Trajectory Optimization Problem	2	5	1	3	6	8	4	7
Wireless Coverage Antenna Placement	3	2	4	7	5	8	1	6
Transmission Network Expansion Planning	1	6	1	1	7	5	1	8
Dynamic Economic Dispatch 1	4	2	3	5	6	1	7	8
Dynamic Economic Dispatch 2	3	1	6	4	5	2	8	7
Static Economic Load Dispatch 1	3	4	7	6	5	8	1	2
Static Economic Load Dispatch 2	2	1	6	3	4	7	5	8
Static Economic Load Dispatch 3	2	1	7	5	4	8	3	6
Static Economic Load Dispatch 4	3	1	7	2	4	8	5	6
Static Economic Load Dispatch 5	2	1	4	5	7	3	8	6

Across real-world instances, behavior is category-dependent. In Transmission Network Expansion Planning and antenna placement/coverage, TRIDENT-DE shows excellent or strongly competitive outcomes with narrow best-mean spreads, indicating trustworthy single-run performance. In a few specialized settings, such as circular antenna design or the Cassini 2 trajectory problem, isolated top scores emerge from specific baselines (e.g., EA4Eig, CMA-ES), consistent with their aptitude for lower effective dimensional subspaces or smoother subregions. Still, when aggregating global evidence via mean-based rankings and win/placement totals, TRIDENT-DE achieves the best overall average rank among all contenders (Table 10), suggesting that its advantage is portable rather than instance-specific.

Table 10. Comparison of Algorithms and Final Ranking. The values highlighted in green indicate the best performance, while those in blue denote the second-best performance.

Algorithm	Best Total	Mean Total	Overall	Average Rank
TRIDENT-DE	37	40	77	2.139
mLSHADE_RL	51	70	121	3.361
UDE3	63	65	128	3.556
CMA-ES	71	81	152	4.222
SaDE	85	86	171	4.750
EA4Eig	89	85	174	4.833
jDE	96	92	188	5.222
CLPSO	124	123	247	6.861

In the energy family, nuances appear. On DED variants, methods with strong adaptive dispersion (e.g., CMA-ES) often secure high placements, reflecting their ability to navigate plateau-like score profiles. Conversely, in ELD-1 without time coupling classical DE flavors may occasionally top the mean ranking, yet TRIDENT-DE remains consistently competitive and close to the optimal operating window, as evidenced by its mean figures in Table 7 and the per-problem ranks in Table 9. Practically, even when a “specialist” baseline dominates a narrow niche, TRIDENT-DE does not collapse in reliability, it maintains a small best-mean gap and stays near the top on average.

Overall, Table 7 reveals two complementary strengths: high best-case performance across a wide variety of instances and consistently strong mean performance that makes those peaks reproducible. When combined with the consolidated standings and Overall Average Rank in Table 9 and Table 10, the picture is clear: TRIDENT-DE delivers strong, stable, and widely transferable performance compared to the alternatives, with only a handful of exceptions where specific competitors exploit landscape idiosyncrasies to claim local wins.

3.6. Neural Network Training with TRIDENT-DE

We conducted an additional set of experiments where TRIDENT-DE was employed as the optimizer for training feedforward artificial neural networks [53,54] Given a training set $\mathcal{D}={\left\{({\mathbf{x}}_i,y_i)\right\}}_{i=1}^M$, with input vectors ${\mathbf{x}}_i\in {\mathbb{R}}^d$ and targets $y_i$ (for classification, either scalar class indices or one-hot vectors), the objective minimized by TRIDENT-DE was the mean-squared training error:

$$E\left(\mathcal{N}(\mathbf{x},\mathbf{w})\right)=\sum _{i=1}^M{\left(\mathcal{N}({\mathbf{x}}_i,\mathbf{w})-y_i\right)}^2,$$

(1)

where $\mathcal{N}(·,\mathbf{w})$ denotes the neural network’s mapping parameterized by the weight (and bias) vector $\mathbf{w}$. In this setup, each candidate solution encoded all trainable parameters of the network, TRIDENT-DE evolved these parameters directly in continuous space. Unless otherwise noted, inputs were standardized to zero mean and unit variance, categorical labels were one-hot encoded when needed, and training used full batches on each fitness evaluation of (1). To reduce overfitting, we monitored validation error for early stopping, in some runs we also added ${\ell }_2$ regularization by augmenting (1) with $\lambda {\parallel \mathbf{w}\parallel }_2^2$ (small $\lambda$), without altering the optimizer.

To gauge performance across heterogeneous conditions, we compiled a broad suite of publicly available classification datasets spanning low to moderate dimensionality and varying class balance. Datasets were sourced from:

• The UCI Machine Learning Repository, https://archive.ics.uci.edu/ (accessed on 18 September 2025) [55].
• The KEEL collection, https://sci2s.ugr.es/keel/datasets.php (accessed on 18 September 2025) [56].
• The StatLib archive, https://lib.stat.cmu.edu/datasets/index (accessed on 18 September 2025).

The experiments were conducted using the following datasets:

• Appendicitis: medical classification of acute appendicitis cases [57].
• Alcohol: records related to alcohol consumption patterns [58].
• Australian: heterogeneous banking/credit transaction data [59].
• Balance: psychophysical balance-scale experiment outcomes [60].
• Cleveland: coronary heart disease dataset analyzed in multiple studies [61,62].
• Circular: synthetic two-dimensional nonlinearly separable data.
• Dermatology: clinical attributes for dermatological diagnosis [63].
• Ecoli: protein localization/functional attributes in E. coli [64].
• Fert: relations between sperm concentration and demographic variables.
• Glass: chemical composition measurements for glass type identification.
• Haberman: breast-cancer survival after surgery.
• Hayes-Roth: classic concept-formation benchmark [65].
• Heart: clinical indicators for heart-disease detection [66].
• HeartAttack: medical features targeting early detection of cardiac events.
• Housevotes: U.S. Congressional voting records by bill/party [67].
• Ionosphere: radar returns measuring ionospheric conditions [68,69].
• Liverdisorder: liver function tests widely studied in the literature [70,71].
• Lymphography:imaging/diagnostic attributes of lymphatic diseases [72].
• Mammographic: features for breast-cancer mass prediction [73].
• Parkinsons: voice/acoustic markers of Parkinson’s disease [74,75].
• Pima: diabetes onset in Pima Indian women [76].
• Phoneme: short-duration speech sounds (phoneme recognition).
• Popfailures: climate/meteorology-related experimental observations [77].
• Regions2: medical attributes related to liver diagnostics [78].
• Saheart: cardiovascular risk factors and outcomes [79].
• Segment: multivariate image segmentation benchmark [80].
• Sonar: acoustic echoes distinguishing metal vs. rock objects [81].
• Statheart: additional heart-disease classification dataset.
• Spiral: synthetic two-class intertwined spiral (nonlinear boundary).
• Student: school performance and demographic indicators [82].
• Transfusion: blood-donation behavior and response modeling [83].
• WDBC: Wisconsin Diagnostic Breast Cancer (malignant vs. benign) [84,85].
• Wine: oenological measurements for wine quality/type discrimination [86,87].
• EEG: brain-signal recordings; cases used—Z_F_S, ZO_NF_S, ZONF_S, Z_O_N_F_S [88,89].
• Zoo: animal taxonomy classification via morphological traits [90].

The Table 11 demonstrates a clear advantage of TRIO over BFGS, Genetic, and ADAM in terms of classification error. TRIO attains an average error of 20.46%, compared to 33.80% for BFGS, 26.46% for Genetic, and 34.08% for ADAM amounting to relative reductions of approximately 39.5% vs. BFGS, 22.7% vs. Genetic, and 40.0% vs. ADAM. At the dataset level, TRIO achieves the lowest error on 34 out of 36 benchmarks, with only two exceptions AUSTRALIAN and LIVERDISORDER where Genetic holds a narrow lead (32.10% vs. 33.97% and 31.11% vs. 31.15%, respectively). TRIO’s dominance extends to both “easier” datasets (e.g., ZONF_S 2.10%, STUDENT 4.38%, POPFAILURES 4.43%, CIRCULAR 4.58%, ZOO 5.60%, WINE 7.47%, WDBC 7.63%) and “harder” ones where all methods incur higher errors (e.g., CLEVELAND, ECOLI, SEGMENT, SPIRAL), consistently delivering the best performance. Overall, the results indicate that TRIO combines low average error with strong robustness (median ≈ 19.58%) across heterogeneous benchmarks, whereas BFGS and ADAM lag systematically, and Genetic is competitive only in a small number of cases.

Table 11. Multi -Dataset Evaluation of Machine-Learning Methods for Classification.

DATASET	TRIDENT-DE	BFGS	GENETIC	ADAM
APPENDICITIS	14.80%	18.00%	18.10%	16.50%
ALCOHOL	20.28%	41.50%	39.57%	57.78%
AUSTRALIAN	33.97%	38.13%	32.10%	35.65%
BALANCE	8.03%	8.64%	8.97%	12.27%
CIRCULAR	4.58%	6.08%	5.99%	19.95%
CLEVELAND	43.55%	77.55%	51.60%	67.55%
DERMATOLOGY	8.51%	52.92%	30.58%	26.14%
ECOLI	44.76%	69.52%	54.67%	64.43%
HABERMAN	26.37%	29.34%	28.66%	29.00%
HAYES-ROTH	35.08%	37.33%	56.18%	59.70%
HEART	18.52%	39.44%	28.34%	38.53%
HEARTATTACK	19.57%	46.67%	29.03%	45.55%
HOUSEVOTES	5.57%	7.13%	6.62%	7.48%
IONOSPHERE	8.34%	15.29%	15.14%	16.64%
LIVERDISORDER	31.15%	42.59%	31.11%	41.53%
LYMOGRAPHY	21.14%	35.43%	28.42%	39.79%
MAMMOGRAPHIC	16.61%	17.24%	19.88%	46.25%
PARKINSONS	17.47%	27.58%	18.05%	24.06%
PIMA	30.67%	35.59%	32.19%	34.85%
POPFAILURES	4.43%	5.24%	5.94%	5.18%
REGIONS2	24.44%	36.28%	29.39%	29.85%
SAHEART	32.67%	37.48%	34.86%	34.04%
SEGMENT	42.67%	68.97%	57.72%	49.75%
SONAR	19.80%	25.85%	22.40%	30.33%
SPIRAL	43.01%	47.99%	48.66%	47.67%
STATHEART	19.59%	39.65%	27.25%	44.04%
STUDENT	4.38%	7.14%	5.61%	5.13%
TRANSFUSION	23.84%	25.84%	24.87%	25.68%
WDBC	7.63%	29.91%	8.56%	35.35%
WINE	7.47%	59.71%	19.20%	29.40%
Z_F_S	9.27%	39.37%	10.73%	47.81%
ZO_NF_S	7.10%	43.04%	21.54%	47.43%
ZONF_S	2.10%	15.62%	4.36%	11.99%
ZOO	5.60%	10.70%	9.50%	14.13%
AVERAGE	20.46%	33.80%	26.46%	34.08%

Using R version 4.5 scripts applied to the empirical results tables, we assessed statistical significance via the p-value criterion. Figure 6 reports the significance encoding (ns for p > 0.05, * for p < 0.05, ** for p < 0.01, *** for p < 0.001, **** for p < 0.0001) across the classification datasets and the models under comparison. All three pairwise contrasts yielded ****—that is, p < 0.0001 for TRIDENT-DE vs. BFGS, TRIDENT-DE vs. GENETIC, and TRIDENT-DE vs. ADAM. These results provide very strong statistical evidence that TRIDENT-DE outperforms the baselines on the examined datasets, making it highly unlikely that the observed gains are attributable to random variation (Figure 6).

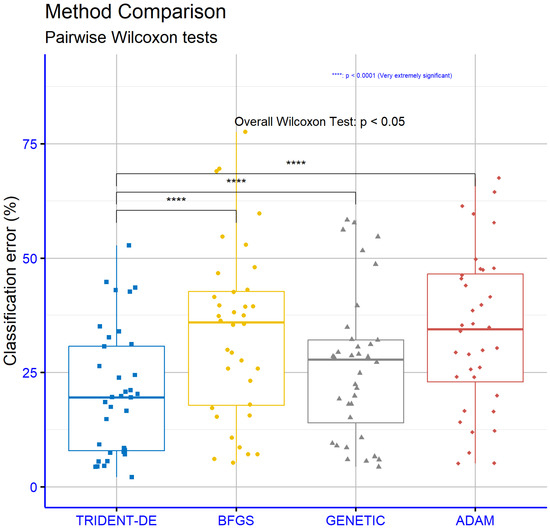
Figure 6. Comparative Statistical Evaluation on Classification Benchmarks.

4. Conclusions

The empirical evidence demonstrates that TRIDENT-DE delivers strong and transferable performance across heterogeneous settings from rugged physical landscapes (Lennard-Jones, Tersoff) to tightly constrained industrial/energy tasks (ELD/DED) and complex real-world applications (TNEP, wireless coverage, orbital design). Aggregated results in Table 7 show competitive best values accompanied by consistently tight best-mean gaps, indicating reproducible quality rather than isolated lucky hits. This picture is reinforced by the detailed standings in Table 9, where TRIDENT-DE maintains top-tier positions on physical potentials and several real-world tasks, while the final consolidated ranking in Table 10 yields the best Overall Average Rank among all contenders evidence of broad portability rather than niche specialization.

Mechanistically, the parameter-sensitivity study in Section 3.3 indicates an intrinsically self-stabilising regime: the principal hyperparameters exert second-order effects across most domains, with targeted leverage for the stagnation threshold $\tau$ and the top-p fraction $\phi$ (p-best) on heavily constrained landscapes. In Lennard-Jones and Tersoff, main-effect ranges remain small near the defaults, consistent with the triple operator ensemble, light jDE-style control on F, C and one-step greedy line refinement acting as dampers against parameter oversensitivity. In energy scheduling (ELD/DED), strict feasibility and plateau-like regions elevate the roles of $\tau$ and $\phi$ as control knobs for timely rejuvenation and exploitation-exploration balance, respectively. This behaviour is quantified in Table 4, Table 5 and Table 6 and the accompanying figures.

Time-scaling evidence (Figure 5) adds a key dimension: wall-clock time grows approximately linearly with size in two representative domains (“GasCycle Thermal Cycle” and “Tandem Space Trajectory”), with no super-linear pathologies. The slightly higher curve of the latter reflects a domain-dependent additive evaluation cost rather than a shift in the algorithm’s scaling rate, yielding predictability under load and a clean separation between stable algorithmic overhead and problem-dependent evaluation burden.

Beyond physical and industrial benchmarks, the experiments in Section 3.6 show that TRIDENT-DE is also an effective trainer for artificial neural networks, directly optimizing weights and biases by minimizing the mean-squared error. Evaluations on a broad suite of public classification datasets (UCI, KEEL, StatLib) consistently yielded lower error rates than BFGS, Genetic, and ADAM, with significance tests confirming p < 0.0001 for all pairwise contrasts against TRIDENT-DE. These results extend the portability of our conclusions from pure black-box optimization to machine-learning settings, indicating that the triple trial-vector ensemble, the one-step greedy refinement, and adaptive micro-restarts translate into robust gains for parameter tuning in learned models.

In sum, the findings articulate a triad of strengths: (i) consistently strong mean performance with small best-mean gaps (Table 7), (ii) dominant consolidated standings across diverse tasks (Table 8, Table 9 and Table 10), and (iii) favourable scaling without hidden overheads (Figure 5). The synergy among the triple trial-vector generator, line refinement, and adaptive micro-restarts distributes the burden of adaptation across exploration, exploitation, and diversity maintenance, explaining why hyperparameter effects remain modest over wide operating regions.

Limitations. Despite the positive aggregate view, certain boundaries are worth noting. In ELD/DED, performance is more sensitive to $\tau$ and $\phi$ under constrained congestion, while defaults are safe operating points, local retuning can further stabilise progress (see Section 3.3). In a few specialised scenarios (e.g., Cassini 2, circular antenna arrays), individual baselines attain isolated wins signalling landscape idiosyncrasies where added specialisation may help. Finally, the time-scaling study rests on two cases, although indicative, a broader scaling sweep (multiple sizes/dimensions/workloads) would strengthen external validity.

Future Work. Several promising avenues emerge. First, higher-level adaptivity (hyper-heuristics) could learn online operator-mix policies using credit assignment and success signals per generation, deepening the self-stabilising behaviour observed in Section 3.3. Second, targeted self-regulation of $\tau$ and $\phi$ in constrained domains (ELD/DED) via bandit-style or Bayesian controllers may reduce plateau effects while preserving diversity. Third, integrating surrogate models for costly evaluations (e.g., lightweight GP/SVR) can leverage the observed linear scaling to maximise efficiency under tight budgets. Fourth, parallelisation (vectorised trials, GPU-friendly line refinement) promises additional wall-clock gains without altering stochastic dynamics. Fifth, extending to multi-objective and hard/soft constrained variants with explicit feasibility enforcement and adaptive penalties would probe robustness in more realistic settings. Finally, a theoretical strand (e.g., Markov-chain or drift analyses) could formalise the interplay among triple operators, restart, and refinement that is empirically evident. These directions follow naturally from Table 7, Table 8, Table 9 and Table 10, Figure 5, and Section 3.3, aiming to convert empirical advantages into systematically scalable and theoretically grounded benefits.