Robust Optimization for IRS-Assisted SAGIN Under Channel Uncertainty

Abstract

With the widespread adoption of space–air–ground integrated networks (SAGINs) in next-generation wireless communications, intelligent reflecting surfaces (IRSs) have emerged as a key technology for enhancing system performance through passive link reinforcement. This paper addresses the prevalent issue of channel state information (CSI) uncertainty in practical systems by constructing an IRS-assisted multi-hop SAGIN communication model. To capture the performance degradation caused by channel estimation errors, a norm-bounded uncertainty model is introduced. A simulated annealing (SA)-based phase optimization algorithm is proposed to enhance system robustness and improve worst-case communication quality. Simulation results demonstrate that the proposed method significantly outperforms traditional multiple access strategies (SDMA and NOMA) under various user densities and perturbation levels, highlighting its stability and scalability in complex environments.

1. Introduction

With the advent of sixth-generation mobile communications (6G), building a global communications infrastructure that offers wide-area coverage, high throughput, and low latency has become a shared objective of academia and industry. In this context, the space–air–ground integrated network (SAGIN) has attracted significant attention as a core architecture to enable ubiquitous connectivity and intelligent services. By organically integrating satellite systems in the space layer, uncrewed aerial vehicles and stratospheric platforms (e.g., high-altitude balloons and high-altitude platforms, HAPs) in the aerial layer, and terrestrial cellular networks on the ground, SAGIN enables coordinated transmission and resource sharing across space, air, and ground. The result is a multi-tier heterogeneous network featuring global coverage, dynamic orchestration, and enhanced resilience. Compared with conventional terrestrial cellular networks, SAGIN offers several salient advantages. First, thanks to the high vantage of satellites and aerial platforms, it can remedy service blind spots in remote areas, over the oceans, and in post-disaster scenarios, markedly improving reachability and universality. Second, the rapid deployment and flexible scheduling of aerial nodes provide efficient backhaul and relay capabilities for emergency tasks, temporary hotspots, and unexpected events, thereby strengthening the network’s spatiotemporal elasticity. Finally, cross-domain resource integration across space, air, and ground lays the foundation for load balancing, hierarchical access, and computation offloading, paving the way for greener and more intelligent communication systems. Despite these advantages—particularly in remote, post-disaster, and emergency settings—practical deployment of SAGIN still faces several challenges. First, due to the highly heterogeneous architecture, there are substantial differences across layers in node density, mobility, and spectrum allocation, making unified protocol design and resource scheduling intrinsically complex. Second, multi-hop links are susceptible to blockage, fading, and disruptions; channel instability is significantly higher than in terrestrial networks, placing stricter demands on channel modeling and robustness. Third, cross-layer optimization is markedly more difficult because time-varying link states hinder real-time acquisition of global network information. Consequently, while SAGIN provides an innovative blueprint for future communications, it calls for more robust and environment-adaptive enhancement mechanisms to ensure stable operation in dynamic and complex conditions.

To address the above challenges, intelligent reflecting surfaces (IRSs)—also referred to as reconfigurable intelligent surfaces (RISs)—have emerged as a promising technology for enhancing coverage and interference resilience in wireless systems. An IRS consists of a large number of programmable, nearly passive reflecting elements whose coefficients (primarily phases) can be tuned to reconfigure the impinging wavefront. In this way, the propagation environment can be shaped and strengthened without injecting additional transmit power. Compared with conventional relaying, IRSs are generally considered energy-efficient because the nearly passive reflecting elements require only minimal biasing and infrequent updates. This advantage is particularly evident in low-rate IoT and sensing scenarios, where sparse reconfiguration suffices. However, RISs are not entirely “zero-power”: the overall system power draw includes the controller (e.g., FPGA or microcontroller), the driver/bias circuits, and the update overhead, which grows with the reconfiguration frequency [1,2]. Recent studies have modeled and measured these contributions, showing that per-element consumption can be negligible with varactor-based designs, while higher update rates or switching elements increase the power burden. Therefore, the oft-cited energy efficiency of RISs must be understood in application-specific contexts.

Despite the demonstrated potential of IRSs in wireless communications, most existing RIS optimization methods presume accurate channel state information (CSI). In the highly dynamic SAGIN setting, however, perfect CSI estimation is practically unattainable. Although several studies have explored CSI-free or CSI-light designs—e.g., minimizing the bit error rate (BER) under limited or no CSI to improve reliability [3,4], or resource allocation in wireless-powered RIS-assisted multiuser systems with hybrid operating modes and energy harvesting constraints [5]—these works typically focus on simplified models that do not capture the complexities of SAGIN or the additional challenges introduced by multi-hop links. These CSI-free designs, however, are generally unsuitable for highly dynamic scenarios such as mobile networks or space–air–ground integrated networks (SAGINs). In such cases, the rapid time variation in the channel due to user mobility and Doppler shifts causes the statistical assumptions underlying CSI-free optimization to break down. Moreover, the cascaded satellite–RIS–user channels introduce significant uncertainties that cannot be effectively compensated without some level of CSI acquisition. The coherence time of the equivalent channel is also considerably shortened, making purely statistical or training-free methods ineffective, as the channel conditions change faster than the system can adapt. Consequently, CSI-free strategies are mainly applicable to quasi-static or low-mobility environments, but they cannot guarantee reliable performance in SAGINs [6].

This work proposes a new robust optimization framework that explicitly accounts for CSI uncertainty when configuring the RIS. Unlike approaches that rely on exact CSI, our method introduces norm-bounded uncertainty sets and enforces worst-case guarantees, thereby sustaining reliable performance under adverse channel conditions. By combining simulated annealing (SA) with Monte Carlo sampling (MCS), the proposed algorithm effectively handles the non-convex optimization inherent to multi-hop topologies while substantially reducing computational overhead, making it suitable for large-scale IRS deployments in SAGINs. The main contributions of this paper can be summarized as follows:

• A multi-hop IRS-SAGIN channel modeling framework is constructed, which incorporates atmospheric turbulence, pointing errors, and line-of-sight (LoS) propagation, thereby providing a more realistic representation of the communication environment.
• CSI uncertainty is incorporated into the IRS optimization problem, and a min–max robust optimization formulation is developed.
• At the algorithmic level, simulated annealing is combined with Monte Carlo sampling to balance global search capability and low-complexity implementation, effectively avoiding the dimensionality curse encountered in traditional convex relaxation methods.

Through this framework, this paper aims to provide a more robust and efficient solution to facilitate the practical deployment of IRS in SAGINs. The remainder of this paper is organized as follows: Section 2 reviews related research on space–air–ground integrated communications, intelligent reflecting surfaces, and robust optimization techniques. Section 3 introduces the system architecture and communication link modeling and formulates the robust optimization problem. Section 4 presents the proposed phase optimization algorithm design and its solution procedure. Section 5 evaluates the performance of different algorithms through simulations. Finally, Section 6 concludes the paper and outlines future research directions.

2. Related Work

2.1. SAGIN Architectures

With the advancement of 6G communications, SAGINs have gradually emerged as a key architecture for enabling global coverage and intelligent services. By integrating satellite communications, high-altitude platforms, and terrestrial cellular networks, SAGIN realizes a unified coordination of multi-domain resources across space, air, and ground. This integration allows the provision of wide-area coverage and highly reliable communication in challenging environments such as disaster relief, remote areas, and high-mobility scenarios [7,8]. In recent years, extensive research efforts have been devoted to SAGINs in terms of system architecture, multi-layer cooperative mechanisms, dynamic link switching strategies, and task-driven resource scheduling methods [9]. For example, Tan et al. developed a comprehensive multi-factor coupled model that jointly considers UAV channel fading, energy consumption, and energy harvesting, and derived the optimal flight altitude to minimize both the energy outage rate and the signal-to-noise ratio (SNR) outage probability [10]. Nguyen et al. proposed a hybrid edge–cloud collaborative architecture that jointly optimizes UAV trajectories, computation offloading, and wireless resource allocation, thereby achieving a balance between energy consumption and latency [11]. These studies provide valuable theoretical foundations for SAGIN modeling and performance analysis. However, practical deployment still encounters highly complex channel environments, multi-hop cooperative links, and frequent blockage effects, all of which impose stringent requirements on stable and reliable communications.

2.2. IRS-Assisted Communications

IRS has recently emerged as a prominent research topic in the field of wireless communications. Composed of a large number of low-cost and programmable passive reflecting elements, IRS can reconfigure incident signals by adjusting the reflection coefficients (primarily the phase shifts) of each element. This enables controllable and enhanced channel environments without introducing additional transmit power. Compared with conventional relay technologies, IRS demonstrates significant advantages in terms of energy consumption, cost, and deployment flexibility, and is regarded as a key enabling technology for realizing reconfigurable intelligent surfaces (RISs). In terrestrial cellular networks, IRS has been widely applied to various representative scenarios. For example, in urban environments with severe building blockages, IRS can be deployed on walls or building facades to improve both indoor and outdoor coverage. In Internet of Things scenarios, IRS has been used for channel redirection and blind-spot compensation. In UAV communications, IRS mounted on aerial platforms can dynamically reconstruct propagation paths to achieve flexible coverage and rapid responsiveness. These applications have fully demonstrated the potential of IRS in enhancing communication performance in complex environments. With the development of SAGINs, researchers have begun to investigate the application of IRS within this architecture to address challenges such as link blockages and highly dynamic propagation conditions. Existing studies have shown that IRS can serve as a passive relay to support LoS-constrained links, thereby alleviating severe blockages between satellites and terrestrial users. By leveraging the mobility of high-altitude platforms or UAVs, IRS can also achieve on-demand three-dimensional beamforming, enhancing both coverage and communication flexibility. Notably, several recent studies have further revealed the potential value of IRS in SAGIN and UAV systems. For instance, OTFS-aided RIS systems have been shown to outperform conventional OFDM in high-Doppler scenarios, demonstrating the robustness of IRS under strongly time-varying channels [12]. UAV-mounted stacked intelligent metasurfaces (SIMs), combined with optoelectronic hybrid neural networks, have enabled high-accuracy direction-of-arrival (DoA) estimation, offering a new solution for the integration of UAV communications and sensing [13]. In addition, a UAV-mounted IRS framework has been proposed for joint user association and phase design, effectively supporting multiuser coverage and resource allocation optimization [14]. Despite these advances, current research on IRS in SAGIN and UAV systems primarily focuses on transmission mechanism optimization or hardware design. Limited attention has been given to robust optimization and low-complexity algorithm design under complex channel uncertainties. Therefore, further research is required to explore the integrated application of IRS in SAGINs, particularly regarding channel modeling and robust optimization in multi-hop topologies and dynamic environments.

2.3. Robust Optimization Under CSI Uncertainty

In multi-hop space–air–ground communication systems, the acquisition of accurate CSI is often hindered by factors such as high platform mobility, unstable feedback links, and frequent environmental blockages. These challenges severely degrade communication performance and system stability. To address this issue, robust optimization has become an important direction in the design of wireless system [15]. Its core objective is to guarantee a minimum level of system performance under CSI uncertainty, thereby improving system reliability and adaptability. Current research on robust optimization mainly focuses on two aspects: uncertainty modeling methods and robust solution frameworks. Among them, the norm-bounded model is widely adopted due to its mathematical tractability and strong representational capability. It typically models the actual channel as the sum of an estimated value and a perturbation term, with a norm constraint imposed on the latter to formulate a worst-case performance objective. This approach has been extensively applied in IRS-, MIMO-, and UAV-enabled systems. Li et al. proposed an analytical framework to investigate the physical layer security (PLS) of hybrid Free-Space Optical (FSO) and Radio Frequency (RF) systems within SAGINs. The study considers the presence of eavesdroppers on both FSO and RF links, as well as the effects of imperfect CSI and malicious jamming. Simulation results demonstrate that the proposed scheme significantly outperforms conventional FSO-RF relaying approaches in terms of secrecy outage probability and secure throughput. In another line of work, Wu et al. explored the deployment of RIS on UAVs within SAGINs to mitigate the degradation caused by long-distance transmission effects [16]. However, existing studies largely overlook the impact of uncertain CSI in IRS-assisted SAGIN systems. This paper aims to address this gap by incorporating CSI uncertainty into the system model and optimization framework.

In multi-objective optimization, the S-Procedure has been widely adopted to address the theoretical and computational challenges posed by the min–max structure in robust formulations. By introducing Lagrangian multipliers, the S-Procedure transforms an infinite set of uncertainty constraints—typically expressed in quadratic forms—into finite-dimensional semidefinite matrix inequalities. This reformulation enables the problem to be solved using convex optimization techniques such as SDP or SOCP. However, such methods often face significant scalability issues in high-dimensional variable spaces or in systems with complex coupling relationships, leading to high computational complexity and slow convergence [17]. To mitigate the above limitations, a growing body of work has explored heuristic optimization for robust communications, particularly when dealing with non-convex, nondifferentiable, or strongly coupled problems. Representative approaches include particle swarm optimization (PSO), genetic algorithms (GAs), ant colony optimization (ACO), and SA [18]. These gradient-free methods are characterized by strong global search capability, ease of implementation, and scalability to large problem sizes. Among them, SA emulates the physical annealing process: by introducing a temperature-controlled acceptance mechanism that occasionally admits suboptimal moves, it effectively avoids premature convergence to local optima. SA has demonstrated promising performance in IRS phase optimization, interference suppression, and multiuser scheduling [19]. Although the effectiveness of robust optimization has been demonstrated in terrestrial communication systems, its application within the SAGIN architecture remains challenging. On the one hand, dynamic coupling and asymmetry across multi-hop links demand more fine-grained modeling. On the other hand, platform-control limitations and energy constraints restrict the optimization space, while uncertainty in perturbations further shrinks the feasible region, thereby increasing the difficulty of computation. Consequently, developing multi-link robust modeling frameworks tailored to SAGINs and incorporating efficient global search optimization strategies is a key direction for improving system reliability and practical deployability.

3. System Model and Poblem Formulation

3.1. Network Model

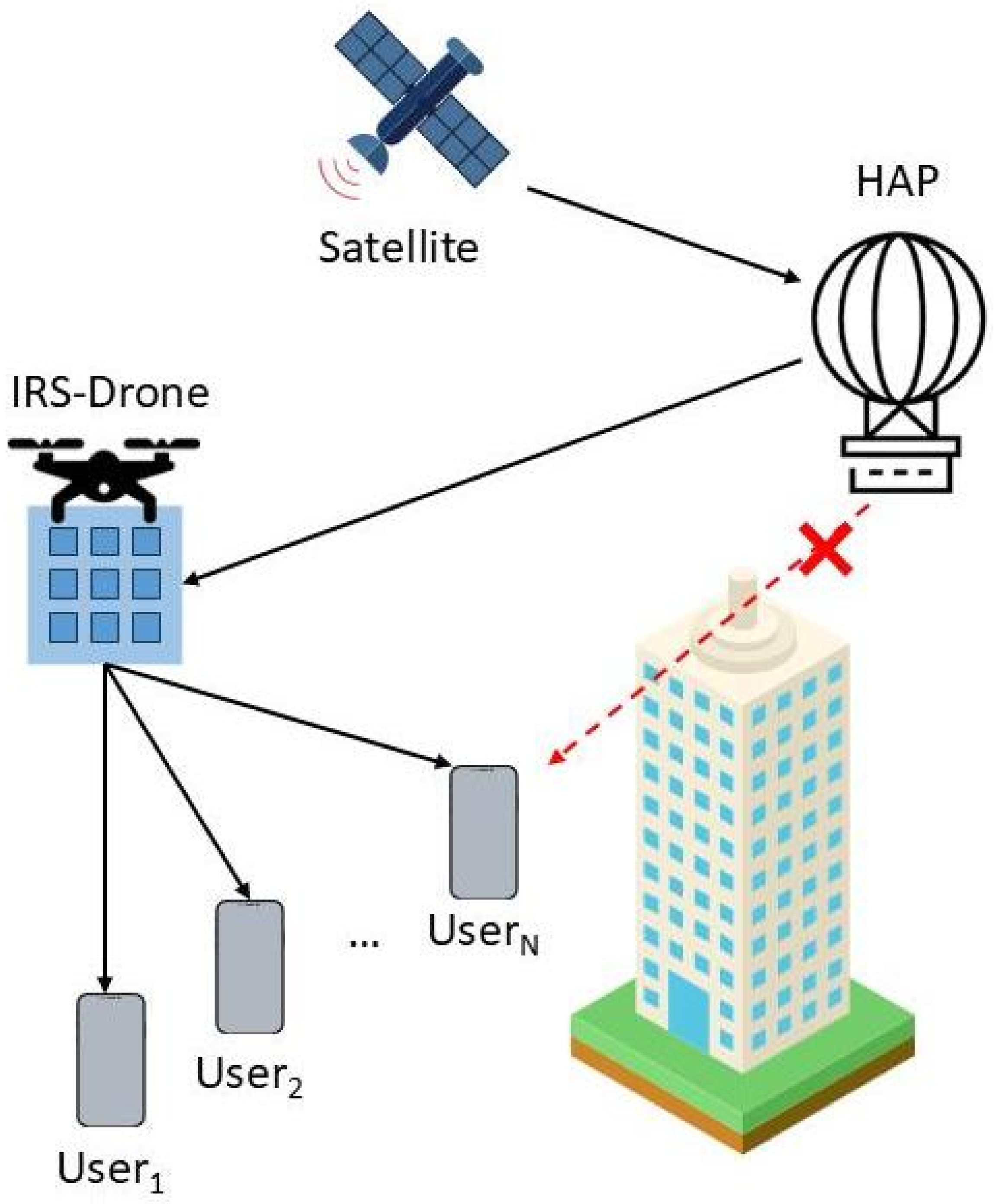
This section considers a representative multi-hop communication scenario in SAGINs, consisting of a satellite node, a high-altitude platform (HAP), an intelligent reflecting surface (IRS), and terrestrial users. The overall link structure follows a four-hop transmission architecture of “satellite–HAP–IRS–terrestrial user” that is designed to ensure reliable communication when severe blockages or link interruptions occur between the satellite and ground terminals. The architecture is illustrated in Figure 1. In this architecture, the satellite node serves as the source, transmitting information signals and establishing a stable long-distance channel with the HAP via an FSO link. Acting as a relay node, the HAP receives the satellite signal and forwards it to the IRS deployed in the aerial domain. The IRS, composed of a large number of programmable passive reflecting elements, reconfigures the incident signals by adjusting phase shifts, thereby reconstructing and enhancing the propagation path. Finally, the reconfigured signal is delivered from the IRS to terrestrial users, completing communication across the three layers of space, air, and ground.

In the subsequent subsections, the channel characteristics of each link will be modeled in detail. Based on this, CSI uncertainty constraints will be introduced to formulate a robust optimization problem, thereby characterizing the system performance in practical deployment scenarios.

3.2. Signal Model

In this section, the multi-hop links in the integrated space–air–ground communication system are modeled, and the received signal expression on the user side is derived. For clarity and to facilitate subsequent derivations, the main notations adopted in this paper are summarized in

Table 1. Notation summary.

Symbol	Description
U	Number of IRSs
M	Number of reflecting elements per IRS
N	Number of terrestrial users
x	Transmit signal from the satellite, with $\mathbb{E}\left[\right|x{|}^2]=1$
$n_k$	Additive white Gaussian noise (AWGN) at the k-th user
$G_{s,r}$	Actual FSO channel gain from satellite to HAP
$G_{r,u}$	Actual RF channel gain from HAP to the u-th IRS
$h_{u,k}$	Actual RF channel gain from the u-th IRS to the k-th user
${\mathit{\vartheta }}_u=[{\vartheta }_{u,1},\dots ,{\vartheta }_{u,M}]$	Phase-control vector of the u-th IRS

.

Specifically, $g_{FSO}$ denotes the path loss of the FSO link, while $g_a$ represents the fading caused by atmospheric turbulence, which is commonly modeled using the Málaga distribution. $G_{s,r}$ refers to the general form of the actual channel gain, with its estimated values and perturbations to be further detailed in Section 3.3. In addition, $g_p$ accounts for the pointing error induced by the misalignment between the satellite’s transmission angle and HAP’s receiving direction, which is defined as follows:

$$\begin{array}{cc}\hfill & G_{s,r}=g_{FSO}{g}_a{g}_p\hfill \end{array}$$

(1)

Here, $g_{\mathrm{FSO}}$ denotes the path loss of the FSO link, $g_a$ represents the fading caused by atmospheric turbulence, which is typically modeled using the Málaga distribution, and $g_p$ accounts for beam misalignment loss resulting from the pointing error between the satellite’s transmission angle and the HAP’s receiving direction. The beam misalignment loss $g_p$ is defined as follows:

$$\begin{array}{cc}\hfill & g_p\approx A_{p}exp\left(-{\displaystyle \frac{2r^2}{s_p^2}}\right)\hfill \end{array}$$

(2)

Here, r denotes the radial displacement caused by pointing error, $A_p$ is the maximum signal gain in the absence of misalignment, and $s_p$ represents the equivalent beam radius at the receiver. Let $G_{r,m}$ denote the signal transmitted from the high-altitude platform to the m-th IRS; the corresponding complex channel gain is given by the following:

$$\begin{array}{c}\hfill G_{r,u}=\sqrt[]{{\beta }_1{\left({\displaystyle \frac{d_1}{d_{r,u}}}\right)}^{{\alpha }_1}}{e}^{j{\varphi }_{r,u}}\end{array}$$

(3)

Here, ${\beta }_1$ denotes the reference path-loss coefficient, $d_{r,u}$ is the distance between the high-altitude platform and the u-th IRS, ${\alpha }_1$ represents the path-loss exponent, and ${\varphi }_{r,u}$ is the phase perturbation term. This link is dominated by a line-of-sight (LoS) component with slight shadow fading, while Rician fading is not considered in this work. Each IRS is responsible for reflecting signals toward ground users within its coverage area. In this network, each IRS consists of M passive reflecting elements. By adjusting the phase shift of each reflecting element, the reflection characteristics can be controlled. The reflection phase shift matrix is defined as follows:

$$\begin{array}{cc}\hfill & \mathrm{\Phi }=diag\left(e^{j{\vartheta }_1},e^{j{\vartheta }_2},\dots ,e^{j{\vartheta }_M}\right),\vartheta \in [0,2\pi )\hfill \end{array}$$

(4)

Here, ${\vartheta }_m$ denotes the phase shift applied by the m-th reflecting element of the IRS. The channel gain between the u-th IRS and the k-th ground user is modeled as follows:

$$\begin{array}{cc}\hfill & h_{u,k}=\sqrt{L_{u,k}}{h}_{u,k}^{\left(s\right)}\hfill \end{array}$$

(5)

Here, $L_{u,k}={\left({\displaystyle \frac{\lambda }{4\pi d_{u,k}}}\right)}^2$ represents the path loss, $h_{m,k}^{\left(s\right)}$ denotes the small-scale fading component, which is typically modeled as a Rayleigh distribution, and $d_{u,k}$ is the distance between the IRS and the ground user. The equivalent signal ultimately received by the k-th user can be expressed as follows:

$$y_k=\underset{\mathrm{multi}\text{-}\mathrm{hop}\mathrm{signal}\mathrm{aggregation}}{\underbrace{{\displaystyle \sum _{u=1}^U\sum _{m=1}^M}{e}^{j{\vartheta }_{u,m}}{G}_{s,r}{G}_{r,u}{h}_{u,k}x}}+n_k,$$

(6)

where $n_k$∼$\mathcal{CN}(0,{\sigma }^2)$ denotes the additive white Gaussian noise (AWGN) at user k. It should be noted that the noise term $n_k$ is introduced only once at the receiver side, rather than being added repeatedly within the double summation. The modeling in this section captures a multi-hop communication process without direct links, making it well-suited for wide-area coverage and obstructed environments in space–air0-ground scenarios. Building on this foundation, the subsequent sections introduce CSI uncertainty modeling and formulate a robust optimization problem to address the impact of channel uncertainty in the communication process.

3.3. Channel Uncertainty Modeling

In SAGINs, CSI uncertainty arises from multiple sources. First, the satellite–HAP FSO link is affected not only by atmospheric turbulence and beam pointing errors, but also by the difficulty of accurately acquiring the statistical parameters of these disturbances in practice. Second, although the HAP–IRS RF link is primarily dominated by LoS channels, estimation errors may still occur in terms of path-loss factors, propagation distances, and phases. Finally, the IRS–user link, in addition to path loss, is further influenced by small-scale fading and environmental blockages, leading to both systematic bias and random perturbations between the estimated and actual CSI. If IRS phase optimization relies solely on estimated channels, the link gain may be either overestimated or underestimated, which can result in significant system performance degradation.

To address these issues, this paper adopts a norm-bounded error model for uncertainty characterization. Under this model, the actual channel is represented as the superposition of the estimated value and a perturbation term, with the perturbation constrained within a norm-bounded set. Unlike models that only consider gain errors, this work simultaneously accounts for uncertainties in path loss, phase variations, and fading across different links, thereby providing a more realistic representation of the complex propagation characteristics in SAGINs. This paper adopts the norm-bounded error model to characterize CSI uncertainty. Let the actual channel of a given link be denoted by g, and its estimated value by $\widehat{g}$; then,

$$g=\widehat{g}+\mathrm{\Delta }g,\parallel \mathrm{\Delta }g\parallel \le ϵ$$

(7)

where $\mathrm{\Delta }g$ denotes the perturbation term, and $ϵ$ represents the error radius, indicating that the actual channel lies within an uncertainty region centered at the estimated value with radius $ϵ$. For convenience in subsequent robust optimization, the uncertainty set can be defined as

$$\mathcal{U}\triangleq \left\{\mathrm{\Delta }:\parallel \mathrm{\Delta }{G}_{s,r}\parallel \le {ϵ}_{sr},\parallel \mathrm{\Delta }{G}_{r,u}\parallel \le {ϵ}_{ru},\parallel \mathrm{\Delta }{h}_{u,k}\parallel \le {ϵ}_{uk}\right\}$$

(8)

3.3.1. Satellite–HAP Link

This link serves as the primary uplink backbone of the system, offering large capacity but being highly sensitive to environmental conditions. The actual channel gain is expressed as

$$G_{s,r}={\widehat{G}}_{s,r}+\mathrm{\Delta }{G}_{s,r},\parallel \mathrm{\Delta }{G}_{s,r}\parallel \le {ϵ}_{sr}$$

(9)

where the estimated channel can be decomposed as

$${\widehat{G}}_{s,r}={\widehat{g}}_{\mathrm{FSO}}{\widehat{g}}_a{\widehat{g}}_p$$

(10)

which corresponds to the free-space path loss ($\widehat{g}\mathrm{FSO}$), the atmospheric turbulence fading ($\widehat{g}a$, typically modeled by the Málaga distribution), and the pointing error factor ($\widehat{g}p$), caused by relative motion and attitude jitter. The aggregated perturbation term $\mathrm{\Delta }Gs,r$ captures both modeling inaccuracies and real-time disturbances associated with these three physical components.

3.3.2. HAP–IRS Link

The HAP operates in the stratosphere, where its link with the IRS is typically dominated by LoS propagation. The link gain is jointly determined by path loss and phase and can be modeled as

$$G_{r,u}={\widehat{G}}_{r,u}+\mathrm{\Delta }{G}_{r,u},\parallel \mathrm{\Delta }{G}_{r,u}\parallel \le {ϵ}_{ru}$$

(11)

where the estimated value follows the Friis model:

$${\widehat{G}}_{r,u}=\sqrt{{\beta }_1{\left({\displaystyle \frac{d_1}{d_{r,u}}}\right)}^{{\alpha }_1}}{e}^{j{\widehat{\varphi }}_{r,u}}$$

(12)

with ${\beta }_1$ denoting the reference path-loss factor, $d_1$ the reference distance, $d_{r,u}$ the propagation distance from the HAP to the u-th IRS, ${\alpha }_1$ the path-loss exponent, and ${\widehat{\varphi }}_{r,u}$ the estimated phase. The perturbation term $\mathrm{\Delta }{G}_{r,u}$ collectively captures deviations arising from path-loss parameters, propagation distance, and phase estimation errors due to meteorological variations and platform attitude fluctuations.

3.3.3. IRS–User Link

IRSs are typically deployed in low-altitude environments or on building surfaces, where the links are significantly affected by blockage and environmental scattering. The overall channel conditions are generally determined by both large-scale path loss and small-scale fading. The actual channel gain between the u-th user and IRS k can be modeled as

$$h_{u,k}={\widehat{h}}_{u,k}+\mathrm{\Delta }{h}_{u,k},\parallel \mathrm{\Delta }{h}_{u,k}\parallel \le {ϵ}_{u,k}$$

(13)

where the estimated channel is given by

$${\widehat{h}}_{u,k}=\sqrt{L_{u,k}}{\widehat{h}}_{u,k}^{\left(s\right)},L_{u,k}={\left({\displaystyle \frac{\lambda }{4\pi d_{u,k}}}\right)}^2$$

(14)

with $L_{u,k}$ denoting the path loss, $d_{u,k}$ the propagation distance between the u-th IRS and the k-th user, and ${\widehat{h}}_{u,k}^{\left(s\right)}$ the small-scale fading, which is typically modeled by a Rayleigh distribution. The perturbation term $\mathrm{\Delta }{h}_{u,k}$ reflects the combined error in path-loss parameters and fading components due to user mobility and variations in blockage conditions.

Through the above link-level modeling, this paper captures the CSI uncertainty characteristics across different propagation paths in a comprehensive manner. While ensuring mathematical tractability, the model also reflects the complex propagation mechanisms inherent in SAGIN environments. However, it should be noted that although the norm-bounded error model effectively enhances robustness, it does not explicitly account for more sophisticated phenomena such as Doppler effects, fast shadowing, or distributional uncertainties. Future research may incorporate time-correlated stochastic processes or probabilistic constraint methods to further improve modeling accuracy and engineering applicability.

3.4. Problem Formulation

Building upon the signal modeling and CSI uncertainty analysis presented in the previous sections, this section formulates a robust optimization problem to ensure reliable communication quality under imperfect CSI. Since the phase control of IRS plays a decisive role in the received signal power, the main objective of this work is to minimize the worst-case degradation of the received SINR, thereby enhancing the robustness of the system under uncertain channel conditions. Specifically, let the received signal of the k-th user be given by Section 3.2. Then, the corresponding SINR can be expressed as

$${\mathrm{SINR}}_k={\displaystyle \frac{{\left|{\sum }_{u=1}^U{\sum }_{m=1}^M{e}^{j{\vartheta }_{u,m}}{G}_{s,r}{G}_{r,u}{h}_{u,k}\right|}^2}{{\sigma }_k^2}}$$

(15)

where ${\sigma }_k^2$ denotes the additive white Gaussian noise (AWGN) power. When CSI uncertainty is considered, the actual SINR is affected by estimation errors, and thus, the system robustness must be ensured under all possible perturbation conditions. The optimization objective of this work is to maximize the minimum SINR among all users, which can be formulated as

$$\underset{\left\{{\vartheta }_{u,m}\right\}}{max}\underset{\mathrm{\Delta }{G}_{s,r},\mathrm{\Delta }{G}_{r,u},\mathrm{\Delta }{h}_{u,k}\in \mathcal{U}}{min}\underset{k=1,\dots ,N}{min}{\mathrm{SINR}}_k$$

(16)

In addition, the phase adjustments of the IRS elements must satisfy the following constraint: the reflection coefficient of each element has a fixed amplitude of unity; that is,

$$|e^{j{\vartheta }_{u,m}}|=1,{\vartheta }_{u,m}\in [0,2\pi ),\forall u,m$$

(17)

Combining the above, the robust optimization problem can be formulated as

$$\begin{array}{cc}\hfill \underset{\left\{{\vartheta }_{u,m}\right\}}{max}& \underset{\mathrm{\Delta }{G}_{s,r},\mathrm{\Delta }{G}_{r,u},\mathrm{\Delta }{h}_{u,k}\in \mathcal{U}}{min}\underset{k=1,\dots ,N}{min}{\mathrm{SINR}}_k\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& |e^{\mathrm{j}{\vartheta }_{u,m}}|=1,{\vartheta }_{u,m}\in [0,2\pi ),\forall u,m\hfill \end{array}$$

(18)

This optimization problem is essentially a non-convex two-layer robust optimization: the outer layer optimizes the IRS phase configuration, while the inner layer searches for the worst-case perturbation within the CSI uncertainty set. As the direct solution of this problem entails prohibitive complexity, the next section introduces a simulated annealing-based approximation algorithm that iteratively searches for a phase control solution with strong robustness.

4. Proposed Scheme

4.1. Robust Optimization Strategy Based on Simulated Annealing

In the previous chapter, the optimization problem $\mathbf{P}\mathbf{1}$ was formulated as a non-convex two-layer robust optimization problem. The outer layer optimizes the IRS phase matrix $\left\{{\vartheta }_{u,m}\right\}$, while the inner layer searches for the worst-case perturbation within the CSI uncertainty set $\mathcal{U}$. Specifically, the problem can be expressed as

$$\mathbf{P}\mathbf{1}:\underset{\left\{{\vartheta }_{u,m}\right\}}{max}\underset{\mathrm{\Delta }\in \mathcal{U}}{min}\underset{k=1,\dots ,N}{min}{\mathrm{SINR}}_k(\left\{{\vartheta }_{u,m}\right\},\mathrm{\Delta })$$

(19)

We first consider the search space of the IRS phase matrix. Suppose the system contains U IRSs, each with M reflecting elements. The total number of optimization variables is then $U\times M$ phase shifts. If each phase shift is continuously distributed in $[0,2\pi )$, the search must be performed over an infinite continuous space, which is intractable. Even when a discretization approximation is applied (e.g., quantizing the phase into Q levels), the complexity still grows as

$$\mathcal{O}\left(Q^{U·M}\right)$$

(20)

For example, when $M=128$ and $Q=8$, the search space size is $8^{128}\approx {10}^{115}$, which is far beyond current computational capabilities.

Second, under CSI uncertainty, the inner-layer problem requires computing the worst-case minimum SINR within the uncertainty set $\mathcal{U}$. Assuming the number of users is N, solving for the worst-case perturbation for each user incurs at least

$$\mathcal{O}(N·C_{\mathrm{worst}})$$

(21)

where $C_{\mathrm{worst}}$ denotes the computational cost of the minimization within the uncertainty set. For large-scale multiuser systems, this cost is further amplified, rendering the direct solution of $\mathbf{P}\mathbf{1}$ infeasible.

In summary, problem $\mathbf{P}\mathbf{1}$ is characterized by high-dimensional variables, non-convex constraints, and stringent robustness requirements. Its computational complexity grows exponentially, making it an NP-hard problem that cannot be efficiently solved within conventional convex optimization frameworks.

To overcome the aforementioned difficulties, this paper adopts the SA method to optimize the IRS phase configuration. Inspired by the annealing process in solid-state physics, the basic principle of SA is as follows: at high temperatures, suboptimal solutions are accepted with a certain probability to enhance global exploration; as the temperature gradually decreases, the acceptance of inferior solutions is restricted, eventually leading to convergence toward a stable solution with superior performance.

In the considered problem, the application of SA can be summarized as follows: In each iteration, a random perturbation is applied to the IRS phase matrix to generate a candidate solution ${\mathbf{\Phi }}^{\prime }$. The performance of this candidate is then evaluated based on the minimum user SINR within the uncertainty set $\mathcal{U}$, namely,

$$f\left({\mathbf{\Phi }}^{\prime }\right)=\underset{\mathrm{\Delta }\in \mathcal{U}}{min}\underset{k=1,\dots ,N}{min}{\mathrm{SINR}}_k({\mathbf{\Phi }}^{\prime },\mathbf{\Delta })$$

(22)

If $f\left({\mathbf{\Phi }}^{\prime }\right)\ge f\left(\mathbf{\Phi }\right)$, the new solution is directly accepted; otherwise, it is accepted with probability

$$p=exp\left(-{\displaystyle \frac{f\left(\mathbf{\Phi }\right)-f\left({\mathbf{\Phi }}^{\prime }\right)}{T}}\right)$$

(23)

where T denotes the current temperature. As the temperature decreases over time, the algorithm gradually converges to a near-optimal solution.

4.2. Monte Carlo Sampling-Based Phase Optimization

To address the robust optimization problem formulated earlier, we design a phase optimization algorithm that combines SA with Monte Carlo sampling, referred to as RIPA (Robust IRS Phase Annealing). The proposed method treats the IRS phase vector as the optimization variable, and under uncertain channel conditions, it leverages probabilistic perturbations and sample-driven worst-case approximation to optimize the performance of the weakest user. Compared with traditional convex relaxation or greedy search methods, the proposed approach maintains strong search capability and convergence performance under complex non-convex constraints.

Given a phase configuration $\mathrm{\Phi }$, the approximate worst-case performance of the received signal power for the users under channel uncertainty is defined as

$$f_{\mathrm{worst}}\left(\mathrm{\Phi }\right)=\underset{s=1,\dots ,S}{min}\sum _{k=1}^N{\left|\sum _{m=1}^M{e}^{j{\vartheta }_m}{G}_{s,r}\left({\widehat{G}}_{r,m}+\delta G_{r,m}^{\left(s\right)}\right)\left({\widehat{h}}_{m,k}+\delta h_{m,k}^{\left(s\right)}\right)\right|}^2$$

(24)

where S denotes the number of perturbation samples. Here, $\delta G_{r,m}^{\left(s\right)}$ and $\delta h_{m,k}^{\left(s\right)}$ represent the perturbations for the HAP–IRS and IRS–user links, respectively, subject to

$$\begin{array}{cc}\hfill |\delta G_{r,m}^{\left(s\right)}{|}^2& \le {ϵ}_{r,m}\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill |\delta h_{m,k}^{\left(s\right)}{|}^2& \le {ϵ}_{m,k}\hfill \end{array}$$

(26)

The above objective function is approximated by generating multiple random samples within the perturbation set and selecting the worst-case performance, thereby characterizing system robustness under uncertain channels. During the optimization process, the simulated annealing algorithm introduces a temperature variable to control the search range and acceptance probability: at high temperatures, suboptimal solutions are accepted with a certain probability to enhance global exploration; as the temperature gradually decreases, the algorithm becomes more stable and eventually converges to a near-optimal solution. The specific procedure is described as Algorithm 1.

Algorithm 1: Robust IRS Phase Annealing (RIPA).

In this section, we have formulated the robust optimization problem for IRS-assisted SAGINs under imperfect CSI and highlighted the inherent challenges posed by its non-convex and high-dimensional structure. To overcome the prohibitive computational complexity of direct solutions, we proposed the RIPA algorithm, which integrates simulated annealing with Monte Carlo sampling. The algorithm effectively balances global exploration and local refinement, enabling robust phase configuration of large-scale IRS with reduced computational overhead. Theoretical analysis further demonstrates that the proposed method achieves polynomial-level complexity while maintaining scalability with respect to the number of reflecting elements and sampling instances. These results establish a practical and robust optimization framework, laying the foundation for the performance evaluation and comparative studies to be presented in the next section.

5. Numerical Results and Analysis

5.1. Experimental Environment and Parameter Setup

To validate the effectiveness of the proposed robust optimization method based on RIPA (Robust IRS Phase Annealing), numerical simulations were conducted on a Python 3.11.3 platform. The system consists of a satellite node, a HAP, an IRS, and multiple terrestrial users, forming a representative multi-hop space–air–ground integrated network. The satellite and HAP are connected via an FSO link, which accounts for path loss, atmospheric turbulence fading (modeled by the Málaga distribution), and pointing errors. The HAP–IRS link is dominated by LoS propagation, with channel gain decaying over distance and perturbed by small phase fluctuations. The IRS–user link is modeled by large-scale path loss combined with small-scale Rayleigh fading.

To capture the estimation errors in CSI, a norm-bounded uncertainty model is adopted. Perturbation samples are generated within the error-bound radius using Monte Carlo sampling, thereby approximating the worst-case performance. For benchmarking, three methods are compared: (i) the proposed RIPA method, which iteratively optimizes the IRS phase vector through simulated annealing while approximating the worst-case channel conditions via Monte Carlo sampling; (ii) random-phase IRS (Random Phase IRS), where phase shifts are uniformly distributed in $[0,2\pi )$; and (iii) a baseline without IRS (Without IRS), where only the direct link is utilized.

System performance is evaluated in terms of the worst-case SINR, defined as the minimum value across all users and perturbation samples, expressed in dB. The main simulation parameters are summarized in

Table 2. Simulation parameter settings.

Parameter	Value/Description
M	[16, 32, 64, 128, 256]
N	[2, 4, 8, 12, 16]
$ϵ$	[0, 0.01, 0.02, 0.05, 0.1]
S	300
L	150
$T_0$	1.0
$\alpha$	0.95
$\delta \varphi$	0.1
${\sigma }^2$	1
$R_{\mathrm{avg}}$	4

.

5.2. Experimental Results and Analysis

Under a unified Monte Carlo evaluation protocol, we compare all methods using two robustness metrics. Let $s\in \{1,\dots ,S\}$ index the perturbation samples and $k\in \{1,\dots ,N\}$ index the users. ${\mathrm{SINR}}_{s,k}$ is denoted by the receiving SINR of user k under sample s, which is jointly determined by the phase vector $\mathit{\theta }$ and the uncertain channel characterized by the radius $\epsilon$; the noise variance is ${\sigma }^2$.

First, the worst-user worst-case SINR is defined as

$$\begin{array}{c}\hfill f_{\mathrm{worst}}\triangleq \underset{s}{min}\underset{k}{min}{\mathrm{SINR}}_{s,k},f_{\mathrm{worst}}^{\mathrm{dB}}=10{log}_{10}\left(f_{\mathrm{worst}}+{10}^{-10}\right)\end{array}$$

(27)

This quantifies the system’s link-assurance capability under the joint ’worst perturbation + worst user’ condition (larger is better). We denote this metric by $f_{\mathrm{worst}}$ and report it in decibels as $f_{\mathrm{worst}}^{\mathrm{dB}}$ in the figures. Second, the robust throughput is defined as

$$\begin{array}{c}\hfill R_{min}\triangleq \underset{s}{min}\sum _{k=1}^N{log}_2\left(1+{\mathrm{SINR}}_{s,k}\right)\end{array}$$

(28)

which represents the system’s usable sum capacity under the most adverse perturbation. Together with $f_{\mathrm{worst}}$, it provides a complementary view of ’worst-user guarantee vs. aggregate capacity’. To ensure the statistical reliability of the reported results, each simulation setting was independently repeated 10 times with different randomly generated channel realizations. The performance metrics (e.g., $f_{\mathrm{worst}}$ and $R_{min}$) were then averaged over these independent trials. By adopting this approach, we mitigate the influence of random fluctuations and guarantee that the presented curves reflect the consistent performance trends rather than accidental outcomes.

5.2.1. Uncertainty-Robustness Analysis

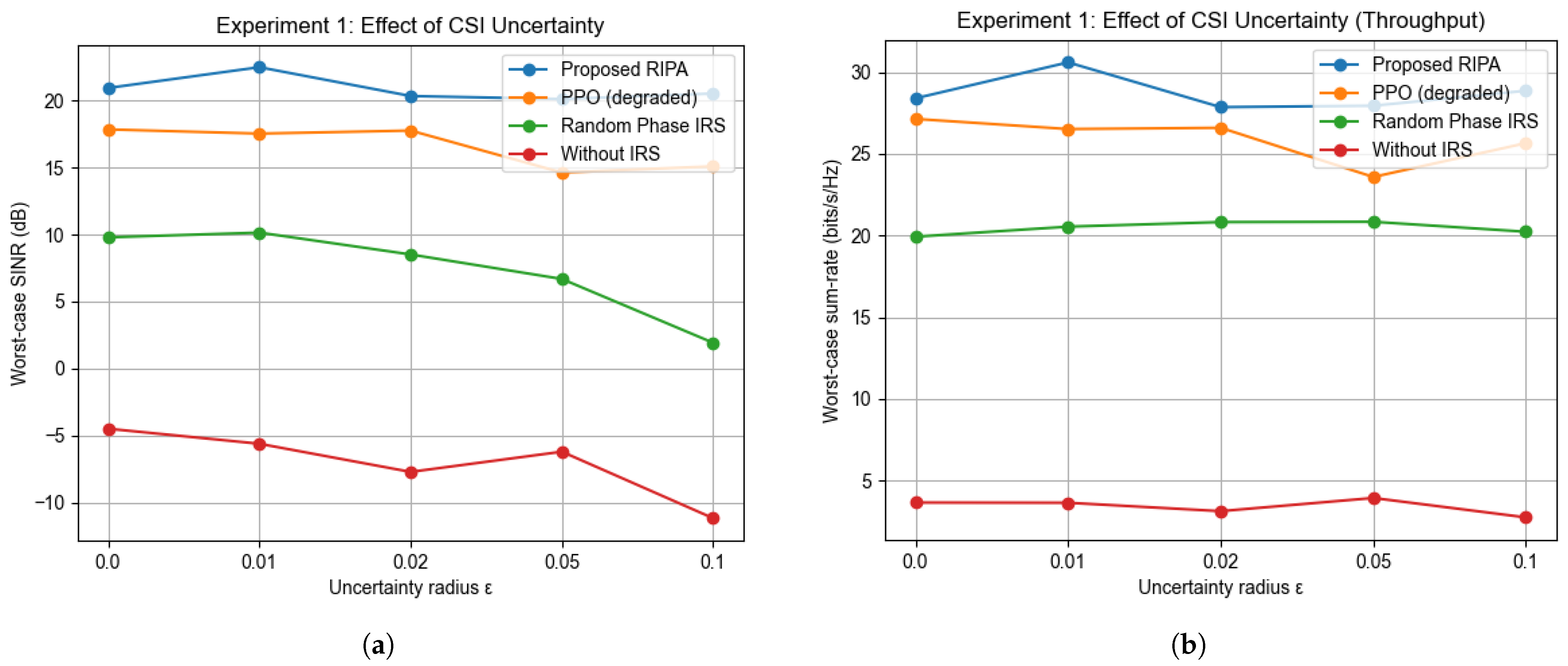
As shown in Figure 2a,b, as the CSI uncertainty radius $\epsilon$ increases, the proposed RIPA exhibits a gentle decline yet consistently leads on both metrics. Specifically, the worst-user worst-case SINR $f_{\mathrm{worst}}$ remains high—about 21–22 dB at $\epsilon =0$—and still stays around 19–21 dB at $\epsilon =0.1$. Correspondingly, the robust throughput $R_{min}$ reaches approximately $30\text{–}31$ bits/s/Hz in the small-perturbation regime and remains at about 26–28 bits/s/Hz at $\epsilon =0.1$, implying an overall relative loss of roughly $15\%$. These results indicate that, under the “worst perturbation + worst user” evaluation paradigm, RIPA is only mildly sensitive to uncertainty and maintains stable robustness.

By contrast, PPO performs close to RIPA when $\epsilon \le 0.02$, but as the uncertainty grows to $\epsilon \ge 0.05$, the gap widens to about 3–4 dB in $f_{\mathrm{worst}}$ and 2–3 bits/s/Hz in $R_{min}$, reflecting limited robustness of the learned policy under stronger perturbations. On the other hand, a random-phase IRS—without phase optimization—shows pronounced degradation of $f_{\mathrm{worst}}$ with $\epsilon$ (dropping from roughly 10 dB to much lower levels), while $R_{min}$ mostly stagnates around 20–21 bits/s/Hz. The no-IRS baseline yields markedly inferior values on both metrics: $f_{\mathrm{worst}}$ often lies in the negative dB region and $R_{min}$ is only about 3–4 bits/s/Hz, thus serving as a practical lower bound. Building on these observations, we subsequently examine the scalability gains brought by increasing the array size to assess how effectively each method converts additional phase degrees of freedom into usable robustness gains.

5.2.2. Scalability Analysis

With the CSI uncertainty radius fixed at $\epsilon =0.05$, we increase the number of IRS elements M. As shown in Figure 3a,b, both curves for RIPA grow approximately linearly with M: the worst-user worst-case SINR $f_{\mathrm{worst}}$ rises from about $12\text{–}14$ dB at $M=16$ to roughly 27 dB at $M=256$, while the robust throughput $R_{min}$ increases from around $19\text{–}20$ bits/s/Hz to about $36\text{–}37$ bits/s/Hz. This steady scaling indicates that RIPA effectively converts the additional phase degrees of freedom provided by more reflecting elements into robust coherent-combining gains. Meanwhile, PPO also improves with M, but its gap from RIPA tends to widen in the large-scale regime: it is typically behind by $2\text{–}4$ dB in $f_{\mathrm{worst}}$ and $2\text{–}5$ bits/s/Hz in $R_{min}$. This behavior is consistent with conservative choices such as quantization and step-size clipping, which limit fine-grained tuning in high-dimensional phase spaces.

By contrast, a random-phase IRS exhibits overall upward trends with M but with pronounced fluctuations, suggesting that unoptimized phases yield only “accidental coherence” that fails to deliver stable gains in the worst-sample sense. The no-IRS baseline is independent of M and remains a lower bound across both metrics. To further isolate the impact of multiuser interference on robustness, we subsequently turn to scaling with the number of users.

5.2.3. Multiuser Scenario Analysis

With $\epsilon =0.05$ and $M=64$ fixed, we increase the number of users N. As shown in Figure 4a, the worst-user worst-case SINR $f_{\mathrm{worst}}$ decreases for all methods as N grows, since a larger user set is more likely to contain an extreme weak user and the limited resources must be split among more users. Even so, RIPA maintains the highest level across the entire range—for example, it drops from about 23 dB at $N=2$ to roughly 13 dB at $N=16$, yet it remains clearly above the alternatives. PPO tracks RIPA but is consistently lower, with the gap widening slightly at larger N. A random-phase IRS exhibits pronounced fluctuations and even enters the negative dB region for certain values of N. The no-IRS baseline stays lowest throughout.

In contrast, Figure 4b shows that the sum-rate metric $R_{min}$ grows approximately linearly with N. RIPA leads over the entire range and exceeds ∼90 bits/s/Hz at $N=16$; PPO follows closely but remains consistently below it. The random-phase IRS falls increasingly behind in the medium-to-large N regime, while the no-IRS case exhibits the most limited gains. Overall, under the joint objectives of fairness (worst-user assurance) and capacity (sum rate), RIPA achieves a more favorable trade-off: despite the inevitable decline in $f_{\mathrm{worst}}$ with growing N, it delivers higher $R_{min}$ in multiuser settings. Finally, to validate the effectiveness and computational cost of the optimization itself, we present convergence tests.

5.2.4. Convergence Validation

As shown in Figure 5, the RIPA metric $f_{\mathrm{worst}}$ rises rapidly over the first few tens of iterations (from roughly $14\text{–}16$ dB to above 19 dB), then approaches its steady value in a stepwise manner, and ultimately converges to about 22 dB after on the order of a hundred iterations. This trajectory aligns with the cooling schedule of simulated annealing: at higher temperatures, occasional downhill moves are admitted to escape local optima; as the temperature decreases, the search stabilizes.

Given a per-iteration objective-evaluation cost of $\mathcal{O}\left(SMN\right)$ and an overall complexity of $\mathcal{O}\left(LSMN\right)$ with L iterations, RIPA achieves a “fast start, stable convergence, and controlled cost” profile at the scales considered in this paper. These properties support extensions to larger deployments and scenarios with real-time constraints.

Generally, this section systematically compares the methods along three axes—uncertainty level, array size, and user population—and corroborates the implementation cost and attainable performance via convergence tests. From Figure 2a,b, as $\epsilon$ increases, RIPA exhibits the smallest performance-degradation slope and consistently leads on both $f_{\mathrm{worst}}$ and $R_{min}$. Next, Figure 3a,b show that both metrics for RIPA grow approximately linearly with M, indicating efficient conversion of additional phase degrees of freedom into robust coherent-combining gains; PPO improves in the same direction but its gap to RIPA widens slightly in the large-scale regime. In tandem with Figure 4a,b, as N increases, all methods experience an inevitable decline in $f_{\mathrm{worst}}$ while $R_{min}$ grows roughly linearly; RIPA achieves a superior fairness–capacity trade-off, maintaining higher worst-user protection and minimum robust throughput under stronger multiuser interference. Finally, Figure 5 confirms that RIPA reaches a steady state with a “fast start–stepwise approach–stable convergence” trajectory at acceptable computational complexity.

Taken together, these results support a consistent conclusion: across multiple key scenarios, RIPA demonstrates stronger robustness, scalability, and implementability than PPO, random-phase IRS, and the no-IRS baseline, offering a more compelling solution for robust system design under uncertain channel conditions.

6. Conclusions

This paper investigates the impact of channel uncertainty on IRS-assisted communications in space–air–ground integrated networks and proposes a robust IRS phase optimization method, namely RIPA (Robust IRS Phase Annealing). In terms of system modeling, a multi-hop architecture was established, consisting of the satellite–high-altitude platform, high-altitude platform–IRS, and IRS–user links. A norm-bounded uncertainty channel model was introduced to effectively capture the influence of CSI estimation errors on system performance in practical environments. On the algorithmic side, to address the resulting min–max non-convex optimization problem, the RIPA algorithm was developed by integrating simulated annealing with Monte Carlo sampling, thereby enhancing the robustness of the worst-case user performance through global search and perturbation-based approximation. In the numerical experiments, RIPA was comprehensively evaluated under different CSI uncertainty levels, IRS array sizes, numbers of users, and iterative convergence behavior. The results demonstrated that RIPA significantly outperforms both random-phase IRS and the baseline without IRS across various complex conditions, showing clear advantages in robustness, scalability, and convergence efficiency.

Despite the progress achieved, several promising directions remain for further exploration. First, the system modeling in this work is mainly based on idealized FSO and LoS assumptions. Future studies could incorporate more complex and dynamic channel models, such as time-varying channels affected by atmospheric stratification, satellite orbital dynamics, or blockage effects, to enhance realism. Second, regarding IRS phase optimization, this paper adopts a heuristic method combining simulated annealing and Monte Carlo sampling. Future research may explore intelligent optimization strategies based on deep reinforcement learning or meta-heuristic algorithms, aiming to further reduce computational complexity and improve convergence speed. Third, this work adopts worst-case user SINR as the primary optimization objective. Future efforts could integrate multiple performance metrics—such as energy efficiency, latency, and coverage—into a unified framework for more comprehensive system evaluation. Finally, this study focuses on a single-IRS scenario, whereas in large-scale deployments, cooperative multi-IRS optimization and joint integration with other reconfigurable metasurfaces will be highly promising research directions.

In conclusion, this paper proposes a robust phase optimization algorithm, RIPA, providing an effective solution for the practical deployment of IRS in space–air–ground integrated communication systems. Future research will help drive this technology from theoretical validation toward real-world implementation, thereby supporting the development of next-generation broadband, reliable, and intelligent global communication networks. It is also worth emphasizing that the channel models adopted in this work still involve certain idealized assumptions. For example, the satellite–HAP link is mainly modeled as FSO transmission without considering the time-varying refractive effects of atmospheric stratification; the HAP–IRS link assumes pure LoS propagation, whereas in practice, it may experience non-line-of-sight interference due to meteorological conditions or obstacles; and the IRS–user link is modeled with Rayleigh fading, yet it does not account for factors such as terrain variations, urban blockages, or user mobility. Therefore, future work could introduce more sophisticated and dynamic channel models, such as combined multipath and time-selective fading models, mixed fading channels incorporating blockage and shadowing effects, or measurement-based statistical models, in order to further enhance the practical applicability of the research outcomes.Beyond the above aspects, future work will pursue (i) a joint robust design that couples IRS phase control with user scheduling, deployment, and energy constraints; (ii) distributed and learning-augmented optimization under limited fronthaul, with explicit modeling of hardware non-idealities and semi-blind/CSI-free reflection training to reduce feedback; and (iii) multi-objective extensions (energy, latency, and coverage), cooperative multi-IRS and ISAC-oriented designs, and over-the-air prototypes to validate practicality.