Abstract
Private Set Intersection Cardinality (PSI-CA) is a cryptographic method in secure multi-party computation that allows entities to identify the cardinality of the intersection without revealing their private data. Traditional approaches assume similar-sized datasets and equal computational power, overlooking practical imbalances. In real-world applications, dataset sizes and computational capacities often vary, particularly in Internet of Things and mobile scenarios where device limitations restrict computational types. Traditional PSI-CA protocols are inefficient here, as computational and communication complexities correlate with the size of larger datasets. Thus, adapting PSI-CA protocols to these imbalances is crucial. This paper explores unbalanced scenarios where one party (the receiver) has a relatively small dataset and limited computational power, while the other party (the sender) has a large amount of data and strong computational capabilities.This paper, based on the concept of commutative encryption, introduces Cuckoo filter, cloud computing technology, and homomorphic encryption, among other technologies, to construct three novel solutions for unbalanced Private Set Intersection Cardinality (PSI-CA): an unbalanced PSI-CA protocol based on Cuckoo filter, an unbalanced PSI-CA protocol based on single-cloud assistance, and an unbalanced PSI-CA protocol based on dual-cloud assistance. Depending on performance and security requirements, different protocols can be employed for various applications.
1. Introduction
1.1. Background
In today’s digital age, data privacy and security have become critically important issues worldwide. With technological advancements and explosive growth in data volumes, individuals and institutions face unprecedented challenges in protecting their privacy. Privacy computing technologies have emerged in response to these challenges, enabling the secure computation and analysis of data without exposing the details of personal information. This is crucial for driving data-driven innovation and services while safeguarding personal privacy and data protection.
Private Set Intersection (PSI) technology is a key technique in the field of privacy computing. It allows two or more parties to identify the common elements in their datasets without revealing any other non-shared data. This technology is highly useful in multiple application scenarios, such as cross-institutional data cooperation, fraud detection, and private contact discovery, without compromising user privacy. It has been applied in various fields, including the genetic testing of fully sequenced human genomes [1], private contact discovery [2], and botnet detection [3]. This study investigates the cardinality of private dataset intersections between two parties, which is an essential aspect of two-party computation (2PC) tasks. Specifically, it involves a sender and a receiver who aim to collaboratively determine the number of common elements in their private datasets. Throughout this process, only the receiver obtains the cardinality of the set intersection, while the sender remains unaware of it. The topic of private-set intersection cardinality is widely researched due to its significant practical applications
1.2. Motivation
While the traditional Private Set Intersection Cardinality (PSI-CA) protocols have been extensively explored in research, real-world applications continue to present unique challenges. Traditional approaches assume similar-sized datasets and equal computational power, overlooking practical imbalances. In real-world applications, dataset sizes and computational capacities often vary, particularly in Internet of Things and mobile scenarios where device limitations restrict computational types. Traditional PSI-CA protocols are inefficient here, as computational and communication complexities correlate with the size of larger datasets. Thus, adapting PSI-CA protocols to these imbalances is crucial.
A compelling example is found in the collaboration between major medical institutions and small health app developers. In this scenario, a large medical institution with extensive patient data and robust computational capabilities collaborates with a small app developer who possesses minimal user data and limited computational resources. The primary goal is to analyze the coverage of health app users within the extensive patient database to assess market penetration and potential partnership opportunities. For instance, the medical institution might want to determine how many of its patients are using the health app to consider recommending it more broadly or collaborating on new features.
This article uses the above scenario as an example to conduct research, but our scenario is not limited to this, and the data types are also diverse. As long as one party has a large number of dataset elements and strong computing and storage capabilities, while the other party has a small number of dataset elements and weak computing and storage capabilities, and both parties want to perform PSI-CA operations, our solution is applicable.
To address the challenges outlined above, this paper delves into the unbalanced Private Set Intersection-Cardinality (PSI-CA) protocols and proposes three innovative unbalanced PSI-CA protocols. In practical applications, different solutions can be chosen based on varying performance and security requirements.
1.3. Main Work
- To address the performance shortcomings of traditional PSI-CA protocols in the face of significant differences in dataset sizes between participants, this paper introduces the first protocol, which is the unbalanced PSI-CA protocol based on Cuckoo filter. This protocol successfully constructs the first unbalanced private intersection cardinality protocol of this article by integrating exchange encryption technologies with Cuckoo filter functionalities for private information retrieval, followed by experimental analysis.
- To alleviate the computational and storage burden on the small health app developer in the first protocol, the paper further proposes an unbalanced PSI-CA protocol based on single-cloud assistance and conducts experimental analysis. This strategy effectively migrates computational and storage tasks to cloud services, significantly optimizing resource utilization efficiency.
- To safeguard against data leakage risks inherent in the unbalanced PSI-CA protocol based on single-cloud assistance, which cannot resist collusion attacks, the paper further designs an unbalanced PSI-CA protocol based on dual-cloud assistance. By employing homomorphic encryption and other security technologies, this scheme resolves potential data leakage risks in the single-cloud protocol while effectively preventing potential collusion attacks.
- Based on the unbalanced PSI-CA protocol based on dual-cloud assistance, this paper also designs the PSI-CA network and establishes corresponding data update strategies, significantly enhancing the practicality of the protocol.
2. Related Works
2.1. Design Framework of Private Set Intersection Protocol
2.1.1. Design Framework Based on Public Key Encryption
The basic idea behind early private-set intersection protocols is to encrypt data elements and then perform comparison operations on the encrypted data. The most widely used technique in this method is homomorphic encryption: The sender encrypts their dataset and sends it to the receiver. The receiver processes these ciphertexts using the properties of homomorphic encryption and returns the results to the sender. The sender then decrypts these results using their own private key to obtain the intersection of the datasets. This public-key-based method generally relies on three main security assumptions [4]:
- Based on Diffie–Hellman (DH) theory: Meadows [5] used the DH key-exchange mechanism, which is based on the discrete logarithm problem, to implement a PSI protocol. In contrast, Huberman et al. [6] explored the use of elliptic curve cryptography in PSI, noting its significant advantages in security and efficiency compared to traditional discrete logarithm-based PSI methods.
- Based on the RSA assumption: DeCristofaro et al. [7] developed a semi-honest PSI protocol using RSA blind signature technology based on the integer factorization problem. Another study [8] showed that PSI schemes based on discrete logarithm cryptography demonstrated higher efficiency compared to those based on integer factorization cryptography.
- Based on homomorphic encryption: Freedman et al. [9] innovatively represented elements as roots of polynomials and encrypted the coefficients of these polynomials using Paillier homomorphic encryption technology, combined with zero-knowledge proofs, to implement a two-party PSI protocol resistant to malicious attacks. In 2016, Freedman et al. [10] further improved computational efficiency through the ElGamal encryption mechanism and reduced the protocol’s computational complexity using Cuckoo Hash technology [4]. Abadi et al. [11] introduced a set representation method based on point-value pairs of d-degree polynomials, implemented through the Paillier encryption scheme, reducing the multiplication complexity from O() to O(d) [4]. Kissner et al. [12] adopted different polynomial representation methods, significantly reducing computational costs to be linearly proportional to the number of participants. Jarecki et al. [13] used additive homomorphic encryption and zero-knowledge proofs to implement pseudorandom functions (PRF). Hazay et al. [14] developed an additive homomorphic encryption scheme that supports threshold decryption for implementing multi-party semi-honest PSI protocols. Dou Jiawei et al. [15] combined Paillier encryption to propose a PSI protocol based on the formula for calculating the area of triangles and rational number encoding.
Public key encryption-based Private Set Intersection (PSI) schemes typically feature fewer communication rounds and are suitable for environments with strong computational capabilities. However, in practice, communication bandwidth and time complexity often pose significant constraints [4].
2.1.2. Design Framework Based on Garbled Circuits
Garbled circuit technology can transform any function into a Boolean circuit, thereby securely computing the function. Early methods based on universal circuits, like the DPSZ scheme [16], demonstrated how to use arithmetic circuits to solve the set intersection problem: the circuit builder encrypts the circuit gates using a symmetric key, then creates a garbled circuit and sends it to the circuit evaluator. The evaluator decrypts specific paths in the garbled circuit to obtain the intersection results, while being unable to access other paths in the circuit. As the circuit depth increases, its construction complexity also increases. Additionally, PSI protocols based on this circuit design can also perform various symmetric function operations, such as calculating the threshold intersection, the number of intersection elements, and their sum. For adversaries under semi-honest conditions, there are two types of garbled circuits: the Yao [17] protocol and the GMW [18] protocol. Pinkas et al. [19,20,21] and Chandran et al., based on hash storage structures and GMW circuits, implemented a more efficient OPRF circuit PSI scheme through private membership tests, reducing the number of comparisons and the depth of circuit equivalence comparisons. Meanwhile, Huang et al. [22] created a semi-honest secure disordered circuit PSI scheme through the combination of Yao circuits, performing equivalence tests and specific sorting on adjacent elements. Despite these advantages, these methods still require additional key calculations and communication processes, such as key exchanges between participants.
2.1.3. Design Framework Based on Oblivious Transfer
Oblivious Transfer (OT) [23] is a cryptographic protocol that allows a sender to transmit information to a receiver without revealing any private information. In the OT protocol, the sender has two options, but the receiver can only obtain information about one of them without access to the other, and the sender does not know which option the receiver has chosen. OT is widely used in many secure areas due to its cryptographic robustness and privacy features. Its applications include secure protocol negotiation, secure online auction systems, and secure voting systems. In 2013, Dong et al. [24] proposed a new data structure—the Garbled Bloom Filter (GBF)—and based on the GBF and OT extension, they introduced a PSI protocol. This protocol utilized efficient symmetric encryption operations and could handle billions of elements. However, this protocol faced two issues: one is that the malicious sender might send incorrect shared information, and the other is that the input datasets are not independent. To address these problems, in 2016, Rindal and Rosulek [25] proposed a new randomized garbled Bloom filter using the “cut-and-choose” technique. They successfully implemented a two-party malicious model PSI protocol. Subsequently, Zhang et al. [26], based on this scheme, further proposed and implemented a multi-party PSI protocol, ensuring malicious security in the presence of two non-colluding servers, with computational and communication costs depending on the number of participants. Pinkas et al. [27], based on the OOS17-OT [28] protocol, built a maliciously secure PSI protocol. Rindal et al. [29], based on the semi-honest secure Schoppmann et al. [30] protocol and the maliciously secure Weng et al. [31] protocol, respectively, proposed maliciously secure and semi-honest secure PSI protocols. Overall, PSI protocols based on oblivious transfer typically feature lower computational and communication overhead.
2.2. PSI-CA
In the research of set intersection cardinality, Ref. [32] put forward a two-party protocol based on the Bloom filter and ElGamal encryption scheme; the trick here is to count how many common zero-bits were in their Bloom filters. Thus, the cardinality of set intersection can be quickly figured out by a formula provided in [33]. The proposal in [34] was analogous to [32], which employed the Goldwasser–Micali encryption algorithm [25] to encrypt the Bloom filter entries.Cristofaro et al. [35] designed the first PSI-CA protocol with linear complexity based on the Decisional Diffie–Hellman (DDH) assumption in the Random Oracle Model (ROM) [36]. However, for the computation cost, both the sender and the receiver need to compute two exponentiations for each item.
3. Related Theories and Technologies
3.1. Multi-Party Secure Computation Security Model
The mathematical concept of Multi-Party Computation (MPC) involves several participants (such as ), each holding private input data (). These participants collaboratively execute a computation of the function with the goal of ensuring that each participant can only access their own computational results, while being unable to ascertain the inputs and results of others. There are generally two security models employed in secure multi-party computation protocols [37,38]:
- Semi-honest model: In this model, participants adhere to the protocol’s execution rules but may attempt to gather other participants’ inputs, outputs, and any accessible information during the execution of the protocol. This model assumes that the participants do not deviate from the established procedural rules but will use all available information to deduce the private data of others.
- Malicious adversary model: Unlike the semi-honest model, the malicious adversary model accounts for the possibility that attackers may manipulate a subset of the participants to perform illicit actions, such as submitting incorrect input data or maliciously altering data to steal the private information of honest participants. Malicious adversaries might also disrupt the protocol by intentionally terminating its execution or by refusing to participate, thus preventing the protocol’s completion.
The security model considered in this paper is the semi-honest security model.
3.2. Cuckoo Filter
Determining whether a particular element belongs to a given set is a common problem in computer science, with widespread applications in bioinformatics, machine learning, computer networks, the Internet of Things, and database systems [39]. Filter data structures such as Bloom filters and Cuckoo filters can approximately determine if an element is part of a specified set and have been extensively applied in network routing [40], information retrieval, file merging [41], spam detection [42], and distributed systems [43].
Filter data structures are used to approximately ascertain if an element belongs to a specific set. In essence, for a given set S and a query element x, the filter can approximately inform the query whether “x is in S”. “Approximately” here implies that if x is actually not in S, the filter has a small error probability p of wrongly indicating that “x is in S”; however, if x is indeed in S, the filter will always correctly return that “x is in S”. Filter data structures sacrifice some query accuracy to enhance space and time efficiency. Unlike data structures that require storing the complete information of each element for precise queries, filters approximate the presence of an element solely through partial information such as hash values or “fingerprints”. Based on this principle, existing filter data structures are mainly categorized into two types: one type uses bit arrays as in Bloom filters; the other type, exemplified by Cuckoo filters, is based on element “fingerprints”.
The Cuckoo filter [44] is an advanced retrieval structure made up of multiple buckets, each capable of containing several bits. Compared to Bloom filters, Cuckoo filters offer the significant advantage of supporting deletion of elements and having higher space efficiency. With equal storage space, Cuckoo filters can achieve more accurate search results and shorter search times. When querying an element, the time complexity for Cuckoo filters is , meaning constant time complexity. This indicates that the execution time for query operations does not increase with the number of elements in the filter, an important performance feature of the Cuckoo filter design. In this paper, Cuckoo filters are used to store data at a large medical institution.
3.3. Paillier Homomorphic Encryption
Homomorphic encryption is an encryption technology that allows computations to be performed on encrypted data and to obtain encrypted results, which, when decrypted, are consistent with the results obtained by performing the same computations directly on the original data. This means that homomorphic encryption enables data to be processed and analyzed without revealing any content. It is an important technology for protecting online privacy, allowing cloud computing services to perform complex data processing tasks on users’ encrypted data without accessing the actual data.
Paillier homomorphic encryption is a public-key cryptosystem that specifically supports homomorphic addition operations on encrypted data. The applications of the Paillier encryption scheme are extensive, and it can be used to protect the privacy and security of data. For example, in distributed computing, the Paillier encryption scheme can be used to encrypt data and transmit it to various nodes for processing, ensuring the security and privacy of the data. Furthermore, the Paillier encryption scheme can also be used to implement homomorphic secret sharing, private-set intersection, and other application scenarios. Overall, the Paillier encryption scheme is an efficient homomorphic encryption scheme with a wide range of application prospects. This paper uses the Paillier cryptosystem in its final scheme. The homomorphic properties utilized in this paper are as follows:
- Additive Homomorphism: If and , then . This allows for performing addition operations on ciphertexts without needing to decrypt them first.
- Scalar Multiplication Homomorphism: If , then . This means that it is possible to perform multiplication operations between a ciphertext and a plaintext scalar without decryption.
This paper will utilize homomorphic encryption technology to construct the third protocol of this paper: Unbalanced PSI-CA Protocol Based on Dual-Cloud Assistance.
4. PSI-CA Protocol Constructed Based on DH Key Exchange Mechanism
Before proposing the first unbalanced PSI-CA protocol of this paper, we introduce Cristofaro’s PSI-CA protocol, constructed based on the DH key-exchange mechanism [35]. As shown in Figure 1, the specific process is as follows, where is the private key of a large medical institution, is the private key of a small health app developer, and H is the hash function negotiated by both parties.
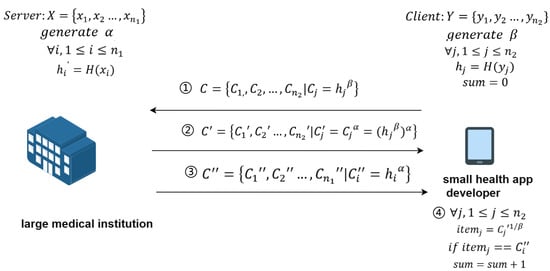
Figure 1.
PSI-CA protocol constructed based on DH key-exchange mechanism.
4.1. Protocol Process
4.1.1. Exchange and Computation Stage
- Receiver Data Encryption: The receiver encrypts with its private key , obtaining , and sends it to the sender.
- Sender Computation: Upon receiving , the sender applies their private key to compute and shuffles it before sending it back to the receiver.
- Sender Data Encryption: The sender encrypts with its private key , resulting in , and sends it to the receiver to facilitate the computation of the intersection cardinality.
4.1.2. Cardinality Calculation Stage
- Receiver Decryption and Computation: The receiver uses the inverse of to decrypt to retrieve . By comparing with , the receiver can calculate the cardinality of the intersection between the two sets.
4.2. Experimental Analysis
For this protocol, experiments were conducted and the runtime was recorded for various combinations of dataset sizes, as shown in Table 1. Cardinality here refers to the number of elements in the participant’s dataset. For example, means that the dataset has elements. The cardinalities mentioned in the following tables all have the same meaning.

Table 1.
Runtime of the PSI-CA protocol constructed based on the DH key-exchange mechanism.
Through the experimental data, an important phenomenon can be observed. Table 1 shows the estimated runtime of the above protocol under different data volume levels. For example: Initially, when the number of elements in Participant One’s dataset is and Participant Two’s dataset is , the runtime of the protocol is 1.8095 s. In this case, there is a noticeable imbalance between the smaller side (Participant One) and the larger side (Participant Two). Now, if we expand the number of elements in Participant One’s dataset (originally the side with fewer elements) to , while keeping Participant Two’s dataset size constant at , the runtime increases to 5.2207 s, approximately three times the original. This indicates that although the runtime increases when the datasets are balanced, the increase is limited. However, if we keep Participant One’s dataset size at and increase Participant Two’s dataset size to (the same scale of change), the runtime dramatically increases to 56.1277 s, approximately 31 times the initial condition. This phenomenon shows that, in unbalanced dataset conditions, increasing the number of elements in the larger dataset significantly affects the efficiency of the protocol.
These results reveal the importance of dataset balance in maintaining efficiency during the implementation of this protocol. Unbalanced datasets not only lead to extended runtimes but can also cause low resource utilization and delays in processing. However, in practical applications, when two parties want to obtain the private-set intersection’s cardinality, their sets are often unequal and have a significant gap. Therefore, the current situation requires the design of a new protocol to eliminate the impact of dataset size imbalance on protocol efficiency.
4.3. Summary of This Chapter
This chapter explores the PSI-CA Protocol built on the Diffie–Hellman (DH) key-exchange mechanism, detailing its processes and experimental analysis. Initially, the protocol employs a DH mechanism for securing data exchanges between two parties, outlined in specific stages: data encryption by the receiver, computation and further encryption by the sender, followed by decryption and intersection cardinality computation by the receiver.
The experimental analysis section provides a practical examination of the protocol’s runtime across varying dataset sizes, demonstrating that imbalances significantly affect efficiency. As the dataset sizes diverge, particularly when a smaller dataset is compared with a rapidly increasing larger dataset, the protocol’s runtime escalates dramatically.
Therefore, there is an urgent need to design a new protocol to alleviate the adverse effects of dataset size imbalance on the performance of the PSI-CA protocol.
5. Unbalanced PSI-CA Protocol Based on Cuckoo Filter
Although Cristofaro’s PSI-CA protocol [35], constructed based on the DH key-exchange mechanism, provides an effective way to compute the intersection’s cardinality of two datasets, especially under the premise of protecting participants’ data privacy, this paper observes that its efficiency is significantly impacted when dataset sizes are extremely unbalanced. In particular, as shown in Table 1, the runtime increases significantly as the size of the larger dataset increases, reflecting the performance limitations of Cristofaro’s PSI protocol when dealing with unbalanced datasets.
In order to overcome these limitations, the first protocol proposed in this paper adopts a different technical strategy, which effectively reduces the computational burden under unbalanced conditions by introducing Cuckoo filter. This not only optimizes the data processing process, but also improves the overall operational efficiency. In the new protocol, the increase in run time is not as dramatic as that in the Cristofaro PSI-CA protocol [35], based on DH key exchange; even with unbalanced dataset sizes, this allows for more efficient and balanced data processing. This improvement is particularly important for datasets of different sizes frequently encountered in practical applications.
Therefore, based on the above introduction, as shown in Figure 2, this paper first proposes a PSI-CA protocol based on the discrete logarithm problem difficulty and the correctness (high false positive rate) of Cuckoo filter. This protocol is divided into two phases; the specific details are as follows.
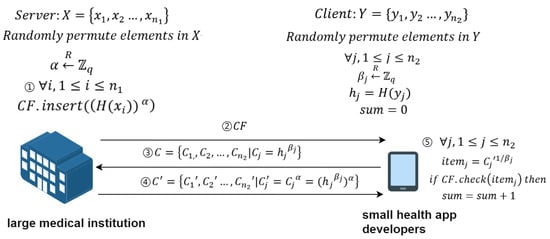
Figure 2.
Unbalanced PSI-CA protocol based on Cuckoo filter.
5.1. Definition of Main Participants and Related Symbols
- Large medical institution represents the party with a larger dataset and greater computational and storage capabilities.
- Small health app developer represents the party with a smaller dataset and lesser computational and storage capabilities.
- X and Y represent the dataset of the large medical institution and the small health app developer, respectively.
- represents the private key of the large medical institution in the Diffie–Hellman encryption algorithm.
- represents the random number generated by the small health app developer for the Diffie–Hellman encryption algorithm.
- H represents the hash function negotiated by the small health app developer and large medical institution for use.
- represents Cuckoo filter, represents the operation of adding an element to the Cuckoo filter, represents the operation of checking whether a specific element exists in the filter.
- represents the i-th element of set X. Similarly, , , etc., also represent similar meanings.
- represents the set containing ciphertexts sent by the small health app developer to the large medical institution.
- represents the set containing ciphertexts sent by the large medical institution to the small health app developer.
- represents the result obtained through a series of exchange and decryption operations, used to retrieve the filter.
- represents the cardinality of the intersection between the two parties.
5.2. Protocol Process
The protocol is divided into two phases, the preprocessing phase and the intersection phase, with specific details as follows.
5.2.1. Preprocessing
In the preprocessing phase, the small health app developer and the large medical institution need to perform a series of preparatory works to ensure the security and efficiency of subsequent interactions. The specific steps are as follows:
- Security parameter negotiation: The small health app developer and the large medical institution agree on the large prime number q used in the DH encryption algorithm and the hash function H used.
- Large Medical Institution Generates Private Key: The large medical institution generates its own private key , used for the Diffie–Hellman (DH) encryption algorithm.
- Data Scrambling: The small health app developer and the large medical institution scramble their own datasets Y and X for randomization, enhancing data privacy and security.
- Small Health App Developer Data Preprocessing: The small health app developer calculates and generates random numbers , used for the Diffie–Hellman (DH) encryption algorithm.
- Creation of Cuckoo Filter: The large medical institution generates a Cuckoo filter by using the operation and sends the filter to the small health app developer for private-set intersection queries with privacy protection.
5.2.2. Cardinality Calculation
In the cardinality calculation phase, the small health app developer and the large medical institution perform a series of carefully designed encryption and decryption operations to blind the small health app developer’s elements securely and compute the intersection cardinality of the two sets. The specific operations are as follows:
- Element Blinding and Interactive Encryption Operations: The small health app developer and the large medical institution interact through a series of asymmetric encryption and decryption operations to blind the small health app developer’s elements. Specifically, the small health app developer calculates and sends C to the large medical institution. The large medical institution uses its private key to compute and sends back to the small health app developer.
- Cardinality Computation: After receiving , the small health app developer checks whether they belong to the filter through the check operation , thereby calculating the cardinality of the intersection of the sets. Specifically, after receiving sent by the large medical institution, the small health app developer computes and uses the result to query the filter to obtain the intersection’s cardinality .
5.3. Correctness Analysis
If , then , then (please see the fifth step in Figure 2) (Step 4 in Figure 2) (Step 3 in Figure 2) .
Thus, through this scheme, the small health app developer can accurately obtain the cardinality of the intersection of both parties.
5.4. Security Analysis
This section will analyze the security of the protocol in detail, mainly its ability to protect the privacy of both parties. Here, the large medical institution is called the sender and the small health app developer is called the receiver.
5.4.1. Definition
denotes the deterministic function of where S denotes the sender and R denotes the receiver. We say that the protocol is secure under the semi-honest model, if the probabilistic polynomial-time algorithms and can be presented as:
where and denote all the information, which an adversary can obtain from party S and party R, respectively. The information includes the input of the party, the output from function f, and the other information that it receives.
5.4.2. Theorem
Let X, Y be two sets from a predefined universe; the set intersection functionality f is defined as: . Given the commutative encryption system, our protocol in Section 5 can compute f securely in the presence of semi-honest adversaries.
5.4.3. Proof
If the Hellman encryption scheme is secure, then the simulators for sender and receiver are guaranteed to exist; we can use them as subroutines when constructing our simulators.
- Sender’s View: We start from the case where the sender is corrupted. We construct a simulator , which receives the sender’s private input and output and generates the view of the sender S in the protocol. We want to show that this view is indistinguishable from the view of S in an execution of the unbalanced PSI-CA protocol based on Cuckoo filter. That is,We first sketch the algorithm of . In the pre-process step, determines a prime number q and chooses a public key with the same security parameter. It constructs a Cuckoo filter in the presence of the ciphertexts, which is all the same as the real execution. Then, fills a set with the same size as Y randomly and determines a key to encrypt each element in utilizing the Hellman encryption scheme randomly. We denote the encryption set result as Y. Last but not least, attempts to obtain the cardinality of the set intersection by querying the Cuckoo filter.From the view of the sender, given the secure Hellman encryption scheme, the distribution of produced by is indistinguishable from the one produced by the real execution. Thus, we can conclude that the simulated view is indistinguishable from the real view.
- Receiver’s View: In this case, the receiver is corrupted. We construct a simulator that is given the private input Y and the output . Similarly, we will prove this view is indistinguishable from the view of the receiver R in the real execution. That is, .We first sketch the algorithm of . In the pre-process step, determines a prime number q and chooses a public key with the same security parameter to encrypt its own set Y. Then, randomly chooses elements from a predefined universe and elements from Y. We denote the new dataset as . Afterward, determines a sender’s key to encrypt the dataset and constructs the Cuckoo filter in the presence of the new dataset’s ciphertext using the parameters determined in the pre-process step. Since the distribution of produced by is indistinguishable from the distribution of X produced by the real execution, we conclude the simulated view is indistinguishable from a real view.
Combining both of the above, we finish our proof.
5.5. Experimental Analysis
For this protocol, experiments were conducted, and the runtime was recorded for various combinations of data volumes, as shown in Table 2. The table also compares the runtime of Cristofaro’s PSI-CA protocol constructed based on the DH key-exchange mechanism [35]. Since preprocessing can be completed offline, the runtime of the unbalanced PSI-CA protocol based on Cuckoo filter refers to the total time of the the cardinality calculation process. The original protocol refers to the PSI-CA protocol constructed based on the DH key-exchange mechanism, and the new protocol refers to the unbalanced PSI protocol based on Cuckoo filter.

Table 2.
Comparison of running time of PSI-CA protocol based on DH key-exchange mechanism and Cuckoo Filter based.
Through the experimental data, this paper can observe several key phenomena. First, when the cardinality of the smaller dataset (number of elements) remains constant while the number of elements in the larger dataset increases rapidly, it is observed that the runtime of the protocol does not change much, remaining consistent. This indicates that, although the size of the large dataset increases dramatically, the efficiency of the protocol is not significantly affected, thereby proving that the design of this protocol can effectively mitigate the negative impact of dataset size imbalance on protocol efficiency. In particular, the overall runtime of the protocol is more related to the cardinality of the smaller dataset and has very low relevance to the cardinality of the larger dataset.
At the same time, this experiment also found that, under balanced dataset conditions, the runtime of the PSI-CA protocol based on the DH key-exchange mechanism and the unbalanced PSI-CA protocol based on Cuckoo filter does not differ significantly. This indicates that, when the sizes of the sets are similar, both protocols can exhibit comparable performance, providing an efficient solution.
5.6. Summary of This Chapter
This chapter presents the development and analysis of an unbalanced PSI-CA protocol that utilizes Cuckoo filter to efficiently handle datasets with significant size disparities. The protocol is designed to overcome the limitations observed in traditional PSI-CA protocols such as Cristofaro’s, which struggles with efficiency under unbalanced conditions.
Experimental analyses demonstrate the protocol’s robustness, showing minimal runtime increases even as dataset sizes grow significantly, which marks a substantial improvement over traditional methods. The protocol proves particularly effective in real-world scenarios where dataset imbalances are common, providing a reliable solution that ensures privacy and efficiency.
In essence, this chapter confirms the efficacy of integrating Cuckoo filter into PSI-CA protocols, offering enhanced performance and security, making it a valuable addition to the field of data privacy and secure computation.
However, in this protocol, the receiver still has to bear the burden of complex cryptographic computations and storing the Cuckoo filter. The next chapter will focus on optimizing this aspect.
6. Unbalanced PSI-CA Protocol Based on Single-Cloud Assistance
The previous chapter has proven that the unbalanced PSI-CA protocol based on Cuckoo filter is more suitable for practical scenarios, especially under unbalanced conditions, this protocol effectively resolves the performance limitations of the PSI protocol constructed using the DH key-exchange mechanism in handling unbalanced datasets. However, there is still room for improvement in this protocol. It is observed that, in this protocol, the small health app developer (receiver) need to store the filter and perform complex cryptographic operations, which can be a significant burden for mobile devices with limited computing power and storage space. A series of encryption operations and the storing filter received from the other party becomes a heavy load. To address this issue, it is considered to transfer most of the receiver’s computational and storage tasks to cloud servers. By delegating tasks to cloud servers, the receiver can significantly reduce computational and storage pressure, especially for a small health app developer with limited capabilities.
This section will introduce cloud computing technology, which allows a small health app developer with limited computing power and storage space to outsource their private data and request cloud platforms to perform related computations. Currently, whether for individual users or large enterprises, entrusting data storage and computation tasks to cloud services has become a common practice. Based on the introduction above, as shown in Figure 3, this chapter proposes a second unbalanced PSI-CA protocol.
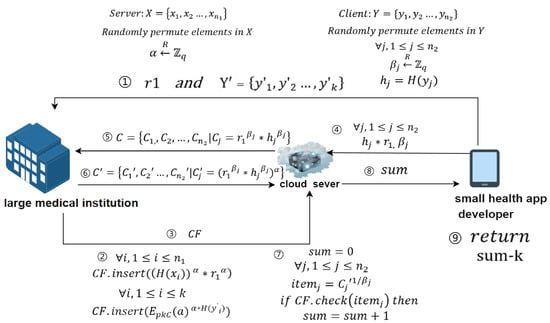
Figure 3.
Unbalanced PSI-CA protocol based on single-cloud assistance.
6.1. Definition of Main Participants and Related Symbols
- Large medical institution represents the party with a larger dataset and greater computational and storage capabilities.
- Small health app developer represents the party with a smaller dataset and lesser computational and storage capabilities.
- Cloud server represents an auxiliary server that assists the receiver in obtaining the intersection’s cardinality operations, undertaking most of the computational and storage pressures.
- X and Y represent the dataset of the large medical institution and the small health app developer, respectively.
- represents the obfuscated dataset sent by the small health app developer to the large medical institution, used to confuse the cloud server and prevent it from obtaining the accurate cardinality of the intersection. k represents the cardinality of the set .
- represents the private key of the large medical institution in the Diffie–Hellman encryption algorithm.
- represents the random number generated by the small health app developer, used to blind the data.
- represents the random number generated by the small health app developer for the Diffie–Hellman encryption algorithm.
- H represents the hash function negotiated for use by the small health app developer and large medical institution.
- represents the Cuckoo Filter, represents the operation to add an element to the Cuckoo filter, represents the operation to check if a specified element exists in the filter.
- represents the i-th element of the set X. Similarly, , , etc., also represent similar meanings.
- represents the set of ciphertexts sent by the small health app developer to the large medical institution.
- represents the set of ciphertexts sent by the large medical institution to the small health app developer
- represents the result obtained through a series of exchange and decryption operations, used to retrieve the filter to obtain the cardinality of intersection.
- represents the variable used to help the small health app developer obtain the cardinality of the intersection, where represents the cardinality of the intersection.
6.2. Protocol Process
6.2.1. Preprocessing
- Security parameter negotiation: Each role discusses the necessary security parameters; all parties share the large prime q used in the DH cryptographic algorithm. The small health app developer and the large medical institution negotiate to generate and the hash function H.
- The small health app developer negotiates with the large medical institution to create an obfuscated dataset ; this dataset is completely useless data, which means that its elements cannot belong to either the small health app developer or the large medical institution collection.
- Large medical institution generates a private key: The large medical institution generates its own private key , for use in the Diffie–Hellman encryption algorithm.
- Data scrambling: The small health app developer and the large medical institution each scramble their own datasets X and Y.
- Small health app developer data preprocessing: The small health app developer calculates , generates random numbers , and calculates .
6.2.2. Outsourcing
- Large medical institution sends data to the cloud server: The large medical institution uses its private key to perform the operation , creates a Cuckoo filter , and sends it to the cloud server.
- Small health app developer sends data to the cloud server: The small health app developer sends the random numbers and to the cloud server. After receiving the data sent by the small health app developer, the cloud server calculates . At this point, the cloud server has saved the small health app developer’s blinded data.
6.2.3. Cardinality Calculation
- Cloud server sends data: The cloud server sends the blinded data to the large medical institution.
- Large medical institution processes data: Upon receiving , the large medical institution uses its private key to calculate and sends the result back to the cloud server.
- Cloud server processes data: After receiving from the large medical institution, the cloud server calculates and uses the result to search . If exists in , then sum is incremented by 1 (initial value of sum is 0).
- Obtaining the intersection cardinality: The small health app developer obtains the cardinality of the intersection by calculating , where k is the cardinality of the set .
6.3. Correctness Analysis
Thus, through this scheme, the small health app developer can accurately obtain the cardinality of the intersection of both parties.
6.4. Security Analysis
In the design of this protocol, the primary security objective is to ensure that, even in a partially trusted cloud environment, neither the small health app developer’s data nor the large medical institution’s data can be accessed or inferred by unauthorized entities. Overall, this protocol, compared to the previous one, merely outsources the tasks, thus inheriting the security of the previous protocol. Specifically, since other participating parties are unaware of the large medical institution’s private key , they cannot deduce the data held by the large medical institution. Similarly, since other parties do not know the small health app developer’s private random number , they cannot deduce the small health app developer’s data.
However, this scheme has inherent security risks, primarily because it does not withstand collusion attacks. If the large medical institution and the cloud server collude, they can jointly deduce the small health app developer’s data. This is possible because the cloud server possesses the blinded data , and if the large medical institution leaks the private key to the cloud server, then both the cloud server and the large medical institution could deduce the small health app developer’s original data . Collusion attacks are a security threat where two or more distinct entities (for example, users, systems, or service providers) secretly cooperate to undermine or circumvent security mechanisms and privacy measures. In cloud computing environments, cloud service providers and cloud users may collude to steal or infer other users’ sensitive data stored on the cloud. In the medical scenario of this article, the intersection represents the patient’s sensitive data, and leaking this information will cause very serious damage.
6.5. Experimental Analysis
6.5.1. Data Storage Volume
In the research of this paper, the experimental analysis of the unbalanced PSI-CA protocol based on single-cloud assistance revealed a key issue: when the small health app developer needs to receive a Cuckoo filter from the large medical institution, this poses a significant challenge for receivers with limited storage capacity. This challenge is magnified when facing large datasets.
To understand this issue deeply, a series of experiments were conducted to measure the volume of the Cuckoo filter needed by the small health app developer under different data sizes. The input data size for the experiments was provided by the large medical institution, reflecting the various data volumes that might be encountered in actual application scenarios. As shown in Table 3, the paper meticulously recorded the specific sizes of Cuckoo filter under different input data volumes, revealing the intrinsic relationship between data volume and filter size. Through experiments, it was discovered that, as the data volume in the large medical institution increased, the storage burden on the small health app developer under the original protocol also increased accordingly, with the size of the Cuckoo filter directly impacted by the input data volume. Especially in the context of the large medical institution containing extensive patient data, this storage pressure is particularly evident.

Table 3.
Size of Cuckoo filter at different data volumes.
Therefore, based on the above analysis and experimental results, it is clear that when the data volume in the large medical institution is excessively large, in other words, when the number of users reaches a certain level, the feasibility of a simple unassisted unbalanced PSI-CA protocol based on Cuckoo filter significantly decreases. This is because the unbalanced PSI-CA protocol based on Cuckoo filter requires small health app developers to directly receive and process a massive Cuckoo filter, which poses a significant challenge for small health app developers with limited storage resources, particularly mobile devices. Small health app developer devices often do not have enough storage space to accommodate these large-volume filter data, let alone process these data to complete PSI-CA operations.
In this context, the introduction of a cloud server scheme shows its unique advantages. By transferring the storage of the filter to the cloud server, the burden on the small health app developer is greatly reduced. By this means, even in situations with a massive number of users and large data volumes, the scheme can still maintain efficient operations and ensure the smooth completion of PSI-CA operations.
In summary, through experimental and theoretical analysis, this section concludes that, in scenarios with large-scale users and massive data volumes, the introduction of a cloud server scheme is more feasible and efficient than the unbalanced PSI-CA protocol based on Cuckoo filter.
6.5.2. Protocol Running Time
For this protocol, as shown in Table 4, the paper conducted experiments and recorded the running time of the protocol under various data volume combinations. Because preprocessing can be completed offline, the running time of the protocol refers to the total time of the outsourcing process and the intersection process. Table 4 also compares the running times of the unbalanced PSI-CA protocol based on Cuckoo filter and the unbalanced PSI-CA protocol based on single-cloud assistance. Here, Protocol 1 refers to the unbalanced PSI-CA protocol based on Cuckoo filter, and Protocol 2 refers to unbalanced PSI-CA protocol based on single-cloud assistance.

Table 4.
Running times of Protocol 1 and Protocol 2 under different data volume combinations.
From the experimental analysis, the following conclusions can be drawn: In cases of smaller data volumes, the performance differences between the two protocols are not significant. However, as the data volume increases, the running time differences between different protocols gradually become apparent. This is because, at certain specific levels, the proportion of communication time is relatively high when the data volume is small, significantly impacting the results. For larger data volumes, where computation time dominates, Protocol 2, by placing computational tasks on the more powerful cloud server, gradually widens the running time difference from Protocol 1. Overall, the use of cloud resources in the unbalanced PSI-CA protocol based on single-cloud assistance significantly reduces running times, especially when dealing with large-scale datasets.
6.6. Summary of This Chapter
This chapter introduces an unbalanced PSI-CA protocol based on single-cloud assistance, which utilizes cloud computing to reduce the computing and storage pressure of the small health app developer compared with previous protocols. Additionally, in the absence of collusion between the large medical institution and the cloud server, the protocol effectively protects data from unauthorized access, ensuring the confidentiality of the data and the privacy of the small health app developer, making it highly suitable for scenarios where the cloud server is fully trusted.
However, it cannot be denied that, although this scheme significantly reduces the computational and storage burden on the small health app developer, its security against collusion attacks is insufficient. In the medical scenario of this article, the intersection represents the patient’s sensitive data, and leaking this information will cause very serious damage. When the possibility of collusion between the cloud server and large medical institution cannot be completely ruled out, the protocol faces security risks and will require further security enhancement measures. Therefore, the next chapter will introduce a more secure solution to address the security deficiencies of the current scheme, ensuring the security and privacy of small health app developer data and large medical institution data in environments where not all parties are fully trustworthy. In other words, the new scheme can resist collusion attacks.
7. Unbalanced PSI-CA Protocol Based on Dual-Cloud Assistance
The previous single-server solution, which efficiently delegated computationally intensive encryption operations such as exponentiation and storage-intensive Cuckoo filter to the cloud server, has indeed alleviated the computational and storage burdens on the small health app developer to a certain extent. This is particularly advantageous for small health app developers with limited computing and storage capabilities, allowing them to operate beyond their hardware constraints. However, security analysis reveals that the unbalanced PSI-CA protocol based on single-cloud assistance has inherent security risks, specifically when collusion between the cloud server and large medical institution is possible, thus compromising its adequacy in protecting small health app developer data privacy.
As shown in Figure 4, to preserve the advantages of the previous scheme—namely reducing computational and storage pressures on the small health app developer—while addressing these security issues, this chapter proposes a new solution. This design aims to enhance the security during data processing, especially against potential collusion attacks.
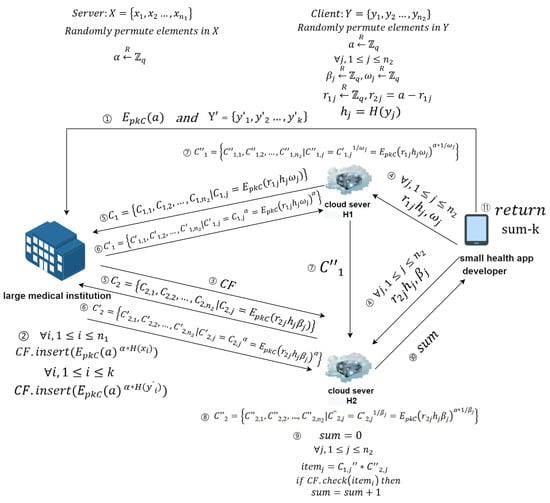
Figure 4.
Unbalanced PSI-CA protocol based on dual-cloud assistance.
7.1. Definition of Main Participants and Related Symbols
- Large medical institution represents the party with a larger dataset and greater computational and storage capabilities.
- Small health app developer represents the party with a smaller dataset and lesser computational and storage capabilities.
- Cloud server : Acts as an auxiliary server for the small health app developer, handling the majority of computation and storage pressures.
- cloud server : Another auxiliary server handling substantial computational and storage demands.
- X and Y represent the dataset of the large medical institution and the small health app developer, respectively.
- represents the obfuscated dataset sent by the small health app developer to the large medical institution, used to confuse the cloud server and prevent it from obtaining the accurate cardinality of the intersection. k represents the cardinality of the set .
- represents the private key of the large medical institution used in the Diffie–Hellman encryption algorithm.
- H: The hash function agreed upon by the small health app developer and the large medical institution for use.
- represents the Cuckoo Filter, where denotes the operation to add elements, and checks for the presence of specific elements.
- : Random exponentials generated by the small health app developer for cloud server , for cloud server .
- a: A secret value held by the small health app developer.
- : Random numbers used by the small health app developer for sending obfuscated data to cloud server , and for where .
- : The ciphertext collection sent from cloud server to the large medical institution, and from ; and are specific elements within these collections.
- and : Processed ciphertext collections returned to and from the large medical institution; and are specific elements within these collections.
- and : Final processed ciphertext collections at and after receiving data from the large medical institution; and are specific elements within these collections.
- represents the result of multiplying and used to query the filter.
- represents the variable used to help the small health app developer obtain the cardinality of the intersection, where represents the cardinality of the intersection.
7.2. Protocol Process
7.2.1. Preprocessing
- Discuss security parameters: Each party discusses the necessary security parameters—the large prime q used in DH encryption and the small health app developer’s public key required for the Paillier encryption system. The small health app developer and the large medical institution negotiate the creation of hash function H.
- The small health app developer negotiates with the large medical institution to create an obfuscated dataset . This dataset is completely useless data, which means that its elements cannot belong to either the small health app developer or the large medical institution collection.
- Small health app developer sends : The small health app developer generates its private secret number a and sends to the large medical institution.
- Large medical institution generates private key: The large medical institution creates its private key , used for the DH encryption algorithm.
- Data scrambling: The small health app developer and the large medical institution each shuffle their respective datasets.
- Small health app developer calculates hashes and generates random numbers: The small health app developer computes and generates random numbers, , , , , and computes , , where .
7.2.2. Outsourcing
- Small health app developer sends data to cloud servers: The small health app developer sends , to cloud server and , to cloud server . computes , and computes . At this point, and hold the small health app developer’s obfuscated data.
- Large medical institution sends data to cloud servers: Using , the large medical institution performs the filter insertion operation to generate a Cuckoo filter and sends it to cloud server . stores the filter sent by the large medical institution.
7.2.3. Intersection
- and send data: and each send their respective collections and to the large medical institution.
- Large medical institution processes data: Upon receiving the data, the large medical institution uses its private key to compute and sends the results back to . It also processes and sends the results back to .
- processes data: After receiving data from the large medical institution, uses the random number to calculate and sends the results to .
- processes data: Upon receiving data from and the large medical institution, calculates . checks if exists in . If exists in , then sum is incremented by 1 (initial value of sum is 0).
- Obtaining the intersection cardinality: The small health app developer obtains the cardinality of the intersection by calculating , where k is the cardinality of the set .
7.3. Correctness Analysis
If , then , which implies that (please see the ninth step in Figure 4) (Step 7 and Step 8 in Figure 4) (Step 6 in Figure 4) (Step 5 in Figure 4) (Step 1 in Figure 4) .
Thus, through this scheme, the small health app developer can accurately obtain the cardinality of the intersection of both parties.
7.4. Security Analysis
Firstly, we consider the security of the small health app developer’s data in the set. In considering security against collusion attacks, it is generally assumed that there is an adversary who possesses the perspective and information of all participating parties except for the protected entity. This means the adversary can access, control, or receive information and resources from all participants except for the small health app developer. In this scenario, the adversary attempts to compromise the system’s security or privacy by aggregating these insights, such as revealing the sensitive data of the small health app developer. If, in this context, the adversary still cannot learn or infer the small health app developer’s data, then it is proven that the data and privacy of the small health app developer are sufficiently secured against collusion attacks.
This section defines a game where the security objective is to maintain confidentiality of the data within the set under semi-honest and collusion conditions. The game for securing the small health app developer’s dataset is as follows:
- The small health app developer runs the preprocessing algorithm, sharing the cryptographic hash function H and the large prime q used in the protocol with the adversary.
- The small health app developer simulates the outsourcing algorithm and sends their (encrypted) input to the adversary.
- The small health app developer and the adversary simulate the intersection algorithm and discard any output.
- The adversary is asked to output a guess of the small health app developer’s input y.
The game is analogized to a deterministic one-way function, such as a public key encryption scheme. Let S be the simulated messages of the small health app developer during the game. Let a one-way function adversary be given the information (public key) and function (ciphertext) c (encrypted y). The advantage of the adversary is defined as the difference between the successful guesses of A and . If this advantage is negligible in the security parameter , then the outsourced private-set intersection is considered secure. That is, let . If , then the protocol is said to be secure.
Specifically, after the steps mentioned above, , , and the large medical institution have a complete view of the process. However, under the two-server architecture, as illustrated in Figure 4:
- In step four of Figure 4, since and are unknown to the adversary, cannot be derived. The adversary can only attempt exhaustive guessing, thus making negligible.
- In subsequent steps, as A does not know the small health app developer’s private key for the Paillier encryption system, it is impractical to decrypt the ciphertexts, making it even more challenging to derive . For instance, , and since the private key used in Paillier’s system by the small health app developer is unknown, decrypting this compound is complex and hence remains secure.
From the analysis above, it is evident that the advantage of is negligible. Therefore, if both cloud servers collude with the large medical institution, they cannot deduce the small health app developer’s original data.
Next, consider the security of the data in the large medical institution’s set. Obviously, apart from the large medical institution itself, none of the parties know the large medical institution’s private key ; hence, even if both cloud servers colluded with the small health app developer, they cannot derive the original data from .
It is particularly noted that, due to the prevalence of attacks on hash functions, further security enhancements are recommended by protecting the hashed data as the raw data.
In addition, due to the existence of obfuscated dataset , two cloud servers cannot know the set cardinality of the large medical institution and the small health app developer.
In conclusion, the dual-server scheme successfully resists collusion attacks under semi-honest conditions. By thoroughly integrating considerations for security and privacy into the protocol design, both the small health app developer’s and the large medical institution’s data are assured of robust protection. This solution not only provides an effective mechanism for private-set intersection but also demonstrates resilience against potential collusion threats.
7.5. Experimental Analysis
7.5.1. Data Computation Volume
When evaluating the performance of these protocols, the computational load borne by the small health app developer is undoubtedly a critical factor. Since all three protocols have been introduced, this section specifically focuses on the computational volume of the small health app developer to accurately gauge and compare the efficiency of the three distinct protocols in operation. Specifically, this section will conduct a detailed analysis and comparison of the main computational tasks that the small health app developer must execute across these protocols to fully assess each protocol’s demand on the small health app developer’s computational resources. This analysis will primarily focus on the types of operations involved, aiming to clarify which protocol demonstrates relative advantages in reducing the small health app developer’s computational burden, thus providing a solid basis for selecting the most appropriate protocol. Below is an analysis of the main types of operations involved in each protocol, focusing primarily on the outsourcing and intersection processes, as the preprocessing can be completed offline.
- Unbalanced PSI-CA protocol based on Cuckoo filter: Two rounds of modular exponentiation operations and filter retrieval.
- Unbalanced PSI-CA protocol based on single-cloud assistance: A single round of multiplication operations.
- Unbalanced PSI-CA protocol based on dual-cloud assistance: Two rounds of multiplication operations.
An analysis of the single-instance time consumption for these four operations offers a practical insight into the computational volume differences:
- Modular Exponentiation Operation: Representing computation-intensive operations, modular exponentiation becomes particularly time-consuming. On a standard hardware setup, the time required for a single modular exponentiation operation depends primarily on the size of the numbers involved and the efficiency of the algorithm.
- Multiplication Operation: Compared to modular exponentiation, multiplication operations execute much faster on modern computing systems, even when involving large numbers. Therefore, whether it is a single round of multiplication in the single-cloud protocol or two rounds in the dual-cloud protocol, the processing times are relatively short.
- Cuckoo Filter Retrieval: Although relatively quick, the retrieval operation for a Cuckoo filter involves memory access, which may make it slightly slower than simple arithmetic operations. The exact time required for this operation depends on the size of the filter and the efficiency of the implementation.
After a detailed analysis and comparison, this section has conducted a thorough exploration of the key computational tasks executed by the small health app developer across the three different protocols. These tasks include modular exponentiation, multiplication operations, and Cuckoo filter retrieval By assessing these types of computations and their specific time consumptions, the following conclusions can be drawn:
- Unbalanced PSI-CA Protocol Based On Cuckoo Filter: Primarily relies on two rounds of modular exponentiation, which are computation-intensive, especially when dealing with large numbers, making it the most time-consuming of all the operations reviewed. Additionally, the filter retrieval operation is also involved.
- Unbalanced PSI-CA Protocol Based On Single-Cloud Assistance: By executing a single round of multiplication, it significantly alleviates the computational burden on the small health app developer. Multiplication operations, even for large numbers, can be done quickly.
- Unbalanced PSI-CA Protocol Based On Dual-Cloud Assistance: Includes two rounds of multiplication operations, also aiming to distribute the computational pressure on the small health app developer. Although it involves two rounds of multiplication, due to the inherent efficiency of the operation, the total processing time remains within an acceptable range.
Through the meticulous assessment of each protocol’s computational types and their time consumptions, it is evident that both the unbalanced PSI-CA protocol based on single-cloud assistance and unbalanced PSI-CA protocol based on dual-cloud assistance exhibit excellent performance in reducing the small health app developer’s computational burden, particularly in the efficient execution of multiplication operations. In contrast, the unbalanced PSI-CA protocol based on Cuckoo filter, while potentially offering stronger security provisions, shows some deficiencies in efficiency and timeliness. Therefore, when choosing an appropriate protocol, a balance should be struck based on actual performance requirements and security needs.
7.5.2. Protocol Running Time
After introducing all three protocols, this section primarily discusses the running times of the protocols. The running time of a protocol is an important benchmark for evaluation in this paper because it directly reflects the protocol’s efficiency in practical operations. The factors affecting the running time of the protocol include computational time and communication time. As shown in Table 5, experiments were conducted to record the running times of the protocols under various data volume combinations. Table 5 also places the running times of the unbalanced PSI -CA protocol based on Cuckoo filter, unbalanced PSI-CA protocol based on single-cloud assistance, and unbalanced PSI-CA protocol based on dual-cloud assistance side by side for comparative analysis. Here, Protocol I refers to the unbalanced PSI-CA protocol based on Cuckoo filter, Protocol II refers to the unbalanced PS-CAI protocol based on single-cloud assistance, and Protocol III refers to the unbalanced PSI-CA protocol based on dual-cloud assistance.

Table 5.
Running times of the three protocols under different data volume combinations.
It is noteworthy that the preprocessing stages of all three protocols can be completed offline, meaning they do not directly contribute to online operation delays. Therefore, the recorded running times in this paper refer to the total time of all processes, excluding preprocessing. Specifically, in Protocol I this primarily refers to the total duration of the intersection process; in Protocols II and III, it refers to the total duration of both the outsourcing and intersection processes.
Through experimental analysis, the paper draws the following conclusions: At smaller data volumes, the performance differences between the three protocols are not significant. However, as the data volume increases, the differences in running times between the protocols become apparent. Generally, the unbalanced PSI-CA protocol based on Cuckoo filter tends to have the longest running time, while the unbalanced PSI-CA protocol based on single-cloud assistance has the shortest running time, and the performance of the unbalanced PSI-CA protocol based on dual-cloud assistance is in the middle. This phenomenon can be explained by the complexity of data handling and the differences in communication overhead among the protocols. The unbalanced PSI-CA protocol based on Cuckoo filter, due to its direct and unoptimized calculations, is less efficient when handling large volumes of data. Nevertheless, at very small data volumes, where the proportion of communication time is relatively high, the impact of data transmission costs on total running time becomes significant. In such cases, the unbalanced PSI-CA protocol based on Cuckoo filter does not necessarily appear inefficient because other protocols might be even less efficient in data transmission. Especially in environments with poor network conditions or limited data transfer rates, the lower communication demands of the unbalanced PSI-CA protocol based on Cuckoo filter might, in some cases, lead to better performance.
Moreover, the running times of the unbalanced PSI-CA protocol based on single-cloud assistance and the unbalanced PSI-CA protocol based on dual-cloud assistance are significantly reduced through distributed computing and the use of cloud resources, especially when dealing with large-scale datasets. In summary, choosing the appropriate protocol requires a comprehensive consideration of factors such as data volume, computational resources, and network environment. In practical applications, understanding the performance characteristics and suitable scenarios of each protocol is crucial for optimizing data processing workflows and enhancing efficiency.
7.6. Summary of This Chapter
The protocol leverages the computational and storage resources of two cloud servers, significantly reducing the burden on the small health app developer by lowering its computational and storage requirements and enhancing the system’s efficiency and availability. Through distributed computing and security measures such as homomorphic encryption, it ensures the privacy of data during transmission and processing, adequately protecting the sensitive information of both the small health app developer and the large medical institution. This solution not only improves the operational efficiency of devices with limited resources but also effectively prevents collusion attacks. Consequently, the unbalanced PSI-CA protocol based on dual-cloud assistance excels in private-set intersection operations, demonstrating both high efficiency and security.
7.7. Extensions
To enhance the practicality of the scheme, this section will explore two key aspects from an engineering practice perspective: the design of the PSI-CA network and the design of the data update mechanism.
First, the design of the PSI-CA network focuses on building an efficient, secure, and scalable network architecture to support large-scale PSI-CA computations.
Second, the design of the data update mechanism involves how to update the datasets stored on the cloud servers without interrupting the service. This is particularly crucial for PSI-CA computation scenarios that require frequent data updates.
7.7.1. PSI-CA Network
As previously described, the small health app developer delegates PSI-CA computations to two cloud servers. In practice, a vast network of cloud servers can be built to support this delegation. The basic system description is as follows.
- Access and Authentication of Cloud Servers: Any server can apply to become a cloud server, also known as a server assistant. These servers must undergo a series of certification processes (including hardware performance verification, security vulnerability scanning, and compliance checks) to ensure they meet security and performance standards. Servers that pass the certification but later violate regulations will be blacklisted and removed. The system maintains platform security and trust through mechanisms such as regular security scans and real-time monitoring, with any violations leading to immediate removal and further investigation of the server.
- Mechanism for Selecting Server Assistants: When needing to perform PSI-CA, small health app developers choose two cloud servers based on their performance (such as processing power, storage capacity, and network bandwidth), stability, security capabilities, and compliance with regulations, among other hard and soft factors. Cloud servers with high availability promises are preferred to minimize the risk of failures.
- Execution Mechanism for PSI-CA Operations: The PSI-CA network supports small health app developer flexibility and system scalability; small health app developers can execute PSI-CA on different large medical institutions by merely changing and obfuscated dataset , without needing to redesign the entire system. This design enhances small health app developer flexibility and the system’s efficiency, reliability, and security.
This system design not only achieves the delegation of PSI-CA computations but also introduces multiple cloud servers into the network, thereby enhancing the system’s flexibility and stability. Additionally, by implementing authentication and maintaining a blacklist for cloud servers, the system can better guarantee the credibility of the cloud servers, enhancing overall security. This flexible yet secure system design provides small health app developers with more options and makes PSI-CA operations more adaptable to various practical requirements.
In summary, under the existing framework, small health app developers can delegate computing and storage tasks to different cloud servers and perform PSI-CA operations on various large medical institutions by using different random numbers, , and obfuscated dataset . This method allows small health app developers to more flexibly use multiple resource nodes and optimize task distribution, thereby further enhancing the overall performance and security of the privacy protection scheme.
7.7.2. Data Updates
To further enhance the practicality of the scheme, this paper also designs a data update mode compatible with the scheme, making the overall scheme more practical and reliable.
- Data Updates on the Large Medical Institution’s Side:As shown in Figure 5, the update details of the large medical institution are as follows:
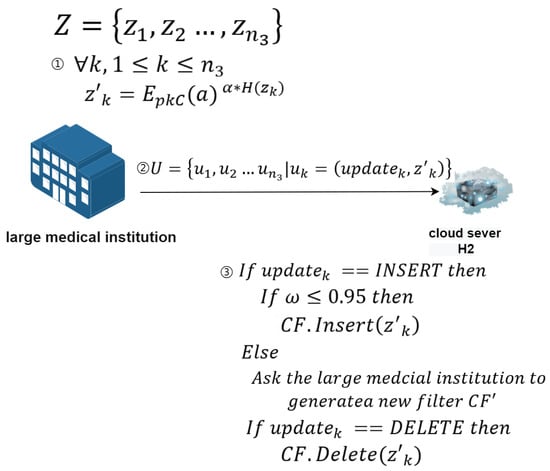 Figure 5. Data updates on the large medical institution’s side.Definition of main participants and related symbols:
Figure 5. Data updates on the large medical institution’s side.Definition of main participants and related symbols:- Large medical institution: Represents the large medical institution that wants to encrypt and upload updated data to cloud server .
- Cloud server : Represents the cloud-assisted server that assists the large medical institution in completing update operations.
- Z represents the set of data to be updated; represents the k-th element of Z.
- represents the load factor of the filter.
- represents the data after encryption processing.
- represents the operation index, used to determine whether the update operation is an insertion or deletion.
- U represents the set of data sent by the large medical institution to the cloud-assisted server ; represents the k-th element of U.
Update process:- The large medical institution has a set of elements Z it wants to insert or delete. These elements are blinded before being sent to cloud server . Specifically, .
- In addition to sending the blinded elements, the large medical institution also sends an identifier variable to inform the small health app developer whether the operation is an insertion or a deletion.
- During an insertion operation, first checks whether the current filter’s load factor exceeds 0.95.
- If the load factor is greater than 0.95, then must request the large medical institution to generate a new filter using all elements to maintain high spatial and lookup efficiency of the filter.
- If the load factor is less than or equal to 0.95, then can directly insert the element into the current filter .
- In a deletion operation, removes the specified element from the filter , a process that does not require generating a new filter.
- Data Updates on the Small Health App Developer’s Side:As shown in Figure 6, the update details of the small health app developer are as follows:
 Figure 6. Data updates on the small health app developer’s side.Definition of main participants and related symbols:
Figure 6. Data updates on the small health app developer’s side.Definition of main participants and related symbols:- Small health app developer: Represents the small health app developer who wants to perform data updates.
- Cloud server represents the cloud-assisted server that assists the small health app developer in completing update operations.
- Cloud server represents the cloud-assisted server that assists the small health app developer in completing update operations.
- Z represents the set of data to be updated; represents the k-th element of Z.
- represents the data after being processed by the hash function H.
- k represents the data index, used to determine the type of update, either insertion or deletion, and to retrieve the updated data based on the index.
- When adding data, represents the data processed through the dual-cloud scheme and sent to the two cloud-assisted servers. When deleting, is null.
- V represents the set of data sent by the small health app developer to the cloud-assisted server ; represents the k-th element of V.
- represents the set of data sent by the small health app developer to the cloud-assisted server ; represents the k-th element of .
Update process:- The small health app developer has a set of elements Z it wants to insert or delete. In both cases, the small health app developer blinds each element and sends them to and , respectively.
- The small health app developer sends a data index K to inform the cloud servers about the type of update, whether it is an insertion or a deletion. If the index is less than , it indicates a deletion operation. In this case, is null, and and delete the corresponding data based on the index.
- If the index is greater than , it indicates an addition operation, and the corresponding calculation results and index are saved.
- After completing a batch of deletion and addition operations, the relative order of the indices also needs to be adjusted. The update process is illustrated in Figure 5.
8. Conclusions and Future Work
8.1. Work Summary
Privacy computing is a technology framework aimed at protecting individual privacy during the process of data use and sharing. It ensures that data can still be effectively utilized without disclosing specific content through various algorithms and protocols. Among many applications of privacy computing, Privacy Set Intersection (PSI-CA) is a common requirement, which allows two or more parties to compute the cardinality of the intersection without revealing their private data.
Traditional PSI-CA protocols are primarily designed for cases where datasets are relatively balanced in size, which often does not apply in real scenarios. In many practical situations, the size disparity between participants’ datasets is significant, necessitating the use of unbalanced PSI-CA protocols. These protocols are specifically designed to handle such disparities, optimizing computational efficiency and privacy protection to cater to a wider range of practical needs. By adopting unbalanced PSI-CA protocols, not only is the processing efficiency improved, but more precise control over data protection is also offered, thus finding broader application in various data-sensitive industries. This paper proposes three protocols: the unbalanced PSI-CA protocol based on Cuckoo filter, the unbalanced PSI-CA protocol based on single-cloud assistance, and the unbalanced PSI-CA protocol based on dual-cloud assistance. Here, the unbalanced PSI-CA protocol based on Cuckoo filter addresses the performance issues of traditional PSI-CA protocols in handling unbalanced datasets. On this basis, the unbalanced PSI-CA protocol based on single-cloud assistance transfers most of the computational and storage burdens from the small health app developer to the cloud, enhancing practicality. Faced with the possibility of collusion attacks, the unbalanced PSI-CA protocol based on dual-cloud assistance employs security mechanisms such as homomorphic encryption to effectively resist these attacks. The main contributions of this paper are summarized as follows:
- Addressing the shortcomings of traditional PSI-CA protocols when dealing with significant data size disparities among participants, this paper proposes the first protocol, namely the unbalanced PSI-CA protocol based on Cuckoo filter.
- Given the complexities of cryptographic operations and storage demands of the small health app developer in the unbalanced PSI-CA protocol based on Cuckoo filter, this paper introduces an unbalanced PSI-CA protocol based on single-cloud assistance. This protocol effectively transfers the majority of computational and storage burdens from the small health app developer to the cloud.
- In response to potential collusion between the cloud and large medical institution in the unbalanced PSI-CA protocol based on single-cloud assistance, this paper proposes a unbalanced PSI-CA protocol based on dual-cloud assistance with security mechanisms like homomorphic encryption, which effectively prevents collusion attacks while offloading computational and storage burdens.
- In view of the practical problems of the unbalanced PSI-CA protocol based on dual-cloud assistance, this paper also designs a PSI-CA network and a data update mode tailored for the unbalanced PSI-CA protocol based on dual-cloud assistance.
8.2. Three Protocols
As shown in Table 6, this section provides a comprehensive summary and recommendations for the three protocols discussed in this paper. The unbalanced PSI-CA protocol based on Cuckoo filter offers high security but involves significant computational and storage demands, making it suitable for clients with strong computational and storage resources. The unbalanced PSI-CA protocol based on single-cloud assistance, while being the fastest and offloading computational burdens to the cloud, poses security risks as it cannot withstand collusion attacks, making it appropriate for scenarios where the cloud is fully trusted. The unbalanced PSI-CA protocol based on dual-cloud assistance offers an ideal balance of runtime, security, and efficiency, making it the most versatile and practical option.

Table 6.
Overall performance summary of the three protocols.
8.3. Future Outlook
Although the protocols proposed in this document are applicable in most scenarios, there are still several aspects that could be optimized for future development:
- All protocols are designed for two-party unbalanced PSI-CA. Extending these protocols to multi-party scenarios is an important future direction, given the practical needs for multi-party computations.
- The protocols are developed under a semi-honest security model. Extending their robustness to malicious models, where adversaries may actively attempt to undermine the protocols, represents a crucial area for further research.
- The current protocols are focused exclusively on PSI-CA. In practical applications, there may be a need to carry out other types of computations, such as PSI-SUM, etc. Expanding the protocols to support a variety of computational types is another significant direction for future work.
Author Contributions
Conceptualization, W.T., S.D. and J.W.; Methodology, W.T., S.D. and J.W.; Software, S.D.; Validation, W.T. and J.W.; Formal analysis, W.T., S.D. and J.W.; Investigation, S.D.; Resources, W.T.; Data curation, W.T.; Writing—original draft preparation, S.D.; Writing—review and editing, W.T., S.D. and J.W.; Visualization, S.D.; Supervision, W.T. and J.W.; Project administration, W.T. and J.W.; Funding acquisition, W.T. and J.W. All authors have read and agreed to the published version of the manuscript.
Funding
Guangdong Key Laboratory of Data Security and Privacy Preserving: 2023B1212060036. National Natural Science Foundation of China under Grant 62272199.
Data Availability Statement
The original data for this article were generated and recorded by ourselves. The data for this article does not originate from a publicly available repository. The authors confirm that the data supporting the findings of this study are available within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bald, P.; Baronio, R.; Cristofaro, E.; Gasti, P.; Tsudik, G. Efficient and secure testing of fully-sequenced human genomes. Biol. Sci. Initiat. 2000, 470, 7–10. [Google Scholar]
- Chen, H.; Laine, K.; Rindal, P. Fast private set intersection from homomorphic encryption. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, Dallas, TX, USA, 30 October–3 November 2017; pp. 1243–1255. [Google Scholar]
- Nagaraja, S.; Mittal, P.; Hong, C.Y.; Caesar, M.; Borisov, N. {BotGrep}: Finding {P2P} Bots with Structured Graph Analysis. In Proceedings of the 19th USENIX Security Symposium (USENIX Security 10), Washington, DC, USA, 11–13 August 2010. [Google Scholar]
- Li, W.; Liu, J.; Zhang, L.; Wang, Q.; He, C. A Survey on Set Intersection Computation for Privacy Protection. J. Comput. Res. Dev. 2022, 59, 1782–1799. [Google Scholar]
- Meadows, C. A More Efficient Cryptographic Matchmaking Protocol for Use in the Absence of a Continuously Available Third Party. In Proceedings of the 7th IEEE Symposium on Security and Privacy, Oakland, CA, USA, 7–9 April 1986; p. 134. [Google Scholar]
- Huberman, B.; Franklin, M.; Hogg, T. Enhancing Privacy and Trust in Electronic Communities. In Proceedings of the 1st ACM Conference on Electronic Commerce, Denver, CO, USA, 3–5 November 1999; pp. 78–86. [Google Scholar]
- DeCristofaro, E.; Tsudik, G. Experimenting with Fast Private Set Intersection. In Proceedings of the International Conference on Trust and Trustworthy Computing, Vienna, Austria, 13–15 June 2012; pp. 55–73. [Google Scholar]
- Pinkas, B.; Schneider, T.; Zohner, M. Faster Private Set Intersection Based on OT Extension. In Proceedings of the 23rd USENIX Security Symposium, San Diego, CA, USA, 20–22 August 2014; pp. 797–812. [Google Scholar]
- Freedman, M.; Nissim, K.; Pinkas, B. Efficient Private Matching and Set Intersection. In Proceedings of the 23rd International Conference on the Theory and Applications of Cryptographic Techniques, Interlaken, Switzerland, 2–6 May 2004. [Google Scholar]
- Freedman, M.J.; Hazay, C.; Nissim, K.; Pinkas, B. Efficient Set Intersection with Simulation-Based Security. J. Cryptol. 2016, 29, 115–155. [Google Scholar] [CrossRef]
- Abadi, A.; Terzis, S.; Dong, C. O-PSI: Delegated Private Set Intersection on Outsourced Datasets. In Proceedings of the 27th IFIP International Information Security and Privacy Conference, Hamburg, Germany, 26–28 May 2015; pp. 3–17. [Google Scholar]
- Kissner, L.; Song, D. Privacy-Preserving Set Operations. In Proceedings of the 25th Annual International Cryptology Conference, Santa Barbara, CA, USA, 14–18 August 2005; pp. 241–257. [Google Scholar]
- Jarecki, S.; Liu, X. Efficient Oblivious Pseudorandom Function with Applications to Adaptive OT and Secure Computation of Set Intersection. In LNCS 5444, Proceedings of the 6th Theory of Cryptography Conference, Francisco, CA, USA, 15–17 March 2009; Springer: Berlin/Heidelberg, Germany; pp. 577–594.
- Hazay, C.; Venkitasubramaniam, M. Scalable Multi-party Private Set-Intersection. In Proceedings of the 20th IACR International Workshop on Public Key Cryptography, Amsterdam, The Netherlands, 28–31 March 2017; pp. 175–203. [Google Scholar]
- Dou, J.; Liu, X.; Wang, W. Efficient and Secure Calculation of Two-Party Sets in the Field of Rational Numbers. Chin. J. Comput. 2020, 43, 1397–1413. [Google Scholar]
- Damgård, I.; Pastro, V.; Smart, N.; Zakarias, S. Multiparty Computation from Somewhat Homomorphic Encryption. In Proceedings of the 32nd Annual Cryptology Conference, Santa Barbara, CA, USA, 19–23 August 2012; Name, E., Ed.; Springer: Berlin/Heidelberg, Germany, 2012. Lecture Notes in Computer Science. pp. 643–662. [Google Scholar]
- Yao, A.C. Protocols for Secure Computations. In Proceedings of the 23rd Annual Symposium on Foundations of Computer Science (SFCS 1982), Chicago, IL, USA, 3–5 November 1982; pp. 160–164. [Google Scholar]
- Micali, S.; Goldreich, O.; Wigderson, A. How to Play Any Mental Game. In Proceedings of the 19th ACM Symposium on Theory of Computing, New York, NY, USA, 1 January 1987; pp. 218–229. [Google Scholar]
- Pinkas, B.; Schneider, T.; Segev, G.; Zohner, M. Phasing: Privateset intersectionusing permutation-basedhashing. In Proceedings of the 24th USENIX Security Symposium, USENIX Association, Washington, DC, USA, 12–14 August 2015; pp. 515–530. [Google Scholar]
- Pinkas, B.; Schneider, T.; Weinert, C.; Wieder, U. Efficient circuit-based PSI via Cuckoo hashing. In Proceedings of the 38th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Darmstadt, Germany, 19–23 May 2019; pp. 125–157. [Google Scholar]
- Pinkas, B.; Schneider, T.; Tkachenko, O.; Yanai, A. Efficient circuit-based PSI with linear communication. In Proceedings of the 39th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, 10–14 May 2019; pp. 122–153. [Google Scholar]
- Huang, Y.; Evans, D.; Katz, J. Private Set Intersection: Are Garbled Circuits Better Than Custom Protocols? In Proceedings of the 19th Network and Distributed System Security Symposium, San Diego, CA, USA, 5–8 February 2012. [Google Scholar]
- Naor, M.; Pinkas, B. Efficient oblivious transfer protocols. In Proceedings of the SODA, Washington, DC, USA, 7–9 January 2001; Volume 1, pp. 448–457. [Google Scholar]
- Dong, C.; Chen, L.; Wen, Z. When private-set intersection meets big data: An efficient and scalable protocol. In Proceedings of the 2013 ACM SIGSAC Conference on Computer & Communications Security, Berlin, Germany, 4–8 November 2013; pp. 789–800. [Google Scholar]
- Rindal, P.; Rosulek, M. Improved private set intersection against malicious adversaries. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Paris, France, 30 April–4 May 2017; pp. 235–259. [Google Scholar]
- Zhang, E.; Liu, F.H.; Lai, Q.; Jin, G.; Li, Y. Efficient multi-party private set intersection against malicious adversaries. In Proceedings of the 2019 ACM SIGSAC Conference on Cloud Computing Security Workshop, London, UK, 11 November 2019; pp. 93–104. [Google Scholar]
- Pinkas, B.; Rosulek, M.; Trieu, N.; Yanai, A. PSIfrom PaXoS: Fast, malicious private set intersection. In Proceedings of the 39th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, 10–14 May 2019; pp. 739–767. [Google Scholar]
- Orrù, M.; Orsini, E.; Scholl, P. Actively secure 1-out-of-n OT extension with application to private set intersection. In Proceedings of the Cryptographers’ Track at the RSA Conference, San Francisco, CA, USA, 14–17 February 2017; pp. 381–396. [Google Scholar]
- Rindal, P.; Schoppmann, P. VOLE-PSI: Fast OPRF and Circuit-PSI from Vector-OLE. IACR Cryptology ePrint Archive. 2021. Available online: https://eprint.iacr.org/2021/266 (accessed on 28 April 2024).
- Schoppmann, P.; Gascón, A.; Reichert, L.; Raykova, M. Distributed vector-OLE: Improved constructions and implementation. In Proceedings of the 26th ACM SIGSAC Conference on Computer and Communications Security, London, UK, 11–15 November 2019; pp. 1055–1072. [Google Scholar]
- Weng, C.; Yang, K.; Katz, J.; Wang, X. Wolverine: Fast, Scalable, and Communication-Efficient Zero-Knowledge Proofs for Boolean and Arithmetic Circuits. Cryptology ePrint Archive. 2020. Available online: https://eprint.iacr.org/2020/925 (accessed on 28 April 2024).
- Egert, R.; Fischlin, M.; Gens, D.; Jacob, S.; Senker, M.; Tillmanns, J. Privately Computing Set-Union and Set-Intersection Cardinality via Bloom Filters. Eur. J. Oper. Res. 2015, 139, 371–389. [Google Scholar]
- Ashok, V.; Mukkamala, R. A Scalable and Efficient Privacy Preserving Global Itemset Support Approximation Using Bloom Filters. In Proceedings of the IFIP Conference on Data and Applications Security and Privacy, Vienna, Austria, 14–16 July 2014; pp. 382–389. [Google Scholar]
- Debnath, S.; Dutta, R. Secure and Efficient Private Set Intersection Cardinality Using Bloom Filter. In Proceedings of the International Information Security Conference, Trondheim, Norway, 9–11 September 2015; pp. 209–226. [Google Scholar]
- De Cristofaro, E.; Gasti, P.; Tsudik, G. Fast and Private Computation of Cardinality of Set Intersection and Union. In Proceedings of the CANS 2012, Darmstadt, Germany, 12–14 December 2012; pp. 218–231. [Google Scholar]
- Jarecki, S.; Liu, X. Fast Secure Computation of Set Intersection. In Proceedings of the SCN 2010, Amalfi, Italy, 13–15 September 2010; Lecture Notes in Computer Science. Volume 6280, pp. 418–435. [Google Scholar]
- Su, G.; Xu, M. A Survey on Secure Multi-party Computation Technology and Applications. Inf. Commun. Technol. Policy 2019, 45, 19–22. [Google Scholar]
- Li, A. Research on Multi-Party Statistical Computations Based on Functional Encryption. Ph.D. Thesis, Wuhan University of Technology, Wuhan, China, 2017. [Google Scholar]
- Wang, H.; Dai, H.; Chen, S.; Chen, Z.; Chen, G. A Survey of Filter Data Structures. Comput. Sci. 2024, 51, 35–40. [Google Scholar]
- Yu, M.; Fabrikant, A.; Rexford, J. BUFFALO: Bloom filter forwarding architecture for large organizations. In Proceedings of the International Conference on Emerging Networking Experiments and Technologies, Rome, Italy, 1–4 December 2009; pp. 313–324. [Google Scholar]
- Li, P.; Luo, B.; Zhu, W.; Xu, H. Cluster-based distributed dynamic Cuckoo filter system for Redis. Int. J. Parallel Emergent Distrib. Syst. 2020, 35, 340–353. [Google Scholar] [CrossRef]
- Wang, F.; Chen, H.; Liao, L.; Zhang, F.; Jin, H. The power of better choice: Reducing relocations in Cuckoo filter. In Proceedings of the International Conference on Distributed Computing Systems, Dallas, TX, USA, 7–10 July 2019; pp. 358–367. [Google Scholar]
- Gur, L.; Lis, D.; Dai, H.; Wang, H.; Luo, Y.; Fan, B.; Basat, R.B.; Wang, K.; Song, Z.; Chen, S.; et al. Adaptive online cache capacity optimization via lightweight working set size estimation at scale. In Proceedings of the USENIX Annual Technical Conference, Boston, MA, USA, 10–12 July 2023; pp. 467–484. [Google Scholar]
- Reviriego, P.; Martínez, J.; Larrabeiti, D.; Pontarelli, S. Cuckoo Filters and Bloom Filters: Comparison and Application to Packet Classification. IEEE Trans. Netw. Serv. Manag. 2020, 17, 2690–2701. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).