Scheduling of Industrial Control Traffic for Dynamic RAN Slicing with Distributed Massive MIMO ^†

Abstract

Industry 4.0, with its focus on flexibility and customizability, is pushing in the direction of wireless communication in future smart factories, in particular, massive multiple-input-multiple-output (MIMO) and its future evolution of large intelligent surfaces (LIS), which provide more reliable channel quality than previous technologies. At the same time, network slicing in 5G and beyond systems provides easier management of different categories of users and traffic, and a better basis for providing quality of service, especially for demanding use cases such as industrial control. In previous works, we have presented solutions for scheduling industrial control traffic in LIS and massive MIMO systems. We now consider the case of dynamic slicing in the radio access network, where we need to not only meet the stringent latency and reliability requirements of industrial control traffic, but also minimize the radio resources occupied by the network slice serving the control traffic, ensuring resources are available for lower-priority traffic slices. In this paper, we provide mixed-integer programming optimization formulations for radio resource usage minimization for dynamic network slicing. We tested our formulations in numerical experiments with varying traffic profiles and numbers of nodes, up to a maximum of 32 nodes. For all problem instances tested, we were able to calculate an optimal schedule within 1 s, making our approach feasible for use in real deployment scenarios.

1. Introduction

The rise of Industry 4.0 brings new challenges in communications. Key ideas in Industry 4.0 include that manufacturing should become more flexible and dynamic, with greater customization and optimization of production, automation, and adaptation, with real-time capability, decentralization, and modularity as important principles for operation [1,2]. In order to realize this vision, there is an ambition to move more and more to wireless communication on the factory floor. Compared with traditional wired deployments, wireless communication allows for easier reconfiguration of the factory floor, adjustments of scheduling and resource allocation, as well as reduced costs since there is no need to install cables for communication. As such, smart factories are a major application domain for new and emerging use cases envisaged to be served by 6G systems [3].

Providing wireless communication in a domain where applications have stringent requirements on reliability and latency is no easy task; however, massive multiple-input-multiple-output (MIMO) [4] is far more promising in this regard than previous wireless technologies. With massive MIMO, the large number of antennas provide a high degree of diversity, improving reliability for industrial applications [5], while an effect known as channel hardening smooths out small-scale variations in the radio channel and provides a much more predictable performance [6]. These effects will be enhanced with the advent of large intelligent surfaces (LIS) [7,8], also known as cell-free distributed massive MIMO, slated to be the next evolution of massive MIMO and a key technology for 6G [3]. In LIS, the number of antennas will increase once again, and they will be deployed in multiple arrays over a wider area, further enhancing spatial diversity and increasing the chances that a user will have antennas located close by and within line-of-sight, providing good channel quality. While there are many other promising technologies in the development of 6G, both for communication [9,10] as well as localization and sensing [11], we focus here specifically on LIS and how it affects scheduling and resource allocation.

To provide a high quality of service (QoS) communication that meets the demands of industrial applications requires not only the underlying physical layer technology, but also appropriate scheduling and resource allocation methods at the link layer. With the concept of networking slicing [12,13], the network is divided into multiple logically separated virtual networks, called slices, each tailored to a particular application or group of users. Each slice can implement policies that optimize quality of service for the particular application it serves. Radio access network (RAN) slicing [14,15] occurs when the network slicing concept is applied to the RAN, with radio resources divided between the slices in such a way as to meet their application requirements. Slicing can be performed either statically, where each slice receives a fixed allocation of resources, or dynamically, where each slice may receive some minimum allocation, but also opportunistically borrow resources from other slices when they are not needed.

In large-scale antenna array systems, such as massive MIMO and LIS, the primary resource to be allocated in the RAN is orthogonal pilot signals. In time division duplex (TDD) massive MIMO systems, during each coherence block—a time-frequency region in which the channel is effectively constant—a user device must transmit a pilot signal in order for the base station to collect its channel state information (CSI) and calculate an appropriate precoding matrix (on the downlink) and combining matrix (on the uplink). Having done so, the device may both transmit and receive in the coherence block, and a large number of devices may transmit and receive simultaneously. However, in each coherence block, there are a limited number of pilot signals available, with the exact number depending on the pilot scheme and how much of the block is dedicated to channel estimation via pilot signals versus transmission of data. Pilot signals then determine which user devices can estimate their channels and thus be spatially multiplexed in the same coherence block, allowing them to make use of the time and frequency resources in the block to transmit simultaneously.

In this paper, we consider the case with both deadline-based industrial control traffic and rate-based background traffic in the system, and develop a scheduling solution for dynamic RAN slicing that accommodates both simultaneously. In previous work [16], we examined the scheduling problem with the objective of overall pilot usage minimization. In a networking slicing context, this would correspond to static slicing, in which each slice is given a fixed allocation and no sharing of resources between slices is possible.

With dynamic slicing, unused pilots allocated to one slice can be borrowed by lower-priority slices, and it is desirable to minimize the actual number of occupied pilot resources, not just the overall size of the slice. This adds considerable complexity to the optimization problem but yields a more efficient use of scarce radio resources. In this paper, we formulate two different mixed-integer programming (MIP) optimization problems, for cases where the frame length for scheduling is constant or variable, where the objective is to minimize the maximum number of pilots per time slot. The industrial control slice takes priority as it serves critical traffic, and so, by minimizing the number of pilots allocated to this slice, we maximize the resources left available for other slices.

We have tested our formulations with numerical experiments with up to 32 nodes and a range of different traffic patterns. The formulation for fixed frame length is unsurprisingly faster to solve than that with variable frame length. Minimizing the number of pilots used per slot is a more difficult objective than minimizing a static slice allocation as we did in our previous work, and so, it results in slower solution times. However, with the help of an iterative solution procedure that we developed, we were able to solve all test cases in less than 1 s. This means that our scheduling solutions are feasible to implement in real-world scenarios, where the active time for a schedule will typically be much longer than the solution times we obtained.

The rest of this paper is organized as follows. Section 2 describes existing work on scheduling and RAN slicing for industrial communications using massive MIMO. Next, Section 3 details the smart factory scenario we target, and Section 4 gives our system model. In Section 5, we then elaborate our optimization formulations. Section 6 outlines the numerical experiments we conducted, and their results are then given in Section 7. Finally, Section 8 concludes this paper.

2. Related Work

The work in this paper follows on from our work in [16], where we considered the problem of scheduling for industrial control traffic in massive MIMO and LIS systems. In the current paper, we target the same use case, however with the addition of dynamic RAN slicing. This requires a new objective for the optimization problems. In [16], the objective we used was to minimize the maximum number of pilots used in any time slot. This assumes that there is a static number of pilots given to the control traffic and minimizes this number. However, this does not necessarily result in the fewest pilots used overall. In a dynamic slicing context, any unused pilots in the industrial control slice can be used by other slices. It is, therefore, better to have a larger base allocation of pilots for the industrial control slice but use fewer of these, leaving them available to be borrowed. In the current paper, we therefore consider a new objective of minimizing the number of pilots used per slot, that is, the pilot rate. This adds significant complexity to the optimization formulation and changes the way it should be solved in order to be feasible for use in real systems.

Pilot allocation and scheduling for massive MIMO is an area that has received a lot of attention and concerted research effort since massive MIMO was first conceived. It is too much to discuss here, but a survey up to 2017 can be found in [17], and a more recent one concerning scheduling in 5G more broadly in [18]. However, thus far, little work has been conducted on user scheduling for massive MIMO in an industrial context, and in this work, even less deals with demanding industrial control traffic. Paper [19] considers the feasibility of supporting ultra-reliable low-latency communications (URLLC) traffic in a massive MIMO system but with grant-free access rather than scheduled access. While grant-free access is the most appropriate for certain types of URLLC traffic, especially sporadic traffic, such as alarms, it is not a good fit for industrial control traffic, which is periodic and frequent and thus lends itself better to a scheduled approach.

Several works investigate massive MIMO as a communications technology for the industrial Internet of Things (IIoT). In [20], the authors consider a single-cell scenario in which a massive MIMO base station serves a much larger number of IIoT devices than its number of antennas. Similarly, [21] investigates whether it is feasible to use massive MIMO for IIoT, again in a single-cell scenario with a large number of low-power IIoT devices, focusing on different precoding techniques rather than link layer user scheduling. In [22], the focus is instead on power allocation in IIoT with massive MIMO, and the pilot and payload power are jointly optimized. While these works share the same industrial domain setting as our work, and in some cases, similar stringent requirements on latency and reliability, their focus is on access for massively many devices, typically with low per-device data rates. We instead focus on industrial control traffic, where the goal is to meet the latency and reliability requirements needed for high-frequency control loops, rather than serve a massive number of devices.

A few works have previously been published on scheduling for industrial communications in massive MIMO systems. In [23], we considered the case of high-priority alarm traffic alongside industrial control traffic; however, in that work, we focused on the alarm traffic and did not provide a scheduling method for the control traffic. In that work, we also did not consider dynamic RAN slicing.

Network slicing was proposed in the years leading up to the release of 5G as a means of providing QoS for its diverse use cases [12,13], and since, has continued to attract significant interest from the research community [24]. In particular, RAN slicing aims to partition the resources in the radio access network between different slices [14,15]. To do this, the particular radio technology must be taken into account. In our case, we consider massive MIMO and LIS systems where spatial multiplexing allows time and frequency resources to be shared between users.

In [25], the authors used deep reinforcement learning to allocate radio resources between slices in a massive MIMO RAN, aiming to optimize the QoS of the slices, including an ultra-reliable low latency (URLLC) slice, into which category our industrial communications use case fits. However, this work was focused on allocation between slices, and divides the time and frequency resource blocks disjointly, without borrowing between slices. We instead consider the scheduling of devices within the industrial control slice, devices share resource blocks but are instead separated via spatial multiplexing with the help of pilot signals, and devices in one slice can borrow unused resources from other slices. Machine learning was also applied to RAN slicing in [26], in this case, with a cascaded convolutional neural network-long short-term memory network but for broadcasting services rather than URLLC traffic. Slicing for low latency services was performed in [27] with the help of an SDN-based framework, but here, the targeted system was the backhaul networks rather than the RAN.

RAN slicing between massive IoT and URLLC use cases is performed in [28] for a cooperative multipoint system; however, they studied bursty URLLC, whereas we consider periodic industrial control traffic. The traffic model in this case significantly impacts how resource allocation can be performed. The work in [29] considers the three canonical 5G use cases: URLLC, enhanced mobile broadband (eMBB), and massive machine-type communication (mMTC), and allocates resource blocks as well as other resources, such as virtual network functions, to different slices within each use case. Mixed-integer programming for throughput optimization was used for RAN slicing in [30], and both the RAN and network routing between the remote radio heads and the baseband unit were considered. However, the traffic model used downlink traffic only, characterized by a required data rate for each user. For our use case of industrial control traffic, it is important to consider periodic transmissions in the traffic model.

There is as yet not much existing work on RAN slicing taking into account the particular spatial multiplexing capabilities of massive MIMO and allocating resources based on pilot signals. Distributed massive MIMO with non-orthogonal slicing was investigated in [31], using mixed-integer programming optimization as we also do in our work. However, in that work, the objective to be optimized was energy efficiency, which we do not consider here, instead aiming for minimal resource usage. Massive MIMO is also the radio technology used in [32], with both pilot contamination and pilot duration taken into account. The objective in that work was, however, to maximize the total system data rate, and each slice was characterized by a required minimum rate.

In this paper, we draw together the threads of dynamic RAN slicing, massive MIMO resource allocation using pilot signals, modeling of industrial control traffic, and scheduling. We continue the work we began in [16] and extend it to the dynamic RAN slicing case. We develop solutions for the scheduling of industrial control traffic that facilitate efficient resource borrowing between slices by minimizing the pilot rate demanded by the industrial control slice, while still meeting its stringent latency and reliability requirements. A summary of this paper’s contributions with respect to the works discussed above is given in

Table 1. Summary of the contributions of this work in relation to existing work.

Traffic Model
[19,20,21,22]	grant-free and mMTC traffic
[23]	alarm traffic
[28]	bursty URLLC traffic
[30]	downlink rate-based traffic
This work	scheduled periodic traffic for industrial control, both uplink and downlink
Slicing and resource allocation
[25,29]	URLLC with allocation between slices
[26]	slicing for broadcasting services
This work	scheduling within industrial control slice, with resource borrowing between slices
Optimization objective
[31]	energy efficiency
[32]	maximization of total system rate
This work	minimal resource usage

.

3. Targeted Scenario

We target a smart factory scenario as in Figure 1. On the factory floor, there are machines and other devices that need to communicate. Some of these require real-time control with low latency and high reliability, for example, robots and other industrial equipment, while other devices do not have strict requirements, for example, Internet of Things (IoT) sensors, smartphones, and other devices used by factory staff. We consider that RAN slicing is applied, with each device category occupying a slice to serve its traffic. In the following, we focus on the real-time control devices, which occupy the highest-priority slice.

In the typical closed-loop control case, the plant (machine or other equipment to be controlled) needs to transmit frequent updates to the controller, and receive control values in return. In our scenario, the controller may be located either on the factory floor or in the local cloud; however, even in the case where the controller is on the factory floor, it may communicate with the plant wirelessly. As such, this communication needs to go via a base station (in the centralized massive MIMO case), or a federation of cooperating contact service points (CSPs) (in the LIS case) [8]. In the following we will focus on the LIS case and refer to the serving CSPs, but our work is equally applicable to cellular massive MIMO systems. The key requirement is that the devices should be served by antennas that are operated coherently, and share the same set of pilot signals. To facilitate communication, end devices send pilot signals to the service CSPs, where there are a limited number of pilot signals in each time slot (coherence interval).

In this work, we do not model the radio channel in detail, but we assume similar characteristics to the Lund massive MIMO testbed LuMaMi [33] for the massive MIMO case, and to the Lund LIS testbed (still under construction) for the LIS case. Both of these use 3.7 GHz as the operating frequency, and uniform rectangular arrays as the antenna configuration. For LIS, the distances between the CSPs can vary, so long as they are operated coherently and thus share the same set of pilot signals and serve the same set of users. However, the maximum possible number of CSPs to serve a group of users and the distance between them is still a matter of active research, especially in low-latency cases where communication of channel state information between the CSPs, needed for coherent operation, can impose a bottleneck. We assume the end devices to be single-antenna devices.

Our problem is then to allocate pilot signals to end devices in time slots such that the communication requirements of the devices are fulfilled while minimizing the resources—pilots—used by the industrial control slice as a whole. Each device should receive sufficiently many pilots to satisfy its traffic demands, both on the uplink and downlink, and should receive a pilot sufficiently frequently enough to ensure stable and effective control. We assume a TDD massive MIMO system, and so, thanks to channel reciprocity, if a device is allocated a pilot in a given time slot, it can both transmit and receive in that slot. A scheduling algorithm determines which devices are allocated pilots in each time slot. The scheduler runs on edge or local cloud computing resources, i.e., in either the second or third layers in Figure 1, depending on how much computational resources are available at each of these layers.

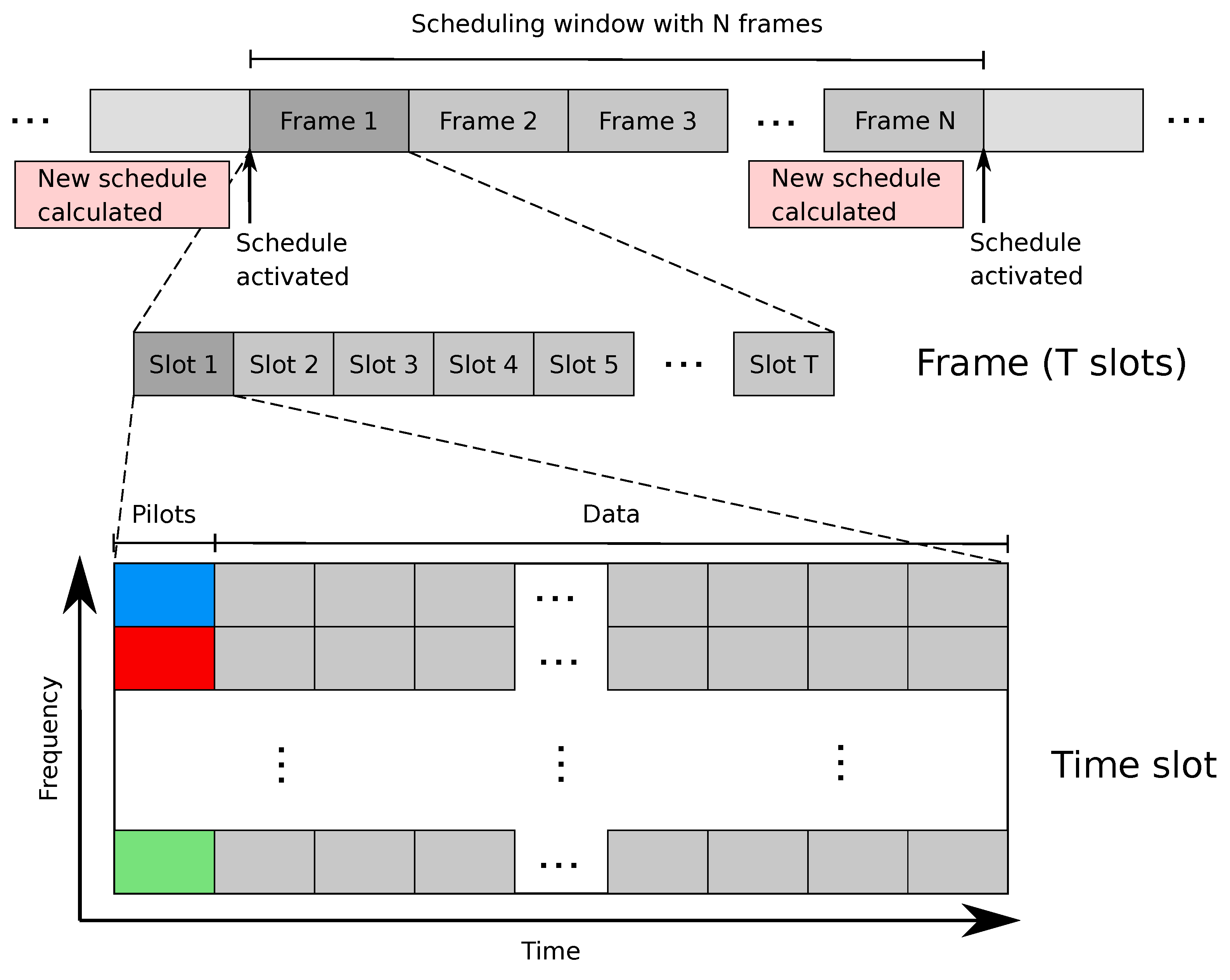
Figure 2 and Figure 3 show how the scheduling works. A number of end devices are served by a number of CSPs (Figure 2). In each scheduling window, the scheduler calculates a schedule that covers a certain number of time slots, which collectively form a scheduling frame (Figure 3). The frame then repeats for the duration of the scheduling window. The time slots are closely related to the wireless channel properties since we consider each time slot as one coherence interval, and thus, the length of a slot depends on the environment as well as the mobility of the users. In cases where the channel coherence time is long, it would also be possible to break each coherence interval into multiple time slots; however, we do not consider this case in this paper.

4. System Model

The notation we use is summarized in

Table 2. Notation.

Parameter	Meaning
$\mathcal{K}$	set of nodes needing to communicate
	$\left(\mathcal{K}=\{1,2,\dots ,K\}\right)$
$\widehat{h}\left(k\right)$	uplink demand rate of node $k\in \mathcal{K}$
$\check{h}\left(k\right)$	downlink demand rate of node $k\in \mathcal{K}$
$d\left(k\right)$	maximum allowable period, in slots, for node $k\in \mathcal{K}$
$\mathcal{S}$	maximal frame (set of slots), $\mathcal{S}=\{1,2,\dots ,S\}$
P	maximum allowable number of pilots per slot
T	frame length ($T\le S$), can be a variable as well
$\mathcal{T}$	feasible frame ($\mathcal{T}=\{1,2,\dots ,T\}$) of length T
$\mathcal{K}\left(T\right)$	set of nodes with $d\left(k\right)<T$
	$\left(\mathcal{K}\left(T\right)=\{k\in \mathcal{K}:d(k)<T\}\right)$
T	frame length ($T\le S$)
$T_k$	last slot of the frame with a pilot allocated to $k\in \mathcal{K}$ ($T_k\le T$)
$t_k$	first slot of the frame with a pilot allocated to $k\in \mathcal{K}$ ($t_k\le T$)
$X^i$	whether or not at least one node is allocated a pilot in slot $i\in \mathcal{S}$
$x_k^i$	whether or not node $k\in \mathcal{K}$ is allocated a pilot in slot $i\in \mathcal{S}$
p	maximum number of pilots used in any slot
$Z_k^i$	binary variables indicating there are remaining slots with pilots allocated to $k\in \mathcal{K}$ later in the frame
$z_k^i$	binary variables indicating there are no slots with pilots allocated to $k\in \mathcal{K}$ earlier in the frame
${\lambda }_i$	binary variables indicating whether slot $i\in \mathcal{S}$ is the last slot in the frame
$\mathbb{B}$	the set $\{0,1\}$
${\mathbb{R}}_{+}$	the set of positive real numbers
${\mathbb{Z}}_{+}$	the set of positive integers

. We have a set $\mathcal{K}=\{1,2,\dots ,K\}$ of nodes (end devices) needing to communicate with the serving CSPs. Communication takes place in frames, where the same pattern of time slots (the frame) is repeated, forming a periodic schedule (see Figure 3). This schedule must satisfy the traffic requirements of all of the end devices. The frame length T, that is, the number of slots in the frame, is a decision variable able to be chosen so as to satisfy the traffic requirements. In the problem formulations, we will assume that the maximal frame length is equal to a given parameter S that is large enough to accommodate a frame that satisfies all nodes’ traffic demands. Thus, we assume that the maximal frame is composed of the slots $i\in \mathcal{S}$, where $\mathcal{S}=\{1,2,\dots ,S\}$, and all other (feasible) frames are composed of slots $\{1,2\dots ,T\}$, where $T\le S$. Determining a suitable value for $\mathcal{S}$ is not entirely straightforward and impacts the performance of the optimization solver. This is a question we will discuss further in Section 7.

Each node $k\in \mathcal{K}$ has three traffic requirements: an uplink demand rate $\widehat{h}\left(k\right)$, a downlink demand rate $\check{h}\left(k\right)$, and a maximum number of slots $d\left(k\right)$ between two consecutive slots in which a pilot is allocated to k. The uplink and downlink demands are traffic rates expressed in slots per frame slot, that is, a number of slots in which the device must transmit (uplink) or receive (downlink) per slot in the frame in order to satisfy the demand. For example, if a node k has an uplink demand rate $\widehat{h}\left(k\right)$ of $0.2$, then for every five slots in the frame, k must transmit in one slot. If the frame lengths were determined to be, say, 20, then k must transmit in at least 4 slots during the frame in order to satisfy its uplink demand. The downlink demand rate works similarly. Here, we do not consider different modulation and coding schemes yielding different data rates, but rather consider that $\widehat{h}\left(k\right)$ and $\check{h}\left(k\right)$ can be satisfied with a fixed number of slots for a given node k and frame length.

Finally, $d\left(k\right)$ gives the maximum number of slots that can elapse between two consecutive transmissions by the device. For example, if $d\left(k\right)=10$, then k must transmit (or receive) at least once every 10 slots. This ensures a given frequency of sending and receiving control updates. Depending on the type of controller and the type of actuator, different devices will have different allowable periods for their control.

In the following section, we provide our optimization formulations based on the above system model. We will first consider the case where the frame length is fixed. This leads to a simpler problem formulation, and is applicable in cases where external constraints enforce a specific frame length, for example, if a frame should be equal to the length of the network’s transmission time interval (TTI). We then consider a variable frame length, which is a more complex problem but can result in better performance in terms of the optimization objectives.

5. Optimization Formulations

In our previous work [16], we minimized the maximum number of pilots used in any slot. This reflects a static resource allocation, in which the industrial control traffic is given a fixed (but minimal) number of pilots, and this allocation applies to all slots. However, it is more efficient to allocate pilots dynamically, if the radio access network supports this. In this case, the industrial control traffic is allocated only to the pilots it requires in any given slot, and all remaining pilots can be used for other traffic. We now consider this case, and therefore, optimize it for the minimal number of pilots used per slot. This gives a measure of efficiency under dynamic slicing that is independent of the frame length.

5.1. Optimization Objective and Constraint Modification

The optimization objective considered in this paper complicates the optimization, compared with our work in [16], since now we seek to minimize the total number of pilots used across all slots. The frame length is variable and is determined by the optimization, but the frame will repeat continually. This means we need to normalize the number of pilots used to the frame length, thus obtaining a pilot rate in pilots used per slot of the frame.

5.2. Formulation FPRM/1: Fixed Frame Length

In the case when the frame length T is a fixed parameter, the formulation to minimize the pilot rate is similar to that in [16] for obtaining a static slice allocation.

$$\begin{array}{cc}\hfill & min\frac{1}{T}{\sum }_{k\in \mathcal{K}}{\sum }_{i\in \mathcal{S}}{x}_k^i\hfill \end{array}$$

(1a)

$$\begin{array}{ccc}\hfill & {\sum }_{i\in \mathcal{T}}{x}_k^i\ge \widehat{h}\left(k\right)T,\hfill & \hfill k\in \mathcal{K}\end{array}$$

(1b)

$$\begin{array}{ccc}\hfill & {\sum }_{i\in \mathcal{T}}{x}_k^i\ge \check{h}\left(k\right)T,\hfill & \hfill k\in \mathcal{K}\end{array}$$

(1c)

$$\begin{array}{ccc}\hfill & {\sum }_{i\in \mathcal{T}}{x}_k^i\ge 1,\hfill & \hfill k\in \mathcal{K}\end{array}$$

(1d)

$$\begin{array}{ccc}\hfill & {\sum }_{j=i-d\left(k\right)+1}^i{x}_k^j\ge 1,\hfill & \hfill k\in \mathcal{K}\left(T\right),d\left(k\right)\le i\le T\\ \hfill & {\sum }_{j=1}^i{x}_k^j+{\sum }_{j=T-\left(d\right(k)-1-i)}^T{x}_k^j\ge 1,\hfill & \hfill \end{array}$$

(1e)

$$\begin{array}{ccc}\hfill & \hfill & \hfill k\in \mathcal{K}\left(T\right),1\le i\le d\left(k\right)-1\end{array}$$

(1f)

$$\begin{array}{ccc}\hfill & {\sum }_{k\in \mathcal{K}}{x}_k^i\le P,\hfill & \hfill i\in \mathcal{T}\end{array}$$

(1g)

$$\begin{array}{ccc}\hfill & x_k^i\in \mathbb{B},\hfill & \hfill k\in \mathcal{K},i\in \mathcal{T}.\end{array}$$

(1h)

The objective function (1a) is however changed to minimize the pilot rate, that is, the number of pilots used per slot in the frame. For the static frame length case, this is equivalent to minimizing the total number of pilots used, but simply normalized to the frame length.

Constraints (1b) and (1c) ensure, respectively, that the uplink and downlink traffic rates are met for each device $k\in \mathcal{K}$. Constraint (1d) requires that every device transmit at least once in the frame, which is not otherwise assured in the case where a device only has periodic traffic, with no rate demand traffic. Constraints (1e) and (1f) together ensure that the periodic traffic requirements are met for each device $k\in \mathcal{K}$, with constraint (1e) covering most of the frame and requiring a transmission at least once every $d\left(k\right)$ slots, while constraint (1f) takes care of the beginning and end of the frame, ensuring that no more than $d\left(k\right)$ slots elapse between the last transmission of one frame and the first transmission of the next. Finally, constraint (1g) makes sure that no more than the maximum allowable number of pilots P is used in any slot, and constraint (1h) gives the domain for the decision variables $x_k^i$.

5.3. Formulation FPRM/2: General

In the case when the frame length T is a decision variable, the problem formulation is significantly more complicated than its counterpart in [16]. This is because, to obtain a MIP formulation, we need to remove the divisions of decision variables that appear in the objective function, i.e., the divisions $\frac{x_k^i}{T},k\in \mathcal{K},i\in \mathcal{S}$. The formulation is as follows.

$$\begin{array}{cc}\hfill & min{\sum }_{k\in \mathcal{K}}{\sum }_{i\in \mathcal{S}}{w}_k^i\hfill \end{array}$$

(2a)

$$\begin{array}{cc}\hfill & T={\sum }_{i\in \mathcal{S}}{X}^i\hfill \end{array}$$

(2b)

$$\begin{array}{cc}\hfill & X^1\ge X^2\ge \cdots \ge X^S\hfill \end{array}$$

(2c)

$$\begin{array}{ccc}\hfill & x_k^i\le X^i,\hfill & \hfill k\in \mathcal{K},i\in \mathcal{S}\end{array}$$

(2d)

$$\begin{array}{ccc}\hfill & {\sum }_{i\in \mathcal{S}}{x}_k^i\ge \widehat{h}\left(k\right)T,\hfill & \hfill k\in \mathcal{K}\end{array}$$

(2e)

$$\begin{array}{ccc}\hfill & {\sum }_{i\in \mathcal{S}}{x}_k^i\ge \check{h}\left(k\right)T,\hfill & \hfill k\in \mathcal{K}\end{array}$$

(2f)

$$\begin{array}{ccc}\hfill & {\sum }_{i\in \mathcal{S}}{x}_k^i\ge 1,\hfill & \hfill k\in \mathcal{K}\end{array}$$

(2g)

$$\begin{array}{cc}\hfill & {\sum }_{i\in \mathcal{S}}{\lambda }^i=1\hfill \end{array}$$

(2h)

$$\begin{array}{cc}\hfill & {\sum }_{i\in \mathcal{S}}i{\lambda }^i=T\hfill \end{array}$$

(2i)

$$\begin{array}{cc}\hfill & u={\sum }_{i\in \mathcal{S}}\frac{1}{i}{\lambda }^i\hfill \end{array}$$

(2j)

$$\begin{array}{ccc}\hfill & w_k^i\le u;w_k^i\le x_k^i;w_k^i\ge u+x_k^i-1,\hfill & \hfill k\in \mathcal{K},i\in \mathcal{S}\end{array}$$

(2k)

$$\begin{array}{ccc}\hfill & {\sum }_{j=i-d\left(k\right)+1}^i{x}_k^j\ge X^i,\hfill & \hfill k\in \mathcal{K},i\in \mathcal{S}:i\ge d\left(k\right)\end{array}$$

(2l)

$$\begin{array}{ccc}\hfill & Z_k^j\ge x_k^i,\hfill & \hfill k\in \mathcal{K},i\in \mathcal{S},1\le j\le i\end{array}$$

(2m)

$$\begin{array}{ccc}\hfill & Z_k^i\le {\sum }_{j=i}^S{x}_k^j,\hfill & \hfill k\in \mathcal{K},i\in \mathcal{S}\end{array}$$

(2n)

$$\begin{array}{ccc}\hfill & T_k={\sum }_{i\in \mathcal{S}}{Z}_k^i,\hfill & \hfill k\in \mathcal{K}\end{array}$$

(2o)

$$\begin{array}{ccc}\hfill & z_k^j\ge x_k^i,\hfill & \hfill k\in \mathcal{K},i\in \mathcal{S},i\le j\le S\end{array}$$

(2p)

$$\begin{array}{ccc}\hfill & z_k^i\le {\sum }_{j=1}^i{x}_k^j,\hfill & \hfill k\in \mathcal{K},i\in \mathcal{S}\end{array}$$

(2q)

$$\begin{array}{ccc}\hfill & t_k={\sum }_{i\in \mathcal{S}}{z}_k^i,\hfill & \hfill k\in \mathcal{K}\end{array}$$

(2r)

$$\begin{array}{ccc}\hfill & (T-T_k)+(S-t_k)\le d\left(k\right)-1,\hfill & \hfill k\in \mathcal{K}\end{array}$$

(2s)

$$\begin{array}{ccc}\hfill & {\sum }_{k\in \mathcal{K}}{x}_k^i\le P,\hfill & \hfill i\in \mathcal{S}\end{array}$$

(2t)

$$\begin{array}{ccc}\hfill & X^i,x_k^i,Z_k^i,z_k^i,{\lambda }^i\in \mathbb{B},\hfill & \hfill k\in \mathcal{K},i\in \mathcal{S}\end{array}$$

(2u)

$$\begin{array}{ccc}\hfill & u,w_k^i\in {\mathbb{R}}_{+},\hfill & \hfill k\in \mathcal{K},i\in \mathcal{S}\end{array}$$

(2v)

$$\begin{array}{ccc}\hfill & T,T_k,t_k\in {\mathbb{Z}}_{+},\hfill & \hfill k\in \mathcal{K}.\end{array}$$

(2w)

In order to express the objective function without variable divisions, we introduce auxiliary variables u and $w_k^i$, $k\in \mathcal{K}$, $i\in \mathcal{S}$. As we will see, u will be constrained to take the value $\frac{1}{T}$, and then each $w_k^i$ will express the value $x_i^{k}u$, i.e., $\frac{x_i^k}{T}$. The sum over all the $w_k^i$ thus gives the pilot rate for the frame.

The frame length T is specified in (2b) by means of binary variables $X^i,i\in \mathcal{S}=\{1,2,\dots ,S\},$ where S is the maximum frame length and $X^i=1$ if, and only if, slot i belongs to the frame. Note that the monotonicity constraint (2c) ensures that the constructed frame is of the required form, i.e., $\mathcal{T}=\{1,2,\dots ,T\}$. Then, constraint (2d) forbids allocating pilots to nodes in the slots outside the frame. As in formulation (1), constraints (2e) and (2f) ensure that each node obtains its required traffic rate on the uplink and downlink, and constraint (2g) forces every node to transmit at least once.

Constraints (2h)–(2j) use binary variables ${\lambda }^i,i\in \mathcal{S}$ (out of which only one is equal to 1 due to constraint (2h)), to first express the current value of variable T (constraint (2i)), and then the current value of $\frac{1}{T}$ (constraint (2j) sets variable u to $\frac{1}{T}$). Finally, constraint (2k) make the values of variables $w_k^i,k\in \mathcal{K},i\in \mathcal{S},$ equal to $x_k^i/T$; this is correct because $u=1/T$ and hence the inequality $u\le 1$ holds.

The next group of constraints makes sure that each node $k\in \mathcal{K}$ transmits at least once in every $d\left(k\right)$ slots. This is mostly done by constraint (2l), which implies that within any sequence of consecutive $d\left(k\right)$ slots in frame $\mathcal{T}$, there is at least one slot with a pilot allocated to node k. Yet, on top of that, we need to ensure that in vector $x_k=(x_k^1,x_k^2,\dots ,x_k^S)$, the number of zeros after the last element equal to 1 plus the number of zeros before the first element equal to 1 will not be more than $d\left(k\right)-1$. This is done by means of constraint (2s), where $T_k$ is the variable that expresses the largest index i with $x_k^i=1$, while the smallest index i with $x_k^i=1$ is equal to $S+1-t_k$ ($t_k$ is a variable). The proper values of $T_k$ are ensured by constraints (2m)–(2o), while the proper value of $t_k$ is implied by constraints (2p)–(2r). In both cases, additional binary variables ($Z_k^i$ and $z_k^i$) are used. The correctness of constraints (2m)–(2o) and (2p)–(2r) is illustrated in Appendix A.

Constraint (2t) once again ensures that the maximum number of pilots is not exceeded, and the remaining constraints give the domains for the decision variables.

6. Numerical Experiments

We conducted a numerical study to investigate the performance of our optimization problems. For each optimization problem, we conducted two sets of experiments. The first set included only periodic traffic (${\sum }_{i\in \mathcal{T}}{x}_k^i\ge 1,\widehat{h}\left(k\right)=\check{h}\left(k\right)=0,k\in \mathcal{K}$), while the second set included both periodic and rate demand traffic (${\sum }_{i\in \mathcal{T}}{x}_k^i\ge 1,\widehat{h}\left(k\right),\check{h}\left(k\right)\ge 0,k\in \mathcal{K}$). We varied the number of nodes from 4 to 32, using only multiples of 2 to facilitate the experiment design, as will be explained further below. We set the maximum number of slots to 15, as this gave us some instances with the number of nodes greater than the maximum frame length, and some less, as well as in practice giving reasonable experiment run times. The details of each set of experiments are given below and are summarized in

Table 3. Experiments.

Experiment	Periodic Traffic	Background Traffic
1A	Short	None
1B	Long	None
1C	Mixed	None
2A	Short	Low
2B	Long	High
2C	Mixed	Mixed

, and a summary of the experimental parameters is given in

Table 4. Experimental parameters.

Symbol	Description	Value
S	total number of slots	15
K	number of nodes	4, 8, 16, 32
D	period (slots)	Short: 2–10, Long: 11–20
h	background traffic rate (transmissions per slot)	low: $0.05$–$0.1$, high: $0.1$–$0.5$
C	coherence interval (ms)	1
p	maximum number of pilots	16
-	solver timeout	$10,800$ s (30 h)

. For each case, we generated and solved 10 problem instances, with periodic and/or background traffic for each uniformly randomly generated from the ranges given in Table 4.

Each formulation was implemented in AMPL and solved using CPLEX on an Intel Xeon E5-2420 CPU with 12 cores and 24 GB of RAM. Our AMPL code, input data for each experiment, and Python code to generate the input data, run the optimizations, and process and plot the results are available online [34].

6.1. Experiment Set 1: Periodic Traffic

In the first set of experiments, we included only periodic traffic, with all background traffic demand rates, both uplink and downlink, set to 0. This reflects cases where there is only control traffic and no other data to be transmitted by the nodes, which is typical for industrial communications if we assume that we have a separate network slice for real-time traffic. For this set of experiments, we tested the effect of the number of nodes (i.e., problem instance size) and how demanding the nodes’ traffic profiles are.

We defined two traffic profiles, one with short periods and one with long periods. We considered industrial processes with a control loop time of between 1 ms and 20 ms, as, for example, in demanding factory automation processes. We therefore set the time slot to 1 ms. Depending on the environment and channel characteristics, the coherence interval may be longer than this, even significantly so; however, for simplicity, we consider the coherence interval and scheduling time slot to be equivalent, i.e., a node must be allocated a pilot in a given slot if it is to transmit or receive in that slot. We exclude processes with a period of 1 ms from the scheduling problem since, if the period is equal to the time slot duration, the node would require a pilot in every time slot, which can be satisfied without any waste of resources with a simple static assignment. We therefore take short periods to be between 2 and 10 ms, and long periods to be between 11 and 20 ms.

For each number of nodes, we conducted three experiments: one in which all nodes had short periods (1A), one in which all nodes had long periods (1B), and one in which the traffic was mixed, with half the nodes having long periods and half having short periods (1C). In each case, for each node, we generated its period uniformly randomly within the range for its traffic profile. In total, we generated 10 problem instances for each case and took the average and 95% confidence interval across the instances.

6.2. Experiment Set 2: Rate Demand Traffic

In the second set of experiments, we add rate demand traffic (i.e., background traffic) as well as the periodic traffic. This reflects use cases where there is additional data to send on top of the control traffic. An example of such a case could be a robot navigating through a factory and performing tasks. Here, periodic data are needed to control the robot, while there may also be streaming data from cameras or other sensors to aid in navigation. This latter type of data is still a high priority as it may be safety-critical, and so, it should be scheduled in the same network slice; however, it is not subject to the same real-time deadlines as for control traffic, and in the case of video, may even be able to suffer some limited packet loss without loss of overall performance, depending on the encoding used. As such, we aim to provide a guaranteed bit rate (specified by the node’s demand rates $\widehat{h}\left(k\right)$ and $\check{h}\left(k\right)$) for this traffic, but do not need to ensure regular transmissions within a given period as for control traffic.

As for the periodic traffic experiments, we define two traffic profiles, with high and low rate demands. In order to investigate the effect of the type of traffic on the performance of the optimization problem, we set the traffic rate demands to be of equal magnitude to the periodic demands. The high traffic demands are set to between $0.1$ and $0.5$ transmissions per slot, thus matching the short periodic demands by simply taking the reciprocal since the traffic rates represent a frequency rather than a period. The low traffic demands are similarly set to between $0.05$ and $0.1$ to match the long-period traffic. In our experiments, we did not distinguish between uplink and downlink demands, so for each node $k\in \mathcal{K}$, $\widehat{h}\left(k\right)=\check{h}\left(k\right)$, and in the following we will refer to the rate demand as simply $h\left(k\right)$.

Once again, we conducted three experiments for each number of nodes. Experiment 2A considered traffic where the periodic demands are dominant, with all nodes having short periods and low rate demands. Conversely, Experiment 2B considered the case where the rate demands are dominant, with long periods and high rate demands. Experiment 2C takes a mixed case, with half the nodes having short periods and low rates, and the other half having long periods and high rates. As for Experiment Set 1, node rates and periods were generated uniformly and randomly within the ranges for their assigned traffic profiles, and we generated 10 problem instances for each experiment and number of nodes, once again taking the average and 95% confidence interval across the instances.

6.3. Formulations

To formulate our optimization problems, we will use mixed-integer programming [35,36]. We ran each of the experiments described above using each of the two formulations: FPRM/1 and FPRM/2. We will first give the results using the general formulation (FPRM/2), as this gives a ground truth for the optimal frame length for each traffic profile and the number of nodes, up to the maximum frame length. The fixed frame length formulation (FRM/2) was then run iteratively, with the frame length starting at 1 slot and increasing to the maximum of 15 slots. This gives an alternative method to find the optimal frame length, meaning that the fixed frame length formulation can be used both in cases where the frame length is indeed static, and in cases where the frame length can vary. In our results, we compare the total solution time for these two approaches to find the optimal frame length, using the general (variable frame length) formulation directly, or iteratively applying the fixed frame length formulation.

In solving the individual optimization problems, we do not specify a solution algorithm but simply invoke the solver, CPLEX. However, CPLEX internally uses branch-and-bound, which, in the worst case, has exponential complexity, although it is lower in the average case. We can thus see the trade-off in complexity for our iterative vs. direct solution method; solving each problem will, in the worst case, take an exponentially longer time as the number of nodes increases, and using the iterative approach then wraps this in a loop (linear complexity) proportional to the number of nodes. This should, in theory, make the iterative method slower; however, as we will see, in practice, FPRM/1 solves much faster than FPRM/2. Here, then, as sometimes occurs with these types of problems, theoretical complexity does not always translate to performance in practice.

7. Results

In this section, we detail the results of the experiments described above. The results are organized by formulation, with the general formulations (FRM/2) first, followed by the fixed frame length formulation (FRM/1).

7.1. Variable Frame Length

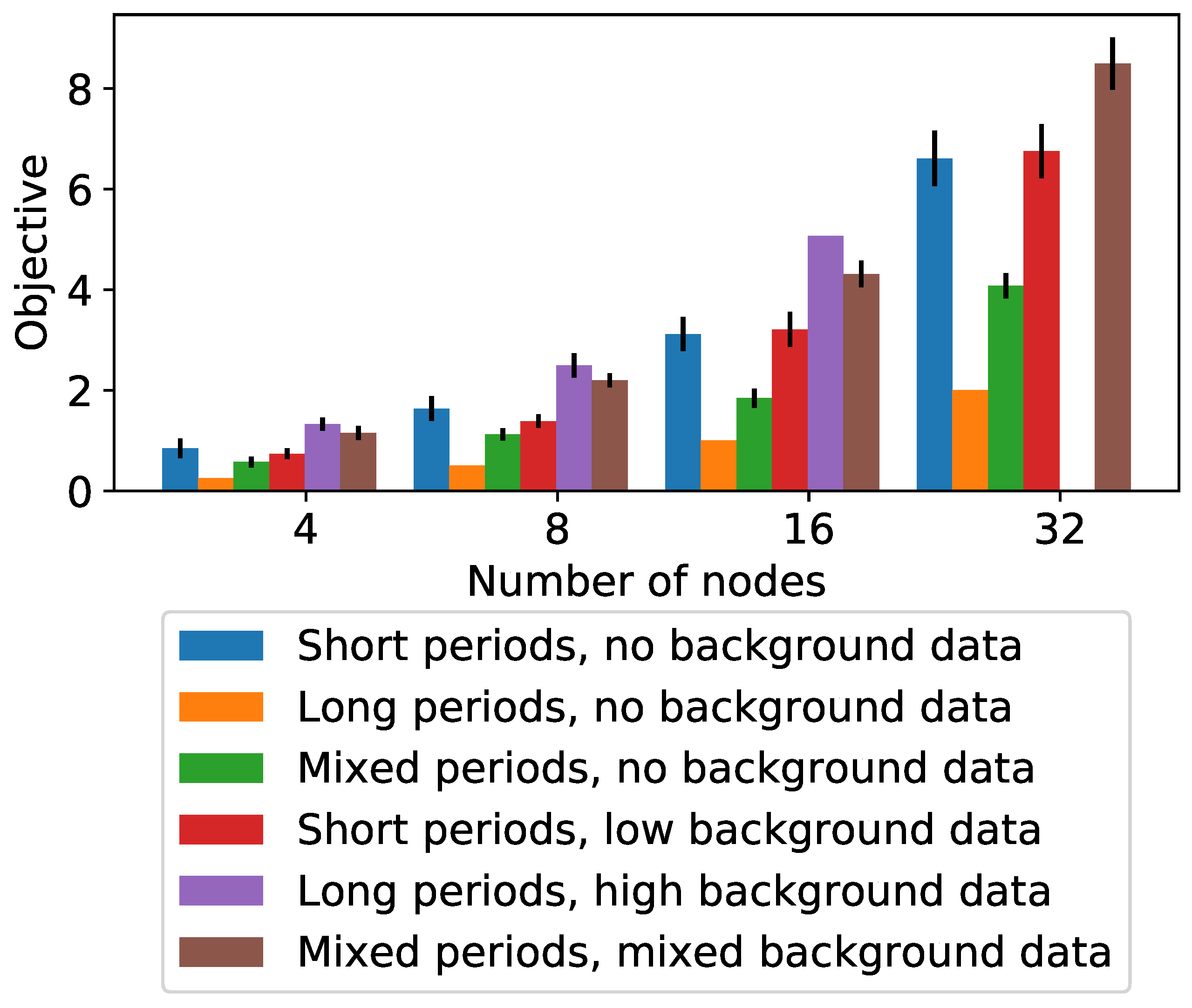
Using the general formulations, FRM/2, for each experiment, we found the optimal schedule according to the formulation objective, along with the corresponding frame length. We also measured the solution time for each case. We see that in terms of objective values, the optimal pilot rate increases with the number of nodes and traffic volume as would be expected (Figure 4). Note that background traffic scales smoothly with the number of slots in the frame, whereas for periodic traffic, there is a quantization effect in cases where the node’s period is longer than the frame. This means that the pilot rate in high background traffic cases is more than that for high periodic traffic cases.

Some larger problem instances were unable to be solved before the timeout of 30 h and are therefore omitted from Figure 4. In particular, none of the problem instances in Experiment 2B (long periods, high background traffic) were able to be solved. Even in instances where the problem could be solved, solution times for this formulation were frequently unacceptably long, often taking several hours. Clearly, FPRM/2 is a much more demanding formulation than FPUM/2 and is not suitable for practical implementation.

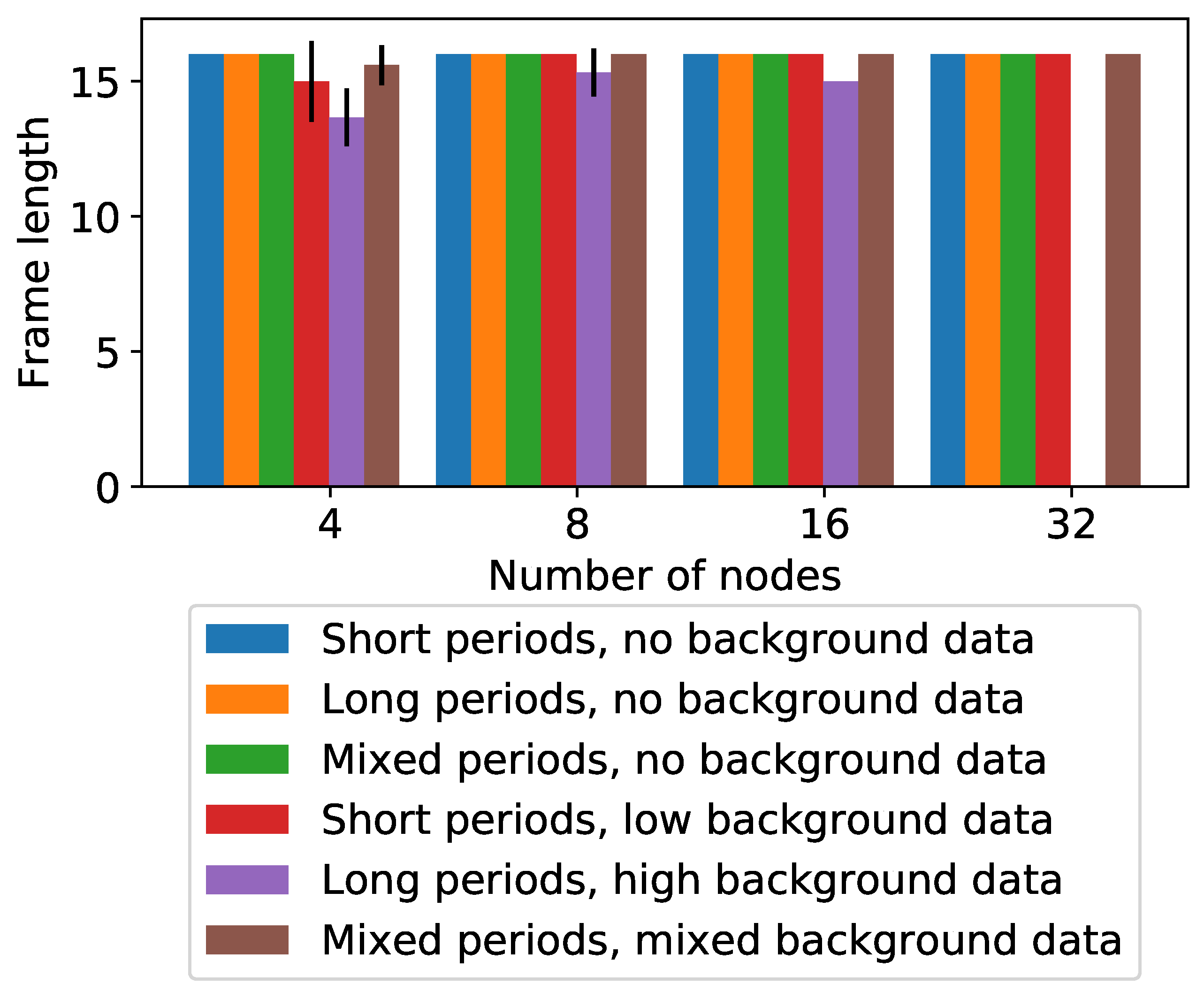
The results for frame length for FPRM/2 are shown in Figure 5. In most cases, the solver selected the maximum allowed frame length of 15 slots. This is understandable as a longer frame allows for greater flexibility in scheduling transmissions, such that they can more often be placed in series instead of parallel, thus using fewer pilots per slot.

7.2. Fixed Frame Length

We now turn to the fixed frame length formulation, FRM/1. One clear application for this formulations is cases where the frame length is fixed by external factors, so, it is more efficient to include it as a parameter rather than a variable in the optimization. However, another potential use is to provide an alternative algorithm for finding an optimal solution in cases where the general formulation takes too long to solve, as we saw in the results for FRM/2. We therefore ran the same experiments as above, but with FRM/1, for each frame length between 1 and 15 (the maximum) inclusive. We then selected the frame length and corresponding solution where the objective value was the lowest, to obtain the final, optimal solution for each experiment.

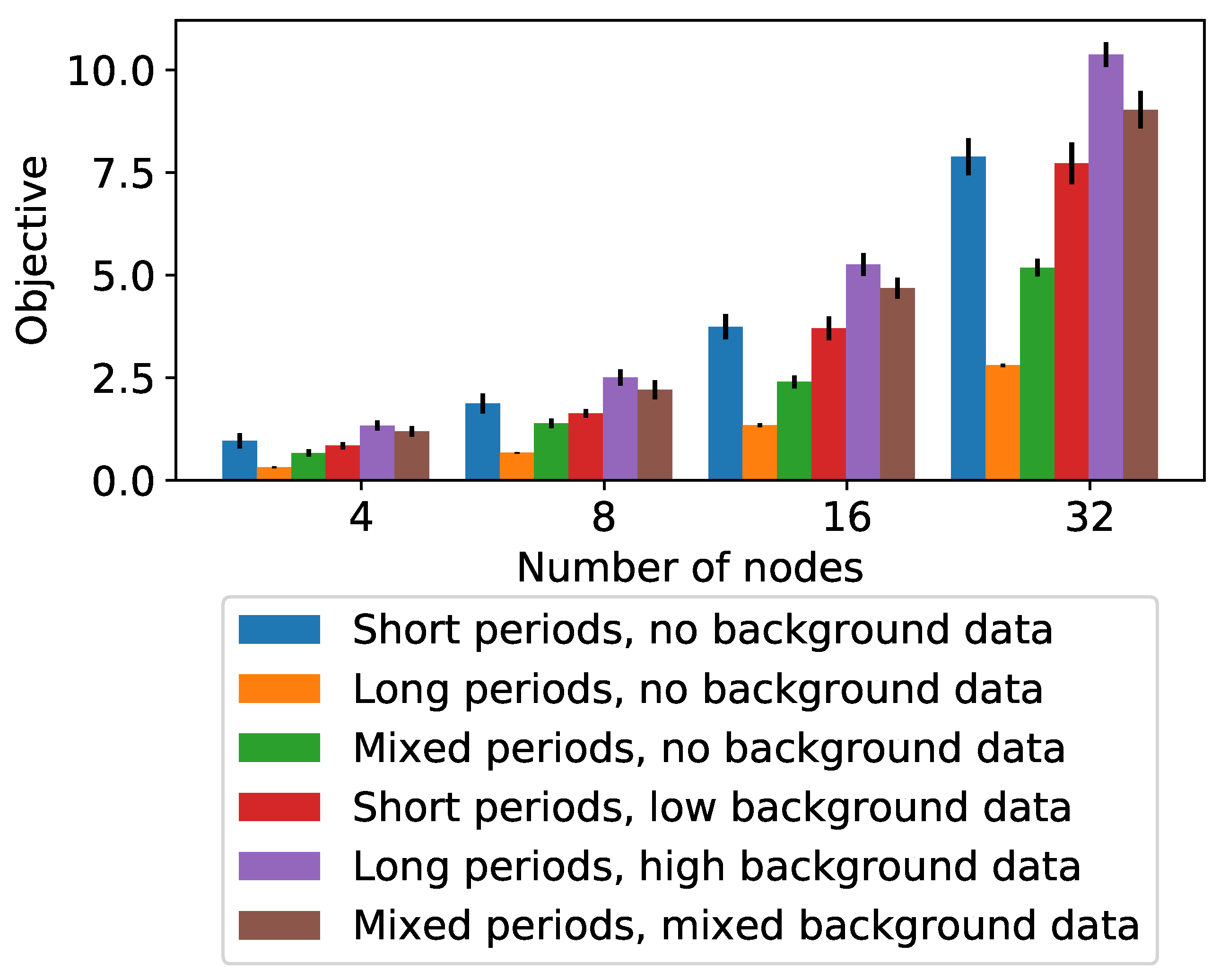
Using this iterative approach with FRM/1, we were able to obtain complete results for minimum pilot rate optimization. The objective values for each experiment are shown in Figure 6. These values were normalized to the obtained frame length.

We see a clear advantage using the iterative approach in terms of solution times (Figure 7). The total solution times here were less than 1 second in all cases for all iterations together. This indicates that the frame length variable adds considerable complexity to the optimization problem in the case of pilot rate minimization, and so a simple linear search as we have performed here is much more efficient. This method makes pilot rate minimization feasible for use in practical scenarios.

The frame lengths obtained with FRM/1 are shown in Figure 8. Once again, these are generally close to the maximum, but with more variance. This indicates that there may be multiple optimal solutions in some cases, and the iterative approach with its more complete search can find more different solutions than what is chosen by the solver when the frame length is a decision variable. It is not clear if it is better to use a shorter or longer frame length, though a shorter frame length could perhaps be advantageous if a retransmission scheme is used in the case of packet errors. The shorter frame length could then give a shorter time to receive (or fail to receive) an acknowledgment and retransmit an erroneous packet.

7.3. Discussion

A clear direction for future work following these results is to widen the range of parameters tested, in particular, the maximum frame length, but also the maximum number of pilots and the traffic profiles. Our focus in this work has been to test the feasibility of solving the different formulations and compare them, and since the solution times for FRM/2 were very long, this limited the parameters that could be included in such a comparison.

However, we now see a clear result in terms of the formulations and solution algorithms that are the best candidates for use in practical deployments. When the frame length is fixed and known in advance, FRM/1 is suitable for use and very efficient to solve. When the frame length is not known and should be solved, the iterative approach using FRM/1 works much better than directly using the general formulation FRM/2. Given this, in future work, we can focus on these feasible methods and test larger problem instances and longer frame lengths.

The frame length is, however, also limited by practical considerations. First of all, it may be desirable to fit one frame within a TTI. For 5G systems, the TTI is variable depending on the type of traffic served, but the TTI chosen may still impose a constraint on usable frame lengths. The frame length may also be limited by considerations, such as error handling and schedule changeover, as both of these functions are likely to be placed at a frame boundary. The higher the granularity desired, the shorter the frame needed.

Similarly, the maximum number of pilots to be used in any slot is likely to be affected by external considerations and cannot be freely set so as to benefit the optimization problems we have presented here. In practice, in 5G massive MIMO systems, the total number of pilots available for all traffic is determined by such factors as the total channel bandwidth and subcarrier spacing, the channel coherence time and frequency, and the pilot signal scheme used. This then must be divided amongst the different network slices—even though the industrial control slice has high priority, some minimum allocation may be needed for other slices, reducing the maximum number of pilots available.

It is thus not straightforward to set these parameters in a general way in a study such as this one. However, in a practical deployment, the factors and constraints discussed above would be known and can thus be used to configure the optimization problems appropriately. Then, our formulations provide a means to schedule both deadline-based, periodic traffic, and rate-based background traffic together in an efficient way that guarantees quality of service requirements for demanding industrial control traffic are met, while also maximizing the radio resources available to be used opportunistically by other slices in a dynamic RAN slicing context.

8. Conclusions

Our work in this paper allows the scheduling of industrial control traffic to be combined with other traffic types through network slicing in either centralized or distributed massive MIMO (also known as LIS) systems. This is highly desirable in an industrial setting, where industrial control traffic must co-exist with other traffic such as from (industrial) Internet of Things sensors, lower-priority data collection for diagnostics and analytics, and staff data traffic. Our optimization formulations are suitable for dynamic RAN slicing, in which other slices can borrow resources from the industrial control traffic when not in use.

We have presented new optimization methods, based on mixed-integer programming, for scheduling industrial control traffic in a dynamic RAN slicing context. We have then evaluated our optimization methods using numerical experiments. We showed that we could schedule both periodic, deadline-based control traffic alongside background traffic, meeting the deadline constraints of the former while satisfying the required data rates for the latter, while minimizing the use of radio resources in terms of pilot signals. Moreover, we could solve our optimization problems quickly, within one second in all cases tested, for up to 32 scheduled nodes, with varying traffic profiles. This makes our methods feasible for use in real-world settings, since the solution time is much shorter than the time over which a computed schedule would be used.

In future work, this research would benefit from larger-scale studies. So far, we have tested scenarios up to 32 nodes as we explored the performance of the different optimization formulations tested. However, we have now identified which methods are the most efficient with the lowest solution times, paving the way to try scenarios with larger numbers of nodes. As well as this, there is further work to be done in refining how the parameters used as input to the optimization problems are determined, in particular, the maximum frame length and maximum number of pilots. Another direction for future work is to implement our methods in an LIS test to conduct more realistic evaluations.