Enhancing Heart Disease Prediction with Federated Learning and Blockchain Integration

Abstract

Federated learning offers a framework for developing local models across institutions while safeguarding sensitive data. This paper introduces a novel approach for heart disease prediction using the TabNet model, which combines the strengths of tree-based models and deep neural networks. Our study utilizes the Comprehensive Heart Disease and UCI Heart Disease datasets, leveraging TabNet’s architecture to enhance data handling in federated environments. Horizontal federated learning was implemented using the federated averaging algorithm to securely aggregate model updates across participants. Blockchain technology was integrated to enhance transparency and accountability, with smart contracts automating governance. The experimental results demonstrate that TabNet achieved the highest balanced metrics score of 1.594 after 50 epochs, with an accuracy of 0.822 and an epsilon value of 6.855, effectively balancing privacy and performance. The model also demonstrated strong accuracy with only 10 iterations on aggregated data, highlighting the benefits of multi-source data integration. This work presents a scalable, privacy-preserving solution for heart disease prediction, combining TabNet and blockchain to address key healthcare challenges while ensuring data integrity.

1. Introduction

Federated learning solves the conflict between data privacy and model performance, allowing institutions to collaboratively enhance their models without sharing sensitive data [1,2]. However, maintaining robust local models across institutions is a challenge due to limited data. This paper explores data expansion techniques in federated learning, focusing on strategies to fortify local models using external datasets. We employ the Comprehensive Heart Disease Dataset and UCI Heart Disease Data to illustrate these techniques. The TabNet model integrates aspects of tree-based models and DNNs [3]. Its architecture accommodates dynamic feature selection and computation, offering a promising solution for data expansion. In light of privacy concerns, we investigate the integration of differential privacy [4] to bolster privacy safeguards in federated learning. Furthermore, we explore the potential of blockchain technology and smart contracts to enhance transparency and coordination in the federated learning process. Through a synergy of these elements, this paper aims to provide insights into effective data expansion strategies in federated learning while maintaining stringent data privacy standards.

The dawn of the digital age has brought immense potential for utilizing data to transform industries, solve complex challenges, and improve decision-making. Amid this, concerns regarding data privacy and security have become paramount. Institutions possess valuable data assets, but the fear of compromising sensitive information often hinders their willingness to collaborate. Federated learning emerges as a solution, allowing institutions to harness the power of data while preserving privacy collectively. In healthcare, where data privacy and patient confidentiality are non-negotiable, the potential for federated learning is even more evident. The ability to collaboratively build predictive models for heart disease, a major global health concern, holds immense promise. However, creating such models while upholding privacy standards presents a significant challenge. This paper is a testament to the marriage of technological innovation and ethical considerations. At its core, it aims to develop a complete system for heart disease prediction while ensuring privacy is not compromised. This paper showcases the technical prowess of building predictive models and underscores the ethical imperative of safeguarding sensitive information. By combining innovation with integrity, the system presented here strives to be a cornerstone in reshaping how data are harnessed for predictive analytics while respecting privacy concerns. The key contributions of this work can be outlined as follows:

• Techniques are explored to expand the available data pool without centralizing sensitive information. By integrating external datasets into the federated learning paradigm, the robustness of local models is enhanced.
• Differential privacy techniques are incorporated to strengthen data protection. This approach ensures that predictive insights do not compromise personal information, fostering participant confidence.
• The potential of blockchain technology and smart contracts is investigated to enhance transparency and trust. Their integration fosters accountability and provides an immutable record of interactions, redefining the governance of federated learning.
• A comprehensive system is presented by integrating data expansion techniques, advanced model architectures, privacy mechanisms, and blockchain technology, demonstrating the feasibility of predictive analytics in healthcare while upholding privacy principles.

The remainder of this paper is structured as follows: Section 2 provides a literature review and a background on federated learning and blockchain technology. Section 3 details the data expansion techniques employed and describes the TabNet model architecture and implementation. Section 4 presents the results and analysis of the model’s performance. Finally, Section 5 concludes the paper by discussing the findings and future research directions.

2. Background

2.1. Literature Review

Recent advancements in federated learning have demonstrated significant potential in heart disease prediction by leveraging distributed data while preserving data privacy [5,6]. Tripathy et al. [7] introduce a federated learning approach that integrates IoT capabilities with Electronic Health Records (EHRs) to predict heart diseases. Employing a soft-margin L1-regularized Support Vector Machine classifier and a cluster primal-dual splitting algorithm enables the methodology to handle high-dimensional data effectively, ensuring enhanced prediction accuracy and data privacy.

Asynchronous updates in federated learning models improve the efficiency and accuracy of predictive models for cardiovascular diseases. The authors of [8] proposed an asynchronous federated learning model using DNNs, incorporating an asynchronous learning technique to update parameters and a temporally weighted aggregation technique. This method significantly reduces communication costs and improves the convergence rates of the models, demonstrating its effectiveness over traditional synchronous federated learning approaches.

Sheller et al.’s [9] research emphasizes federated learning’s potential to facilitate multi-institutional medical research without compromising patient data privacy, and its design allows for the collaborative training of algorithms without direct data exchange, aligning with strict data privacy regulations like GDPR and HIPAA. Enhancements in federated learning efficiency and accuracy promote its adoption across various medical fields, enabling global research collaborations utilizing large, diverse datasets.

The study by Liang et al. [10] examines the application of federated learning to manage heart disease data across Internet of Medical Things (IoMT) devices, focusing on privacy without compromising data utility. The paper details how federated learning allows for local data processing, enhancing data security in distributed healthcare environments. This approach addresses key data privacy and utility challenges within the rapidly evolving smart healthcare landscape.

In [11], the authors introduce split learning as a privacy-preserving technique for healthcare applications, particularly in heart disease prediction. The paper demonstrates how deep learning models can be trained on segmented data, ensuring that sensitive patient information remains localized and secure. This method facilitates collaborative research while maintaining strict data privacy, marking a significant contribution to secure medical data processing.

2.2. Federated Learning

Federated learning is essentially a distributed machine learning technique or machine learning framework. The goal of federated learning is to improve the effectiveness of AI models by enabling common modelling while ensuring data privacy, security, and legal compliance. First proposed by Google in 2016 [12], federated learning was initially used to solve the problem of updating models locally for Android phone end-users; it is particularly suited to scenarios in which data cannot be centrally managed due to privacy concerns, regulatory constraints, or technological limitations. Federated learning leverages the power of distributed computing to collaboratively train models without the need to share devices or nodes between raw data [13,14,15].

2.2.1. Horizontal Federated Learning

Horizontal federated learning refers to a scenario where participants belong to the same business sector or domain but serve different user groups. This approach is suitable when there is a high overlap in the features collected by different participants but little overlap in the users they serve. For instance, hospitals located in different regions may offer similar services (and thus collect similar features) but cater to different patients (resulting in different samples) [16].

The horizontal federated learning process follows these key steps:

Step 1: Each participant computes the model gradients locally using their data. These gradients are masked using encryption techniques such as homomorphic encryption, differential privacy, or secret sharing. The masked gradients (encrypted data) are then sent to the aggregation server.

Step 2: The server performs secure aggregation, often using a weighted average based on homomorphic encryption.

Step 3: The aggregated results are returned to each participant.

Step 4: Each participant decrypts the aggregated gradients and updates their local model parameters accordingly.

Incorporating differential privacy into the federated learning framework ensures that participants’ data remains secure throughout this process. Differential privacy is achieved by adding controlled noise to the gradients shared between participants and the central server. This noise prevents the leakage of sensitive information from any individual participant’s dataset, even if adversaries have significant auxiliary knowledge.

The parameter $ϵ$, known as the privacy budget, governs the trade-off between privacy and accuracy. Smaller $ϵ$ values provide stronger privacy guarantees by introducing more noise, which can slightly reduce model accuracy. Conversely, larger $ϵ$ values reduce the noise, leading to better accuracy but weaker privacy protections. We implemented differential privacy within the federated averaging (FedAvg) algorithm. Each participant adds noise to their local model updates before sending them to the central server for aggregation. Although differential privacy introduces some computational trade-offs, the model’s overall performance remains robust, with privacy protections upheld throughout training.

In traditional machine learning, data are typically centralized in a data center for model training and prediction. However, horizontal federated learning distributes the data and computations across different machines. As shown in Figure 1, each participant downloads the model from the central server, trains it locally with their data, and sends the updated model parameters back to the server. The server then aggregates these updates and distributes the refined model to all participants. This decentralized approach ensures that raw data are never shared, maintaining privacy while allowing for collaborative model training. Moreover, each machine operates independently in this setup, making predictions based on its locally updated model [17].

However, federated learning can be implemented through various approaches, such as FedAvg, aggregating updates using a weighted average [1], and FedProx, which addresses non-IID data challenges. Additionally, asynchronous federated learning allows for model updates without waiting for all participants, improving communication efficiency. Advanced techniques like personalized federated learning further adapt models to participants’ unique data characteristics, enhancing overall performance.

2.2.2. Federated Averaging Algorithm

The computation of the federated averaging algorithm is controlled by three key parameters: parameter $\rho$, which refers to the fraction of clients that perform computations in each round; parameter S, which refers to the number of training steps performed by each client on the local dataset in each round; and parameter M, which refers to the size of the mini-batch used for client updates. We use $M=\infty$ to denote that the complete local dataset is processed as a batch. In this algorithm, $\rho$ controls the global batch size. When $\rho =1$, it indicates gradient descent (non-random selection of training data) using the full training data (also known as full-batch gradient descent) on all data owned by all participants. We still select the batch by using all the data on the selected participants. This baseline algorithm is known as FederatedSGD, where gradients are computed and sent to the server, assuming that the datasets owned by different participants are independently and identically distributed (IID-compliant) and that the batch selection mechanism differs from random selection. In federated learning with k participants, the goal is to have collaborative optimization of the empirical loss function:

$$L\left(w\right)={\displaystyle \frac{1}{\left|D\right|}}\sum _{k=1}^K\left|D_k\right|·L_k\left(w\right)$$

(1)

where $|D_k|$ is a dataset for participant k, D is the union of all datasets for K participants, and $L_k\left(w\right)$ is the local loss function computed over $|D_k|$ for participant k.

In the federated learning setup, the initial global model weights $w_0$ are distributed to all clients at the beginning of training. These initial weights are randomly initialized or derived from a pre-trained model, ensuring all participants begin with the same parameters before local updates. Once the initial weights are distributed, the central coordinator (or server) manages the training process. Participants update their local models during each round using distributed gradient descent with a fixed learning rate $\eta$. Each participant k computes $g_k=\nabla L_k\left(w_t\right)$, the average gradient of its local data at the current model parameter $w_t$. The coordinator aggregates these gradients and updates the global model parameters as follows:

$$w_{t+1}\leftarrow w_t-\eta \sum _{k=1}^K{\displaystyle \frac{|D_k|}{\left|D\right|}}{g}_k$$

(2)

In Equation (2), $g_k=\nabla L_k\left(w_t\right)$ represents the direction of the steepest increase in the loss function. By subtracting the gradient, the model parameters $w_t$ move in the direction that reduces the loss, which is the core principle of gradient descent. The term $\eta$ is the learning rate, which determines the size of the step taken toward the negative gradient. This update rule ensures that the weights are adjusted to minimize the loss function, improving the model’s performance over time. The coordinator can send the updated model parameters $w_{t+1}$ to the participants or send the average gradient to compute the updated model locally. This method, known as gradient averaging, works similarly to model averaging. We use an equivalent federated model training method [18]:

$$\forall k,w_{t+1}^{\left(k\right)}\leftarrow {\overline{w}}_t-\eta g_k$$

(3)

$${\overline{w}}_{t+1}\leftarrow \sum _{k=1}^K{\displaystyle \frac{n_k}{n}}{w}_{t+1}^{\left(k\right)}$$

(4)

where $n_k$ is the number of data points in $D_k$, and n is the number of data points in D. Each client performs one or more steps of gradient descent locally and sends the updated parameters back to the server, which computes a weighted average and sends the aggregated model parameters to all participants.

2.3. Blockchain

Blockchain is a decentralized, distributed digital ledger technology that securely and transparently records transactions. It consists of blocks containing a set of transactions cryptographically linked to the previous block. One of the defining features of blockchain is its immutability, meaning that once a transaction is recorded, it cannot be altered or deleted without consensus from network participants [19]. In federated learning, blockchain enhances transparency, accountability, and data integrity by creating a tamper-proof record of model updates and interactions between nodes [20]. This ensures that all participants can verify the authenticity of updates throughout the training process, fostering trust among decentralized entities.

A key component of blockchain technology is smart contracts—self-executing agreements with contract terms directly written into code. These contracts automatically enforce predefined rules once specific conditions are met, removing the need for intermediaries. In federated learning, smart contracts streamline governance and coordination by automating processes such as local model updates, managing communication rounds, and distributing rewards or incentives to participants. This decentralization ensure that the federated learning process follows agreed protocols without relying on a centralized authority. The ERC-20 standard [21] is employed in our system, offering a structured framework for token management, including functions for total supply tracking, balance management, and seamless token transfers. The approval mechanism within ERC-20 allows token holders to delegate permissions, while real-time event tracking ensures transparency in token transfers and balance updates. In this study, we integrate blockchain technology to enhance transparency, verifiability, and integrity within the federated learning framework. A decentralized ledger system, such as Vfchain, enables the verification and auditability of model updates without compromising data privacy. By storing cryptographic hashes of model updates and using a consensus mechanism enforced by smart contracts, blockchain ensures that tampering is prevented and only valid updates are recorded. This immutable ledger creates a comprehensive audit trail of all transactions, which is crucial for maintaining trust and accountability, particularly in sensitive fields like healthcare.

However, integrating blockchain technology into our federated learning framework introduces some computational overhead. This is primarily due to the cryptographic operations required for transaction verification, smart contract execution, and ensuring the immutability of model updates. The overhead largely stems from the consensus mechanism, which involves validating and storing model updates on the blockchain. This can impact the time required for model aggregation in federated learning, particularly as the number of participants or the frequency of model updates increases. Although this computational burden may introduce delays, especially in real-time applications, it is a manageable trade-off in environments where security, transparency, and trustworthiness are the primary concerns.

3. Model Construction and Training Setup

This section outlines the construction of the model architecture, the choice of hyperparameters, the training procedure, and the evaluation metrics used in our federated learning setup. The model’s construction involves selecting appropriate hyperparameters and configuring them to work within the federated learning setup. The key parameters introduced in this paper are further elaborated below to allow for accurate reconstruction and verification.

• Learning Rate ($\eta$): The learning rate used in our model is set to 1 × 10⁻³. This parameter controls how much the model needs to change in response to the error each time the weights are updated. It is crucial to balance convergence speed and stability, with values typically ranging between 1 × 10⁻⁴ and 1 × 10⁻¹ depending on the data.
• Batch Size (M): The mini-batch size is set to 512, denoted as M. This setup allows each client to process the dataset in smaller batches for local training before sending updates to the server.
• Client Selection Fraction ($\rho$): The fraction of clients participating in each communication round is set to 1. This parameter, $\rho$, controls the portion of clients that perform computation in each round, and a value of 1 represents full participation in the federated learning process.
• Training Steps (S): Each client performs S training steps locally, where $S=100$. This step controls how much computation each client performs before sending updates to the central server.

We utilize the TabNet architecture because it handles tabular data effectively while leveraging attention-based mechanisms for feature selection.

Table 1. Model architecture and training parameters.

Component	Details
Model Architecture	TabNet
Hyperparameters	Learning Rate: 1 × 10−3, Batch Size: 512, Client Selection Fraction: $\rho =1$, Training Steps: $S=100$
Loss Function	Binary Cross Entropy
Optimizer	Adam
Training Procedure	Random shuffling, Early stopping, Model checkpointing
Evaluation Metrics	Accuracy, Training Loss

overviews the key parameters used during training. The TabNet architecture was selected for its ability to balance interpretability and performance when dealing with tabular data. Its attention-based feature selection mechanism is particularly useful in distributed environments like federated learning, where transparency and efficiency are key. The TabNet model outputs a probability score between 0 and 1, representing the likelihood of heart disease. Scores ≥0.5 indicate a higher risk (positive), while those <0.5 indicate lower risk (negative). This probabilistic output offers more nuanced predictions compared to binary classification.

Hyperparameters: These settings control the learning process. In this case, we set the learning rate to 1 × 10⁻³, which balances efficient convergence with stability. A batch size of 512 ensures that a sufficiently large subset of data is used during each training iteration, enhancing the model’s ability to generalize while keeping memory requirements reasonable.

Loss Function: We used the Binary Cross Entropy (BCE) loss function, which is well suited for binary classification tasks, such as predicting whether a patient is at risk of heart disease. BCE calculates the difference between the predicted probabilities and the actual binary class labels (0 or 1), penalizing incorrect predictions more heavily the further they are from the true label. The formula for BCE is as follows:

$$\mathrm{BCE}=-{\displaystyle \frac{1}{N}}\sum _{i=1}^N\left[y_{i}log\left(p_i\right)+(1-y_i)log(1-p_i)\right]$$

(5)

where $y_i$ is the true label, $p_i$ is the predicted probability for each sample i, and N is the total number of samples.

Optimizer: The Adam optimizer was selected for its ability to adapt the learning rate during training, making it well-suited for large and noisy datasets. Adam combines the advantages of RMSprop and momentum-based methods, leading to faster convergence without requiring extensive hyperparameter tuning.

Training Procedure: Several strategies were employed to ensure robust training. Random shuffling of the training data helps prevent the model from learning patterns specific to the order of the data, enhancing generalization. Early stopping monitors the validation loss and halts training when no improvement is observed, preventing overfitting. Additionally, model checkpointing is employed to save the best-performing model during training, ensuring that the final model retains the best performance.

Accuracy: Accuracy measures the ratio of correctly predicted instances to the total number of predictions. It evaluates how well the model’s predictions match the actual outcomes. For heart disease prediction task, accuracy is defined as

$$\mathrm{Accuracy}={\displaystyle \frac{\mathrm{Number}\mathrm{of}\mathrm{Correct}\mathrm{Predictions}}{\mathrm{Total}\mathrm{Number}\mathrm{of}\mathrm{Predictions}}}$$

(6)

This metric is particularly useful in binary classification tasks like heart disease prediction, where we assess the model’s ability to distinguish between positive (patients with heart disease) and negative (patients without heart disease) cases.

Training Loss: Training loss is calculated using the Binary Cross Entropy (BCE) loss function, which penalizes incorrect predictions. The BCE loss function is commonly used for binary classification problems. The formula for BCE loss is

$$\mathrm{BCE}\mathrm{Loss}=-{\displaystyle \frac{1}{N}}\sum _{i=1}^N\left[y_{i}log\left(p_i\right)+(1-y_i)log(1-p_i)\right]$$

(7)

where $y_i$ is the true label (0 or 1), $p_i$ is the predicted probability, and N is the total number of samples. This loss function helps guide the optimization process during training, with the goal of minimizing the error between predicted and true values.

3.1. Data Expansion

Multiple institutions participate in federated learning, each maintaining its dataset to protect privacy and prevent the disclosure of confidential information. Additionally, the local models at these institutions must undergo frequent fine-tuning to maintain high performance and remain relevant to evolving data features. This process necessitates the availability of diverse datasets to support continuous adaptation and improvement.

The first dataset is the Comprehensive Heart Disease Dataset [22], which combines five popular heart disease datasets and contains 1190 instances with 11 features. The second dataset is UCI Heart Disease Data [23], a collection of various numerical variables used for multivariate numerical data analysis. It consists of 14 attributes: age, sex, chest pain type, resting blood pressure, serum cholesterol, fasting blood sugar, resting electrocardiographic results, maximum heart rate achieved, exercise-induced angina, oldpeak (ST depression induced by exercise relative to rest), the slope of the peak exercise ST segment, number of major vessels, and Thalassemia. These attributes provide information about different aspects related to cardiovascular health and can be used to analyze and understand patterns and relationships within the data. We use padding for the data because the second dataset contains two features not present in the first dataset: the number of major vessels and Thalassemia. As is the case with most methods used in deep learning, we set these two features to 0.

3.2. TabNet Model Architecture

For tasks using tabular data, tree-based models have better performance than other models, and Boosting tree-based models like XGBoost [24] and LightGBM [25] have become the standard in data mining competitions nowadays. In this project, we need to keep updating the local models by online learning. However, the tree-based model can only be retrained with the whole dataset because the decision tree structure will be destroyed and rebuilt in the training process. Consequently, we chose TabNet, a DNN model with a fixed model structure that also features tree-based models. It has the advantages of interpretability and sparse feature selection of tree-based models while retaining the end-to-end and representation learning features of DNNs.

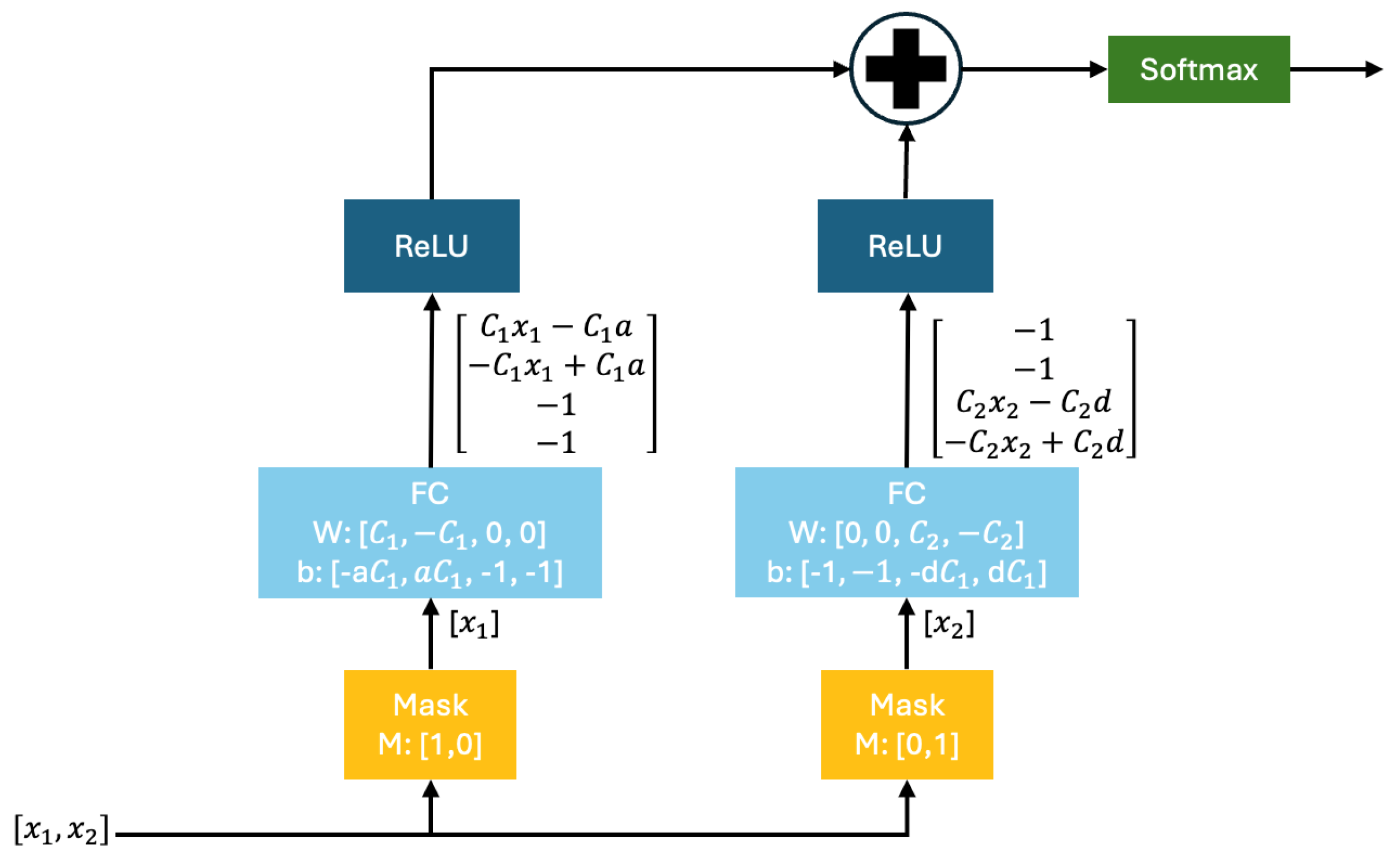
(1) Building a decision tree using a DNN. Figure 2 illustrates a DNN structured similarly to a decision tree. This architecture processes inputs through masked, fully connected (FC) layers that isolate specific features. Non-linearity and classification are achieved through ReLU and softmax layers, respectively. The diagram also details how weight (W) and bias (b) influence decision paths, where both W and b are represented as four-dimensional vectors, corresponding to different layers of the network. Initially, input features $x_1$ and $x_2$ are filtered by mask layers, then passed through fully connected layers with explicitly set weights and biases. Variables like C and D represent feature transformation and decision layers, while a refers to the attention mechanism applied during feature selection.

Weights and biases are key to transforming and combining input features to make predictions. Weights, learned during training, adjust the strength of connections between neurons, while biases shift activation functions for better data fitting. In TabNet, the attention mechanism uses weights to emphasize essential features and suppress irrelevant ones, while biases further refine layer outputs, ensuring the model captures complex relationships. These parameters enable the TabNet model to process tabular data and make accurate predictions efficiently.

The ReLU activation function sums up the outputs of the two FC layers and passes through a softmax activation function as the final output.

Let us compare it with the decision tree process. We can find that each layer of this neural network corresponds to the corresponding step of the decision tree: The mask layer corresponds to feature selection in the decision tree, which is well understood; FC layer+ReLU corresponds to the threshold judgment. Take $x_1$ as an example:

After passing through the FC layer, followed by ReLU activation, the model ensures that only one element of the output vector remains positive (i.e., greater than zero). In contrast, the other elements are set to zero. This process mirrors the conditional decisions made in a decision tree, where a single decision path is chosen based on feature thresholds.

This corresponds to the conditional judgment of the decision tree; finally, the results of all the conditional judgments are added up, and the final output is obtained through a softmax layer.

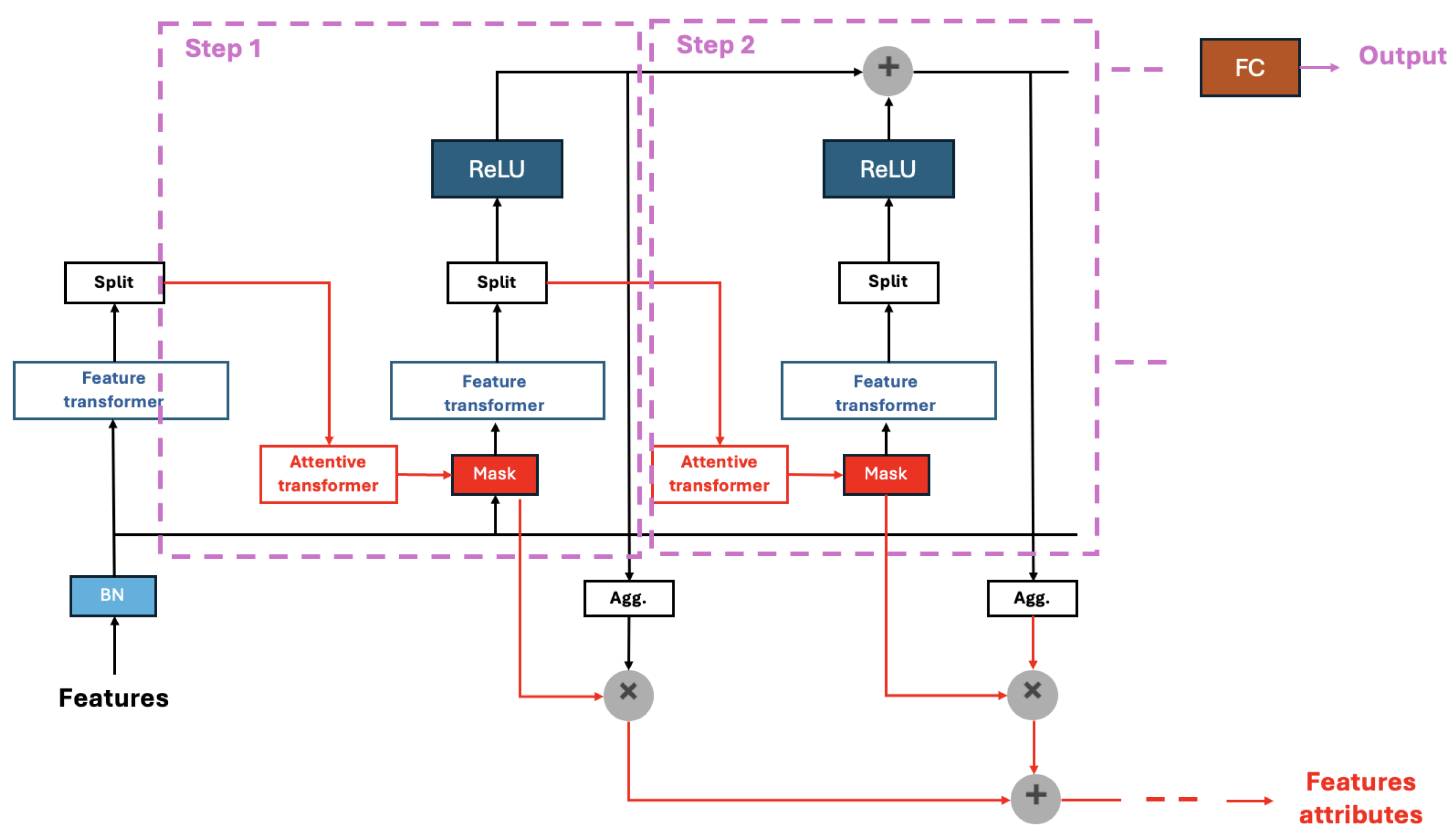
(2) The model structure of TabNet is illustrated in Figure 3. This figure outlines the architecture of TabNet for tabular data processing, showcasing the sequence of operations, including batch normalization, feature transformation, attentive transformation, masking, and aggregation, which culminate in the output through ReLU activation and a fully connected layer. This model shares a framework similar to traditional neural networks, functioning as an additive model with multiple processing steps. The input to the model consists of features with dimensions $B\times D$, where B represents the batch size and D denotes the dimension of the features. The output of the model is a vector representing the classification result.

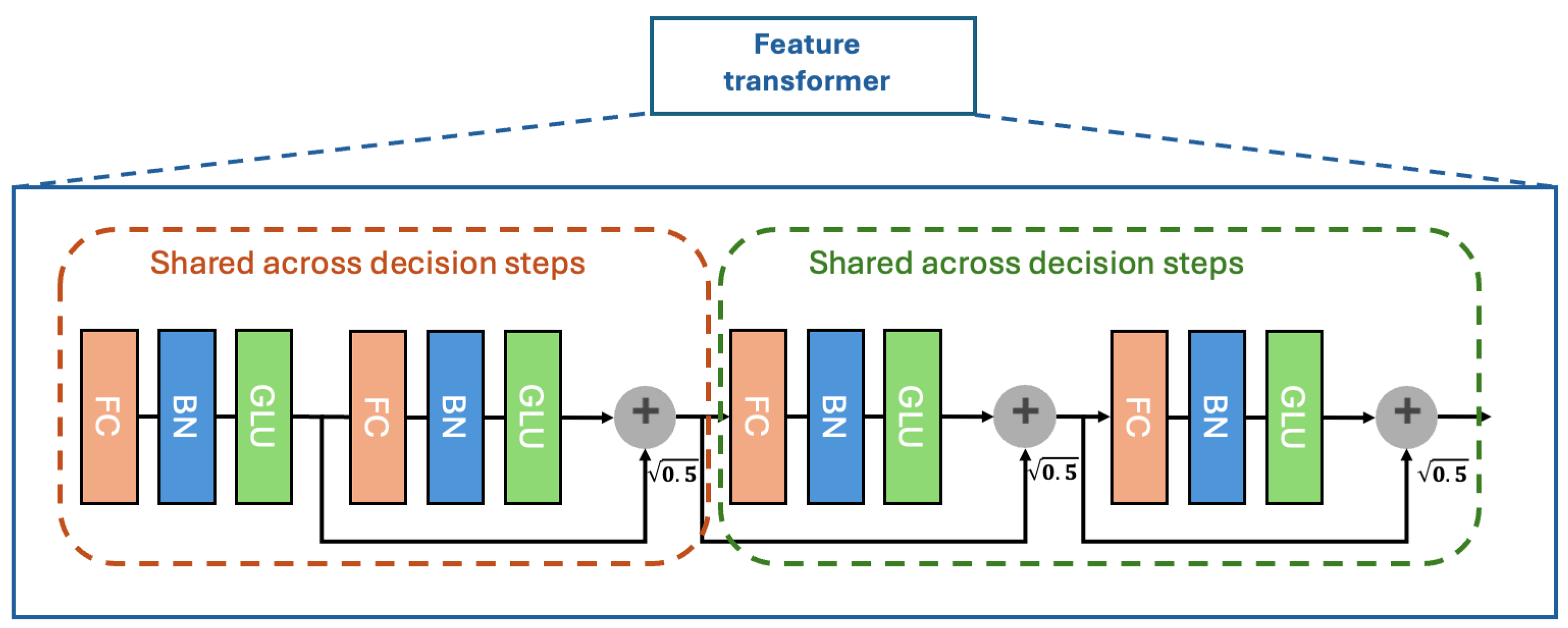
BN denotes the batch normalization layer. The Feature transformer layer is similar to the role of the previous FC layer, which related to feature calculation and is more complex. The structure is shown in Figure 4. The Feature transformer layer consists of two parts. The parameters of the first half of the layer are shared; that is, they are trained together on all steps, while the second half is not shared and is trained separately on each step. This is carried out considering that for each step, the input is the same features (the mask layer only masks some features and does not change others), so we can use the same layers for the common part of feature computation first and then see to different parts using different layers later. In addition, we can see that the residual connection is used in the layer, multiplied by $\sqrt{0.5}$ to ensure the network’s stability.

The split layer cuts the vector output from the Feature transformer layer into two parts, one of which is used to compute the final output of the model, while the other is used to compute the mask layer for the next step. The attentive transformer layer computes the mask layer of the current step based on the result of the previous step, as Figure 5 shows. The sparsemax layer can be understood as a sparse version of the softmax layer. The feature attribute output portrays the global importance of the feature. The model first sums the output vectors of a step of the model to obtain a scalar, reflecting this step’s importance for the final result. Then, it is multiplied by the mask matrix of this step to reflect the importance of each feature, and the global importance of the feature is obtained by adding up the results of all steps.

The federated averaging algorithm (FedAvg) enables decentralized training of the TabNet model across participants while preserving data privacy. Each participant trains a local TabNet model, computes updates, and sends them to a central server. The server aggregates these updates using a weighted average based on the dataset size, creating a global TabNet model, which is then shared back with participants. This cycle repeats until model convergence, combining TabNet’s strengths with privacy-preserving federated learning.

4. Results and Analysis

This section presents the findings from implementing the TabNet model on the Comprehensive Heart Disease Dataset and the UCI Heart Disease Data. We evaluate the model’s performance using various metrics and analyze the training and testing outcomes. Additionally, we compare the effectiveness of different training epochs to identify the setup that provides high accuracy and robustness in heart disease prediction.

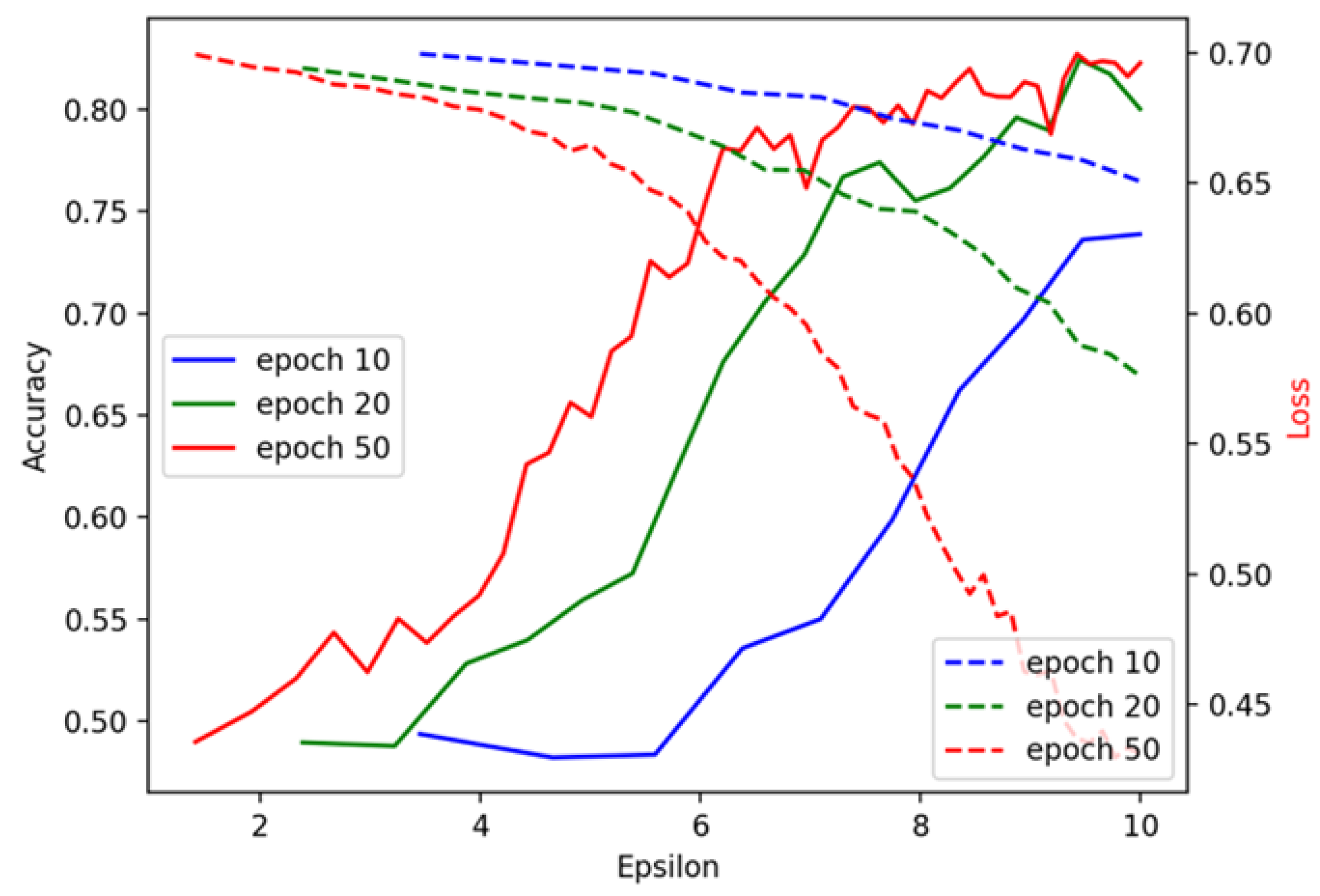
Figure 6 and Figure 7 present the training results on the UCI and Cleveland datasets under the specified setup. Both figures suggest that 10 epochs are insufficient for the model to converge, as the accuracy and loss metrics improve significantly with additional iterations. Performance stabilizes between 20 and 50 epochs, with 20 epochs being sufficient for both datasets to achieve strong results. Since the UCI dataset is smaller than the Cleveland dataset, the latter achieves a higher training accuracy (0.825) than the former (0.534). In both cases, model accuracy rapidly increases during the first 10 epochs, stabilizing at around 20 epochs, indicating that further training yields diminishing returns. The consistent decrease in training loss across both datasets shows effective learning and model convergence. Additionally, the Cleveland dataset’s higher accuracy is likely due to its larger size and greater feature diversity, contributing to better model generalization. These findings demonstrate that the TabNet model performs well on the Cleveland dataset, achieving high accuracy and convergence, but shows limited effectiveness on the UCI dataset. While the model exhibits robust performance on the Cleveland dataset, the results from the UCI dataset suggest challenges in achieving similarly high accuracy, possibly due to the dataset’s smaller size and lower feature diversity. As such, the model balances accuracy and computational effort more effectively on the Cleveland dataset.

To prevent overfitting, early stopping can be utilized to determine the optimal number of epochs. By monitoring the validation loss during training, we can stop the process once the model begins to overfit, thereby preventing a decline in accuracy with increased epochs. This ensures that the model maintains generalization to new data. Future work could explore additional methods, such as cross-validation, to systematically evaluate performance and further refine the optimal number of training epochs.

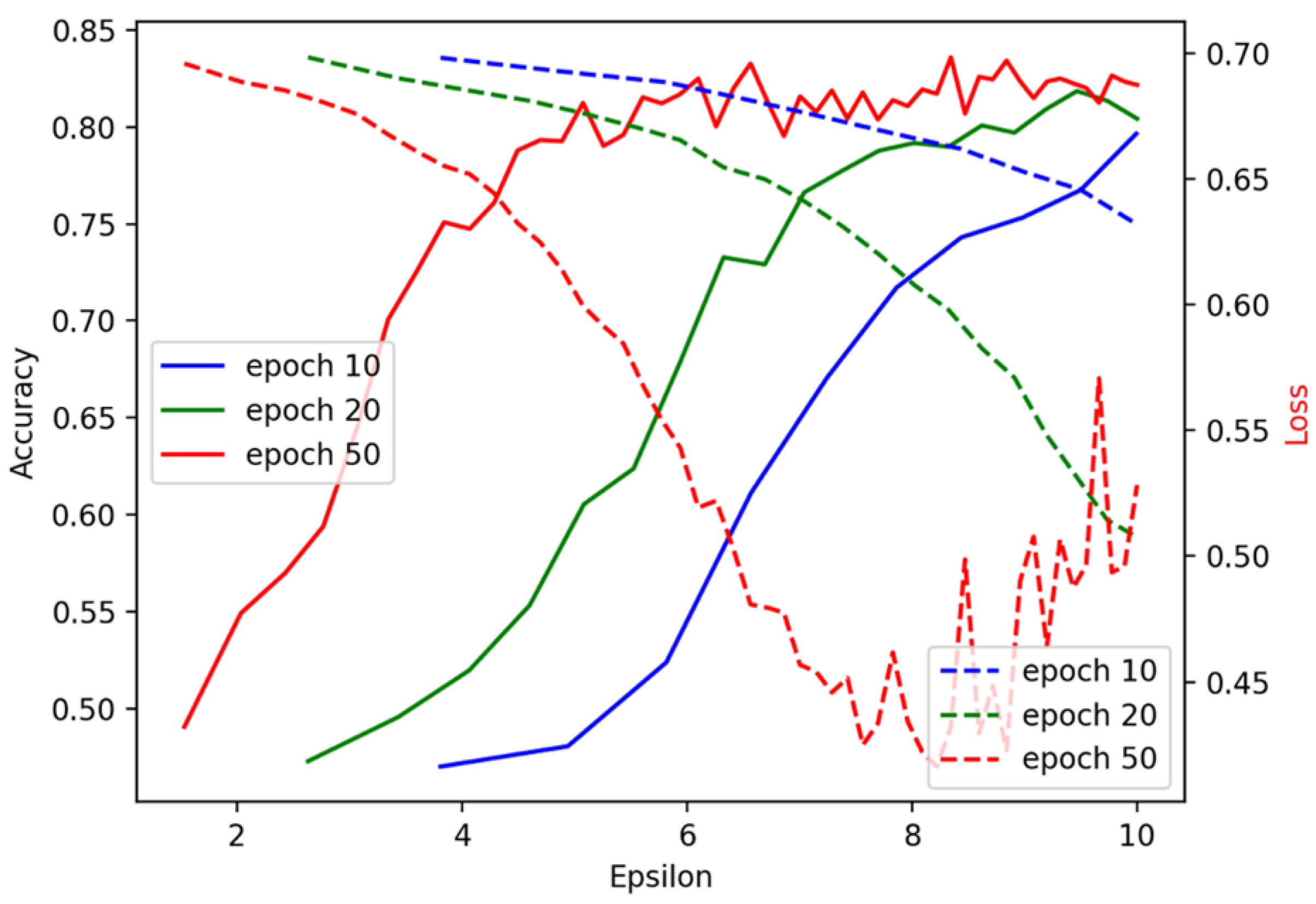
Figure 8 illustrates the trends of accuracy and loss for both the Cleveland and aggregated datasets, where the model exhibits similar performance on both. After expanding the dataset, the model achieves high accuracy in 10 iterations. As epsilon ($ϵ$) approaches 8, the training loss increases, suggesting that the model has reached a local minimum. Epsilon ($ϵ$) serves as the privacy budget in the context of differential privacy, governing the trade-off between data privacy and model accuracy. A smaller epsilon value provides more robust privacy protection but can reduce model accuracy, whereas a larger epsilon enhances accuracy at the expense of privacy. In our federated learning framework, epsilon ($ϵ$) controls the level of noise introduced into model updates during training. This noise prevents individual participants’ data from being reverse-engineered or extracted from the aggregated updates, ensuring privacy while facilitating effective collaborative learning across institutions. The figure demonstrates that, with the expanded dataset, the model reaches high accuracy after just 10 iterations. The increase in training loss, when epsilon reaches 8, indicates that the model has reached a local minimum, marking the point where further improvements in accuracy are balanced by increasing privacy trade-offs. Overall, this figure highlights the significance of using an aggregated dataset. Combining data from multiple sources improves the model’s generalization and robustness, which is essential for enhancing performance across different conditions.

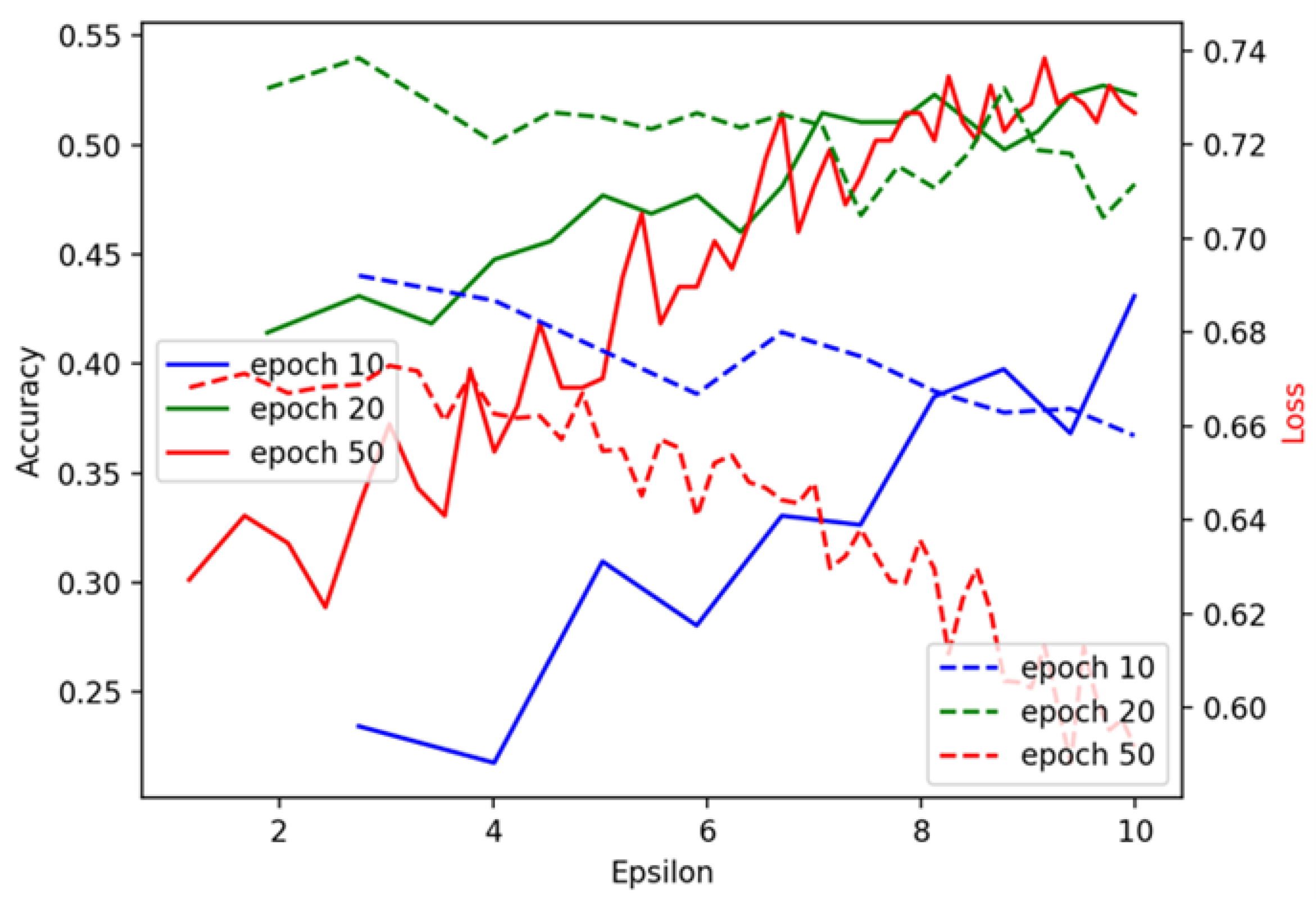
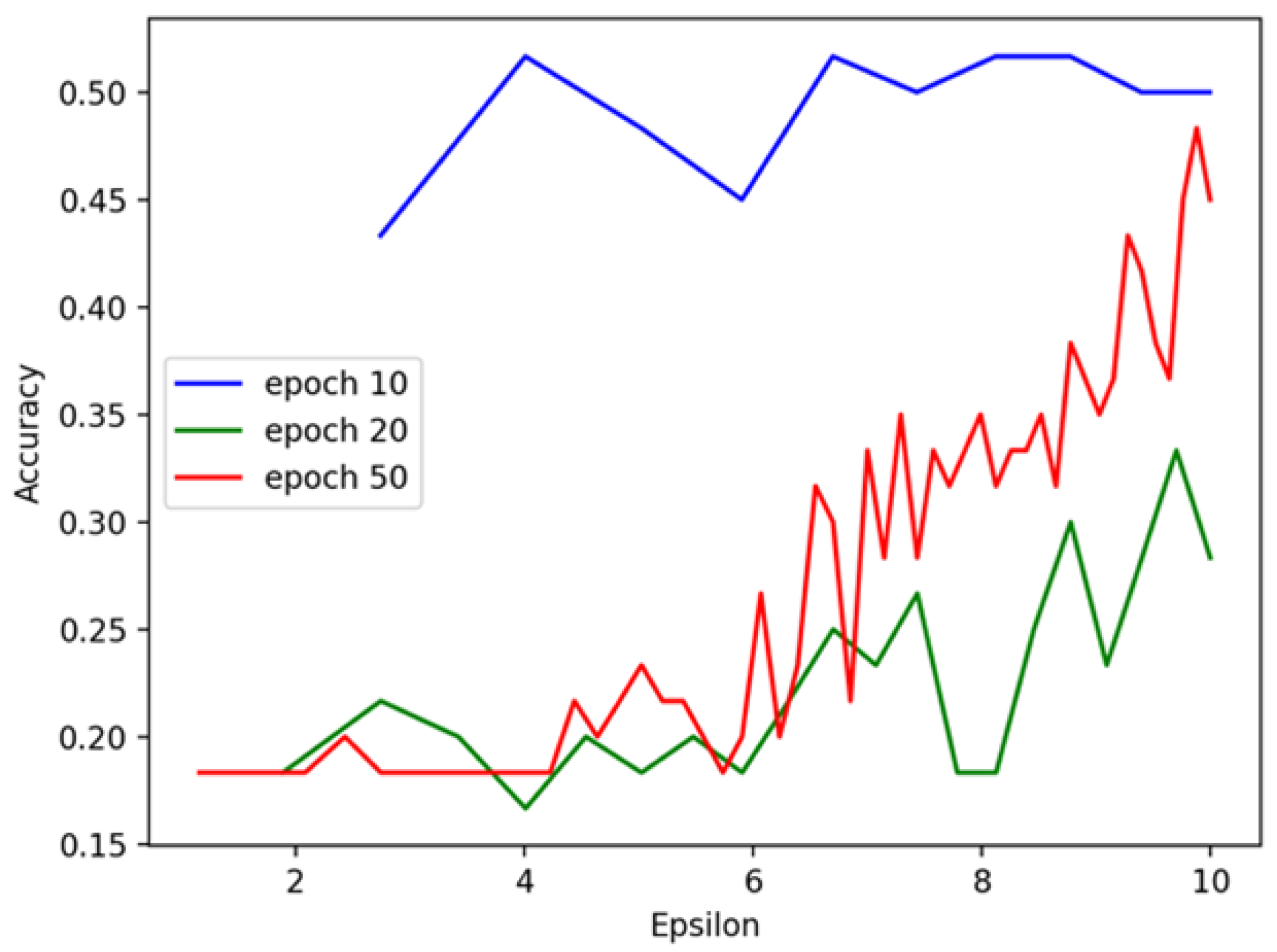
Figure 9 and Figure 10 show testing results during the training process. From Figure 10, we observe that the model trained with 50 epochs initially performs significantly better than those trained with 10 and 20 epochs. However, as epsilon ($ϵ$) increases, the accuracy of all models begins to converge, and by the time epsilon reaches 10, their performance levels off. This indicates that the privacy budget ($ϵ$) plays a critical role in controlling the performance gains and, when relaxed, models trained with fewer epochs can perform similarly to those trained with more epochs. This trend suggests that, under looser privacy constraints, additional training does not necessarily yield performance benefits. In contrast, the results using the UCI dataset, shown in Figure 9, exhibit an unexpected pattern. The model trained with 10 iterations consistently outperforms those trained with 20 or 50 iterations, reaching the highest accuracy when epsilon ($ϵ$) is less than 4. This abnormal result could be attributed to overfitting when more iterations are used, especially under stricter privacy constraints. The Cleveland dataset seems to benefit from early stopping, with fewer iterations preventing the model from overfitting, which may explain the better generalization performance with only 10 iterations. The differences observed in Figure 9 and Figure 10 provide valuable insights into how training duration and the privacy budget impact model performance. These figures underscore the importance of balancing privacy constraints with model accuracy and tailoring training configurations to the specific characteristics of the dataset.

The poorer performance of the TabNet model on the UCI Heart Disease dataset, with an R2 score of 0.4 (Figure 6 and Figure 9), can be attributed to several factors. The UCI dataset is smaller and less diverse than the Cleveland dataset, limiting the model’s ability to capture complex patterns. This, combined with fewer features, reduces its predictive power. The smaller sample size also makes the model prone to overfitting, especially with more epochs, resulting in high training accuracy but poor generalization on test data. Additionally, class imbalance and the model’s sensitivity to hyperparameter tuning further contribute to weaker performance. These factors reflect the dataset’s limitations rather than a fundamental flaw in the TabNet model. Future work could address these issues through data augmentation, class balancing, and hyperparameter optimization.

Figure 11 shows the model’s performance on the aggregated test data. The trend is similar to the Cleveland dataset, with the key difference being that the test accuracy increases gradually in the later stages of training. As epsilon ($ϵ$) increases, the model’s accuracy rises more smoothly on the aggregated data compared to the Cleveland data. This suggests a more consistent generalization performance when using aggregated datasets, likely due to the diversity of data sources. Given that accuracy ranges from 0 to 1 and epsilon ranges from 1 to 10, we designed a more balanced metric that considers the ratios of accuracy and epsilon and their respective magnitudes. Our approach utilizes a combination of exponential functions to evaluate performance under different privacy constraints. This figure supports the idea that combining data from multiple sources in an aggregated form enhances model stability and ensures better accuracy across varying epsilon values. The formula for the metric can be defined as follows:

$$\mathrm{Balanced}\mathrm{Metrics}=w_1·exp\left(\mathrm{accuracy}\right)+w_2·exp(-ϵ)$$

(8)

$BalancedMetrics$ will be larger as $accuracy$ approaches 1 and $ϵ$ approaches 1. When $accuracy$ is close to 0, the contribution from the first term will be minimal, and when $ϵ$ is close to 1, the contribution from the second term will be minimal. We chose $w_1=0.7$ and $w_2=1$ to give more weight to the contribution from $epsilon$, which presents more privacy than accuracy.

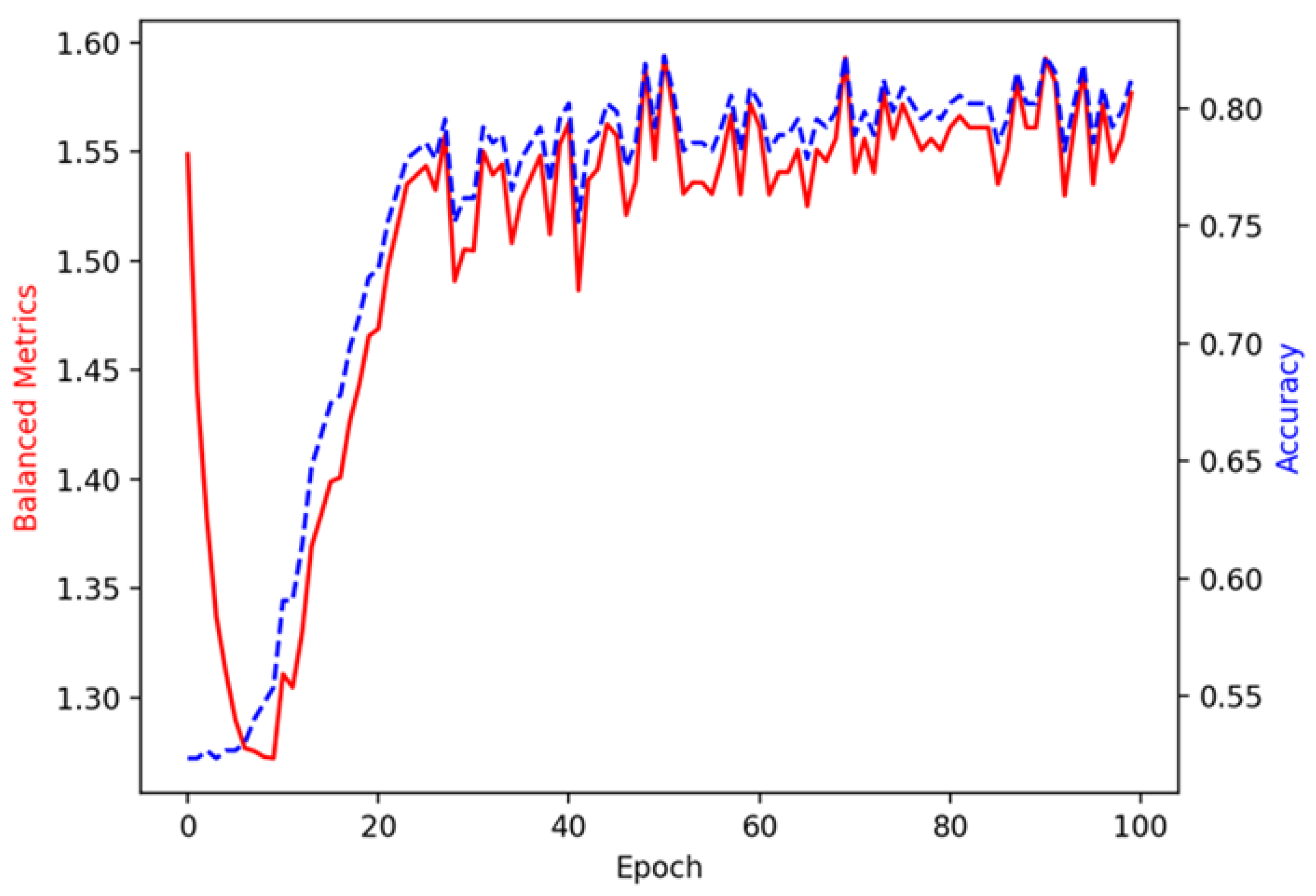
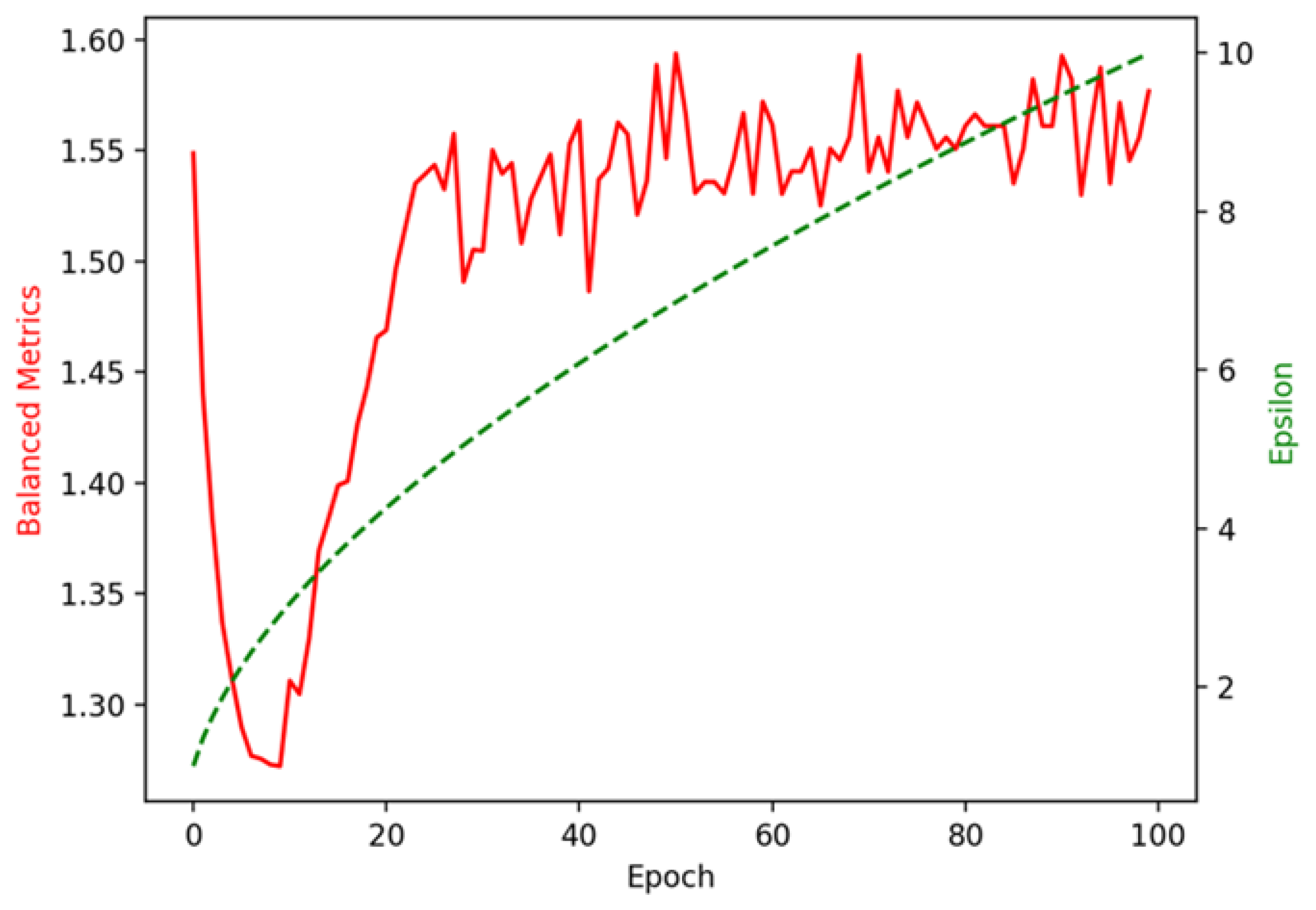
Figure 12 and Figure 13 show the trend of $BalancedMetrics$ with epoch compared with the trend of accuracy or epsilon in 100 iterations. The value of $BalancedMetrics$ is high when $accuracy$ and $ϵ$ tend to zero. Then, as $accuracy$ and $ϵ$ rise in the training process, $BalancedMetrics$ first plummets and then grows significantly. After that, the trend of $BalancedMetrics$ with epoch coincides with the accuracy trend. This indicates that, initially, privacy is strongly preserved when accuracy and epsilon are both low, leading to a highly balanced metrics score. However, as the model improves its accuracy and epsilon increases (which reduces privacy), the balanced metrics decrease temporarily. This drop is likely due to the trade-off between privacy and accuracy, as the model focuses on improving performance. Interestingly, after this drop, the $BalancedMetrics$ grows again as accuracy improves, showing that the model achieves a better balance between privacy and accuracy after the initial trade-off. After a certain point in training, the trend of $BalancedMetrics$ coincides with the accuracy trend, suggesting that the model has stabilized its performance. The highest $BalancedMetrics$ (1.594) is obtained at 50 epochs, with an accuracy of 0.822 and an $ϵ$ of 6.855. This result suggests that at 50 epochs, the model strikes a favourable balance between privacy protection (controlled by $ϵ$) and performance (measured by accuracy). The model demonstrates effective performance at this stage while maintaining reasonable privacy protection.

5. Conclusions

Integrating technology with privacy considerations is essential in the evolving landscape of data-driven advancements. This paper explores heart disease prediction through federated learning, emphasizing the balance between innovation and ethical responsibility. By developing a comprehensive system incorporating data expansion techniques, the TabNet model, differential privacy mechanisms, and blockchain technology, we have demonstrated the potential to create effective predictive models while maintaining data privacy collaboratively. This work underscores the transformative power of federated learning, allowing institutions to tackle complex challenges collectively while safeguarding sensitive information. This paper’s key contribution lies in integrating privacy-preserving techniques within predictive analytics. We successfully maintained high model performance without sacrificing privacy by applying the TabNet model and leveraging differential privacy. Blockchain technology enhanced transparency and accountability in the federated learning process, ensuring data integrity across institutions. The proposed approach was validated on real-world datasets (UCI Heart Disease and Cleveland datasets), where the model achieved high accuracy and balanced metrics under various privacy settings. Specifically, the best results were observed with 50 epochs and a privacy budget ($ϵ$) of 6.855. This demonstrates that the method effectively balances privacy protection and predictive power.

This method can be applied in healthcare institutions, such as hospitals and medical research centers, where collaborative data modelling is critical and privacy must be preserved. Several future research directions arise from this study. First, further exploration of advanced privacy-preserving techniques, such as combining differential privacy with homomorphic encryption, could enhance data security without compromising performance. Second, a comparative analysis between federated learning and non-federated approaches could provide insights into trade-offs between security, performance, and resource efficiency. Additionally, while the TabNet model has demonstrated promise, further investigation into its limitations is needed. Future work could focus on improving interpretability in real-world healthcare settings by incorporating explainable AI techniques like Shapley values or LIME. Moreover, exploring the scalability of TabNet in large-scale applications and comparing it with models like XGBoost or LightGBM could lead to more optimized solutions for handling larger datasets. A hybrid approach, combining TabNet’s strengths with other models, could also enhance performance in large-scale deployments.