Abstract
The rapid urbanization trend underscores the need for effective management of city resources and services, making the concept of smart cities increasingly important. This study leverages the IMD Smart City Index (SCI) dataset to analyze and rank smart cities worldwide. Our research has a dual objective: first, we aim to apply a set of unsupervised learning models to cluster cities based on their smartness indices. Second, we aim to employ supervised learning models such as random forest, support vector machines (SVMs), and others to determine the importance of various features that contribute to a city’s smartness. Our findings reveal that while smart living was the most critical factor, with an importance of 0.259014. Smart mobility and smart environment also played significant roles, with the importance of 0.170147 and 0.163159, respectively, in determining a city’s smartness. While the clustering provides insights into the similarities and groupings among cities, the feature importance analysis elucidates the critical factors that drive these classifications. The integration of these two approaches aims to demonstrate that understanding the similarities between smart cities is of limited utility without a clear comprehension of the importance of the underlying features. This holistic approach provides a comprehensive understanding of what makes a city ’smart’ and offers a robust framework for policymakers to enhance urban living standards.
1. Introduction
Rapid urbanization and the increasing complexity of city management have brought smart cities to the forefront of urban planning discussions. However, despite the growing attention to smart city rankings, there is still a limited understanding of what makes a city truly ’smart’. Existing methodologies for comparing cities often rely on aggregate indices or subjective assessments, which fail to capture the nuanced contributions of various factors like governance, infrastructure, and mobility. This lack of clarity leaves policymakers with incomplete guidance on which areas to prioritize for smart city development.
This study addresses this gap by introducing a dual-analysis framework that leverages unsupervised and supervised learning models to both cluster cities and assess the importance of various features contributing to their smartness. By focusing on data-driven insights, we aim to provide a more precise and actionable understanding of urban intelligence, enabling policymakers to make informed decisions about where to allocate resources and which urban dimensions to prioritize. This focused approach provides a clearer roadmap for improving city smartness and ensuring sustainable urban growth.
Smart cities have emerged as a pivotal paradigm in contemporary urban policy, driven by the rapid urbanization projected by the United Nations Department of Economic and Social Affairs. By 2050, it is estimated that two-thirds of the global population will reside in urban areas, necessitating innovative urban planning and management approaches. Smart cities leverage technology and data to enhance the quality of life, improve the efficiency of urban services, and promote sustainability.
The study of smart cities greatly benefits from the application of artificial intelligence (AI) and machine learning (ML) models, which are essential for understanding urban environments’ complex and multifaceted nature. Unsupervised learning models, such as clustering algorithms, allow us to identify inherent patterns and groupings within vast datasets, revealing hidden structures and relationships among cities.
The United Nations Department of Economic and Social Affairs (https://www.un.org/development/desa/pd/, accessed on 1 September 2024) predicts that by 2050 at least two persons out of three will be living in urban areas. Figure 1 shows the past and future percentages of the urban population. The plot highlights the increasing trend in the world’s more- and less-developed regions. The barplot was created using data from United Nations, Department of Economic and Social Affairs, Population Division (2019). World Urbanization Prospects: The 2018 Revision (ST/ESA/SER.A/420). New York: United Nations (https://population.un.org/wup/Publications/Files/WUP2018-Report.pdf accessed on 1 September 2024).
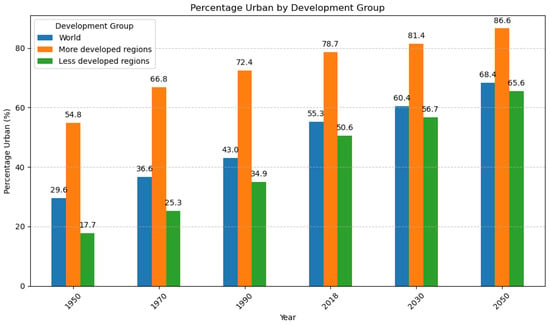
Figure 1.
Percentage of urban population between 1950 and 2050.
While presently there are 31 megacities (i.e., cities with more than 10 million inhabitants), their number will grow to about 43 by 2030. The major city growth rate is predicted to be in developing countries (population.un.org/wup/Maps/ accessed on 1 September 2024). Urbanization (i.e., the socio-economic process of environmental and social mutation from rural to urban) is the result of many factors, among which spatial and urban planning, investments in building and infrastructure, and economy. The increase in urban population will be driven by several factors, including natural population growth, rural-to-urban migration, and the geographic expansion of urban areas through annexation and conversion of rural localities into urban settlements. Thus, there are upcoming unexpected challenges for the infrastructure (housing), transportation, energy provisioning, economy, environment, education, employment, public services, and healthcare of cities. The yearly Sustainable Development Goals report analyzes the 17 goals of the 2030 Agenda for Sustainable Development, highlighting the current situation and future predictions. Goal 11 is “Sustainable cities and communities”. Presently, approximately one quarter of the global population resides in squalid, densely populated urban areas, living in extreme poverty. Building high-quality infrastructure and providing everyone with access to basic services are crucial for improving the preparedness and resilience of cities for recovering from and responding to future crises. Considering the increasing trend of irregular urban sprawl, urgent actions are required for housing, transportation, and services in slums. The World Cities Report (www.un-ilibrary.org/content/periodicals/2518654x accessed on 1 September 2024) [1] analyzes the upcoming scenarios for cities, including the different features of cities, the degree of urbanization, inequalities, economies, green perspectives, urban planning, public health, governance, resilience, and innovation and technological advancements. Innovation and technology are pivotal for sustainable cities, as digitalization and automation are transforming economies and urban features. Plus, the need for decarbonization is enhancing green and smart technologies. Smart cities have become a dominant paradigm in contemporary urban policy, steadily gaining prominence each day. Smart cities with a dense concentration of people enhance dynamic resource sharing, networking, and collaboration, providing innovation. Consequently, the development and improvement of buildings, energy, transport, water, waste, air pollution, and greenness are crucial.; thus, there exists an urge for smart city transformation of public services, social innovation, and the public sector. Numerous municipal administrations are adopting a smart city agenda to plan objectives for the future.
As urban development advances and cities become increasingly smarter, it becomes essential to investigate the disparities in smartness among cities, identify the key factors driving the development of urban intelligence, and determine the primary elements that distinguish more advanced smart cities from their counterparts.
Several indexes and classifications rank smart cities according to various factors, thresholds, and characteristics. Each methodology considers and assigns varying levels of importance to different attributes according to what are thought to be the best indicators of smartness (and future development) of a city. Although some of the aforementioned factors are measurable (e.g., economic aspects), some others are not (e.g., social aspects), thus the difficulty of numerically expressing smartness.
Ericsson computed the Networked Society City Index (NSCI, www.ericsson.com/en/reports-and-papers/networked-society-insights accessed on 1 September 2024), stating that ICT is fundamental for creating new opportunities for innovation and growth. The latest available report, dated 2016, highlights the need for cities to rethink themselves to be able to completely exploit ICT upcoming innovations. The authors list characteristics of a future networked society (a concept thought to be more extensive than that of smart cities): (i) resilience, (ii) collaboration, (iii) participation, (iv) mobility, (v) strong and visionary leadership, (vi) new regulatory frameworks, and (vii) a holistic approach. The Networked Society City Index assesses and ranks cities according to their sustainable urban development (accessed via 8 variables and 31 proxies from the (i) social, (ii) economic, and (iii) environmental categories) and ICT maturity (accessed via 7 variables and 18 proxies from the ICT (i) infrastructure, (ii) affordability, and (iii) usage categories). The outputted ranking highlights the relationship between investments in ICT and a city’s ecological, economic, and social progress, meaning that cities with above-average investments in ICT infrastructure typically excel in areas such as infrastructure, environmental protection, public safety, and healthcare.
Kearney’s Global Cities Report (www.kearney.com/service/global-business-policy-council/gcr accessed on 1 September 2024) ranks the world’s cities, rating the rate of attraction, retainment, and generation of global flows of capital, people, and ideas in cities. Two quantitative measures are available: the Global Cities Index (GCI) for measuring the current performance and the Global Cities Outlook (GCO) for performance forecasts. GCI assesses a total of 29 metrics divided into five categories. On the other hand, GCO assesses 13 indicators divided into four categories. Each category weighs the final score of a city. For GCI, business activity and human capital are the factors that contribute the most to smartness. GCO, instead, gives the same importance to the considered factors.
The IMD Smart City Index (SCI, www.imd.org/smart-city-observatory/home/ accessed on 1 September 2024) relies on individuals’ opinions collected through surveys. The perceptions of 120 residents for each city are assessed by the availability of infrastructure and technological services. Both are judged concerning five dimensions: (i) health and safety, (ii) mobility, (iii) activities, (iv) opportunities, and (v) governance. Weights of the five areas are not predetermined: respondents are asked to select five city priorities from 15 indicators. The weight of each category in the final calculation is adjusted based on the number of selected indicators that fall within that category. Thus, no indicator is thought to be the most influential on smartness in overall assessments. The final score for each city is calculated using weighted data from the past three years: the most recent year’s weight is 3 and the least recent year’s weight is 1.
IESE rates cities via its Cities in Motion Index (CIMI, www.iese.edu/insight/articles/smart-sustainable-cities-in-motion/ accessed on 1 September 2024), yearly adding new indicators of cities health such as the number of private startups worth more than 1 billion dollars or corporations listed in the Fortune Global 500. The index considers 114 indicators, divided into 9 categories: (i) human capital, (ii) social cohesion, (iii) economy, (iv) governance, (v) environment, (vi) mobility and transportation, (vii) urban planning, (viii) international profile, and (ix) technology. Each of the categories has a relative weight, as reported in Table 1. CIMI assigns the highest level of importance to the economy as a factor as a smartness indicator.

Table 1.
Categories and weights for the computation of the main smart city indexes.
The Smart City Strategy Index (SCSI, www.rolandberger.com/en/Insights/Publications/Smart-City-Strategy-Index-Vienna-and-London-leading-in-worldwide-ranking.html accessed on 1 September 2024) evaluates the extent and ambition of urban centers based on the essential components of a Smart City since 2017. The index considers 12 criteria (i.e., categories, with a total of 31 subcategories) that are thought to be representative of the development of a successful smart city strategy: budget, buildings, energy and environment, mobility, education, health, government, infrastructure, policy and legal framework, stakeholders, coordination, and plan. Each category has a weight depending on its overall importance, and a final weighted score is calculated. The index attributes a high importance to infrastructure and policy and legal framework as indicators of smartness.
The Smart EcoCity Index (SEC, www.smartecocity.com/smartecocity-index/ accessed on 1 September 2024) assesses three dimensions of a smart city: equity (i.e., the city’s quality of life and social inclusion), environment (i.e., the city’s sustainable practices and reduction of environmental impact), and economy (i.e., involvement of citizens, governance, innovation and resilience plans). The index considers eight categories of factors for accessing the final score: (i) transport and mobility, (ii) sustainability, (iii) governance, (iv) innovation economy, (v) digitalization, (vi) cybersecurity, (vii) living standards, and (viii) expert perception. Each accounts differently in the computation of the final score. Transport and mobility are thought to play the most prominent role in determining the smartness of a city.
The majority of the indexes discussed so far consider sustainability, smartness, urbanization, and quality of life as key factors to characterize smart cities. Table 1 reports the categories for each indicator and their weights.
The IMD Smart City Index (SCI) provides a comprehensive set of variables that reflect different aspects of a city’s smartness, including smart living, smart mobility, smart governance, smart economy, smart people, and smart environment. These dimensions form the core of the data used in the analysis. The focus then moves into the unsupervised learning phase, where clustering techniques such as k-means, hierarchical clustering, Gaussian mixture models (GMMs), and self-organizing maps (SOMs) are employed. These methods are used to categorize cities into clusters based on their performance across these smart city dimensions. This step helps identify similarities and patterns among cities, grouping them into categories that exhibit common traits in their smartness profiles.
Once the clusters are identified, the research shifts focus to determining the relative importance of the features contributing to a city’s classification. At this stage, supervised learning models like random forest, support vector machines (SVMs), and gradient boosting are used. These models are trained on the data to assess which dimensions of smartness—such as smart mobility or smart governance—have the greatest impact on a city’s overall ranking. This analysis reveals which aspects are the most critical in determining whether a city is classified as highly smart or not.
The results from these models highlight that some dimensions, like smart living, consistently play a significant role in driving a city’s smartness score, offering key insights for policymakers. The flow of the research thus moves from categorization through clustering to understanding the underlying factors through feature importance analysis. This dual approach provides both a macro-level view of how cities compare to one another and a micro-level understanding of which factors cities should focus on to improve their smartness.
The research concludes by synthesizing the findings into actionable insights for city planners and policymakers. By knowing which dimensions of smartness to prioritize, urban leaders can focus their efforts on specific areas that will have the most significant impact, thereby improving the overall smartness and livability of their cities. The study’s flow effectively bridges the gap between data analysis and practical policy recommendations, offering a roadmap for smart city development.
The originality of this article lies in ranking smart cities through a dual-analysis framework. Firstly, it applies a range of unsupervised learning models to cluster cities based on the IMD Smart City Index (SCI) dataset. This clustering reveals intrinsic groupings and patterns among cities that are often overlooked in traditional rankings. Secondly, it employs supervised learning models, such as random forest and support vector machines (SVMs), to determine the importance of various features that contribute to a city’s smartness. By integrating these two methodologies, the study not only provides a nuanced classification of smart cities but also identifies the critical factors driving these classifications.
As per Figure 2, this work is organized as follows. Section 2 discusses the related work. Section 3 reviews the background of the models used, while Section 4 describes the experiments performed on the dataset. Section 5 comments on the results. Finally, Section 6 draws the conclusions and the directions of more extended research.
Figure 2.
Visual representation of the work’s structure.
2. Related Work
Recent studies have increasingly focused on various aspects of smart city development and management. Researchers have developed and refined numerous indicators to capture the complexity of urban smartness. Smart city rankings offer a comparative perspective.
Son et al. [2] presented a thorough literature review to explore the use of artificial intelligence (AI) in urban planning. Using the PRISMA protocol, the work conducted a systematic review of 91 publications sourced from Scopus and Web of Science databases, identifying key AI applications in areas like urban data analytics, infrastructure management, disaster management, and development control.
The main contribution of this paper is its identification of AI’s potential to enhance smart and sustainable city planning. The review highlights how early AI adopters in urban planning are paving the way for broader implementation, emphasizing the importance of collaboration between stakeholders. The study also underscores AI’s reliance on big data and the need for the convergence of artificial and human intelligence to address urbanization challenges. In this sense, this review offers crucial insights into the future integration of AI in urban planning and its potential to support sustainable development goals, particularly through more efficient urban governance, environmental monitoring, and infrastructure management. Information and communication technology enables the digital infrastructure that supports various urban systems and services Data warehousing and big data analytics are fundamental in real-time data collection, storage, and analysis, which are crucial for decision-making processes. Cities increasingly rely on predictive models powered by AI and machine learning to optimize services such as traffic management, energy consumption, and public safety. The integration of these technologies into smart city frameworks enhances the efficiency and responsiveness of urban systems.
Similarly, content management and collaboration tools play a significant role in smart city governance. They facilitate better communication between city authorities and citizens, enhancing the delivery of public services. These tools promote transparency and active citizen participation, which are essential for ensuring effective governance in a smart city. Without a robust system for managing content and streamlining workflows, cities might struggle to meet the growing demand for fast and efficient public service responses.
Additionally, computer network platforms form the backbone of smart cities by ensuring the seamless flow of data between various systems, from IoT sensors to communication networks. The efficiency of services such as intelligent transport systems, smart grids, and healthcare systems depends on the reliability of these networks. Their role in enabling real-time interaction between different components of the urban ecosystem is crucial to the functioning of smart cities.
The concept of social mining should not be overlooked. By analyzing data from social media and other digital footprints, cities can gain valuable insights into citizen behavior, preferences, and concerns. This information can guide urban planners and policymakers in creating adaptive and responsive city services, enhancing the overall quality of life in urban areas.
Finally, the IoT (Internet of Things) is fundamental to the smart city vision as it connects devices and sensors that generate real-time data across urban environments. However, this interconnectedness also makes cities vulnerable to cybersecurity threats. Ensuring robust protections is critical to maintaining the integrity and functionality of urban systems, especially in sectors like transportation and healthcare, which could be severely affected by breaches. Lytras et al. [3] focused on bridging the gap between smart city services and the needs and expectations of end-users. The study clustered smart city services into categories based on perceptions and expectations through a pilot survey. The authors highlighted the importance of aligning technology providers and policymakers with citizen needs, emphasizing ICT-enabled services. The paper’s originality lies in its introduction of a practical toolkit for querying user perceptions and expectations, helping policymakers and businesses respond effectively to citizens’ needs, thus enhancing the relevance and usability of smart city services.
Researchers have leveraged different techniques in their studies, including clustering methods, to evaluate what makes a city “smart” and therefore consider and rank different available cities, commenting on their results. The analyses are conducted at various levels, including national, continental, and global scales.
Okonta et al. [4] reviewed the current smart city software applications landscape, analyzing multiple case studies aimed at enhancing sustainability and resilience and classifying their benefits into six possible action areas: governance, economy, environment, people, mobility, and living. The authors suggested that implementing smart city software applications and integrating them across various domains are crucial for tackling all the challenges that might become apparent in the future.
Yigitcanlar et al. [5] examined the key factors that affect a smart city’s transformation readiness, suggesting that both ICT and non-ICT factors influence the outcome. The authors performed a statistical investigation on the Australian region, performing multiple regression analyses on features that affect urban smartness levels. The conclusion of the work is that 65% of smart city transformation readiness is influenced by (i) proximity to the domestic airport, (ii) low level of remoteness, (iii) high population density, (iv) low unemployment rate, and (v) high labor productivity.
Liu [6] observed that current city evaluation research faces challenges such as unclear goals, inadequate theoretical foundations, redundant indices, poor comparability, lack of consideration for urban diversity, excessive focus on rankings, and insufficient validation and feedback. Additionally, there is a need for a more systematic interpretation of evaluation systems’ composition, principles, and uncertainties. Mills et al. [7] explored possible smart city objectives and actionable future practices. The main smart city capacities are identified as (i) technology exploitation, (ii) innovation, (iii) collaboration, and (iv) ecosystem orchestration.
Artificial intelligence (AI) and particularly ML play a vital role in determining the importance of various features that contribute to a city’s smartness [8]. By analyzing these features, it is possible to identify the key drivers of urban performance and prioritize areas for improvement. This insight is indispensable for policymakers and urban planners aiming to enhance the quality of urban life. The integration of both supervised and unsupervised learning models is paramount. Unsupervised learning uncovers the underlying patterns without prior labels, offering a broad understanding of urban similarities and differences. Supervised learning, with its focus on feature importance, provides detailed and actionable insights. Excluding one in favor of the other would result in an incomplete analysis, missing either the holistic view provided by unsupervised methods or the specific, actionable insights from supervised techniques.
Clustering plays a crucial role in the development and management of smart cities, as it involves grouping a set of objects in such a way that objects in the same group are more similar to each other than to those in other groups. Cities can be clustered in multiple ways, as explored by recent literature. The analyzed papers focus on clustering and then ranking of cities but often lack explainability on what are thought to be meaningful parameters and why. The following paragraphs show what work has been performed so far in the scope of smart city clustering.
Janusz et al. [9] studied the advancements of the implementation of smart cities in the Visegrad Group (V4). The cities were divided into clusters for the final assessment and classification using a dendrogram of similarity. The study evidenced that the best smart city scores are obtained by cities that are western and thus nearer to the European Union, implying that historical, socio-economic, political, and possibly geographic factors might influence a city’s smartness.
Cantuarias-Villessuzanne et al. [10] clustered 40 European smart cities depending on the activities implemented by the cities, outputting three clusters: (i) cities with emerging smart strategies, (ii) technology-oriented cities, and (iii) quality-life oriented smart cities. The clustering was performed for sustainability evaluation and ranking purposes. Clusters were obtained via principal component analysis (PCA).
Correia et al. [11] clustered and ranked European cities through the comparison of the number of existing projects by weighted category, considering population density. Four main categories were created via PCA: (i) infrastructure and transport, (ii) sectorial initiatives, (iii) territorial competencies, and (iv) community. PCA was applied to the projects to find the relationships between categories.
Ciacci et al. [12] assessed which Italian provincial municipalities aligned with the smart sustainable city (SSC) paradigm using the Pena’s distance method (DP2). Then, the authors applied a k-means variant with five fixed centroids and discovered that clusters of SSCs form at a macro-geographical level. Northern municipalities belonged to the cluster containing cities that identified the most with the smart sustainable city model.
Kutty et al. [13] clustered and ranked smart cities using the fuzzy c-means partitioning technique. The cities were evaluated first via partitioning them into low-, medium-, and high-performing cities and then via a comparative analysis considering a three-criteria decision model (based on sustainability, resilience, and livability) where the analytical hierarchy process (AHP) is combined with the Evaluation based on distance from average solution (EDAS) approach under a spherical fuzzy environment.
Recent studies in smart city rankings and feature importance analyses have explored various methodologies to understand better the dimensions that contribute most significantly to a city’s “smartness”. One study by Gazzeh [14] combined content analysis and the analytic hierarchy process (AHP) to create a robust ranking system for sustainable smart city (SSC) indicators. This study emphasized the importance of governance, livability, and public services, while interestingly downplaying the role of technology and ICT, challenging the widespread assumption that these are the most crucial factors. This study’s combined ranking system serves as a decision-making tool, helping prioritize smart city initiatives based on available resources and strategic goals.
Another study by Dashkevych et al. [15] took a systematic literature review approach to identify the key criteria for smart city identification and ranking. Their work highlighted the use of ML techniques, such as dynamic factor analysis, to better understand how cities can be evaluated based on their innovation capacity, infrastructure, and social inclusion.
Our approach consists of a data-centric and ML-driven approach to analyze the IMD Smart City Index dataset. The focus shifts to unsupervised and supervised learning models, specifically clustering and feature importance, to categorize cities based on “smart” features and determine which factors are most influential in urban development. This detailed, technical exploration contrasts with the broader literature review and ranking approaches discussed in the other two works. In particular, Dashkevych et al. adopted a more qualitative and comprehensive review of existing literature on smart city criteria. Their research identified 48 distinct metrics used across various studies to define and assess smart cities, categorizing these metrics into technology, living conditions, and environmental sustainability. Their emphasis is on cataloging these criteria rather than deploying statistical models to analyze them, which is the core focus of our work.
On the other hand, Gazzeh’s article moves in a somewhat different direction, integrating content analysis and the analytic hierarchy process (AHP) to rank indicators for sustainable smart cities. This ranking system is meant to assist policymakers by prioritizing aspects of smart city development. Gazzeh’s work focuses on practical decision-making tools for urban planners, positioning technology as one of several factors rather than the dominant driver, which contrasts with your data-driven focus on feature importance and clustering.
Finally, it may be beneficial to compare the present article against a work by Silvestri et al. [16]. Both focus on the use of advanced technologies to improve urban environments through smart city concepts, but they approach the subject from different perspectives and methodologies.
Our paper is primarily concerned with understanding how cities can be grouped or clustered based on their performance in various dimensions of smartness, such as smart mobility, smart governance, smart living, and more. The main contribution is the application of clustering algorithms, such as k-means and Gaussian mixture models, to identify patterns in how cities perform across these dimensions. The focus is also on determining the feature importance of these dimensions, identifying which aspects most significantly impact a city’s classification. The goal of this study is to guide policymakers in improving their cities by focusing on the dimensions that most affect urban intelligence. The paper emphasizes machine learning techniques, especially clustering, and feature importance analysis, which provides insights into which areas cities should prioritize for becoming smarter.
In contrast, the paper by Silvestri et al. provides a technical framework for integrating heterogeneous data and managing complex urban systems. This article introduces a novel architecture that enables the seamless deployment and integration of various subsystems within smart cities, leveraging technologies such as digital twins (DT), cloud computing, and data lakes. Its main contribution lies in creating an IT infrastructure that allows urban data to be collected, stored, integrated, and visualized efficiently. This architecture also supports the deployment of real-time applications and workflows that enhance the functionality of urban intelligence systems. The paper’s key focus is on the technical execution of smart city systems, ensuring they can manage and process large, heterogeneous datasets effectively, while also providing a user-friendly interface for city administrators to make data-driven decisions.
As evidenced by the papers presented in this section, the literature includes various studies that employ clustering techniques in the context of smart cities. However, in most cases, a single method is utilized and applied to a specific aspect of smart cities. The emergence of issues such as unclear goals, redundant indices, and a lack of comprehensive methodological applications highlights the need for more systematic interpretation of evaluation systems and a more integrated approach to employing IT solutions in smart city development. It is also important to integrate smart city software applications across various domains. Effective implementation and coordination of these technologies are crucial for addressing future urban challenges and improving city management. A holistic approach, incorporating diverse methodologies and comprehensive analysis, is essential for advancing smart city development.
3. Background
The analysis of smart cities involves a comprehensive evaluation of various indices to understand their development, performance, and growth. To achieve this, unsupervised learning models are employed to cluster smart cities based on these specific indices. Clustering provides insights into the natural groupings and similarities among cities, facilitating the identification of patterns and trends.
On the other hand, supervised learning models are used to determine the importance of different features contributing to these indices. By deciphering feature importance, these models help in understanding which factors most significantly impact the performance and development of smart cities. The models chosen for this study are particularly well suited for these tasks, enabling robust and interpretable analysis of the data.
The following sections discuss the methodologies and mathematical foundations of supervised and unsupervised ML models. Each technique is presented with its theoretical background and application to the clustering and analysis of smart city indices.
3.1. Unsupervised Learning
Clustering methods like k-means, hierarchical clustering, GMM, and SOM are well suited for analyzing smart city indices as they reveal patterns and group cities with similar characteristics.
k-means is ideal when the number of clusters is known, efficiently minimizing variance within clusters, and works well for grouping cities based on similar features such as development and governance. Hierarchical clustering, which builds a hierarchy of clusters, is useful when the number of clusters is unknown. It allows visualization through dendrograms, showing how clusters merge and providing insights at different levels of similarity.
GMM offers a probabilistic approach, assigning cities to multiple clusters with varying probabilities. It is effective when clusters overlap or when they are not well separated, providing flexible clustering. SOM, a neural network, visualizes high-dimensional data by preserving topological properties, making it ideal for interpreting complex relationships in smart city data.
Each method offers unique strengths—k-means and GMM focus on cluster assignment, while hierarchical clustering and SOM provide deeper structural insights into the data—making them suitable for understanding different aspects of smart city development.
3.2. k-Means
k-means (see, for example, [17]) is a popular unsupervised learning algorithm used for clustering data into k distinct, non-overlapping subsets. The goal is to partition a set of n data points into k clusters, in which each point belongs to the cluster with the nearest mean, serving as a prototype of the cluster.
Given a set of observations , where each observation is a d-dimensional vector, k-means clustering aims to partition the n observations into k clusters to minimize the within-cluster sum of squares (WCSS):
where is the mean of the points in cluster :
The algorithm proceeds as follows:
- Initialize k cluster centroids randomly.
- Assign each data point to the nearest centroid, forming k clusters.
- Recalculate the centroids of the clusters by computing the mean of the points assigned to each cluster.
- Repeat steps 2 and 3 until the centroids do not change significantly or a maximum number of iterations is reached.
k-means aims to find the partition that minimizes the total intra-cluster variance, which is equivalent to minimizing the WCSS. In this sense, the optimal value of k parameter can be estimated using the silhouette index and the elbow method. This approach is used to determine the optimal number of clusters k in k-means clustering. It involves running the algorithm for a range of k values and plotting the WCSS against k. The optimal k is found at the “elbow” point where the rate of decrease in WCSS slows down.
k-means clustering partitions the data space into regions, with each region corresponding to one of the k cluster centroids. These regions can be visualized using a geometric concept known as a Voronoi diagram [18]. In a Voronoi diagram, the space is divided into cells based on the distance to a specific set of points, called sites. Each cell contains all the points that are closer to its site than to any other site.
A Voronoi diagram is a partitioning of a plane into regions based on the distance to a specified set of points. These points are often referred to as sites or generators.
Given a set of distinct points in the Euclidean plane, the Voronoi diagram is a subdivision of the plane into n regions, each associated with one point. The region associated with the point consists of all points in the plane that are closer to than to any other point in P.
Mathematically, the Voronoi cell for a site is defined as follows:
where denotes the Euclidean distance between points x and p.
The Voronoi diagram can be characterized using a set of properties.
Each Voronoi cell is a convex polygon. This follows from the definition since the intersection of half-spaces (regions defined by linear inequalities) results in a convex shape. The edges of the Voronoi cells are portions of the perpendicular bisectors of the line segments joining pairs of sites. For two sites and , the perpendicular bisector is given by the following:
A Voronoi vertex is a point that is equidistant from three or more sites. These vertices are the points of intersection of the perpendicular bisectors of the line segments connecting the sites. To construct a Voronoi diagram, literature offers different algorithmic approaches (see, for example, Fortune’s algorithm [19]).
3.3. Hierarchical Clustering
Hierarchical clustering (see, for example, [20]) is a method of cluster analysis that seeks to build a hierarchy of clusters. This technique involves the iterative fusion or division of clusters based on a measure of similarity or dissimilarity between data points. In agglomerative hierarchical clustering (bottom-up approach), each data point starts as its own cluster, and pairs of clusters are merged sequentially based on a linkage criterion (such as single, complete, or average linkage) until all data points form a single cluster. The process is typically visualized in a dendrogram, where the vertical axis represents the distance at which clusters are merged.
Conversely, in divisive hierarchical clustering (top-down approach), a single cluster containing all data points is progressively split into smaller clusters.
A key advantage of hierarchical clustering is that it does not require a predefined number of clusters, allowing for a flexible analysis of the data’s structure. However, it is computationally intensive, particularly for large datasets, and is sensitive to noise and outliers, which can distort the clustering outcome.
The distance metric (e.g., Euclidean or Manhattan) and linkage method selected significantly influence the final clustering solution, and their choice depends on the data’s characteristics.
3.4. SOM
Self-organizing maps (SOMs, [21]) are a type of artificial neural network used for unsupervised learning. SOMs are particularly useful for dimensionality reduction and clustering, enabling the visualization of high-dimensional data in a low-dimensional (typically two-dimensional) space. The primary objective of a SOM is to produce a low-dimensional, discretized representation of the input space, preserving the topological properties of the data.
A SOM consists of a grid of neurons, each associated with a weight vector of the same dimensionality as the input data. During the training process, input vectors are presented to the network, and the neurons compete to respond to the input. The neuron whose weight vector is closest to the input vector (according to a specified distance metric, typically the Euclidean distance) is declared the winner. This neuron, along with its topological neighbors, adjusts its weight vector to become more similar to the input vector. This process, repeated over many iterations, causes the map to self-organize and produce a meaningful clustering of the input data.
Let be an input vector, and let be the weight vector associated with the neuron located at position on the grid. The training process of a SOM involves, as per Algorithm 1, the different steps.
| Algorithm 1 Self-Organizing Map (SOM) Training |
|
where the Best Matching Unit (BMU) is the neuron whose weight vector is closest to the input vector (this is calculated using the Euclidean distance).
The result of the training process is a topologically ordered map where similar input vectors are mapped to nearby neurons, enabling the visualization of the high-dimensional input space in a low-dimensional grid. This characteristic makes SOMs a powerful tool for exploratory data analysis and visualization.
3.5. Gaussian Mixture Models
Gaussian mixture models (GMM, [22]) are probabilistic models that assume the data are generated from a mixture of several Gaussian distributions with unknown parameters. GMMs are used for clustering, density estimation, and as generative models for data.
A GMM is defined as a weighted sum of K Gaussian component densities. The probability density function of a GMM is given by the following:
where are the mixture weights, are the mean vectors, are the covariance matrices of the Gaussian components, and represents all the parameters of the model.
The parameters of a GMM can be estimated using the expectation-maximization (EM) algorithm, which iteratively improves the estimates of the parameters. The EM algorithm consists of two steps: the expectation (E) step and the maximization (M) step.
In the E step, the algorithm calculates the posterior probabilities (responsibilities) for each data point to belong to each Gaussian component:
In the M step, the parameters are updated using the current responsibilities:
where and N is the total number of data points.
GMMs are used for clustering because they can model complex data distributions with multiple peaks, unlike k-means which assumes spherical clusters. GMMs provide a soft clustering approach where each data point is assigned a probability of belonging to each cluster, which is more informative than hard clustering. Also, GMMs are suitable for density estimation and can generate new samples from the learned distribution. GMMs are flexible in representing data distributions and can model clusters of different shapes and sizes. They provide probabilistic cluster assignments, which can be useful for uncertainty quantification. However, GMMs have limitations, including sensitivity to initialization and the assumption that each cluster follows a Gaussian distribution. They can also be computationally expensive, especially for high-dimensional data and many components.
For clustering tasks, GMMs can provide more accurate and flexible cluster assignments compared to k-means, especially when the data have non-spherical clusters. GMMs can also be used for anomaly detection by identifying data points with low probability under the learned model. Furthermore, GMMs can be integrated into more complex models, such as hidden Markov models (HMMs), to model sequential data.
Models Evaluation
In addition to the aforementioned elbow and silhouette methods, this work considers further model performance evaluation techniques. In particular, the Davies–Bouldin index is used to evaluate the quality of clustering. It is defined as follows:
where:
- n is the number of clusters.
- is the average distance between each point in cluster i and the centroid of cluster i (intra-cluster distance).
- is the distance between the centroids of clusters i and j (inter-cluster distance).
- The formula computes the similarity between each cluster i and the cluster most similar to it (the maximum similarity between i and any other cluster j).
The Davies–Bouldin index measures the ratio of within-cluster scatter () to between-cluster separation (). The index is the average of the worst-case ratio for each cluster.
A lower Davies–Bouldin index indicates better clustering, meaning that the clusters are compact (low ) and well separated (high ).
Furthermore, The Calinski–Harabasz index is used to evaluate the quality of clustering. It is defined as follows:
where
- N is the total number of data points.
- k is the number of clusters.
- Tr() is the trace of the between-cluster dispersion matrix.
- Tr() is the trace of the within-cluster dispersion matrix.
The Calinski–Harabasz index measures the ratio of the sum of between-cluster dispersion to within-cluster dispersion. A higher value indicates that the clusters are well separated and more compact. Specifically,
- High values indicate better-defined clusters (high between-cluster variance and low within-cluster variance).
- Low values suggest poor clustering (high within-cluster variance or low between-cluster variance).
3.6. Supervised Learning
Random forests and gradient boosting can capture non-linear relationships, which are common in real-world data, making them highly effective in assessing the influence of individual features. These models naturally provide feature importance scores by evaluating how much each feature reduces prediction error or impurity, offering direct insight into their significance.
SVMs can also handle high-dimensional data and provide feature weights that help assess feature significance. These models work well with various types of data, whether categorical or continuous, without requiring extensive preprocessing, and they are flexible enough to deal with both types.
Moreover, these models also quantitatively evaluate feature impact, with random forests computing feature importance based on the decrease in prediction error. This quantitative evaluation further enhances the models’ interpretability and ability to highlight the most significant features. Thus, these models are particularly well suited for determining feature importance due to their flexibility, interpretability, and ability to handle complex data structures.
3.7. Random Forests
Random forests [23] are an ensemble learning method used for both classification and regression tasks. They work by constructing multiple decision trees during training and aggregating their results. For classification, the final prediction is the mode of the classes predicted by individual trees. For regression, the final prediction is the mean of the predictions from all trees. This method leverages the power of multiple models to improve accuracy and control overfitting.
The main idea is to combine the predictions of several base estimators to reduce variance and enhance generalization. Each tree in a random forest is trained on a different random subset of the training data, using a technique called bagging (bootstrap aggregating). This approach creates diverse trees, which reduces the risk of overfitting to the training data.
First, bootstrap sampling is applied to the training dataset , generating B bootstrap samples by sampling with replacement.
Each bootstrap sample is used to train a decision tree . During the training of each tree, at each node, a random subset of features is selected, and the best split among these features is found.
For aggregation, in classification tasks, the final prediction for an input is obtained by majority voting:
In regression tasks, the final prediction for an input is obtained by averaging:
Here, B denotes the number of trees, represents the prediction of the b-th tree, and is the set of all features.
By averaging multiple decision trees, each trained on different parts of the training data and different features, random forests utilize the law of large numbers to improve the stability and accuracy of the model.
3.8. Linear SVM
Linear SVMs [24] aim to create a robust classifier by finding the hyperplane that best separates the classes, ensuring maximum margin, and minimizing classification errors on new data. The goal of a linear SVM is to find a hyperplane defined by , where is the normal vector to the hyperplane and b is the bias term. The objective is to maximize the margin , which is the distance between the hyperplane and the nearest data point of each class.
This can be formulated as an optimization problem
subject to the following constraints:
Here, represents the input vectors, and are the corresponding class labels.
To solve this problem, we typically use Lagrange multipliers, leading to the dual form of the problem
subject to
The solution to the dual problem gives the values of , which are then used to find the optimal hyperplane parameters and b. The final decision function for classifying a new point is as follows:
3.9. Gradient Boosting
A gradient boosting model [25] can be trained using the following steps:
First, initialize the model with a constant value:
where L is the loss function, and are the true values.
For each iteration to M, where M is the total number of iterations:
Compute the residuals (pseudo-residuals):
Fit a new base learner (e.g., a decision tree) to the residuals:
Update the model:
where is the learning rate, controlling the contribution of each tree.
The final model after M iterations is as follows:
Gradient boosting iteratively adds weak learners to the model, focusing on reducing the errors made by the previous models. This approach leverages the power of gradient descent optimization to minimize the loss function and improve predictive accuracy.
4. Experiments
4.1. Dataset Description
The considered dataset is derived from IMD Smart City Index (SCI, https://www.imd.org/smart-city-observatory/home/, available at https://www.kaggle.com/datasets/magdamonteiro/smart-cities-index-datasets/data accessed on 1 September 2024), and it refers to 2020. It is composed of 102 observations and 11 features. The most relevant ones are introduced in the following.
Smart mobility measures the efficiency and effectiveness of transportation systems within a city. It evaluates aspects such as public transportation availability, traffic management, and the integration of technology to facilitate the smooth and sustainable movement of people and goods. A high score in smart mobility indicates a city’s capability to offer efficient, accessible, and environmentally friendly transportation options.
Smart environment assesses the city’s commitment to environmental sustainability and its efforts to reduce pollution and manage natural resources responsibly. This index includes metrics related to air quality, waste management, renewable energy usage, and green spaces. A higher score in smart environment reflects a city’s proactive approach to maintaining a clean and healthy environment for its residents.
Smart government evaluates the effectiveness, transparency, and responsiveness of a city’s government. It looks at how well the city uses technology to provide public services, engage with citizens, and ensure accountability. High scores in smart government indicate a city that leverages digital platforms to enhance governance and foster civic participation.
Smart economy measures the economic dynamism and innovation capacity of a city. This index considers factors such as the presence of high-tech industries, startup ecosystem, economic growth, and employment rates. A city with a high smart economy score is one that promotes innovation, supports business development, and maintains a vibrant economic environment.
Smart people assesses the human and social capital within a city. It includes metrics related to education, lifelong learning opportunities, social inclusiveness, and the ability of citizens to adapt to new technologies. A higher score in smart people indicates a city that invests in its residents’ skills and knowledge, fostering a community that is educated, engaged, and adaptable.
Smart living evaluates the quality of life in a city, focusing on factors such as housing, healthcare, safety, and cultural and leisure activities. This index measures how well a city ensures the well-being and happiness of its residents. High scores in smart living reflect a city’s success in providing a safe, healthy, and enjoyable living environment.
The Smart City Index is a composite score that aggregates the evaluations from the various dimensions of a smart city, providing an overall assessment of how smart a city is. This index gives a holistic view of a city’s performance across mobility, environment, governance, economy, people, and living conditions.
Finally, the Smart City Index relative to Edmonton compares each city’s overall smart city Index to that of Edmonton, serving as a benchmark. This relative index highlights how each city stands compared to Edmonton’s performance as a smart city, providing a contextual understanding of a city’s ranking and achievements.
4.2. Models
In the following, the clusters are visualized in a two-dimensional space using the PCA dimensionality reduction method (see, for example, [26]).
4.3. k-Means
Based on the analysis of the elbow method, the silhouette index, and the gap statistics approaches, some insights were drawn about the optimal number of clusters (k).
Using the elbow method, a significant drop in the within-cluster sum of squares (WCSS) up to k = 5 was observed. After this point, the reduction in WCSS starts to flatten, forming an “elbow”, suggesting that k = 5 is a good choice for the number of clusters. Furthermore, the silhouette score for k = 5 is 0.61, indicating that the clusters are well separated and distinct. This score supports the selection of k = 5, as it strikes a good balance between intra-cluster compactness and inter-cluster separation.
Finally, the gap statistic for k = 5 was calculated to be 0.47, which is the highest gap value compared to other k-values. This further confirms that k = 5 is the optimal number of clusters, as it indicates the largest gap between the total within-cluster variation and expected variation under a random distribution. Further measures depicted in Table 2 are provided by the Davies–Bouldin index, equal to 0.89.

Table 2.
Clustering performance metrics for k-means with .
Similarly, the Calinski–Harabasz index for k = 5 is 431.20. Higher values indicate that the clusters are well separated and compact, meaning the k-means clustering performs well.
Cluster Analysis
The clustering generated by the k-means model is depicted in Figure 3 and in Table 3. Cluster 0 (in red) includes cities such as Milan, Brussels, Dublin, and Barcelona, which are major European hubs known for balancing cultural heritage with urban development. These cities are prominent economic centers with investments in infrastructure, public transportation, and urban services. Cities like Rome, Florence, and Lisbon are significant cultural and historical landmarks, yet they are integrating modern smart city initiatives. Smaller cities like Bratislava and Ljubljana are emerging as leaders in smart governance and environmental sustainability, while Tel Aviv stands out as a technology hub in the Middle East. This cluster focuses on integrating modern infrastructure while maintaining cultural integrity and governance improvements.
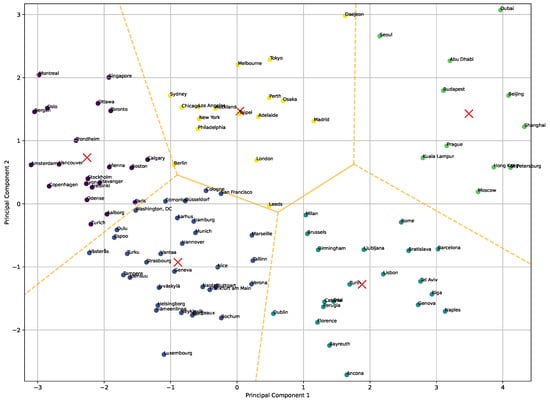
Figure 3.
k-means clustering for .

Table 3.
k-means clustering for .
Cluster 1 (in green) includes major metropolitan areas from across the globe, such as Los Angeles, New York, Chicago, London, Sydney, and Tokyo. These cities are recognized for their massive urban populations and advanced infrastructure. They face challenges related to urban density and environmental sustainability but have made significant strides in transportation systems, smart governance, and digital innovation. Taipei, Melbourne, Auckland, and Osaka are leaders in green energy and public transportation. Madrid and Daejeon add to the mix as smart cities with strong technological advancement and urban mobility initiatives. This cluster represents cities that are fast-paced, with heavy investment in technology and a focus on enhancing urban living for large populations.
Cluster 2 (in blue) features rapidly developing cities like Abu Dhabi, Seoul, Dubai, Shanghai, Moscow, and Beijing. These cities are characterized by large-scale investment in modern infrastructure and technology. They are innovation driven, with strong urban planning and futuristic development projects. Hong Kong, Budapest, and Prague have emerging tech economies, while Kuala Lumpur focuses on becoming a global technology hub. These cities share an emphasis on smart infrastructure, public services, and large-scale urbanization, often driven by rapid economic development and technological advancement.
Cluster 3 (in purple) includes cities such as Oslo, Amsterdam, Copenhagen, Stockholm, and Vienna, which are leaders in sustainability and urban living standards. These Northern and Central European cities have strong public welfare systems, green energy initiatives, and extensive public transportation networks. Cities like Montreal, Singapore, and Zurich are recognized for their innovation and quality of life. Washington, DC, Boston, and Ottawa stand out as governmental and academic centers with strong emphasis on smart governance. This cluster consists of cities that are globally recognized for their high quality of life, sustainability, and innovation in public services.
Finally, Cluster 4 (in orange) brings together cities like Västerås, Düsseldorf, Reykjavik, Munich, and Hamburg—all known for their smart mobility and environmental policies. These cities often lead in implementing sustainable technologies and urban planning. Frankfurt am Main and San Francisco are global financial centers, while cities like Strasbourg and Geneva are known for strong governance and international cooperation. Smaller cities like Hämeenlinna, Tampere, and Oulu have leveraged smart city technologies to improve urban living standards. This cluster reflects cities that have advanced in integrating environmental sustainability with smart infrastructure, public services, and governance. The dashed and continuous lines represent different types of boundaries. Continuous Lines denote the main, direct boundaries between regions, often showing where the influence of one central point (e.g., a city or data point) transitions to another. In contrast, dashed lines often represent secondary or less definitive boundaries, possibly indicating areas with weaker or shared influence between multiple points or where boundaries are less rigid. The cluster centroids are represented by an X character.
4.4. Hierarchical Clustering
The dendrogram in Figure 4 provides a hierarchical clustering of the cities based on their smart city indices (the performance metrics are summarized in Table 4). The method used is the Ward linkage method, which is often used when the goal is to minimize the variance within clusters. It tends to produce clusters that are compact and similar in size, making it effective when the dataset is expected to have spherical clusters. In this case, using smart city metrics, Ward linkage ensures that cities grouped into the same cluster are more similar in terms of their smart city characteristics (e.g., mobility, environment, governance) compared to cities in other clusters.
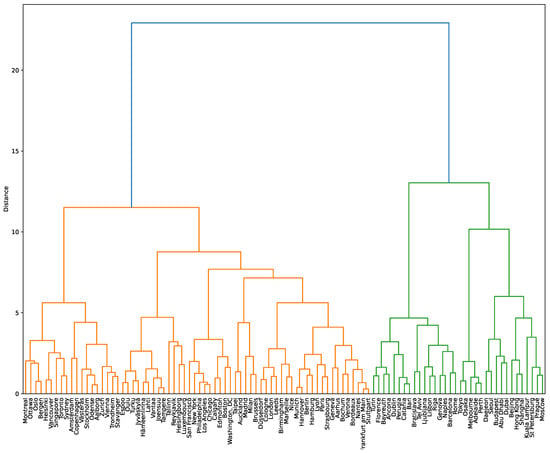
Figure 4.
Dendrogram of smart city indices.

Table 4.
Clustering performance metrics for the hierarchical clustering model.
Having identified five clusters, the silhouette score of 0.3750 suggests that the clusters are moderately well-defined but there may be some overlap. The Davies–Bouldin index of 0.8920 shows that the clusters are relatively distinct, with a value closer to 0 indicating better-defined clusters. This score indicates fairly good performance. The Calinski–Harabasz index of 65.32 reflects the ratio of between-cluster dispersion to within-cluster dispersion. A higher value indicates better-defined clusters. These metrics together suggest that the hierarchical clustering model performs moderately well.
Cluster Analysis
The height at which two clusters are joined together represents the distance or dissimilarity between them. Cities are divided into two major clusters at the highest level, represented by the two main branches of the dendrogram. The left major cluster includes cities such as Montreal, Oslo, Helsinki, and Amsterdam. These cities tend to have high scores in smart mobility, environment, and government indices. The sub-clusters within this major cluster represent cities with even more similar characteristics. For example, Oslo and Helsinki are joined at a lower level, indicating they are very similar in their smart city indices. The right major cluster includes cities such as Shanghai, Beijing, Dubai, and Moscow. These cities are distinguished by their high scores in smart economy and smart living indices. The sub-clusters show further granularity. For instance, Beijing and Shanghai are closely related, reflecting their similar scores across various smart city dimensions. The height of the branches indicates the level of similarity or dissimilarity. Cities like Montreal and Oslo are joined at a higher level than Beijing and Shanghai, indicating that the former pair is more similar to each other than to the latter pair. This hierarchical structure helps to identify groups of cities with similar smart city characteristics. The hierarchical clustering displayed in the dendrogram provides insight into the relative similarities and differences among cities based on their smart city indices. Cities that are grouped at lower levels of the dendrogram are more similar to each other than to those joined at higher levels. Table 5 recaps the content of each cluster.

Table 5.
Smart cities based on hierarchical clustering.
4.5. Gaussian Mixture Models
As per Table 6, the clustering performance results for the Gaussian mixture model reveal several insights. The silhouette score of 0.4010 suggests that the clusters are reasonably well-defined, although there may still be some overlap between them, while the result points to moderate clustering quality, there is room for improvement in terms of distinct separation.

Table 6.
Clustering performance metrics for the GMM model.
The Davies–Bouldin index, with a value of 0.7514, indicates that the clusters are fairly distinct from each other.
The Calinski–Harabasz index is 87.15, which indicates that the model has created clusters with reasonable separation, but as with the silhouette score, there could be further improvement. Overall, these metrics together suggest that the model is performing moderately well, but optimizing the clustering approach or tuning parameters may enhance the results.
Cluster Analysis
In the GMM clustering plot of Figure 5 and Table 7, the cities in Cluster 0 are primarily from Europe and North America, including Oslo, Amsterdam, Boston, Zurich, and Paris. These cities are known for their strong infrastructure, high quality of life, and leadership in smart city initiatives, particularly in sustainability, public services, and governance. Cluster 1 features cities like San Francisco, Milan, Brussels, Dublin, and Rome, which are prominent cultural and economic centers. These cities face the challenge of balancing historical preservation with modern smart city technologies, focusing on tourism, cultural heritage, and enhancing urban living standards. Cluster 2 contains large global metropolitan areas such as Los Angeles, New York, Berlin, Tokyo, and Sydney. These cities are major financial hubs and urban megacities with diverse populations. They are investing heavily in smart infrastructure and technology to address challenges like urban density and sustainability. Lastly, Cluster 3 includes cities from rapidly developing regions like Abu Dhabi, Dubai, Hong Kong, Moscow, and Shanghai. These cities are characterized by rapid urbanization, large-scale investments in modern infrastructure, and technology-driven economic growth. Each cluster reflects cities with similar levels of urbanization, technological advancement, and governance, showcasing their approaches to smart city development.
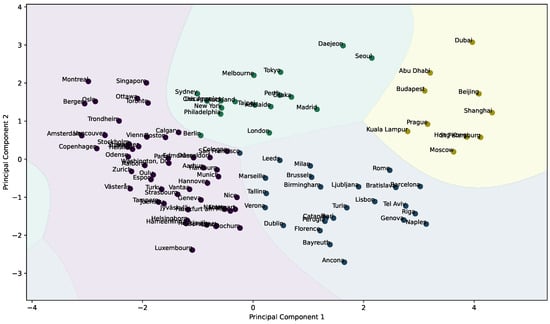
Figure 5.
Gaussian mixture model (GMM) clustering of smart city indices.

Table 7.
GMM clustering of smart cities.
4.6. SOM
The performance evaluation of the SOM model is denoted by Table 8. While the silhouette score points to moderate clustering quality, both the Davies–Bouldin index and Calinski–Harabasz index suggest that the clusters are well separated and compact, indicating that the model is performing at a good level. There is room for refinement, but overall, the clustering is reasonably effective.

Table 8.
Clustering performance metrics for the SOM model.
Cluster Analysis
The SOM plot in Figure 6 for clustering smart cities exhibits overlapping clusters (a summary is provided by Table 9). This scenario may arise because of the variability in the dataset (cities that are similar in some indices but different in others might appear in overlapping regions). The presence of Aalborg, Paris, Washington DC, Edmonton, Oulu, and Berlin in two overlapping clusters can be attributed to their diverse and multifaceted characteristics.
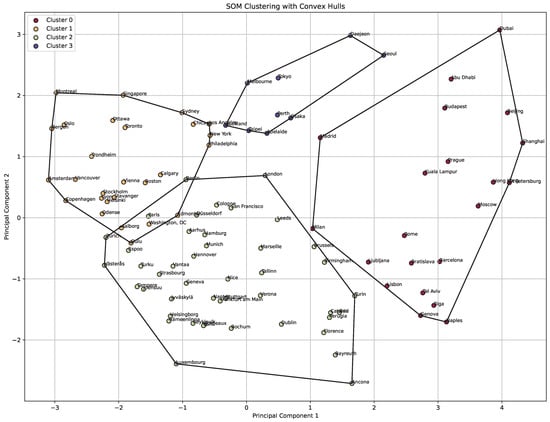
Figure 6.
Self-organizing map (SOM) clustering of smart city indices with convex hulls.

Table 9.
SOM clustering of smart city indices in tabular form.
The cities in Cluster 0 include cities that are located primarily in Asia and Oceania, with strong economic growth and significant investments in urban infrastructure. They are characterized by large populations and rapid technological advancements. Cities like Tokyo, Osaka, and Taipei are major innovation hubs in smart technology and urban mobility, while Melbourne, Perth, and Auckland are known for their high living standards and focus on smart city initiatives. Collectively, these cities are distinguished by robust public transportation systems, growing urban populations, and sustainability-oriented urban planning.
The cities in Cluster 1 include numerous cities from Europe and the United States. These cities are economic powerhouses, with strong urban infrastructure and significant investments in smart city initiatives. Major financial and business centers such as London, Geneva, Frankfurt, and San Francisco lead in innovation-driven policies and advanced transportation networks. At the same time, historical cities like Rome, Milan, and Florence are balancing the preservation of cultural heritage with modern smart city initiatives. This cluster also includes smaller European cities, such as Ljubljana, Catania, and Bari, which are focused on improving smart mobility and environmental initiatives. Overall, the cities in this cluster emphasize sustainability, smart governance, and integrating technological growth with cultural preservation.
Cluster 2 includes cities such as Madrid, Abu Dhabi, Seoul, Dubai, Budapest, and several major Asian and Eastern European metropolises. These cities are known for rapid urbanization and cutting-edge technological advancements. Places like Shanghai, Beijing, Hong Kong, and Seoul lead in urban mobility, high-speed internet infrastructure, and automation. Meanwhile, Dubai and Abu Dhabi stand out in the Middle East for their modern infrastructure and transformation into global technology hubs. Eastern European cities like Moscow, St. Petersburg, and Budapest have embraced large-scale smart city initiatives to enhance public services, transportation, and sustainability. The commonality among these cities is their rapid population growth, heavy investment in smart technology, and focus on integrating these advancements into urban planning.
In Cluster 3, we find cities like Oslo, Amsterdam, Copenhagen, Stockholm, Montreal, Vienna, Singapore, and many more from North America and Europe. These cities are recognized leaders in smart governance, quality of life, sustainability, and innovation. Cities like Amsterdam, Copenhagen, Stockholm, and Oslo are often seen as global pioneers in smart city initiatives, particularly in sustainability, green energy, and reducing carbon footprints. North American cities such as New York, Toronto, Chicago, and Los Angeles have made significant strides in upgrading transportation, smart governance, and infrastructure. Cities like Helsinki, Vienna, and Zurich are known for their exceptional quality of life, clean energy solutions, and advanced urban mobility systems. The cities in this cluster are united by their mature smart city programs, strong governance, and focus on innovation in public services such as transportation, healthcare, and energy.
This overlapping indicates that urban areas cannot always be distinctly categorized due to their complex and diverse attributes. Therefore, such overlaps provide a more nuanced understanding of their urban dynamics and the multi-dimensional aspects of smart city development.
4.7. Features Importance Analysis
Non-numeric columns such as Id, City, Country, and the target column SmartCity_Index have been dropped from the features used for modeling. The target variable SmartCity_Index is isolated for prediction. A total of 80% of the data are used for training and 20% are used for testing, ensuring that the model is trained on one portion of the data and evaluated on another to assess its generalization ability. After the training process, the model makes predictions on the test set. Several performance metrics are computed to evaluate its effectiveness: (i) the mean squared error (MSE), which measures the average squared difference between actual and predicted values; (ii) the root mean squared error (RMSE), the square root of the MSE and a more interpretable measure; (iii) the R-squared () value, which explains the proportion of variance in the target variable that is predictable from the features, and finally, (iv) Average across 5 folds. Cross-validation involves splitting the data into several folds or subsets. In 5-fold cross-validation, the dataset is divided into 5 equal parts. The model is trained on 4 parts and validated on the remaining 1 part. This process is repeated 5 times, each time using a different fold for validation while training on the rest.
4.8. Random Forest
A random forest regressor is used to model the relationship between the features and the target variable. After the training process, the model makes predictions on the test set. Several performance metrics are computed to evaluate its effectiveness.
The MSE value is 60512.58, RMSE is 245.99, and the value is 0.899. This indicates that approximately 89.9% of the variance in the SmartCity_Index is explained by the model. However, the average across 5 folds is −0.0693. The high , compared to the negative during cross-validation, highlights that the models’performance is unstable across different data splits. High variability and outliers in the dataset are likely contributing to the overfitting problem. although these are intrinsic characteristics of the cities.
4.9. SVM
The MSE is 8990.17, while the RMSE is 94.82, which indicates that, on average, the model’s predictions deviate from the actual values by approximately 95 units, suggesting a reasonable level of accuracy. A value of 0.985 shows that the model explains 98.5% of the variance in the target variable, meaning it captures almost all the patterns within the data. The cross-validated average score, calculated as 0.747, indicates that the model generalizes relatively well compared to Random Forest.
4.10. Gradient Boosting
In this case, MSE is 52320.73, RMSE is 228.73, and has a score of 0.9135. The MSE value suggests that the model is performing reasonably well. The score of 0.9128 indicates that the model explains about 91.28% of the variance in the target variable. The average cross-validation of 0.2011 indicates that the Gradient Boosting model’s performance during cross-validation is not consistent. Similar to the Random Forest, the Gradient Boosting model appears to be overfitting.
- Model parameterization
With regard to model parameterization, different considerations have been applied:
- The random forest model deploys 100 trees, which is a standard choice for balancing computational cost and model accuracy. Increasing the number of trees generally improves performance but also increases computation time.
- The SVM model employs a linear kernel. This choice is appropriate as it makes it easier to interpret feature weights, as the model essentially performs a linear regression.
- The gradient boosting model uses default parameters, although the model’s performance can often be improved by tuning parameters such as the number of boosting stages, the learning rate, and the maximum depth of the individual trees.
- Conclusion
Based on the evaluation of the three ML models—Random Forest, Gradient Boosting, and SVM—it is evident that both Random Forest and Gradient Boosting suffer from substantial overfitting. Instead, the SVM is chosen as the preferred model due to its superior stability and generalizability, making it the most appropriate model for understanding the contributions of various features to the prediction task, as denoted by Table 10.

Table 10.
Feature importance (descending order) according to SVM model.
5. Discussion
The following discussion is articulated according to two parts. The first proposes some recommendations on how clustering models support urban planning, reviewing future trends and strategies, including the importance of visualization in decision-making. The second part reviews the results deriving from the experiments.
5.1. Urban Planning and Clustering
By employing machine learning methods such as k-means clustering, hierarchical clustering, GMM, and SOM, this study highlights the ability of clustering to reveal patterns and similarities among cities based on their smartness. These techniques help policymakers understand how different cities compare in terms of dimensions like smart living, smart mobility, and smart governance. The research emphasizes that cities in the same cluster share common strengths, offering insights into which areas need improvement and which cities can serve as models for others. This approach allows for more informed, data-driven urban planning.
The future trends in urban planning will increasingly rely on advanced AI techniques, such as clustering, to make sense of the vast amounts of urban data generated by smart cities. These techniques enable city planners to prioritize interventions, allocate resources efficiently, and focus on improving areas that most significantly contribute to urban quality of life, such as healthcare, transportation, and environmental sustainability. The ability to cluster cities and assess their performance across different dimensions allows for more targeted and strategic urban policies that can be tailored to specific urban contexts.
Visualization and user interfaces (UI) will play a crucial role in transforming these complex data analyses into actionable insights for decision-makers. Effective visualization tools can turn data from clustering models into intuitive dashboards, enabling urban planners and policymakers to quickly grasp the performance of their city across various metrics. This helps in identifying which policies are working and where adjustments are needed. For instance, cities that score highly in smart living but lag in smart mobility can be easily identified through well-designed visual dashboards, allowing for immediate strategic focus.
Furthermore, the integration of these data insights into decision-making platforms enables real-time monitoring of urban performance. Future smart city strategies will benefit from the development of user-friendly interfaces that not only visualize these clusters and trends but also allow city administrators to simulate potential interventions and see their predicted outcomes. By visualizing data in accessible ways, city leaders can better engage with stakeholders, including citizens and businesses, to co-create solutions that enhance the overall urban environment.
Clustering in urban planning offers a method to analyze and group cities, driving better-targeted interventions and policies. Future trends point to more sophisticated AI-driven analyses supported by strong visualization tools and intuitive user interfaces, which will become essential for informed decision-making and effective management of smart city initiatives. This approach will enable cities to become more adaptive, resilient, and responsive to the evolving needs of their populations.
5.2. Clustering Analysis
The clustering of smart city indices has been analyzed using several methods. In particular, according to the elbow method, k-means clustering divides the cities into five distinct clusters. Cities within each cluster are relatively close to each other, indicating similar smart city indices. This method is straightforward but may not capture complex relationships between cities.
The dendrogram shows a hierarchical relationship between cities, providing a detailed view of similarities and differences. It is useful for understanding the nested structure of clusters but can be complex to interpret for large datasets. This method can identify more nuanced relationships but may be less intuitive than k-means. SOM clustering uses a neural network approach to map high-dimensional data into a lower-dimensional space. It effectively visualizes complex relationships and provides clear boundaries using convex hulls, but the interpretation of clusters can be less direct. Moreover, it accounts for overlapping clusters.
The feature importance values provide insight into the relative contribution of each feature to the models’ predictions. The results show that smart living is by far the most important feature, with an importance of 0.259014. This suggests that smart living contributes significantly more to the model’s ability to predict the target variable compared to the other features. Its dominant importance may indicate that this aspect of smart city development has the most direct impact on the overall Smart City Index.
Smart mobility comes in second, with an importance of 0.170147. While its contribution is lower than smart living, it still plays an important role in the model’s predictions, indicating that mobility infrastructure and services are key factors in the development of a smart city.
Smart environment follows closely behind, with an importance of 0.163159. This suggests that environmental factors are an important driver in the Smart City Index, although less impactful than smart living and mobility.
Smart economy, with an importance of 0.149919, indicates that economic factors contribute meaningfully to the model’s predictions, though not as much as smart living, mobility, and environment. Economic factors play a supporting role in determining the Smart City Index.
Smart people has a importance of 0.137956, suggesting that human capital and social elements of the city have a moderate influence on the prediction of the target variable, slightly less than the economic aspects.
Smart government has the lowest importance, with a value of 0.119805. This indicates that governance factors, while still relevant, are less critical in the overall prediction of the Smart City Index compared to the other features. Its relatively low importance could imply that the data being modeled place less emphasis on governance in determining smart city performance.
6. Conclusions and Future Work
In this study, we have analyzed the smartness of cities using both unsupervised and supervised learning models. Applying unsupervised learning techniques such as k-means clustering, hierarchical clustering, SOM, and GMM provided valuable insights into the natural groupings and similarities among the cities based on their smart city indices. These clustering methods revealed intrinsic patterns and allowed for a comparative analysis of the cities, highlighting the distinct characteristics of each cluster.
Furthermore, the use of an SVM model enabled us to determine the importance of various features contributing to a city’s smartness. The integration of these methodologies offers a robust framework for understanding what makes a city ’smart’ and provides actionable insights for policymakers and urban planners to enhance urban living standards.
This research opens several avenues for future work. Firstly, expanding the dataset to include more recent data and additional features can provide a more comprehensive analysis and capture the dynamic nature of smart city development. Incorporating real-time data streams from IoT devices and social media could further enhance the granularity and accuracy of the analysis.
Secondly, exploring advanced ML techniques such as deep learning and reinforcement learning could offer new perspectives and improve the performance of clustering and feature importance analysis. Techniques like graph-based clustering and network analysis could be particularly useful in understanding the complex interdependencies and relationships between different aspects of smart cities.
Thirdly, a deeper investigation into the impact of socio-economic and cultural factors on the smartness of cities can provide a more holistic view. This includes examining how these factors influence residents’ perceptions and how they can be integrated into the existing indices to create a more inclusive and representative measure of smart city performance.
Lastly, developing interactive and user-friendly visualization tools can aid in the dissemination of findings to a broader audience, including policymakers, urban planners, and the general public. These tools can help stakeholders better understand the data and make informed decisions to drive the smart city agenda forward.
Author Contributions
Conceptualization, E.B.; methodology, E.B.; software, E.B. and A.G.; validation, A.G.; formal analysis, E.B.; investigation, A.G.; resources, E.B.; writing—original draft preparation, E.B.; writing—review and editing, A.G.; supervision, E.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data and software are available at https://github.com/EBarbierato/smart_cities_clust_feat_imp, accessed on 1 September 2024.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| TLA | Three letter acronym |
| LD | Linear dichroism |
References
- United Nations iLibrary. World Cities Report; United Nations: San Francisco, CA, USA, 2022. [Google Scholar] [CrossRef]
- Son, T.H.; Weedon, Z.; Yigitcanlar, T.; Sanchez, T.; Corchado, J.M.; Mehmood, R. Algorithmic urban planning for smart and sustainable development: Systematic review of the literature. Sustain. Cities Soc. 2023, 94, 104562. [Google Scholar] [CrossRef]
- Lytras, M.D.; Visvizi, A.; Sarirete, A. Clustering Smart City Services: Perceptions, Expectations, Responses. Sustainability 2019, 11, 1669. [Google Scholar] [CrossRef]
- Okonta, D.E.; Vukovic, V. Smart cities software applications for sustainability and resilience. Heliyon 2024, 10, e32654. [Google Scholar] [CrossRef]
- Yigitcanlar, T.; Degirmenci, K.; Butler, L.; Desouza, K.C. What are the key factors affecting smart city transformation readiness? Evidence from Australian cities. Cities 2022, 120, 103434. [Google Scholar] [CrossRef]
- Liu, H. City evaluation methodology: An overview. Dili Yanjiu 2024, 43, 596–620. [Google Scholar] [CrossRef]
- Mills, D.E.; Pudney, S.; Gomes, R.C.; Sarturi, G. Smart City Capacities: Extant Knowledge and Future Research for Sustainable Practical Applications. Sustainability 2024, 16, 3719. [Google Scholar] [CrossRef]
- Zamponi, M.E.; Barbierato, E. The Dual Role of Artificial Intelligence in Developing Smart Cities. Smart Cities 2022, 5, 728–755. [Google Scholar] [CrossRef]
- Janusz, M.; Kowalczyk, M. How Smart Are V4 Cities? Evidence from the Multidimensional Analysis. Sustainability 2022, 14, 10313. [Google Scholar] [CrossRef]
- Cantuarias-Villessuzanne, C.; Weigel, R.; Blain, J. Clustering of European Smart Cities to Understand the Cities’ Sustainability Strategies. Sustainability 2021, 13, 513. [Google Scholar] [CrossRef]
- Correia, D.; Marques, J.L.; Teixeira, L. Assessing and Ranking EU Cities Based on the Development Phase of the Smart City Concept. Sustainability 2023, 15, 13675. [Google Scholar] [CrossRef]
- Ciacci, A.; Ivaldi, E.; González-Relaño, R. A Partially Non-Compensatory Method to Measure the Smart and Sustainable Level of Italian Municipalities. Sustainability 2021, 13, 435. [Google Scholar] [CrossRef]
- Kutty, A.A.; Kucukvar, M.; Onat, N.C.; Ayvaz, B.; Abdella, G.M. Measuring sustainability, resilience and livability performance of European smart cities: A novel fuzzy expert-based multi-criteria decision support model. Cities 2023, 137, 104293. [Google Scholar] [CrossRef]
- Gazzeh, K. Ranking Sustainable Smart City Indicators Using Combined Content Analysis and Analytic Hierarchy Process Techniques. Smart Cities 2023, 6, 2883–2909. [Google Scholar] [CrossRef]
- Dashkevych, O.; Portnov, B.A. Criteria for Smart City Identification: A Systematic Literature Review. Sustainability 2022, 14, 4448. [Google Scholar] [CrossRef]
- Silvestri, S.; Tricomi, G.; Bassolillo, S.R.; De Benedictis, R.; Ciampi, M. An Urban Intelligence Architecture for Heterogeneous Data and Application Integration, Deployment and Orchestration. Sensors 2024, 24, 2376. [Google Scholar] [CrossRef]
- Hamerly, G.; Elkan, C. Learning the k in k-means. Adv. Neural Inf. Process. Syst. 2003, 16. Available online: https://proceedings.neurips.cc/paper_files/paper/2003/file/234833147b97bb6aed53a8f4f1c7a7d8-Paper.pdf (accessed on 24 September 2024).
- Aurenhammer, F.; Klein, R. Voronoi Diagrams. Handb. Comput. Geom. 2000, 5, 201–290. [Google Scholar]
- De Berg, M. Computational Geometry: Algorithms and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Decelle, A.; Seoane, B.; Rosset, L. Unsupervised hierarchical clustering using the learning dynamics of restricted Boltzmann machines. Phys. Rev. 2023, 108, 014110. [Google Scholar] [CrossRef]
- Kohonen, T. Self-organized formation of topologically correct feature maps. Biol. Cybern. 1982, 43, 59–69. [Google Scholar] [CrossRef]
- Rasmussen, C. The infinite Gaussian mixture model. Adv. Neural Inf. Process. Syst. 1999, 12. Available online: https://proceedings.neurips.cc/paper_files/paper/1999/file/97d98119037c5b8a9663cb21fb8ebf47-Paper.pdf (accessed on 24 September 2024).
- Genuer, R.; Poggi, J.M.; Genuer, R.; Poggi, J.M. Random Forests; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Chang, Y.W.; Lin, C.J. Feature ranking using linear SVM. In Proceedings of the Causation and Prediction Challenge. PMLR, Hong Kong, China, 3–4 June 2008; pp. 53–64. [Google Scholar]
- Konstantinov, A.V.; Utkin, L.V. Interpretable machine learning with an ensemble of gradient boosting machines. Knowl.-Based Syst. 2021, 222, 106993. [Google Scholar] [CrossRef]
- Maćkiewicz, A.; Ratajczak, W. Principal components analysis (PCA). Comput. Geosci. 1993, 19, 303–342. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).