Abstract
The Internet of Things (IoT) consists of complex and dynamically aggregated elements or smart entities that need decentralized supervision for data exchanging throughout different networks. The artificial bee colony (ABC) is utilized in optimization problems for the big data in IoT, cloud and central repositories. The main limitation during the searching mechanism is that every single food site is compared with every other food site to find the best solution in the neighboring regions. In this way, an extensive number of redundant comparisons are required, which results in a slower convergence rate, greater time consumption and increased delays. This paper presents a solution to optimize search operations with an enhanced ABC (E-ABC) approach. The proposed algorithm compares the best food sites with neighboring sites to exclude poor sources. It achieves an efficient mechanism, where the number of redundant comparisons is decreased during the searching mechanism of the employed bee phase and the onlooker bee phase. The proposed algorithm is implemented in a replication scenario to validate its performance in terms of the mean objective function values for different functions, as well as the probability of availability and the response time. The results prove the superiority of the E-ABC in contrast to its counterparts.
1. Introduction
IoT refers to the network of inter-relating physical objects that have the ability to exchange data among a network at a remarkable speed for smart and intelligent devices. [1,2,3,4]. The data from smart devices are collected in an aggregated manner to be shared in a secure way for dependable solutions. The IoT enables such physical entities to sense, discover, recognize, think, communicate and share data in a variety of applications [5,6]. The IoT-based system reduces the human workload in multiple domains [7,8,9,10]. IoT-enabled structures are complicated and dynamic in nature. Thus, there are many significant challenges that have to be solved. Artificial intelligence (more specifically, swarm intelligence) deals with such complex problems well because of its superior properties such as robustness and flexibility [11]. SI generates benefits for IoT-enabled structures, which can be shaped as a swarm of simple devices or can incorporate swarm intelligence-based algorithms to attain global objectives [12]. In this way, a global optimum can be obtained at the system level by starting with basic rules for individual behaviors and interactions. This capability to self-organize is essential to adapt systems to changing environmental circumstances, to scale effectively and to ensure robust functioning for a system’s long-term viability.
Cloud computing describes the on-demand provision of services like data storage, data processing, etc. Cloud-based systems are most commonly used in fields like WSNs, IoT, big data, etc., In the IoT, the cloud maintains central repositories for these applications, where big data can be saved to analyze and alert stakeholders and to protect from possible losses [13]. The cloud server is considered as the primary or main server that is responsible for providing services as needed; therefore, the big data from massive IoT devices are usually processed through fog servers and then stored in the cloud. A large amount of replicated data is also saved in the cloud, which should be eliminated to save storage. Cloud-based systems minimize the expenses of IT systems or networks by enabling cost-effective, extensible, flexible and widely available resources from anywhere and at any time. These systems are able to transfer the enormous data packages that are assembled by the IoT [14,15,16].
This paper presents the enhanced ABC mechanism to improve the optimization performance. The main objective is to improve the searching mechanisms. This work solves the identified problem by choosing different criteria for employed and onlooker bees to choose their food sources. The main contributions of this work are as follows:
- This work explores the schemes that utilize either standard ABC-based schemes or modified versions to achieve better performance in terms of optimization;
- The proposed work resolves the issue of excessive time consumption during the search mechanism for the employed bee phase and onlooker bee phase in modified versions of the ABC;
- The proposed algorithm eliminates redundant comparisons when finding suitable solutions, where every single food site is compared with every other food site. We obtain the finest food sites in contrast to neighboring sites, which results in the exclusion of poor sources;
- Next, the enhanced version of the ABC algorithm is executed by data centers in order to find the optimal path for data replicas. Finally, the proposed E-ABC algorithm’s results are validated in comparison to its counterparts.
The rest of the manuscript is organized as follows. Section 2 presents a literature review for data sharing and replication techniques. The proposed solution is presented in Section 3. Section 4 discusses the efficiency of the proposed scheme; moreover, it presents a comparison of the E-ABC with some other well-known algorithms. Finally, Section 5 concludes our work.
2. Literature Review
In this section, schemes that cover ABC algorithm-based solutions are explored while considering its optimization. The literature is categorized into standard ABC schemes, variants of the ABC and optimized data-sharing and replication-based techniques.
2.1. Standard ABC Schemes
This sub-section explores standard artificial bee colony (ABC) algorithm-based solutions to achieve optimization. The SI-based optimized ABC is inspired by the foraging behavior of honey bee swarms. It consists of three types of bees: an employed bee, an onlooker bee and scout bees. Employed bees search for food sources, analyze the amount of nectar and return to the dancing area and perform their dance. Onlooker bees observe the employed foragers’ dances from their hives and choose a food site accordingly. The third type of bees, named scout bees, are independent of employed and onlooker bees. In the ABC, the honey bee swarms explore the area and search for food sources; once they find sufficient sources, these bees memorize the locations of these sources before they leave the hive. Afterwards, these bees start dancing in the dancing zone; this dance conveys the food source’s location to the other bees that reside in the hive [17].
The ABC is applicable in numerous fields, such as continuous optimal problems, data clustering, data replication, image classification, task scheduling and network reconfiguration complexity. The ABC is known for its simplicity, minimal parameters and robust global search capability [18]. The ABC is applicable to numerous fields, including research, social sciences, data clustering, neural networks and many more. Moreover, it can be utilized in cloud computing to reduce load balancing [19]. The ABC approach is most commonly utilized in finding optimal solutions. The unique problem-solving method of the ABC algorithm makes it superior to other algorithms [20]. The scout bees examine food sites randomly, as seen in Figure 1.
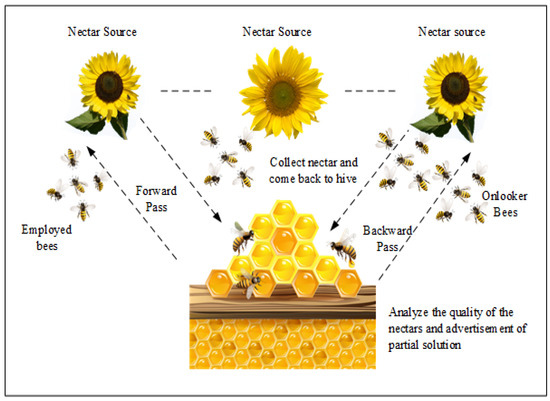
Figure 1.
Intelligent behavior of bees in ABC.
2.2. Enhanced Variants of ABC Schemes
This sub-section explores the variants of the ABC algorithm where researchers have modified the existing functionality to achieve better results as per its applicability. Karaboga et al. presented an enhanced version of the ABC algorithm named the quick artificial bee colony algorithm (qABC). In qABC, the authors pointed out that onlooker bees choose their food sources differently as compared to employed bees. Thus, a new definition for the onlooker bee is introduced in qABC, while, in the original ABC technique, both the employed and onlooker bees select their food sources using the same formula. Another modification introduced in this algorithm is that it chooses a solution in neighboring areas using the mean Euclidian distance. Moreover, the efficiency of qABC was tested on various benchmark functions considering the neighborhood radius. The experimental outcomes prove the efficiency of the qABC algorithm [21]. Aslan et al. presented an improved quick artificial bee colony algorithm (iqABC). A new definition for exploitation is presented in this work for the purpose of enhancing the early convergence rate without affecting the final solutions. To attain encouraging results, four different search schemas are added in the ABC algorithm. Additionally, a finestLimit parameter is added in the workflow of the standard ABC algorithm. Experiments were performed for the finestLimit parameter and various benchmark problems were used to test the performance of the iqABC algorithm while comparing it with some other well-known algorithms. The results show the efficiency of the iqABC algorithm over other preceding algorithms [22]. Sumin Li et al. present the IABC algorithm, which enhances the modified search strategy of the GABC with a dynamic inertia weight factor. Experimental results demonstrate that the IABC outperforms both the standard ABC and GABC in terms of search accuracy and convergence speed [23]. Li et al. presented an improved algorithm named EMABC-NS that utilizes multi-strategy collaboration and a neighborhood search. It incorporates information from both the global best individual and nearby individuals during the search, enhancing the search strategy for employed and onlooker bees. The introduction of a modification rate (MR) randomizes the solution dimensions. The EMABC-NS outperforms competitors in benchmark functions and engineering problems, demonstrating its effectiveness in practical applications [24]. Cui et al. presented an ABC algorithm named FOABC that uses fractional-order calculus to enhance the local search capabilities by incorporating memory properties. The FOABC refers to past foraging behaviors stored in memory when generating new candidate solutions. An improved search strategy in the employed bee phase balances diversification and intensification. Experimental results on CEC benchmark problems show the FOABC’s superiority over other ABC variants and its effectiveness in practical applications like robot path planning [25]. Tingyu et al. presented an enhanced MaOABC-TA algorithm, incorporating two archives (convergence and diversity) and three search strategies, inspired by the Two_Arch2 method. A new probability selection strategy prioritizes diverse solutions. Experimental comparisons with 10 MaOEAs and 3 AfBCs on benchmark sets reveal that MaOABC-TA outperforms the others in terms of the inverted generational distance (IGD) and hypervolume (HV) values [26].
2.3. Data Sharing and Replication-Based Techniques
ABC-based schemes are applicable in the identification of replication in data and files. The solutions in the literature attempt to identify replicas as food sources using the ABC and its variants. Mansouri et al. presented a scheme named prefetching-aware data replication (PDR). The connection is found among the data replicas while obtaining the data from increasingly popular remote sites. To accomplish data replicas, the PDR utilizes fuzzy logic. The structure of the PDR is based on four elements: the access number, the replica cost, the duration since the last access for replicas and data availability [27]. Najjar et al. [28] introduced a robust spanning tree technique in the IoT and named it RST-IoT. The presented technique is used for tree construction. It utilizes the ABC approach to produce appropriate trees for great productivity. The major advantage of adopting this approach is that it produces trees that are close to optimum. The generated trees are arranged in accordance with their preferences. The simulation findings show that RST-IoT outperforms previous methods with regard to stability and energy usage. Saleem et al. [29] described a multi-objective based optimization technique to select and place data replicas. The presented approach uses the artificial bee colony algorithm to achieve optimal solutions and is called the multi-objective optimized ABC algorithm (MOABC). In the presented approach, the ABC is used to place the replicated data in the finest possible location in terms of the shortest distance and lowest cost. Moreover, the MOABC uses the knapsack technique to save money while achieving load balancing across data centers. In this approach, the data centers employ artificial bee colonies to determine the optimal data replication sequence. The suggested technique is implemented to investigate the effectiveness and accessibility of data as well as the cost-optimality of replicas. The resultant outcomes demonstrate that the MOABC produces effective solutions and outperforms competing methods.
Cui et al. [30] presented the ABC with dynamic composition, where bees are dynamically assigned on the basis of a searching space limit, as compared to the existing ABC schemes that involve a fixed ratio of employed and onlooker bees, which restricts the utilization of the available resources when searching for the best food. Kruekaew et al. presented an enhanced scheme named HABC_LJF for virtual machines that aimed to improve task scheduling and load balancing [31]. Li et al. [32] demonstrated an ABC-based hybrid approach that aimed to solve task scheduling. Liu et al. presented an efficient fog computing resource-scheduling strategy to address inefficiencies in IoT edge networks with increasing data input. Utilizing particle swarm optimization (PSO), the strategy optimizes the load balance, computation time and energy consumption within a single fog cluster. Additionally, the particle swarm genetic joint optimization artificial bee colony algorithm (PGABC) optimizes task scheduling among fog clusters, further reducing the delay and energy consumption. Experimental results demonstrate that the PGABC outperforms the GABC, the ABC and the PSO in reducing time delays [33].
2.4. Comparative Discussion and Problem Statement
The standard ABC algorithm [17] exhibits strong exploration properties but lacks efficiency in exploitation. With only two adjustable parameters (colony size and maximum cycle number), it is simple to implement and flexible, allowing easy adjustments. Modifications to the search equation in some schemes enhance the efficiency and convergence speed. Researchers have explored hybrid techniques, combining the ABC with other algorithms and hybridizing the ABC with data clustering algorithms for improved performance in terms of accuracy, convergence rates, efficiency and robustness. In this section, a comparative analysis of existing schemes is presented to explore the optimization ability of enhanced ABC-based schemes, as illustrated in Table 1.

Table 1.
Summary of existing ABC-based schemes.
The main problem during the search operation is that the standard ABC algorithm [17] utilizes the same criteria for both employed and onlooker bees to choose food sources. However, employed and onlooker bees choose their food sources differently. A modified variant named qABC [21] resolves this issue, but it performs a large number of comparisons to find the best solution. It compares each source with every other source in the neighborhood. Consequently, it leads to several issues, such as slow convergence rates, greater time consumption and increased delays.
3. Proposed Solution
We present the enhanced ABC (E-ABC), in which the employed bee phase and onlooker bee phase of the ABC algorithm enhance the searching mechanism for better optimization. It presents a solution for the selection of the finest food site with higher quality than other algorithms. In order to obtain a faster convergence speed, the search schemas of the employed bees and onlooker bees are improved. Existing schemes [17,33] also use a similar framework or structure. The list of notations is shown in Table 2.

Table 2.
List of notations.
There are three phases, namely the employee bee phase, onlooker bee phase and replication position optimization phase, which describe the workflow of the proposed ABC, as shown in Figure 2. In the ABC algorithm, the search schemas rely on the exploitation and exploration abilities of bees to attain enhanced convergence rates. Prior to these modules, first, the food sites are initialized at random. Subsequently, the acquired food sites are examined and their values are estimated using the objective function. In the initial stage, control parameters such as the colony size, maximum iterations, maximum number and limit are initialized. Food sites are initiated at random, ranging between (0, 1), computed as + rand (0, 1) × (), where i denotes the total number of food sites set by scout bees and ranges from 1 to sn. Moreover, m ranges between 1 and d, where d represents the number of optimum parameters depicted so as to minimize the objective function. In addition to this, li and ui represent the lower and upper bounds of the parameter , respectively.

Figure 2.
Main phases of the proposed E-ABC scheme.
3.1. Employed Bee Phase
The frequency of perturbation in the original ABC algorithm is inflexible, which means that the frequency is fixed and, as a result, the convergence rate of the ABC algorithm becomes slower. This is because, if the purpose is to generate a new solution vi, in this case, only a single parameter of root solution xi is modified, which results in a slower convergence rate. Hence, a new parameter MR is used in the employed bee phase and onlooker bee phase. MR corresponds to the modification rate, which is a randomly appointed number that ranges between 0 and 1. Thus, in the present work, the value for the newly generated solution is computed by utilizing the modification rate, as given in Equation (1).
As discussed earlier, the MR has a value from 0 to 1; k is a random number that ranges from 1 to SN and it has an index that must be different from i. Furthermore, as a result of the large amount of comparisons, the time consumption is high. It also affects the quality of the global best solution. In the qABC, there is an opportunity to eliminate the possibility of selecting certain solutions since the focus is on selecting the best possible solutions. The literature also shows that due to this undesired behavior, sometimes, the original ABC performs better than the qABC. Thus, considering these factors that cause the algorithm’s poor performance, a new parameter named finestLimit is included in the ABC, as in the iqABC algorithm. However, the difference between the present work and the iqABC is that, in the iqABC, the workflow is reverted to the original ABC in such cases. However, in the proposed algorithm, a modified definition is used for this case, which helps in modifying the flow from the finestLimit parameter to the new modification rate phase as Vfinest,j = xfinest,j + (xfinest,j − xi,j).
Furthermore, random food sources are produced in the population at the start of the algorithm. Following this, a comparison is performed between the total evaluations totalEval and maximum evaluations maxEval, as shown in step 2. A counter named EBPTrials is activated if maxEval exceeds totalEval or is equal to totalEval in step 3. The counter counts how many times xfinest fails to enhance the employed bee phase (EBP) to the finestLimit value. The comparison determines whether the finest limit EBP will be employed or not. In the case where the value of finestLimit exceeds the EBPTrials value or they are both equal, then the ith employed will generate a solution in the neighboring region with the help of Equation (2) from [19], as in step 8 and 19. If the value of the trial at index ifinest is zero, then the value for EBP is revised; otherwise, its value will be increased and EBPTrials is also incremented accordingly in step 13. If the scenario is the opposite, where the best limit is less than EBPTrials, then the ith employed generates a solution that guides the employed bee to the related food source, as shown in Algorithm 1.
| Algorithm 1: Food Source Identification by Employee Bee |
| Input: SN, Output: Selected Food Source 1. for = 1 to SN do 2. if then 3. if then 4. send employee bees to the finest food site 5. = get finest food site index, = finest food site 6. Generate 7. = new food source 8. if then 9. Replace 10. trial() = 0 11. else 12. trial() = trial() + 1 13. EBPTrials = EBPTrials + 1 14. end if 15. send employee bees to the finest food site 16. else 17. send employee bees to the relevant food sites 18. = new food site using Equation (1). 19. if fit() ≥ fit() then 20. Replace , Set trial(i) = 0 21. else 22. trial(i) = trial(i) + 1 23. end if 24. send employed bees to the related food source 25. end if 26. 27. end if 28. end for |
3.2. Onlooker Bee Phase
At the start, the SN sources are initialized at random in the population and probabilistic values for fitness are computed to choose food sources. The SN depicts the size of the population. Afterwards, all changes that are made in the employed bee phase are also implemented here. A comparison between totalEval and maxEval is performed and the total bees are contrasted with SN. A new solution in the neighboring region is generated if the best limit exceeds OBPTrials or is equal to OBPTrials. The new candidate solution is generated as Vfinest,j = xfinest,j + (xfinest,j − xs,j). Here, xs is a source/site selected by the onlooker bees and it possesses jth parameter xs,j, while vfinest is a newly generated solution that possesses jth parameter vfinest,j. It utilizes Equation (1) when OBPTrials is greater than or equal to the finest limit value, as shown in step 7 of Algorithm 2.
| Algorithm 2: Finest Food Site Selection by Onlooker Bee |
| Input: SN, food sites Output: , 1. for i = 1 to SN do 2. p() = 3. end for 4. Set totalBee = 1, Set currentBee = 1 5. while do 6. if rand(0,1) ≤ p() then 7. if then 8. send onlooker bees to the finest food site 9. = get finest food site index 10. = finest food site 11. = new food site 12. if fit() ≥ fit() then 13. Set = , trial() = 0 14. else 15. trial() = trial() + 1 16. OBPTrials = OBPTrials + 1 17. end if 18. send onlooker bees to finest food site 19. else 20. = a new food site through Equation (1) 21. if fit() ≥ fit() then 22. = 23. trial(currentBee) = 1 24. else 25. trial(currentBee) = trial(currentBee) + 1 26. end if 27. send onlooker bees to the chosen food site 28. end if 29. totalEval = totalEval + 1 30. totalBee = totalBee + 1 31. end if 32. currentBee = currentBee + 1 33. if currentBee ≥ SN then 34. currentBee = 1 35. end if 36. end while |
3.3. Optimized Replication Position
The E-ABC is applied to assess replicas and place them through nodes in a cloud environment considering a shorter path. The E-ABC offers cost-effective optimal solutions and attains burden sharing or load balancing via data centers (DCs). Accessing and placing the DCs at the correct positions is crucial. The suggested solution demonstrates replication access and suitable deployment in the cloud through nodes. We obtain the quickest route between the DCs at the lowest cost and utilize a heterogeneous method to locate replicas at the finest position, in an optimized way, using statistical distribution. The costs and quantity of available data replications differ amongst the DCs. In the given scheme, employee bees are capable of acquiring and depositing data correctly at the DCs at the lowest possible cost. All the DCs are linked hierarchically and circularly across all levels. Users are at the system’s exterior level, and they may use the DCs to transmit jobs to replicas in order to obtain the best results at the lowest cost, duration and distance. Placing data replications at locations closer to users, at an acceptable cost, via the DCs is a difficult task; thus, AI-based techniques are used to achieve the objective of optimized data replication and placement in the DCs. The E-ABC employs an improved variant of the ABC, which decreases the number of comparisons and achieves high data accessibility while reducing delays. Next, we will discuss the optimal replica position.
The users reside at the system’s outermost position and have the ability to transmit tasks to replication in order to attain the best possible place in terms of time, distance and cost. Accessing and placing the DCs at the appropriate position is achieved through nodes in cloud computing. Thus, to achieve the excellent capability of selecting nodes with cost-effectiveness and a shorter path among data centers, and to accomplish optimum data replication, a heterogeneous approach is utilized. Moreover, at the same time, all the DCs are connected at all levels, both hierarchically and circularly. Considering these points, it is concluded that accessing the DCs and placing them at appropriate positions is very important concerning honeybees, since these bees are liable to explore the lowest-cost path efficiently. Data replicas reside at the DCs in order to fulfill the user’s tasks. Geometric distribution and Zipf are used with the purpose of allocating replicas and placing files between data centers that are nearer to users. Zipf is calculated as It is used for the placement of replicated files among the different DCs that are very close to the users. Here, α represents the factor data replication distribution and α ranges between 0 ≤ α < 1, while i = 1, …, n. The geometric distribution is another important factor that is used to randomly allocate and place replication files ideally together with various parameters. The value for the GD can be obtained using . Here, p represents access to a replica file. The DC provides better efficiency with respect to speed, data accessibility and reliability and has a higher fault tolerance rate, which results in a higher cost. Considering the cloud environment, the replication cost is a crucial element. Thus, the total cost of the system should be managed in a better way. Every DC has a cost to replicate data, which is strongly associated with each data center. The cost among various data centers is calculated on the basis of the replication number across each data center. In cloud computing, it is very important to access replicas with the minimum cost and place them closer to the user. The replica cost for data file can be computed using Equation (3), where x represents the total number of DCs, represents the cost for file replication at data center and represents the number of replicas of at
4. Results and Discussion
In this section, the performance of the given scheme, E-ABC, is reviewed. This section also presents configuration specifics and details of the experimental findings by introducing a testbed for the implementation of the ABC algorithm. For the backend, we set up a testbed on the C#/ASP.net code through WCF services to implement the ABC algorithm and deploy it on the Windows AZURE cloud. The replicated data files of different applications and software publicly available are physically placed at virtual machines as data centers on the Windows Azure cloud. The front-end of the web application is deployed on a machine with the Windows 10 operating system, 8 GB RAM and 2 processors of the 7th generation with 2.9 GHz and 2.7 GHz. The application initiates a call to the WCF service functions to execute the ABC algorithm and its variants. Initial graphs give information about the convergence speed of the proposed scheme and show the comparison with some standard and well-known variants of the ABC algorithm. After proving the efficiency of the given algorithm, it is implemented in data replication scenarios. Moreover, eight well-known benchmark functions are employed for experimentation. In addition to this, initially, the efficiency of the proposed scheme is analyzed with respect to the finestLimit parameter and numerous functions, including Rastrigin, Dixen Price, Ackley and Griewank, as given in CEC [8]. The base schemes are ABC [17], qABC [21], GABC, iqABC [22] and MOABC [29].
4.1. Evaluation of Performance in Terms of finestLimit Parameter
In this section, experiments are conducted with respect to the finestLimit parameter. In order to analyze the efficiency of the proposed E-ABC, numerous benchmark functions and their base functions are utilized in the experiments. The functions are uni-modal, while other functions, such as , are multimodal functions. Furthermore, the colony size is taken as 20, and the maximum fitness values are taken as 500 and 1500 for 10 dimensions and 30 dimensions, respectively. The limit value is calculated as (colony size x dimensions)/2, and 20 independent runs are conducted with various seeds, as in [8].
Convergence refers to a mathematical concept that can be defined as a series of components that ultimately reaches a single value, known as a limit. Convergence itself is not an algorithm; rather, it is a value that an algorithm manipulates or iterates on. The phrase “fast convergence speed” is used in this study; the term “fast” specifies the algorithm’s convergence rate, and it demonstrates how quickly the ABC converges towards excellent-quality solutions. The value of the limit is calculated as , where CS denotes the colony size and D denotes the dimension [18].
The convergence speed for the proposed E-ABC is examined on Rotated Bent Cigar function , as shown in Figure 3a. It shows the dominance of the E-ABC in contrast to four well-known algorithms, namely the original ABC, quick ABC, global ABC and improved qABC algorithms. The graphical results present the mean objective value versus fitness evaluations. Considering an example where the fitness evaluation value is noted as 500, the mean value against 500 is observed as 8 × 103 for the standard ABC, 7.5 × 103 for the GABC, 5 × 103 for the qABC, 3 × 103 for the iqABC and 2.5 × 103 for the E-ABC. The results reveal that the proposed E-ABC achieves a 45.83% better convergence rate as compared to the ABC. It provides 41.67%, 20.83% and 4.17% better results than the GABC, the qABC and the iqABC, respectively. Figure 3b elucidates the convergence speed with respect to Shifted and Rotated Schwefel function . The results show that the E-ABC achieves the optimal solution, in contrast to the other base schemes. The convergence graph for Shifted and Rotated HappyCat function is shown in Figure 3c. The results show that when the mean objective function value is 1000, the proposed E-ABC reaches the optimal value, while the other schemes require more time to approach the optimal value. Figure 3d presents Shifted and Rotated HGBat function regarding the convergence rate. From the graph, it is clear that the E-ABC reaches the mean objective value of 6 × 102 when the value of the fitness evaluation is five hundred, while the iqABC achieves the same goal when the fitness evaluation value is 1000. The other base schemes require even more time to approach the optimal solution.

Figure 3.
Convergence values for (a) , (b) , (c) and (d) .
4.2. Comparisons of Algorithms on Benchmark Functions
Classical benchmark functions are utilized in order to perform experiments. These benchmark functions are diverse in nature, as some of them are unimodal and some are multimodal and have different characteristics. Moreover, some functions are separable while others are not. For this experiment, the highest fitness value is taken as 50,000, while overall 30 independent runs are conducted against different seeds and we observe the mean objective value for these functions. The effectiveness of these functions is examined on the Rastrigin function regarding the convergence rate, as shown in Figure 4a. For this purpose, the average objective amount for the finest solution is noted. The results show the improved results for the proposed E-ABC as compared to the ABC, qABC and iqABC.

Figure 4.
Convergence speed for (a) Rastrigin, (b) Dixen price, (c) Ackley and (d) Griewank functions.
Next, we consider a scenario where experiments are performed for the convergence speed for the well-known function named the Dixen price function, as depicted in Figure 4b. The efficiency of the proposed E-ABC scheme along with the other three algorithms is examined by noting the average value for the objective function against the fitness evaluation value. The results show that our proposed algorithm completely surpasses its counterparts. After the Dixen price, we implement the E-ABC for the Ackley function in order to test the effectiveness of the proposed E-ABC, as shown in Figure 4c. The graph provides a comprehensive view of the convergence speed for the average value of the objective function against the fitness value. From the results, it is clearly seen that the E-ABC approaches the optimal solution prior to other algorithms when tested on the Griewank function, as shown in Figure 4d.
4.3. Data File Availability
Devices that provide maximum accessibility for the longest duration are said to be trustworthy and scalable. The device should be accessible whenever a user requests data file availability. If a device collapses or if any errors or malfunctions occur, the device is said to be unavailable or unreliable. As a result, guaranteeing maximum file accessibility is critical in cloud-based environment. The probability of data file availability (dfa) is determined using Equation (4) [17], where shows the number of blocks and shows the number of replicas of a file. The cumulative value for block access probability (bap) is also calculated. Case-1 illustrates a structure in which all data file blocks are placed at the DC together. Case-2 shows a situation where the blocks are situated on different DCs individually. The access to replicas for each cost value varies between 0 and 50. From the experimental results, it is noticed that the file availability depends on the cost. As the cost rises, the probability of file accessibility also rises, as shown in Figure 5a, where is observed for the probability. For the cost value of 20, the file availability probability is 0.85, i.e., 85%. As the cost increases, the probability of file availability also increases.

Figure 5.
Probability of file availability is shown in (a,b), presenting the average response time.
4.4. Response Time
The response time is the time that it takes for a system to respond to a service. It depends on the route selected for transmission. The average response time (ART) is given in Equation (5), where is the sending time and is the receiving time of cloudlet k in user j. Moreover, denotes the number of cloudlets for user j [34].
The response time to examine the rising number of cloudlets is elaborated in Figure 5b. The efficiency of the proposed E-ABC with respect to the response time or delay is tested and the results are compared with those of the MOABC and DCR2S. Considering these circumstances, we note the response time in seconds against the number of cloudlets for all considered schemes. For a number of cloudlets of 800, the mean response time is observed as 34 s for the DCR2S, 16 s against the MOABC and 9 s for the presented scheme, E-ABC. From these values, a considerably decreased response time for the E-ABC is noticed. The E-ABC provides 67.5% better results than the DCR2S and 20% better than the MOABC.
5. Conclusions
This work performs optimized data sharing in the IoT, where the search mechanism of the employed bee phase and onlooker bee phase is enhanced using the E-ABC algorithm. The system identifies optimized ways to identify sources that can perform searching in an efficient manner, which reduces redundant operations as well. It optimizes the node identification process with the shortest paths while accessing replicas in files placed at central repositories. A testbed is set up to validate the performance of the proposed E-ABC for data replications in contrast to existing schemes. The experimental results prove the superiority of the proposed E-ABC algorithm compared to its counterparts in terms of the convergence rate for different functions, the probability of file accessibility and the response rate. The E-ABC algorithm offers a 65% better average response time when compared with DCR2S and improves the average response time of MOABC by 20% when the count of cloudlets is taken as 1000. The probability of file accessibility for the proposed scheme is observed to be 85% when the total cost is 20. In the future, file-level de-duplication techniques will be analyzed for possible optimization. Furthermore, we will examine the impact of failed devices handling searching tasks and carrying desired information.
Author Contributions
Conceptualization, A.A., A.U. and M.S.R.; Data curation, A.A., A.U. and I.A.; Funding acquisition, M.S.R., F.A. and A.U.; Investigation, F.A., I.A., M.S.R. and A.U.; Methodology, A.A., A.U. and M.S.R.; Project administration, F.A. and M.S.R.; Software, A.A. and A.U.; Supervision, A.U. and M.S.R.; Validation, M.S.R., F.A. and I.A.; Visualization, A.A., M.S.R. and I.A.; Writing—original draft, A.A., A.U., M.S.R. and I.A.; Writing—review and editing, M.S.R. and F.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research work was funded by the Institutional Fund Projects under grant No. (IFPHI-114-611-2020). Therefore, the authors gratefully acknowledge the technical and financial support of the Ministry of Education and King Abdulaziz University, DSR, Jeddah, Saudi Arabia.
Data Availability Statement
There is no specific dataset linked to this work.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kök, İ.; Okay, F.Y.; Muyanlı, Ö.; Özdemir, S. Explainable Artificial Intelligence (XAI) for Internet of Things: A Survey. IEEE Internet Things J. 2023, 10, 14764–14779. [Google Scholar] [CrossRef]
- Chen, W.; Qiu, X.; Cai, T.; Dai, H.N.; Zheng, Z.; Zhang, Y. Deep Reinforcement Learning for Internet of Things: A Comprehensive Survey. IEEE Commun. Surv. Tutor. 2021, 23, 1659–1692. [Google Scholar] [CrossRef]
- Latif, S.; Driss, M.; Boulila, W.; Huma, Z.e.; Jamal, S.S.; Idrees, Z.; Ahmad, J. Deep learning for the industrial internet of things (Iiot): A comprehensive survey of techniques, implementation frameworks, potential applications, and future directions. Sensors 2021, 21, 7518. [Google Scholar] [CrossRef] [PubMed]
- Franco, J.; Aris, A.; Canberk, B.; Uluagac, A.S. A Survey of Honeypots and Honeynets for Internet of Things, Industrial Internet of Things, and Cyber-Physical Systems. IEEE Commun. Surv. Tutor. 2021, 23, 2351–2383. [Google Scholar] [CrossRef]
- Salih, K.O.M.; Rashid, T.A.; Radovanovic, D.; Bacanin, N. A Comprehensive Survey on the Internet of Things with the Industrial Marketplace. Sensors 2022, 22, 730. [Google Scholar] [CrossRef]
- Fotia, L.; Flávia, D.; Giancarlo, F. Trust in edge-based internet of things architectures: State of the art and research challenges. ACM Comput. Surv. 2023, 55, 1–34. [Google Scholar]
- Selmy, H.A.; Mohamed, H.K.; Medhat, W. Big data analytics deep learning techniques and applications: A survey. Inf. Syst. 2024, 120, 102318. [Google Scholar] [CrossRef]
- Torabi, E.; Ghobaei-Arani, M.; Shahidinejad, A. Data replica placement approaches in fog computing: A review. Clust. Comput. 2022, 6, 3561–3589. [Google Scholar] [CrossRef]
- Öztürk, Ş.; Ahmad, R.; Akhtar, N. Variants of Artificial Bee Colony algorithm and its applications in medical image processing. Appl. Soft Comput. J. 2020, 97, 106799. [Google Scholar] [CrossRef]
- Hansen, E.B.; Bøgh, S. Artificial intelligence and internet of things in small and medium-sized enterprises: A survey. J. Manuf. Syst. 2021, 58, 362–372. [Google Scholar] [CrossRef]
- Sun, W.; Tang, M.; Zhang, L.; Huo, Z.; Shu, L. A survey of using swarm intelligence algorithms in IoT. Sensors 2020, 20, 1420. [Google Scholar] [CrossRef] [PubMed]
- Alsalibi, B.; Mirjalili, S.; Abualigah, L.; Yahya, R.I.; Gandomi, A.H. A Comprehensive Survey on the Recent Variants and Applications of Membrane-Inspired Evolutionary Algorithms. Arch. Comput. Methods Eng. 2022, 29, 3041–3057. [Google Scholar] [CrossRef]
- Yahia, H.S.; Zeebaree, S.R.M.; Sadeeq, M.A.M.; Salim, N.O.M.; Kak, S.F.; Al-Zebari, A.A.; Salih, A.A.; Hussein, H.A. Comprehensive Survey for Cloud Computing Based Nature-Inspired Algorithms Optimization Scheduling. Asian J. Res. Comput. Sci. 2021, 8, 1–16. [Google Scholar] [CrossRef]
- Shakarami, A.; Ghobaei-Arani, M.; Shahidinejad, A.; Masdari, M.; Shakarami, H. Data Replication Schemes in Cloud Computing a Survey. Cluster Comput. 2021, 24, 2545–2579. [Google Scholar] [CrossRef]
- Hassan, W.; Chou, T.-S.; Tamer, O.; Pickard, J.; Appiah-Kubi, P.; Pagliari, L. Cloud computing survey on services, enhancements and challenges in the era of machine learning and data science. Int. J. Inform. Commun. Technol. 2020, 9, 117. [Google Scholar] [CrossRef]
- Pu, Q.; Xu, C.; Wang, H.; Zhao, L. A novel artificial bee colony clustering algorithm with comprehensive improvement. Vis. Comput. 2022, 38, 1395–1410. [Google Scholar] [CrossRef]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization; Technical Report-tr06; Computer Engineering Department, Engineering Faculty, Erciyes University: Kayseri, Türkiye, 2005; Volume 200, pp. 1–10. [Google Scholar]
- Xiao, S.; Wang, H.; Wang, W.; Huang, Z.X.M. Artificial bee colony algorithm based on adaptive neighborhood search and Gaussian perturbation. Appl. Soft Comput. 2021, 100, 106955. [Google Scholar]
- Alatawi, H.S.; Sharaf, S.A. Review of Load Balancing Algorithms Inspired by Artificial Bee Colony Algorithm in the Cloud Computing. Int. J. Wirel. Commun. Netw. Technol. 2023, 12, 14–27. [Google Scholar]
- Kaya, E.; Gorkemli, B.; Akay, B.; Karaboga, D. A review on the studies employing artificial bee colony algorithm to solve combinatorial optimization problems. Eng. Appl. Artif. Intell. 2022, 115, 105311. [Google Scholar]
- Karaboga, D.; Gorkemli, B. A quick artificial bee colony (qABC) algorithm and its performance on optimization problems. Appl. Soft Comput. J. 2014, 23, 227–238. [Google Scholar] [CrossRef]
- Aslan, S.; Badem, H.; Karaboga, D. Improved quick artificial bee colony (iqABC) algorithm for global optimization. Soft Comput. 2019, 23, 13161–13182. [Google Scholar] [CrossRef]
- Li, S.; Zhang, W.; Hao, J.; Li, R.; Chen, J. Artificial Bee Colony Algorithm Based on Improved Search Strategy. In Artificial Intelligence and Mobile Services–AIMS 2023; Yang, Y., Wang, X., Zhang, L.J., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2023; Volume 14202. [Google Scholar]
- Li, X.; Zhang, S.; Yang, L.; Shao, P. Neighborhood-search-based enhanced multi-strategy collaborative artificial Bee colony algorithm for constrained engineering optimization. Soft Comput. 2023, 27, 13991–14017. [Google Scholar]
- Cui, Y.; Hu, W.; Rahmani, A. Fractional-order artificial bee colony algorithm with application in robot path planning. Eur. J. Oper. Res. 2023, 306, 47–64. [Google Scholar]
- Ye, T.; Wang, H.; Zeng, T.; Omran, M.G.; Wang, F.; Cui, Z.; Zhao, J. An improved two-archive artificial bee colony algorithm for many-objective optimization. Expert Syst. Appl. 2024, 236, 121281. [Google Scholar]
- Mansouri, N.; Javidi, M.M. A new Prefetching-aware Data Replication to decrease access latency in cloud environment. J. Syst. Softw. 2018, 144, 197–215. [Google Scholar] [CrossRef]
- Najjar-Ghabel, S.; Yousefi, S.; Farzinvash, L. Reliable data gathering in the Internet of Things using artificial bee colony. Turk. J. Electr. Eng. Comput. Sci. 2018, 26, 1710–1723. [Google Scholar] [CrossRef]
- Salem, R.; Salam, M.A.; Mohamed, A.A. An Artificial Bee Colony Algorithm for Data Replication Optimization in Cloud Environments. IEEE Access 2020, 8, 51841–51852. [Google Scholar] [CrossRef]
- Cui, Y.; Hu, W.; Rahmani, A. Improved artificial bee colony algorithm with dynamic population composition for optimization problems. Nonlinear Dyn. 2022, 107, 743–760. [Google Scholar] [CrossRef]
- Kruekaew, B.; Kimpan, W. Enhancing of artificial bee colony algorithm for virtual machine scheduling and load balancing problem in cloud computing. Int. J. Comput. Intell. Syst. 2020, 13, 496–510. [Google Scholar] [CrossRef]
- Li, J.-Q.; Han, Y.-Q. A hybrid multi-objective artificial bee colony algorithm for flexible task scheduling problems in cloud computing system. Clust. Comput. 2020, 23, 2483–2499. [Google Scholar] [CrossRef]
- Liu, W.; Li, C.; Zheng, A.; Zheng, Z.; Zhang, Z.; Xiao, Y. Fog Computing Resource-Scheduling Strategy in IoT Based on Artificial Bee Colony Algorithm. Electronics 2023, 12, 1511. [Google Scholar]
- Chen, Q.; Liu, B.; Zhang, Q.; Liang, J.J.; Suganthan, P.N.; Qu, B.Y. Problem Definitions and Evaluation Criteria for CEC 2015 Special Session on Bound Constrained Single-Objective Computationally Expensive Numerical Optimization. In Proceedings of the 2015 IEEE Congress on Evolutionary Computation, Sendai, Japan, 25–28 May 2015; pp. 84–88. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).