Machine Learning: Models, Challenges, and Research Directions

Abstract

Machine learning techniques have emerged as a transformative force, revolutionizing various application domains, particularly cybersecurity. The development of optimal machine learning applications requires the integration of multiple processes, such as data pre-processing, model selection, and parameter optimization. While existing surveys have shed light on these techniques, they have mainly focused on specific application domains. A notable gap that exists in current studies is the lack of a comprehensive overview of machine learning architecture and its essential phases in the cybersecurity field. To address this gap, this survey provides a holistic review of current studies in machine learning, covering techniques applicable to any domain. Models are classified into four categories: supervised, semi-supervised, unsupervised, and reinforcement learning. Each of these categories and their models are described. In addition, the survey discusses the current progress related to data pre-processing and hyperparameter tuning techniques. Moreover, this survey identifies and reviews the research gaps and key challenges that the cybersecurity field faces. By analyzing these gaps, we propose some promising research directions for the future. Ultimately, this survey aims to serve as a valuable resource for researchers interested in learning about machine learning, providing them with insights to foster innovation and progress across diverse application domains.

1. Introduction

Machine learning (ML) applications have recently found extensive use across various domains, including cyber-security [1]. These cyber-security applications have attained widespread adoption in research and commercial systems, establishing themselves as indispensable components [2,3]. Building a compelling and influential secure ML application is a complex and time-consuming undertaking. It requires high-quality data and the selection of an appropriate model, which can achieve optimal architecture through hyperparameter tuning [4]. Numerous factors have to be taken into consideration when building a successful machine learning model. To develop a thriving security ML application, the initial step involves collecting raw signals and generating a dataset. However, this process often encounters challenges, such as inconsistencies, imputations, and redundancies, which can lead to inaccurate results [5,6,7]. Therefore, employing proper data pre-processing techniques becomes imperative in the development of any successful machine learning application [8,9]. The second step is to choose a machine learning model. These ML models can be classified into four categories: supervised, semi-supervised, unsupervised, and reinforcement learning. Supervised models use a labeled dataset for the training process to achieve the desired outputs [3]. In contrast, unsupervised models are trained using unlabeled datasets without any supervision. Semi-supervised models are combinations of supervised and unsupervised models, which train the model using a small number of labeled samples and a high number of unlabeled samples [4,5], while reinforcement learning models are trained based on rewarding the desired actions or punishing undesired behaviors. In such models, the agent attempts to interpret the environment, act, and learn via trial and error [6,7,8].

The subsequent step is to ensure that the trained model achieves optimality. ML models involve many parameters. These parameters have to be optimized using hyperparameter tuning techniques [9,10,11,12,13,14,15]. A hyperparameter tuning technique is an algorithm that finds the best parameters of an ML model with the best performance. Examples of these tuning techniques include genetic algorithms, random search, and grid search [13]. For instance, in the work described in [14], the authors used a tuning technique, a tree-structured parzen estimator, to optimize the parameters of several boosting-based models, such as adaptive boosting, categorical boosting, and gradient boosting. Examples of the parameters that have to be optimized are the estimator number and learning. The number of estimators indicates the number of the trees in the forest, whereas the learning rate shows how fast the model learns. The number of the estimators and the learning rate were set to 100 and 0.29, respectively, after applying the tree-structured parzen estimator tuning technique. The simulation results showed exponential improvements in the performance of these selected ML models as a result of optimizing their parameters using a hyperparameter tuning technique.

Another study [16] used a grid search to improve the performance of several traditional and ensemble ML models, namely K nearest neighbor, naïve bayes, random forest, and stacking in detecting intrusions on the smart grid. Examples of the hyperparameters are the number of neighbors, weight, and size of the leaves used in the K nearest neighbor model. The number of neighbors refers to the number of the nearest neighbors in the voting procedure which occurs in K nearest neighbor model, while the weight in this model refers to the given weights to the nearest K point using the kernel function. The size of the leaves manages the minimum number of points in a node and effectively adjusts the tradeoff between the cost of node traversal and the cost of a brute-force distance estimate. Their results showed a significant improvement using the optimized parameters.

The hyperparameter tuning process varies significantly across different types of machine learning models due to the various hyperparameter types (discrete, categorical, and continuous) that need to be optimized for each model [16,17,18,19]. This process can be carried out through manual testing or automatic optimization. However, manual testing comes with several limitations, including difficulties in dealing with numerous parameters [20], complex models, extended and costly evaluations, and non-linear hyperparameter interactions [17]. Consequently, automatic hyperparameter optimization has emerged as a practical solution for numerous domain applications [18,21,22]. The primary objective of automatic hyperparameter optimization is to streamline the hyperparameter tuning process effectively [23,24]. By employing these techniques, the model performance can be significantly improved while reducing the need for human efforts. Consequently, the models can make accurate predictions and their performance analyzed using performance metrics [9,19,25].

In this survey, we aim to provide a review of recent techniques related to the entire machine learning process, encompassing data pre-processing, models, and optimization approaches. We provide an in-depth exploration of various security machine learning models, including supervised, semi-supervised, unsupervised, and reinforcement learning. Furthermore, we analyze some of the challenges and potential research directions within the domain of machine learning. In summary, the main contributions of this paper are as follows:

• Brief discussion of data pre-processing;
• Detailed classification of supervised, semi-supervised, unsupervised, and reinforcement learning models;
• Study of known optimization techniques;
• Challenges of machine learning in the field of cybersecurity.

The survey is organized as follows. First, we discuss related published surveys in the domain of machine learning in Section 2. Then, we discuss the existing machine learning models in Section 3. Section 4 discusses the different phases of machine learning and summarizes several existing approaches in each phase. Section 5 explores the current challenges and future directions. Finally, Section 6 gives a conclusion.

2. Related Work and Research Methodology

A number of surveys related to machine learning in various domains, including cybersecurity, have been published over the last decade. Table 1 gives an overview of some of these surveys with the covered and uncovered topics. As shown in this table, some of these surveys only focused on one or two specific learning categories. For instance, in [26,27,28,29,30], the authors surveyed several supervised learning models applied to different applications and explored fundamental concepts in machine learning. In addition, the authors of [26] analyzed several hyperparameter techniques and their significance in developing successful machine learning systems. Other surveys focused on unsupervised or reinforcement learning. For example, the authors of [31] provided a comprehensive analysis of unsupervised models, while the authors of [32] emphasized the importance of semi-supervised models and provided a concise discussion of these models. In contrast, the authors of [33] focused solely on the hardware architecture of reinforcement learning models, offering an overview of various reinforcement learning approaches with an emphasis on their hardware implementations.

Other surveys compared various learning approaches. Examples of such surveys can be found in [34,35,36,37], where the authors discussed well-known supervised and unsupervised models, highlighting their respective strengths and limitations. In [38], the authors categorized machine learning models into three main classes, unsupervised, supervised, and reinforcement learning, providing a detailed description of these categories specifically in the context of computer architecture and system design. In [39], the authors also provided a comparison of three different machine learning models: supervised, unsupervised, and semi-supervised models. In [40], the authors focused on comparing self-, semi-, and unsupervised models for classifying images. The authors of [41,42,43,44,45] also discussed different machine learning models, namely supervised, semi-supervised, unsupervised, and reinforcement learning algorithms. These surveys focused on particular domains, such as software-defined networking and the Internet of Things.

However, the existing literature reviews [26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45] did not focus on all four types of machine learning models, particularly in the cybersecurity research field which affects many types of networks, including 5G/6G, unmanned aerial systems/vehicles, the Internet of Things, smart vehicles, and wireless sensor networks. In all these research areas, systems use Internet for communication, which is prone to cyberattacks. In addition, these studies [26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45] did not cover other crucial phases of machine learning, such as data pre-processing and hyperparameter tuning techniques. In this paper, we provide a survey on machine learning, data pre-processing methods, and hyperparameter tuning approaches. Additionally, we propose a taxonomy for machine learning classification models that covers supervised, unsupervised, semi-supervised, and reinforcement learning models. Through this taxonomy, our goal is to offer the readers a comprehensive understanding of the diverse landscape of machine learning models. In summary, this survey aims to address these gaps in the existing studies by providing a comprehensive resource that sheds light on data pre-processing, machine learning techniques, and hyperparameter tuning.

Table 1. List of related review papers.

Reference	Year	Study Highlights	Coverage of Data Pre-Processing and Hyperparameter Tuning		Coverage of Machine Learning
			Data Pre-Processing	Hyperparameter Tuning Approach	Supervised Learning	Unsupervised Learning	Semi-Supervised Learning	Reinforcement Learning
[34]	2021	Describes the known deep learning models, their principles, and characteristics.			✓	✓
[41]	2019	Focuses on limited machine learning techniques on only software-defined networking.			✓	✓	✓	✓
[39]	2022	Investigates the known issues in the field of system designs that can be solved using machine learning techniques.			✓	✓		✓
[26]	2021	Presents a detailed description of a few supervised models and their optimization techniques.		✓	✓
[32]	2021	Provides an overview of semi-supervised machine learning techniques with their existing algorithms.					✓
[38]	2022	Provides the state of the art, challenges, and limitations of supervised models in the field of maritime risk analysis.			✓
[33]	2022	Reviews hardware architecture of reinforcement learning algorithms.						✓
[28]	2022	Presents the existing algorithm for wireless sensor networks and describes the existing challenges of using such techniques.			✓
[29]	2016	Describes most of the known supervised algorithms for classification problems.			✓
[35]	2019	Provides a description of known supervised and unsupervised models.			✓	✓
[36]	2021	Discusses supervised and unsupervised deep learning models for intrusion detection systems.			✓	✓
[37]	2021	Surveys existing supervised and unsupervised techniques in smart grid.			✓	✓
[40]	2021	Explains known algorithms for image classifications.			✓	✓	✓
[31]	2022	Illustrates the unsupervised deep learning models and summarizes their challenges.				✓
[42]	2023	Discusses techniques for energy usage in future			✓	✓	✓	✓
[43]	2020	Reviews various ML techniques in the security of the Internet of Things.			✓	✓	✓	✓
[44]	2020	Proposes a taxonomy of machine learning techniques in the security of Internet of Things.			✓	✓	✓	✓
[38]	2019	Surveys the taxonomy of machine learning models in intrusion detection systems.			✓	✓		✓
[45]	2022	Gives ML techniques in industrial control systems.	✓		✓	✓	✓	✓
[30]	2022	Proposes the taxonomy of intrusion detection systems for supervised models.			✓

Table 1. List of related review papers.

Reference	Year	Study Highlights	Coverage of Data Pre-Processing and Hyperparameter Tuning		Coverage of Machine Learning
			Data Pre-Processing	Hyperparameter Tuning Approach	Supervised Learning	Unsupervised Learning	Semi-Supervised Learning	Reinforcement Learning
[34]	2021	Describes the known deep learning models, their principles, and characteristics.			✓	✓
[41]	2019	Focuses on limited machine learning techniques on only software-defined networking.			✓	✓	✓	✓
[39]	2022	Investigates the known issues in the field of system designs that can be solved using machine learning techniques.			✓	✓		✓
[26]	2021	Presents a detailed description of a few supervised models and their optimization techniques.		✓	✓
[32]	2021	Provides an overview of semi-supervised machine learning techniques with their existing algorithms.					✓
[38]	2022	Provides the state of the art, challenges, and limitations of supervised models in the field of maritime risk analysis.			✓
[33]	2022	Reviews hardware architecture of reinforcement learning algorithms.						✓
[28]	2022	Presents the existing algorithm for wireless sensor networks and describes the existing challenges of using such techniques.			✓
[29]	2016	Describes most of the known supervised algorithms for classification problems.			✓
[35]	2019	Provides a description of known supervised and unsupervised models.			✓	✓
[36]	2021	Discusses supervised and unsupervised deep learning models for intrusion detection systems.			✓	✓
[37]	2021	Surveys existing supervised and unsupervised techniques in smart grid.			✓	✓
[40]	2021	Explains known algorithms for image classifications.			✓	✓	✓
[31]	2022	Illustrates the unsupervised deep learning models and summarizes their challenges.				✓
[42]	2023	Discusses techniques for energy usage in future			✓	✓	✓	✓
[43]	2020	Reviews various ML techniques in the security of the Internet of Things.			✓	✓	✓	✓
[44]	2020	Proposes a taxonomy of machine learning techniques in the security of Internet of Things.			✓	✓	✓	✓
[38]	2019	Surveys the taxonomy of machine learning models in intrusion detection systems.			✓	✓		✓
[45]	2022	Gives ML techniques in industrial control systems.	✓		✓	✓	✓	✓
[30]	2022	Proposes the taxonomy of intrusion detection systems for supervised models.			✓

Offering the readers a holistic understanding of machine learning applications in different domains, such as cybersecurity.

3. Machine Learning Models

As previously mentioned, machine learning models can be classified in four categories: supervised, semi-supervised, unsupervised, and reinforcement learning. Each of these categories includes several types, as shown in Figure 1. The supervised models can be grouped into six types: tree, Bayesian, instance, regularization, neural network, and ensemble-based models. Unsupervised models are categorized into clustering, dimensionality reduction, and neural network techniques. Semi-supervised models can also be categorized into inductive and transductive models, whereas reinforcement models are classified into model-based and model-free techniques [46,47,48,49,50,51,52,53,54,55,56]. The following subsection gives a detailed description of each of these categories, as well as a list of the models used in each category.

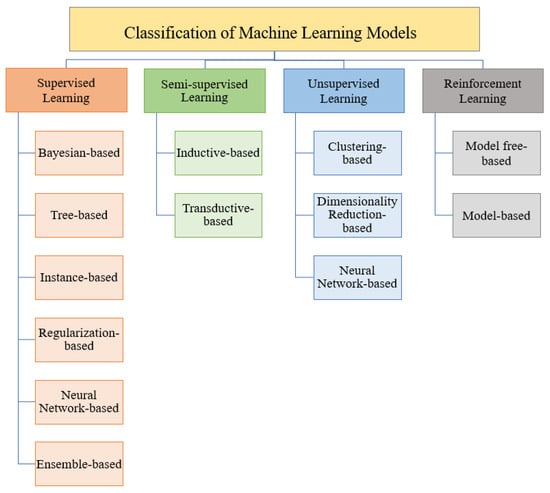
Figure 1. Classification of machine learning models.

3.1. Supervised Learning

Supervised learning models learn from labeled training data, where the input-output pairs are provided. The model generalizes patterns in the data to make predictions or classify new, unseen inputs. It relies on a supervisor to guide the learning process and correct predictions. Therefore, human intervention plays an important role in creating the labeled data and precise models based on known parameters. In the following, a mathematical concept of a supervised model is provided as follows.

A supervised ML model is a parametrized function $f_p$ which can show the input data $\overrightarrow{x }$ $\in {\mathbb{X}}^{\mathrm{d}}$to the output data y $\in \mathbb{Y}$. In general, input data are defined as a vector of features. For a classification, ${\mathbb{X}}^{\mathrm{d}}$is a d-dimensional vector space and $\mathbb{Y}$ is the set of classes. This function trains the data to predict the label of the new data precisely, which has not been seen previously. In concrete, the main steps of such an approach can be divided into two steps [56].

Model Training: The aim of the training process is to identify the optimal parameters which can precisely achieve the relationship among $\mathbb{X}$ and $\mathbb{Y}.$ To address such an aim, a training dataset $D=\left\{{\overrightarrow{x}}_i,{ y}_i\right\}{}_{i=1 }^N$with N samples is required. The loss function is employed to compute the difference between two outputs, such as the ground truth $y_i$ and the predicted $f_p$ (${\overrightarrow{x}}_i$). In such training, the loss function has to be minimized, as presented in Equation (1):

$$p_o=arg min\left({\sum }_{i}L(y_i,f_p \left({\overrightarrow{x}}_i\right))+\mathsf{\Omega }\left(p\right)\right)$$

(1)

where $p_o$ is the optimal parameter, $\mathsf{\Omega }$ is a regularization term for penalizing model complexity and avoiding overfitting problems, and $p$ is defined as a parameter that is not optimized.

Model prediction: After model training has been performed and optimal parameters $p_o$are achieved, from the given input ${\overrightarrow{x}}_i$ the corresponding output can be obtained as $y=f_p \left({\overrightarrow{x}}_i\right).$This process is called prediction or inference. The prediction accuracy over a testing dataset $D_t$can be calculated to evaluate the model’s performance [57].

As shown in Figure 2, the supervised ML models can be classified into six classes: tree, Bayesian, tree, regularization, instance, neural network, and ensemble-based models.

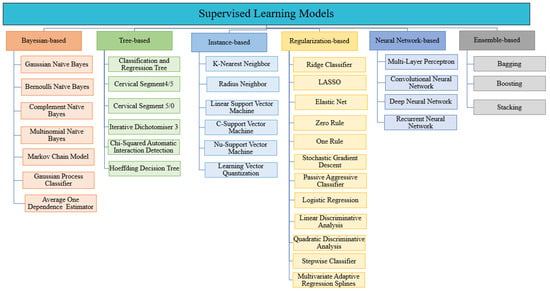
Figure 2. Classification of supervised machine learning models.

Bayesian models provide a robust framework for handling uncertainty, offering comprehensive probability distributions for parameters. This helps in decision-making under ambiguity, which is an important advantage. Additionally, they excel at integrating prior knowledge, enhancing predictive accuracy, particularly in data-scarce environments. Their adaptability to complex relationships and ability to prevent overfitting through regularization are further strengths. However, Bayesian models can be computationally demanding, especially for complex models or large datasets. In addition, subjectivity in choosing priors may introduce bias, and interpreting results can be challenging for non-experts. Scalability issues may also arise with extensive datasets, necessitating careful consideration of computational resources.

In this study, we discuss seven supervised Bayesian-based models, namely multinomial naïve Bayes, hidden Markov chain, Gaussian naïve Bayes, Bernoulli naïve Bayes, complement naïve Bayes, Gaussian process classifier, and average one-dependence estimators.

In tree-based models, predictions are generated by building a tree-like structure using a hierarchy of if-then rules to partition the features in the training dataset. The basic elements of a tree are branches and nodes, which can be root, internal, or leaf nodes. The partitions can be selected according to different metrics, namely entropy, Gini index, classification error, information gain, gain ratio, and twoing criteria [58]. Tree-based models provide several benefits, such as high accuracy and ease of interpretation without any excessive data preprocessing. These models, as shown in Figure 2, consist of several supervised models, including classification and regression tree, cervical segment 4/5, cervical segment 5/0, iterative dichotomiser 3, chi-square automatic interaction detection, and Hoeffding decision tree.

Instance-based learning, memory-based learning, refers to a group of ML techniques that can adapt to unseen data and are commonly used for real-time data processing. These methods use the concepts of the nearest neighbor optimization algorithm to classify or predict data. The memory-based algorithms mainly follow the simplest instance-based learning framework, instance based one (IB1), which includes three core functions, namely similarity function, concept description updater, and classification function [59]. These algorithms, based on the previous functions’ description, require a large amount of memory to store the data. Memory-based models delay the processing until a new instance is classified or predicted, which is known as the lazy learning pattern. Lazy learning has the advantage of estimating the target function locally and differently for each new instance [60,61]. As a result, instance-based methods have a lot of flexibility and multiple options when it comes to designing the objective functions. They are frequently used to build test instance models which consist of five techniques, namely radius neighbor, K-nearest neighbors, C-support vector machine, linear support vector machine, and nu-support vector machine, as shown in Figure 2.

Regularization-based models are critical learning algorithms that are used to appropriately fit a function on the training set and prevent overfitting problems by adding some extra information to the models [62]. In these models, an additional penalty term, extra information, in the error function is added to tune the models and control the fluctuating function [63]. The reduction in the value of an error is called the shrinkage method, and it is the core aspect of the regularization-based technique. The shrinkage function may lead to variance reduction, which is very effective in large datasets, especially when the data are from a high dimensional environment [64]. Regularization-based models can be classified into ridge classifier, least absolute shrinkage and selection operator, elastic net, one rule, zero rule, stochastic gradient descent, passive aggressive classifiers, logistic regression, linear discriminant analysis, quadratic discriminant analysis, stepwise classifier, and multivariate adaptive regression spines, as shown in Figure 2.

Neural networks, also known as artificial neural networks (ANN), are an important subset of machine learning techniques that are inspired by the human brain. These techniques can be effectively used in classification, clustering, pattern recognition, and predictions. The great potential of such techniques is to provide high-speed processing in parallel implementation. ANNs are widely used universal function approximations for different numerical paradigms due to their high rate of self-learning, adaptivity, fault tolerance, and nonlinearity features of these techniques [65,66]. A universal function approximation refers to how a neural network can approximate any function used in its training and validation. In addition, these techniques are easy to use and more precise in comparison with techniques with large inputs [67]. Supervised neural networks can also be classified into four categories: multi-layer perceptron, convolutional neural networks, deep neural networks, and recurrent neural networks, as illustrated in Figure 2.

Ensemble-based machine learning techniques, also known as multiplier classifier systems, train and integrate several learners to address a problem. In these techniques, the generalization capacity of an ensemble learner is broadly stronger than an individual learner [68,69]. Although this theory holds more for weak learners, strong traditional learners give better performance results. Additionally, ensemble models usually provide better results when there is a diversity among the combined base learners [70]. These models provide several benefits, including low variance, high performance, and the removal of noise and biased data. Moreover, these models are robust, which can decrease the spread or dispersion of the predictions. Despite the benefits of these models, they deal with several shortcomings, including the lack of simplicity and explainability, generalization, and high prediction time [71].

Ensemble-based models are classified into three different types, bagging, boosting, and stacking, as shown in Figure 3. The Bagging model, known as the bootstrap aggregation technique, can minimize the variance and thereby improve the prediction [71,72]. Boosting models use a sequential iterative technique to combine multiple weak individual learners into one strong learner with a better performance. To generate the output of this strong learner, a relationship based on a weighted average or voting is established between the basic learners with different distributions [73]. Finally, stacking, known as stack generalization, is another type of ensemble learning technique that includes heterogeneous weak learners. Stacking models may provide some benefits, such as increasing the robustness and improving the performance [74]. These techniques ensure a higher performance in comparison with any single contributing model. Table 2 provides the characteristics, advantages, and disadvantages of these supervised classification techniques.

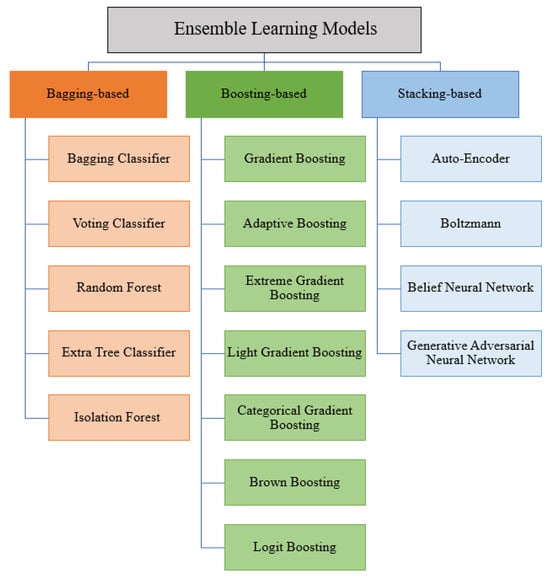
Figure 3. Examples of ensemble supervised models.

Table 2. Characteristics, limitations, and strengths of classification categories [56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74].

Classification Category	Characteristics	Advantages	Disadvantages
Bayesian- Based	Dealing with uncertain data.	Ability to quantify the uncertainty; Capacity for the incorporation of prior knowledge in a principled manner; Useful for small datasets.	High computational costs; Difficulty with selecting priors.
Tree- based	Data splitting-based; Non-parametric method.	High accuracy; Ease of interpretation; Handling large datasets.	Prone to overfitting; Non-robust.
Instance- based	Adapting for new and real-time data.	Capacity to adapt to new and real-time data; Ability to change the similarity function for each instance at each prediction step; Fast training process.	High computational costs; Expensive memory usage.
Regularization-based	Regularizing the coefficient estimates towards zero; Generalization.	Reduction in model variance with no increase in bias; Reducing the overfitting issues; Simplicity; Computational efficiency.	Dimensionality reduction; High bias error.
Neural network-based	Storing information on an entire network; Distributed memory; Ability of parallel processing.	Ability to detect all possible interactions between predictor variables; Availability of multiple training processes; High rate of adaptability.	Requiring large datasets; High computational power; Black box nature; Prone to overfitting;
Ensemble-based	Combine multiple learners	Low variance; High performance; Removing noise and biased data.	High inference time; Lack of simplicity; Lack of generalization.

3.2. Semi-Supervised Learning

Semi-supervised learning models are algorithms that learn from both labeled and unlabeled data. They use a small set of labeled examples alongside a larger pool of unlabeled data to make predictions or classifications. These models are advantageous when labeling data is costly or time-consuming, as it maximizes the utility of available resources. Semi-supervised learning often achieves higher accuracy than purely supervised models. However, it relies heavily on the quality of initial labeling, which can introduce bias, and may struggle with highly complex tasks that require a substantial amount of labeled data for effective training [60].

The following are the main mathematical concepts of semi-supervised learning models.

In semi-supervised models, the set of training samples is defined as $L=\left\{\left(X_i, Y_i\right)| X_i\in R^d, Y_i \in \Omega , i=1,\dots ,L\right\}$. In these models, every sample consists of a dimensional feature space, d, where $X_i$ is the input sample, $Y_i$ is the class label $X_i$, and $\mathsf{\Omega }=\left\{T_1,\dots \dots \dots \dots T_K\right\}$ presents the target classes. In addition, $\mathrm{U}=\left\{X_j^{*}| j=1,\dots \dots \dots ,u\right\}$ is the set of unlabeled data. Semi-supervised models consist of different categories, namely dimensionality reduction, clustering, and regression. In this survey, we only focus on classification semi-supervised models. The main steps of semi-supervised models can be divided, as follows:

Model training: The important process is to use unlabeled data samples to create a learner that performs better than the one based on labeled data. Thus, a set of learning training samples $L$ is presented. Using these models, a loss functions can be applied to weights representing class labels and cluster assumptions (based on the defined model).

Model Prediction: Once the model has been trained with the optimal parameters, it predicts the learners’ accuracy over test data samples, which they exceed compared to learners using labeled data.

Semi-supervised models are generally considered direct extensions of supervised models. These models can be divided into inductive- and transductive-based models, as illustrated in Figure 4. Table 3 outlines the characteristics, advantages, and disadvantages of these models. Inductive-based models can create predictions for any objects in the input vector, while unlabeled data samples can be applied when training the classifier [75,76]. When the training process concludes, the predictions of new samples will be completely independent of each other. In inductive-based models, cluster-label and pre-training-based models, the given data can be extracted from unlabeled data [77]. However, wrapper-based inductive models, including self-training, co-training, and boosting models, only use labeled data to train classifiers, and then use the predictions to create more labeled data. Afterwards, the unlabeled data are pseudo-labeled in a wrapper-supervised manner, and an inductive classifier is constructed. While, intrinsically semi-supervised models combine unlabeled data with optimization functions to extend the process of labeled data to unlabeled data [78].

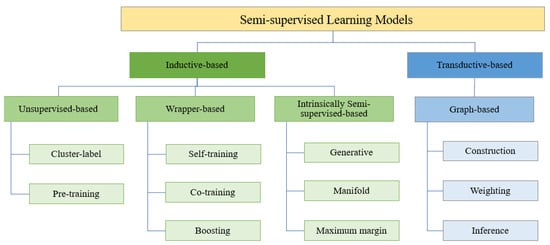
Figure 4. Classification of semi-supervised learning models.

Table 3. Characteristics, limitations, and strengths of semi-supervised models [76,77,78,79,80,81].

Classification Category	Characteristics	Advantage	Disadvantage
Inductive- Based	Generates a model that can create predictions for any sample in the input space	The predictions of new samples are independent of old samples	The same model can be used in training and predicting new data samples
Transductive- based	Predictive strengths are limited to objects that are processed during the training steps	No difference between the training and testing steps	No distinction between the transductive algorithms in a supervised manner

Transductive models are another category of semi-supervised learning models that do not create a model for the whole input space. These models do not differentiate between the training and testing phases. They are widely performed based on the graph-based approach, in which data samples are connected via graphs, and their data are grown with the edges of the graph [79]. These graph-based models (generative, manifold, and maximum margin) deal with three phases, namely graph construction, weighting, and inference [80]. In graph construction, the set of input data is used to generate the graph where the nodes show data samples are connected via the edge [79,81]. In graph weighting, the edges are weighted to show pairwise similarity between the data samples. In graph inference, the graph is applied to highlight the labels compared to the unlabeled data samples. More details about these models and characteristics can be found in [80].

3.3. Unsupervised Learning

Unsupervised machine learning methods analyze and cluster unlabeled outputs using a set of inputs. Clustering of samples is widely used to uncover hidden patterns, structures, or data knowledge in unlabeled datasets [24,57]. The following are mathematical concepts of unsupervised models.

An unsupervised machine learning model is a parameterized function $g_{\theta }$ which consists of the input data $\overrightarrow{x }$ $\in X^d$ with no outputs. In this model, input data refers to a feature’s vector. In addition, $X^d$ is a d-dimensional vector space. The data have to be trained accurately to predict the data label, which is not known. The steps of unsupervised models are described as follows.

Model Training: This process involves the identification of the optimal parameters that can help more accurately find a pattern between data samples and their outputs. So, a training dataset D = ${\left\{{\overrightarrow{x}}_i\right\}}_{i=1}^N$with N number of samples is provided. A loss function is defined to compute the difference between data inputs and the outputs. The aim of training unsupervised models is to diminish the loss function in the training set and achieve the optimal results.

Model Prediction: After model training and when optimal parameters have been presented from the input $\overrightarrow{x}$, the model can discover the inherent structure of unlabeled data, and the prediction accuracy over a testing dataset $D_t$can be computed to evaluate the performance of the model.

Unsupervised models can be divided into cluster-based, dimensionality reduction-based, and neural network-based models, as illustrated in Figure 5. A clustering-based model groups the data into categories based on their characteristics and similarities and clusters them together. This group is capable of finding homogeneous subgroups in the given data, and their results can be used to group observations (features) into distinct groups. These groups help the interpretation and assessment of data. These methods are usually easy to implement; however, their complexity is high [75]. As shown in Figure 5, cluster-based models include K-means, C-means, linear discriminative analysis, hierarchical clustering, non-negative matrix factorization, and density-based spatial clustering with noise.

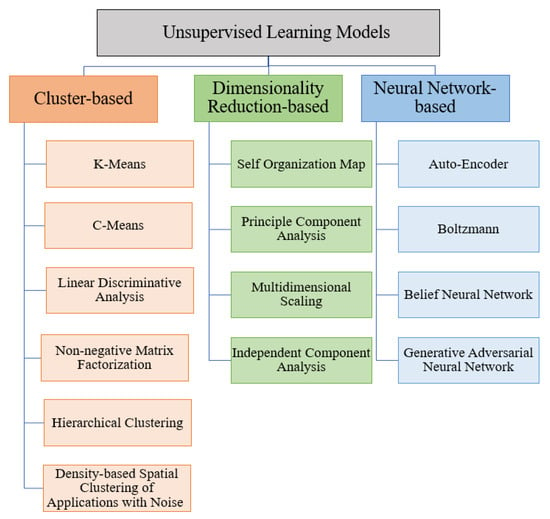
Figure 5. Overview of unsupervised learning models.

Dimensionality reduction-based models refer to the number of features in a dataset, which are represented as columns. In unsupervised learning, such models aim to decrease the features’ number in training and testing. Models like these can summarize relationships between samples with a reduced number of dimensions. Using these approaches facilitates the visualization and preprocessing of complicated datasets. Dimensionality reduction-based models can reduce time and storage, although they may face data loss [75]. AS shown in Figure 5, these categories include self-organization maps, principal component analysis, multidimensional scaling, and independent component analysis.

Another category of unsupervised models is neural network-based models, which belong to both supervised and unsupervised categories. These models can identify interactions between predictors and have high adaptability. Despite these benefits, they require huge datasets to process and have a high tendency to overfit. In addition, neural network-based models usually face high computational power. Auto-encoders, generative adversarial neural networks, Boltzmann, and belief neural networks, are among the neural-network-based unsupervised models, as shown in Figure 5. Table 4 lists the characteristics, the limitations, and strengths of these models.

Table 4. Characteristics, limitations, and strengths of unsupervised models [74,75].

Classification Category	Characteristics	Advantages	Disadvantages
Cluster-based	Divides uncategorized data into similar groups;	Easy implementation.	High complexity.
Dimensionality reduction-based	Decreases the number of features in the given dataset;	Decrease time and storage.	Data loss.
Neural network-based	Inspiration of human brains.	Can detect the interactions among predictor variables; Availability of multiple training processes; High adaptability.	Require huge datasets; High computational power; Tendency to overfit.

3.4. Reinforcement Learning

Reinforcement learning (RL) models are another ML category that trains an agent to learn in an interactive environment by getting feedback from its own experiences and actions. Reinforcement learning trains the models to learn the optimal actions in an environment to get maximum rewards. These optimal actions can be performed through interactions with an environment and their responses. In the absence of a supervisor, the learner has to explore the sequence of their actions independently, which maximizes the rewards [82]. Advantages of reinforcement learning include their ability to handle dynamic and complex environments, making them suitable for tasks like robotics control and game playing. They also excel in scenarios with sparse or delayed feedback. However, they often require extensive training and may struggle with high-dimensional state spaces. Additionally, defining a suitable reward function can be challenging, and poorly designed rewards may lead to suboptimal behavior. Furthermore, exploration strategies need to be carefully balanced to avoid excessive trial-and-error.

In general, an agent attempts to sequentially learn the decision-making challenges through modeling the Markov Decision Process (MDP). At a timestep t, the agent receives an observation of an environment $P_t\in P$, where P indicates the state space, and the agent can choose a behavior $B_t$ $\in R\left(P_t\right)$ based on the environment reaction. In this context, $B\left(P_t\right)$ is the set of all possible actions of state $P_t$. Then, the agent has a reward $R_{t+1}$. Then, the state $P_{t+1}$ and reward $R_{t+1}$ depend on the previous state of $P_t$ and the behavior of $R_t$. During the learning process, the agent also learns to maximize the cumulative rewards, shown as the expected reward return $E_t$, using a discount rate $Y$ using the following equation [83]:

$$D_{t }={\sum }_{k=0}^{\infty }{Y}^k{R}_{t+k+1}\hspace{1em}\hspace{1em}\hspace{1em}0\le Y\le 1$$

(2)

The agent also follows a rule that maps from the states to the probabilities of every action. The value of such a rule depends on the expected discounted return, calculated as follows:

$$V_{\pi }\left(p\right)=E_{\pi }\left[D_{t }\right| P_t=p]$$

(3)

Moreover, the action value function $T_{\pi }\left(p, b\right)$refers to the expected return from state p and behavior $b$:

$$T_{\pi }\left(p,b\right)=E_{\pi }\left[D_{t }\right| P_t=p, B_t=b]$$

(4)

The optimal action value with rule $\pi$ is defined as follows:

$$q_{*}\left(p,b\right)=\underset{\pi }{\max }{T}_{\pi }\left(p,b\right)$$

(5)

In reinforcement learning models, optimal equations can be used to improve the rule followed by an agent iteratively.

RL models can be classified into model-based and model-free-based techniques, as shown in Figure 6. Model-based techniques are defined as learning an optimal behavior by making predictions about the consequence of the actions. This process can happen by taking actions and observing the outcomes that include the next state and the immediate reward. In contrast, model-free-based techniques, such as policy optimization and Q learning-based techniques, are data-based optimal control methods that aim to learn an optimal control policy in the absence of a process model. The main difference between the model-based and model-free-based techniques is the interaction between the agent and the environment [84]. Table 5 summarizes the characteristics, strengths, and limitations of model-based and model free-based techniques. More details can be found in [15,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113].

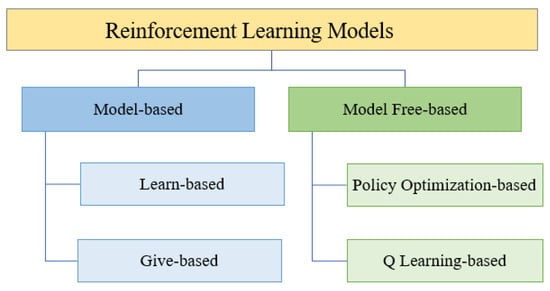
Figure 6. Overview of reinforcement learning models.

Table 5. Characteristics, advantages, and disadvantages of classification categories of reinforcement Learning [15,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113].

Classification Category	Characteristics	Advantage	Disadvantage
Model-based	Optimal actions are learned via a model	Few interactions between the agent and the environment; Quick convergence to optimal solutions.	Relies on transition models; Accuracy of the model can positively/negatively impact the learning process.
Model free-based	No transition of a probability distribution or reward associated with the Markov decision process	No prior transition knowledge needed; Easy implementation.	High damage rate.

4. Machine Learning Processes

In general, this process begins with data collection and pre-processing, involving the acquisition and curation of relevant datasets. Subsequently, an ML model is selected based on the problem’s nature, such as classification, regression, or clustering. The model selection is followed by the training phase, during which the model learns patterns and relationships in the data by iteratively adjusting its parameters to minimize a predefined error metric. This phase involves the division of the given dataset into training and validation sets to evaluate the performance of the model.

After training, the model undergoes evaluation using a separate test dataset to assess its generalization ability. If the performance of the model meets the desired criteria, it can be configured for real-world security applications. ML processes are characterized by a continuous cycle of refining and iterating performed on the models to achieve higher accuracy and robustness, making them an essential tool for solving complex problems across various domains. To briefly discuss these steps, overviews of data pre-processing, tuning approaches, and evaluation metrics are provided.

4.1. Data Pre-Processing

One of the main key factors on developing a successful ML system is the availability and quality of the utilized datasets and benchmarks [15,49]. However, data collection in various fields can present several challenges, including the difficulty in establishing real datasets due to safety [48], security [50], privacy [48,50,101], and other concerns. To address this issue, numerous studies have focused on identifying rare conditions and simulating datasets to uncover essential data patterns [15,51,52,53,101,102,103,104,105,106,107,108,109]. Ensuring the optimal performance of ML models requires high-quality datasets, making data preprocessing a crucial step in the machine learning process. In the preprocessing phase, raw data are converted into a practical format. In addition, dataset often contain imperfections like inconsistencies, redundancy, noise, and missing values [54], which can impact model performance. Therefore, proper processing steps are important to enhance the quality and reliability of the model’s decisions [55]. Data preprocessing encompasses data reduction, data transformation, discretization, data cleaning, and imbalanced learning to prepare the data for effective ML [110].

Table 6 presents a comprehensive summary of key data pre-processing techniques across various processes, including data transformation, cleaning, reduction/increasing, discretization, and imbalanced learning. Data transformation techniques convert data from one format to another one. This is achieved through two main techniques: normalization and standardization. Data cleaning includes tasks such as filling in missing values, handling noisy data, and treating outliers. In the context of data reduction/increasing, redundant and irrelevant information can be identified and removed or added using techniques like feature extraction, feature selection, and instance generation. Discretization is an approach that reduces the number of data values by converting them into a smaller set of discrete values. In cases of imbalanced class distribution, balanced learning techniques are crucial to avoid low performance. Balancing the class distribution is achieved through under-sampling and over-sampling techniques, ensuring the best performance results [56,110,111,112,113].

Table 6. Summary of data preprocessing steps with their techniques [15,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,101,102,103,104,105,106,107,108,109,110,111,112,113].

Data Preprocessing Steps	Methodology	Technique	Highlights
Data transformation	Standardization and normalization	Unit vector normalization	Extract the given data, and convert them to a usable format
		Max abs scalar
		Quantile transformer scalar
		Robust scalar Min-max scaling
		Power transformer scalar
		Unit vector normalization
		Standard scalar
Data cleaning	Missing value imputation	Complete case analysis	Loss of efficiency, strong bias, and complications in handling data.
		Frequent category imputation
		Mean/median imputation
		Mode imputation
		End of tail imputation
		Nearest neighbor imputation
		Iterative imputation
		Hot and cold deck imputation
		Exploration imputation
		Interpolation imputation
		Regression-based imputation
	Noise treatment	Data polishing
		Noise filters
Data reduction/ increasing	Feature selection	Wrapper	Decrease or increase the number of samples or features that are not important in the process of training
		Filter
		Embedded
	Feature extraction	Principle component analysis
		Linear discriminative analysis
		Independent component analysis
		Partial least square
		Multifactor dimensionality reduction
		Nonlinear dimensionality reduction
		Autoencoder
		Tensor decomposition
	Instance generation	Condensation algorithms
		Edition algorithms
		Hybrid algorithms
Discretization	Discretization-based	Chi-squared discretization	Loss of information, simplicity, readability, and faster learning process
		Efficient discretization
Imbalanced learning	Under-sampling	Random under-sampling	Presents true evaluation results
		Tomek links
		Condensed nearest neighbor
		Edited nearest neighbor
		Near-miss under-sampling
	Oversampling	Random oversampling
		Synthetic minority oversampling technique
		Adaptive synthetic
		Borderline-synthetic minority oversampling technique

4.2. Tuning Approaches

The performance of ML models relies on the engineered features or the hyperparameter settings [89,90]. Creating a successful machine learning model requires a complicated process, which involves identifying an appropriate algorithm and using an optimal architecture by tuning its hyperparameters (HPs) [91,92,93,94,95]. These parameters can be categorical, discrete, and continuous values.

Hyperparameter tuning methods can be manual or automatic [96,97,98,99,100]. Manual tuning is an ineffective approach due to the complex ML models and non-linear hyperparameter interactions [15,101,102]. However, automatic tuning techniques speed up the process of detecting the optimal parameters of a model using specific optimization methods. Several hyperparameter tuning techniques exist. These types, as shown in Table 7, have different strengths and limitations [89,103].

Table 7. Characteristics, advantages, and disadvantages of tuning approaches [89,103,104,105,106,107,108,109,110,111,112,113].

Hyperparameter Methods	Strengths	Limitations
Grid search	Simple.	Only effective with categorical hyperparameters; Takes a long time to find hyperparameters.
Random search	Performs parallelization; More effective than a grid search.	Does not rely on previous results; Cannot perform well with conditional hyperparameters.
Genetic algorithm	No need for good initialization; Performs well with all types of hyperparameters.	Weak performance for parallelization.
Gradient-based techniques	Quick convergence speed for continuous hyperparameters.	Detects local optimum; Supports continuous hyperparameters.
Bayesian optimization-Gaussian process	Quick convergence speed for continuous hyperparameters.	Weak performance for parallelization.
Particle swarm optimization	Good with parallelization; Performs well with all types of hyperparameters.	Needs good initialization.
Bayesian optimization-tree structure parzen estimator	Maintain conditional dependencies; Performs well with all types of dependencies.	Weak performance for parallelization.
Hyperband	Good performance with parallelization.	Does not provide satisfactory results with conditional hyperparameters.
Bayesian optimization-SMAC	Good performance with parallelization.	Weak performance for parallelization.
Population-based	Simultaneously optimizes the parameters and trains the model; Improves the flexibility of the machine learning model; Finds adaptive parameters rather than a fixed set of hyperparameters.	Can be challenging to find hyperparameters in some scenarios; Finding adaptive parameters may not be suitable for some cases.

4.3. Evaluation Metrics

Evaluation metrics are essential to investigate the performance of ML models. These metrics differ depending on the application and the category of the models. For instance, supervised learning models require different metrics than reinforcement learning models. Below are short descriptions of the most common metrics and their mathematical equations.

4.3.1. Evaluation Metrics for Supervised Learning

Accuracy: This represents the correct predictions made by an ML model. It is calculated, as presented in Equation (6), where $T_P$ presents the true positive, $T_N$ denotes the true negative, $F_P$ is the false positive, and $F_N$ is the false negative.

$$\mathrm{Accuracy}=\frac{T_P+T_N}{T_P+T_N+F_P+F_N}\times 100$$

(6)

Precision: This shows the number of true positives divided by the total number of true positive and false positive. It can be calculated by:

$$\mathrm{Precision}=\frac{T_P}{T_P+F_P}\times 100$$

(7)

Recall (Detection Rate): This metric computes the number of the positive samples correctly classified to the total number of the positive samples. This metric, as shown in Equation (8), can indicate the model’s ability to classify positive samples among other samples.

$$\mathrm{Recall}=\frac{T_P}{T_P+F_N}$$

(8)

F1-Score: This metric is derived from the recall and the precision, where the precision is defined in Equation (7) and the recall is given by Equation (8). It is given by:

$$\mathrm{F}1\text{-}\mathrm{Score} \frac{2T_P}{2T_P+F_p+F_N}$$

(9)

Area under the receiver operating characteristics curve (AUC): The receiver operating characteristic (ROC) can visualize a tradeoff among sensitivity and specificity in an ML model. This curve is considered as a plot of the true positive rate (TPR) to the false positive rate (FPR). This metric is calculated using Equation (10), where x presents the varying AUC parameter.

$$\mathrm{Area} \mathrm{Under} \mathrm{Curve}={{\displaystyle \int }}_{x=0}^1\frac{T_P}{T_P+F_N} \left({(\frac{F_P}{F_P+T_N})}^{-1}\left(x\right)\right)dx$$

(10)

False Alarm Rate: False alarm rate, false positive rate, is the probability of a false alarm being raised. This metric can be computed by:

$$\mathrm{False} \mathrm{Alarm} \mathrm{Rate}=\frac{F_p}{T_N+F_P}$$

(11)

Misdetection Rate: It indicates the percentage of misclassified samples. It is given by:

$$\mathrm{Misdetection} \mathrm{Rate}=\frac{F_N}{T_P+F_N}$$

(12)

Mean Absolute Percentage Error: It is used to evaluate the accuracy of forecasting models. It calculates the average percentage difference between the predicted and the actual values.

$$Mean Absolute Percentage Error=\frac{1}{n}{\sum }_{t=1}^n\left|\frac{A_{t-F_t}}{A_t}\right|$$

(13)

where, n is the number of the summation times that the iteration happens, $A_t$ denotes the actual value at time t, and $F_t$ is the predicted value at time t.

Processing Time: This refers to time taken to train, test, and predict the results. It can represents the time required to predict or analyze malicious signals compared to non-malicious signals.

Training Time per Sample: This refers to the time taken to train a model on a single sample of the dataset. It represents the amount of time required to process and learn from the features and labels of an individual sample during the training phase.

Memory Usage: This is the amount of memory or storage space that is required by a model during its entire process. It represents the amount of memory resources utilized to store and process the model’s parameters, intermediate computations, and other relevant data.

4.3.2. Evaluation Metrics for Unsupervised Learning Models

Silhouette Score: It computes the similarity of each data point in one cluster to data points of the neighboring clusters. The higher values indicate that the data points are well-clustered and have clear separation.

Davies–Bouldin Index: It calculates the average similarity among every cluster and its most similar clusters. A lower Davies–Bouldin index indicates better clustering, with smaller values representing tighter and more distinct clusters.

Calinski–Harabasz Index: This index evaluates the ratio of the between-cluster variance to the within-cluster variance. Higher values indicate a better separation between clusters, implying that the data are well-clustered.

Dunn Index: This metric assesses the rate of the minimum inter-cluster distance to the maximum intra-cluster distance. A higher Dunn index presents better clustering, as it shows smaller distances within clusters and larger distances between clusters.

Inertia (Within-Cluster Sum of Squares): Inertia calculates the total distance among data points within the same cluster. Lower inertia values presents denser and more compact clusters.

Gap Statistic: The gap statistic compares the clustering algorithm performance to the performance of random clustering. A larger gap indicates that the algorithm’s clustering is better than random.

Adjusted Rand Index: It measures the similarity between true class labels and the labels assigned by the clustering algorithm, correcting for chance. The higher values indicate better clustering agreement.

Normalized Mutual Information: It measures the mutual information between true class labels and cluster assignments, normalized to account for chance. A higher Normalized Mutual Information indicates better clustering quality.

Homogeneity, Completeness, and V-measure: These three metrics, homogeneity, completeness, and their harmonic mean (V-measure), assess different aspects of clustering quality. Homogeneity computes how pure each cluster is with respect to a single class. Completeness measures how well all instances of a given class are assigned to the same cluster. V-measure combines both homogeneity and completeness into a single metric.

Spectral Gap: The spectral gap measures the gap between eigenvalues of a similarity matrix or Laplacian graph. A larger spectral gap indicates more distinct clusters.

4.3.3. Evaluation Metrics for Semi-Supervised Learning Models

Log-Likelihood: In semi-supervised learning, where generative models like Gaussian mixture models (GMMs) or variational autoencoders (VAEs) are used, log-likelihood can be a crucial metric. It measures how well the model captures the underlying data distribution.

Pseudo-label Accuracy: In semi-supervised learning, pseudo-labels are assigned to unlabeled data points based on model predictions. Pseudo-label accuracy measures the accuracy of these pseudo-labels, providing insights into how well the model is utilizing unlabeled data.

Consistency Regularization: Some semi-supervised learning methods use consistency regularization as a metric to quantify the model’s stability by comparing predictions on perturbed versions of the same input. Higher consistency indicates better generalization.

Active Learning Metrics: In semi-supervised learning with active learning, metrics such as query density and query diversity are used. Query density measures how well the model selects informative data points for labeling, while query diversity assesses the variety of data points selected.

Entropy: Entropy measures the uncertainty of model predictions. Lower entropy indicates a higher confidence in predictions, which can be a valuable metric when dealing with unlabeled data.

4.3.4. Evaluation Metrics for Reinforcement Learning Models

Cumulative Reward (Return): Cumulative reward, also called return, is the sum of rewards received by the agent over a sequence of actions in an episode. It measures the agent’s ability to maximize its long-term objectives.

Average Reward: Average reward calculates the expected value of the rewards received per time step or per episode. It provides a measure of the agent’s efficiency and effectiveness in achieving its goals.

Discounted Sum of Rewards: In some cases, it is important to consider future rewards with less weights. The discounted sum of rewards applies a discount factor,(gamma, to give more importance to immediate rewards while still considering long-term consequences.

Episodic vs. Continuing Tasks: Depending on the task, you may need to use different evaluation methods. Episodic tasks have a clear beginning and end for each episode, while continuing tasks continue indefinitely. The choice of evaluation metric can vary accordingly.

Exploration Rate: Exploration is crucial in reinforcement learning. Evaluating the agent’s exploration rate assists in determining if it is effectively exploring the environment to uncover optimal policies or if it is becoming trapped in suboptimal ones.

Learning Curve: A learning curve plots the agent’s performance (e.g., cumulative reward) over time, showing how quickly it converges to an optimal or near-optimal policy. It helps to monitor the learning progress.

Q-value Convergence: In Q-learning and other value-based methods, the convergence of Q-values can be evaluated to assess whether the agent has learned an accurate value function.

Policy Convergence: For policy-based methods, such as policy gradients or REINFORCE, the convergence of the agent’s policy can be evaluated to determine if it has found an optimal or near-optimal policy.

Exploration–Exploitation Trade-off Metrics: Metrics like epsilon (ε)-greedy exploration rate, Boltzmann exploration, or UCB (Upper Confidence Bound) help assess how well the agent balances exploration (attempting new actions) and exploitation (selecting the best-known actions).

Success Rate: In tasks where there is a specific goal or objective (e.g., reaching a target in a maze), the success rate measures the percentage of episodes in which the agent successfully achieves the goal.

Entropy of Policy: Policy entropy quantifies the level of uncertainty in the agent’s action selection. Higher entropy indicates more exploration, while lower entropy suggests a more deterministic policy.

Time to Solve: This metric measures the time or number of steps it takes for the agent to achieve a predefined level of performance or solve a task. It helps assess efficiency.

Sample Efficiency: Sample efficiency evaluates how quickly the agent learns from its interactions with the environment, considering the number of episodes or steps required to reach a certain level of performance.

Table 8 summarizes the possible evaluation metrics for each ML category, as discussed above.

Table 8. Evaluation metrics for supervised, semi-supervised, unsupervised, and reinforcement learning models.

Category	Metric Name
Supervised Learning	Accuracy; Recall; F1-score; False alarm rate; Precision; AUC; Misdetection rate; Mean absolute percentage error; Processing time; Prediction time; Memory size; Training time per sample.
Unsupervised Learning	Silhouette score; Dunn index; Inertia (within-cluster sum of squares Gap statistic; Davies–Bouldin index; Adjusted rand index; Normalized mutual information; Homogeneity, completeness, and V-measure; Calinski–Harabasz index; Spectral gap.
Semi-Supervised Learning	Accuracy; Precision; Recall; F1-score; AUC; False alarm rate; Misdetection rate; Mean absolute percentage error; Processing time; Prediction time; Memory size; Training time per sample; Log-Likelihood; Pseudo-label Accuracy; Consistency Regularization; Active Learning Metrics; Entropy.
Reinforcement Learning	Cumulative reward (return); Average reward; Discounted sum of rewards; Episodic vs. continuing tasks; Exploration rate; Learning curve; Q-value convergence; Policy convergence; Exploration–exploitation trade-off metrics; Success rate; Entropy of policy; Time to solve; Sample efficiency.

5. Challenges and Future Directions

Machine learning has witnessed remarkable advancements in recent years, but it still faces numerous challenges and ongoing research directions. Some of the prominent areas of focus are shown in Table 9.

Table 9. Current challenges in ML [114,115,116,117,118,119,120,121,122,123,124,125].

Challenges	Descriptions
Interpretability and Explain-ability	Complex model architecture; Black-box models; User-friendly explanations; Interpretable features; Trade-off with performance.
Bias and Fairness	Data and algorithm bias; Inadvertent exhibition of biases or discrimination against specific groups; Biases in decision support systems.
Adversarial Robustness	Adversarial data poisoning; Computation and resource constraints; Data model complexity; Adversarial attacks and their transability.
Privacy and Security	Safeguarding user data and models against privacy breaches and attacks; Secure federated learning, and differential privacy.
Reinforcement Learning	Low efficiency; Low stability; Low generalization capability; Exploration–exploitation trade-offs, off-policy learning, and safe reinforcement learning.
Quantum Computing	Conflicting objectives; Multiple criteria optimization; Algorithm development; Non-convexity; High-dimensional search spaces; Computational resource constraints.
Multi-Criteria Models	Trade-off complexity; Non-convexity; High dimensionality; Preference modeling; Computational resources; Interpretability; Scalability.

Interpretability and Explain-ability: Machine learning models are considered black boxes because of their complexity. Therefore, their outputs are usually not understood. Thus, there is a pressing demand for understanding and explaining their decision-making processes. Achieving interpretability and explain--ability is vital for establishing trust and ensuring best efficiency [114,115,116,117,118,119,120,121,122].

Bias and Fairness: Machine learning algorithms use datasets built by humans, so these models can inadvertently exhibit biases or discriminate against specific groups. Consequently, reducing overfitting and promoting fairness in machine learning models are important research objectives. This entails the development of methods to classify biases, as well as the design of algorithms that exhibit fairness and lack bias across diverse demographic groups [114,115,116,117].

Adversarial Robustness: Machine learning models are vulnerable to adversarial attacks, wherein slight, imperceptible alterations to input data can result in misclassification or erroneous predictions. Research is actively focused on constructing robust models that resist adversarial attacks. Techniques such as adversarial training, defensive distillation, and robust optimization are employed to enhance model resilience [117,118].

Privacy and Security: The increased utilization of machine learning in sensitive domains raises concerns regarding privacy and security. Safeguarding user data and models against privacy breaches and attacks becomes crucial. Research directions involve the development of privacy-preserving machine learning techniques like secure multi-party computation, federated learning, and differential privacy [114,115,116,117,118,119,120,121,122].

Reinforcement Learning: In some fields and cases, there are limited real data available. For instance, in cybersecurity, data from attacks can be very limited and, in some cases, performing attacks to obtain data is not allowable. Reinforcement learning addresses the limited data availability challenge. However, existing reinforcement models have lower efficiency than conventional machine learning models. Therefore, research efforts concentrate on enhancing the efficiency, stability, and generalization capabilities of reinforcement learning algorithms. Topics include exploration–exploitation trade-offs, off-policy learning, and safe reinforcement learning [115,116,117,118,119,120,121,122].

Multi-Criteria Models: In the rapidly evolving landscape of machine learning, new trends are emerging to enhance decision-making and computational capabilities. For example, multi-criteria models are gaining prominence, enabling more sophisticated and nuanced decision-making processes. These models can be considered to account for multiple, often conflicting, criteria and objectives [123]. Multi-criteria models in machine learning involve optimizing decision-making processes when there are multiple conflicting objectives to consider, such as cost, accuracy, and interpretability. Developing machine learning algorithms that can handle these conflicting objectives and make trade-offs between them efficiently remains a significant challenge. Common approaches include multi-objective optimization techniques, Pareto front exploration, and preference modeling. Integrating these approaches into machine learning models effectively is complex due to several issues, including non-convexity, high-dimensional search spaces, and computational resource constraints. Addressing these problems is crucial for creating robust multi-criteria machine learning models capable of making informed decisions that balance diverse objectives and preferences in real-world applications.

Quantum Computing: Quantum computing represents a revolutionary frontier in machine learning. Quantum computing can offer the potential for exponential speed up in solving complex optimization and pattern recognition tasks. By harnessing the principles of quantum mechanics, quantum computing may revolutionize the field, opening doors to previously insurmountable challenges and unlocking new frontiers in ML and data analysis [124,125]. Quantum computing holds significant promise for addressing complex problems in machine learning by leveraging quantum phenomena such as superposition and entanglement. One prominent challenge in classical machine learning is solving optimization problems, and quantum algorithms like the quantum approximate optimization algorithm and the variational quantum eigensolver show potential for faster optimization convergence. Additionally, quantum ML models, such as quantum support vector machines and quantum neural networks aim to provide quantum advantages over classical counterparts in tasks like classification and regression. However, quantum computing in machine learning is still in its infancy, facing challenges related to error correction, hardware scalability, and the need for quantum data encoding schemes. As the field matures and quantum technologies advance, quantum computing can be a potential candidate to revolutionize ML by tackling complex optimization and modeling challenges more efficiently.

These challenges and research directions represent only a fraction of the vast landscape within machine learning. These challenges underscore the complexity of machine learning and researchers and practitioners strive to overcome the limitations and advance the capabilities of these systems. The field continues to rapidly evolve, driven by the necessity to confront these challenges and extend the frontiers of what is achievable with these models.

6. Conclusions

This paper highlights a summary of machine learning cyber-security applications, covering data pre-processing, models, and optimization techniques applicable across various domains. The survey discusses fundamental concepts, current advancements, components of machine learning cyber-security applications, and existing challenges. A major contribution of this survey is the classification of machine learning models into four categories: supervised, semi-supervised, unsupervised, and reinforcement learning. Through this classification, we introduce a taxonomy of existing developments in machine learning classification models based on their shared characteristics. Optimization techniques are necessary techniques in developing optimal and successful machine learning algorithms, and we provide a concise discussion of these techniques. Additionally, we outline open challenges and potential research directions to inspire practical and future research endeavors.