Energy Saving Strategy of UAV in MEC Based on Deep Reinforcement Learning
Abstract
:1. Introduction
- (1)
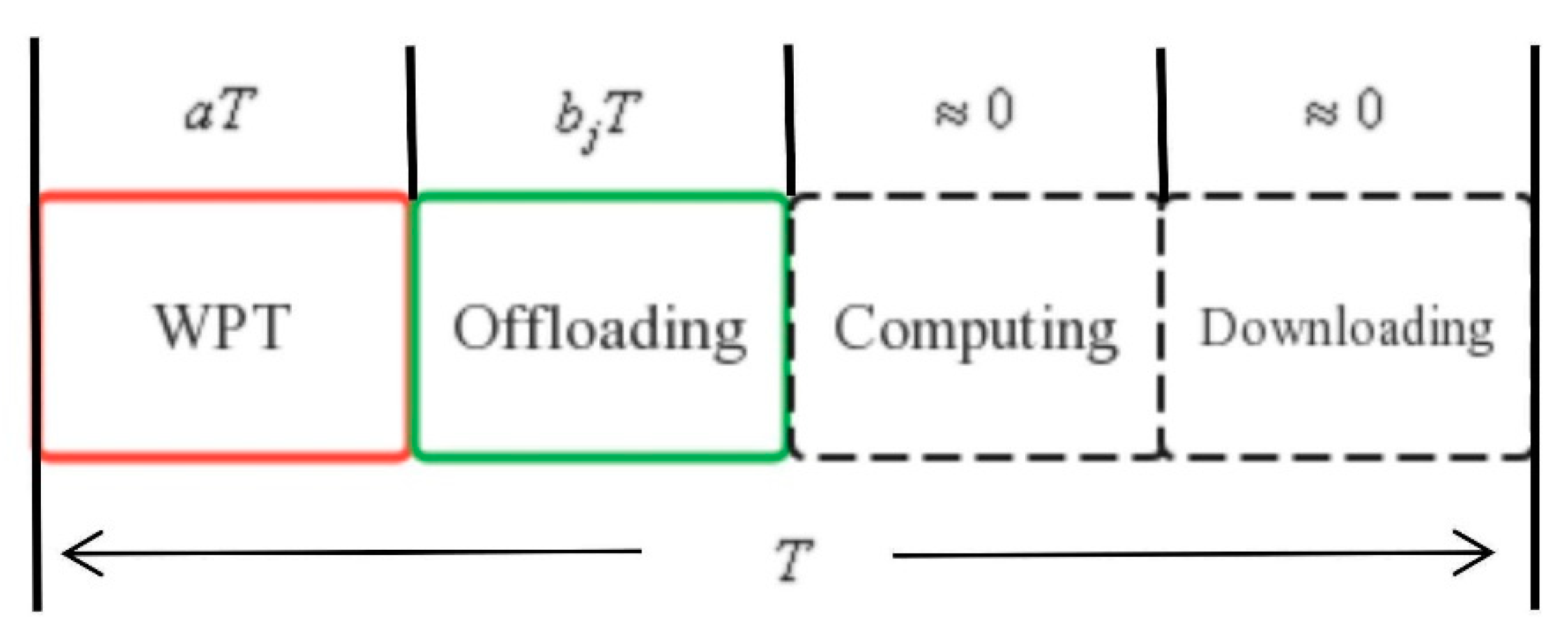
- The MEC system that we consider consists of a multi-antenna AP with an edge server placed on the ship and multiple UAVs with a single antenna. The AP can provide wireless energy for the UAV and can also be used to receive UAV computing tasks. The UAV computing task adopts the binary offload method, and the offload scheduling is implemented based on the time division multiple access (TDMA) communication protocol. In order to achieve the research goal of maximizing the residual energy of the UAV, we propose an optimization scheme to jointly optimize the UAV time and communication resources. The research objective is formalized as the problem of maximizing the residual energy of UAV.
- (2)
- The formalized problem of maximizing the residual energy is a non-convex problem and difficult to solve. However, once the offloading decision is given, the problem can be transformed into a convex problem, which can be solved by a convex optimization method. Therefore, we split the target problem into two sub-problems: the time resource allocation problem and task offloading problem. Firstly, we use the convex optimization method to solve the time resource allocation problem, and then obtain an online task offloading strategy that maximizes the residual energy of the UAV in wireless fading environments based on the DOTO algorithm.
- (3)
- To reduce the computational complexity of the DOTO algorithm, we propose a new adaptive quantization method, which reduces the quantization action of the algorithm with the increase in the time block. Under the condition of ensuring the quality of the offloading strategy, the exponentially increased delay due to the increase in the number of devices is reduced so as to be almost unchanged.
- (4)
- Simulation experiments show that the DOTO algorithm proposed for the research objective of maximizing the UAV’s residual energy in MEC can provide users with an online computing offloading strategy that is superior to other traditional benchmark schemes. Moreover, when there is a UAV in the MEC system that exits the system due to insufficient power or failure, or if a new UAV is connected to the system, the DOTO algorithm can still quickly converge to provide an effective online computing task offloading strategy for the MEC system in time.
2. Related Work
3. System Model
3.1. Energy Transfer Model
3.2. Local Computing Model
3.3. Offloading Computing Model
4. Problem Formulation and Solution
4.1. Problem Formulation
4.2. Problem Analysis and Solution
4.2.1. Computing Task Offloading Decision Problem
4.2.2. Time Resource Allocation Problem
5. The DOTO Algorithm
5.1. Algorithm Overview
5.2. Offload Function Iteration
- (1)
- Initially, set the value to . During training, all alternatives generated by the KNN quantization method are sorted by Euclidean distance.
- (2)
- Each time block records the index value corresponding to the maximum residual energy offloading action. Every time block, compare the largest in the time block with the in the time block, and select the largest value as the next iteration.
- (3)
- In order to avoid excessive training loss caused by an overly small value, when , we set the value as , i.e., the value range of is .
5.3. Offload Policy Update
| Algorithm 1 The DOTO algorithm |
| Input:: wireless channel gain at each time block ; : the number of time
blocks; : training interval; : the number of quantized actions; |
| Output: optimal offloading decision ; 1: Initialize the DNN with random parameters and empty memory; 2: for do 3: Generate a relaxed offloading action ; 4: Quantize into binary actions ; 5: Compute for all by solving ; 6: Select the optimal offloading decision ; 7: Update experience replay pool by adding ; 8: if mod then 9: Randomly select training samples ; 10: Update using the Nadam algorithm; 11: end 12: if mod = 0 then 13: Update by ; 14: end 15: end |
6. Simulation Results
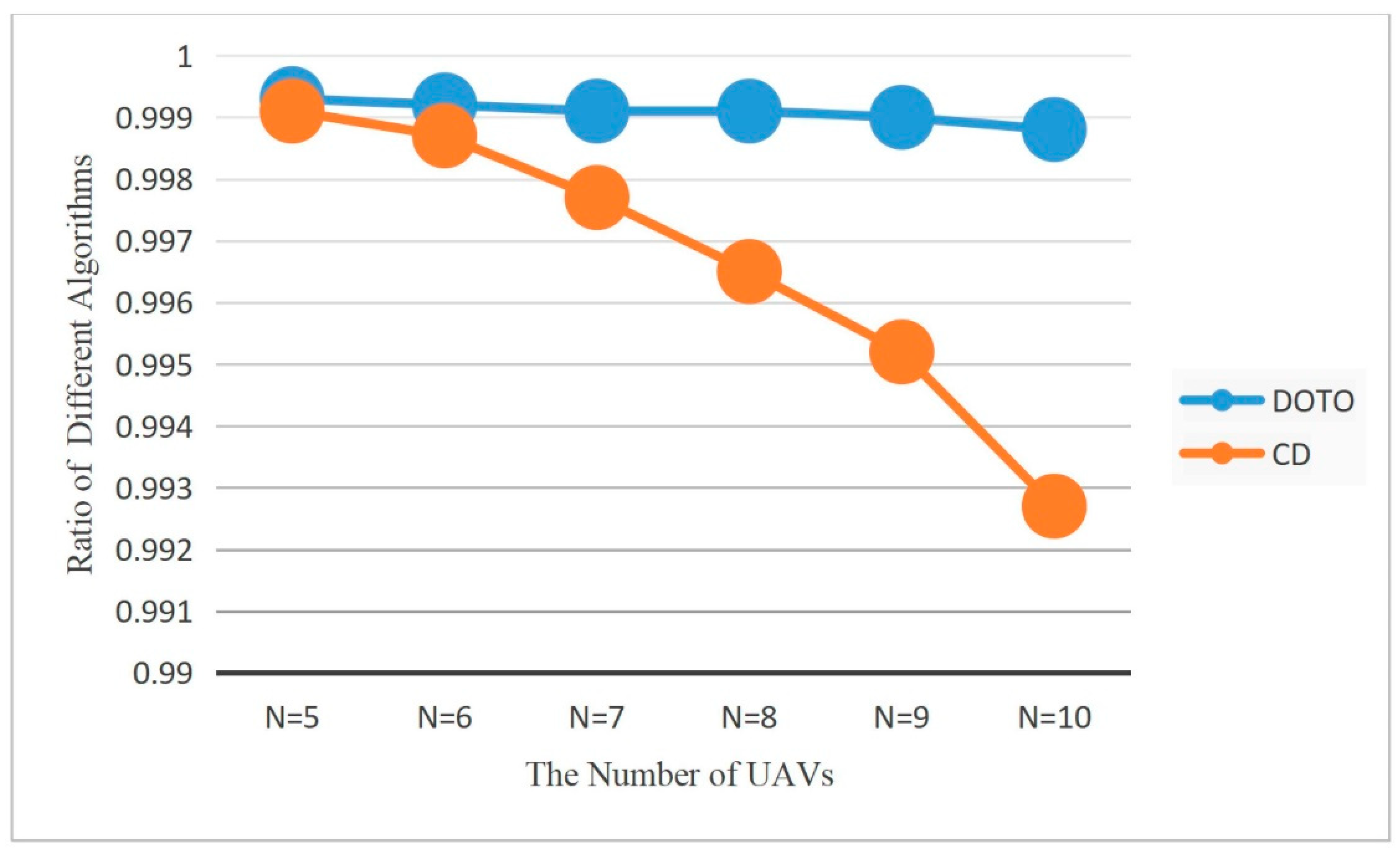
6.1. Performance of Algorithm
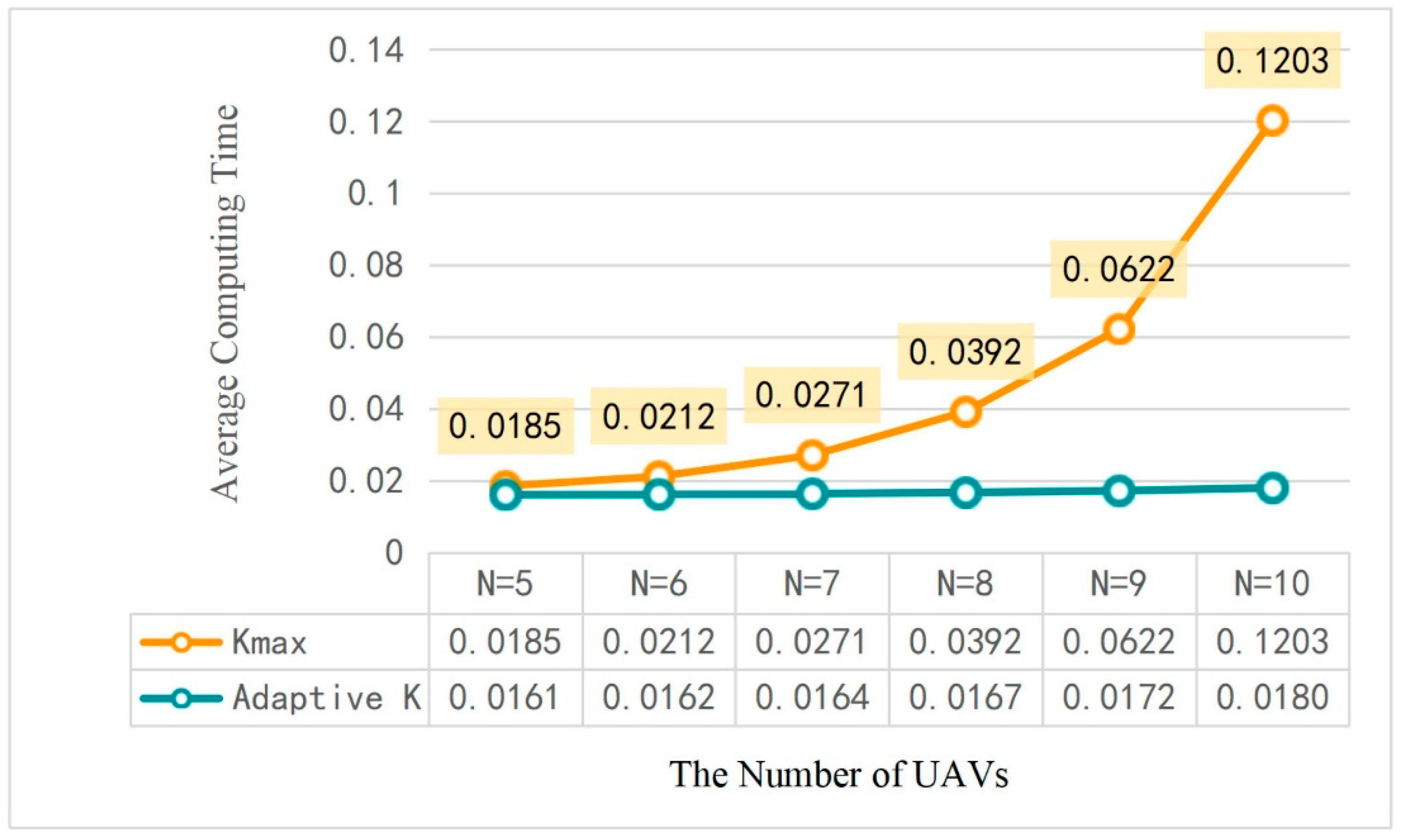
6.2. Adaptive Value Setting Method
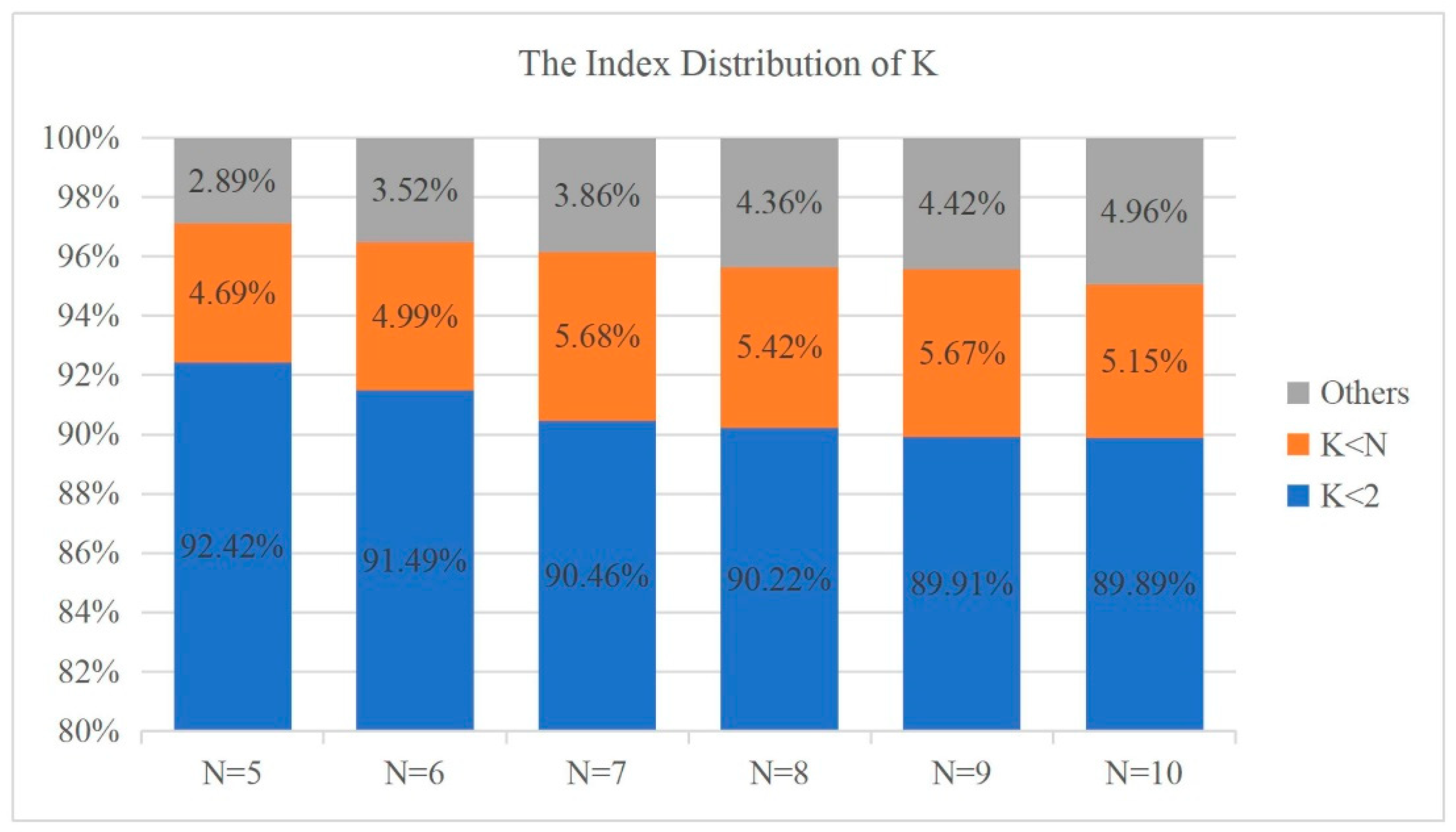
6.3. The Effects of Different Parameters
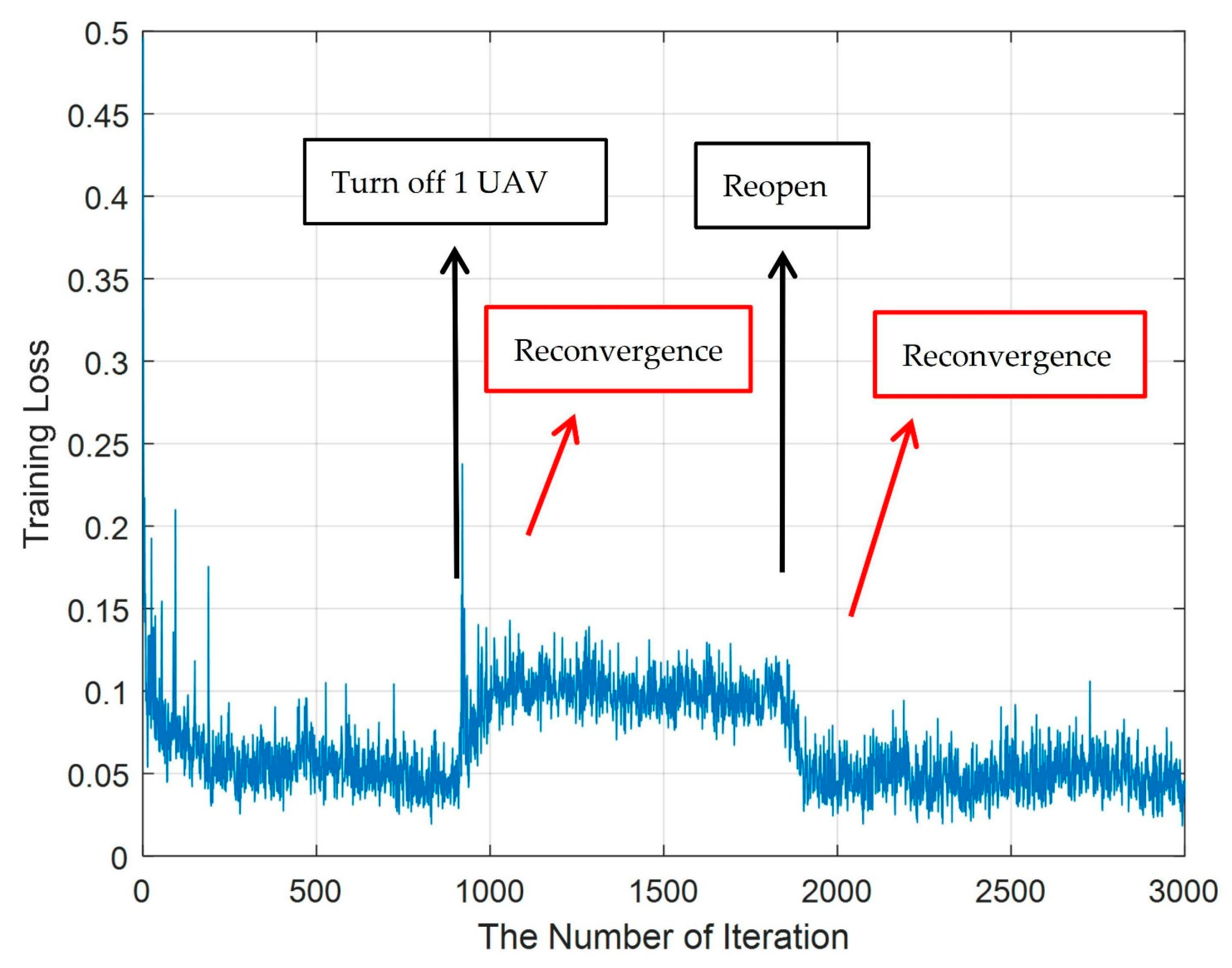
6.4. Switching UAV On or Off
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abd Elaziz, M.; Abualigah, L.; Ibrahim, R.A.; Attiya, I. IoT Workflow Scheduling Using Intelligent Arithmetic Optimization Algorithm in Fog Computing. Comput. Intell. Neurosci. 2021, 2021, 9114113. [Google Scholar] [CrossRef] [PubMed]
- Dhelim, S.; Ning, H.; Farha, F.; Chen, L.; Atzori, L.; Daneshmand, M. IoT-Enabled Social Relationships Meet Artificial Social Intelligence. IEEE Internet Things J. 2021, 8, 17817–17828. [Google Scholar] [CrossRef]
- Martinez-Alpiste, I.; Golcarenarenji, G.; Wang, Q.; Alcaraz-Calero, J.M. Search and Rescue Operation Using UAVs: A Case Study. Expert Syst. Appl. 2021, 178, 114937. [Google Scholar] [CrossRef]
- Rozlosnik, A.; Infrarroja, S.T.; de Bustamante, S. Potential Contribution of the Infrared Industry in the Future of IoT/IIoT. In Proceedings of the 14th Quantitative InfraRed Thermography Conference, Berlin, Germany, 25–29 June 2018; pp. 25–29. [Google Scholar]
- Al-Turjman, F.; Zahmatkesh, H.; Al-Oqily, I.; Daboul, R. Optimized Unmanned Aerial Vehicles Deployment for Static and Mobile Targets’ Monitoring. Comput. Commun. 2020, 149, 27–35. [Google Scholar] [CrossRef]
- Avgeris, M.; Spatharakis, D.; Dechouniotis, D.; Kalatzis, N.; Roussaki, I.; Papavassiliou, S. Where There Is Fire There Is Smoke: A Scalable Edge Computing Framework for Early Fire Detection. Sensors 2019, 19, 639. [Google Scholar] [CrossRef] [Green Version]
- Liu, P.; Xu, G.; Yang, K.; Wang, K.; Li, Y. Joint Optimization for Residual Energy Maximization in Wireless Powered Mobile-Edge Computing Systems. KSII Trans. Internet Inf. Syst. (TIIS) 2018, 12, 5614–5633. [Google Scholar]
- Li, L.; Xu, G.; Liu, P.; Li, Y.; Ge, J. Jointly Optimize the Residual Energy of Multiple Mobile Devices in the MEC–WPT System. Future Internet 2020, 12, 233. [Google Scholar] [CrossRef]
- Hu, X.; Wong, K.K.; Yang, K. Wireless Powered Cooperation-Assisted Mobile Edge Computing. IEEE Trans. Wirel. Commun. 2018, 17, 2375–2388. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, A.; Ahmed, E. A Survey on Mobile Edge Computing. In Proceedings of the International Conference on Intelligent Systems & Control, Coimbatore, India, 7–8 January 2016. [Google Scholar]
- Mao, Y.; You, C.; Zhang, J.; Huang, K.; Letaief, K.B. A Survey on Mobile Edge Computing: The Communication Perspective. IEEE Commun. Surv. Tutor. 2017, 19, 2322–2358. [Google Scholar] [CrossRef] [Green Version]
- Yu, Z.; Xu, G.; Li, Y.; Liu, P.; Li, L. Joint Offloading and Energy Harvesting Design in Multiple Time Blocks for FDMA Based Wireless Powered MEC. Future Internet 2021, 13, 70. [Google Scholar] [CrossRef]
- Huang, L.; Bi, S.; Zhang, Y.-J.A. Deep Reinforcement Learning for Online Computation Offloading in Wireless Powered Mobile-Edge Computing Networks. IEEE Trans. Mob. Comput. 2019, 19, 2581–2593. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.; Wang, P.; Niyato, D.; Kim, D.I.; Han, Z. Wireless Networks with RF Energy Harvesting: A Contemporary Survey. IEEE Commun. Surv. Tutor. 2014, 17, 757–789. [Google Scholar] [CrossRef] [Green Version]
- Gao, H.; Ejaz, W.; Jo, M. Cooperative Wireless Energy Harvesting and Spectrum Sharing in 5G Networks. IEEE Access 2016, 4, 3647–3658. [Google Scholar] [CrossRef]
- Mao, Y.; Zhang, J.; Letaief, K.B. Dynamic Computation Offloading for Mobile-Edge Computing with Energy Harvesting Devices. IEEE J. Sel. Areas Commun. 2016, 34, 3590–3605. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.; Xing, H.; Xu, J. Real-Time Resource Allocation for Wireless Powered Multiuser Mobile Edge Computing with Energy and Task Causality. IEEE Trans. Commun. 2020, 68, 7140–7155. [Google Scholar] [CrossRef]
- Wang, Y.; Sheng, M.; Wang, X.; Wang, L.; Li, J. Mobile-Edge Computing: Partial Computation Offloading Using Dynamic Voltage Scaling. IEEE Trans. Commun. 2016, 64, 4268–4282. [Google Scholar] [CrossRef]
- Wang, C.; Liang, C.; Yu, F.R.; Chen, Q.; Tang, L. Computation Offloading and Resource Allocation in Wireless Cellular Networks with Mobile Edge Computing. IEEE Trans. Wirel. Commun. 2017, 16, 4924–4938. [Google Scholar] [CrossRef]
- Bi, S.; Zhang, Y.J. Computation Rate Maximization for Wireless Powered Mobile-Edge Computing with Binary Computation Offloading. IEEE Trans. Wirel. Commun. 2018, 17, 4177–4190. [Google Scholar] [CrossRef] [Green Version]
- Tran, T.X.; Pompili, D. Joint Task Offloading and Resource Allocation for Multi-Server Mobile-Edge Computing Networks. IEEE Trans. Veh. Technol. 2018, 68, 856–868. [Google Scholar] [CrossRef] [Green Version]
- Guo, S.; Xiao, B.; Yang, Y.; Yang, Y. Energy-Efficient Dynamic Offloading and Resource Scheduling in Mobile Cloud Computing. In Proceedings of the IEEE INFOCOM 2016-The 35th Annual IEEE International Conference on Computer Communications, San Francisco, CA, USA, 10–14 April 2016; pp. 1–9. [Google Scholar]
- Dinh, T.Q.; Tang, J.; La, Q.D.; Quek, T.Q. Offloading in Mobile Edge Computing: Task Allocation and Computational Frequency Scaling. IEEE Trans. Commun. 2017, 65, 3571–3584. [Google Scholar]
- Dulac-Arnold, G.; Evans, R.; van Hasselt, H.; Sunehag, P.; Lillicrap, T.; Hunt, J.; Mann, T.; Weber, T.; Degris, T.; Coppin, B. Deep Reinforcement Learning in Large Discrete Action Spaces. arXiv 2015, arXiv:1512.07679. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-Level Control through Deep Reinforcement Learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Bi, S.; Huang, L.; Wang, H.; Zhang, Y. Stable Online Computation Offloading via Lyapunov-Guided Deep Reinforcement Learning. In Proceedings of the ICC 2021-IEEE International Conference on Communications, Montreal, QC, Canada, 14–23 June 2021. [Google Scholar]
- Naouri, A.; Wu, H.; Nouri, N.A.; Dhelim, S.; Ning, H. A Novel Framework for Mobile-Edge Computing by Optimizing Task Offloading. IEEE Internet Things J. 2021, 8, 13065–13076. [Google Scholar] [CrossRef]
- You, C.; Huang, K.; Chae, H. Energy Efficient Mobile Cloud Computing Powered by Wireless Energy Transfer. IEEE J. Sel. Areas Commun. 2016, 34, 1757–1771. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Giannakis, G.B. Power-Efficient Resource Allocation for Time-Division Multiple Access over Fading Channels. IEEE Trans. Inf. Theory 2008, 54, 1225–1240. [Google Scholar] [CrossRef]
- Wang, F.; Xu, J.; Wang, X.; Cui, S. Joint Offloading and Computing Optimization in Wireless Powered Mobile-Edge Computing Systems. IEEE Trans. Wirel. Commun. 2017, 17, 1784–1797. [Google Scholar] [CrossRef]
- Zhou, F.; Wu, Y.; Hu, R.Q.; Qian, Y. Computation Rate Maximization in UAV-Enabled Wireless-Powered Mobile-Edge Computing Systems. IEEE J. Sel. Areas Commun. 2018, 36, 1927–1941. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Liu, T.; Zhu, Y.; Yang, Y. A Deep Reinforcement Learning Approach for Online Computation Offloading in Mobile Edge Computing. In Proceedings of the 2020 IEEE/ACM 28th International Symposium on Quality of Service (IWQoS), Hangzhou, China, 15–17 June 2020. [Google Scholar]
- Bi, S.; Huang, L.; Wang, H.; Zhang, Y. Lyapunov-Guided Deep Reinforcement Learning for Stable Online Computation Offloading in Mobile-Edge Computing Networks. IEEE Trans. Wirel. Commun. 2021, 20, 7519–7537. [Google Scholar] [CrossRef]
- Min, M.; Xiao, L.; Chen, Y.; Cheng, P.; Wu, D.; Zhuang, W. Learning-Based Computation Offloading for IoT Devices with Energy Harvesting. IEEE Trans. Veh. Technol. 2019, 68, 1930–1941. [Google Scholar] [CrossRef] [Green Version]
- Zhao, N.; Ye, Z.; Pei, Y.; Liang, Y.-C.; Niyato, D. Multi-Agent Deep Reinforcement Learning for Task Offloading in UAV-Assisted Mobile Edge Computing. IEEE Trans. Wirel. Commun. 2022, 1. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Z.-Y.; Min, L.; Tang, C.; Zhang, H.-Y.; Wang, Y.-H.; Cai, P. Task Offloading and Trajectory Control for UAV-Assisted Mobile Edge Computing Using Deep Reinforcement Learning. IEEE Access 2021, 9, 53708–53719. [Google Scholar] [CrossRef]
- Herbert, S.; Wassell, I.; Loh, T.-H.; Rigelsford, J. Characterizing the Spectral Properties and Time Variation of the In-Vehicle Wireless Communication Channel. IEEE Trans. Commun. 2014, 62, 2390–2399. [Google Scholar] [CrossRef]
- Mao, S.; Leng, S.; Yang, K.; Huang, X.; Zhao, Q. Fair Energy-Efficient Scheduling in Wireless Powered Full-Duplex Mobile-Edge Computing Systems. In Proceedings of the GLOBECOM 2017-2017 IEEE Global Communications Conference, Singapore, 4–8 December 2017; pp. 1–6. [Google Scholar]
- Boyd, S.; Boyd, S.P.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Calmet, J.; Benhamou, B.; Caprotti, O.; Henocque, L.; Sorge, V. (Eds.) Artificial Intelligence, Automated Reasoning, and Symbolic Computation. In Prceeedings AISC 2002 and Calculemus 2002, Marseille, France, 1–5 July 2002; Springer: Berlin/Heidelberg, Germany, 2002; Available online: https://link.springer.com/book/10.1007/3-540-45470-5 (accessed on 7 July 2022).
- Tato, A.; Nkambou, R. Infusing Expert Knowledge into a Deep Neural Network Using Attention Mechanism for Personalized Learning Environments. Available online: https://www.frontiersin.org/articles/10.3389/frai.2022.921476/full (accessed on 7 July 2022).
- Dozat, T. Incorporating Nesterov Momentum into Adam; ICLR 2016 Workshop; 11 March 2016. Available online: https://openreview.net/pdf/OM0jvwB8jIp57ZJjtNEZ.pdf (accessed on 7 July 2022).




| Training Interval | Ratio of Residual Energy to Optimal Decision | Convergence Performance |
|---|---|---|
| 2 | 0.9985 | convergence fluctuates greatly |
| 5 | 0.9990 | convergence fluctuates greatly |
| 10 | 0.9991 | convergence |
| 20 | 0.9990 | convergence |
| 40 | non-convergence | |
| 80 | non-convergence |
| Experience Replay Pool | Training Sample | Ratio of Residual Energy to Optimal Decision | Convergence Performance |
|---|---|---|---|
| 64 | 64 | 0.9987 | convergence fluctuates greatly |
| 128 | 64 | 0.9986 | convergence fluctuates greatly |
| 128 | 0.9984 | convergence fluctuates greatly | |
| 256 | 64 | 0.9988 | convergence |
| 128 | 0.9988 | convergence fluctuates greatly | |
| 256 | 0.9987 | convergence fluctuates greatly | |
| 512 | 64 | 0.9988 | convergence |
| 128 | 0.9989 | convergence fluctuates greatly | |
| 256 | 0.9989 | convergence fluctuates greatly | |
| 1024 | 64 | 0.9990 | convergence |
| 128 | 0.9991 | convergence | |
| 256 | 0.9990 | convergence | |
| 2048 | 64 | 0.9989 | slow convergence |
| 128 | 0.9991 | slow convergence | |
| 256 | 0.9990 | convergence |
| Training Sample | Ratio of Residual Energy to Optimal Decision | Convergence Performance |
|---|---|---|
| 16 | non-convergence | |
| 32 | 0.9985 | convergence fluctuates greatly |
| 64 | 0.9990 | convergence |
| 128 | 0.9991 | convergence |
| 256 | 0.9990 | convergence |
| 512 | 0.9988 | convergence fluctuates greatly |
| 1024 | 0.9985 | convergence fluctuates greatly |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, Z.; Xu, G.; Liu, Z.; Ge, J.; Wang, W. Energy Saving Strategy of UAV in MEC Based on Deep Reinforcement Learning. Future Internet 2022, 14, 226. https://doi.org/10.3390/fi14080226
Dai Z, Xu G, Liu Z, Ge J, Wang W. Energy Saving Strategy of UAV in MEC Based on Deep Reinforcement Learning. Future Internet. 2022; 14(8):226. https://doi.org/10.3390/fi14080226
Chicago/Turabian StyleDai, Zhiqiang, Gaochao Xu, Ziqi Liu, Jiaqi Ge, and Wei Wang. 2022. "Energy Saving Strategy of UAV in MEC Based on Deep Reinforcement Learning" Future Internet 14, no. 8: 226. https://doi.org/10.3390/fi14080226
APA StyleDai, Z., Xu, G., Liu, Z., Ge, J., & Wang, W. (2022). Energy Saving Strategy of UAV in MEC Based on Deep Reinforcement Learning. Future Internet, 14(8), 226. https://doi.org/10.3390/fi14080226





