Missing Data Imputation in the Internet of Things Sensor Networks
Abstract
:1. Introduction
2. Motivation and Contribution
- As various imputation techniques exist in the literature, when faced with real-life missing instances where there is no ground truth data, it is important to have imputation approaches that will embed the capability of selecting optimal algorithms for imputing missing values. We propose an imputation algorithm called BFMVI that is capable of choosing appropriate techniques for filling-in missing instances based on the nature and characteristics of the missing data.
- We also propose a reverse error score function RES(r) that is based on double Root Mean Squared Error (RMSE) calculations on two final imputation estimates to obtain the final imputation result for filling in missing instances.
- We experimentally demonstrate that considering highly correlated auxiliary variables in the imputation model will impute efficient predictors which will significantly improve the RMSE and MAE scores.
- Our proposed BFMVI algorithm shows a better performance as opposed to alternative benchmark techniques when missing values occur at different rates and consecutive periods of time.
3. Related Works
4. Experiments
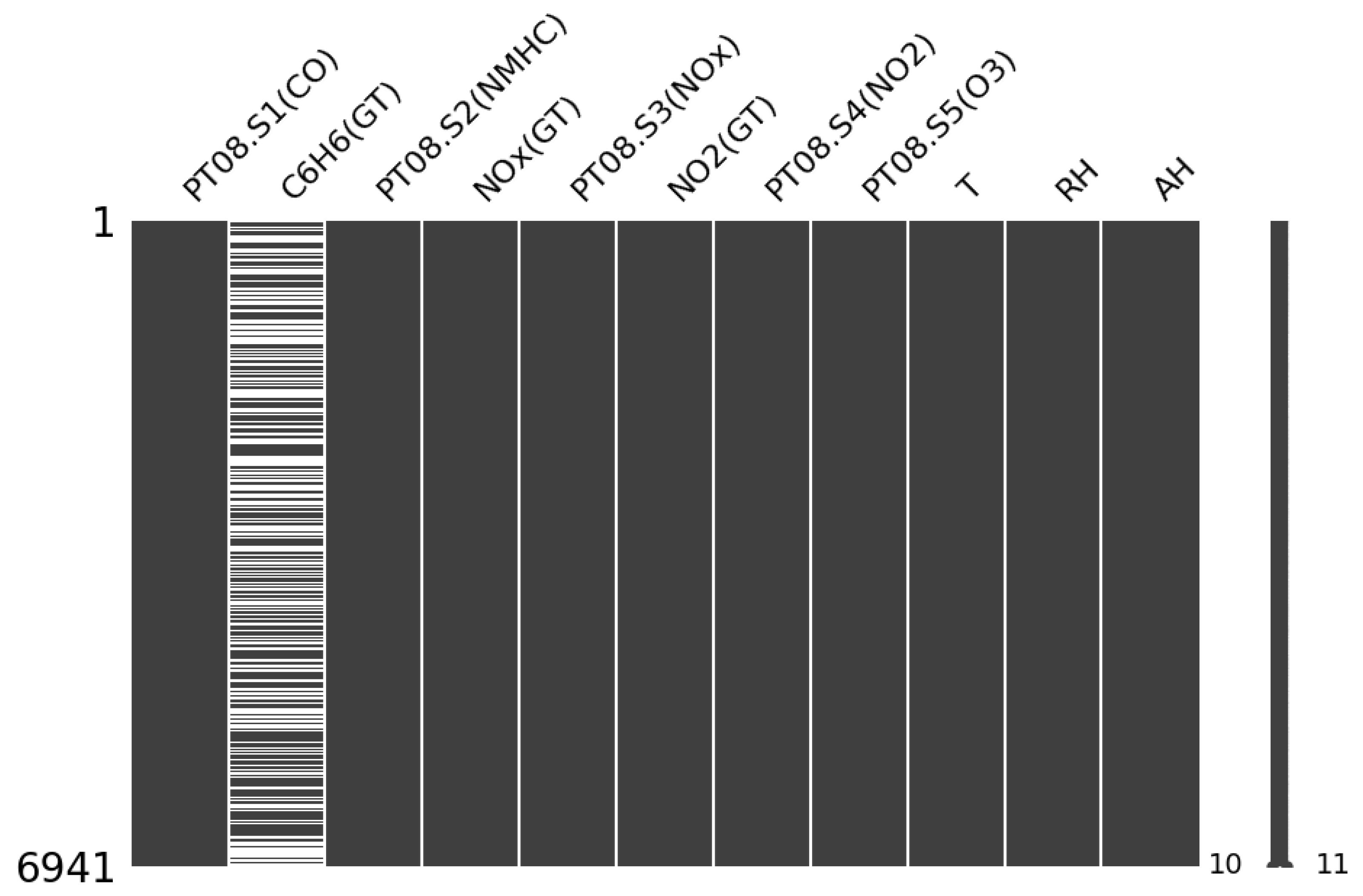
4.1. Dataset Description
4.2. Methodology
- (i)
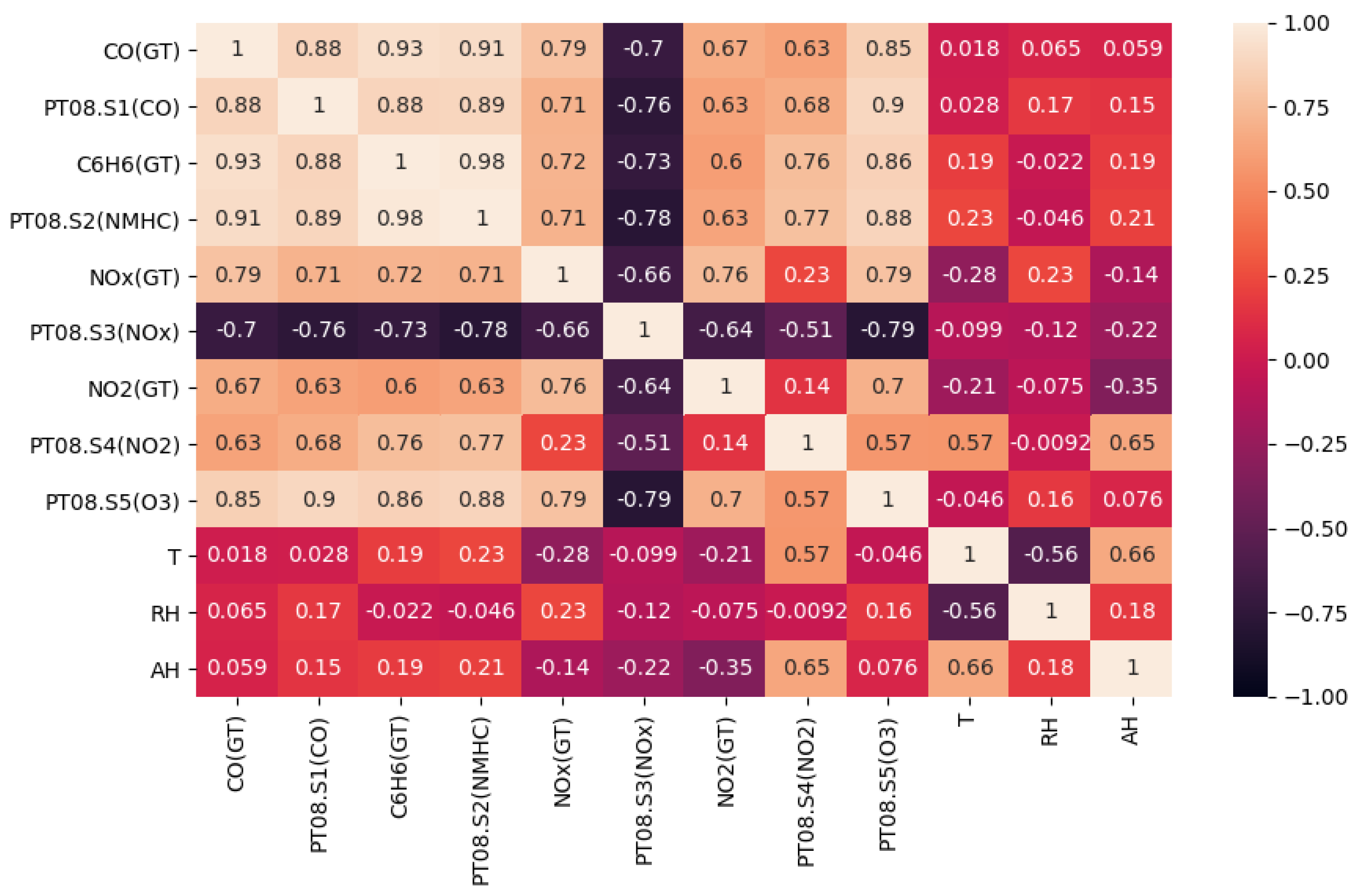
- We evaluated the correlation between each feature as seen in Figure 2; features that exhibited strong correlation with the variable (CH) that required imputation were used in the imputation model.
- (ii)
- We created missingness at arbitrary points on the target variable.
- (iii)
- We imputed missing values using the different imputation techniques.
- (iv)
- The accuracy off all the imputation techniques were assessed and compared using their Root Mean Squared Error (RMSE) indicator.
- (v)
- We analysed the effect of each imputation technique on the sensor calibration and compared the results to the calibration result of each imputation method.
- (a)
- We simulated missingness on a single variable at random, where missing ratio r = (10%, 20%, 30% and 40%).
- (b)
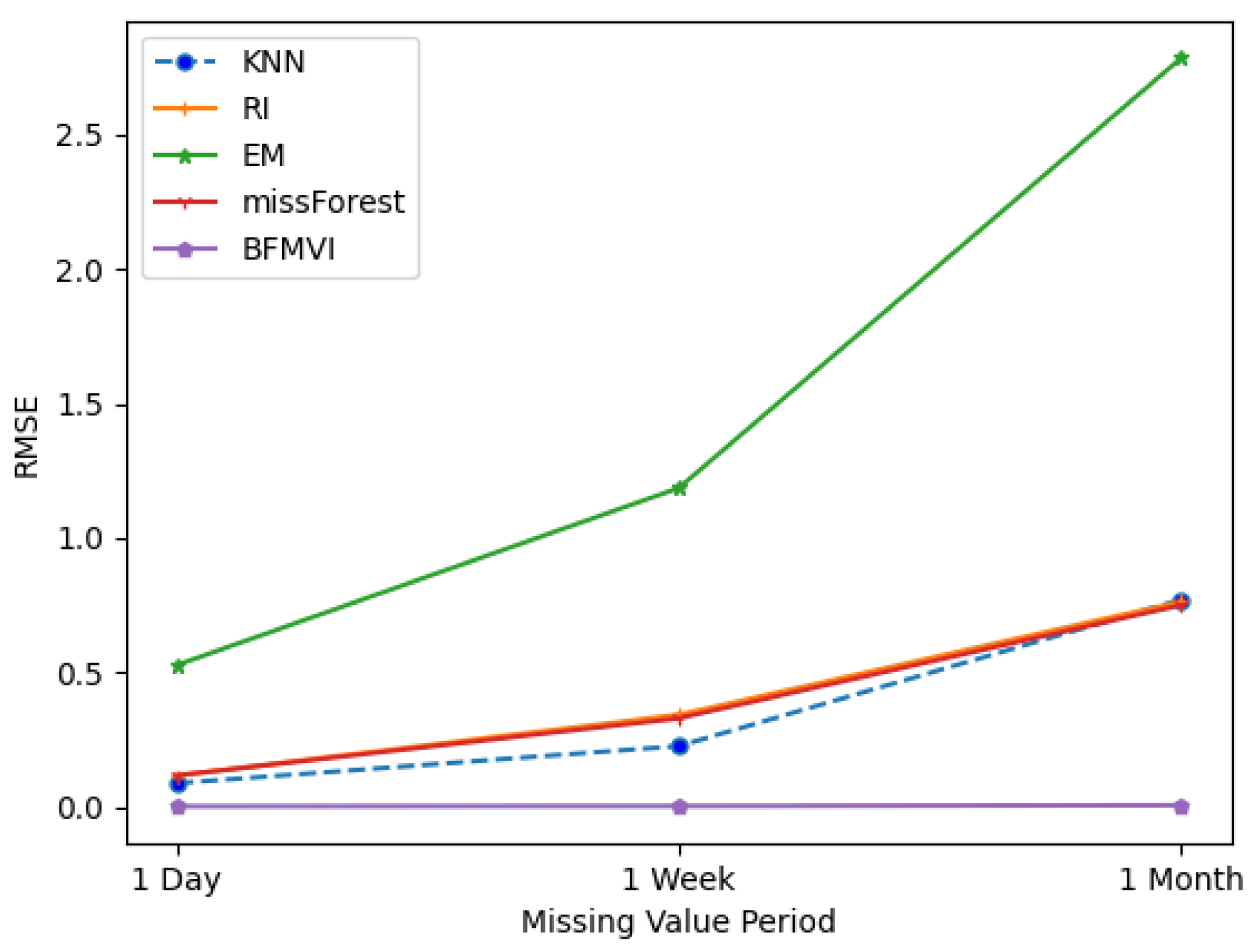
- We simulated missing values on one variable, occurring over p consecutive time periods where p = (1 day, 1 week and 1 month).
4.2.1. Expectation Maximization Imputation (EMI)
4.2.2. K-Nearest Neighbour (KNN) Imputation
4.2.3. MissForest
4.2.4. Regression Imputation
4.3. Our Approach
4.3.1. Stage 1: Partitioning the Dataset
4.3.2. Stage 2: Defining the Imputation Strategy
- representing the values that are present in the variable
- representing the values that are missing in the variable
- representing the observations, = {1,…,n}\ of the predictor variable in
- representing the observations, of the predictor variable in
- The missing values in each cluster matrix are located.
- The kNN vectors are defined by; with , where represents the rows of the matrix , and is the distance given by Equation (1).
- For each point in , the distance (x, y) between the missing point and nearest imputed value is stored in a similarity array .
- The array is sorted in descending order and the top K data for in is selected for imputation.
- For each matrix the data was split into four parts similar to the RF method where a regression model was trained on the response and predictor variable .
- The trained regression model is then used to predict the missing values in .
4.3.3. Step 3: Selecting the Best Fit Estimation
| Algorithm 1k-Best Fit Estimation Model. |
Input: Incomplete matrix X (n x p). Parameter: , missing value: vs. Output: Dataset with Imputed values .
|
4.4. Model Evaluation
5. Results
5.1. Imputation
5.2. Sensor Calibration
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| RI | Regression Imputation |
| EM | Expectation Maximization |
| kNN | kNeareast-Neighbour |
| BFMVI | Best Fit Missing Value Imputation |
| MLR | Multi-linear Regression |
| DT | Decision Tree |
| RF | Random Forest |
References
- Lee, G.H.; Han, J.; Choi, J.K. MPdist-based missing data imputation for supporting big data analyses in IoT-based applications. Future Gener. Comput. Syst. 2021, 125, 421–432. [Google Scholar] [CrossRef]
- Al-Aqrabi, H.; Johnson, A.P.; Hill, R.; Lane, P.; Alsboui, T. Hardware-intrinsic multi-layer security: A new frontier for 5G enabled IIoT. Sensors 2020, 20, 1963. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Al-Aqrabi, H.; Liu, L.; Hill, R.; Antonopoulos, N. A multi-layer hierarchical inter-cloud connectivity model for sequential packet inspection of tenant sessions accessing BI as a service. In Proceedings of the 2014 IEEE International Conference on High Performance Computing and Communications, 2014 IEEE 6th International Symposium on Cyberspace Safety and Security, 2014 IEEE 11th International Conference on Embedded Software and System (HPCC, CSS, ICESS), Paris, France, 20–22 August 2014; pp. 498–505. [Google Scholar]
- Al-Aqrabi, H.; Hill, R.; Lane, P.; Aagela, H. Securing manufacturing intelligence for the industrial internet of things. In Proceedings of the Fourth International Congress on Information and Communication Technology, Singapore, 22 January 2019; pp. 267–282. [Google Scholar]
- De Vito, S.; Massera, E.; Piga, M.; Martinotto, L.; Di Francia, G. On field calibration of an electronic nose for benzene estimation in an urban pollution monitoring scenario. Sens. Actuators B Chem. 2008, 129, 750–757. [Google Scholar] [CrossRef]
- Mazzeo, N.A.; Venegas, L.E. Evaluation of turbulence from traffic using experimental data obtained in a street canyon. Int. J. Environ. Pollut. 2005, 25, 164–176. [Google Scholar] [CrossRef]
- Loy-Benitez, J.; Heo, S.; Yoo, C. Imputing missing indoor air quality data via variational convolutional autoencoders: Implications for ventilation management of subway metro systems. Build. Environ. 2020, 182, 107135. [Google Scholar] [CrossRef]
- Chen, Y.; Lv, Y.; Wang, F.Y. Traffic flow imputation using parallel data and generative adversarial networks. IEEE Trans. Intell. Transp. Syst. 2019, 21, 1624–1630. [Google Scholar] [CrossRef]
- Sanjar, K.; Bekhzod, O.; Kim, J.; Paul, A.; Kim, J. Missing data imputation for geolocation-based price prediction using KNN–mcf method. ISPRS Int. J. Geo-Inf. 2020, 9, 227. [Google Scholar] [CrossRef] [Green Version]
- Wells, B.J.; Chagin, K.M.; Nowacki, A.S.; Kattan, M.W. Strategies for handling missing data in electronic health record derived data. Egems 2013, 1, 1035. [Google Scholar] [CrossRef]
- Ehrlinger, L.; Grubinger, T.; Varga, B.; Pichler, M.; Natschläger, T.; Zeindl, J. Treating missing data in industrial data analytics. In Proceedings of the 2018 Thirteenth International Conference on Digital Information Management (ICDIM), Berlin, Germany, 24–26 September 2018; IEEE: Piscataway, NJ, USA; pp. 148–155. [Google Scholar]
- Read, S.H. Applying Missing Data Methods to Routine Data Using the Example of a Population-Based Register of Patients with Diabetes. Ph.D. Thesis, University of Edinburgh, Edinburgh, UK, 4 July 2015. [Google Scholar]
- Osman, M.S.; Abu-Mahfouz, A.M.; Page, P.R. A survey on data imputation techniques: Water distribution system as a use case. IEEE Access 2018, 6, 63279–63291. [Google Scholar] [CrossRef]
- Graham, J.W. Missing data analysis: Making it work in the real world. Annu. Rev. Psychol. 2009, 60, 549–576. [Google Scholar] [CrossRef] [Green Version]
- Azur, M.J.; Stuart, E.A.; Frangakis, C.; Leaf, P.J. Multiple imputation by chained equations: What is it and how does it work? Int. J. Methods Psychiatr. Res. 2011, 20, 40–49. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; He, Z.; Sun, L. A Bayesian tensor decomposition approach for spatiotemporal traffic data imputation. Transp. Res. Part C Emerg. Technol. 2019, 98, 73–84. [Google Scholar] [CrossRef]
- Stekhoven, D.J.; Bühlmann, P. MissForest—non-parametric missing value imputation for mixed-type data. Bioinformatics 2012, 28, 112–118. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mesquita, D.P.; Gomes, J.P.P.; Rodrigues, L.R. Artificial neural networks with random weights for incomplete datasets. Neural Process. Lett. 2019, 50, 2345–2372. [Google Scholar] [CrossRef]
- Snow, D. MTSS-GAN: Multivariate Time Series Simulation Generative Adversarial Networks. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3616557 (accessed on 2 May 2022).
- Xie, R.; Jan, N.M.; Hao, K.; Chen, L.; Huang, B. Supervised variational autoencoders for soft sensor modeling with missing data. IEEE Trans. Ind. Inf. 2019, 16, 2820–2828. [Google Scholar] [CrossRef]
- Peralta, M.; Jannin, P.; Haegelen, C.; Baxter, J.S. Data imputation and compression for Parkinson’s disease clinical questionnaires. Artif. Intell. Med. 2021, 114, 102051. [Google Scholar] [CrossRef]
- Bowman, S.R.; Vilnis, L.; Vinyals, O.; Dai, A.M.; Jozefowicz, R.; Bengio, S. Generating sentences from a continuous space. arXiv 2015, arXiv:1511.06349. [Google Scholar]
- Agbo, B.; Qin, Y.; Hill, R. Best Fit Missing Value Imputation (BFMVI) Algorithm for Incomplete Data in the Internet of Things. In Proceedings of the 5th International Conference on Internet of Things, Big Data and Security (IoTBDS 2020), Prague, Czech Republic, 7–9 May 2020; pp. 130–137. Available online: https://www.scitepress.org/Papers/2020/95782/95782.pdf (accessed on 4 April 2022).
- Okafor, N. Missing Data Imputation on IoT Data Networks: Implications for On-site Sensor Calibration. IEEE Sens. J. 2021, 21, 22833–22845. [Google Scholar] [CrossRef]
- Little, R.J.; Rubin, D.B. Statistical Analysis with Missing Data; John Wiley & Sons: Hoboken, NJ, USA, 2019; Available online: https://www.wiley.com/en-us/Statistical+Analysis+with+Missing+Data%2C+3rd+Edition-p-9780470526798 (accessed on 4 April 2022).
- Bashir, F. Handling of Missing Values in Static and Dynamic Data Sets. PhD Thesis, University of Sheffield, Sheffield, UK, 2019. Available online: https://etheses.whiterose.ac.uk/23283/ (accessed on 4 April 2022).
- Alsaber, A.R.; Pan, J.; Al-Hurban, A. Handling complex missing data using random forest approach for an air quality monitoring dataset: A case study of Kuwait environmental data (2012 to 2018). Int. J. Environ. Res. Public Health 2021, 18, 1333. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B (Methodol.) 1977, 39, 1–22. [Google Scholar]
- Zhang, L.; Pan, H.; Wang, B.; Zhang, L.; Fu, Z. Interval Fuzzy C-means Approach for Incomplete Data Clustering Based on Neural Networks. J. Internet Technol. 2018, 19, 1089–1098. [Google Scholar]
- Gupta, A.; Lam, M.S. Estimating missing values using neural networks. J. Oper. Res. Soc. 1996, 47, 229–238. [Google Scholar] [CrossRef]
- Ravi, V.; Krishna, M. A new online data imputation method based on general regression auto associative neural network. Neurocomputing 2014, 138, 106–113. [Google Scholar] [CrossRef]
- Guastella, D.A.; Marcillaud, G.; Valenti, C. Edge-based missing data imputation in large-scale environments. Information 2021, 12, 195. [Google Scholar] [CrossRef]
- Spinelle, L.; Gerboles, M.; Villani, M.G.; Aleixandre, M.; Bonavitacola, F. Field calibration of a cluster of low-cost available sensors for air quality monitoring. Part A: Ozone and nitrogen dioxide. Sens. Actuators B Chem. 2015, 215, 249–257. [Google Scholar] [CrossRef]
- UCI Air Quality Data Set. Available online: https://archive.ics.uci.edu/ml/datasets/air+quality (accessed on 2 February 2022).
- Phan, T.-T.-H.; Caillault, É.P.; Lefebvre, A.; Bigand, A. Dynamic time warping-based imputation for univariate time series data. Pattern Recognit. Lett. 2020, 139, 139–147. [Google Scholar]
- Liang, J.; Bentler, P.M. An EM algorithm for fitting two-level structural equation models. Psychometrika 2004, 69, 101–122. [Google Scholar] [CrossRef]
- Muthén, B.; Shedden, K. Finite mixture modeling with mixture outcomes using the EM algorithm. Biometrics 1999, 55, 463–469. [Google Scholar] [CrossRef]
- Neale, M.C.; Boker, S.M.; Xie, G.; Maes, H.M. Statistical Modeling; Department of Psychiatry, Virginia Commonwealth University: Richmond, VA, USA, 1999; Available online: http://ftp.vcu.edu/pub/mx/doc/mxmang10.pdf (accessed on 4 April 2022).
- Raudenbush, S.W.; Bryk, A.S. Hierarchical Linear Models: Applications and Data Analysis Methods; SAGE: Newbury Park, CA, USA, 2002; Available online: https://us.sagepub.com/en-us/nam/hierarchical-linear-models/book9230 (accessed on 4 April 2022).
- Neal, R.M.; Hinton, G.E. A view of the EM algorithm that justifies incremental, sparse, and other variants. In Learning in Graphical Models; Springer: Dordrecht, The Netherlands, 1998; pp. 355–368. Available online: https://link.springer.com/chapter/10.1007/978-94-011-5014-9_12 (accessed on 4 April 2022).
- Bilmes, J.A. A gentle tutorial of the EM algorithm and its application to parameter estimation for Gaussian mixture and hidden Markov models. Int. Comput. Sci. Inst. 1998, 4, 126. [Google Scholar]
- Maillo, J.; Ramírez, S.; Triguero, I.; Herrera, F. kNN-IS: An Iterative Spark-based design of the k-Nearest Neighbors classifier for big data. Knowl. Based Syst. 2017, 117, 3–15. [Google Scholar] [CrossRef] [Green Version]
- Amirteimoori, A.; Kordrostami, S. A Euclidean distance-based measure of efficiency in data envelopment analysis. Optimization 2010, 59, 985–996. [Google Scholar] [CrossRef]
- Emmanuel, T.; Maupong, T.; Mpoeleng, D.; Semong, T.; Banyatsang, M.; Tabona, O. A Survey On Missing Data in Machine Learning. J. Big Data 2021, 8, 1–37. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Yang, L.T.; Chen, Z.; Xia, F. A High-Order Possibilistic C-Means Algorithm for Clustering Incomplete Multimedia Data. IEEE Syst. J. 2015, 11, 2160–2169. [Google Scholar] [CrossRef]
- Zhao, L.; Chen, Z.; Yang, Z.; Hu, Y.; Obaidat, M.S. Local similarity imputation based on fast clustering for incomplete data in cyber-physical systems. IEEE Syst. J. 2018, 12, 1610–1620. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Maresca, P. The Running Time of an Algorithm. Ser. Softw. Eng. Knowl. Eng. 2003, 13, 17–32. [Google Scholar] [CrossRef]
| Imputation Method | Avg. Computational Complexity (s) | Missing Rate | RMSE | MAE | |
|---|---|---|---|---|---|
| KNN | 0.82 | 10% | 0.941595 | 0.984187 | 0.216405 |
| 20% | 1.410407 | 0.964461 | 0.452831 | ||
| 30% | 1.831899 | 0.964461 | 0.694035 | ||
| 40% | 1.930442 | 0.933555 | 0.861461 | ||
| RI | 0.85 | 10% | 0.802989 | 0.98831 | 0.193356 |
| 20% | 1.206893 | 0.97327 | 0.392866 | ||
| 30% | 1.630087 | 0.949827 | 0.61114 | ||
| 40% | 1.722670 | 0.943538 | 0.771931 | ||
| EM | 2.28 | 10% | 3.083324 | 0.824947 | 0.719108 |
| 20% | 4.507154 | 0.608994 | 1.435791 | ||
| 30% | 5.445520 | 0.405416 | 2.189204 | ||
| 40% | 6.398958 | 0.152979 | 2.914241 | ||
| missForest | 1.71 | 10% | 0.835237 | 0.987369 | 0.197484 |
| 20% | 1.231309 | 0.972118 | 0.392628 | ||
| 30% | 1.631028 | 0.949937 | 0.60595 | ||
| 40% | 1.746202 | 0.941935 | 0.77397 | ||
| BFMVI | 3.39 | 10% | 0.011758 | 0.999998 | 0.000599 |
| 20% | 0.029012 | 0.999985 | 0.001917 | ||
| 30% | 0.215160 | 0.999165 | 0.006739 | ||
| 40% | 0.169418 | 0.999483 | 0.006136 |
| Missing Period | KNN | RI | EM | missForest | BFMVI |
|---|---|---|---|---|---|
| 1 Day | 0.0872 | 0.115932 | 0.526072 | 0.11624 | 0.001016 |
| 1 Week | 0.225566 | 0.341941 | 1.185411 | 0.328895 | 0.002169 |
| 1 Month | 0.770596 | 0.763162 | 2.785029 | 0.750043 | 0.005263 |
| Imputation Method | Performance Measure | MLR | DT | RF |
|---|---|---|---|---|
| Original Data | RMSE | 1.105198 | 2.675627 | 1.307132 |
| R | 0.977588 | 0.852582 | 0.967482 | |
| MAE | 0.782843 | 1.924280 | 0.941910 | |
| KNN | RMSE | 0.921755 | 1.831899 | 1.443856 |
| R | 0.983985 | 0.939847 | 0.961877 | |
| MAE | 0.711107 | 0.694035 | 0.703279 | |
| RI | RMSE | 0.85446 | 1.630087 | 1.28414 |
| R | 0.985646 | 0.949827 | 0.968328 | |
| MAE | 0.656718 | 0.61114 | 0.622812 | |
| EM | RMSE | 2.529208 | 5.450468 | 4.118277 |
| R | 0.757888 | 0.403799 | 0.530481 | |
| MAE | 1.928332 | 2.196589 | 2.132884 | |
| MissForest | RMSE | 0.823423 | 1.631028 | 1.287602 |
| R | 0.986708 | 0.949937 | 0.968244 | |
| MAE | 0.634978 | 0.60595 | 0.61483 | |
| BFMVI | RMSE | 0.031015 | 0.201528 | 0.195777 |
| R | 0.999982 | 0.999268 | 0.999308 | |
| MAE | 0.023258 | 0.006227 | 0.010485 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agbo, B.; Al-Aqrabi, H.; Hill, R.; Alsboui, T. Missing Data Imputation in the Internet of Things Sensor Networks. Future Internet 2022, 14, 143. https://doi.org/10.3390/fi14050143
Agbo B, Al-Aqrabi H, Hill R, Alsboui T. Missing Data Imputation in the Internet of Things Sensor Networks. Future Internet. 2022; 14(5):143. https://doi.org/10.3390/fi14050143
Chicago/Turabian StyleAgbo, Benjamin, Hussain Al-Aqrabi, Richard Hill, and Tariq Alsboui. 2022. "Missing Data Imputation in the Internet of Things Sensor Networks" Future Internet 14, no. 5: 143. https://doi.org/10.3390/fi14050143
APA StyleAgbo, B., Al-Aqrabi, H., Hill, R., & Alsboui, T. (2022). Missing Data Imputation in the Internet of Things Sensor Networks. Future Internet, 14(5), 143. https://doi.org/10.3390/fi14050143








