1. Introduction
A smart grid is the intellectualization of a power grid, also known as “power grid 2.0”. It is based on an integrated and high-speed two-way communication network. Compared with traditional power grids, the smart grid has better controllability and observability. It can solve the problems of low energy utilization, poor interaction, and difficult security and stability analysis of traditional power systems. At the same time, the real-time regulation based on energy flow is convenient for the access and use of distributed new energy generation and distributed energy storage systems. In general, a smart grid has three remarkable characteristics. Firstly, the smart grid is highly observable. This means that the management center can monitor the information of each node of the power system with the help of information network technology. Secondly, power generation can dynamically interact with power consumption. This means that the optimal dispatching is carried out using real-time power generation and user information. Thirdly, the smart grid is reliable. This means that the smart grid can automatically recover from system shocks and alarms, and adjust for system instability in advance. In general, a smart grid realizes the observability, interaction, safety, economy, efficiency, and reliability of a power grid through the application of advanced sensing and measurement technology, a control method, and a decision-support system. In smart grids, the security of communication and data privacy are extremely important components. Once the data communication of the power grid system is damaged or privacy data are compromised, society and governments pay a high cost.
The research of most scholars has been based on public key infrastructure. For example, Nicanfar et al. [
1] proposed to build a generator for key distribution to ensure the communication security of smart grids; however, this was not operable in practice. Tsai and Lo et al. [
2] proposed an identity-based encryption algorithm in cryptography to complete anonymous key distribution. However, if the key is leaked in this distribution process, it leads to the insecurity of the whole system. In addition, some scholars [
3,
4,
5,
6] completed the key distribution process by introducing Elliptic Curve Cryptography (ECC), and realized anonymity on the basis of ensuring the security of distribution. Some scholars introduced other encryption means, such as certificates [
7], signatures [
8] or hash functions [
9] to further ensure security and anonymity. The complexity of calculation is a common problem in the above schemes. In addition, these schemes cannot resist inside attackers.
In smart grid systems, the aim is to deploy more miniaturized intelligent gateways, so that power transactions can be completed more flexibly. Intelligent gateways are generally provided by third parties, so that the key distribution channels are exposed to the outside. Although these key management schemes based on public key infrastructure are quite mature, these schemes cannot guarantee the security of these channels. In practice, there are two main solutions in the research of smart grids for a large number of distributed devices. First, blockchain technology is a potential solution to this problem. Wang et al. [
10] proposed a blockchain-based secure and lightweight authentication protocol for smart grids (blockSLAP). This scheme solves the problem of centralized registration authority, and has higher performance compared to the common ECC scheme; however, it cannot solve the problems of batch verification and registration. Second, certificateless public key cryptography is another potential solution to this problem. Jennifer et al. [
11] proposed a secure and effective anonymous certification signature for a key distribution scheme for smart grids. This scheme allows authorized users to generate their private key using partial keys from the key generation center. In addition, the proposed scheme also realizes the elasticity of key escrow.
However, the existing solutions based on blockchain require the terminal equipment to have high computing power to complete relevant calculations. At the same time, although the traditional certificateless key scheme avoids the elasticity of key escrow, the users’ partial private keys still come from third-party institutions, and this distribution process cannot be supervised by users. In addition, the bilinear pairing operation in the process of certificateless cryptography also requires that the terminal equipment has high computing power. Therefore, it is necessary to design a trusted, efficient, and secure key management method for lightweight devices. In order to achieve the goal, our contributions are as follows:
We designed a five-tier architecture of a smart grid based on blockchain. The architecture re-divides the smart grid into four layers and establishes a blockchain layer in the dispatching center, power plants, transmission stations, and transformer substations. The blockchain layer records the key distribution process and system parameters to supervise the dispatching center and avoid tampering with the system parameters. It ensures that the key distribution process is trusted and prevents the intelligent gateway from participating in the operation of the blockchain.
We improved the traditional certificateless public key cryptography and proposed a lightweight certificateless group key agreement method without pairing based on blockchain for smart grids. This method allows the key distribution process to be completed without bilinear pairing, which reduces the computation of intelligent gateways. At the same time, combined with the group key based on a logical key tree, the dynamic distribution and revocation of the key are realized.
The rest of the paper is organized as follows:
Section 2 introduces the theoretical support for the related technologies used in our proposed information acceleration strategy.
Section 3 introduces entities in the five-tier architecture of the smart grid based on blockchain and these five layers.
Section 4 introduces the key distribution of our method and a process of node authentication, joining and leaving.
Section 5 presents informal proof showing that the proposed method achieves the security requirements described, and discusses the results in the context of other related papers.
Section 6 shows the results of computational performance and compares them with those of other similar schemes.
Section 5 summarizes the paper and outlines future work.
2. Background Knowledge
In this section, we introduce the related technologies of blockchain and certificateless public key cryptography, which provide theoretical support for our proposed information acceleration strategy.
1. In essence, blockchain is a distributed database built by multiple independent nodes. Each node has independent storage and equal status. The data structure of blockchain can be described by the block, transaction and chain. The block is the basic storage unit in the blockchain, and records all the transaction information of each node within a certain time. Each block is linked by a random hash (also known as a hash algorithm), and then a chain is formed. Transactions in blocks are organized by a Merkle tree structure. Any change in the data in a block will cause a change in the total hash value of the transaction. This results in the disconnection of the blockchain from the block. Therefore, it can be ensured that the data are not easily tampered with, are difficult to forge, and are traceable [
12].
The blockchain can be divided into the public blockchain, the private blockchain, and the consortium blockchain according to the degree of centralization. The public blockchain is a completely open chain that participants can fully access. The private blockchain consists of a single node that can record and maintain data in a ledger. The private blockchain is usually not open to external participants. The private blockchain platform is used for an organization or an enterprise; only authorized entities can join the system. The consortium blockchain is recorded and maintained by predetermined nodes. Whether a participant can access a consortium blockchain system is determined by the predetermined nodes. The consortium blockchain is an integration of semi-public and semi-private systems that has specific purposes for organizations and participants [
13]. It retains other characteristics of blockchain and gradually becomes the mainstream in the field of commercial applications.
Blockchain was a foundational element in the development of cryptocurrency; it was extended for use in various industrial scenarios to build trust and consensus within distributed systems. Blockchain-enabled systems and services have improved authentication, integrity, and immutability [
14]. This means blockchain can promote the realization of secure, privacy preserving, and trusted smart grid developments [
15].
2. Certificateless public key cryptography (CL-PKC) refers to the technology of key distribution based on a public key cryptosystem without the help of certificate. It is a classic and widely used technical scheme in public key cryptography. CL-PKC is a typical representative certificateless cryptography, which is widely cited by current security workers. This scheme does not need a certificate managed key, and does not fully trust the key materials from the key generation center (KGC). In this scheme, the node judges whether the received key material is legal, and combines the legal part of the private key with the secret value held by itself to obtain the complete node private key. The following outlines the process of CL-PKC [
16]:
(1) System Initialization
For initialization, KGC performs the following steps:
KGC selects a master private key
and computes a master public key
, then chooses two hash functions in Formula (1).
Then, KGC publishes these parameters in Formula (2).
(2) Partial-Private-Key-Generate
KGC computes the partial private key of user
in Formula (3).
(3) User-Key-Generate
The user randomly selects a secret value
, and the private key and public key are computed using Formula (4).
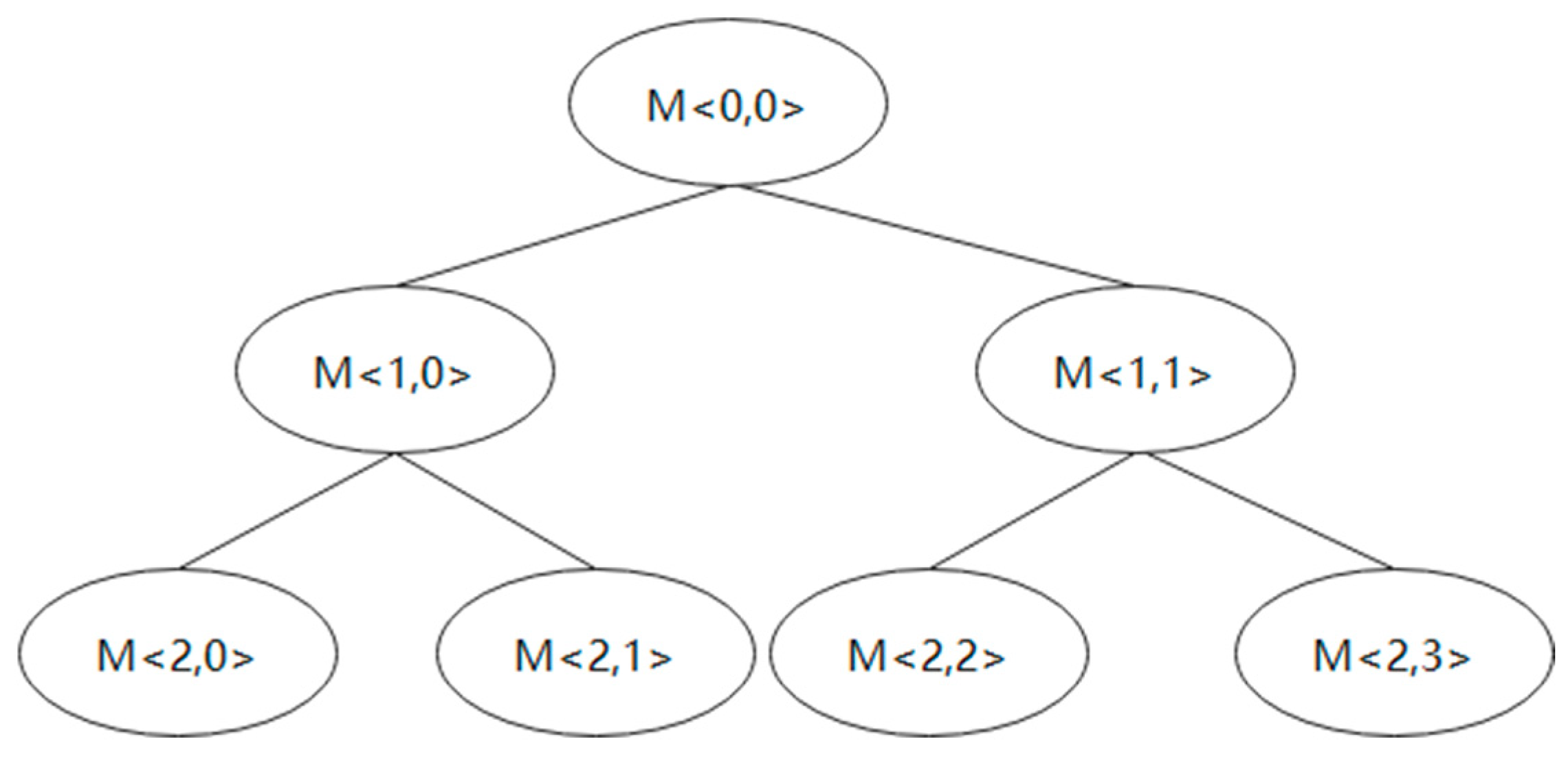
3. In the logical key tree, the group controller maintains a key tree; each node of the tree corresponds to a key, and the leaf node of the tree corresponds to the group members (the members do not include the group controller). The group controller knows all the keys, and the key known by each group member comes from the node on the path from the leaf node corresponding to the group member to the root node. It is called a logical key tree because it is only a data structure maintained by the group controller, and its non-leaf nodes do not correspond to group members [
17]. A leaf node in the key tree represents an individual group member. The key tree root corresponds to the group key
. All other inner nodes represent the subgroup keys
, each of which is held by the group members that are descendants of the corresponding inner nodes. An example of a logical key tree is shown in
Figure 1.
3. Five-Tier Architecture of Smart Grid Based on Blockchain
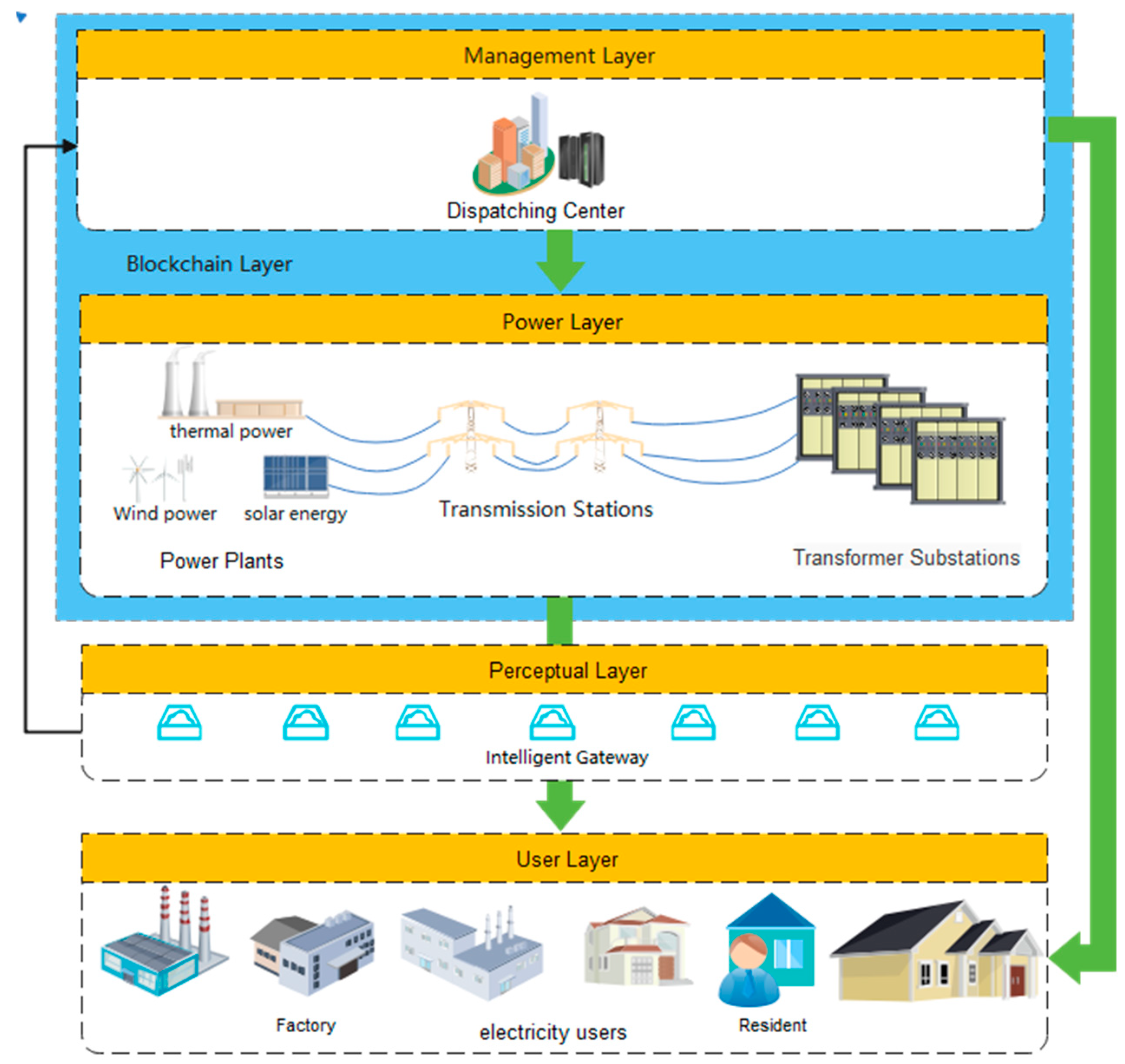
As shown in
Figure 2, we divide the smart grid into five layers based on the structure of the smart grid: management layer, power layer, perceptual layer, user layer and blockchain layer. Here, we introduce these five layers.
(1) Management Layer
In the management layer, the main entity is the dispatching center, which undertakes the dispatching of the whole power system. The dispatching center includes the network control centers for energy management and distribution management systems. It can also be used for scheduling and trading purposes; information about the availability of power (transfer power, operating reserve) or order information is transmitted to or from the power layer. Therefore, the entity can control all entities of the power layer, the perceptual layer, and the user layer. In addition, as the center of the smart grid, the dispatching center is responsible for the responsibilities of KGC. KGC acts as a third party between the power layer, perceptual layer, and user layer. A certificateless scheme is used to avoid the key escrow problem by allowing KGC to only provide a partial key.
(2) Power Layer
The power layer mainly includes three entities: power plants, transmission stations, and transformer substations. The power plants convert bulk energy into electrical energy and are usually directly connected to the transmission stations. The transmission stations transmit electrical energy from generation sources over longer distances. The transformer substations distribute the electric energy delivered by the transmission stations to power consumers. In order to reduce fault clearing times by faster fault identification, the transformer substations need to be atomized. The transmission stations and the transformer substations are typically remotely controlled and supervised by an operator of the dispatching center. They transmit metering information and equipment condition information. In this layer, these entities jointly complete the distribution process of power for the user layer. In the process of key distribution, the channel between the power layer and the management layer is in the internal private network of the power system, which is generally considered to be trusted.
(3) Perceptual Layer
In the perceptual layer, the main entity is the intelligent gateway, which may comprise a variety of sensing devices, such as smart meters and smart car charging piles. The smart gateway collects the power usage and relevant information in its responsible area. The management receives the information returned by the intelligent gateway and reschedules the whole power system by analyzing the data.
(4) User Layer
In the user layer, electricity consumers are the main entity. These consumers may be residents and factories, which apply process automation to control and supervise manufacturing processes and energy consumption or generation. As users, they receive power directly from the power layer, but the relevant power use will be uniformly dispatched by the management.
(5) Blockchain Layer
The management and power layers jointly form the blockchain layer. The blockchain mainly stores the key distribution process in the dispatching center to realize the supervision of the key distribution process. At the same time, the public key parameters are stored in the blockchain to prevent malicious attackers from tampering with system parameters.
4. A Lightweight Certificateless Group Key Agreement Method without Pairing Based on Blockchain for a Smart Grid
In this section, we propose a lightweight certificateless group key agreement method without pairing based on blockchain for a smart grid. This method enables the management layer to distribute the key based on a certificateless key without pairing under supervision in the initialization and registration phase. Then, we redesign the two-node authentication process, referring to the establishment mechanism of the logical key tree from [
18]. In addition, considering that the joining and leaving of nodes are dynamic, we establish a group key reconstruction process based on joining and leaving of intelligent gateway nodes. The proposed method includes four phases: initialization and registration, authentication and establishment, joining, and leaving. Next, we describe these phases.
4.1. Initialization and Registration Phase
The initialization and registration phase consists of three phases: system setup, partial key extraction, and user key generation.
(1) System Setup
When the system is initialized, the entities at the management layer and the power layer jointly build the consortium blockchain. The dispatching center as a super node has the right to account. The dispatching center as KGC randomly generates the base point: and the elliptic curve on the prime field . Then, the dispatching center generates the long-term master key and the long-term public key . The will be uploaded to the blockchain by a smart contract and disclosed in the system.
(2) Partial Key Extraction
The dispatching center will give intelligent gateway an identity . The dispatching center chooses a random value and computes , , and . Then, the dispatching center secretly transmits to the intelligent gateway and uploads this to the blockchain by the smart contract. The intelligent gateway can validate whether receives its partial private key.
(3) User Key Generation
The intelligent gateway randomly chooses a secret value and computes . Then, the intelligent gateway revives its private keys and public key .
4.2. Authentication and Key Establishment Phase
The authentication and key establishment phase consists of two phases: key exchange for two adjacent intelligent gateways and group key generation.
(1) Key Exchange for Two Adjacent Intelligent Gateways
The intelligent gateway
needs to exchange the key with its adjacent intelligent gateway
. From the initialization and registration phase,
has private keys
and a public key
and
has private keys
and a public key
.
sends
to
. Receiving this message,
chooses a random
and computes
. Then,
sends
to
.
also needs to choose a random
and computes
after receiving this message. Then,
sends
to
. Then,
and
can compute the shared secret key.
computes:
The shared secret key is:
(2) Group Key Generation
The shared secret key of
and
is (7) from the previous phase. Refer to
and
for the process of sharing the secret key; the shared secret key of
and
is:
It is necessary to select
and
to achieve
from the logical key tree structure in
Section 2.
selects its private keys
and public keys
, and
selects its private keys
and public keys
. After negotiation,
and
obtain their shared secret key:
Then, obtains encrypted with from and obtains encrypted with from . Finally, the shared secret is shared between with .
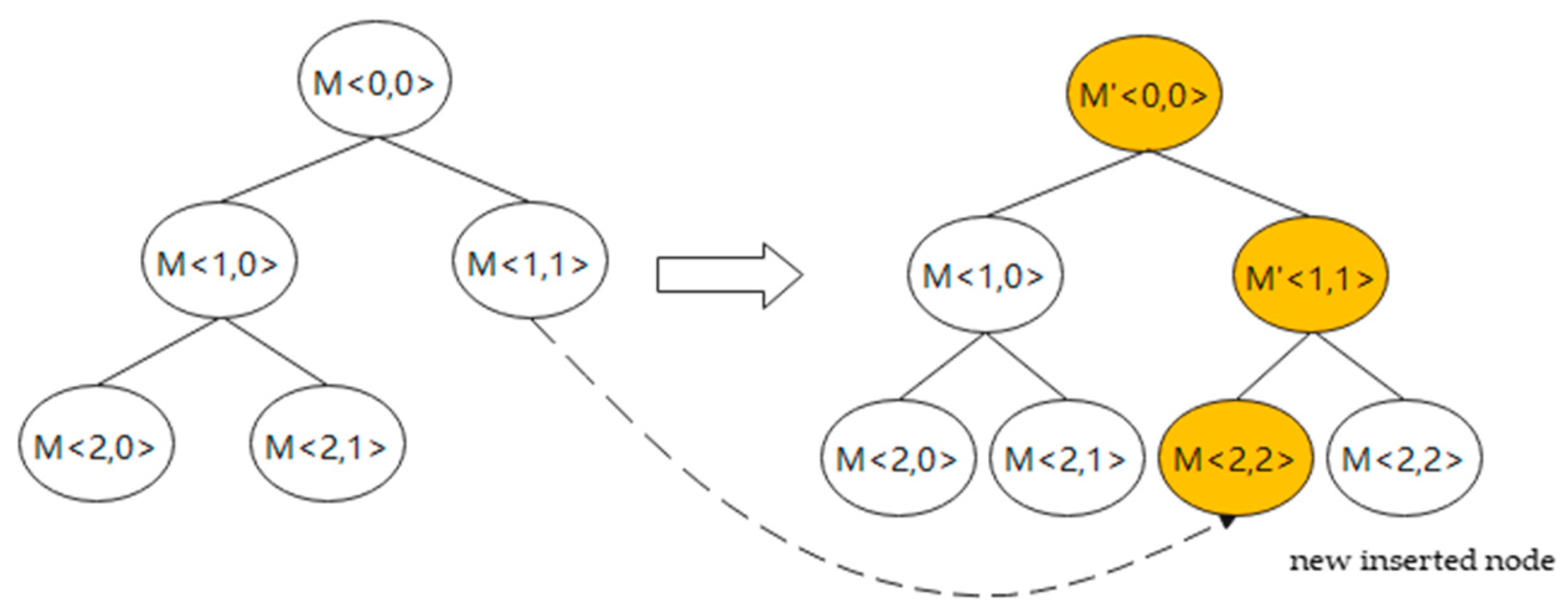
4.3. Group Key Update for Intelligent Gateway Node Join
In this section, the joining of the new intelligent gateway node is described. The group key is updated after the join to ensure backward secrecy. The process is as follows.
(1) The new intelligent gateway node
needs to broadcast its public key
in the group. Then, the new inserted node of logical key tree is inserted with the rightmost leaf node in the subtree rooted at the insertion node. Furthermore, there are two possibilities according to whether the new inserted node has the sibling node, as shown on
Figure 3 and
Figure 4:
(a) If the new inserted node does not have the sibling node, needs to compute and sends to . On the other hand, computes , and sends to . Then, and computes , .
(b) If the new inserted node has the sibling node, needs to compute and sends to . On the other hand, computes , and sends to . Then, and computes .
(2) Irrespective of whether the new inserted node has a sibling node, the final group key will change. The difference between the two cases is whether the group key is directly or indirectly affected.
(3) The new group key is encrypted by the shared secret key broadcast to each node of the network.
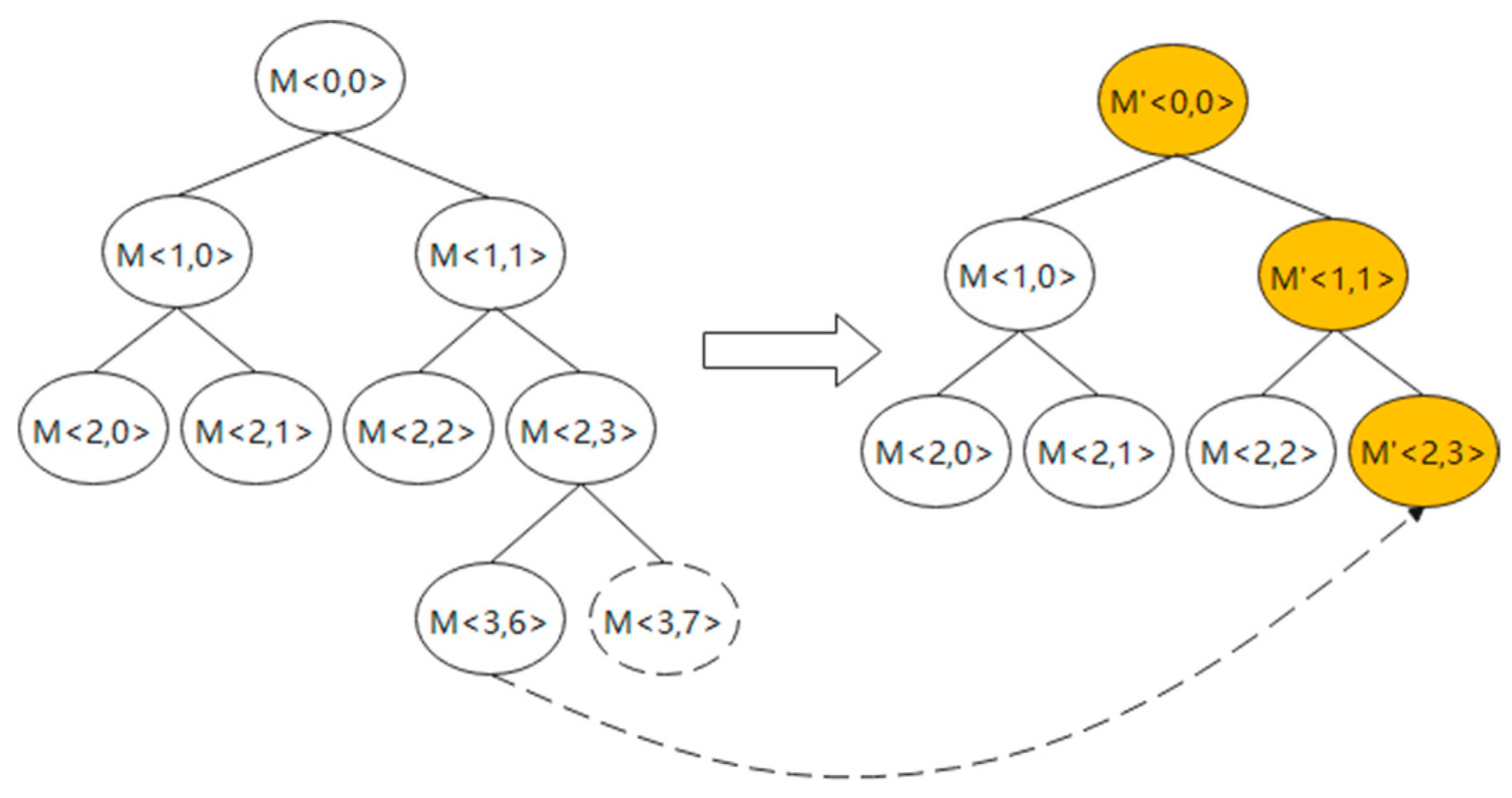
4.4. Group Key Update for Intelligent Gateway Node Leave
Leaving the intelligent gateway node is completed through the following steps, as shown in
Figure 5.
(1) When the public key of an intelligent gateway node is revoked, its parent node or brother node broadcasts messages, and the logical key tree deletes the node and its parent node.
(2) The rightmost leaf node in the subtree rooted at the leaving member’s sibling node reselects a random number, and the node makes a key exchange with its current sibling node.
(3) The new group key is encrypted by the shared secret key broadcast to each node of the network after generating a new group key.
5. Security Analysis and Discussion
In this section, we present an informal proof showing that the whole method achieves the security requirements described. In additional, we provide a discussion and comparison with similar works.
5.1. Security Properties Analysis
We consider both type I and type II adversaries. A type I adversary does not know the master key of KGC but may replace the public key of an arbitrary entity with a value of its choice, whereas a type II adversary knows the master key but cannot replace the target entity’s public key.
(1) Security of Key Distribution
Even during the distribution process, a malicious attacker can obtain the partial key of . Since attackers cannot obtain the secret value , which is chosen randomly by , they cannot complete the push process from the partial key to the complete key . Therefore, we can ensure security of key distribution.
(2) Perfect Forward/Backward Security
Irrespective of whether the intelligent gateway node joins or leaves, the group key will change due to the particularity of the logical key tree structure. Therefore, there is no doubt that the disclosure of the current session key will not lead to the disclosure of the previous session key, nor will it pose a security threat to the subsequent session key.
(3) Resist Private Key Disclosure
When the private key of each intelligent gateway node is obtained by a malicious attacker, the malicious attacker can compute ; however, the malicious attacker cannot compute and without and to obtain the group key.
(4) Resist Temporary Information Disclosure
Even if both nodes leak and at the same time, the malicious attacker can compute ; however, the malicious attacker cannot compute and from to obtain the group key .
(5) Resist the MITM Attack
An adversary A may try to modify the message that send to . However, the message is encrypted through the session key . If A wants to complete the modification, A needs to know the private keys of all nodes, which is difficult.
(6) Resist the Eavesdropping Attack
An adversary A may intercept the messages exchanged in the communication link. However, the communication between any two nodes will be encrypted through the session key . When A does not know the private keys of all nodes, it is impossible to directly calculate the session key.
5.2. Security Properties Discussion
We compared three existing works of key management in terms of some security properties of the whole method.
Table 1 shows the comparison among the three protocols based on ECC, certificateless degree, and blockchain technology.
As shown in
Table 1, the methods of Refs. [
11,
19] require an extra computational overhead for bilinear pairing or blockchain. Although this article also uses blockchain to record the key distribution process of KGC, it does not add computational overhead or reduce authentication efficiency during the certification phase. Furthermore, Ref. [
11] and this article are based on a certificateless approach; thus, they provide key escrow resilience whereby the KGC only has to provide half of a private key to the user. Refs. [
5,
11,
19] use a private key to complete the encryption process or temporary information to a generate session key, so are unable to resist the security threat caused by key disclosure.
6. Performance Analysis and Comparison
In this section, we present performance analysis and a comparison of the computation cost in the authentication and key establishment phase. We investigated the key management of the smart grid based on ECC, the certificateless approach and blockchain technology to complete the comparison with our scheme.
Table 2 shows the execution time of different cryptographic elements which are based on an Alibaba cloud sever that has a 2.9 GHz Intel Xeon E3-1240v6 processor and 2 GB random access memory. The results presented in
Table 2 and
Table 3 show the comparative computational cost. In this article, (5) and (6) need to be calculated twice, and (6), (7) and (8) need to be calculated once to complete the whole authentication process; thus, the computational cost of our method is 12
+ 2
+ 6
.
The results show that although our scheme has little improvement in computational overhead compared with [
5], it shows a sharp improvement compared with [
11,
19], and we provides key escrow flexibility and a trusted key distribution process compared with [
5].
7. Conclusions
This paper proposes an authenticated certificateless group key agreement method without pairing based on blockchain for smart grids, which mainly solves the key management problem of large-scale intelligent gateway nodes with limited computing power. Then, the KGC key distribution process is uploaded to the blockchain. This means KGC cannot prevent the distribution of the partial keys, which are stored in the blockchain, thus realizing the effective supervision of KGC. Furthermore, KGC stores the relevant system parameters in the blockchain to prevent malicious attackers from modifying the parameters, which would result in the collapse of the key management system. We also realize a certificateless key management scheme without bilinear pairing based on blockchain by combining the group key technology based on the logical key tree. This means that our scheme has lower computational overhead compared to similar schemes. Security and performance analysis show that the proposed approach can achieve lower computational overhead and greater safety compared to similar key management schemes.
In the future, we will improve the existing group key based on the logical key tree. The group key scheme combined in this paper cannot deal with the joining and leaving of a large number of intelligent gateway nodes; thus, the existing group key scheme should be improved and designed to efficiently complete the joining and leaving of a large number of nodes. The future method can achieve more efficient management of intelligent gateway node keys.