Financial Market Correlation Analysis and Stock Selection Application Based on TCN-Deep Clustering
Abstract
1. Introduction
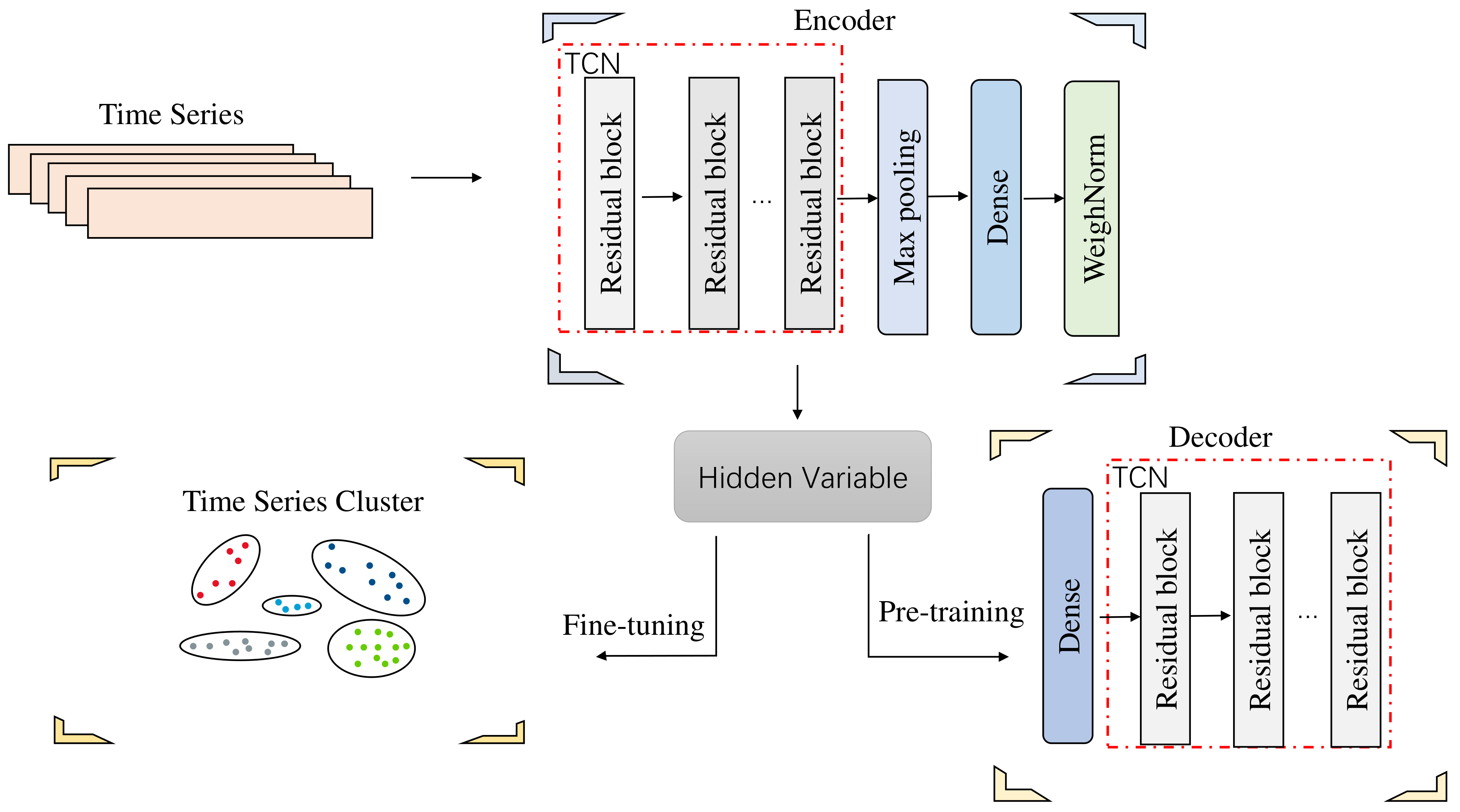
2. Financial Time-Series Deep Clustering Network: TCN-Deep Clustering
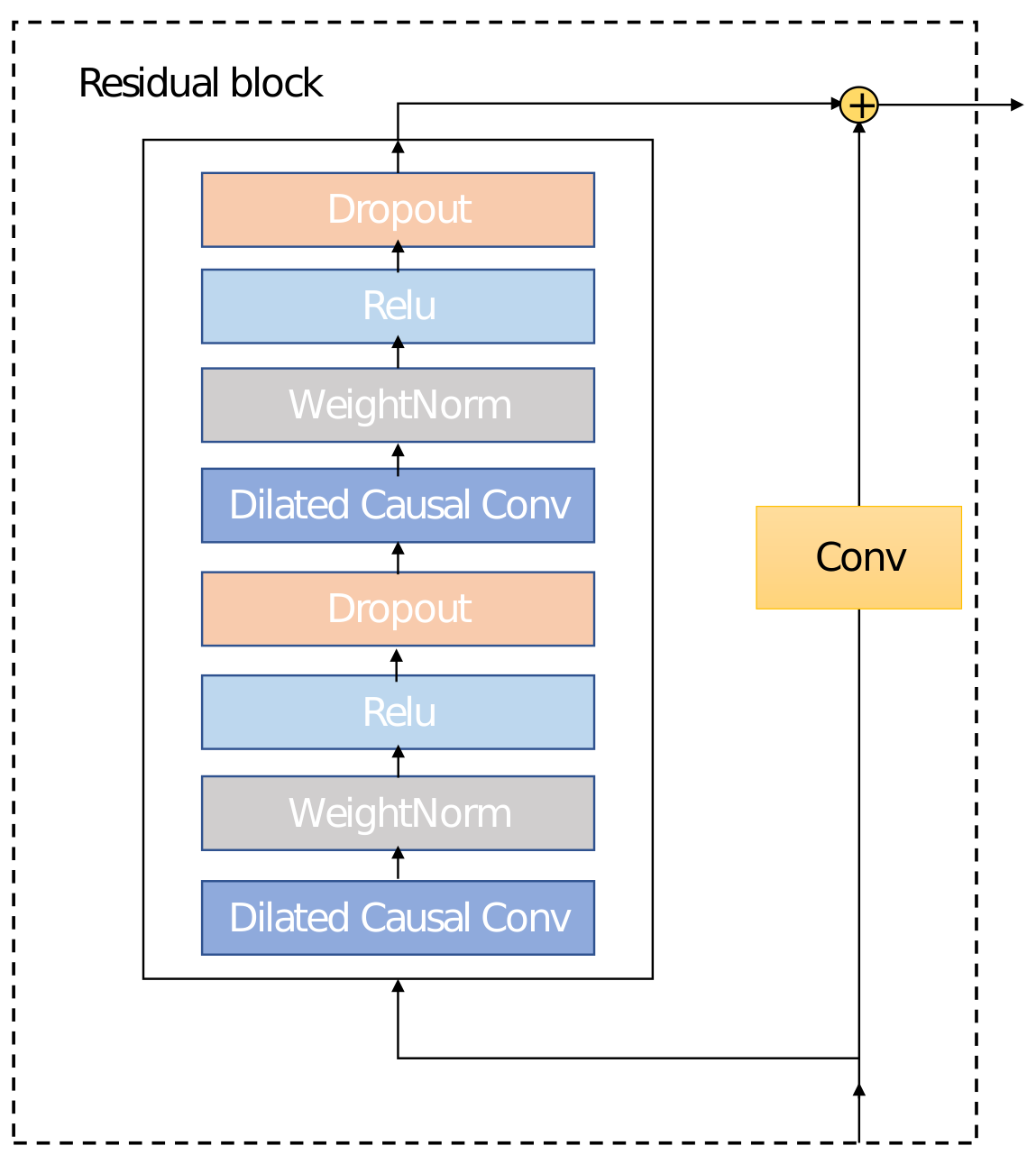
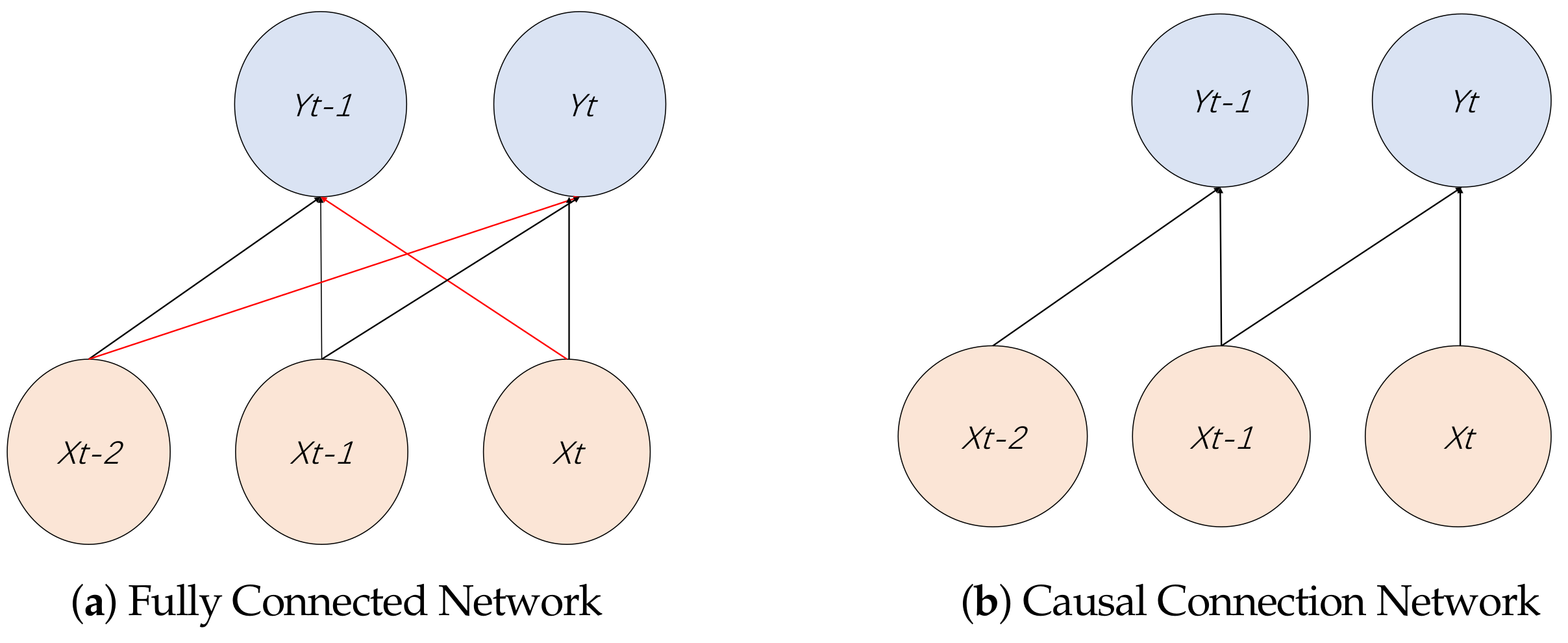
2.1. Autoencoder Network of TCN
2.2. Training Process
2.2.1. Time-Series Feature Extraction
2.2.2. Time-Series Clustering Optimization
2.3. TCN-Deep Clustering Algorithm
| Algorithm 1: TCN-Deep Clustering Algorithm. |
Model: TCN-Deep Clustering Input: Data set D; Number of clusters K; Maximum iteration N; Pre-trained iteration ; Output: Clustering results S; 1 K-means initialize the clustering center 2 for to : 3 , autoencoder preliminary feature extraction. 4 for to N: 5 Encoder extraction of input features: 6 Calculating the soft distribution of with cluster class center 7 Assign input data to clusters; Obtain S 8 Calculating the target distribution 9 Calculating 10 Based on Adam, to update cluster centers and encoder parameters 11 end if Cluster assignment is less than the threshold |
3. Experimental Settings and Results
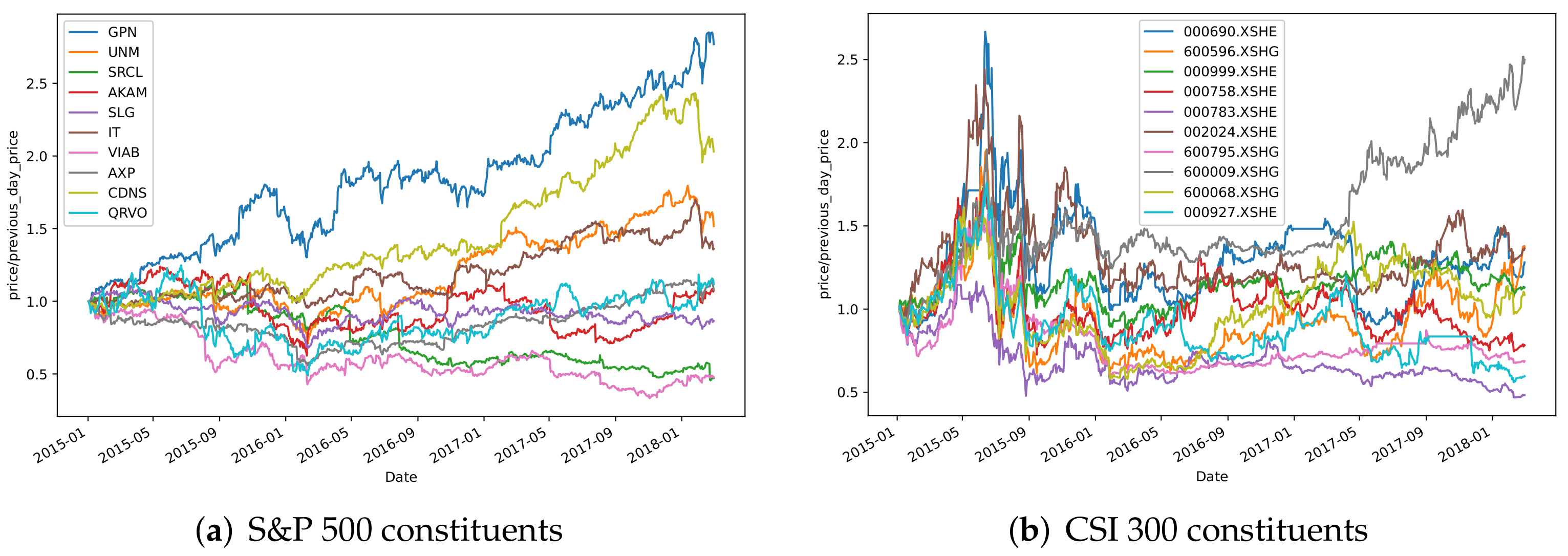
3.1. Data Description
3.2. The Number of Clusters
3.3. Parameter Settings
3.4. Evaluation Indicators
3.4.1. SC
3.4.2. CH
3.4.3. DB
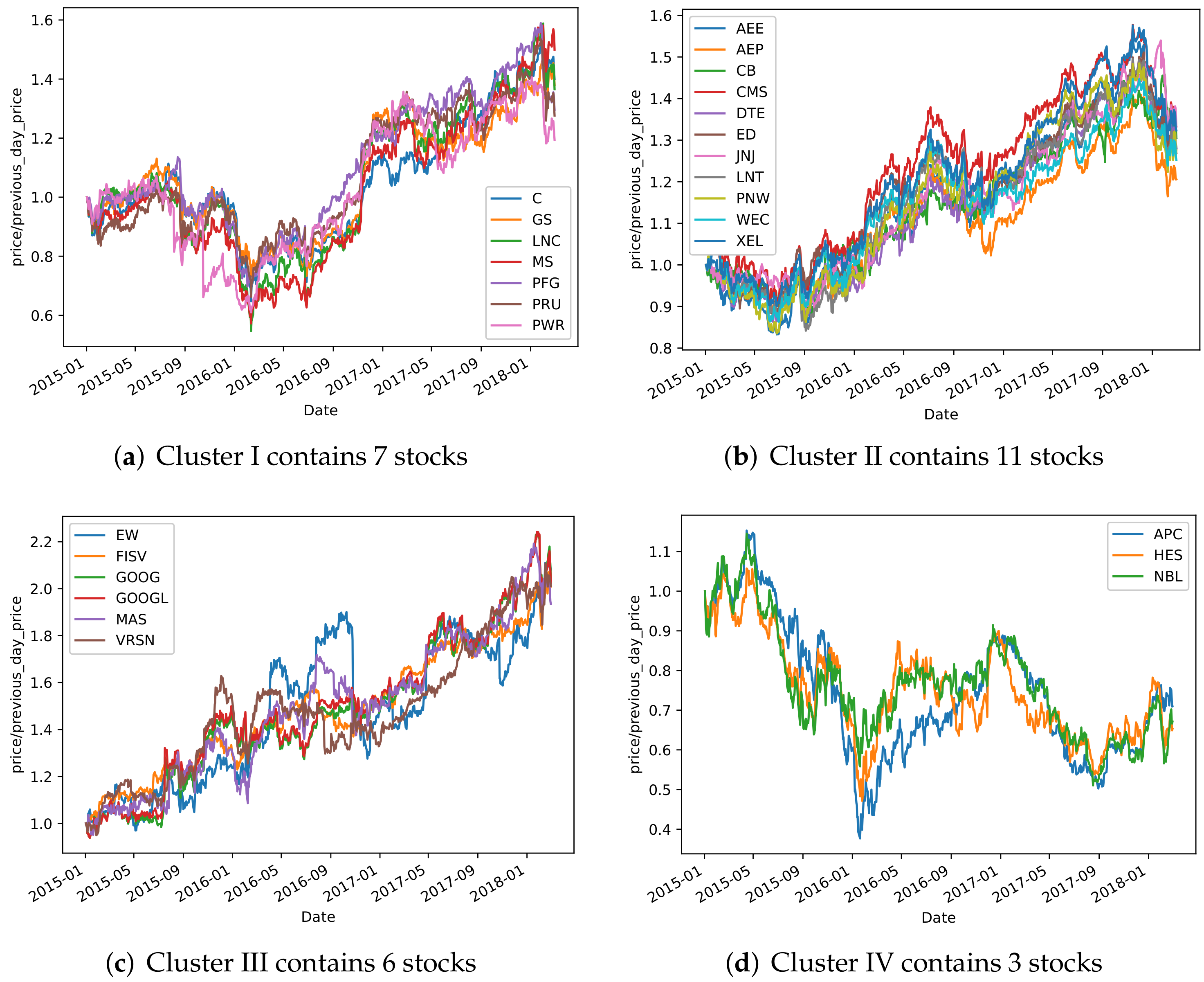
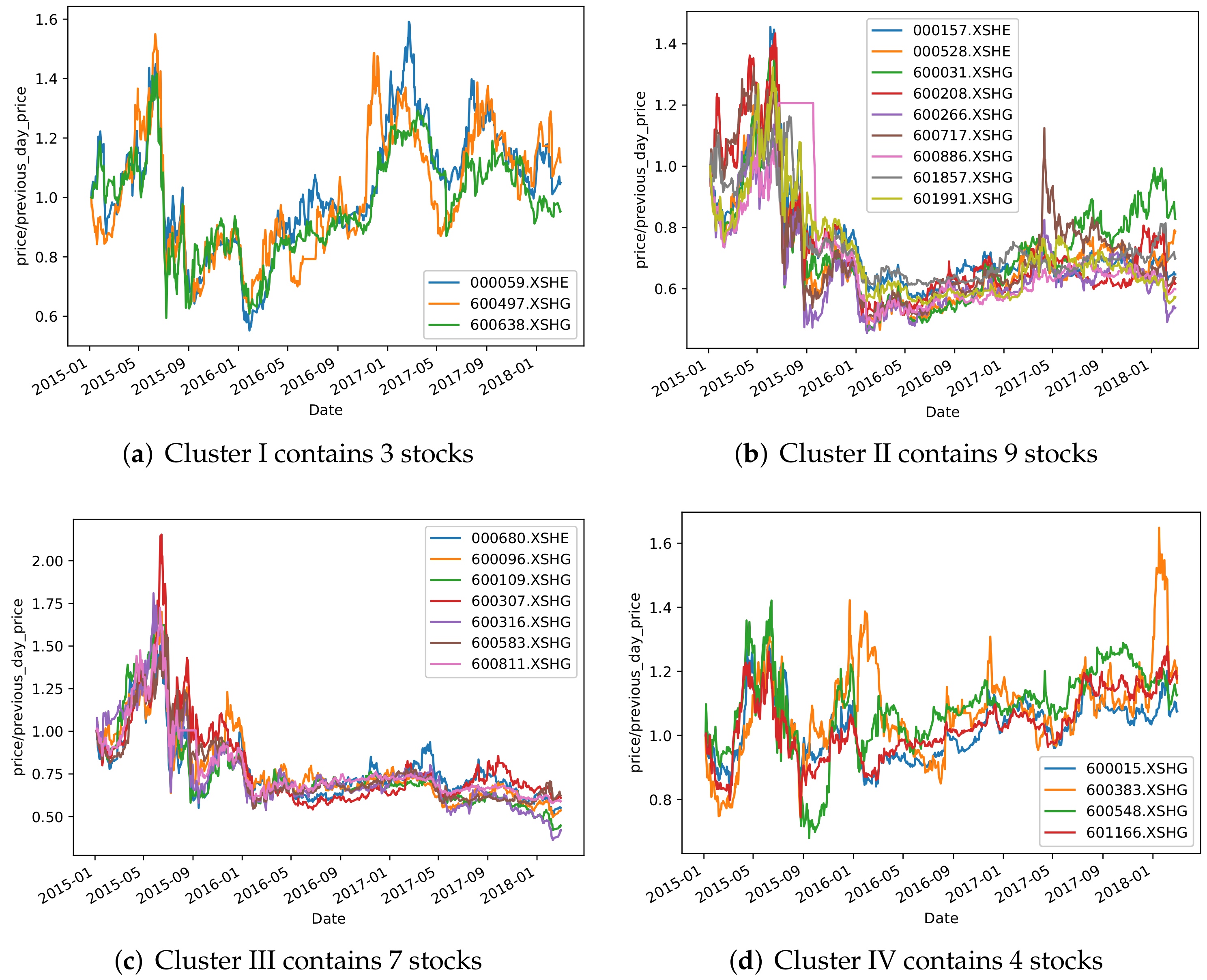
3.5. Results and Analysis
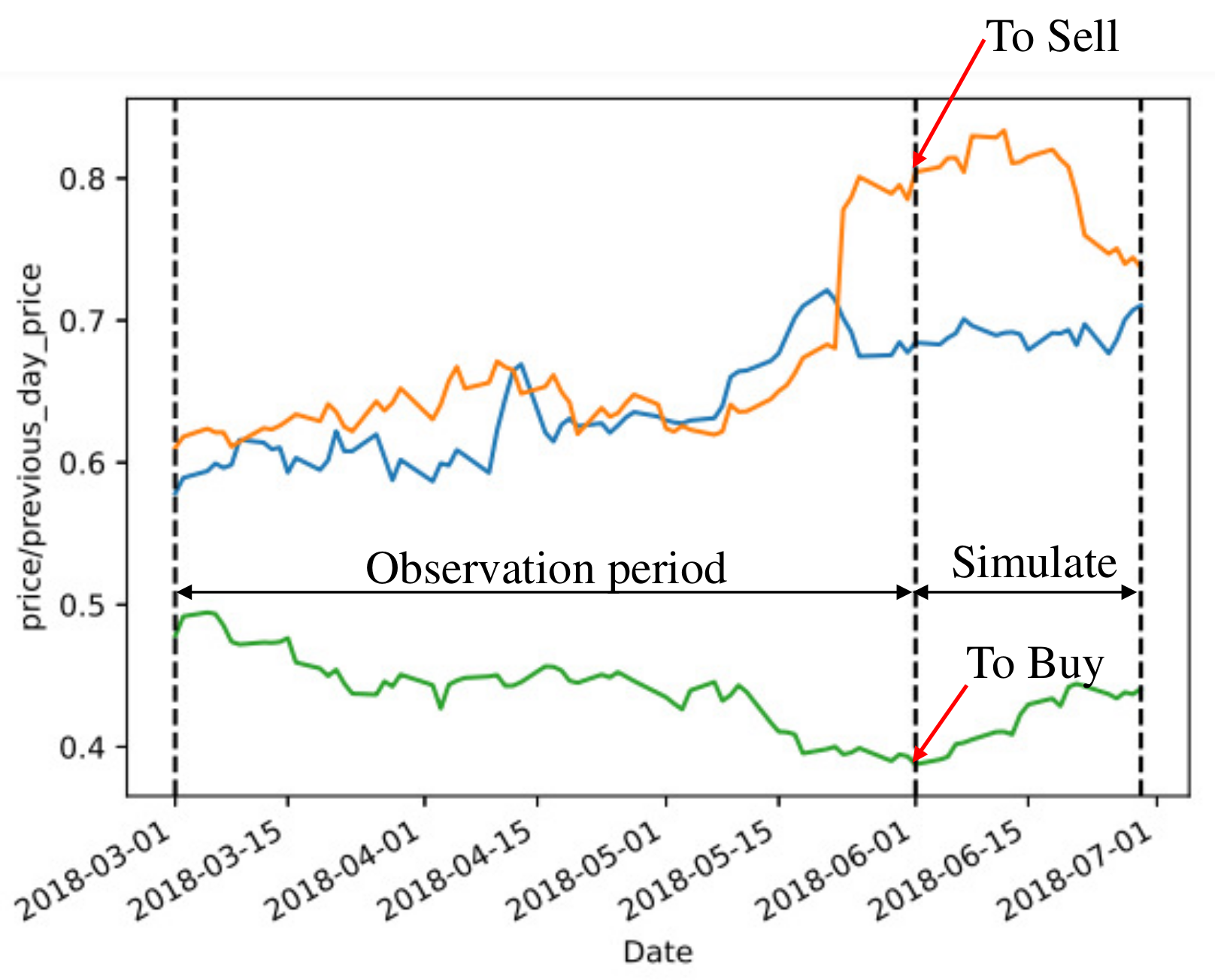
4. Backtest Analysis
Construction of Stock Selection Strategy Based on Clustering Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yu, P.; Yan, X. Stock price prediction based on deep neural networks. Neural Comput. Appl. 2020, 32, 1609–1628. [Google Scholar] [CrossRef]
- Lee, S.W.; Kim, H.Y. Stock market forecasting with super-high dimensional time-series data using ConvLSTM, trend sampling, and specialized data augmentation. Expert Syst. Appl. 2020, 161, 113704. [Google Scholar] [CrossRef]
- Karim, F.; Majumdar, S.; Darabi, H. Insights into LSTM fully convolutional networks for time series classification. IEEE Access 2019, 7, 67718–67725. [Google Scholar] [CrossRef]
- Feng, F.; He, X.; Wang, X.; Luo, C.; Liu, Y.; Chua, T.-S. Temporal relational ranking for stock prediction. ACM Trans. Inf. Syst. (TOIS) 2019, 37, 27. [Google Scholar] [CrossRef]
- Sawhney, R.; Agarwal, S.; Wadhwa, A.; Derr, T.; Shah, R.R. Stock selection via spatiotemporal hypergraph attention network: A learning to rank approach. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtually, 2–9 February 2021; Volume 29, pp. 497–504. [Google Scholar]
- Hajizadeh, E.; Ardakani, H.D.; Shahrabi, J. Application of data mining techniques in stock markets: A survey. J. Econ. Int. Financ. 2010, 2, 109–118. [Google Scholar]
- Dimitriou, D.; Kenourgios, D.; Simos, T. Are there any other safe haven assets? Evidence for “exotic” and alternative assets. Int. Rev. Econ. Financ. 2020, 69, 614–628. [Google Scholar] [CrossRef]
- Kaufman, L.; Rousseeuw, P.J. Finding Groups in Data: An Introduction to Cluster Analysis; John Wiley Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Zhao, F.; Gao, Y.; Li, X.; An, Z.; Ge, S.; Zhang, C. A similarity measurement for time series and its application to the stock market. Expert Syst. Appl. 2021, 182, 115217. [Google Scholar] [CrossRef]
- Rakthanmanon, T.; Keogh, E. Fast shapelets: A scalable algorithm for discovering time series shapelets. In Proceedings of the 2013 SIAM International Conference on Data Mining, Austin, TX, USA, 2–4 May 2013; SIAM: Philadelphia, PA, USA, 2013; pp. 668–676. [Google Scholar]
- Keogh, E.; Ratanamahatana, C.A. Exact indexing of dynamic time warping. Knowl. Inf. Syst. 2005, 7, 358–386. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, L.; Chen, T.Y.; Towey, D.; Kuo, F.-C.; Huang, R.; Guo, Y. Test case prioritization for object-oriented software: An adaptive random sequence approach based on clustering. J. Syst. Softw. 2018, 135, 107–125. [Google Scholar] [CrossRef]
- Sun, L.; Wang, K.; Balezentis, T.; Streimikiene, D.; Zhang, C. Extreme point bias compensation: A similarity method of functional clustering and its application to the stock market. Expert Syst. Appl. 2021, 164, 113949. [Google Scholar] [CrossRef]
- Tian, K.; Zhou, S.; Guan, J. Deepcluster: A general clustering framework based on deep learning. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Skopje, Macedonia, 18–22 September 2017; Springer: Cham, Switzerland, 2017; pp. 809–825. [Google Scholar]
- Lafabregue, B.; Weber, J.; Gançarski, P.; Forestier, G. End-to-end deep representation learning for time series clustering: A comparative study. Data Min. Knowl. Discov. 2022, 36, 29–81. [Google Scholar] [CrossRef]
- Min, E.; Guo, X.; Liu, Q.; Zhang, G.; Cui, J.; Long, J. A survey of clustering with deep learning: From the perspective of network architecture. IEEE Access 2018, 6, 39501–39514. [Google Scholar] [CrossRef]
- Caron, M.; Bojanowski, P.; Joulin, A.; Douze, M. Deep clustering for unsupervised learning of visual features. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 132–149. [Google Scholar]
- Xie, J.; Girshick, R.; Farhadi, A. Unsupervised deep embedding for clustering analysis. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016; pp. 478–487. [Google Scholar]
- Guo, X.; Gao, L.; Liu, X.; Yin, J. Improved deep embedded clustering with local structure preservation. In Proceedings of the IJCAI—International Joint Conference on Artificial Intelligence, Melbourne, Australia, 19–25 August 2017; pp. 1753–1759. [Google Scholar]
- Li, F.; Qiao, H.; Zhang, B. Discriminatively boosted image clustering with fully convolutional auto-encoders. Pattern Recognit. 2018, 83, 161–173. [Google Scholar] [CrossRef]
- Hu, Z.; Liu, W.; Bian, J.; Liu, X.; Liu, T.Y. Listening to chaotic whispers: A deep learning framework for news-oriented stock trend prediction. In Proceedings of the Eleventh ACM International Conference on Web Search and Data Mining, Los Angeles, CA, USA, 5–9 February 2018; pp. 261–269. [Google Scholar]
- Bai, S.; Kolter, J.Z.; Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Caliński, T.; Harabasz, J. A dendrite method for cluster analysis. Commun. Stat. Theory Methods 1974, 3, 1–27. [Google Scholar] [CrossRef]
- Davies, D.L.; Bouldin, D.W. A cluster separation measure. IEEE Trans. Pattern Anal. Mach. Intell. 1979, 2, 224–227. [Google Scholar] [CrossRef]


| Index | Stocks | Training Set | Observation Set | Simulation Set |
|---|---|---|---|---|
| 01/01/2015 | 01/03/2018 | 01/06/2018 | ||
| 01/03/2018 | 01/06/2018 | 01/07/2018 | ||
| CSI 300 | 290 | 1155 | 92 | 30 |
| S&P 500 | 478 | 1155 | 92 | 30 |
| No | Type | Layer | Output Shape | Parameters |
|---|---|---|---|---|
| 1 | —— | Input_1 (InputLayer) | (None, None, 1) | 0 |
| 2 | Encoder (Layer 1) | residual_block_1 | (None, None, 40) | 5162 |
| 3 | Encoder (Layer 2) | residual_block_2 | (None, None, 40) | 9762 |
| 4 | Encoder (Layer 3) | residual_block_3 | (None, None, 40) | 9762 |
| 5 | Encoder (Layer 4) | residual_block_4 | (None, None, 40) | 9762 |
| 6 | Encoder (Layer 5) | residual_block_5 | (None, None, 40) | 9762 |
| 7 | Encoder (Layer 6) | residual_block_6 | (None, None, 160) | 103,202 |
| 8 | Encoder (Layer 7) | global_max_pooling1d | (None,160) | 0 |
| 9 | Encoder (Layer 8) | dense | (None, 320) | 51,520 |
| 10 | Encoder (Layer 9) | activation | (None, 320) | 0 |
| 11 | Decoder (Layer 10) | dense | (None, 796) | 255,516 |
| 12 | Decoder (Layer 11) | reshape | (None, 796, 1) | 0 |
| 13 | Decoder (Layer 12) | decoder_residual_block_1 | (None, 796, 40) | 5162 |
| 14 | Decoder (Layer 13) | decoder_residual_block_2 | (None, 796, 40) | 9762 |
| 15 | Decoder (Layer 14) | decoder_residual_block_3 | (None, 796, 40) | 9762 |
| 16 | Decoder (Layer 15) | decoder_residual_block_4 | (None, 796, 40) | 9762 |
| 17 | Decoder (Layer 16) | decoder_residual_block_5 | (None, 796, 40) | 9762 |
| 18 | Decoder (Layer 17) | decoder_residual_block_6 | (None, 796, 1) | 170 |
| Indicator | General Clustering | Deep Clustering | |||
|---|---|---|---|---|---|
| K-Means | K-Shape | Spectral | DEC | TCN-Deep Clustering | |
| SC | 0.1088 | 0.1086 | 0.1021 | 0.1256 | 0.1168 |
| CH | 116.8139 | 114.3262 | 107.0936 | 120.6435 | 130.9683 |
| DB | 1.0986 | 1.1563 | 1.1595 | 1.0553 | 0.9360 |
| Indicator | General Clustering | Deep Clustering | |||
|---|---|---|---|---|---|
| K-Means | K-Shape | Spectral | DEC | TCN-Deep Clustering | |
| SC | 0.1272 | 0.1215 | 0.1023 | 0.1315 | 0.1329 |
| CH | 54.0336 | 54.5807 | 34.3582 | 51.1134 | 63.68 |
| DB | 0.9992 | 1.0509 | 1.0295 | 0.9162 | 0.8175 |
| S&P 500 | Different Thresholds | ||||
|---|---|---|---|---|---|
| Th = 0.02 | 0.04 | 0.08 | 0.1 | ||
| To buy | 1.0113 | 1.0068 | 1.0081 | 1.0077 | 1.0125 |
| To sell | 1.0070 | 1.0025 | 1.0066 | 0.9899 | 0.9866 |
| Average | 1.0048 | 1.0048 | 1.0048 | 1.0048 | 1.0048 |
| CSI 300 | Different Thresholds | ||||
|---|---|---|---|---|---|
| Th = 0.02 | 0.04 | 0.06 | 0.08 | 0.1 | |
| To buy | 0.9455 | 0.9192 | 0.9253 | 0.9290 | 0.9476 |
| To sell | 0.9135 | 0.9454 | 0.9256 | 0.9104 | 0.9245 |
| Average | 0.9214 | 0.9214 | 0.9214 | 0.9214 | 0.9214 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cen, Y.; Luo, M.; Cen, G.; Zhao, C.; Cheng, Z. Financial Market Correlation Analysis and Stock Selection Application Based on TCN-Deep Clustering. Future Internet 2022, 14, 331. https://doi.org/10.3390/fi14110331
Cen Y, Luo M, Cen G, Zhao C, Cheng Z. Financial Market Correlation Analysis and Stock Selection Application Based on TCN-Deep Clustering. Future Internet. 2022; 14(11):331. https://doi.org/10.3390/fi14110331
Chicago/Turabian StyleCen, Yuefeng, Mingxing Luo, Gang Cen, Cheng Zhao, and Zhigang Cheng. 2022. "Financial Market Correlation Analysis and Stock Selection Application Based on TCN-Deep Clustering" Future Internet 14, no. 11: 331. https://doi.org/10.3390/fi14110331
APA StyleCen, Y., Luo, M., Cen, G., Zhao, C., & Cheng, Z. (2022). Financial Market Correlation Analysis and Stock Selection Application Based on TCN-Deep Clustering. Future Internet, 14(11), 331. https://doi.org/10.3390/fi14110331







