Abstract
As part of studies that employ health electronic records databases, this paper advocates the employment of graph theory for investigating drug-switching behaviors. Unlike the shared approach in this field (comparing groups that have switched with control groups), network theory can provide information about actual switching behavior patterns. After a brief and simple introduction to fundamental concepts of network theory, here we present (i) a Python script to obtain an adjacency matrix from a records database and (ii) an illustrative example of the application of network theory basic concepts to investigate drug-switching behaviors. Further potentialities of network theory (weighted matrices and the use of clustering algorithms), along with the generalization of these methods to other kinds of switching behaviors beyond drug switching, are discussed.
1. Introduction
Information and Communication Technologies (ICTs) are major players in society nowadays. The ubiquitous presence of Internet-connected computer systems (via smartphones, tablets, wearable devices) in daily life allows us to virtually obtain all kinds of information, and at the same time, a lot of information about human behavior is systematically stored in databases [1,2,3]. Among others, health and medical services have been radically transformed by the ICT progress over recent decades. In this regard, a pivotal role has been played by health care databases, which contain information about individuals’ health and related behaviors [4,5,6,7,8,9,10,11]. ICTs allow continuously and automatically updating administrative databases as soon as an event takes place (the prescription of a drug made by a physician, medical procedures, diagnoses information, records of health services, etc.).
In this paper, we will focus on analyzing electronic health records database data related to drug prescription and, specifically, drug switching. Traditional methods employed for investigating drug-switching behaviors are often unable to determine the actual switching pattern. Here, we propose the use of network theory to improve the analyses of these kinds of data. A previous contribution on this topic [12] was limited to advocating the application of network theory for investigating switching behaviors. Therefore, we provide a step-by-step user guide, along with a ready-to-use Python script for obtaining an adjacency matrix from raw data.
1.1. Getting Data from an Electronic Records Database
When considering health electronic records databases, there are essentially two types of repositories [13]: medical records databases (information is recorded as part of clinical outpatient care) and administrative databases (information is recorded for monitoring and controlling health expenditures). Both kinds of databases contain information about prescription drugs and medical diagnoses.
Of note, within the European Union, a researcher willing to analyze an electronic records database must take into consideration the General Data Protection Regulation (GDPR). This regulation was put into effect on 25 May 2018, and specifies responsibilities and requirements on entities that handle personal data. Needless to say, the Ethical Committee Approval for an administrative database analysis-based study must comply with GDPR. In this regard, we recommend further exploring this topic in the literature dedicated to GDPR and health research [14,15,16,17].
To satisfy storage, security and privacy constraints of medical records, recent literature has explored the possibility of using blockchain-based approaches [18,19], also taking into account GDPR compliance [20]. Our primary source of data, though, still relies on extraction from traditional Relational Database Management Systems (e.g., [5]). More broadly speaking, it is important to clarify how information is recorded in the healthcare database under scrutiny. Depending on the country, healthcare information is stored in different ways. This may have an impact on the results of the analyses. For example, what happens when a patient changes medical doctor or hospital? The answer depends on the organization of the healthcare system of the country. The Italian healthcare system is regionally based. Usually, some fields of the administrative database records can change (medical doctor, hospitals), while the overall process is still handled within the specific region. Before carrying out the analysis of the database, it is critical to explore these issues to understand the limitations of the study.
1.2. The Importance of Investigating Drug-Switching Behaviors
After a physician consultation, the patient usually receives a treatment plan (e.g., drug prescriptions, dietary habits, performing or avoiding physical activities). However, the patient may or may not follow medical advice. The term compliance (also called adherence) refers to behavior in which the patient follows the physician’s instructions. Compliance becomes critical in the case of chronic illness medication, where the patient must take a specific drug (or different drugs in sequence) for a prolonged interval of time. There is no way for the physician to directly ascertain the compliance of the patient. However, drugs consumption can be inferred from administrative and medical databases, and although the prescription of a drug does not necessarily correspond to the consumption of that drug, it can be considered a good indicator [5,20,21,22]. It is worth noting that statistical analysis of these kinds of databases is not straightforward because they are commonly characterized by records of tens of thousands of people (or more) for several years. A row is created when a new event related to a patient occurs (e.g., a new prescription, an update about a new medical condition). Table 1 reports a simplified extract of a few lines of a typical database.

Table 1.
An illustrative example of a health records database.
Following previous contributions [12,23], here, we will focus on a specific issue that can answer questions such as, “Given a certain drug, what are the other drugs with which a switch is more likely?”. This is an example of switching behavior, which is particularly important within health literature [24,25,26]. Under certain circumstances, a physician may ask a patient to switch medication. For example, within the psychiatric field, there are circumstances (especially for patients who require long-term treatment) where switching the current antipsychotic medication to another antipsychotic drug is required because adverse effects were observed or the response to treatment is inadequate [27]. Information about how prescriptions of various drugs change in sequence is stored in the aforementioned databases. Thus, their analysis may contribute to ascertaining what kind of switch pattern is associated with the best clinical outcome (reduction of adverse effects and optimal clinical response).
Investigating drug-switching patterns is a critical aspect also in the domain of behavior change interventions [28,29,30,31]. In order to obtain the best clinical outcome, patients have to switch drugs in the way prescribed by the physician. The adherence to physician’s guidelines depends on several variables (e.g., intentions, beliefs, habits, motivation). Traditionally, health psychology has proposed several theoretical models to design behavior change interventions that can help to improve adherence [32,33]. More recently, cognitive-oriented forms of interventions have been proposed. Exploiting the sensitivity to the context of cognitive processes [34,35,36,37,38] and, in particular, decision making [39,40,41,42], the so-called “Nudge approach” proposes changing the architecture of choice (i.e., the design in which choices are presented to decision makers) in order to obtain nonforced compliance [43]. The Nudge theory is based on indirect suggestions and default behavior. In other terms, the context in which a certain choice is made is organized in order to induce automatic and effortless behaviors [44,45,46,47] that are associated with better adherence. The comparison of different types of intervention (e.g., Nudge-based or classic behavior change intervention) aiming at a specific drug-switching pattern could greatly benefit from a more accurate method of inferring the actual patients’ behavior.
Furthermore, studying drug switching may also be relevant for investigating potential differences between generic and brand-name drugs. It is not unusual for the pharmacist—having taken note of the doctor’s prescription—to ask the patient to choose between the branded or the generic drug. This takes on weight if we consider that the scientific literature [48,49] reports that two typologies of drugs may be different in terms of tolerability or efficacy. Thus, investigating drug-related switching behaviors can be extremely useful in the case of chronic diseases where patients may switch continuously from branded drugs to generic ones unbeknownst to the physician. Assessing the relationship between the observed switch pattern with clinical outcomes may give physicians new insights into the therapeutic intervention.
1.3. The Statistical Analysis of Drug-Switching Behavior
In the previous section, we described the relevance of using databases for investigating drug-switching behaviors. However, the analyses commonly employed in previous studies are usually characterized by some limitations. Indeed, studies are often limited to a comparison between the group of patients who have switched drugs with the group who have not switched in a given interval of time [50,51,52]. Then, the groups can be compared by employing an adherence index such as the Medical Possession Ratio (MPR). When the health records database provides information about only a few different types of drugs, the commonly employed approach is very effective. However, when the number of different types of drugs increases along with the dimension of the number of rows of the database, these methods can miss the real complexity of the switching behaviors of patients.
Among the wide range of mathematical tools usefully employed within healthcare, graph theory [53,54] could be an ideal tool to investigate switching behavior by means of database analysis (as previously suggested in the health domain [12] and in other fields, such as marketing research [55]). This paper aims to offer a simple and straightforward introduction to basic concepts of graph theory in order to exploit its potentialities as a tool to analyze switching behavior. The ideal reader is a healthcare researcher that can find here a ready-to-use guide to carry out the analysis of drug-switching behavior.
In the following sections, first, the elementary concepts of graph theory relevant for this paper will be introduced. Then, after a description of the basic characteristics of illustrative electronic health records databases, an example of the application of graph theory for analyzing switching behavior will be displayed (including a Python script for obtaining the adjacency matrix necessary for network analysis).
2. Fundamentals of Graph Theory
In this section, we will provide a very basic introduction to the fundamental concepts of graph theory. We will avoid a formal approach in favor of a more discursive presentation in order to allow researchers without a mathematical background (or mathematical aptitude) to easily understand this topic. A formal introduction can be found in the books of Kolaczyk et al. [53] or Luke [54].
From a mathematical point of view, a network (also called graph) consists of a set of nodes (or vertices) and a set of connections between nodes, the edges (or links). A network can be either directed or undirected. A directed network is characterized by edges that point in only one direction (from a node to another node). When links between edges are not oriented in a specific direction (i.e., they are generic connections), the network is an undirected network. In this paper, we will deal with directed networks, which represent an ideal approach to model switching behaviors.
Calling V the set of nodes and E the set of edges, a graph G can be defined as a pair G = (V, E). In a directed graph, E is the set of ordered pairs of vertices (that is, an edge is associated with two distinct nodes). A graph can be represented by using an adjacency matrix A, a square n x n matrix, where n is the number of nodes. Each element Ai,j is different from zero if node i is connected to node j by an edge in the graph. The value of each element of the matrix represents the weight of the connection between two nodes. Because we are considering directed graphs, it is necessary to specify that weights stand for the link from the starting node (reported on rows, for example) to the destination node (thus reported on the columns in this example). Adjacency matrices of directed graphs can be asymmetric of course, and in the case of recurrent connections on the same node, the main diagonal elements may be nonzero.
Within the study of network topology, several measures can be defined. First, it is necessary to clarify the meaning of some terms. A walk is a sequence (finite or infinite) of links that joins a sequence of nodes. A walk, in which all links are distinct is called a trail. Finally, a trail, in which all nodes (and thus all edges) are distinct is defined as a path.
The distance between two nodes is the length of the shortest directed (in the case of a directed graph, as the case object of this study) path. Of course, there may be more than a single shortest path between two nodes.
In order to evaluate the structure of a graph, the average path length that is the mean value of the shortest paths for all possible pairs of graph vertices can be computed. Generally, it is considered an efficiency measure of the information flow of the network. Taking into account the distance between each pair of vertices, the greatest length of any of these paths is called the diameter of the network.
In a directed graph, each node is characterized by the in-degree value (the number of incoming links) and an out-degree (the number of outgoing links). The centrality degree values represent a sort of popularity index [56]. As the number of incoming links (or outgoing, in other cases) increases, the importance of a node within the network increases too.
Other useful measures are the node betweenness centrality and closeness. Node betweenness centrality allows understanding the importance of a node in the “flow management” of the network. Indeed, the interaction between two nonadjacent nodes A and B is related to the nodes placed on the path between A and B. Node betweenness centrality of a node X is the ratio between the number of shortest paths (between any pair of vertices in the network) that passes through X and the total number of shortest paths existing between any couple of nodes in the network.
The closeness of a node W is the reciprocal of the sum of every shortest path between node W and all other nodes in the graph. High values of closeness indicate that node W is “near” to all other nodes. It is important to note that closeness is an average tendency of a node to be isolated or close to other vertices.
A network can also be characterized by weights that measure the strength of connections between nodes. The application of indexes based on the weights of the network is beyond the scope of this paper; however, taking into account the weights of the graph may be extremely interesting in the study of switching behavior adjacency matrix.
3. From Electronic Records Databases to Adjacency Matrix
Electronic health databases may contain a huge amount of diverse information. Here, we will focus on a simplified and illustrative example of drug prescription. Table 1 represents the basic information needed for switch behavior analysis with graph theory. The considered variables are: the identification number of each patient ID (ID), the date of prescription (DD/MM/YEAR) and the kind of drug (CODE, labeled with numbers) (In this example, the variable CODE refers to the kind of drug. However, this variable can represent other behavior that an individual may show or adopt (choosing food in a cafeteria, see a particular doctor with different specialization, and so on)).
Whenever someone (identified by their personal ID) receives a prescription drug from the physician, that information is recorded in the database. The kind of drug is reported in the CODE column. It is important to note that this kind of database (especially when the number of entries is very large) often needs to be cleaned out (false or wrong IDs, impossible dates, duplicate records and so on). A crucial step to performing switching behavior analysis based on network theory consists of obtaining an adjacency matrix from the database. In Appendix A, a simple Python script is reported that achieves this result. The output of the Python code is a weighted adjacency matrix with the drugs codes on the rows/columns. The weights represent the number of switches from one drug to another. As mentioned earlier, this paper does not focus on the weighted matrix but rather on an unweighted direct adjacency matrix. An example of analysis will be described in the next section.
4. A Working Example
Let us suppose we have an electronic database that, after the application of the Python script in Appendix A, is transformed in the adjacency matrix represented in the graph of Figure 1.
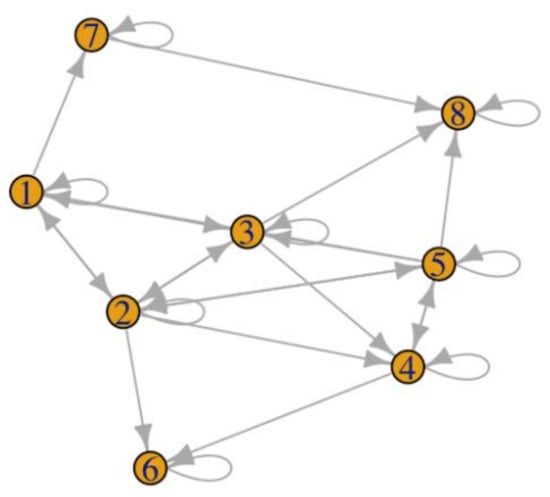
Figure 1.
Example of a graph generated from an adjacency matrix with 8 different types of drugs.
This is not an example based on real data, but it may be considered a plausible situation. The eight nodes may represent eight different types of pharmaceutical equivalent drugs (i.e., same active ingredients, same dosage form and method of administration, identical in concentration/strength), branded or not. A sample of patients in a given interval of time switched between these different drugs, as represented in the adjacency matrix of Figure 1.
We are going to compare this setting (called Case Study) with a reference scenario with a fully connected network (Figure 2). It represents a situation where a sample of patients switches from a specific drug to any other drug (given the eight drugs under scrutiny). This may represent an actual situation. Fully connected networks are often used as a benchmark to compare the features of a given network [53,54,57].
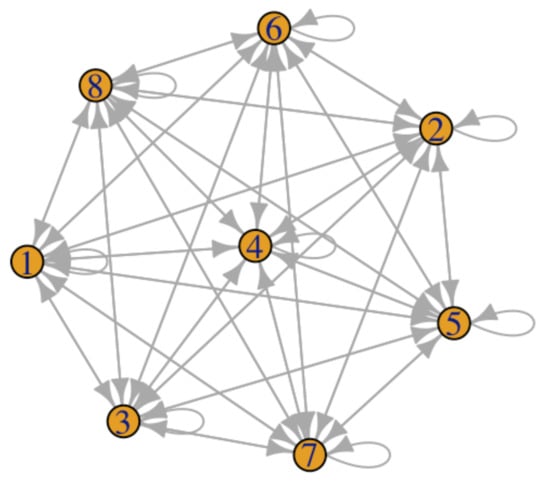
Figure 2.
Fully connected adjacency matrix with 8 different types of drugs.
Network analyses have been performed with the statistical software R [58] (in particular using the packages tidyverse [59] and igraph [60]), which easily allows computing the degree, the in-degree, the out-degree, betweenness centrality and closeness for each node and for the two scenarios (Table 2). They are computed giving as input the graph and provide the outputs as defined in Section 2. Appendix B reports the R script employed to obtain the data presented here.

Table 2.
Degree, in-degree, out-degree, betweenness centrality and closeness for each node and for the two scenarios.
Drug 2, Drug 3 and Drug 5 have the highest degree (thus, they are more the center of switching behaviors). However, Drugs 2 and 3 have the same in-degree (switching to that drug) equal to four (likewise other kinds of drug, for example, Drugs 1, 4 and 8) and higher than Drug 5 (in-degree equal to three). The high degree scores of these three drugs depend mainly on the out-degree (switching to another drug). It is easy to observe that in the fully connected network, there are no differences among nodes for degree, in-degree and out-degree where all the values have the highest possible amount.
When drugs are switched in sequence, Drug 5 is the most “central” (with a betweenness centrality equal to 5.50), followed by Drugs 1 and 2. This means that these drugs are a sort of recurrent “bridge” between other drugs. In other terms, they have a crucial role in the flow of drug switching. The differences among nodes in closeness values are not so high, but results confirm that Drugs 2, 3 and 5 are nearer (in terms of switching) to other drugs. Again, in the fully connected network, the distribution of betweenness centrality and closeness are uniform: specifically, equal to zero for each node and equal to 0.14 for betweenness centrality and closeness, respectively.
Lastly, the diameter of the Case Study network is three, whereas the diameter of the fully connected network is one, confirming that the former is “larger” (i.e., there are some drugs that do not switch directly to each other) than the fully connected network.
5. Discussion and Conclusions
This paper aimed to promote the use of network theory as a method to investigate switching behaviors (in particular, drug switching). The current and shared approach is usually based on classical statistical analyses (to compare individuals who have switched in a given period with those who have not switched) [51,61,62]. However, this approach is unable to grasp the real complexity and switching pattern that a health database may contain. Network theory may represent a useful tool for analyzing switching behavior for healthcare researchers. In this contribution, we reported a brief list of network theory fundamental concepts, a Python script that allows obtaining an adjacency matrix from the basic information of a healthcare database and an illustrative example of the application of graph analysis. Focusing only on the analysis of an unweighted directed adjacency matrix, it was possible to see how network theory indexes can be very informative about the switching pattern about drugs. Indeed, in some cases, it may be observed a fully connected network, whereas in other cases, the database analysis could reveal a situation more similar to the reported Case Study where some drugs play a more central role in switching patterns compared to other more peripheral.
Here, we focused on a basic analysis in order to propose to healthcare researchers a ready-to-use guide to get started. However, compared to the simple analyses presented in this paper, it could be useful to integrate them with the computation of indexes based on the weights of the adjacency matrix [53,54]. Indeed, the Python script reported in this paper produces a weighted matrix, and the weights can allow obtaining useful insight about switching behaviors. Typically, the highest weights are found in correspondence to switches towards the same drug [20]. However, with regard to the switch from one drug to another, it could be useful to differentiate which kind of switch is more frequent. The importance of also taking into account the weight between nodes is testified by studies that observed how weighted networks are successful in simulating real-world networks [63,64]. The use of an adjacency matrix opens also the possibility to employ clustering algorithms [65,66]. Clustering allows dividing the whole sample of nodes into subsamples that maximize intracluster similarities and intercluster sparsity. In other terms, the basic idea is that the nodes in the same cluster are closer to each other than the nodes in other clusters. Thus, this analysis can allow detecting subsets of drugs that tend to switch to each other.
The use of network theory to analyze drug switching may allow obtaining deeper insights about patients’ behaviors and their health compared to current approaches. Determining what kind of drug-switching pattern is associated with the best outcome or if there is no difference in health outcomes when switching between branded and nonbranded drugs may result in beneficial effects in terms of well-being and financial sustainability of the healthcare system.
This paper is focused on drug switching as a peculiar example of information taken by health records databases, but it is important to note that this approach can be generalized to other health-related behaviors (e.g., the consumption of water with different amounts of calcium [67], the investigation of the influence of nudging strategies to different health behaviors [68] or the study of placebo/nocebo effects [69,70]). Every behavior or event automatically recorded in a database that can be switched is of course amenable to the proposed approach.
We hope that this contribution may represent a user guide to improve the investigation of switching behavior inferred from health records databases through the deployment of network theory.
Author Contributions
Conceptualization, G.G. and F.G.; formal analysis, G.G.; methodology, G.G., F.G. and M.R.; software development, M.R.; writing—original draft preparation, G.G.; writing—review and editing, F.G. and M.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not Applicable, the study does not report any data.
Acknowledgments
We are grateful to Alessandro Lazzeri for useful insights.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The following flowchart describes the algorithm (Figure A1):
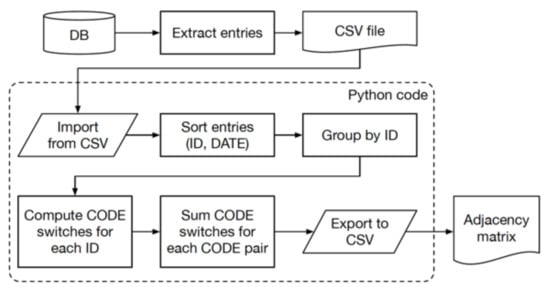
Figure A1.
Algorithm flowchart.
The Python code starts by reading the input list of prescriptions in Comma Separated Values (.csv) format and creating the corresponding Pandas DataFrame. After sorting the values by ascending ID and DATE (i.e., all IDs in increasing order, with the same IDs all adjacent, and then in each group, rows ordered by date), we use the groupby function to obtain a group for each ID. The helper function compute_complete_switches (group) is applied to each group in order to obtain a dictionary with, for each CODE (top-level key), an inner dictionary (again with CODE as key, second-level key) with the number of switches from the outer CODE to the inner CODE. The groups.apply function applies the helper function to each group and then returns the aggregate of all the dictionaries as a new DataFrame. Finally, the get_adjacency_matrix (input_frame, codes) function creates an n x n matrix with indices corresponding to CODEs. By iterating over the dictionary, it updates the value in the corresponding cell by adding the number of switches in the group of the input_frame. The result is returned as a new Pandas DataFrame and saved back in CSV format.

Appendix B

References
- Barsocchi, P.; Cimino, M.G.; Ferro, E.; Lazzeri, A.; Palumbo, F.; Vaglini, G. Monitoring elderly behavior via indoor position-based stigmergy. Pervasive Mob. Comput. 2015, 23, 26–42. [Google Scholar] [CrossRef]
- Watanabe, Y.; Hirano, Y.; Asami, Y.; Okada, M.; Fujita, K. A unique database for gathering data from a mobile app and medical prescription software: A useful data source to collect and analyse patient-reported outcomes of depression and anxiety symptoms. Int. J. Psychiatry Clin. Pract. 2017, 21, 318–321. [Google Scholar] [CrossRef] [PubMed]
- Guazzini, A.; Yoneki, E.; Gronchi, G. Cognitive dissonance and social influence effects on preference judgments: An eye tracking based system for their automatic assessment. Int. J. Hum. Comput. Stud. 2015, 73, 12–18. [Google Scholar] [CrossRef]
- Giudici, F.; Cavalli, T.; Giusti, F.; Gronchi, G.; Batignani, G.; Tonelli, F.; Brandi, M.L. Natural history of MEN1 GEP-NET: Single-center experience after a long follow-up. World J. Surg. 2017, 41, 2312–2323. [Google Scholar] [CrossRef] [PubMed]
- Cianferotti, L.; Parri, S.; Gronchi, G.; Marcucci, G.; Cipriani, C.; Pepe, J.; Raglianti, M.; Minisola, S.; Brandi, M.L. Affiliations expand Prevalence of chronic hypoparathyroidism in a Mediterranean region as estimated by the analysis of anonymous healthcare database. Calcif. Tissue Int. 2018, 103, 144–150. [Google Scholar] [CrossRef] [PubMed]
- Vannucci, L.; Masi, L.; Gronchi, G.; Fossi, C.; Carossino, A.M.; Brandi, M.L. Calcium intake, bone mineral density, and fragility fractures: Evidence from an Italian outpatient population. Arch. Osteoporos. 2017, 12, 40. [Google Scholar] [CrossRef]
- Jha, A.K.; DesRoches, C.M.; Campbell, E.G.; Donelan, K.; Rao, S.R.; Ferris, T.G.; Shields, A.; Rosenbaum, S.; Blumenthal, D. Use of electronic health records in US hospitals. N. Engl. J. Med. 2009, 360, 1628–1638. [Google Scholar] [CrossRef] [PubMed]
- Baldacci, F.; Policardo, L.; Rossi, S.; Ulivelli, M.; Ramat, S.; Grassi, E.; Palumbo, P.; Giovannelli, F.; Cincotta, M.; Ceravolo, R.; et al. Reliability of administrative data for the identification of Parkinson’s disease cohorts. Neurol. Sci. 2015, 36, 783–786. [Google Scholar] [CrossRef] [PubMed]
- Shao, Y.; Durmus, N.; Zhang, Y.; Pehlivan, S.; Fernandez-Beros, M.-E.; Umana, L.; Corona, R.; Addessi, A.; Abbott, S.A.; Smyth-Giambanco, S.; et al. The Development of a WTC Environmental Health Center Pan-Cancer Database. Int. J. Environ. Res. Public Health 2021, 18, 1646. [Google Scholar] [CrossRef]
- Concheiro-Moscoso, P.; Martínez-Martínez, F.J.; Miranda-Duro, M.d.C.; Pousada, T.; Nieto-Riveiro, L.; Groba, B.; Mejuto-Muiño, F.J.; Pereira, J. Study Protocol on the Validation of the Quality of Sleep Data from Xiaomi Domestic Wristbands. Int. J. Environ. Res. Public Health 2021, 18, 1106. [Google Scholar] [CrossRef]
- Wu, M.-H.; Li, C.-Y.; Pan, H.; Lin, Y.-C. The Relationship between Scabies and Stroke: A Population-Based Nationwide Study. Int. J. Environ. Res. Public Health 2019, 16, 3491. [Google Scholar] [CrossRef] [PubMed]
- Gronchi, G. The Use of Network Theory for Analyzing Switching Behaviors: Assessing Cognitive and Educational-Based Intervention for Promoting Health. Front. Psychol. 2018, 9, 1095. [Google Scholar] [CrossRef]
- Hennessy, S. Use of health care databases in pharmacoepidemiology. Basic Clin. Pharmacol. Toxicol. 2006, 98, 311–313. [Google Scholar] [CrossRef] [PubMed]
- Demotes-Mainard, J.; Cornu, C.; Guérin, A.; Bertoye, P.H.; Boidin, R.; Bureau, S.; Chrétien, J.M.; Delval, C.; Deplanque, D.; Dubray, C.; et al. How the new European data protection regulation affects clinical research and recommendations? Therapies 2019, 74, 31–42. [Google Scholar] [CrossRef]
- Puljak, L.; Mladinić, A.; Iphofen, R.; Koporc, Z. Before and after enforcement of GDPR: Personal data protection requests received by Croatian Personal Data Protection Agency from academic and research institutions. Biochem. Med. 2020, 30, 363–370. [Google Scholar] [CrossRef]
- Kanwal, T.; Anjum, A.; Khan, A. Privacy preservation in e-health cloud: Taxonomy, privacy requirements, feasibility analysis, and opportunities. Clust. Comput. 2021, 24, 293–317. [Google Scholar] [CrossRef]
- Raikwar, M.; Gligoroski, D.; Kralevska, K. SoK of used cryptography in blockchain. IEEE Access 2019, 7, 148550–148575. [Google Scholar] [CrossRef]
- Hasselgren, A.; Rensaa, J.A.H.; Kralevska, K.; Gligoroski, D.; Faxvaag, A. Blockchain for Increased Trust in Virtual Health Care: Proof-of-Concept Study. J. Med. Internet Res. 2021, 23, e28496. [Google Scholar] [CrossRef]
- Hasselgren, A.; Wan, P.K.; Horn, M.; Kralevska, K.; Gligoroski, D.; Faxvaag, A. GDPR Compliance for Blockchain Applications in Healthcare. In Proceedings of the International Conference on Big Data, IOT and Blockchain (BIBC 2020), Dubai, United Arab Emirates, 24–25 October 2020. [Google Scholar]
- Cianferotti, L.; Parri, S.; Gronchi, G.; Rizzuti, C.; Fossi, C.; Black, D.M.; Brandi, M.L. Changing patterns of prescription in vitamin D supplementation in adults: Analysis of a regional dataset. Osteoporos. Int. 2015, 26, 2695–2702. [Google Scholar] [CrossRef]
- Ingrasciotta, Y.; Bertuccio, M.P.; Crisafulli, S.; Ientile, V.; Muscianisi, M.; L’Abbate, L.; Pastorello, M.; Provenzano, V.; Scorsone, A.; Scondotto, S.; et al. Real World Use of Antidiabetic Drugs in the Years 2011–2017: A Population-Based Study from Southern Italy. Int. J. Environ. Res. Public Health 2020, 17, 9514. [Google Scholar] [CrossRef]
- Bounoure, F.; Mouly, D.; Beaudeau, P.; Bentayeb, M.; Chesneau, J.; Jones, G.; Skiba, M.; Lahiani-Skiba, M.; Galey, C. Syndromic Surveillance of Acute Gastroenteritis Using the French Health Insurance Database: Discriminatory Algorithm and Drug Prescription Practices Evaluations. Int. J. Environ. Res. Public Health 2020, 17, 4301. [Google Scholar] [CrossRef] [PubMed]
- Glerum, P.J.; Maliepaard, M.; de Valk, V.; Burger, D.M.; Neef, K. Drug switching in The Netherlands: A cohort study of 20 active substances. BMC Health Serv. Res. 2020, 20, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Glerum, P.J.; Neef, C.; Burger, D.M.; Yu, Y.; Maliepaard, M. Pharmacokinetics and Generic Drug Switching: A Regulator’s View. Clin. Pharmacokinet. 2020, 59, 1065–1069. [Google Scholar] [CrossRef] [PubMed]
- Langman, M.; Kahler, K.H.; Kong, S.X.; Zhang, Q.; Finch, E.; Bentkover, J.D.; Stewart, E.J. Drug switching patterns among patients taking non-steroidal anti-inflammatory drugs: A retrospective cohort study of a general practitioners database in the United Kingdom. Pharmacoepidemiol. Drug Saf. 2001, 10, 517–524. [Google Scholar] [CrossRef] [PubMed]
- Linton, D.; Procyshyn, R.M.; Elbe, D.; Lee, L.H.N.; Barr, B.M. A retrospective study of antipsychotic drug switching in a pediatric population. BMC Psychiatry 2013, 13, 248. [Google Scholar] [CrossRef] [PubMed]
- Keks, N.; Schwartz, D.; Hope, J. Stopping and switching antipsychotic drugs. Aust. Prescr. 2019, 42, 152–157. [Google Scholar] [CrossRef]
- Fishbein, M.; Ajzen, I. Theory-based behavior change interventions: Comments on Hobbis and Sutton. J. Health Psychol. 2005, 10, 27–31. [Google Scholar] [CrossRef] [PubMed]
- Fjeldsoe, B.S.; Marshall, A.L.; Miller, Y.D. Behavior change interventions delivered by mobile telephone short-message service. Am. J. Prev. Med. 2009, 36, 165–173. [Google Scholar] [CrossRef]
- Abraham, C.; Michie, S. A taxonomy of behavior change techniques used in interventions. Health Psychol. 2008, 27, 379–387. [Google Scholar] [CrossRef] [PubMed]
- Steinmetz, H.; Knappstein, M.; Ajzen, I.; Schmidt, P.; Kabst, R. How effective are behavior change interventions based on the theory of planned behavior? A three-level meta-analysis. Z. Psychol. 2016, 224, 216–233. [Google Scholar]
- Room, J.; Hannink, E.; Dawes, H.; Barker, K. What interventions are used to improve exercise adherence in older people and what behavioural techniques are they based on? A systematic review. BMJ Open 2017, 7, e019221. [Google Scholar] [CrossRef]
- Kini, V.; Ho, P.M. Interventions to improve medication adherence: A review. JAMA 2018, 320, 2461–2473. [Google Scholar] [CrossRef] [PubMed]
- Helson, H. Studies of Anomalous Contrast and Assimilation. J. Opt. Soc. Am. 1963, 53, 179–184. [Google Scholar] [CrossRef]
- Higgins, E.T.; Lurie, L. Context, categorization, and recall: The “change-of-standard” effect. Cogn. Psychol. 1983, 15, 525–547. [Google Scholar] [CrossRef]
- Righi, S.; Gronchi, G.; Marzi, T.; Rebai, M.; Viggiano, M.P. You are that smiling guy I met at the party! Socially positive signals foster memory for identities and contexts. Acta Psychol. 2015, 159, 1–7. [Google Scholar] [CrossRef]
- Pierguidi, L.; Righi, S.; Gronchi, G.; Marzi, T.; Caharel, S.; Giovannelli, F.; Viggiano, M.P. Emotional contexts modulate intentional memory suppression of neutral faces: Insights from ERPs. Int. J. Psychophysiol. 2016, 106, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Kenrick, D.T.; Gutierres, S.E. Contrast effects and judgments of physical attractiveness: When beauty becomes a social problem. J. Pers. Soc. Psychol. 1980, 38, 131–140. [Google Scholar] [CrossRef]
- Takemura, K. The effect of decision frame and decision justification on risky choice. Jpn. Psychol. Res. 1993, 35, 36–40. [Google Scholar] [CrossRef][Green Version]
- De Martino, B.; Kumaran, D.; Seymour, B.; Dolan, R.J. Frames, biases, and rational decision-making in the human brain. Science 2006, 313, 684–687. [Google Scholar] [CrossRef]
- Levi, H.R.; Jackson, R.C. Contextual factors influencing decision making: Perceptions of professional soccer players. Psychol. Sport Exerc. 2018, 37, 19–25. [Google Scholar] [CrossRef]
- Tracy, C.S.; Dantas, G.C.; Moineddin, R.; Upshur, R.E. Contextual factors in clinical decision making: National survey of Canadian family physicians. Can. Fam. Physician 2005, 51, 1106–1107. [Google Scholar] [PubMed]
- Thaler, R.H.; Sunstein, C.R. Nudge: Improving Decisions about Health, Wealth, and Happiness. Theory; Penguin Books: London, UK, 2008. [Google Scholar]
- Gronchi, G.; Giovannelli, F. Dual process theory of thought and default mode network: A possible neural foundation of fast thinking. Front. Psychol. 2018, 9, 1237. [Google Scholar] [CrossRef] [PubMed]
- Sloman, S.A. The empirical case for two systems of reasoning. Psychol. Bull. 1996, 119, 3–22. [Google Scholar] [CrossRef]
- Evans, J.S.B. In two minds: Dual-process accounts of reasoning. Trends Cogn. Sci. 2003, 7, 454–459. [Google Scholar] [CrossRef]
- Osman, M. An evaluation of dual-process theories of reasoning. Psychon. Bull. Rev. 2004, 11, 988–1010. [Google Scholar] [CrossRef] [PubMed]
- Andermann, F.; Duh, M.S.; Gosselin, A.; Paradis, P.E. Compulsory generic switching of antiepileptic drugs: High switchback rates to branded compounds compared with other drug classes. Epilepsia 2007, 48, 464–469. [Google Scholar] [CrossRef] [PubMed]
- Kesselheim, A.S.; Misono, A.S.; Lee, J.L.; Stedman, M.R.; Brookhart, M.A.; Choudhry, N.K.; Shrank, W.H. Clinical equivalence of generic and brand-name drugs used in cardiovascular disease: A systematic review and meta-analysis. JAMA 2008, 300, 2514–2526. [Google Scholar] [CrossRef]
- Saag, M.S.; Powderly, W.G.; Schambelan, M.; Benson, C.A.; Carr, A.; Currier, J.S.; Dubé, M.P.; Gerber, J.G.; Grinspoon, S.K.; Grunfeld, G.; et al. Switching antiretroviral drugs for treatment of metabolic complications in HIV-1 infection: Summary of selected trials. Top. HIV Med. 2002, 10, 47–51. [Google Scholar]
- Ideguchi, H.; Ohno, S.; Takase, K.; Ueda, A.; Ishigatsubo, Y. Outcomes after switching from one bisphosphonatesphosphonate to another in 146 patients at a single university hospital. Osteopor. Int. 2008, 19, 1777–1783. [Google Scholar] [CrossRef]
- Martin, B.C.; Wiley-Exley, E.K.; Richards, S.; Domino, M.E.; Carey, T.S.; Sleath, B.L. Contrasting measures of adherence with simple drug use, medication switching, and therapeutic duplication. Ann. Pharmacother. 2009, 43, 36–44. [Google Scholar] [CrossRef]
- Kolaczyk, E.D.; Csárdi, G. Statistical Analysis of Network Data with R; Springer: New York, NY, USA, 2014; Volume 65. [Google Scholar]
- Luke, D.A. A User’s Guide to Network Analysis in R; Springer: London, UK, 2015. [Google Scholar]
- Iacobucci, D.; Henderson, G.; Marcati, A.; Chang, J. Network analyses of brand switching behavior. Int. J. Res. Mark. 1996, 13, 415–429. [Google Scholar] [CrossRef]
- Hansen, D.L.; Shneiderman, B.; Smith, M.A.; Himelboim, I. Social network analysis: Measuring, mapping, and modeling collections of connections. In Analyzing Social Media Networks with NodeXL; Morgan Kaufmann: Burlington, MA, USA, 2011; pp. 31–51. [Google Scholar]
- Palla, G.; Derényi, I.; Farkas, I.; Vicsek, T. Uncovering the overlapping community structure of complex networks in nature and society. Nature 2005, 435, 814–818. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020; Available online: https://www.R-project.org/ (accessed on 29 August 2021).
- Wickham, H.; Averick, M.; Bryan1, J.; Chang, W.; D’Agostino McGowan, L.; François, R.; Grolemund, G.; Hayes, A.; Henry, L.; Hester, J. Welcome to the tidyverse. J. Open Source Soft. 2019, 4, 1686. [Google Scholar] [CrossRef]
- Csardi, G.; Nepusz, T. The igraph software package for complex network research. J. Complex Syst. 2006, 1695, 1–9. [Google Scholar]
- Ganguli, R. Rationale and strategies for switching antipsychotics. Am. J. Health Syst. Pharm. 2002, 59, S22–S26. [Google Scholar] [CrossRef]
- Thiebaud, P.; Patel, B.V.; Nichol, M.B.; Berenbeim, D.M. The effect of switching on compliance and persistence: The case of statin treatment. Am. J. Manag. Care 2005, 11, 670–674. [Google Scholar]
- Bellingeri, M.; Bevacqua, D.; Scotognella, F.; Alfieri, R.; Cassi, D. A Comparative Analysis of Link Removal Strategies in Real Complex Weighted Networks. Sci. Rep. 2020, 10, 3911. [Google Scholar] [CrossRef] [PubMed]
- Bellingeri, M.; Bevacqua, D.; Scotognella, F.; Cassi, D. The Heterogeneity in Link Weights May Decrease the Robustness of Real-World Complex Weighted Networks. Sci. Rep. 2019, 9, 10692. [Google Scholar] [CrossRef]
- Rodriguez, M.Z.; Comin, C.H.; Casanova, D.; Bruno, O.M.; Amancio, D.R.; Costa, L.D.F.; Rodrigues, F.A. Clustering algorithms: A comparative approach. PLoS ONE 2019, 14, e0210236. [Google Scholar] [CrossRef]
- Gronchi, G.; Guazzini, A.; Massaro, E.; Bagnoli, F. Mapping cortical functions with a local community detection algorithm. J. Complex Netw. 2014, 2, 637–653. [Google Scholar] [CrossRef]
- Vannucci, L.; Fossi, C.; Quattrini, S.; Guasti, L.; Pampaloni, B.; Gronchi, G.; Giusti, F.; Romagnoli, C.; Cianferotti, L.; Marcucci, G.; et al. Calcium intake in bone health: A focus on calcium-rich mineral waters. Nutrients 2018, 10, 1930. [Google Scholar] [CrossRef]
- Vlaev, I.; King, D.; Dolan, P.; Darzi, A. The theory and practice of “nudging”: Changing health behaviors. Public Adm. Rev. 2016, 76, 550–561. [Google Scholar] [CrossRef]
- Palermo, S.; Giovannelli, F.; Bartoli, M.; Amanzio, M. Are Patients with Schizophrenia Spectrum Disorders More Prone to Manifest Nocebo-Like-Effects? A Meta-Analysis of Adverse Events in Placebo Groups of Double-Blind Antipsychotic Trials. Front. Pharmacol. 2019, 10, 502. [Google Scholar] [CrossRef] [PubMed]
- Zaccara, G.; Giovannelli, F.; Schmidt, D. Placebo and nocebo responses in drug trials of epilepsy. Epilepsy Behav. 2015, 43, 128–134. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).