1. Introduction
Nowadays, new technologies are evolving at an exponential pace, and the consequential technological advancements achieved through them are blurring the lines between the physical, digital and biological worlds [
1]. These advancements constitute the basis of the fourth industrial revolution (also called Industry 4.0), which is principally constituted of progress in the areas of artificial intelligence (AI), robotics, nanotechnology, quantum computing, energy storage systems and the internet of the things (IoT) [
2]. As Industry 4.0 continues changing the world, new challenges arise in different branches of society, one of them being education; thus, Education 4.0 comes into existence.
In general, science and engineering education needs, learning and teaching methods are continuously and rapidly changing in order to adapt to the incoming innovation challenges caused by the digital transformation of industries. Therefore, one of the main objectives of Education 4.0 is to generate updated curricula at the undergraduate level that allows students to develop technological progress and knowledge that, in a future, can be usable for the welfare of society.
As stated by [
3], one of the main pillars for the creation of this new curricula is competency development. This approach will allow students to apply the acquired knowledge towards real-life situations rather than only memorizing and repeating data. In the context of Education 4.0, competencies are considered to be sets of skills, attributes and behaviors that allow the successful realization of an specific task [
4]. According to [
3], in the case of scientific and engineering education, new curricula must focus on driving the development of the following competencies: virtual collaboration, resilience, social intelligence, novel and adaptive thinking, load cognition management, sense-making, new media literacy, design mindset, transdisciplinary approach and computational skills. Nevertheless, in an effort to make the most out of these competencies, students must also learn how they can be used to acquire a deeper knowledge on disruptive technologies.
Among these technologies, there is the area of Human–Computer Interaction (HCI), which studies the interaction between the human body as the control and a computer as the acting device [
5,
6]. HCI can use either physiological movements (i.e., body motion detection [
7,
8], eye tracking [
9,
10], tongue movement, etc.), spoken word recognition [
11,
12] and/or electrical signals produced by the human body (i.e., muscular or brain activation [
13,
14,
15]) as the control signals. HCI has been used for augmented reality [
16,
17,
18], control of exoskeletons [
19], rehabilitation robots [
15,
20], spelling devices [
21], video games or daily devices [
22,
23,
24] and many others [
16,
25,
26].
Particularly, the use of brain signals as control patterns is known as Brain–Computer Interfaces (BCI). These types of interfaces have the advantage of not requiring any type of movement; therefore, they can be used by people with motion impairment, where, in many cases, the brain activity remains intact (i.e., people with Lock-in-Syndrome [
27,
28]). Although there has been great progress in the BCI field, it is still necessary to further improve to make them work better for different subjects and on a daily basis [
14,
28]. As a consequence, many experiments and new researchers are still needed; thus, the importance of applying the Education 4.0 paradigm towards science and engineering students.
Kuhn [
29] said that the development of science consists of past research on scientific achievements that have plenty of support from the scientific community to create new and improved models or paradigms for further research. Hence, it is necessary to fully understand what was done and how it works before developing new technology. This becomes problematic since BCI is a multidisciplinary field, which requires knowledge from many areas, such as engineering (e.g., statistics, signal analysis and control theory), computer science (e.g., machine learning and software development), medicine (e.g., physiology, anatomy, neuroscience and psychology) and many others to create expertise. Otherwise, it would require a lot of time to identify problems and develop solutions.
Knowing all the theories is not enough, testing is also required before any real-life application of BCI can be fully developed. Specifically, medical experimentation requires careful processes to prove a hypothesis, especially since it is going to be used by humans and it has a direct connection with technology. Therefore, in medical experimentation, three main things need to be considered: first, the use of medical equipment is limited due to it being complex to use, expensive or with a busy schedule; second, faulty experimentation could be harmful or tiresome for the subjects; and third, medical experimentation requires many repetitions to guarantee that it works and will not damage the patient. Thus, experimentation needs to be carefully performed; otherwise, a bad design of the experiment translates into a waste of time and/or money or inflicted damage to the patient.
All of these problems can be solved by becoming an expert and applying the basics. Under normal circumstances, becoming an expert in all these areas and knowing all these tasks is complex and very time-consuming because of the transdisciplinary nature of BCI. For that reason, it is important for students to have a starting point in this field where experimentation and analysis can be performed without harming any subject while allowing them to develop competencies such as adaptive thinking, sense-making, design mindset, transdisciplinary approach and computational skills. Furthermore, the involvement of applied knowledge, logical interpretation, adoption of digital tools and construction of real learning scenarios through practical projects are some of the pillars that constitute the basis of Education 4.0 [
30]. Hence, a way to introduce this paradigm on future engineers and scientists is to use practical approaches that help them acquire new skills, learn how theory and practice are linked, understand how to correctly structure and test hypotheses, know how to develop problem-solving techniques or simply to understand how to work with new equipment and to gather, manipulate and/or interpret data [
31].
One way to achieve this is to provide students the option to learn over a testing bench or workbench, in which they can try out different protocols and verify their correctness without trying them on a human. This would help them acquire knowledge about the development of experiments, as well as how to manipulate data and understand results. It is very important to remark that the learning process over a workbench must be carried out over a similar context to the real subject to learn [
32] and that it must be done using technologies that are similar to the ones that would be used for a real-life application [
33].
To develop this workbench, it is important to understand how science and technology are usually taught. In general, the aim of education in science and technology is to inform people who live in a world with high dependency on technology. It is important to notice that science cannot be taught disjointed from the world because of the many relationships between science and society, especially through the countless applications of science and technology [
34,
35]. Thus, it is of high importance for future scientists and engineers to learn science and technology based on their own experience and their knowledge about the world and their surroundings [
36]. This translates into learning through practical approaches over things that are related to them as individuals.
Having said that, the main objective of this study is to serve as educational material for science and engineering students and teachers that are dabbling in the Education 4.0 paradigm. Ultimately, this will help students to acquire expertise on a disruptive and transdisciplinary technology, such as BCI, while developing computational skills, adaptive and sense-making thinking. In order to achieve this objective, this work first explains the basics behind Brain–Computer Interfaces and five different artificial intelligence algorithms: Kohonen Self-Organizing Maps (SOM), Artificial Neural Networks (ANN), Linear Discriminant Analysis (LDA), Supported Vector Machines (SVM) and Restricted Boltzmann Machines (RBM). Furthermore, for this work to be fully in line with the Education 4.0 paradigm, we present a test bench for students to learn the applicability of the previous algorithms towards BCI and how to interpret the outcomes of the given experimentation. The proposed test bench in this work consists of a two-class Motor Image database obtained by [
37], which includes three different bipolar EEG recordings and three monopolar EOG recordings.
This article goes first through a review of Brain–Computer Interfaces with BCI control paradigms, signal processing, including signal acquisition and feature extraction, and Pattern Recognition methods. In the latter, an introduction to AI techniques is given, exploring two linear and two neural network classifiers and one more neural network that creates an internal representation of the signal. Furthermore, a bibliographic comparison is conducted to cover their corresponding advantages and disadvantages. Afterward, these algorithms are tested over a BCI database to show and compare their potential and performance.
3. Signal Processing
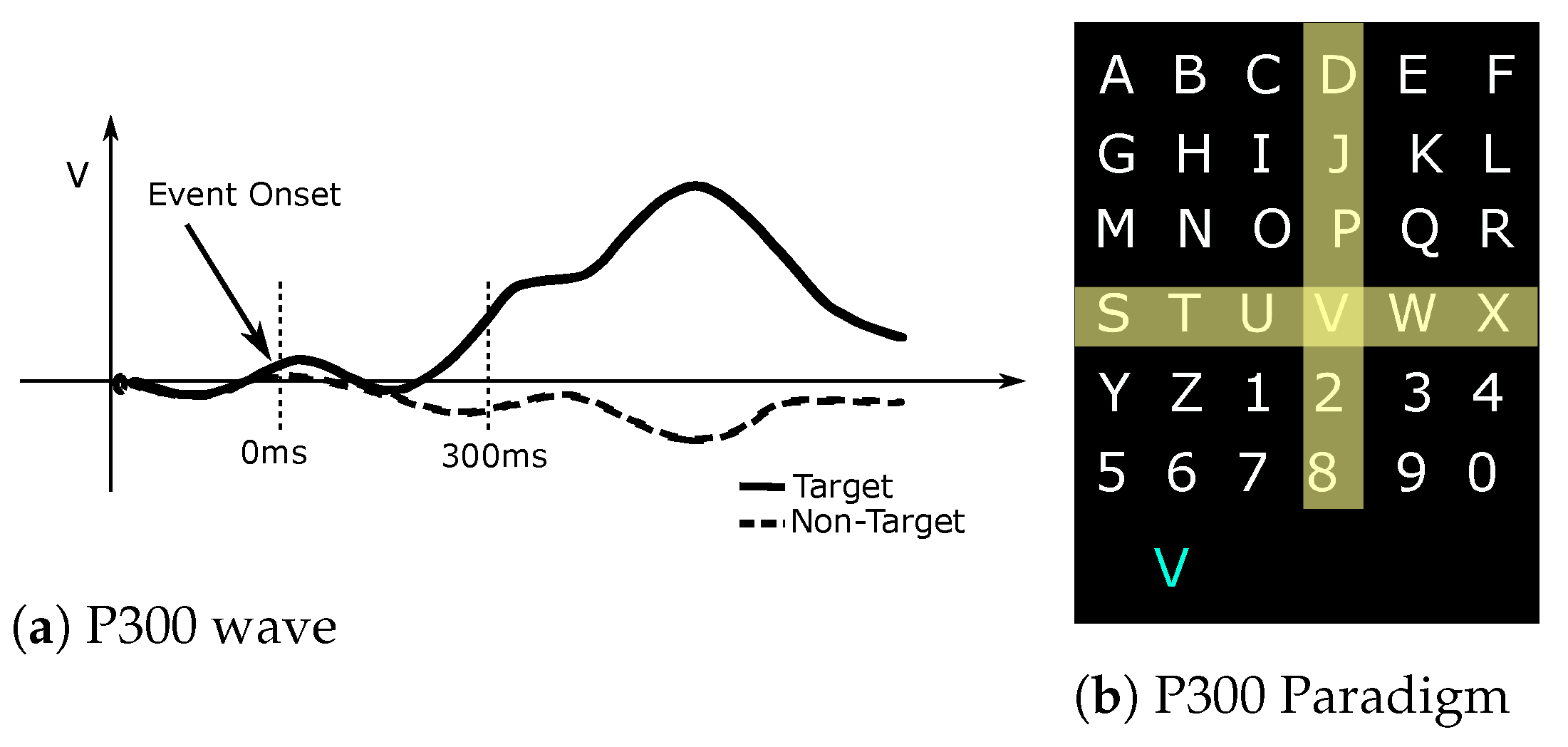
Decoding brain states is problematic since they have a poor signal-to-noise ratio, variability between trials (in different sessions or even on the same session), high dimensionality data, highly location-dependent data, etc. [
50]. Thus, for correct decoding, the usage of brain signals requires several steps, starting from signal acquisition (e.g., EEG and ECoG recordings), feature extraction, pattern recognition and, finally, translation into control signals (
Figure 1).
3.1. Signal Acquisition
The brain is composed of billions of neurons that communicate using electrical signals. These signals are produced at similar locations between individuals, yet it is not fully understood why they are emitted there and what their intentions are. However, it is still important to know when they are produced and their location, which reflects the normal or abnormal activity of the brain and user intentions.
Many techniques have been developed to record brain activity (e.g., EEG, ECoG, single-neuron recording, PET, fMRI, MEG and FNIR) [
14,
51]. Despite all of them being able to record brain activity, in this work, we will focus on EEG. The reason behind this is that the other enlisted techniques are either invasive, expensive or have high latency.
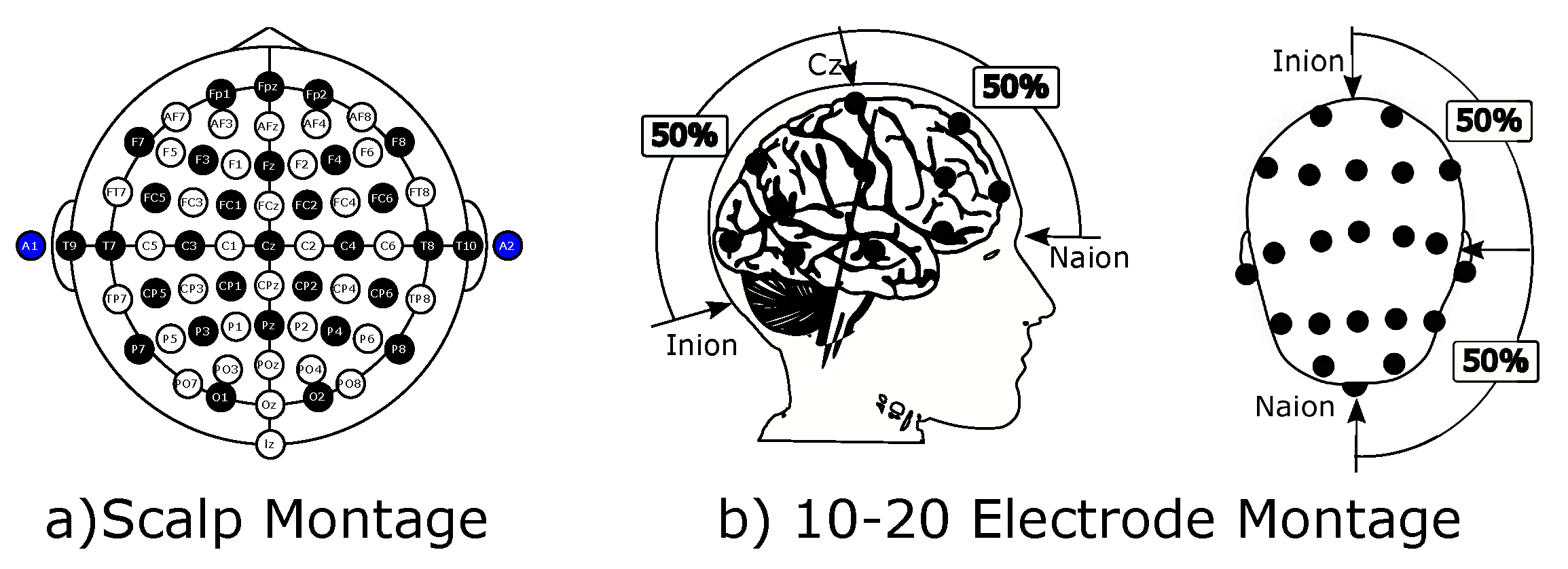
EEG recordings are done using electrodes attached to the surface of the scalp, and each electrode measures the potential difference from a reference electrode and itself [
51]. Correspondingly, these potentials reflect activity within the brain, and to avoid unwanted signal noise due to poor connection, the electrodes must have good contact with the area of interest. Furthermore, for understanding and repeatability, it is of great interest to know exactly where the electrodes are commonly located. For that reason, international 10–20 electrode systems are used, which consist of making an arc grid over the scalp that starts at specific locations, where the Nasion and Inion are the longitudinal references and the right and left preauricular are the lateral references (see
Figure 3). The corresponding name of each arc crossing represents a location of the brain lobes, which is helpful for the spatial analysis of recorded signals.
Furthermore, since EEG signals go through several layers of muscle, skin and bone, having a correct measure of the brain signal requires a process of amplification and filtering to improve the signal quality.
First, the amplification helps increase the low-signal amplitude (∼10–20 V), which is not easy to interpret using common displays, recorders or AC/DC converters. Notably, amplifiers must fulfill some requirements such as noise rejection and guarantee equipment and patient protection.
Then, filtering is done to reduce either the environmental noise (e.g., power lines and electrical and/or surrounding medical equipment) or the physiological noise (e.g., muscle activation, eye movement, and/or blinking) [
52]. Dealing with environmental noise is usually easier than dealing with physiological noise. Environmental noise can be avoided by removing most of the sources of electromagnetic signals from the recording room and its vicinity. Furthermore, one of the most common techniques is to use a notch filter at 50 or 60 Hz that helps by removing the noise of the electric power lines’ artifacts. For physiological noise, one of the most common approaches is to incorporate physiological signals in the recordings and subtract them from the EEG. Other methods include telling the subject to remain still, not blink and hold the gaze during the study; however, this is usually difficult and can introduce even more noise because of the voluntary attention needed to control those body actions.
3.2. Feature Extraction Methods
The second component is feature extraction. Once you have selected the correct control signal, it is necessary to find a way to better represent it. BCI mainly use four kinds of feature extraction methods to represent the signal: temporal methods (i.e., signal amplitude and auto-regressive), frequency methods (i.e., band power and power spectral densities), time-frequency methods (STFT and wavelets) and some others (e.g., coherency, phase synchronization, etc.). The selection of one of these methods will depend completely on the desired control command for classification. Thus, depending on the transformation, it is recommended that EEG recordings have a high sampling rate and more than a single electrode for a better signal recording.
4. Pattern Recognition
The third component is pattern recognition, which is the one that translates the feature into a control signal. The main problem in this step of the BCI is that the brain signals are highly variable and would be hard, if not impossible, to manually translate into control signals. Then, in the light of solving this problem, the use of Artificial Intelligence (AI) is highly beneficial. Given that there are many techniques and their applications in science are vast, it is required to understand the basics of AI techniques, what each technique can do and how they are developed. Thus, students must see what a real application of these techniques can do, especially in BCI.
In particular, this work focuses on five AI algorithms: Kohonen Self-Organizing Maps (SOM), Artificial Neural Networks (ANN) trained by Backpropagation, Linear Discriminant Analysis (LDA), Supported Vector Machines (SVM) and Restricted Boltzmann Machines (RBM), as well as their applicability to BCI. These techniques were chosen because each one brings different properties that are interesting to be analyzed. In the case of SOM, as an unsupervised network that does not require labels, it is capable of creating an internal representation of the system. On the other hand, neural networks facilitate their training by using the error to correct its internal representation. Linear discriminant analysis is the most used technique used for BCI due to its simplicity and adaptability but with the limitation of working only for binary classification. Furthermore, Support Vector Machines is selected to be tested in this work since it is one of the most used classification techniques and has high separability capabilities. Finally, the Restricted Boltzmann Machine algorithm is analyzed as a different technique for BCI that explores and characterizes both the signals and their classes together, creating an internal map of them.
4.1. Kohonen Self-Organizing Maps
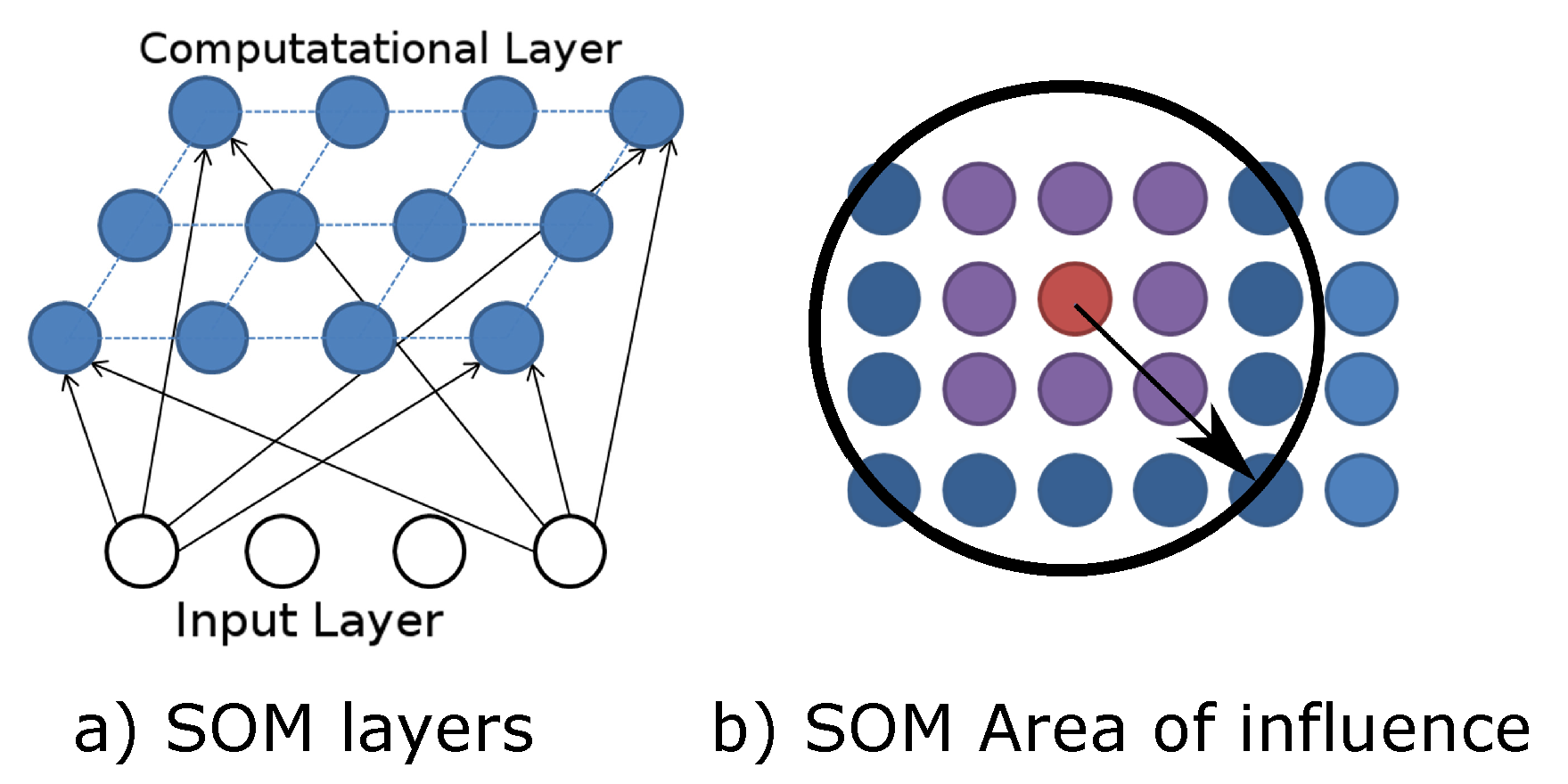
A Self-Organizing Map (SOM) [
53] is an unsupervised neural network that produces a discrete representation of an input space, which is referred to as a map. This algorithm is used as a clustering or dimensionality reduction method and consists of an input layer and a computational layer (
Figure 4a) conformed to nodes or neurons. Each node has a topological position and has a number of weights equal to the number of inputs (
, with
n as the number of inputs,
;
number of nodes, where
). The SOM method calculates the Euclidean distance between an entry vector and the weights of each node:
and chooses the lowest distance to one node as the best or winning node. This node is referred to as the Best Matching Unit or BMU.
Once the BMU is found, the nodes in the neighbor (i.e., influence area) of the BMU and the BMU itself are selected, and their weights are updated (
Figure 4b). The BMU’s influence area is calculated as
, with
as the lattice width at the instant
and
as the updating constant of
. After the area is selected, the weights are updated using the equation below:
where
and
represent the learning rate and influence rate at the instant of time
t. As training time advances, the learning rate and influence rate diminish their effect by:
where
is the initial learning rate, and
is the update constant of
. With this learning technique, the inputs with similar characteristics will cluster together around a given node, while inputs with different characteristics will cluster apart in other different nodes. The steps of this method can be seen in Algorithm 1.
| Algorithm 1: SOM Pseudo-code. |
| Input network: |
| Training set ; Learning and influence rate & = () |
| Init network: |
| Initialize the weights to a small random value |
| Train network: |
| Loop until : |
| Select random input: |
| Compute the distances: |
| Select BMU |
| Calculate area of influence: |
| Update weights: |
| Update learning and influence rate: |
| Output network: Weights w |
4.2. Fisher’s Linear Discriminant Analysis
Linear Discriminant Analysis (LDA), also known as Fisher’s LDA, uses a linear hyperplane to separate the data representing each of the two classes (see
Figure 5).
The hyperplane is obtained by projecting high-dimensional data onto a line. The objective of this projection is to maximize the distance between the means of the two classes while minimizing the variance within each class. This defines the Fisher criterion, which is maximized over all linear projections,
w:
where
represents the mean of the projections of classes 1 and 2 (
), and
represents the variance of these projections (
), where
is the projected samples
. Based on these equalities, we can rewrite Fisher’s criterion as a function of
w in the following way:
where
and
measure the separation between means of both classes and the within-class scattering, respectively. Given the previous equation, we can find its maximum by solving the generalized eigenvalue problem as follows:
Solving this problem will result in a collection of eigenvectors w and their corresponding eigenvalues . Then, these eigenvectors must be sorted according to their eigenvalues from biggest to smallest, and finally, a set of k eigenvectors is chosen to create a weight matrix w, which is the representation of the new space in which the data are going to be projected. Algorithm 2 gives the basic steps for LDA.
| Algorithm 2: LDA Pseudo-code. |
| Input network: |
| Training set |
| Train network: |
| Calculate the means |
| Calculate and |
| Get the eigenvectors and values: (), () |
| Obtain the matrix |
| Sort the eigenvectors and chose the k ones with the bigger eigenvalues |
| Form a matrix |
| Output network: Returns Matrix W |
4.3. Supported Vector Machine
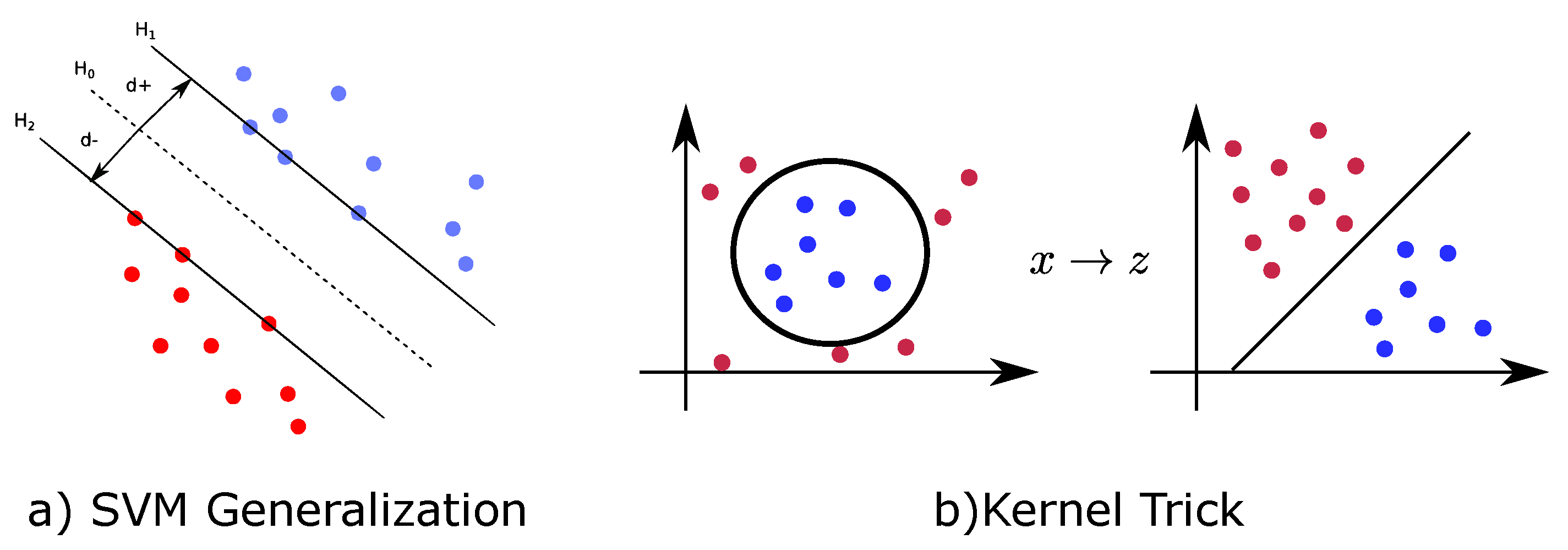
Supported Vector Machines (SVM) are supervised models that search how to separate two classes using a discriminative hyperplane. SVM searches for a hyperplane that maximizes the separation margins of the system, i.e., the distances between the classes of the training points. In
Figure 6a, these distances are shown as
and
.
As it can be seen in the previous Figure, the hyperplanes divide the input data in two different regions, one considered to be positive (
for
) and the other to be negative (
for
). Thus, the hyperplanes, as shown in
Figure 6a, are defined as
and
. Those conditions can be combined into
. The main objective is that the classifier has a margin as big as possible, i.e., maximize the distance between both hyperplanes, defined as
. This is the same as minimizing the function
constrained to the condition of
.
Although SVM is a linear classifier, it can be extended to non-linear using the ‘kernel trick’, which maps the data into a different space (
Figure 6b) where the data can be linearly separated. Furthermore, SVM is a binary classification but can be easily converted into a multi-class classifier using the technique of one vs. the rest, where a classifier is made for each class and discriminated against the rest of the classes. The winning class is the one with the higher final confidence value. The steps for SVM can be seen in Algorithm 3.
| Algorithm 3: SVM Pseudo-code. |
| Input network: |
| Training set: |
| Regularization Parameter: C |
| Tolerance and maximum number of iterations |
| Init network: |
| Initialize and |
| Train network: |
| Quadratic Programing such as SMO |
| Output network: |
| Lagrange Multipliers: |
| Threshold: |
4.4. Backpropagation
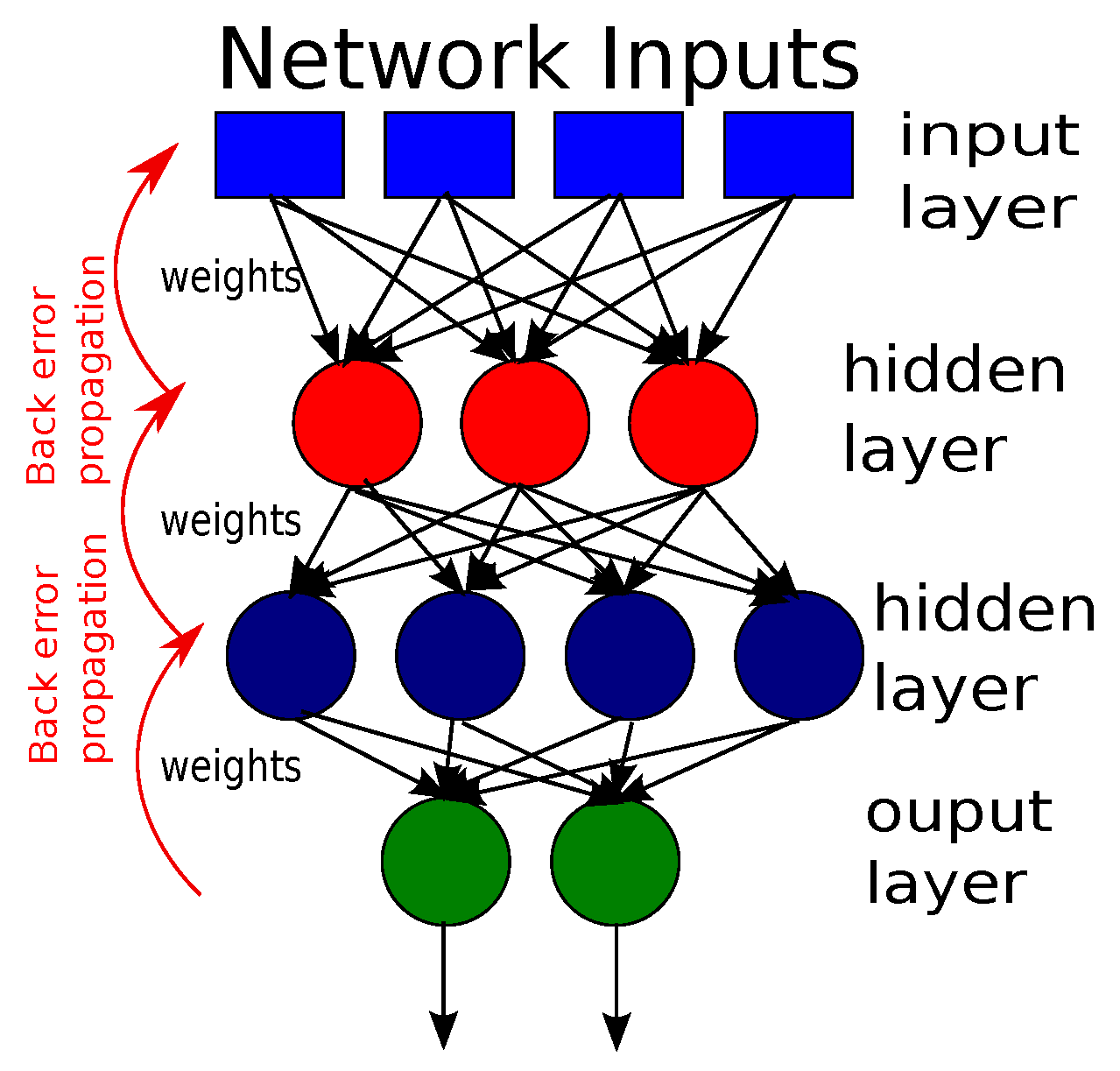
Backpropagation (BP) is a common technique for training Artificial Neural Networks (ANN), where, in few words, the error is propagated backwards so that the network can learn by itself and adapt depending on previous mistakes [
54] (
Figure 7). The main objective of the BP algorithm is to minimize the error function in a weight space using the gradient descent method. The combination of weights that minimize the error of the function is considered the solution to the learning problem. To use the gradient descent method, first, we must guarantee that the error function and the activation function are continuous and differentiable. One of the activation functions that is usually implemented for BP is the sigmoid function,
, of which a derivative exists and is continuous
. The activation function of a neuron calculates the sum of the inputs
times the weights
plus the bias of that particular neuron
. In the particular case of the sigmoid function:
where the output of the system is composed by the outputs of each neuron,
. The method of BP searches to minimize the error between the generated output
and the original output, i.e., the target
. This error can be represented through the mean sum squared loss function:
To minimize error, the weights need to be corrected using the gradient descent:
where each weight is updated using
, with
being the learning constant. The weights are updated iteratively until
using:
With this, all weights are updated with the intent of error minimization. Once the error is minimized, the network can be used on unseen data to check out its performance.
The resulting method can be described in Algorithm 4.
| Algorithm 4: Artificial Neural Network trained with BackPropagation. |
| Input network: |
| Training set ; Learning and influence rate and = () |
| Init network: |
| Initialize the weights and bias b to a small random value |
| Train network: |
| Loop until : |
| repeat |
| Chose random input |
| Forward Propagation: |
| for All MLP Layers |
| Use 7 to each of the layers until the output layer |
| end for |
| Backward Propagation: |
| Calculate quadratic error according to 8 |
| for All MLP Layers do |
| Calculate each of the deltas using |
| end for |
| Update weights using |
| until when it converges |
| Output: |
| Weights |
| Use trained network for classification |
| Results: Activity Labels A of the unlabeled data
|
4.5. Restricted Boltzmann Machines
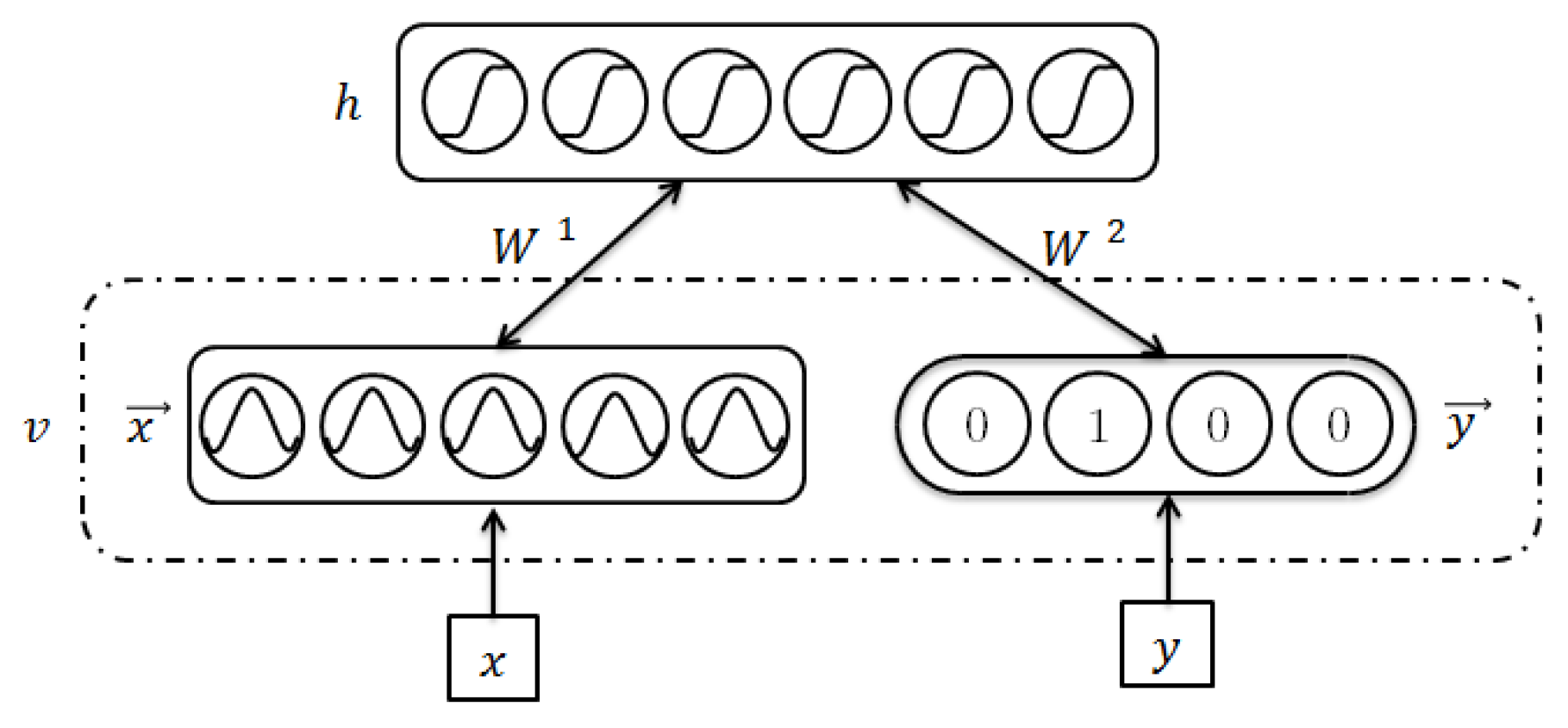
A special type of ANN is the one developed by Hinton [
55], known as Restricted Boltzmann Machines (RBM). RBMs are two-layer neural networks of stochastic units, divided into
visible units
and
hidden units
, which have symmetrical connected weights (see
Figure 8). The visible units represent the data, while the hidden units are known as feature extractors. RBMs pretend to be model dependencies over visible variables. The probability
is known as the Boltzmann distribution, which has an energy function described as:
with
as the symmetric weights,
and
as the bias of the visible and hidden units, respectively, and
. The two conditional distributions over the variables, i.e., hidden given the visible and visible given the hidden, are given by:
and
where
represents the activation function. Since the hidden variables cannot be observed, we need an algorithm that improves the RBM representation of the system. This algorithm is called Contrastive Divergence (CD) [
56], which allows fitting the probability
to a certain set of observations (e.g., EEG signals).
The pseudo code for RBM can be seen in Algorithm 5.
| Algorithm 5: RBM Pseudo-code using Contrastive Divergence-k. |
| % Notation: means x is set to value b |
| % means x is sampled from p |
| Input network: |
| Training pair |
| Learning rate |
| Init network: |
| Train network: |
| |
| Loop Gibbs sampling |
| % Positive phase |
| |
| % Negative phase |
| |
| |
| end Loop |
| |
| % Updates |
| for ∈ do |
| |
| end for |
| Output network: Return weights and biases |
4.6. Advantages and Disadvantages of the Methods
It is intended to test the efficacy of the proposed methods for BCI, but, before doing that, it may be convenient to clarify the advantages and disadvantages of each method.
Table 1 is a listing of the main characteristics of each of them.
4.7. Accuracy and Cross Validation
In general, it is important to know how well a given method performs over a specific task; thus, it is important to calculate its accuracy. Therefore, to calculate the accuracy, the Mean Square Error (
MSE) was used, as shown in Equation (
14), with
and
as the observed and predicted outputs.
Another important measure to be done is how the classification method is going to behave when dealing with independent data, i.e., how general the method is. It is important to check that the method does not overfit, which means that it obtains a perfect score when dealing with training data but has a poor performance when it is exposed to unseen data. One way to overcome this problem is to observe the performance of the classifier over a training dataset and then verify it using a test dataset; this is the basic idea behind a technique called cross validation. However, we still have the problem that the behavior of the system may depend heavily on which data points are used for training and which ones are used for training. Thus, the algorithm may yield different results depending on how the data was divided into the training and testing datasets.
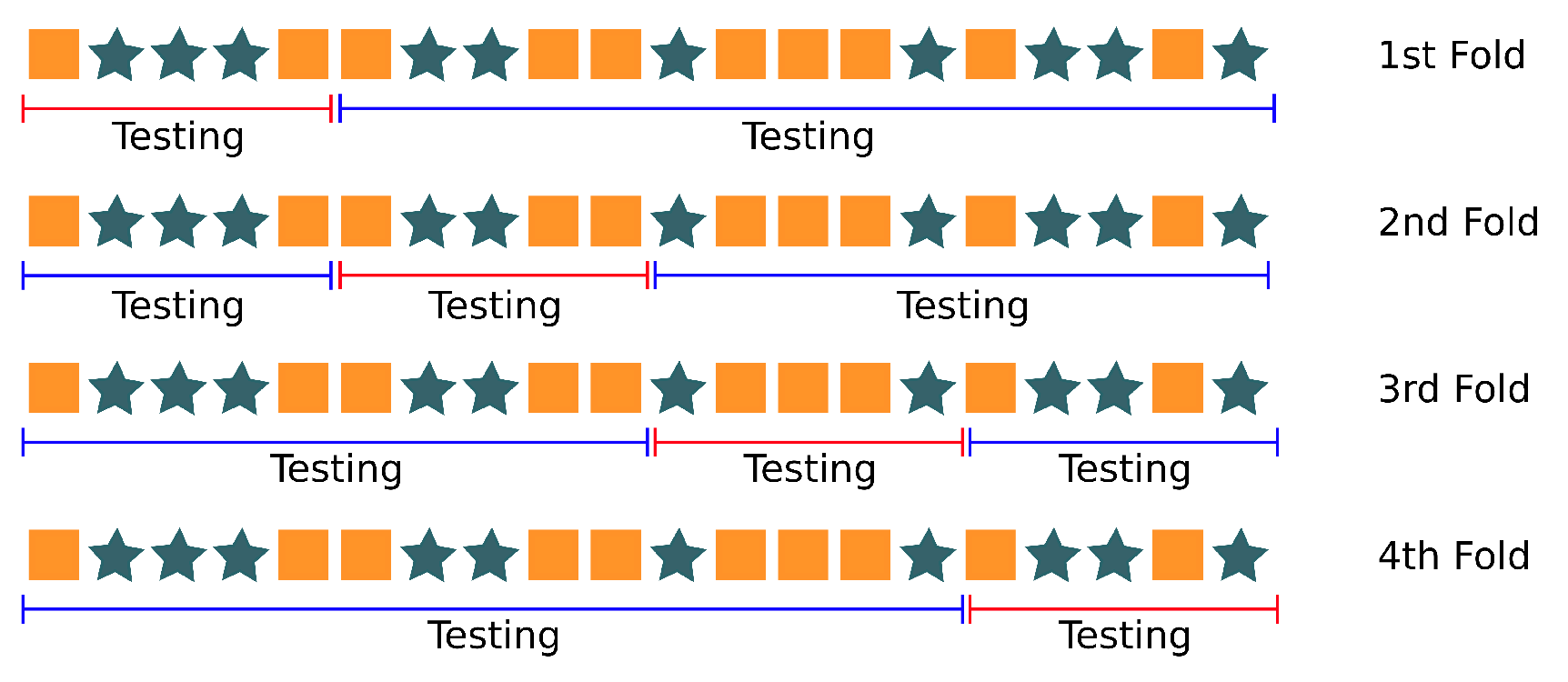
One of the most used methods to overcome this problem is known as K-fold Cross-Validation. This technique is based on splitting the data set into
k smaller sets and repeat the training and testing
k times. Each time the algorithm uses one different testing dataset, the other
datasets are used for training. Then, the validation results are averaged to obtain the overall performance of the algorithm (see
Figure 9). This testing procedure allows us to describe how well the classifier performs using different datasets.
5. Method
To test the previously described techniques, we used the dataset from [
37] (a link to this dataset can be found in
Appendix C), consisting of EEG and EOG recordings from ten naive right-handed subjects (six male and four female) with an average age of
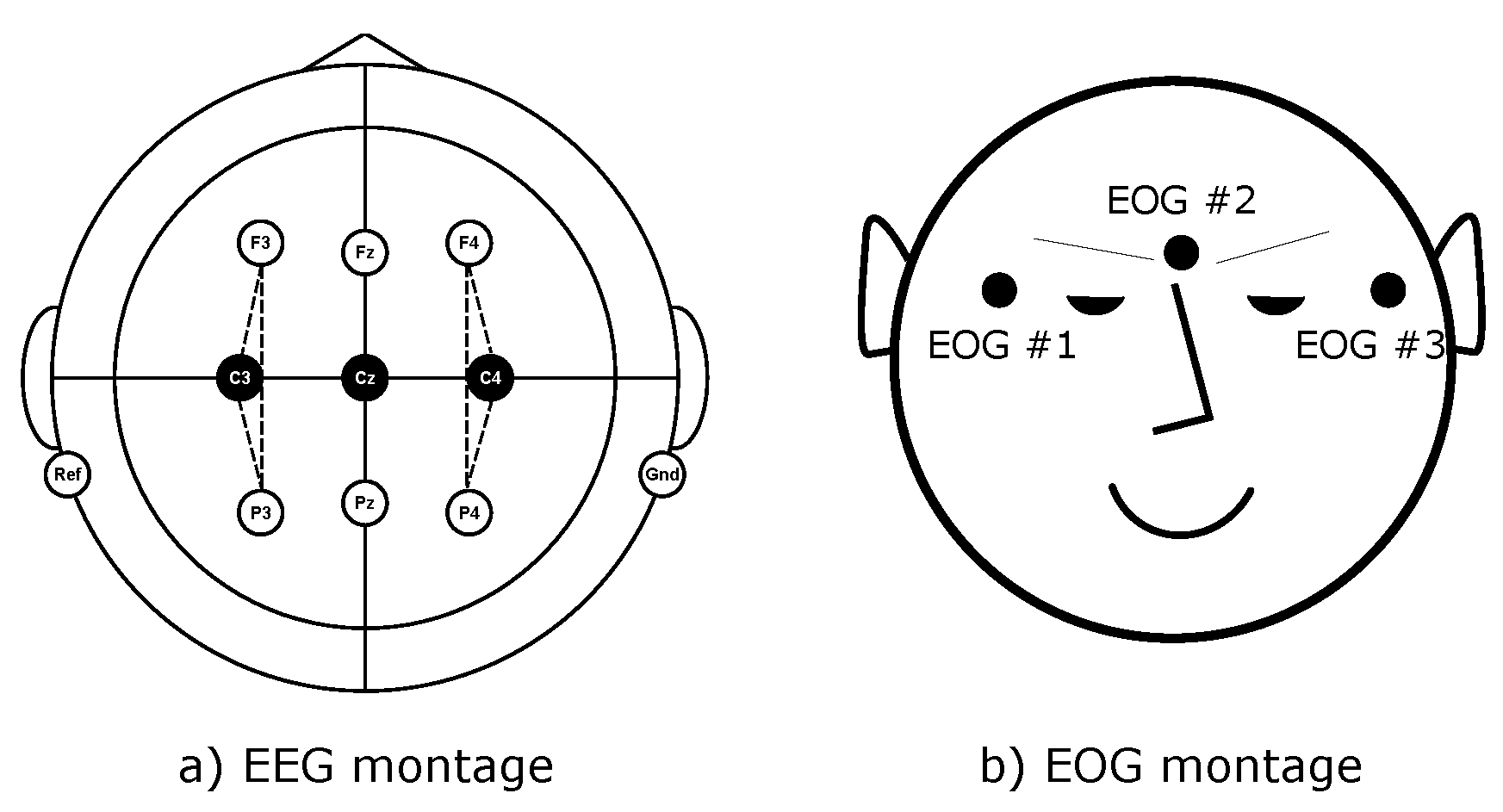
years. Furthermore, the participants had normal or corrected-to-normal vision during the experiments. The gathered data consisted of three bipolar EEG recordings (C3, Cz and C4) with a sampling frequency of 250 Hz and the electrode Fz as the EEG ground, as shown in
Figure 10a. The recorded signals had a dynamic range of
V, which were analog bandpass filtered (0.5–100 Hz) and notch filtered (50 Hz). At the same time, EOG data were recorded using three monopolar electrodes (
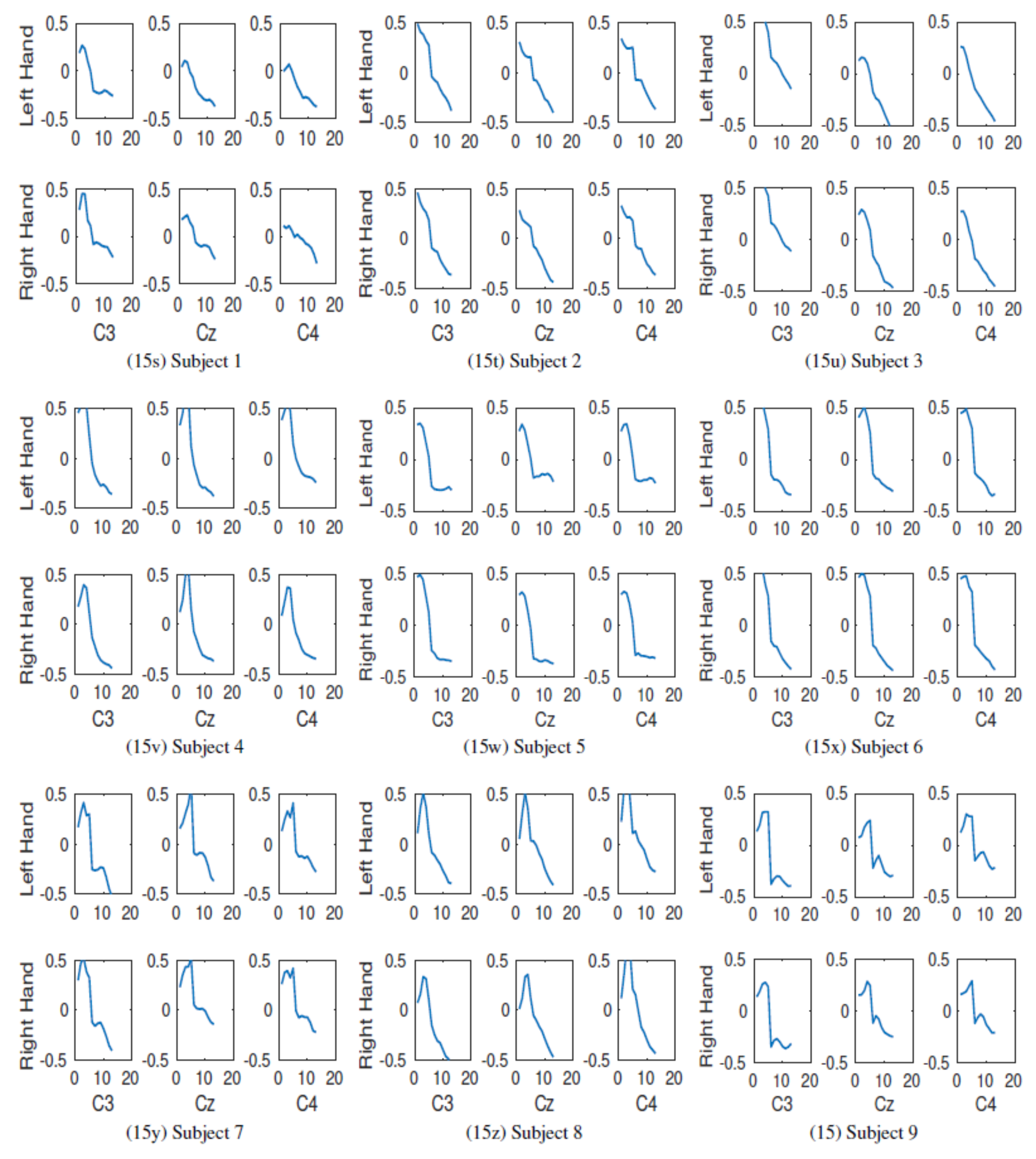
Figure 10b) with a dynamic voltage range of ±1 mV.
Each subject participated in five sessions, two without feedback and three with feedback. At the beginning of each session, a 5-minute recording of continuous eye behavior was made to estimate the EOG artifact correction coefficients. These recordings were divided as follows: eyes open during 2 min, eyes closed during 1 min and eyes moving during 1 min (see
Appendix A).
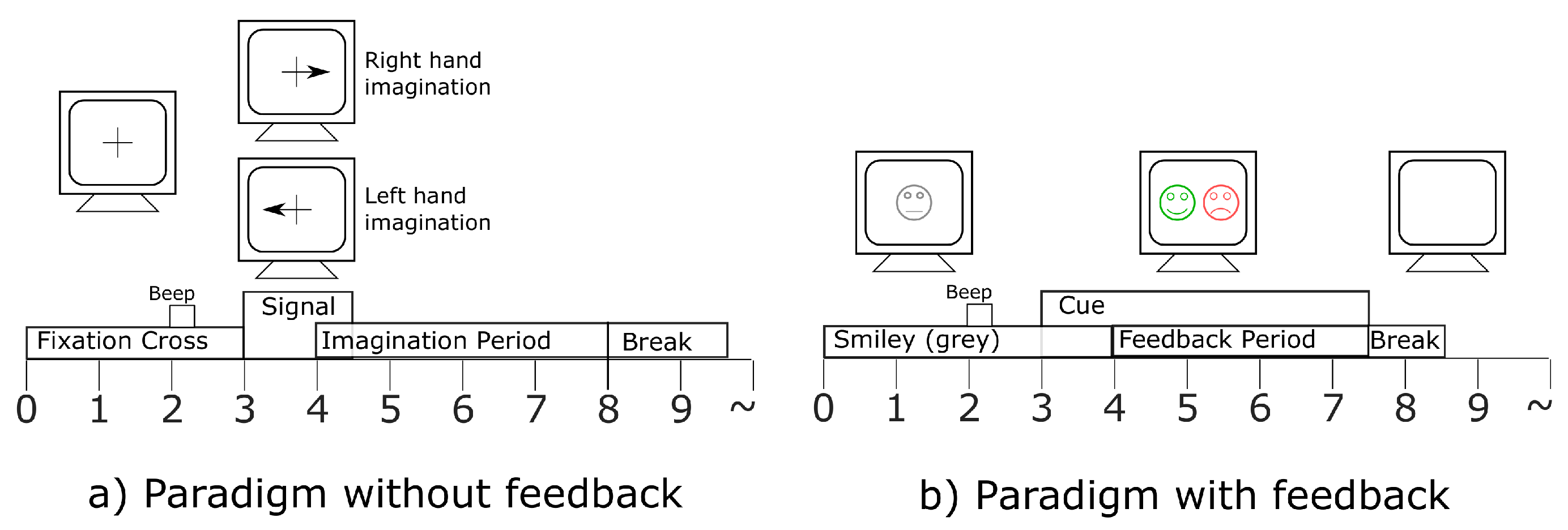
The sessions without feedback were done using a cue-based paradigm (
Figure 11a), in which each subject had to perform motor imagery (MI) depending on the visual cue shown in the monitor. Each trial started with a fixated cross and an additional short warning tone. Then, after some seconds, the visual cue consisting of an arrow pointing either to the right or to the left appeared for 1.25 s. Afterward, the subject had to maintain the corresponding MI for a period of 4 s. In between trials, a short break of a random period between 1.5 and 2.5 s was given to avoid adaptation.
The three feedback sessions consisted of four runs with twenty trials for each type of motor imagery. These sessions were carried out using smiley feedback (see
Figure 11b), which the initial state was centered and gray-colored. At the second two, a warning tone was emitted, which preceded a cue that lasted from second 3 to 7.5. According to the given cue, subjects had to move the smiley to the left or right by imagining hand movements towards those directions. The smiley changed color from gray to green or red and the curvature of the mouth from happy to sad if the direction was either correct or incorrect according to the cue, respectively.
Data Processing
Two different approaches were designed for the data processing step. The first one consisted of testing the performance of the classifiers with a large range of frequency bands and without any EOG removal. To do this, the data were transformed into a frequency domain between (8–30) Hz, which is the range in which changes in amplitude occur. Then, the second approach was to reduce the frequency bands into two different ranges, (8–12) Hz and (22–30) Hz, and the EOG was removed using the previously proposed regression.
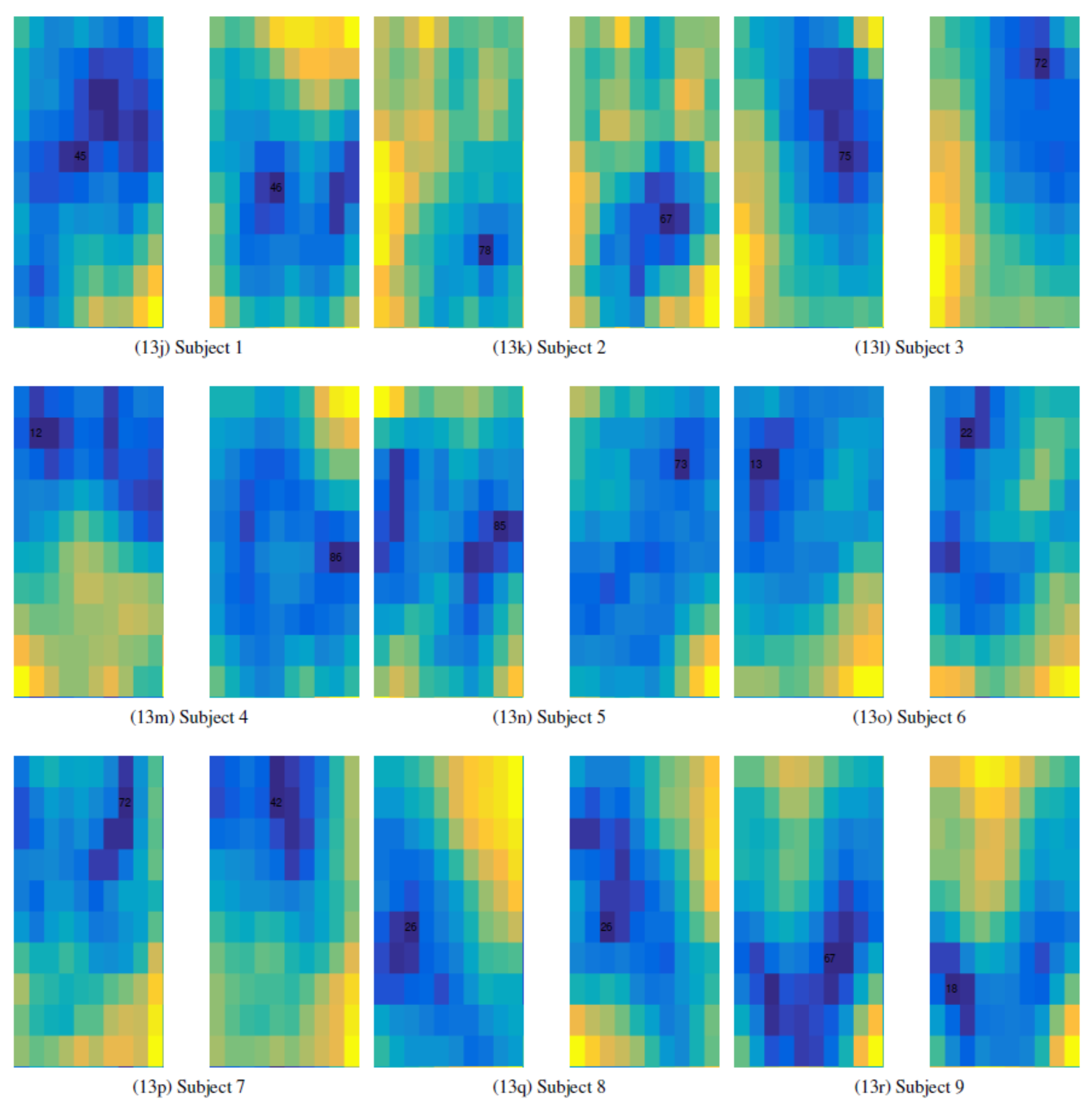
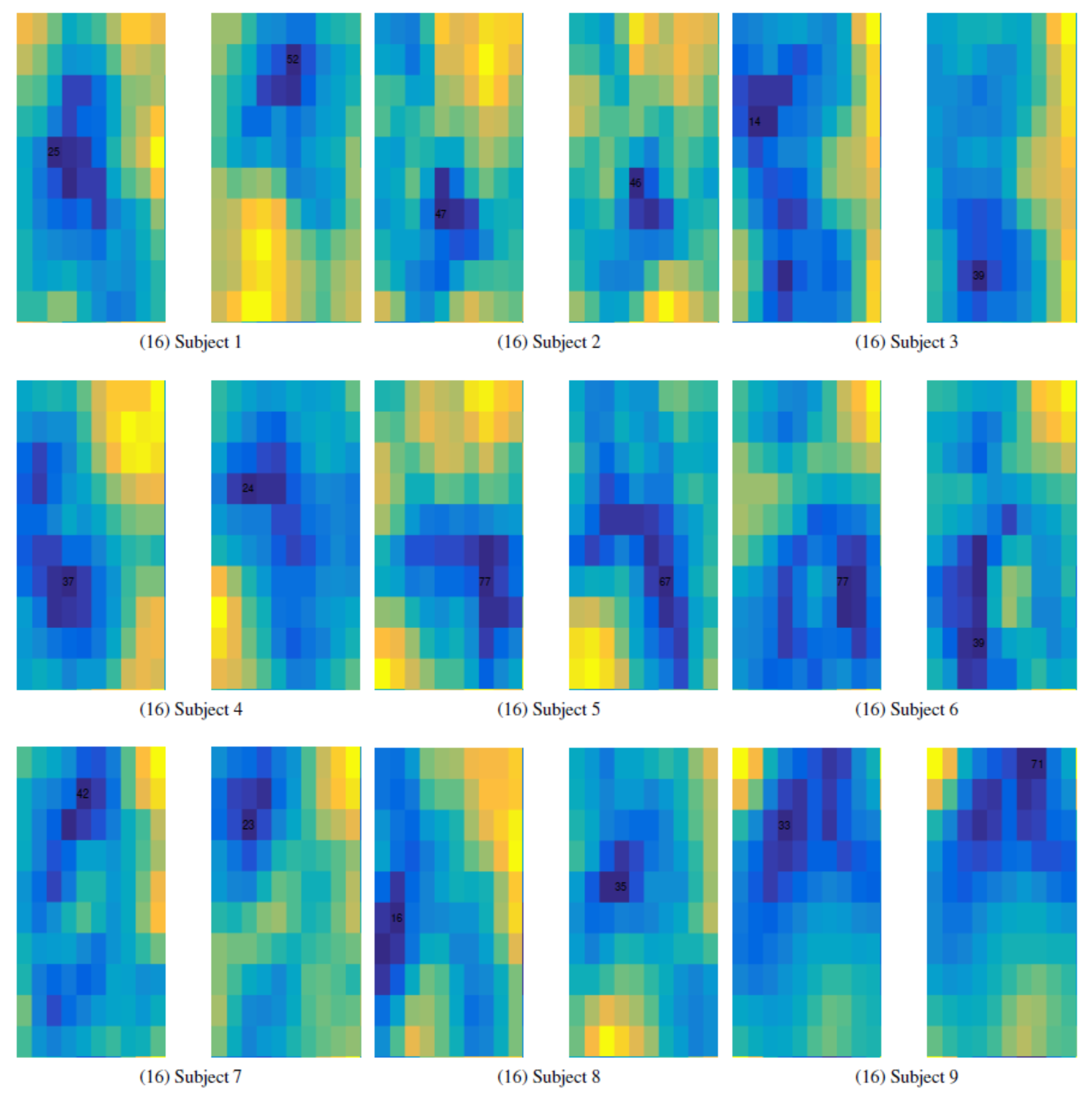
A specific SOM was trained for over 50 epochs for each one of the nine subjects to obtain an internal representation of both classes in order to observe if they could be easily discriminated against. Each SOM had 100 units distributed in a 10 × 10 matrix (see
Figure 12), an initial learning rate
, an initial lattice width of (
) and updating constants
and
.
Being an unsupervised method, the training dataset was used to tune the weights of the SOM, and the testing dataset was used to observe the final internal representation that it could generate. In this case, the first three sessions were used as training data and the remaining two as testing data.
The other techniques were supervised methods, where the testing dataset was used to check the final classification accuracy of each method. K-fold cross-validation was done to better evaluate the results of these algorithms, with . In other words, the data were split so that one of the recorded sessions was considered as testing data and the reminding sessions as training data. This process was repeated five times, then the accuracy was averaged.
As LDA calculates the mean and scatter matrices, it does not require any specific training parameter, so the process is as straightforward as shown in
Section 4.2. For the SVMs, since this problem is a binary classification problem, there was no need to use any expansion method. However, the SVMs were trained on a radial basis using the kernel function
, which is one of the most common kernels used for BCI. The box constraint parameter
was used since it gave the best overall results.
A 1000-neuron Artificial Neural Network was trained using backpropagation, which had a learning rate of and a momentum of . The weights were initialized through a normal distribution . The ANN has trained over 100 sweeps (or epochs) with batches of 100 randomly selected EEG trials.
Finally, the RBM initial training parameters (weights, biases and rates) were obtained from [
56] and adapted after some preliminary analysis. The RBM was trained over 100 epochs, each comprising Contrastive Divergence updates derived from 10 Gibbs sampling iterations (CD10). The training datasets were composed of mini-batches of 100 randomly selected EEG trials. The weights were drawn from a normal distribution
for the Gaussian-Binary connections and
for the Softmax-Binary connections, with each bias initialized at zero. The weights and biases were updated with a learning rate of
and a momentum of
with an increment of
at
and
of the learning process. The step-up value of 0.1 was selected because higher increments made the learning unstable. A cost value of
was selected since it facilitated the learning process of CD by increasing the mixing rate of the Markov chain.
All the algorithms were implemented using Matlab™ on Windows™ 7 professional 64-bit operating system. The computer used to run the algorithms had an Intel® CPU E5-2618L v3 @ 2.30 Ghz with 16 cores and 24 GB RAM.
7. Discussions and Conclusions
7.1. Discussions on the Results
Frequency band of (8–12) Hz and no EOG filtering: The results showed that for subject 4, 7 and 9, the SOM mapping has a better separation capacity (see
Figure 14 (Subject 4), (Subject 7) and (Subject 9)) than for the rest of the subjects. Likewise, this effect is also represented on
Table 2 (using
Figure 12), where the winner neurons for the two classes are far apart from each other.
Correspondingly, a similar effect occurs for the classification methods (
Table 3), where the same subjects, plus subjects 1, 5 and 8, showed training and testing accuracy higher than chance level ≥60∼80% for LDA, BP and RBM. However, for the other subjects, it is not easy to discriminate between both classes, which is illustrated in
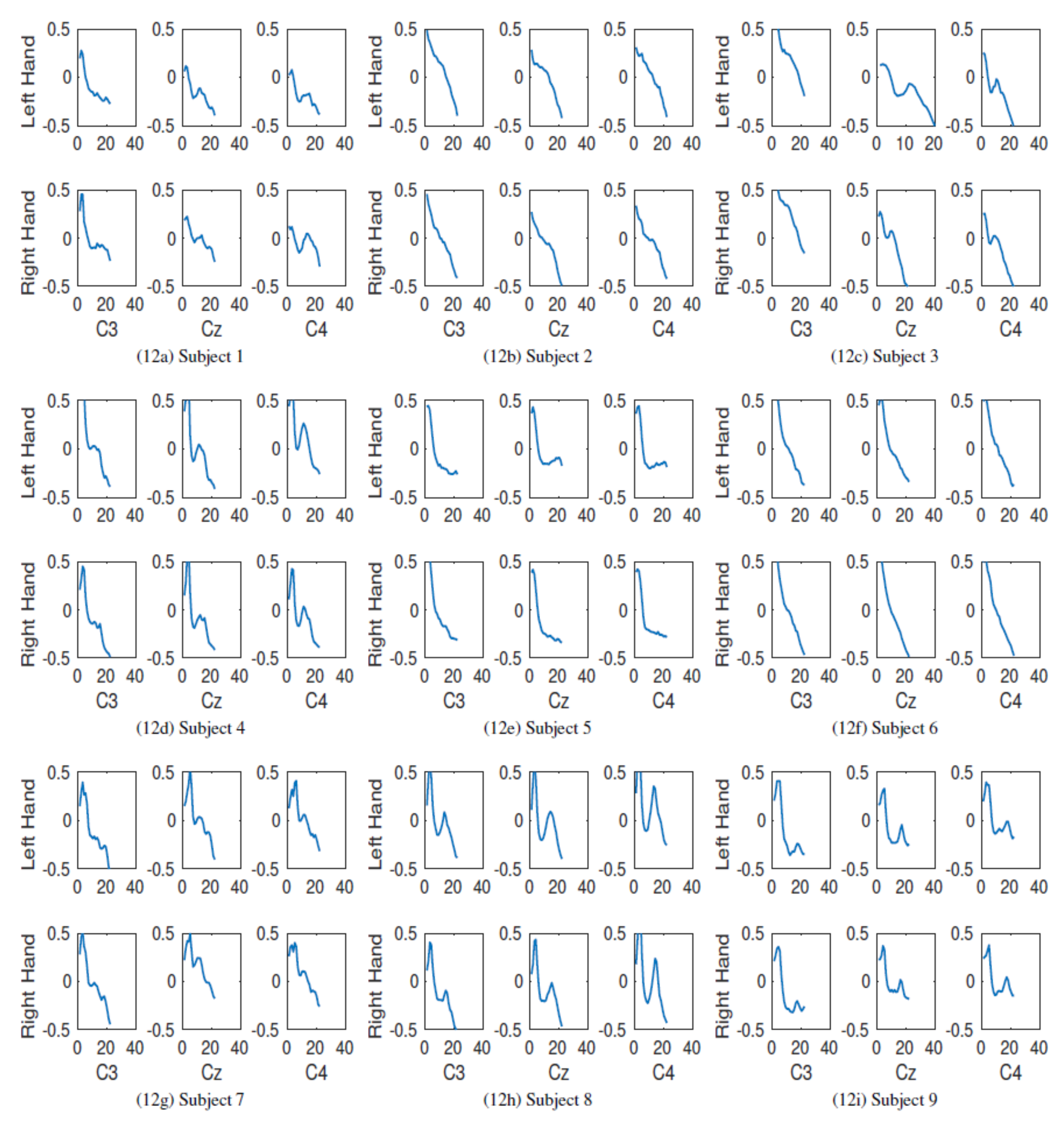
Figure 13, where there is no observable difference between the EEG frequency response among these subjects. It is important to notice that the SVM method did not show any discrimination capacity for any subject when applied to the testing dataset. This might be due to the kernel being too general and not working well on high dimension signals.
Frequency bands of (8–12) Hz and (22–30) Hz and EOG reduction: Using the band reduction and the EOG regression method, the results for SOM showed now that the best separation capacity was obtained for subjects 1, 3, 6, 8 and 9.
Although in the case of the classification techniques, there was a slight improvement for subjects 1, 4 and 8 in the accuracy percentage (
Table 5), and there was no significant improvement over subjects 7 and 9, which already had good results on the (8–30) Hz band. In this case, it is assumed that there were some hidden attributes for subjects 1, 4 and 8 that were found due to the band reduction or filtering. However, these procedures did not necessarily help the other subjects, where the selected bands may not be optimal or the EOG contamination was not an important factor in their classification. In addition, there was no improvement over the accuracy for the subjects that already performed poorly. In these cases, even the limited band and noise reduction technique could not help to uncover if there was any difference between the classes.
Lastly, for the SVM method, the accuracy was low for every subject except for subjects 4, 5 and 8. In general, the accuracy of SVM highly depends on finding the correct kernel to map the function, meaning that the initial parameters introduced for mapping into a higher dimension were not optimal for this database. Furthermore, SVM usually has problems discriminating when the same parameters are used in every individual, which means that it may require a specific setup for each subject.
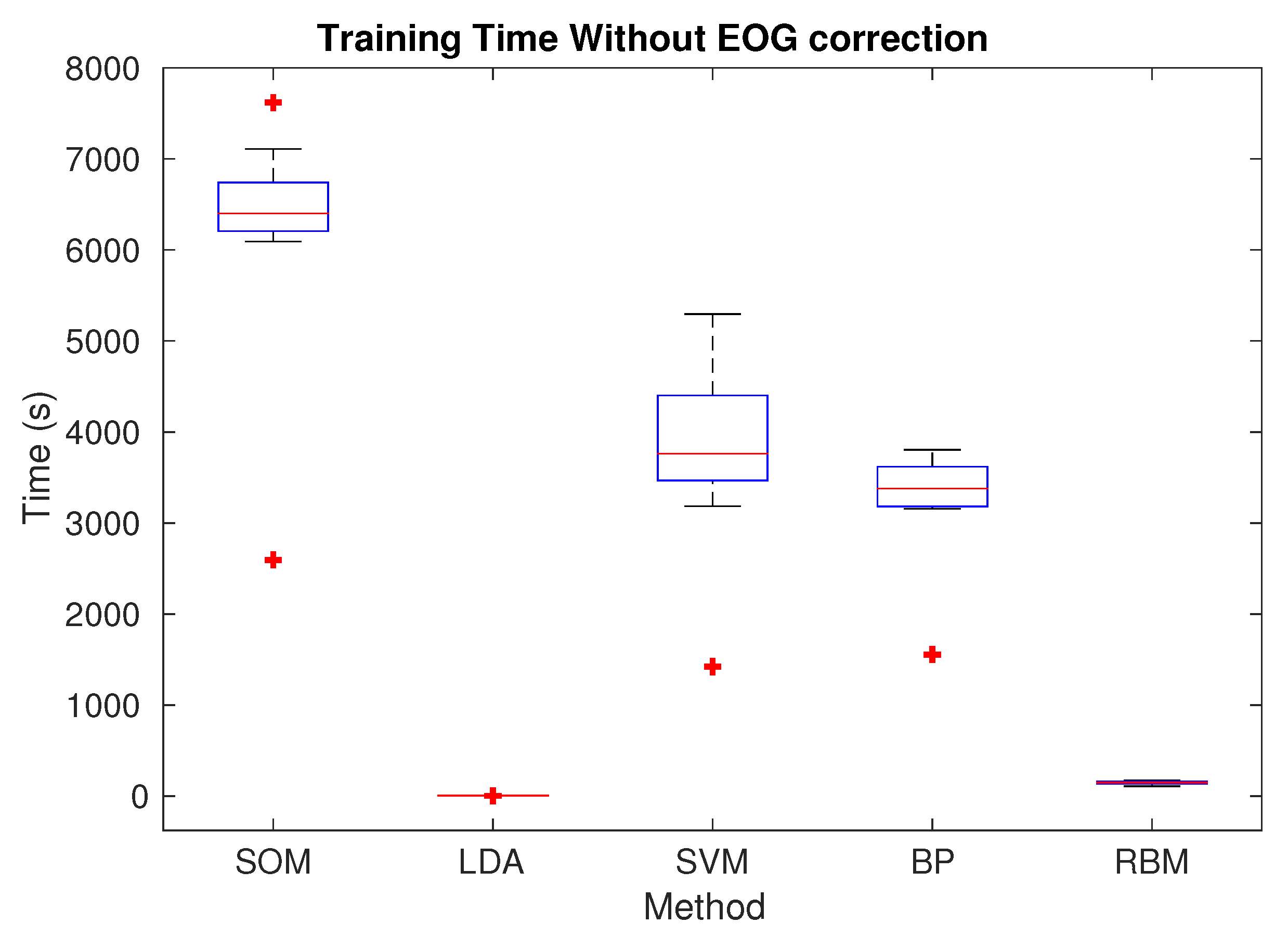
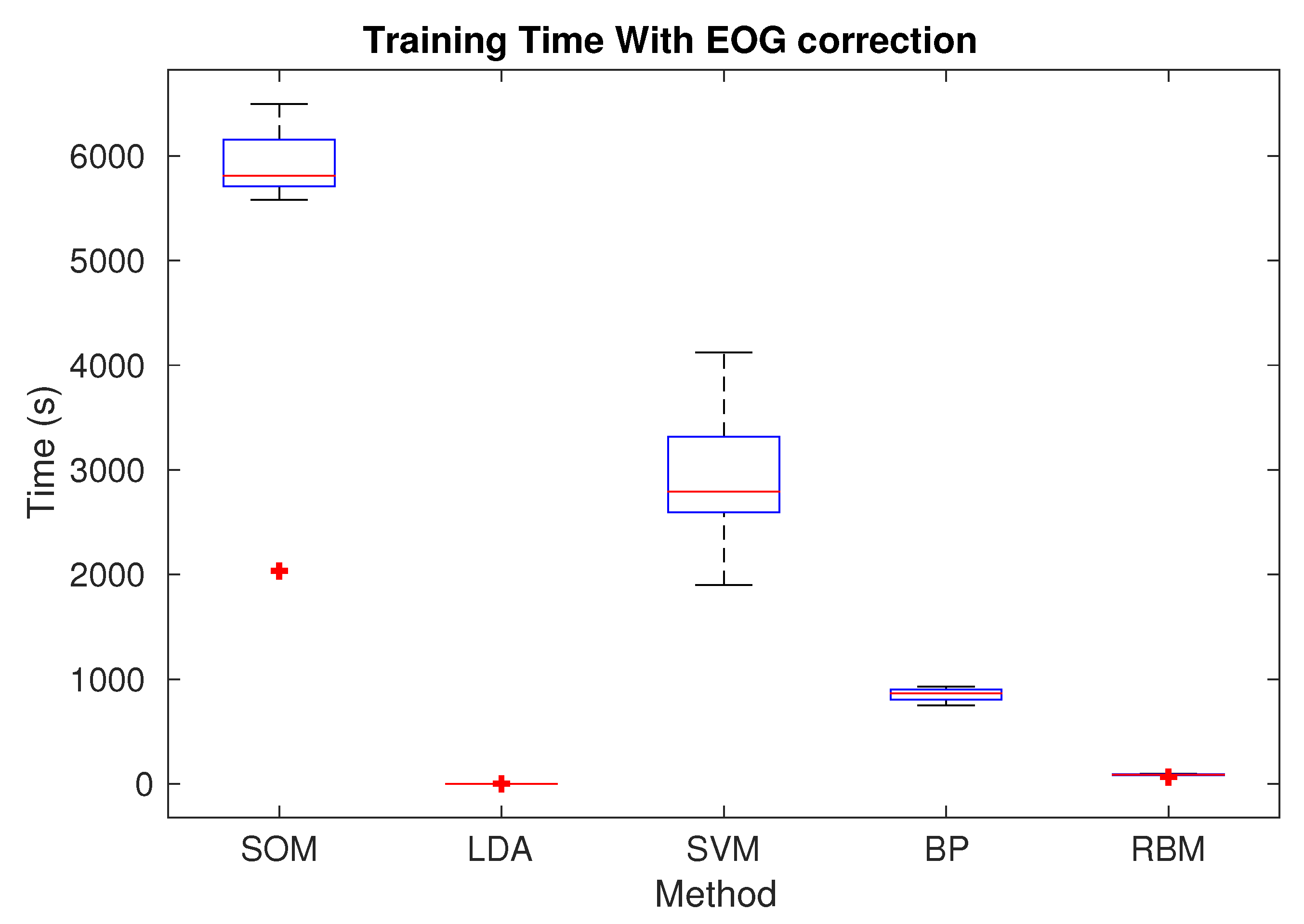
In the case of processing times, the training time is reduced using the limited frequency bands and regression method. This is a natural consequence of having a reduced dimensionality of data. Furthermore, while comparing the processing times between the presented methods, it can be observed that SOM has the largest ones, followed by SVM. The former could be due to the process of inserting the data one by one to adjust the map, which could be improved using a batch method. On the other hand, SVM needs to solve a quadratic optimization problem with a large data set and a small box constraint, which limits the algorithm convergence speed. Moreover, it can be observed that the BP method is slower than the RBM method. The reason behind this is that the ANN had many more neurons than the RBM (1000 neurons for BP over 64 neurons for RBM). However, other numbers of neurons for the BP did not give as high accuracy as those obtained.
Finally, although LDA indeed is the fastest of all the presented algorithms by far, which is one of the reasons why its one of the most used methods for BCI, it has the problem of not being easily adaptable to a high number of classes, thus needing different methods for multi-class problems.
7.2. Conclusions
With the aim of driving the development of competencies for future engineers and scientists, schools require curricula that is in line with the technological progress and demands of Industry 4.0. Consequently, Education 4.0 is searching for new ways to introduce students to emerging technologies, such as artificial intelligence, and how they are applied on real-life situations.
Accordingly, Education 4.0 is responsible for helping future professionals begin being familiar with the area of artificial intelligence, and, at the same time, it must provide them with the opportunity of testing the acquired knowledge by applying it to real-life scenarios. Therefore, in the scope of the Education 4.0 framework, teachers and students are in need of updated educational material that helps them embrace their path towards teaching and learning more about the technologies that are being used in the incoming industrial revolution. Hence, the main objective of this work was to provide updated teaching/learning material that allows students to have an introduction to a cutting edge technology, such as BCI, which is used for several real-life applications, while providing them with the basic knowledge of five different AI techniques and how they can be applied over the basics of BCI experimentation.
These different AI techniques were presented through a brief review of the methods and their corresponding pseudo-codes while also presenting the results of their implementation on BCI so that students become aware of the problems and possible outcomes of these experiments. This implementation was done over a test bench that consists on EEG and EOG recordings obtained from [
37]. From the obtained results, it is important for students to notice that the obtained behavior of each method made sense with the information presented in
Table 1; however, the main problem in this work was that none of them was able to always discriminate or even discriminate similarly to all subjects.
Through the description of the AI techniques and the analysis of the results of applying them over the proposed BCI test bench, this work allows students to learn the basic theory of SOM, LDA, ANN-BP, SVM and RBM, as well as giving the guidelines for the application of those techniques over real-life BCI problems. Furthermore, teachers that are beginning to work under the Education 4.0 paradigm can use this work as introductory material to BCI and artificial intelligence, and the proposed test bench can be used by them as a reinforcement exercise or project to test the understanding of students posterior to a BCI or AI lesson.
Notwithstanding of the contribution of this work to the development of updated curricula for the Education 4.0 framework, there is still a lot of work to do. To allow students to achieve a better comprehension of the presented methods, it is important to make an improved test bench with different band sizes as in [
37] or use some other type of filter or dimensionality reduction method such as Common Spatial Patterns [
69] (this can be seen in
Appendix B), which is also part of the current state-of-the-art BCI. Additionally, more advanced artificial intelligence techniques for BCI classification can be explored to provide students with additional information about algorithms that are not only applied on BCI but also on other areas of Industry 4.0.