Abstract
Privacy protection has been an important concern with the great success of machine learning. In this paper, it proposes a multi-party privacy preserving machine learning framework, named PFMLP, based on partially homomorphic encryption and federated learning. The core idea is all learning parties just transmitting the encrypted gradients by homomorphic encryption. From experiments, the model trained by PFMLP has almost the same accuracy, and the deviation is less than 1%. Considering the computational overhead of homomorphic encryption, we use an improved Paillier algorithm which can speed up the training by 25–28%. Moreover, comparisons on encryption key length, the learning network structure, number of learning clients, etc. are also discussed in detail in the paper.
1. Introduction
In the big data era, data privacy has become one of the most significant issues. Thus far, there exist plenty of security strategies and encryption algorithms which try to ensure that sensitive data would not be compromised. In addition, among them, most of the security strategies assume that only those who have secret keys can access the confidential data. However, with the wide use of machine learning, especially the centralized machine learning, in order to train a useful model, data should be collected and transferred to a central point. Therefore, for those private and sensitive data, it will inevitably face the risk of data leakage. Thus, how to do machine learning on private datasets without data leakage is a key issue for sharing intelligence.
Based on privacy protection, machine learning with multi-party privacy protection could help users of all parties to jointly learn with each other’s data, on the premise of ensuring the security of their own data [1,2,3]. Among them, federated learning [4,5] is a typical one that could help to solve the privacy problems under the multi-party computation. In this paper, we developed a privacy protected machine learning algorithm, named PFMLP, based on homomorphic encryption. Basically, the model is trained jointly by gradient learning under the protection of multi-party privacy. In detail, the model is optimized by gradient descent in each iteration, and one could learn from other users’ data by transmitting the gradient. However, according to member inference attack mentioned in [6], malicious users in the training might use the plaintext gradient to train a shadow model to compromise the data security of other users. Thus, we introduce homomorphic encryption against this attack, which allows one to perform calculations on encrypted data without decrypting it. In addition, the result of the homomorphic operation after decryption is equivalent to the operation on the plaintext data [7]. Since the operation is not able to identify the data being operated in the whole process of homomorphic operation, the security of privacy data can be guaranteed.
The multi-party privacy protected machine learning based on homomorphic encryption proposed in the paper has a wide range of scenarios in practical applications. In addition, the main contributions of the work are as follows:
- -
- It provides a multi-party privacy protected machine learning framework that combines homomorphic encryption and federated learning to achieve the protection of data and model security during model training. In addition, the proposed framework can maintain the privacy data security when multiple parties learn together.
- -
- It verifies that the model trained by our proposed algorithm has a similar accuracy rate as the model trained by traditional methods. From experiments on the MNIST and metal fatigue datasets, the accuracy deviation does not exceed 1%.
- -
- About the time overhead of homomorphic encryption, it analyzes the impact of different key lengths and network structures, and finds that, as the key length increases or the structure becomes more complicated, the time overhead increases. Trade-off between performance and security level should pay more attention.
The organization of the rest of the paper is as follows. The related work is summarized briefly in Section 2. In Section 3, the federated network algorithm and Paillier federated network algorithm are discussed in more detail from the point of security, interaction, and network structure. The experimental results are presented in Section 4 and Section 5 summarizes the whole paper.
2. Related Work
2.1. Distributed Machine Learning
Distributed machine learning is a kind of multi-node machine learning which was designed to improve the performance, increase the accuracy, and scale the data to a large amount easily. In NIPS 2013, a distributed machine learning framework was proposed [8]. It proposed a state synchronous parallel model to solve the problem of ordinary synchronization or to train in a massive data volume and massive model size. In 2015, Xing et al. proposed a general framework for solving the data and model parallel challenges systematically in large-scale machine learning [9]. Xie et al. proposed an effective factor broadcast (SFB) calculation model, which is effective and efficient in distributed learning of a large matrix parameterized model [10]. Wei et al. maximized the efficiency of network communication under a given network bandwidth among machines to minimize parallel errors while ensuring the theoretical fusion for large-scale data parallel machine learning applications [11]. Kim et al. proposed a distributed framework STRADS, which optimized the throughput for classical distributed machine learning algorithms [12].
In distributed deep learning, in 2012, Jeffrey et al. proposed Google’s first-generation deep learning system Disbelief, and split a model into 32 nodes for calculation [13]. In 2013, data and model parallelism in distributed machine learning were introduced into deep learning and implemented in the InfiniBand network [14]. In 2014, Seide et al. theoretically compared the efficiency of distributed SGD (stochastic gradient descent) training in model and data parallel, and pointed out that increasing the size of minibatch can improve the efficiency of data training [15,16].
2.2. Secure Multi-Party Computation and Homomorphic Encryption
Since distributed machine learning is based on a center dispatching tasks to the outside, and, in this case, data are transparent to the system, and data privacy cannot be protected effectively. Generally, distributed learning involves multi-party computing, which often gives the complicated or unknown computing process to a third party. In 1986, Yao proposed the Garbred Circuit method based on the millionaire problem, which can be used to solve general problems, including almost all two-party password problems [17]. In addition, then, in 1998, Goldreich proposed the concept of secure multi-party computation (SMPC) [18]. Thus far, SMPC is regarded as a subfield of cryptography that enables distributed parties to jointly compute an arbitrary functionality without revealing their won private inputs and outputs.
Currently, homomorphic encryption has become a commonly used method in SMPC. In 1978, Rivest et al. proposed the concept of homomorphic encryption for bank applications [19]. As one of the first public-key cryptosystems, the well known RSA (Rivest-Shamir-Adleman) has multiplicative homomorphism [20,21]. In 1999, the Paillier algorithm was invented [22]. Since Paillier satisfied the addition of homomorphism, it has been widely used in cloud ciphertext retrieval, digital auction, digital elections, and some other privacy protected applications. In 2009, Craig Gentry first proposed a fully homomorphic encryption (FHE) algorithm based on ideal lattices which satisfied both additive homomorphism and multiplicative homomorphism [23]. Since FHE has extremely high security, it has been widely used [24,25,26]. Especially in cloud computing, homomorphic encryption has made great contributions to privacy protection [27].
Besides that, differential privacy is also a privacy assurance technique used to prevent privacy leakage by adding noise to the samples [28,29,30]. Since introducing noise, when the amount of data is small, the influence of noise will inevitably affect the model training. How to reduce the influence is a big challenge.
2.3. Federated Learning
Concerning the data privacy protection and multi-party joint learning, a machine learning named federated learning was proposed by Google in 2016 [31]. As a multi-party cooperative machine learning, federated learning has gradually attracted much attention in research and industry [32,33]. At the beginning, the purpose of federated learning was to help the Android users to solve the problem of updating their models locally. Furthermore, federated learning can be applied in various fields of machine learning. In 2019, Google scientists mentioned that they built a scalable production system for joint learning in the field of mobile devices based on tensorflow [34]. In addition, in 2019, more related works have been proposed. Wang focused on the problem of learning model parameters when data distributed across multiple edge nodes, without sending raw data to a centralized node [35]. There is also some work focusing on federated transfer learning, such as the framework designed in [36], that can be flexibly applied to various secure multi-party machine learning. About performance, in [37], it proposed a framework SecureBoost with almost the same accuracy compared with the five privacy protection methods.
Federated learning has been widely used in various fields. For example, the Gboard system designed by Google realizes keyboard input prediction while protecting privacy and helping users improve input efficiency [38,39]. In the medical field, patients’ medical data are sensitive, thus federated learning is very useful [40,41]. Besides this, natural language processing [42] and recommendation systems [43] are also applicable for federated learning as well.
In addition, in recent years, there is a lot of work on privacy protection machine learning worthy of attention. Zhou et al. proposed using differential privacy to protect privacy in machine learning, and SMC was used to reduce the noise caused by differential privacy [44,45]. In 2020, Zhang et al. proposed a batchcrypt algorithm, which is based on the optimization of the FATE framework [46]. It encodes a batch of quantized gradients as a long integer, and then encrypts it at one time, which improves the efficiency of encryption and decryption by reducing the amount of calculation. Wei Ou et al. proposed a vertical federated learning system for Bayesian machine learning with homomorphic encryption, which can achieve 90% of the performance of a single union server training model [47].
3. Method and Algorithm
3.1. Multi-Sample Cooperative Learning Based on a Federated Idea
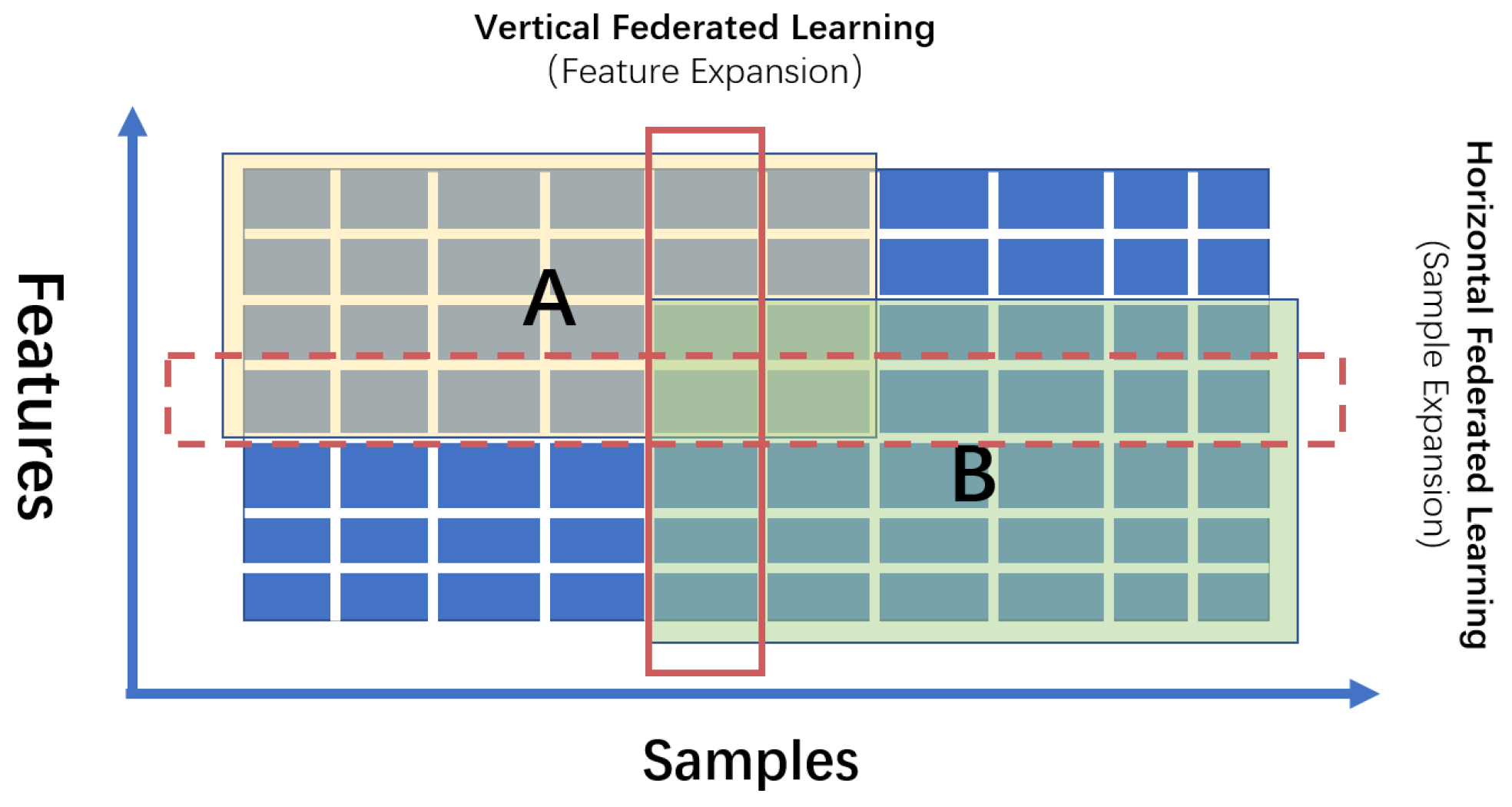
The idea of federated learning is that, in the case of data areolation, through the interactions of intermediate variables in the training process, one can use the information of other party’s data to optimize their own model, as shown in Figure 1. From the different data split, federated learning can be divided into two categories, horizontal federated learning (sample expansions), and vertical federated learning (feature expansions).
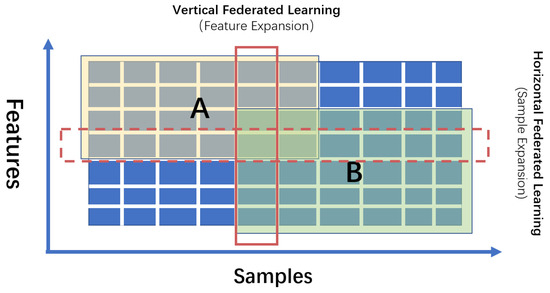
Figure 1.
Two different kinds of federated learning from sample or feature expansions. A is the data owner of yellow rectangle area, and B is the data owner of green rectangle area.
The idea of horizontal federated learning is machine learning with sample expansions. Supposing that D represents data, X represents features, Y represents samples, and I represents the data index. Horizontal federal learning can be represented as:
It indicates that different users have different data which may or may not have intersections. The main idea of horizontal federated learning is to help multiple users using their own data to jointly train a reliable model, while ensuring the privacy and security of data. However, for sample expansions, the data of all parties need to be aligned first to ensure that all parties involved in the training have the same feature domain. This helps all parties build the same model architecture and iterate synchronously. Similarly, for vertical federated learning, all the participants have samples with different features.
3.2. Federated Network Algorithm
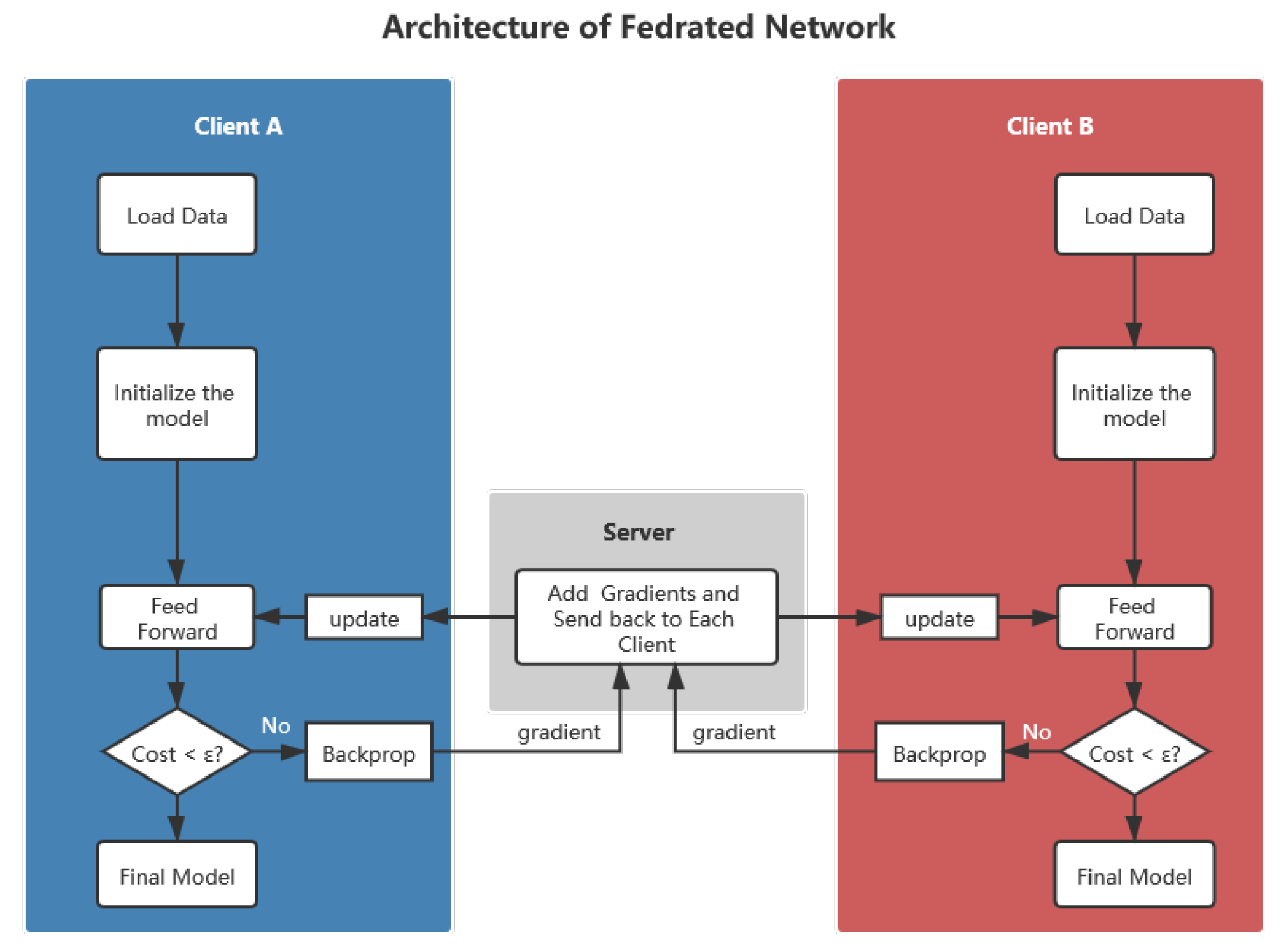
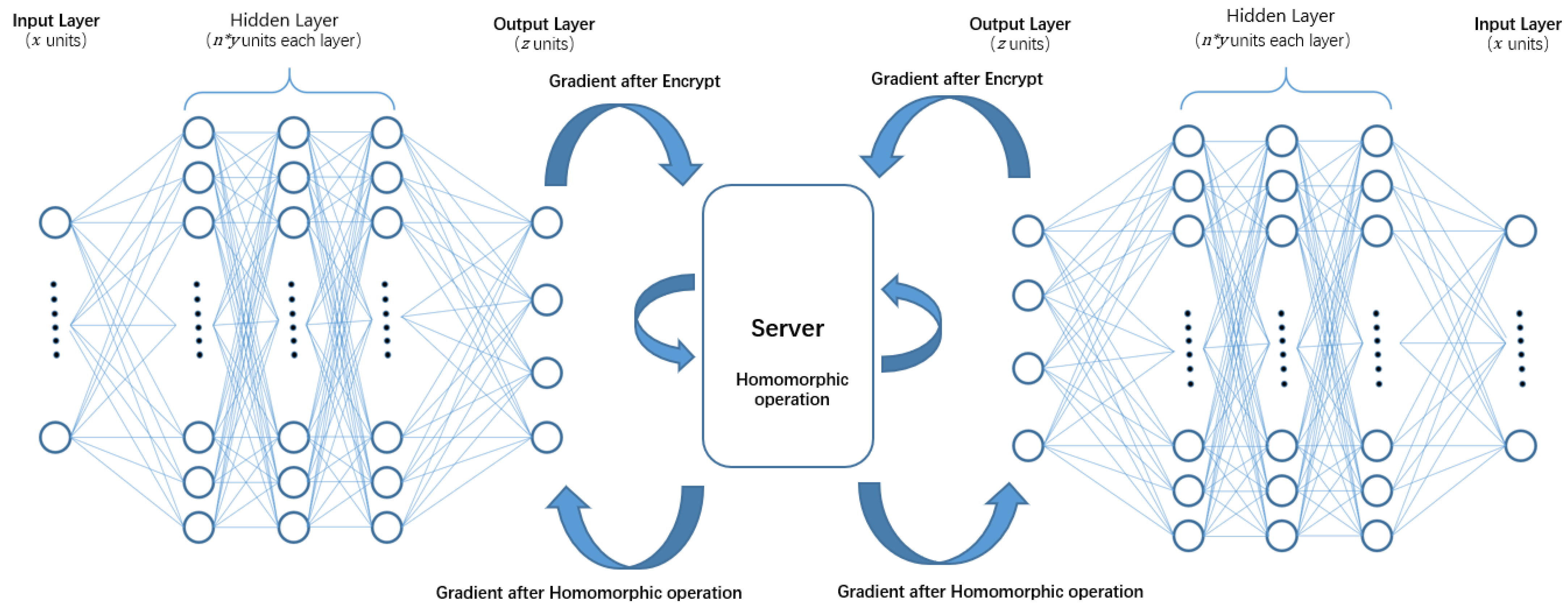
The main target of federated learning network proposed in this paper is to help all parties jointly train the same model by passing intermediate variables in the training process. Considering that most neural networks are trained by gradient descent, here, we choose gradients as its intermediate variables. Although the gradient cannot represent all the data directly, it can represent the relationship between the model and the data which facilitate model training. The architecture of federated learning network is shown in Figure 2, and it contains a computing server and several learning clients.
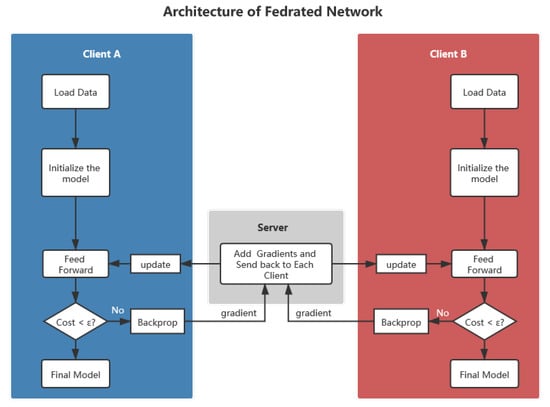
Figure 2.
The architecture of the federated neural network.
3.2.1. Learning Client
For learning clients, they have their own private data and, supposing all the data have been aligned, their quantitative dimensions with other learning participants. For the learning client, the main functions include initializing the same initial model with other clients, training data locally, extracting gradients during the training, computing the gradients with computing server, collecting server responses, passing the results, updating the model, and iterating repeatedly until the model converges.
3.2.2. Computing Server
The computing server is an intermediate platform in the learning process. The main functions are receiving the gradient information from multiple learning clients, performing calculations on the gradients, integrating the information learned by multiple models, and transmitting the result to each learning client separately.
3.3. Federated Multi-Layer Perceptron Algorithm
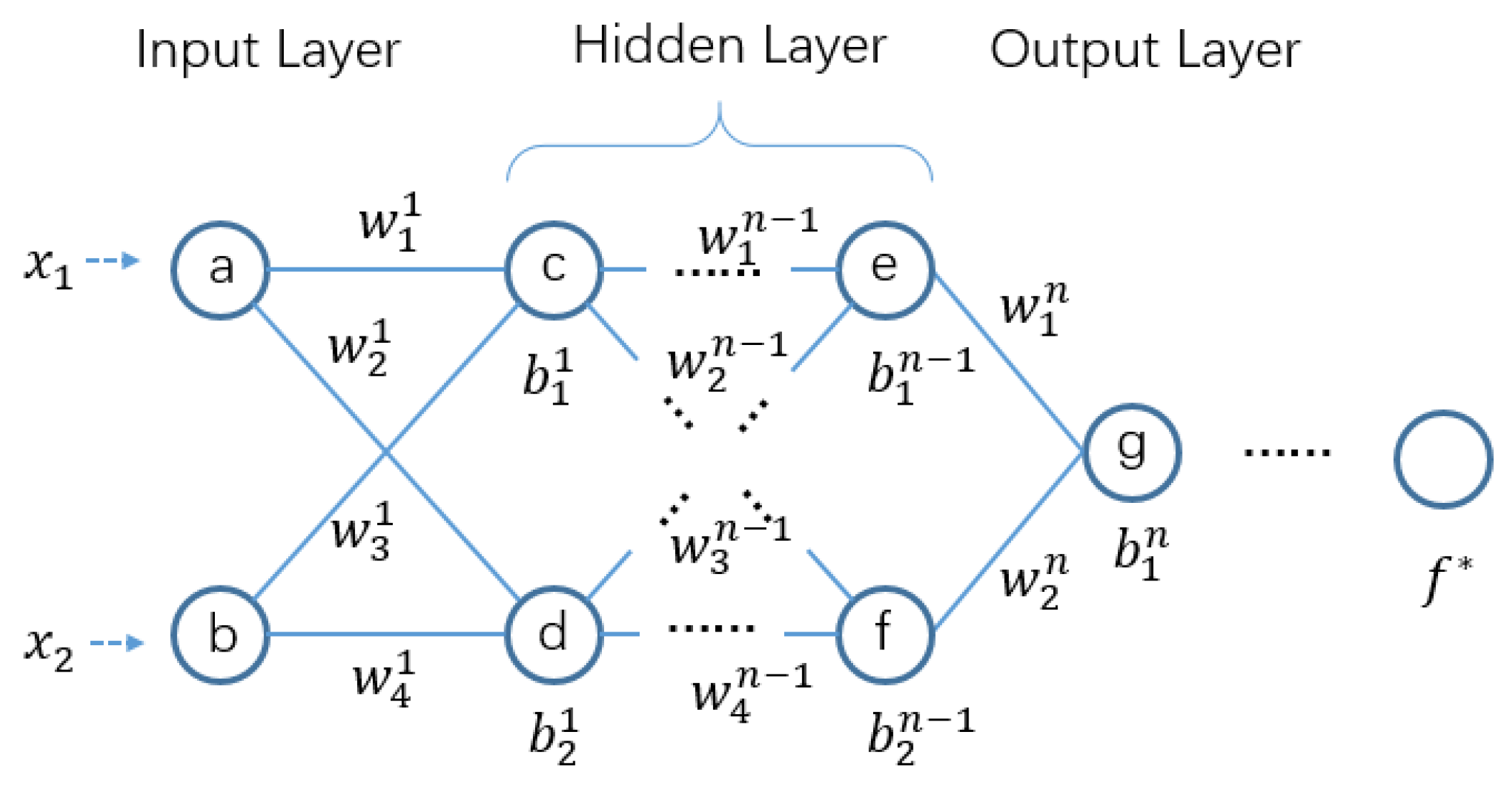
Here, we propose a federated multi-layer perceptron algorithm (FMLP) based on the traditional multi-layer perceptron. FMLP can train a simple model for each client in a multi-party data areolation environment through gradients’ sharing. The multi-layer perceptron, also known as a deep feed-forward network, is a typical deep learning model. An example of its architecture is shown in Figure 3.
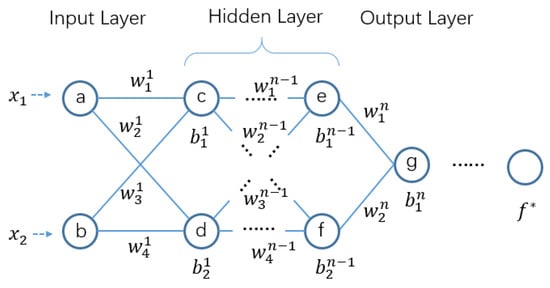
Figure 3.
Multi-layer perceptron model.
All the parameters and their meanings involved in the algorithm are shown in Table 1.

Table 1.
The parameters and descriptions in the PFMLP algorithm.
Supposing the parameter of the model is , the learning rate of training is . The data set can be represented as . The purpose of the model is to approximate a distribution . The forward process of the network is to calculate the output of the training that can be defined as:
The loss function that calculates the distance between the output and the ideal value can be defined as:
The function of the back-propagation is to calculate the gradients and propagate them from the loss function backwards to help the network adjust the parameters according to the gradient to reduce the error between the output value and the ideal one. The back-propagation process can be defined as:
The model-update process is to adjust the network parameters based on the gradient obtained by backpropagation, which can be expressed as:
Through the federated network realized by MLP, we can get a federated MLP (FMLP). Then, a copy of the MLP model is stored in the local memory of each learning client. It contains an input layer with x units, n hidden layers with y units each, and an output layer with z units. The size of x depends on the feature dimensions of the input data. In addition, the size of z depends on the required output of the network that is closely dependent on target output of the real applications.
The main function of the computing server is to fuse the gradient data, helping the model to accelerate the gradient descent while learning the data from each client. Before the model is updated, each learning client passes the gradients to the computing server for model training. In addition, then the computing server integrates all the gradient data from all clients, and returns the calculated new gradient to each client for model updates. Finally, when the loss of each client is less than , the model converges. In addition, then all the clients can get the same federated model. The specific steps of FMLP are shown in Algorithm 1.
| Algorithm 1 Federated Multi-Layer Perceptron |
|
3.4. Paillier Federated Network
The federated network proposed in this paper allows multiple parties to perform cooperative machine learning with isolated data. However, in practice, what the cracker actually needs is not only the data provided by the participants, but also the final model trained by multiple parties.
According to a member inference attack proposed by Shokri et al. in 2017, the cracker can invade the server and infer several shadow models from the data in the server. Based on the idea of ensemble learning, the cracker can finally get a prediction that is similar to the model trained by actual cooperation based on these shadow models. In other words, the federated model under this condition can only solve the data security problem, not the model security.
Therefore, for model security, homomorphic encryption can be introduced into the federated learning. In addition, the core idea of homomorphic encryption is, after encrypting plaintext a to ciphertext c, the result of performing some operations on c in the ciphertext space, which is equivalent to the result of encryption operations on a in plaintext space. The encryption operation can be expressed as:
In Equation (6), E represents an encryption algorithm, and a and b represent two different plain texts. ⊕ and ⊗ represent operators. If the operation is a multiplication operation, then the homomorphic encryption satisfies the multiplicative homomorphism, for instance, the RSA algorithm [20]. If the operation is an addition operation, the homomorphic encryption algorithm satisfies the additive homomorphism. The Paillier algorithm is the most famous one [22]. In addition, if the algorithm satisfies both additive and multiplicative homomorphism at the same time, then the encryption algorithm satisfies full homomorphism [23]. Since in MLP we need to sum the gradient data, the Paillier algorithm can thus be used to do homomorphic encryption.
3.4.1. Paillier Algorithm
As mentioned above, Paillier encryption is a partially homomorphic encryption satisfying additive homomorphism. It can be divided into three parts: key generation, encryption, and decryption.
Key generation: First of all, select two primes p and q that are sufficiently large and equal length that also satisfy . Then, calculate n and as:
An integer g is selected randomly and satisfies , so that n can divide the order of g. Then, define to calculate as:
Thus far, we can get the public key as and the private key as .
Encryption: Assuming the plaintext is m, and the ciphertext is c, the encryption process with the public key can be noted as:
Decryption: Accordingly, using a private key to decrypt the ciphertext c and the plaintext m is:
3.4.2. Improved Paillier Algorithm
However, due to the high complexity of the Paillier algorithm when doing encryption and decryption, it will affect the efficiency of network training. Therefore, we use an improved version of Paillier, and the correctness and efficiency of the optimization have been proved in detail in [48].
Key generation: Use as the divisor, if replaces the position of the in the private key. We can modify g in the public key and ensure that the order of g is .
Encryption: Assuming that the plaintext is m, the ciphertext is c, and r is a random positive integer, and satisfies that r is less than . The improved encryption process can be shown as:
Decryption: The Decryption process can be shown as:
It can be seen from the above algorithms that the biggest advantage of using instead of is in the decryption. The number of power operations has changed from times to times. Since is a divisor of , the time overhead has been significantly reduced. The computational complexity of Native Paillier is , and the computational complexity of improved Paillier is [49].
3.4.3. Architecture of the Paillier Federated Network
Here, we use Paillier encryption to protect the gradient data. Thus, even if crackers compromise the computing server, they cannot know the specific information of the gradient data from each learning client. In addition, it is impossible for crackers to use these encrypted gradient data to train shadow models.
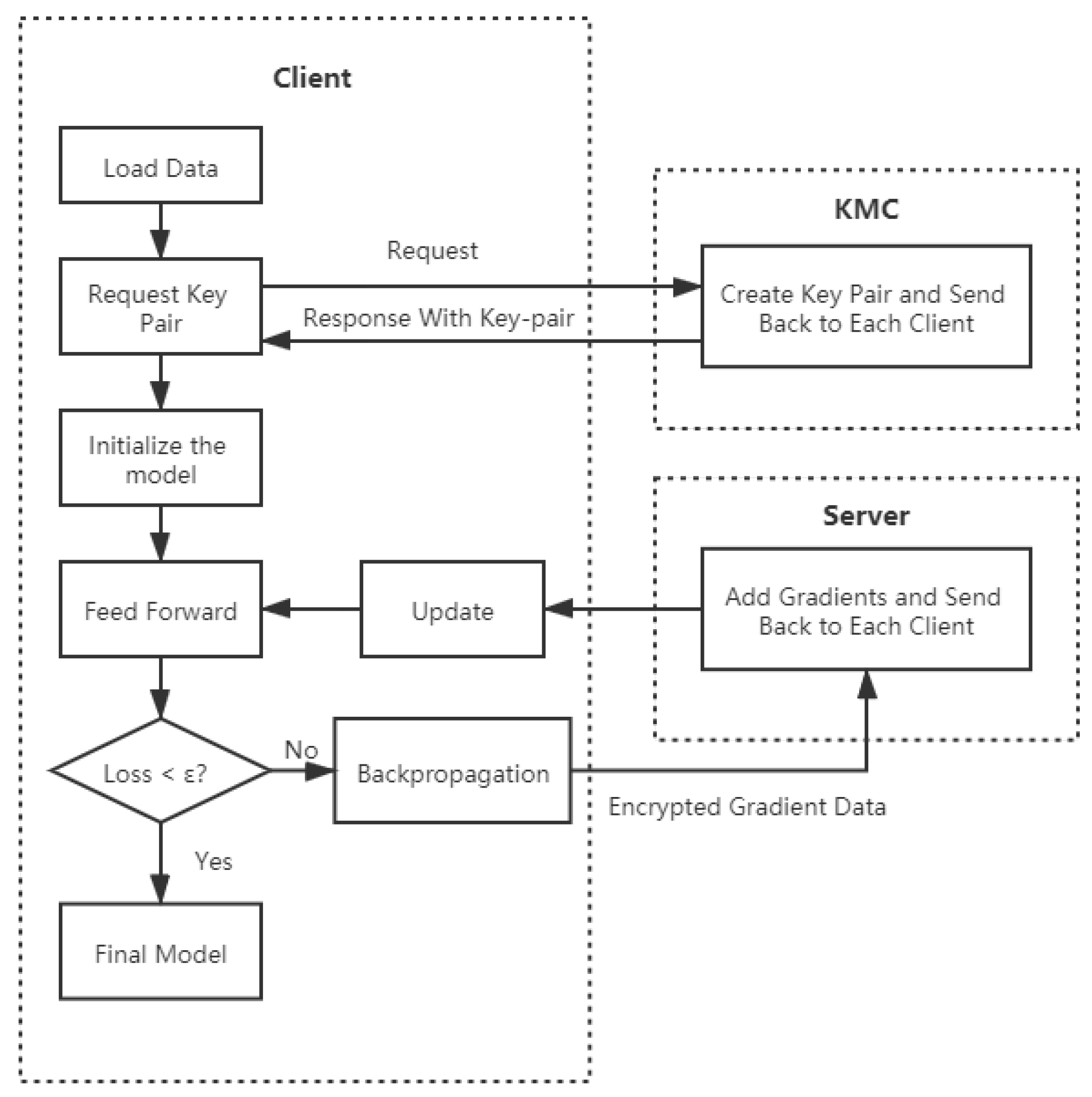
Since Paillier encryption requires key pairs, in order to generate and manage key pairs, we add a key management center (KMC) in the algorithm. The Paillier federated network is shown in Figure 4. It includes KMC, computing server, and several learning clients.
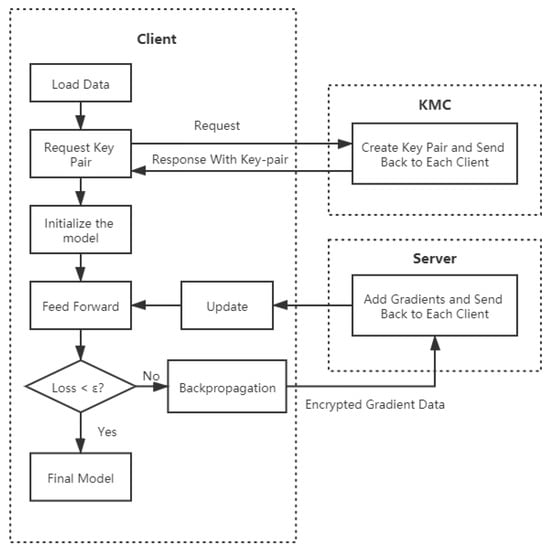
Figure 4.
The architecture of a Paillier federated network.
3.5. Paillier Federated Multi-Layer Perceptron (PFMLP)
The basic structure of PFMLP is quite similar to FMLP. Since PFMLP needs to interact with KMC, the learning client should send a request to the KMC before training starts. The KMC confirms that each participant is online, and then generates key pairs and returns them to learning clients. After getting the key pairs, each learning client performs multi-party machine learning based on encrypted data. The flow chart of PFMLP is shown in Figure 5.
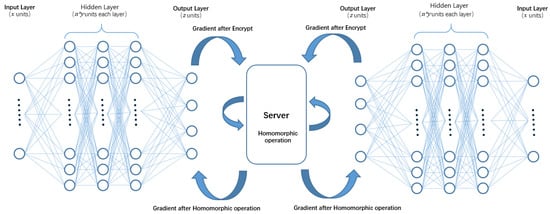
Figure 5.
The flow chart of the Paillier federated multi-layer perceptron algorithm.
Compared with FMLP, PFMLP adds another three parts: (1) Encryption and decryption operations in the learning clients; (2) Homomorphic operations in the computing server; and (3) Generation and distribution of key pairs in the key management center (KMC). In PFMLP, it contains learning clients, computing server, and KMC. The algorithm for learning clients is shown in Algorithm 2.
| Algorithm 2 PFMLP in the Learning Client |
|
The learning client does not immediately update the local model after calculating the gradient for each learning iteration. It homomorphically encrypts the gradient data and transmits it to the computing server, and then waits for the server to return the new encrypted gradient data after doing homomorphic operation. For the decryption phase, once the client decrypts the new encrypted gradient data, it can update the local model of each learning client with the new gradient. Thus, the new gradient contains other client’s private data implicitly, in order to protect the data privacy indirectly.
Since PFMLP performs Paillier encryption on the gradient data, even if the computing server is compromised by a cracker, the leaked data only show the encrypted gradient data . Thus, the threat of inference attacks can be avoided.
The algorithm for KMC is shown in Algorithm 3. In addition, its main functions are generating and distributing key pairs. That is, when it receives a request from a learning client, it generates a key pair and distributes it to the client.
| Algorithm 3 PFMLP in KMC |
|
For the computing server, it performs homomorphic operations on the encrypted gradient data provided by each learning client. In addition, when the computing server receives a request from a client, it performs homomorphic operations on the encrypted data and returns the results to the client. The PFMLP algorithm for computing server is shown in Algorithm 4. Since the computing server does not obtain the key throughout the whole process, all of these guarantee the data privacy during the model training.
| Algorithm 4 PFMLP in the Computing Server |
|
3.6. Algorithm Security Analysis
In PFMLP, the key management center is only responsible for key generation and can not access any data. For the key management center, it does not even know what data the client has encrypted with the key, so it cannot collude with other parties to access the data illegally.
The data received by the computing server is the ciphertext encrypted by the client, and all operations are homomorphic operation without a decryption process. It means that, on the computing server, all data are in the encrypted format, so, even if the server is compromised, the plaintext data cannot be obtained.
The learning client obtains the key pair from the key management center, and then sends the encrypted gradient data to the computing server; after that, the computing server returns the result that is still in the encrypted format to the client after the calculation is completed. During the whole process, the client cannot access the data of other clients. The only data participated in the process is the data uploaded and the result returned, and they are all in the encrypted format, which can ensure data security.
If an attacker wants to obtain data by attacking the computing server or a communication channel, he/she can only get the ciphertext. Since we can change the key pair during each iteration, even if the attacker is lucky enough to crack a few rounds of training results, he/she cannot obtain the final result. Even if the attacker is a participant, he/she cannot obtain data from other clients due to the client security analysis described above.
4. Experiments and Results Analysis
4.1. Experimental Datasets and Environment
Two datasets are used for verifications: MNIST and Metal fatigue strength data. For the MNIST handwritten dataset [50], it contains 60,000 training samples and 10,000 testing samples. In addition, the neural network model consists of 784 input layers, two hidden layers with a default number of 64 units, and an output layer with 10 output units.
About metal fatigue data, it only has 437 records coming from the NIMS MatNavi open dataset [51]. MatNavi is one of the world’s largest materials databases, including polymers, ceramics, alloys, superconducting materials, composites, and diffusion databases. Here, we select 437 pieces of metal fatigue strength data from MatNavi to build a regression model to test different metals, like carbon steel, low alloy steel, carburizing steel, and spring steel, under different testing conditions, such as different components, rolled product characteristics, and subsequent heat treatment. Each piece of metal fatigue data contains 15-dimensional features and 1-dimensional labels. According to the fatigue dataset, we divide it into four categories as shown in Table 2. The model structure used in the experiment includes one input layer with 15 units (15 dimensions), three hidden layers with 64 units, and one output layer with four units. The network structure of PFMLP is shown in Table 3.

Table 2.
Fatigue dataset for multi-classification tasks.

Table 3.
The network structure of PFMLP.
Here, the represents the data of the . In order to evaluate the PFMLP algorithm and its optimization methods, several comparative experiments were designed from three perspectives: (1) the prediction accuracy of the federated multi-layer perceptron and the single-node multi-layer perceptron; (2) the time consumption of the model training using different key length; (3) the time consumption of the model training with different sizes of hidden layer units; and (4) the impact of different numbers of learning clients on model performance.
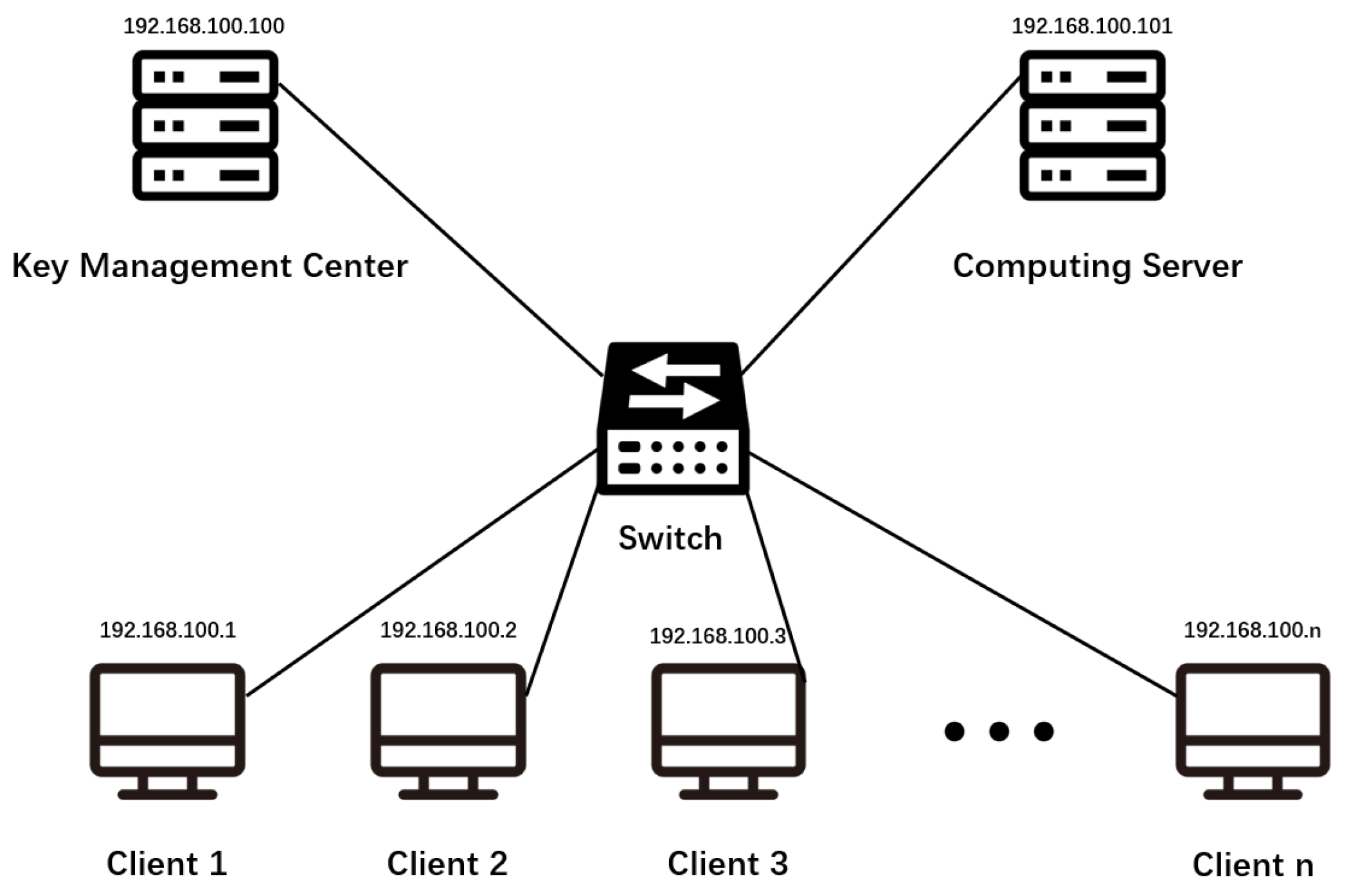
The experimental environment is in Windows 10, Python 3.6 with scikit-learn 0.21.3 and phe 1.4.0. We deployed a computing server, a KMC, and multiple clients in the local area network, and established communication between machines through the Socket. The specific network deployment is shown in Figure 6.
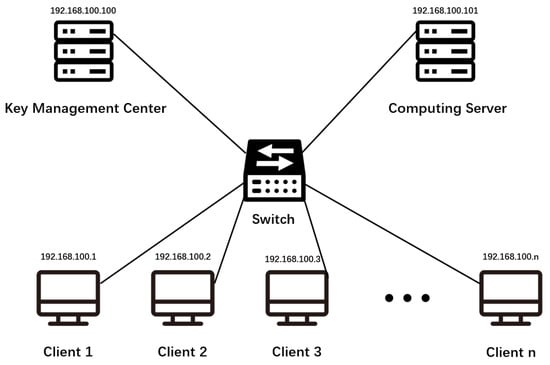
Figure 6.
The network deployment in the experimental environment.
4.2. Accuracy Comparison
For comparison, the PFMLP and MLP algorithms use the same network structure for model training while learning the same dataset. Supposing that there are two learning clients, we split each dataset into two subsets and distribute them to two learning clients.
For the MNIST dataset, we select the first 4000 data as the train-set , and then divide the 4000 pieces of data into two parts, respectively: , . The testing data use 10,000 testing sets provided by MNIST.
Meanwhile, we select 400 pieces of data from the metal fatigue strength dataset, and divide them into two equal subsets for model training. Supposing that the original data are , randomize the original data noted as . The two sub-datasets are , . In addition, then we use 70% as the training set and the remaining 30% as the testing set. In addition, the experimental result is shown in Table 4.

Table 4.
Comparison results of prediction accuracy of MLP and PFMLP on two datasets.
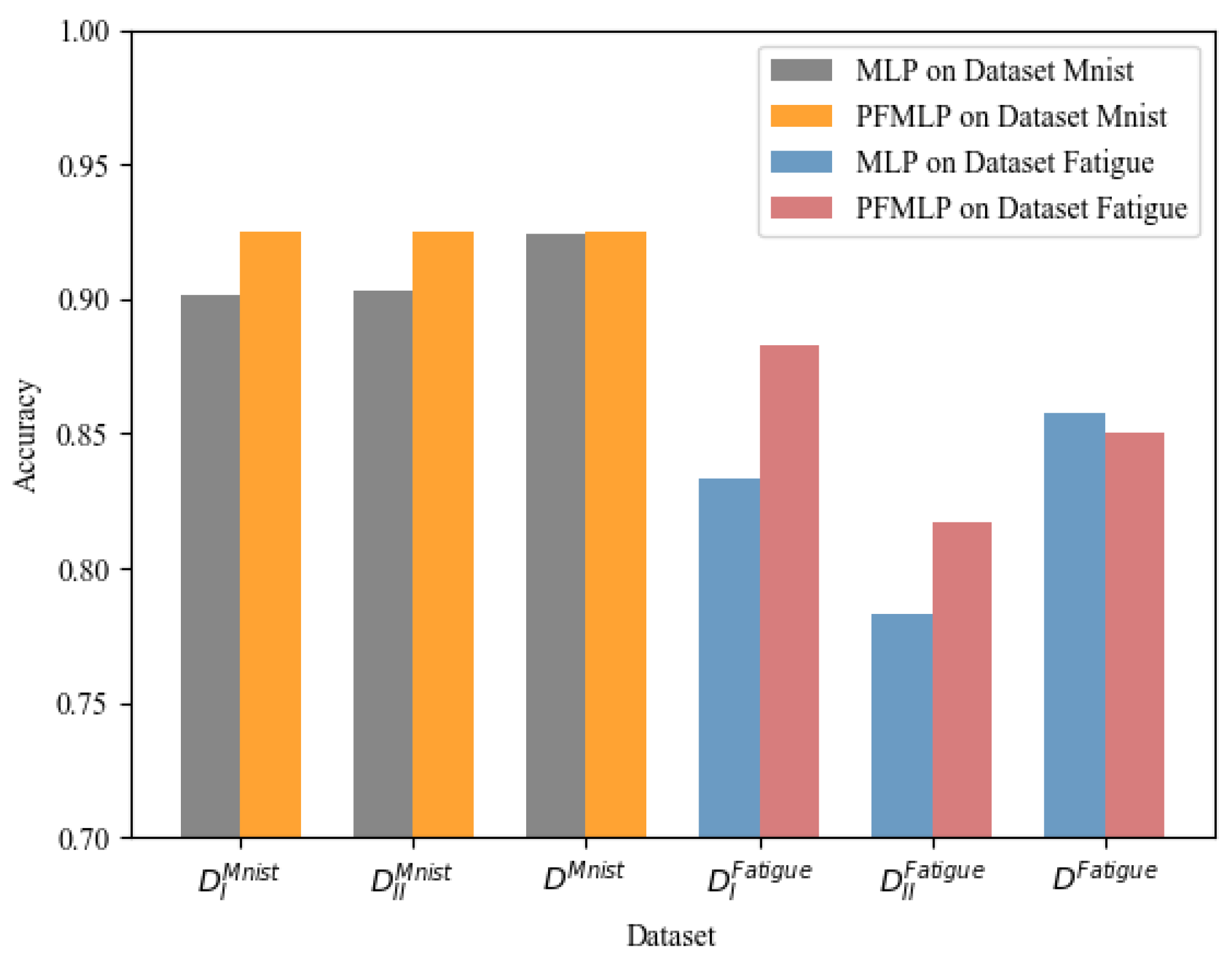
From Table 4, it shows that the model trained by PFMLP is more accurate than that of local MLP. The final model trained by PFMLP is almost equivalent to or even better than that of the model trained by MLP using all data from each client.
The experiments on the MNIST dataset show that the model trained by PFMLP can reach an accuracy rate of 0.9252 on the testing set, while the model trained by MLP using all of the data of training set can reach an accuracy rate of 0.9245, just 0.007 lower than that of the PFMLP algorithm.
For the metal fatigue strength dataset, since models on each client learned from the same PFMLP, we can perform a weighted average of the results of the two experiments based on the amount of the testing set, and get a final prediction accuracy rate of 0.85. Compared with the MLP model with an accuracy rate of 0.858 after learning all the data, the accuracy rate has only decreased by 0.008.
Therefore, from the experimental results on two datasets, it shows that the PFMLP algorithm can train a model with almost the same accuracy rate as the MLP on all data from multiple parties. Detailed results are shown in Figure 7.
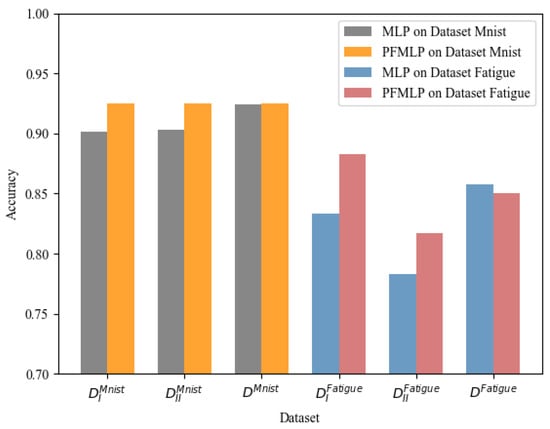
Figure 7.
Prediction accuracy between MLP and PFMLP.
4.3. Comparison of Model Training Time for Different Key Lengths
Due to the threat of membership inference attacks, transmitting gradient data in plain text may be exploited by a malicious user to train his own shadow models. The privacy related data security of other clients will be violated. Here, we use Paillier homomorphic encryption in PFMLP. In addition, the encryption is operated during the gradient data transmission, and homomorphic operations are performed in the computing server to ensure that the encrypted gradient data will not be leaked, even if the server has security vulnerabilities.
In Paillier, the key length is an important factor that affects the security level. Generally, the longer the key length, the higher the security level. However, using a long key, the time overhead for generating the ciphertext also increases. For the MNIST and metal fatigue dataset, three comparison experiments are conducted. In addition, the model structure is fixed, and different key lengths are the core factors of time cost of model training. Table 5 shows the details.

Table 5.
Impact of different key lengths on total training time.
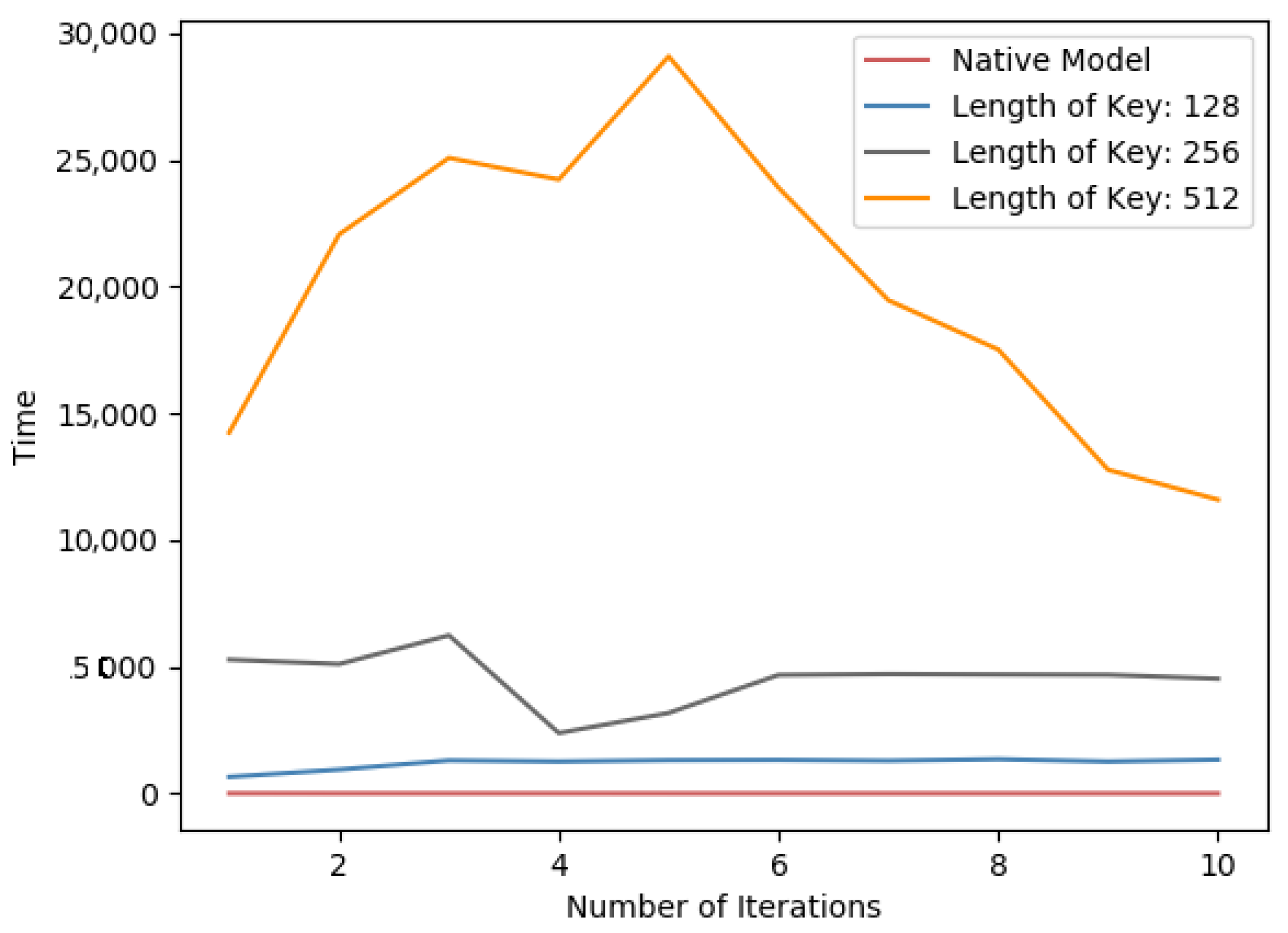
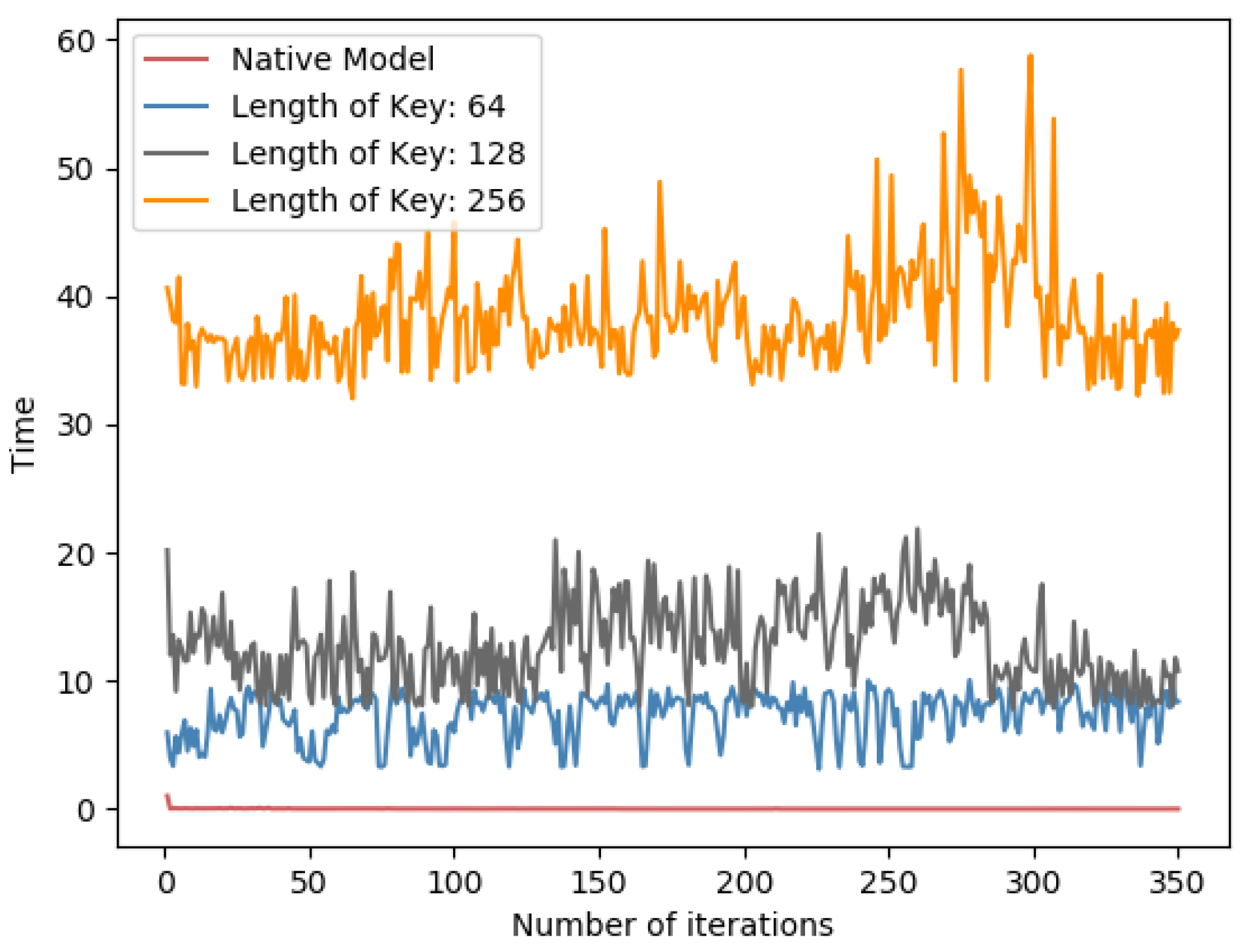
From Table 5 in both datasets, the impact of Paillier key length is proportional to the time consumption. Meanwhile, as in Figure 8 and Figure 9, it is a line chart of the training time for each round of learning for PFMLP on two datasets. Since in each round, it requires the encryption and decryption of gradient data, and the encrypted gradient is transmitted to the computing server for further operation, it is reasonable that, as the key length increases, the time overhead of each round of training increases. Thus, we can choose an appropriate key length that is a trade-off between security level and time performance. In addition, in order to upgrade the security level, we can update the key in each round of training. In this way, even if a certain round of keys is cracked, it will not affect the security of the overall training process to achieve the higher level of data security.
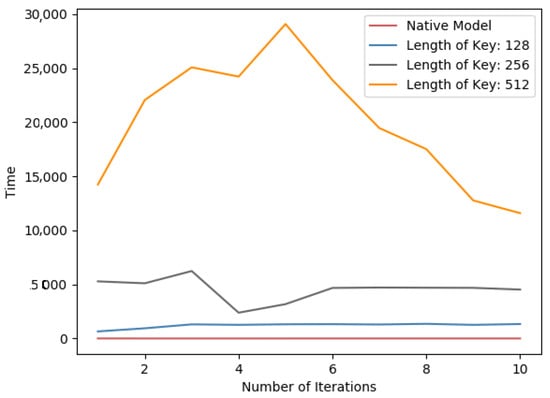
Figure 8.
Per-iterations time spent on the MNIST dataset for different key lengths.
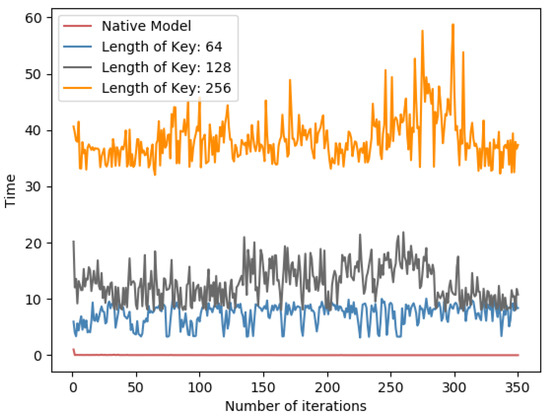
Figure 9.
Per-iterations time spent for different key lengths on the fatigue dataset.
From the above experiment, it shows that, under the same model and the same key length, 4000 pieces of data take 358.14 s per iteration, 8000 data 733.69 s, and 12,000 data 1284.06 s. Thus, it says that the time overhead is positively related to the amount of encrypted data.
We use the Improved Paillier algorithm to conduct experiments on the MNIST dataset, and compare the time costs of encryption and decryption with the same gradient data in the same round of iterations, as shown in Table 6.

Table 6.
The impact of different key lengths on the iteration time of each round.
From Table 6, it shows that, comparing with the Native Paillier algorithm, the improved Paillier has significantly improved the performance of encryption and decryption by nearly 25–28%.
4.4. Comparison of Training Performance with Different Sizes of Hidden Layers
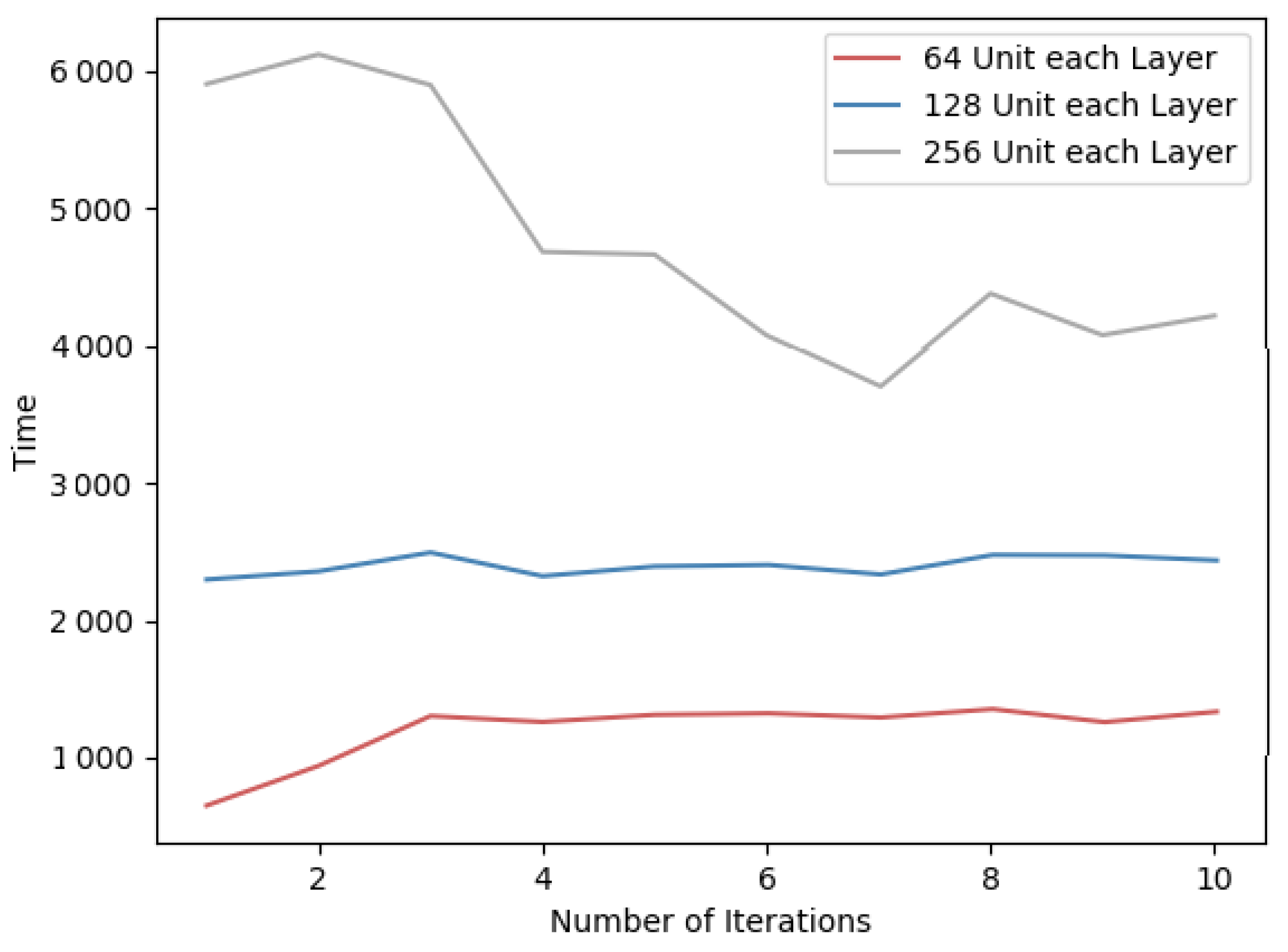
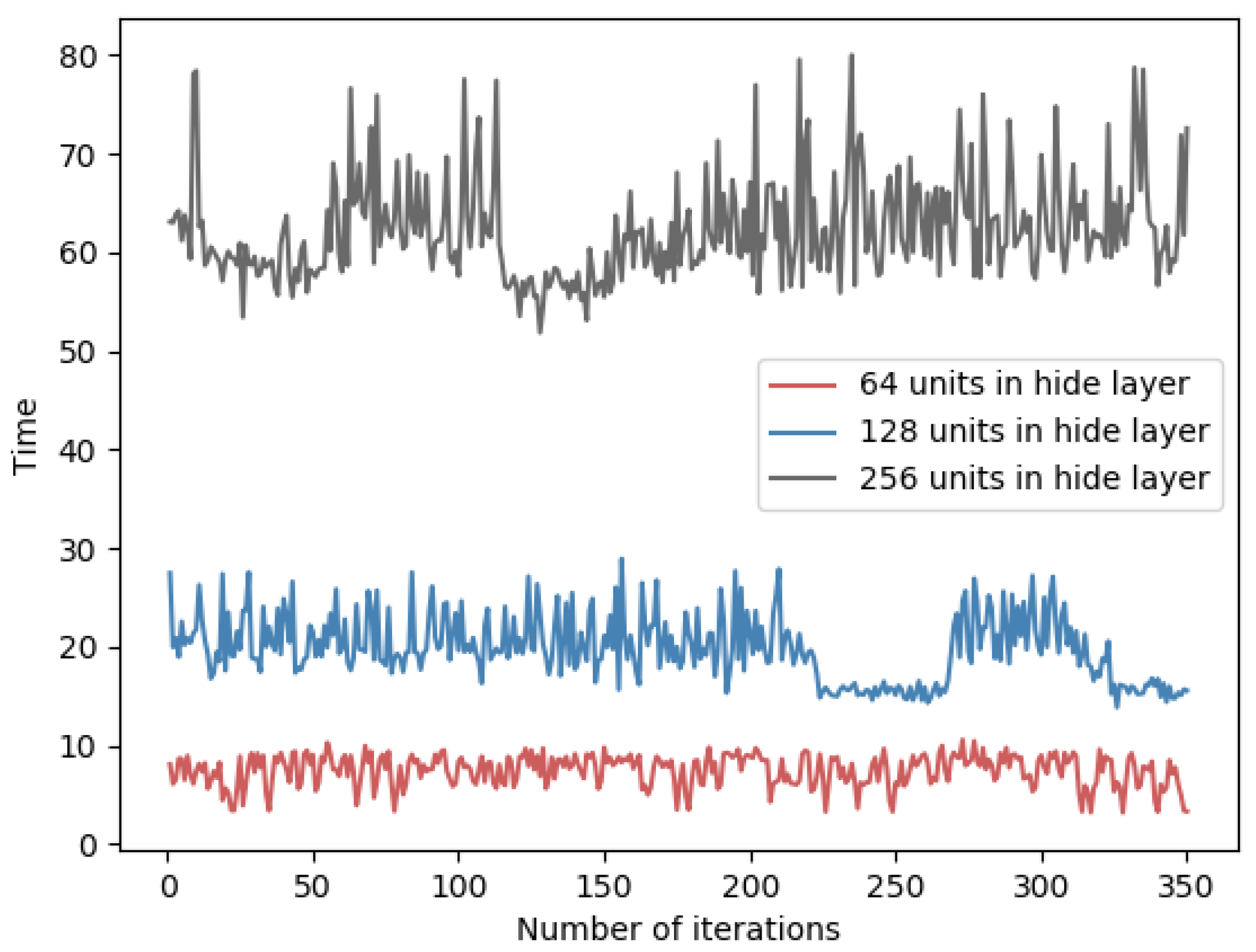
For neural networks, the size of each layer will affect the time performance of forward and backward propagation. In general, it shows a positive correlation between the network size and the training time. Here, we design several comparative experiments on two datasets, and the results are shown in Table 7. Specifically, the time overhead of each round of training is indicated in Figure 10 and Figure 11.

Table 7.
Impact of different hidden layer sizes on total training time.
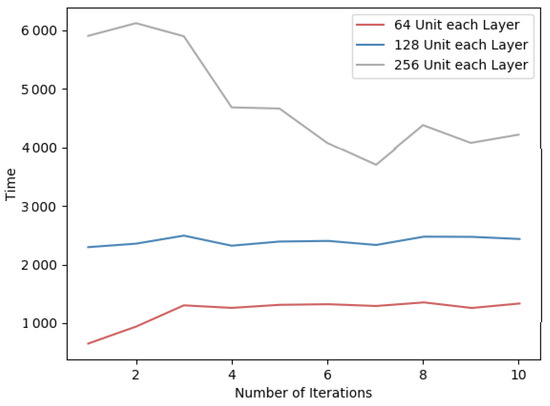
Figure 10.
Per-iteration time spent on the MNIST dataset for different sizes of hidden layers.
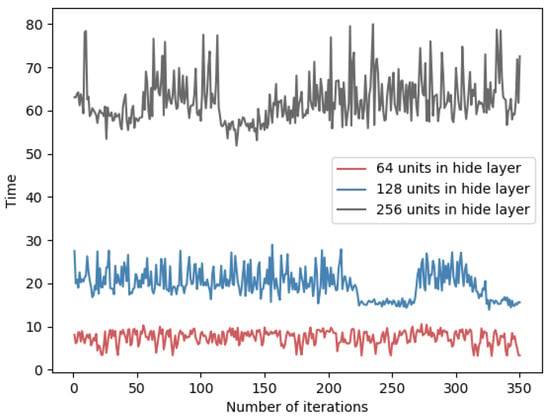
Figure 11.
Per-iteration time spent on fatigue dataset for different sizes of hidden layers.
Therefore, since the algorithm requires encryption for the gradient matrix and more hidden layer units, the time overhead will increase proportionally. In addition, as the number of units in the hidden layer increases, the amount of data to be transmitted in the network also increases. In order to reduce the time overhead of the PFMLP algorithm, under the premise of ensuring the accuracy, the number of hidden layers and each hidden layer units should be reduced as much as possible.
4.5. Different Numbers of Learning Clients on Training Accuracy and Time Overhead
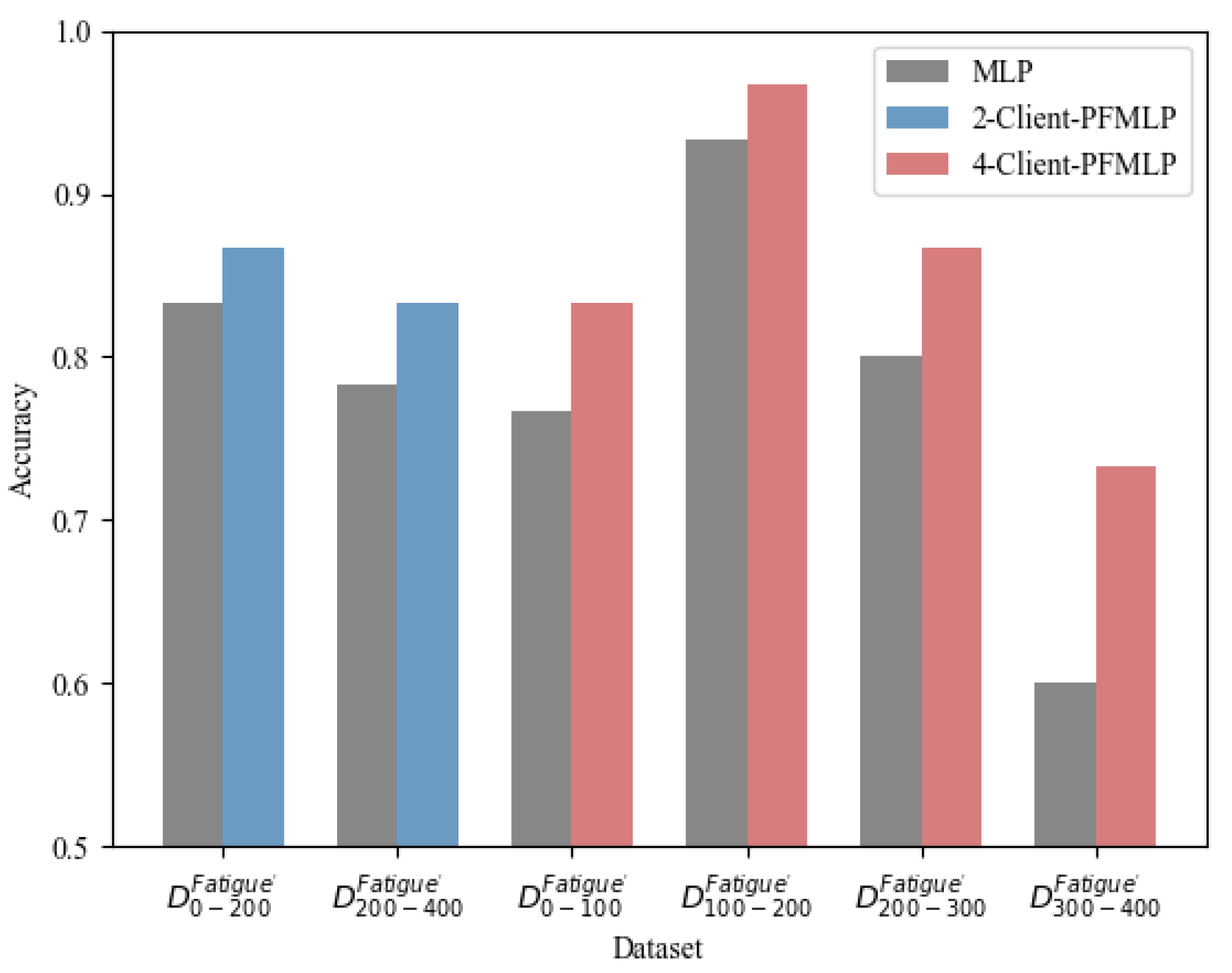
PFMLP can support multi-party machine learning. In addition, theoretically, as the number of clients increases, the learning algorithm should guarantee similar accuracy and even shorter time overhead during model training. Here, we design a comparative experiment with single node (MLP), two clients (2-Client-PFMLP) and four clients (4-Client-PFMLP) on the metal fatigue strength dataset. In addition, the experimental results are shown in Table 8. Here, the local accuracy is the accuracy rate of the model’s prediction accuracy on the local test data set. The logical accuracy is the average accuracy on each client. The detailed results are shown in Figure 12.

Table 8.
The accuracy of PFMLP with different learning clients on the metal fatigue dataset.
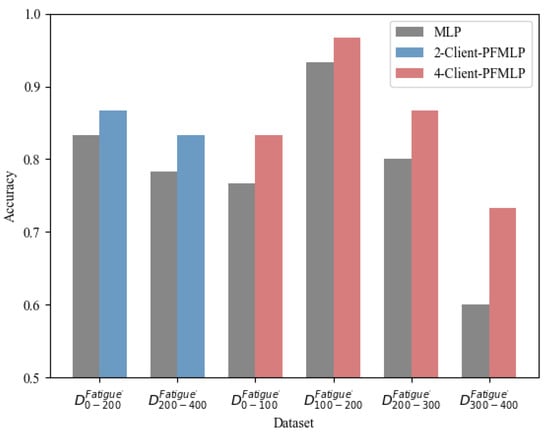
Figure 12.
Accuracy comparisons among single-node MLP, 2-client and 4-client PFMLP on the fatigue dataset.
From Figure 12, the multi-client-PFMLP algorithm has significantly improved the prediction accuracy. The logical accuracy rate is almost the same for two and four learning clients. Compared with the local training of the divided data, the local accuracy of PFMLP training has been improved. Especially in extreme cases, the accuracy is amplified. For example, in a 4-Client-PFMLP experiment, the last learning client obviously has outlier data, and the accuracy of PFMLP is higher than that of MLP. The second learning client has a local accuracy rate up to 93.3%, and using PFMLP still improves by 3.4%.
In addition, it can be seen from Table 8 that the number of clients has almost no effect on the performance of the model trained by PFMLP. They are all close to the performance of the model trained by a single MLP that collects data from all participants. Meanwhile, since the core idea of N-Client-PFMLP is based on batch expansion, once each client has less data, they will learn a smaller size of batch per round. Thus, the time overhead of the training process will be reduced.
5. Conclusions and Future Work
Multi-party privacy protected machine learning proposed in this paper can help multiple users to perform machine learning without leaking their own private data due to the integration of homomorphic encryption and federated learning. Especially in privacy data protection, the algorithm can train common models in the case of data areolation. Experiments of the PFMLP algorithm show that the model trained by PFMLP has a similar effect as the model trained using all data on a single machine. All parties just transmit the gradient data and gradient fusion is performed by homomorphic operations in the central computing sever. The learning model is updated based on the new gradient data after homomorphic operations. However, homomorphic encryption will inevitably cause some performance problems, such as the additional overhead of the encryption and decryption process which will greatly affect the training efficiency. In addition, the network structure, encryption/decryption key length, and key replacement frequency, etc. also affect the final performance.
About the future work, firstly, more powerful and scalable federated learning should be considered, like vertical federated learning algorithms splitting the features into different clients. Secondly, highly efficient homomorphic encryption algorithms will accelerate the learning performance. Finally, a more robust privacy protected learning algorithm should be given more attention, including those hybrid algorithms, anti-malicious attack clients algorithms, etc.
Author Contributions
Conceptualization, H.F. and Q.Q.; methodology, H.F. and Q.Q.; software, H.F.; validation, H.F.; formal analysis, H.F. and Q.Q.; investigation, H.F. and Q.Q.; data curation, H.F.; writing—original draft preparation, H.F.; writing—review and editing, Q.Q.; visualization, H.F.; supervision, Q.Q.; project administration, Q.Q.; funding acquisition, Q.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the “National Key Research and Development Program of China, Grant No. 2018YFB0704400” and the “Key Program of Science and Technology of Yunnan Province, Grant No. 202002AB080001-2”.
Data Availability Statement
Data that support the findings of this study is available from the corresponding author upon reasonable request.
Acknowledgments
This work is partially sponsored by the National Key Research and Development Program of China (2018YFB0704400), Key Program of Science and Technology of Yunnan Province (202002AB080001-2), Research and Development Program in Key Areas of Guangdong Province (2018B010113001). The authors gratefully appreciate the anonymous reviewers for their valuable comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bonawitz, K.; Ivanov, V.; Kreuter, B.; Marcedone, A.; McMahan, H.B.; Patel, S.; Ramage, D.; Segal, A.; Seth, K. Practical secure aggregation for privacy-preserving machine learning. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, Dallas, TX, USA, 30 October–3 November 2017; pp. 1175–1191. [Google Scholar]
- Giacomelli, I.; Jha, S.; Joye, M.; Page, C.D.; Yoon, K. Privacy-preserving ridge regression with only linearly-homomorphic encryption. In International Conference on Applied Cryptography and Network Security; Springer: Berlin/Heidelberg, Germany, 2018; pp. 243–261. [Google Scholar]
- Hall, R.; Fienberg, S.E.; Nardi, Y. Secure multiple linear regression based on homomorphic encryption. J. Off. Stat. 2011, 27, 669. [Google Scholar]
- Konečný, J.; McMahan, H.B.; Yu, F.X.; Richtárik, P.; Suresh, A.T.; Bacon, D. Federated learning: Strategies for improving communication efficiency. arXiv 2016, arXiv:1610.05492. [Google Scholar]
- Yang, Q.; Liu, Y.; Chen, T.; Tong, Y. Federated machine learning: Concept and applications. ACM Trans. Intell. Syst. Technol. (TIST) 2019, 10, 1–19. [Google Scholar] [CrossRef]
- Shokri, R.; Stronati, M.; Song, C.; Shmatikov, V. Membership inference attacks against machine learning models. In Proceedings of the 2017 IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 22–26 May 2017; pp. 3–18. [Google Scholar]
- Yi, X.; Paulet, R.; Bertino, E. Homomorphic encryption. In Homomorphic Encryption and Applications; Springer: Berlin/Heidelberg, Germany, 2014; pp. 27–46. [Google Scholar]
- Ho, Q.; Cipar, J.; Cui, H.; Lee, S.; Kim, J.K.; Gibbons, P.B.; Gibson, G.A.; Ganger, G.; Xing, E.P. More effective distributed ml via a stale synchronous parallel parameter server. Adv. Neural Inf. Process. Syst. 2013, 2013, 1223–1231. [Google Scholar] [PubMed]
- Xing, E.P.; Ho, Q.; Dai, W.; Kim, J.K.; Wei, J.; Lee, S.; Zheng, X.; Xie, P.; Kumar, A.; Yu, Y. Petuum: A new platform for distributed machine learning on big data. IEEE Trans. Big Data 2015, 1, 49–67. [Google Scholar] [CrossRef] [Green Version]
- Xie, P.; Kim, J.K.; Zhou, Y.; Ho, Q.; Kumar, A.; Yu, Y.; Xing, E. Distributed machine learning via sufficient factor broadcasting. arXiv 2015, arXiv:1511.08486. [Google Scholar]
- Wei, J.; Dai, W.; Qiao, A.; Ho, Q.; Cui, H.; Ganger, G.R.; Gibbons, P.B.; Gibson, G.A.; Xing, E.P. Managed communication and consistency for fast data-parallel iterative analytics. In Proceedings of the Sixth ACM Symposium on Cloud Computing, Kohala Coast, HI, USA, 27–29 August 2015; pp. 381–394.
- Kim, J.K.; Ho, Q.; Lee, S.; Zheng, X.; Dai, W.; Gibson, G.A.; Xing, E.P. Strads: A distributed framework for scheduled model parallel machine learning. In Proceedings of the Eleventh European Conference on Computer Systems, London, UK, 18–21 April 2016; pp. 1–16. [Google Scholar]
- Dean, J.; Corrado, G.; Monga, R.; Chen, K.; Devin, M.; Mao, M.; Ranzato, M.; Senior, A.; Tucker, P.; Yang, K.; et al. Large scale distributed deep networks. In Proceedings of the 25th International Conference on Neural Information Processing Systems, Siem Reap, Cambodia, 13–16 December 2012; pp. 1223–1231. [Google Scholar]
- Coates, A.; Huval, B.; Wang, T.; Wu, D.; Catanzaro, B.; Andrew, N. Deep learning with cots hpc systems. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. 1337–1345. [Google Scholar]
- Seide, F.; Fu, H.; Droppo, J.; Li, G.; Yu, D. On parallelizability of stochastic gradient descent for speech dnns. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 235–239. [Google Scholar]
- Watcharapichat, P.; Morales, V.L.; Fernandez, R.C.; Pietzuch, P. Ako: Decentralised deep learning with partial gradient exchange. In Proceedings of the Seventh ACM Symposium on Cloud Computing, Santa Clara, CA, USA, 5–7 October 2016; pp. 84–97. [Google Scholar]
- Yao, A.C.-C. How to generate and exchange secrets. In Proceedings of the 27th Annual Symposium on Foundations of Computer Science (sfcs 1986), Toronto, ON, Canada, 27–29 October 1986; pp. 162–167. [Google Scholar]
- Goldreich, O. Secure Multi-Party Computation; Manuscript. Preliminary Version; CiteSeerX: University Park, PA, USA, 1998; Volume 78. [Google Scholar]
- Rivest, R.L.; Adleman, L.; Dertouzos, M.L. On data banks and privacy homomorphisms. Found. Secur. Comput. 1978, 4, 169–180. [Google Scholar]
- Calderbank, M. The Rsa Cryptosystem: History, Algorithm, Primes; Fundamental Concepts of Encryption; University of Chicago: Chicago, IL, USA, 2007. [Google Scholar]
- Somani, U.; Lakhani, K.; Mundra, M. Implementing digital signature with rsa encryption algorithm to enhance the data security of cloud in cloud computing. In Proceedings of the 2010 First International Conference On Parallel, Distributed and Grid Computing (PDGC 2010), Solan, India, 28–30 October 2010; pp. 211–216. [Google Scholar]
- Paillier, P. Public-key cryptosystems based on composite degree residuosity classes. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Prague, Czech Republic, 14–18 May 1999; pp. 223–238. [Google Scholar]
- Gentry, C. Fully homomorphic encryption using ideal lattices. In Proceedings of the Forty-First Annual ACM Symposium on Theory of Computing, Washington, DC, USA, 31 May–2 June 2009; pp. 169–178. [Google Scholar]
- Dijk, M.V.; Gentry, C.; Halevi, S.; Vaikuntanathan, V. Fully homomorphic encryption over the integers. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Monaco and Nice, France, 30 May–3 June 2010; pp. 24–43. [Google Scholar]
- Ibtihal, M.; Hassan, N. Homomorphic encryption as a service for outsourced images in mobile cloud computing environment. In Cryptography: Breakthroughs in Research and Practice; IGI Global: Hershey, PA, USA, 2020; pp. 316–330. [Google Scholar]
- Makkaoui, K.E.; Ezzati, A.; Beni-Hssane, A.; Ouhmad, S. Fast cloud–paillier homomorphic schemes for protecting confidentiality of sensitive data in cloud computing. J. Ambient. Intell. Humaniz. Comput. 2020, 11, 2205–2214. [Google Scholar] [CrossRef]
- Çatak, F.; Mustacoglu, A.F. Cpp-elm: Cryptographically privacy-preserving extreme learning machine for cloud systems. Int. J. Comput. Intell. Syst. 2018, 11, 33–44. [Google Scholar] [CrossRef] [Green Version]
- Abadi, M.; Chu, A.; Goodfellow, I.; McMahan, H.; Mironov, I.; Talwar, K.; Zhang, L. Deep learning with differential privacy. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016; pp. 308–318. [Google Scholar]
- Dwork, C.; Roth, A. The algorithmic foundations of differential privacy. Found. Trends Theor. Comput. Sci. 2014, 9, 211–407. [Google Scholar] [CrossRef]
- Zhu, T.; Ye, D.; Wang, W.; Zhou, W.; Yu, P. More than privacy: Applying differential privacy in key areas of artificial intelligence. arXiv 2020, arXiv:2008.01916. [Google Scholar] [CrossRef]
- Gilad-Bachrach, R.; Dowlin, N.; Laine, K.; Lauter, K.; Naehrig, M.; Wernsing, J. Cryptonets: Applying neural networks to encrypted data with high throughput and accuracy. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 201–210. [Google Scholar]
- Yuan, J.; Yu, S. Privacy preserving back-propagation neural network learning made practical with cloud computing. IEEE Trans. Parallel Distrib. Syst. 2013, 25, 212–221. [Google Scholar] [CrossRef]
- Shokri, R.; Shmatikov, V. Privacy-preserving deep learning. In Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security, Denver, Colorado, 12–16 October 2015; pp. 1310–1321. [Google Scholar]
- Bonawitz, K.; Eichner, H.; Grieskamp, W.; Huba, D.; Ingerman, A.; Ivanov, V.; Kiddon, C.; Konecny, J.; Mazzocchi, S.; McMahan, H.B.; et al. Towards federated learning at scale: System design. arXiv 2019, arXiv:1902.01046. [Google Scholar]
- Wang, S.; Tuor, T.; Salonidis, T.; Leung, K.K.; Makaya, C.; He, T.; Chan, K. Adaptive federated learning in resource constrained edge computing systems. IEEE J. Sel. Areas Commun.s 2019, 37, 1205–1221. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Chen, T.; Yang, Q. Secure federated transfer learning. arXiv 2018, arXiv:1812.03337. [Google Scholar]
- Cheng, K.; Fan, T.; Jin, Y.; Liu, Y.; Chen, T.; Yang, Q. Secureboost: A lossless federated learning framework. arXiv 2019, arXiv:1901.08755. [Google Scholar]
- Yang, T.; Andrew, G.; Eichner, H.; Sun, H.; Li, W.; Kong, N.; Ramage, D.; Beaufays, F. Applied federated learning: Improving google keyboard query suggestions. arXiv 2018, arXiv:1812.02903. [Google Scholar]
- Hard, A.; Rao, K.; Mathews, R.; Ramaswamy, S.; Beaufays, F.; Augenstein, S.; Eichner, H.; Kiddon, C.; Ramage, D. Federated learning for mobile keyboard prediction. arXiv 2018, arXiv:1811.03604. [Google Scholar]
- Sheller, M.J.; Reina, G.A.; Edwards, B.; Martin, J.; Bakas, S. Multi-institutional deep learning modeling without sharing patient data: A feasibility study on brain tumor segmentation. In Proceedings of the International MICCAI Brainlesion Workshop, Granada, Spain, 16 September 2018; pp. 92–104. [Google Scholar]
- Huang, L.; Shea, A.L.; Qian, H.; Masurkar, A.; Deng, H.; Liu, D. Patient clustering improves efficiency of federated machine learning to predict mortality and hospital stay time using distributed electronic medical records. J. Biomed. Inform. 2019, 99, 103291. [Google Scholar] [CrossRef] [Green Version]
- Chen, M.; Mathews, R.; Ouyang, T.; Beaufays, F. Federated learning of out-of-vocabulary words. arXiv 2019, arXiv:1903.10635. [Google Scholar]
- Ammad-Ud-Din, M.; Ivannikova, E.; Khan, S.A.; Oyomno, W.; Fu, Q.; Tan, K.E.; Flanagan, A. Federated collaborative filtering for privacy-preserving personalized recommendation system. arXiv 2019, arXiv:1901.09888. [Google Scholar]
- Truex, S.; Baracaldo, N.; Anwar, A.; Steinke, T.; Ludwig, H.; Zhang, R.; Zhou, Y. A hybrid approach to privacy-preserving federated learning. In Proceedings of the 12th ACM Workshop on Artificial Intelligence and Security, London, UK, 15 November 2019; pp. 1–11. [Google Scholar]
- Xu, R.; Baracaldo, N.; Zhou, Y.; Anwar, A.; Ludwig, H. Hybridalpha: An efficient approach for privacy-preserving federated learning. In Proceedings of the 12th ACM Workshop on Artificial Intelligence and Security, London, UK, 15 November 2019; pp. 13–23. [Google Scholar]
- Zhang, C.; Li, S.; Xia, J.; Wang, W.; Yan, F.; Liu, Y. Batchcrypt: Efficient homomorphic encryption for cross-silo federated learning. In Proceedings of the 2020 USENIX Annual Technical Conference (USENIX ATC 20), online, 15–17 July 2020; pp. 493–506. [Google Scholar]
- Ou, W.; Zeng, J.; Guo, Z.; Yan, W.; Liu, D.; Fuentes, S. A homomorphic-encryption-based vertical federated learning scheme for rick management. Comput. Sci. Inf. Syst. 2020, 17, 819–834. [Google Scholar] [CrossRef]
- Jost, C.; Lam, H.; Maximov, A.; Smeets, B.J. Encryption performance improvements of the paillier cryptosystem. IACR Cryptol. ePrint Arch. 2015, 864, 2015. [Google Scholar]
- Ogunseyi, T.B.; Bo, T. Fast decryption algorithm for paillier homomorphic cryptosystem. In Proceedings of the 2020 IEEE International Conference on Power, Intelligent Computing and Systems (ICPICS), Shenyang, China, 28–30 July 2020; pp. 803–806. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- MatNavi, N. Materials Database. [DB/OL] 15 June 2013. Available online: http://mits.nims.go.jp/index_en.html (accessed on 20 October 2020).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).