Two-Layer Network Caching for Different Service Requirements

Abstract

Network caching is a technique used to speed-up user access to frequently requested contents in complex data networks. This paper presents a two-layer overlay network caching system for content distribution. It is used to define some caching scenarios with increasing complexity, which refers to real situations, including mobile 5G connectivity. For each scenario our aim is to maximize the hit ratio, which leads to the formulation of NP-complete optimization problems. The heuristic solutions proposed are based on the theory of the maximization of monotone submodular functions under matroid constraints. After the determination of the approximation ratio of the greedy heuristic algorithms proposed, a numerical performance analysis is shown. This analysis includes a comparison with the Least-Frequently Used (LFU) eviction strategy adapted to the analyzed systems. Results show very good performance, under the hypotheses of either known or unknown popularity of contents.

1. Introduction

The proliferation of service types accessible through the Internet has radically changed the behavior of Internet users. Contents are continuously generated by both the organizations that leverage the capillary diffusion of the Internet, and the individual users. The resulting situation is characterized by a plethora of contents, consisting of images, videos, game updates, containerized applications and many other types. These contents represent the context that holds together the networked behavioral nature of the users. This huge volume service data is stored in repositories, typically located in large data centers and often accessible through a cloud-computing interface. The user requests determine the so-called $popularity$ of contents. A typical approach for taking advantage of this feature for both improving the customer services and relieving the network load, is caching contents. It essentially consists of temporarily storing popular contents in suitable network locations, different from repositories where they are originally stored and forward user requests towards such locations instead of repositories. Temporary storage could be done in different network elements, such as in browsers’ caches, in Content Distribution Network (CDN) servers [1,2], in base stations of cellular networks [3], in servers delivering metafiles for networked bioinformatics services [4], in caches of Information Centric Networking architectures [5,6] and in Service and Network Function Virtualization platforms [4]. The approach of caching content is not recent. For example, the Domain Name Service (DNS) has been using it for decades. Nevertheless, the current data consumption rate has induced companies, such as YouTube [7], Facebook [8] and Netflix [9], to make an extensive use of caches distributed over networks. This interest has also stimulated theoretical studies [10]. The network caching, which is the subject of this paper, is indeed one of the most popular research areas on caching. In fact, although a lot of research has been done on content replication strategies and content eviction policies in individual caches, the aggregate performance of a hierarchy of caches still needs to be analyzed in depth.

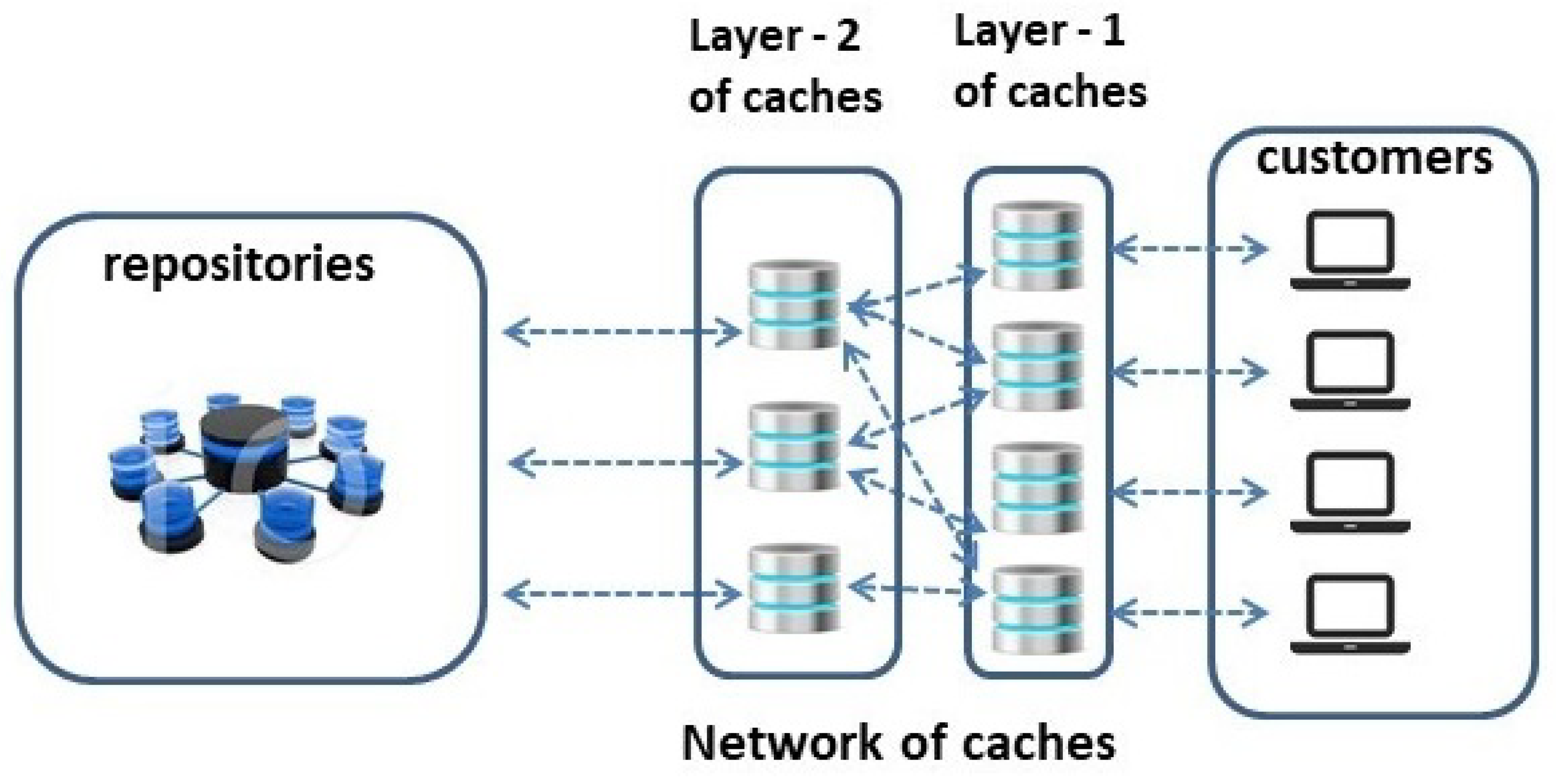
In this paper, we consider a two-layer hierarchy of caches. This cache organization is widely used in operation (for example by Facebook [8]), since the interaction between caches positioned at different depths in the network can help improve the effects of caching. In this work we assume that it is indifferent for a user to take an item from the cache closest to him, or from the furthest one, in the second caching level. In fact, we assume that the latter can be allocated at the most in the edge of the network, where the storage resources cannot be very large but the access latency for the contents is not significant. Therefore we do not consider any penalty if a content is available in second level caches. Furthermore, we stress that in this paper we do not specify in detail all the details to implement the content access service, but rather focus on the algorithms that are used to populate the caches. In this regard, it is worth considering that a complete caching protocol, which is beyond the scope of the paper, should include details relevant to keeping the caching system active when exceptions happen, such as network malfunctions, or getting rid of corrupted chunks, or even managing memory failures. Another aspect to be managed is the introduction of a robust cache authentication for avoiding making the system vulnerable to spoofing and similar attacks. Thus our contribution, which is algorithmic, needs to be included in a detailed protocol for it to be used in operation.

Furthermore, since many types of caching system exist, which cannot be addressed all in a single paper, we organized our proposal for contributing to CDN systems.

The original contribution of the paper is as follows:

• We identify a caching problem, to be further specialized in separate case studies. For this problem we propose a solution consisting of a cache management algorithm based on a hierarchical 2-layer caching structure.
• We show that the proposed algorithm outperforms the Least-Frequently Used (LFU) policy [11,12]. The performance metric used for this comparison is the probability of finding contents in caches, also referred to as hit ratio. It is indeed the main performance metric of any caching system.
• We specialize the basic caching problem and the relevant solution in other specific network caching scenarios. Each scenario is a variation of the basic caching problem, characterized by particular requirements in terms of content management and specific network limitations. For each scenario we formulate an optimization problem, which results to be NP-complete and propose some feasible solutions for pre-loading caches in order to maximize the hit ratio. Each solution consists of a greedy algorithm. We show that each proposed algorithm is characterized by guaranteed approximation performance. This property is based on recent results related to the maximization of submodular functions subject to matroid constraints.
• We analyze each model under the hypothesis of both known and unknown content popularity. The former hypothesis is used to analyze the asymptotically achievable hit ratio, and the latter is used for analyzing the proposals under more realistic conditions. All greedy algorithms have been implemented numerically, and integrated in a simulator. For the numerical analysis we selected some values of the configuration parameters that refer to the scenario of the distribution of movies through a content distribution network. Numerical results confirm the expectations.

The paper is organized as follows—the Section 2 includes some background information. The Section 3 shows the mathematical model of each considered scenarios, the associated optimization problems, the relevant greedy heuristics and the theoretical analysis. The numerical results are illustrated in Section 4. Some final considerations can be found in Section 5. Appendix A includes some basic introduction to the matroid theory and a theorem useful in the theoretical analysis.

2. Background

In this section, we describe the general network caching problem that is the background of this paper.

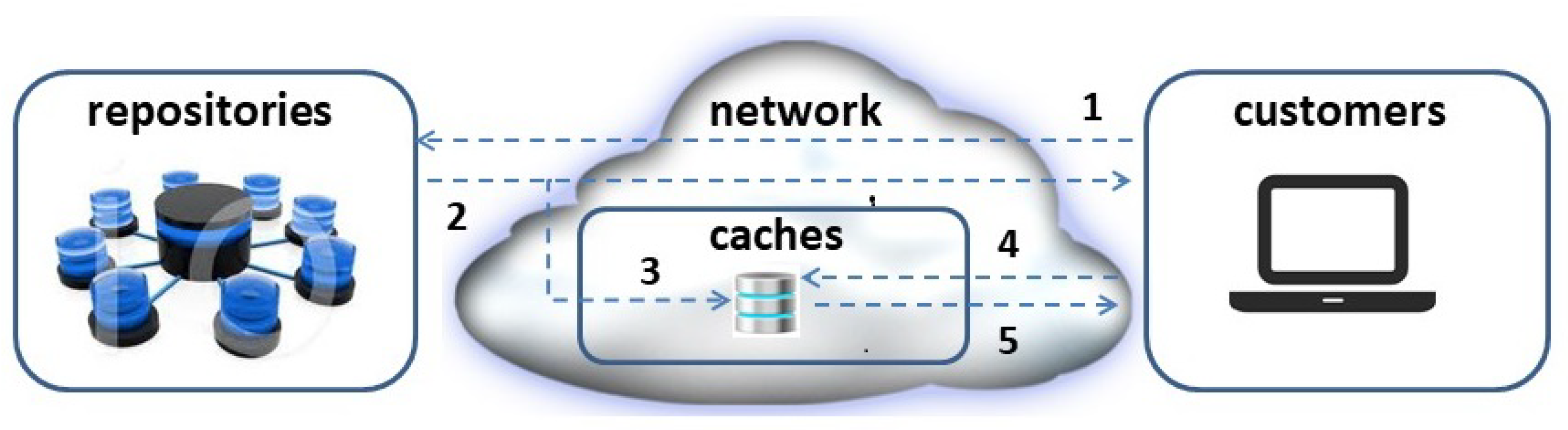
We assume the presence of a logical network of caches, having a known topology, connecting repositories with customers. With reference to Figure 1, we consider a generic content distribution system having the purpose of providing customers with the desired contents. In this paper the terms “customers”, “clients”, and "users" are used interchangeably. Customers’ requests (1) are routed through the network towards the repositories that store the desired contents. A contacted repository can either send the requested contents (2), if its location is the most convenient, or the only one, for providing the requesting customer with the content, or inform the client that the content is available in a cache closer to it. If deemed convenient, the content can be pre-fetched (3) in any caches in the network or even during their propagation through the network if it is frequently requested by customers.This way, the client can issue a content request to the indicated cache (4) and download it (5).

This simple network caching model includes some crucial aspects that need to be considered. The most important ones are the content replication strategy and the content eviction (or cache replacement) policy. The first one consists of the strategy used to distribute content replicas through the network of caches. The second one consists of the policy used to replace the cached replicas with other ones, if this is considered convenient. The principal known replication strategies and eviction policies are presented in the remainder of this Section.

The effectiveness of caching largely depends on the distribution of the content popularity [9,13]. In this paper, the popularity of a content indicates its mass probability of being requested. If the content size and popularity are the same for all of them, it is clear that the hit ratio in a given cache equals the ratio between the cache size and the catalogue size. If the popularity of contents is different, it is possible to take advantage of the difference between popularity values for increasing the hit ratio by preferably caching the most popular contents. In what follows, we assume that the content popularity follows the Mandelbrot-Zipf $\left(MZ\right)$ distribution. According to this distribution, the probability that a content is at popularity rank i, out of a catalog size M, is:

$$P_{MZ}\left(i\right)=\frac{K}{{\left(i+q\right)}^{\alpha }},$$

(1)

where $K={\displaystyle \frac{1}{{\sum }_{i=1,\dots ,M}\frac{1}{{\left(i+q\right)}^{\alpha }}}}$, and $\alpha$ and q are parameters of the distribution. This is a very general model, customizable by suitable parameter values, largely used to represent the distribution of popularity characterizing real processes [12]. It is also commonly agreed that the popularity of a significant portion of IP traffic follows this distribution. For example, a very good matching was observed for the Web traffic [14], YouTube [15] and Bit Torrent [16].

Another important aspect of cache management is the computational cost of the caching strategy. It typically corresponds to a feasible solution, sufficiently close to the optimum, of an optimization problem. If the strategy requires heavy content-wise management, it could result in being impractical.

Recently, given the proliferation of overlay networks, the proposals relating to caching systems are concerning the external part of the networks, which is close to the users. Some proposals have emerged for the management of caching on Fog nodes, characterized by scarcity of resources, but useful to contain the latency of access to services and to preserve data privacy. A caching management protocol for edge nodes is presented in [17].

In the same line of research that involves the use of network resources at the edges to create caches, regarded as elements of a more complex network, the survey [18] presents the state-of-the-art relating to caching at Edge nodes based on machine learning algorithms. The authors formulate a taxonomy based on network hierarchy and describe a number of related algorithms of supervised, unsupervised, and reinforcement learning.

In this paper, we consider different caching problems, typical of different applications and network environments, over a hierarchical cache network topology. All these problems are NP -complete. For all of them, we propose a feasible solution based on the theory of submodular function maximization bound to matroid constraints. These problems are formulated and analyzed in Section 3.

2.1. Individual Cache Management

A large number of cache replacement policies have been proposed over time. They refer to different usage of caches, such as disk buffering, WEB proxies, ICN and other [5,6,17]. A comprehensive description cannot be included in this paper. In what follows we introduce some of them, selected by their relevance with our proposals although, to the best of our knowledge, no solutions exist for the problems analyzed in this paper. The simplest conceivable approach is the First In First Out (FIFO). It consists of managing a cache as a FIFO queue. The Least Recently Used (LRU) policy [11,12] refines the FIFO approach in that when an uncached content is requested, the cached element that has been requested less recently is replaced with the requested one. In this case, the cache management becomes more complex since it is necessary to keep an “age” metric updated for each cached item, whatever the implementation of this metric is. The LRU policy has inspired a family of other proposals. A variation of LRU is q-LRU [13], where any new requested content is stored in the cache with probability q. The eviction policy is LRU. k-LRU [13] is another variant of the LRU policy. It consists of a chain of virtual LRU caches attached to the real one. Newly arrived contents are “stored” in the last virtual cache, and any hit before its removal cause an advancement in the chain, until the physical cache is entered. In some particular cases, when the use of contents has a circular nature, it might be convenient to evict the most recently used (MRU) contents [6]. This situation can occur when users request a movie and the chunks of the related file are always sent from the first to the last ones.

A significant change of strategy has been brought by the Least-Frequently Used (LFU) policy [11,12]. It aims at populating a cache with the most popular contents. Assuming the content popularity to be known and constant over time, this policy maximizes the hit ratio. A practical implementation of it consists of counting references to the contents of the whole catalog. If a content that arrives at a cache has a higher reference count than the minimum of the cached contents, the latter is replaced by the arrived content. A family of proposals followed the basic LFU policy. All of them assume variable popularity over time and aim to quickly replace cached content that has suffered a sudden drop in popularity. The variant LFU with Dynamic Aging (LFUDA) [12] requires that the reference count of a content is incremented by a cache age when it enters the cache and when a cached object is hit. The proposal in [19], called TinyLFU, consists of maintaining an approximate representation of the access frequency of the recently accessed items. This proposal in based on the Bloom filter theory. Its aim is to implement a lightweight estimation, although sufficiently reliable, that leverages frequency-based cache admission policy that adapts to skewed access distributions. The Frequency Based Replacement (FBR) [20] combines LRU and LFU policies. It makes use of LRU content ordering in the cache, but the eviction policy is based on the reference count. The Least Frequent Recently Use (LFRU) [21] policy consists of organizing caches in two partitions, called privileged and unprivileged. The privileged one is managed by using the LRU policy, whilst the unprivileged partition makes use of an approximated LFU, for which content eviction metrics are computed on limited time windows.

2.2. Networks of Caches

In this subsection, we consider the aspects related to both content replication strategies and coordinated cache management. A hierarchical cache organization, rooted at a single content repository, is presented in [22]. Cooperative cache management algorithms for minimizing bandwidth occupancy and maximizing hit ratio are proposed. The Leave Copy Everywhere (LCE) content replication strategy [5,6], consists in replicating the contents on all the caches present in the path followed by the content for its delivery to the requesting customers. An LCE variant is the so-called Conditional LCE (CLCE), for which a cache node stores an arriving content if it satisfies a qualifying condition [21]. Another strategy is the Leave a Copy Down (LCD) [23], which consists of replicating contents only downward the location of a cached copy on the path to the requesting client. Move Copy Down (MCD) [6] is a strategy consisting of moving a cached content from the cache where is found to the connected downward cache. Leave Copy Probability (LCP) [6] is a strategy according to which a content copy is cached with a given probability p in the caches staying in the path to the requesting customers. In the strategy Centrality-based caching [6], a content is stored in the cache node having the highest betweenness centrality. A significant strand of research on cache networks is related to coded caching, which is worth of mention although it is not in the scope of our proposal. In [24] the authors investigated coded caching in a multiserver network of different types. Servers are connected to multiple caches implemented in clients. The Multi Queue caching algorithm [25] consists of a hierarchical organization of LRU queues in a cache. Each hierarchical level is associated with an expected lifetime. The position of a content at a given hierarchy level is determined by its request counts within the expected lifetime and the contents at the lowest hierarchy level are candidates for eviction. The a-NET was proposed in [26]. It approximates the behavior of multi-cache networks by making use of other approximation algorithms designed for isolated LRU caches. An analytical model of an uncooperative two-level LRU caching system is presented in [27]. A Time-to-Live based policy is proposed in [28] and performance is determined for both a linear network and a tree network with a root cache and multiple leaf caches with infinite buffer size. In the context of content centric networking, content placement schemes and request routing are tightly coupled. The relevant optimization problems typically consists maximization of a submodular functions subject to matroid constraints [29,30]. Such mathematical framework is also used in this paper.

3. Model

3.1. Statistical Model of Content Requests

Most of proposals on cache management have been analyzed by using the Independent Reference Model (IRM) [13,27]. According to it, contents belong to a fixed catalogue and their popularity is constant over time. In addition, customers’ requests form a sequence of i.i.d. random variables and the request arrival process is memory-less.

For what concerns the size of items, due to the common practice of chunking large contents if their size exceeds a given value, in many papers it is modeled as a constant value [13]. In this paper, we consider both constant and variable content size. The reason of considering also variable content size is that in some situations it can be requested to cache all content chunks or nothing.

For what concerns the catalog size, considering it fixed in the era of Big Data could be considered an excessive simplification. However, if we limit the analysis to the set of contents that collects a high percentile of the popularity distribution, the number of contents that are worth of being considered is relatively small. For example, by using (1) for $q=8$, $M={10}^6$, and $\alpha =1.3$, it results that ${10}^5$ and $4\times {10}^5$ contents account for a percentile of probability of about $97\%$ and $99\%$, respectively.

3.2. Hierarchy of Caches

Consider a cache of size K and the popularity distribution in (1). Under the assumption of IRM, it is trivial to argue that the maximum hit ratio is achieved when the K positions in the cache are occupied by the first K components of (1), ordered by decreasing probability, and the relevant mean hit ratio equals

$$P_{hit,max}=\sum _{i=1}^K{P}_{MZ}\left(i\right).$$

(2)

In this paper, we consider a 2-layer hierarchy of caches. The first layer of caches in connected with customers, which can be regarded either as individual final users or groups of them. In the first case a layer-1 cache serves a single user, as it typically happens in film distribution networks. In the second case, a layer-1 cache serves a community of homogeneous users, as it happens in community networks. Cache hierarchy could also be a consequence of a path-pinning routing techniques used in overlay networks [31], as sketched in Figure 2. A real deployment of a two-layer hierarchy of caches in an overlay network is shown in [8].

We assume that customers request contents from the same catalogue. Nevertheless, the popularity of a content could be different for each customer.

When a content is requested, if it is already cached, request is forwarded to either the layer-1 cache connected to the requesting user or to any connected layer-2 caches, depending on where the content is cached. As already mentioned, we assume that it is indifferent for the user to find content in the nearest cache or in the second level cache. Therefore we do not introduce any penalty in the use of the second level cache, because we assume that it is still in the proximity of the user, as in an edge network. Furthermore, we do not deal with the application protocol used to access the two caches.

Our proposal, illustrated in what follows, consists of pre-loading caches by using different algorithms. These algorithms are compared with the LFU cache management policy, since it is a well known and sound reference.

In order to make a fair comparison between our proposal and LFU, we adapted the LFU policy to the analyzed hierarchy of caches as follows. When a content is returned from repositories it is preferably cached in one of the layer-2 caches serving the requesting customer. In case the LFU policy does not allow caching the content in any of the layer-2 caches, it is sent the layer-1 cache and evaluated for caching therein. This way, contents are not replicated in different caches as it would happen by executing LFU independently in all caches with a consequent waste of cache memory.

Before formulating the optimization problem we discuss the expected effects of caching a content in layer-2 and layer-1 caches.

The use of layer-2 caches is strategic for obtaining high hit ratio values. In fact, a content cached in a layer-2 cache can be accessed by multiple customers, while a content in a layer-1 cache can be accessed by a single customer. However, since the popularity of contents may be different among different customers, it is necessary to solve non-trivial optimization problems for populating caches. The objective is to maximize the hit ratio, by taking advantage of both layer-1 and layer-2 caches. Hence, once layer-2 caches are populated, finding the suitable contents to be cached into a layer-1 cache is simple. For each customer, it is sufficient to make use of (2) and cache the contents that are not accessible in layer-2 caches with decreasing popularity until the layer-1 cache is filled. In order to manage length contents, we will use the density of popularity concept. Thus, the role of layer-1 caches in the caching problem could appear quite trivial. Nevertheless, some other important contributions can also be identified. In case of sub-optimal population of layer-2 caches, the presence of layer-1 caches could be highly beneficial for the hit ratio. Sub-optimal content selection could be due to either the usage of heuristic solutions of NP-complete caching problems, or short-term statistical fluctuations in the rate of requests causing errors in the estimation of content popularity. Since the estimated content popularity is used to populate caches, some contents that should be optimally stored in the layer-2 caches cloud be cached in the layer-1 caches. This would happen at the expense of the exclusion of contents having lower popularity, but sufficiently high for being selected for layer-1 caches in the optimal allocation. Thus, layer-1 caches increase the system resilience to any suboptimal content selection for layer-2 caches. This effect is highlighted in Section 4 by evaluating the percentage of hits occurring in layer-1 caches in different case studies.

3.3. Caching Problems

In this section, we identify different caching problems, starting from a basic one, analyze their complexity, propose heuristic solutions, and determine their computational cost. We present the principal used notation in

Table 1. Principal Notation.

Variable	Meaning
i:	index of layer-1 caches (or attached users);
j:	index of layer-2 caches;
m:	index of variable-length items;
$\xi$:	index of fixed-length items (or fixed-length chunks of variable length items);
${\xi }^{*}$:	index of selected $\xi$ for caching;
$m^{*}$:	index of selected m for caching;
$\left\{m^{+}\right\}$:	pre-selected set of items for selection;
${\varphi }_{i,j}=1$	if the layer-1 cache i is connected with the layer-2 cache j, otherwise ${\varphi }_{i,j}=0$;
$\Phi$:	$[W\times |K_2\left|\right]$ matrix of the ${\varphi }_{i,j}$ values
$g_{j,\xi }=1$	if item $\xi$ is in layer-2 cache j, otherwise $g_{i,\xi }=0$;
$q_{i,\xi }=1$	if item $\xi$ is in layer-1 cache i, otherwise $q_{i,\xi }=0$;
$\zeta (\xi ,m)=1$	if a chunk $\xi$ is part of an item m;
$\Xi$:	set of items;
$K_2$:	set of layer-2 caches;
$K_{2,j}$:	size of j-th layer-2 cache;
$K_{1,i}$:	size of i-th layer-1 cache;
$P_{MZ,i}\left(\xi \right)$:	Zipf-Mandelbrot popularity of content $\xi$ for user i;
$\mathbf{P}$:	$[W\times C]$ popularity matrix.
C:	cardinality of the set of items;
W:	cardinality of the set of customers;
${\epsilon }_j$:	set of items stored in cache j;
${\lambda }_i:$	mean request rate of user i;
$d\left(m,i\right)$:	density of popularity of item m for user i;
$\mathbf{D}$:	$[W\times C]$ matrix of $d\left(m,i\right)$ values.
$b_{min}:$	minimum bandwidth for transmitting a chunk;
$b_{i,j}$:	the bandwidth used to transfer items from cache j to customer i.
$B_j$:	output bandwidth at the j-th cache server
$\tau :$	maximum download time;
${\sigma }_{i,j}:$	probability that layer-1 cache i is connected with the layer-2 cache j.
${\mathit{P}}_{hit,i}$:	hit ratio at layer-1 cache i.
${\mathit{P}}_{hit,K2}$:	hit ratio at layer-2 caches.
$\mathbf{T}$:	$\left[1\times |K_2|\right]$ vector of layer-2 cache occupation thresholds.

.

3.3.1. Case1: Fixed-Size Items

This case study is the basic caching problem, the simplest one in this paper. The contents are the same size. The content popularity value can change from user to user and remain constant over time. In addition, the popularity value is known in advance for investigating the asymptotic performance. This model can be used to represent the access to contents of similar size, which is significantly lower than the cache size, for a time period in which the content popularity may be realistically assumed to be stationary. For example, a single day access to Instagram pictures can be modeled in this way. In fact, the trend of such content popularity after some time from publication can be estimated quite reliably, generally it does not show significant variations for a few days. We decided to include this problem in order to show some basic elements of our approach, which results to be light, and compare it with the optimal hit ratio determined by (2). Subsequent case studies will be characterized by higher complexity.

For an item $\xi$ requested by the user i, the hit ratio $P_{hit}$ is given by the probability of finding it either at the layer-1 cache or at any of the layer-2 caches reachable by i, that is, $\{cachej:{\varphi }_{i,j}=1\}$.

We assume the content popularity and the matrix ${\varphi }_{i,j}$ are given. The caching problem can be formulated as follows.

Problem 1.

$$\begin{array}{ccc}\hfill & & \underset{q_{i,\xi }{g}_{j,\xi }}{max}{P}_{hit}\hfill \\ & & st\hfill \\ & & \sum _{\xi =1}^C{g}_{j,\xi }\le K_{2,j}\forall j\in \left[1,|K_2|\right]\hfill \\ & & \sum _{\xi =1}^C{q}_{i,\xi }\le K_{1,i}\forall i\in \left[1,W\right]\hfill \\ & & g_{j,\xi },q_{i,\xi }\in \left\{0,1\right\}.\hfill \end{array}$$

(3)

The first two constraints are due to the finite size of caches. Problem 1 can be split in two subproblems. To show this, we first show the following Lemma.

Lemma 1.

For any content placement in layer-2 caches, the optimal content placement in cache i is found by selecting the items having higher popularity for customer ith from the set of the contents not already cached in layer-2 caches, that is, $\{\xi \in \Xi :{\varphi }_{i,j}{g}_{j,\xi }=0$$,\forall j\}$.

Proof. 

Let $P_{hit,i,1}$ be the hit ratio obtained by selecting items as mentioned above by customer ith. Assume by contradiction that ∃ an item ${\xi }_x\in \Xi$ \${\bigcup }_{j=1}^{K_2}\left\{\xi \in \Xi :{\varphi }_{i,j}{g}_{j,\xi }=1:q_{i,\xi }=0\right\}$ and an item ${\xi }_y\in \left\{\xi \in \Xi :q_{i,\xi }=1\right\}$ such that swapping them in cache i, the resulting hit probability $P_{hit,i,2}>P_{hit,i,1}$. Nevertheless, given the content selection by decreasing popularity generating to $P_{hit,i,1}$, it results that

$$P_{hit,i,2}\left(\xi \right)=P_{MZ,i}\left({\xi }_y\right)+P_{hit,i,1}-P_{MZ,i}\left({\xi }_x\right)\le P_{hit,i,1},$$

(4)

which contradicts the assumption.   □

Theorem 1.

Problem 1 can be decomposed in two subproblems, each relevant to layer-1 and layer-2 caching, respectively.

Proof. 

Let ${\left\{\xi \right\}}_{opt}=\left\{\xi :\exists g_{j,\xi }=1\vee q_{i,\xi }=1\right\}$ be the optimal content placement due to the optimal solution of Problem 1. This solution can be written as ${\left\{\xi \right\}}_{opt}={\left\{\xi \right\}}_{K1}\bigcup {\left\{\xi \right\}}_{K2}$, where ${\left\{\xi \right\}}_{K1}=\left\{\xi :q_{i,\xi }=1\right\}$ and ${\left\{\xi \right\}}_{K2}=\left\{\xi :\exists g_{j,\xi }=1\right\}$ are the set of items stored in layer-1 cache and layer-2 caches, respectively. Due to Lemma 1, given ${\left\{\xi \right\}}_{K2}$, ${\left\{\xi \right\}}_{K1}$ follows.    □

Hence, Problem 1 can be written as follows:

Problem 2.

$$\begin{array}{ccc}\hfill & & \underset{q_{i,\xi }{g}_{j,\xi }}{max}{P}_{hit}=\underset{g_{j,\xi }}{max}{P}_{hit,K2}+\sum _{i=1}^W\underset{q_{i,\xi }:{\varphi }_{i,j}{g}_{j,\xi }=0}{max}{P}_{hit,i}\hfill \\ & & st\hfill \\ & & \sum _{\xi =1}^C{g}_{j,\xi }\le K_{2,j}\forall j\in \left[1,|K_2|\right]\hfill \\ & & \sum _{\xi =1}^C{q}_{i,\xi }\le K_{1,i}\forall i\in \left[1,W\right]\hfill \\ & & g_{j,\xi },q_{i,\xi }\in \left\{0,1\right\}.\hfill \end{array}$$

(5)

Since the part of the optimization problem relevant to layer-1 caches is readily solved through Lemma 1, the remaining problem to be solved is the following:

Problem 3.

$$\begin{array}{ccc}\hfill & & \underset{g_{j,\xi }}{max}{P}_{hit,K2}\hfill \\ & & st\hfill \\ & & \sum _{\xi =1}^C{g}_{j,\xi }\le K_{2,j}\forall j\in \left[1,|K_2|\right]\hfill \\ & & g_{j,\xi }\in \left\{0,1\right\}.\hfill \end{array}$$

(6)

$P_{hit,K2}$ can be written considering that an item requested by a customer could be cached in one or more than one layer-2 connected caches. This replication could be due to the different content popularity distribution for the customers connected to the same layer-2 cache.

Figure 3 is a graphical representation of the parameters defined above. The example in this figure shows how they combine for including the popularity of a content in the optimization function, for a given user, by caching it in two out three reachable caches, indicated by ones in the $\left(i,j\right)$ plane.

$$P_{hit,K2}=\sum _{i=1}^W\sum _{\xi =1}^C\left(\underset{j=1}{\overset{|K_2|}{\bigvee }}{\varphi }_{i,j}{g}_{j,\xi }\right)P_{MZ,i}\left(\xi \right).$$

(7)

Since the OR function in (7) is monotone not decreasing, and the marginal contribution for caching an additional item is not increasing with the size of the set of the previously cached items, the function $P_{hit,K2}$ is $submodular$ [32].

It is very easy to show that the inequality constraints in (6) can be mapped into a uniform matroid, with the ground set corresponding to the set of items. Some details on uniform matroids are reported in Appendix. Thus, the optimization problem consists of the maximization of a monotone submodular function over the independent sets of a matroid. This class of problems has been studied in depth [32]. They can be hastened by the use of greedy algorithms with known achievable performance.

Looking at the maximization function (7), the atomic elements that can be greedily selected to increase its value are the individual items. The marginal contribution due to caching each element requested by a user i in the j-th cache depends on both its popularity for user i and the presence of the same element in other caches connected to the other users that can be served also by the j-th cache. Thus, the OR function affects the $state$ of the cache before caching an additional element. When no items are already cached, the item that is greedily cached first is the one that adds the maximum amount of popularity. That is

$${\xi }^{*},j^{*}=argmax\sum _{i=1}^W{\varphi }_{j,i}{P}_{MZ,i}\left(\xi \right)=argmax\left({\Phi }^T\mathbf{P}\right),$$

(8)

where $\Phi$ is the $[W\times |K_2\left|\right]$ matrix including the elements ${\varphi }_{i,j}$ and P is the $[W\times C]$ popularity matrix initialized by the $P_{MZ,i}\left(\xi \right)$ values for each referred item.

Once an item ${\xi }^{*}$ is cached in $j^{*}$, in order to allow selecting the same ${\xi }^{*}$ element to be cached in other layer-2 caches, that is to implement the OR function in case the same ${\xi }^{*}$ element is already cached in some layer-2 caches, the popularity matrix is updated as follows:

$$\mathbf{P}(i,{\xi }^{*})\leftarrow \mathbf{P}(i,{\xi }^{*})\left(1-{\Phi }^T(j^{*},i)\right)\forall i\in [1,W].$$

(9)

This way, all users connected to the cache $j^{*}$ will not contribute to the optimization metric if ${\xi }^{*}$ is cached in another cache.

In order to compare the maximum popularity value of the contents for different users, it is necessary to weight the popularity values with the mean request rate of each customers.

In synthesis, we propose the heuristic solution Algorithm1 illustrated in Code 1 for Problem 3. Note that row 7 of Algorithm1 makes a greedy random selection of content ${\xi }^{*}$ and cache $j^{*}$ if multiple pairs that maximize the optimization function exist.

Code 1 Solution to Problem 3.

1: functionAlgorithm1($\Xi ,\Phi ,\mathbf{P}$, $K_2$, $\left\{{\lambda }_i\right\}$)→${\epsilon }_j$ 2:     ${\epsilon }_j\leftarrow \varphi \forall j$                   ▷ initialization 3:     $step\leftarrow 1$ 4:     $T_j\leftarrow 0\forall j$         ▷ thresholds on the cache occupation 5:     $\mathbf{P}(i,\xi )\leftarrow \mathbf{P}(i,\xi ){\lambda }_i\forall i$ 6:     while $(\exists$$j:$$T_j<K_{2,j})\wedge (step\le C)$do▷ core of the greedy algorithm 7:         ${\xi }^{*},j^{*}\leftarrow$ random argmax$\left({\Phi }^T\mathbf{P}\right)$ 8:         if $T_{j^{*}}=K_{2,j}$ then 9:            $\varphi (i,j^{*})\leftarrow 0\forall i$ 10:         end if 11:         $T_{j^{*}}\leftarrow T_{j^{*}}+1$ 12:         step ← step+1 13:         $\mathbf{P}(i,{\xi }^{*})\leftarrow \mathbf{P}(i,{\xi }^{*})\left(1-{\Phi }^T(j^{*},i)\right)\forall i\in [1,W]$ 14:         ${\epsilon }_{j^{*}}\leftarrow {\epsilon }_{j^{*}}\cup \left\{{\xi }^{*}\right\}$ 15:     end while 16:     return ${\epsilon }_j$ 17: end function

The algorithm completes in $K={\sum }_{j=1}^{|K_2|}{K}_{2,j}$ iterations. Let $M_{opt}$ denote the optimum solution, that is the maximum achievable value of $P_{hit,K2}$, and $M_i$ the metric produced by Algorithm1 at step i. Given the greedy nature of the algorithm and submodularity of the optimization function, it follows that

$$\sum _{i=1}^W{\varphi }_{j^{*},i}\mathbf{P}(i,{\xi }^{*})\ge \frac{1}{K}\left(M_{opt}-M_i\right).$$

(10)

that is equivalent to say that

$$M_{i+1}-M_1\ge \frac{1}{K}\left(M_{opt}-M_i\right).$$

(11)

Hence

$$\begin{array}{ccc}\hfill M_{i+1}& \ge & M_1+\frac{1}{K}\left(M_{opt}-M_i\right)=\frac{1}{K}{M}_{opt}+\left(1-\frac{1}{K}\right)M_i\hfill \\ & \ge & \frac{1}{K}{M}_{opt}+\left(1-{\left(1-\frac{1}{K}\right)}^i\right)\left(1-\frac{1}{K}\right)M_{opt}\hfill \\ & =& \left(1-{\left(1-\frac{1}{K}\right)}^{i+1}\right)M_{opt}.\hfill \end{array}$$

(12)

At the final step of the algorithm

$$\begin{array}{ccc}\hfill M_K& \ge & \left(1-{\left(1-\frac{1}{K}\right)}^K\right)M_{opt}\ge \left(1-\frac{1}{e}\right)M_{opt},\hfill \end{array}$$

(13)

since ${\left(1-\frac{1}{K}\right)}^K\le \frac{1}{e}$. This is a good result since in [32] the authors show that the maximum approximation ratio of a greedy algorithm over a matroid constraint is $\left(1-\frac{1}{e}\right)M_{opt}$ unless P = NP.

Under the hypothesis that $C>>K$, as expected in operation, the complexity of the Algorithm1 is determined by row 7 of it, consisting of a $\left[\right|K_2|\times W]$ and $[W\times C]$ matrix products plus a max determination out of $|K_2|\times C$ elements iterated K times. Thus, the complexity of Algorithm 1 is $O\left(W\right|K_2\left|CK\right)$. If we restrict the set of contents considered to a subset having the higher popularity and are actually candidate for caching, the size of this subset is proportional to K, thus making the complexity of Algorithm1 $O\left(W\right|K_2\left|K^2\right)$.

In what follows, we consider variations to the basic caching problem in order to refer to different classes of applications.

3.3.2. Case 2: Variable-Size Items

In this case study, we remove the hypothesis of equal-size items. This model can be useful when the number of items that can be cached is relatively small and the specific size of each can significantly affect the hit ratio.

Given the different sizes of the items, in order to consider it in the optimal use of the available cache memory, we introduce the concepts of density of popularity. It is defined as the ratio $d(m,i)=\frac{P_{MZ,i}\left(m\right)}{size\left(m\right)},\forall i\in [1,W]$. In what follows D denotes the $[W\times C]$ matrix of the elements $d(m,i)$. The Problem 3 changes as follows:

Problem 4.

$$\begin{array}{ccc}\hfill & & \underset{g_{j,\xi }}{max}{P}_{hit,K2}\hfill \\ & & st\hfill \\ & & \sum _{m=1}^C{g}_{j,m}size\left(m\right)\le K_{2,j}\forall j\in \left[1,|K_2|\right]\hfill \\ & & g_{j,m}\in \left\{0,1\right\}.\hfill \end{array}$$

(14)

Note that, in this formulation, the caching problem is combined with the zero-one knapsack problem, which is known to be NP-complete. $Cost$ of items, $value$ of items, and available $budget$ attributes of the knapsack problem correspond to $item$  $size$, $item$  $popularity$, and $cache$  $size$ of the caching problem. For the knapsack problem an arbitrarily good polynomial time algorith, based on dynamic programming exists [33], providing a metric $M=(1-ϵ)M_{opt}$. However, due to the submodularity of the optimization function in Problem 4, it is necessary to use a different approach. Also in this case it is very easy to show that the inequality constraints in (14) can be mapped into a uniform matroid. More details how matroid constraints combine with the knapsack problem can be found in [34]. Hence, also in this case the problem can be faced through a heuristic greedy algorithm which selects items according to their density of popularity. It is listed in Code 2.

As for the analysis of performance and complexity, the use of content size does not alter the analysis shown for Algorithm1. Therefore, the computational cost of Algorithm1 is equal to that of Algorithm2 (see Code 2).

Code 2 Solution to Problem 4.

1: functionAlgorithm2($\Xi ,size\left(m\right)\forall m\in \Xi ,\Phi ,\mathbf{D}$, $K_2$, $\left\{{\lambda }_i\right\}$)→${\epsilon }_j$ 2:     ${\epsilon }_j\leftarrow \varnothing \forall i,j$                    ▷ initialization 3:     $step\leftarrow 1$ 4:     $T_j\leftarrow 0\forall j$           ▷ thresholds on the cache occupation 5:     $d(m,i)\leftarrow d(m,i){\lambda }_i\forall m,i$ 6:     while (∃$j:$$T_j<K_{2,j})\wedge (step\le C)$do   ▷ core of the greedy algorithm 7:         $m^{*},j^{*}\leftarrow$ max-size $argmax\left({\Phi }^T\mathbf{D}\right)$ 8:         if $T_{j^{*}}+size\left(m^{*}\right)>K_{2,j}$ then 9:            $\varphi (i,j^{*})\leftarrow 0\forall i$ 10:         end if 11:         $T_{j^{*}}\leftarrow T_{j^{*}}+size\left({\xi }^{*}\right)$ 12:         step ← step+1 13:         $\mathbf{P}(i,m^{*})\leftarrow \mathbf{P}(i,m^{*})\left(1-{\Phi }^T(j^{*},i)\right)\forall i\in [1,W]$ 14:         ${\epsilon }_{j^{*}}\leftarrow {\epsilon }_{j^{*}}\cup \left\{m^{*}\right\}$ 15:     end while 16:     return ${\epsilon }_j$ 17: end function

A variant of Problem 4 consists of taking advantage of parallel downloading from layer-2 caches. This means that different chunks of an item can be cached in different caches, under the constraint that the entire item is cached. For example, this could be necessary to support a real-time financial service, which requires an entire dataset in a very short time.

In order to write constraints, we introduce an additional notation for items. We denote that the chunk $\xi$ is part of an item m as $\zeta (\xi ,m)$. We also denote the total number of chunks as $C_1$. The problem can be formulated as follows.

Problem 5.

$$\begin{array}{ccc}\hfill & & \underset{g_{j,\xi }}{max}\left\{\sum _{i=1}^W\sum _{\xi =1}^{C_1}\left(\underset{j=1}{\overset{|K_2|}{\bigvee }}{\varphi }_{i,j}{g}_{j,\xi }\right)P_{MZ,i}\left(\xi \right)\right\}\hfill \\ & & st\hfill \\ & & \sum _{\xi =1}^C{g}_{j,\xi }\le K_{2,j}\forall j\in \left[1,|K_2|\right]\hfill \\ & & \sum _{\xi =1}^{C_1}\underset{j=1}{\overset{|K_2|}{\bigvee }}{\varphi }_{i,j}{g}_{j,\xi }\zeta (\xi ,m)=\left|m\right|\forall m\in [1,C],\hfill \\ & & g_{j,\xi }\in \left\{0,1\right\}.\hfill \end{array}$$

(15)

From the practical viewpoint, the difference between Problems 4 and 5 is appreciable when the size of aggregates is such that just few of them can be cached.

Although the two problems could appear quite similar, from the algorithmic viewpoint the Problem 5 introduces significant issues, due to the possibility of caching contents in different layer-2 caches. The relevant greedy algorithm Algorithm2bis follows in Code 3.

Code 3 Solution to Problem 5.

1: functionAlgorithm2bis($\Xi ,size\left(m\right)\forall m\in \Xi ,\Phi ,\mathbf{D}$, $K_2$, $\left\{{\lambda }_i\right\}$)→${\epsilon }_j$ 2:     ${\epsilon }_j\leftarrow \varnothing \forall i,j$                         ▷ initialization 3:     $step\leftarrow 1$ 4:     $T_j\leftarrow 0\forall j$                ▷ thresholds on the cache occupation 5:     $d(m,i)\leftarrow d(m,i){\lambda }_i\forall i$ 6:     while (∃$j:$$T_j<K_{2,j})\wedge (step\le C)$do       ▷ core of the greedy algorithm 7:         $m^{*},\left\{j^{*}\right\}\leftarrow$Procedure1$\left(\Phi ,\mathbf{D},\mathbf{T},\left|K2\right|,\Xi \right)$ 8:         step ← step+1 9:         ${\epsilon }_{j^{*}}\leftarrow {\epsilon }_{j^{*}}\cup \left\{m^{*}\right\}$ 10:         cache $m^{*}$ distributing items over $\left\{j^{*}\right\}$ and update T 11:     end while 12:     return ${\epsilon }_j$ 13: end function     1: functionProcedure1($\Phi ,\mathbf{D},\mathbf{T},|K_2|,\Xi$)$\to m^{*},\left\{j^{*}\right\}$ 2:     $\left\{m^{+}\right\}$$\leftarrow \varnothing$, $\left\{m^{*}\right\}$$\leftarrow \varnothing$ 3:     $\mathsf{{\rm Y}}={\Phi }^T\mathbf{D}$ 4:     while $\mathsf{{\rm Y}}\ne$ [0] do 5:         $\left\{m^{+}\right\}$←$argma{x}_m\left(\mathsf{{\rm Y}}\right)$ 6:         for all $m\in \left\{m^{+}\right\}$do        ▷ check if sufficient cache storage is available 7:            $L_m\leftarrow 0$                ▷ space available for content $\xi$ in caches 8:            for all $j\in \{j:(j,m^{+})=max\left(\mathsf{{\rm Y}}\right)\}$ do 9:                $L_m\leftarrow L_m+K_{2,j}-T_j$ 10:                if $L_m\ge size\left(m\right)$ then 11:                    $\left\{m^{*}\right\}\leftarrow m$ 12:                end if 13:            end for 14:         end for 15:         $m^{*}=$ max-size $\left\{m^{*}\right\}$$,\left\{j^{*}\right\}\leftarrow \{j:(j,m^{*})=max\left(\mathsf{{\rm Y}}\right)\}$ 16:         return $m^{*},\left\{j^{*}\right\}$ 17:         if $\left\{m^{*}\right\}$ = ∅then               ▷ descrease the max $\mathsf{{\rm Y}}={\Phi }^T\mathbf{D}$ 18:            $\mathsf{{\rm Y}}(m^{+},\{j\in (j,m^{+})=max\left({\Phi }^T\mathbf{D}\right)\})\leftarrow 0$   ▷ values corresponding to 19:            $newmax\leftarrow {max}_m\mathsf{{\rm Y}}(m^{+},:)$           ▷ the $m^{+}$ columns to the 20:            $\mathsf{{\rm Y}}(m^{+},\{j\in (j,m^{+})\})\leftarrow newmax$         ▷ second largest ones 21:         end if 22:     end while 23:     return $\varnothing ,\varnothing$                        ▷ no solution found 24: end function

Procedure1 in Code 3 searches for the maximum density of popularity value for the uncached contents (row 4). If some identified contents in $\left\{m^{+}\right\}$ are large enough to be stored in caches reachable by users that generate the maximum density of popularity, the largest content is returned together with the caches where it can be stored (row 16). Otherwise a particular management is necessary, which is the peculiar part of Procedure1. It is the management of the matrix $\mathsf{{\rm Y}}$ when the size of the selected contents $\left\{m^{+}\right\}$ is greater than the room available in the identified caches that optimize the overall score. In this case, the density of popularity of these contents is reduced to the second score value of the columns indexed by $\left\{m^{+}\right\}$. In this way, the number of caches that can be used increases, and the content could be allocated in the following iteration. If no contents are selected, empty sets are returned (row 23). The computational cost of the procedure is determined by the iterated maximum search in $\mathsf{{\rm Y}}$$=\left[\right|K_2|\times C]$, which is linear with the size of $\mathsf{{\rm Y}}$, since all the other operations require a lower effort. It multiplies with the complexity of Algorithm2. The result is the price to pay for caching entire items in chunks in a greedy way in different caches.

For what concerns the approximation ratio, note that constraints of Problems 4 and 5 clearly define uniform matroids (see Appendix A). The submodular maximization function is the same as in Problem 3. Following the same steps of the proof relevant to Algorithm1, it is easy to find that the achievable approximation ratio it is the same as for Algorithm1.

3.3.3. Case 3: Guaranteed Download Time

In this case we introduce an additional performance guarantee. Our aim is to maximize the hit ratio and ensure a maximum download time $\tau$ for the whole item. For this purpose, it is necessary to introduce other constraints. Also in this case we include the possibility of downloading different chunks of the same content simultaneously, from different layer-2 caches. Given the need to ensure the download time, also the bandwidth of links between layer-2 caches and users is an issue generating a constraint. Essentially, it is necessary to ensure download time for all chunks, while respecting the limitation on the output bandwidth at all cache servers. This limitation is due to technology used, the bandwidth of links, and the operating conditions, such as thermal noise and interference at the receiver site in case of radio links. The minimum bandwidth necessary for transmitting a chunk is $b_{min}=\frac{size\left(\xi \right)}{\tau }$. Let $b_{i,j}$ be the bandwidth used to transfer contents from cache j to customer i. Clearly $B_j\ge {\sum }_i{b}_{i.j}$, where $B_j$ is the output bandwidth of the j-th cache server. The problem can be formulated as follows:

Problem 6.

$$\begin{array}{ccc}\hfill & & \underset{g_{j,\xi }}{max}\left\{\sum _{i=1}^W\sum _{\xi =1}^C\left(\underset{j=1}{\overset{|K_2|}{\bigvee }}{\varphi }_{i,j}{g}_{j,\xi }\right)P_{MZ,i}\left(\xi \right)\right\}\hfill \\ & & st\hfill \\ & & \sum _{\xi =1}^C{g}_{j,\xi }\le K_{2,j}\forall j\in \left[1,|K_2|\right]\hfill \\ & & \sum _{\xi =1}^C{g}_{j,\xi }\le \frac{B_j}{b_{min}}\forall j\in \left[1,|K_2|\right]\hfill \\ & & \sum _{\xi =1}^C{\varphi }_{i,j}{g}_{j,\xi }\le \frac{b_{i,j}}{b_{min}}\forall i\in \left[1,W\right]\forall j\in \left[1,|K_2|\right]\hfill \\ & & \sum _{\xi =1}^C\underset{j=1}{\overset{|K_2|}{\bigvee }}{\varphi }_{i,j}{g}_{j,\xi }\zeta (\xi ,m)=\left|m\right|\forall m\in [1,Q],\forall j\in \left[1,|K_2|\right]\hfill \\ & & g_{j,\xi }\in \left\{0,1\right\}.\hfill \end{array}$$

(16)

Note that for each user all items of an aggregate have the same popularity. Therefore, if sufficient bandwidth and storage are available, they are selected sequentially. Note also that the first two sets of constraints of Problem 4 are reduced to a single set, relevant to the minimum thresholds.

In Algorithm3 (see Code 4), the elements of the [$W\times |K_2|$] matrix FB are the free bandwidth of links connecting a user i and a cache j.

As for the asymptotic complexity of the algorithm, all changes due to the additional constraints introduce a complexity of the same order as that present in Algorithm1. Thus the complexity of Algorithm3 is the same as Algorithm2bis. For what concerns the performance, all constraints of the Problem 6 map into uniform matroids. Theorem A1 in the Appendix shows that the intersection of independents of uniform matroids are independent sets of a uniform matroid. The submodular maximization function is the same as Algorithm1. Following the same steps of the proof for Algorithm1, it is easy to find that the guaranteed approximation ratio of Algorithm3 is the same as Algorithm1.

Code 4 Solution to Problem 6.

1: functionAlgorithm3($\Xi ,\Phi ,\mathbf{P}$, $K_2$, $\left\{{\lambda }_i\right\}$,$\left\{B_j\right\}$, $b_{min}$, M)→${\epsilon }_j$ 2:     ${\epsilon }_j\leftarrow \varnothing \forall j$                          ▷ initialization 3:     $step\leftarrow 1$ 4:     $T_{1,j}\leftarrow 0,\forall j$                     ▷ counters of cache usage 5:     $T_{2,i,j}\leftarrow 0,\forall i,j$                    ▷ counters of link usage 6:     FB ← [free link bandwidths] 7:     $d(m,i)\leftarrow d(m,i){\lambda }_i\forall m,i$ 8:     while $\left(\exists j:T_{1,j}<min\left(K_{2,j},\frac{B_j}{b_{min}}\right)\right)\wedge \left(\exists i:T_{2,i}<\frac{b_{i,j}}{b_{min}}\right)\wedge \left(step\le C\right)$ do 9:         $m^{*},\left\{j^{*}\right\}$←Procedure2$\left(\Phi ,\mathbf{D},{\mathbf{T}}_1,\left|K2\right|,\Xi ,\mathbf{FB}\right)$        ▷ see Code 5 10:         step ← step+1 11:         if $T_{1,j^{*}}+1\le min\left(K_{2,j},\frac{B_j}{b_{min}}\right)\wedge T_{2,i,j^{*}}\le b_{i,j^{*}}\forall i:{\varphi }_{i,j^{*}}=1$ then 12:            ${\epsilon }_{j^{*}}={\epsilon }_{j^{*}}\cup \left\{m^{*}\right\}$ 13:            cache $m^{*}$ distributing items over $\left\{j^{*}\right\}$ 14:            update ${\mathbf{T}}_1$ and [${\mathbf{T}}_2]$ and FB 15:            $P(i,m^{*})\leftarrow P(i,m^{*})\left(1-{\Phi }^T(\left\{j^{*}\right\},i)\right)\forall i\in [1,W]$ 16:         else 17:            $\varphi (i,j^{*})\leftarrow 0\forall i$ 18:         end if 19:     end while 20:     return ${\epsilon }_j$ 21: end function

Code 5 Procedure used in Algorithm3.

1: functionProcedure2($\varphi ,\mathbf{D},{\mathbf{T}}_1,\left|K_2\right|,\Xi ,\mathbf{FB}$)$\to {\xi }^{*},\left\{j^{*}\right\}$ 2:     $\left\{m^{+}\right\}$←∅, $\left\{m^{*}\right\}$←∅ 3:     $\mathsf{{\rm Y}}={\Phi }^T\mathbf{D}$ 4:     while $\mathsf{{\rm Y}}\ne$ [0] do 5:         $\left\{m^{+}\right\}$←${max}_m\mathsf{{\rm Y}}$ 6:         for all $m\in \left\{m^{+}\right\}$ do 7:            $L_m\leftarrow 0$                  ▷ space available for content m in caches 8:            for all $j\in \{j:(j,m^{+})=max\left(\mathsf{{\rm Y}}\right)\}$ do 9:                $L_m\leftarrow L_m+K_{2,j}-T_{1,j}$ 10:            end for 11:            if $\left(L_m\ge size\left(m\right)\right)\wedge \left({\sum }_{j\in (j,m^{*})}\mathbf{FB}(:,j)\ge b_{min}\right)$ then 12:                $\left\{m^{*}\right\}\leftarrow m$ 13:            end if 14:            $m^{*}=$ max-size $\left\{m^{*}\right\}$ 15:            $\left\{j^{*}\right\}\leftarrow \{j:(j,m^{*})=max\left({\Phi }^T\mathbf{D}\right)\}$ 16:            return $m^{*},\left\{j^{*}\right\}$ 17:            if $\left\{m^{*}\right\}=\varnothing$ then 18:                $\mathsf{{\rm Y}}(m^{+},\{j\in (j,m^{+})\})\leftarrow 0$    ▷ decrease the max $\mathsf{{\rm Y}}$ values of {$m^{+}$} 19:                $newmax\leftarrow {max}_m\mathsf{{\rm Y}}(m^{+},:)$       ▷ columns to the second ones 20:                $\mathsf{{\rm Y}}(m^{+},\{j\in (j,m^{+})\})\leftarrow newmax$ 21:            end if 22:         end for 23:     end while 24:     return $\varnothing ,\varnothing$                       ▷ no solution found 25: end function

3.3.4. Case 4: Random Connections

In this case, in addition to the constraints above, we assume that each logical link is associated with a bandwidth ranging between 0 and a maximum value. In this view, the presence of a content in two caches accessible by the same user is not a redundancy but a solution to have the content accessible with the desired probability.

A simple approach for introducing an effective caching system in this environment is to guarantee the presence of elements in caches $in$ $expectation$. This problem has a formulation and a corresponding solution that can be derived from the problems already analyzed by replacing the ${\varphi }_{i,j}$ binary values with probability values of active connections between users and caches. In this way, it is possible to weight the popularity of contents for each customer with the probability of connection with caches. This approach would lead to the maximization of the expected popularity of the cached contents, without any specific guarantees. Although this case study could be of interest in operation, no significant algorithmic novelties can be added with respect to the previous cases. Thus, we present a more challenging problem that can be formulated by using stochastic network connections between users and layer-2 caches. This problem consists of maximizing the popularity of cached contents while providing the same guarantees of Problem 3, along with a given probability bound of accessing them. In more detail, we still include the possibility of taking advantage of parallel content download. This means that contents can be of different size and they can be split in portions of arbitrary size, in order to cache them in the free cache memory. In addition, we require that the entire content is cached. Since the links between users and layer-2 caches are stochastic, we consider a probability threshold $P_t$ of accessing the cached contents. This is the probability value for which the cached contents are considered available to users. Below this probability value, the caching service is considered unacceptable. Since the probability of links can be lower than $P_t$, in order to obtain the desired probability it is possible to replicate contents, or a portion of them, in different caches. In what follows, we assume statistically independent links, so in case of storing the same replica of content in different caches, the probability of having the content available can be found by considering statistically independent events. In synthesis, a content can be split and cached in different caches for having the whole of it available, and any portion of it can replicated in any caches for obtaining the desired access probability. This case study may be representative of different challenging situation that have recently generated research interests. For example, some edge computing applications, typical of 5G systems, leverage real time capabilities of cellular systems. Layer 2 caches with performance guarantees may either be implemented in the edge, for example, in the intersection of different network slices. The stochastic nature of the radio links make the proposed case study of interest. In what follows ${\sigma }_{i,j}$ indicates the probability of the link $(i,j)$. The relevant problem can be formulated as as follows:

Problem 7.

$$\begin{array}{ccc}\hfill & & \underset{g_{j,\xi }}{max}\left\{\sum _{i=1}^W\sum _{\xi =1}^C\left(\underset{j=1}{\overset{|K_2|}{\bigvee }}{\varphi }_{i,j}{g}_{j,\xi }\right)P_{MZ,i}\left(\xi \right)\right\}\hfill \end{array}$$

(17)

$$\begin{array}{ccc}& & st\hfill \\ & & \sum _{\xi =1}^C{g}_{j,\xi }\le K_{2,j}\forall j\in \left[1,|K_2|\right]\hfill \\ & & \sum _{\xi =1}^C{g}_{j,\xi }\le \frac{B_j}{b_{min}}\forall j\in \left[1,|K_2|\right]\hfill \\ & & \sum _{\xi =1}^C{\varphi }_{i,j}{g}_{j,\xi }\le \frac{b_{i,j}}{b_{min}}\forall i\in \left[1,W\right]\forall j\in \left[1,|K_2|\right]\hfill \\ & & \sum _{\xi =1}^C\underset{j=1}{\overset{|K_2|}{\bigvee }}{\varphi }_{i,j}{g}_{j,\xi }\zeta (\xi ,m)=\left|m\right|\forall m\in [1,Q],\forall j\in \left[1,|K_2|\right]\hfill \\ & & \sum _{j=1}^{|K_2|}{\sigma }_{i,j}{g}_{j,\xi }\ge P_t\forall i\in \left[1,W\right]\forall \xi cached\hfill \\ & & g_{j,\xi }\in \left\{0,1\right\}.\hfill \end{array}$$

(18)

This formulation of the problem still includes an optimization function with a value easy to increment by a greedy approach, which consists in maximizing the marginal increase of the optimization function at each selection of contents. Notice that the link probability values appear in the constraint (18) only, and not in the optimization function. The users that can access layer-2 caches with a probability greater than $P_t$ are not influenced by the constraint (18). Similarly, the caches such that $mi{n}_i{\sigma }_{i,j}\ge P_t$ can be used regardless (18). For what concerns the other caches, if we combine them for storing the same contents, so that $1-{\prod }_{j=1}^{|K_2|}\left(1-mi{n}_i{\sigma }_{i,j}\right)\ge P_t$, then the constraint (18) can be removed and the Problem 7 is equal to the Problem 6. In other words, we propose to use the Algorithm3 also for solving the Problem 7 with a substantial difference. Instead of considering the physical caches, in Code 6 Algorithm3 is applied to virtual caches ones. They are caches that are defined by combining the physical caches so that the constraint (18) is satisfied for any usage of them. A $\mathit{j}$-th virtual cache corresponds to a physical one if $mi{n}_i{\sigma }_{i,j}\ge P_t$. The other physical caches are pre-processed so that their physical storage capacity is partitioned and combined so that (18) is satisfied while providing the maximum bandwidth to be used by Algorithm3.

Figure 4 shows an example. Consider a single user connected with five caches. The cache size and the link probabilities are shown in Figure 4a, along with the threshold probability $P_t$. The three caches with link probability values higher than $P_t$ are selected, and the other ones are shown in Figure 4b. These two caches are combined. The process begins by considering the cache with largest size in order to obtain the maximum intersection. The relevant probabilities are combined in order to satisfy the threshold $P_t$. Thus, the size of the largest cache is split in two portions. The smallest one, corresponding to the intersection of the two caches, is combined with the other caches to form a virtual cache satisfying the threshold $P_t$. The other portion is left for any future usage, as shown in Figure 4c. The resulting set of four caches satisfying the threshold $P_t$ is shown in Figure 4d. When the Algorithm3 selects a virtual cache, the content is actually stored in all the physical caches that correspond to the virtual cache. In case of multiple users, in order to provide a set of virtual caches that can be greedily selected for maximizing the marginal increase of (17), the cache combination is done by using the link probabilities of each user, and at each step the minimum of the obtained probabilities is compared with $P_t$. The relevant procedure is shown in what follows.

Code 6 Alternative procedure to be used in Algorithm3 with virtual caches.

1: functionProcedure3(${\sigma }_{i,j},P_t,\left|K_2\right|,K_{2,j}$)→ mapping $\left\{j_v\right\}\leftrightarrow \left\{j\right\}$ 2:                        ▷$\left\{j_v\right\}$ denotes the set of virtual caches 3:     move caches from $K_2$ to the set of virtual caches: $\left\{j_v\right\}\leftarrow$$\{j:mi{n}_i{\sigma }_{i,j}\ge P_t\}$ 4:     sort remaining set R=$\{j:mi{n}_i{\sigma }_{i,j}<P_t\}$ by decreasing size 5:     while ${\prod }_{j\in R}\left(1-mi{n}_i{\sigma }_{i,j}\right)\ge P_t$ do 6:         combine caches by decreasing size until $mi{n}_i$${\sum }_{j=1,j\in R}^{j=j_F}{\sigma }_{i,j}\ge P_t$ 7:         virtual cache $j_{virt}=\{j_1\dots J_F\}$ 8:         size $\left(j_{virt}\right)\leftarrow size\left(j_F\right)$ 9:         ${\sigma }_{j_{virt},i}\leftarrow {\sigma }_{j_F,i}\forall i\in \left[1,W\right]$ 10:         for all $index\in \{j_1,\dots ,j_{F-1}\}$ do 11:            $\{size\left(j_{index}\right)-size\left(j_F\right)\}$ 12:         end for 13:         move $\left\{j_v\right\}\leftarrow \{j_1\dots J_F\in$ R } as a virtual cache 14:         sort remaining set R=$\{j:mi{n}_i{\sigma }_{i,j}<P_t\}$ by decreasing size 15:     end while 16: end function

Note that in case of equal size layer-2 caches, the steps 13 and 14 are not necessary. In this case, it is easily to see that the worst case computational cost of the procedure is $K_2^2$, corresponding the extreme case that each cache probability is below the threshold $P_t$ and each cache is combined with all others. After the Procedure3 is accomplished, Algorithm3 can be used to allocate contents to virtual caches, and this allocation is used to store contents in physical caches.

3.4. Population of Layer-1 Caches

Once layer-2 caches are populated, layer-1 caches can be easily populated by selecting, for each user, the most convenient contents not cached in the reachable layer-2 caches. The criterion used may either be the content popularity for fixed content size, or density of popularity for variable content size. The Procedure4 in Code 7 below is for fixed content size. The extension to variable content size is straightforward.

Code 7 Layer-1 cache population for fixed content size.

1: functionProcedure4($K_1,\Xi ,size\left(\xi \right)\forall \xi ,W,\left\{g_{j,\xi }\right\}$)$\to \left\{q_{i,\xi }\right\}$ 2:     $\mathit{content}\_\mathit{index}=0$ 3:     for all $i\in$ {customers} do 4:         while (layer-1 cache $free\_space>0$)$\wedge \left(content\_index<C\right)$ do 5:            ${\xi }^{*}\leftarrow argmax\left(P_{MZ,i}\left(\xi \right)\times size\left(\xi \right)\right)$ 6:            $P_{MZ,i}\left(\xi \right)\leftarrow 0$           ▷ not selectable in the next step 7:            if $size\left({\xi }^{*}\right)\le$ layer-1 cache $\mathit{free}\_\mathit{space}$ then 8:                cache content ${\xi }^{*}$ in layer-1 cache, $q_{i,{\xi }^{*}=1}$ 9:                $\mathit{content}\_\mathit{index}\leftarrow \mathit{content}\_\mathit{index}+1$ 10:                $\mathit{free}\_\mathit{space}\leftarrow \mathit{free}\_\mathit{space}-size\left({\xi }^{*}\right)$ 11:            end if 12:         end while 13:     end for 14: end function

3.5. Summary of Algorithmic Approaches

Table 2. Summary of Problems and relevant Algorithms.

Problem	Problem Features	Algorithms
Problem 2:	addressing layer-1 caching in (5) in a basic setting: equal-size items and stationary requests pattern	Procedure4 in Code 7
Problem 3:	addressing layer-2 caching in (6) in a basic setting: equal-size items and stationary requests pattern	Algorithm1 in Code 1
Problem 4:	addressing layer-2 caching in (14) with variable size items and stationary requests pattern	Algorithm2 in Code 2
Problem 5:	addressing layer-2 caching in (15) with variable size items and stationary requests pattern, taking advantage of parallel downloading	Algorithm2bis and Procedure1, both in Code 3
Problem 6:	addressing layer-2 caching in (16) with variable size items and stationary requests pattern, taking advantage of parallel downloading and guaranteeing to complete the download within a maximum download time	Algorithm3 in Code 4, and Procedure2 in Code 5
Problem 7:	addressing layer-2 caching in (17) with variable size items and stationary requests pattern in a topology with random connections, taking advantage of parallel downloading and guaranteeing to complete the download within a maximum download time	Algorithm3 in Code 4, and Procedure3 (virtual caches) in Code 6

recaps the mapping between the problems defined in this paper and the algorithms and procedures defined to solve them. For each problem, we have indicated the equations used to model it, its main distinguishing features, and which algorithm is used to address these features.

4. Numerical Results

In this section we present some results of the numerical analysis of the caching problems illustrated above, performed by using a simulator specifically implemented [35]. The simulation general parameters were chosen according to the description of some existing popular content distribution systems [7,8,9]: $C=2000$, $|K_2|=3$, $W=10$; the size of layer-1 caches was set equal to the size of layer-2 caches; layer-1 caches and layer-2 caches are fully connected, that is ${\varphi }_{i,j}=1\forall i,j$. From the algorithmic viewpoint, this is the most challenging cache interconnection. As for the traffic model, we used $\alpha =1.3$ and $q=4$. In the experiments with equal content size, all volumes are normalized to the individual content size. So the size of each item equals 1. In experiments with variable content size, all volumes are normalized to the minimum value. For what concerns the content size, the value range that can be observed in operation is extremely variable. For these experiments we inspired to the typical file size of a movie, which depends on various factors, such as the length, resolution and encoding. In this paper we report the numerical results relevant to a range between 0.5 to 2.5 gigabytes, resulting in a normalized uniform distribution between 1 and 5. Some variations in this range do not significantly change results. In the experiments with a constraint on the link bandwidth, we assumed that $b_{i,j}/b_{min}=30$ units. In the experiments with stochastic links, we used a probability threshold $P_t=0.8$ and assumed that each link has a probability of being active ${\sigma }_{i,j}=0.7$. In order to analyze the proposal in more realistic experiments, we introduced the estimation of the content popularity. In this paper we report the performance of two extreme situations, relevant to a length of the estimation window N, equal to 2000 and 10,000 inter-arrival times, respectively. In fact, a low value should be used when the popularity of content, especially those requested most frequently, is expected to change rapidly. A value of 2000, for a cache serving content in a restricted area, could be used for a stationary period of content popularity of the order of a few minutes. A value equal to 10,000 is used to manage slower variations, however evident. Even slower variations, such as those that occur on time scales in the order of hours, allow for very reliable estimates, therefore with performance that approach the ideal one, corresponding to the hypothesis of known popularity values. All hit ratio values shown in the following figures are plotted with the 99% confidence interval. The initial set of experiments, relevant to equal size items, with and without popularity estimation, are finalized to evaluate the capability of the proposed algorithm to approach the optimal known values of hit ratio, evaluated by means of (2), considering the actual size of the layer-1 caches and the sum of the size of layer-2 caches accessible by each user. Since the main elements of Algorithm2bis are included in Algorithm3, the set of algorithms implemented are Algorithm1, Algorithm3 and Algorithm4 for equal-size contents, and Algorithm2, Algorithm3, and Algorithm4 for variable size items. Please note that Algorithm4 corresponds to Algorithm3 used in conjunction with Procedure3 . In addition, a comparison with LFU is presented in order to compare the proposal with one of the most appreciated solutions.

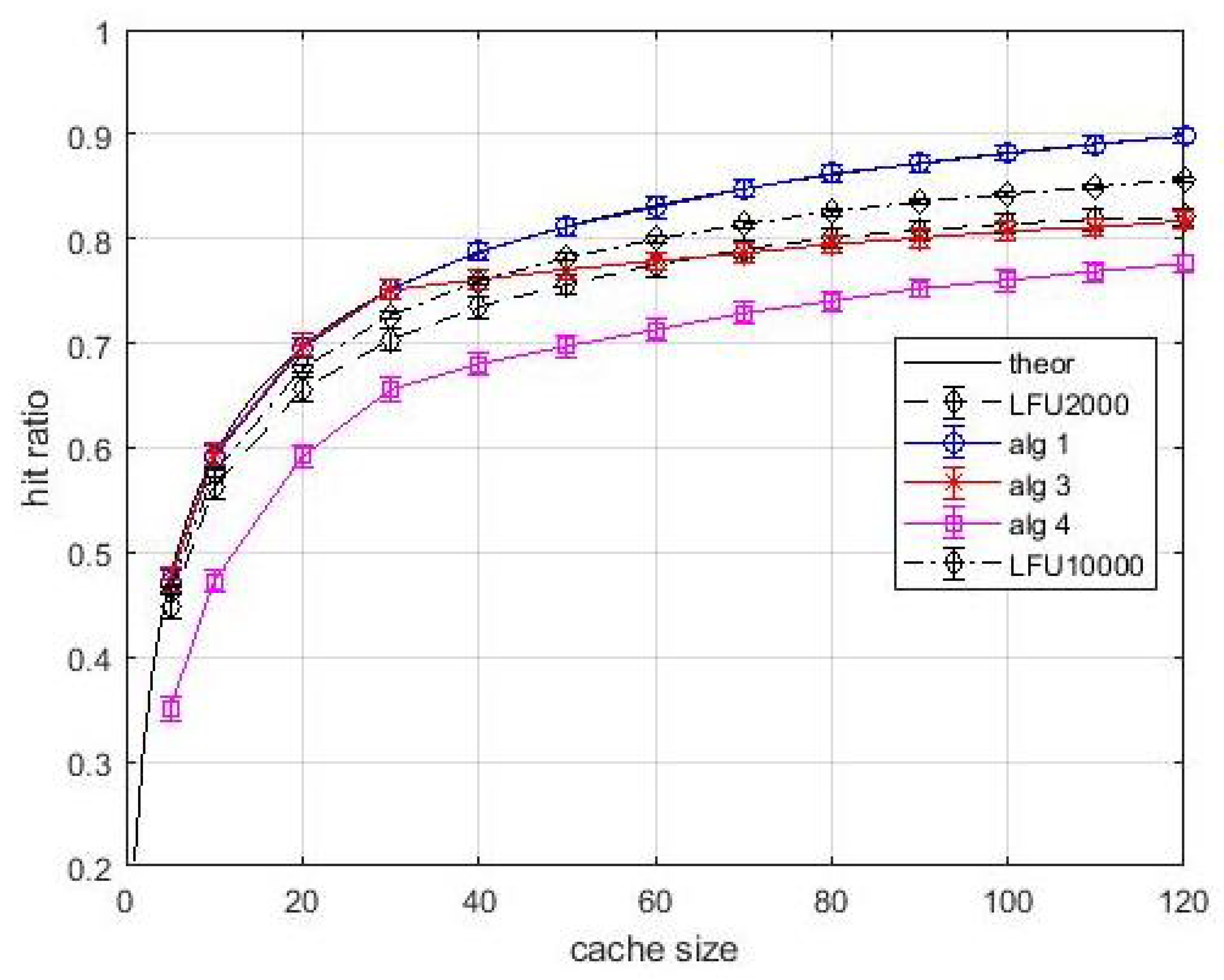
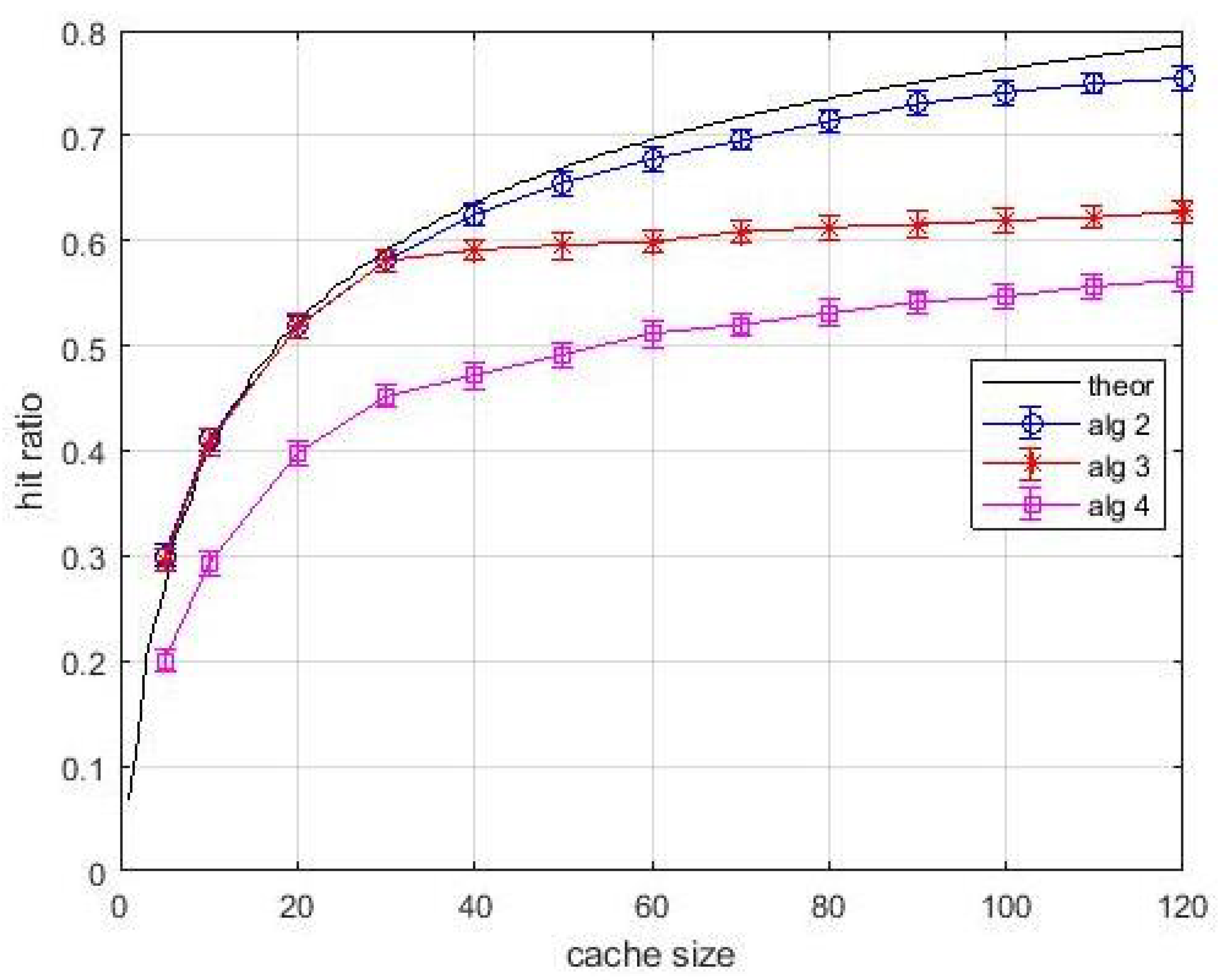
Figure 5 shows the hit ratio vs. cache size. The popularity of each item is the same for all users. The solid black line is relevant to the optimal value which is easily determined by using (2) when caches are loaded with the items by decreasing popularity, or popularity density, starting with layer-2 caches. Thus, the black solid curve is the performance upper bound. Note that this upper is just a baseline, and our proposal in based on estimated popularity values. In our analysis the LFU content estimation windows are equal to 2000 and 10,000 inter-arrival times, respectively. Note that the only meaningful comparison in this figure and in the following ones is between Algortithm1 and LFU, since all other performance curves are relevant to different caching problems. The first general observation is that the 99% confidence intervals are very tight, so the estimate is accurate. We can observe that Algortithm1 produces hit ratio values coincident with the upper bound. Hence, in this easy situation, the greedy approach not only guarantees $\left(1-1/e\right)$ approximation ratio, but can converge towards the optimum. The LFU performance is lower than that of Algortithm1 for both estimation windows. This is indeed an expected behavior since the LFU policy requires the estimate of the frequency of arrival of contents. However, for avoiding a biased comparison, the hit statistics were collected after a start-up time of an estimation window. Although the performance gap between Algortithm1 and LFU in this case study was expected, the fact that the proposed greedy approach converges towards the optimum is an encouraging result before proceeding to analyze more complex situations. For what concerns Algortithm3, the effects of bandwidth constraints are evident. In fact, until the number of parallel contents that can be transmitted is higher than the cacheable contents, the performance of Algortithm3 is the same as Algortithm1. When the link bandwidth happens to be the actual bottleneck for allocating further contents, the rate of performance improvement with the cache size decreases. This improvement, although it occurs at a slower rate, is due only to layer-1 caches. This is another confirmation of the importance of layer-1 caches. As for the Algortithm4, in addition to the bandwidth limitations, we consider the stochastic links between layer-1 and layer-2 caches. Note that all links have a probability of being active that is lower than the probability acceptance threshold. However, due to the introduction of virtual caches, which is central in Algortithm4, the caching system is turned from unavailable to available with an appreciable performance, although not at the same level of the other situations analyzed above.

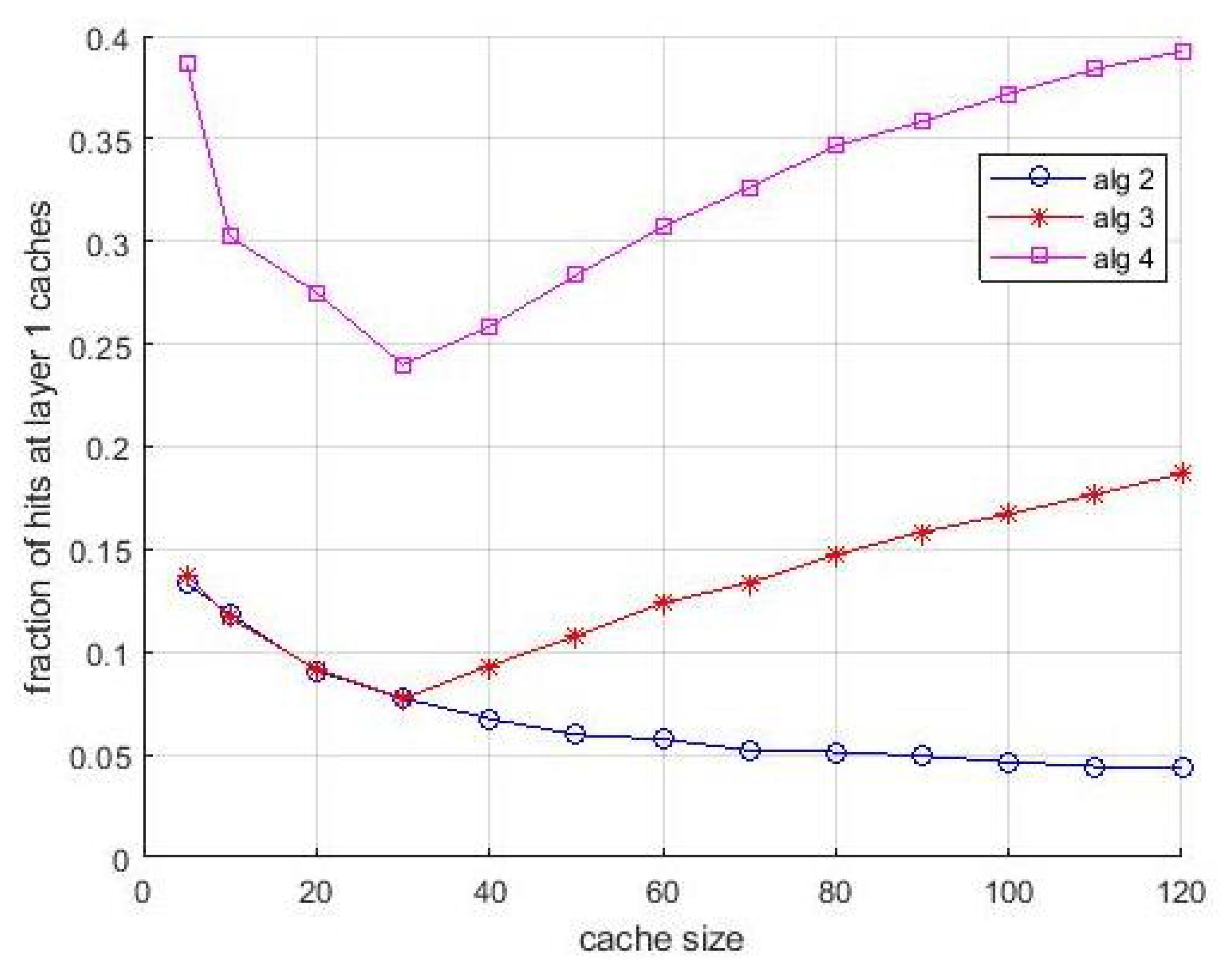
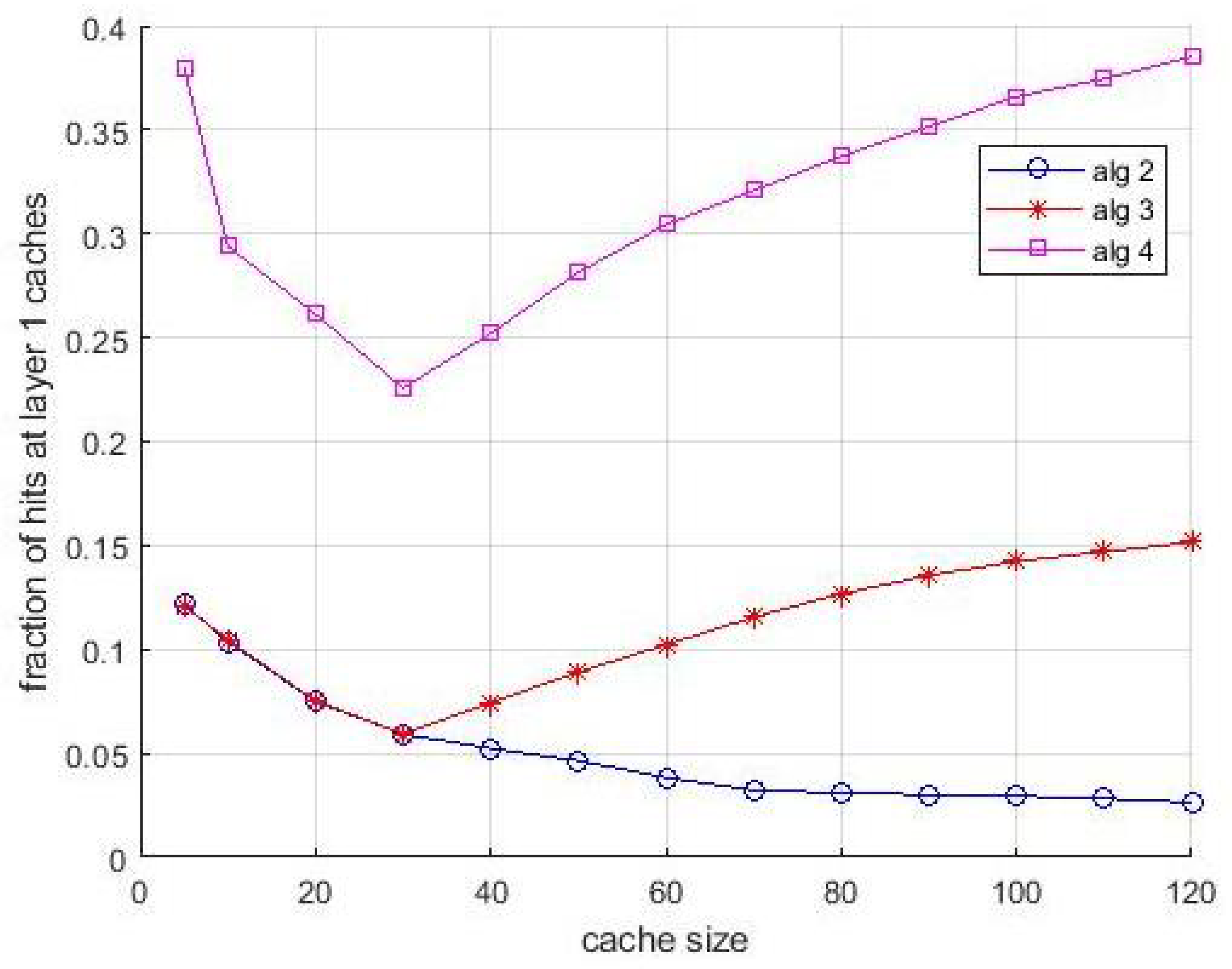
It is interesting to associate the observations of the performance shown in Figure 5 with the behavior shown in Figure 6. It shows the fraction of hits collected at the layer-1 caches vs. cache size. This figure confirms the compensating role of the layer-1 caches when the allocation in layer-2 caches is not optimal. For some situations, in particular for Algortithm3 and Algortithm4, this fraction is significant, and for both algorithms the effect of bandwidth limitations is even more evident. Notice that the evidence of this compensating effect is not only an interesting result per se, but makes the performance difference between the algorithms observed in Figure 5 even more evident. The asymptotic difference in Figure 6 between Algortithm1 and LFU is due to the first miss that happens in caches the first time an item is requested. The presence of multiple caches compensate this effect almost totally, since if a content is cached in a layer-2 cache, the first miss for that content does not happen for the other users that can access the cache for receiving the same content.

For what concerns the performance of the proposed algorithms when the content popularity is estimated, Figure 7 and Figure 8 show the hit ratio for fixed content size. Popularity is estimated by using the LFU estimation procedure, based on a sliding window, for all algorithms. Note that our approach could be used in conjunction with other estimation algorithms, such as that one used for implementing the TinyLFU [19]. Hence, in the case of pre-allocation of contents, that is for Algortithm1, Algortithm3, and Algortithm4, the popularity values estimated by LFU during an estimation window are used, so that the comparison is fair. 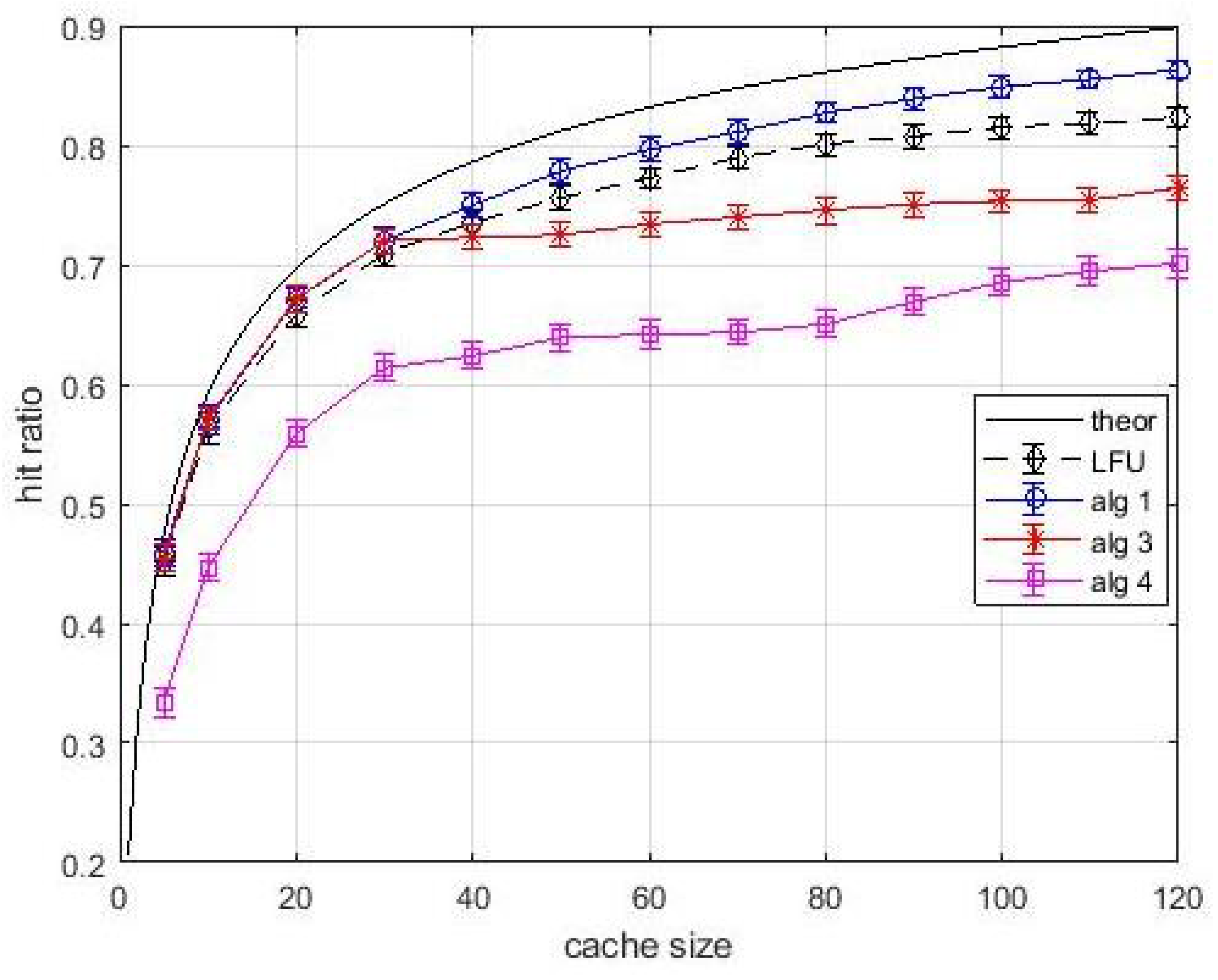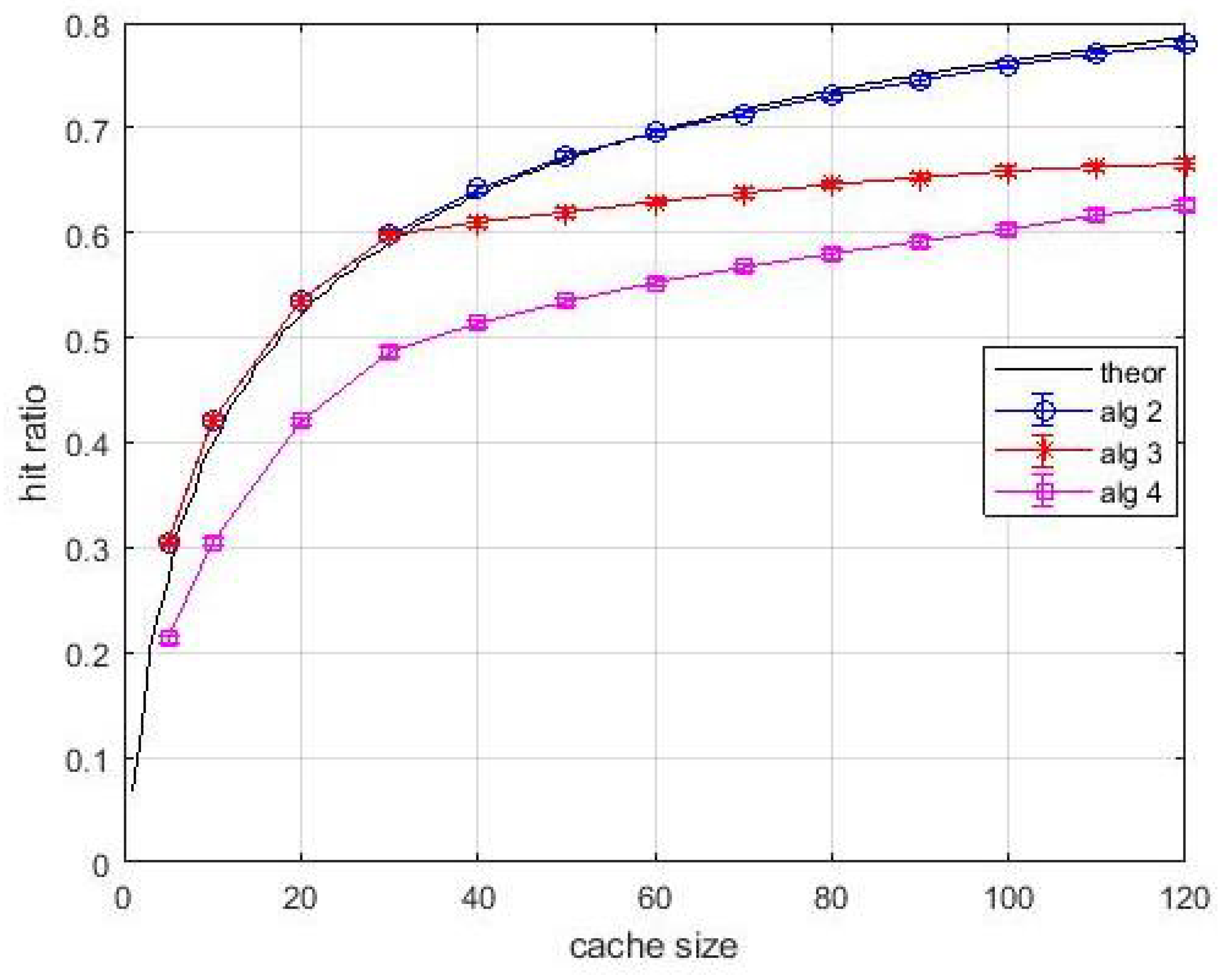Figure 7, relevant to an estimation window of 2000 interarrival times, shows that the performance of Algortithm1 is lower than the theoretical one. The performance degradation is due to the use of estimated popularity values. Nevertheless, Algortithm1 still outperforms LFU. A slight performance degradation is observed also for Algortithm3 and Algortithm4. 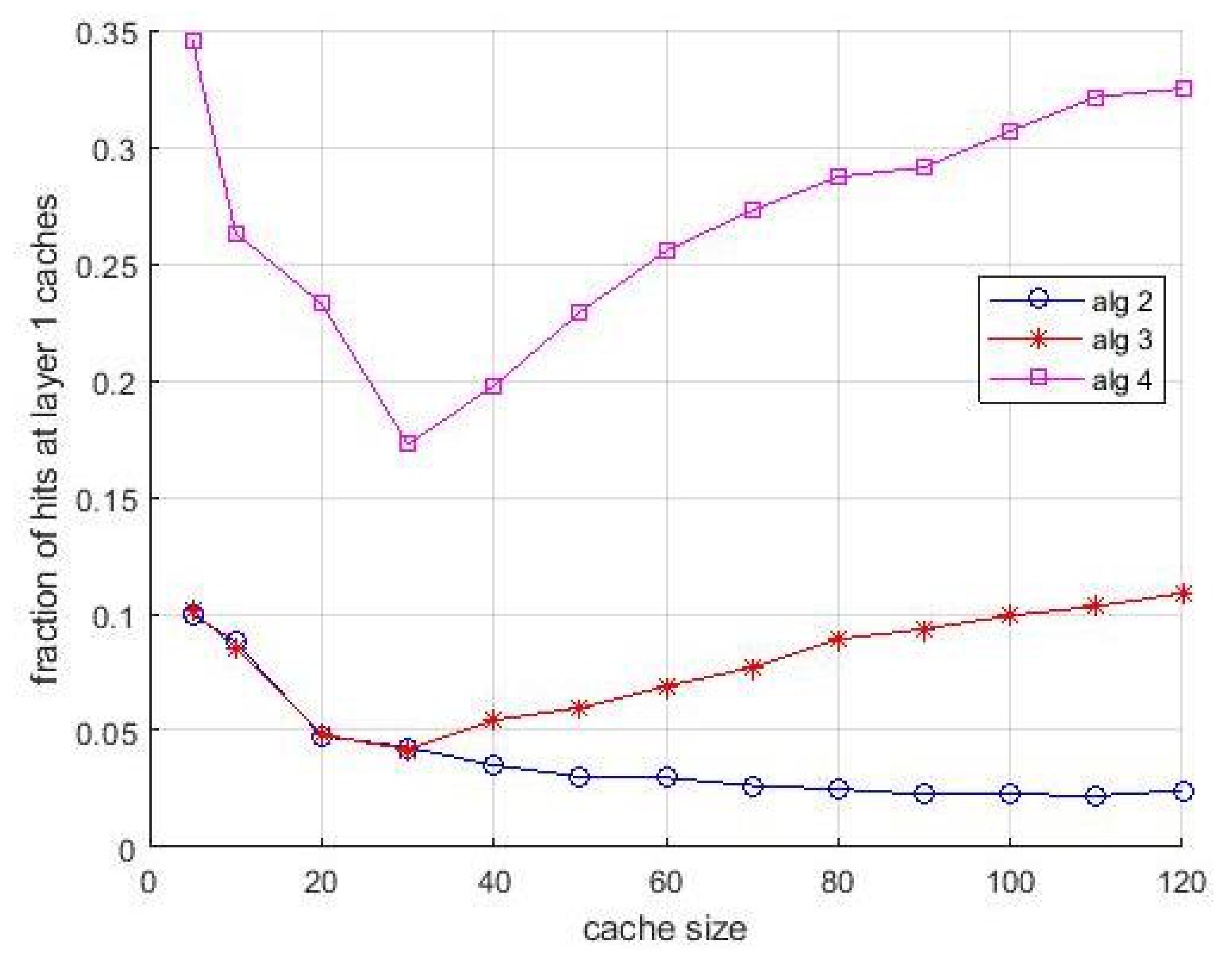It is interesting to observe in Figure 8 that the performance degradation is present also in layer-1 caches. This effect can be explained with the coarse estimation of the popularity of less frequently requested items over an (almost) fixes window. These items are typically found in layer-1 queues. However, their contribution to the average hit ratio is quite limited, and the observed degradation is acceptable. 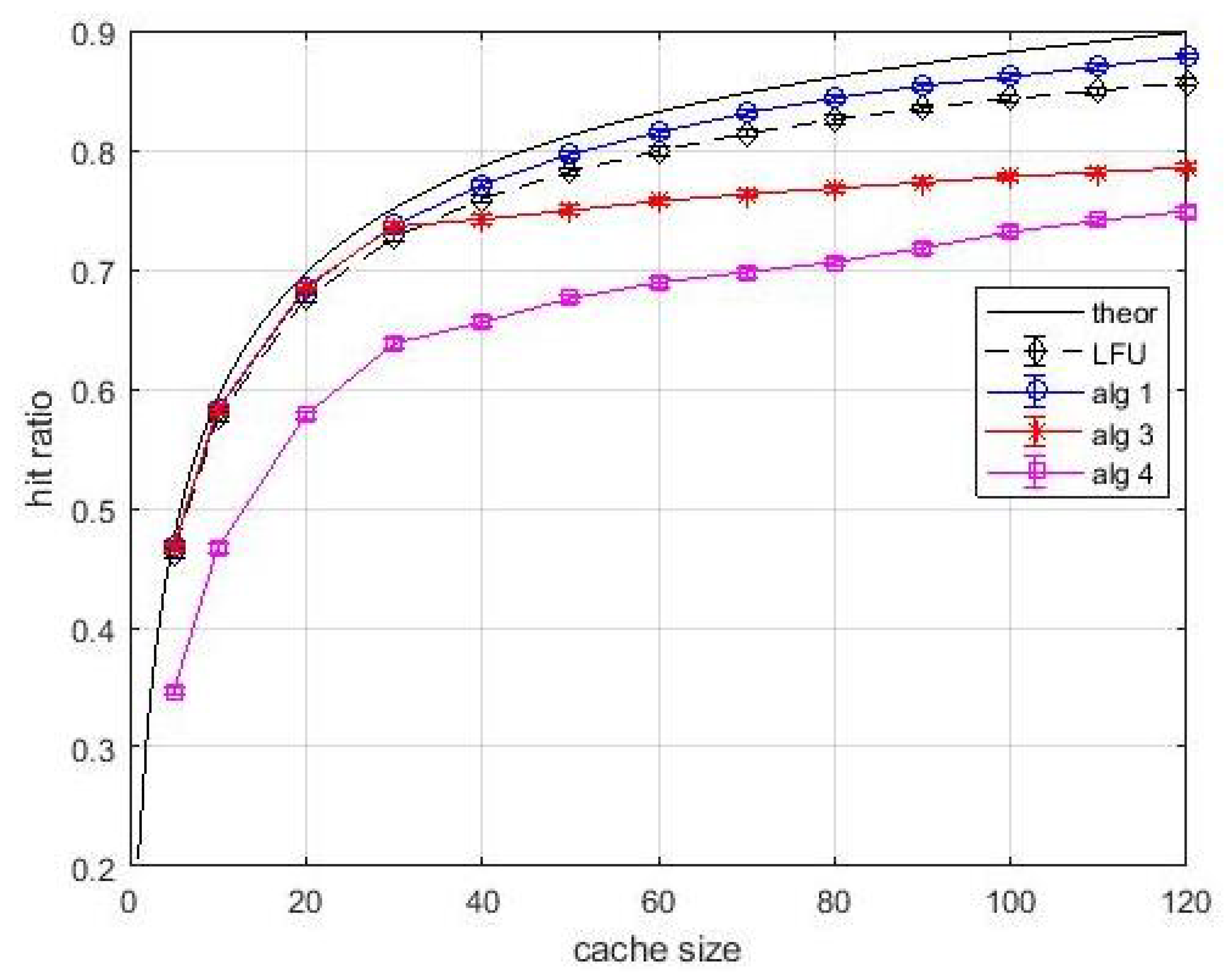If the estimation window increases to 10,000 inter-arrival times, in Figure 9 and Figure 10 we can observe that the performance degradation is negligible. Algortithm1 still outperforms LFU, and in case of Algortithm3 and Algortithm4 the performance is mostly determined by bandwidth limitations and stochastic links than by estimated popularity values. Given the well assessed performance comparison between Algortithm1 and LFU, the following experiments, based on variable content size, will focus in Algortithm2, which is the extension of Algortithm1 for handling variable size, Algortithm3 and Algortithm4.

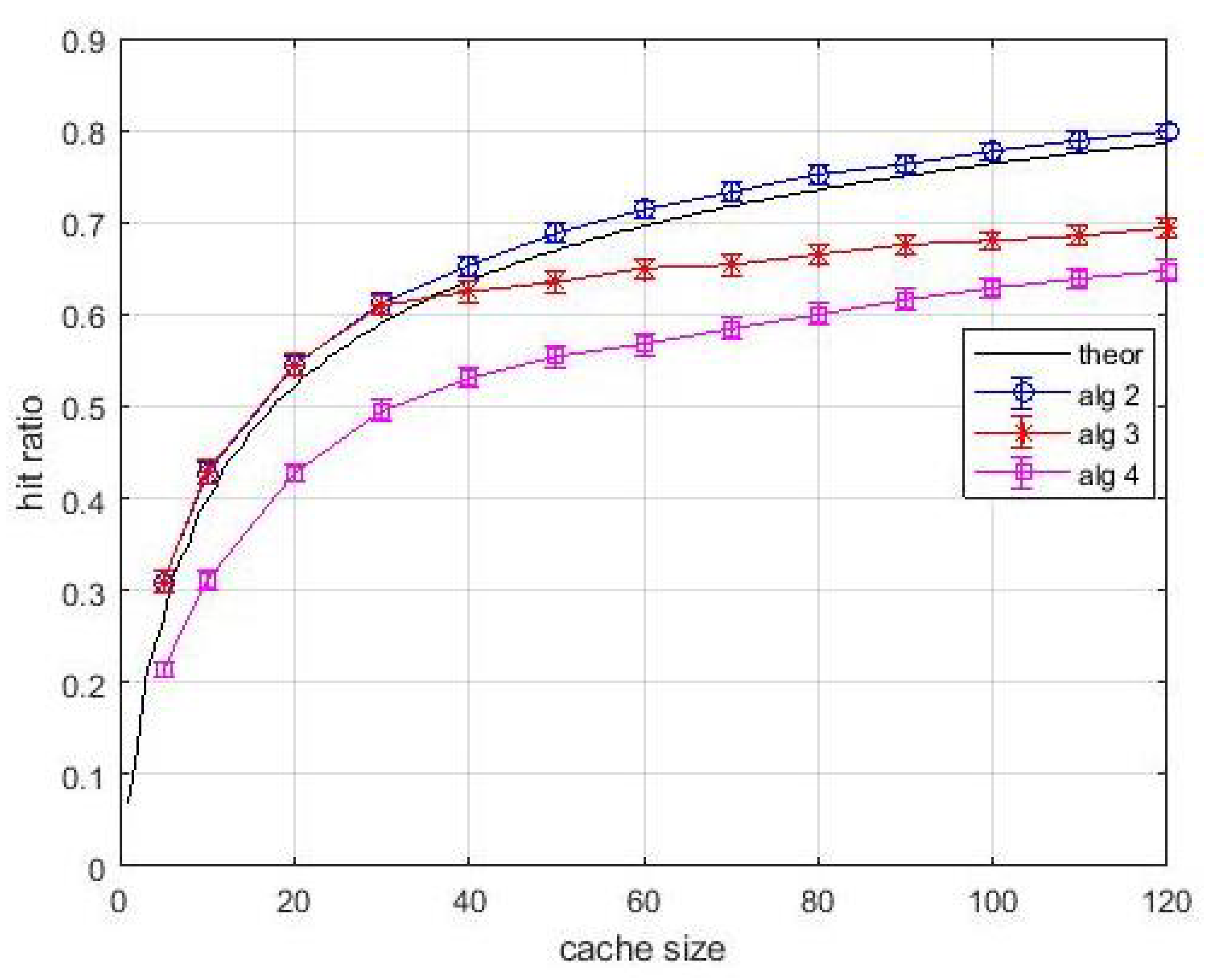
Figure 11 and Figure 12 are relevant to an experiment with known content popularity and variable content size. The curve labelled as theoretical shows the hit ratio computed by (2) by considering popularity only. Differently, the proposed algorithms make use of the density of popularity. This choice is done for highlighting the benefits due to the use of this approach. In fact, we can observe in Figure 11 that curve relevant to Algortithm2 is above the theoretical one. The effect of resource constraints are still evident for Algortithm3 and Algortithm4, but the known popularity makes the effect of layer-1 queues appreciable. It can be observed both in Figure 11, in the rate of performance improvement for increasing size of caches and in the neatness of Figure 12, which shows a significant and steadily increasing contribution of layer-1 caches. Hence, the variable content size has not impaired the performance achievable by the proposed algorithms.

When popularity is unknown, it is estimated as in the previous experiments, through a preliminary estimation during a sliding window of 2000 and 10,000 interarrival times, respectively. Figure 13 and Figure 14 are relevant to first case. The theoretical curve is the same as in Figure 11. We can observe a slight decrease of the hit ratio, negligible for small cache size, tolerable for large ones. Most of considerations done for Figure 12 are valid also for Figure 14. However, the not perfect popularity estimation has an impact on the hit rate in layer-1 caches. We stress that this decrease of the hit rate in layer-1 caches is not due to a decrease of their compensation capabilities, since their size allow caching some items that had to be cached in layer-1 caches. It is due to the coarse estimation of the popularity of items that are requested rarely by users. In fact, the overall penalty in the hit rate is quite tolerable.

This observation is confirmed by Figure 15 and Figure 16, which are relevant to the longer estimation window. In this case, although popularity values are estimated, the level of the observed performance is considerable.

The main outcomes of our performance evaluation campaign are summarized in in

Table 3. Summary of performance evaluation results.

Case	Configuration Parameters	Main Performance Evaluation Results
Case 1:	fixed item size, known content popularity	Algorithm1 outperforms LFU and approaches theoretical limit (2). Known popularity makes the effect of layer-1 queues appreciable
Case 2:	fixed item size, popularity estimation with $N=$ 2000	Algorithm1 outperforms LFU, but it is below the theoretical limit (2)
Case 2:	fixed item size, popularity estimation with $N=$ 10,000	Algorithm1 slightly outperforms LFU, the distance from theoretical limit (2) is not so significant thanks to the longer N
Case 3:	known content popularity and variable content size	Algorithm2 outperforms theoretical limit (2) thanks to the usage of density of popularity, LFU is not considered. Known popularity makes the effect of layer-1 queues appreciable
Case 4:	variable content size and popularity estimation with $N=$ 2000	Algorithm2 approaches theoretical limit (2), LFU is not considered. Estimated popularity makes hit ratio to decrease and less appreciable the effect of layer-1 queues
Case 4:	variable content size and popularity estimation with $N=$ 10,000	Algorithm2 nearly overlaps to theoretical limit (2) thanks to long N, LFU is not considered. Long estimation window N makes less remarkable the performance penalty

. It focuses mainly on the best performing algorithm and its comparison with theoretical limit and with LFU (only for fixed item size). Clearly, Algorithm3 and Algorithm4, working with stronger constraints, will suffer of performance degradation. This has already been commented with figures and it is not captured in Table 3.

5. Conclusions

This paper considers a networked caching architecture based on a two-layer hierarchy, used to define some content distribution scenarios, with different complexity. The proposed caching strategies for each scenario are based on greedy algorithms with guaranteed approximation ratio, according to the theory of monotone function maximization subject to matroid constraints. In our proposals, layer-2 caches have the main role to maximize the hit ratio, while layer-1 results to have a compensating role for sub-optimal usage of layer-2 caches. These algorithms were also analyzed through an extensive simulation campaign, which highlighted the contribution of each hierarchical layer of caches to the obtained hit ratio values.The numerical analysis included also a comparison with the well-known LFU eviction strategy, adapted to the analyzed systems. Results show very good performance, under the assumption of either known or unknown content popularity. The future research objective consists of optimal caching for mobile users and variable connection with layer-2 caches.