A Classification Method for Academic Resources Based on a Graph Attention Network
Abstract
1. Introduction
2. Related Work
3. Definition
3.1. Definition of Notations
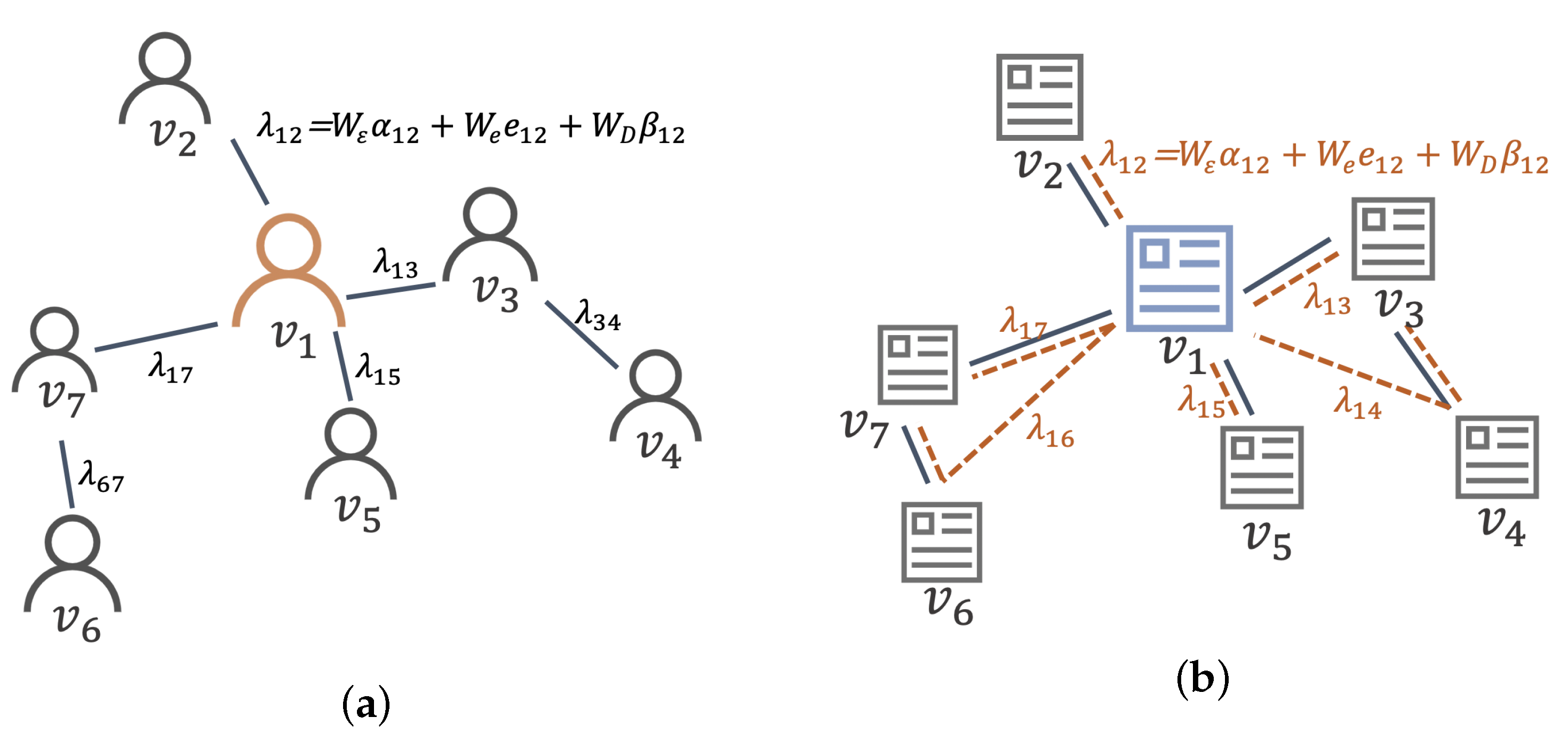
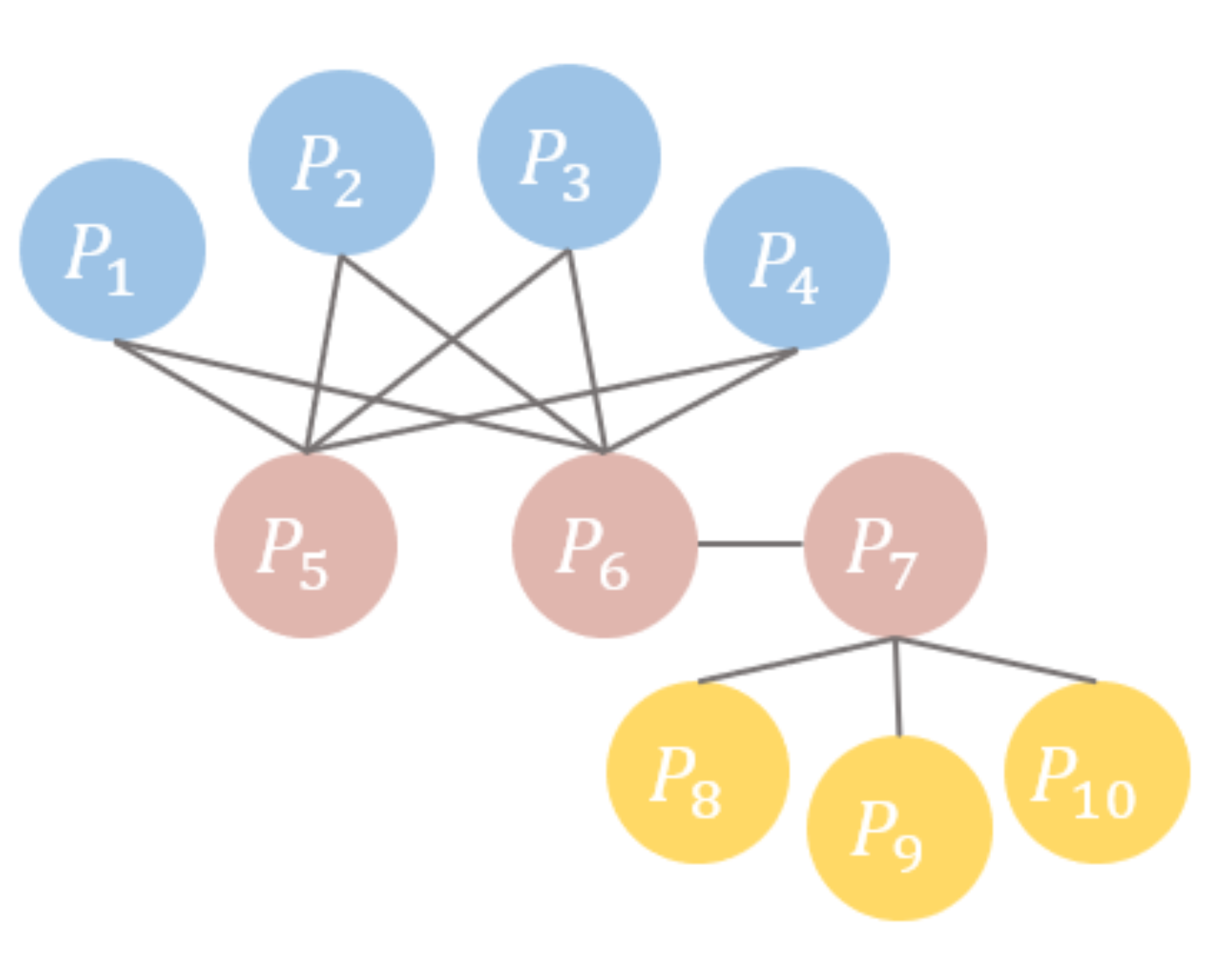
3.2. Academic Resource Networks
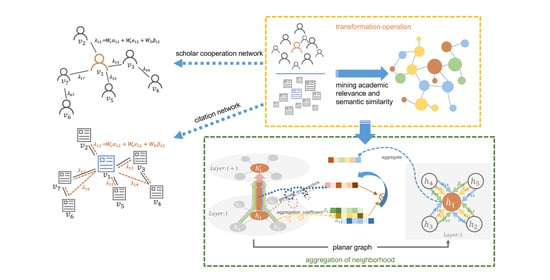
4. Proposed Method
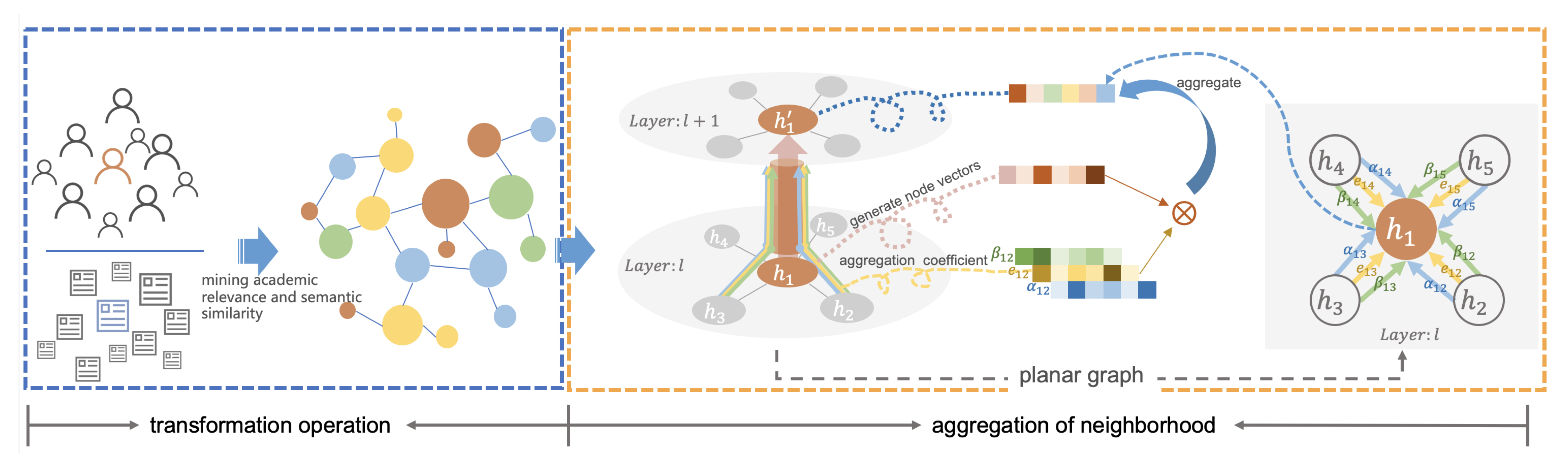
4.1. Mining and Representation of Academic Relevance
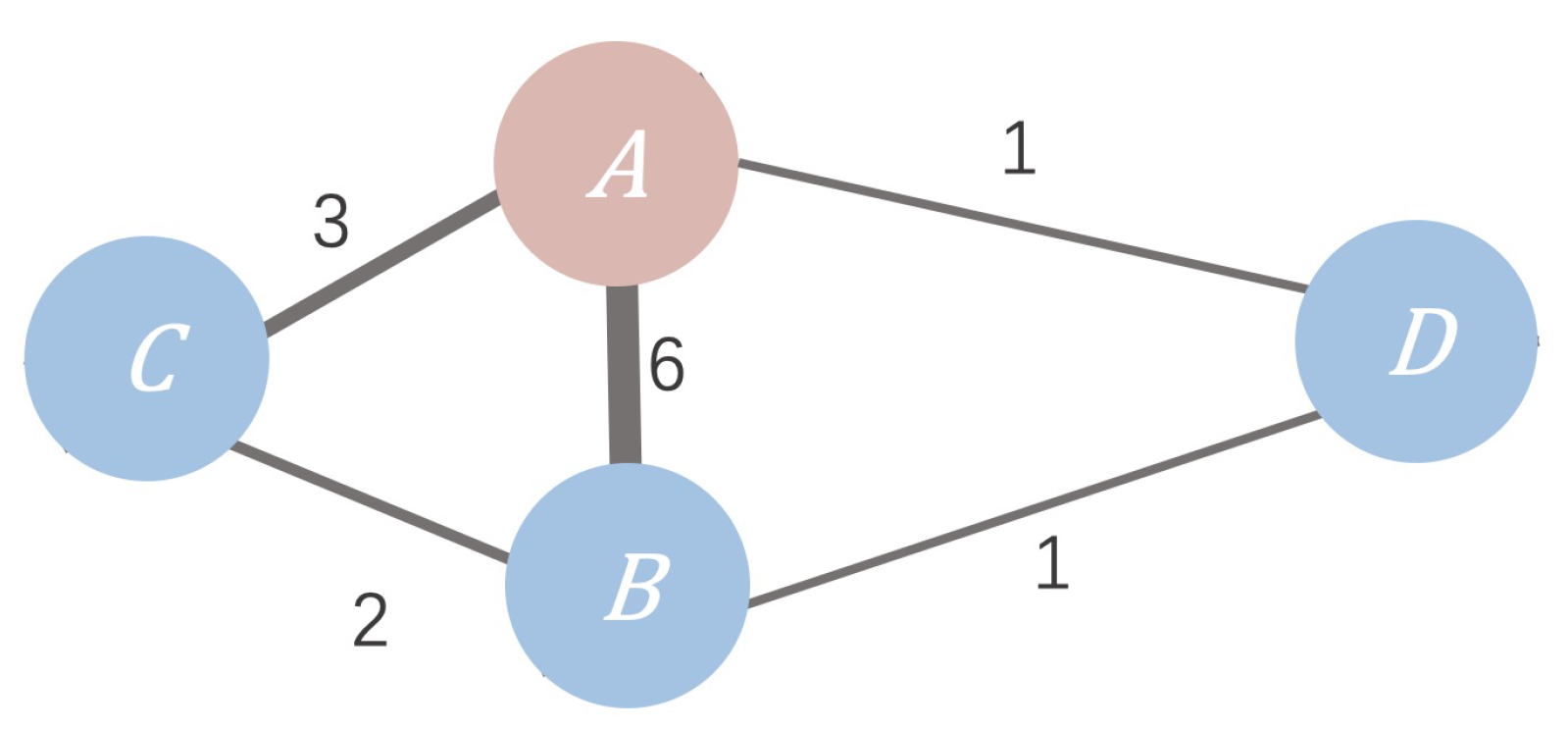
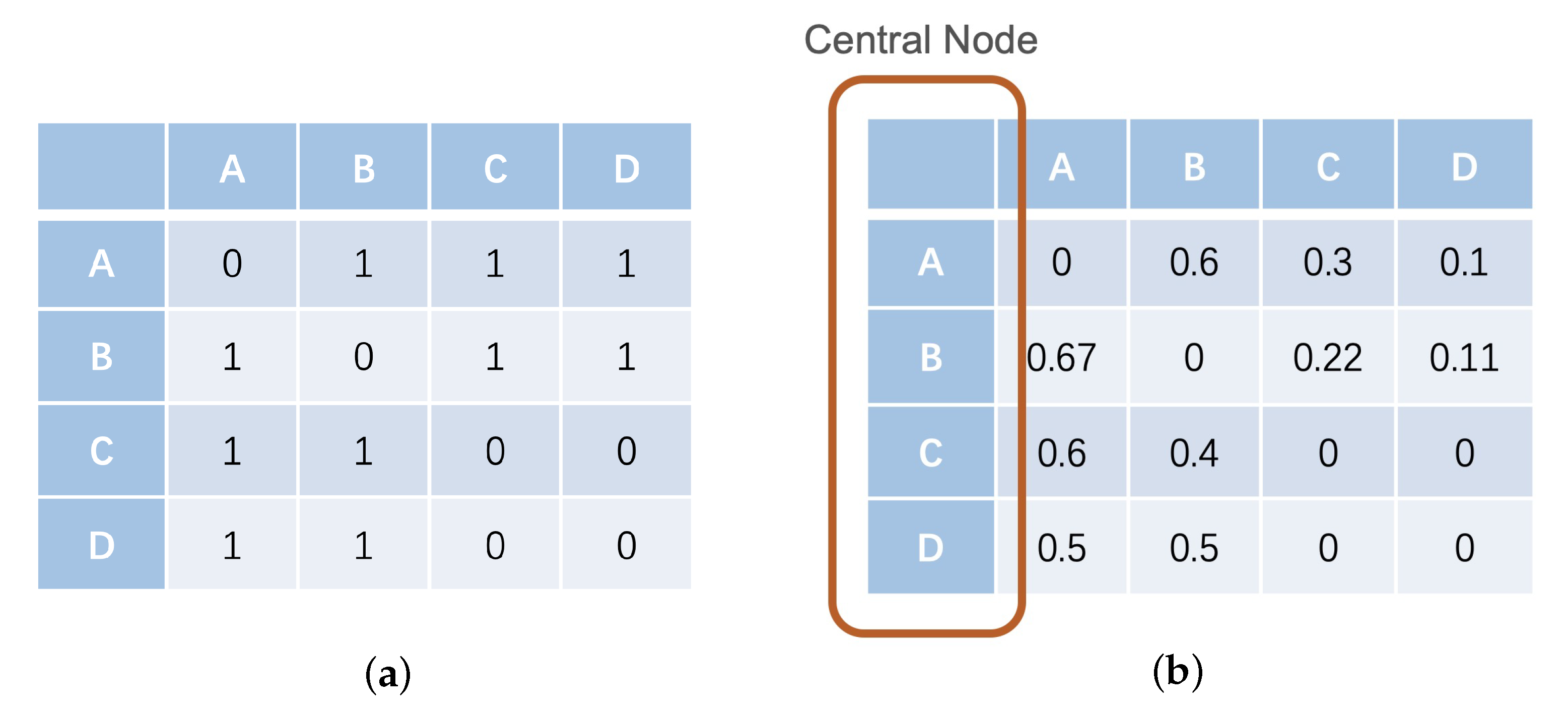
- We calculate the degree matrix D of a network of N nodes, where is the degree of node .
- The influence of neighboring node j on central node i is expressed as the ratio of the degree of node j to the degree of node i, which can be obtained according to Equation (1).
- The influence factor of each node and are obtained through normalization according to Equation (2).
4.2. Aggregation Based on an Attention Mechanism
5. Experiment
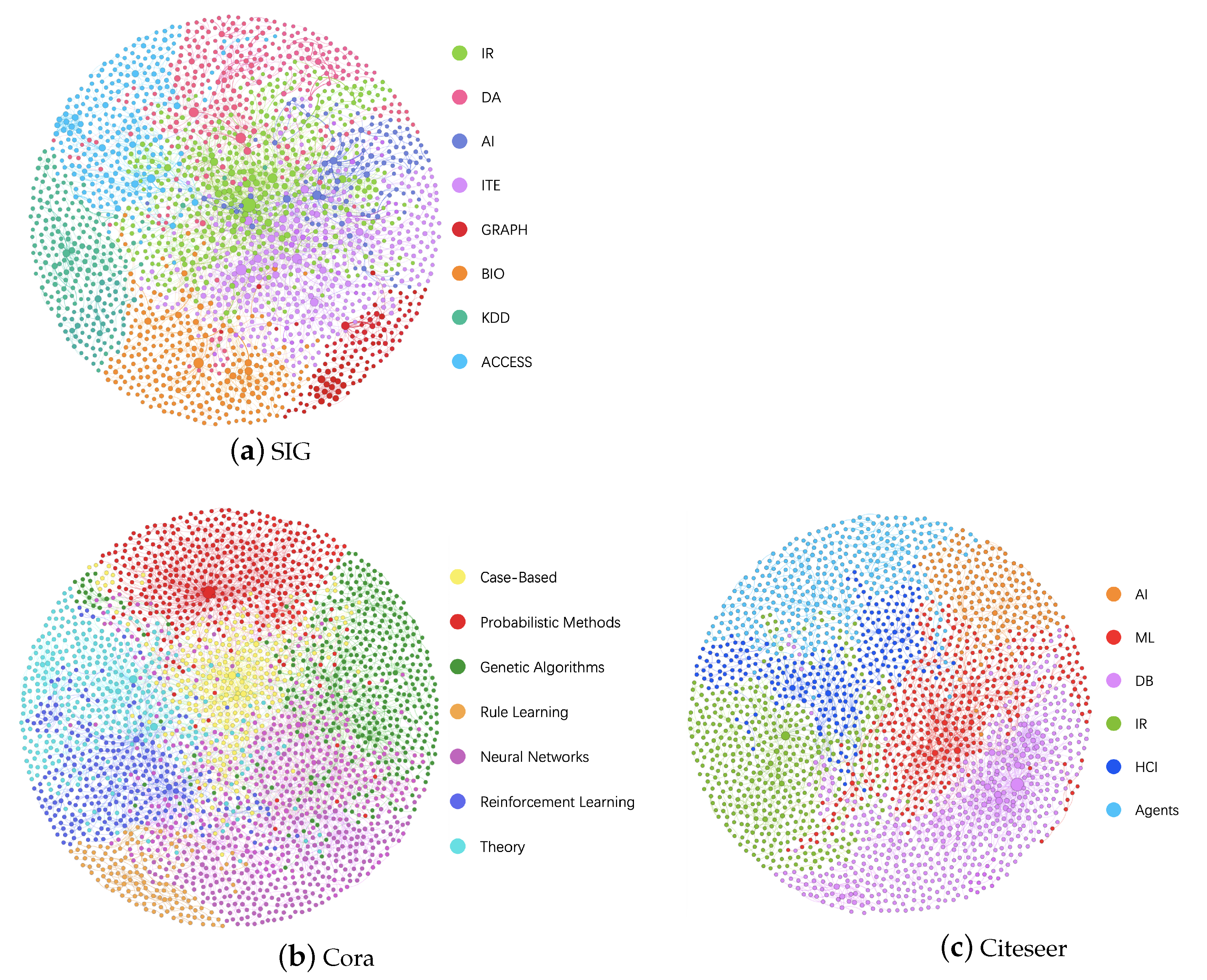
5.1. Datasets
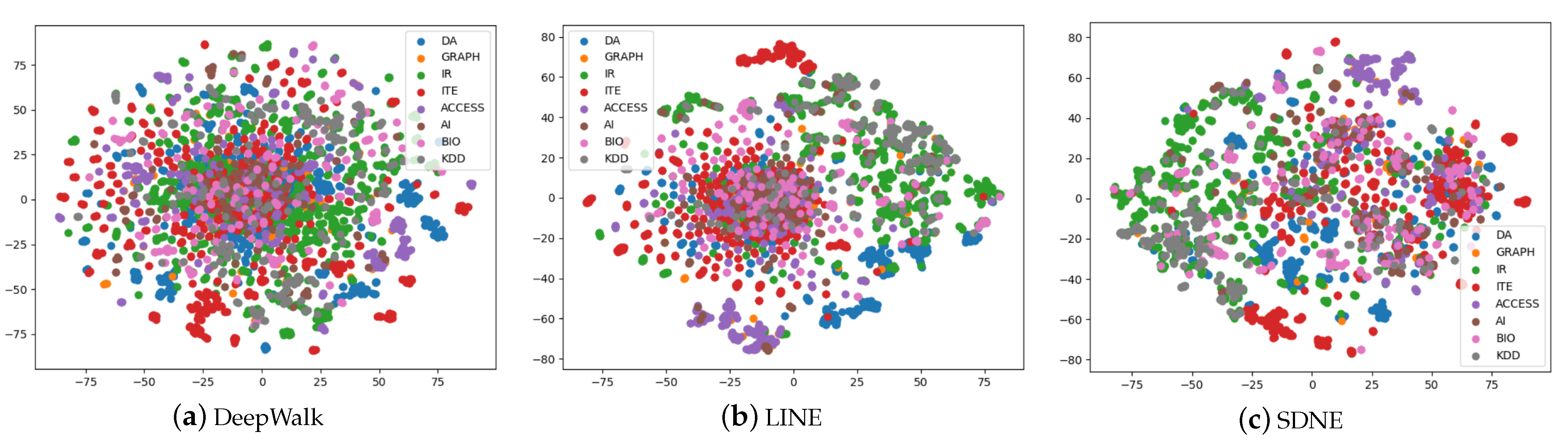
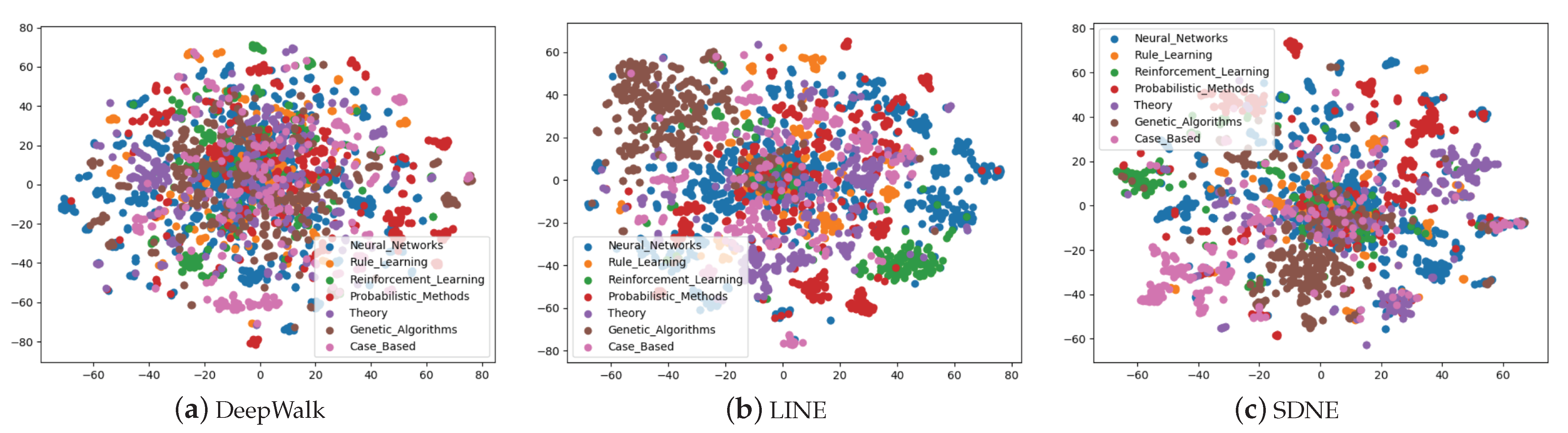
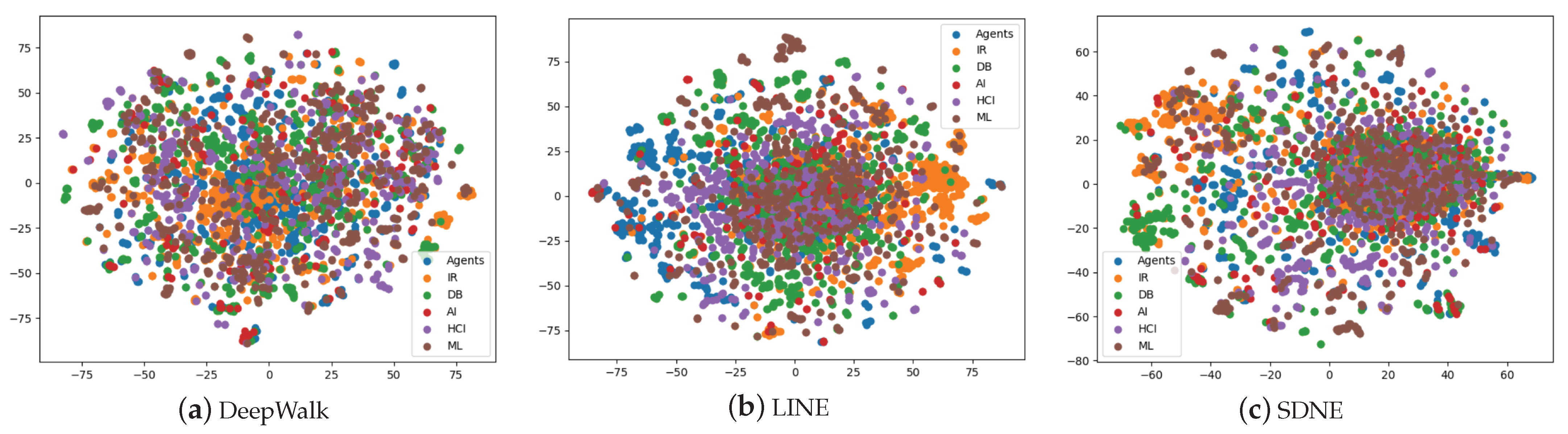
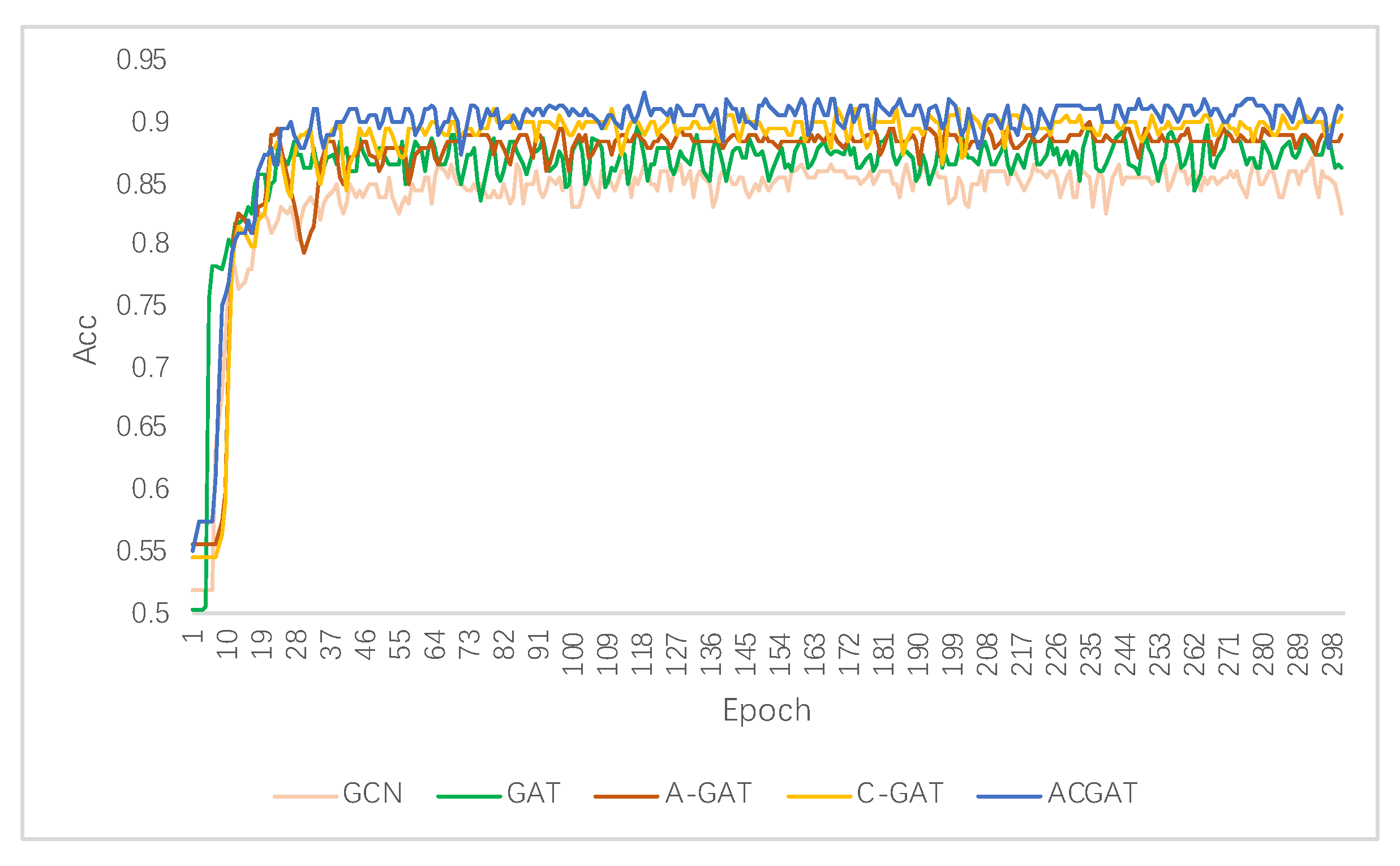
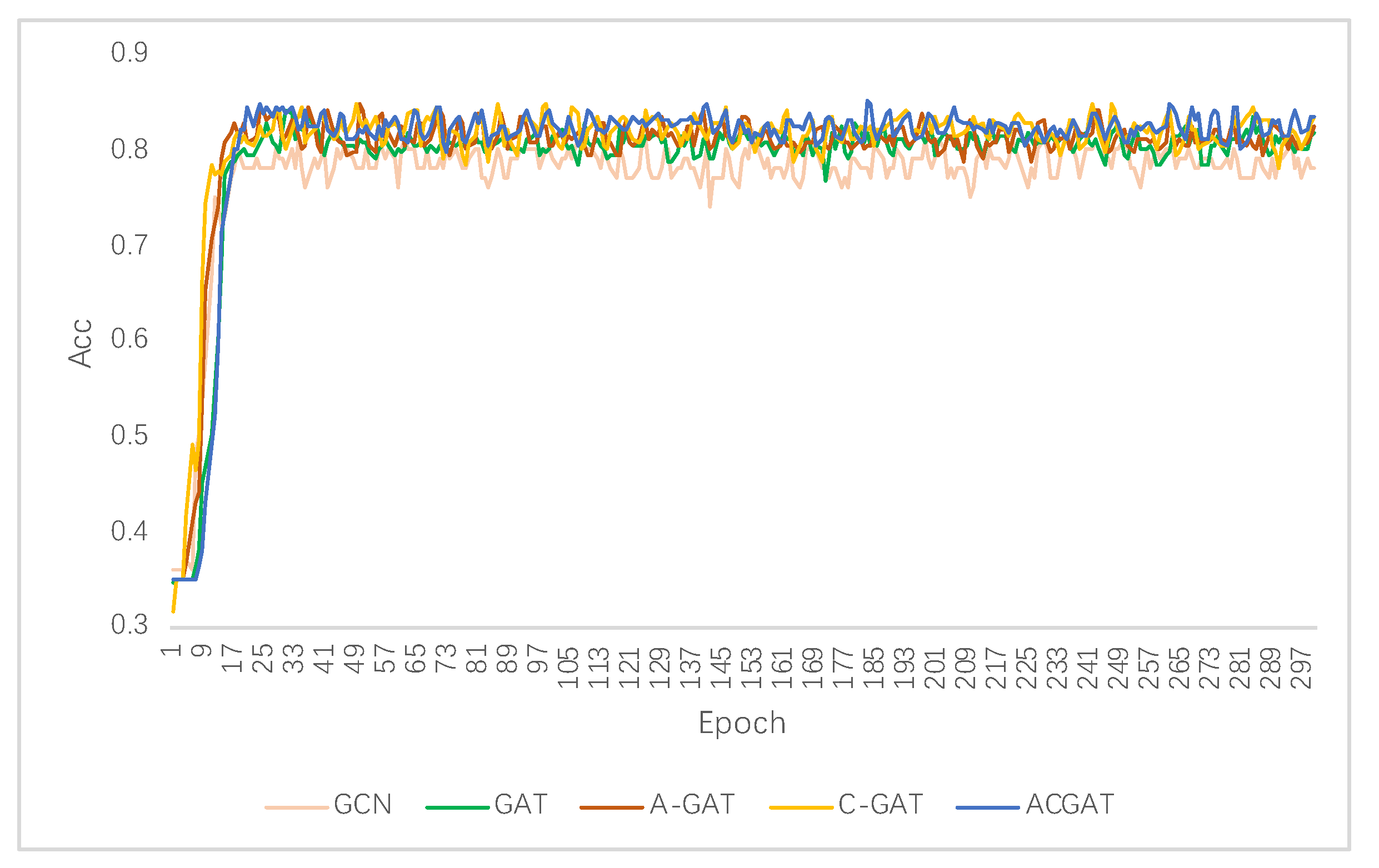
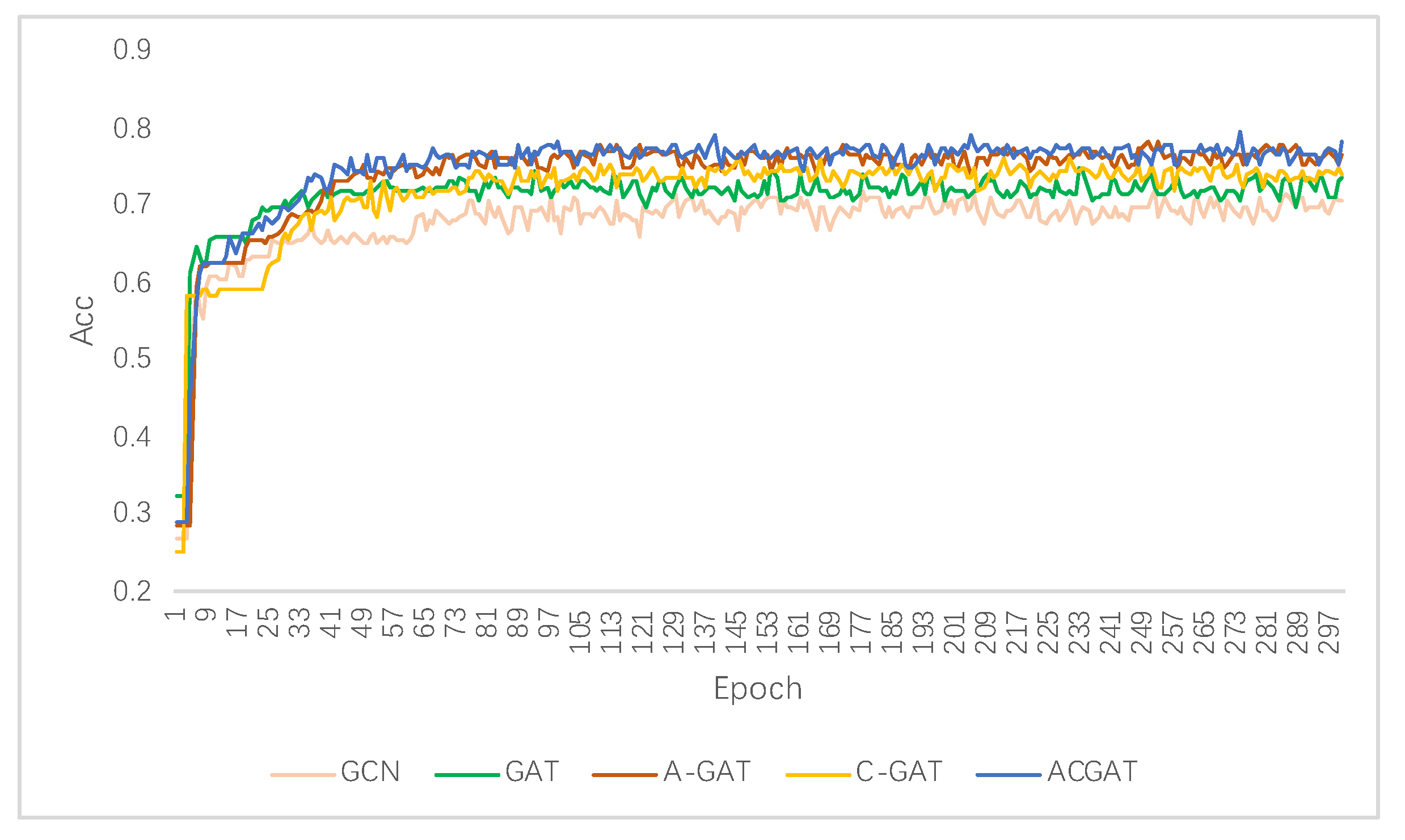
5.2. Experimental Analysis
- Micro-F1: We calculate this metric globally by counting the total true positives, false negatives, and false positives, and then calculate F1.
- Macro-F1: We calculate this metric for each label and find its unweighted mean. This does not take label imbalance into account.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lin, S.; Zheng, D. Big Data to Lead a New Era for “Internet+”: Current Status and Prospect. In Proceedings of the Fourth International Forum on Decision Sciences; Li, X., Xu, X., Eds.; Springer: Singapore, 2017; pp. 245–252. [Google Scholar]
- Fidalgo-Blanco, A.; Sánchez-Canales, M.; Sein-Echaluce, M.L.; García-Peñalvo, F.J. Ontological Search for Academic Resources. In Proceedings of the Sixth International Conference on Technological Ecosystems for Enhancing Multiculturality, Salamanca, Spain, 24–26 October 2018. [Google Scholar]
- Guo, G. Decision support system for manuscript submissions to academic journals: An example of submitting an enterprise resource planning manuscript. In Proceedings of the 2017 International Conference on Machine Learning and Cybernetics (ICMLC), Ningbo, China, 9–12 July 2017. [Google Scholar]
- Correia, F.F.; Aguiar, A. Patterns of Information Classification. In Proceedings of the 18th Conference on Pattern Languages of Programs, Portland, OR, USA, 21–23October 2011. [Google Scholar]
- Gong, L.; Cheng, Q. Exploiting Edge Features for Graph Neural Networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–21 June 2019. [Google Scholar]
- Sina, S.; Rosenfeld, A.; Kraus, S. Solving the Missing Node Problem Using Structure and Attribute Information. In Proceedings of the 2013 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining, Niagara Falls, ON, Canada, 25–28 August 2013. [Google Scholar]
- Fei, H.; Huan, J. Boosting with Structure Information in the Functional Space: An Application to Graph Classification. In Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 24–28 July 2010. [Google Scholar]
- Chen, S.; Huang, S.; Yuan, D.; Zhao, X. A Survey of Algorithms and Applications Related with Graph Embedding. In Proceedings of the 2020 International Conference on Cyberspace Innovation of Advanced Technologies, Guangzhou, China, 4–6 December 2020. [Google Scholar]
- Ahmed, A.; Shervashidze, N.; Narayanamurthy, S.; Josifovski, V.; Smola, A.J. Distributed Large-Scale Natural Graph Factorization. In Proceedings of the 22nd International Conference on World Wide Web; Association for Computing Machinery: New York, NY, USA, 2013; pp. 37–48. [Google Scholar] [CrossRef]
- Cao, S.; Lu, W.; Xu, Q. GraRep. In Proceedings of the 24th ACM International on Conference on Information and Knowledge Management-CIKM, Melbourne, Australia, 19–23 October 2015. [Google Scholar]
- Perozzi, B.; Al-Rfou, R.; Skiena, S. DeepWalk: Online Learning of Social Representations. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014. [Google Scholar]
- Tang, J.; Qu, M.; Wang, M.; Zhang, M.; Yan, J.; Mei, Q. LINE: Large-scale Information Network Embedding. Line Large-Scale Inf. Netw. Embed. 2015. [Google Scholar] [CrossRef]
- Grover, A.; Leskovec, J. node2vec: Scalable Feature Learning for Networks. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Zheng, D.; Wang, M.; Gan, Q.; Zhang, Z.; Karypis, G. Learning Graph Neural Networks with Deep Graph Library. In Proceedings of the Companion Proceedings of the Web Conference 2020, Taipei, Taiwan, 20–24 April 2020. [Google Scholar]
- Song, X.; Yang, H.; Zhou, C. Pedestrian Attribute Recognition with Graph Convolutional Network in Surveillance Scenarios. Future Internet 2019, 11, 245. [Google Scholar] [CrossRef]
- Zhang, C.; Song, D.; Huang, C.; Swami, A.; Chawla, N.V. Heterogeneous Graph Neural Network. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019. [Google Scholar]
- Che, M.; Yao, K.; Che, C.; Cao, Z.; Kong, F. Knowledge-Graph-Based Drug Repositioning against COVID-19 by Graph Convolutional Network with Attention Mechanism. Future Internet 2021, 13, 13. [Google Scholar] [CrossRef]
- Niepert, M.; Ahmed, M.; Kutzkov, K. Learning Convolutional Neural Networks for Graphs. In International Conference on Machine Learning; PMLR: Cambridge, MA, USA, 2016. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph Attention Networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Gilmer, J.; Schoenholz, S.; Riley, P.; Vinyals, O.; Dahl, G. Neural Message Passing for Quantum Chemistry. In International Conference on Machine Learning; PMLR: Cambridge, MA, USA, 2017. [Google Scholar]
- Lin, L.; Wang, H. Graph Attention Networks over Edge Content-Based Channels. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, San Diego, CA, USA, 22 August 2020. [Google Scholar]
- Shanthamallu, U.S.; Thiagarajan, J.J.; Spanias, A. A Regularized Attention Mechanism for Graph Attention Networks. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020. [Google Scholar]
- Zhukovskiy, M.; Gusev, G.; Serdyukov, P. Supervised Nested PageRank. In Proceedings of the 23rd ACM International Conference on Conference on Information and Knowledge Management, Shanghai, China, 3–7 November 2014. [Google Scholar]
- Meyer-Brötz, F.; Schiebel, E.; Brecht, L. Experimental evaluation of parameter settings in calculation of hybrid similarities: Effects of first- and second-order similarity, edge cutting, and weighting factors. Scientometrics 2017, 111, 1307–1325. [Google Scholar] [CrossRef]
- Ortega-Arranz, H.R.; Llanos, D.; Gonzalez-Escribano, A. The shortest-path problem: Analysis and comparison of methods. Synth. Lect. Theor. Comput. Sci. 2014, 1, 1–87. [Google Scholar] [CrossRef]
- Low, J.X.; Choo, K.W. Classification of Heart Sounds Using Softmax Regression and Convolutional Neural Network. In Proceedings of the 2018 International Conference on Communication Engineering and Technology, Singapore, 24–26 February 2018. [Google Scholar]
- Jiang, T.; Cheng, J. Target Recognition Based on CNN with LeakyReLU and PReLU Activation Functions. In Proceedings of the 2019 International Conference on Sensing, Diagnostics, Prognostics, and Control (SDPC), Beijing, China, 15–17 August 2019. [Google Scholar]
- Jia, X.; Li, W. Text classification model based on multi-head attention capsule neworks. J. Tsinghua Univ. (Sci. Technol.) 2020, 60, 415. [Google Scholar] [CrossRef]
- Sen, P.; Namata, G.; Bilgic, M.; Getoor, L.; Galligher, B.; Eliassi-Rad, T. Collective Classification in Network Data. AI Mag. 2008, 29, 93. [Google Scholar] [CrossRef]
- Wang, D.; Cui, P.; Zhu, W. Structural Deep Network Embedding. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; Association for Computing Machinery: New York, NY, USA, 2016; pp. 1225–1234. [Google Scholar] [CrossRef]
- Vidyapu, S.; Vedula, V.S.; Bhattacharya, S. Quantitative Visual Attention Prediction on Webpage Images Using Multiclass SVM. In Proceedings of the 11th ACM Symposium on Eye Tracking Research & Applications, Denver, CO, USA, 25–28 June 2019. [Google Scholar]
- Lin, Z.; Lyu, S.; Cao, H.; Xu, F.; Wei, Y.; Samet, H.; Li, Y. HealthWalks: Sensing Fine-Grained Individual Health Condition via Mobility Data. Proc. ACM Interactive Mobile Wearable Ubiquitous Technol. 2020, 4, 1–26. [Google Scholar] [CrossRef]
- Shim, H.; Luca, S.; Lowet, D.; Vanrumste, B. Data Augmentation and Semi-Supervised Learning for Deep Neural Networks-Based Text Classifier. In Proceedings of the 35th Annual ACM Symposium on Applied Computing, Brno, Czech Republic, 30 March–3 April 2020. [Google Scholar]
- Chen, Y.; Hu, S.; Zou, L. An In-depth Analysis of Graph Neural Networks for Semi-supervised Learning. In Semantic Technology; Wang, X., Lisi, F.A., Xiao, G., Botoeva, E., Eds.; Springer: Singapore, 2020; pp. 65–77. [Google Scholar]
| Notations | Descriptions |
|---|---|
| G | A graph. |
| V | The set of nodes in a graph. |
| A node . | |
| E | The set of edges in a graph. |
| N | The number of nodes, . |
| The feature vector of a set of nodes. | |
| F | The dimension of the node features. |
| The academic association commonality coefficient. | |
| The weighted coefficients of the association commonality. | |
| The association influence coefficient. | |
| The semantic similarity coefficient. | |
| A | The influence factor matrix. |
| D | The degree matrix, D. |
| The degree of node . | |
| M | The number of neighbors of a node v. |
| The shared attention mechanism. | |
| The neighbors of a node v. | |
| W | The sharing parameter. |
| Splicing operation. | |
| Learning parameters, including the academic semantic relevance, academic association commonality, and influence coefficient. | |
| The final coefficient. | |
| The activation function. | |
| K | The multi-attention number. |
| Datasets | Nodes | Edges | Features | Classes | |
|---|---|---|---|---|---|
| Scholar cooperation network | SIG | 3669 | 10,399 | 3664 | 8 |
| Citation network | Cora | 2708 | 5429 | 1433 | 7 |
| Citeseer | 3312 | 4732 | 3708 | 6 | |
| Dataset Metrics (%) | SIG | Cora | Citeseer | |||
|---|---|---|---|---|---|---|
| Micro-F1 | Macro-F1 | Micro-F1 | Macro-F1 | Micro-F1 | Macro-F1 | |
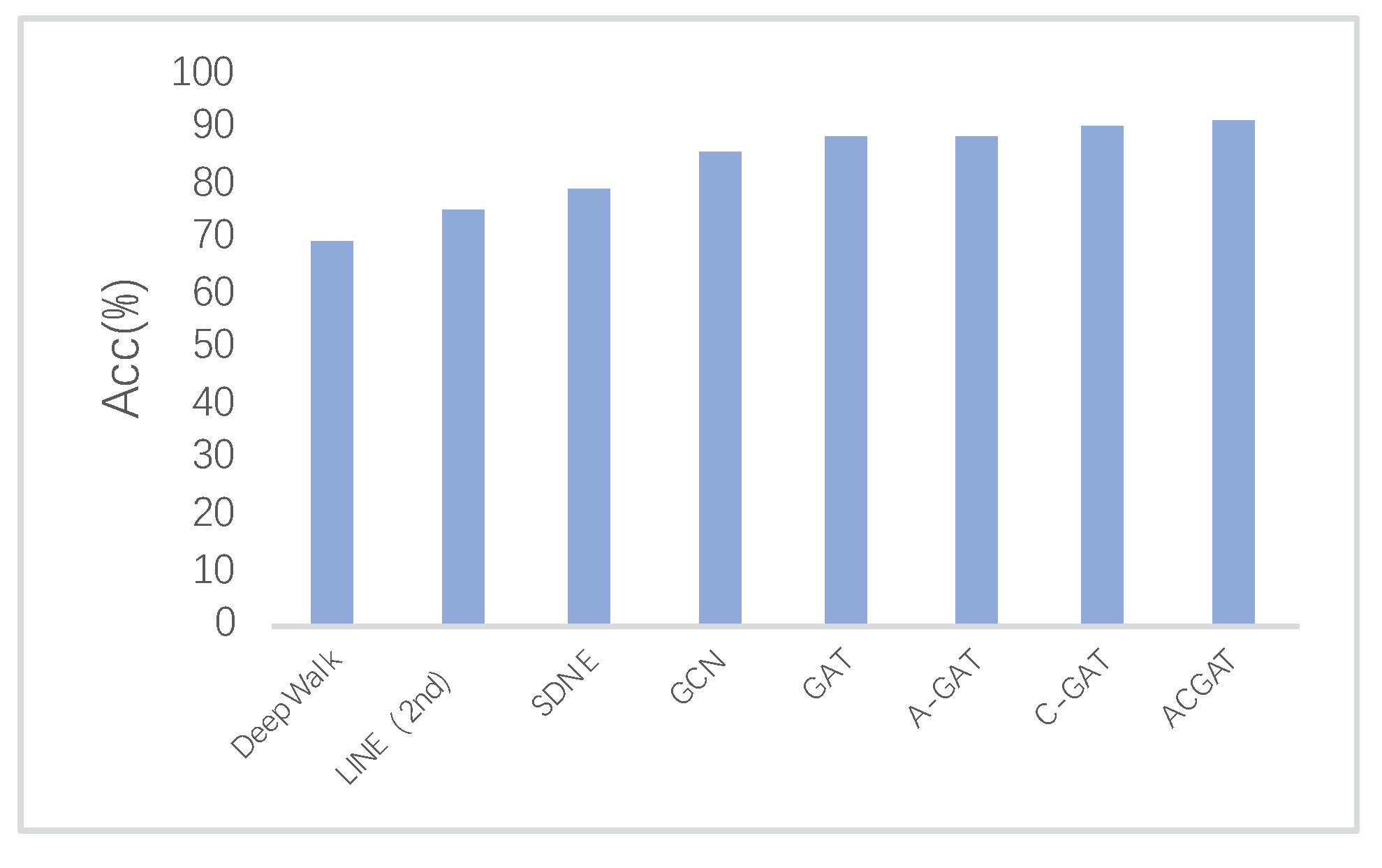
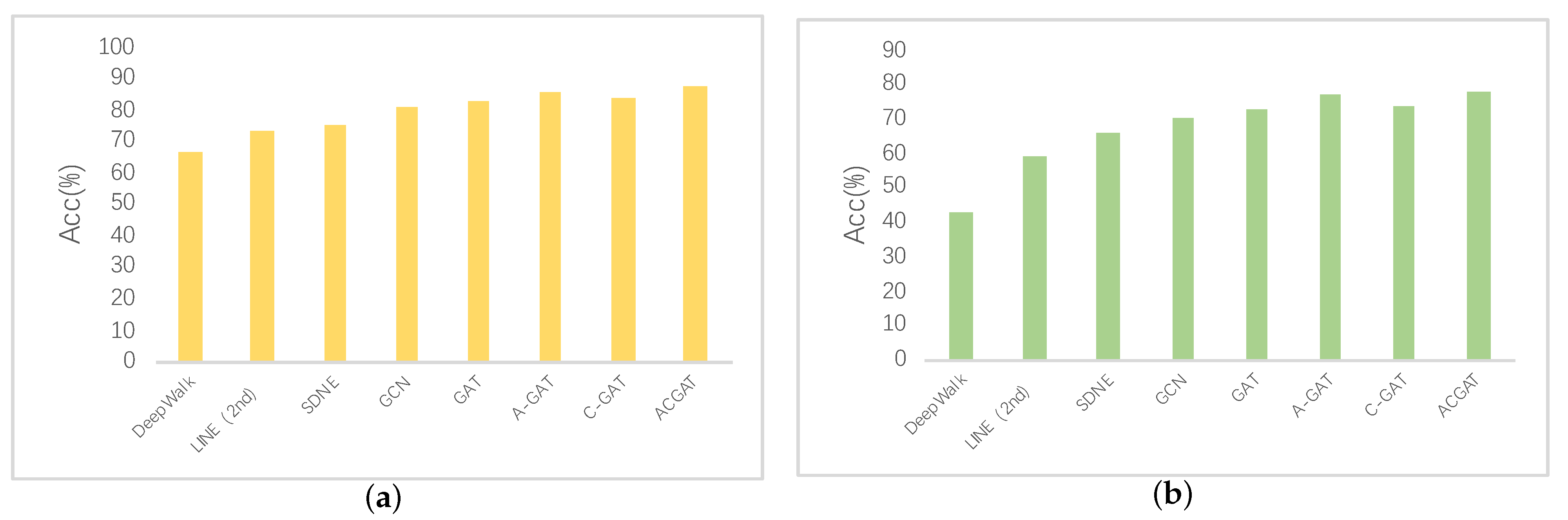
| DeepWalk | 60.91 | 53.66 | 57.75 | 54.12 | 41.63 | 35.70 |
| LINE | 65.28 | 56.52 | 62.55 | 61.23 | 54.49 | 49.34 |
| SDNE | 69.23 | 60.01 | 70.11 | 67.47 | 60.01 | 55.38 |
| GCN | 75.31 | 69.32 | 78.72 | 71.38 | 64.35 | 58.21 |
| GAT | 80.20 | 77.65 | 86.83 | 78.84 | 68.72 | 64.36 |
| A-GAT | 83.11 | 75.27 | 88.71 | 83.26 | 73.26 | 69.24 |
| C-GAT | 86.26 | 81.39 | 88.43 | 85.17 | 71.11 | 66.83 |
| ACGAT | 90.67 | 85.22 | 92.62 | 88.54 | 74.69 | 70.30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; Li, Y.; Pan, C.; Wang, J. A Classification Method for Academic Resources Based on a Graph Attention Network. Future Internet 2021, 13, 64. https://doi.org/10.3390/fi13030064
Yu J, Li Y, Pan C, Wang J. A Classification Method for Academic Resources Based on a Graph Attention Network. Future Internet. 2021; 13(3):64. https://doi.org/10.3390/fi13030064
Chicago/Turabian StyleYu, Jie, Yaliu Li, Chenle Pan, and Junwei Wang. 2021. "A Classification Method for Academic Resources Based on a Graph Attention Network" Future Internet 13, no. 3: 64. https://doi.org/10.3390/fi13030064
APA StyleYu, J., Li, Y., Pan, C., & Wang, J. (2021). A Classification Method for Academic Resources Based on a Graph Attention Network. Future Internet, 13(3), 64. https://doi.org/10.3390/fi13030064