Abstract
In a community with an aging population, helping each other is a must society function. Lacking mutual trust makes the need for a fair and transparent service exchange platform on top of the public service administration’s list. We present an efficient blockchain-based TimeBank realization with a newly proposed dynamic service matching algorithm (DSMA) in this work. The Hyperledger Fabric (or Fabric in short), one of the well-known Consortium Blockchains, is chosen as our system realization platform. It provides the identity certification mechanism and has an extendable network structure. The performance of a DSMA is measured by the waiting time for a service to get a match, called the service-matching waiting time (SMWT). In our DSMA, the decision as to whether a service is to get a match or wait for a later chance depends dynamically on the total number of contemporarily available services (i.e., the thickness of the service market). To better the proposed TimeBank system’s service quality, a Dynamic Tuning Strategy (DTS) is designed to thicken the market size. Experimental results show that a thicker market makes on-chain nodes have more links, and in turn, they find a match easier (i.e., consume a shorter SMWT).
1. Introduction
Helping each other is vital in an outbreak of influenza and viruses, especially in the current COVID-19 pandemic, and the TimeBank system is an implementable mutual-assistance-building mechanism [1,2]. TimeBank is a reciprocity-based service trading system in which the amount of time spent (i.e., seconds, minutes, or hours) are the statutory currencies. With time banking, a person with one skill set can bank and trade hours of work for equal hours of work in another skill set instead of paying or being paid for services. The hours banked are always changed equally relating to the services rendered. This equality intends to foster ties in communities and, by making all contributions valued similarly, encourage balance in the communities themselves.
In decentralized markets, users create alternative socio-economic systems through resource sharing, such as services, materials, and knowledge. However, today’s shared economic model tends to rely on a centralized organization to act as a broker or an arbitrator, merely connecting two parties on a supply and demand basis. On the other hand, a centralized company will control everyone’s information and use it to create fair values. Besides, a centralized company can hide information that is not conducive to the system and thus causes system information inequality between users and the company.
Blockchain technology [3] can remove intermediate brokers, a technical solution that does not rely on third parties to store, verify, and transmit through its decentralized nodes. In a blockchain, every node is connected in a peer-to-peer manner and can trade without mutual trust, making a system manager redundant. The blockchain’s peer-to-peer connections enable users to secure and decide to share and exchange services or values. Furthermore, the blockchain has several specific features suitable for integrating with the concept of a shared economy. The first is transparency. All members in the blockchain network can see all the validated data of each other. The second is immutability. That is, the recorded data is nearly impossible to modify. Once the information has been written into the ledger, it is hard to change. In other words, the information on the ledger is trustworthy. Spyros and Christodoulou [4] gave a comprehensive survey of the blockchain, discussing its advantages and possible drawbacks and its implications for the future of the Internet and human lives and societies. Besides some general introduction and discussion about disruptive changes and unique blockchain values, the authors also described several major blockchain applications with the highest prospective advantages. For example, they discussed the most notable subset of innovative blockchain applications—Smart Contracts, DAOs (Decentralized Autonomous Organizations), and super secure networks—at the end of their work.
However, in the applications of time banking, identity authentication is a must [5]. Conventionally, the exchange of services needs to be carried out face to face because it is necessary to review the identity and confirm the security of involved members. Joshi et al. [6] conducted a comprehensive survey on blockchain technology by discussing its structure to different consensus algorithms as well as its challenges and opportunities from a perspective of data security and privacy. Similarly, reference [7] gives a thorough review and systematizes all cryptographic concepts already used in blockchain. Moreover, the authors present a list of cryptographic skills which have not yet been applied but have immense potential to improve the current blockchain solutions. The above-mentioned security-sensitive requirement is the main reason why we use Hyperledger Fabric. Even though we do not need an intermediate manager to pair two sides with matching conditions, a particular organization (Certificate Authority: CA) must validate the network’s identities of on-chain members. A verified member will get a digital certificate to prove his or her identity, and when a smart contract is invoked, the authentication is restored to evidence the corresponding membership.
On the one hand, in a licensed blockchain, the on-chain information can only be queried by legal members, and only valid members can invoke smart contracts [8]. On the other hand, if a permissionless blockchain platform is used, everyone can join the blockchain network, and none can guarantee the safety of on-chain members. Moreover, when the system is constructed based on blockchain, there is no central server to handle everyone’s matching needs. In the direct implementation of a naive dynamic matching algorithm on the blockchain, the corresponding complexity is too high to be used in practice.
In this paper, we embed the matching algorithm in each validated node (i.e., a local algorithm is used) until the market’s thickness (or size) reaches an economic scale. The rest of the paper is organized as follows: Section 2 presents the related works and the Fabric Blockchain’s backgrounds and the dynamic matching issues about time banking. In Section 3, we overview the whole newly proposed TimeBank system. Section 4 introduces all of the functional modules in the design and addresses our system’s detailed settings. The effects of dynamic matching strategies on the two-sided market model are explained and discussed in Section 5. Finally, Section 6 and Section 7 present the experimental results and conclusions, respectively.
2. Background and Related Work
2.1. Blockchain Technology
Satoshi Nakamoto conceptualized the first blockchain in 2008. He presented the design of using a secure hash function for chaining blocks into the first blockchain platform, Bitcoin [1], which provides the most successful decentralized electronic cash system. Bitcoin is a digital ledger-based system using the proof-of-work (PoW) consensus algorithm and a few other technologies to help verify transactions and create a global peer-to-peer (p2p), decentralized cryptocurrency. In 2014, a new blockchain platform was born called Ethereum. Ethereum is proposed by Vitalik Buterin [9]. Vitalik suggested the usage of smart contracts for providing programming capability to the blockchain. Moreover, one can execute smart contracts on a blockchain base using simple business logic, and the involved data are immutable and transparent. Finally, the internet-like nature of blockchain means that anyone of interest can join the blockchain network anonymously. Due to its trustworthy and decentralized nature, blockchain technology has been successfully applied to solve social business and social credit issues [10,11,12], besides its regular banking industry applications [13,14,15].
The adopted blockchain platform, called Hyperledger Fabric [16], belongs to the category of permissioned blockchains, in which the member’s identification is strictly restricted. Fabric delivers high degrees of confidentiality, flexibility, resiliency, and scalability. These characteristics make the solution developed based on Fabric suitable for lots of industrial applications. The membership service in Fabric’s Permissioned Model can be integrated with various standard identity management systems. Fabric adopted a novel architectural approach to support this flexibility and improved how the blockchain responds to non-determinism, resource exhaustion, and performance attacks. Fabric can also create channels enabling a group of participants to create separate transaction ledgers. This capability is essential for networks where some participants may not want to have a competitor for each transaction.
Inspired by the pre-described characteristics of permissioned blockchain and the requirements of a TimeBank system, we realized a blockchain-based TimeBank system based on the Hyperledger Fabric framework [5]. Our TimeBank provided a grading system allowing involved members to give each other a grade to reflect their degrees of satisfaction about the system’s services. This grading system incentivized the members to provide a better quality of service and adopt a friendlier attitude for receiving a service, which may positively endorse the development of a worldwide TimeBank system. For simplicity, the system realized in [5] matched up the posted services with a naive matching method, i.e., the matching between services’ supply-and-demand tasks was done intuitively and conducted directly through autonomous smart contracts. Once people complete their service exchange, the one who provides the service can execute the token transferring function to get their time credit as a return. Although the flexibility of this naive approach has been proved by the simulation conducted in [5], we believe that to fit the dynamic nature of the supply-and-demand of a practical mutual assistance community, a more effective matching algorithm is a must. Therefore, this work presents an efficient blockchain-based TimeBank realization with a newly proposed dynamic service matching algorithm (DSMA) to achieve the goal mentioned above.
2.2. Dynamic Matching
The dynamic matching process’s conduction is based on the system users’ (or nodes) preferences for the conditions or attribute compatibility. The “kidney-exchange process” [17] is the most closely related scenario to our study about dynamic supply-and-demand matching on a time-varying network. In general, we encode a kidney exchange instance as a directed compatibility graph G = (V, E) and construct one vertex for each patient-donor pair in the pool. Then, an edge e is created from vertex vi to vertex vj if the patient in vj wants and is compatible with the donor kidney of vi. A paired donor is willing to give her kidney if and only if the patient in her vertex vi receives a kidney. We also encode our TimeBank instance as a bi-directional directed compatibility graph and construct one vertex for each SP and each SR in the market. Clearly, in our system model, SP plays a similar role as a donor and SR as a patient. And an edge is created from vertex vi to vertex vj if the SR in vj is compatible with the SP’s matching criteria in vi and vice versa. Since the edge is bi-directional, we can simplify it as an undirected one.
Another topic related to our research is the Stable Marriage Problem (SMP). In mathematics, economics, and computer science, SMP is the problem of finding a stable matching between two equally sized sets of elements given each element’s ordering preferences. In 1962, David Gale and Lloyd Shapley proved the Gale-Shapley algorithm [18] to solve this problem. There are also related papers discussing the SMP issue in different scenarios [19]. The most significant difference between SMP and our research is that the SMP problem is a preference-based matching issue, and our study focuses on the compatibility-based matching issue. In the future, our system may also integrate with the preference-based matching mechanism.
M. Akbarpour [20] considered a model where compatibilities are based on a random graph model. Researches indicated that waiting for the thickening of the market size will yield significant gains if the planner knows the departure time. There are other studies on Imbalanced Markets [21,22], in which the exchanges of markets are conducted by easy-to-match and hard-to-match agents.
Kurino [23] and Bloch and Houy [24] studied the housing market’s overlapping generation models. In their models, agents have a deterministic schedule in arrivals and departures. Besides, the market’s housing side is infinitely durable and static, and houses do not have preferences over agents.
As pre-described, this work applies the strategy of market size thickening to a blockchain-based TimeBank system’s operations. To simplify the analyses, we treat balancing supply-and-demand in a TimeBank as finding a match in a “two-sided market” [25], which means in the proposed platform, there are two distinct user groups that provide each other with network benefits.
3. System Overview
3.1. Application Scenario Overview
In time banking applications, we need to investigate the service-exchange process the system executed. Currently, the critical business of a TimeBank is to provide services in exchange for time credits, where one can use time credits to exchange for other people’s services. Before introducing the service–exchange process of a TimeBank, four conventions need to be addressed first:
- “Service” represents a collective term of different useful and desirable skills for disabled or aged people, such as cleaning a house, repairing a machine, driving to a hospital, and so on.
- The time credit value is measured according to the service’s time spent, regardless of the service’s substances. For example, cleaning a house for one hour gets the same time credit as taking care of an elderly citizen for one hour.
- Members of the system can be divided into two clusters: The Service Providers (SPs) and the Service Receivers (SRs). SPs provide services in their spare time, while SRs seek assistance from others in their required instance.
- The provision of services is not immediate. For example, Uber is a kind of prompt service provider. However, in a TimeBank, if Bob needs someone to help babysit his child on Saturday, Bob has to issue the request a few days before.
In the proposed TimeBank system, SPs and SRs match the supply-and-demand services on the Fabric blockchain. The service-exchange process of the system consists of the following three main steps:
- (1)
- Step 1: Members need to post their service inquiries to the blockchain, where the service inquiries have two types. SPs post the supply inquiry, and SRs post the demand inquiry. Then, the service inquiry reveals the user’s specific content of the supply or demand service, and it will be posted to the blockchain through the client-side application software, as shown in Figure 1.
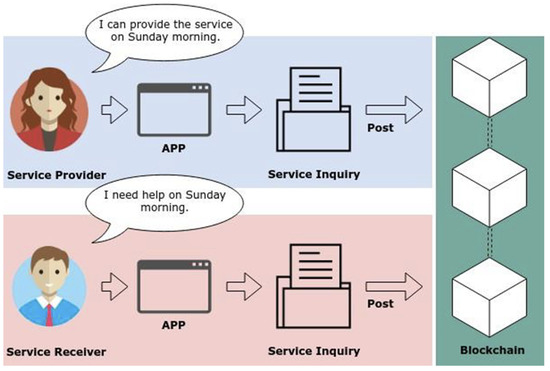 Figure 1. The processes of posting SP’s and SR’s service inquiries on the blockchain.
Figure 1. The processes of posting SP’s and SR’s service inquiries on the blockchain. - (2)
- Step 2: The supply-and-demand service inquiry keeps looking for candidates who match up with the matching criteria until a matching strategy is pursued. In this work, a market thickness-based dynamic tuning matching strategy is adopted. In a nutshell, each service inquiry decides when to match with others, according to the market’s thickness.
- (3)
- Step 3: Before SP provides the pre-negotiated service to SR, the TimeBank system will help SP check SR’s account balance to ensure it has enough time credit for paying the mandatory service charge. Similarly, the TimeBank system will help SR send the pre-negotiated time credit to SP after SP did complete the service.
3.2. Network Structure Overview
In our system, there are SPs, SRs, and a neutral certificate authority (CA). The neutral CA reviews the applicants who want to join the network and sends the identity certificate after validation. Based on the issued identity certificate, users’ footprints can be tracked by our system if they do something illegal. Moreover, the service-exchange must be conducted face-to-face between SRs and SPs since members’ safety is the top priority. CA can also revoke the identity certificate for the member who had menaced other members.
After the enrollment, valid users get permission to invoke chaincodes and query the on-chain data. There are two different channels in the network of our TimeBank system (cf. Figure 2):
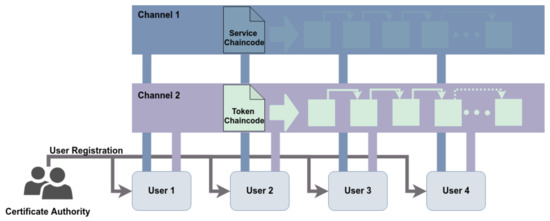
Figure 2.
The underlying architecture of the proposed TimeBank system is founded based on Hyperledger Fabric’s multi-channel network.
- Service Channel (SC): Processes in SC managing all service inquiries and handling the matching process. Users evoke SC for posting their queries then match their supply-and-demand attributes with the other members in this channel.
- Token Channel (TC): Processes in TC managing all users’ accounts and balances. If a service-exchange is accomplished, evoking TC confirms whether the corresponding service status on SC is completed, then approves sending the token to SPs from associated SRs.
In summary, the proposed system is designed based on Fabric’s multiple-channel architecture to increase the system’s scalability. Because TimeBanks are community-based institutions, the circulatory nature of time credits is also limited. Therefore, multiple TimeBanks are allowed to join in the proposed system. All TimeBanks in the network share the same TC, but each of them has its own SC. Each SC manages its community’s services, and the services cannot match each other if they belong to different SCs.
3.3. System Assumption
Before exploring our TimeBank system’s operational behavior, guided by the proposed matching mechanism, some system-related assumptions must be addressed to make our discussions more focused. Firstly, each service inquiry has a fixed available time when the members post it onto the blockchain. Because each service inquiry’s response is not immediate, SPs and SRs can wait for a while after a service inquiry is posted. Setting the period of available time also helps SPs and SRs know whether the service inquiry has been successfully matched or not. Second, different to the traditional server-client-based system where users need to call the matching function on the local-side after the service is posted and cannot continuously execute the match function, in the proposed approach, there is no global planner to handle the match process. Each inquiry tries to evoke the match function through the service chaincodes autonomously during the available time until a match is found. Third, since all SPs and SRs find their partners in the Fabric network, so the Fabric network can be viewed as a market of the proposed TimeBank. The stochastic nature of the arrivals of SPs and SRs to the market complicates our analysis a lot. For simplifying the analyses, we take dynamic market matching methodologies into account and assume that the supply and demand of the market is balanced. In the rest of our discussions, a market that fulfills the above assumption is called a two-sided market. For a two-sided market, some works focus on the incentive strategy design for enhancing selling [26], which achieves a balance between supply and demand through an advanced pricing or rewarding strategy. This paper discusses the matching strategy based on the pre-described “waiting for matching” or, equivalently, the “thickening market” strategy.
4. Functional Modules of the Proposed System
4.1. User Registration Module
Fabric is a permissioned blockchain, so all on-chain members must complete their user registration process before evoking or querying the on-chain information.
Figure 3 shows the interaction between an applicant and CA in the user registration process. First, the applicant sends a registration request to CA through his or her client App, and the application contains the applicant’s real identity. Second, after the registration, CA sends and stores the public and the private keys and the identity certificate on the user’s wallet. Third, CA calls token chaincodes to create a user’s account, where the user’s time token is stored.
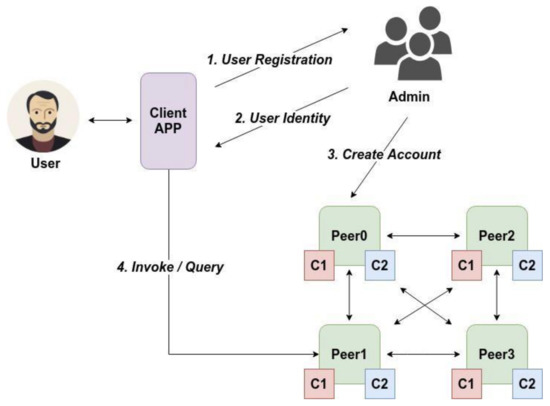
Figure 3.
The interaction with the CA in the user registration process.
Every time a user invokes the chaincodes, Fabric blockchain checks the validity of the identity certificate. Cryptography techniques allow users to present their credentials to others for proving their identities, as long as the other parties trust the certificate issuer. By reading and checking the certificate, one can make sure that the user’s information has not been tampered with.
4.2. Service Inquiry Posting Module
An enrolled member with an issued key pair and wallet can start to post service inquiries on the Fabric blockchain. Using the issued key pair, a valid member accesses the peer, uploads his or her service inquiry, and evokes a service posting function, called the service proposal, in the form of service chaincodes. Then, the service proposal is posted on SC. For maximizing the liquidity and circulation of Time Coins, each posted service has a fixed available time slot for waiting for the match up with other qualified services, which fulfilled the conditions defined in each service inquiry.
Each service inquiry has a lifecycle on the blockchain, and Figure 4 shows the transition diagram of the corresponding state machine of the service inquiry. The states of service inquiries can be divided into five stages: NewPost, Candidate, Designation, Confirmation, and Expiration, which precisely depict the life cycle. Although a service will be terminated sooner or later, the related data are recorded on the blockchain forever. The state information will help the system query for services that can be matched with high probability. Furthermore, the state promotes the system to solve the potential double-spending problem. We will mention the details about the double-spending problem in the next section.
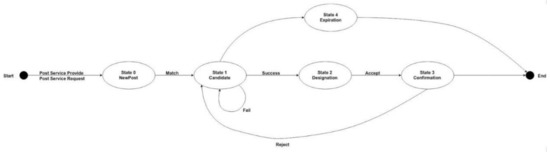
Figure 4.
The transition diagram of the corresponding state machine of the service inquiry.
4.3. Service Inquiry Evoking Module
We represent each matching process as a set of chaincodes, which are instantiated on the blockchain by the market’s two-side users (i.e., SPs and SRs). The enrolled members published their services inquiries in SC (cf. Table 1). The types of services, denoted as servicetype, are divided into the following two kinds: request and provide.

Table 1.
The parameters in the service proposal.
Each newly posted service inquiry, as mentioned above, has a fixed available time. Each service inquiry attempts to evoke the match function in the Service Chaincodes at a fixed period until it is matched. In our system, the “Number of Available Invokes (NOAI)” records the number of times each service inquiry does invoke the match function. Whenever a match function executes for a service inquiry, the number in NOAI is decreased by one. Let “serviceClass” denote the classes of service substances of a TimeBank.
Figure 5 shows some service substances taken from TimeBanks USA and their supply-versus-demand ratios. It is worth mentioning that the number of offers may not be realistic. When someone wants to join the TimeBanks USA, they need to tell the system what services they can provide. When someone needs help, the TimeBanks USA’s staff will use the phone to ask members to provide the service. Therefore, the number of members who can provide services must be less than the number of offers in the figure. For simplicity, we select the three most demanded services as the service substances in the proposed system, including HelpatHome, CommunityActivities, and Home.
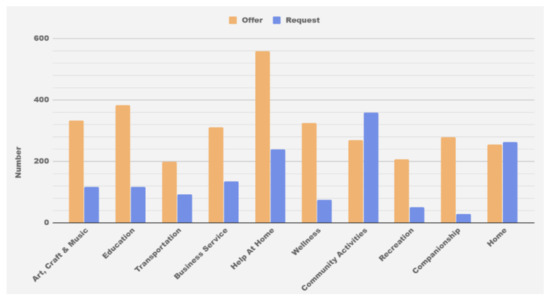
Figure 5.
Relative service ratios of supply-versus-demand measured in TimeBank USA.
The service chain codes will classify these service inquiries in the blockchain according to the associated service states. In our system, each service inquiry becomes the matching candidate for another service if they have the same “serviceClass” and need to be within the same available time interval. We use “serviceTime” to record the time interval for supplying or demanding services. The “serviceTime” in a service-post plays a critical role in justifying the service’s qualifications to be a candidate.
4.4. Service Matching Module
Figure 6 shows the detailed transaction flow of the service matching process. First, an SR posts his or her service inquiry onto the blockchain. If the posting process is successful, the service inquiry’s state changes to the state “NewPost.” Second, as long as that service inquiry is alive, the client app will automatically invoke the match function at a fixed frequency. And the state of the service inquiry will be searchable by other services when its state is denoted as a “Candidate.” After posting the service inquiry, our system will upload the service-related data to the blockchain. The target SR will find the candidate SP’s service inquiry when the matching function is invoked next time. Third, after the service inquiries of the SP and the SR fulfill a matching strategy, the target SR sets the “serviceOwner” of the matched SP to himself or herself and vice versa. Finally, the SP can choose to accept or not accept this service match. If not, both parties will return to their candidate state and continue to look for other compatible service inquiries.
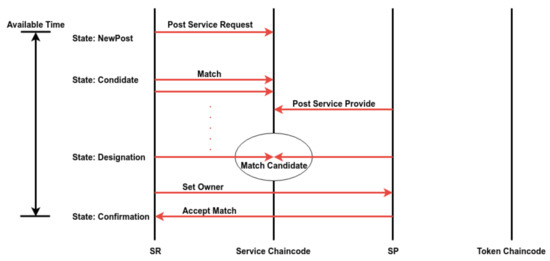
Figure 6.
The transaction flow diagram of the service matching phase.
5. Dynamic Matching Strategies in Two-Sided Markets
5.1. The Model
This Section models the dynamic service matching tasks on blockchain as a continuous-time stochastic process in a market with two-side binding participants, in which each node denotes a valid service inquiry posted on the blockchain. In other words, two linked nodes stand for a candidate-matched pair, and each link represents a potential matching relationship between the two ends of the link. The two nodes with potential matching relationships are called neighbors. We use N(ni) to denote the number of neighbors of node ni.
Once a service inquiry is posted on a node, we say that the node is entering the market, and as pre-described, users in the market can be divided into SPs and SRs. For simplicity, a user in the market is denoted by the symbol xi, where xi ∈ {SP, SR}, i = 1,2,3,… Without loss of generality, we assume users arrive at the market with an average time interval Tn according to a Poisson process, where n denotes the time interval cycle. The probability of an SP arriving at the market is Pr[SP], and that of an SR is Pr[SR]. Moreover, we assume that the amounts of supply and demand in the market are equal. Hence, Pr[SP] = Pr[SR] = 0.5. Assume all the matched services will leave the market immediately, and each SP and SR have a fixed average available time Ta. Therefore, each user has examined n services when they leave the market without being matched, where n = Ta/Tn. If a node has not been matched during its available time, it will leave the market immediately as pre-described. This work assumes a standard matching cycle time is Tx; if a service cannot match with others in Tx, it will wait until the next cycle to find a match again. Therefore, each service can invoke match processes up to m times in its lifecycle, where m = Ta/Tx. Furthermore, let p denote the probability of two random service inquiries that are compatible, where p is related to the services’ type, class, and available time.
5.2. The Greedy and the Patient Matching Strategies
Previous dynamic matching studies [20] showed that simple local algorithms that select appropriate time-matching agents but do not take advantage of the global network structure could perform near complexity optimal algorithms.
Suppose every node has some time to wait for matching in the market. Each node tends to find a match when the node itself becomes critical, the market size becomes thicker, and the number of objects that can be paired increases. Since the market gets thicker, each node has more choice to match or to be matched. Therefore, we can divide the simple local algorithm into the greedy and patient algorithms. The greedy algorithm means that any node tries to find a match as soon as possible when it arrives at the market. If no match can be found, the node will remain in the market. The patient algorithm means that any node gets a match only when it becomes critical, where the node has exhausted its available time. In the following, we try to explain the main idea of [20] without involving too much mathematics.
As shown in Figure 7, the node ni where i = 1, 2, …, 5 arrives at the market in order. If each node matches immediately upon arrival, nodes n1 will find a match whenever node n2 comes at the market, and then no node can be matched with node n3 when it arrives at the market. On the one hand, if each node prefers to wait for a while, nodes n1 will have the other matching choices. This situation is an example of the so-called timing issue. On the other hand, at this moment, node n1 could choose nodes n2 or n3 but not both of them; this situation clearly shows a structural issue.
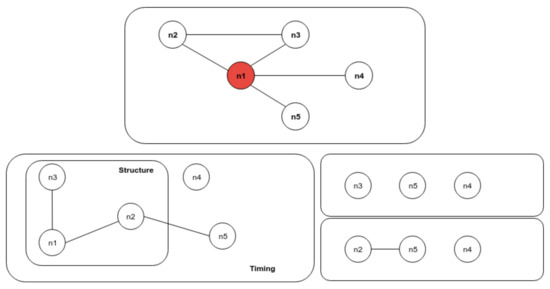
Figure 7.
Timing issue of the matching process. (Upper) The matching conditions among active nodes in the market; (Bottom) different market states caused by different node Ni’s matching choice.
Notice that choosing the node which benefits the whole market will complicate the system a lot. For example, if node n1 is aware that its match with node n3 will make nodes n2 and n5 get matched, it leads to a better system state than its choice to match with node n2 directly. However, to reach such a better system state, one must globally compute all the possible linking situations of the market. Clearly, it will take O(n2) complexity if the market size is n. Another fact is, in the dynamic matching market, if any node arrives at the market or leaves the market, all the linking possibilities must be recalculated. Unfortunately, our system is blockchain-based, and there is no centralized planner and/or executor to handle the above-mentioned global computation. Therefore, it is better to postpend the actual match somewhat to thicken the market size, which may increase the overall system matching rate.
Furthermore, timing and structural issues are related to each other. If each node waits for a while to find a match, the number of nodes in the market will increase, and the nodes will have more possible links among each another. On the other hand, if the market already has sufficient thickness, each node’s choice will not impact its system structure much. For example, in Figure 8, if n1 matches any of its neighbors, the other nodes can always find someone to match with. Compared with Figure 7, in which, if n1 selects its match with n2, the choice will make nodes n3 and n5 unable to find matches, this choice causes a higher loss to the market.
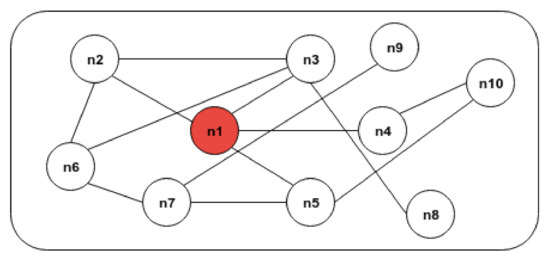
Figure 8.
Structural issue of the matching process: the node’s connecting structure depends on the market’s thickness. All other modes can still find matches even if node N1 matches any of its connected neighbors immediately.
For measuring the density of a market, we define the density parameter as d = np, where d is the number of expected node links that do not match anyone yet. After each node enters the market, there is a fixed available time, Ta. If a node continues to wait for the entire available time, the node will meet the other n nodes during this time period. Then the number of expected links of the node will be np.
5.2.1. Greedy Algorithm
A greedy algorithm means that any node tries to find a match as soon as possible when it arrives at the market. If no match can be found, the node will remain in the market. Figure 9a shows our greedy algorithm’s processing snapshots, with four continuous-time units, in a market. When n3 arrives at the market, it immediately matches n1 and leaves the market. Therefore, any node that remains in the market will have not have a link with any others; and they can only wait for matches with nodes arriving at the market later. In other words, nodes in the market get matched when they become critical and leave the market in pairs. The market size will be highly concentrated on a fixed range if we continuously apply a greedy algorithm to the market. This phenomenon implies that a balance between the arrival rate and the departure rate is reached. The departure nodes include those leaving the market immediately after they found matches successfully and those leaving without a match because of lifecycle expiration.
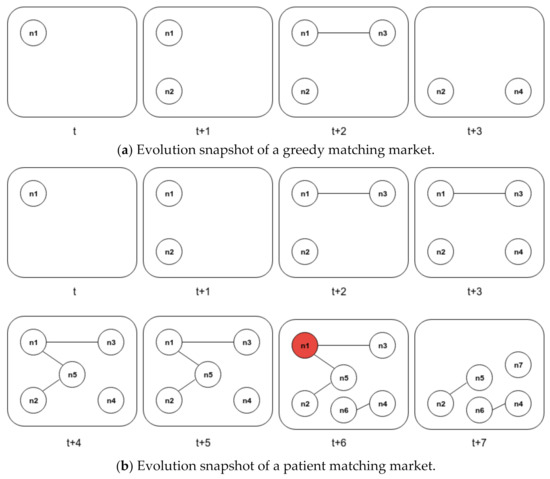
Figure 9.
Dynamic matching market under (a) the greedy algorithm and (b) the patient algorithm.
Now let y denote the number of nodes in the market, then we can express the market arrival rate under the greedy algorithm as:
where the probability p equals to d/n.
Equation (1) can be understood as any node getting a match when it arrives at the market, while the nodes added to the market are those who did not find matches with the other nodes in the market. On the other hand, we can express the departure rate in the market as:
Equation (2) can be understood by considering the following two cases:
(i) Leave without matched: suppose we use Ta as a time unit in the equation. After a Ta, there are n nodes, on average, arriving at the market. However, as all nodes are assumed to not have found matches, all the in-system nodes will leave the market after a Ta is passed. Therefore, the number of departure nodes equals the number of nodes n in the market. (ii) Get a match, then leave: When the node arrives at the market and gets a match immediately, the number of nodes in the market will be reduced accordingly because the matched node will leave the market right away. Therefore, the balance equation of the size of a stable market, under the greedy matching algorithm, can be written as:
By solving Equation (3), we can find the abovementioned highly concentrated market size that is:
While the loss of the market under the greedy algorithm can be defined as the ratio of the node arrival rate to its departure counterpart, that is:
5.2.2. Patient Algorithm
The patient algorithm means any node is getting a match only when it becomes critical, where critical is a node that has exhausted its available time. Figure 9b shows the processing snapshots of our patient algorithm, with eight continuous-time units, in which when node n1 becomes critical, it randomly matches one of its neighbors. Because the patient algorithm is applied, our system will postpone the possible matching and keep the nodes in the market, and therefore, increase the node density of the market. At this moment, any node that enters the market will be kept in the market. If the number of nodes in the market changes from y to y − 1, this is caused only by the on-market node’s timeout. On the other hand, if a node matches with another node, there will be two nodes leaving the market simultaneously. Therefore, the departure rate equals the expected number of nodes in the market that cannot find matches. We can express the greedy algorithm’s departure rate as
and the leaving rate of the matched nodes as:
Equation (6) says nodes in the market get matched when they become critical and leave the market in pairs. Therefore, the equation of the balanced market size can be deduced as:
Like the greedy case, the market size will highly concentrate on a fixed range if we continuously apply a patient algorithm to the market. There is a straightforward way to find the highly concentrated range. Assume that any arriving node matches with none of the critical nodes; then the market size should be n. On the other hand, if all critical nodes do find their corresponding matches, then the market size would be n/2. Because when the arrival rate is n, the market size is y, and all of them found their matches, then the leaving rate should be 2y. At the equilibrium state, n = 2y, so that y will be n/2.
Based on the concentrated node number of the market, the loss of the market under the patient algorithm can be computed as the ratio of the node arrival rate to the departure ratio, that is
The computed system losses with respect to the number of expected links per node, d, for the patient and the greedy matching strategies, are shown in Figure 10.
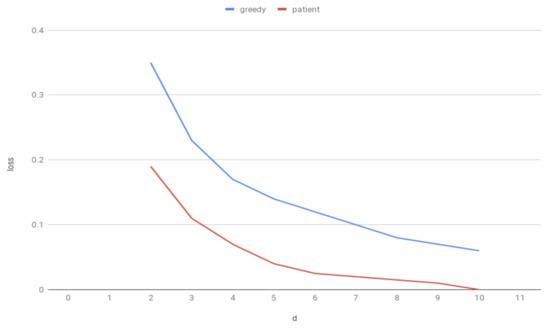
Figure 10.
System losses vs. the number of expected links per node, d, if the patient and the greedy matching strategies are adopted.
Experimental results, presented in Section 6, confirm that the patient algorithm gets more matches in the market. However, it also costs too much time to find a match. Moreover, patient algorithms are more suitable for use in large markets.
5.3. Dynamic Tuning Strategy
As pre-described, our TimeBank is a community-based system. There are a limited number of market members; therefore, the system performance is susceptible to the market’s quantity. For promoting the embrace of TimeBank, we should enlarge her node density (or number of active members) to an economic scale to provide attractive system performance. Therefore, in this paper, a market thickness-based dynamic matching strategy is presented for bettering our system performance. The basic idea is that “increase the possible links per node does give each node more matching candidates.” However, in a blockchain-based TimeBank, all of the matching strategies are realized on chaincodes. That means the on-ledger matching strategy does not have the flexibility to meet the dynamically changed market conditions. For example, if the market is very thick, but all nodes are programmed to follow the patient algorithm, it will cost a lot of time to find a match. Therefore, we need a more flexible (or dynamic changing) strategy to handle different real market situations.
In some sense, a Dynamic Tuning Strategy (DTS) will also thicken the market to reduce system losses, just like the patient algorithm. But DTS does not need to postpone the match of a node until the node becomes critical. In this work, a system parameter decides whether the market prefers the patient algorithm or the greedy one that is defined to control the system’s preference about the patient or greedy during the matching process. When the market is thin, all in-market nodes prefer to take a patient-oriented strategy. On the other hand, when the market is thick, all the nodes prefer not to wait too long to get a match.
Since a blockchain-based system does not have a global planner, the matching process must be run by all users. When someone posts a service inquiry to the blockchain, the corresponding node will invoke the matching function, and this matching function should be DTS-based. Conceptually, the proposed DST mechanism is a mixture of the pre-described greedy and patient mechanisms, and this will be detailed in the next subsection.
(1) Voting Mechanism: After a user posted their service proposal on the blockchain, the corresponding node queries match related data of the other inquiries on the blockchain. This work assumes that Ni is the set of neighbors to a service Si, where a neighbor to the service Si means the matching condition of that node is compatible with that of the Si. Furthermore, we also denote the set of the voting states as V for each posted service inquiry, where the collection of voting states, V, consists of the following two elements:
- vp: the state of the service inquiry tends to be patient for the current market;
- vg: the state of the service inquiry tends to be greedy for the current market.
Every time the user invokes a DTS-based matching, the service inquiry can flag itself with vote state vp or vg and write the chosen state into the set V in the service inquiry, as shown in Algorithm 1.
| Algorithm 1: Dynamic Tuning Strategy |
 |
If Si does not have any neighbors, it means Si does not comply with other service inquiries’ matching conditions in the current market. Si cannot complete the match process at this time, so it prefers waiting for other nodes. This waiting will thicken the market for finding neighbors; therefore, Si will flag its voting state to vp when invoking DTS-based matching, which means that it expects every other node to wait for matching patiently.
If Si has neighbors, there are other service inquiries in the market whose matching conditions comply with that of Si. Since Si has neighbors, it prefers completing the match as soon as possible. Therefore, the Si will flag its voting state to vg, which means that Si embraces the greedy market strategy more. Figure 11 depicts the block diagram of the proposed DTS for matching, and its detailed processing flow is shown in Figure 12.
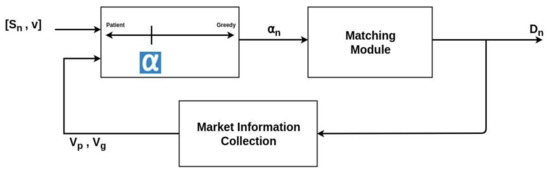
Figure 11.
The block diagram of the proposed DTS-based matching mechanism.
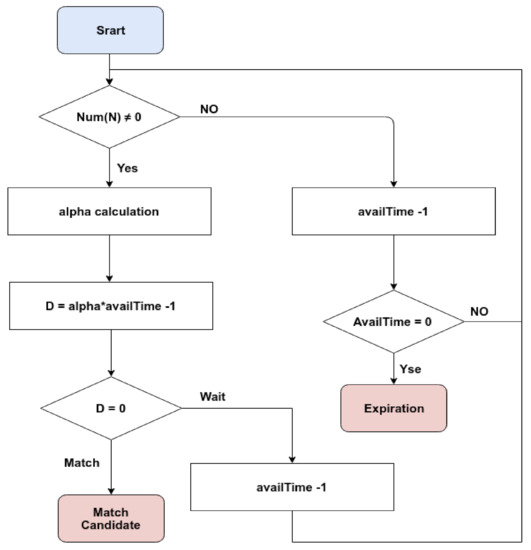
Figure 12.
The detailed processing flow of the proposed DTS-based matching algorithm.
After voting, if the number of Si’s neighbors is greater than zero, then Si investigates the voting states of other service inquiries in the blockchain and calculates its value as . In this work, is defined as the ratio of the number of vp to the current market size. That is,
First, let us consider two extreme cases for further discussion:
- If all nodes in the market do not have any neighbors, all inquiries will change their voting states to vp. At this time, α = 1, and our DTS-based matching is equivalent to that of a patient algorithm. All nodes in the market have a consistent choice: to wait patiently.
- If all nodes in the market do have neighbors, all inquiries will change their voting states to vg. At this time, α = 0, and our DTS-based matching effect is equivalent to a greedy algorithm, and all nodes in the market have a consistent choice: to match as soon as possible.
Second, from Equation (1), the value of α will be dynamically tuned according to the ratio of the number of vp to the market’s total votes. As the system members’ voting states are changing, the strategy for matching should also be altered dynamically.
(2) Decision Function: The realization of the proposed DTS depends on the following Match Decision Function:
TH = m − ⌊m ∗ α⌋,
In Equation (3), NOAI denotes the number of available times remained in the lifecycle interval for the service inquiry, m is the maximum time of the service inquiry when invoking a matching process in its lifecycle. For example, if m = 10 and the service inquiry Si have failed to get match four times in the current pairing procedure, then NOAI = 6. Assuming α = 0.5, then TH = 5. Now (NOAI − TH) = 6 − 5 = 1, D = Wait, and Si will continue to wait until the next call for the matching function. As one more matching period passed, Si in the new matching process will have NOAI = 5. Assuming α = 0.5 again, then D = Match, and the corresponding Si will try its best to match one of its neighbors and leave the market. Furthermore, the longer a node remains on the market, the easier it finds a match. Therefore, all nodes in the market will operate according to the remaining feasible time and have the characteristics mentioned above.
6. Experiment Result
In this work, we simulate the whole process starting from users’ stochastically arrivals to the blockchain, posting their service inquiries, and then waiting to find a match. Our experimental system and simulation are built and conducted on a personal computer with Intel 6700K CPU, 24GB RAM, and Ubuntu 16.04. The Fabric version is 1.4 and all the nodes are running in Docker, where the version is 18.09.3.
Our matching experiments consist of two parts. The first is an experiment of matching under the greedy and patient algorithms. The second is to simulate finding a match in the real market scenario under the greedy, the patient, and the DTS-based matching algorithms. The pre-described system losses are used to measure the corresponding performances.
In our simulation:
- The average arrival time interval is 5 s and follows a Poisson Process.
- The total number of services is 250.
- The matching period is 40 s.
- The available time is 200 s.
Figure 12 presents the simulation results under the two static algorithms. The market will highly concentrate on the corresponding quantity ranges under both algorithms. In the greedy algorithm, the concentration range should be approximately (6, 15), while the patient algorithm’s results should be close to (20, 40).
Table 2 shows the system performances under the different three algorithms. The loss of the greedy algorithm is the largest, but the waiting time is the shortest. While the patient algorithm causes the smallest loss, however, it takes the longest waiting time to find a match. The loss obtained in the DTS-based matching algorithm is only slightly worse than that of the patient algorithm, but it dramatically reduces the waiting time. That is to say, if a DTS-based matching algorithm is used, users can save more than half of the waiting time, and the loss can be controlled to an acceptable range. More importantly, as for the average neighbors, the greedy algorithm gives only one neighbor to one node when it finds a match.

Table 2.
The performance comparison among three different strategies.
In Figure 13, we use a DTS-based matching algorithm to simulate the matching scenario in the time banking system. Unlike previous simulations, no service will arrive at the market after a certain point in time. This simulation will show that when the service to the market changes drastically, the system’s strategy will automatically tune the alpha and maximize the overall matching rate.
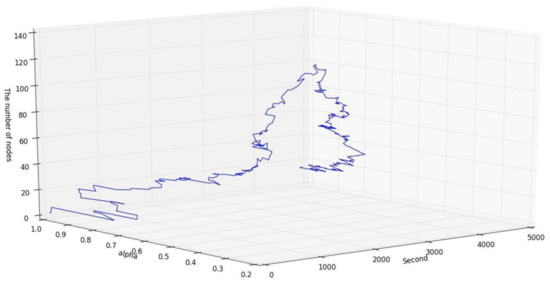
Figure 13.
Simulated market sizes and alpha values for the DTS-based matching algorithms.
From the results of the simulation, we can divide it into the following three phases:
- (1)
- When the system begins running, the market would be very tiny, so the hasty increment due to each service’s vote caused the value of α to change substantially. On the other hand, because the market size is small and the probability of matching is low, α will be biased towards 1, and the timing strategy of the system tends to wait.
- (2)
- When the market gets thicker, α will slowly be decreasing, and the corresponding value change will become smoother, representing services in the market that can get matched in shorter waiting times.
- (3)
- When the service’s arrival is interrupted, α will gradually increase, allowing the market to maintain its match rate based on the proposed waiting mechanism.
From the simulation results, we observed that DTS could stabilize the market thickness of TimeBanks in the community-based mutual assistance systems and effectively provide a high matching rate. Compared to the static matching algorithms, DTS flexibly changes the timing strategy based on the number of nodes in the market and the number of links of each node. TimeBanks in different communities do have different arrival rates and matching rates. Its dynamic nature makes the DTS-based approach not need to have to re-design different matching algorithms according to different markets’ characteristics. As nodes arrive in the market in sequence, the algorithm will automatically tune to the appropriate timing strategy.
7. Conclusions and Future Work
In an era of outbreaking influenza and viruses, especially the COVID-19 pandemic, the necessity and importance of building mutual assistance within communities has increased significantly. As shown in this work, with the aid of modern technology such as blockchain, TimeBank systems [2,27] could manifest their value in building community, inclusion, volunteerism, and social assistance. As stated in [28], the theory of matching algorithms has focused mostly on static environments until recently. In other words, little is known in the case where all participants arrive and depart dynamically, like the one we faced in a Timebank system. Our work helps bridge this gap by introducing and realizing a simpler dynamic matching algorithm that works when any one of the SPs or the SRs can arrive or depart online.
In summary, this paper presents a blockchain-based TimeBank system with a service-exchange and flexible matching mechanism. Since we realized our TimeBank on Fabric, its blockchain nature brings data transparency, high scalability, and the fairness of matching to the system. However, building systems on the blockchain also have some challenges and compromises. For example, the blockchain cannot globally compute the system’s optimal matching parameters and need the user to run the matching process locally. In a nutshell, the proposed dynamic tuning strategy increases each node’s neighbors’ number without costing a much longer waiting time. When the market structure changed, becoming thicker or thinner, we dynamically adjusted the matching policy accordingly.
Shortly, we will integrate the user’s grading mechanism [5] into our matching mechanism. This integration will allow the system to select matching objects regarding users’ personal preferences. The integrated system is expected to enhance the matching quality because user experiences and feedbacks are considered. Moreover, as pointed out by one of the anonymous reviewers, Xuheng Lin et al., in their position paper [28], proposed a Blockchain-Enabled Decentralized Time Banking System (BlendTBS) for encouraging people in the community to be engaged in mutual serving relationships. For achieving this goal, BlendTBS rewards the residents who commit to socially beneficial activities. Notice that the SP and the SR can use different matching strategies independently when the market’s supply and demand are uneven. If there are many SRs but just a few SPs in the market, the SR’s matching policy may be greedier than SP. In the practical matching algorithm design, we believe that an incentive mechanism [26] or a rewarding mechanism [27] for dealing with unbalanced supply and demand must also be considered carefully.
Moreover, as mentioned in [27], a small-scale study was planned to examine the utility of BlendTBS to a traditional community on the island of Aneityum, Republic of Vanuatu. We believe that our dynamic matching algorithm might help enhance the applicability of BlendTBS, especially when the community scale is enlarged. Finally, as suggested by one of the anonymous reviewers, Table 3 is added to show the three mentioned TimeBank systems’ specific contributions.

Table 3.
The similarities and differences of the three mentioned TimeBank systems.
Author Contributions
Funding acquisition, J.-L.W.; Investigation, Y.-T.L.; Methodology, Y.-T.L.; Project administration, J.-L.W.; Software, J.-J.L.; Writing—original draft, J.-J.L.; Writing—review & editing, J.-L.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Edgar, S.C. Time Dollars: The New Currency That Enables Americans to Turn Their Hidden Resources—Time—Into Personal Security and Community Renewal; Rodale Press: Emmaus, PA, USA, 1992. [Google Scholar]
- Edger, S.C. No More Throw-Away People: The Co-Production Imperative, 2nd ed.; Essential Books: London, UK, 2000. [Google Scholar]
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 5 March 2021).
- Makridakis, S.; Klitos, C. Blockchain: Current Challenges and Future Prospects/Applications. Available online: https://www.researchgate.net/publication/338951665_Blockchain_Current_Challenges_and_Future_ProspectsApplications (accessed on 26 February 2021).
- Lee, Y.-T.; Lin, J.-J.; Jane, Y.-J.H.; Wu, J.-L. A Time Bank System Design on the Basis of Hyperledger Fabric Blockchain. Future Internet 2020, 12, 83. [Google Scholar] [CrossRef]
- Prashanth, J.A.; Han, M.; Wang, Y. A Survey on Security and Privacy Issues of Blockchain Technology. Available online: https://www.researchgate.net/publication/325173502_A_survey_on_security_and_privacy_issues_of_blockchain_technology (accessed on 26 February 2021).
- Raikwar, M.; Gligoroski, D.; Kralevska, K. SoK of Used Cryptography in Blockchain. IEEE Access 2019, 7, 550–575. [Google Scholar] [CrossRef]
- Mike, E. Smart Contracts: Terminology, Technical Limitations and Real-World Complexity. Law Innov. Technol. 2017. [Google Scholar] [CrossRef]
- Buterin, V. Ethereum: A Next Generation Smart Contract and Decentralized Application Platform. 2013. Available online: https://github.com/ethereum/wiki/wiki/White-Paper (accessed on 5 March 2021).
- Xu, R.; Lin, X.; Dong, Q.; Chen, Y. Constructing trustworthy and safe communities on a blockchain-enabled social credits system. In Proceedings of the 15th EAI International Conference on Mobile and Ubiquitous Systems: Computing, Networking and Services, New York, NY, USA, 9 November 2018; pp. 449–453. [Google Scholar]
- Schweizer, A.; Schlatt, V.; Urbach, N.; Fridgen, G. Unchaining Social Businesses-Blockchain as the Basic Technology of a Crowdlending Platform. In Proceedings of the 38th International Conference on Information Systems, Seoul, South Korea, 10–13 December 2017; Available online: http://www.fimrc.de/Paperbibliothek/Veroeffentlicht/712/wi-712.pdf (accessed on 5 May 2020).
- Mukkamala, R.R.; Vatrapu, R.; Ray, P.K.; Sengupta, G.; Halder, S. Converging blockchain and social business for socio-economic development. In Proceedings of the IEEE International Conference on Big Data, Seattle, WA, USA, 10–13 December 2018; pp. 3039–3048. [Google Scholar]
- Guo, Y.; Liang, C. Blockchain application and outlook in the banking industry. Financ. Innov. 2016, 2, 24. [Google Scholar] [CrossRef]
- Peters, G.W.; Panayi, E. Understanding modern banking ledgers through blockchain technologies: Future of transaction processing and smart contracts on the internet of money. In Banking beyond Banks and Money; Springer: Berlin/Heidelberg, Germany, 2016; pp. 239–278. [Google Scholar]
- Wu, T.; Liang, X. Exploration and practice of inter-bank application based on blockchain. In Proceedings of the 12th International Conference on Computer Science and Education (ICCSE), Houston, TX, USA, 22–25 August 2017; pp. 219–224. [Google Scholar]
- Androulaki, E.; Barger, A.; Bortnikov, V.; Cachin, C.; Christidis, K.; De Caro, A.; Enyeart, D.; Ferris, C.; Laventman, G.; Manevich, Y.; et al. Hyperledger fabric: A distributed operating system for permissioned blockchains. In Proceedings of the 13th ACM SIGOPS European Conference on Computer Systems, Porto, Portugal, 23–26 April 2018. [Google Scholar]
- Freedman, R.; Borg, J.S.; Walter, S.-A.; Dickerson, J.P.; Conitzer, V. Adapting a Kidney Exchange Algorithm to Align with Human Values. Artif. Intell. 2020, 283, 103261. [Google Scholar] [CrossRef]
- Gale, D.; Shapley, L.S. College Admissions and the Stability of Marriage. Am. Math. Monthly 1962, 69, 9–15. [Google Scholar] [CrossRef]
- Iwama, K. A Survey of the Stable Marriage Problem and Its Variants. In Proceedings of the IEEE Informatics Education and Research for Knowledge-Circulating Society, Kyoto, Japan, 17 January 2008. [Google Scholar]
- Akbarpour, M. Thickness and Information in Dynamic Matching Markets. J. Political Econ. 2020, 128, 783–815. [Google Scholar] [CrossRef]
- Ashlagi, I. On Matching and Thickness in Heterogeneous Dynamic Markets. Op. Res. 2019, 67, 905–1208. [Google Scholar] [CrossRef]
- Ashlagi, I. Matching in Dynamic Imbalanced Market. arXiv 2019, arXiv:1809.06824v2. [Google Scholar] [CrossRef]
- Kurino, M. House Allocation with Overlapping Agents: A Dynamic Mechanism Design Approach; Jena Economic Research Papers; Friedrich-Schiller-University Jena: Jena, Germany, 2009. [Google Scholar]
- Bloch, F.; Houy, N. Optimal assignment of durable objects to successive agents. Econ. Theory 2012, 51, 13–33. [Google Scholar] [CrossRef]
- Rochet, J.-C.; Tirole, J. Platform Competition in Two-Sided Markets. J. Eur. Econ. Assoc. 2003, 1, 990–1029. [Google Scholar] [CrossRef]
- Ramon, C.-M.; Llanes, G. Investment Incentives in Open-Source and Proprietary Two-Sided Platforms. J. Econ. Manag. Strategy 2015, 24, 306–324. [Google Scholar] [CrossRef]
- Lin, X.; Xu, R.; Chen, Y.; Lum, J.K. A blockchain-enabled decentralized time banking for a new social value system. In Proceedings of the 2019 IEEE Conference on Communications and Network Security (CNS), IEEE, Washington, DC, USA, 10–12 June 2019. [Google Scholar]
- Burq, M. Dynamic Matching Algorithms. Ph.D. Thesis, MIT Sloan School of Management, Cambridge, MA, USA, 2019. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).