Abstract
The reporting of incidents of misconduct, violence, sexual assault, harassment, and other types of crime that constitute a major concern in modern society is of significant value when investigating such incidents. Unfortunately, people involved in such incidents, either as witnesses or victims, are often reluctant to report them when such reporting demands revealing the reporter’s true identity. In this paper, we propose an online reporting system that leverages Identity-Based Cryptography (IBC) and offers data authentication, data integrity, and data confidentiality services to both eponymous and anonymous users. The system, called ARIBC, is founded on a certificate-less, public-key, IBC infrastructure, implemented by employing the Sakai–Kasahara approach and by following the IEEE 1363.3-2013 standard. We develop a proof-of-concept implementation of the proposed scheme, and demonstrate its applicability in environments with constrained human, organizational and/or computational resources. The computational overheads imposed by the scheme are found to be well within the capabilities of modern fixed or mobile devices.
1. Introduction
Incidents, such as misconduct, violence, sexual assault, harassment, and other types of crime occur frequently in social circumstances, such as in educational institutions at all levels or the workplace; such incidents constitute a major concern in modern society.
The reporting of such incidents is of significant value for both investigating the incident itself, and for recognizing potential problems before they evolve into serious incidents. However, difficulties exist in encouraging observers to make the incidents known to the competent authority on one hand, and in handling the reports on the other. Witnesses and victims alike are frequently reluctant to report an incident due to a number of reasons, including fear of retaliation by the perpetrator(s), fear of not being believed, insecurity, and fear of getting into trouble. As a result, a significant percentage of incidents go unreported; this is particularly the case with sexual assault and property theft crimes [1]. Further, when an observer does report an incident, they frequently do so more than once, in particular during the investigation process. Thus, a number of reports by the same person on the same incident or more than one related incidents (as e.g., in the case of financial misconduct or crime) may be submitted; the investigating authorities need to attribute these to the same reporter, in order to handle them properly and use them effectively.
Online reporting systems have provided a means for overcoming the latter obstacle. However, the approach most commonly followed in such systems is to associate each report with the verified identity of the reporter or by an incident ID, assigned to the first submitted report. Whereas this greatly facilitates the management of the reporting process, it fails to address the reporters’ concerns regarding the disclosure of their true identity; this can be resolved by allowing anonymous reporting. Even though anonymous reporters were, in the past, perceived to be less credible than identified ones when reporting to the authorities via one-way communication, the perceived credibility of the reporter was recently found not to be statistically different when using two-way communication. Further, investigators have been found to allocate statistically similar amounts of effort to investigate anonymous and identified reports [2]. These results support the use of anonymous, two-way communication in online reporting systems. Anonymous reporters would benefit from the ability to maintain an active dialogue with investigators without jeopardizing their own safety or the effectiveness of the investigation.
In this paper, we propose ARIBC, an online reporting system that leverages Identity Based Cryptography. The proposed system is based on the Sakai–Kasahara Key Encryption (SAKKE) schemes [3] and the BLMQ (Barreto, Libert, McCullagh, Quisquater) signature scheme. The latter is essentially the Sakai–Kasahara signature scheme [4] that was proposed in [5]. ARIBC offers two-way secure communication between the reporter and the authorities by means of encryption; two-way source authentication and data integrity by means of digital signatures; option to the reporter to remain anonymous; independence from other authentication and authorization infrastructures; ease of implementation and use.
The remainder of the paper is structured as follows: In Section 2 we review related work. In Section 3 the structure and the operational processes of the ARIBC are presented. In Section 4 we discuss implementation issues, and in Section 5 we discuss the security of the ARIBC, and its advantages and drawbacks when compared to alternative approaches. Finally, in Section 6 we summarize our conclusions.
2. Related Work
Many law enforcement agencies around the world have online reporting systems in operation. The vast majority of these support the reporter in communicating with the agency either via e-mail or via a website. As such, they usually do not have any privacy protection controls in place, they do not support two-way communication (between the agency and the reporter), and they can only associate reporters with reports by means of a report ID, assigned to the first submitted report. This functionality may suffice for satisfying the basic needs of an agency, but more sophisticated solutions are needed to fully support the reporting process. Accordingly, several online reporting schemes, that serve diverse purposes, have been proposed in the literature, and some have been implemented and are operational. Some of these systems support anonymous reporting, whilst others require the reporters to be eponymous and to identify themselves either with the authority to which they report (e.g., the police) or to a third party (mediator); only a few schemes support both modes of reporting.
An anonymous, web-based online reporting system that combines natural language processing with insights from the cognitive interview approach to obtain more information from witnesses and victims is described in [6,7,8]. Another anonymous reporting system was proposed for use in reporting and for following up on incidents, accidents and the like in [9]. Zou et al. proposed ReportCoin, a Blockchain-based anonymous reporting system integrating an incentive mechanism [10]. The Say Something Anonymous Reporting System is a youth violence prevention program from Sandy Hook Promise, a national violence prevention organization, that allows youth and adults to submit secure and anonymous safety concerns to help identify and intervene upon individuals at-risk before they hurt themselves or others [11].
When it comes to eponymous reporting schemes, Sakpere et al. presented a system (Cry Help App) that was developed to enable residents of a university community, situated in an environment with constrained technological resources, to facilitate secure and covert crime reporting [12]. Shih et al. proposed an online illegal event reporting scheme based on cloud technology, which can process illegal activity reports from the reporting event to the issuing of a reward [13]. Obada-Obieh et al. in [14] described an Online Third Party Reporting System (O-TPRS) that was developed by VESTA Social Innovation Technologies [15]. A prototype crime reporting system that relies on four reporting forms, namely a complaint or dispatch reporting form; a crime event report form; a follow-up investigation report form; and an arrest report form was described in [16]. An application that can be used by citizens to report and manage their complaints effectively was proposed in [17]. A mobile infrastructure for detecting, reporting and tracking down criminal perpetrators using a mobile device was proposed in [18]. Eponymous online reporting systems commonly use a Public Key Infrastructure (PKI) to securely identify the reporters.
Whereas eponymous systems clearly support two-way, repeated, secure communication between the reporter and the authority receiving the report, existing anonymous schemes cannot offer this functionality. Further, existing anonymous reporting systems cannot be linked to a reward process, unless a form of electronic currency (such as e.g., bitcoin) is used, as in [10]. However, this solution inherits all the limitations and downsides of such currency.
The concept of a Public-key Cryptographic scheme that would use a publicly known distinctive characteristic of identity as its public key was first introduced by Shamir in 1984 [19]. Any type of identifier, e.g., email address, social security number, telephone number can be used, as long as it can uniquely identify the user and is readily available to the party that uses it. The corresponding private component would be generated by a trusted key generation center. The main motivation for this approach is to eliminate the need for certificates and their management; this is why such schemes are called certificate-less IBC schemes and are considered simpler and less resource-demanding solutions than certificate-based PKIs. Even though Shamir proposed the idea, he was only able to develop an identity-based signature (IBS) scheme based on the RSA primitive. Only in the early 2000’s did the emergence of cryptographic schemes based on pairings on elliptic curves result in the construction of feasible and secure IBC schemes [3,20,21]. An early survey of IBC schemes appeared in [22]. IBC schemes have found use in many diverse applications, including mobile ad-hoc network security [23]; secure e-mail implementations [24,25]; cloud security [26]; healthcare systems [27,28,29]; e-Government environments [30]; smart grid security [31]; and aviation and maritime navigation and tracking [32,33]. The distinguishing features, the benefits and the drawbacks of IBC against those of the more traditional PKI have been discussed in [34,35].
The Sakai–Kasahara Key Encryption (SAKKE) scheme [3], and a variant of the Elliptic Curve Digital Signature algorithm (ECDSA) optimized for use with the Sakai–Kasahara scheme is part of the MIKEY-SAKKE protocol [36,37,38], that was proposed in 2016 by the National Cyber Security Centre of the UK [39]. MIKEY-SAKKE “is designed for government and relevant enterprises to enable secure, cross-platform multimedia communications” and integrates the MIKEY (Multimedia Internet KEYing) framework [40].
In this work the Sakai–Kasahara IBC schemes [3] and the BLMQ signature scheme proposed in [5,41] are used. Further, the guidelines of the IEEE 1363.3-2013 “Standard for Identity-Based Cryptographic Techniques using Pairings” [42] have been followed. The standard describes IBC schemes that use pairings to implement data encryption, digital signatures, data signcryption, and exchanges of symmetric ciphers keys. Additionally, the standard presents formalized algorithms for calculating pairings with the appropriate parameters to satisfy industry-standard security requirements as defined in [43]. The security of the algorithms and techniques employed in this paper has been analyzed in [4,42,44].
3. Structure of the ARIBC
3.1. ARIBC Entities
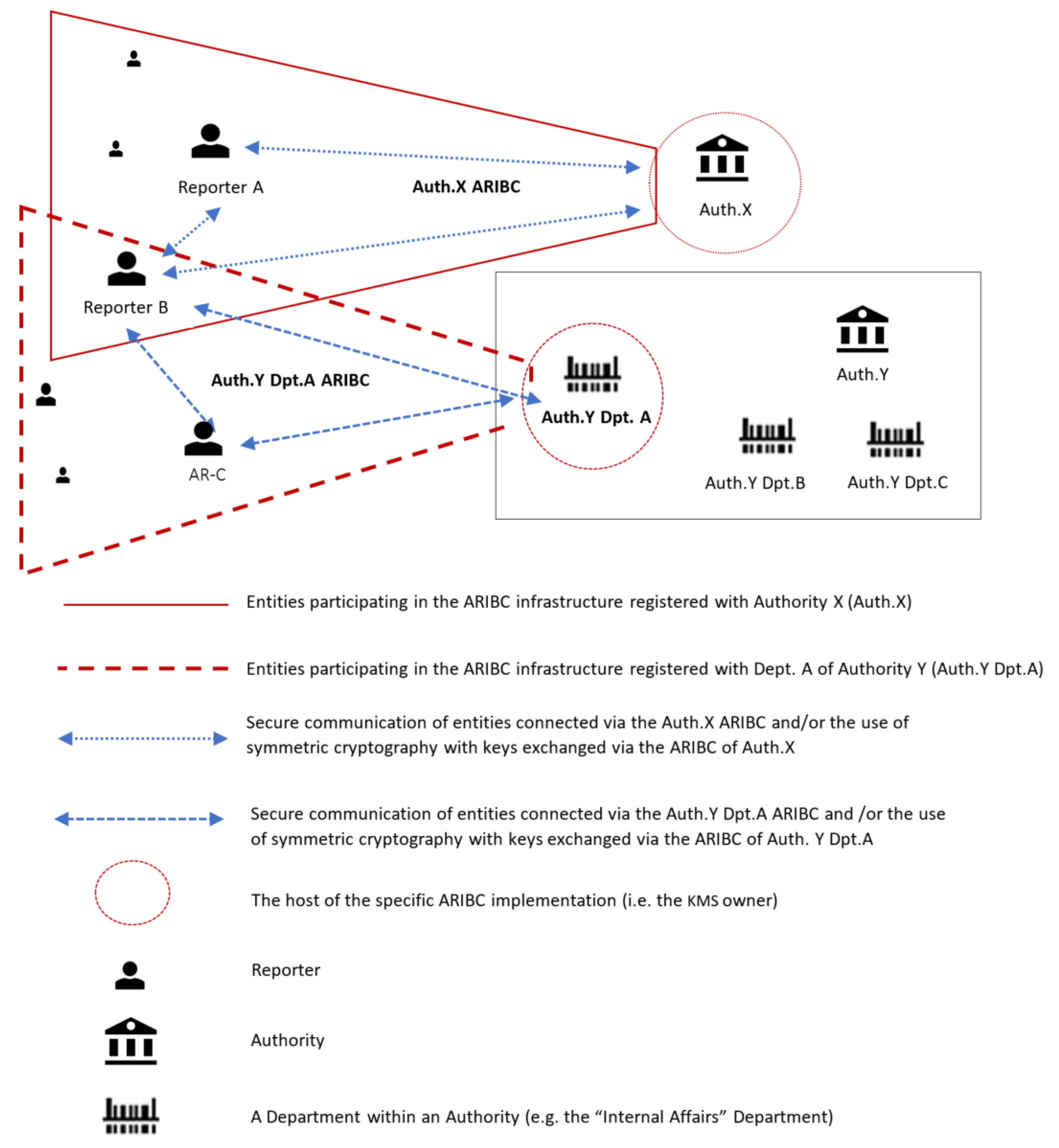
As shown in Figure 1, the ARIBC’s interactive entities are reporters, authorities, and possibly departments (or individual investigators) within authorities.
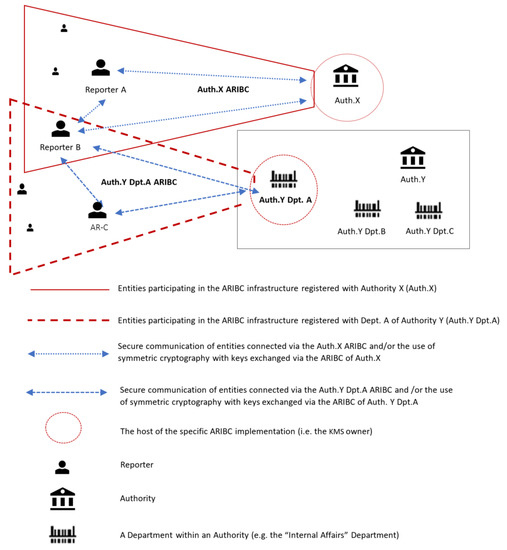
Figure 1.
The interactive entities of ARIBC.
In Figure 1, authority X hosts an instance of ARIBC. A number of reporters, including Reporter A and Reporter B have registered with Authority X and can communicate securely with it. Department A of Authority Y also hosts an instance of ARIBC, with which a number of reporters, including Reporters B and C have registered. Note that a reporter may have registered with more than one instances of ARIBC. Both instances of ARIBC offer to their registered reporters confidential communication, authentication and integrity services. Note also that reporters registered with either instance of the ARIBC can securely communicate with each other as well; however, such communication cannot be in their capacity as reporters of a particular incident, because no entity other than each reporter him/herself and the authority to which the report has been submitted has the knowledge to associate an incident with a reporter of the incident.
3.2. Notation
The notations shown in Table 1 will be used in the sequel.

Table 1.
ARIBC notations.
3.3. ARIBC Setup Phase
The establishment of an ARIBC instance requires setting up a central trusted coordinator, that is responsible for generating the private keys of the users using their public identifiers (IDs). This coordinator, who is also the operator of the ARIBC instance, is referred to as the ARIBC Key Management Server (ARIBC-KMS); this is the dominant and most sensitive entity in an IBC scheme and should be trusted a priori by all entities that interact with the ARIBC. Setting up the ARIBC-KMS entails:
- defining a security parameter to be used for calculating a number of system parameters, henceforth referred to as Public Parameters (PP), which will be made public;
- selecting a random master secret, henceforth referred to as Master (Server) Secret key (KSAK), which will be kept private;
- computing the ARIBC public key, henceforth referred to as Master (Server) Public key (), which will be made public;
- selecting the hash functions to be used; and
- publishing and .
3.3.1. Definition of Public Parameters
The security level of the ARIBC instance is determined by the chosen size of its security parameter (t). This is defined as the size (in bits) of a prime number p, that defines the order of the bilinear map cyclic groups , , that will be generated in subsequent steps. The security level of each ARIBC instance is proportional to the size of t, but its efficiency is inversely proportional to it. Thus, the value of this parameter needs to be selected carefully, to achieve the right balance between efficiency and level of security of each ARIBC instance. Therefore, the value of the security parameter should be defined by a methodical investigation of the special needs and characteristics of the Authority in which the ARIBC instance is to be established. In this work we describe a generic ARIBC instance, following the general guidelines and suggestions in the IEEE 1363.3-2013 standard [42].
We then find a prime number and we generate three bilinear map cyclic groups , , (target) of prime order p, by following the guidelines in [5,44,45].
Next, we establish a random number generator R by following the RFC5091, FIPS186-2 or X9.62 standards. To this end, we choose as a random generator of and we find the appropriate random generator of , so that an efficient isomorphism such that exists. We denote by e the bilinear pairing mapping . To improve the efficiency of the ARIBC implementation, we pre-calculate and store the constant pairing value .
3.3.2. Selection of the Master (Server) Secret Key
We randomly pick the Master (Server) Secret key of the ARIBC instance, where p is the order of the bilinear map cyclic groups . The is even more security-sensitive than the Master Private Key of a Certification Authority in an X.509 PKI, because an adversary that knows the Master Private Key of a Certification Authority of a PKI is only able to create spoofed certificates of public keys; this is in contrast to an adversary who knows the , who is able to create the private key for any user. Accordingly, the operator of the ARIBC instance is responsible for taking all necessary measures to ensure the security and availability of the KSAK, and the appropriate procedures for recovering it, should the need arise.
One way to solve the problem that the key generation center gets to know the entire private keys of all users is the use of certificate-less public key cryptography [46]. In this approach the key generation center only computes a partial private key of user A, based on the identity ; the user combines this partial private key with some secret information (only known to the user). Then the user combines the secret information with the public parameters of the key generation center to obtain the user’s public key. The advantage of this approach is that this public key no longer needs to be certified, since it contains the identity of the user, and if the key generation center is trusted (and the public parameters of the key generation center are authentic) one can rasonably assume that the user associated to really corresponds to A and holds the corresponding private key.
3.3.3. Computation of the ARIBC Public Key
We compute the Master (Server) Public-key () that derives from the chosen Master (Server) Secret key (KSAK) by using elliptic curve multiplication. is computed as the product of times the generator point of , ,47]. Note that it is equally secure to define and .
3.3.4. Selection of Hash Functions
Five cryptographic hash functions are to be used in the signing and encryption procedures, as follows:
- :, where p = “prime order” of , , is a cryptographic hash function viewed as a random oracle for hashing the of the receiver [45]; according to [42], the SHA family [48] is to be used, with the specific SHA function determined according to the value of the security parameter. Note that needs to be converted from a bit-string to an octet string before being used. Further details may be found in sections 5.2.6 and 6.1.1 of [42]. is used both in the authenticity and integrity service, and in the confidentiality service.
- : is a cryptographic hash function viewed as a random oracle. is used only in the authenticity and integrity service.
- : is a cryptographic hash function, typically of the SHA family, viewed as a random oracle for XOR-ing the transmitted data. Further details may be found in sections 5.6.4 and 6.2.1 of [42]. is used only in the confidentiality service.
- : is used to derive a blinding coefficient. is used only in the confidentiality service.
- : is used for XoR-ing with the plaintext. is used only in the confidentiality service.
Note that the transmitted data may be either communication messages or the key to be used with a symmetric algorithm, such as e.g., the Advanced Encryption Standard (AES), to encrypt subsequent communication.
3.3.5. Publication of Public Information
The operator of the ARIBC publishes the Master (Server) Public-key (); and the ARIBC Public Parameters (ARIBC-PP), i.e., (, , , e, , , , , , , , , ). These parameters are static and the users of the ARIBC instance may download them only once and store them for subsequent use.
3.4. The Reporter Registration Phase
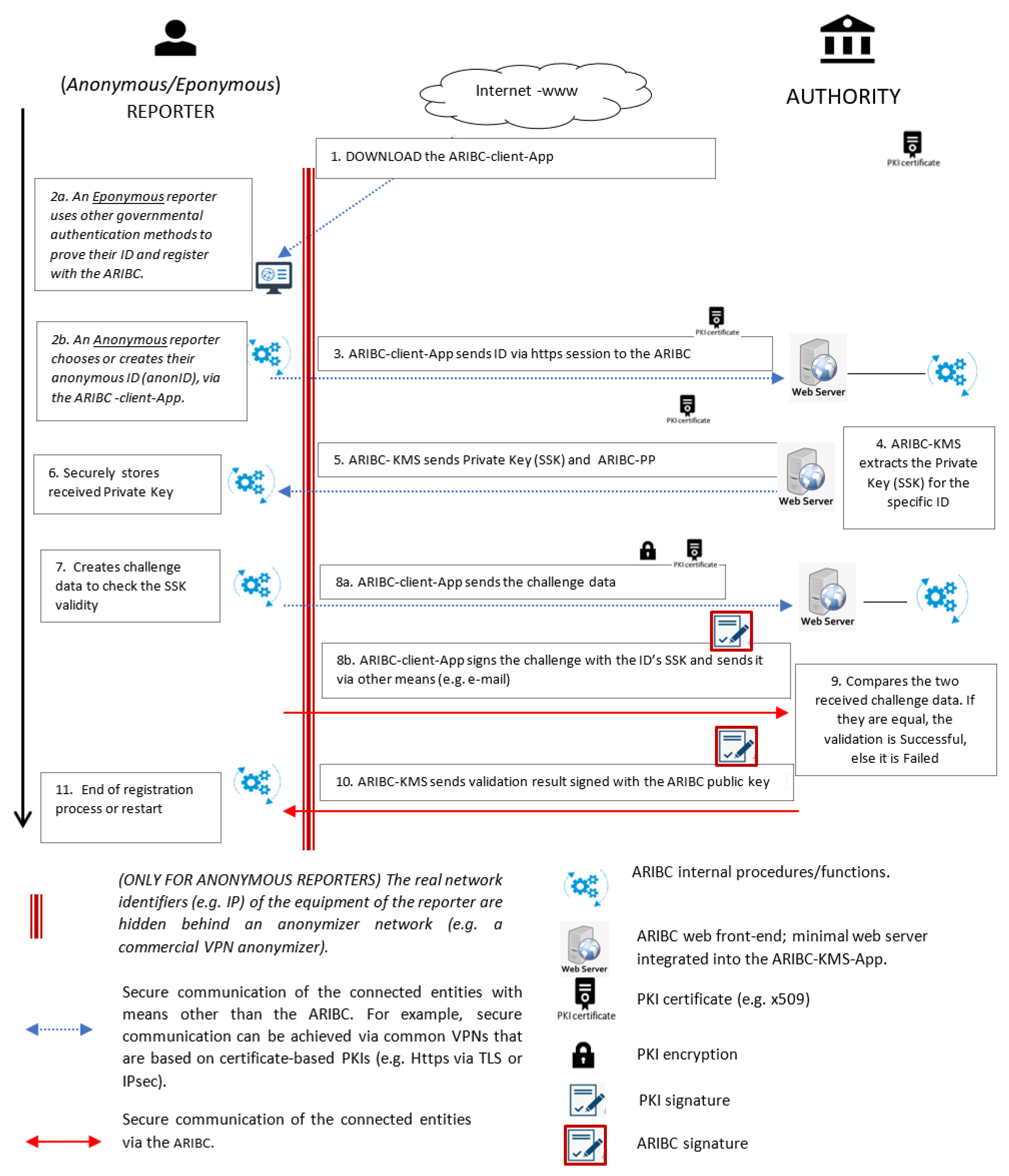
ARIBC supports both anonymous and eponymous reporters. The registration of eponymous reporters can be done either with or independently of the ARIBC instance operator. Accordingly, different procedures may be followed to ensure the real identity of the reporter, so as to satisfy the requirements of each ARIBC instance. For example, similar to the procedure typically followed for secure identification of certificate-based PKI users, the reporter visits the ARIBC instance operator and identifies her/himself by means of an official identification document (e.g., ID card, passport). The registration of anonymous reporters is performed with the ARIBC instance operator itself.
A client-side application, called ARIBC-client-App, has been designed to implement the procedures involved with ARIBC anonymous and eponymous reporter registration. There are two variants of the ARIBC-client-App: one as a smartphone application, the other as a standalone desktop application. The ARIBC-client-APP offers a user-friendly environment that makes the ARIBC services easy to use by the average user. The application allows the reporter to connect to the ARIBC using privacy-enhancing schemes such as e.g., an anonymizer service and/or a location privacy preservation service.
The registration procedures for both the anonymous and the eponymous reporter are shown compactly in Figure 2. In Figure 2 blue-colored arrows indicate communication protected by TLS VPN (i.e., a typical https/TLS connection that uses a typical site certificate), whilst red-colored arrows indicate communication protected by means of the ARIBC services. Note that the anonymous reporter needs to select (or create) her/his to be subsequently linked to her/his private key. This can be any string, including the output of a cryptographic hash function of the reporter’s choice. If this option is followed by the reporter, it is also possible, should the reporter wish, for example, to benefit from a reward, to prove her/his identity by presenting the key to decrypt her/his (hashed) .
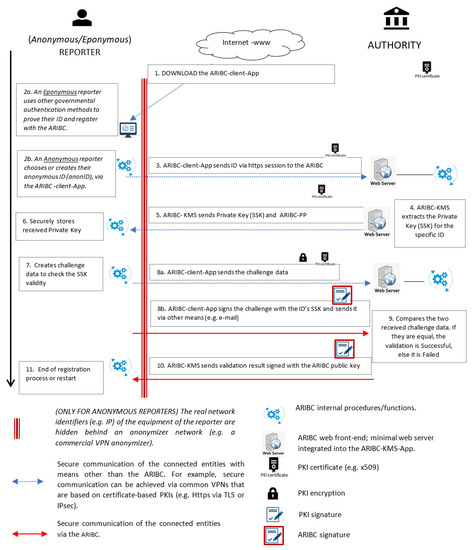
Figure 2.
ARIBC user registration process.
3.5. Extraction of the Private Keys (SSKs)
The ARIBC uses the reporter’s ID and combines it with the Public Parameters (PP) and the Master (Server) Secret key (KSAK) of the ARIBC to extract the corresponding Private (Secret) Key (SSK), of the reporter. The steps are as follows [47]:
- Represent as a string of bits in .
- Compute the cryptographic hash ; see hash in Section 3.3.4 “Selection of hash functions”.
- Compute .
3.6. Services Offered by the ARIBC
3.6.1. Integrity and Authenticity Service
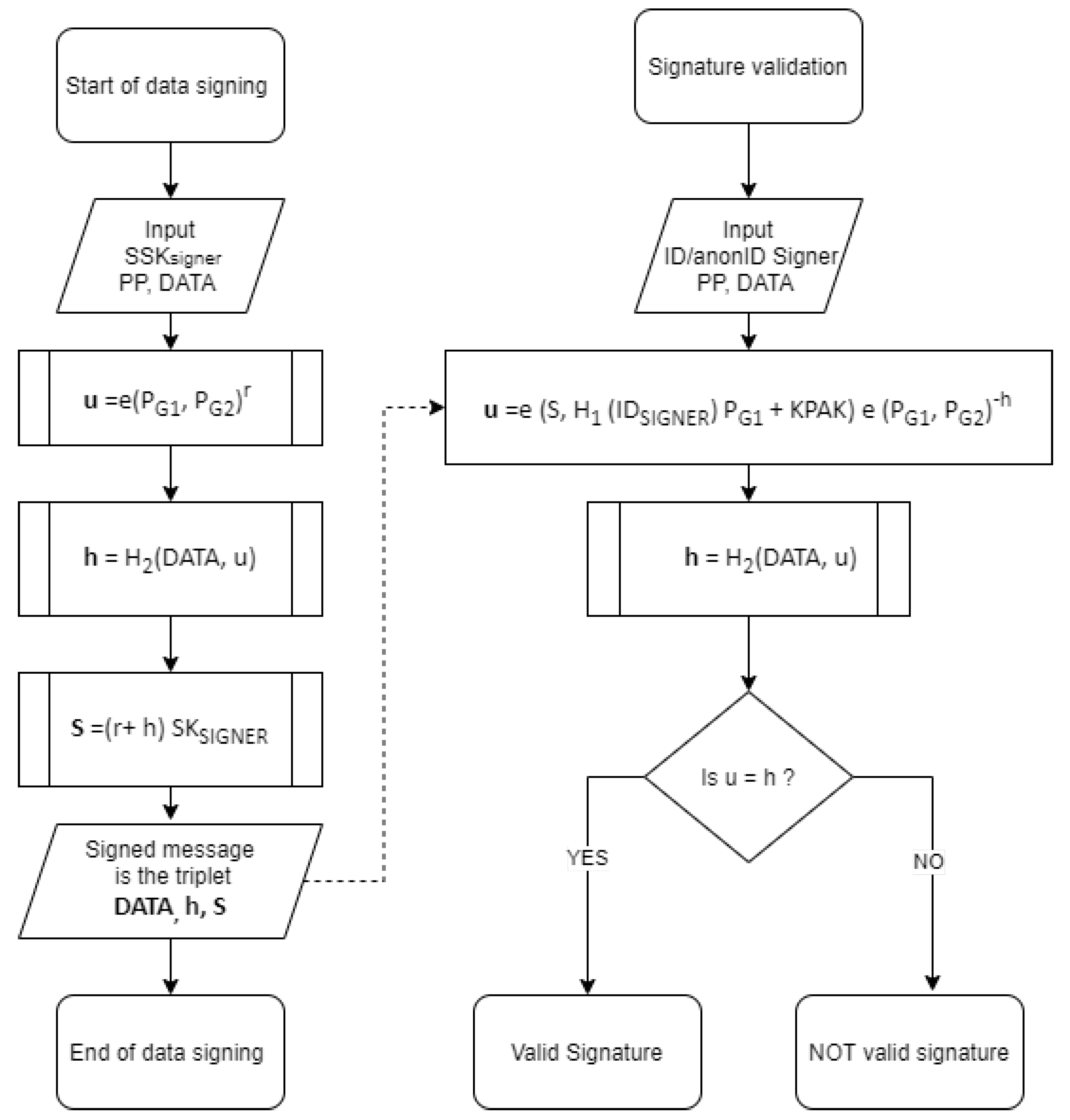
The ARIBC offers the capability of signing all types of data of the ARIBC instance operator and of its registered users. Anyone, including users not registered with the ARIBC, can verify the signature, consequently the authenticity and integrity of the signed data. Two entities are involved in the signing process, namely the Signer and the Verifier. The Signer signs the data with her/his digital signature and the Verifier verifies the validity of the signature and thus the authenticity and integrity of the signed data. The Signer can be any registered user of the ARIBC that has a valid Private Key issued by the specific ARIBC-KMS. The Verifier can be anyone, s/he only needs the publicly available of the Signer and the Public Parameters of the specific ARIBC-KMS to validate the signature. The Integrity and authenticity service is implemented by means of the Signature Generation operation and the Signature Verification operation, which are based on the BLMQ identity-based signatures operations [5,42]. Note that we choose to define , to avoid arithmetic during verification; a description with , and signed messages in would be equally secure, while keeping the signature as short as possible in practice.
The input to the Signature Generation operation consists of:
- The DATA to be signed , (where = length of the DATA in bits);
- The ARIBC Public Parameters (, , , e, , , , , , );
- The private key of the Signer ; and
The computations performed in the Signature Generation operation are:
- , where e is the bilinear pairing mapping, ;
- , where is the hash function defined in the initial setup phase of the ARIBC; and
- .
The output (i.e., the signed data) of the Signature Generation operation is the following triplet:
The input to the Signature Verification operation consists of:
- The to be validated;
- The ARIBC-KMS Public Parameters () , , ); and
- the publicly available of the Signer.
The computations performed in the Signature Verification operation are:
- ; and
The output of the Signature Verification operation is a verdict on whether the signature is Valid (if ) or Invalid (otherwise). Both the signature generation and the signature verification processes described above are shown in graphical form in Figure 3.
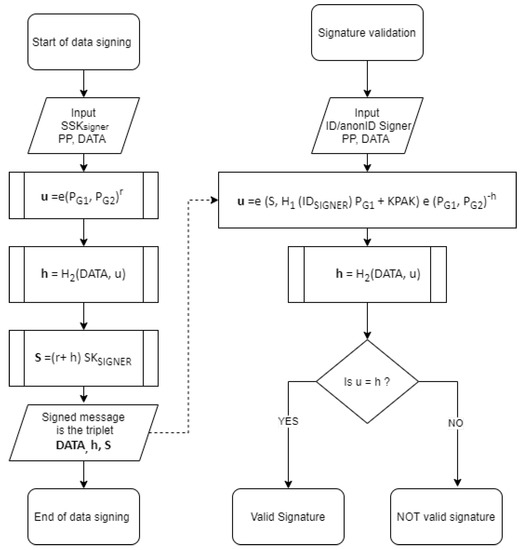
Figure 3.
ARIBC signature generation and signature verification processes.
3.6.2. Confidentiality Service
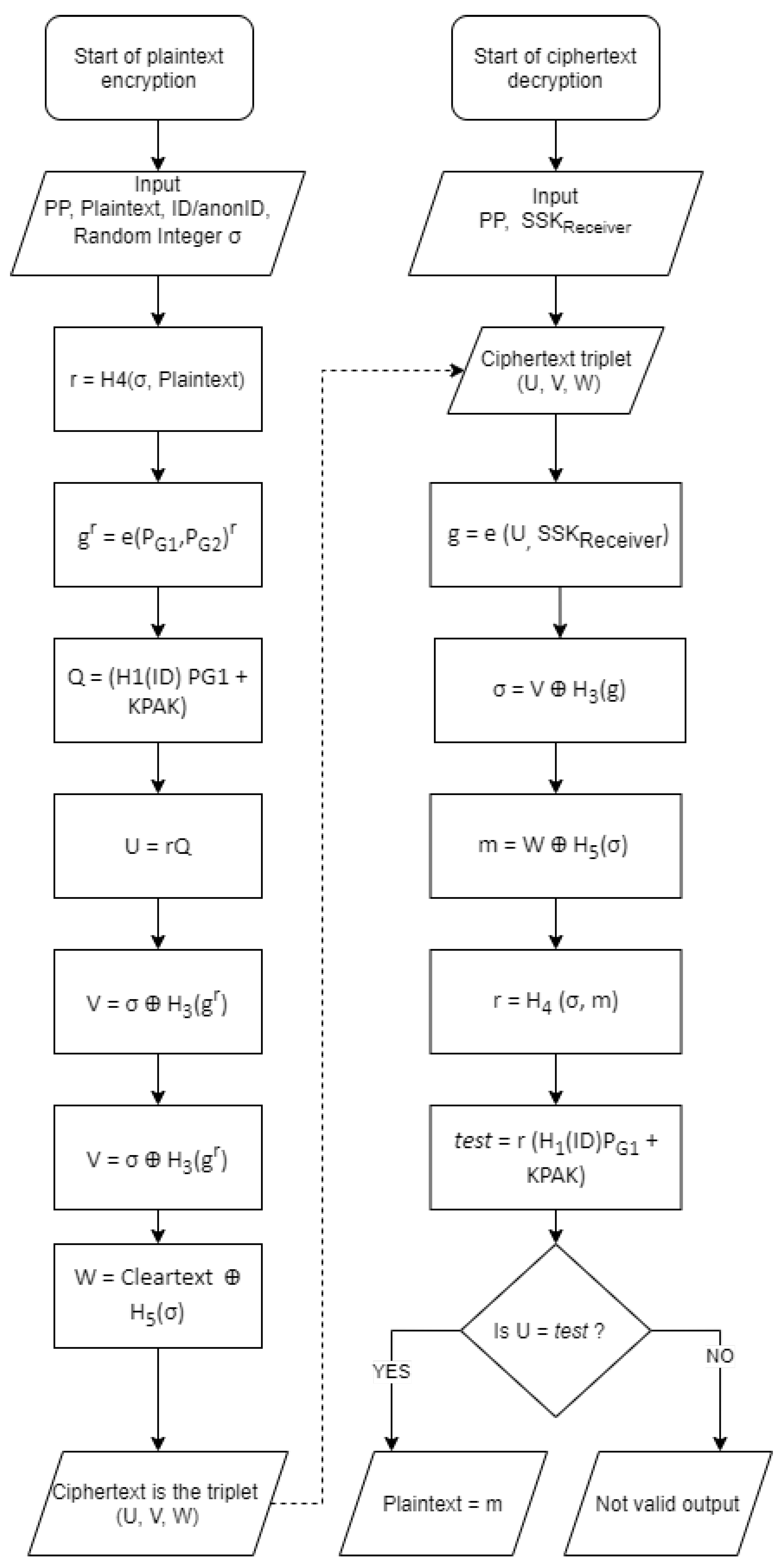
If the of a user is known (because the user her/himself chose to publish it), the user’s public key is also known (or can be computed, by using the user ID and the public parameters of the authority). Thus, anyone can send an encrypted message to that user. The recipient can decrypt the message using the corresponding private key. As the use of asymmetric encryption is not efficient for long messages, the most common use of the confidentiality service is for sharing a symmetric key to be used for exchanging subsequent confidential messages. The confidentiality service is implemented by means of the Encryption operation and the Decryption operation. Hereafter, we present the adaptation to our proposal of the SK-IBE scheme algorithms as presented in section 3 of [44].
The input to the Encryption operation consists of:
- The , (where = length of the data in bits) to be encrypted;
- The ARIBC Public Parameters,ARIBC-PP =
- A random integer , generated with the random number generator R; and
- The receiver’s .
The computations performed in the Encryption operation are:
- ; where :
- ;
- ; where : ,
- ;
- ; where :
- ; where :
The output of the Encryption operation is the triplet (Ciphertext)
The input to the Decryption operation consists of:
- The ARIBC Public ParametersARIBC-PP = ;
- The Private Key () of the recipient ; and
- The Ciphertext .
The computations performed in the Decryption operation are:
- ;
- ;
- ;
- ;
The output of the Decryption operation is , unless , in which case the retrieved data () should be discarded, as they correspond to an invalid . Both the encryption and the decryption processes described above are shown in graphical form in Figure 4.
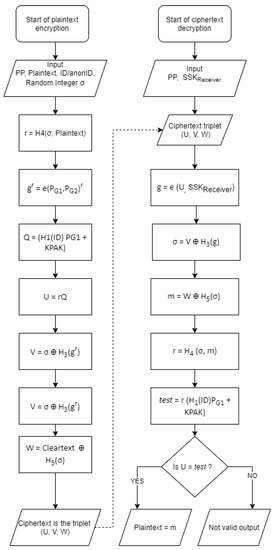
Figure 4.
ARIBC encryption and decryption processes.
4. Implementation
With an eye towards examining the suitability of the proposed ARIBC scheme, which is an amalgam of relatively new IBC schemes and well-known, time-tested IT-security technologies, to real-world applications, we developed a proof-of-concept implementation. By leveraging the algorithms in RFC6507, we developed code that implements (a) the creation of the key-pair (KSAK/KPAK) of the KMS; (b) the extraction of the key-pair (SSK/PVT) of a new user; (c) the signing of a message; and (d) the verification of the signature. To this end, instead of using a rather complicated and insufficiently documented open-source implementation of the Sakai–Kasahara scheme that is available in [49], we chose to write our own code. The code makes use of cryptographic libraries provided by the “Legion of the Bouncy Castle” (www.bouncycastle.org (accessed on 8 January 2021)) with an MIT-type license. Our code is validated by setting the values of the cryptographic parameters equal to those of the test data specified in RFC6507 and comparing the results. Additionally, we followed the RFC6507 recommendation to use curves and base points defined in FIPS 186-4 [50].
The main elements of our implementation are the following:
- Setup of a custom Key Management Service (KMS).
- Definition of the accepted format for identifiers for the authority, and a custom method for deriving these from the users’ public IDs.
- PC with the following specifications: Intel ® Core ™ i7-5600U CPU @ 2.60Hz, RAM: 16GB and OS: 64-bit Windows 10 Pro.
- Custom Java code that implements the algorithms in RFC6507.
- Security parameter n = 256 bits.
- The NIST P-256 elliptic curve, (p256r1 variant)
- The NIST-recommended generator G.
- Hashing with the SHA-256 algorithm (as defined in FIPS 180-4 [48]).
4.1. ARIBC Communication and Computation Overhead
The communication and computation overheads imposed by the ARIBC depend on the security level that has been chosen at the initial setup phase. Stronger security implies larger cryptographic parameters, and these in-turn imply more communication and computational overhead. The following estimates are derived based on the work in [5,45,47].
4.1.1. Authentication and Integrity Service
For the authentication and integrity service, because the signature is the cryptographic tuple , the communication overhead is the sum of the length of h (in bits) plus the length of S (in bits). Table 2 [45] depicts estimates of the length of h and S, with “point compression” when using three different security options, namely Super Singular (SS) curves at 80-bit security (first column); MNT curves at 80-bit security (second column); or MNT curves at 128-bit security (column).

Table 2.
Signature operation communication overhead.
In ARIBC, the signing process takes two scalar point multiplications, and the verification process takes one scalar point multiplication and one pairing evaluation. According to [47], back in 2008 these processes were taking 1.56 msec and 3.60 msec respectively, on an Athlon XP at 2 GHz under a supersingular-curve (SS) of embedding degree k = 6 over F397. Clearly, this overhead is negligible when modern smartphones and PCs are used. Indeed, the overhead of the BLMQ signature scheme under Windows, Android, and Linux was measured in [41] and was found to be as in Table 3 (values extracted from Figure 4 in [41]. The first column in this table lists the operations whose overhead was measured, and each one of the following columns lists the overhead time (in msec) corresponding to implementation in one of the three environments.

Table 3.
BLMQ signature scheme overhead under Windows, Android, and Linux.
The overheads we measured with our implementation are as follows:
- Negligible overhead for the creation of the key-pair () of the KMS.
- Computation time of almost 1 sec for the extraction of the key-pair () for a new user.
- Computation times of almost 1 sec for both the signing of a message and the verification of the signature.
4.1.2. Confidentiality Service
The estimated communication overhead of the Ciphertext triplet , (where = length of the data in bits), with “point compression” on Super Singular (SS) curves at 80bit security, MNT at 80-bit security and MNT at 128-bit security is as shown in Table 4, whose structure is similar to that of Table 2.

Table 4.
Confidentiality service communication overhead.
When it comes to the computational overhead of the confidentiality service, the same arguments as for the signing and verification process stand, and the same methodology can be applied. The general computational overhead estimates presented here are based on the work in [3], where the indicative sizes with “point compression” optimizations for the , , and groups, for standard elliptic curve types are given. These values are for Super-Singular (SS) elliptic curve at 80-bit security as follows: = 160 bits, = 512 bits, = 512 bits, = 1024 bits. For MNT elliptic curve at 128-bit security: = 256 bits, = 512 bits, = 3072 bits, = 3072 bits. An “indicative” time unit as the time needed for point multiplication on a random 171-bit elliptic curve for a random 160-bit exponent is defined in [3]. Under the above settings, and for Super-Singular (SS) elliptic curve at 80-bit security: Secret (Private) key extraction costs 2 time units, encryption costs 6 time units and decryption costs 104 time units. For MNT elliptic curve at 128-bit security: Secret (Private) key extraction costs 100 time units, encryption costs 36 time units and decryption costs 1506 time units. Finally, the BLMQ Signcryption scheme, that has similar characteristics, needs 2.65 msec to Sign and Encrypt for one group exponentiation and two scalar point multiplications [5]. Therefore, the processing time for Decryption and Verification is 6.09 msec for one group exponentiation and 2 pairing evaluations.
As with the authenticity and integrity service, these overheads are negligible on modern technology computing devices.
5. Discussion
5.1. The Security of the ARIBC
The security of the proposed scheme depends on choices made regarding the implementation on the one hand, and on the underlying cryptographic protocols and techniques on the other. The former include:
- The choice of the public parameters and of the elliptic curve in particular. In our implementation we selected the security parameter to be 256 bits and the NIST P-256 elliptic curve [42,45,51].
- The measures to secure the Master (Server) Secret key. The Master (Server) Secret key needs protection analogous to that of the private key of any Certification Authority in a X.509-based PKI; this entails the use of a special hardware security module [52] and/or the KMS to be offline, as in the case of a commercial implementation of an SK-based scheme called “Cryptify” (https://www.cryptify.com/cryptifys-implementation-of-mikey-sakke/ (accessed on 8 January 2021).
- The measures to secure the sharing of the SSKs of the anonymous reporters. In our proposal, we use time-tested technologies such as the TLS protocol for confidentiality and the X.509-based PKI certificate for the authentication of the KMS of the authority. Eponymous reporters may receive their SSKs in a secure device (e.g., a USB token) when they present themselves to the authority to register.
The cryptographic security of the employed BLMQ signature scheme is based on the Diffie–Hellman inverse (DHI) family of primitives [42]. The signature created by the scheme “...has a security reduction to an assumption that is related to (and actually weaker than) the q-Bilinear Diffie-Hellman inverse (q-BDHI) assumption”. The created signature is the proof of possession by the signer of the SSK. On the other hand, the security of SK-IBE is based on the q-BDHI assumption and has been proved in [44,45]. More details on the security of the underlying cryptographic mechanisms and protocols can be found in [42] and [45]; security concerns about IBC are discussed in [4].
5.2. Advantages and Drawbacks of the ARIBC
When comparing the ARIBC against alternatives reviewed in Section 2, the following can be noted:
- In terms of functionality, the ARIBC supports both eponymous and anonymous reporters. Moreover, it allows an initially anonymous reporter to later revoke her/his anonymity, should s/he so chooses, so as to allow her/his participation in a reward scheme.
- Contrary to simple, web-based applications with no supporting identification infrastructure, the ARIBC allows secure two-way communication between authorities and reporters.
- In terms of implementation, the ARIBC is simpler to implement than schemes based on traditional PKI. A reporter’s public key is derived from her/his identity, hence no pre-enrollment is required, unless the reporter chooses to become eponymous at the registration phase.
- Being based on IBC, the ARIBC requires neither certificate management nor a key revocation mechanism, in contrast to traditional PKI-based schemes.
- Being based on IBC, the ARIBC has an inherent key escrow mechanism. Whether this characteristic of IBC-based schemes constitutes a drawback or not depends on the context of the particular application scenarios. In the case of anonymous reporting, the conjecture (to be confirmed experientially by means of user acceptance studies) is that it is not. For eponymous reporters, solutions to the key-escrow problem such as the one in [53] can be considered.
6. Conclusions
We proposed a novel scheme that supports online eponymous and anonymous reporting, and is based on identity-based cryptography. The proposed scheme allows for secure, continued two-way communication between anonymous reporters and the pertinent authorities, thus successfully addressing the reporters’ concerns whilst ensuring the integrity and effectiveness of the investigation. The scheme may also support a reward scheme, should the reporter wishes to retain the option of proving her/his identity at a later stage. The proposed scheme enjoys a number of advantages over existing alternatives, most notable among them being its ease of implementation, even with limited resources, bot at the server and the client-side. We developed a proof-of-concept implementation of the proposed scheme, and demonstrated the applicability of the scheme in environments with constrained resources (human, organizational and/or computational). This implementation allows for measuring overheads imposed by the scheme, which were found to be well within the capabilities of modern fixed or mobile devices. Our plans for future research include the full implementation of the ARIBC system; experimentation with it towards validation; assessment of its security by means of pen testing; empirical investigation of the stakeholders’ acceptance of the proposed scheme; and assessment of its usability.
Author Contributions
Conceptualization, A.G., S.K.; methodology, A.G.; software, A.G.; validation, A.G.; formal analysis, A.G.; writing—original draft preparation, A.G.; writing—review and editing, S.K.; visualization, A.G., S.K.; supervision, S.K.; project administration, S.K. Both authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not Applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Auto Thefts Most Likely to Be Reported, Murders Most Likely to Be Solved. Available online: https://www.pewresearch.org/fact-tank/2020/11/20/facts-about-crime-in-the-u-s/ft_20-11-12_crimeintheus_5/ (accessed on 26 December 2020).
- Young, J.; Courtney, J.; Bennett, R.; Ellis, T.; Posey, C. The impact of anonymous, two-way, computer-mediated communication on perceived whistleblower credibility. Inf. Technol. People 2020. [Google Scholar] [CrossRef]
- Sakai, R.; Kasahara, M. ID based Cryptosystems with Pairing on Elliptic Curve. IACR Cryptol. EPrint Arch. 2003, 2003, 54. [Google Scholar]
- Moody, D.; Peralta, R.; Perlner, R.; Regenscheid, A.; Roginsky, A.; Chen, L. Report on pairing-based cryptography. J. Res. Natl. Inst. Stand. Technol. 2015, 120, 11–27. [Google Scholar] [CrossRef]
- Barreto, P.S.L.M.; Libert, B.; McCullagh, N.; Quisquater, J.J. Efficient and Provably-Secure Identity-Based Signatures and Signcryption from Bilinear Maps. In Advances in Cryptology—ASIACRYPT 2005, Proceedings of the 11th International Conference on the Theory and Application of Cryptology and Information Security, Chennai, India, 4–8 December 2005; Roy, B., Ed.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 515–532. [Google Scholar]
- Ku, C.H.; Iriberri, A.; Leroy, G. Crime Information Extraction from Police and Witness Narrative Reports. In Proceedings of the 2008 IEEE Conference on Technologies for Homeland Security, Waltham, MA, USA, 12–13 May 2008; pp. 193–198. [Google Scholar] [CrossRef]
- Iriberri, A.; Leroy, G. Natural Language Processing and e-Government: Extracting Reusable Crime Report Information. In Proceedings of the 2007 IEEE International Conference on Information Reuse and Integration, Las Vegas, IL, USA, 13–15 August 2007; pp. 221–226. [Google Scholar] [CrossRef]
- Iriberri, A.; Leroy, G.; Garrett, N. Reporting On-Campus Crime Online: User Intention to Use. In Proceedings of the 39th Annual Hawaii International Conference on System Sciences (HICSS’06), Kauai, HI, USA, 4–7 January 2006; Volume 4, p. 82. [Google Scholar] [CrossRef]
- Ferraro, E.F. Anonymous Reporting System. 2015. Available online: https://patents.google.com/patent/US9135598 (accessed on 26 December 2020).
- Zou, S.; Xi, J.; Wang, S.; Lu, Y.; Xu, G. Reportcoin: A Novel Blockchain-Based Incentive Anonymous Reporting System. IEEE Access 2019, 7, 65544–65559. [Google Scholar] [CrossRef]
- Say Something Anonymous Reporting System. Available online: https://www.saysomething.net/ (accessed on 26 December 2020).
- Sakpere, A.B.; Kayem, A.V.D.M.; Ndlovu, T. A Usable and Secure Crime Reporting System for Technology Resource Constrained Context. In Proceedings of the 2015 IEEE 29th International Conference on Advanced Information Networking and Applications Workshops, Gwangiu, Korea, 24–27 March 2015; pp. 424–429. [Google Scholar] [CrossRef]
- Shih, T.F.; Chen, C.L.; Syu, B.Y.; Deng, Y.Y. A Cloud-Based Crime Reporting System with Identity Protection. Symmetry 2019, 11, 255. [Google Scholar] [CrossRef]
- Obada-Obieh, B.; Spagnolo, L.; Beznosov, K. Towards Understanding Privacy and Trust in Online Reporting of Sexual Assault. In Proceedings of the Sixteenth Symposium on Usable Privacy and Security (SOUPS 2020), Boston, MA, USA, 9–11 August 2020; USENIX Association: Washington, DC, USA, 2020; pp. 145–164. [Google Scholar]
- Vesta Social Innovation Technologies. Available online: https://www.vestasit.com/ (accessed on 26 December 2020).
- Jimoh, R.G.; Ojulari, K.; Enikuomehin, O. A Scalable Online Crime Reporting System. Afr. J. Comput. ICT 2014, 7, 11–20. [Google Scholar]
- Tabassum, K.; Shaiba, H.; Shamrani, S.; Otaibi, S. e-Cops: An Online Crime Reporting and Management System for Riyadh City. In Proceedings of the 2018 1st International Conference on Computer Applications Information Security (ICCAIS), Riyadh, Saudi Arabia, 4–6 April 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Agangiba, W.A.; Agangiba, M.A. Mobile Solution for Metropolitan Crime Detection and Reporting. J. Emerg. Trends Comput. Inf. Sci. 2014, 4, 916–921. [Google Scholar]
- Shamir, A. Identity-Based Cryptosystems and Signature Schemes. In Advances in Cryptology, Proceedings of the Workshop on the Theory and Application of Cryptographic Techniques, Santa Barbara, CA, USA, 18–22 August 1985; Blakley, G.R., Chaum, D., Eds.; Springer: Berlin/Heidelberg, Germany, 1985; pp. 47–53. [Google Scholar]
- Joux, A. A One Round Protocol for Tripartite Diffie–Hellman. J. Cryptol. 2004, 17, 263–276. [Google Scholar] [CrossRef]
- Boneh, D.; Franklin, M. Identity-Based Encryption from the Weil Pairing. In Advances in Cryptology—CRYPTO 2001, Proceedings of the 21st Annual International Cryptology Conference, Santa Barbara, CA, USA, 19–23 August 2001; Kilian, J., Ed.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 213–229. [Google Scholar]
- Baek, J.; Newmarch, J.; Safavi-naini, R.; Susilo, W. A Survey of Identity-Based Cryptography. Proceedings of Australian Unix Users Group Annual Conference, Flinders St, Melbourne, 1–3 September 2004. [Google Scholar]
- Zhao, S.; Aggarwal, A.; Frost, R.; Bai, X. A survey of applications of identity-based cryptography in mobile ad-hoc networks. IEEE Commun. Surv. Tutor. 2012, 14, 380–399. [Google Scholar] [CrossRef]
- Faraj Al-Janabi, S.T.; Abd-alrazzaq, H.K. Combining Mediated and Identity-Based Cryptography for Securing E-Mail. In Digital Enterprise and Information Systems, Proceedings of the DEIS 2011, London, UK, 20–22 July 2011; Ariwa, E., El-Qawasmeh, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 1–15. [Google Scholar]
- Karatop, A.G.; Savaş, E. An Identity-Based Key Infrastructure Suitable for Messaging and Its Application to e-Mail. In Proceedings of the 4th International Conference on Security and Privacy in Communication Netowrks (SecureComm’08), Istanbul, Turkey, 22–25 September 2008; Association for Computing Machinery: New York, NY, USA, 2008. [Google Scholar] [CrossRef]
- Yu, Y.; Au, M.H.; Ateniese, G.; Huang, X.; Susilo, W.; Dai, Y.; Min, G. Identity-Based Remote Data Integrity Checking With Perfect Data Privacy Preserving for Cloud Storage. IEEE Trans. Inf. Forensics Secur. 2017, 12, 767–778. [Google Scholar] [CrossRef]
- Aditia, M.K.; Paida, S.; Altaf, F.; Maity, S. Certificate-less Public Key Encryption For Secure e-Healthcare Systems. In Proceedings of the 2019 IEEE Conference on Information and Communication Technology, Allahabad, India, 6–8 December 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Ssembatya, R.; Kayem, A.V.D.M. Secure and Efficient Mobile Personal Health Data Sharing in Resource Constrained Environments. In Proceedings of the 2015 IEEE 29th International Conference on Advanced Information Networking and Applications Workshops, Gwangiu, Korea, 24–27 March 2015; pp. 411–416. [Google Scholar] [CrossRef]
- Kamarudin, N.H.; Yussoff, Y.M. Authentication scheme interface for mobile e-health monitoring using unique and lightweight identity-based authentication. AIP Conf. Proc. 2016, 1774, 050016. [Google Scholar] [CrossRef]
- Aljeaid, D.; Ma, X.; Langensiepen, C. Biometric identity-based cryptography for e-Government environment. In Proceedings of the 2014 Science and Information Conference, Warsaw, Poland, 7–10 September 2014; pp. 581–588. [Google Scholar] [CrossRef]
- Lim, H.W. On the Application of Identity-Based Cryptography in Grid Security. Ph.D. Thesis, Royal Holloway, University of London, London, UK, 2006. [Google Scholar]
- Baek, J.; Hableel, E.; Byon, Y.J.; Wong, D.; Jang, K.; Yeo, H. How to Protect ADS-B: Confidentiality Framework and Efficient Realization Based on Staged Identity-Based Encryption. IEEE Trans. Intell. Transp. Syst. 2017, 18, 690–700. [Google Scholar] [CrossRef]
- Goudossis, A.; Katsikas, S. Towards a secure automatic identification system (AIS). J. Mar. Sci. Technol. 2019, 24, 410–423. [Google Scholar] [CrossRef]
- Paterson, K.G.; Price, G. A comparison between traditional public key infrastructures and identity-based cryptography. Inf. Secur. Tech. Rep. 2003, 8, 57–72. [Google Scholar] [CrossRef]
- Girish; Phaneendra, H. Identity-Based Cryptography and Comparison with traditional Public key Encryption: A Survey. Int. J. Comput. Sci. Inf. Technol. 2014, 5, 5521–5525. [Google Scholar]
- Groves, M. Elliptic Curve-Based Certificateless Signatures for Identity-Based Encryption (ECCSI). Available online: https://tools.ietf.org/html/rfc6507 (accessed on 20 February 2021).
- Groves, M. Sakai-Kasahara Key Encryption (SAKKE). Available online: https://tools.ietf.org/html/rfc6508 (accessed on 20 February 2021).
- Groves, M. MIKEY-SAKKE: Sakai-Kasahara Key Encryption in Multimedia Internet KEYing (MIKEY). Available online: https://tools.ietf.org/html/rfc6509 (accessed on 20 February 2021).
- National Cyber Security Centre. MIKEY-SAKKE Frequently Asked Questions. Available online: https://www.ncsc.gov.uk/guidance/mikey-sakke-frequently-asked-questions (accessed on 20 February 2021).
- Arkko, J.; Keranen, A.; Mattsson, J. IANA Rules for MIKEY (Multimedia Internet KEYing). Available online: https://tools.ietf.org/html/rfc6309 (accessed on 20 February 2021).
- Zhong, S.; Ren, W.; Zhu, T.; Ren, Y.; Choo, K.R. Performance and Security Evaluations of Identity- and Pairing-Based Digital Signature Algorithms on Windows, Android, and Linux Platforms: Revisiting the Algorithms of Cha and Cheon, Hess, Barreto, Libert, Mccullagh and Quisquater, and Paterson and Schuldt. IEEE Access 2018, 6, 37850–37857. [Google Scholar] [CrossRef]
- Identity-Based Cryptographic Techniques Using Pairings; IEEE Standard 1363.3-2013; IEEE Standards Association: Piscataway, NJ, USA, 2013.
- Barker, E. Recommendation for Key Management Part 1: General; SP 800-57 Revision 5; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2020. [Google Scholar]
- Chen, L.; Cheng, Z. Security Proof of Sakai-Kasahara’s Identity-Based Encryption Scheme. Cryptogr. Coding 2005, 3796, 442–459. [Google Scholar]
- Boyen, X. A tapestry of identity-based encryption: Practical frameworks compared. Int. J. Appl. Cryptogr. 2008, 1, 3–21. [Google Scholar] [CrossRef]
- Al-Riyami, S.S.; Paterson, K.G. Certificateless Public Key Cryptography. In Advances in Cryptology—ASIACRYPT 2003, Proceedings of the 9th International Conference on the Theory and Application of Cryptology and Information Security, Taipei, Taiwan, 30 November–4 December 2003; Laih, C.S., Ed.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 452–473. [Google Scholar]
- Barreto, P.; Deusajute, A.; De, E.; Cruz, S.; Pereira, G.; Silva, R. Toward efficient certificateless signcryption from (and without) bilinear pairings. In Proceedings of the VIII Simpósio Brasileiro em Segurança da Informação e de Sistemas Computacionais, Gramado, Rio Grande do Sul, Brazil, 1–5 September 2008. [Google Scholar]
- Secure Hash Standard (SHS); Standard; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2015.
- Mikey-Sakke Crypto Library and Demonstration Code for ECCSI/ SAKKE (RFC 6507 and 6508). Available online: https://github.com/jim-b/ECCSI-SAKKE (accessed on 3 February 2021).
- Digital Signature Standard (DSS); Standard; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2013.
- Chen, L.; Moody, D.; Regenscheid, A.; Randall, K. Recommendations for Discrete Logarithm-Based Cryptography: Elliptic Curve Domain Parameters; Special Publication 800-186; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2019; p. 78. [Google Scholar]
- Security Requirements for Cryptographic Modules; Standard; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2019.
- Oh, J.; Lee, K.; Moon, S. How to Solve Key Escrow and Identity Revocation in Identity-Based Encryption Schemes. In Information Systems Security, Proceedings of the First International Conference (ICISS 2005), Kolkata, India, 19–21 December 2005; Jajodia, S., Mazumdar, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 290–303. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).