Collaborative Filtering Based on a Variational Gaussian Mixture Model
Abstract
1. Introduction
- We propose a new variational autoencoder CF model (i.e., a Gaussian mixture model for latent factor distribution for CF (GVAE-CF)). Specifically, we change the single Gaussian posterior distribution in the standard variational autoencoder to a Gaussian mixture model (GMM), and we propose a GMM-based variational autoencoder neural network structure for CF. The model can effectively learn the relationships of users and items.
- We re-derive the variational lower bound of the variational autoencoder.
- We compare the latent space representations of the standard VAE and GVAE-CF to study the GVAE-CF internal mechanism of the GVAE-CF.
2. Background and Related Work
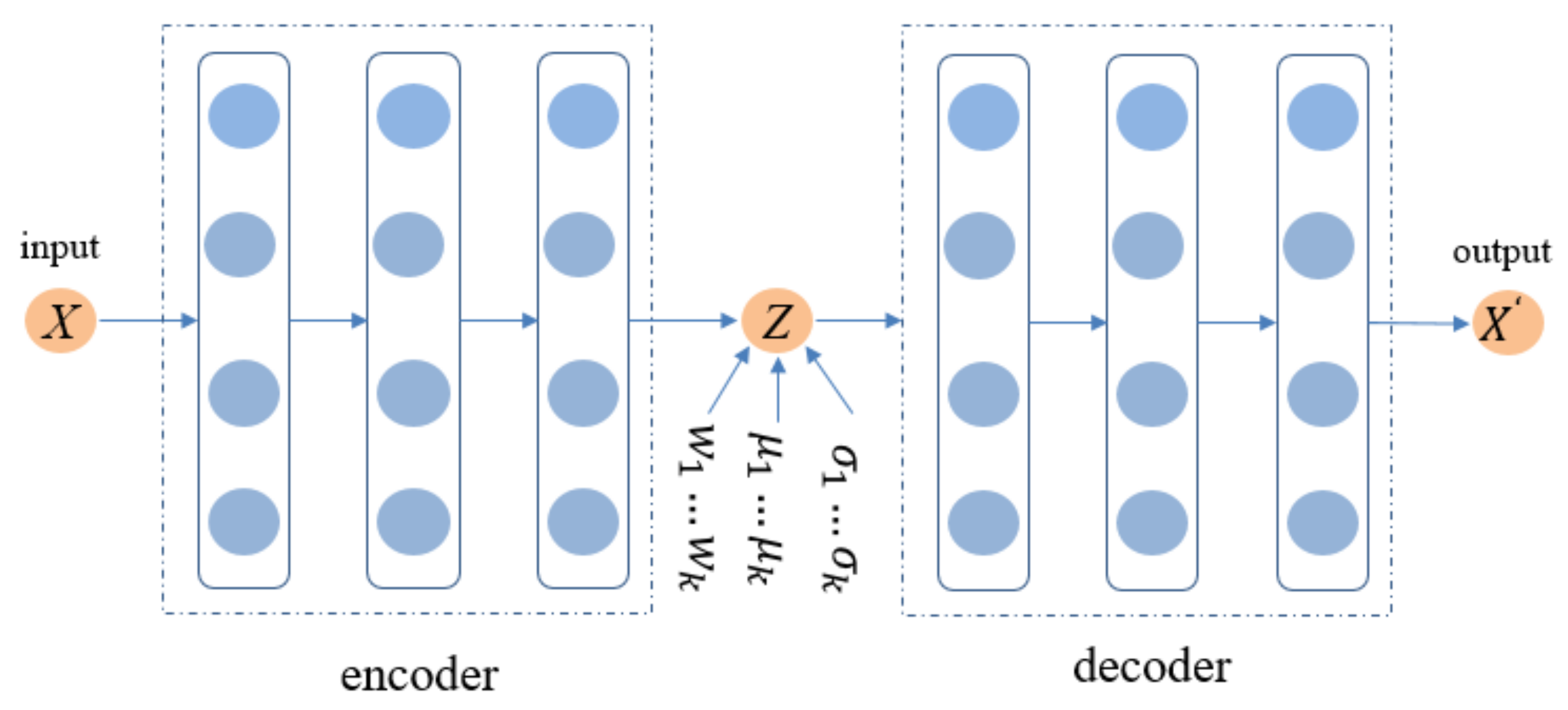
3. Method
3.1. Variational Autoencoder
3.2. Variational Autoencoder Based on the GMM for CF
| Algorithm 1 GVAE-CF uses stochastic gradient descent algorithm to optimize the parameters |
Input: Rating matrix
|
4. Results
4.1. Datasets
4.2. Metrics
4.3. Experimental Setup
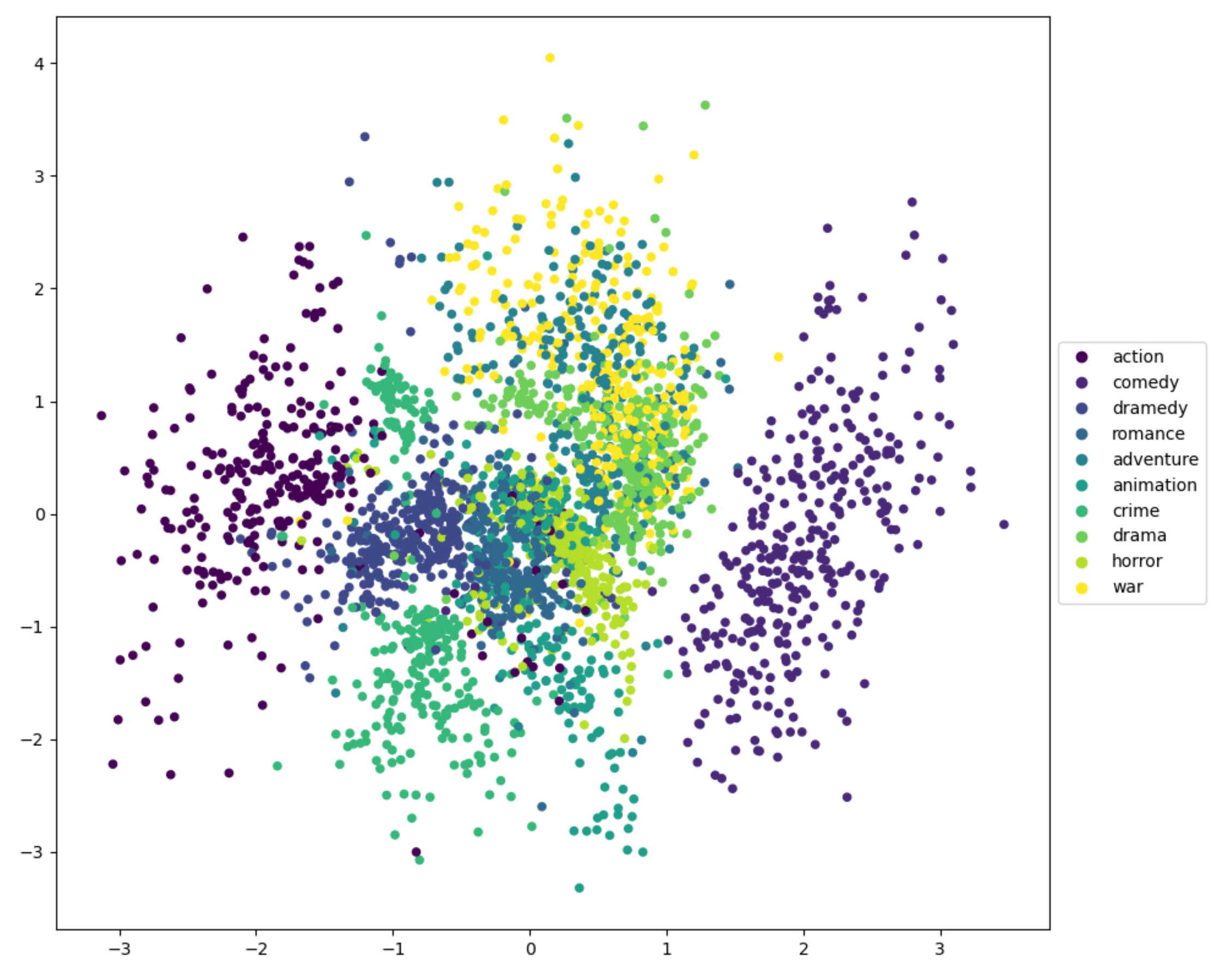
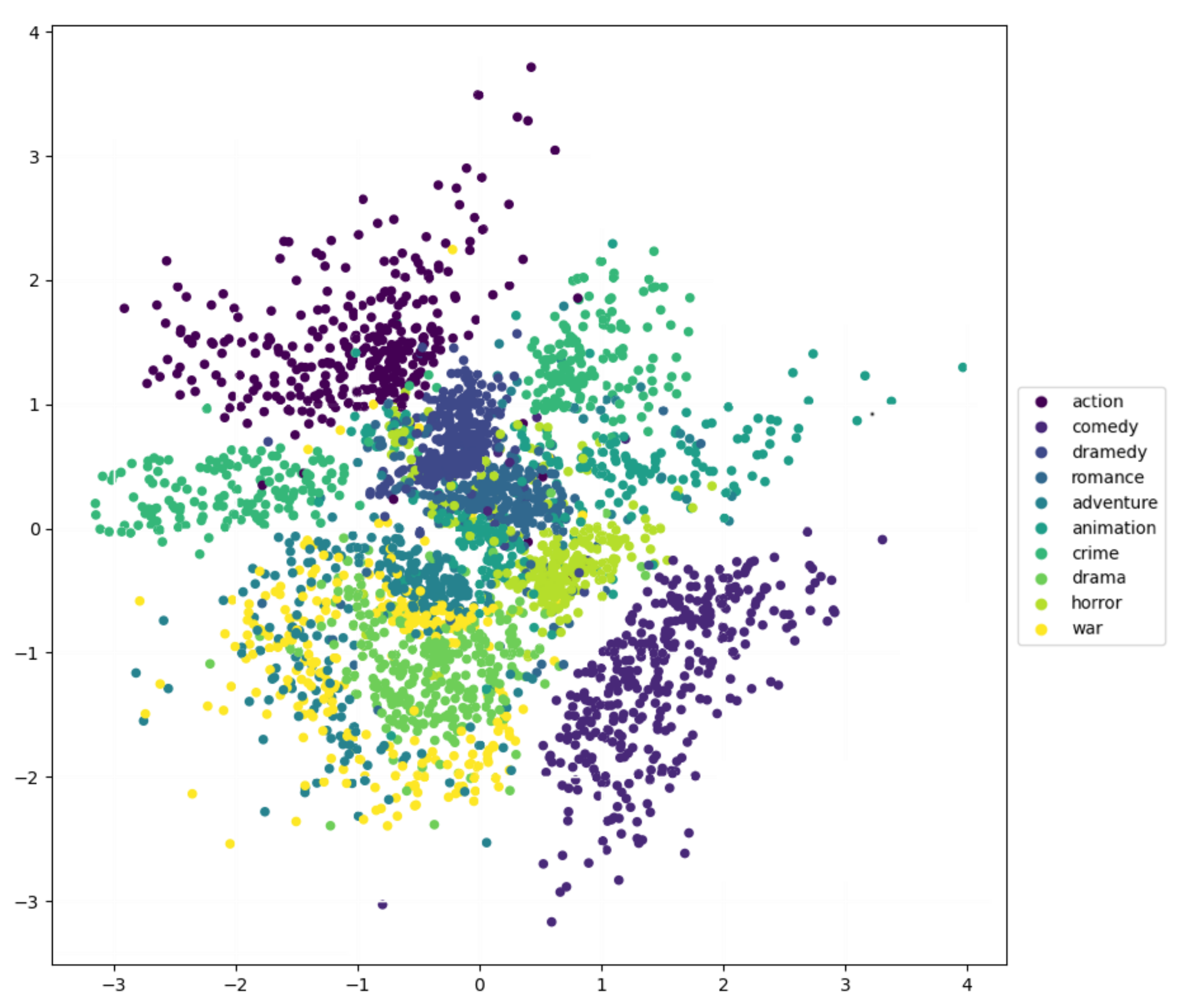
4.4. Latent Space Exploration
4.5. Discussion
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CF | Collaborative filtering |
| GVAE-CF | Variational autoencoder that uses a Gaussian mixture model for the |
| latent factor for CF distribution | |
| VAEs | Variational autoencoders |
| NDCG | Normalized discounted cumulative gain |
| GMM | Gaussian mixture model |
| GAN | Generative adversarial network |
| KL | Kullback-Liebler |
| ELBO | Evidence lower bound |
| RecVAE | Recommender VAE |
| SVD | Singular value decomposition |
References
- Resnick, P.; Varian, H.R. Recommender systems. Commun. ACM 1997, 40, 56–58. [Google Scholar] [CrossRef]
- Pazzani, M.J.; Billsus, D. Content-based recommendation systems. In The Adaptive Web; Springer: Berlin, Germany, 2007; pp. 325–341. [Google Scholar]
- Thomas, X. Content-Based Personalized Recommender System Using Entity Embeddings. arXiv 2020, arXiv:2010.12798. [Google Scholar]
- Zarei, M.R.; Moosavi, M.R. An adaptive similarity measure to tune trust influence in memory-based collaborative filtering. arXiv 2019, arXiv:1912.08934. [Google Scholar]
- Zhao, Z.D.; Shang, M.S. User-based collaborative-filtering recommendation algorithms on hadoop. In Proceedings of the 2010 Third International Conference on Knowledge Discovery and Data Mining, IEEE, Jinggangshan, China, 2–4 April 2010; pp. 478–481. [Google Scholar]
- Zhang, L.; Liu, G.; Wu, J. Beyond Similarity: Relation Embedding with Dual Attentions for Item-based Recommendation. arXiv 2019, arXiv:1911.04099. [Google Scholar]
- Goldberg, D.; Nichols, D.; Oki, B.M.; Terry, D. Using collaborative filtering to weave an information tapestry. Commun. ACM 1992, 35, 61–70. [Google Scholar] [CrossRef]
- Ding, X.; Yu, W.; Xie, Y.; Liu, S. Efficient model-based collaborative filtering with fast adaptive PCA. In Proceedings of the 2020 IEEE 32nd International Conference on Tools with Artificial Intelligence (ICTAI), Baltimore, MD, USA, 9–11 November 2020; pp. 955–960. [Google Scholar]
- Severinski, C.; Salakhutdinov, R. Bayesian Probabilistic Matrix Factorization: A User Frequency Analysis. arXiv 2014, arXiv:1407.7840. [Google Scholar]
- Chae, D.K.; Kang, J.S.; Kim, S.W.; Lee, J.T. Cfgan: A generic collaborative filtering framework based on generative adversarial networks. In Proceedings of the 27th ACM International Conference on Information and Knowledge Management, Torino, Italy, 22–26 October 2018; pp. 137–146. [Google Scholar]
- Kang, W.C.; Fang, C.; Wang, Z.; McAuley, J. Visually-aware fashion recommendation and design with generative image models. In Proceedings of the 2017 IEEE International Conference on Data Mining (ICDM), New Orleans, LA, USA, 18–21 November 2017; pp. 207–216. [Google Scholar]
- Hu, Y.; Koren, Y.; Volinsky, C. Collaborative filtering for implicit feedback datasets. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; pp. 263–272. [Google Scholar]
- Mnih, A.; Salakhutdinov, R.R. Probabilistic matrix factorization. In Advances in Neural Information Processing Systems; MIT Press: London, UK, 2008; pp. 1257–1264. [Google Scholar]
- Liang, D.; Krishnan, R.G.; Hoffman, M.D.; Jebara, T. Variational autoencoders for collaborative filtering. In Proceedings of the 2018 World Wide Web Conference, Lyon, France, 23–27 April 2018; pp. 689–698. [Google Scholar]
- Kim, D.; Suh, B. Enhancing VAEs for collaborative filtering: Flexible priors & gating mechanisms. In Proceedings of the 13th ACM Conference on Recommender Systems, Copenhagen, Denmark, 16–20 September 2019; pp. 403–407. [Google Scholar]
- Shenbin, I.; Alekseev, A.; Tutubalina, E.; Malykh, V.; Nikolenko, S.I. RecVAE: A new variational autoencoder for top-N recommendations with implicit feedback. In Proceedings of the 13th International Conference on Web Search and Data Mining, Houston, TX, USA, 3–7 February 2020; pp. 528–536. [Google Scholar]
- Gopalan, P.; Hofman, J.M.; Blei, D.M. Scalable Recommendation with Hierarchical Poisson Factorization. arXiv 2013, arXiv:1311.1704. [Google Scholar]
- Billsus, D.; Pazzani, M.J. Learning collaborative information filters. In Icml; AAAI: Palo Alto, CA, USA, 1998; Volume 98, pp. 46–54. [Google Scholar]
- Alquier, P.; Cottet, V.; Chopin, N.; Rousseau, J. Bayesian matrix completion: Prior specification. arXiv 2014, arXiv:1406.1440. [Google Scholar]
- Alexandridis, G.; Siolas, G.; Stafylopatis, A. Enhancing social collaborative filtering through the application of non-negative matrix factorization and exponential random graph models. Data Min. Knowl. Discov. 2017, 31, 1031–1059. [Google Scholar] [CrossRef]
- Liang, D.; Altosaar, J.; Charlin, L.; Blei, D.M. Factorization meets the item embedding: Regularizing matrix factorization with item co-occurrence. In Proceedings of the 10th ACM Conference on Recommender Systems; ACM: New York, NY, USA, 2016; pp. 59–66. [Google Scholar]
- Lee, W.; Song, K.; Moon, I.C. Augmented variational autoencoders for collaborative filtering with auxiliary information. In Proceedings of the 2017 ACM on Conference on Information and Knowledge Management; ACM: New York, NY, USA, 2017; pp. 1139–1148. [Google Scholar]
- Askari, B.; Szlichta, J.; Salehi-Abari, A. Joint Variational Autoencoders for Recommendation with Implicit Feedback. arXiv 2020, arXiv:2008.07577. [Google Scholar]
- Altosaar, J. Tutorial-What is a Variational Autoencoder. Available online: https://jaan.io/what-is-variational-autoencoder-vae-tutorial/ (accessed on 30 January 2021).
- Blei, D.M.; Kucukelbir, A.; McAuliffe, J.D. Variational inference: A review for statisticians. J. Am. Stat. Assoc. 2017, 112, 859–877. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Rezende, D.J.; Mohamed, S.; Wierstra, D. Stochastic backpropagation and approximate inference in deep generative models. arXiv 2014, arXiv:1401.4082. [Google Scholar]
- Harper, F.M.; Konstan, J.A. The movielens datasets: History and context. ACM Trans. Interact. Intell. Syst. 2015, 5, 1–19. [Google Scholar] [CrossRef]
- Bennett, J.; Lanning, S. The netflix prize. In Proceedings of KDD Cup and Workshop; ACM: New York, NY, USA, 2007; Volume 2007, p. 35. [Google Scholar]
- Dong, X.; Yu, L.; Wu, Z.; Sun, Y.; Yuan, L.; Zhang, F. A hybrid collaborative filtering model with deep structure for recommender systems. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 1309–1315. [Google Scholar]
- Li, S.; Kawale, J.; Fu, Y. Deep collaborative filtering via marginalized denoising auto-encoder. In Proceedings of the 24th ACM International on Conference on Information and Knowledge Management; ACM: New York, NY, USA, 2015; pp. 811–820. [Google Scholar]
- Rendle, S.; Freudenthaler, C.; Gantner, Z.; Schmidt-Thieme, L. BPR: Bayesian personalized ranking from implicit feedback. arXiv 2012, arXiv:1205.2618. [Google Scholar]
- Kabbur, S.; Ning, X.; Karypis, G. Fism: Factored item similarity models for top-n recommender systems. In Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; ACM: New York, NY, USA, 2013; pp. 659–667. [Google Scholar]
- Yang, S.H.; Long, B.; Smola, A.J.; Zha, H.; Zheng, Z. Collaborative competitive filtering: Learning recommender using context of user choice. In Proceedings of the 34th International ACM SIGIR Conference on Research and Development in Information Retrieval, Beijing, China, 24–28 July 2011; pp. 295–304. [Google Scholar]
- Croft, W.B.; Metzler, D.; Strohman, T. Search Engines: Information Retrieval in Practice; Addison-Wesley Reading: Boston, MA, USA, 2010; Volume 520. [Google Scholar]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef] [PubMed]
- Ning, X.; Karypis, G. Slim: Sparse linear methods for top-n recommender systems. In Proceedings of the 2011 IEEE 11th International Conference on Data Mining, Vancouver, BC, Canada, 11–14 December 2011; pp. 497–506. [Google Scholar]
- Wu, Y.; DuBois, C.; Zheng, A.X.; Ester, M. Collaborative denoising auto-encoders for top-n recommender systems. In Proceedings of the Ninth ACM International Conference on Web Search and Data Mining; ACM: New York, NY, USA, 2016; pp. 153–162. [Google Scholar]
| Method | Recall@20 | Recall@50 | NDCG@100 |
|---|---|---|---|
| WMF [12] | 0.314 | 0.466 | 0.341 |
| SLIM [37] | 0.370 | 0.495 | 0.401 |
| CDAE [38] | 0.391 | 0.523 | 0.418 |
| Mult-DAE [14] | 0.387 | 0.524 | 0.419 |
| Mult-VAE [14] | 0.395 | 0.537 | 0.426 |
| RecVAE [16] | 0.414 | 0.521 | 0.420 |
| GVAE-CF | 0.408 ± 0.002 | 0.520 ± 0.002 | 0.431 ± 0.002 |
| Method | Recall@20 | Recall@50 | NDCG@100 |
|---|---|---|---|
| WMF | 0.314 | 0.466 | 0.341 |
| SLIM | 0.370 | 0.495 | 0.401 |
| CDAE | 0.391 | 0.523 | 0.418 |
| Mult-DAE | 0.387 | 0.524 | 0.419 |
| Mult-VAE | 0.395 | 0.537 | 0.426 |
| RecVAE | 0.414 | 0.521 | 0.420 |
| GVAE-CF | 0.416 ± 0.001 | 0.524 ± 0.001 | 0.431 ± 0.001 |
| Method | Recall@20 | Recall@50 | NDCG@100 |
|---|---|---|---|
| WMF | 0.252 | 0.346 | 0.259 |
| SLIM | 0.261 | 0.372 | 0.269 |
| CDAE | 0.264 | 0.396 | 0.275 |
| Mult-DAE | 0.277 | 0.401 | 0.351 |
| Mult-VAE | 0.279 | 0.427 | 0.362 |
| RecVAE | 0.296 | 0.421 | 0.372 |
| GVAE-CF | 0.301 ± 0.002 | 0.429 ± 0.002 | 0.381 ± 0.002 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, F.; Liu, F.; Liu, S. Collaborative Filtering Based on a Variational Gaussian Mixture Model. Future Internet 2021, 13, 37. https://doi.org/10.3390/fi13020037
Yang F, Liu F, Liu S. Collaborative Filtering Based on a Variational Gaussian Mixture Model. Future Internet. 2021; 13(2):37. https://doi.org/10.3390/fi13020037
Chicago/Turabian StyleYang, FengLei, Fei Liu, and ShanShan Liu. 2021. "Collaborative Filtering Based on a Variational Gaussian Mixture Model" Future Internet 13, no. 2: 37. https://doi.org/10.3390/fi13020037
APA StyleYang, F., Liu, F., & Liu, S. (2021). Collaborative Filtering Based on a Variational Gaussian Mixture Model. Future Internet, 13(2), 37. https://doi.org/10.3390/fi13020037







