Software Design and Experimental Evaluation of a Reduced AES for IoT Applications

Abstract

IoT devices include RFID tags, microprocessors, sensors, readers, and actuators. Their main characteristics are their limited resources and computing capabilities, which pose critical challenges to the reliability and security of their applications. Encryption is necessary for security when using these limited-resource devices, but conventional cryptographic algorithms are too heavyweight and resource-demanding to run on IoT infrastructures. This paper presents a lightweight version of AES (called LAES), which provides competitive results in terms of randomness levels and processing time, operating on GF(2⁴). Detailed mathematical operations and proofs are presented concerning LAES rounds design fundamentals. The proposed LAES algorithm is evaluated based on its randomness, performance, and power consumption; it is then compared to other cryptographic algorithm variants, namely Present, Clefia, and AES. The design of the randomness and performance analysis is based on six measures developed with the help of the NIST test statistical suite of cryptographic applications. The performance and power consumption of LAES on a low-power, 8-bit microcontroller unit were evaluated using an Arduino Uno board. LAES was found to have competitive randomness levels, processing times, and power consumption compared to Present, Clefia, and AES.

1. Introduction

NIST launched its lightweight cryptography project in 2013, highlighting the need for lightweight cryptographic algorithms that meet the requirements of constrained environments with limited processing speeds, resources, and energy. In 2015, NIST convened the 1st Lightweight Cryptography Workshop to explore concerns such as application security and resource needs in limited environments, as well as the possibilities for future lightweight primitive standardization. NIST’s 2nd Lightweight Cryptography Workshop (2016) decided to create a portfolio to discuss lightweight algorithms through an open process, similar to the criteria for block cipher selection. In October 2020, NIST’s 4th Lightweight Cryptography Workshop (held virtually) negotiated different aspects of the candidates and acquired useful feedback for the preference of the finalists [1].

This research addresses the problem of conventional cryptographic algorithms being inappropriate for IoT systems, due to requiring complex computations, and being consequently slow and energy-consuming [2,3]. The security of IoT applications heavily depends on robust and resilient lightweight cryptographic algorithms, which can balance the trade-offs between the requirements of IoT-constrained devices and the need to provide rigorous security for data transmission [4]. The design of novel lightweight cryptographic algorithms should address three main constraints that can influence the design process, usually referred to as the design trade-offs for lightweight cryptographic algorithms [5,6]: security, performance, and the cost of the cryptographic algorithm. For example, although a longer key and an increased number of rounds may offer higher levels of security, the cost and performance of the algorithm may be adversely affected. Balancing these factors is an ongoing challenge. IoT-constrained devices, such as wireless sensors, need to provide rigorous security for transmitting huge volumes of data while eluding several attacks and vulnerabilities [7,8]. In order to achieve security when using these limited-resource devices, encryption is required; however, conventional cryptographic algorithms are too heavyweight and resource-demanding to run effectively on IoT infrastructures [9].

Cryptographic algorithm output should be random, so that output analysis cannot predict the algorithm. An algorithm of this kind is said to be indistinguishable from a random permutation [10,11]; therefore, it is crucial to use statistical randomness tests to evaluate algorithm output. As indicated by NIST, the randomness test should take place in the early stages of cryptographic algorithm design, to determine whether or not the cryptographic algorithm is suitable for a particular cryptographic application; further cryptanalysis can then be applied to assess the robustness of its design. Usually, if a cryptographic algorithm fails the randomness test, a relationship exists between the plaintext and ciphertext bits that can be discovered through the use of the relevant cryptanalytic tools and analysis.

This paper is motivated by the advances of the information technology era, which have led to increased connections between different types of IoT devices with special security requirements based on multiple constraints. It is almost impossible to use common cryptographic algorithms to meet these different cryptographic constraints, considering application contexts and available resources [6,12,13]. Usually, IoT devices are characterized by limited power resources (e.g., the limited computational power of microprocessors and microcontrollers), limited memory size, compact hardware implementation, and limited battery life. The research community and the International Organization for Standardization (ISO) were prompted to standardize the principle of lightweight cryptography in ISO/IEC 29192-2012, a multi-part international standard that specifies the prerequisites, guidance, and design recommendations for lightweight cryptographic algorithms.

1.1. Contribution

A successful approach to designing a new lightweight cryptographic algorithm must use the modality of a trusted, well-known cryptographic algorithm applicable in a heavyweight cryptographic approach under the constraints of a lightweight one. This approach was successfully used to design the DESL [12] based on DES, and the DESXL [12] based on DESX. This paper investigates the same approach by proposing a lightweight cryptographic algorithm based on the Advanced Encryption Standard (AES), which we call Lightweight Advanced Encryption Standard (LAES). This paper extends the design and evaluation of [13], and makes the following main contributions.

• Design and construction: Our approach utilizes the modality of a trusted cryptographic algorithm in proposing a reduced version of AES, LAES, which is more amenable to lightweight applications germane to the IoT.
• Evaluation of randomness and performance: This paper evaluates LAES performance with existing well-known lightweight cryptographic algorithms (Present, Celfia, and AES). The four algorithms were challenged in identical scenarios to encrypt a range of images of varying sizes. The randomness level of each algorithm was measured using three metrics (i.e., frequency, block, and run tests), while the remaining metrics were used to determine their time efficiency.
• Evaluation based on the microcontroller: The performance of LAES was tested on a low-power, 8-bit microcontroller using an Arduino Uno board. The evaluation outcomes of LAES and its counterparts were compared and analyzed using six measures [14]. These measures aimed to evaluate the proposed LAES from a different perspective: The average required encryption time for block, round and entire process, average CPU cycle required for encrypting block and round, as well as measuring the average power and battery charge consumption required for encrypting a block.

1.2. Road Map

This paper is organized as follows. The Related Work section discusses recent applications operating on IoT devices while requiring a certain degree of security, reviews some literature on the applications of NIST randomness tests for verifying cryptographic algorithms, and briefly discusses some well-known lightweight cryptographic algorithms designed to provide security for IoT applications. The Material and Methods section presents the LAES design. The following section presents the main components of transformation for LAES encryption rounds that are mainly derived from AES. The Results and Evaluation section presents the randomness and performance evaluation of LAES and its counterparts, based on frequency test, block test, runs test, and processing time. Six different measures for LAES were conducted using an 8-bit microcontroller Arduino Uno board (MCU). Finally, the conclusion section summarizes the main findings.

2. Related Work

2.1. Lightweight Cryptographic Applications

The world is witnessing the unprecedented growth of interconnected devices in almost every aspect of life. IoT devices and applications are now proliferating in every industry, including automobiles, health, and appliances, in addition to smart homes and smart cities, and monitoring systems for power, electricity, water, and gas [15]. IoT services and applications that could operate on billions of IoT nodes increasingly demand more robust lightweight cryptographic algorithms to secure their operations. These futuristic IoT services and applications include social IoT, and IoT search engines, services computing, recommendation systems, analytics, and experimental platforms [16,17]. Since the IoT trend first began, many researchers and institutions have introduced lighter-weight encryption algorithms to enhance security in a variety of IoT applications, including health applications, smart homes and cities, monitoring, tracking and surveillance, and location-based services (LBSs) [18,19].

The authors in [20] proposed a novel cryptographic technique named KE-IBE, which relies on identity-based cryptography (IBC) and overcomes its key escrow issue. The researchers presented a privacy-preserving eHealth solution to ensure patient privacy and better fulfill IoT environment requirements. The technique provides anonymity while running at a reasonable speed. In the same context of medical applications for IoT, the authors in [21] improved an intrusion detection approach for the Internet of Medical Things (IoMT). The authors highlighted that sensitive patient data transmitted over IoMT can be vulnerable to different types of attacks, such as man-in-the-middle, remote hijacking, password guessing, DoS attacks, and many others. The authors utilized the grey wolf technique to optimize the feature extraction process. The proposed approach resolved the problem of local minimum optimization and obtained faster convergence compared to counterpart optimizers. The proposed approach provided an enhancement of 15% for accuracy and reduced time complexity by 32%, based on comprehensive experiments and benchmarking using an intrusion detection dataset.

Data visualization was used by [22] to propose a technique for zero-day malware detection using a similarity matrix. This approach is useful for IoT environments where big data are generated and collected from different sources, such as servers, network sensors, and mobile devices. The authors of [23] addressed the challenge raised by the rapid growth of multimedia texts, audio, images, and videos that are continuously generated and must be transmitted securely every second. These researchers proposed a secure surveillance framework for healthcare applications using intelligent integration of the efficient chaotic map to extract data in a monitored scene using a visual sensor (camera). Their results showed that the proposed framework fulfilled the security requirements for surveillance applications.

The authors in [24] showed an augmented reality (AR) application in a smart city. Using smartphones and augmented reality technologies, it enables citizens to access crucial information such as bus routes, transportation arrival times, and tourism attractions in an easy and effective manner. Images and geo-location markers activate AR information, which is delivered via a secure IoT infrastructure. The IoT infrastructure is built on bus-mounted IoT devices that move information to linked cloud servers via a secure platform. System security is ensured by the use of lightweight cryptography in conjunction with low-power IoT devices. As explained in [25], the system is built on an attribute-based encryption (ABE) scheme for fine-grained access control without a lengthy user permission process.

Table 1. Comparison between lightweight approaches.

Study	Context IoT Application	Security Objective	Improvement Concern for IoT
[20,26]	IoT eHealth	Privacy-preserving eHealth system to achieve patient privacy and address IoT environment requirements more effectively using Identity-Based Cryptography	Low communication computation, memory, and energy consumption
[20,21]	Internet of Medical Things (IoMT)	Improve an intrusion detection approach for the IoMT	Increased accuracy and reduction in the time required for training the classification model
[21,23]	Surveillance for IoT healthcare application	Intelligent integration of chaotic encryption to secure the healthcare application	Competitive and real-time encryption throughput
[23,24]	Application of augmented reality (AR) within a smart city	System security guaranteed through deployment of lightweight encryption used with low-powered IoT devices	Fine-grained access control without a lengthy user authorization process

compares the lightweight approaches discussed in this section.

2.2. NIST Tests for Cryptographic Algorithms

NIST recommends several techniques to verify the randomness of binary sequences generated from cryptographic algorithms and pseudorandom number generators. In April 2010, the NIST test suite was first presented in a special publication (800-22rev1a) [10]. NIST tests are used for hypothesis testing and are usually conducted to determine if a data sample shows that a certain condition is true for an entire population. The tests are designed to evaluate data sequences for a specific null hypothesis. If the outcome of the test satisfies the null hypothesis, it is concluded that the data sequence is random. Conversely, if the outcome of the test satisfies the alternative hypothesis, then it is concluded that the data sequence is not random. Each test examines the data sequence based on the null hypothesis, to determine whether the cryptographic algorithm is producing random values.

The NIST test suite [10,27] has been used to assess the randomness of several cryptographic algorithms [28,29,30,31]. The competition process for selecting the AES involves a rigorous series of randomness evaluations. The experiment was fixed to 0.01 significance. The author in [28] evaluated several cryptographic algorithms, including Rijndael, Serpent, Twofish, RC6, and Mars, highlighting the fact that the randomness of the ciphertext is correlated with a specific number of rounds for each cryptographic algorithm. For example, Rijndael passed the randomness tests after the 3rd round, Serpent and RC6 after the 4th, and Mars after the 6th.

The authors in [29] presented a framework based on the NIST suite to evaluate the randomness outcomes of cryptographic algorithms. The proposed framework used three NIST statistical tests to evaluate the randomness of block ciphers and stream ciphers, including TEA, Camellia, and LEX. The results of statistical tests indicated the percentage of successes from different generated sequence lengths. The authors concluded that the selected cryptographic algorithms showed a reliable degree of randomness based on the selected NIST tests.

2.3. Development and Evaluation

The author of [32] found that AES is not appropriate for constrained environments, such as RFID tags and sensor networks; therefore, they proposed a lightweight cryptographic algorithm called Present, based on substitution–permutation network primitives. Present works on a block length of 64 bits, supporting two options for key lengths of 80 and 128 bits. For lightweight applications requiring moderate security levels, the authors recommended deploying the cryptographic algorithm using the 80-bit key length mode. Present consists of 31 rounds of encryption that use a single 4-bit S-box and a single-bit permutation table. The authors also showed that Present is robust against different types of attacks, such as differential and linear cryptanalysis [33,34].

Celfia [35] is a lightweight cryptographic algorithm proposed by Sony Corporation labs. Celfia components are based on a Feistel networking structure divided into four data lines. Celfia uses two F-functions, each with 32 bits, for each encryption round. The F-functions were developed based on the concept of the diffusion switching mechanism (DSM) [36], and two different S-boxes were employed to enhance the overall diffusion. The number of rounds was therefore reduced to 10, 11, or 12 for the key lengths of 128, 192, and 256 bits (respectively). Celfia has shown robustness against different types of attacks and a processing encryption time comparable to that of AES.

Mini-AES [37] was designed for educational purposes rather than to be considered for use secure applications. This algorithm is designed to operate in the finite field of GF(2⁴). The plaintext is divided into blocks of 16 bits, each of which enters an encryption round that consists of four main components: NibbleSub, ShiftRow, MixColumn, and KeyAddition. 16-bit key length is used in Mini-AES encryption rounds. Mini-AES components operate in the same manner as Rijndael [38], but the design of the components is not justified in the finite field of GF(2⁴). The work of [37] also illustrated the vulnerability of Mini-AES to square attacks. The work of [39] presented another AES variant that operates in GF(2⁴) with the objective of performing cryptanalysis experiments on a simplified AES version, in order to understand how attacks might work. Their results suggested that the simplified version of AES is still robust against algebraic and man-in-the-middle attacks. The work of [40] highlighted the importance of the design trade-off between robust security solutions and performance optimization in terms of the area of system chips, power consumption, and memory utilization for lightweight applications. They implemented AES using the Xilinx ISE-13.2 suite and provided full pipeline encryption and decryption to utilize silicon costs. The authors also highlight the benefits of lightweight cryptographic algorithms and integrated 8-bit Kogge stone adder with x-tea to provide faster computation for large applications. The work of [41] also designed a variant of the AES S-Box to maximize performance, achieve high throughput, and utilize area efficiency. The problem of arithmetic implementations usually consuming exorbitant amounts of power is solved by implementing a solution for S-BOX construction based on Galileo’s field. The proposed solution is implemented using Die-to-Die (D2D) and With-In-Die (WID) variations.

Table 2. Comparison between cryptographic algorithms.

Cryptographic Algorithm	Block Size (Bit)	Key Size (Bit)	Number of Rounds	Structure	Proposed Use	Limitation
AES	128	28/192/256	10/12/14	SPN	Conventional applications	Requires a large number of hardware resources
Present	64	80/128	31	SPN	RFID tags and sensor networks	Less throughput than Celfia
Celfia	128	128/192/256	18/22/26	Feistel network	Very limited resource environment	Provides less memory utilization compared with Present
Mini-AES	16	16	10	SPN	Educational purposes	Not applicable for real IoT environments

compares the cryptographic algorithms discussed in this section. We focused mainly on AES, Present, and Celfia due to the fact that, among multiple block ciphers, both Present and Celfia have been certified and published in ISO/IEC 29192-2:2019 [42] as suitable cryptographic algorithms for lightweight applications. AES also has gained a lot of popularity in the era of lightweight encryption for the purpose of secure transmission between IoT devices, due to its friendly software implementation [43]; however, [32] indicated that AES is not suitable for extremely constrained environments, such as RFID tags and wireless sensor networks, and they stressed the need for a new optimized block cipher. More recently, it was reported that AES may not act as an ultimate choice for the IoT environment, due to the fact that it requires extensive hardware resources [43]. The software evaluation of [44] compared Present and Celfia in terms of security strength, performance, and resource utilization, demonstrating that Present requires fewer memory footprints than Celfia, due to the fact that the latter utilizes two S-boxes; however, Present requires more encryption time and average CPU cycles than Celfia.

3. Materials and Methods

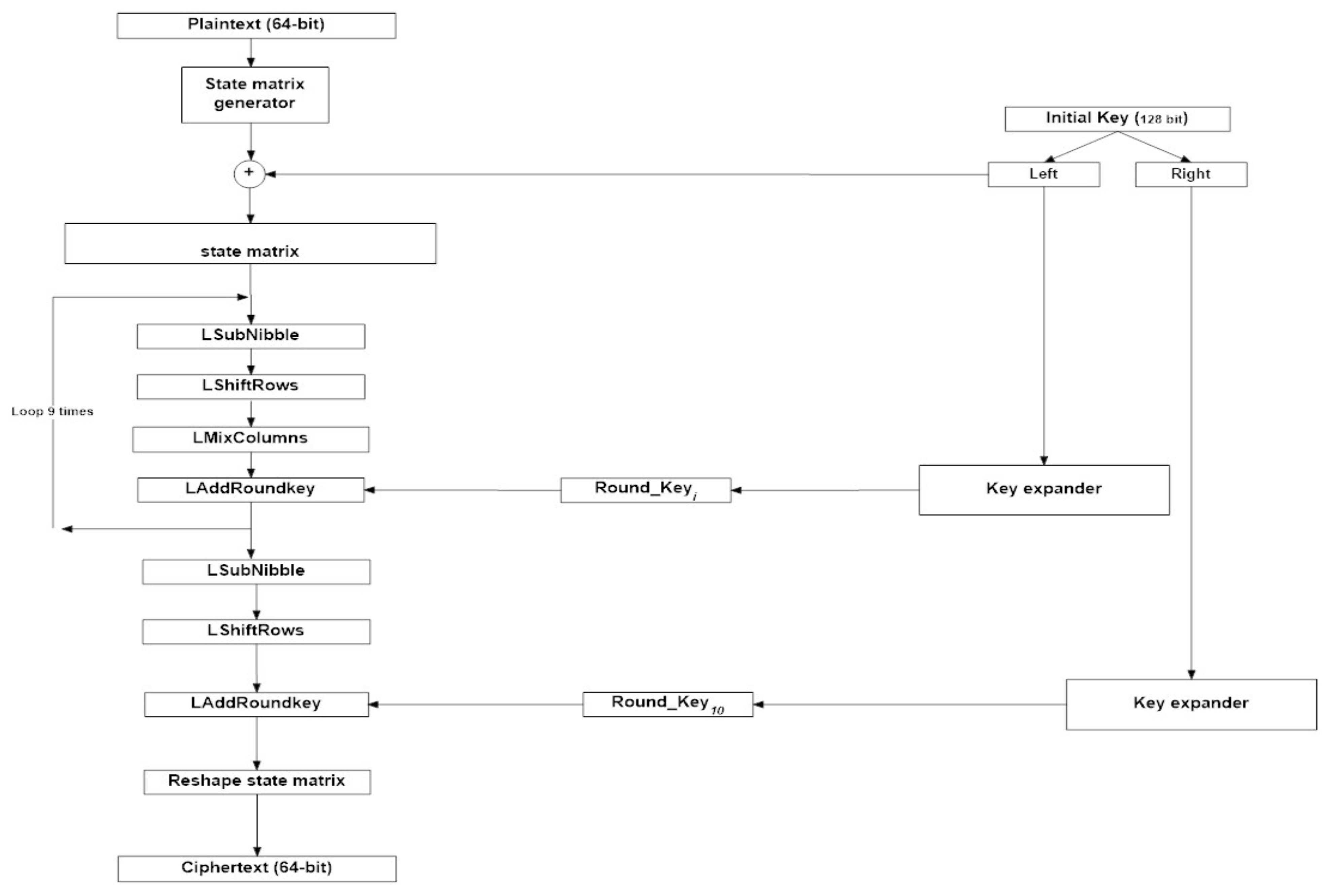
The design of LAES takes into consideration the following modifications: S-box arrangements, operation of finding the inverse in GF(2⁴), affine transformation, and key expansion process. These changes allow the algorithm to operate on 64-bit plaintext input. This section presents an overview of the main components of the proposed 64-bit LAES cryptographic algorithm that uses a 128-bit encryption key. The LAES consists of ten rounds that use an expanded key generated from the initial key. 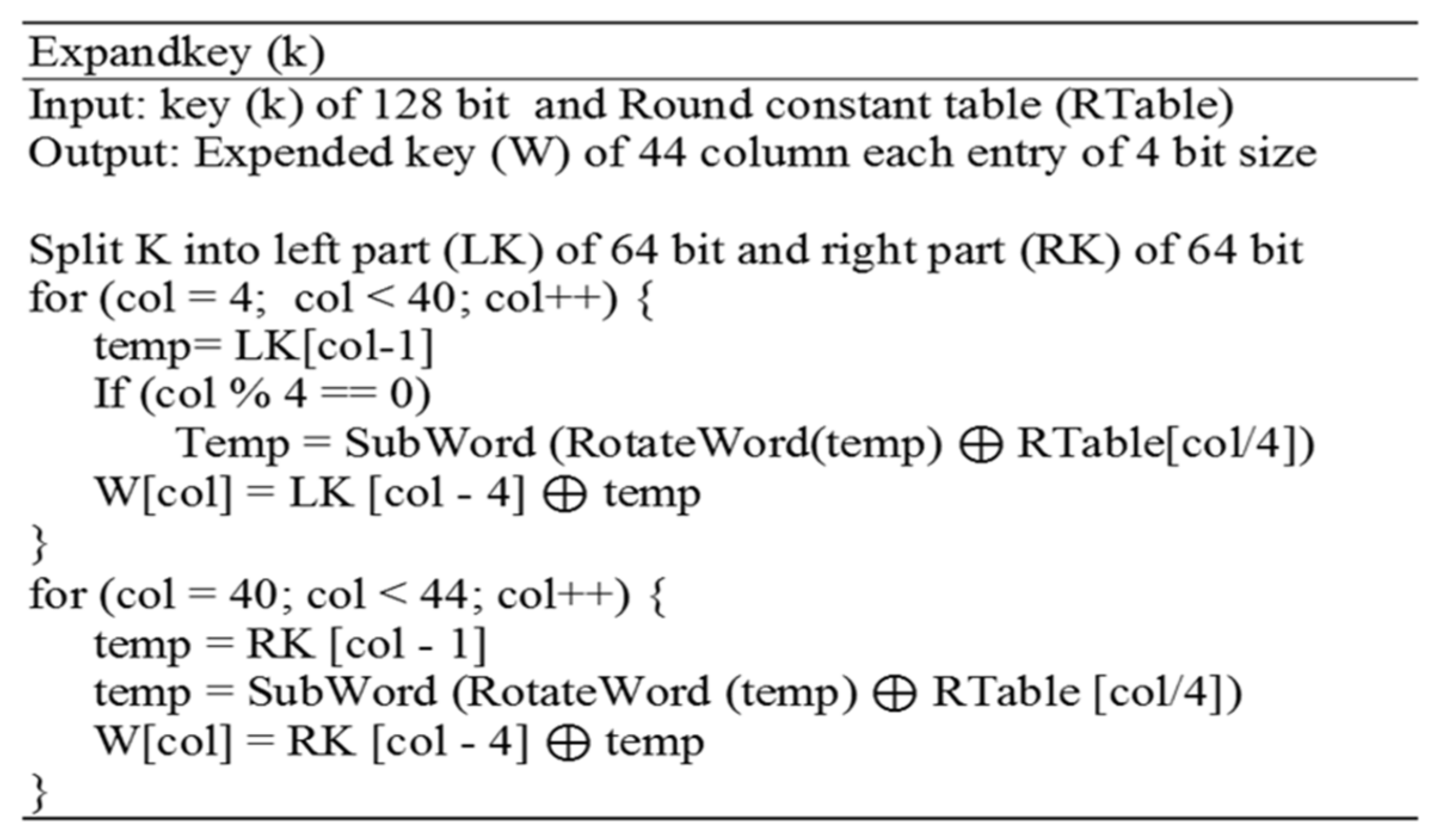The operation of LAES is described as follows, as illustrated in Figure 1 and Figure 2 (the major components are described in the next section):

• The plaintext is divided into 64-bit blocks using a state matrix generator, which reshapes the 64 bits into 4 × 4 matrix, whereby each element has 4 bits.
• The encryption key is divided into two 64-bit parts. The left part of the key is XORed with the text generated from the state matrix generator, to obtain the state matrix text. The left part is fed to the key expander to generate the round keys for the first nine rounds.
• The state matrix text is substituted to the S-box using the LSubNibble component, which enhances non-linearity during each round.
• Each row in the resulting 4 × 4 matrix text obtained from step 3 is rotated cyclically by offsets of 0, 1, 2, and 3. This step is inherited mainly from the original AES, to enhance the diffusion and confusion of the LAES.
• The mixing column has the same objectives of the previous step, multiplying the resulting matrix from step 4 by a constant matrix that has entries from GF(2⁴).
• The key expander generates a round key based on the left part key. The generated round keys are dependent on each other. The matrix generated in step 5 is XORed with the round key.
• Steps 3 to 6 are repeated nine times.
• The resultant text after the ninth round is processed using steps 3, 4, and 6. The key expander generates the key round based on the right part of the key.
• Finally, the resulting matrix is reshaped into a 64-bit vector, which represents the ciphertext.

3.1. S-Box and Inv S-Box Generation

This section illustrates the process of generating the S-box and its inverse. This process reduces the finite field of GF(2⁸) that represents the basic primitive polynomial in AES into GF(2⁴), to represent the basic primitive polynomial in the design of LAES. This reduction is intended to simplify both the software and hardware design, and to speed up the process of generating and looking up the entries of the S-box and Inv S-box [45].

3.2. Substitution Table

The generation of the substitution tables of S-box and Inv S-box in LAES is based on a primitive polynomial of GF(2⁴), defined as f(x) = x⁴ + x + 1, where x is a 4-bit input. The multiplicative inverse of x is computed, and then the affine transformation is applied to it. The output from the affine transformation forms an entry to the S-box lookup table. In GF(2⁴) the expected input to the S-box is a hexadecimal number. Inv S-box is constructed in a basically similar way; however, the 4-bit input to the Inv S-box is manipulated by the affine transformation, then the multiplicative inverse is computed. The output of this computation forms the entries of the Inv S-box lookup table. The S-box and the Inv S-box are used in the processes of encryption, decryption, and key expansion to directly substitute a 4-bit value with another 4-bit value of the same finite field.

3.3. Multiplicative Inverse

Table 3. Inversion table computation over GF(2⁴).

Primitive Polynomial	Inverse in Primitive Polynomial	x	x−1
0	0	0 0 0 0	0 0 0 0
1	x0	0 0 0 1	0 0 0 1
x	x	0 0 1 0	1 0 0 1
x2	x2	0 1 0 0	1 1 0 1
x3	x3	1 0 0 0	1 1 1 1
x4	x4 = x + 1	0 0 1 1	1 1 1 0
x5	x5 = x. x4 = x2 + x	0 1 1 0	0 1 1 1
x6	x6 = x. x5 = x3 + x2	1 1 0 0	1 0 1 0
x7	x7 = x. x6 = x3 + x + 1	1 0 1 1	0 1 0 1
x8	x8 = x. x7 = x2 + 1	0 1 0 1	1 0 1 1
x9	x9 = x. x8 = x3 + x	1 0 1 0	1 1 0 0
x10	x10 =x. x9 = x2 + x + 1	0 1 1 1	0 1 1 0
x11	x11 = x. x10 = x3 + x2 + x	1 1 1 0	0 0 1 1
x12	x12 = x. x 11 = x3 + x2 + x + 1	1 1 1 1	1 0 0 0
x13	x13 = x. x12 = x3 + x2 + 1	1 1 0 1	0 1 0 0
x14	x14 = x. x13 = x3 + 1	1 0 0 1	0 0 1 0

describes the computation of the inverse of 4-bit values over the finite field of GF(2⁴). The details of this calculation can be found in [46], describing the multiplicative inverse of a polynomial function over GF(2p).

Table 4. Inversion table values in hexadecimal.

Input $\left({\mathit{x}}^{}\right)$	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
Output ($x^{-1}$)	0	1	9	E	D	B	7	6	F	2	C	5	A	4	3	8

represents the inversion values in hexadecimal.

3.4. Affine Transformation

The affine transformation can be achieved in the finite field GF(2⁴) modulo of the irreducible polynomial x⁴ + x + 1 using Equation (1), for 0 ≤ i < 4, where bi is the ith bit of the 4-bit input (b), and Ci is the ith bit of a 4-bit constant (C = 0110 b). For example, the affine transformation of 0 is computed by first finding the inverse of 0 from Table 4, then the affine transformation is computed using the constant C.

• b₀’ = b₀ ⊕ b₂ ⊕ b₃ ⊕ c₀ = 0 ⊕ 0 ⊕ 0 ⊕ 0 = 0
• b₁’ = b₁ ⊕ b₃ ⊕ b₀ ⊕ c₁ = 0 ⊕0 ⊕ 0 ⊕ 1 = 1
• b₂’ = b₂ ⊕ b₀ ⊕ b₁ ⊕ c₂ = 0 ⊕ 0 ⊕ 0 ⊕ 1 = 1
• b₃’ = b₃ ⊕ b₁ ⊕ b₂ ⊕ c₃ = 0 ⊕ 0 ⊕ 0 ⊕ 0 = 0

b_i’ = b_i ⊕ b_(i+2) mod 4 ⊕ b_(i+3) mod 4 ⊕ C_i

(1)

Similarly, this transformation can be achieved in a matrix notation in GF(2⁴) modulo with the irreducible polynomial f(x) = x⁴ + x + 1 using Equation (2), where matrix A is invertible over GF(2), and C could be a compatible constant number in GF(2⁴). In this design, we set the constant C to 616, which is equal to the vector 0110. Matrix A used in the current implementation is represented as follows:

$$A=\left[\begin{array}{cccc}1& 0& 1& 1\\ 1& 1& 0& 1\\ 1& 1& 1& 0\\ 0& 1& 1& 1\end{array}\right]$$

where A has an inverse over GF(2), given by:

$$A^{-1}=\left[\begin{array}{cccc}1& 1& 1& 0\\ 0& 1& 1& 1\\ 1& 0& 1& 1\\ 1& 1& 0& 1\end{array}\right]$$

$$x\prime =A·\left(x^{-1}\oplus C\right)$$

(2)

The S-box table is constructed using Table 4 and Equation (1). The entry of the S-box that corresponds to an input x is computed first by finding the inverse of x from Table 4, then applying the affine transformation in Equation (1) to the output of Table 4. This produces the S-box lookup shown in

Table 5. S-box lookup.

Input $\left(\mathit{x}\right)$	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
Output ($x^{\prime }$)	6	1	A	E	7	4	2	5	9	8	0	C	3	B	F	D

.

Table 6. Inv S-box.

Input $\left({\mathit{x}}^{\prime }\right)$	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
Output ($x$)	A	1	6	C	5	7	0	4	9	8	2	D	B	F	3	E

shows the Inv S-box lookup table used in the decrypting function. The entries of the Inv S-box table are computed after the multiplicative inverse is applied to the output of Equation (3). Table 6 illustrates the entries for the Inv S-box over GF(2⁴).

$$x={(A^{-1}·\left(x^{\prime }\oplus c\right))}^{-1}$$

(3)

3.5. Key Expander

The 128-bit length of the LAES key keeps the design persistent in terms of the agent’s brute force attack, in comparison to the smaller key size used in previous studies [32,35]. The key is divided into two halves, each of which is a 64-bit 4 × 4 matrix. Each entry in the matrix consists of 4 bits, instead of the 8 bits in AES.

The key expander simply expands the left part of the key during each round until the ninth round of LAES is completed. The right part of the key is then expanded during the final round. The basic principles of AES key expansion were followed in the design of LAES [38]:

• The total number of round key bits is equal to the block length multiplied by the number of rounds, plus 1.
• The key is expanded into an expanded key.
• Round keys are taken from this expanded key.

The S-box lookup and the round constant tables are used during the expansion process of generating 36 new columns from the left part and 4 new columns from the right part. The S-box lookup and the round constant tables are used to minimize the correlation between the key parts, and to eliminate symmetricity and enhance the non-linearity of the expanded key, which affects the LAES diffusion property.

The left part of the key consists of 64 bits arranged into a 4 × 4 matrix, where each entry has 4 bits. The matrix is then expanded by joining 40 more columns. Considering that the initial values of key columns are C (0), C (1), C (2), and C (3), the new columns are defined as in Equation (4).

$$C\left(i\right)=\left\{\begin{array}{c}C\left(i-4\right) \oplus C\left(i-1\right) , i \% 4 \ne 0\\ C\left(i-4\right) \oplus Tr\left(C\left(i-1\right)\right), i \% 4=0\end{array}\right.$$

(4)

where Tr(C(i − 1)) is the transformation of C(i − 1) obtained as follows. Let the elements of C(i − 1) have the values a, b, c, and d. Shift-left these elements cyclically to obtain b, c, d, and a, then replace each of these values with the corresponding element in the S-box lookup table, to obtain the values e, f, g, and h. Finally, Tr(C(i − 1)) is the column vector that equals e ⊕ r(i), f, g, and h, in which r(i) is a round constant of the ith round. In this way, columns C(4) … C(39) are generated from the initial four columns of the left part key. The final four columns generated (C(40), C(41), C(42), and C(43)) from the right part of the key are obtained using a similar algorithm. Figure 3 illustrates the algorithm of key expansion in LAES.

3.6. Round Constant Reconstruction

The round constant table of AES needs to be reconstructed to GF(2⁴), which in this case comprises a 10 × 4 matrix of zeros except for the first column, which contains 4-bit values conforming with powers of 2 modulo for the primitive polynomial x⁴ + x + 1. The polynomial nature of this multiplication by 2, which is actually a bit-shifting to the left, does not have any influence on the result as long as the product does not exceed a value of 15; therefore, the first four elements are obtained by the multiplication of 2 over GF(2⁴). Once the value exceeds 15, one more bit is needed to represent the generated value, and this is not achievable for one entry value in GF(2⁴) and the value is folded back into GF(2⁴) by modular reduction.

Table 7. Round constant table.

Round Number	1	2	3	4	5	6	7	8	9	10
Round constant	1	2	4	8	3	6	C	B	5	A

shows the round number and its corresponding round constant.

3.7. Mix Column Permutation

The AES constant matrix was selected based on factors that provide the encryption and decryption process with less computation and higher diffusion power [38]. These factors include the linearity over GF(2) and the invertibility of the constant matrix. The matrix should be invertible to perform the decryption process and support a quick handing process. As per AES, an entry of 0 or 1 requires no multiplication process [38]. In LAES, the choice of the coefficients of C(x) are 3, 2, 1, and 0, which allows easier implementation for software and hardware multiplication process. Columns of the state matrix are considered as a polynomial over GF(2⁴) modulo x⁴ + x + 1, with a fixed polynomial C(x) = 3x³ + 1x² + 1x + 2. Although the polynomial x⁴ + x + 1 is not irreducible, the operation is invertible, since the polynomial C(x) is co-prime to x⁴ + x + 1.

The coefficients of the polynomial C(x) and the polynomial of state column matrix are in themselves polynomials in GF(2⁴). The inverse of C(x) is C-1 (x) = 9x³ + Ex² + Bx + 4, which is needed to construct the matrix in the decryption process.

The 0th column of the constant matrix can be represented by s3,0x³ + s2,0x ² + s1,0x + s0,0, where the coefficient 3 in C(x) is actually the polynomial x + 1 in GF(2⁴), the coefficient 1 is the polynomial 1, and the coefficient 2 is the polynomial x in GF(2⁴).

The multiplication by C(x) modulo x⁴ + x + 1 can also be represented as a matrix transformation. For example, if we take the 0th column, which has four elements (s0,0, s1, 0, s2, 0, s3, 0), the mix columns component produces the 0th column of the result (s’0,0, s’1, 0, s’2, 0, s’3, 0), in the manner seen below. Similarly, the operation is repeated for the other columns.

$$\left[\begin{array}{c}s{\prime }_{0,0}\\ s{\prime }_{1,0}\\ s{\prime }_{2,0}\\ s{\prime }_{3,0}\end{array}\right]=\left[\begin{array}{cccc}x& x+1& 1& 1\\ 1& x& x+1& 1\\ 1& 1& x& x+1\\ x+1& 1& 1& x\end{array}\right]\cdot \left[\begin{array}{c}{s}_{0,0}\\ s_{1,0}\\ s_{2,0}\\ s_{3,0}\end{array}\right]$$

3.8. Encryption Process in LAES

The main transformations components of LAES encryption rounds are mainly inherited from the original AES; however, the AES encryption components operate on GF (2⁸), while the LAES encryption components operate on GF(2⁴). This means that the components of the LAES operate by following the same logical operations of the AES, but the entries of each component are completely different, and operate on a smaller scale. For example, the S-box in the AES is a lookup table of 256 entries, while the S-box of the LAES is a lookup table of 16 entries. The input to the encryption process is a block of 64 bits, and it is reshaped into 4 × 4 matrix. This matrix is called a state matrix, which is modified based on the encryption rounds until the 10th round of the encryption is completed. The first nine rounds of LAES consist of four transformation components: LSubNibble, LShiftRows, LMixColumns, and LAddRoundKey. The final round of LAES contains only three transformations components, similar to the AES, which are LSubNibble, LShiftRows, and LAddRoundKey, as described below.

LSubNibble: This component is used to perform the simple transformation of the state matrix bits into another matrix based on the S-box lookup table (see Table 5). For example, the state matrix entry of 0 will be transferred into 6. Different bits of the state matrix are transformed into different bits from the S-box lookup table. The S-box is intended to provide an invertible transformation of the state matrix entries during this component, which is inverted by the LInvSubNibble in the decryption process by the entries of the Inv S-box (see Table 6). In AES, the S-box is a 16 × 16 matrix covering a total of 256 bytes, represented in hexadecimal, and indexed in a column and row pattern. The work in [45] indicated that the SubBytes component in AES has an egregious processing time and power consumption, and the use of smaller lookup tables with sizes ranging from 16 to 128 bytes has become more reliable for obtaining higher speeds to meet the needs of different lightweight applications, such as smartphone applications, sensor networks, smart cards, and RFID. In LAES, the S-box and the Inv S-box are reduced into 16 nibbles, indexed from 1 to 16, which is expected to improve the processing speed of LAES and provide the required confusion for lightweight applications.

LShiftRows: This component operates similar to the ShiftRows in AES, by shifting the entries of each row of the state matrix cyclically. The LShiftRows operates on a state matrix of 64 bits. The shift is made by certain offsets of 0, 1, 2, and 3 for rows 1 to 4 of the state matrix, respectively. The objective of this component is to avoid the columns of the state matrix form being linearly independent, and to enhance the overall diffusion of the encryption process. For the decryption process, the LInvShiftRows component cyclically shifts the rows of the state matrix to the right by certain offsets of 0, 1, 2, and 3 for rows 1 to 4 of the state matrix, respectively.

LMixColumns: In this component, the state matrix obtained from the LSubNibble is diffused to provide a further level of diffusion following the operation performed by LShiftRows component. The LMixColumns performs permutation at the column level of the state matrix, which provides another level of diffusion over the LShiftRows component.

The LMixColumns transformation is computed as illustrated in Equation (5), where S’ is the new state matrix, P is the polynomial coefficient, and S is the current state matrix.

$$S^{\prime }=P\cdot S$$

(5)

This transformation can be defined by the polynomial coefficient matrix multiplication on the state matrix as follows:

$$\left[\begin{array}{cccc}{s^{\prime }}_{0,0}& {s^{\prime }}_{0,1}& {s^{\prime }}_{0,2}& {s^{\prime }}_{0,3}\\ {s^{\prime }}_{1,0}& {s^{\prime }}_{1,1}& {s^{\prime }}_{1,2}& {s^{\prime }}_{1,3}\\ {s^{\prime }}_{2,0}& {s^{\prime }}_{2,1}& {s^{\prime }}_{2,2}& {s^{\prime }}_{2,3}\\ {s^{\prime }}_{3,0}& {s^{\prime }}_{3,1}& {s^{\prime }}_{2,3}& {s^{\prime }}_{3,3}\end{array}\right]=\left[\begin{array}{cccc}2& 3& 1& 1\\ 1& 2& 3& 1\\ 1& 1& 2& 3\\ 3& 1& 1& 2\end{array}\right]\cdot \left[\begin{array}{cccc}{s}_{0,0}& s_{0,1}& s_{0,2}& s_{0,3}\\ s_{1,0}& s_{1,1}& s_{1,2}& s_{1,3}\\ s_{2,0}& s_{2,1}& s_{2,2}& s_{2,3}\\ s_{3,0}& s_{3,1}& s_{2,3}& s_{3,3}\end{array}\right]$$

The inverse mix column transformation, called LInvMixColumns, is defined by the following matrix multiplication:

$$\left[\begin{array}{cccc}9& E& B& 4\\ 4& 9& E& B\\ B& 4& 9& E\\ E& B& 4& 9\end{array}\right]\cdot \left[\begin{array}{cccc}{s}_{0,0}& s_{0,1}& s_{0,2}& s_{0,3}\\ s_{1,0}& s_{1,1}& s_{1,2}& s_{1,3}\\ s_{2,0}& s_{2,1}& s_{2,2}& s_{2,3}\\ s_{3,0}& s_{3,1}& s_{2,3}& s_{3,3}\end{array}\right]=\left[\begin{array}{cccc}{s^{\prime }}_{0,0}& {s^{\prime }}_{0,1}& {s^{\prime }}_{0,2}& {s^{\prime }}_{0,3}\\ {s^{\prime }}_{1,0}& {s^{\prime }}_{1,1}& {s^{\prime }}_{1,2}& {s^{\prime }}_{1,3}\\ {s^{\prime }}_{2,0}& {s^{\prime }}_{2,1}& {s^{\prime }}_{2,2}& {s^{\prime }}_{2,3}\\ {s^{\prime }}_{3,0}& {s^{\prime }}_{3,1}& {s^{\prime }}_{2,3}& {s^{\prime }}_{3,3}\end{array}\right]$$

LAddRoundKey: This component XORs the state matrix and the round key. The LAddRoundKey is a simple transformation that affects every bit of the state matrix. LAddRoundKey and the other LAES components provide the required level of confusion and diffusion. The InvLAddRoundKey is the component that performs the inverse of LAddRoundKey transformation. The decryption process is the reverse of the transformation components of the encryption process. The input to the decryption process is the ciphertext processed by the invertible components.

4. Results and Evaluation

LAES was assessed and compared against the well-known lightweight crypto algorithms Celfia and Present. The evaluation was conducted using several measures designed based on the guidance of the NIST statistical test suite for cryptographic applications [27]: frequency test, block test, runs test, effective (total) encryption time, average encryption time for a single block, and average encryption time for a single round. Facing identical cases, the three algorithms were challenged to encrypt various images with sizes from 1 KB up to 4 MB. The experiments included the encryption of around 15,000 image files. The randomness level was measured using the first three measures, while the rest were used to indicate the encryption latency for LAES and its counterparts.

4.1. Frequency Test

The frequency test is an important measure that assesses whether the number of zeros and ones in a sequence are equivalent, as would be expected for a truly random sequence [10]. This test computes a p-value for a series of bits to determine its randomness; if the computed p-value is less than 0.01, this means that the sequence is not random [14]. To compute the p-value for a binary sequence X, where Xi represents the ith bit of the sequence, the bits are first converted into +1 and −1 values. This process is conducted by converting the zero binary digits to −1 and the ones to +1; then, Equation (6) is applied to find the sequence sum (S) that has a length of (N). Sobs is then calculated to find the absolute value of the sum using Equation (7). Finally, the p-value is calculated using Equation (8), where erfc is a function as explained by [10]:

$$S={\displaystyle \sum }_{i=0}^N{X}_i$$

(6)

$$S_{obs}=\frac{\left|S\right|}{\sqrt{N}}$$

(7)

$$p-vlaue=erfc\left(\frac{S_{obs}}{\sqrt{2}}\right)$$

(8)

Figure 4 displays the rate of success for frequency testing obtained from the cipher output of LAES 128, Present 128, Clefia 128, and AES on various sizes of files. The x-axis identifies the success rate for each cryptographic algorithm on a specific size of the file, and the y-axis identifies the file size. It can be seen that very good randomness properties were exhibited by all of the algorithms, with success rates generally ranging between 80–100%. The trend lines for the LAES and its counterparts also show anticipated performance for cryptographic algorithms that are supposed to produce a random cipher (to avoid exposing confidential information), which could be useful for undesired cryptoanalysis. It can be seen that the percentage of success increased with a larger file size, which is attributable to the statistical features of the test, which is directly affected by the large number of sequences generated from larger file sizes (which usually have a higher volume of chaotic data).

4.2. Block Test

The focus of this test is the ratio of ones and zeros in the sequence. It begins by partitioning the sequence into blocks, as indicated in Equation (9), where M is the block length, n is the length of the sequence, and N is the number of blocks [14]. π_i, which indicates the proportion of ones, is calculated using Equation (10) for each M-bit block, where 1 ≤ i ≤ N. Equation (11) calculates X²(obs) to measure how well the ones within a given M-bit block match the expected 50% value. The p-value is finally computed using Equation (12), where igamc is a function as explained by [10]. A p-value of less than 0.01 is considered to indicate failure (i.e., a non-random sequence). This test can be viewed as a restricted version of frequency test, where each block of the sequence is examined individually; if one block fails the test, then the overall success rate for the sequence is degraded.

$$N=⎣\frac{n}{M}⎦$$

(9)

$${\pi }_i=\frac{{{\displaystyle \sum }}_{j=1}^M{X}_{\left(i-1\right)M+j}}{M}$$

(10)

$$X^2\left(obs\right)=4M{\displaystyle \sum }_{i=1}^N{\left({\pi }_i-\frac{1}{2}\right)}^2$$

(11)

$$P-value=igamc\left(\frac{N}{2},\frac{X^2\left(obs\right)}{2}\right)$$

(12)

Figure 5 shows the block test success rate achieved by LAES 128, Present 128, Clefia 128, and AES on files of different sizes. The x-axis identifies the rate of success for each crypto algorithm on a specific size of file, and the y-axis identifies the size of the files. Figure 5 shows that the randomness trend lines for the algorithms are above 40%. The trend lines for the LAES show a higher success rate for larger files, almost similar to the AES trend line. This indicates that despite the higher number of rounds in the LAES counterparts, it was able to produce a higher degree of diffusion on files consisting of a higher number of blocks.

4.3. Runs Test

This test evaluates the total number of runs in the sequence. The non-empty elements that consist of adjacent equal values in the sequence are considered a run. The main purpose of the runs test is to determine whether the number of runs of ones and zeros of various lengths is as expected for a random sequence [10]. The test starts by conducting a frequency test as a prerequisite; if the frequency test fails, then the run test is not applicable, and the p-value is set to zero. If the frequency test is passed, then Equation (13) is applied to count the number of ones in the sequence X, where X_i represents the ith bit of the sequence, and n is the length of the sequence. The total number of runs V_n(obs) is then computed as shown in Equation (14), where R(i) equals zero if X_i and X_i+1 are identical, and one otherwise. Finally, Equation (15) computes the p-value. If the p-value is less than 0.01, this means that the sequence failed the test [14].

$$\pi =\frac{{{\displaystyle \sum }}_i^n{X}_i}{n}$$

(13)

$$V_n\left(obs\right)={{\displaystyle \sum }}_{i=1}^{n-1}R\left(i\right)+1$$

(14)

$$P-value=\left(\frac{\left|V_n\left(obs\right)-2n\pi \left(1-\pi \right)\right|}{2\sqrt{2n}\pi \left(1-\pi \right)}\right)$$

(15)

Figure 6 shows the runs test success rate obtained from the cipher output of LAES 128, Present 128, Clefia 128, and AES on files of various sizes. The x-axis identifies the success rate for each crypto algorithm on a specific size of the file, and the y-axis identifies the file size. The figure shows very good randomness outcomes for the algorithms, and success rates ranging between 80–100%. The trend lines for LAES and its counterparts show very close success rates.

To conclude the results of these three tests, a random sequence should consist of a finite number of elements, with each element of the sequence being generated with uniform probability; in other words, a binary random sequence should have equal probabilities, and be unpredictable and uniform [47]. The outcome performance of LAES regarding the frequency, block, and run tests satisfy the properties required by cryptographic algorithms and outperform its counterparts. For example, the trend line for LAES outperforms Celia, Present, and AES for both frequency test and run test, and is very close to AES in block test for large file sizes. This indicates that the cipher produced by LAES satisfies the properties of binary random sequence with a high degree of confidence.

4.4. Processing Time

The time efficiency of LAES and its counterparts were measured using three metrics, as shown in Figure 7, Figure 8 and Figure 9. Figure 7 shows the effective (total) encryption time achieved by LEAS and its counterparts. It illustrates that the encryption time of LEAS increases modestly with file size, but in contrast, it increases exponentially for Present and AES. This behavior is attributable to Present having a large number of rounds (n = 31). While Celfia demonstrates a lower encryption time than Present, the lowest encryption time was achieved by LEAS, with an average difference of 79.7%, 95.0%, and 97.4% lower than Celfia, Present, and AES, respectively. These outcomes also conform to the outcomes displayed in Figure 8, indicating the required encryption time for a single block.

Figure 9 shows the encryption time for a single round achieved by LEAS, Present, Celfia, and AES. LEAS evidently outperforms both Present and Celfia regardless of file size, with an average difference of 79.8% and 82.7% lower (respectively). This is due to the deceleration propagated from the key generation process in Present, and the bit permutation method it uses. Celfia also shows relatively slower round encryption time compared to LAES due to its internal structure, which is based on a generalized Feistel structure, with four data lines having two 32-bit F-functions per round (comprising two different 8-bit S-boxes), followed by a diffusion matrix multiplication [35]. This elaborate process slows down Celfia compared to LAES.

4.5. Microcontroller-Based Evaluation

This section assesses the performance and simplicity achieved by the encryption process for LAES and its counterparts in terms of CPU cycles, consumed power, and the amount of charge required. This experiment used an 8-bit microcontroller Arduino Uno board (MCU). The popularity of the Arduino board is due to its ease of use, its extendibility for managing a large number of sensors, and the fact that installation and maintenance of its components are inexpensive [48]. The Arduino Uno board has been used in many lightweight IoT applications, including smart cities [49], wearable sensor-based IoT sensors [50], temperature measurement devices [51], and heart rate monitoring systems [52].

The Arduino Uno used in this experiment was powered and connected to computers through a USB port. It can also be powered via an AC/DC adapter. The experimental setup and specifications are similar to those used by [14], whereby sketch programming was used to implement the proposed LAES and its counterparts on the Arduino board. When the board was turned on, the cyclic encryption mode started immediately, and a built-in timer was used to measure the time required for each cycle. A fixed-size block of random data was encrypted 10,000 times, and several measures were obtained using a multimeter to compute the average power consumption for block encryption.

Table 8. Evaluation outcomes based on the 8-bit microcontroller Arduino Uno board.

Measures	Cryptographic Algorithms (Block Size/Key Size/Number of Rounds)
	Present (64/128/31)	Clefia (128/128/18)	AES (128/128/10)	LAES (64/128/10)
Average block encryption time (us)	3212	2846	4834	1920
Average number of CPU cycles for the block encryption	51,392	45,536	77,344	30,720
Average round encryption time (us)	103.613	158.11	483.40	120.23
Average number of CPU cycles per encryption round	1658	2530	7734	1550
Average power consumption for block encryption (mWh)	1.10189 × 10−4	9.80289 × 10−5	1.71876 × 10−4	6.37333 × 10−5
Average battery charge consumption for block encryption (mAh)	2.20379 × 10−5	1.96058 × 10−5	3.43751 × 10−5	1.27467 × 10−5

shows the results of the evaluation for LAES and its counterparts using the measures below, which aimed to evaluate the proposed LAES from a different perspective: the average required encryption time for (1) block, (2) round, and (3) entire process; the average CPU cycle required for (4) encrypting block and (5) round; (6) the average power and battery charge consumption required for encrypting a block.

The evaluation results show that LAES outperforms its counterparts in the specified measures. LAES required fewer CPU cycles, less power, and less charge consumption for block encryption. As indicated in Table 8, the number of CPU cycles per encryption round required by Present is less than LAES, AES, and Clefia; however, the fact that Present requires 31 rounds for block encryption causes the cipher to consume additional CPU cycles and energy. Clefia requires more CPU cycles and energy than Present and LAES, due to some complex operations during the encryption round and the key generation strategy. LAES shows promising performance in terms of the number of CPU cycles required, as well as efficient energy consumption and battery charge consumption for block encryption, which are important measures for resource-constrained devices in IoT.

5. Conclusions

This paper presents a streamlined AES variant called LAES that employs a key whitening technique and operates on GF(2⁴). We evaluated and compared the operation of LEAS with three lightweight cryptographic algorithms: Celfia, Present, and AES. The evaluation was conducted using randomness analysis and time efficiency using six measures: the frequency (Monobit) test, the block test, the runs test, effective (total) encryption time, average encryption time for a single block, and average encryption time for a single round. The four algorithms were assessed with similar scenarios. The evaluation showed that LAES achieves comparable randomness to Celfia, Present, and AES for most scenarios in terms of randomness testing. The randomness average of LAES increases with relatively larger files; however, in terms of effective (total) encryption time, average encryption time for a single block, and average encryption time for a single round, the results for LEAS were clearly lower than those of Present and Celfia. This supports our objective to achieve high randomness levels with lower encryption time. The evaluation revealed outstanding improvements (i.e., reductions) in processing time and power consumption for LAES compared to Present, Clefia, and AES. Furthermore, LAES and its counterparts were evaluated and compared based on different measures using an 8-bit microcontroller Arduino Uno board. LAES required fewer CPU cycles, less power, and less charge consumption for the block encryption.

In future work, we plan to perform different cryptoanalysis techniques such as linear and differential attacks for LAES, and to evaluate its hardware implementation in order to measure its energy consumption and footprint compared to other well-known lightweight cryptographic algorithms. We also plan to implement the proposed LAES on hardware to evaluate the number of gates it requires and compare it with its counterparts. Another possible research direction will focus on evaluating LAES with different types of big data, including multimedia data such as audio and video. The proposed LAES will also be implemented and evaluated on real IoT applications that manipulate sensitive data, such as eHealth, smart homes and cities, tracking and surveillance, and location-based services applications.