Fine-Scale Population Estimation Based on Building Classifications: A Case Study in Wuhan
Abstract
:1. Introduction
- (1)
- This paper proposes a building classification method with POI data. The text classification method, frequency-inverse document frequency (TF-IDF), is applied to calculate the POI data to obtain functional classifications of buildings (Section 2).
- (2)
- Based on the results of building classification, this paper establishes a population estimation model at a subdistrict scale. Firstly, this paper makes statistics on the relevant characteristics of buildings. Secondly, by calculating the importance of each building feature, a certain number of variables are selected, in turn, to establish a fine-scale population estimation model (Section 2).
- (3)
- This paper conducts experiments on the real dataset in Wuhan. The experimental results show that our approach achieves a lower error rate, which provides a new solution to the estimation for fine-scale populations (Section 3).
2. Materials and Methods
2.1. Study Site and Data Source
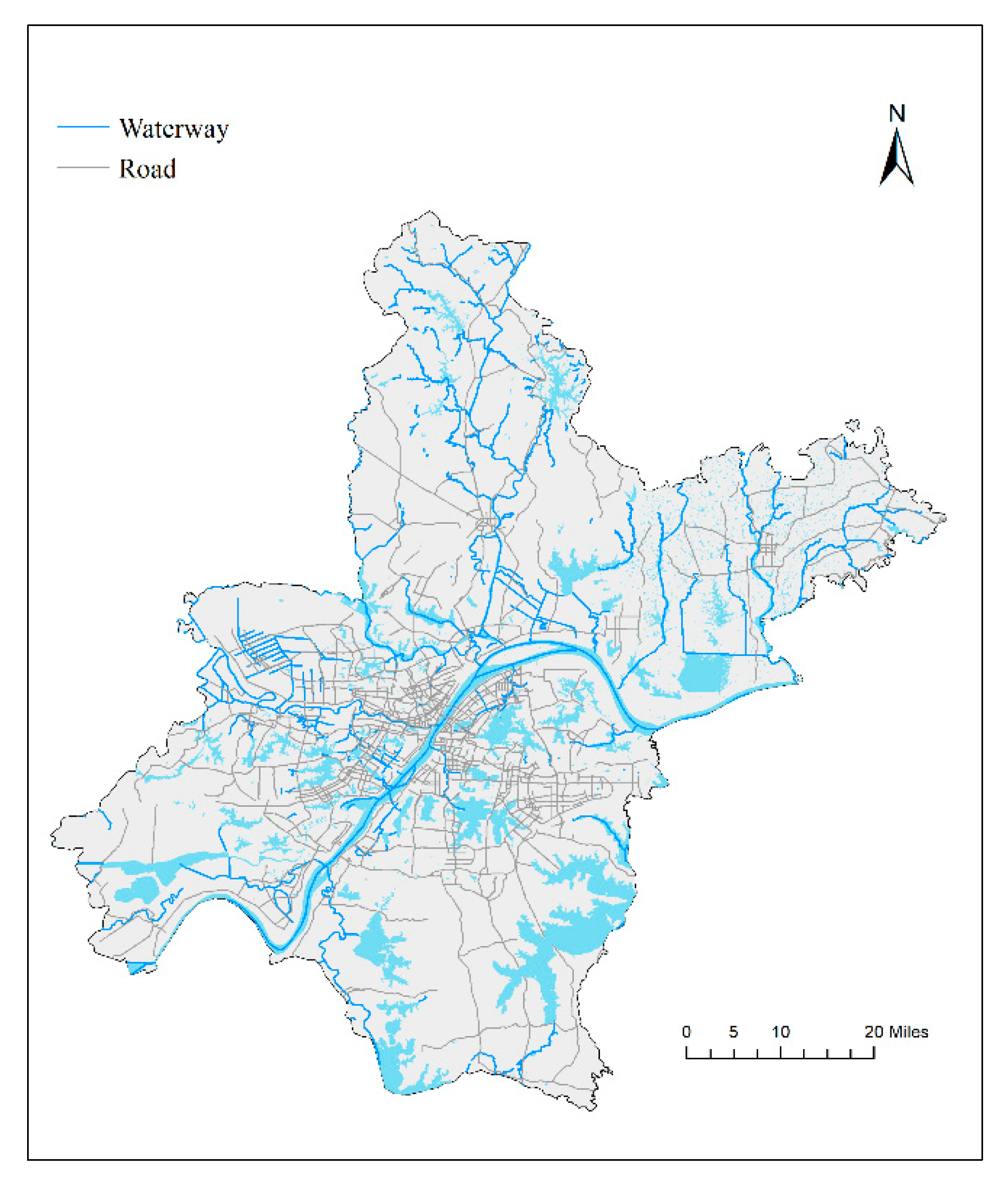
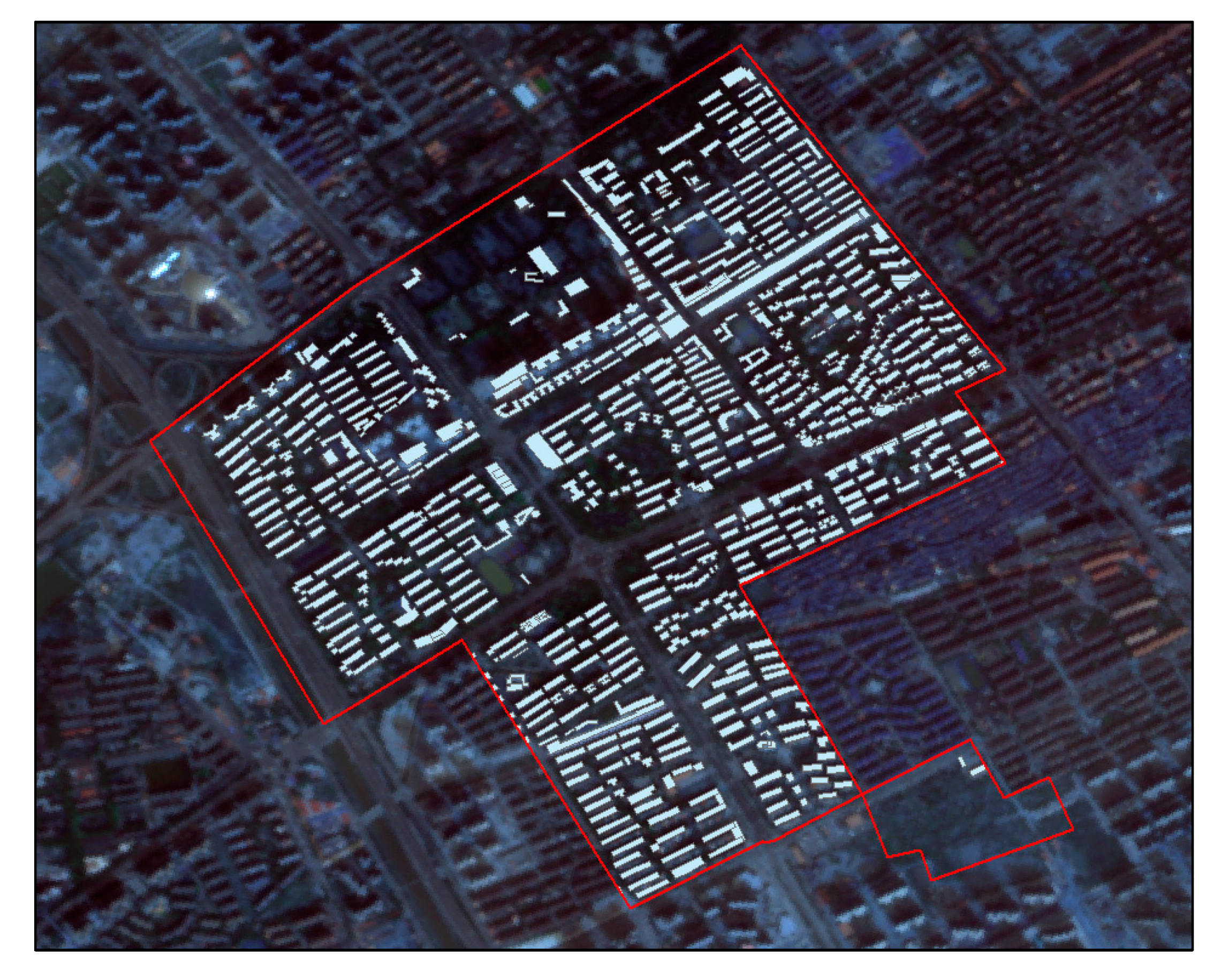
2.1.1. Study Area
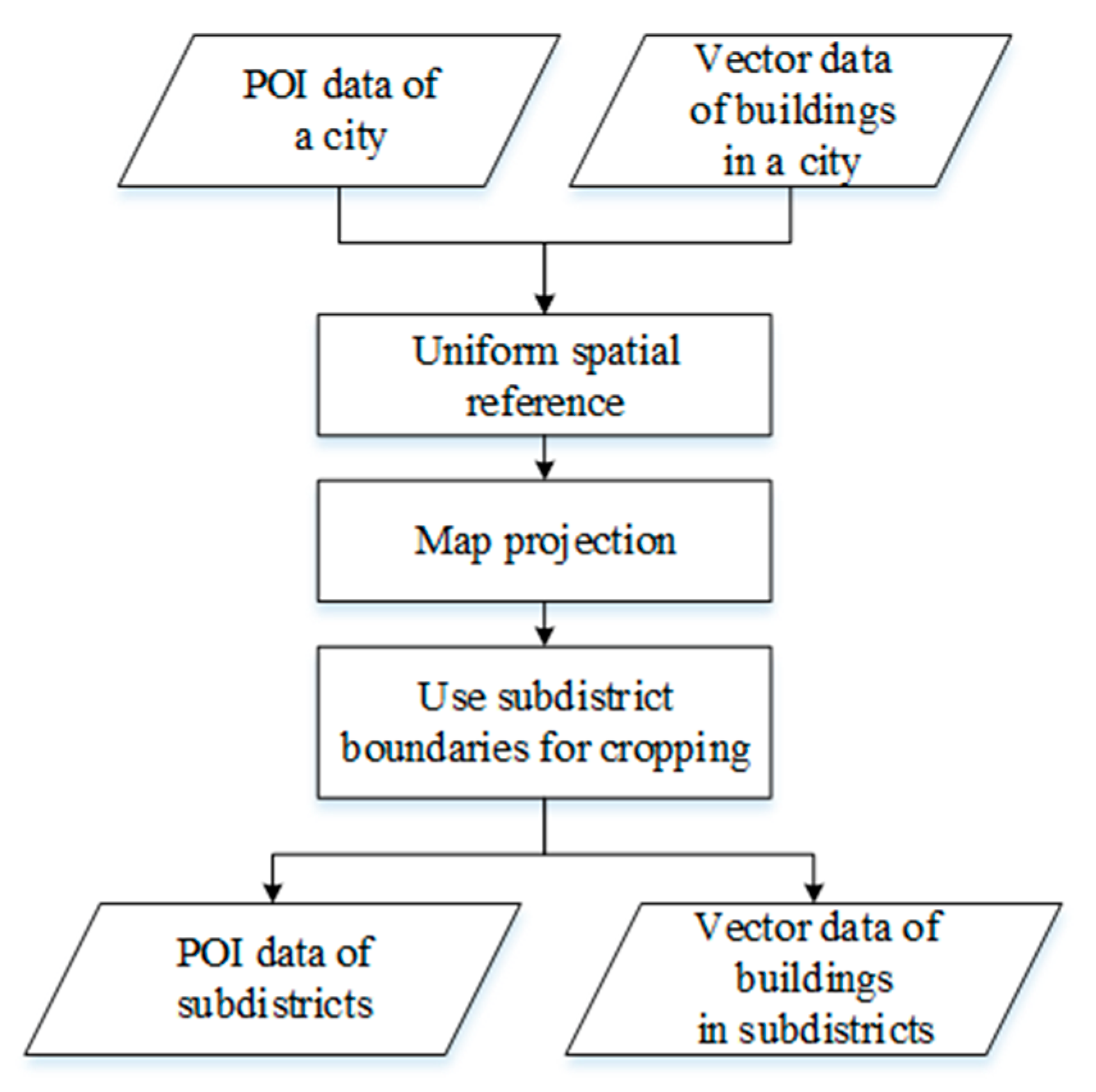
2.1.2. Data Source
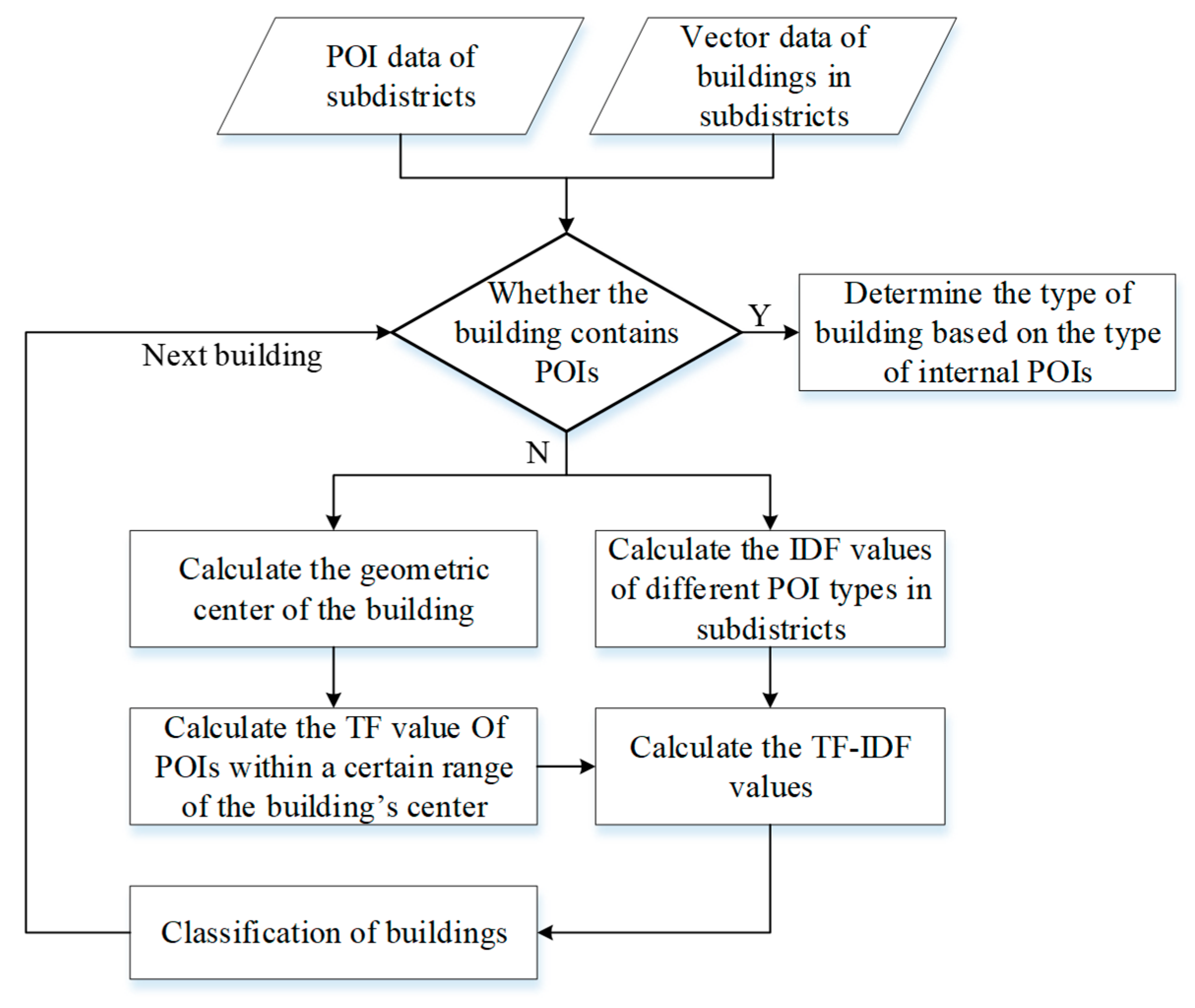
2.2. Classification of Urban Buildings
2.2.1. Geometric Relationships and Classification of Space
- (1)
- If a building is located in an area with only residential type POIs, the building is a residential building.
- (2)
- If a building is located in an area with both commercial service POIs and residential POIs, the building is a low-rise commercial building with residences above.
- (3)
- For buildings without POIs, the type is predicted with the TF-IDF method.
2.2.2. Classification of Buildings with the TF-IDF Method
2.3. Population Estimation at Fine-Scale
2.3.1. Classification of Buildings with the TF-IDF Method
2.3.2. Population Estimation Model
2.3.3. Model Estimation
3. Results and Discussions
3.1. Establishment of Population Estimation Model
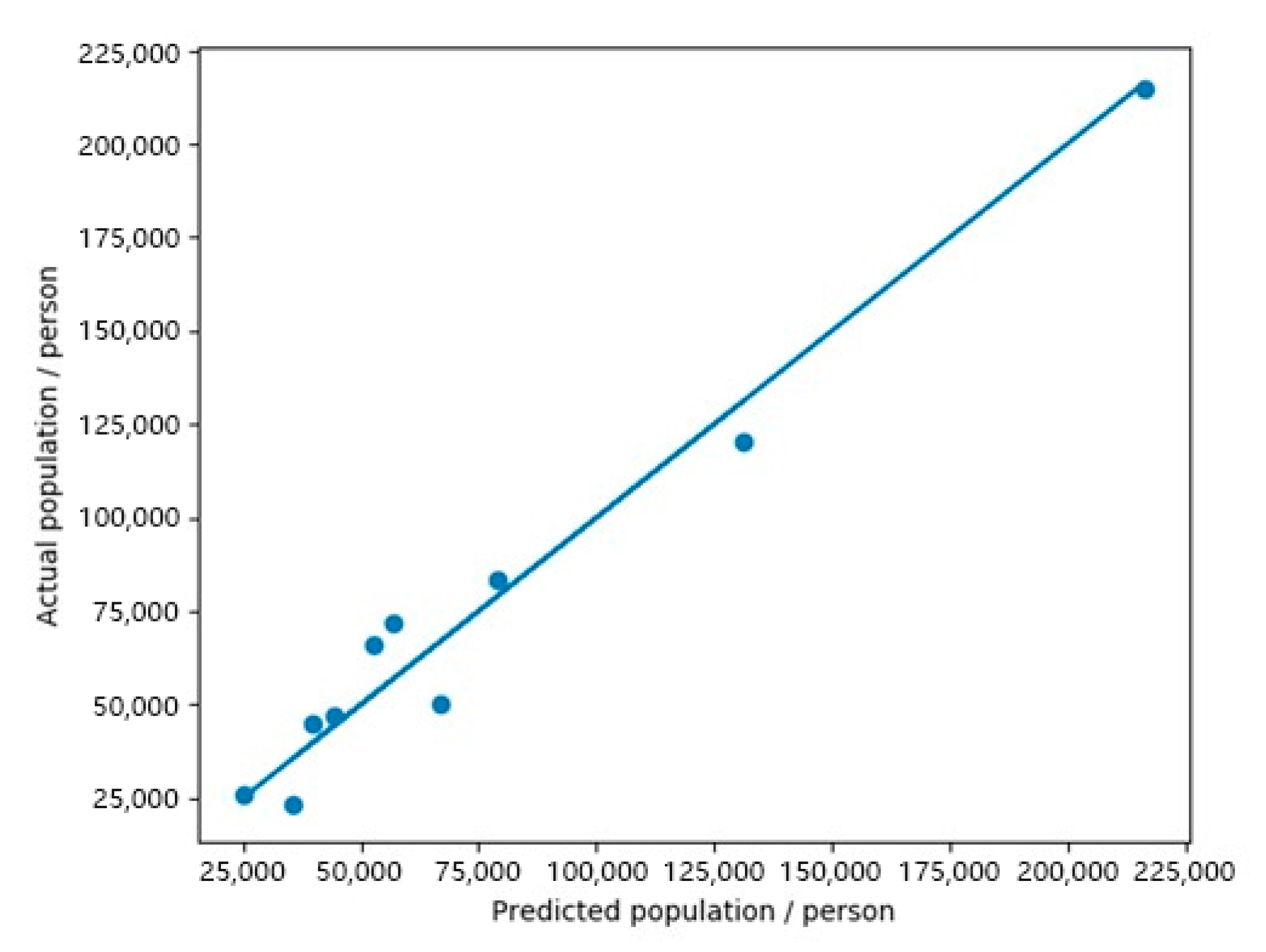
3.2. Evaluation of Model Estimation Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bai, C.; Lei, X. New trends in population aging and challenges for China’s sustainable development. China Econ. J. 2020, 13, 3–23. [Google Scholar] [CrossRef]
- Liu, X.; Clarke, K.; Herold, M. Population density and image texture. Photogramm. Eng. Remote Sens. 2006, 72, 187–196. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Tian, Y.; Zhou, Y.; Liu, W.; Lin, C. Fine-scale population estimation by 3D reconstruction of urban residential buildings. Sensors 2016, 16, 1755. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xie, J.; Zhou, J. Classification of urban building type from high spatial resolution remote sensing imagery using extended MRS and soft BP network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3515–3528. [Google Scholar] [CrossRef]
- Liao, S.B.; Li, Z.H. Relationship between Population Distribution and Land Use and Spatialization of Population Census Data. Resour. Environ. Yangtze Basin 2004, 13, 557–561. [Google Scholar]
- Jiang, D.; Yang, X.H.; Wang, N.B.; Liu, H.H. Study on Spatial Distribution of Population Based on Remote Sensing and GIS. Adv. Earth Sci. 2002, 17, 734–738. [Google Scholar]
- Picornell, M.; Ruiz, T.; Borge, R.; García-Albertos, P.; de la Paz, D.; Lumbreras, J. Population dynamics based on mobile phone data to improve air pollution exposure assessments. J. Expo. Sci. Environ. Epidemiol. 2019, 29, 278–291. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.L.; Singh, S. Video analysis of human dynamics—A survey. Real-Time Imaging 2003, 9, 321–346. [Google Scholar] [CrossRef]
- Tsou, M.H. Research challenges and opportunities in mapping social media and Big Data. Cartogr. Geogr. Inf. Sci. 2015, 42 (Suppl. 1), 70–74. [Google Scholar] [CrossRef]
- Qian, J.; Liu, Z.; Du, Y.; Wang, N.; Yi, J.; Sun, Y.; Zhou, C. Multi-Level Inter-Regional Migrant Population Estimation Using Multi-Source Spatiotemporal Big Data: A Case Study of Migrants in Hubei Province during the Outbreak of COVID-19 in Wuhan. In Mapping COVID-19 in Space and Time; Springer: Cham, Switzerlands, 2021; pp. 169–188. [Google Scholar]
- Leyk, S.; Gaughan, A.E.; Adamo, S.B.; de Sherbinin, A.; Balk, D.; Freire, S.; Rose, A.; Stevens, F.R.; Blankespoor, B.; Frye, C.; et al. The spatial allocation of population: A review of large-scale gridded population data products and their fitness for use. Earth Syst. Sci. Data 2019, 11, 1385–1409. [Google Scholar] [CrossRef] [Green Version]
- Wardrop, N.A.; Jochem, W.C.; Bird, T.J.; Chamberlain, H.R.; Clarke, D.; Kerr, D.; Bengtsson, L.; Juran, S.; Seaman, V.; Tatem, A.J. Spatially disaggregated population estimates in the absence of national population and housing census data. Proc. Natl. Acad. Sci. USA 2018, 115, 3529–3537. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yao, Y.; Liu, X.; Li, X.; Zhang, J.; Liang, Z.; Mai, K.; Zhang, Y. Mapping fine-scale population distributions at the building level by integrating multisource geospatial big data. Int. J. Geogr. Inf. Sci. 2017, 31, 1220–1244. [Google Scholar] [CrossRef]
- Patel, N.N.; Stevens, F.R.; Huang, Z.; Gaughan, A.E.; Elyazar, I.; Tatem, A.J. Improving large area population mapping using geotweet densities. Trans. GIS 2017, 21, 317–331. [Google Scholar] [CrossRef]
- Kontokosta, C.E.; Johnson, N. Urban phenology: Toward a real-time census of the city using Wi-Fi data. Comput. Environ. Urban Syst. 2017, 64, 144–153. [Google Scholar] [CrossRef]
- Chen, R.; Sharman, R.; Rao, H.R.; Upadhyaya, S.J. Coordination in emergency response management. Commun. ACM 2008, 51, 66–73. [Google Scholar] [CrossRef]
- Nara, A.; Yang, X.; Machiani, S.G.; Tsou, M.H. An integrated evacuation decision support system framework with social perception analysis and dynamic population estimation. Int. J. Disaster Risk Reduct. 2017, 25, 190–201. [Google Scholar] [CrossRef]
- Khodabandelou, G.; Gauthier, V.; Fiore, M.; El-Yacoubi, M.A. Estimation of static and dynamic urban populations with mobile network metadata. IEEE Trans. Mob. Comput. 2018, 18, 2034–2047. [Google Scholar] [CrossRef] [Green Version]
- Feng, T.T.; Gong, J.Y. Investigation on Small-area Population Estimation Based on Building Extraction. Remote Sens. Technol. Appl. 2010, 25, 323–327. [Google Scholar]
- Wang, Z.Y.; Pan, Y.Q.; Huangfu, G.Y.; Li, T.G.; Ge, L.L. A Summary of Population Prediction Methods in Urban Plan. Resour. Dev. Mark. 2009, 25, 237–240. [Google Scholar]
- Pan, Z.Q.; Liu, G.H. The Research Progress of Areal Interpolation. Prog. Geogr. 2002, 21, 152–156. [Google Scholar]
- Lian, T. Population Estimation at the Building Level Based on Random Forest and Nighttime Light Data. Master’s Thesis, East China Normal University, Shanghai, China, 2019. [Google Scholar]
- Jie, Y. Population Estimation of Different Administrative Scales Based on DMSP/OLS Lighting Data. Master’s Thesis, Southwest Jiaotong University, Sichuan, China, 2018. [Google Scholar]
- Cao, L.Q.; Li, P.X.; Zhang, L.P. Urban Population Estimation Based on the DMSP/OLS Night-time Satellite Data—A Case of Hubei Province. Remote Sens. Inf. 2009, 1, 83–87. [Google Scholar]
- Amaral, S.; Monteiro, A.M.; Câmara, G.; Quintanilha, J.A. DMSP/OLS night-time light imagery for urban population estimates in the Brazilian Amazon. Int. J. Remote Sens. 2006, 27, 855–870. [Google Scholar] [CrossRef]
- Tripathy, B.R.; Tiwari, V.; Pandey, V.; Elvidge, C.D.; Rawat, J.S.; Sharma, M.P.; Prawasi, R.; Kumar, P. Estimation of urban population dynamics using DMSP-OLS night-time lights time series sensors data. IEEE Sens. J. 2016, 17, 1013–1020. [Google Scholar] [CrossRef]
- Xiao, D.S.; Yang, S. A review of population spatial distribution based on nighttime light data. Remote Sens. Land Resour. 2019, 31, 10–19. [Google Scholar]
- Tomás, L.; Fonseca, L.; Almeida, C.; Leonardi, F.; Pereira, M. Urban population estimation based on residential buildings volume using IKONOS-2 images and lidar data. Int. J. Remote Sens. 2016, 37 (Suppl. 1), 1–28. [Google Scholar] [CrossRef] [Green Version]
- Feng, T.T. Urban Small Area Population Estimation Based on High-Resolution Remote Sensing Data. Ph.D. Thesis, Wuhan University, Wuhan, China, 2010. [Google Scholar]
- Feng, J. Urban Small Area Population Estimation Based on High-resolution Remote Sensing Data. Master’s Thesis, East China Normal University, Shanghai, China, 2012. [Google Scholar]
- Lu, Z.; Im, J.; Quackenbush, L.; Halligan, K. Population estimation based on multi-sensor data fusion. Int. J. Remote Sens. 2010, 31, 5587–5604. [Google Scholar] [CrossRef]
- Wu, S.S.; Wang, L.; Qiu, X. Incorporating GIS Building Data and Census Housing Statistics for Sub-Block-Level Population Estimation. Prof. Geogr. 2008, 60, 121–135. [Google Scholar] [CrossRef]
- Khoshelham, K.; Nardinocchi, C.; Frontoni, E.; Mancini, A.; Zingaretti, P. Performance evaluation of automated approaches to building detection in multi-source aerial data. ISPRS J. Photogramm. Remote Sens. 2010, 65, 123–133. [Google Scholar] [CrossRef] [Green Version]
- Qu, C.; Ren, Y.H.; Liu, Y.L.; Li, Y. Functional Classification of Urban Buildings in High Resolution Remote Sensing Images through POI-assisted Analysis. J. Geo-Inf. Sci. 2017, 19, 831–837. [Google Scholar]
- Dong, G.; Li, R.; Jiang, J.; Wu, H.; McClure, S.C. Multigranular Wavelet Decomposition-Based Support Vector Regression and Moving Average Method for Service-Time Prediction on Web Map Service Platforms. IEEE Syst. J. 2019, 14, 3653–3664. [Google Scholar] [CrossRef]
- Lu, D.; Wang, Y.; Yang, Q.; Su, K.; Zhang, H.; Li, Y. Modeling spatiotemporal population changes by integrating DMSP-OLS and NPP-VIIRS nighttime light data in Chongqing, China. Remote Sens. 2021, 13, 284. [Google Scholar] [CrossRef]
- Dong, C.; Yin, S.; Zhang, Y. A model of urban fine-scale population estimation based on multi-agent. Sci. Surv. Mapp. 2019, 44, 113–119. [Google Scholar]


| Classification | Reclassification |
|---|---|
| automobile service, automobile sales, automobile maintenance, motorcycle service, catering service, shopping service, life service, sports and leisure service, accommodation service, corporate enterprise, financial and insurance service, business residence: industrial park, business residence: building, business residence: business residence related | commercial service |
| medical and health care services, scenic spots, government institutions and social organizations, scientific, educational and cultural services, transportation facilities, road ancillary facilities, public facilities | public service |
| business residence: residential area, place name and address information: door number information | residential building |
| Variable Name | Importance |
|---|---|
| HighbuildingNum | 0.231080 |
| BuildingAreacovered | 0.160503 |
| MidbuildingArea | 0.158064 |
| MidbuildingNum | 0.156951 |
| HighbuildingArea | 0.144724 |
| LowbuildingNum | 0.100244 |
| LowbuildingArea | 0.048434 |
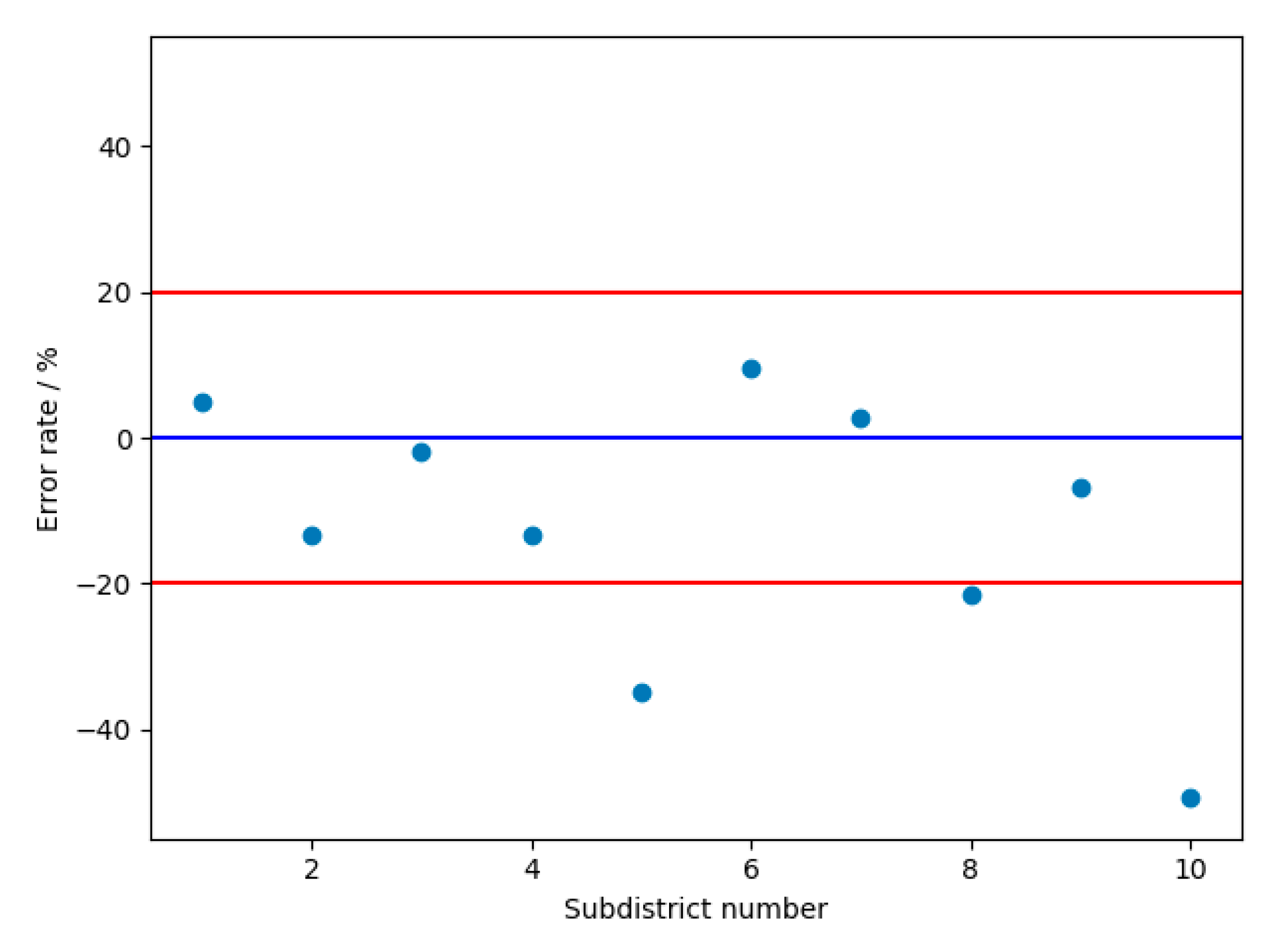
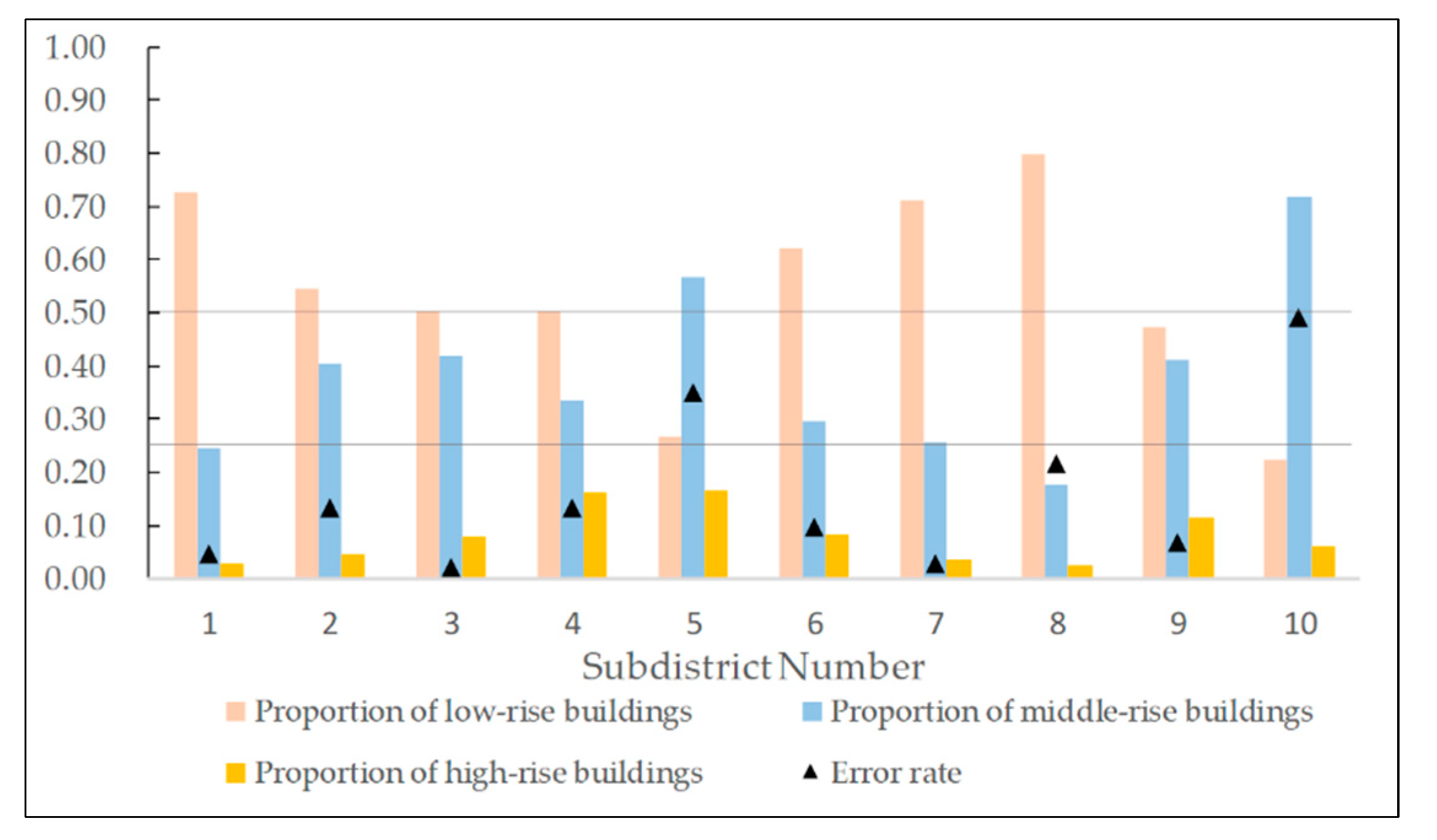
| Subdistrict Name | Actual Population | Predicted Population | Estimation Error | Error Rate |
|---|---|---|---|---|
| Liangdao Subdistrict | 64,704 | 67,818 | 3114 | 4.81% |
| Cuiwei Subdistrict | 44,529 | 38,604 | 5925 | −13.31% |
| Luonan Subdistrict | 230,583 | 225,938 | 4645 | −2.01% |
| Shuita Subdistrict | 19,426 | 16,859 | 2567 | −13.21% |
| Dazhi Subdistrict | 35,087 | 22,799 | 12,288 | −35.02% |
| Erqi Subdistrict | 81,312 | 89,207 | 7894 | 9.71% |
| Huanghelou Subdistrict | 60,909 | 62,573 | 1664 | 2.73% |
| Minquan Subdistrict | 36,387 | 28,539 | 7848 | −21.57% |
| Siwei Subdistrict | 32,234 | 30,054 | 2180 | −6.76% |
| Ganghuacun Subdistrict | 77,222 | 39,195 | 38,027 | −49.24% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Li, R.; Jiang, J.; Meng, Y. Fine-Scale Population Estimation Based on Building Classifications: A Case Study in Wuhan. Future Internet 2021, 13, 251. https://doi.org/10.3390/fi13100251
Wang S, Li R, Jiang J, Meng Y. Fine-Scale Population Estimation Based on Building Classifications: A Case Study in Wuhan. Future Internet. 2021; 13(10):251. https://doi.org/10.3390/fi13100251
Chicago/Turabian StyleWang, Shunli, Rui Li, Jie Jiang, and Yao Meng. 2021. "Fine-Scale Population Estimation Based on Building Classifications: A Case Study in Wuhan" Future Internet 13, no. 10: 251. https://doi.org/10.3390/fi13100251
APA StyleWang, S., Li, R., Jiang, J., & Meng, Y. (2021). Fine-Scale Population Estimation Based on Building Classifications: A Case Study in Wuhan. Future Internet, 13(10), 251. https://doi.org/10.3390/fi13100251







