Exploring Time-Series Forecasting Models for Dynamic Pricing in Digital Signage Advertising
Abstract
:1. Introduction
- -
- To review the widely used time-series forecasting models, providing an abstract of the different models that can potentially be applied for dynamic pricing.
- -
- To discuss the relationship of data characteristics to the time-series forecasting models from each category.
- -
- To investigate the applicability of the model selection framework based on the data characteristics of the dataset in DSA.
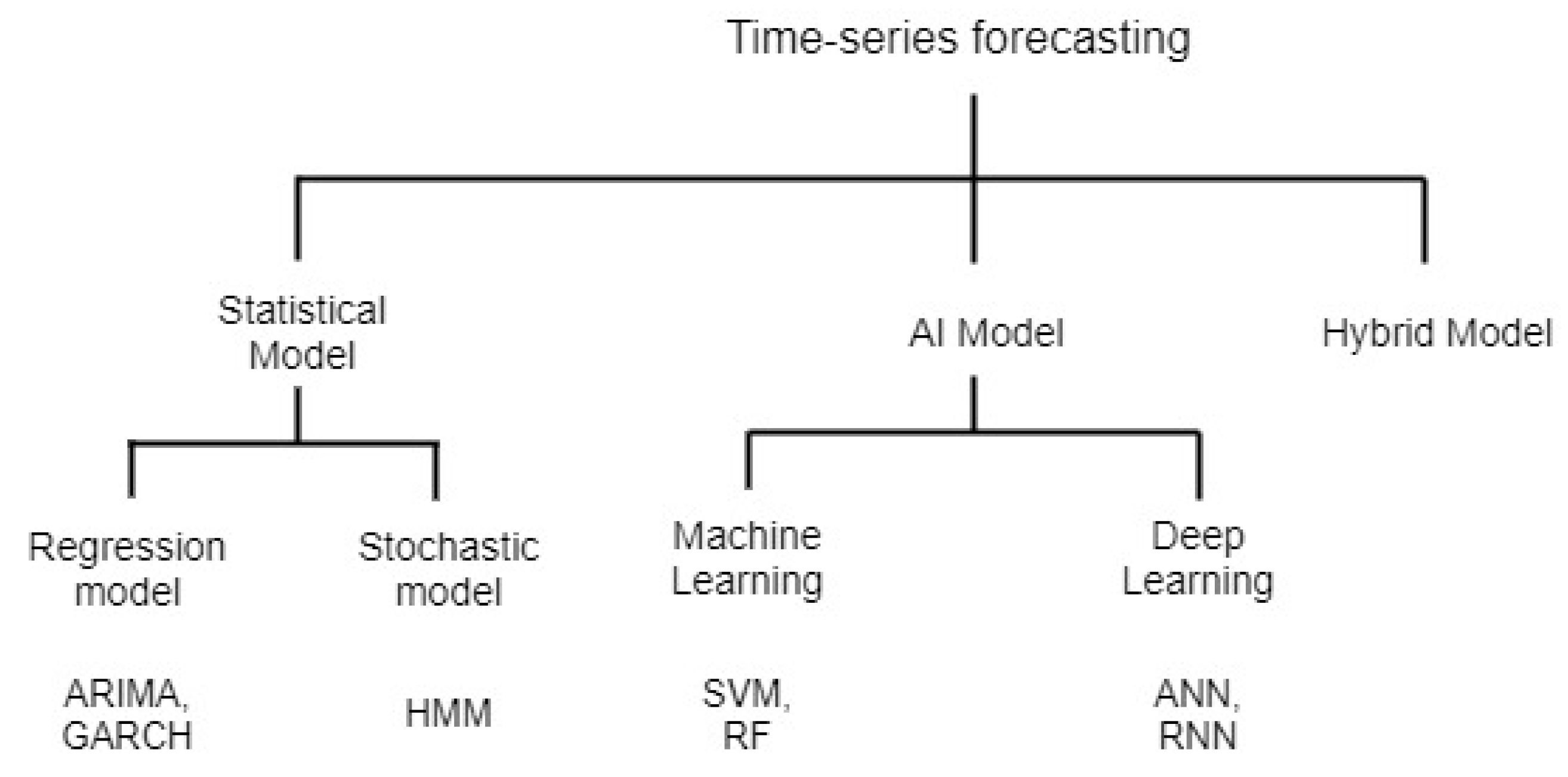
2. Review on Time-Series Forecasting Studies
2.1. Statistical Model
2.1.1. Regression Model
Autoregressive Integrated Moving Average (ARIMA)
Generalized Autoregressive Conditional Heteroscedasticity (GARCH)
2.1.2. Stochastic Model
Hidden Markov Model (HMM)
2.2. Artificial Intelligence Model (AI)
2.2.1. Machine Learning Model (ML)
Support Vector Machine (SVM)
Random Forest (RF)
2.2.2. Deep Learning Model
Artificial Neural Network (ANN)
Recurrent Neural Network (RNN)
2.3. Hybrid Model
3. Discussion
3.1. Summary of Suitable Data Characteristics for the Included Models
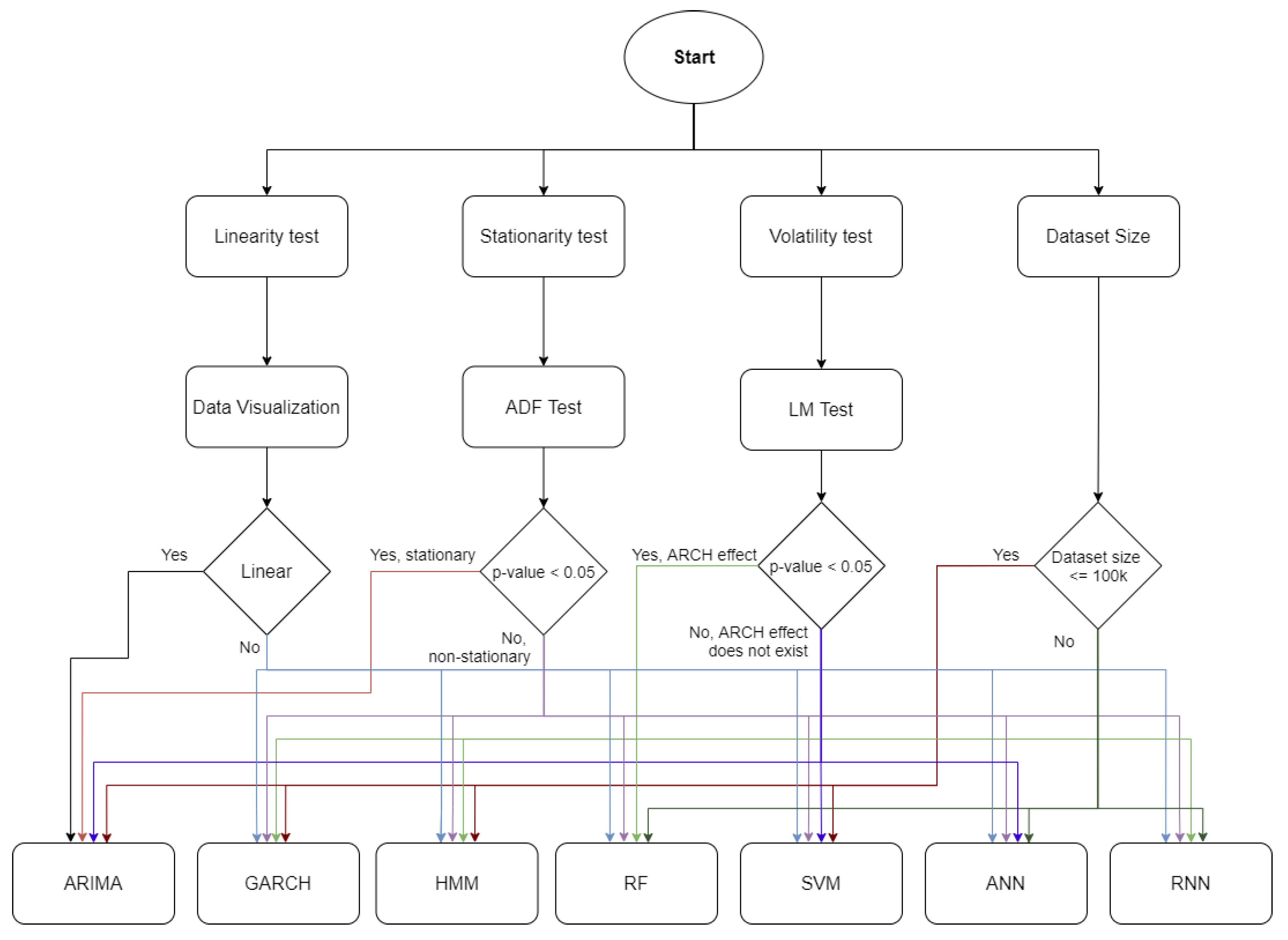
3.2. DSA Data Analysis and Proposed Framework for Optimal Model Selection
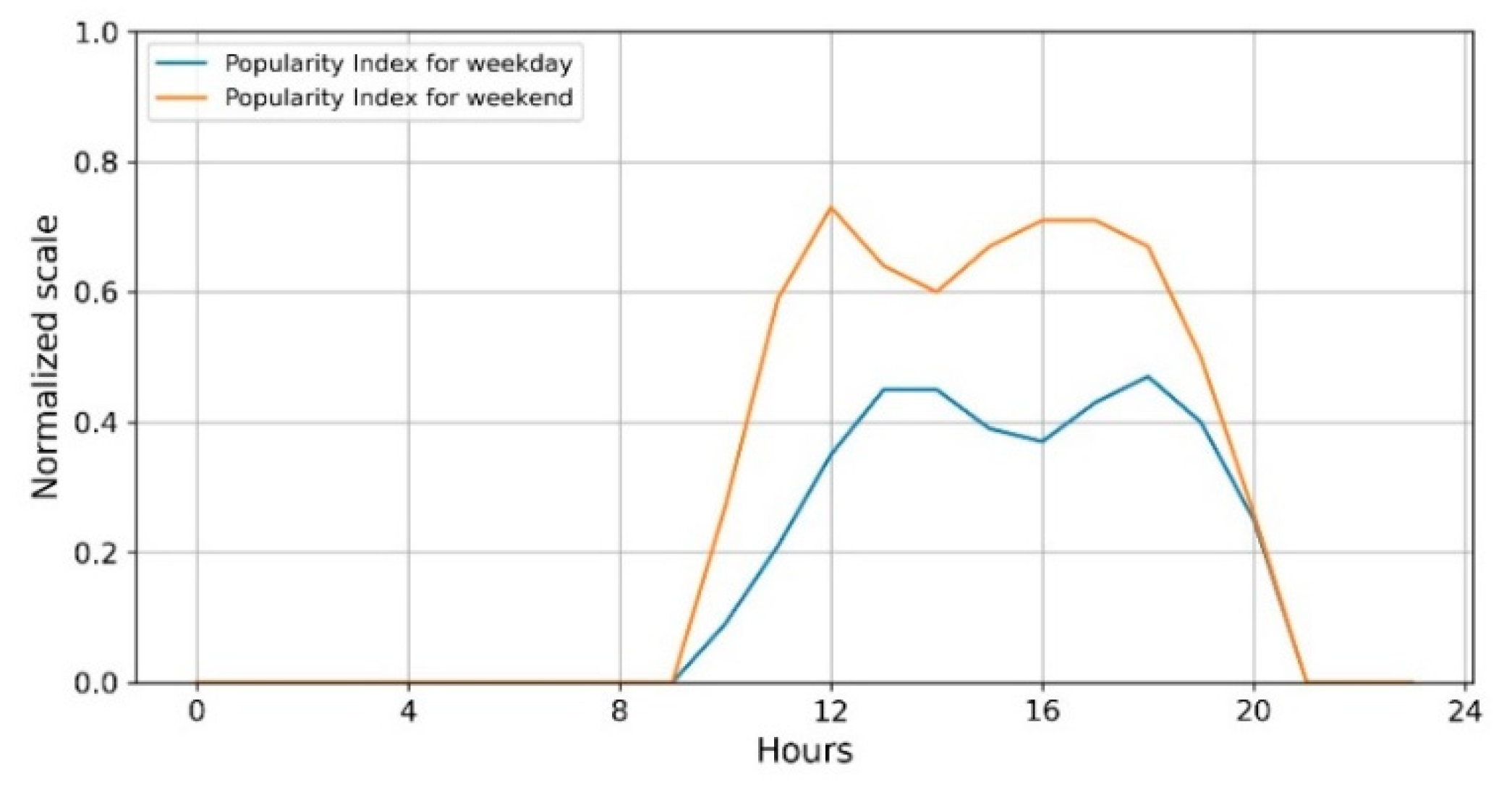
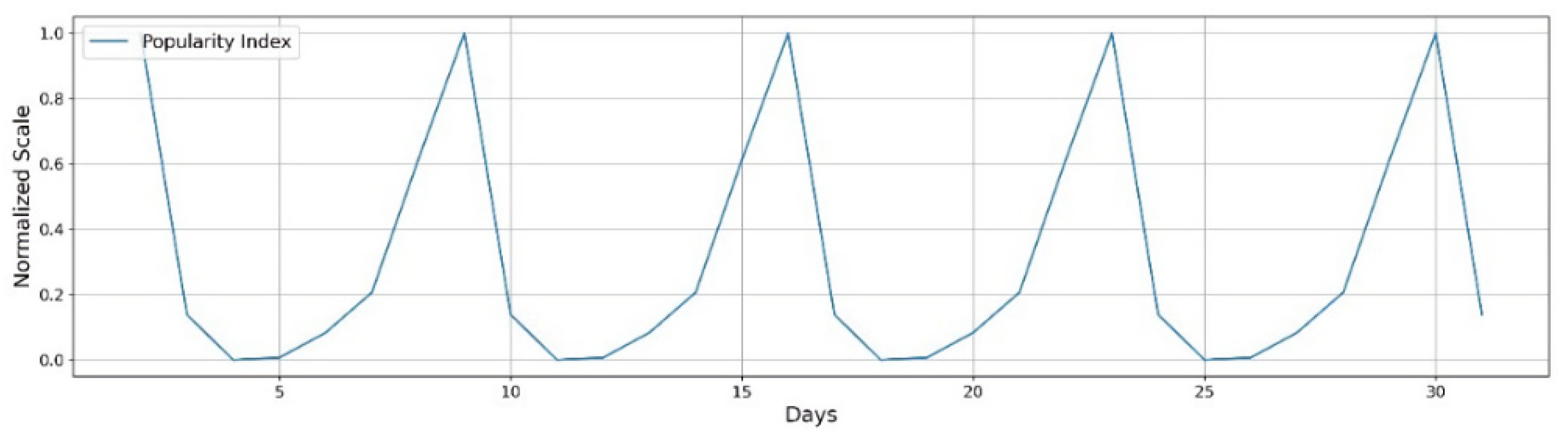
3.2.1. Location
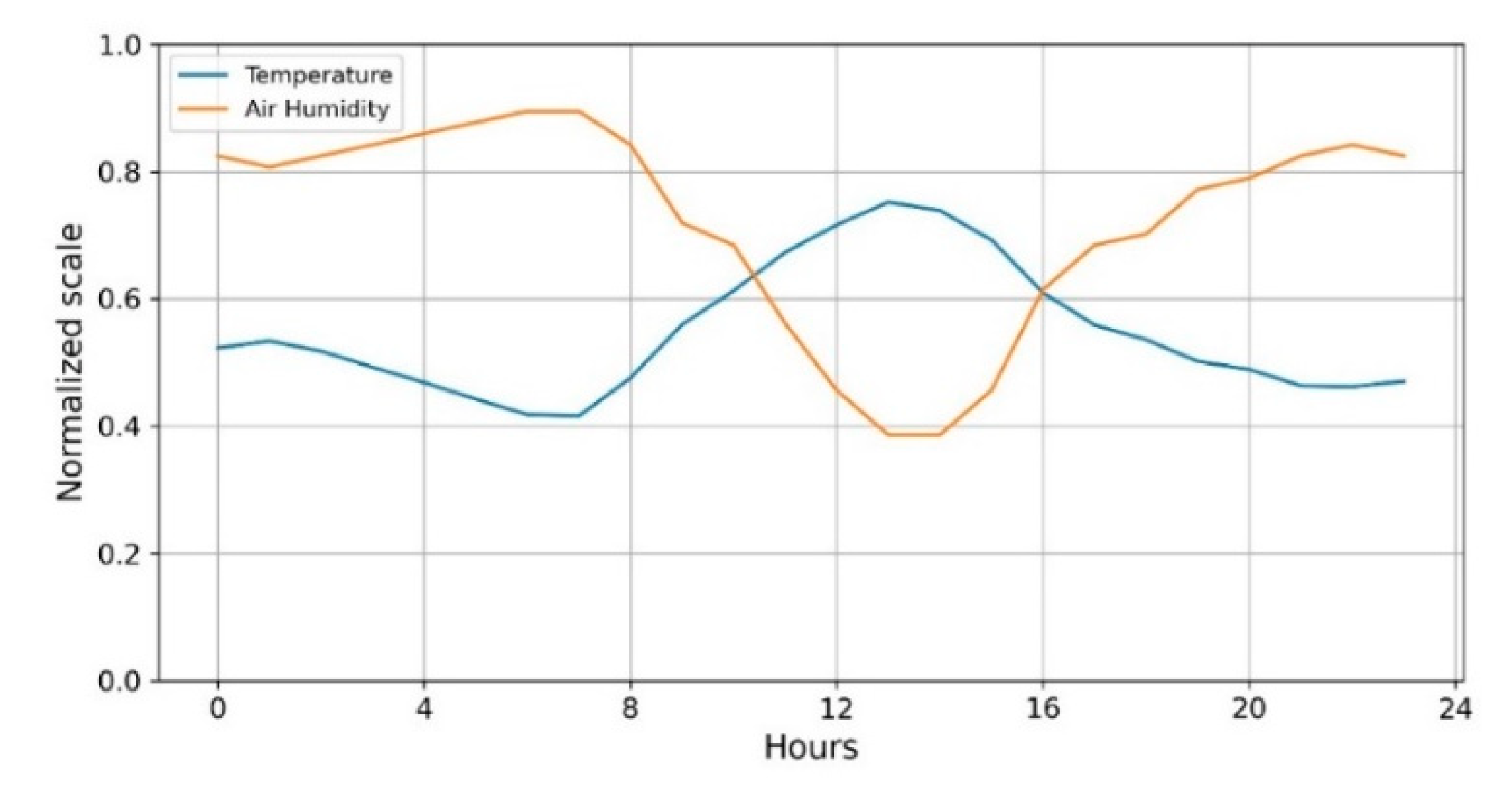
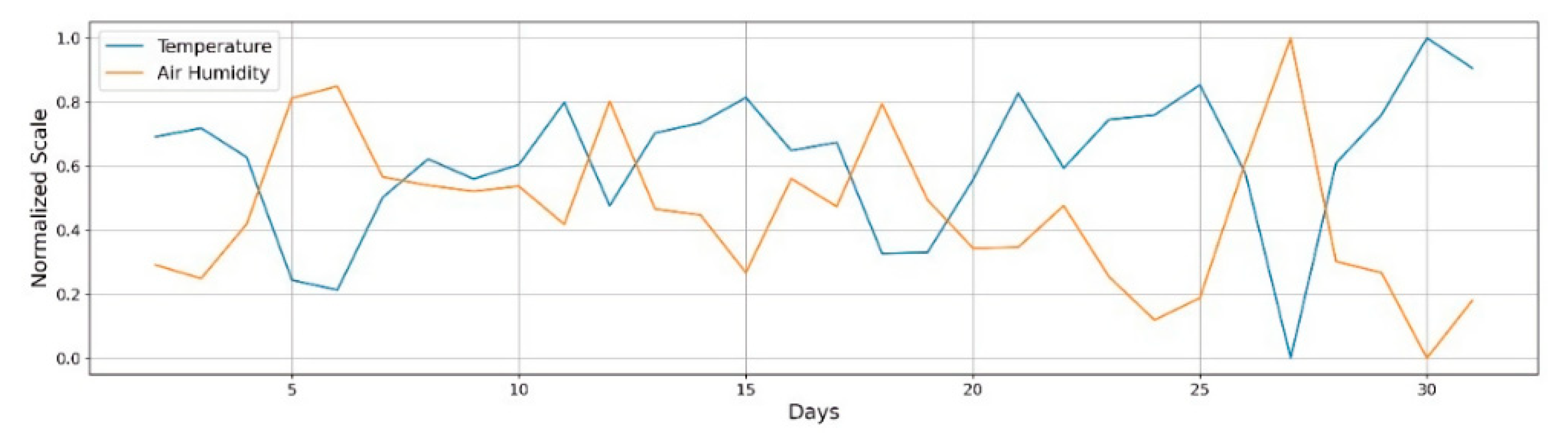
3.2.2. Weather and Temperature
4. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bauer, C.; Dohmen, P.; Strauss, C. A conceptual framework for backend services of contextual digital signage. J. Serv. Sci. Res. 2012, 4, 271–297. [Google Scholar] [CrossRef]
- O’Driscoll, C. Real-Time, Targeted, Out-Of-Home Advertising with Dynamic Pricing. Trinity College Dublin. 2019. Available online: https://www.scss.tcd.ie/publications/theses/diss/2019/TCD-SCSS-DISSERTATION-2019-012.pdf (accessed on 12 September 2021).
- Choi, H.; Mela, C.; Balseiro, S.; Leary, A. Online Display Advertising Markets: A Literature Review and Future Directions. Inf. Syst. Res. 2020, 31, 556–575. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, C. Dynamic pricing strategy and coordination in a dual-channel supply chain considering service value. Appl. Math. Model. 2018, 54, 722–742. [Google Scholar] [CrossRef]
- Athiyarath, S.; Paul, M.; Krishnaswamy, S. A Comparative Study and Analysis of Time Series Forecasting Techniques. SN Comput. Sci. 2020, 1, 175. [Google Scholar] [CrossRef]
- Wang, D.; Luo, H.; Grunder, O.; Lin, Y.; Guo, H. Multi-step ahead electricity price forecasting using a hybrid model based on two-layer decomposition technique and BP neural network optimized by firefly algorithm. Appl. Energy 2017, 190, 390–407. [Google Scholar] [CrossRef]
- Sehgal, N.; Pandey, K.K. Artificial intelligence methods for oil price forecasting: A review and evaluation. Energy Syst. 2015, 6, 479–506. [Google Scholar] [CrossRef]
- Gao, W.; Aamir, M.; Shabri, A.B.; Dewan, R.; Aslam, A. Forecasting Crude Oil Price Using Kalman Filter Based on the Reconstruction of Modes of Decomposition Ensemble Model. IEEE Access 2019, 7, 149908–149925. [Google Scholar] [CrossRef]
- Mahalakshmi, G.; Sridevi, S.; Rajaram, S. A survey on forecasting of time series data. In Proceedings of the 2016 International Conference on Computing Technologies and Intelligent Data Engineering (ICCTIDE’16), Kovilpatti, India, 7–9 January 2016; pp. 1–8. [Google Scholar]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Hyndman, R.J. Forecasting: Principles and Practice, 2nd ed.; OTexts: Melbourne, Australia, 2018. [Google Scholar]
- Lama, A.; Jha, G.K.; Paul, R.K.; Gurung, B. Modelling and Forecasting of Price Volatility: An Application of GARCH and EGARCH Models. Agric. Econ. Res. Rev. 2015, 28, 73. [Google Scholar] [CrossRef]
- Mittal, R.; Gehi, R.; Bhatia, M.P.S. Forecasting the Price of Cryptocurrencies and Validating Using Arima. Int. J. Inf. Syst. Manag. Sci. 2018, 1, 5. [Google Scholar]
- Ariyo, A.A.; Adewumi, A.O.; Ayo, C.K. Stock Price Prediction Using the ARIMA Model. In Proceedings of the 2014 UKSim-AMSS 16th International Conference on Computer Modelling and Simulation, Cambridge, UK, 26–28 March 2014; IEEE: Washington, DC, USA, 2014; pp. 106–112. [Google Scholar]
- Rotela Junior, P.; Salomon, F.L.R.; de Oliveira Pamplona, E. ARIMA: An Applied Time Series Forecasting Model for the Bovespa Stock Index. Appl. Math. 2014, 5, 3383–3391. [Google Scholar] [CrossRef] [Green Version]
- Wahyudi, S.T. The ARIMA Model for the Indonesia Stock Price. Int. J. Econ. Manag. 2017, 11, 223–236. [Google Scholar]
- Cherdchoongam, S.; Rungreunganun, V. Forecasting the Price of Natural Rubber in Thailand Using the ARIMA Model. King Mongkut’s Univ. Technol. North. Bangk. Int. J. Appl. Sci. Technol. 2016, 7. [Google Scholar] [CrossRef]
- Udomraksasakul, C.; Rungreunganun, V. Forecasting the Price of Field Latex in the Area of Southeast Coast of Thailand Using the ARIMA Model. Int. J. Appl. Eng. Res. 2018, 13, 550–556. [Google Scholar]
- Verma, V.K.; Kumar, P. Use of ARIMA modeling in forecasting coriander prices for Rajasthan. Int. J. Seed Spices 2016, 6, 42–45. [Google Scholar]
- Jadhav, V.; Reddy, B.V.C.; Gaddi, G.M. Application of ARIMA Model for Forecasting Agricultural Prices. J. Agric. Sci. Technol. 2017, 19, 981–992. [Google Scholar]
- KumarMahto, A.; Biswas, R.; Alam, M.A. Short Term Forecasting of Agriculture Commodity Price by Using ARIMA: Based on Indian Market. In Advances in Computing and Data Sciences; Singh, M., Gupta, P.K., Tyagi, V., Flusser, J., Ören, T., Kashyap, R., Eds.; Communications in Computer and Information Science; Springer: Singapore, 2019; Volume 1045, pp. 452–461. ISBN 9789811399381. [Google Scholar]
- Bandyopadhyay, G. Gold Price Forecasting Using ARIMA Model. J. Adv. Manag. Sci. 2016, 4, 117–121. [Google Scholar] [CrossRef]
- Yang, X. The Prediction of Gold Price Using ARIMA Model. In Proceedings of the 2nd International Conference on Social Science, Public Health and Education (SSPHE 2018), Sanya, China, 28–27 November 2018; Atlantis Press: Sanya, China, 2019. [Google Scholar]
- Contreras, J.; Espinola, R.; Nogales, F.J.; Conejo, A.J. ARIMA models to predict next-day electricity prices. IEEE Trans. Power Syst. 2003, 18, 1014–1020. [Google Scholar] [CrossRef]
- Zhou, M.; Yan, Z.; Ni, Y.; Li, G. An ARIMA approach to forecasting electricity price with accuracy improvement by predicted errors. In Proceedings of the IEEE Power Engineering Society General Meeting, Denver, CO, USA, 6–10 June 2004; Volume 2, pp. 233–238. [Google Scholar]
- Jakasa, T.; Androcec, I.; Sprcic, P. Electricity price forecasting—ARIMA model approach. In Proceedings of the 2011 8th International Conference on the European Energy Market (EEM), Zagreb, Croatia, 25–27 May 2011; pp. 222–225. [Google Scholar]
- Carta, S.; Medda, A.; Pili, A.; Reforgiato Recupero, D.; Saia, R. Forecasting E-Commerce Products Prices by Combining an Autoregressive Integrated Moving Average (ARIMA) Model and Google Trends Data. Future Internet 2018, 11, 5. [Google Scholar] [CrossRef] [Green Version]
- Ping, P.Y.; Miswan, N.H.; Ahmad, M.H. Forecasting Malaysian gold using GARCH model. Appl. Math. Sci. 2013, 7, 2879–2884. [Google Scholar] [CrossRef]
- Yaziz, S.R.; Zakaria, R. Suhartono ARIMA and Symmetric GARCH-type Models in Forecasting Malaysia Gold Price. J. Phys. Conf. Ser. 2019, 1366, 012126. [Google Scholar] [CrossRef]
- Xing, D.-Z.; Li, H.-F.; Li, J.-C.; Long, C. Forecasting price of financial market crash via a new nonlinear potential GARCH model. Phys. Stat. Mech. Appl. 2021, 566, 125649. [Google Scholar] [CrossRef]
- Tripathy, S.; Rahman, A. Forecasting Daily Stock Volatility Using GARCH Model: A Comparison Between BSE and SSE. IUP J. Appl. Financ. 2013, 19, 71–83. [Google Scholar]
- Virginia, E.; Ginting, J.; Elfaki, F.A.M. Application of GARCH Model to Forecast Data and Volatility of Share Price of Energy (Study on Adaro Energy Tbk, LQ45). Int. J. Energy Econ. Policy 2018, 8, 131–140. [Google Scholar]
- Li, H.; Xiong, H.; Li, W.; Sun, Y.; Xu, G. A power price forecasting method based on nonparametric GARCH model. In Proceedings of the 2008 Third International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, Nanjing, China, 6–9 April 2008; pp. 285–290. [Google Scholar]
- Bhardwaj, S.P.; Paul, R.K.; Singh, D.R.; Singh, K.N. An Empirical Investigation of Arima and Garch Models in Agricultural Price Forecasting. Econ. Aff. 2014, 59, 415. [Google Scholar] [CrossRef]
- Garcia, R.C.; Contreras, J.; vanAkkeren, M.; Garcia, J.B.C. A GARCH Forecasting Model to Predict Day-Ahead Electricity Prices. IEEE Trans. Power Syst. 2005, 20, 867–874. [Google Scholar] [CrossRef]
- Hassan, M.R.; Nath, B. Stock market forecasting using hidden Markov model: A new approach. In Proceedings of the 5th International Conference on Intelligent Systems Design and Applications (ISDA’05), Warsaw, Poland, 8–10 September 2005; pp. 192–196. [Google Scholar]
- Hassan, M.R. A combination of hidden Markov model and fuzzy model for stock market forecasting. Neurocomputing 2009, 72, 3439–3446. [Google Scholar] [CrossRef]
- Dimoulkas, I.; Amelin, M.; Hesamzadeh, M.R. Forecasting balancing market prices using Hidden Markov Models. In Proceedings of the 2016 13th International Conference on the European Energy Market (EEM), Porto, Portugal, 6–9 June 2016; pp. 1–5. [Google Scholar]
- Date, P.; Mamon, R.; Tenyakov, A. Filtering and forecasting commodity futures prices under an HMM framework. Energy Econ. 2013, 40, 1001–1013. [Google Scholar] [CrossRef] [Green Version]
- Valizadeh Haghi, H.; Tafresh, S.M.M. An Overview and Verification of Electiricity Price Forecasting Models. In Proceedings of the 2007 International Power Engineering Conference (IPEC 2007), Singapore, 3–6 December 2007. [Google Scholar]
- Zhang, J.; Wang, J.; Wang, R.; Hou, G. Forecasting next-day electricity prices with Hidden Markov Models. In Proceedings of the 2010 5th IEEE Conference on Industrial Electronics and Applications, Taichung, Taiwan, 15–17 June 2010; pp. 1736–1740. [Google Scholar]
- Bon, A.T.; Isah, N. Hidden Markov Model and Forward-Backward Algorithm in Crude Oil Price Forecasting. IOP Conf. Ser. Mater. Sci. Eng. 2016, 160, 012067. [Google Scholar] [CrossRef] [Green Version]
- Shaaib, A.R. Comparative Study of Artificial Neural Networks and Hidden Markov Model for Financial Time Series Prediction. Int. J. Eng. Inf. Technol. 2015, 1, 7. [Google Scholar]
- Xie, W.; Yu, L.; Xu, S.; Wang, S. A New Method for Crude Oil Price Forecasting Based on Support Vector Machines. In Computational Science—ICCS 2006; Alexandrov, V.N., van Albada, G.D., Sloot, P.M.A., Dongarra, J., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006; Volume 3994, pp. 444–451. ISBN 978-3-540-34385-1. [Google Scholar]
- Qi, Y.-L.; Zhang, W.-J. The Improved SVM Method for Forecasting the Fluctuation of International Crude Oil Price. In Proceedings of the Electronic Commerce and Business Intelligence International Conference, Beijing, China, 6–7 June 2009. [Google Scholar]
- Khashman, A.; Nwulu, N.I. Support Vector Machines versus Back Propagation Algorithm for Oil Price Prediction. In Advances in Neural Networks—ISNN 2011; Liu, D., Zhang, H., Polycarpou, M., Alippi, C., He, H., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6677, pp. 530–538. ISBN 978-3-642-21110-2. [Google Scholar]
- Yu, L.; Zhang, X.; Wang, S. Assessing Potentiality of Support Vector Machine Method in Crude Oil Price Forecasting. EURASIA J. Math. Sci. Technol. Educ. 2017, 13, 7893–7904. [Google Scholar] [CrossRef]
- Jing Jong, L.; Ismail, S.; Mustapha, A.; Helmy Abd Wahab, M.; Zulkarnain Syed Idrus, S. The Combination of Autoregressive Integrated Moving Average (ARIMA) and Support Vector Machines (SVM) for Daily Rubber Price Forecasting. IOP Conf. Ser. Mater. Sci. Eng. 2020, 917, 012044. [Google Scholar] [CrossRef]
- Makala, D.; Li, Z. Prediction of gold price with ARIMA and SVM. J. Phys. Conf. Ser. 2021, 1767, 012022. [Google Scholar] [CrossRef]
- Swief, R.A.; Hegazy, Y.G.; Abdel-Salam, T.S.; Bader, M.A. Support vector machines (SVM) based short term electricity load-price forecasting. In Proceedings of the 2009 IEEE Bucharest PowerTech, Bucharest, Romania, 28 June–2 July 2009; pp. 1–5. [Google Scholar]
- Mohamed, A.; El-Hawary, M.E. Mid-term electricity price forecasting using SVM. In Proceedings of the 2016 IEEE Canadian Conference on Electrical and Computer Engineering (CCECE), Vancouver, BC, Canada, 15–18 May 2016. [Google Scholar]
- Saini, D.; Saxena, A.; Bansal, R.C. Electricity price forecasting by linear regression and SVM. In Proceedings of the 2016 International Conference on Recent Advances and Innovations in Engineering (ICRAIE), Jaipur, India, 23–25 December 2016; pp. 1–7. [Google Scholar]
- Ma, Z.; Zhong, H.; Xie, L.; Xia, Q.; Kang, C. Month ahead average daily electricity price profile forecasting based on a hybrid nonlinear regression and SVM model: An ERCOT case study. J. Mod. Power Syst. Clean Energy 2018, 6, 281–291. [Google Scholar] [CrossRef]
- Akın, B.; Dizbay, İ.E.; Gümüşoğlu, Ş.; Güdücü, E. Forecasting the Direction of Agricultural Commodity Price Index through ANN, SVM and Decision Tree: Evidence from Raisin. Ege Acad. Rev. 2018, 18, 579–588. [Google Scholar]
- Kumar, M. Forecasting Stock Index Movement: A Comparision of Support Vector Machines and Random Forest. Available online: https://ssrn.com/abstract=876544 (accessed on 1 July 2021).
- Lahouar, A. Day-ahead load forecast using random forest and expert input selection. Energy Convers. Manag. 2015, 103, 1040–1051. [Google Scholar] [CrossRef]
- Mei, J.; He, D.; Harley, R.; Habetler, T.; Qu, G. A random forest method for real-time price forecasting in New York electricity market. In Proceedings of the 2014 IEEE PES General Meeting|Conference & Exposition, National Harbor, MD, USA, 27–31 July 2014; pp. 1–5. [Google Scholar]
- Sharma, G.; Tripathi, V.; Mahajan, M.; Kumar Srivastava, A. Comparative Analysis of Supervised Models for Diamond Price Prediction. In Proceedings of the 2021 11th International Conference on Cloud Computing, Data Science & Engineering (Confluence), Noida, India, 28–29 January 2021; pp. 1019–1022. [Google Scholar]
- Ramakrishnan, S.; Butt, S.; Chohan, M.A.; Ahmad, H. Forecasting Malaysian exchange rate using machine learning techniques based on commodities prices. In Proceedings of the 2017 International Conference on Research and Innovation in Information Systems (ICRIIS), Langkawi, Malaysia, 16–17 July 2017; pp. 1–5. [Google Scholar]
- Liu, D.; Li, Z. Gold Price Forecasting and Related Influence Factors Analysis Based on Random Forest. In Proceedings of the Tenth International Conference on Management Science and Engineering Management; Xu, J., Hajiyev, A., Nickel, S., Gen, M., Eds.; Advances in Intelligent Systems and Computing; Springer: Singapore, 2017; Volume 502, pp. 711–723. ISBN 978-981-10-1836-7. [Google Scholar]
- Khaidem, L.; Saha, S.; Dey, S.R. Predicting the direction of stock market prices using random forest. arXiv 2016, arXiv:1605.00003. [Google Scholar]
- Jha, G.K.; Sinha, K. Agricultural Price Forecasting Using Neural Network Model: An Innovative Information Delivery System. Agric. Econ. Res. 2013, 26, 229–239. [Google Scholar]
- Yamin, H.; Shahidehpour, S.; Li, Z. Adaptive short-term electricity price forecasting using artificial neural networks in the restructured power markets. Int. J. Electr. Power Energy Syst. 2004, 26, 571–581. [Google Scholar] [CrossRef]
- Ozozen, A.; Kayakutlu, G.; Ketterer, M.; Kayalica, O. A combined seasonal ARIMA and ANN model for improved results in electricity spot price forecasting: Case study in Turkey. In Proceedings of the 2016 Portland International Conference on Management of Engineering and Technology (PICMET), Honolulu, HI, USA, 4–8 September 2016; pp. 2681–2690. [Google Scholar]
- Ranjbar, M.; Soleymani, S.; Sadati, N.; Ranjbar, A.M. Electricity Price Forecasting Using Artificial Neural Network. Int. J. Electr. Power Energy Syst. 2011, 33, 550–555. [Google Scholar]
- Sahay, K.B.; Singh, K. Short-Term Price Forecasting by Using ANN Algorithms. In Proceedings of the 2018 International Electrical Engineering Congress (iEECON), Krabi, Thailand, 7–9 March 2018. [Google Scholar]
- Verma, S.; Thampi, G.T.; Rao, M. ANN based method for improving gold price forecasting accuracy through modified gradient descent methods. IAES Int. J. Artif. Intell. IJ-AI 2020, 9, 46. [Google Scholar] [CrossRef]
- Laboissiere, L.A.; Fernandes, R.A.S.; Lage, G.G. Maximum and minimum stock price forecasting of Brazilian power distribution companies based on artificial neural networks. Appl. Soft Comput. 2015, 35, 66–74. [Google Scholar] [CrossRef]
- Prastyo, A.; Junaedi, D.; Sulistiyo, M.D. Stock price forecasting using artificial neural network: (Case Study: PT. Telkom Indonesia). In Proceedings of the 2017 5th International Conference on Information and Communication Technology (ICoIC7), Melaka, Malaysia, 17–19 May 2017; pp. 1–6. [Google Scholar]
- Wijesinghe, G.W.R.I.; Rathnayaka, R.M.K.T. ARIMA and ANN Approach for forecasting daily stock price fluctuations of industries in Colombo Stock Exchange, Sri Lanka. In Proceedings of the 2020 5th International Conference on Information Technology Research (ICITR), Moratuwa, Sri Lanka, 2–4 December 2020; pp. 1–7. [Google Scholar]
- Sun, X.; Ni, Y. Recurrent Neural Network with Kernel Feature Extraction for Stock Prices Forecasting. In Proceedings of the 2006 International Conference on Computational Intelligence and Security, Guangzhou, China, 3–6 November 2006; pp. 903–907. [Google Scholar]
- Li, W.; Liao, J. A comparative study on trend forecasting approach for stock price time series. In Proceedings of the 2017 11th IEEE International Conference on Anti-counterfeiting, Security, and Identification (ASID), Xiamen, China, 27–29 October 2017; pp. 74–78. [Google Scholar]
- Wang, Y.; Liu, Y.; Wang, M.; Liu, R. LSTM Model Optimization on Stock Price Forecasting. In Proceedings of the 2018 17th International Symposium on Distributed Computing and Applications for Business Engineering and Science (DCABES), Wuxi, China, 19–23 October 2018; pp. 173–177. [Google Scholar]
- Siami-Namini, S.; Tavakoli, N.; Siami Namin, A. A Comparison of ARIMA and LSTM in Forecasting Time Series. In Proceedings of the 2018 17th IEEE International Conference on Machine Learning and Applications (ICMLA), Orlando, FL, USA, 17–20 December 2018; pp. 1394–1401. [Google Scholar]
- Du, J.; Liu, Q.; Chen, K.; Wang, J. Forecasting stock prices in two ways based on LSTM neural network. In Proceedings of the 2019 IEEE 3rd Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chengdu, China, 15–17 March 2019; pp. 1083–1086. [Google Scholar]
- Tandon, S.; Tripathi, S.; Saraswat, P.; Dabas, C. Bitcoin Price Forecasting using LSTM and 10-Fold Cross validation. In Proceedings of the 2019 International Conference on Signal Processing and Communication (ICSC), Noida, India, 7–9 March 2019; pp. 323–328. [Google Scholar]
- Chaitanya Lahari, M.; Ravi, D.H.; Bharathi, R. Fuel Price Prediction Using RNN. In Proceedings of the 2018 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Bangalore, India, 19–22 September 2018; pp. 1510–1514. [Google Scholar]
- Vidya, G.S.; Hari, V.S. Gold Price Prediction and Modelling using Deep Learning Techniques. In Proceedings of the 2020 IEEE Recent Advances in Intelligent Computational Systems (RAICS), Thiruvananthapuram, India, 3–5 December 2020; pp. 28–31. [Google Scholar]
- Mandal, P.; Senjyu, T.; Urasaki, N.; Yona, A.; Funabashi, T.; Srivastava, A.K. Price Forecasting for Day-Ahead Electricity Market Using Recursive Neural Network. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–8. [Google Scholar]
- Zhu, Y.; Dai, R.; Liu, G.; Wang, Z.; Lu, S. Power Market Price Forecasting via Deep Learning. In Proceedings of the IECON 2018 —44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 4935–4939. [Google Scholar]
- Ugurlu, U.; Oksuz, I.; Tas, O. Electricity Price Forecasting Using Recurrent Neural Networks. Energies 2018, 11, 1255. [Google Scholar] [CrossRef] [Green Version]
- Weng, Y.; Wang, X.; Hua, J.; Wang, H.; Kang, M.; Wang, F.-Y. Forecasting Horticultural Products Price Using ARIMA Model and Neural Network Based on a Large-Scale Data Set Collected by Web Crawler. IEEE Trans. Comput. Soc. Syst. 2019, 6, 547–553. [Google Scholar] [CrossRef]
- Tang, L.; Diao, X. Option pricing based on HMM and GARCH model. In Proceedings of the 2017 29th Chinese Control and Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; pp. 3363–3368. [Google Scholar]
- Wang, Y.; Guo, Y. Forecasting method of stock market volatility in time series data based on mixed model of ARIMA and XGBoost. China Commun. 2020, 17, 205–221. [Google Scholar] [CrossRef]
- Pai, P.-F.; Lin, C.-S. A hybrid ARIMA and support vector machines model in stock price forecasting. Omega 2005, 33, 497–505. [Google Scholar] [CrossRef]
- Zhang, J.-L.; Zhang, Y.-J.; Zhang, L. A novel hybrid method for crude oil price forecasting. Energy Econ. 2015, 49, 649–659. [Google Scholar] [CrossRef]
- Zhu, B.; Wei, Y. Carbon price forecasting with a novel hybrid ARIMA and least squares support vector machines methodology. Omega 2013, 41, 517–524. [Google Scholar] [CrossRef]
- Shabri, A.; Samsudin, R. Daily Crude Oil Price Forecasting Using Hybridizing Wavelet and Artificial Neural Network Model. Math. Probl. Eng. 2014, 11. [Google Scholar] [CrossRef] [Green Version]
- Safari, A.; Davallou, M. Oil price forecasting using a hybrid model. Energy 2018, 148, 49–58. [Google Scholar] [CrossRef]
- Bissing, D.; Klein, M.T.; Chinnathambi, R.A.; Selvaraj, D.F.; Ranganathan, P. A Hybrid Regression Model for Day-Ahead Energy Price Forecasting. IEEE Access 2019, 7, 36833–36842. [Google Scholar] [CrossRef]
- Huang, Y.; Dai, X.; Wang, Q.; Zhou, D. A hybrid model for carbon price forecasting using GARCH and long short-term memory network. Appl. Energy 2021, 285, 116485. [Google Scholar] [CrossRef]
- Shafie-khah, M.; Moghaddam, M.P.; Sheikh-El-Eslami, M.K. Price forecasting of day-ahead electricity markets using a hybrid forecast method. Energy Convers. Manag. 2011, 52, 2165–2169. [Google Scholar] [CrossRef]
- Kristjanpoller, W.; Minutolo, M.C. Gold price volatility: A forecasting approach using the Artificial Neural Network–GARCH model. Expert Syst. Appl. 2015, 42, 7245–7251. [Google Scholar] [CrossRef]
- Hassan, M.R.; Nath, B.; Kirley, M. A fusion model of HMM, ANN and GA for stock market forecasting. Expert Syst. Appl. 2007, 33, 171–180. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, W.; Lou, Y. Forecasting Stock Prices Using a Hybrid Deep Learning Model Integrating Attention Mechanism, Multi-Layer Perceptron, and Bidirectional Long-Short Term Memory Neural Network. IEEE Access 2020, 8, 117365–117376. [Google Scholar] [CrossRef]
- Nisha, K.G.; Sreekumar, K. A Review and Analysis of Machine Learning and Statistical Approaches for Prediction. In Proceedings of the 2017 International Conference on Inventive Communication and Computational Technologies (ICICCT), Coimbatore, India, 10–11 March 2017. [Google Scholar]
- Young, W.L. The Box-Jenkins approach to time series analysis and forecasting: Principles and applications. RAIRO-Oper. Res. 1977, 11, 129–143. [Google Scholar] [CrossRef] [Green Version]
- Babu, C.N.; Reddy, B.E. Selected Indian stock predictions using a hybrid ARIMA-GARCH model. In Proceedings of the 2014 International Conference on Advances in Electronics Computers and Communications, Bangalore, India, 10–11 October 2014; pp. 1–6. [Google Scholar]
- Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Xue, T.; Eugene Stanley, H. Comparison of Econometric Models and Artificial Neural Networks Algorithms for the Prediction of Baltic Dry Index. IEEE Access 2019, 7, 1647–1657. [Google Scholar] [CrossRef]
- Baum, L.E.; Petrie, T. Statistical Inference for Probabilistic Functions of Finite State Markov Chains. Ann. Math. Stat. 1966, 37, 1554–1563. [Google Scholar] [CrossRef]
- Liu, D.; Cai, Z.; Li, X. Hidden Markov Model Based Spot Price Prediction for Cloud Computing. In Proceedings of the 2017 IEEE International Symposium on Parallel and Distributed Processing with Applications and 2017 IEEE International Conference on Ubiquitous Computing and Communications (ISPA/IUCC), Guangzhou, China; 2017; pp. 996–1003. [Google Scholar]
- Mamon, R.S.; Erlwein, C.; Bhushan Gopaluni, R. Adaptive signal processing of asset price dynamics with predictability analysis. Inf. Sci. 2008, 178, 203–219. [Google Scholar] [CrossRef]
- Ky, D.X.; Tuyen, L.T. A Higher order Markov model for time series forecasting. Int. J. Appl. Math. Stat. 2018, 57, 1–18. [Google Scholar]
- Williams, C. A brief introduction to Artificial Intelligence. In Proceedings of the OCEANS ’83, San Francisco, CA, USA, 29 August–1 September 1983. [Google Scholar]
- Angra, S.; Ahuja, S. Machine learning and its applications: A review. In Proceedings of the 2017 International Conference on Big Data Analytics and Computational Intelligence (ICBDAC), Chirala, India, 23–25 March 2017; pp. 57–60. [Google Scholar]
- Ramírez-Amaro, K.; Chimal-Eguía, J.C. Machine Learning Tools to Time Series Forecasting. In Proceedings of the 2007 Sixth Mexican International Conference on Artificial Intelligence, Special Session (MICAI), Aquascalientes, Mexico, 4–10 November 2007; pp. 91–101. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Syntaktische Merkmale und Kategorien. Deutsche Syntax Deklarativ; DE GRUYTER: Berlin, Germany, 1999; pp. 1–13. ISBN 978-3-484-30394-2. [Google Scholar]
- Auria, L.; Moro, R.A. Support Vector Machines (SVM) as a Technique for Solvency Analysis. SSRN Electron. J. 2008, 20, 577–588. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Hu, D. Comparison of SVM and LS-SVM for Regression. In Proceedings of the 2005 International Conference on Neural Networks and Brain, Beijing, China, 13–15 October 2005; Volume 1, pp. 279–283. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Felizardo, L.; Oliveira, R.; Del-Moral-Hernandez, E.; Cozman, F. Comparative study of Bitcoin price prediction using WaveNets, Recurrent Neural Networks and other Machine Learning Methods. In Proceedings of the 2019 6th International Conference on Behavioral, Economic and Socio-Cultural Computing (BESC), Beijing, China, 28–30 October 2019; pp. 1–6. [Google Scholar]
- Istiake Sunny, M.A.; Maswood, M.M.S.; Alharbi, A.G. Deep Learning-Based Stock Price Prediction Using LSTM and Bi-Directional LSTM Model. In Proceedings of the 2020 2nd Novel Intelligent and Leading Emerging Sciences Conference (NILES), Giza, Egypt, 24–26 October 2020; pp. 87–92. [Google Scholar]
- Mcculloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biol. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Dumitru, C.; Maria, V. Advantages and Disadvantages of Using Neural Networks for Predictions. Ovidius Univ. Ann. Econ. Sci. Ser. 2013, 13, 444–449. [Google Scholar]
- Welch, R.L.; Ruffing, S.M.; Venayagamoorthy, G.K. Comparison of feedforward and feedback neural network architectures for short term wind speed prediction. In Proceedings of the 2009 International Joint Conference on Neural Networks, Atlanta, GA, USA, 14–19 June 2009. [Google Scholar]
- Deb, C.; Zhang, F.; Yang, J.; Lee, S.E.; Shah, K.W. A review on time series forecasting techniques for building energy consumption. Renew. Sustain. Energy Rev. 2017, 74, 902–924. [Google Scholar] [CrossRef]
- Kothapalli, S.; Totad, S.G. A real-time weather forecasting and analysis. In Proceedings of the 2017 IEEE International Conference on Power, Control, Signals and Instrumentation Engineering (ICPCSI), Chennai, India, 21–22 September 2017; pp. 1567–1570. [Google Scholar]
- Cheung, Y.-W.; Lai, K.S. Lag order and critical values of the augmented Dickey–Fuller test. J. Bus. Econ. Stat. 1995, 13, 277–280. [Google Scholar]
- Saia, R.; Boratto, L.; Carta, S. A Latent Semantic Pattern Recognition Strategy for an Untrivial Targeted Advertising. In Proceedings of the 2015 IEEE International Congress on Big Data, New York, NY, USA, 27 June–2 July 2015; pp. 491–498. [Google Scholar]
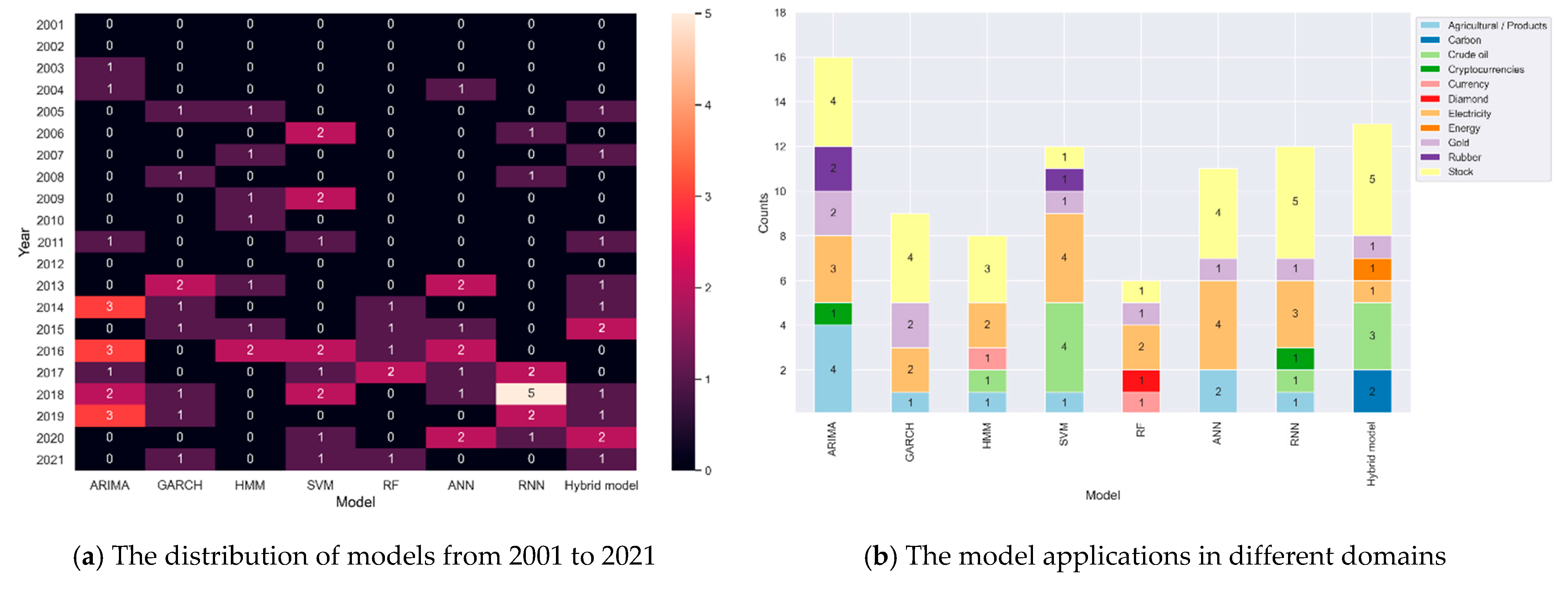



| Category | Model | Count | Time Range | References |
|---|---|---|---|---|
| Regression Model | ARIMA | 14 | 2003–2019 | [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27] |
| GARCH | 9 | 2005–2021 | [12,28,29,30,31,32,33,34,35] | |
| Stochastic Model | HMM | 8 | 2007–2016 | [36,37,38,39,40,41,42,43] |
| Machine Learning | SVM | 12 | 2005–2021 | [44,45,46,47,48,49,50,51,52,53,54,55] |
| RF | 6 | 2006–2021 | [56,57,58,59,60,61] | |
| Deep Learning | ANN | 10 | 2004–2020 | [62,63,64,65,66,67,68,69,70] |
| RNN | 12 | 2006–2020 | [71,72,73,74,75,76,77,78,79,80,81,82] | |
| Hybrid Model | Regression + Stochastic | 1 | 2017 | [83] |
| Regression + ML | 4 | 2005–2021 | [84,85,86,87] | |
| Regression + DL | 6 | 2014–2021 | [88,89,90,91,92,93] | |
| Stochastic + DL | 1 | 2007 | [94] | |
| DL + DL | 1 | 2020 | [95] |
| Domain | Author | Dataset | Model | Result |
|---|---|---|---|---|
| Cryptocurrencies | Mittal et al., 2018 [13] | Cryptocurrencies (2013 to May 2018) | ARIMA | Accuracy of 86.424 |
| Stock | Ayodele et al., 2014 [14] | New York Stock Exchange and Nigerian Stock Exchange | ARIMA | R2 of 0.0033 and 0.9972 |
| Rotela Junior et al., 2014 [15] | Bovespa Index (January 2000 to December 2012) | ARIMA | MAPE of 0.064 | |
| Setyo, 2017 [16] | Indonesia Composite Stock Price Index | ARIMA | MAPE of 0.8431 | |
| Rubber | Sukanya and Vichai, 2016 [17] | Bangkok and World natural rubber price (January 2002 to December 2015) | ARIMAX | MAPE of 1.11 |
| Latex | Chalakora and Vichai, 2018 [18] | Central Rubber Market of Hat Yai, Thailand | SARIMA | MAPE of 24.60 and RMSE of 14.90 |
| Agricultural and e-commerce product | Verma et al., 2016 [19] | Agricultural Produce Market Committee, Ramganj (May 2003 to June 2015 | ARIMA | MAPE of 6.38 |
| Jadhav et al., 2017 [20] | Price of cereal crops in Karnataka (2002 to 2016) | ARIMA | MAPE of 2.993, 1.859, 1.255 paddy, ragi, and maize, respectively | |
| Carta et al., 2018 [27] | Amazon product’s prices, with Google Trends data used as exogenous features | ARIMA | Achieves the lowest average MAPE of 4.77 | |
| Anil Kumar et al., 2019 [21] | Price in market Kadiri, India (January 2011 to December 2015) | ARIMA | MAPE of 2.30 | |
| Gold | Banhi and Gautam, 2016 [22] | Multi Commodity Exchange of India (November 2003 to January 2014) | ARIMA | MAPE of 3.145 |
| Yang, 2019 [23] | World Gold Council (July 2013 to June 2018) | ARIMA | Relative error of less than 1.2% | |
| Electricity | Contreras et al., 2003 [24] | Spanish and Californian electricity market of 2000 | ARIMA | Mean errors of less than 11% |
| Mingzhou et al., 2004 [25] | California power market of 1999 | ARIMA | MSE of 0.1148 | |
| Tina et al., 2011 [26] | EPEX power exchange | ARIMA | MAPE of 3.55 |
| Domain | Author | Dataset | Model | Result |
|---|---|---|---|---|
| Oil | Lama et al., 2015 [12] | Cotlook A (April 1982 to March 2012) | GARCH, EGARCH | EGARCH achieved the best performance with RMSE of 14.41 |
| Gold | Ping et al., 2013 [28] | Kijaang Emas prices (July 2001 to September 2012) | GARCH | MAPE of 0.809767 |
| Yaziz et al., 2019 [29] | Malaysia gold price (January 2003 to June 2014) | ARIMA, GARCH, ARIMA-GARCH | ARIMA-GARCH achieved the most optimal result with a price error less than 2 | |
| Stock | Xing et al., 2021 [30] | West Texas Intermediate (January 2015 to May 2018) and CSI300 (May 2015 to 2016) | GARCH with nonlinear function | AIC of −1119.77 and −11373.6 for CSI300 and WTI dataset |
| Tripathy and Raahman, 2013 [31] | Bombay Stock Exchange and Shanghai Stock Exchange (1990 to 2013) | GARCH | AIC of −5.512662 and −5.260705 for BSE and SSE dataset | |
| Erica et al., 2018 [32] | Adaro energy share price (January 2014 to December 2016) | GARCH | MAPE of 2.16 | |
| Power | Hong Li et al., 2008 [33] | Power price in California of 2000 | NP-GARCH, GARCH, ARIMA | NP-GARCH achieved the lowest MPE of 3.62 and 4.86 |
| Agricultural Product | Bhardwaj et al., 2014 [34] | Gram price in Delhi (January 2007 to April 2012) | GARCH, ARIMA | GARCH achieved the best performance with an average error of less than 2 |
| Electricity | Garcia et al., 2005 [35] | Spanish and Californian Power Market (September 1999 to November 2000) and (January 2000 to December 2000) | GARCH | FMSE of less than 6 and 69 for Spanish and Californian market |
| Domain | Author | Dataset | Model | Result |
|---|---|---|---|---|
| Stock | Hassan and Nath, 2005 [36] | Four airline stock indexes | HMM | MAPE of less than 6.850 for included stocks |
| Hassan, 2009 [37] | Six different stock prices | Fuzzy logic model and HMM | MAPE of less than 4.535 | |
| Dimoulkas, 2016 [38] | Nordic BM | HMM, ARIMA | HMM has the best accuracy of 73% | |
| Commodity | Date et al., 2013 [39] | Financial market commodity prices | HMM | RMSE of 0.08502 |
| Electricity | Valizadeh Haghi and S. M. Moghaddas Tafresgu, 2007 [40] | Spanish spot market of 2005 | HMM | |
| Jianhua Zhang et al., 2010 [41] | Electricity market data of August 2009 | HMM | MAPE of 4.1598 | |
| Oil | Bon and Isah, 2016 [42] | WTI dataset for oil prices of 2015 | HMM | |
| Financial | Shaaib, 2015 [43] | Foreign currency exchange rate of Euro against USD (April 2007 to February 2011) | HMM, ANN | HMM achieved the best performance with MSE of less than 0.04 |
| Domain | Author | Dataset | Model | Result |
|---|---|---|---|---|
| Crude oil | Xie et al., 2006 [44] | WTI crude oil price (January 1970 to December 2003) | SVM, ARIMA, BPNN | SVM has the best performance with RMSE of 2.1921 |
| Qi and Zhang, 2009 [45] | OPEC, DJAIS and AMEX oil index | SVM | Error rate of 16.23% | |
| Khashman and Nwulu, 2011 [46] | WTI crude oil price (2002 to 2008) | SVM, ANN | SVM has the highest correct prediction rate of 81.27 | |
| Yu et al., 2017[47] | WTI crude oil price | SVM, ARIMA, FNN, ARFIMA, MS-ARFIMA, Random walk, SVM | SVM has the best performance with highest Diebold–Mariano test score | |
| Rubber | Jing Jong et al., 2020 [48] | Bulk latex | ARIMA | ARIMA-SVM achieved the lowest MAPE of 0.3535 |
| Gold | Makala and Li, 2021 [49] | World Gold Council (1979 to 2019) | SVM, ARIMA | SVM achieved the best result with an RMSE of 0.028 |
| Electricity | Swief et al., 2009 [50] | PJM (March 1997 to April 1998) | SVM | MAPE of 1.3847 |
| Mohamed and El-Hawary, 2016 [51] | New England ISO (2003 to 2010) | SVM | MAPE of 8.0386 | |
| Saini et al., 2016 [52] | Australian Electrical Market | SVM | MAPE of less than 1.78 | |
| Ma et al., 2018 [53] | ERCOT | SVM | MAPE of 6.57 | |
| Agricultural | Akın et al., 2018 [54] | Raisin World Export dataset | SVM, ANN | SVM is better than ANN with an accuracy of 0.888 |
| Stock | Kumar et al., n.d. [55] | Financial time-series data | SVM, RF | SVM outperform the RF by 1.04% of hit ratio |
| Domain | Author | Dataset | Model | Result |
|---|---|---|---|---|
| Load | Lahouar and Ben Hadj Slama, 2015 [56] | Tunisian Company of Electricity and Gas (January 2009 to August 2014) | RF, ANN, SVM | RF has the lowest MAPE of less than 4.2302 |
| Electricity | Mei et al., 2014 [57] | NYISO | RF, ANN, ARIMA | RF has the lowest MAPE of 12.05 |
| Diamond | Sharma et al., 2021 [58] | Kaggle | RF, Decision Tree, Lasso, Ada Boost, Ridge Gradient Boosting, Linear Regression, Elastic Net | RF has the lowest RMSE of 581.905423 |
| Exchange rate | Ramakrishnan et al., 2017 [59] | Department of Statistic Malaysia, World Bank, Malaysia Palm Oil Council, Malaysian Rubber Export Promotion Council, Federal Reserve Bank | RF, NN, SVM | RF has the lowest RMSE of 0.018 |
| Gold | Liu and Li, 2017 [60] | DJIA, S&P500, USDX | RF | RF showed a promising result in predicting the different datasets, with prediction performance up to 0.99 |
| Stock | Khaidem et al., 2016 [61] | Samsung, GE and, Apple stock | RF | Accuracy of higher than 86.8396 |
| Domain | Author | Dataset | Model | Result |
|---|---|---|---|---|
| Agricultural | Jha and Sinha, 2013 [62] | Soybean price from SOPA, rapeseed-mustard from Delhi | ANN, ARIMA, TDNN | ARIMA obtained better result for soybean price forecasting with an RMSE of 5.43, hybrid ARIMA-TDNN has better performance with an RMSE of 3.46 |
| Electricity | Yamin et al., 2004 [63] | Californian power market (January 1999 to September 1999) | ANN | MAPE of less than 9.23 |
| Ozozen et al., 2016 [64] | EPIAS (2014 to 2015) | ANN, ARIMA, ARIMA-ANN | The hybrid model achieved an MAPE of 4.08 | |
| Ranjbar et al., 2016 [65] | Ontario power market (January 2003 to December 2003) | ANN | MAPE of 9.51 | |
| Sahay and Singh, 2018 [66] | Historical power data (2007 to 2013) | Backpropagation algorithm | MAPE of 6.60 | |
| Gold | Verma et al., 2020 [67] | Gold price from investing site, (January 2015 to December 2018) | GDM, RP, SCG, LM, BR, BFGS, OSS | GDM algorithm has the lowest MAPE of 4.06 |
| Stock | Laboissiere et al., 2015 [68] | CEBR3, CSRN3 | ANN | MAE of 0.0009 and 0.0042 for CEBR3 and CSRN3 |
| Prastyo et al., 2017 [69] | Daily stock closing prices from Wanjawa and Lawrence | ANN | RMSE of 0.1830 | |
| Wijesinghe and Rathnayaka, 2020 [70] | Colombo stock exchange | ANN, ARIMA | ANN has the lowest MAPE of 0.1783 |
| Domain | Author | Dataset | Model | Result |
|---|---|---|---|---|
| Stock | Sun and Ni, 2006 [71] | Yahoo Finance (April 2005 to August 2005) | RNN | Accuracy of 0.9784 |
| Li and Liao, 2017 [72] | China stock market (2008 to 2015) | RNN, LSTM, MLP | LSTM has the highest performance with an accuracy of 0.473 | |
| Wang et al., 2018 [73] | Yunnan Baiyao stock data | LSTM | Accuracy of 50–65% | |
| Sima et al., 2018 [74] | Yahoo Finance (January 1985 to August 2018) | LSTM, ARIMA | ARIMA and LSTM achieved an RMSE of 5.999 and 0.936, respectively | |
| Du et al., 2019 [75] | American Apple stock data of 2008 | LSTM | MAE of 0.155 | |
| Cryptocurrency | Tandon et al., 2019 [76] | Coin Market Cap website | LSTM, RF, Linear Regression | LSTM has the best performance with an MAE of 0.1518 |
| Fuel | Chaitanya Lahari et al., 2018 [77] | Historical data from major metropolitan cities | RNN | Accuracy of above 90% |
| Gold | S and S, 2020 [78] | World Gold Council | LSTM | RMSE of 7.385 |
| Electricity | Mandal et al., 2007 [79] | PJM | RNN | MAPE of less than 10 |
| Zhu et al., 2018 [80] | New England ISO and PJM | LSTM, SVM, DT | LSTM has the best performance with an MAPE of lower than 39 | |
| Ugurlu et al., 2018 [81] | Turkish electricity market of 2016 | LSTM, GRU, ANN | GRU has the best performance with an MAE of 5.36 | |
| Agricultural | Weng et al., 2019 [82] | Beijing Xinfadi Market (August 2015 to July 2018) | RNN, ARIMA, BPNN | The RNN achieved the best performance with the lowest AAE of 0.49, 0.21, 0.15 |
| Domain | Author | Dataset | Model | Result |
|---|---|---|---|---|
| Tang and Diao, 2017 [83] | WIND database (January 2010 to September 2016) | HMM-GARCH | RMSE of 0.0238 and 0.0075 | |
| Stock | Pai and Lin, 2005 [85] | Ten stocks dataset (October 202 to December 2002) | ARIMA, SVM, ARIMA-SVM | Hybrid model has the lowest MAE for the included ten stocks |
| Raiful Hassan et al., 2007 [94] | Daily stock price of Apple, IBM, and Dell from Yahoo Finance | ANN-GA-HMM | MAPE of 1.9247, 0.84871, and 0.699246 for the stock, respectively | |
| Wang and Guo, 2020 [84] | Ten stocks dataset (2015 to 2018) | DWT-ARIMA-GSXGB | RMSE of less than 20.3013 for the worst case, the general cases have an RMSE of less than 0.3 | |
| Chen et al., 2020 [95] | Yahoo Finance (September 2008 to July 2019) | MLP-Bi-LSTM with AM | MAE of 0.025393 | |
| Crude oil | Shabri and Samsudin, 2014 [88] | Brent crude oil prices and WTI crude oil prices | ANN, WANN | WANN has the best performance with MAPE of 1.31 and 1.39 for Brent and WTI dataset |
| Zhang et al., 2015 [86] | WTI and Brent crude oil (January 1986 to 2005) and (May 1987 to June 2005) | EEMD-LSSVM-PSO-GARCH | MAPE of 1.27 and 1.53 for WRI and Brent dataset | |
| Safari and Davallou, 2018 [89] | OPEC crude oil prices (January 2003 to September 2016) | ESM-ARIMA-NAR | MAPE of 2.44, obtained the lowest error compared to other single models | |
| Energy | Bissing et al., 2019 [90] | Iberian electricity market (February to July 2015) | ARIMA -MLR and ARIMA-Holt winter | ARIMA-Holt Winter has better performance with an MAPE of less than 5.07 for different day forecasting |
| Carbon | Zhu and Wei, 2013 [87] | European Climate Exchange (ECX) of December 2010 and December 2012 | ARIMA-LSSVM | RMSE of 0.0311 and 0.0309 for DEC10 and DEC12 |
| Huang et al., 2021 [91] | EUA futures from Wind database | VMD-GARCH and LSTM | VMS-GARCH has the best performance with first ranking in terms of RMSE, MAE and MAPE | |
| Electricity | Shafie-khah et al., 2011 [92] | Spanish electricity market of 2002 | Wavelet-ARIMA-RBFN | Error variances of less than 0.0049 |
| Gold | Kristjanpoller and Minutolo, 2015 [93] | Gold Spot Price and Gold Future Price from Bloomberg (September 1999 to March 2014) | ANN-GARCH | MAPE of 0.6493 and 0.6621 |
| Model | Linear | Nonlinear | Stationary | Non-Stationary | Volatile | Non-Volatile | Large Dataset | Small Dataset |
|---|---|---|---|---|---|---|---|---|
| ARIMA | ✓ | ✓ | ✓ | ✓ | ||||
| GARCH | ✓ | ✓ | ✓ | ✓ | ||||
| HMM | ✓ | ✓ | ✓ | ✓ | ||||
| SVM | ✓ | ✓ | ✓ | ✓ | ||||
| RF | ✓ | ✓ | ✓ | ✓ | ||||
| ANN | ✓ | ✓ | ✓ | ✓ | ||||
| RNN | ✓ | ✓ | ✓ | ✓ |
| Factors | Example | Attention Level | Price |
|---|---|---|---|
| Location | High popularity, High rating of surrounding public facilities, business | Increase ↑ | Increase ↑ |
| Weather and temperature | Raining, extremely high or low temperature and air humidity | Decrease ↓ | Decrease ↓ |
| Environmental Factor | Linearity | Stationary | Volatility | Dataset Size | Selected Model | |
|---|---|---|---|---|---|---|
| Location | Popularity index | No | No | No | ≤100 K | SVM |
| Weather | Temperature | Yes | Yes | No | ARIMA | |
| Air humidity | Yes | Yes | No | ARIMA | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, Y.-F.; Ong, L.-Y.; Leow, M.-C.; Goh, Y.-X. Exploring Time-Series Forecasting Models for Dynamic Pricing in Digital Signage Advertising. Future Internet 2021, 13, 241. https://doi.org/10.3390/fi13100241
Tan Y-F, Ong L-Y, Leow M-C, Goh Y-X. Exploring Time-Series Forecasting Models for Dynamic Pricing in Digital Signage Advertising. Future Internet. 2021; 13(10):241. https://doi.org/10.3390/fi13100241
Chicago/Turabian StyleTan, Yee-Fan, Lee-Yeng Ong, Meng-Chew Leow, and Yee-Xian Goh. 2021. "Exploring Time-Series Forecasting Models for Dynamic Pricing in Digital Signage Advertising" Future Internet 13, no. 10: 241. https://doi.org/10.3390/fi13100241
APA StyleTan, Y.-F., Ong, L.-Y., Leow, M.-C., & Goh, Y.-X. (2021). Exploring Time-Series Forecasting Models for Dynamic Pricing in Digital Signage Advertising. Future Internet, 13(10), 241. https://doi.org/10.3390/fi13100241








