Abstract
Consensus mechanisms are a core feature for handling negotiation and agreements. Blockchain technology has seen the introduction of different sorts of consensus mechanism, ranging from tasks of heavy computation to the subtle mathematical proofs of Byzantine agreements. This paper presents the pioneer Delegated Byzantine Fault Tolerance (dBFT) protocol of Neo Blockchain, which was inspired by the Practical Byzantine Fault Tolerance (PBFT). Besides introducing its history, this study describes proofs and didactic examples, as well as novel design and extensions for Neo dBFT with multiple block proposals. Finally, we discuss challenges when dealing with strong Byzantine adversaries, and propose solutions inspired on PBFT for current weak-synchrony problems and increasing system robustness against attacks. Key Contribution: Presents an overview of the history of PBFT-inspired consensus for blockchain, highlighting its current importance on the literature, challenges and assumptions. Contributes to the field of Distributed Consensus, proposing novel extensions for the Neo dBFT (dBFT 2.0+, dBFT 3.0 and dBFT 3.0+), with new insights on innovative consensus mechanisms.
1. Introduction
The emergence of the Bitcoin cryptocurrency [1] boosted the popularity of various applications of blockchain technology, focusing not only on the financial sector, but also several other industries. There are plenty of different areas in which blockchain has been applied, from the gaming industry to decentralized exchanges, tokenization of fiat currencies and securities, the peer-review process, data registries, among others. To cover the needs of each distinct use, different solutions have been designed for Distributed Ledger Technologies (DLTs) [2].
The organization of DLT systems based on “information chunks”, or blocks, gained momentum under the umbrella of blockchain technologies. These systems typically organize operations, or transactions, in a total-order that forms an immutable ledger, which by means of cryptography techniques is able to resist many types of attacks in a decentralized (permission-less) network. As a core mechanism of any blockchain one can find a consensus strategy for managing blocks, in which autonomous agents form a Peer-to-Peer (P2P) network topology. These agents behave like a multi-agent system, reaching agreements throughout negotiation protocols which include voting, auctions or bargain [3]. Among these, Proof-of-Work (PoW) consensus mechanisms remain the most prolific, used in the most famous blockchain projects to date, Bitcoin and Ethereum [4]. On the PoW consensus, computational power is used to perform calculations that can vary in difficulty, adjusted according to the computational capacity of the network guided by a desired block-time. PoW mechanisms include a fork resolution strategy, in which competing branches of global block ordering are resolved, usually following a longest chain logic.
The hard challenges faced by consensus systems were deeply explored in the 1980s, as well as their limits when dealing with faulty processes [5]. A promising family of fault-resistant consensus is based on the classical Byzantine Generals problem [6], which is the basis of the term Byzantine Fault Tolerance (BFT). The Practical Byzantine Fault Tolerance (PBFT) algorithm [7] was the first to resist to such Byzantine attacks while preserving a total-order of independent operations, up to the limit of f Byzantine nodes from a total of . Some authors proposed enhancements over PBFT, such as the Spinning BFT [8] and Redundant BFT [9], in order to increase robustness of network when dealing with systematic Byzantine attacks, eventually at the expense of increasing network communication.
Neo Blockchain [10] was a pioneer project extending PBFT for blockchain, allowing a set of N independent nodes to be elected on a decentralized network, in order to maintain a public ledger by means of the innovative Delegated Byzantine Fault Tolerance (dBFT) consensus. In fact, dBFT can be seen as one of the core components of the Neo network, as it allows a set of N nodes (called Consensus Nodes) to cooperate in a global decentralized network, with optimal resilience against byzantine faults: up to nodes. Besides the groundbreaking contributions of PBFT, dBFT includes ideas also discussed in other works from the literature. One example is a round-robin selection of primary nodes, also found in Spinning BFT, that drastically reduces the attack surface on consensus, reducing damage when the primary node is the faulty one.
The dBFT goes far beyond an ordinary component that provides global ordering, since its nodes are also representatives (or delegates) of the entire Neo Blockchain network, elected by NEO token owners. Consensus Nodes enforce on-chain governance, while dBFT ensures all these decisions (including transaction computation) are viewed consistently by all nodes in the network, as a unique Global State. In this sense, an unique feature of dBFT (and Neo Blockchain since its conception) is its capability to provide Single Block Finality (or One Block Finality− 1BF), such that every decision is final once approved/signed by consensus nodes (or simply ), where f is the maximum accepted limit for faulty nodes. This was devised as one of the core goals of the platform and enforced since early design phases of the project; however it is not a trivial task to achieve. Even counting on the existing PBFT background, it was necessary to move one step further for elaborating dBFT. Due to performance limitations on the peer-to-peer layer, the first version of dBFT included only two of the three PBFT phases to reduce message burden. As soon as network capabilities were further improved, the project moved towards a complete three-phase consensus, called dBFT 2.0. In this sense, this work further discusses the theoretical background behind PBFT-based consensus for blockchain, and proposes several extensions for dBFT, namely: dBFT 2.0+, dBFT 3.0 and dBFT 3.0+.
This study elaborates on existing consensus technologies for blockchain and DLTs, indicating promising directions for the next generation of consensus on Neo Blockchain. Using didactic examples and innovative definitions, we demonstrate the existing challenges, as well as current proposals on how to deal with them. Ultimately, this paper has the following major contributions:
- (i)
- Presents an overview of PBFT consensus for blockchain, presenting its general properties and those required for blockchain applications;
- (ii)
- Defines operations conditions for a Byzantine consensus over a decentralized P2P network;
- (iii)
- Introduces potential improvements to Neo dBFT 2.0 algorithm, namely dBFT 2.0+, also discussing crucial weak-synchrony challenges for 1BF on blockchain;
- (iv)
- Presents a novel dBFT algorithm, namely dBFT 3.0, in which redundant primaries are used to increase consensus robustness.
- (v)
- Discusses future possible extensions over dBFT 3.0, namely dBFT 3.0+, to cope with other types of attacks and innovative byzantine node detection techniques.
This paper is organized into five sections, besides this introduction. Section 2 provides background on Byzantine fault tolerant technologies and its fundamental concepts. Section 3 presents a brief history of the dBFT algorithm, with details of its first implementation. Section 4 describes its evolution to dBFT 2.0, including achievements and existing limitations, as well as presenting a solution for solving weak-synchrony problems and also act as a tool for byzantine node detection. Section 5 introduces the proposed design for an upgraded version of the current Neo Consensus, namely dBFT 3.0. Finally, Section 6 draws some final considerations and future extensions.
2. Background
2.1. Twenty Years of Practical Byzantine Fault Tolerance
Over 20 years ago, the groundbreaking work on PBFT by Miguel Castro and Barbara Liskov [7] had finally demonstrated the practical feasibility of dealing with systematic byzantine (The term Byzantine was coined by Leslie Lamport [6], on the Byzantine Generals Problem, which simply represents a faulty machine that shows arbitrary behavior, thus invalidating or even attacking the protocol itself.) faults in a distributed system, even in face of a very strong adversary. The resiliency of such system was proven to be optimal, resisting up to f faulty/byzantine nodes, from a total of replicated state machines [11]. The reason nodes are required is also straightforward due to the hostile nature of the considered network: messages can be delayed, delivered out of order, duplicated, or even lost. Since f nodes can be faulty, you need to be able to decide after communicating with the other nodes (). However, even when you receive f responses from them, you still cannot know if those are the faulty ones or not. Maybe the others were just delayed, so you need extra confirmations to be certain of the truth.
2.2. Network Properties
We present requirements on the underlying network for dBFT-inspired consensus protocols.
2.2.1. General Network Properties
The PBFT work presented the following properties:
- (P.1)
- fail to deliver messages
- (P.2)
- delay messages
- (P.3)
- duplicate messages
- (P.4)
- message delivery out of order
2.2.2. Decentralized Network Properties
We introduce additional network constraints for a public DLT ecosystem, named off-chain governance requirements:
- (P.5)
- network communication is performed by collaborative nodes that can join and leave at will
- (P.6)
- in order to ensure safety, interested parties must be able to verify public information, performing an in-time participation on the correct network
Because of its public and decentralized nature, a P2P design is usually adopted for DLT networks, satisfying (P.5). Although it may not be beneficial in terms of efficiency, it favors resiliency. The in-time requirement (P.6) is generally assumed, as one depends on actively receiving and sending messages via a specific protocol, with online worldwide data validation, as this is what differentiates official networks (aka. MainNet) from others (TestNet, PrivateNet, …). Constraint (P.6) can be relaxed depending on other architectural properties, such as the expected time to generate consensus/decisions (may vary from seconds up to minutes/hours). To effectively collaborate on the network (P.5), a node must be up to date at a minimum given time threshold.
2.2.3. Blockchain Network Properties
Finally, we present Blockchain Conditions:
- (P.7)
- client requests (aka. transactions) are processed in batches (aka. blocks), and are chained together by linking them to previous blocks
- (P.8)
- to satisfy (P.5) and (P.7), pending requests are usually managed via a memory pool mechanism, which aggregates requests not yet executed
According to (P.8), mempool is naturally non-deterministic, since there is no guarantee that two nodes will have precisely the same pending requests at any given moment of time.
2.3. Message Delivery
Most works consider an asynchronous scenario, where messages are delayed, but will eventually arrive. This way, previous works argue that guaranteed delivery of messages can be achieved by replaying messages, as a way to circumvent (P.1), a strategy that we will call .
In practice, there is no central authority or absolute control over the P2P network (including its software), so it is very hard to guarantee that certain properties hold, including . Software bugs and upgrades on different clients (at different times) may generate unexpected behavior, leading to eventual message loss and temporary disruption of the P2P channel. These disruptive events may also be caused by external decisions related to off-chain governance and the incentive model for the network.
This way, a well designed and healthy decentralized network can guarantee at least that messages are almost always delivered, with the exception of extremely rare events (where it can eventually halt), which we call . In our perspective, this modeling is a better approximation of a public decentralized blockchain ecosystem. This path is also in line with decisions of public blockchain projects, such as Neo, that do not expose the public IPs of consensus nodes, nor connect them directly (thus they depend on a healthy network to be able to communicate).
Therefore, in this work, we will explore alternative models to deal with (P.1), namely and . This may not be a good approach to devise correctness proofs, yet it is useful to argue for pros and cons of existing consensus models.
Ensuring Message Delivery on Peer-To-Peer: Challenges
Purely asynchronous consensus depends on guaranteed message delivery for the underlying network [12], which is not a trivial property to assume for a decentralized network. To relay messages and avoid duplication, techniques such as Bloom Filters and probabilistic tables are usually employed [10]. Although this strongly favors efficiency and reduces overall memory usage, there is a risk of completely denying genuine messages, due to conflicts of previously generated message hashes. The probability of this event may be very small, yet not negligible in practice if the consensus mechanism depends on assuming all messages are eventually delivered.
One way to reduce the probability of such failures, is to have separated filters for Priority (consensus) and Non-priority messages. Since most messages is of non-priority (transactions, blocks, etc.), they may overload the probabilistic tables with information that may cause non-deterministic conflicts on priority messages. With less info on priority tables (and perhaps a larger size), the conflict probability that yields false positives on message relay is reduced.
Dealing with adversaries that may intentionally drop messages, thus not relaying them, is even harder. To guarantee that priority messages arrive, one must enforce redistribution for every new node that connects to it, keeping a history of messages that may help current consensus to evolve, and dropping past messages that are not necessary anymore. Nodes should also disconnect and reconnect to others periodically, as stable bonds could lead to situations where a strong adversary can control important nodes and routes inside peer-to-peer.
2.4. Adversarial Model
We consider a very strong adversary (similar to [7]), which is capable of:
- (A.1)
- coordinating faulty nodes, with arbitrary failures
- (A.2)
- delaying communication (as seen in Section 2.2.1)
- (A.3)
- completely block the network and drop messages, in extremely rare situations (This condition is due to previous decentralized peer-to-peer discussions, according to . Please note that it is assumed that it can only happen rarely, otherwise the adversary would simply halt all communications during all times.)
- (A.4)
- delaying any correct node, up to a polynomial time limit (We consider the same delay conditions as [7], where delays can never grow exponentially.)
- (A.5)
- explore issues of byzantine fault tolerance privacy, as leaked information from non-faulty replicas can be explored by byzantine agents
We also consider the following limitations on the adversary:
- (L.1)
- it is compute bound, such that it cannot subvert the given public-key cryptography or generate hash collisions
- (L.2)
- it cannot fake message authentication, due to (L.1)
- (L.3)
- correct nodes have independent implementations and infrastructure, such that no general failure can be explored
The (A.4) is a weak-synchrony assumption, thus allowing a non-violation of the celebrated FLP result [5] that forbids the existence of purely asynchronous consensus (from a deterministic perspective). On the other hand, there exists recent works in the literature that propose efficient purely asynchronous consensus [13], claiming that its “non-deterministic nature” during decision-making allows circumvention of the FLP result. In this case, condition (A.4) is not required to hold, which we will call . This will require an asynchronous network, so (A.3) is not expected to hold anymore, which we name .
2.5. PBFT Discussion
We have presented basic concepts that support the development of the most recent (and efficient) consensus systems. Most of these concepts date back to PBFT [7], a consensus proven to have optimal resilience while handling byzantine faults. PBFT handles safety in an asynchronous manner, being correct according to linearizability [14], but it depends on a weak synchrony (A.4) to guarantee liveness. PBFT has three phases in its algorithm: pre-prepare, prepare and commit.
In short, PBFT intends to find a global order for a given set of operations (more details will follow later). To accomplish that, it divides its nodes into two types: one primary and a set of backups. The primary performs the ordering (giving an unique sequence number to each operation), while the others verify it, being capable of fully replacing the primary when it appears to have failed (by means of a protocol called view change). There are many interesting extensions of PBFT, and some of them will be cited along this paper. We will focus a little bit now on the main character of the story: the pioneer dBFT consensus for blockchain.
3. A Brief History of dBFT
The first version of the dBFT is introduced at Section 3.1. A problem in its implementation, which impaired 1BF, is described at Section 3.2 and Section 3.3. Finally, Section 3.4 presents the direction that dBFT 2.0 took for handling the issue.
3.1. dBFT 1.0
The first version of dBFT just included two phases: PrepareRequest and PrepareResponse (corresponding to PBFT’s pre-prepare and prepare). This was a necessary simplification, due to high communication costs and natural efficiency issues faced by a first prototype. Removing the third phase allowed consensus to perform much faster, especially necessary in a P2P network with the potential for large delays. In practice, it demonstrated how strong the adversary really is, according to (A.2).
We will begin by demonstrating three “good cases” for dBFT 1.0: (a) no replica is faulty (Figure 1); (b) one replica is faulty, but not primary (Figure 2) (c) primary is faulty, requiring a change view (Figure 3).

Figure 1.
Perfect case. Request sent and received by Primary (replica 0). Everyone relays block .

Figure 2.
Good case (faulty non-primary replica 2). Request sent and received by Primary (replica 0). All except 2 relays block .
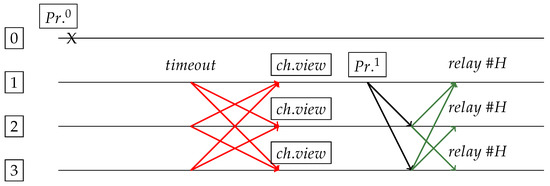
Figure 3.
Primary 0 is dead and no proposal is made. Replicas will change view after timeout (red lines) due to not receiving each other’s responses in time. Replica 1 becomes the new primary () and successfully generates block .
3.2. Forks and Sporks
One side effect of the decision to forego the third phase was that, due to network delays, even when no byzantine node was present among Consensus Nodes, multiple valid blocks could be eventually forged (at the same blockchain height). During community discussions, this phenomena was once called a spork, highlighting its difference from a classic chain fork (which happens naturally in blockchains without 1BF, such as Bitcoin [1]). Unlike a classic fork that allows further endless continuations after each block, in the spork phenomena a valid block was created by orphaned immediately, and progress could continue on the other block. Although not explicitly forking the network, it could potentially generate issues, as non-consensus nodes that accepted the orphaned block would never give up on it (due to 1BF policy). These affected nodes would then require a manual software restart, parsing the whole chain again, in order to finally attach the correct block on top of its chain.
The reason behind this phenomena was simple: some primary node could eventually propose a valid block, receiving support from enough nodes (at least ), but these same nodes could only receive messages from each other after a long time (due to (A.2)). This would cause a view change, since the given timeout for that view has expired (for at least, ‘M‘ replicas), so another backup would become primary and propose another valid block for that same height, receiving again enough signatures from its colleagues (at least ). This situation is presented in Figure 4 and Figure 5.
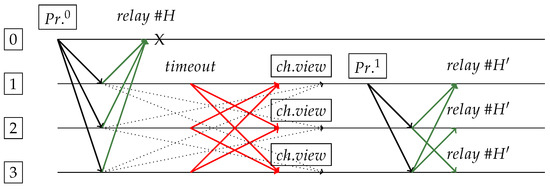
Figure 4.
Request sent and received by replica 0 ( means primary of view 0). Others will not follow it, since they will change view (red lines) due to not receiving each other’s responses (green lines) in time. Replica 1 becomes new primary () and generates “spork” (blocks and are in same height but with different contents). The “X" indicates a complete node crash. Ignored messages are dotted lines (received after a change view has already occurred).
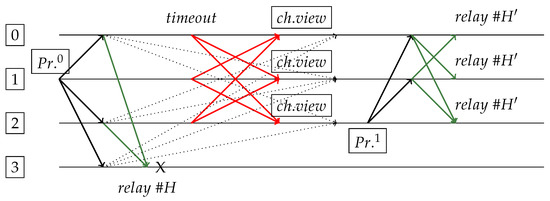
Figure 5.
Request sent by replica 1 and PrepareResponse to replica 3. Primary and others will not follow it, since they will change view due to not receiving each other’s responses. Replica 2 becomes new primary and generates “spork” (blocks and ).
An important explanation was still lacked. The adversary is very strong as we know, but the problem seemed to happen only from time to time, sometimes these “sporks” took nearly a month to happen again. The peer-to-peer network had large delays, but since Neo blocks are generated every 15 s, and the first view change only happened at twice this value, we would require a delay of at least 30 s on the network for a spork to happen. Yet, it kept happening from time to time.
3.3. Sporks Explained
The dBFT does not have a unified notion of “time”, so every node has its own independent timer. Each of them timeout when they believe the primary has failed (with exactly the same timeout value T), but note that this may happen in completely different moments. The reason is that each node depends on the persist time of the previous block to start its next timer, since it is local information (and trusted regardless of primary node, differently from the block timestamp itself).
Therefore, one possibility for a spork to happen naturally is that the primary has already been delayed (by perhaps a delayed reception of the previous block). In this sense, primary starts to work and finishes its valid block just in time for all the others to expire their timers, as detailed in Figure 6. And just in that precise moment, none of them happen to receive any message from each other nor the delayed primary, so puff: we get a spork.
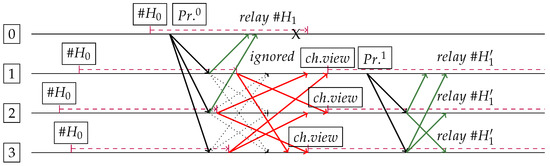
Figure 6.
More “realistic” case analogous to Figure 4, when Primary proposal is naturally delayed due to a delay on previous Block persistence (event ). Timeouts are set to time units (in purple), where v is view number. Please note that most prepare response messages are ignored after Change View has started, even with a regular and very small delay. Since Primary was already delayed in relation to others, time to respond was actually minimal before a protocol change occurred on replicas 1, 2 and 3.
This time difference is still a challenging issue on dBFT 2.0, which will be further discussed during dBFT 3.0 proposal. So how does dBFT deal with delays on block proposals (avoiding large differences on block timestamps)? In short: the current time difference between nodes is allowed up to vary up to several minutes (10 min until 2019, changed to around 2 min), so we still need another mechanism that further reduces this difference (up to second/millisecond scale). Clock drifting is a real problem, but nodes can collaborate with each other guaranteeing that a much smaller time difference is tolerated.
3.4. Towards a Solution for Sporks
The solution to sporks was evident: dBFT needed a third phase. It was clear that block signatures could not be exposed to the network before the replica was confident that other nodes would follow it, otherwise multiple valid blocks could be generated at each height (as seen in Figure 4, Figure 5 and Figure 6). This issue is related to adversarial condition (A.5), where byzantine agents can aggregate signatures from replicas (sent on prepare response), allowing the creation of a valid block even if all replicas i finally decided to relay after a change view.
An interesting characteristic of this issue, from a practical/applied point-of-view, is that it only happened eventually (a few times a year), even on a blockchain with systematic block generation (average 15 s). Considering that all replicas are non-faulty, only a very “unlucky” combination of delays could lead to such scenario. From a theoretical perspective, the issue is easy to be reproduced but not with a trivial fix, as we will see in the next section.
4. dBFT 2.0
The development of dBFT 2.0 had specifically targeted a solution to the “sporks”. This was consistent to a scenario where code quality has been drastically improved (This value is an average from the ones unofficially reported by several core developers, during this project phase in 2018.) (up to 100×), due to several code optimizations and the adoption of the Akka framework (removing several locks from consensus/blockchain system). In this new scenario, the adoption of a third phase for consensus was no longer deemed prohibitive to keep achieving slightly over the 15-s average block-time in practice.
4.1. Effects of a Third Phase
Figure 7 and Figure 8 shows good operation cases for dBFT 2.0, while Figure 9 demonstrates a commit signature exposure.
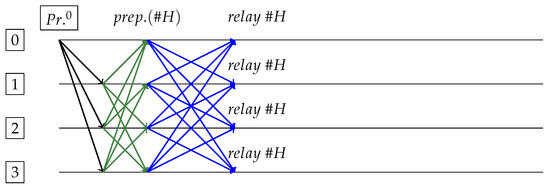
Figure 7.
Perfect case. Request sent and received by Primary (replica 0). After responses/proposal, replica is for block . Everyone relays block after commit phase (in blue).
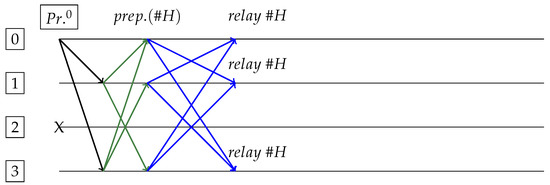
Figure 8.
Good case (faulty non-primary replica 2). Request sent and received by Primary (replica 0). After responses/proposal, replica is for block . All except 2 relays block after commit phase (in blue).
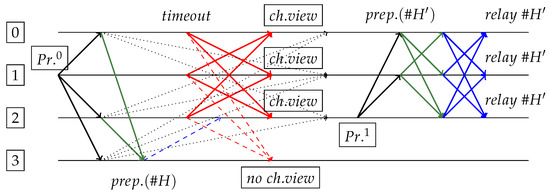
Figure 9.
Request sent by replica 1 and PrepareResponse to replica 3 that becomes Prepared for . Replica 3 exposes its commit signature, so it will deny any view change message. Others may change view (due to message delays) and replica 2 becomes new primary, generating valid (and unique) block (no spork happens).
An interesting feature of dBFT 2.0 is its capability to quickly achieve consensus, with lightweight payloads and independent messages. On the other hand, some challenges arise due to the delivery of messages out of order (P.4) and especially adversarial conditions such as large/variable delays (A.2). One may fear that pending consensus messages may cause unexpected effects after a replica is already committed, and for this reason, change view phase enforces that previous payloads are not received anymore (focus is on the new consensus round). Figure 10 presents how NEO is currently handling this using a synchrony condition.
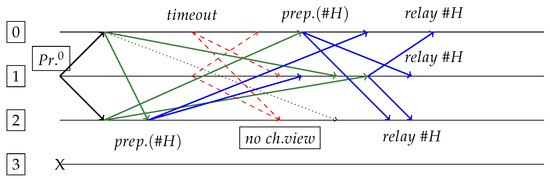
Figure 10.
Request sent by replica 1 and PrepareResponse to replica 2 that becomes Prepared for . Replica 3 is dead. Replicas 0 and 1 want to change view, but are unable due to recovery synchrony condition (where prepared replicas and dead replicas). This prevents nodes from changing view, when next view would be unable to capture necessary signatures to form a block. In this case, system resolves naturally when the minimal number of messages arrive at destination (even with large delays).
As presented in Figure 10, the synchrony condition is helpful to handle extreme situations, especially when a node is permanently dead. In practice, it would be better to avoid this kind of condition, which is not present on classic PBFT, for example. But why is it needed here and not there? Although quite subtle, adversarial and network conditions that serve as the basis for dBFT are slightly more complex than those for PBFT. One must keep in mind that in PBFT, requests are independent, and this is also assumed by many other consensus mechanisms such as Spinning and Redundant BFT [9]. In fact, RBFT and others directly assume some propagation phase that largely reduces these issues (by having requests synchronized between replicas). Unfortunately, this is unfeasible in practice for dBFT, since the mempool is naturally non-deterministic, and replicas are not directly connected between them, but through a decentralized P2P network where things may not work the way you would prefer. Anyway, by fully understanding PBFT mechanisms we may also shed some light on elaborating recovery mechanisms, such as this aforementioned synchrony condition, for dBFT 2.0 and its next generations.
4.2. How Does PBFT Handles Consistency across Views?
PBFT considers the task of totally ordering a given set of requests, sent directly by each client to the expected primary replica. If this first transmission fails, it will keep retrying, but now also send to other replicas. In PBFT, three-phase consensus happens at the level of each independent request, by attributing an unique sequence number n to each request, and guaranteeing that all non-faulty replicas will eventually agree to it.
Please note that consensus may finish in different times, for different requests, due to network delays. That is why, from time to time, it is important to create checkpoints that aggregate several past decisions into a bigger package, and guaranteeing that all non-faulty replicas also agree to that package. At this point, if some request was pending for too long, it needs to be resolved for the process to go on. Hopefully, these checkpoints only happen from time to time, and if this time is long enough, they would not interfere/lock the next consensus round.
This is very different from a blockchain, by totally ordering bigger chunks of requests, respectively called blocks and transactions. For dBFT, the primary selects a chunk of transactions and forms a block, with an unique hash identifier, including a nonce and timestamp. The task of backup nodes is to validate that information. However, what happens then, when somehow a commit is performed by some node, and only then a change view occurs?
For PBFT, change views have the remarkable capability of keeping the sequence number n of any possible committed node in the past (non-faulty ones at least), so new views are not likely to change that number. To perform this, view change messages carry all available information of each participant node, and just like magic, having nodes participating in the change view is enough to guarantee that a new (and honest) primary will keep that same number n for that same request. This guarantees that replicas in future views will commit at same sequence number that they could have committed before (and the same is valid for those who have already committed).
This is not a trivial task on a blockchain. A faulty primary may propose transactions that do not exist, and because of that, a non-faulty primary may propose a valid block that gets rejected (by timeouts) if other replicas cannot get/validate that information quickly enough. Yet, although heavily non-deterministic, the mempool typically spreads information quickly enough to give enough information for backups to validate any block sent by a non-faulty primary (within the time limit). However, if a new primary assumes the task of block proposal (after change view), it is currently free to re-create the block in any way it wishes, thus possibly dropping all efforts made on a previous view.
We argue that replicas could give simple, but important hints to a new primary, in order to reduce possible block proposal conflicts on higher views.
4.3. Aggregating Extra Information on dBFT 2.0: The dBFT 2.0+
We believe that some simple information can help a new primary to propose the creation of a block which is identical (or at least very similar to previous ones, which would help to speed-up consensus). The following strategy could be adopted:
- Replicas can inform which txs are present (or not) by providing a bit array (one bit per transaction index on block) connected to previous proposal;
- If supports the same transaction, it is guaranteed to exist (and be valid). If support that transaction, it is fundamental that the next primary should include it since at, least, honest nodes are going to realize the aforementioned guarantee;
- If a sufficient amount of transactions are present (within a threshold), next primary could propose the same block, resolving all possible issues with nodes committed in the past.
We can still certainly devise more strategies here, and although this increases the burden of a view change message, this is the last opportunity that a replica will have to express itself and avoid future issues. Thus, for ensuring commit consistency across views, replicas can agree on the same block, even after change views, by following these proposed set of strategies. If a non-faulty replica committed on view v, it means that agreed, meaning that at least non-faulty nodes agree (they have all block transactions, which are valid). A change view requires agreement, so as long as non-faulty nodes include all info during view change (including known proposal and responses) at least one non-faulty replica will re-issue the same valid block that could have been previously committed.
Thus, new primary will issue a new proposal (called NewView on PBFT) including extra view change info and the new proposal itself (repeated proposals may be easily eclipsed using simple sign hash techniques). So, it may have two options: if it responded already on view v, it must re-issue the block on (it is proven that it has participated). If it did not participate, then it may issue a new one. As aforementioned, an interesting strategy involves a bit vector sent by nodes, so it can be known which transaction were commonly agreed by non-faulty replicas (just sum ) on previous rounds, so it accelerates the next block to also include those transactions, although global hash will change this time. If it does not change, nodes can reuse the responses from last round in a direct response-commit pack, thus skipping new phases if something improved in the meantime (during view change). This way, it becomes very hard for byzantine primary to maliciously participate on view v, and then forcefully change hash on .
We should note that such targeted attacks (see Figure 11) are even harder to perform on a decentralized P2P network than when replicas are directly connected to themselves. This gives another strong justification for the P2P design (P.5). Consistency should be carried through phases, which is why aggregate messages are necessary for safety (and that is why delayed messages from previous phases must always be discarded).
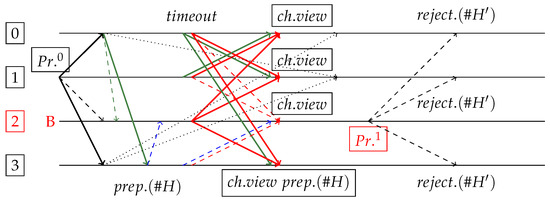
Figure 11.
Failed attack on dBFT 2.0+, where replica is malicious. Request sent by non-faulty replica (on view 0) makes non-faulty replica commit. Due to delays, no one receives messages from , and malicious pretends that messages were not received (neither the prepare request from , response from , or commit from ). Byzantine requests a change view on timeout, and all nodes do the same (even committed replica ). Please note that ViewChange messages also carry prepares and responses for non-faulty replicas, so necessarily become aware of a valid proposal ( confirmations). This way, new primary cannot maliciously propose a new block , and if it was honest, it would re-propose on view 1. If re-proposed, would again respond to it, including its previous commit (adjusted to view 1). Please note that will never issue a different signature, in any case. Eventually all non-faulty replicas will agree on (even if they need to change view again).
A more complex attack is presented in Figure 12. Please note that these attacks depend on a malicious agent deliberately hiding known information, thus allowing the next primary to change proposal hash. As already highlighted, this cannot happen in PBFT, because all order proposals (sequence numbers n) can only be performed by primaries, with signed information. Therefore, if a single agent presents information during change view, this information helps the decision-making of the next primary to preserve all previous orderings (thus allowing precise commits, even in different views). One thing that remains unknown for PBFT, is a case when a byzantine primary issues double signatures, and in a similar way to Figure 12, replicas end up receiving conflicting orderings during change view. It is not clear how to deal with that intentional malicious case, which is very different from simple crash failures. A more detailed description of PBFT can be found on [15], specifically focusing on change view details and assumptions (including the necessity of ViewChangeAck messages since regular payload is not signed).
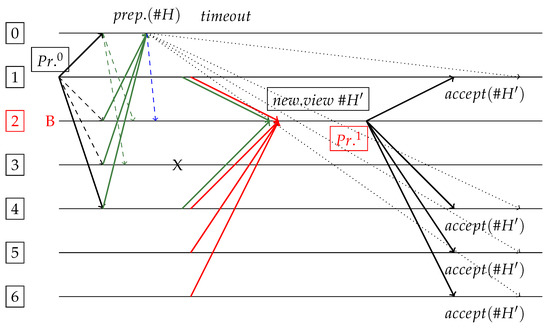
Figure 12.
Complex attack on dBFT 2.0+, where replica is malicious. Byzantine helps commit, and then it assumes new proposal . By unfortunate delays, replicas and are unaware of previous proposal from , and delays prevented to participate on next view change, which “elects” byzantine . Although proposal is effectively informed during view change (always at least one non-faulty will inform), there is not enough confirmations of to force malicious primary to keep it (then it starts a new one ). Replica dies after response to (this can also be considered a malicious attack under quota ). As long as delays are large enough, replicas may form a new block .
The example detailed in Figure 12 is not that bad since the system would converge to (instead of ). In this sense, byzantine replicas would not gain much benefit from the attack, as block is still valid. If any conflicting messages arrive to replicas (at any future time), they would have information to blacklist , and if this happens during consensus, honest replicas would directly trigger another change view together with blacklisting, thus possibly returning to proposal . This is very complex because, as soon as non-faulty replicas respond to , they could only send message during another change view round, otherwise they would be helping to possibly generate a spork, which is not possible unless some of them commit to . If this happens, perhaps at some point (future change view), replicas could become aware that no consensus is possible anymore, and try to fully reset the round (including blacklistings). The worst aspect of this situation is that Byzantine can wait calmly until this event occurs (due to unfortunate delays), and immediately respond accordingly to generate the issue.
5. Promising dBFT Extensions: Towards dBFT 3.0
A further evolution of dBFT 2.0 may help dBFT to achieve better efficiency on consensus, and also to allow broader community participation on the process (boosting network decentralization). This section presents a possible direction that is worth exploring and can improve system resilience and robustness. Following this reasoning, we introduce a weak-synchronous extension of current dBFT 2.0 with two concurrent speakers. In addition, it also discusses an analogous algorithm with primaries (Section 5.3).
5.1. Design Principles
The dBFT 3.0 proposal intends to improve dBFT 2.0 in the following manner:
- (X.1)
- allowing multiple “simultaneous” block proposals (in same view)
- (X.2)
- remove the “special status” of a single primary node: by having (X.1), a single faulty replica cannot delay block generation
- (X.3)
- community participation: by having (X.1), one can afford letting “unvoted” and “highly staked” guest nodes to participate on consensus without risking the network safety, eventually contributing and also earning fees
- (X.4)
- in-time consensus: exact T seconds with block finality (on average)
Some interesting extensions can also be included, such as:
- (X.5)
- community interaction messages from nodes via p2p
We believe that (X.5) could incentivize the early reporting of failures (or even scheduled ones) via P2P, and instantly pass information to users via integration with social networks, wallets and traditional messaging systems. This can also be used (although in a limited way) to provide new monetization means for consensus nodes, by exploring its visibility and “status”, to merchandise for its affiliate projects via P2P.
5.2. dBFT 3.0-WS2: Double Proposals on dBFT
A known weakness of PBFT, dBFT and other primary-based consensus (spinning, etc.) is that consistent primary failures will always trigger a change view (losing time every round). In the spirit of dBFT 3.0 with multiple proposals, one way to extend single block proposal limitation (single primary) is to simply extend it to two primaries. We were hopefully able to design such system in a safe manner, by introducing an extra Pre-Commit Phase. We call this consensus as dBFT 3.0 with weak synchrony and two primaries (dBFT 3.0-WS2). An interesting property of dBFT 3.0-WS2 is that although it may require four phases to achieve consensus, for the great majority of cases (obtained from big set of experiments especially performed to detect such cases), the system could shortcut directly to Commit Phase, leading to three-phase consensus. This happens when the network is synchronous, and the first primary is not faulty.
The general strategy is quite similar to dBFT 2.0, which we present step-by-step for dBFT 3.0-WS2:
- (W.1)
- Replicas receive past block with timestamp
- (W.2)
- Primary 0 of next block on view 0, i.e., , set next timeout to , while Primary 1 of same view 0, i.e., , sets its to (extra seconds, e.g., for a parameter )
- (W.3)
- If Primary 0 is well, it will release a good proposal on time
- (W.4)
- If network delays are not huge (good case), non-faulty replicas will receive proposal and respond to it. In this case, Primary 1 does not need to send proposal , but there may be good reasons to do it anyway, as discussed further on.
- (W.5)
- dBFT 3.0 still follows dBFT 2.0 pattern of PrepareRequest and PrepareResponse phases, but, with an additional Pre-Commit phase, which operates as follows:
- (a)
- pre-commit to Primary 0 is sent when a node has Preparations (PrepareResponse and the PrepareRequest hashes) to Primary 0 among Preparations payloads already received
- (b)
- pre-commit to Primary 1 is sent when, at least, Preparations for Primary 1 are obtained
- (W.6)
- The interesting point of Pre-Commit phase is that it can be skipped completely if response to Primary 0 are obtained. Then, commit to Primary 0 can be directly sent.
- (W.7)
- This strategy allows Primary 0 to have priority over 1, thus resolving consensus very quickly, and directly triggering a Commit message (with signature release that cannot be undone)
- (W.8)
- If no commit is issued, and the timer expires, replicas will issue a change view (same as dBFT 2.0)
As with dBFT 2.0+, in the next round, some interesting strategies are possible such as trying to stick to previous strong proposals (with next primary re-proposing them). In this sense, allowing newer responses to them and resolve the undecided situations, in which the network does not have enough Preparations for Primary 0 neither to Primary 1. This strategy could be called dBFT 3.0+.
5.2.1. Byzantine Attacks on dBFT 3.0-WS2: Towards dBFT 3.0+
Byzantine nodes can be faulty up to f, and systematically not replying to messages may cause undecided situations to arise, requiring a change view. This happens to likely be the worst action a byzantine actor can perform on dBFT 3.0-WS2 (shutdown its own replica), as discussed in the following paragraphs.
Malformed proposals or responses are not smart attacks, since they are directly detected and will trigger a temporary blacklist action on that replica. They cannot fake other identities as well, due to public-key cryptography. A byzantine primary can still propose a “valid” block, but including certain transactions that are not found on mempool (or does not even exist), according to (P.8). However, this byzantine action still cannot force nodes to commit to a bad proposal, as every non-faulty response to that proposal would require a non-faulty replica to actually have all the transactions (guaranteeing that block is valid after all).
On the other hand, a tricky thing that a byzantine node can try to do is to respond simultaneously to multiple proposals (also using network asynchrony in its favor), in the hope of committing other nodes to follow different proposals. There are two ways of circumventing this malicious attack, according to the global strategy of the network. One thing is certain: any detected double proposal will issue a blacklist on that node, with all side effects it will have according to off-chain governance. Here are the options for a dBFT 3.0-WS2+:
- To detect double proposals efficiently (and blacklist faster), one can aggregate pre-commits before issuing/following a commit (pre-commits should carry known preparations). This leaves no space for byzantine nodes to pass undetected (In empirical experiments this appeared to be true in all cases tested. Feeling up to now indicates that it will be nearly impossible for a byzantine node to pass unnoticed from double responses, thus certainly being blacklisted, and the spork prevented.)
- To be more speculative, one may follow pre-commits fast strategies (thus allowing the skipping of one phase in most cases), and issuing a blacklist on byzantine node only after it is detected (perhaps after issuing its own commit, which may cause a spork)
The question is: what are the interests of a consensus node in issuing a double response, in trying to spork when values are at stake? This question does not need even to be fully resolved as a matter. One node may be more speculative according to the responses of some more trusted replica, while being more conservative according to other (perhaps towards an unknown guest node). Many flavors are possible here (both for consensus and network nodes), according to the overall network policy and values at stake. We believe that this opens even more doors for academic discussions on the topic, allowing different solutions to different implementations of consensus node for dBFT 3.0-WS2.
5.2.2. Validation Experiments
To validate the idea of dBFT 3.0-WS2, we have performed some experiments (Source code available at: https://github.com/NeoResearch/dbft3-spork-detect). Experiments consisted of verifying existing scenarios (from a randomized perspective due to exponential number of scenarios), and analyze the respective achieved agreements. The intention is to discover which scenarios can generate sporks, if any. We believe this is a faster approach to validate the idea, before devising possibly complex proofs. This approach is also supported by the fact that indeed, some scenarios may lead to lack of decision on first phase. We discovered that for only 12% of cases, such situations could be presented (with simultaneous presence of network delays and Byzantine agents).
Table 1, Table 2, Table 3, Table 4 and Table 5 present, in a condensed representation, a summary of some key cases selected from the experiments. Notation means that agreement to proposal 0 was sent by replica i, what implies that and are proposals (others are responses), while − means that no message arrived.

Table 1.
dBFT 3.0-WS2: Good Case for Primary 0. No faulty node. All nodes received confirmations for 0, meaning that at least one non-faulty agrees with replica 0, after responses/proposals. System commits globally at 0.

Table 2.
dBFT 3.0-WS2: Good Case for Primary 1. Primary 0 is faulty (or too slow). Replicas agree with primary 1 after responses/proposals for it. System commits globally at 1.

Table 3.
dBFT 3.0-WS2: Undecided Case 0 (). For subset , no agreement currently exists with zeros (priority) or ones. No faulty node, but requires pending messages to arrive, or network will change view.

Table 4.
dBFT 3.0-WS2: Speed-up Case of () with Byzantine node . Node uses speed-up condition to directly commit to 0. A delay of messages could easily generate a need for change views due to the Byzantine attack of .

Table 5.
dBFT 3.0-WS2: Faulty Case with . For subset , no agreement currently exists with zeros (priority) or ones. Replica 2 is faulty, but other replicas cannot know if it will recover to resolve commit, so system will change view due to an undecided situation.
5.3. Towards Generalized Speakers Proposals
Please note that dBFT 3.0-WS2 already achieves proposals for in a consensus (double proposal). Thus, it does not seem impossible to design similar mechanisms, on practice, for and beyond. However, more challenges will emerge if we move to proposals, such as:
- extra complications on commit rules (need to revise priorities for the third proposer)
- extra edge cases to monitor (need to perform extra simulations for each possible Byzantine role)
- extra messages on network (higher burden on network due to extra messages)
Thus, we argue that if this generalized -strategy is indeed necessary (or just keep it fixed to 2 simultaneous proposals), since blacklisting mechanisms of dBFT 3.0-WS2 already allow close monitoring of nodes and could “solve” failure issues (blacklisting is especially effective when nodes are consistently faulty). When multiple nodes are constantly faulty, some off-chain governance (such as voting) may typically “solve this problem”, while the only issue of having multiple failed nodes is extra change views (as on dBFT 2.0).
A comparison of features in existing dBFT version is presented in Table 6 (namely dBFT 1.0 and dBFT 2.0), while Table 7 summarizes a comparison of the variants proposed in this paper (namely dBFT 2.0+, dBFT 3.0-WS2 and dBFT 3.0-WS2+) (At this point, we consider dBFT 3.0-WS2 and dBFT 3.0 as synonyms, since dBFT 3.0 would refer to the “standard name” of the third-generation dBFT, if proposal dBFT 3.0-WS2 is officially accepted by Neo Core Developers. To the present date, dBFT 2.0 is the official consensus algorithm on Neo Blockchain.).

Table 6.
Comparison for existing dBFT variants

Table 7.
Comparison for the dBFT variants proposed in this study
6. Conclusions and Future Works
In this paper, we explore variants of PBFT-inspired consensus for blockchain, focusing on the dBFT consensus of the Neo Blockchain and raising theoretical background for the underlying peer-to-peer network and for blockchains. We analyze the first and second generations of dBFT consensus (dBFT 1.0 and 2.0), which have been running on Neo’s Mainnet. Inspired by the common challenge faced by consensus of guaranteeing one block finality (without issues related to chain forks or sporks), this paper explores possible Byzantine attacks and frequent natural network failures.
Based on a deep understanding and generalization of the PBFT principles extended to 1BF on blockchain, we introduce improvements for the second generation of dBFT 2.0 (namely dBFT 2.0+). It involves the use of proofs during change views, which can help the system to avoid isolated committed nodes in normal operations (without intentional Byzantine agents), reinforcing that committing locally implies in committing globally.
This study also presents directions for a third generation with multiple block proposals, namely dBFT 3.0, by adding an additional consensus negotiation phase (being composed of four phase: PrepareRequest, PrepareResponse, Pre-Commit and Commit). We analyze the impacts on consensus liveness considering a double speakers proposal, which is experimentally validated, estimating that network instability issues could be faced on 12% of cases (requiring change views). A speed-up mechanism is also verified, indicating that only three of the four consensus phases would be typically used on practice (the additional Pre-Commit phase could be skipped). In addition, blacklisting techniques that could restrain Byzantine attackers are highlighted, which would keep a track of the “consensus message trails”.
For the future, we intend to expand the analysis of the replicated speakers proposal for a greater number of nodes, then, verifying the impact of the proposed strategy when nodes propose blocks simultaneously. We also plan to compare with pure asynchronous consensus implementations and validate them using network message delivery assumptions by performing real-scenario network simulations.
Author Contributions
The group of authors contain researchers with a variety of backgrounds, from applied Computers Scientists to specialists in Optimization, Cryptography and Game Theory. The team has been formed throughout the open-source project Neo, which connected these members into different events that they participated together in the USA, China and Brazil. In particular, I.M.C. devised the relationship between the PBFT foundations and the state-of-the-art of dBFT. He was able to design the didactic representation used throughout this work, detecting several possible scenarios and designing the proposed extension together with V.N.C., which assisted the writing of the paper and the comprehension of the historical versions of the dBFT consensus. R.P.A. assisted in the revision of the paper and didactic examples. W.Y.Q. assisted the team with game theory discussions for understanding the motivation for Byzantine attacks and studying the current economic model of Neo Blockchain. B.D.R. assisted with revisions and studies on Redundant speakers, so as fruitful discussions on the nature of decentralized networks. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been done in partnership with NeoResearch, a worldwide open-source community and support of Neo Foundation. Igor M. Coelho was partially supported by the Brazilian funding agency CNPq (PQ-2 313777/2018-7).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| 1BF | One Block Finality |
| BFT | Byzantine Fault Tolerance |
| dBFT | Delegated Byzantine Fault Tolerance |
| dBFT 2.0 | Delegated Byzantine Fault Tolerance 2.0 |
| dBFT 2.0+ | dBFT 2.0 with improvements |
| dBFT 3.0 | Delegated Byzantine Fault Tolerance 3.0 |
| dBFT 3.0-WS2 | Delegated Byzantine Fault Tolerance 3.0 with two concurrent speakers |
| dBFT 3.0-WS2+ | dBFT 3.0-WS2 with change view information sharing |
| DLT | Distributed Ledger Technology |
| FLP | Fischer, Lynch and Paterson |
| P2P | Peer-to-Peer |
| PBFT | Practical Byzantine Fault Tolerance |
| PoW | Proof-of-Work |
References
- Nakamoto, S. Bitcoin: A Peer-To-Peer Electronic Cash System. 2008. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 29 July 2020).
- Bashir, I. Mastering Blockchain: Distributed Ledger Technology, Decentralization, and Smart Contracts Explained; Packt Publishing Ltd: Birmingham, UK, 2018. [Google Scholar]
- Coelho, V.N.; Cohen, M.W.; Coelho, I.M.; Liu, N.; Guimarães, F.G. Multi-agent systems applied for energy systems integration: State-of-the-art applications and trends in microgrids. Appl. Energy 2017, 187, 820–832. [Google Scholar] [CrossRef]
- Vujičić, D.; Jagodić, D.; Ranđić, S. Blockchain technology, bitcoin, and Ethereum: A brief overview. In Proceedings of the 2018 17th International Symposium Infoteh-Jahorina (Infoteh), Istočno Sarajevo, Republika Srpska, 21–23 March 2018; pp. 1–6. [Google Scholar]
- Fischer, M.J.; Lynch, N.A.; Paterson, M.S. Impossibility of Distributed Consensus with One Faulty Process. J. ACM 1985, 32, 374–382. [Google Scholar] [CrossRef]
- Lamport, L.; Shostak, R.; Pease, M. The Byzantine generals problem. ACM Trans. Program. Lang. Syst. (TOPLAS) 1982, 4, 382–401. [Google Scholar] [CrossRef]
- Castro, M.; Liskov, B. Practical Byzantine fault tolerance. OSDI 1999, 99, 173–186. [Google Scholar]
- Veronese, G.S.; Correia, M.; Bessani, A.N.; Lung, L.C. Spin one’s wheels? Byzantine fault tolerance with a spinning primary. In Proceedings of the 2009 28th IEEE International Symposium on Reliable Distributed Systems, Niagara Falls, NY, USA, 27–30 September 2009; pp. 135–144. [Google Scholar]
- Aublin, P.; Mokhtar, S.B.; Quéma, V. RBFT: Redundant Byzantine Fault Tolerance. In Proceedings of the 2013 IEEE 33rd International Conference on Distributed Computing Systems, Philadelphia, PA, USA, 8–11 July 2013; pp. 297–306. [Google Scholar] [CrossRef]
- Hongfei, D.; Zhang, E. NEO: A Distributed Network for the Smart Economy; Technical Report. NEO Foundation, 2015. Available online: https://docs.neo.org/docs/en-us/basic/whitepaper.html (accessed on 29 July 2020).
- Bracha, G.; Toueg, S. Asynchronous consensus and broadcast protocols. J. ACM 1985, 32, 824–840. [Google Scholar] [CrossRef]
- The Honey Badger of BFT Protocols. Available online: https://github.com/initc3/HoneyBadgerBFT-Python (accessed on 18 August 2019).
- Miller, A.; Xia, Y.; Croman, K.; Shi, E.; Song, D. The honey badger of BFT protocols. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016; pp. 31–42. [Google Scholar]
- Herlihy, M.P.; Wing, J.M. Axioms for concurrent objects. In Proceedings of the 14th ACM SIGACT-SIGPLAN Symposium on Principles of Programming Languages, Munich, Germany, 21–23 January 1987; pp. 13–26. [Google Scholar]
- Castro, M.; Liskov, B. Practical Byzantine fault tolerance and proactive recovery. ACM Trans. Comput. Syst. (TOCS) 2002, 20, 398–461. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).