A Probabilistic VDTN Routing Scheme Based on Hybrid Swarm-Based Approach

Abstract

The probabilistic Delay Tolerant Network (DTN) routing has been adjusted for vehicular network (VANET) routing through numerous works exploiting the historic routing profile of nodes to forward bundles through better Store-Carry-and-Forward (SCF) relay nodes. In this paper, we propose a new hybrid swarm-inspired probabilistic Vehicular DTN (VDTN) router to optimize the next-SCF vehicle selection using the combination of two bio-metaheuristic techniques called the Firefly Algorithm (FA) and the Glowworm Swarm Optimization (GSO). The FA-based strategy exploits the stochastic intelligence of fireflies in moving toward better individuals, while the GSO-based strategy mimics the movement of glowworm towards better area for displacing and food foraging. Both FA and GSO are executed simultaneously on each node to track better SCF vehicles towards each bundle’s destination. A geography-based recovery method is performed in case no better SCF vehicles are found using the hybrid FA–GSO approach. The proposed FA–GSO VDTN scheme is compared to ProPHET and GeoSpray routers. The simulation results indicated optimized bundles flooding levels and higher profitability of combined delivery delay and delivery probability.

1. Introduction

DTNs refers to Delay Tolerant Networks, a particular category of the ad-hoc networks characterized by consistent low density levels which result in an intermittent connectivity between nodes [1]. The architecture of DTNs [2] is the appropriate communication paradigm for numerous applications such as the ones spread in [3]. DTN routing relies on the Store-Carry-and-Forward (SCF) principle [4] which consists of storing bundles (data packets) in the buffer cache of the host node for undefined duration when better relay nodes to forward bundles are not available. The bundle is carried until at least one better relay node opportunity arises. Then, the bundle are either replicated or forwarded to the selected SCF node according to the adopted routing policy of the DTN protocol [5].

The DTN routing have been extended to vehicular networks (VANETs) introducing the Vehicular DTNs (VDTNs) seen in the intermittent routing conditions that characterize different vehicular mobility scenarios [6]. The SCF principle is more required for VDTNs than DTNs so that the vehicular communication constraints such as high speed, traffic lights, predefined mobility direction and radio obstacles are better handled [7].

The probabilistic, or prediction-based, VDTN forwarding is one of the most effective routing policies in DTN-based networks [8]. This DTN routing mode consists of exploiting the forwarding historic of nodes to predict their future routing abilities in order to make SCF forwarding decision and define the appropriate buffer management policy [9]. The illustration of the prediction-based routing mode amongst the VDTN routing categories is spread in [10].

The probabilistic DTN routing has been cited in few taxonomies such as in [11] which introduced the founded DTN routers based on the Probabilistic Routing Protocol using History of Encounters and Transitivity (PRoPHET) [12], deriving different modifications on the basis of delivery predictability concept notably the contact duration and the distance-based delivery probability.

The swarm optimization is one of the most effective techniques for combinatorial and hard problems [13]. Such approaches have been opted for solving the problem of routing in conventional VANETs [14] and responded with improved performances comparing to the conventional routing solutions. Hence, the challenge of extending the stochastic swarm computation techniques to the vehicular DTN routing became highly solicited. The bio-inspired metaheuristics are the mostly optimization techniques adapted to the stochastic search of better candidate solutions which fits with the nature of probabilistic routing in VDTNs. Such optimization methods have been involved in VANET routing enhancement, as in [15], which discussed realized bio-inspired routing contributions in VANETs. As illustration, the social-based DTN routing has been discussed as well by [16] showing the utility of human social behaviors as grouping in improving the quality of SCF routing.

In this paper, we propose an extension of the bio-inspired DTN routing through the application of a new swarm-based forwarding strategy for VDTNs founded on the stochastic search of two combined swarm-inspired techniques.

This manuscript is organized as follows: Section 2 gathers together the literature works in probabilistic VDTN routing field. Section 3 introduces the implemented swarm-inspired optimization approaches for supporting probabilistic VDTN routing. Section 4 details the suggested swarm VDTN solution with illustrated examples. Section 5 follows with the simulation phase and discussed results. Section 6 finalizes with the conclusion and perspectives of this work.

2. Literature Review

The probabilistic DTN routing has been developed widely in VANETs to face consistently-sparse networks.

PRoPHET [12], a greedy-based predictive DTN routing scheme founded on the concept of delivery predictability (DP). The DP measures the ability of encountering nodes to forward bundles towards their destinations into a variable named the encounter predictability value. Nodes continuously exchange any updates indicating higher predictability values of neighbors than the one of bundle carrier node. Further, to the direct probability between two nodes (‘A’ and ‘B’ for instance), The DP supports transitive predictability values liaising between nodes having common direct contacts. This property extends the DP impact for larger neighborhood areas. Thus, a meeting table regrouping direct and indirect historic contacts is saved on each node. A third DP characteristic called the data aging is mandatory to temporarily update the predictability values.

Probabilistic Bundle Relaying Scheme (PBRS) [17] hybrid DTN router combines knowledge-based and prediction-based forwarding modes. PBRS finds the prediction of the required duration to deliver every bundle to its destination for each candidate SCF node. Thus, the notion of release probability (Pr) is introduced for this purpose by referring to node speed as the evaluation parameter to calculate the probability of passing a bundle to another node. The Pr value is expected to cut down the bundle’s store time in buffer cache so that the total delivery delay is cut down consequently.

PRoPHET-based Spray-and-Wait (SnW) [18] is a combined ProPHET-SnW protocol which integrates the probabilistic concept of PRoPHET on SnW router [19]. The ProPHET’s DP is performed during the spray phase, where L copies of each bundle are forwarded to the nodes providing higher delivery probability values. When the number of copies is reduced to 1, the SnW’s wait phase is triggered. ProPHET-based SnW adopts also a buffer management mechanism to control buffer cache overflow efficiently by checking the bundles’ size to meet the remaining buffer space of available candidate SCF nodes. This policy contributes to increase the delivery probability.

Improved PRoPHET [20] is a hybrid Epidemic-ProPHET router. Epidemic (ER) [21] is enabled in early steps of forwarding operation which helps to propagate quickly bundle copies. While ProPHET follows in advanced stages of routing process to improve orientation of spread copies by ER. ProPHET is enabled when either a hop count threshold or a predefined number of forwarded bundles are reached.

PRoPHET+ [22] is a modified version of PRoPHET conceived to improve the selection of bundles’ carrier by introducing the delivery value ($V_D$) on the next-SCF node selection on the basis of a predefined threshold comparison. The $V_D$ is calculated for every candidate next-SCF node following the $V_D$’s evaluation function in Equation (1) which is composed from four weighted parameters:

• Buffer parameter ($V_B$), which is the difference between remaining buffer space ratio minus the bundle size.
• Power parameter ($V_P$), which is the remaining power from the difference between device power and the minimum power for sending and receiving bundles.
• Popularity parameter ($V_O$), which is the ratio of number of performed transmissions on the maximum number of transmissions.
• Bandwidth parameter ($V_A$), which is the ratio between received node’s bandwidth and host’s bandwidth.

$$V_D=(W_B\times V_B)+(W_P\times V_P)+(W_A\times V_A)+(W_O\times V_O)+(W_R\times V_R)$$

(1)

$W_B$, $W_P$, $W_A$ and $W_O$ are respectively the affected weights for the predefined evaluation parameters.

A candidate node handles the bundle if it has higher $V_D$ than the predefined $V_D$ threshold. The best $V_D$ is used as a tiebreaker when numerous better candidate SCF nodes are available.

Delivery Probability Routing (DPR) [23] is an enhanced SnW router supported by a delivery probability mechanism. The latter consists of implementing a probability vector which regroups the network contacts. DPR updates this vector in both spray phase and wait phase where every node exchanges its probability vector with its contacts. This approach serves optimizing the spray phase by adjusting the remaining quota of the number of each bundle copies. Consequently, the wait phase is triggered separately for each bundle depending on the quality of the available contacts’ delivery probability values. As a result, the bundles having relay nodes with higher delivery probability get quicker to the wait phase.

HOMME-ProPHET [24] is another variety of ProPHET which includes the meeting historic of previous hops to the delivery predictability of known nodes in order to improve the routing decision of SCF node selection. Thus, the calculation of delivery predictability of each candidate SCF node considers the previous bundles’ passed nodes. Each bundle stores a probabilistic metric which estimates its delivery predictability based on its hop count and the historic of passed hops. This approach helps to take the forwarding decision by differentiating between bundles considering the quality of passed path until the host node and quality of the available delivery predictability values.

Schedule-ProPHET [25] is another probabilistic DTN router for Internet-of-Things (IoT) conceived to enhance the transmission and storage capacities of ProPHET by introducing two buffer scheduling mechanisms on the basis of delivery predictability. The latter orientates the priority of bundles in the buffer cache for either forwarding or deleting decisions. The first mechanism is the bundle management which defines the dropping priority for bundles in the case of full buffer cache. The second mechanism is the bundle transfer which includes the bundle transfer to the last destination, delivery predictability, information exchange and path selection. The latter regards the traffic load and hop count as tiebreaker to the paths having tied accumulated delivery predictability values.

Social Grouping-Based Routing (SGBR) [26] is a social-based DTN router extracted from the grouping behavior of taxi vehicles following their trajectories. SGBR considers the meeting frequency between nodes to approximate the connectivity predictability between each node and a group of nodes increasingly. The purpose is to limit the multiple-copy forwarding of bundle copies to such groups so that the ratio of overheads is reduced. On the other hand, the single-copy forwarding is performed within grouped nodes. Increasingly, the meeting historic between every pair of nodes is built in order to update the node’s connectivity degree which is the major parameter of nodes grouping. The connectivity degree is limited by a predefined threshold for acting the decision between forwarding or dropping bundles.

AntProPHET [27] is an ACO-inspired ProPHET-based router inspired from the food foraging of the swarm of ants. AntProPHET reduces the probabilistic selection of the next-SCF node to the process of food nest tracking by ants to enhance the bundles’ delivery probability regarding reducing the ratio of generated overheads. Thus, the PRoPHET’s predictability calculation is updated following the pheromone concentration decay formulae in Equation (2) where the nodes offering higher pheromone values are more likely to be selected as bundles’ carrier node.

$${\tau }_{ij}=(1-\phi ).{\tau }_{ij}+\phi .{\tau }_0$$

(2)

$\phi$ is the pheromone decay coefficient and ${\tau }_0$ the initial pheromone value.

3. Critics

The discussed literature exposes numerous lacks of the ProPHET-enhanced routers:

• The majority of discussed probabilistic DTN protocols are conceived for MANET-DTNs considering generic buffer storage limitation, low node speed, random mobility scenarios, etc.
• The delivery probability calculation is based on restricted historic-of-encounter parameters neglecting other important routing indicators around the node’s historic forwarding statistics and geographic position.
• The restriction of the SCF vehicle selection on the historic of encounters between nodes is not enough to detect the best relay nodes.
• The notion of prediction-based SCF selection in the discussed literature works is static and lacks the use of geographic position of candidate relay nodes.

4. Suggested Swarm-Inspired Metaheuristics

We introduce in this section the suggested swarm-based approaches for improving the quality of probabilistic VDTN routing:

4.1. Firefly Algorithm (FA)

The FA [28] is a swarm-inspired metaphor conceived for global optimization problems. FA models the impact of interactive attractiveness between fireflies based on their generated light intensity which is reflected by its brightness level. The latter controls their movement respecting that the less brightening fireflies moves toward the brighter ones. Fireflies use light attraction to grab other entities like prey, which is mandatory to its life activities.

The light intensity of any given firefly i is proportional to its distance to any other firefly j and it is calculated using Equation (3):

$$I=\frac{I_S}{|r^2|}$$

(3)

Considering:

• $I_S$ the initial light intensity.
• r represents the distance between fireflies i and j.

The brightness value ($\beta$) of a firefly agent reflects the intensity value (I) and is calculated based on the initial brightness (${\beta }_0$) as mentioned in Equation (4):

$$\beta ={\beta }_0\times {exp}^{-\gamma r}$$

(4)

The attractiveness value ($\alpha$) is extracted from $\beta$ value as calculated in Equation (5):

$$\alpha ={\alpha }_0\times {exp}^{-\gamma r^2}$$

(5)

Consequently, the movement of a firefly i toward a better firefly entity j is a stochastic process calculated using the Equation (6):

$$x_i^{t+1}=x_i^t+{\alpha }_{ij}(x_j^t-x_i^t)+Rand$$

(6)

Considering:

• $x_i^t$: the position of firefly i at instant t.
• $x_i^{t+1}$: the position of firefly i at instant t+1.
• $x_j^t$: the position of firefly j at instant t.
• $Rand$: a randomization parameter between 0 and 1.

The pseudo-code of the FA in Algorithm 1.

Algorithm 1. Pseudo-code of FA metaheuristic.

1: Initialize fitness function $f\left(element\right)$ for each firefly agent $element$. 2: Initialize positions of fireflies. 3: Calculate initial Brightness $F{A}_{Brightness}$ intensity for all fireflies. 4: Check $N_{LIST}$ for $Bdle$; 5: while$Ma{x}_{Iteration}$ not reached do 6:     for each $Firefly\left(i\right)$ in $Firefl{y}_{Population}$ do 7:         for each $Firefly\left(j\right)$ in $Firefl{y}_{Population}$ do 8:            $Firefly{\left(i\right)}_{BRIGHTNESS}$ = Calculate_brightness (i); 9:            $Firefly{\left(j\right)}_{BRIGHTNESS}$ = Calculate_brightness (j); 10:           if $Firefly{\left(j\right)}_{BRIGHTNESS}$ > $Firefly{\left(i\right)}_{BRIGHTNESS}$ then 11:                Move $Firefly\left(i\right)$ toward $Firefly\left(j\right)$ = $Can{d}_{SCF}$; 12:           end if 13:         end for 14:     end for 15:     Evaluate new solutions 16:     Rank fireflies and deduce best local best firefly $firefl{y}_{GBest}$ 17: end while

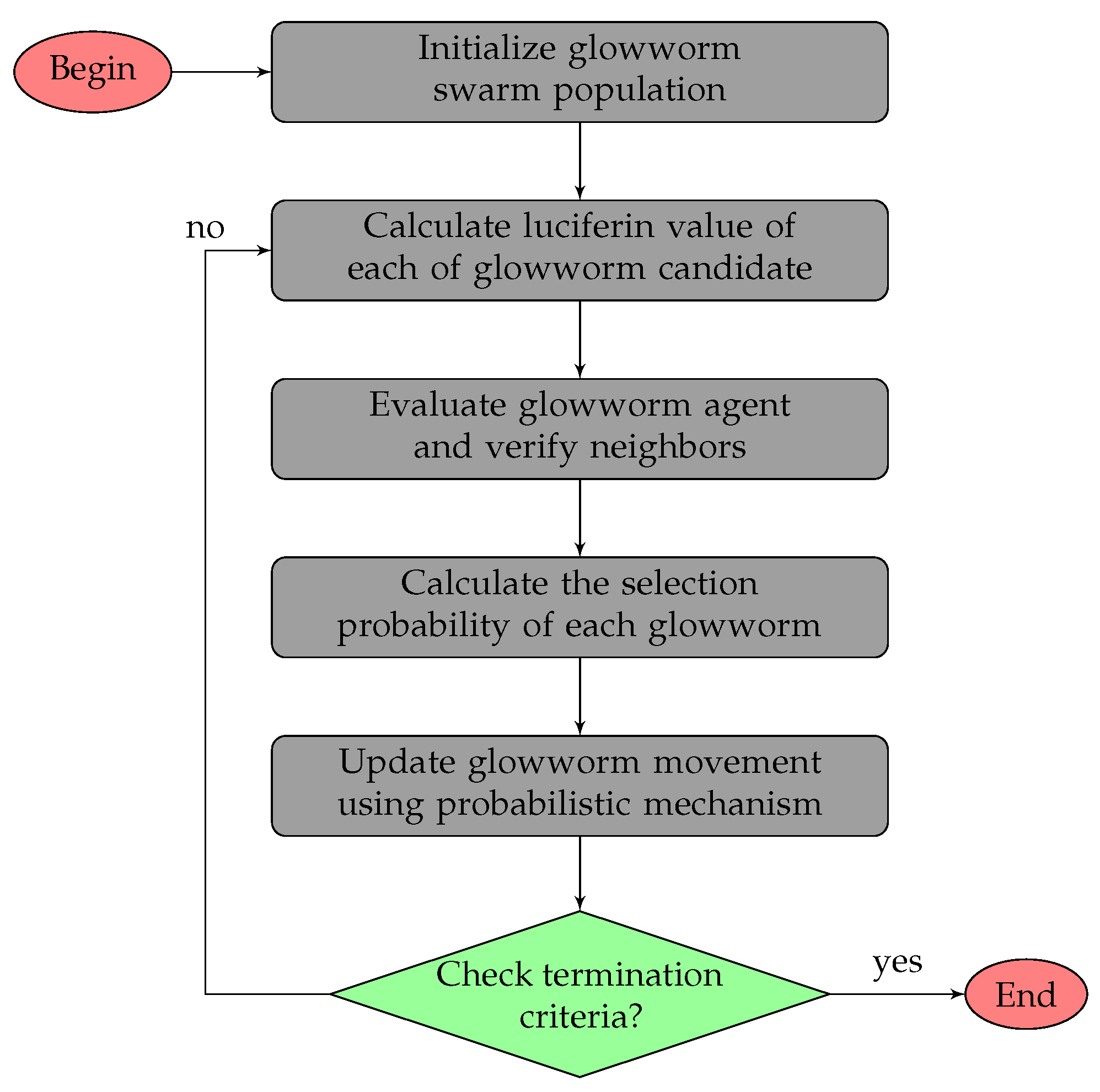
4.2. Glowworm Swarm Optimization (GSO)

The Glowworm Swarm Optimization (GSO) is a swarm-inspired metaphor approach proposed by Krishnanand and Ghose [29] and reflects the grouped movement of glowworm particles controlled by a luminescent quantity named luciferin. The latter controls the interactive behaviors between glowworms in tracking food and organizing their swarm. This behavior is modeled by the GSO along four distributed steps:

• Initialization phase: constitutes the construction of initial population of candidate solutions.
• Neighbors search: models the interaction between adjacent glowworm entities to discover better positions.
• Luciferin update: translates the previous operation by moving to better partial solutions.
• Location update: regroups the local solutions to approach the best global solution.

GSO is a variant of the Ant Colony Optimization (ACO) [30] that offers solutions to continuous functions. GSO proved better positive convergence results than ACO in the multimodal functions proving its ability to detect multiple local optima.

The luciferin intensity value ($L_j$) of glowworm agent is updated from two instant points (t) to (t + 1) following Equation (7):

$$L_j(t+1)=(1-\rho )L_j\left(t\right)+(\gamma \times F\left(p_j\left(t\right)\right))$$

(7)

Considering:

• $L_j$: the luciferin value.
• $\rho$: the update factor with $0<\rho <1$.
• F: the fitness function.
• $\gamma$: the luciferin enhancement constant.

Equation (8) calculates for each glowworm agent the probability of selection ($Pro{b}_{ij}$) according to its updated luciferin value as following:

$$Pro{b}_{ij}\left(t\right)=\frac{L_j\left(t\right)-L_i\left(t\right)}{{\sum }_{k=1}^{N_j}(L_k\left(t\right)-L_i\left(t\right))}$$

(8)

Considering:

• $N_j$: the number of candidate glowworms of glowworm i.
• $(L_j-L_i)$: the luciferin difference between glowworms j and i.

The illustration of the GSO is given in Figure 1.

5. Proposed VDTN Solution

According to our opinion, it is necessary to adjust the selection of next-SCF vehicle dynamically to the unpredictable drastic density changes. VDTNs are characterized by high mobility speed, hence the links between vehicles can be reformulated and split continuously and the disconnection time changes suffer this evolution as a results.

Thus, we introduce a combined swarm-based approach to cover this problem by adjusting the next-SCF vehicle selection with the assistance of the Firefly Algorithm (FA) and the Glowworm Swarm Optimization (GSO). Both approaches seek to find stochastically the optimum available SCF vehicle for each bundle towards its destination, according to a predefined set of SCF selection parameters.

5.1. SCF Vehicle Selection

This procedure is the fundamental operation of DTN routing and depends on the active contacts of every bundle’s host vehicle. Bundles are relayed between vehicles when better detected SCF vehicles are met according to the fitness evaluation of bundle towards its destination from the host using either FA or GSO techniques.

Each candidate SCF vehicle is evaluated based on a predefined score formula in Equation (9) which defines both FA fitness and GSO fitness evaluation procedures. This fitness value is calculated based on the following evaluation parameters:

• Number of relayed bundles ($N{b}_{Relays}$): indicates the ability of node to participate in bundles forwarding.
• Average buffer time ($Av{g}_{Buffer\_time}$): indicates also the degree of participation of node in relaying bundles between nodes.
• Number of active contacts ($N{b}_{Contacts}$): indicates the connectivity degree of node to the network.
• Average lifetime of active contacts ($Av{g}_{Lifetime}$): indicates also the connectivity consistency of the node to its neighborhood.
• Relative speed difference ($Re{l}_{Delta\_Speed}$) of candidate SCF node: including the absolute speed difference and the direction angle to the destination which indicates the geographic forwarding quality of the node.

$$\begin{array}{c}\hfill Swar{m}_{fitness}=(W_1\times N{b}_{Relays})+(W_2\times Av{g}_{Buffer\_time})+(W_3\times N{b}_{Contacts})+\\ \hfill (W_4\times Av{g}_{Lifetime})+(W_5\times Re{l}_{Delta\_Speed})\end{array}$$

(9)

The weights $W_1$, $W_2$, $W_3$, $W_4$, $W_5$ are affected to the fitness parameters consecutively. Equal weight values are affected to the fitness parameters: $W_1=0.2$, $W_2=0.2$, $W_3=0.2$, $W_4=0.2$ and $W_5=0.2$.

The calculated $Swar{m}_{fitness}$ value constitutes the evaluation score of each candidate relay vehicle for every buffered bundle in the framework of the SCF selection.

It is worth noting that there may be some cases where there is no better candidate nodes. Then, the host vehicle continues to carry the bundle until two changes occur:

• Either the new contact opportunity is met, and the host vehicle compares its fitness with the new contact to check a likely change about the best SCF vehicle,
• otherwise, a periodic update is performed to refresh the comparison of the host with its active contact so that any change about the best SCF vehicle is stated.

5.2. Firefly-Based SCF Node Selection

The FA is implemented to support the knowledge-based VDTN routing phase since we believe its adaptive quality to mimic the increasing forwarding quality of the SCF principle used for DTN routing. Fireflies offers the progressive characteristic of passing from a solution to a better one. This property is identical to SCF hops when forwarding or replicating bundles from source to destination vehicles. For VDTN routing, the FA seeks the anticipation of near-optimum relay SCF vehicles that speed up delivering bundles according to a list of predefined brightness parameters that seek optimizing replication/forwarding balance moreover to buffer residence time. In our solution, a customized FA is implemented to be adapted with the intermittent routing that characterizes VDTN networks.

The mapping between the FA elements and VDTN routing components is illustrated in

Table 1. Vehicular Delay Tolerant Network (VDTN)/Firefly Algorithm (FA) mapping.

VDTN Components	FA Elements
VDTN vehicle	Firefly agent
Next-SCF vehicle	Adjacent neighboring firefly
Forwarding quality	Luminescence
Destination vehicle	Brightest firefly

.

The initial brightness (${\beta }_0$) and attractiveness (${\alpha }_0$) values are set for each bundle on the source vehicle to a predefined value Equation (10):

$${\beta }_0={\alpha }_0=1+\frac{1}{E{D}_{Host,Dest}}$$

(10)

$E{D}_{Host,Dest}$ is the euclidean distance between the bundle’s host and destination vehicles. It is worth noticing that ${\alpha }_0$ gets increasing proportionally when the ED to the bundle’s destination gets closer.

Each candidate VDTN node’s brightness is calculated following Equation (11):

$$\beta =(1+\frac{1}{E{D}_{Host,Dest}})\times {exp}^{\frac{-\gamma }{Swar{m}_{fitness}}}$$

(11)

Considering:

• $\beta$: the up-to-date vehicle’s brightness for the stored bundle copy.
• ${\beta }_0$: the initial brightness of the bundle which is set for all nodes carrying a copy of this bundle.
• $Swar{m}_{fitness}$: the brightness fitness of the current hop’s neighbor for the given bundle.
• The absorption factor of our solution is calculated basing on the fitness value.

We deduce the vehicle attractiveness ($\alpha$) in Equation (12) for a given bundle towards its destination from the calculated brightness ($\beta$):

$$\alpha =(1+\frac{1}{E{D}_{Host,Dest}})\times {exp}^{\frac{-\gamma }{{\left(Swar{m}_{fitness}\right)}^2}}$$

(12)

The next position of each bundle b is calculated relative to each candidate’s next-SCF vehicle j amongst the current host’s active contacts following Equation (13):

$$x_b^{t+1}=x_b^t+{\alpha }_{bj}(x_j^t-x_b^t)+Rand$$

(13)

Considering:

• $x_b^t$: the bundle’s position towards the next-SCF candidate j at instant t.
• $x_b^{t+1}$: the bundle’s position towards the next-SCF candidate j at instant t+1.
• ${\alpha }_{bj}$: the attractiveness value of the candidate next-SCF vehicle j on bundle b.
• $x_j^t$: the position of next-SCF vehicle candidate j at instant t.

The candidate vehicle, which provides the best position $x_b^{t+1}$ for the bundle b, is the most likely to be selected from the host node as the next SCF vehicle that with handle the carried bundle b.

5.3. Glowworm-Based SCF Node Selection

Similarly to the FA-based approach, the probabilistic selection of GSO is used to optimize the selection of next-SCF node. The GSO seeks completing FA when the latter fails in detecting better SCF relay nodes.

The mapping between the GSO elements and VDTN routing components is illustrated in

Table 2. VDTN/GSO mapping.

VDTN Components	GSO Elements
VDTN vehicle	Glowworm agent
Next-SCF vehicle	Adjacent neighboring glowworm
Forwarding quality	Luciferin
Destination vehicle	Prey or Food source

:

The predefined SCF fitness formula is applied to update the luciferin evolution from the bundle’s host t to all candidate SCF vehicles t+1. The luciferin update formula is upgraded to the SCF node selection in Equation (14):

$$L\left(candidate\right)=(1-\rho )L\left(host\right)+(\gamma \times Swar{m}_{fitness}(host,candidate))$$

(14)

Considering:

• $L\left(candidate\right)$: the candidate node’s luciferin value.
• $L\left(host\right)$: the bundle carrier node’s luciferin value.
• $Swar{m}_{fitness}(host,candidate)$: the fitness function.
• $\rho$: the luciferin decay constant.
• $\gamma$: the luciferin enhancement constant.

The luciferin update formula by replacing the constants $\rho$ and $\gamma$ is calculated in Equation (15):

$$L\left(candidate\right)=(1-0.1)L\left(host\right)+(0.1\times Swar{m}_{fitness}(host,candidate))$$

(15)

According to the GSO process, the selection probability of passing a bundle from host to a candidate SCF vehicle ($Pro{b}_{host,candidate}$) is applied to extract the optimum SCF vehicle according to the probability values of all candidate nodes as following in Equation (16):

$$Pro{b}_{host,candidate}\left(t\right)=\frac{L_{candidate}\left(t\right)-L_{host}\left(t\right)}{{\sum }_{k=1}^{Cand\_List}(L_k\left(t\right)-L_{host}\left(t\right))}$$

(16)

Considering:

• $Pro{b}_{host,candidate}\left(t\right)$: the selection probability of a candidate vehicle from the bundle’s at period t.
• $L_{host}\left(t\right)$: the luciferin value of the bundle’s host vehicle at period t.
• $L_{candidate}\left(t\right)$: the luciferin value of a candidate vehicle relatively to the bundle’s destination at period t.
• $Cand\_List$: the luciferin value of a candidate vehicle at period t.

The candidate with the highest value is more likely to be selected as next-SCF vehicle of the bundle.

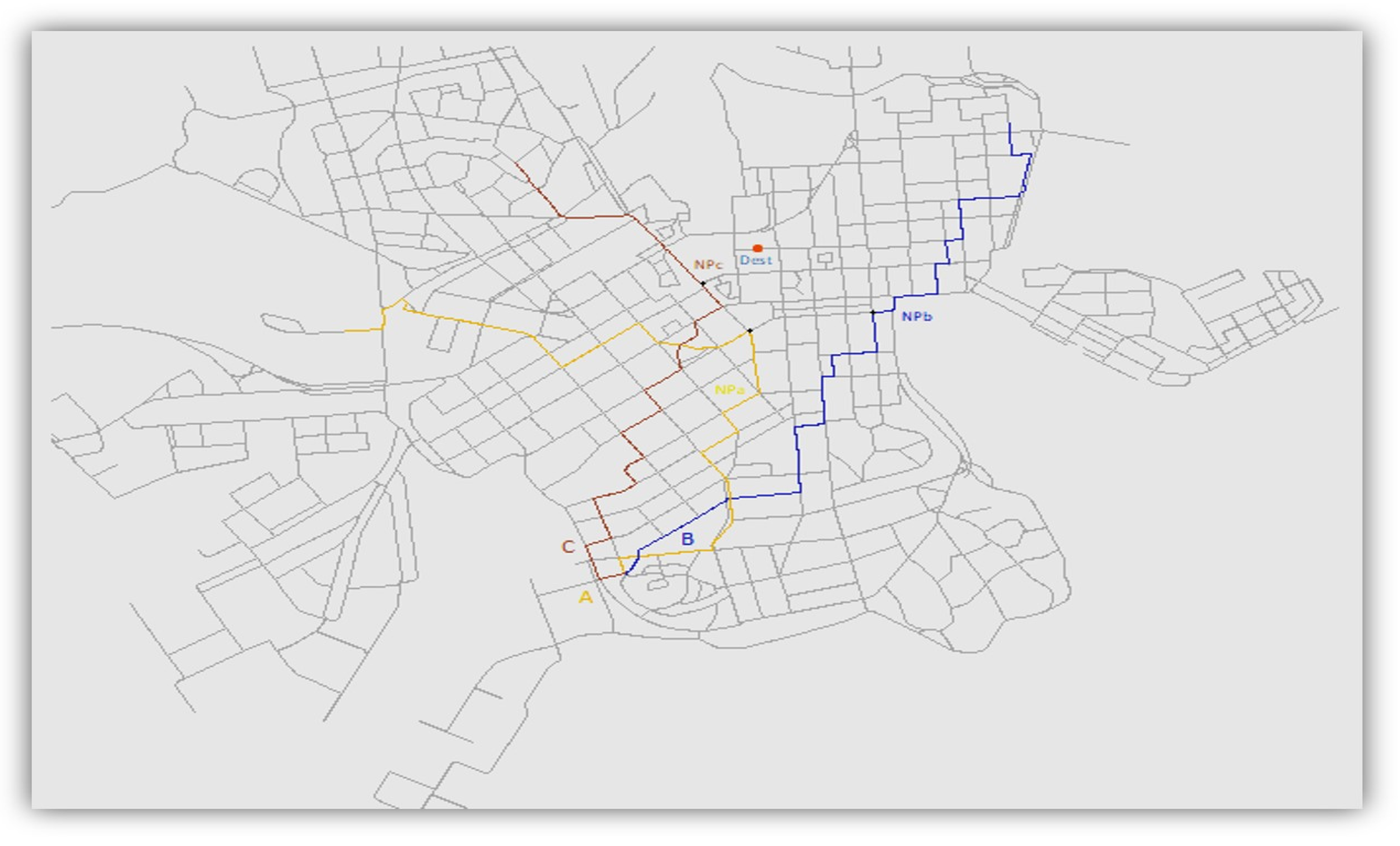
5.4. Geography-Based Recovery Forwarding

Both FA and GSO approaches are exposed to the unavailability of the next-SCF vehicles which offer better relay quality for undefined long periods. This situation forces to find a recovery mechanism to avoid the uncontrolled delivery delays generated by long buffer store time.

Thus, the Minimum Estimated Time of Delivery (METD) concept, as proposed in GeOpps [31] and GeoSpray [32], is switched by passing bundle copies to the vehicles which can reach closer positions to the destination than the bundle’s holder node.

As introduced in the METD, the estimated time of arrival between the candidate vehicle i and selected $N{P}_i$ (ETA($Host$,$N{P}_i$)) in Equation (17), and between the latter and the destination ETA($N{P}_i$,D) in Equation (18) is based.

$$ET{A}_{Host,NP\left(i\right)}=Av{g}_{Path\_Speed\left(i\right)}\times Dis{t}_{Host,NP\left(i\right)}$$

(17)

$$ET{A}_{NP\left(i\right),D}=Av{g}_{Path\_Speed\left(i\right)}\times Dis{t}_{NP\left(i\right),D}$$

(18)

Considering:

• $Av{g}_{Path\_Speed\left(i\right)}$: the extracted average speed from the GPS-calculated path of candidate vehicle i.
• $Dis{t}_{Host,NP\left(i\right)}$: the distance between the bundle’s carrier node and the nearest point of candidate vehicle i.
• $Dis{t}_{NP\left(i\right),D}$: the distance between the nearest point of candidate vehicle i and the destination.

For each candidate SCF vehicle i’s NP ($NP\left(i\right)$), the ETA is recuperated from GPS to calculate the METD in Equation (19).

$$MET{D}_i=ET{A}_{Host,NP\left(i\right)}+ET{A}_{NP\left(i\right),D}$$

(19)

The condition on which the decision to forward bundles to the next-hop nodes is based on Equation (20):

$$MET{D}_{Host}\le \frac{1}{2}\times MET{D}_{Cand\left(i\right)}$$

(20)

Considering:

• $MET{D}_{Host}$: the measured METD of the bundle’s host node.
• $MET{D}_{Cand\left(i\right)}$: the measured METD of candidate node i.

The proposed restriction of the number of METD-based selected vehicles is justified by the minimization of overheads, as the bundle forwarding is limited to candidates offering a least twice better METD quality than the bundle’s host vehicle.

The mapped illustrated use case in Figure 2 explains the proposed restricted METD mechanism.

As shown in this example, the GPS-traced path of the current bundle’s carrier (vehicle B) is compared to other available SCF candidate nodes (vehicles A and C). We notice that both vehicles B and C gather better METD values than bundle host B with $MET{D}_C<MET{D}_A<MET{D}_B$ but only node C meets the condition $MET{D}_C<\frac{1}{2}\times MET{D}_B$; thus, node C is selected as the next SCF vehicle of the forwarded bundle.

5.5. Synthesis

The presented flowchart in Figure 3 covers the entire forwarding cycle of bundle from the source to destination vehicle.

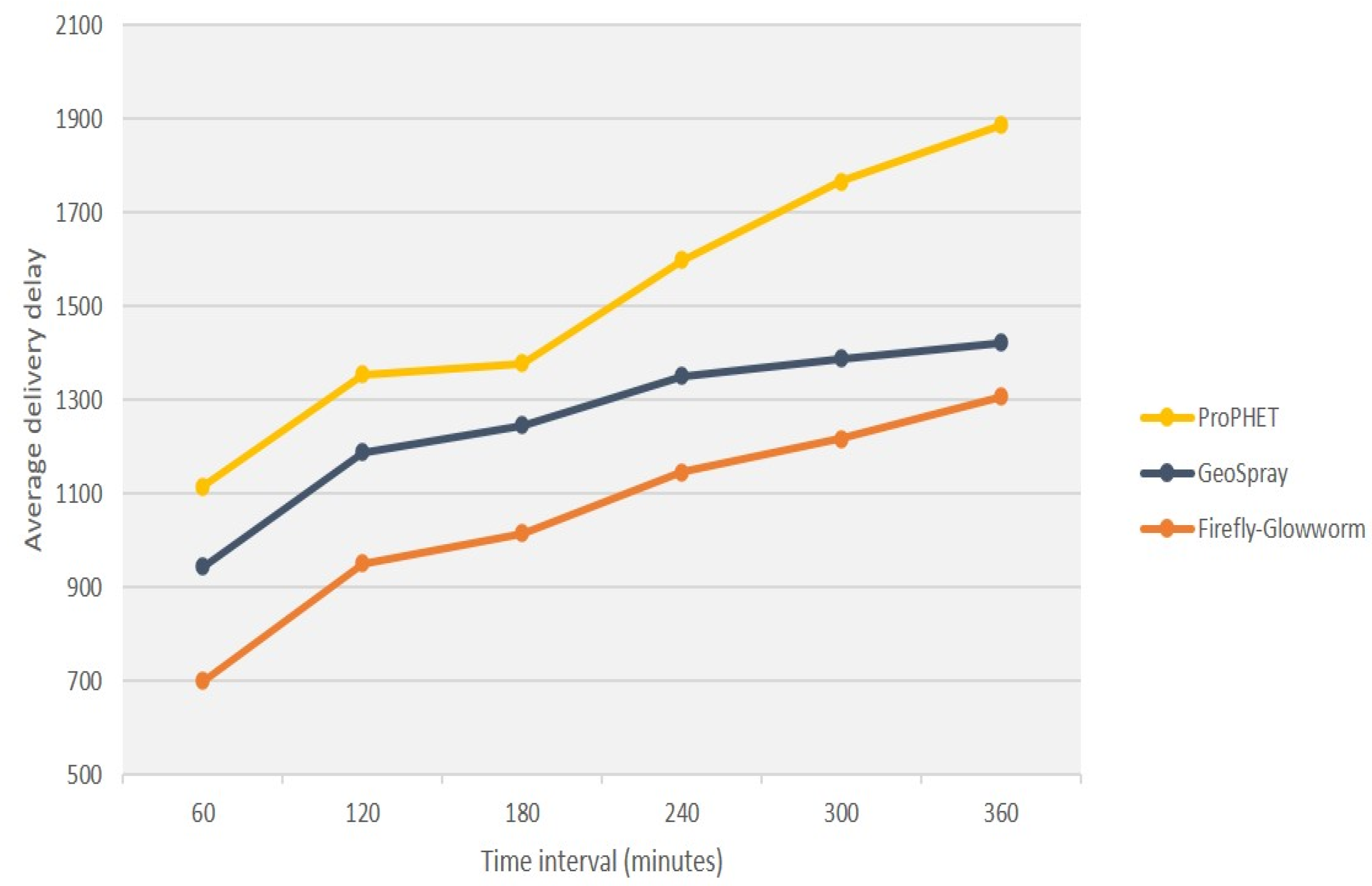
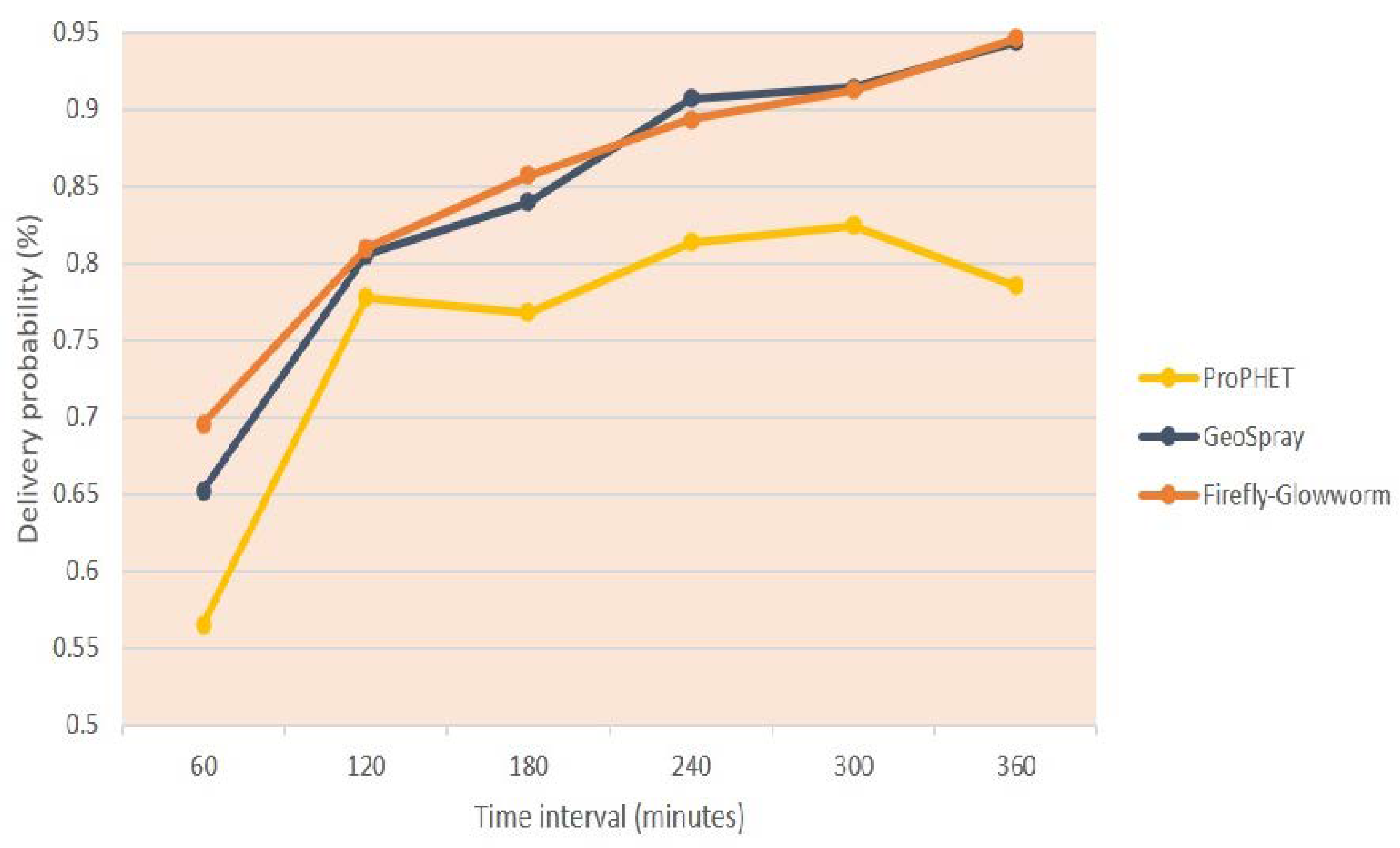
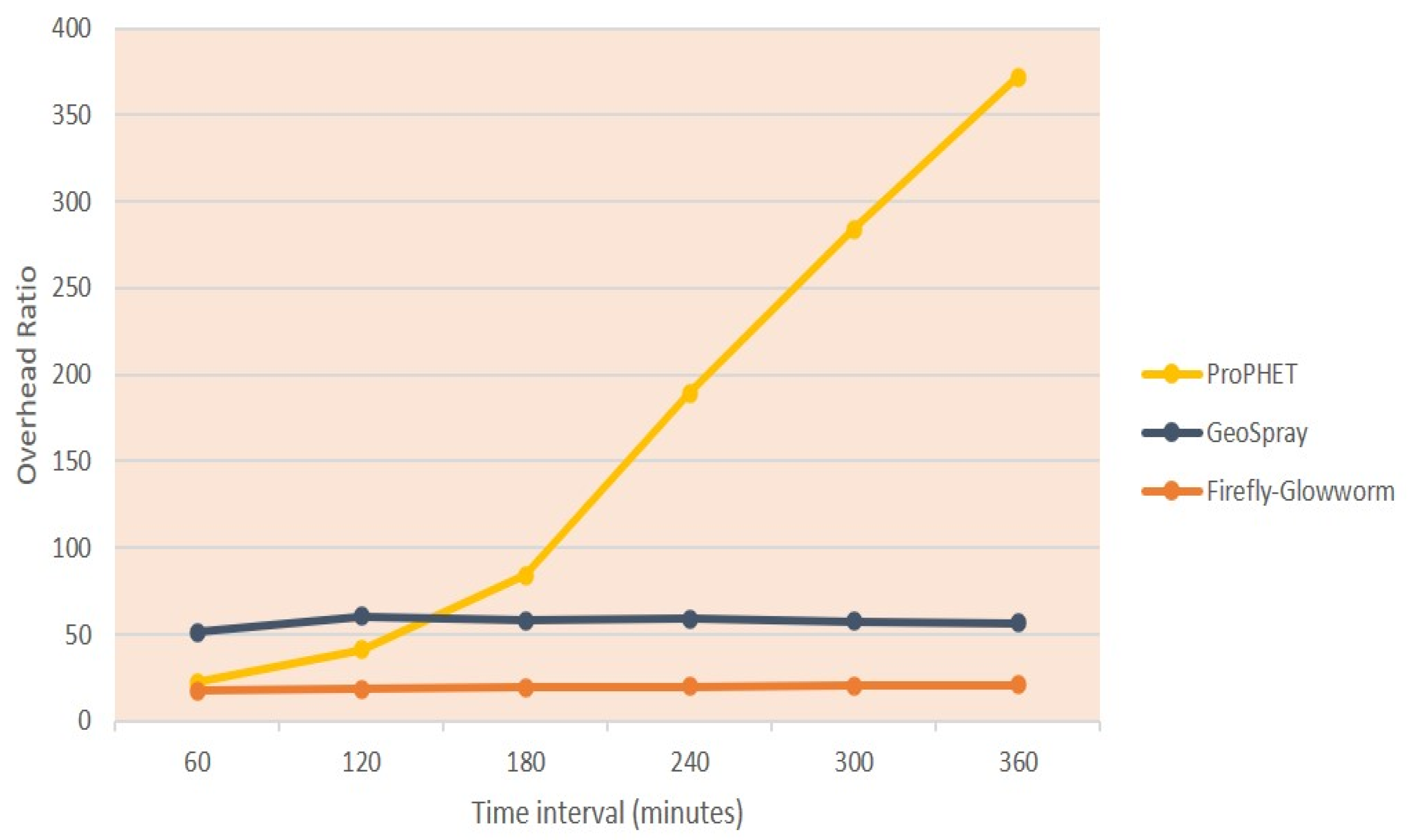
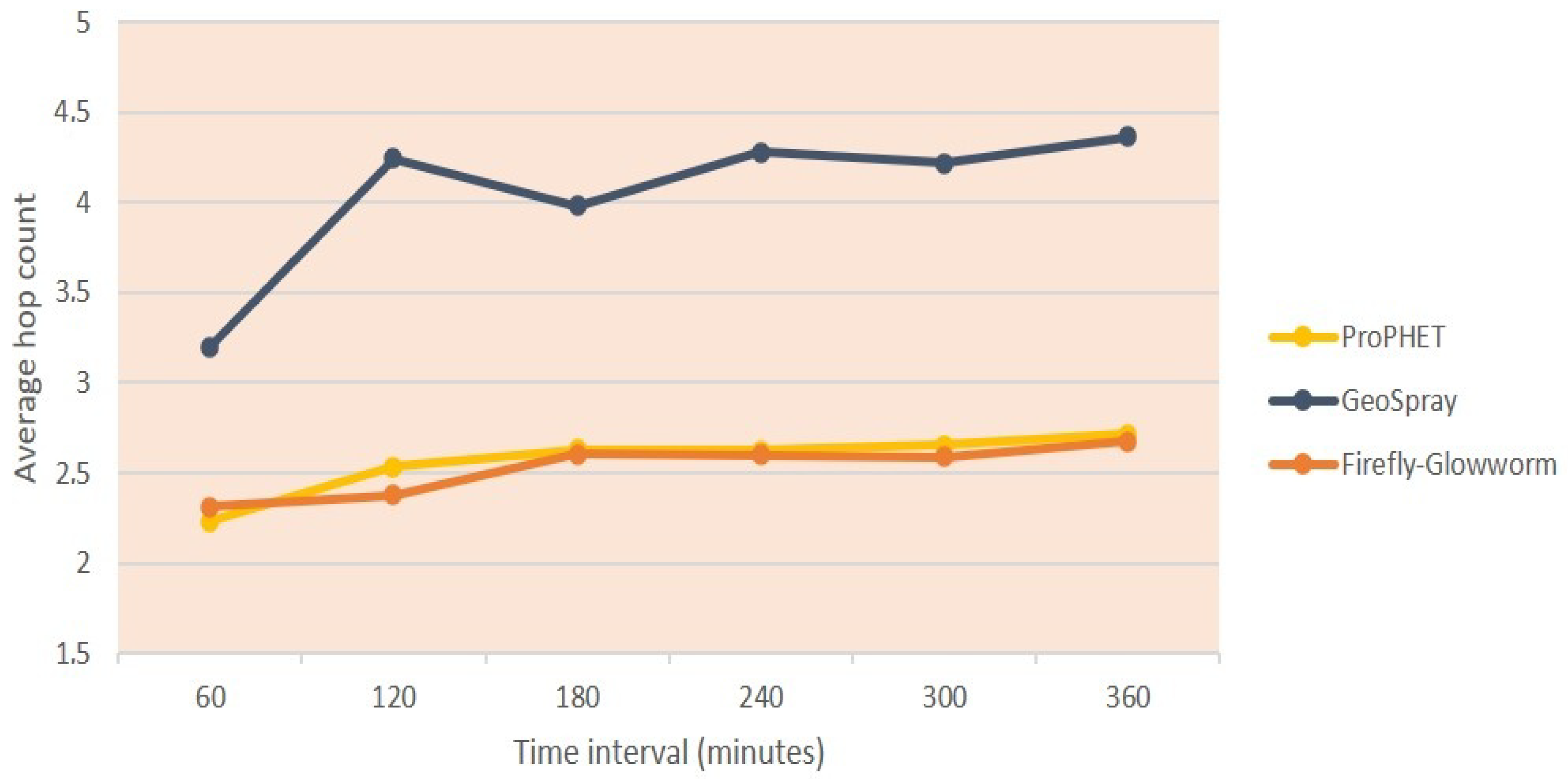
6. Experimental Tests and Discussed Results

The proposed scheme is implemented using the Opportunistic Network Environment (ONE) [33] simulator, a DTN-destined routing simulator for extendable VDTN routing; the proposed Swarm-VDTN router (Firefly–Glowworm) is compared to probabilistic DTN routing router namely ProPHET and a geographic VDTN protocol (GeoSpray). ProPHET protocol is available in ONE 1.4.1 version and GeoSpray is given for simulation by manuscript author Pr. Vasco N. G. J. Soares. The Helsinki city shown in Figure 4 is set as ONE mobility model for the simulation tests. The latter return the major VDTN performance indicators which are:

• Average latency: is calculated as the average end-to-end forwarding delay of all delivered bundles including the SCF time.
• Delivery probability: returns the packet delivery ratio (PDR) including the number of generated copies.
• Overhead ratio: which calculates the ratio between the number of generated undelivered copies and the number of delivered copies.
• Number of flooded bundles: returns the total accumulated amount of replicated copies of all flooded bundles.
• Number of dropped bundles: returns the total accumulated amount of lost copies of all flooded bundles.
• Average hop count: the average length of traversed trajectories traversed by the delivered bundles between the corresponding source and destination nodes.

Table 3. Configuration settings of simulation tests.

Parameter	Value
VDTN simulator	ONE (1.4.1 version)
Mobility scenario	Helsinki city model
Simulated area’s size	4.5 × 3.4 Km
Simulation time	21,600 S (6 H)
Number of vehicles	50 nodes
Mobility models	Cars	Shortest Path Map-based Movement
	Buses	Bus Movement
	Taxis	Map Route Movement
Vehicles speed ranges	Cars	[10∼52 Km/H]
	Buses	[12∼35 Km/H]
	Taxis	[15∼45 Km/H]
Transmission range	35 M
Buffer size	40∼60 MBit
Pause time	20∼120 S
Bundle TTL	30 Min

introduces the configuration settings set for the simulation tests of the proposed VDTN solution (Firefly–Glowworm). The simulations are tracked following equal back-to-back time intervals to evaluate the consistency limits of the swarm-VDTN router comparing to the comparison VDTN protocols.

According to Figure 5, the swarm-VDTN generates reduced delivery delay comparing to GeoSpray and surpasses largely the probabilistic ProPHET. This can be justified by the effectiveness of alternated SCF vehicle selection using FA and GSO.

According to Figure 6, the swarm-VDTN reaches close delivery probability ratios to the geographic VDTN routing (GeoSpray) while it surpasses regularly the probabilistic ProPHET model. This indicates the utility of the implemented METD-based forwarding recovery mechanism when the hybrid FA–GSO fails in detecting better SCF vehicles toward every bundle’s destination.

According to Figure 7, the swarm-VDTN reduces considerably the number of distributed bundle copies especially comparing to ProPHET. Indeed, this aspect is the major advantage of the hybrid FA–GSO-based SCF vehicle selection, by restricting the flooding of bundles to nodes which offer optimized relay quality either geographically or probabilistically.

According to Figure 8, the swarm-VDTN reduces ratio of routing overheads as a result of reduced bundles flooding results.

According to Figure 9, the swarm-VDTN shortens the forwarding trajectory to approximately the same levels of ProPHET surpassing the geographic model of GeoSpray. This allows to reduce network resource utilization and minimize the number of dropped copies. This metric constitutes one of the advantages of probabilistic routing in VDTNs whose SCF vehicle selection is independent from geographic calculation of vehicles’ position which shows the superiority of probabilistic approaches for this performance indicator.

According to Figure 10, the swarm-VDTN does not drop bundle copies similarly to GeoSpray, while ProPHET suffer from increasing number of dropped copies gradually with time. This result is the consequence of the flooding performances and an indicator of the effectiveness of the proposed hybrid bio-inspired probabilistic-geographic approach.

7. Conclusions

In this paper, we proposed a new bio-inspired probabilistic VDTN router based on the combination of two swarm-based approaches, namely the FA and GSO metaheuristics, to solve the problem of SCF vehicle selection in VDTN routing. The proposed model alternates with a geography-based recovery forwarding to cover the lack of nodes in critical stages of bundle routing. The proposed swarm-based router considers both forwarding historic and current forwarding abilities of vehicles as routing parameters for the probabilistic evaluation of candidate SCF relay nodes for both FA and GSO methods.

Following the collected performances from the simulated urban mobility scenario, the proposed swarm-inspired VDTN router has been successful in optimizing the bundle flooding and the average delivery delays, while it alternates the best performances in the delivery probability of the compared GeoSpray model and the optimized route length of the probabilistic ProPHET model. The proposed router showed also an effective management of large buffer cache capacities which characterizes vehicular nodes by the swarm-based controlled forwarding timing of bundles.

This contribution introduced the novelty of alternate swarm computation for VDTN routing and the hybridization of probabilistic and geographic SCF routing which opens further perspectives on the application of enhanced bio-metaheuristic techniques in the VDTN routing optimization. Other VDTN routing modes such as the knowledge-based forwarding can be used to cover the shortages of probabilistic and geographic DTN forwarding modes in the framework of the swarm-inspired optimization methodologies. Further work on the basis of this solution will focus on improving the quality of swarm computation techniques in order to improve the profitability of the SCF selection process.