1. Introduction
The use of Network Function Virtualization (NFV) can bring advantages and challenges at the same time. One of the main challenges is the optimized placement of the virtualized functions based on the characteristics and available resources of the network [
1]. In most cases, Virtualized Network Functions (VNF) form a chain of Network Functions (NF) with predefined parameters that are referred to as a Service Graph (SG) [
1]. The placement of all NFs in a SG is a Network Function Embedding Problem (NFEP). NFEP is defined as mapping the Virtual Network Functions (VNF) and the links between them to the physical network. NFEP can be solved by modeling it as an optimization problem that can be solved using different Linear Programming (LP) solvers/tools [
1]. Such optimization models are proven to be NP-hard and are not scalable. The alternative solution is to design a heuristic that can provide near-optimal solutions with lower complexity. While there have been numerous proposed heuristics for NFEP in wired and wireless networks, the focus has mostly been on providing results close to an optimal solution. Consequently, the proposed heuristics became quite complex and highly time-consuming for larger networks, limiting their scalability. In contrast, in this paper, we explore
simple heuristics and their benefits/drawbacks. We aim to design a heuristic that is as simple as possible, allowing it to be time-efficient/scalable and therefore applicable to larger networks. We are particularly interested in the case of multi-hop wireless networks, with their more severe bandwidth-constraints, but believe that the insights from this work could also apply to other networks where NFs have to be placed, such as data centre networks, wired access networks, or the next generation of cellular networks.
To design a simple heuristic we break our design process into four heuristics that each include one more parameter than the previous heuristic. The following briefly summarizes the four heuristics.
Random placement: The first heuristic places NFs randomly in the network and connects the source and destination of the request to the NFs based on their order in the SG via a shortest path. This heuristic can be used as a benchmark to show the worst result that can be expected, placing NFs randomly.
Shortest path placement: The second heuristic considers the shortage of BW in wireless multi-hop networks due to the presence of interference. This heuristic first finds a shortest path between source and destination of a request by using the Dijkstra algorithm and places NFs along the shortest path based on their order in the service graph.
All shortest path placement: The third heuristic considers the probability of having more than one shortest path and chooses the one with more nodal resources along the path. The main idea here is to increase the chance of placing the current request successfully. In this heuristic, we rank the shortest paths based on their available nodal resources and select the one ranked first. NFs will be placed along the chosen shortest path based on their order in the SG.
Fast and Cost-Efficient (FACE) placement: The fourth and last heuristic is named FACE. FACE uses the same method as the all shortest path heuristic to choose a shortest path but places NFs differently. In placing the NFs, FACE gives priority to the one that has fewer options for placement.
We compare the results gathered from the four mentioned heuristics, an optimization model, and an alternative heuristic. The collected results show that the optimization model has highest execution time in comparison to all explored heuristics. However, it can reach the best results in terms of number of accepted requests. Our comparison between heuristics shows that the shortest path heuristic can place as many requests as the more complex ones with comparable cost. It can be seen through the gathered results that adding additional complexities will not only increase the execution time and computational resources needed to find a placement for NFs. It also does not improve the number of accepted requests or decrease the cost of NFs placement.
The rest of the paper is organized as follows. The next section reviews related work.
Section 3 introduces our proposed placement heuristics,
Section 4 shows the performance comparison of all 6 placement methods studied, and the paper concludes in
Section 5.
Table 1 lists all acronyms used throughout this paper.
2. Related Work
NFEP can be solved via using mathematical methods or by designing a heuristic algorithm. Although mathematical models provide an optimal solution, they are complex and proven to be NP-hard [
2]. The alternative is to design a heuristic that can provide near-optimal solutions with less computational demand and near optimal performance. Although there is (potentially) some performance loss (in our case the acceptance rate of new requests) between the heuristic algorithms and direct solving method, heuristic algorithms have advantage in computational complexity when solving large-scale network optimization problems [
3]. There exists a wide range of heuristics proposed for VNF placement. The proposed methods are designed based on the objectives of their authors. Our goal here is to design a heuristic that can place (ideally) as many requests as the mathematical model while reducing the resource consumption by SGs. Here we review recently proposed heuristics that provide novel methods for mapping SGs’ NFs to a physical network and compare them in terms of their complexity and performance.
The heuristic proposed by the authors of [
4] breaks a SG into the NFs and the links connecting them. The proposed multi-stage algorithm finds all possible options for each NF and defines a cost for each option based on the cost of traveling from previously placed NFs to the current NF according to the path it should take. The algorithm runs in
where
n is the number of nodes in the physical network and
m is the number of NFs per SG. The use of a multi-stage algorithm may make it easier to find a solution for placing each NF but the solution does not minimize the cost for the whole SG. The results are not compared against a simple version of the proposed solution to demonstrate how breaking the problem into sub-problems and the other considered parameters contributes to the reported results. In another example, the authors of [
5] used Dynamic Programming (DP) to organize the problem into smaller interdependent sub-problems of placing each VNF and the virtual link connected to it towards the next VNF. The solutions for the sub-problems are then aggregated to compose the overall chain placement. Similar to [
4,
5] breaks the problem of SG placement into the placement of each NF and the virtual link connected to it. However, providing a solution that minimizes the resource consumption by a NF and the link connected to it does not ensure that the final solution minimizes the cost of the whole SG placement. In [
5] there is a lack of evaluations against very simple placement approaches. Finally, in another similar approach we have a three step placement algorithm proposed in [
6]. The proposed algorithm in [
6] first computes the list of physical node candidates for each VNF, then sorts them based on the number of physical node candidates for placement in increasing order. In the last step, the heuristic computes the placement cost of that VNF and its virtual link to the physical network and chooses the one with the lowest cost. The same problem arises here as the placement focuses on placement of each NF instead of the whole SGs. The results in [
6] are not compared against a simpler version of the provided heuristic such as the one that starts from the first NF of the SG instead of sorting the NFs based on their number of candidates. Such a comparison would demonstrate how this step of the algorithm contribute to improving the results.
The authors in [
7] break the placement problem into placing NFs and connecting them. In the first step, the proposed heuristic in [
7] places the NFs based on their resource demand. The heuristic in [
7] gives priority to the NF with the highest demand and place it in the cheapest node of the network. The value of each node is obtained from a formula that considers the available resource capacity, the price for each resource unit, and the ability to connect to other nodes. The placed NFs then connect through the available shortest path. Although the proposed algorithm considers multiple factors in obtaining a node for placement of NFs it does not consider the whole chain of NFs in its placement and may end up taking a path much longer than the shortest path from source to destination.
Ref. [
8] proposes an algorithm that considers NF placement, routing, and the traffic changing affect of NFs. The proposed heuristic is based on the observation that some NFs can increase a flow’s BW, e.g., by adding authentication headers, or decrease a flow’s BW by compressing, filtering, etc. The Least-First-Greatest-Last (LFGL) algorithm proposed in [
8] starts from the NFs that decrease the BW usage and uses the Dijkstra algorithm to identify the closest node to the source. The LFGL algorithm then places the NFs decreasing the traffic rate in the closest node to the source until there is no space and then advances to the second closest node and so on. The process of placement is the same for the increasing BW usage NFs, except it starts from the destination node and places the NFs increasing the BW usage closer to the destination. The endpoints of the first and the second stage of the placement are then connected through a shortest path. The LFGL heuristic assumes that we have the freedom to re-organize the order of NFs within a SG. This may not be realistic, as in most cases the order of NFs cannot be changed (once a flow is encrypted, for example, it would become difficult to filter it based on payload attributes). The results in [
8] do not provide a comparison between LFGL and a simpler version of the proposed heuristic to show the effectiveness of the considered parameters.
In designing a heuristic the challenge is to consider the parameters that can improve the performance of an algorithm and avoid the ones that only complicate the model. [
9] proposes a solution called Simple Lazy Facility Location (SLFL) that optimizes the placement of VNF instances in response to on-demand workload. Upon new demand arrival, a combination of installation, migrations, and reassignments can be applied to optimize the placement [
9]. In each case, the cost of migrating the already deployed VNF, installing the new VNF instance, or adding to the already deployed VNFs are being compared with each other and the one with the lowest cost will be considered. Although it is mentioned that SLFL runs in polynomial time, its execution time is not reported. A performance comparison between SLFL and a model that places the NFs randomly does not show the effect of the parameters considered in the heuristic on the number of accepted requests.
The heuristic algorithm proposed in [
10] works based on the centrality matrix. The centrality for each node in [
10] is defined as the sum of the total size of flows which have their shortest path going through that node. They assume that the source and destination of all flows are known and determine the node that has the most total traffic volume passing through. The main goal of the algorithm in [
10] is to activate fewer licenses of a certain type of NF. At each iteration, the algorithm compares the cost of activating a new NF in the node with the highest centrality with the cost of the flow traversing through already placed NFs and only activates a new one if it decreases the placement cost. Ref. [
11] propose different heuristics and compares their performance in terms of the maximum number of requests that can be placed in a network. Between the proposed heuristics in [
11] only one, named heuristic-A, is not combined with a proposed mathematical model. Heuristic-A places requests one by one along the shortest path between source and destination. The other heuristics, heuristic-B, B+, B+COR, and C are all being combined with the mathematical model to reduce their execution time. As the proposed mathematical model in [
11] aims at solving the placement problem for all flows at once, the flows are divided into the groups. These heuristics start from the first group and solve the optimization problem for this group. Based on the solution, the problem is updated again and being solved for the next group. Heuristic B randomly groups the requests, heuristic C is the same as B but also consider minimizing the number of used cores in the network. Heuristic B+COR sorts nodes in ascending order based on the number of flows passing through them. Less crowded nodes are selected first to distribute the load away from bottleneck nodes. It is stated that B+COR can place more requests in the network in comparison to other proposed heuristics. However, [
11] did not compare the execution time of the models and only considered the maximum number of the flows that each heuristic can place in the same network. As we will show later in our results, the more complex heuristics combined with a mathematical model may bring better results in terms of the number of accepted requests but suffer from high execution time and therefore are not applicable to large scale networks.
Another attempt in simplifying the problem of VNF placement is to reduce the complexity of the mathematical model by reducing the size of the search space. One example is the heuristic proposed in [
12]. A sampling-based Markov approximation (MA) approach is proposed in [
12] to solve the NP-hard problem which requires a long convergence time. The method begins with a random feasible solution and iterates the process of transformation from the current solution to another feasible solution until the steady-state distribution of the Markov chain appears. To reduce the execution time, the solution space is reduced to a subset of randomly chosen nodes that satisfy the resource demands of a request. It is been stated that the problem can be solved in polynomial time but the execution time of the algorithm is not being reported or compared with other proposed heuristics with similar time complexity. Additionally, the subset of nodes could be chosen based on more sophisticated parameters to reach a near optimal solution faster. Another example is [
13], where the proposed heuristic narrows the target search space of VNF placement by introducing a smaller accessible scope to which the possible locations of VNFs are confined. The requests are categorized based on their source and destination. The nodes with lowest sum of distance from source and destination are in the accessible scope of the request. The size of each accessible scope for each set of requests is proportional to the total traffic volume of those requests. It is shown in [
13] that the size of the accessible scope will impact the time efficiency and performance of the NF placement. Considering all nodes to be in the accessible scope will not reduce the execution time but will provide the acceptance ratio of the optimization model. On the other hand, a very small accessible scope will decrease the execution time but also the acceptance ratio. This approach considers the whole SG and its source and destination. Unlike previous heuristics it does not choose the reduced search space randomly. In the design of one of our heuristics we adopted this idea to narrow the search space and showed in our results that this method can provide near optimal number of accepted requests, and reduce average cost and execution time.
In our design of a heuristic, we start from the simplest model and add parameters one by one to be able to measure their impact on the performance of the number of accepted requests. Compared to wired networks, multihop wireless networks such as MANETs, VANETs, or wireless sensor networks suffer from severe bandwidth (BW) limitations. That is due to several reasons: typical wireless technologies operate at lower transmission rates, compared to wired technologies such as Ethernet, etc. Also, when multihop wireless networks are built up from devices using a single radio, flows interfere with themselves (a node that is a relay between source and destination can only either receive or transmit, but not both at the same time). Finally, wireless technologies typically experience significant interference (either from other flows or due to the above self-interference), drastically lowering the available BW for each link. We therefore emphasize minimizing the BW consumption while placing as many requests as possible. We compare the performance of the proposed heuristics with the heuristic proposed in [
13] and an optimization model proposed in [
1] that formulates and solves an Integer Linear Programming (ILP) model for wireless multi-hop networks.
3. Placement Heuristics
As discussed in the previous section, the main focus of the models proposed for embedding VNFs into a physical network is on designing a heuristic that can achieve near-optimal results. However, the main reason for avoiding optimization models is their complexity and high execution time. Here we aim at exploring how much complexity is required and what benefit we can achieve with simple heuristics, studying a sequence of four, increasingly complex, heuristics. Each heuristic is designed to show the effect of the added parameter on the number of accepted requests, the average cost of the resources consumed by a SG, and the execution time of the algorithm. We start from the simplest heuristic and in each heuristic consider an additional parameter in the NFs’ placement.
In all heuristics, it is assumed that requests arrive one at a time and are placed separately. Each request has a duration, once an accepted request expires, it will be removed from the network and the associated used resources will be released. Each SG request has a specific source and destination, nodal resource demand for each NF, and a BW demand for all virtual links. The physical network consists of nodes with a given amount of nodal resource and links with a specific available BW. We only consider a single nodal resource and its consumption. The nodal resource could represent memory, storage, or CPU resources of a physical node. The model is designed for a wireless multi-hop network and considers the effect of interference in BW consumption. To include the effect of interference in the BW consumption we use an interference model widely used in the literature called the protocol model [
14].
The protocol interference model defines an interference set for each link in the physical network. The interference set for each link consists of all the links
that are connected to the nodes in the transmission range
R of the sender or receiver.
represents the distance between node
u and
.
captures that transmission on the link between node
u and
v will reduce the available BW of all the links whose transmitter is within the transmission range of the sender
u or the receiver
v.
3.1. Random Placement
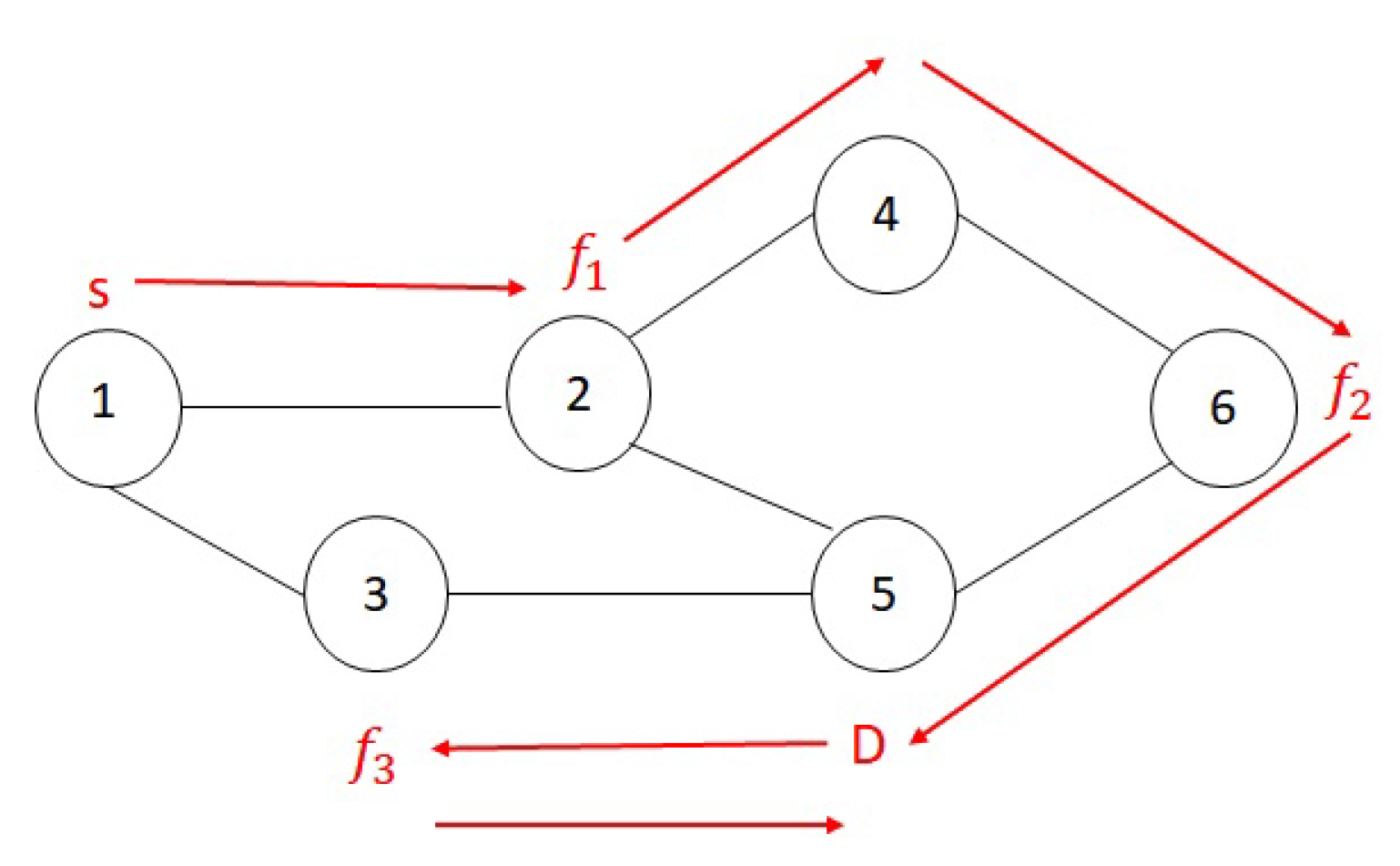
The first heuristic is the simplest algorithm that can be used for embedding the NFs of an SG into a physical network. The random placement heuristic can be divided into two parts: placing the NFs and connecting the NFs. To place a NF, the algorithm randomly chooses a node that has sufficient nodal resources. In this stage, if there is no node with sufficient nodal resource for any of the NFs the request will be rejected. If all NFs are placed successfully, the algorithm moves to the connecting stage. The algorithm starts from the source and connects it to the node used for placement of the first NF of the SG, finding a shortest hop path via Dijkstra algorithm. This process of connecting nodes continues until the node that contains the last NF of the SG connects to the destination. As the path from source to destination that passes all the NFs based on their order is identified, BW availability will be checked. BW consumption is based on the summation of the BW consumed by passing each link and due to interference.
To describe this heuristic and the next ones better, consider the following example of an SG placement that will be solved by all of the heuristics. Assume we have a wireless multi-hop network with six nodes. Nodal resources of the nodes in the wireless network are
units, and the available BW of the links in the physical network are all 20 units. The nodal resource demand of a SG of 3 NFs is
and the BW demand of the request is 2 units. The SG’s source is node 1 and its destination is node 5.
Figure 1 shows the topology of the physical network and a random placement of the SG. As can be seen, although all three NFs could have been placed in the source node and the shortest path between source and destination is only two hops, the length of the chosen path is six hops, consuming significantly more BW.
3.2. Shortest Path Placement
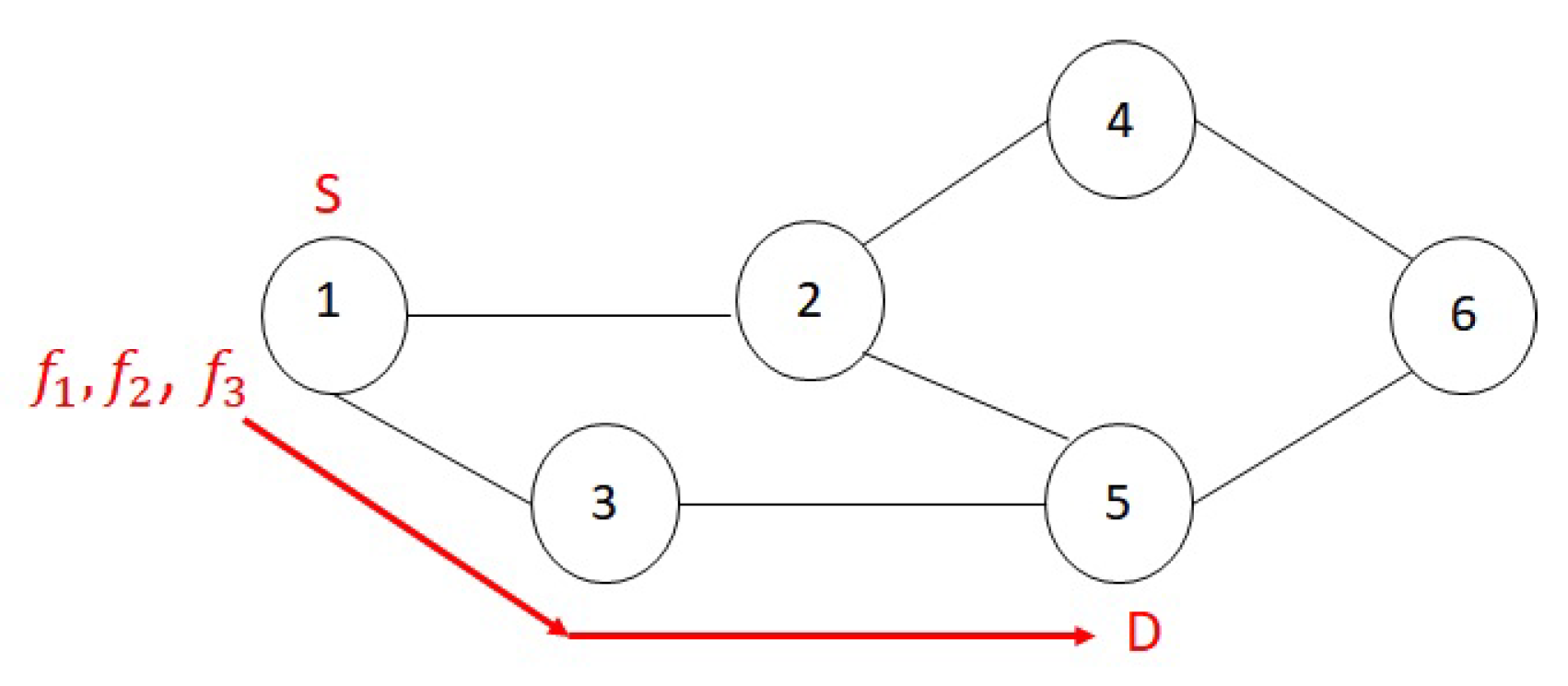
The presence of interference in wireless multi-hop networks causes a scarcity of BW. To reduce BW consumption, our second heuristic first finds a shortest path between source and destination of the SG request via Dijkstra’s algorithm. NFs then will be placed along the shortest path. The shortest path will be checked for availability of sufficient BW to accommodate this flow, considering both the actual links used and the impact on adjacent links due to interference. Should any link exceed their available BW the request gets rejected. The shortest path placement places the first NF in the first node of the path that has sufficient nodal resources. The next NF of the SG will be placed in the same node as the previous NF if possible, otherwise it will be placed in the next node along the shortest path with sufficient available nodal resource. This process continues until all NFs are placed. If any of the NFs cannot be placed due to a lack of nodes with sufficient nodal resources, the request gets rejected.
Figure 2 shows the shortest path placement applied to the same example as the previous section. We can see from the example that this model reduces the BW consumption in comparison to the random placement.
3.3. All Shortest Path Placement
Our third heuristic takes advantage of the fact that there can be more than one shortest path between a source and destination. To increase the probability of accepting a request, this heuristic searches for all shortest paths in the network and chooses the one that has a maximum-minimum nodal resource. The search for all shortest paths is performed by using a search method similar to Breadth First Search (BFS). BFS explores the links of the graph to discover the node that is reachable from the source node. It computes the shortest distance (in terms of number of hops) from the source to each reachable node in the graph. We modified BFS to start from the source and end when it reaches the destination node. Also, in addition to the distance, we record the shortest paths themselves. In our search for shortest paths we define an array and a set for each node u in the physical network:
: An array that represents the shortest distance (number of hops) from the source node.
: A set which records nodes involved in each shortest path found from source node to node u.
The initial value of
for all nodes is infinity, except for the source node which is equal to 0, and initially set of
for all nodes is empty. The search algorithm starts traversing the physical network graph and while visiting neighbor
y of node
x it compares the value of
with
. If
is greater than
,
describes a path longer than the shortest path. So we decrease
to
and assign
to
. If
, we found another shortest path to node
y. In this case,
is the union of
and
. The pseudo-code of this search algorithm is presented as Algorithm 1. This algorithm finds all possible shortest paths for any pairs of nodes. The output of the algorithm is
, which is a set of shortest paths from a source nod
x to a destination node
in the physical network.
| Algorithm 1 Finding all shortest paths. |
![Futureinternet 12 00161 i001 Futureinternet 12 00161 i001]() |
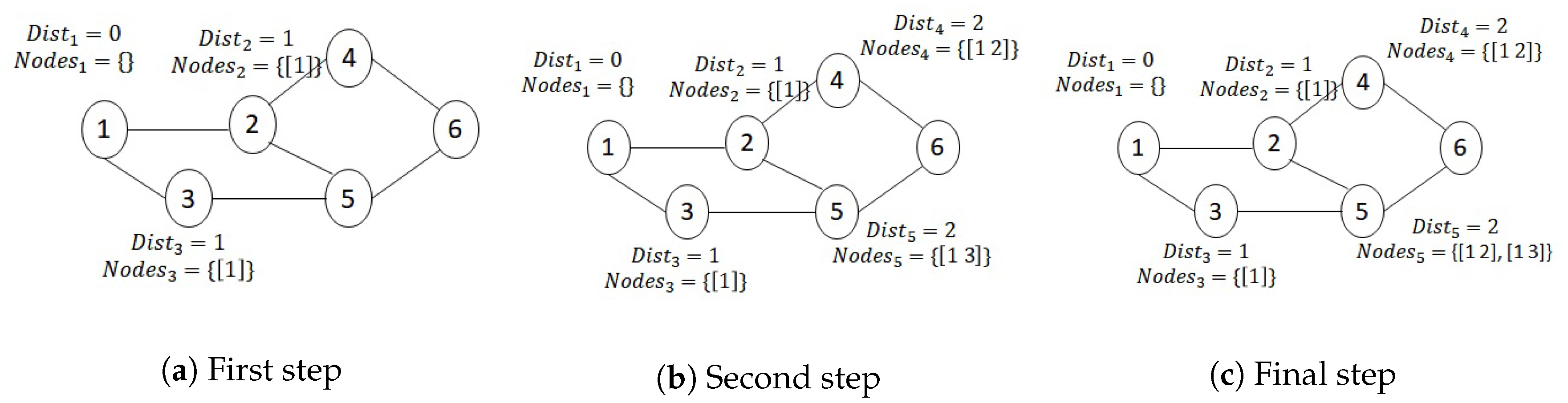
The following example demonstrates how we update the parameters of each node during the search for all shortest paths. As shown in
Figure 3, we consider a network of 6 nodes and want to find all shortest paths from node 1 to 5. In the first stage, we update the parameters of the source node’s neighbors, which are nodes 2 and 3.
Figure 3a shows the first stage and updated parameters of the neighbors of node 1.
Figure 3b shows the second stage, after we updated the parameters for neighbors of node 2. In the final stage, when processing node 5,
. So we update
to the union of
and
.
Figure 3c shows the final stage. All available shortest paths from 1 to 5 are recorded in
.
We applied this all shortest path heuristic to the same example in the previous sections and the resulting placement is shown in
Figure 4. Between the source and destination of the SG there are two shortest paths
, and
. The maximum-minimum resource belongs to the second path. All NFs are placed in the source node as the policy here is to place them in the first node that has sufficient nodal resources.
3.4. Fast and Simple Heuristic Algorithm (FACE)
The final heuristic uses the same method as the previous heuristic in choosing a shortest path. Additionally, the FACE algorithm keeps a decreasing list of shortest paths based on their maximum-minimum nodal resource. In each stage of the placement process, if the placement was not possible for the chosen shortest path, it tries the next shortest path in the list. The following strategy will be deployed to place the NFs along the chosen shortest path.
The NFs are sorted based on the number of possible candidate nodes in an increasing order. A candidate node parameter is defined for each NF of the SG and is equal to the number of nodes along the shortest path that can be used for the placement of that specific NF. In choosing the nodes along the shortest path we consider two parameters: a node has to provide sufficient nodal resources, and the NFs that previously were placed. The order of the NFs in the SG is fixed and we cannot re-organize them. Furthermore, we do not want to have a placement that passes a physical link more than once. E.g. if the third NF of the SG is being placed in the second node of the shortest path, subsequent NFs in the SG cannot be placed in the first node. The candidate nodes are being chosen based on the placement of previous NFs to avoid loops and backtracking in the placement. If there are no candidate nodes for any of the NFs at any stage of placement, the chosen path is infeasible and the placement process will choose the next shortest path with maximum-minimum nodal resource and repeat the process of NF placement.
To place the chosen NF in one of the nodes along the shortest path we sort its candidate nodes based on their index difference and choose the node with the lowest index difference. The index of the nodes along the shortest path is equal to their order in the shortest path e.g., the source node’s index is one. The index of a NF is equal to its order in the SG, e.g., the index of the first NF of the SG is one and the index of second NF is two. We compare the index of the chosen NF with the index of the candidate nodes and choose the one with the minimum index difference with the chosen NF. In the end, the available resources of the nodes, BW of the links, and the list of candidate nodes for the remaining NFs will be updated.
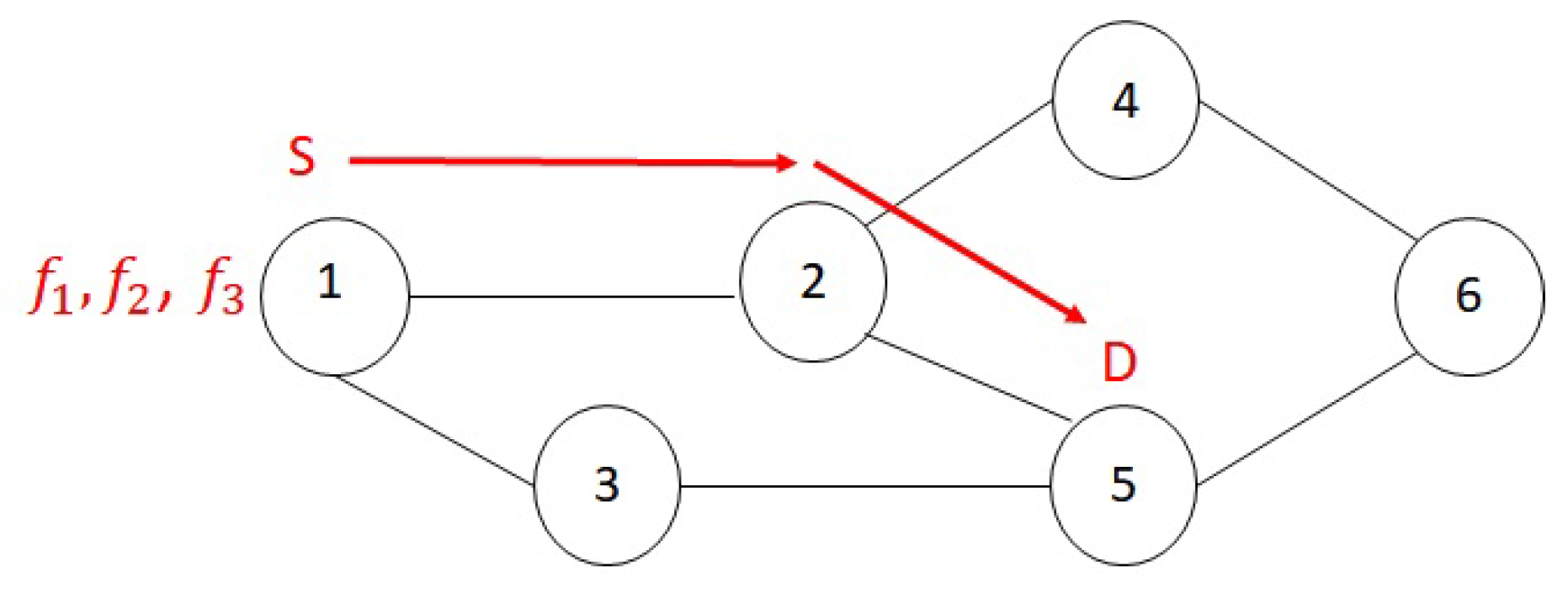
We applied FACE heuristic to the same example as previous sections.
Figure 5 shows the result of placement by FACE heuristic. As all of NFs had three options for placement, the algorithm started from the first NF and placed it in the node with minimum index difference, which is the source node. The second NF is placed in the second node of the chosen shortest path as it has minimum index difference and the third NF is placed in the third node of the chosen shortest path.
3.5. Accessible Scope Heuristic
We also implemented one heuristic proposed in the literature that limits the location of VNFs to nodes on the shortest path(s). The accessible scope heuristic [
13] reviewed earlier introduces the notion of accessible scope to which the possible locations of VNFs are confined. Based on a flow’s source and destination, nodes with lowest sum of distance from source and destination are in the accessible scope of the request. In essence, these are all nodes on all shortest paths. Once the search space is thus narrowed, an optimal placement algorithm then solves the placement problem on this smaller subproblem. In our implementation, we use the model described in the next subsection.
3.6. Optimization Model
In our previous work [
15] we proposed an optimization model for placement of the SGs in wireless multi-hop networks. That model uses Integer Linear Programming (ILP) to place a chain of NFs, subject to constraints on nodal resources, link bandwidth, connectivity, and interference. The objective of the optimization model is to minimize the mapping cost, defined as the sum of BW consumed by the actual flows, the bandwidth lost in adjacent links due to interference, and the consumption of nodal resources. As the results in [
15] show, the execution time for placing SGs even in small networks grows fast, even for small networks of 20 to 40 nodes.
3.7. Summary
This section reviews 6 possible ways of solving the network function placement problem, from randomly placing the NFs to solving a complex optimization model. As the latter results will show, the more complex solutions require more computational time to arrive at a solution per request, which limits their applicability to smaller networks. The question then becomes how much complexity is really needed to achieve reasonably good results. Or in other words: if we choose a simpler solution, do we loose out on performance (number of accepted requests, costs of placement)?
4. Modeling Environment and Results
Two platforms are being used to solve the placement problems: MATLAB to implement our heuristic algorithms, and AMPL to solve the mathematical optimization model and the alternative heuristic proposed in [
13]. AMPL is a modeling language designed to be used for solving optimization problems such as linear and non-linear programming problems [
16]. We used AMPL to solve the optimization model and the compared heuristic as it works with a wide range of solvers. We used BARON for solving our optimization model in AMPL as described in more detail in [
16]. Unlike AMPL, which is designed for solving optimization models, MATLAB allows us to develop our heuristic algorithm for VNF placement.
The wireless topologies are generated with the use of the method proposed in [
17]. The nodes are randomly deployed in a square area, based on a uniform distribution. We generate topologies with 20, 30, 40, and 100 nodes, the network area grows with the number of nodes. We keep the average node density constant, consequently the network size ranges from
m
for the 20 nodes network to
m
for the 40 nodes network [
17]. Nodes in the wireless network are directly connected if their distance is less than or equal to the transmission range of the nodes. This transmission range is constant for all nodes and we verified that all of the generated topologies are connected.
We used the same parameter values as [
1] in order to be able to compare our results. The nodal resource of nodes and the bandwidth of links are values uniformly distributed between 100 and 150 in the first network scenarios. In later scenarios, we increase the available BW and the nodal resource availabilities to observe their impact on the performance of the heuristics. Flows arrive over time, following a Poisson process with an average rate of four flows per 100 time units. Each flow has a lifetime, exponentially distributed with an average of
time units and is accompanied by a SG, defining the required NFs and their interconnection to handle this flow. There are 6 NFs per request. The nodal resource demands of each NF follow a uniform distribution between 1 and 20. The bandwidth requirement of all links of the request is the same and chosen uniformly from between 1 and 50 units.
4.1. Performance Metrics
To measure the performance of our proposed heuristics and compare their performance with each other, we used the following metrics.
Accepted requests: The total number of accepted requests during a simulated network lifetime of 20,000 s.
Average Cost: Average of the BW and nodal resource units used for the deployed requests that are not expired. Please note that this includes the bandwidth of links actually used by flows, as well as the bandwidth consumed on adjacent links due to interference.
Execution time: The total time that it takes to place all requests over the simulated network lifetime of 20,000 s.
Each data point is the average of 10 runs, generating a new random topology and sequence of flow arrivals each time. In addition to the average, we also plot the 95% confidence intervals.
4.2. Results
In order to evaluate the relative performance of our heuristics and to determine the time it takes to solve the placement problem, we designed three scenarios.
In a first scenario, we applied our heuristic models to wireless multi-hop networks of increasing size to evaluate their performance in terms of the time it takes to solve the placement problem and their success in placing the requests. To benchmark our results, we applied the Integer Linear Programming (ILP) model for wireless multi-hop networks introduced in [
1] to the same topologies and the same set of requests as our heuristic models. We compared our results with the accessible scope heuristic proposed in [
13] that we reviewed earlier.
In a second scenario, we focus on the first four proposed heuristics and apply them to a larger size network of 100 nodes to compare their performance in terms of the number of accepted requests, average cost, and execution time. In this scenario, we maintain the number of nodes and increase the available links’ BW.
In a third scenario, similar to the second scenario, we compare the performance of our proposed heuristics as resource availability changes. Here we increase the nodal resource of the nodes while keeping the number of nodes constant at 100. In this scenario, in addition to comparing the relative performance of the proposed heuristics, we can also identify the impact of increasing nodal resources on the number of accepted requests.
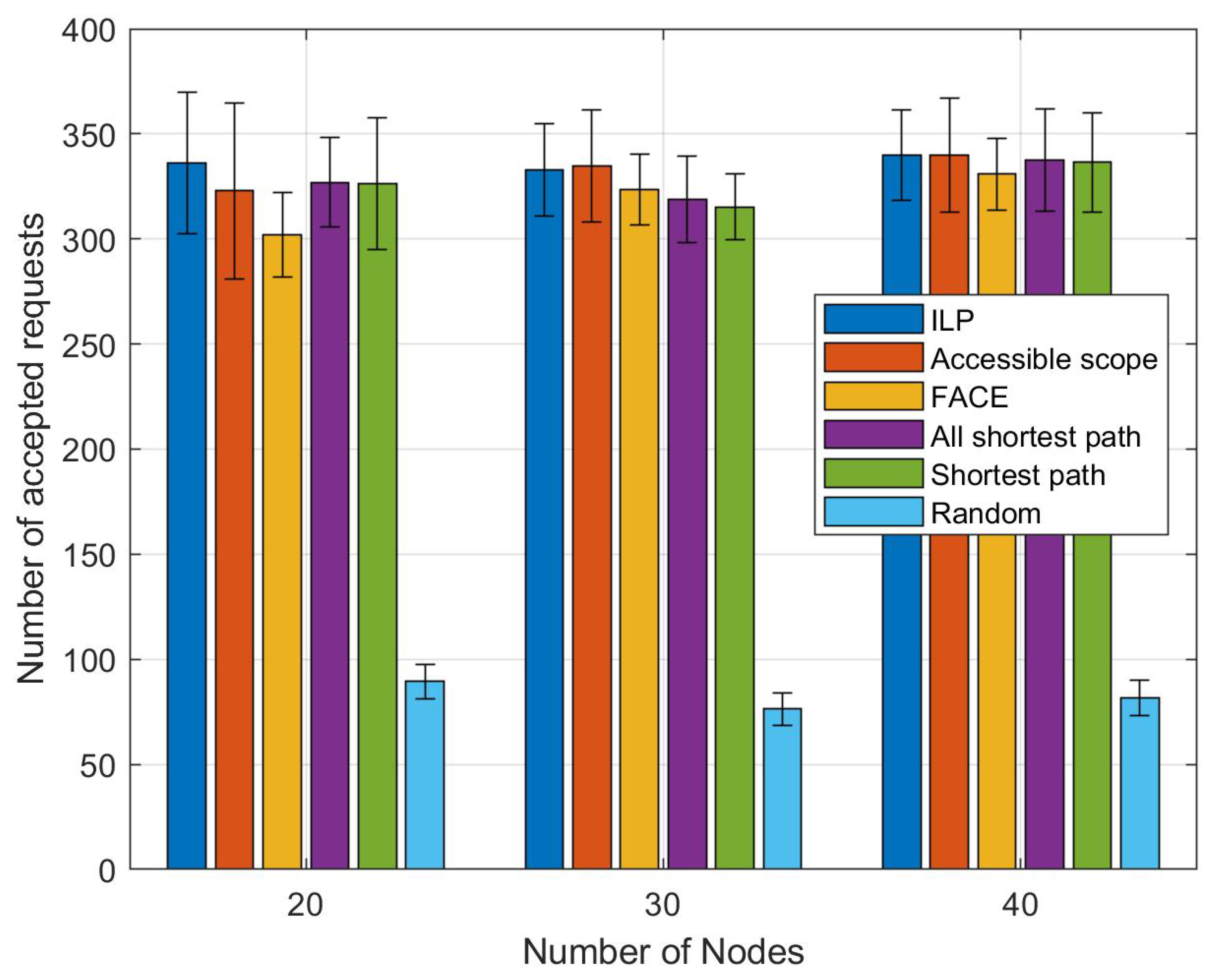
Figure 6 shows the average number of accepted requests and their 95 % Confidence Intervals (CI) for a simulated network lifetime of 20,000 s. We applied our 4 heuristics, the accessible scope heuristic, and the ILP model to the same physical networks and the same set of requests. We increased the number of nodes from 20 to 30 and 40 nodes. For each network size, we repeated the experiment 10 times with different network topologies, averaged the number of accepted requests and calculated the corresponding 95 % CI. The most surprising part of the results is that the average number of accepted requests is almost the same for all heuristics, except for the random placement strategy. The differences in the average acceptance rates, as indicated by the 95 % confidence intervals, are not statistically significant. It may seems counter-intuitive that, for a 30 node network, the ILP has a slightly lower average acceptance rate than the accessible scope heuristic. However, as we have shown in [
1], accommodating placement requests one at a time (as we did here) will impact future placement requests. In this case, ILP successfully placed a request along nodes on a non-shortest path. This reduced available resources, preventing the placement of subsequent requests. The shortest path heuristics would have failed to place such a request, resulting in more resources remaining available to place future requests.
While the four heuristics are quite different in terms of their level of complexity, the shortest path heuristic can place the same number of requests as the complicated accessible scope heuristic or even FACE. All the steps added to our heuristic after the focusing on (a randomly determined) shortest path do not improve the number of accepted requests. However, these steps add complexity and as we can see in
Table 2 increases the execution time. For a 40 node network, applying an optimization model takes almost 10 times as long as the accessible scope heuristic, 100 times longer than FACE, and almost 1000 times longer than the simple shortest path heuristic. Randomly placing network functions in the network actually takes longer (in our implementation), as we repeatedly need to discover shortest paths between consecutively placed NFs. In a network where such information is readily available, for example in the centralized controller of an SDN architecture, randomly placing NFs and placing them in a best-effort manner along the shortest path between source and destination would have approximately the same, minimal, time complexity.
We also collected the execution times for the 4 simpler heuristics for a 100 node network. Again, the results clearly show the superior performance of the simple shortest path heuristic. The time listed here (2.3 s) is the average time to process all arriving requests. With, on average, four requests arriving per 100 time units, and the simulations running for 20,000 time units, we process approximately 800 requests in 2.3 s, so each request individually takes slightly less than 3 ms. This indicates quite clearly that this heuristic scales well for larger networks, allowing processing arriving new flows in real time. Unlike more complex approaches, the execution time of our simple heuristic is related to the number of nodes in the shortest path, not the number of nodes in the network.
The advantage of the simple shortest path heuristic is that it provides a total number of accepted requests close to the optimization model in a timely manner. The all-shortest path and FACE heuristic incur a pre-processing step to calculate all shortest paths for all possible source and destinations in the network. This is a one-time process and does not depend on the number of requests. We excluded this one time calculation of all shortest paths for all pairs of nodes from their execution time. However, in case of dynamic topologies, we may have to run these steps multiple times, potentially each time a new request arrives.
Limiting the placement heuristic to a shortest path will not eliminate the optimal placement in most cases. Over 97 % of the requests are being placed along a shortest path by the optimization model. However, this focus on the shortest path(s) results in a huge decrease in the execution time of all heuristics compared to the optimization model. In terms of the average cost, as the number of accepted requests are similar for heuristics that use a shortest path for placement of the NFs, we end up with more or less the same BW costs. The only potential difference would be the impact of interference, which only the last three approaches explicitly consider during the placement process. However, at least for the results presented here, this impact made little difference overall.
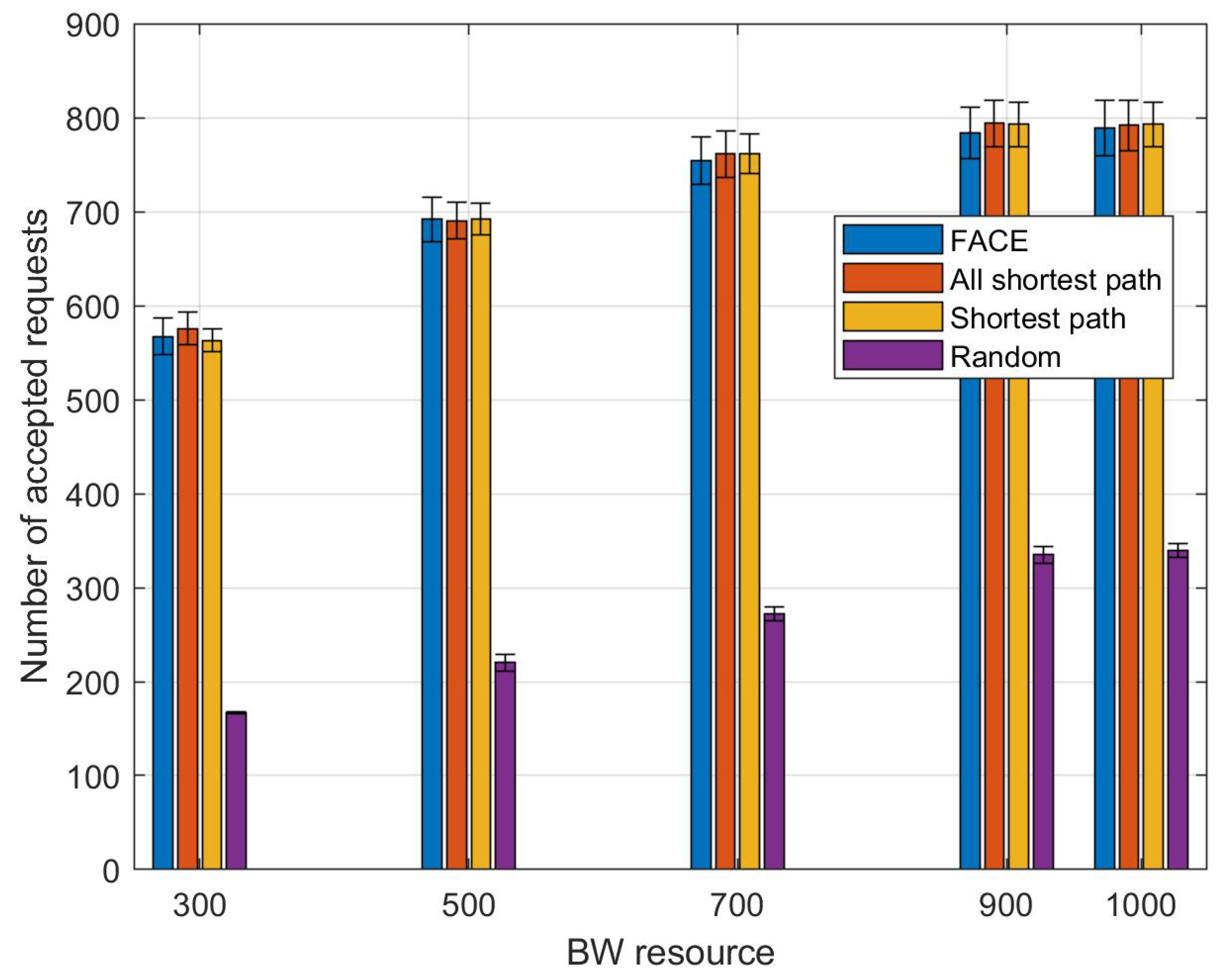
In the second scenario, we apply our 4 proposed heuristics to a 100 nodes network. We chose a network with 100 nodes in order to have more shortest paths available for each pair of nodes in comparison to smaller networks and be able to compare the performance of the all-shortest path and FACE with the one that only considers one shortest path. We vary the uniform distribution that the physical links’ BW is chosen from to model increased bandwidth availability. The intervals are [300, 400], [500, 600], [700, 800], [900, 1000], [1000, 1100]. As can be seen from
Figure 7, the average number of accepted requests increases as we increase the initially available links’ BW. The x-axis is labeled by the beginning of each BW interval. We can observe that the average number of accepted requests remains similar for all heuristics (except for the random placement). High consumption of BW due to the presence of interference makes BW a bottleneck for NF placement in wireless multi-hop networks. Increasing the available BW will mitigate the impact of this bottleneck, and increased the number of accepted requests uniformly for all heuristics. As discussed above, for each simulation run, we have about 800 flow arrivals. If we increase the bandwidth sufficiently (to at least 900 units per link), essentially all flows can be accommodated, independent of the heuristic, as long as NFs are place on a shortest path between source and destination.
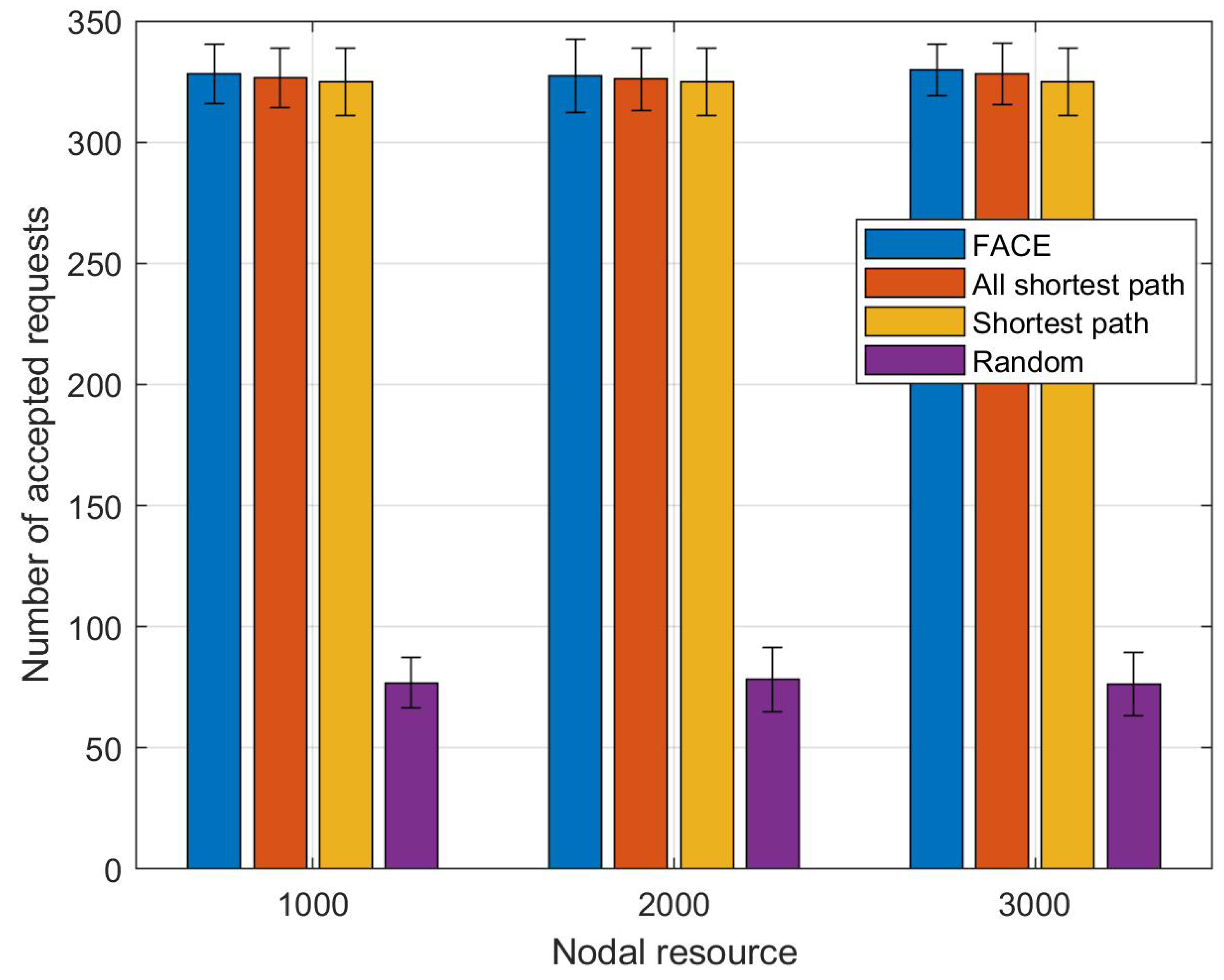
Finally, in the last scenario, for a network of 100 nodes, we increase the nodal resource by increasing the uniform distribution that the nodal resource is chosen from. The intervals are [1000, 1100], [2000, 2500], and [3000, 3500].
Figure 8 shows the acceptance ratio, again the x-axis is labeled by the beginning of each nodal resource interval. Unlike the results shown in
Figure 7, increasing the nodal resource does not results in an increase in the average number of accepted requests. We conclude that bandwidth is a more significant factor in multi-hop wireless networks. Again we see that the performance of the shortest path, the all shortest path, and the FACE heuristics are the same in terms of the average number of accepted requests. As our results show for all scenarios, the difference in performance (in terms of accepted requests) between the shortest path heuristic and the optimal solution as shown in
Figure 6 is not statistically significant. Any heuristic that can beat the simple heuristic would therefore also have to outperform the optimal solution. We therefore do not expect such a superior heuristic to exist.
5. Conclusions
One main challenge in the use of NFVs is to optimally map the SG requests to the physical network. As optimal placement methods are NP-hard and cannot be applied to large networks, we have to design a heuristic with lower complexity that is scalable and can reach near optimal results. Although there exists a wide range of heuristics proposed for VNF placement, none has focused on design a simple heuristic that is time efficient and hence scalable. We explored four heuristics, ranging from very simple to more complex, involving backtracking, in order to identify the simplest possible method that can place a high number of requests in the network in a timely manner.
We compared the performance of our four heuristics with a mathematical model and a popular heuristic proposed in the literature. Our results show that randomly placing NFs, as expected, produces poor results (low acceptance rate, high costs). So some effort is warranted in placing NFs. However, and somewhat unexpected, the simple shortest path heuristic can reach similar results as more complex heuristics. Additional steps, added to the all shortest paths and the FACE heuristic, do not increase the number of accepted requests. Even more complex heuristics such as the accessible scope heuristic [
13] do not improve the acceptance rate. In fact, as shown in
Figure 6, all these approaches provide, statistically speaking, the same performance as an optimization model. However, as shown in
Table 2, the simpler the heuristic, the faster its execution time. The simplest shortest path heuristic can process a newly arriving flow in a few milliseconds in a network of 100 nodes, arguing for its scalability and suitability for real-time admission control.
We explored the effect of increasing BW and nodal resources on the performance of each heuristic. However, we kept the request arrival rate and network density constant. Going forward, we will more thoroughly evaluate and compare the performance of the various heuristics as we vary these parameters as well, resulting in networks that are more lightly or highly loaded.
We also plan to explore possible ways to improve the performance of the shortest path heuristic. Baed on the results presented here, improving the heuristic in a scenario where we process flow arrivals one at a time by more selectively placing NFs among candidate nodes will be of limited benefit. However, in [
5] we already showed that considering already placed flows jointly with a new flow arrival (placement request) may result in more accepted requests overall. While that work used small networks and the optimization model, we plan to extend this to the heuristic approaches as well. The added complexity of such an approach is that such an approach potentially moves some of the already placed NFs. We therefore would need to consider which NFs can be moved and at what cost. This “reconfiguration costs” needs to be considered in a complete solution. Jointly considering multiple requests will also increase the heuristic’s execution time, potentially limiting its scalability.